Structural Optimization of Heat Sink for Thermoelectric Conversion Unit in Personal Comfort System
Abstract
:1. Introduction
- (1)
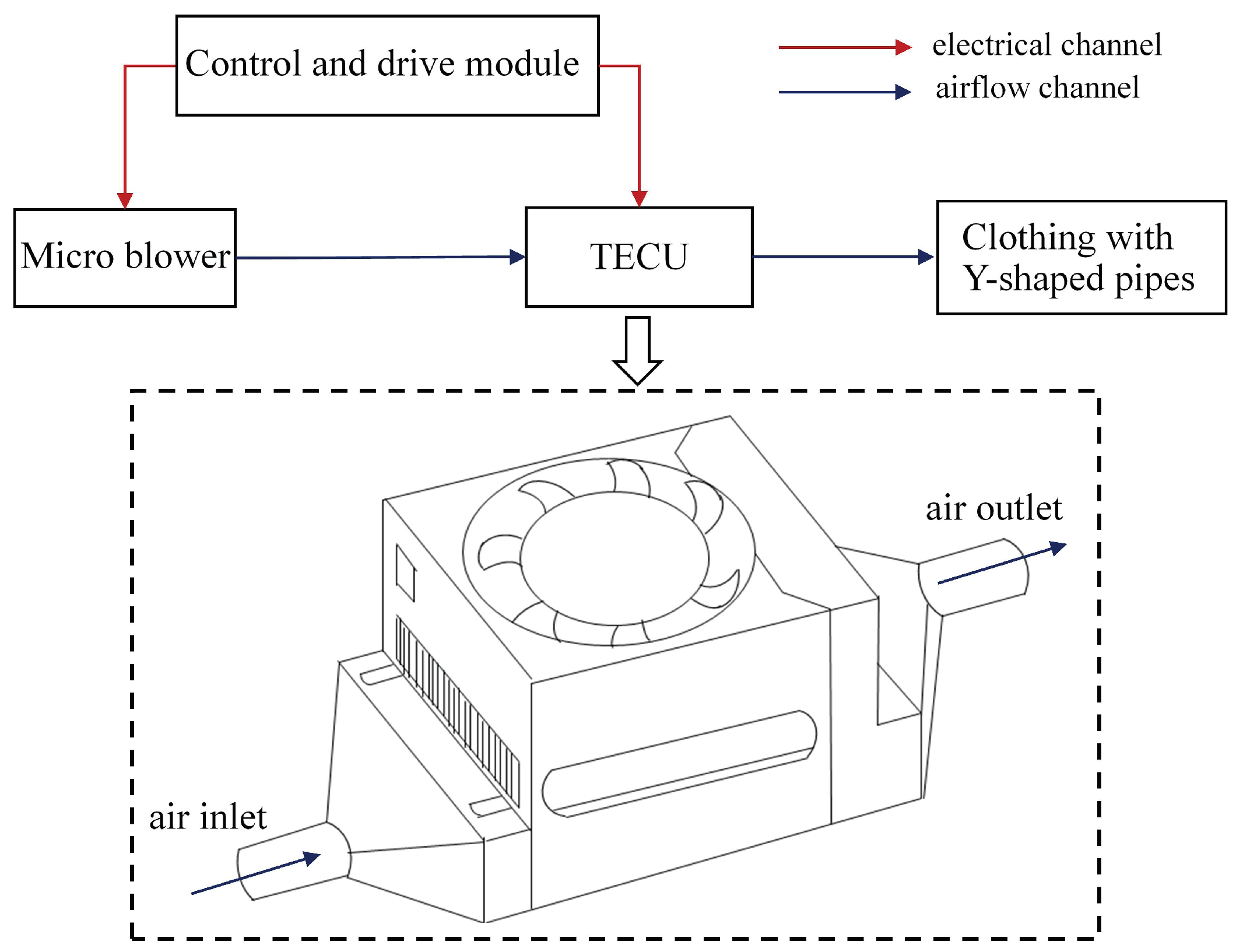
- The heat exchange mechanism of TEM is analyzed. On this basis, the structural design of the attached heat sink is summarized as a multiobjective optimization problem.
- (2)
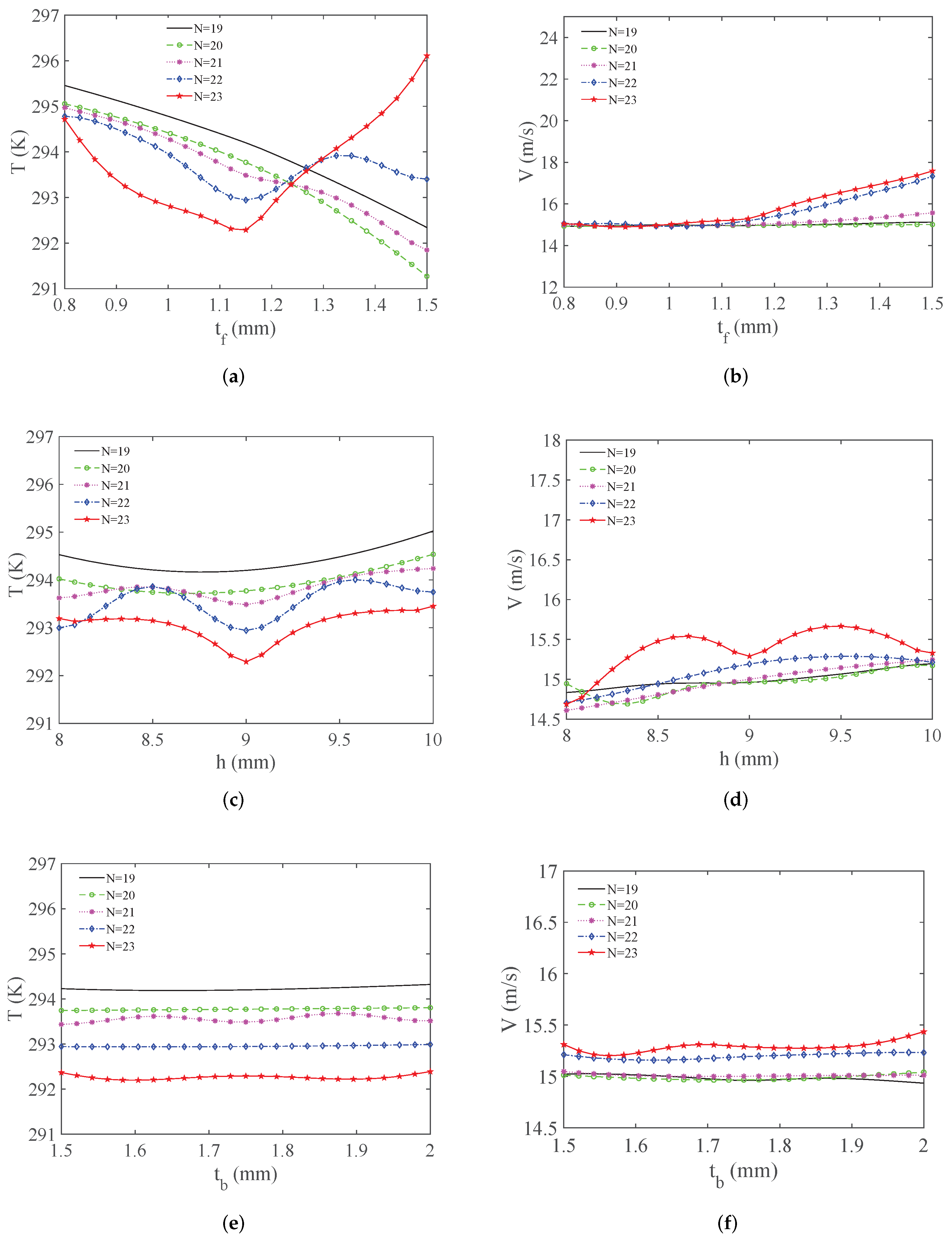
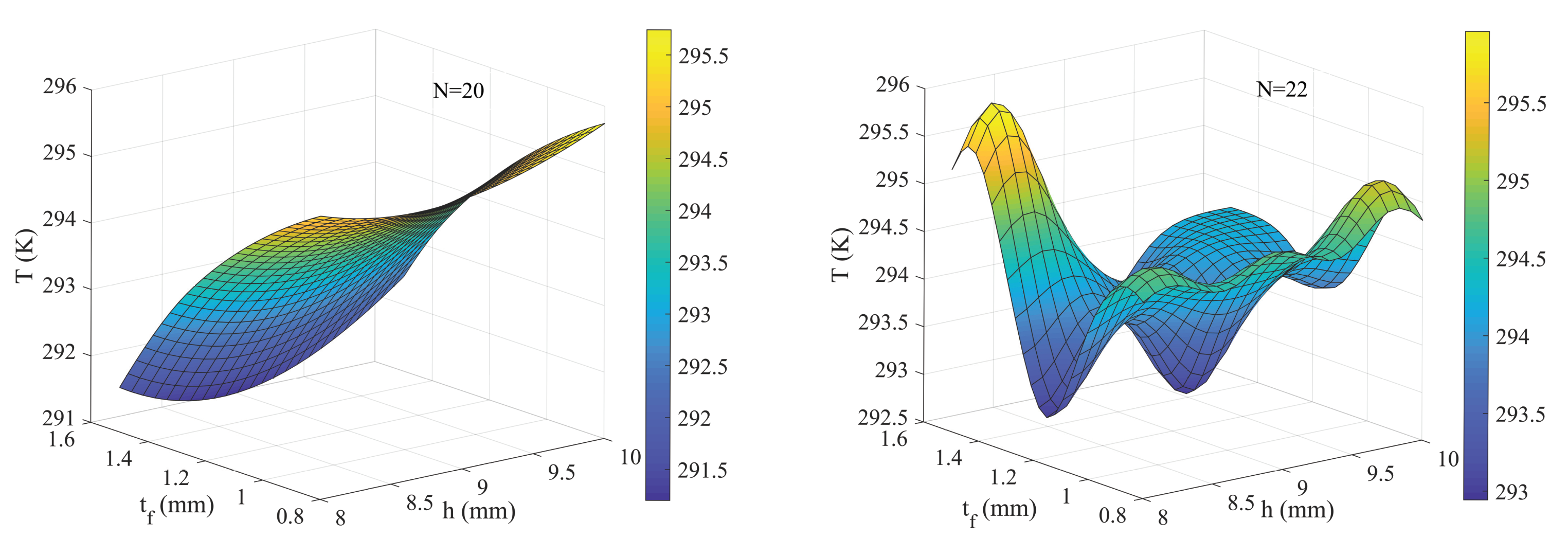
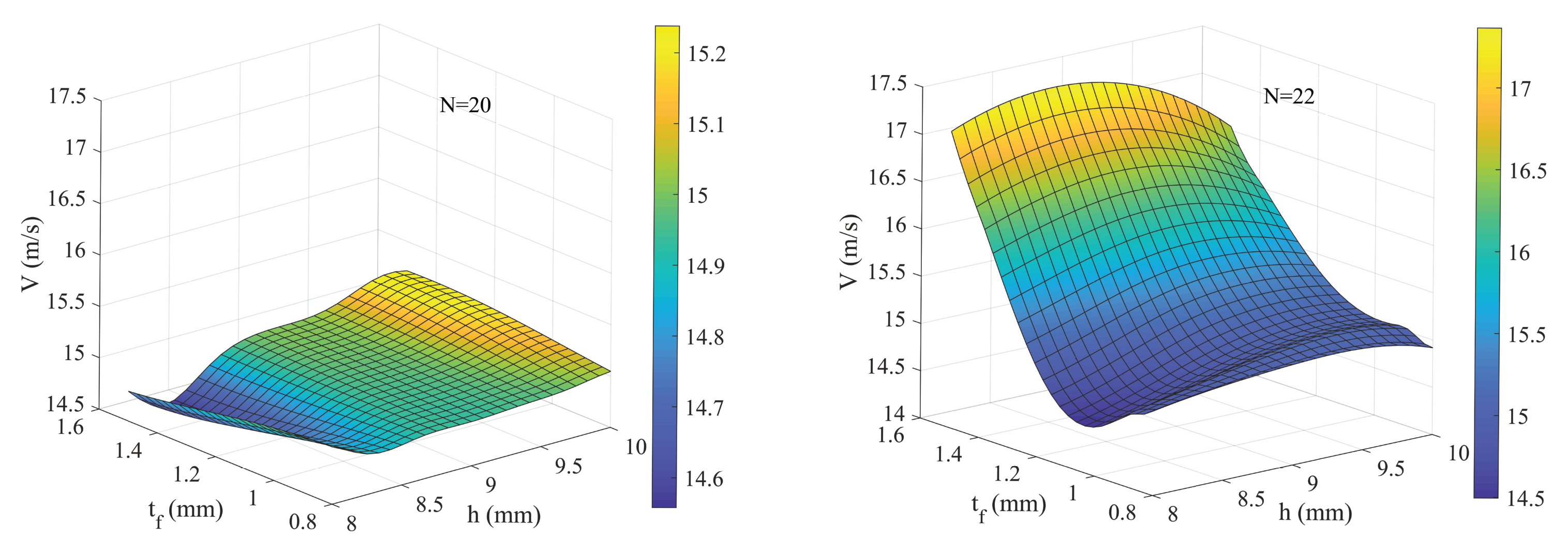
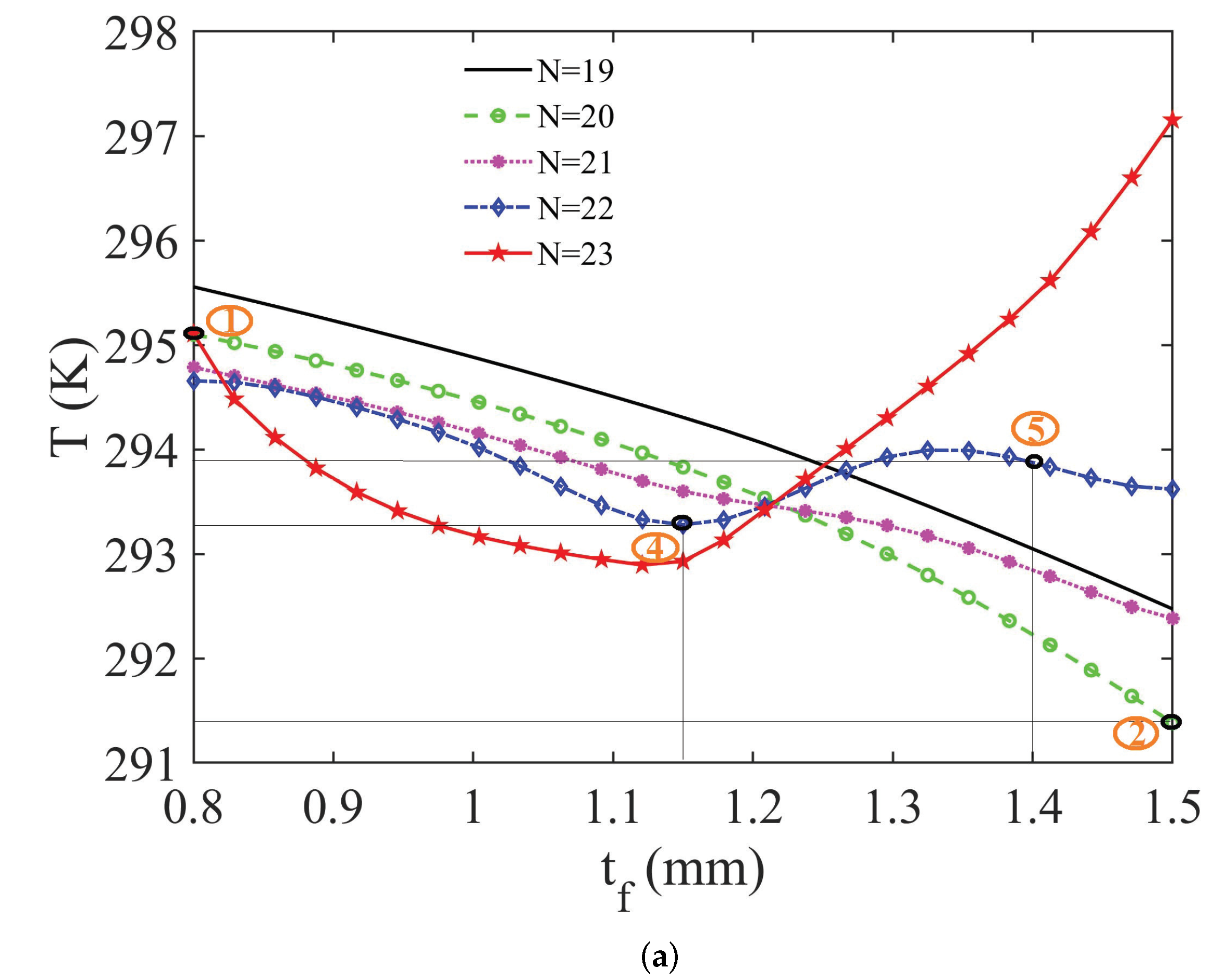
- Based on the established computational fluid dynamics (CFD) model of the heat exchange procedure, the main parameters of the cold-side plate-fin heat sink are optimized with the aid of multiobjective a genetic algorithm (MOGA). In addition, parameter sensitivity analysis is provided, and the number of rows and fin thickness show significant influence on optimization objectives.
- (3)
- Based on the simulation results, experimental tests are carried out. Results demonstrate that the developed structural optimization can effectively enhance the efficiency of heat exchange between the heat sink and the airflow in the TECU, which helps enhance personal thermal comfort.
2. Problem Formulation
3. Simplified CFD Model for Heat Exchange
3.1. Meshing and Boundary Conditions
3.2. Simulation Settings
4. Structural Optimization of the Heat Sink
4.1. Optimization Steps Based on a MOGA
4.2. Optimization Results and Analysis
- *
- The optimization is performed under the conditions of a fixed cold-side substrate temperature, inlet airflow temperature and inlet airflow velocity (see Table 1).
- *
- Additional thermal effects, such as air density variation, radiant heat transfer, phase change heat transfer, etc., are neglected.
- *
- The cavity of the simulation model is completely enclosed. However, the actual assembled model inevitably has the phenomenon of air leakage, which leads to the error of the airflow velocity.
5. Experimental Tests
5.1. Testing Platform for the TECU
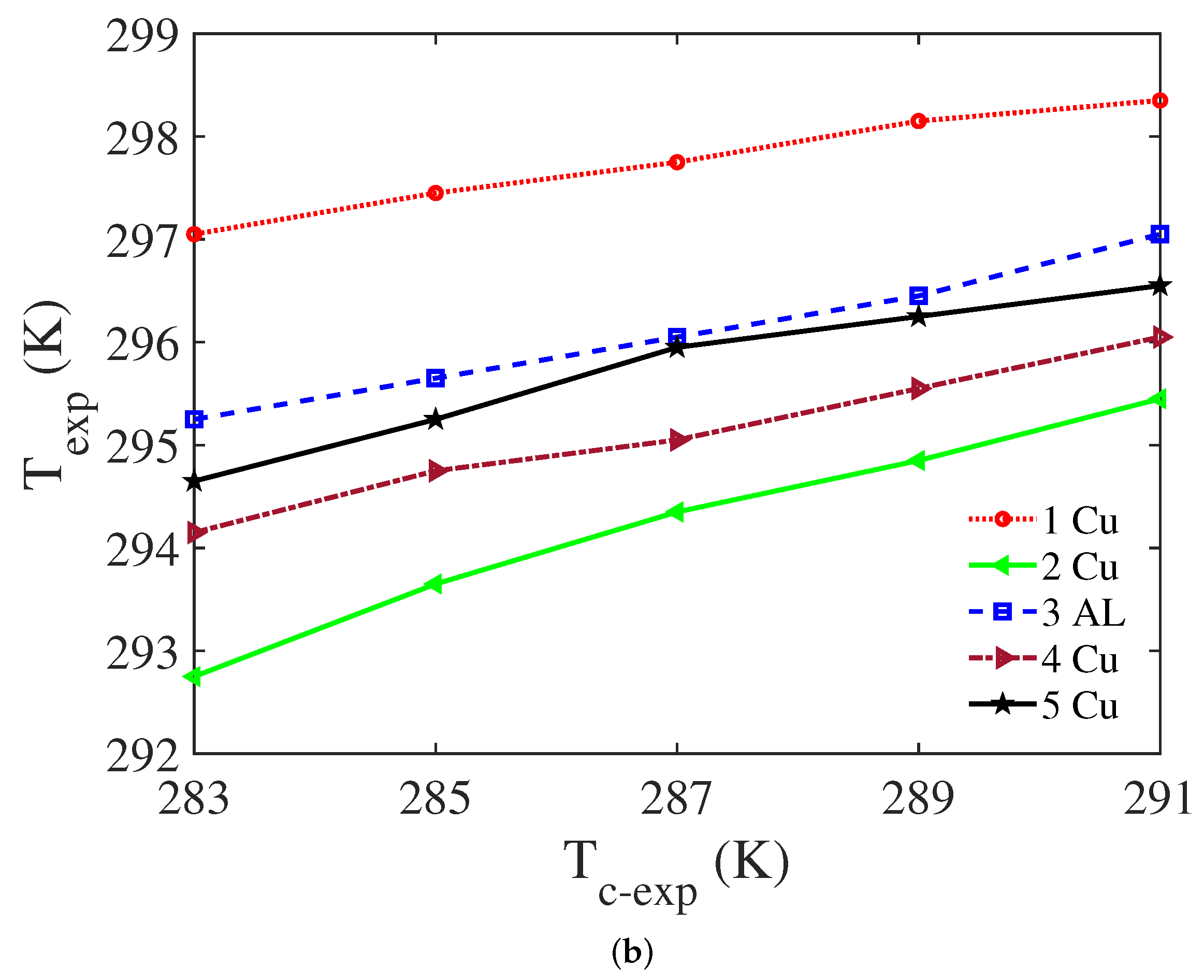
5.2. Experimental Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| ASHRAE | American society of heating, refrigerating and air-conditioning engineers |
| TEM | thermoelectric module |
| TECU | thermoelectric conversion unit |
| CFD | computational fluid dynamics |
| PCS | personal comfort system |
| MOGA | multiobjective genetic algorithm |
| HVAC | heating, ventilation and air-conditioning |
| COP | coefficient of performance |
| COPc | coefficient of cooling performance |
| heat absorbed on the cold side, W | |
| heat released on the hot side, W | |
| I | electric current, A |
| cold-side temperature, K | |
| hot-side temperature, K | |
| seebeck coefficient | |
| R | electric resistance, |
| K | thermal conductance, W/m·K |
| P | input power, W |
| T | average outlet temperature, K |
| V | average outlet airflow velocity, m/s |
| W | width of heat sink, mm |
| L | length of heat sink, mm |
| N | number of fin rows |
| thickness of base, mm | |
| thickness of fin, mm | |
| h | height of fin, mm |
| s | spacing between fins, mm |
| generic variable | |
| diffusion coefficient | |
| generalized source term |
References
- Liu, Y.; Yan, H.; Lam, J. Thermal comfort and building energy consumption implications—A review. Appl. Energy 2014, 115, 164–173. [Google Scholar]
- Chaudhuri, T.; Soh, Y.C.; Li, H.; Xie, L. A feedforward neural network based indoor-climate control framework for thermal comfort and energy saving in buildings. Appl. Energy 2019, 248, 44–53. [Google Scholar] [CrossRef]
- Huang, Y.; Niu, J.L. A review of the advance of HVAC technologies as witnessed in ENB publications in the period from 1987 to 2014. Energy Build. 2016, 130, 33–45. [Google Scholar] [CrossRef]
- Ashrant, A.; Burcin, B.G. Energy Consequences of Comfort-driven Temperature Setpoints in Office Buildings. Energy Build. 2018, 177, 33–46. [Google Scholar]
- Kim, J.; Schiavon, S.; Brager, G. Personal comfort models–A new paradigm in thermal comfort for occupant-centric environmental control. Build. Environ. 2018, 132, 114–124. [Google Scholar] [CrossRef] [Green Version]
- Taub, M.L. Power to the People: Personal Control in Offices for Thermal comfort and ENERGY Savings. Master’s Thesis, University of California, Berkeley, CA, USA, 2013. [Google Scholar]
- Lassen, N. Case study of personal heaters in a Plus energy building—Simulations of potential energy savings and results from a field test. IOP Conf. Ser. Earth Environ. Sci. 2019, 352, 012051. [Google Scholar] [CrossRef]
- Vesely, M.; Molenaar, P.; Vos, M.; Li, R.; Zeiler, W. Personalized heating–Comparison of heaters and control modes. Build. Environ. 2016, 112, 223–232. [Google Scholar] [CrossRef] [Green Version]
- Rawal, R.; Schweiker, M.; Kazanci, O.B.; Vardhan, V.; Lin, D. Personal Comfort Systems: A review on comfort, energy, and economics. Energy Build. 2020, 214, 109858. [Google Scholar] [CrossRef]
- Zhao, D.; Lu, X.; Fan, T.; Wu, Y.S.; Lou, L.; Wang, Q.; Fan, J.; Yang, R. Personal thermal management using portable thermoelectrics for potential building energy saving. Appl. Energy 2018, 218, 280–291. [Google Scholar] [CrossRef]
- Ma, Z.; Zhao, D.; She, C. Personal Thermal Management Techniques for Thermal Comfort and Building Energy Saving. Mater. Today Phys. 2021, 20, 100465. [Google Scholar] [CrossRef]
- Lou, L.; Shou, D.; Park, H.; Zhao, D.; Fan, J. Thermoelectric air conditioning undergarment for personal thermal management and HVAC energy saving. Energy Build. 2020, 226, 110374. [Google Scholar] [CrossRef]
- Wang, Z.; Warren, K.; Luo, M.; He, X.; Smith, M.J. Evaluating the comfort of thermally dynamic wearable devices. Build. Environ. 2019, 167, 106443. [Google Scholar] [CrossRef]
- Hong, S.A.G.; Seo, J.K.; Wang, J.; Liu, P.; Meng, Y.S.; Xu, S.; Chen, R. Wearable thermoelectrics for personalized thermoregulation. Sci. Adv. 2019, 5, eaaw0536. [Google Scholar] [CrossRef] [Green Version]
- Ga, L.; Zhang, Z.; Xu, D. Performance of thermoelectric conversion device with power management module based on shallow soil-air temperature difference. Case Stud. Therm. Eng. 2021, 28, 101582. [Google Scholar] [CrossRef]
- Zhao, D.; Tan, G. A review of thermoelectric cooling: Materials, modeling and applications. Appl. Therm. Eng. 2014, 66, 15–24. [Google Scholar] [CrossRef]
- Seo, Y.M.; Ha, M.Y.; Park, S.H.; Lee, G.H.; Kim, Y.S.; Park, Y.G. A numerical study on the performance of the thermoelectric module with different heat sink shapes. Appl. Therm. Eng. 2017, 128, 1082–1094. [Google Scholar] [CrossRef]
- Zhou, Y.; Yu, J. Design optimization of thermoelectric cooling systems for applications in electronic devices. Int. J. Refrig. 2012, 35, 1139–1144. [Google Scholar] [CrossRef]
- Lin, Z.; Tan, H.; Yu, J. Analysis on optimal heat exchanger size of thermoelectric cooler for electronic cooling applications. Energy Convers. Manag. 2013, 76, 685–690. [Google Scholar]
- Zhu, L.; Yu, J. Optimization of heat sink of thermoelectric cooler using entropy generation analysis. Int. J. Therm. Sci. 2017, 118, 168–175. [Google Scholar] [CrossRef]
- Yu, X.A.; Zl, A.J.A. Man-portable cooling garment with cold liquid circulation based on thermoelectric refrigeration. Appl. Therm. Eng. 2021, 200, 117730. [Google Scholar]
- Chen, L.; Liu, R.; Shi, X. Design and fabrication of thermoelectric devices. In Thermoelectric Materials and Devices; Elsevier: Amsterdam, The Netherlands, 2021; pp. 221–267. [Google Scholar] [CrossRef]
- Ranjbar, B.; Mehrpooya, M.; Marefati, M. Parametric design and performance evaluation of a novel solar assisted thermionic generator and thermoelectric device hybrid system. Renew. Energy 2021, 164, 194–210. [Google Scholar] [CrossRef]
- Min, C.; Snyder, G.J. Analytical and numerical parameter extraction for compact modeling of thermoelectric coolers. Int. J. Heat Mass Transf. 2013, 60, 689–699. [Google Scholar]
- Schaffer, J.D. Multiple Objective Optimization with Vector Evaluated Genetic Algorithms. In Proceedings of the International Conference on Genetic Algorithm and Their Applications, Pittsburg, PA, USA, 24–26 July 1985; pp. 93–100. [Google Scholar]
- Srinivas, N.; Deb, K. Multiobjective Optimization Using Nondominated Sorting in Genetic Algorithms. Evol. Comput. 1994, 2, 1301–1308. [Google Scholar] [CrossRef]
- Deb, K.; Goel, T. Controlled Elitist Non-dominated Sorting Genetic Algorithms for Better Convergence. In Proceedings of the First International Conference on Evolutionary Multi-Criterion Optimization, Zurich, Switzerland, 7–9 March 2001; pp. 385–399. [Google Scholar]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef] [Green Version]
- Konak, A.; Coit, D.W.; Smith, A.E. Multi-objective optimization using genetic algorithms: A tutorial. Reliab. Eng. Syst. Saf. 2006, 91, 992–1007. [Google Scholar] [CrossRef]
- Park, S.K.; Lee, S.B.; Lee, W.C. Goal-Pareto based NSGA-II Algorithm for Multiobjective Optimization. J. Korean Inst. Commun. Inf. Sci. 2007, 32, 1079–1085. [Google Scholar]




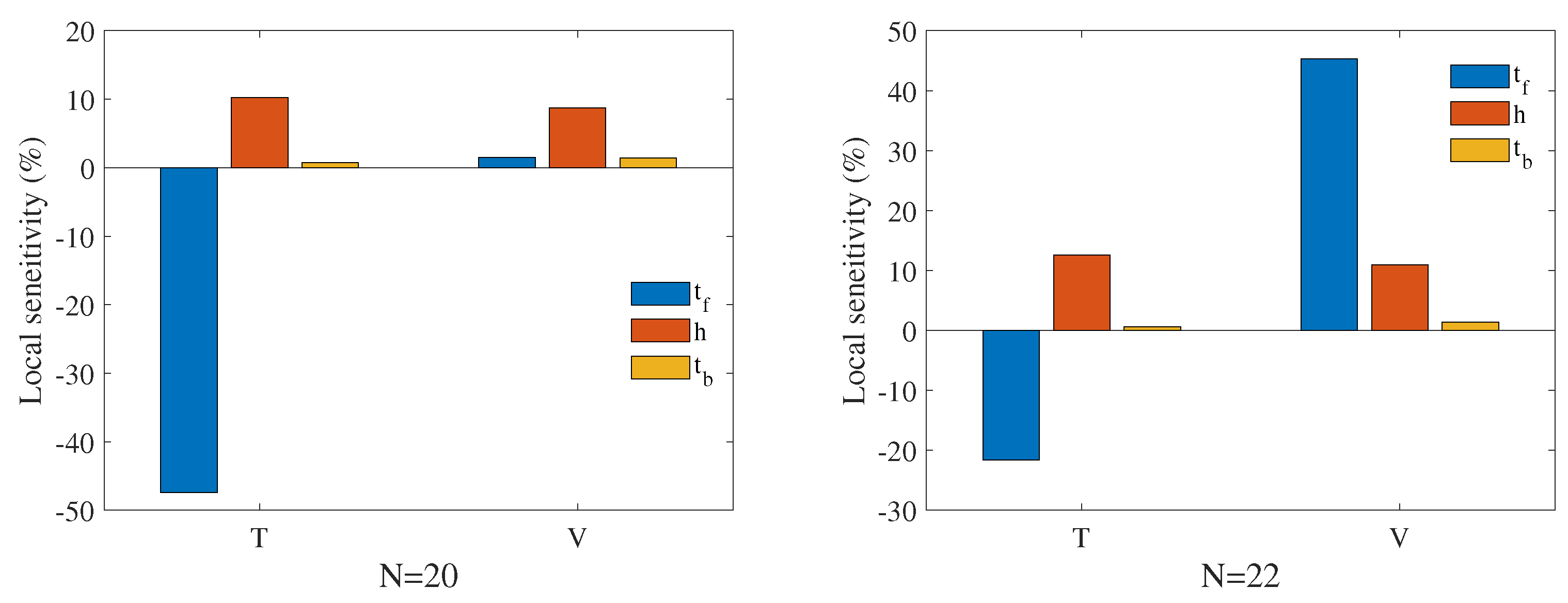



| Parameter | Setting | Unit |
|---|---|---|
| Inlet airflow velocity | 15 | m/s |
| Inlet airflow temperature | 27 | C |
| Ceramic substrate temperature | 12 | C |
| Air density | 1.225 | kg/m |
| Parameters | (mm) | (mm) | h (mm) | N | s (mm) |
|---|---|---|---|---|---|
| hot side | 2 | 0.5 | 9 | 25 | 1.15 |
| cold side | 1.5–2 | 0.8–1.5 | 8–10 | 19–23 | 0.25–1.38 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xue, W.; Cao, X.; Zhang, G.; Tan, G.; Liu, Z.; Li, K. Structural Optimization of Heat Sink for Thermoelectric Conversion Unit in Personal Comfort System. Energies 2022, 15, 2781. https://doi.org/10.3390/en15082781
Xue W, Cao X, Zhang G, Tan G, Liu Z, Li K. Structural Optimization of Heat Sink for Thermoelectric Conversion Unit in Personal Comfort System. Energies. 2022; 15(8):2781. https://doi.org/10.3390/en15082781
Chicago/Turabian StyleXue, Wenping, Xiao Cao, Guangfa Zhang, Gang Tan, Zilong Liu, and Kangji Li. 2022. "Structural Optimization of Heat Sink for Thermoelectric Conversion Unit in Personal Comfort System" Energies 15, no. 8: 2781. https://doi.org/10.3390/en15082781
APA StyleXue, W., Cao, X., Zhang, G., Tan, G., Liu, Z., & Li, K. (2022). Structural Optimization of Heat Sink for Thermoelectric Conversion Unit in Personal Comfort System. Energies, 15(8), 2781. https://doi.org/10.3390/en15082781








