Forced Oscillation Grid Vulnerability Analysis and Mitigation Using Inverter-Based Resources: Texas Grid Case Study
Abstract
:1. Introduction
2. Forced Oscillation Vulnerability Analysis and Mitigation
2.1. Framework of the Algorithm
2.2. Forced Oscillation Vulnerability Analysis Method
2.3. Actuator Selection of Forced Oscillation Controller via IBRs
2.4. Forced Oscillation Mitigation Method
3. Texas Power System Case Study
3.1. Synthetic Texas Power System Model Description
3.2. Grid Vulnerability Analysis
3.2.1. Frequency Dimension Scanning
3.2.2. Location Dimension Scanning
3.3. Actuator Selection of Forced Oscillation Controller via IBRs
3.4. Forced Oscillation Control via IBRs
4. Conclusions
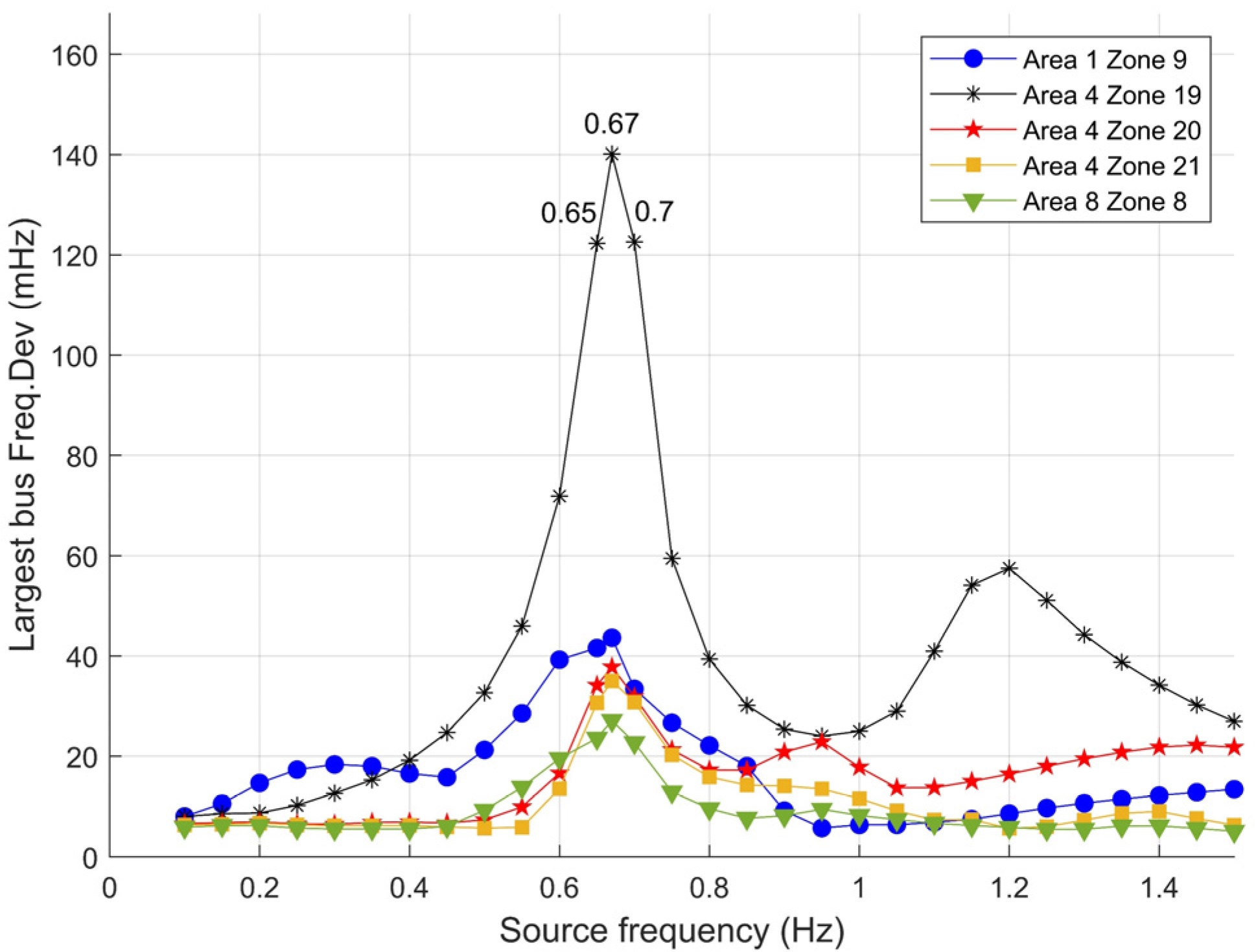
- Based on frequency dimension scanning, forced oscillation at or close to the natural oscillation excites the largest peak–peak frequency deviation in the entire system.
- When the forced oscillation source is located at the areas that have high participation of the natural oscillations, the forced oscillation will be further magnified throughout the system and significantly impact the system stability.
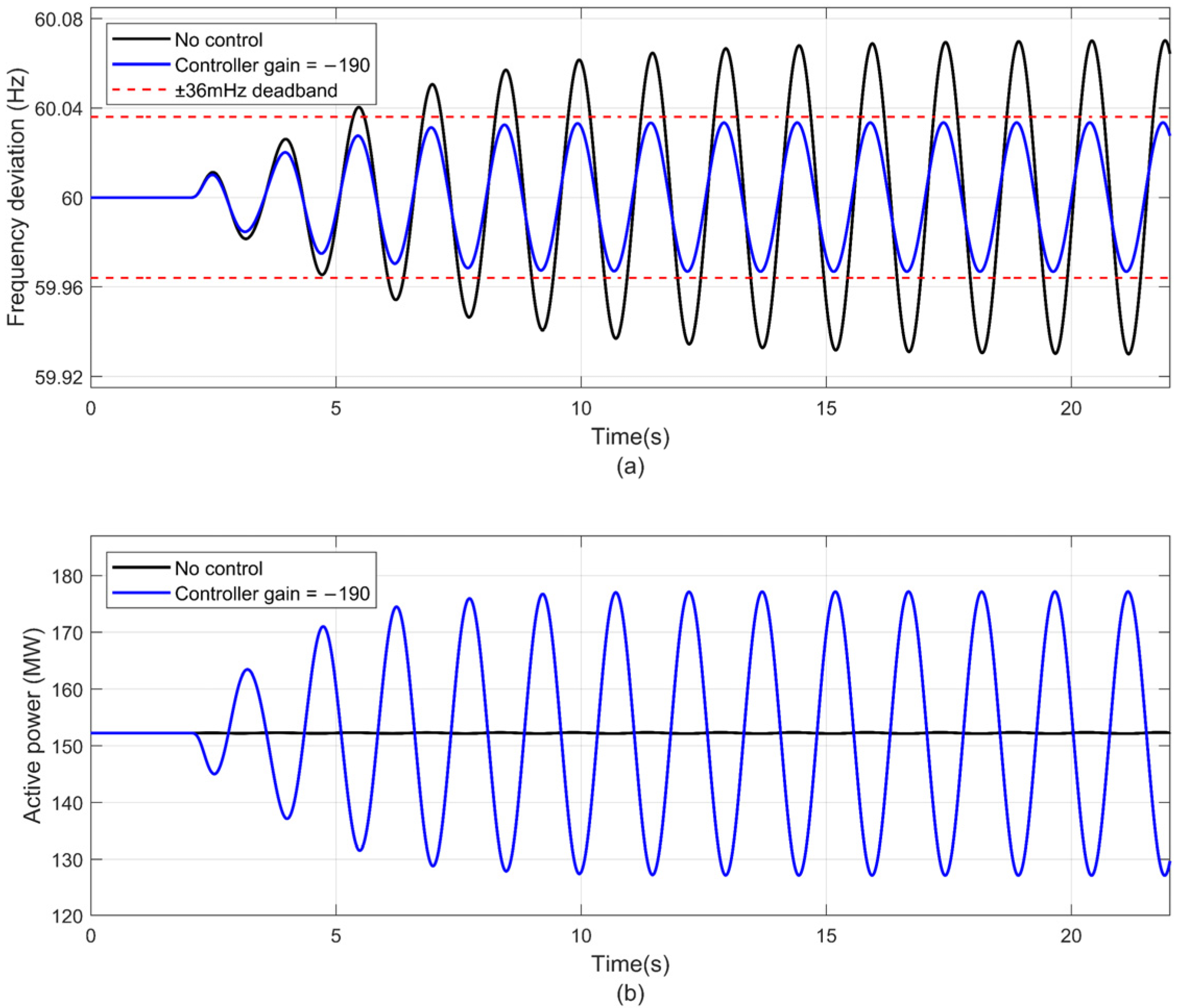
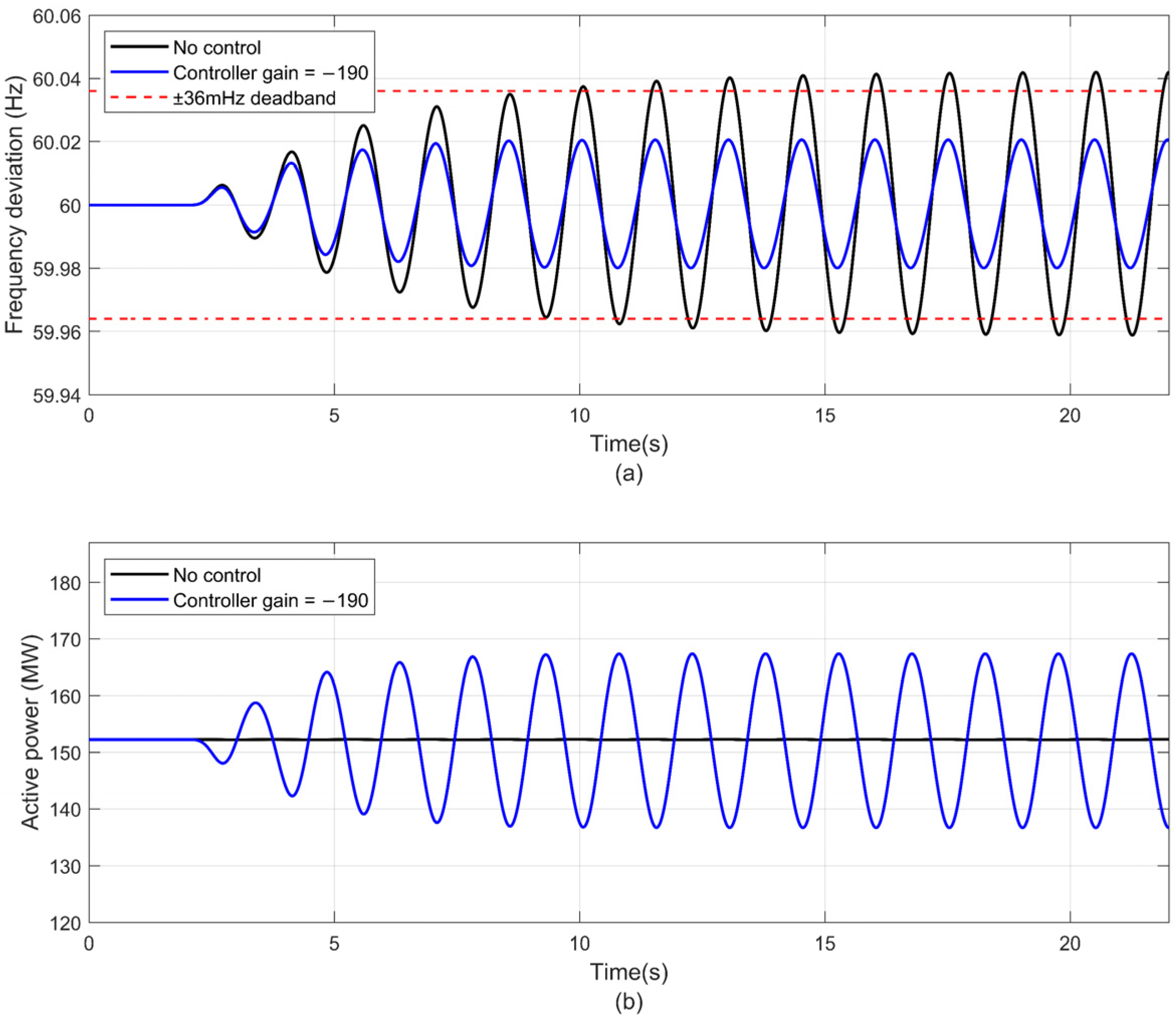
- Active power modulation control through IBRs with local measurement was effective in reducing the frequency deviation that was caused by the forced oscillation. This will allow the operator to have sufficient time to locate and disconnect the forced source.
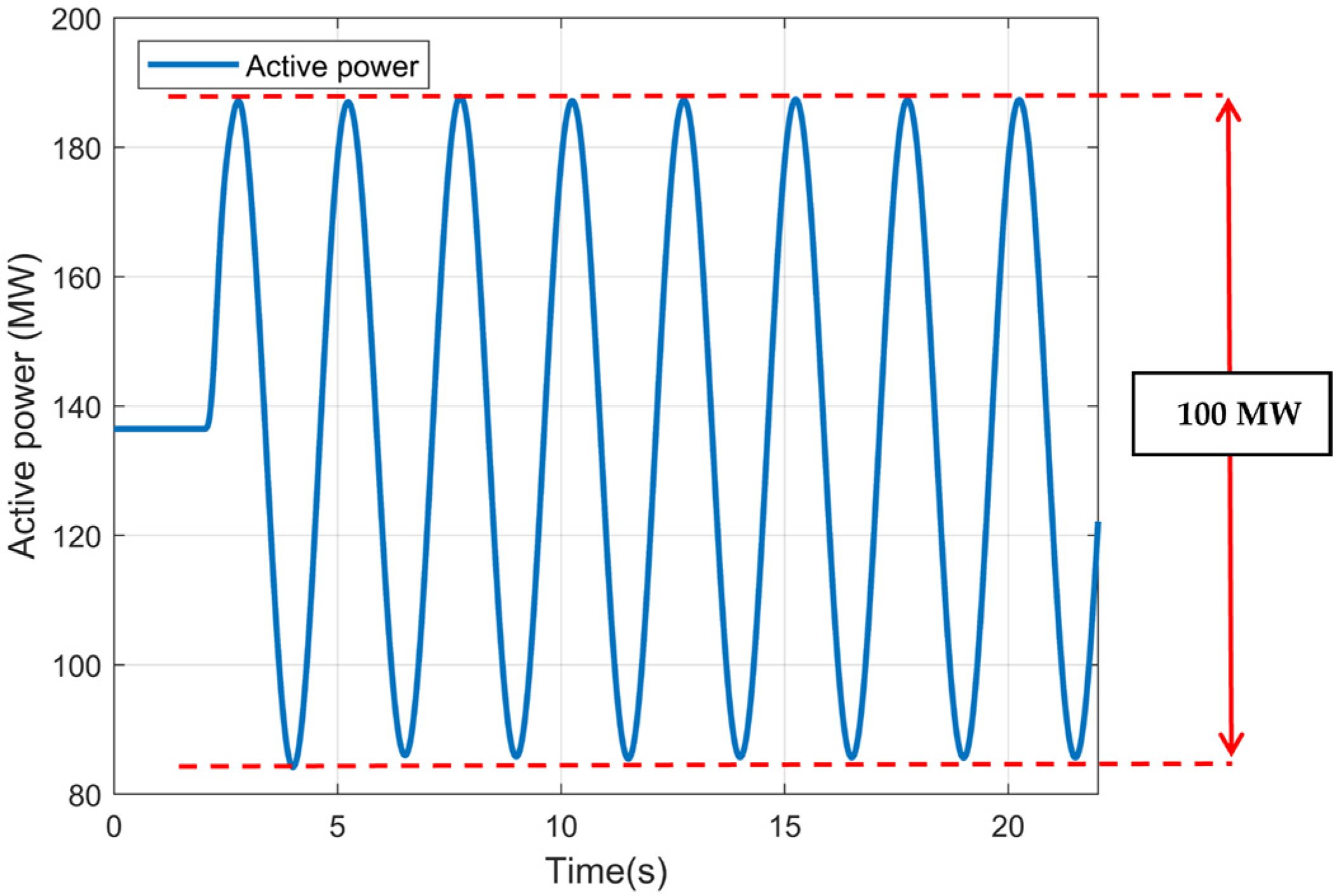
- The proposed forced oscillation controller can reduce all the zones’ frequency deviation to a safety level in the synthetic Texas power grid when the actuator is close to the forced source. The largest peak–peak bus frequency deviation can be reduced by more than 50%, to 66.6 mHz (in the range of governor deadband ±36 mH) with appropriate control gain.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Reliability Guideline: Forced Oscillation Monitoring and Mitigation; The North American Electric Reliability Corporation (NERC): Atlanta, GA, USA, 2017; Available online: https://www.nerc.com/comm/PC_Reliability_Guidelines_DL/Reliability_Guideline_-_Forced_Oscillations_-_2017-07-31_-_FINAL.pdf (accessed on 27 December 2021).
- Ghorbaniparvar, M. Survey on forced oscillations in power system. J. Mod. Power Syst. Clean Energy 2017, 5, 671–682. [Google Scholar] [CrossRef]
- Power System Oscillatory Behaviors: Sources, Characteristics, and Analyses; North American SynchroPhasor Initiative (NASPI), USA, Technical Report, May 2017. Available online: https://www.pnnl.gov/main/publications/external/technical_reports/PNNL-26375.pdf (accessed on 27 December 2021).
- Khan, M.A.; Pierre, J.W. Detection of Periodic Forced Oscillations in Power Systems Using Multitaper Approach. IEEE Trans. Power Syst. 2019, 34, 1086–1094. [Google Scholar] [CrossRef]
- Zuhaib, M.; Rihan, M.; Saeed, M.T. A novel method for locating the source of sustained oscillation in power system using synchrophasors data. Prot. Control Mod. Power Syst. 2020, 5, 30. [Google Scholar] [CrossRef]
- Ye, H.; Liu, Y.; Zhang, P.; Du, Z. Analysis and Detection of Forced Oscillation in Power System. IEEE Trans. Power Syst. 2017, 32, 1149–1160. [Google Scholar] [CrossRef]
- Su, C.; Hu, W.; Chen, Z.; Hu, Y. Mitigation of power system oscillation caused by wind power fluctuation. IET Renew. Power Gener. 2013, 7, 639–651. [Google Scholar] [CrossRef]
- Srinivasan, D.; Trung, L.T.; Singh, C. Bidding and cooperation strategies for electricity buyers in power markets. IEEE Syst. J. 2014, 10, 422–433. [Google Scholar] [CrossRef]
- Xiao, D.; AlAshery, M.K.; Qiao, W. Optimal price-maker trading strategy of wind power producer using virtual bidding. J. Mod. Power Syst. Clean Energy Early Access. 2021, 1–3. [Google Scholar] [CrossRef]
- Surinkaew, T.; Emami, K.; Shah, R.; Islam, S.; Mithulananthan, N. Forced Oscillation in Power Systems with Converter Controlled-Based Resources–A Survey with Case Studies. IEEE Access 2021, 9, 150911–150924. [Google Scholar] [CrossRef]
- Estevez, P.G.; Marchi, P.; Galarza, C.; Elizondo, M. Non-Stationary Power System Forced Oscillation Analysis Using Synchrosqueezing Transform. IEEE Trans. Power Syst. 2021, 36, 1583–1593. [Google Scholar] [CrossRef]
- Eastern Interconnection Oscillation Disturbance January 11, 2019 Forced Oscillation Event; The North American Electric Reliability Corporation (NERC): Atlanta, GA, USA, 2019; Available online: https://www.nerc.com/pa/rrm/ea/Documents/January_11_Oscillation_Event_Report.pdf (accessed on 27 December 2021).
- Rogers, G. Power System Oscillations; Kluwer Academic Publishers: New York, NY, USA, 2000. [Google Scholar]
- Venkatraman, A.; Markovic, U.; Shchetinin, D.; Vrettos, E.; Aristidou, P.; Hug, G. Improving Dynamic Performance of Low-Inertia Systems Through Eigensensitivity Optimization. IEEE Trans. Power Syst. 2021, 36, 4075–4088. [Google Scholar] [CrossRef]
- Tan, A.; Lin, X.; Sun, J.; Lyu, R.; Li, Z.; Peng, L.; Khalid, M.S. A Novel DFIG Damping Control for Power System with High Wind Power Penetration. Energies 2016, 9, 521. [Google Scholar] [CrossRef] [Green Version]
- Sarmadi, S.A.N.; Venkatasubramanian, V. Inter-Area Resonance in Power Systems from Forced Oscillations. IEEE Trans. Power Syst. 2016, 31, 378–386. [Google Scholar] [CrossRef]
- Chevalier, S.; Vorobev, P.; Turitsyn, K. A Bayesian Approach to Forced Oscillation Source Location Given Uncertain Generator Parameters. IEEE Trans. Power Syst. 2019, 34, 1641–1649. [Google Scholar] [CrossRef] [Green Version]
- Feng, S.; Zheng, B.; Jiang, P.; Lei, J. A Two-Level Forced Oscillations Source Location Method Based on Phasor and Energy Analysis. IEEE Access 2018, 6, 44318–44327. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhu, L.; Xiao, H.; Liu, Y.; Farantatos, E.; Patel, M.; Darvishi, A.; Fardanesh, B. An Adaptive Wide-Area Damping Controller via FACTS for the New York State Grid Using a Measurement-Driven Model. In Proceedings of the 2019 IEEE Power & Energy Society General Meeting (PESGM), Atlanta, GA, USA, 8 August 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Zhu, Y.; Liu, C.; Wang, B.; Sun, K. Damping control for a target oscillation mode using battery energy storage. J. Mod. Power Syst. Clean Energy 2018, 6, 833–845. [Google Scholar] [CrossRef] [Green Version]
- Saadatmand, M.; Gharehpetian, C.B.; Moghassemi, A.; Guerrero, J.M.; Siano, P.; Alhelou, H.H. Damping of Low-Frequency Oscillations in Power Systems by Large-Scale PV Farms: A Comprehensive Review of Control Methods. IEEE Access 2021, 9, 72183–72206. [Google Scholar] [CrossRef]
- Feng, S.; Wu, X.; Jiang, P.; Xie, L.; Lei, J. Mitigation of Power System Forced Oscillations: An E-STATCOM Approach. IEEE Access 2018, 6, 31599–31608. [Google Scholar] [CrossRef]
- Xu, Y.; Bai, W.; Zhao, S.; Zhang, J.; Zhao, Y. Mitigation of forced oscillations using VSC-HVDC supplementary damping control. Electr. Power Syst. Res. 2020, 184, 106333. [Google Scholar] [CrossRef]
- Lin, Z.; Yu, W.; Jiang, Z.; Zhang, C.; Zhao, Y.; Dong, J.; Wang, W.; Liu, Y.; Farantatos, E.; Ramasubramanian, D.; et al. A Comprehensive Method to Mitigate Forced Oscillations in Large Interconnected Power Grids. IEEE Access 2021, 9, 22503–22515. [Google Scholar]
- Surinkaew, T.; Shah, R.; Nadarajah, M.; Muyeen, S.M. Forced Oscillation Damping Controller for an Interconnected Power System. IET Gener. Transm. Distrib. 2020, 14, 339–347. [Google Scholar] [CrossRef]
- ACTIVSg2000: 2000-Bus Synthetic Grid on Footprint of TEXAS. Available online: https://electricgrids.engr.tamu.edu/electric-grid-test-cases/activsg2000/ (accessed on 20 December 2021).
- Generic Solar Photovoltaic System Dynamic Model Specification; Prepared by Western Electricity Coordinating Council (WECC) Renewable Energy Modeling Task Force: Salt Lake City, UT, USA, 2012; Available online: https://www.wecc.org/_layouts/15/WopiFrame.aspx?sourcedoc=/Reliability/WECC%20Solar%20PV%20Dynamic%20Model%20Specification%20-%20September%202012.pdf&action=default&DefaultItemOpen=1 (accessed on 21 February 2022).
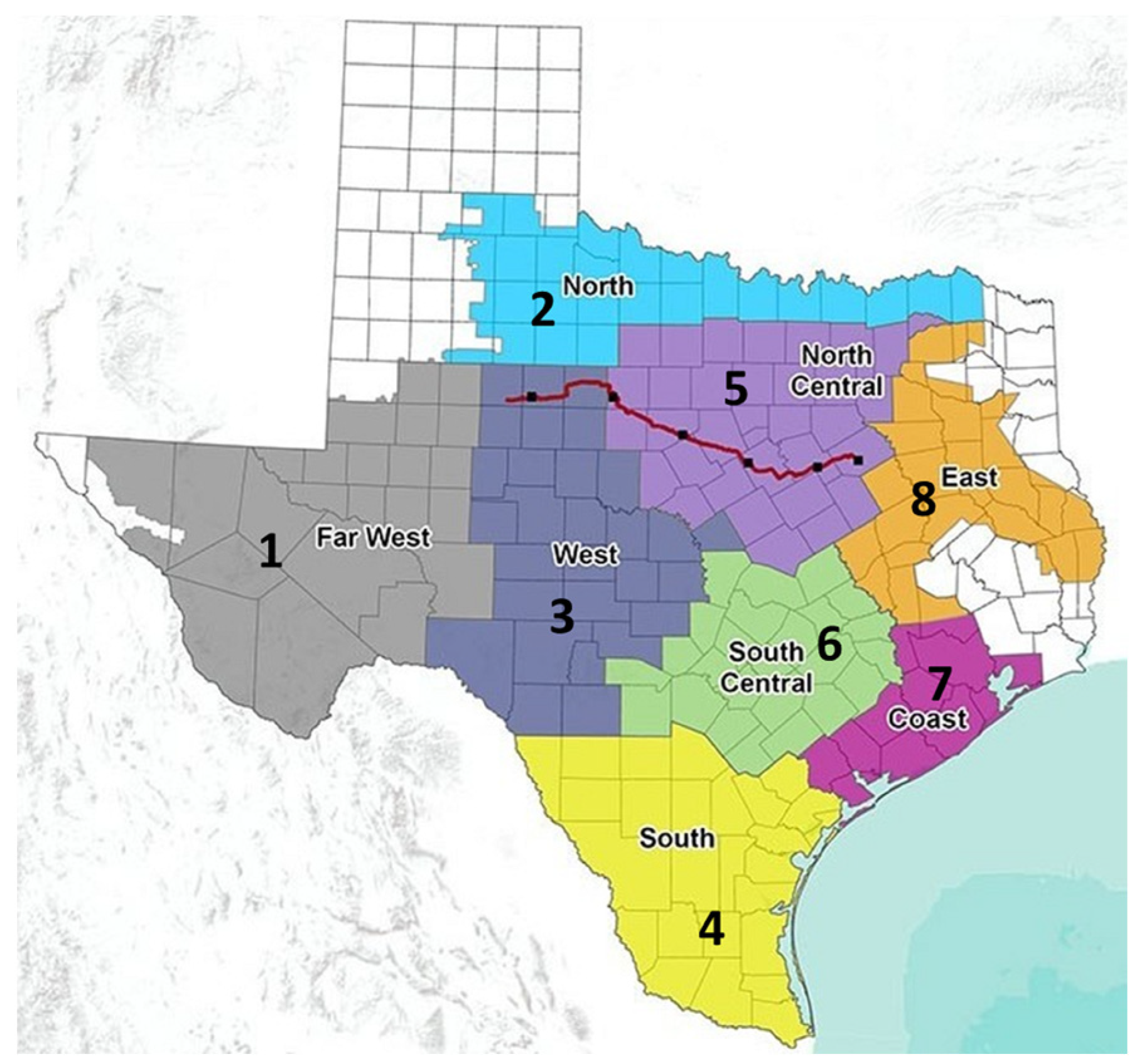
- ERCOT Load Zones. Available online: https://www.lonestartransmission.com/what-we-do/ercot-load-zones.html (accessed on 23 February 2022).

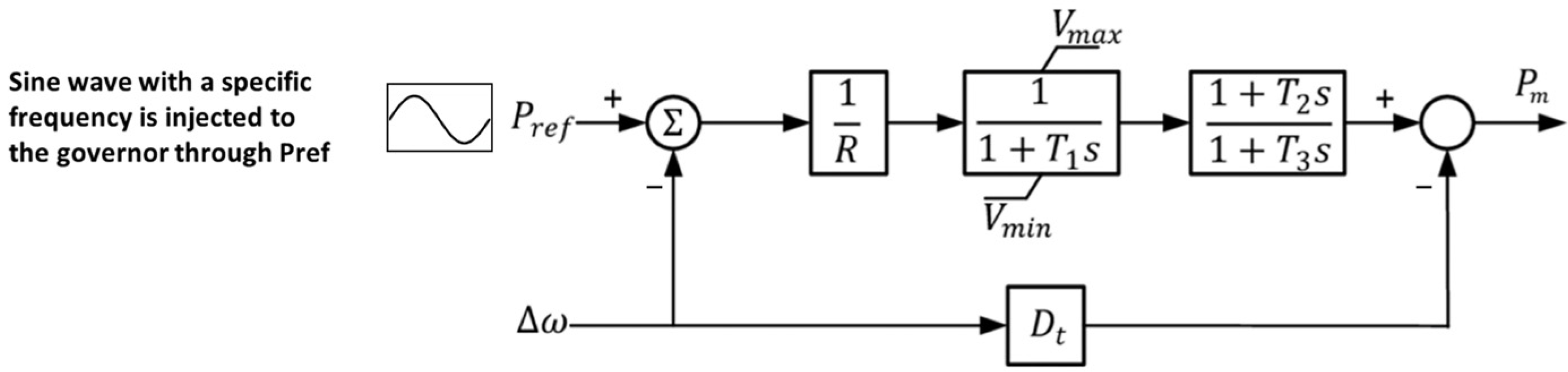


| R | T1 | Vmax | Vmin | T2 | T3 | Dt |
|---|---|---|---|---|---|---|
| 20 | 0.1 | 99 | −99 | 0.1 | 0.1 | 0 |
| Generator Location | Generator Bus NO. | Participation Factor (0.67 Hz) | Participation Factor (0.60 Hz) |
|---|---|---|---|
| Area 4 Zone 19 | 4192 | 1.00 | 0.14 |
| Area 4 Zone 21 | 4058 | 0.72 | 0.01 |
| Area 4 Zone 20 | 4115 | 0.40 | 0.22 |
| Area 8 Zone 8 | 8080 | 0.19 | 0.77 |
| Area 1 Zone 9 | 1051 | 0.18 | 1.00 |
| Area 5 Zone 12 | 5063 | 0.18 | 0.01 |
| Area 2 Zone 11 | 2023 | 0.18 | 0.76 |
| Area 5 Zone 18 | 5319 | 0.17 | 0.73 |
| Source Location | Area—Zone with Largest Bus Frequency Deviation | Peak–Peak Bus Frequency Deviation (mHz) |
|---|---|---|
| Area 4 Zone 19 | Area 4 Zone 19 | 140.090 |
| Area 1 Zone 9 | Area 4 Zone 19 | 43.622 |
| Area 4 Zone 20 | Area 4 Zone 19 | 37.798 |
| Area 4 Zone 21 | Area 4 Zone 19 | 34.996 |
| Area 8 Zone 8 | Area 4 Zone 19 | 30.780 |
| Area 5 Zone 12 | Area 4 Zone 19 | 27.221 |
| Area 7 Zone 4 | Area 4 Zone 19 | 27.125 |
| Area 2 Zone 11 | Area 4 Zone 19 | 26.910 |
| Area 7 Zone 3 | Area 4 Zone 19 | 25.536 |
| Area 5 Zone 18 | Area 4 Zone 19 | 24.451 |
| Area 7 Zone 2 | Area 4 Zone 19 | 23.359 |
| Area 3 Zone 28 | Area 3 Zone 28 | 23.172 |
| Area 8 Zone 7 | Area 4 Zone 19 | 19.345 |
| Area 7 Zone 5 | Area 4 Zone 19 | 18.532 |
| Area 5 Zone 14 | Area 4 Zone 19 | 18.099 |
| Area 5 Zone 16 | Area 4 Zone 19 | 17.938 |
| Area 6 Zone 22 | Area 4 Zone 19 | 17.764 |
| Area 5 Zone 13 | Area 4 Zone 19 | 17.663 |
| Area 5 Zone 17 | Area 4 Zone 19 | 15.185 |
| Area 6 Zone 26 | Area 4 Zone 19 | 13.886 |
| Area 7 Zone 6 | Area 4 Zone 19 | 12.948 |
| Area 6 Zone 25 | Area 4 Zone 19 | 11.598 |
| Area 6 Zone 23 | Area 4 Zone 19 | 9.652 |
| Area 7 Zone 1 | Area 7 Zone 4 | 9.191 |
| Source Location | Oscillation Frequency (Hz) | Area—Zone with Largest Bus Frequency Deviation | Peak–Peak Bus Frequency Deviation (mHz) |
|---|---|---|---|
| Area 1 Zone 9 | 0.1 | Area 7 Zone 4 | 8.00 |
| Area 1 Zone 9 | 0.15 | Area 7 Zone 4 | 10.53 |
| Area 1 Zone 9 | 0.2 | Area 7 Zone 4 | 14.67 |
| Area 1 Zone 9 | 0.25 | Area 7 Zone 4 | 17.33 |
| Area 1 Zone 9 | 0.3 | Area 7 Zone 4 | 18.35 |
| Area 1 Zone 9 | 0.35 | Area 7 Zone 4 | 18.00 |
| Area 4 Zone 19 | 0.4 | Area 4 Zone 19 | 19.19 |
| Area 3 Zone 28 | 0.45 | Area 3 Zone 28 | 25.22 |
| Area 4 Zone 19 | 0.5 | Area 4 Zone 19 | 32.63 |
| Area 4 Zone 19 | 0.55 | Area 4 Zone 19 | 45.95 |
| Area 4 Zone 19 | 0.6 | Area 4 Zone 19 | 71.88 |
| Area 4 Zone 19 | 0.65 | Area 4 Zone 19 | 122.30 |
| Area 4 Zone 19 | 0.67 | Area 4 Zone 19 | 140.09 |
| Area 4 Zone 19 | 0.7 | Area 4 Zone 19 | 122.58 |
| Area 4 Zone 19 | 0.75 | Area 4 Zone 19 | 59.45 |
| Area 4 Zone 19 | 0.8 | Area 4 Zone 21 | 39.37 |
| Area 4 Zone 19 | 0.85 | Area 4 Zone 21 | 30.16 |
| Area 3 Zone 28 | 0.9 | Area 3 Zone 28 | 30.35 |
| Area 3 Zone 28 | 0.95 | Area 3 Zone 28 | 31.79 |
| Area 3 Zone 28 | 1 | Area 3 Zone 28 | 31.78 |
| Area 3 Zone 28 | 1.05 | Area 3 Zone 28 | 33.20 |
| Area 4 Zone 19 | 1.1 | Area 4 Zone 19 | 40.93 |
| Area 4 Zone 19 | 1.15 | Area 4 Zone 19 | 54.10 |
| Area 4 Zone 19 | 1.2 | Area 4 Zone 19 | 57.49 |
| Area 4 Zone 19 | 1.25 | Area 4 Zone 19 | 51.09 |
| Area 4 Zone 19 | 1.3 | Area 4 Zone 19 | 44.23 |
| Area 3 Zone 28 | 1.35 | Area 3 Zone 28 | 46.49 |
| Area 3 Zone 28 | 1.4 | Area 3 Zone 28 | 48.79 |
| Area 3 Zone 28 | 1.45 | Area 3 Zone 28 | 51.21 |
| Area 3 Zone 28 | 1.5 | Area 3 Zone 28 | 53.53 |
| Area-Zone | Peak–Peak Bus Frequency Deviation (mHz) | Bus Frequency Deviation Reduction (mHz) | |
|---|---|---|---|
| No Control | With Control | ||
| Area 1 Zone 9 | 13.00 | 5.99 | 7.01 |
| Area 2 Zone 11 | 18.41 | 8.53 | 9.88 |
| Area 2 Zone 10 | 14.74 | 6.76 | 7.98 |
| Area 3 Zone 27 | 13.44 | 6.19 | 7.25 |
| Area 3 Zone 28 | 7.83 | 3.62 | 4.21 |
| Area 4 Zone 19 | 140.09 | 66.60 | 73.49 |
| Area 4 Zone 20 | 51.11 | 23.64 | 27.47 |
| Area 4 Zone 21 | 101.95 | 47.10 | 54.85 |
| Area 5 Zone 12 | 16.07 | 7.43 | 8.65 |
| Area 5 Zone 13 | 12.95 | 5.99 | 6.95 |
| Area 5 Zone 14 | 15.29 | 7.08 | 8.21 |
| Area 5 Zone 15 | 12.01 | 5.55 | 6.46 |
| Area 5 Zone 16 | 18.39 | 8.52 | 9.87 |
| Area 5 Zone 17 | 17.52 | 8.11 | 9.41 |
| Area 5 Zone 18 | 16.24 | 7.51 | 8.72 |
| Area 6 Zone 22 | 13.46 | 6.24 | 7.22 |
| Area 6 Zone 23 | 8.19 | 3.78 | 4.40 |
| Area 6 Zone 24 | 25.01 | 11.57 | 13.44 |
| Area 6 Zone 25 | 7.85 | 3.63 | 4.23 |
| Area 6 Zone 26 | 13.53 | 6.27 | 7.26 |
| Area 7 Zone 1 | 1.27 | 0.54 | 0.73 |
| Area 7 Zone 2 | 14.98 | 6.94 | 8.03 |
| Area 7 Zone 3 | 13.10 | 6.07 | 7.03 |
| Area 7 Zone 4 | 15.47 | 7.17 | 8.30 |
| Area 7 Zone 5 | 13.27 | 6.15 | 7.12 |
| Area 7 Zone 6 | 11.20 | 5.19 | 6.01 |
| Area 8 Zone 7 | 11.97 | 5.54 | 6.43 |
| Area 8 Zone 8 | 19.28 | 8.93 | 10.35 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alshuaibi, K.; Zhao, Y.; Zhu, L.; Farantatos, E.; Ramasubramanian, D.; Yu, W.; Liu, Y. Forced Oscillation Grid Vulnerability Analysis and Mitigation Using Inverter-Based Resources: Texas Grid Case Study. Energies 2022, 15, 2819. https://doi.org/10.3390/en15082819
Alshuaibi K, Zhao Y, Zhu L, Farantatos E, Ramasubramanian D, Yu W, Liu Y. Forced Oscillation Grid Vulnerability Analysis and Mitigation Using Inverter-Based Resources: Texas Grid Case Study. Energies. 2022; 15(8):2819. https://doi.org/10.3390/en15082819
Chicago/Turabian StyleAlshuaibi, Khaled, Yi Zhao, Lin Zhu, Evangelos Farantatos, Deepak Ramasubramanian, Wenpeng Yu, and Yilu Liu. 2022. "Forced Oscillation Grid Vulnerability Analysis and Mitigation Using Inverter-Based Resources: Texas Grid Case Study" Energies 15, no. 8: 2819. https://doi.org/10.3390/en15082819
APA StyleAlshuaibi, K., Zhao, Y., Zhu, L., Farantatos, E., Ramasubramanian, D., Yu, W., & Liu, Y. (2022). Forced Oscillation Grid Vulnerability Analysis and Mitigation Using Inverter-Based Resources: Texas Grid Case Study. Energies, 15(8), 2819. https://doi.org/10.3390/en15082819









