Power Hardware-in-the-Loop Test of a Low-Cost Synthetic Inertia Controller for Battery Energy Storage System
Abstract
:1. Introduction
2. A Low-Cost Controller for Distributed Synthetic Inertia
3. Experimental Tests of Synthetic Inertia Control by Means of a Battery Energy Storage System
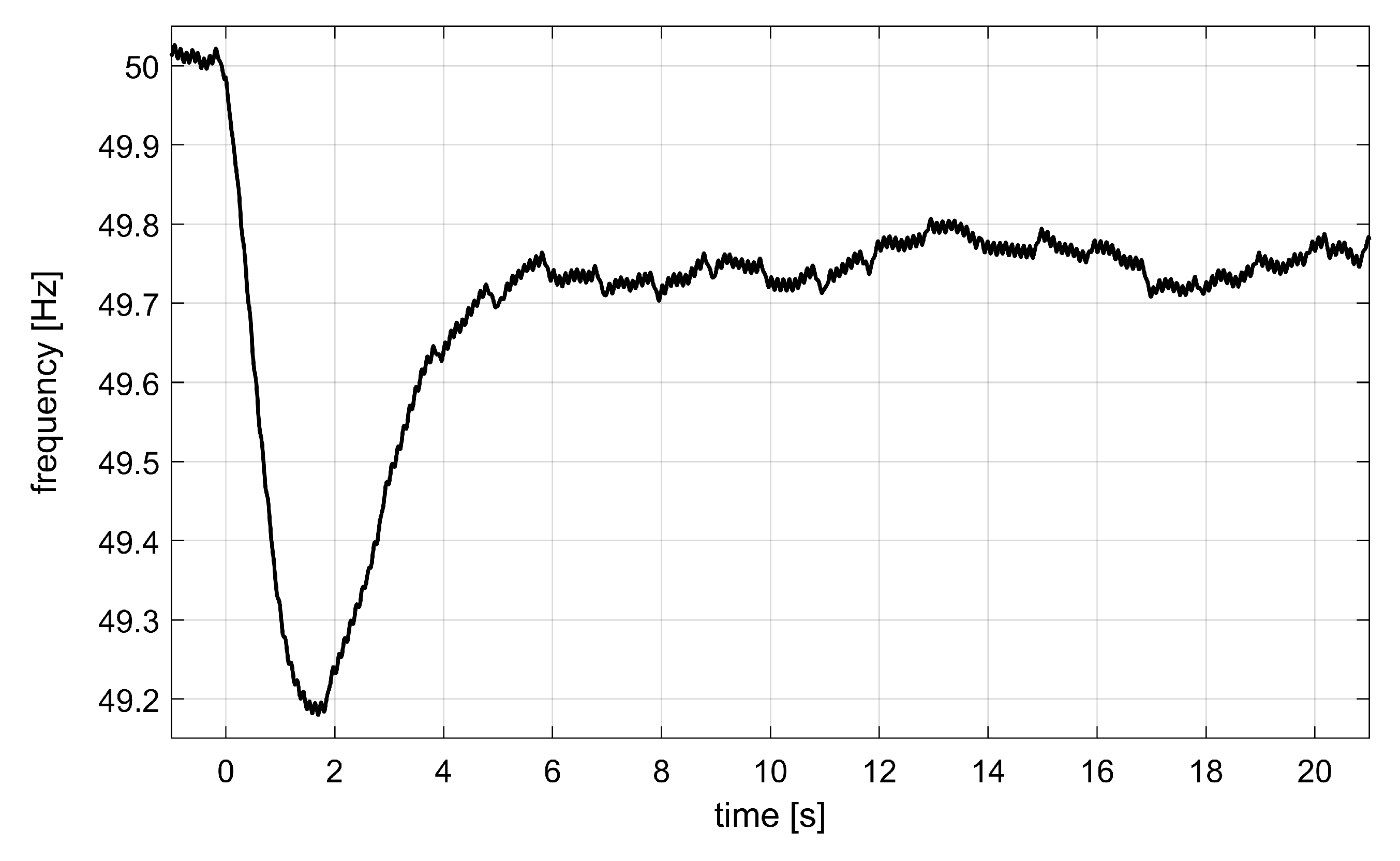
3.1. System Model and Frequency Response without Synthetic Inertia
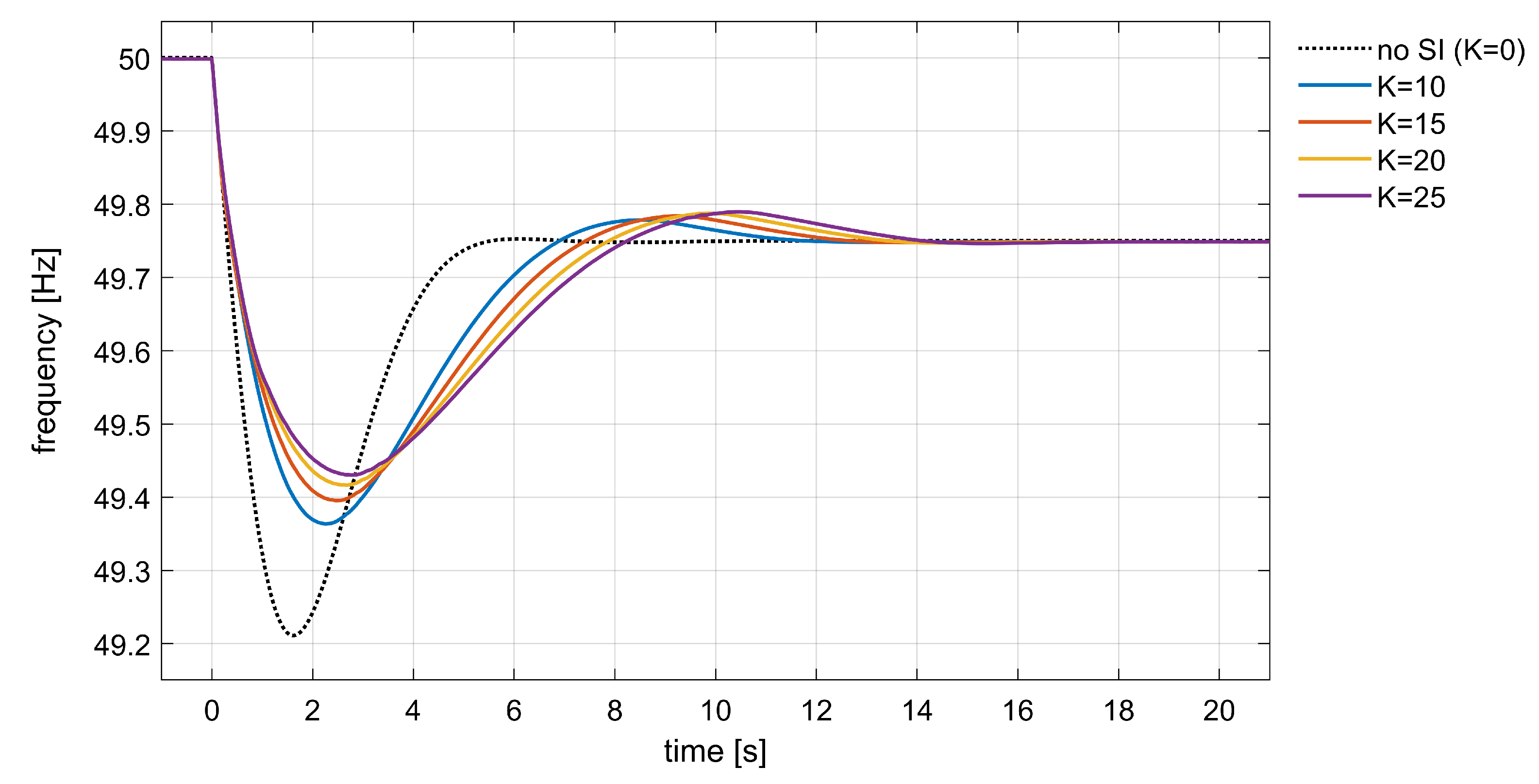
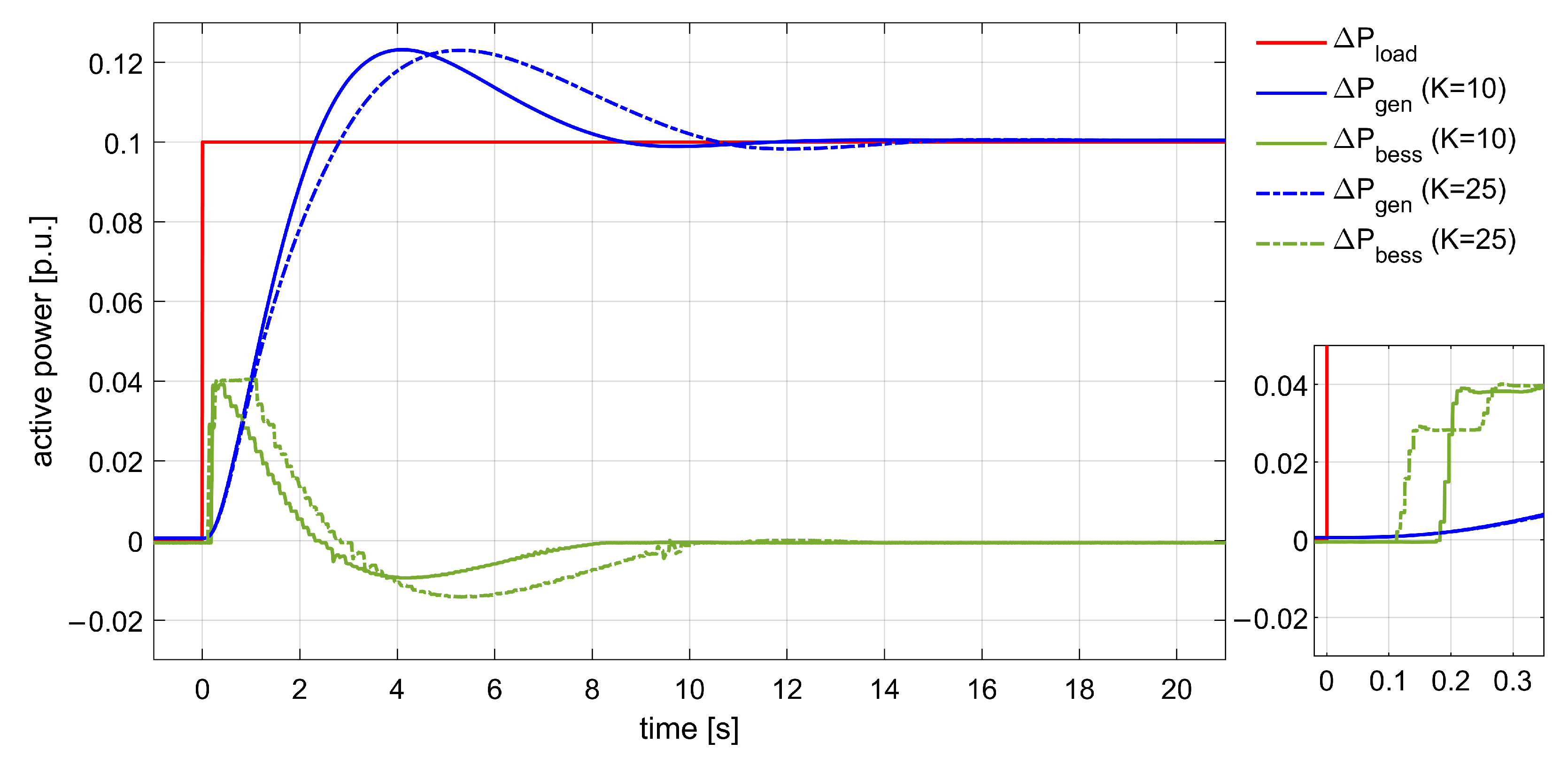
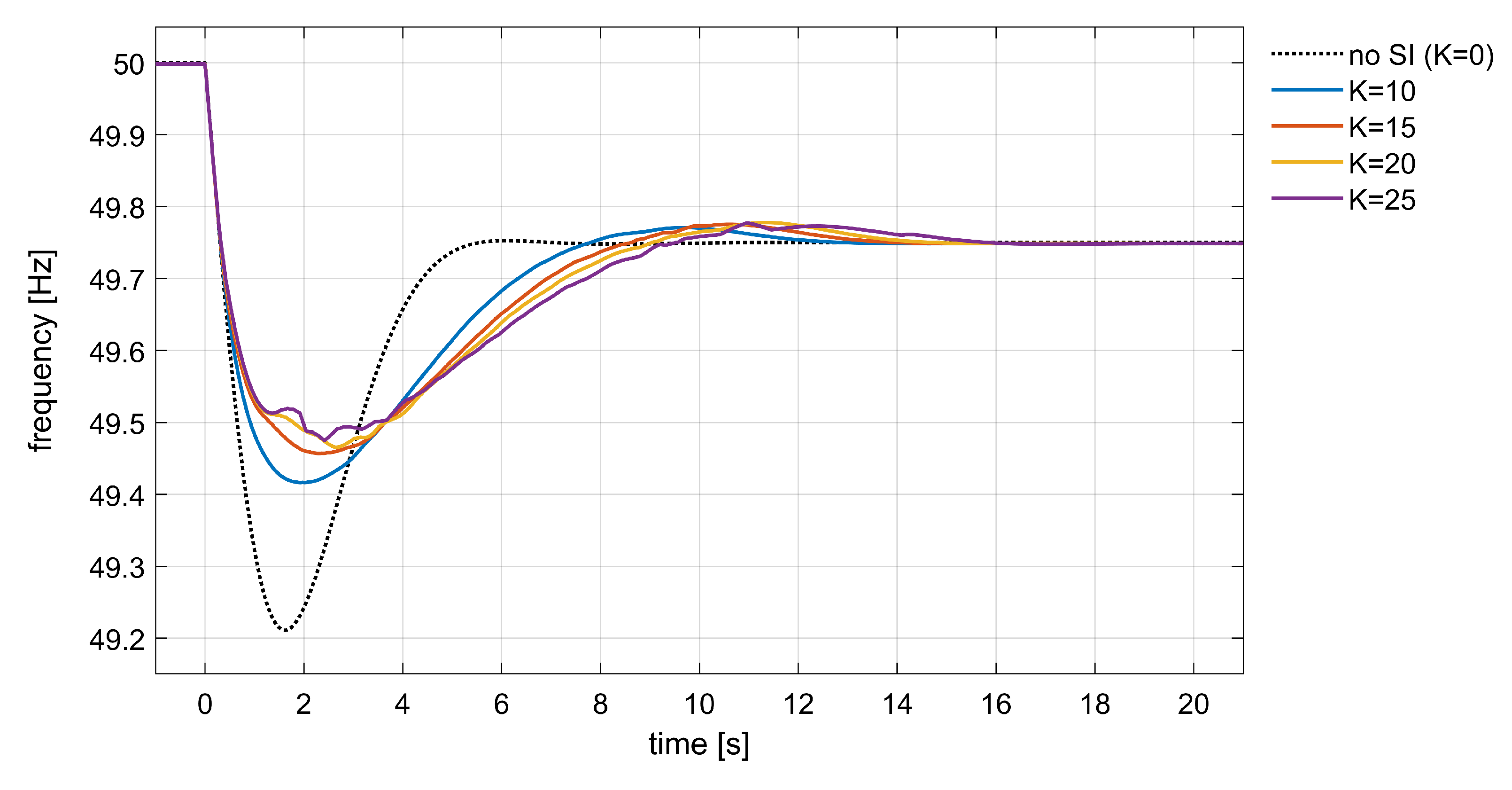
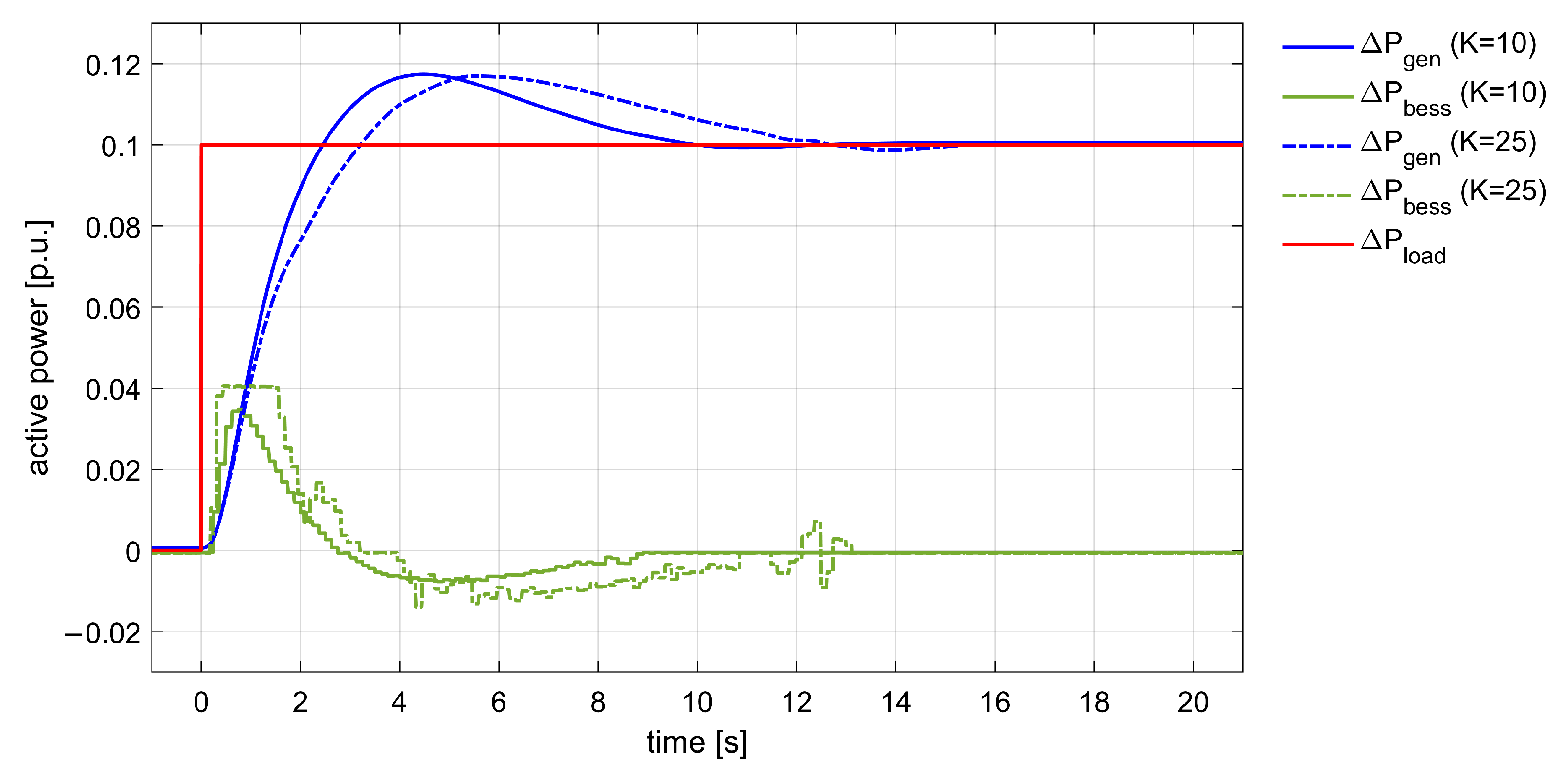
3.2. PHIL Tests of Synthetic Inertia by Means of BESS
4. Power Hardware-in-the-Loop Tests with the Single-Board SI Controller
4.1. Algorithm for Fast Frequency Measurement
- (1)
- An initial guess is made (for example, the frequency period measured at the previous acquisition).
- (2)
- Having considered , two more values in its neighborhood are selected, and .
- (3)
- , , and are evaluated in correspondence of values , and , respectively.
- (4)
- A new value is calculated as the abscissa of the vertex of the parabola passing through the three points , and .
- (5)
- A narrow neighborhood of is analyzed assuming a equal to the sampling period and repeating steps 2–4.
- (6)
- The measured frequency is , with .
4.2. Influence of Measurement Errors
4.3. Tests with Filtered RoCoF Measurements
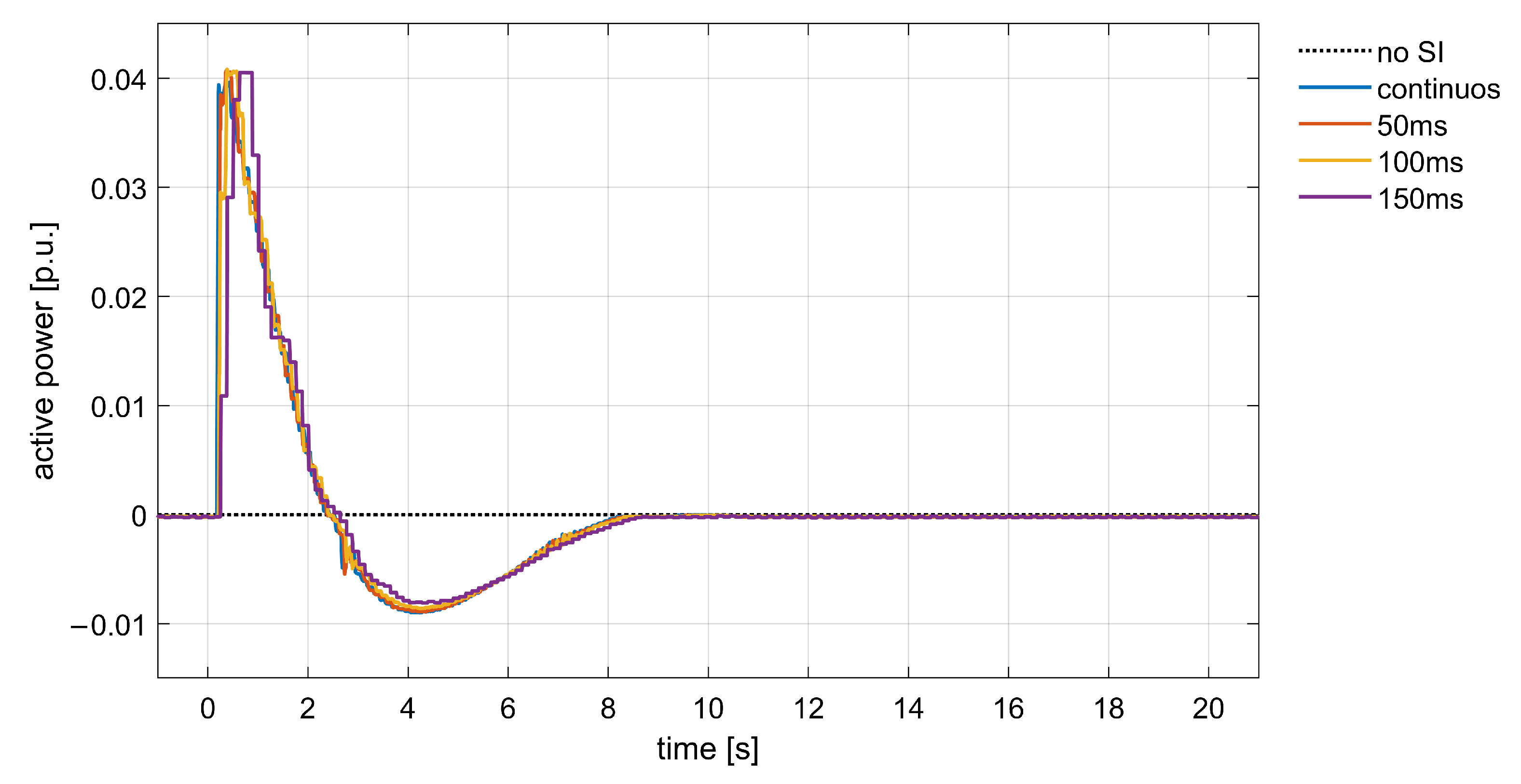
4.4. Frequency Measurement Reporting Time
4.5. Discussion and Future Developments
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Morch, A.Z.; Siface, D.; Gerard, H.; Kockar, I. Market architecture for TSO-DSO interaction in the context of European regulation. In Proceedings of the 16th International Conference on the European Energy Market (EEM), Ljubljana, Slovenia, 18–20 September 2019; pp. 1–5. [Google Scholar] [CrossRef] [Green Version]
- ENTSO-E. Rate of Change of Frequency (RoCoF) Withstand Capability; Technical Report; ENTSO-E: Brussels, Belgium, 2018. [Google Scholar]
- Winter, W.; Elkington, K.; Bareux, G.; Kostevc, J. Pushing the limits: Europe’s new grid: Innovative tools to combat transmission bottlenecks and reduced inertia. IEEE Power Energy Mag. 2015, 13, 60–74. [Google Scholar] [CrossRef]
- ENTSO-E. Need for Synthetic Inertia (SI) for Frequency Regulation; Technical Report; ENTSO-E: Brussels, Belgium, 2017. [Google Scholar]
- Fang, J.; Zhang, R.; Tang, Y.; Hongchang, L. Inertia Enhancement by Grid-Connected Power Converters with Frequency-Locked-Loops for Frequency Derivative Estimation. In Proceedings of the 2018 IEEE Power Energy Society General Meeting (PESGM), Portland, OR, USA, 5–10 August 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Bruno, S.; Giannoccaro, G.; La Scala, M. A Demand Response Implementation in Tertiary Buildings Through Model Predictive Control. IEEE Trans. Ind. Appl. 2019, 55, 7052–7061. [Google Scholar] [CrossRef]
- Subramanian, L.; Debusschere, V.; Gooi, H.B.; Hadjsaid, N. A Distributed Model Predictive Control Framework for Grid-Friendly Distributed Energy Resources. IEEE Trans. Sustain. Energy 2021, 12, 727–738. [Google Scholar] [CrossRef]
- Fang, J.; Li, X.; Tang, Y. Grid-Connected power converters with distributed virtual power system inertia. In Proceedings of the 2017 IEEE Energy Conversion Congress and Exposition, ECCE 2017, Cincinnati, OH, USA, 1–5 October 2017. [Google Scholar] [CrossRef]
- Chamorro, H.R.; Sanchez, A.C.; Øverjordet, A.; Jimenez, F.; Gonzalez-Longatt, F.; Sood, V.K. Distributed synthetic inertia control in power systems. In Proceedings of the 2017 International Conference on ENERGY and ENVIRONMENT (CIEM), Bucharest, Romania, 19–20 October 2017; pp. 74–78. [Google Scholar] [CrossRef] [Green Version]
- Martínez-Sanz, I.; Chaudhuri, B.; Junyent-Ferré, A.; Trovato, V.; Strbac, G. Distributed vs. concentrated rapid frequency response provision in future great britain system. In Proceedings of the 2016 IEEE Power and Energy Society General Meeting (PESGM), Boston, MA, USA, 17–21 July 2016; pp. 1–5. [Google Scholar] [CrossRef]
- The SmartNet Consortium. Deliverable 1.2—Characterization of Flexibility Resources and Distribution Networks; Technical Report; The SmartNet Consortium: Torino, Italy, 2017. [Google Scholar]
- Bruno, S.; De Carne, G.; Iurlaro, C.; Rodio, C.; Specchio, M. A SOC-feedback Control Scheme for Fast Frequency Support with Hybrid Battery/Supercapacitor Storage System. In Proceedings of the 2021 6th IEEE Workshop on the Electronic Grid (eGRID), New Orleans, LA, USA, 8–10 November 2021; pp. 1–8. [Google Scholar] [CrossRef]
- Kuga, R.; Esguerra, M.; Chabot, B.; Avendano Cecena, A. EPIC 2.05: Inertia Response Emulation for DG Impact Improvement. Technical Report. 2019. Available online: https://www.pge.com/pge_global/common/pdfs/about-pge/environment/what-we-are-doing/electric-program-investment-charge/PGE-EPIC-Project-2.05.pdf (accessed on 30 March 2022).
- Fang, J.; Tang, Y.; Li, H.; Li, X. A Battery/Ultracapacitor Hybrid Energy Storage System for Implementing the Power Management of Virtual Synchronous Generators. IEEE Trans. Power Electron. 2018, 33, 2820–2824. [Google Scholar] [CrossRef]
- Conte, F.; Di Vergagni, M.C.; Massucco, S.; Silvestro, F.; Ciapessoni, E.; Cirio, D. Synthetic Inertia and Primary Frequency Regulation Services by Domestic Thermal Loads. In Proceedings of the 2019 IEEE EEEIC/I and CPS Europe 2019, Genova, Italy, 11–14 June 2019. [Google Scholar] [CrossRef]
- Trovato, V.; Sanz, I.M.; Chaudhuri, B.; Strbac, G. Advanced Control of Thermostatic Loads for Rapid Frequency Response in Great Britain. IEEE Trans. Power Syst. 2017. [Google Scholar] [CrossRef] [Green Version]
- Rezkalla, M.; Zecchino, A.; Pertl, M.; Marinelli, M. Grid frequency support by single-phase electric vehicles employing an innovative virtual inertia controller. In Proceedings of the 2016 51st International Universities Power Engineering Conference (UPEC), Coimbra, Portugal, 6–9 September 2016; pp. 1–6. [Google Scholar] [CrossRef] [Green Version]
- Bruno, S.; Giannoccaro, G.; Iurlaro, C.; Scala, M.L.; Rodio, C.; Sbrizzai, R. Fast Frequency Regulation Support by LED Street Lighting Control. In Proceedings of the 2021 IEEE International Conference on Environment and Electrical Engineering and 2021 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I CPS Europe), Bari, Italy, 7–10 September 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Bruno, S.; Giannoccaro, G.; Iurlaro, C.; Scala, M.L.; Rodio, C. A Low-cost Controller to Enable Synthetic Inertia Response of Distributed Energy Resources. In Proceedings of the 2020 IEEE International Conference on Environment and Electrical Engineering and 2020 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Madrid, Spain, 9–12 June 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Rodio, C.; Giannoccaro, G.; Bruno, S.; Bronzini, M.; La Scala, M. Optimal Dispatch of Distributed Resources in a TSO-DSO Coordination Framework. In Proceedings of the 12th AEIT International Annual Conference, AEIT 2020, Catania, Italy, 23–25 September 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Orrù, L.; Petrocchi, L.; Siviero, A.; Silletti, F.; Lisciandrello, G.; Albimonti, G.; Ronzio, D.; Losa, I.; Lazzaro, M. H2020 OSMOSE Project: The Italian demonstrator. Testing flexibilities resources in a coordinated approach. In Proceedings of the 2021 IEEE PES Innovative Smart Grid Technologies Europe (ISGT Europe), Espoo, Finland, 18–21 October 2021; pp. 1–5. [Google Scholar] [CrossRef]
- Daly, P.; Qazi, H.W.; Flynn, D. RoCoF-Constrained Scheduling Incorporating Non-Synchronous Residential Demand Response. IEEE Trans. Power Syst. 2019, 34, 3372–3383. [Google Scholar] [CrossRef]
- Tosato, P.; Macii, D.; Brunelli, D. Implementation of phasor measurement units on low-cost embedded platforms: A feasibility study. In Proceedings of the 2017 IEEE International Instrumentation and Measurement Technology Conference, Turin, Italy, 22–25 May 2017. [Google Scholar] [CrossRef]
- ENTSO-E. Frequency Measurement Requirements and Usage; Technical Report Version 7; ENTSO-E: Brussels, Belgium, 2018. [Google Scholar]
- Romano, P.; Paolone, M. Enhanced Interpolated-DFT for Synchrophasor Estimation in FPGAs: Theory, Implementation, and Validation of a PMU Prototype. IEEE Trans. Instrum. Meas. 2014, 63, 2824–2836. [Google Scholar] [CrossRef]
- Zhang, Z.; Fu, P.; Gao, G.; Jiang, L.; Wang, L. A Rogowski Digital Integrator with Comb Filter Signal Processing System. IEEE Trans. Plasma Sci. 2018, 46, 1338–1343. [Google Scholar] [CrossRef]
- Haque, M.E.; Sakib Khan, M.N.; Islam Sheikh, M.R. Smoothing control of wind farm output fluctuations by proposed Low Pass Filter, and Moving Averages. In Proceedings of the 2015 International Conference on Electrical Electronic Engineering (ICEEE), Rajshahi, Bangladesh, 4–6 November 2015; pp. 121–124. [Google Scholar] [CrossRef]
- Bruno, S.; Giannoccaro, G.; Scala, M.L.; Lopopolo, G. First activities and power-hardware-in-the-loop tests at the public research laboratory LabZERO. In Proceedings of the 2018 110th AEIT International Annual Conference, AEIT 2018, Bari, Italy, 3–5 October 2018; pp. 1–6. [Google Scholar] [CrossRef]
- De Carne, G.; Bruno, S.; Liserre, M.; La Scala, M. Distributed Online Load Sensitivity Identification by Smart Transformer and Industrial Metering. IEEE Trans. Ind. Appl. 2019, 55, 7328–7337. [Google Scholar] [CrossRef]
- Donnini, G.; Carlini, E.; Giannuzzi, G.; Zaottini, R.; Pisani, C.; Chiodo, E.; Lauria, D.; Mottola, F. On the Estimation of Power System Inertia accounting for Renewable Generation Penetration. In Proceedings of the 2020 AEIT International Annual Conference (AEIT), Catania, Italy, 23–25 September 2020; pp. 1–6. [Google Scholar] [CrossRef]
- ENTSO-E. Future System Inertia 2; Technical Report; ENTSO-E: Brussels, Belgium, 2020. [Google Scholar]


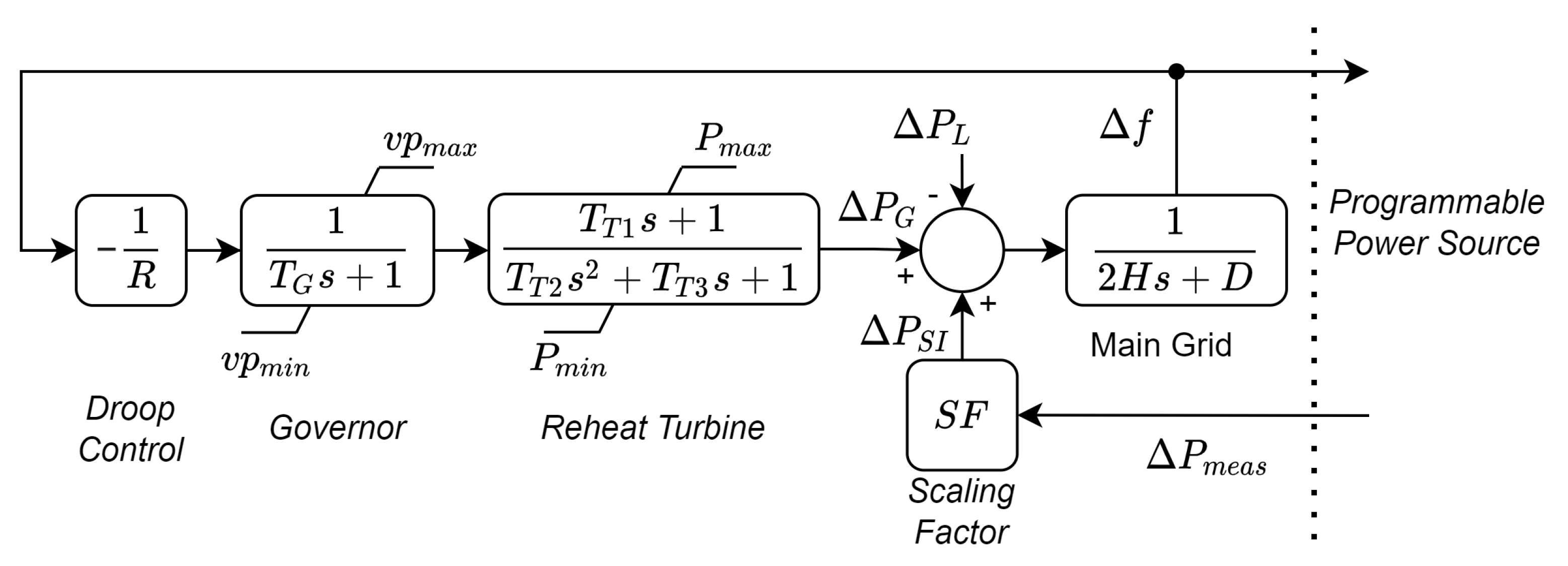
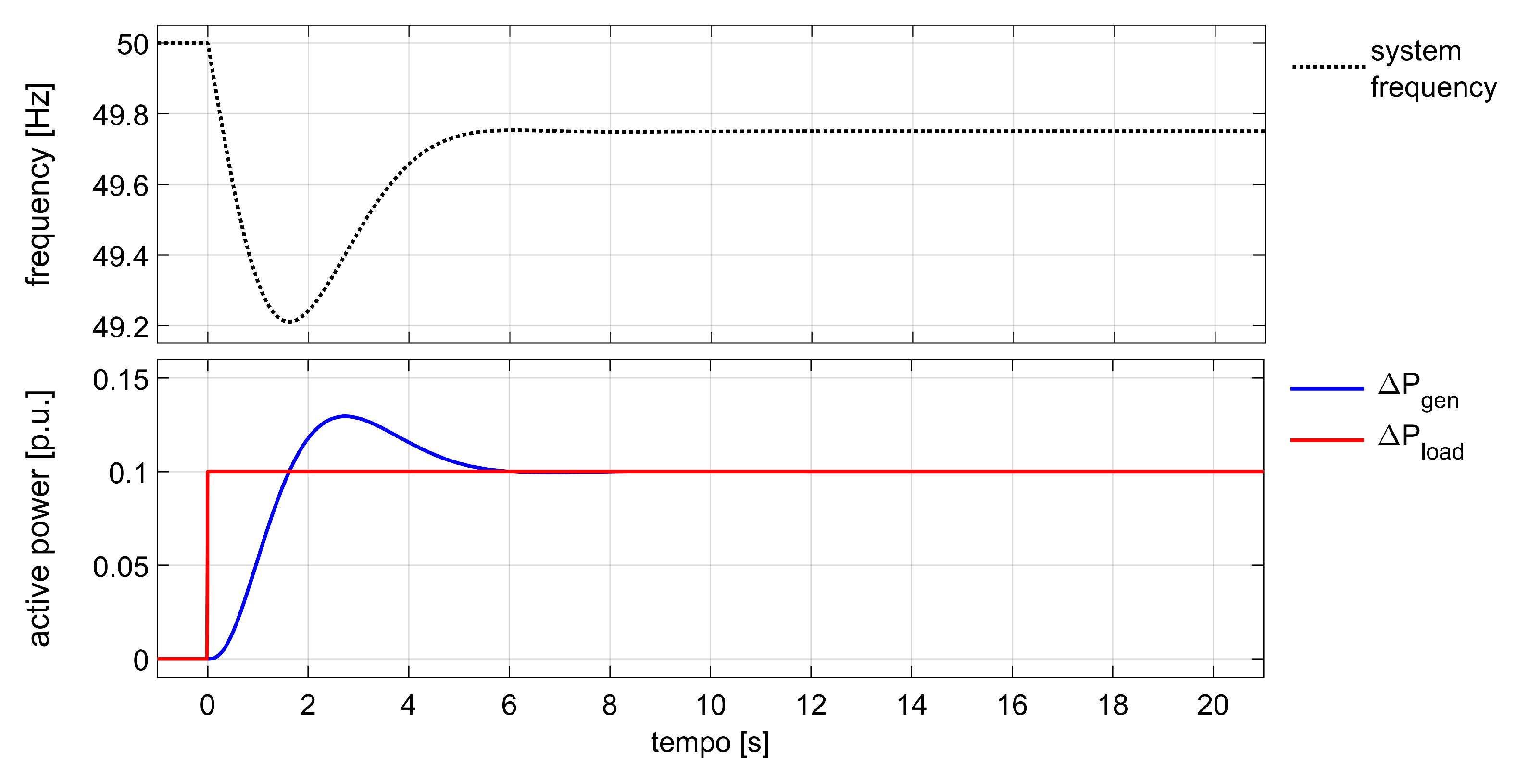
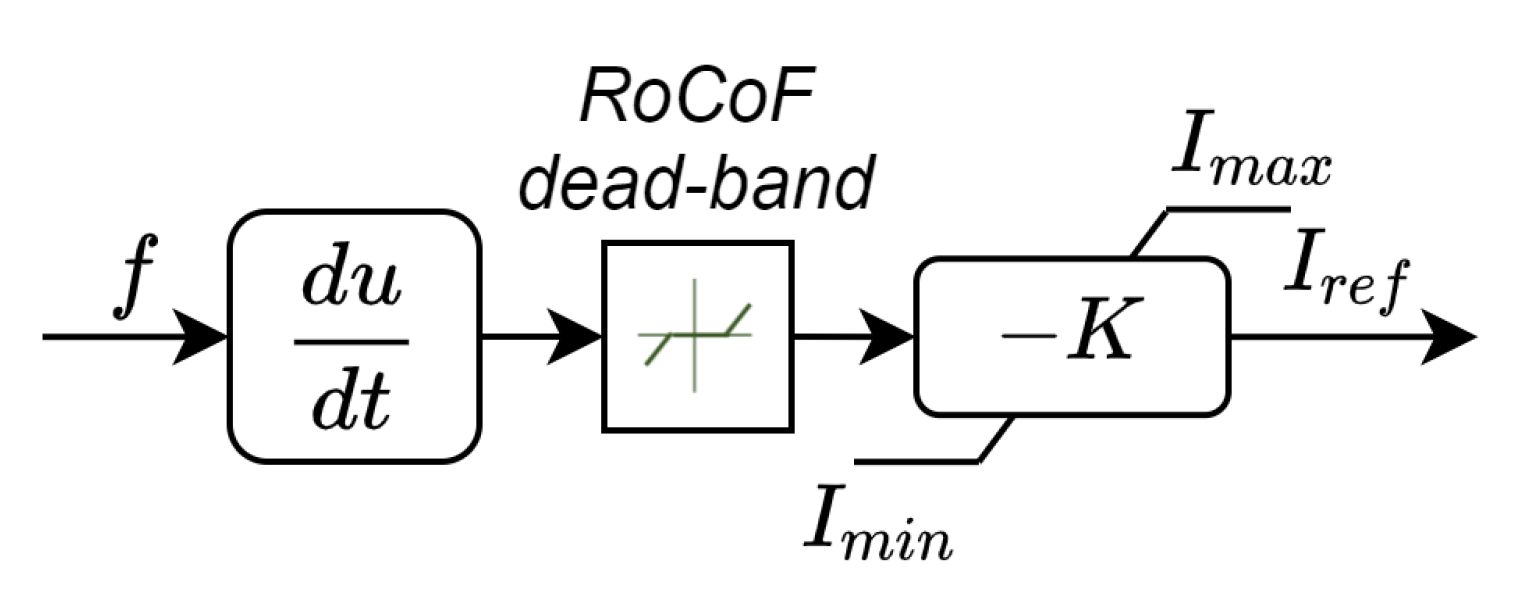





| R | H | D | |||||
|---|---|---|---|---|---|---|---|
| [p.u.] | [s] | [s] | [s] | [s] | [s] | [p.u./kW] | |
| 0.050 | 0.20 | 2.1 | 2.1 | 7.3 | 3.0 | 0.020 | 0.0116 |
| Gain K [A/(Hz/s)] | Frequency Reporting Time [s] | Fall Time [s] | Average RoCoF [Hz/s] | Time nadir [s] | Frequency nadir [Hz] | Overshoot [%] | Settling Time [s] |
|---|---|---|---|---|---|---|---|
| 0 | - | 0.242 | 0.824 | 1.616 | 49.211 | 0.050 | 5.063 |
| 10 | inst. | 0.307 | 0.650 | 2.285 | 49.364 | 0.057 | 10.764 |
| 15 | inst. | 0.310 | 0.645 | 2.483 | 49.396 | 0.068 | 11.896 |
| 20 | inst. | 0.312 | 0.640 | 2.672 | 49.417 | 0.076 | 12.800 |
| 25 | inst. | 0.321 | 0.623 | 2.770 | 49.430 | 0.080 | 13.547 |
| 10 | 0.050 | 0.278 | 0.720 | 2.254 | 49.367 | 0.056 | 10.795 |
| 10 | 0.100 | 0.260 | 0.769 | 2.209 | 49.371 | 0.053 | 10.842 |
| 10 | 0.150 | 0.243 | 0.824 | 2.181 | 49.380 | 0.049 | 10.949 |
| Gain K [A/(Hz/s)] | Frequency Reporting Time [s] | Alpha | Fall Time [s] | Average RoCoF [Hz/s] | Time nadir [s] | Frequency nadir [Hz] | Overshoot [%] | Settling Time [s] |
|---|---|---|---|---|---|---|---|---|
| 0 | - | - | 0.242 | 0.824 | 1.616 | 49.211 | 0.050 | 5.063 |
| 10 | ∼0.050 | 0.10 | 0.246 | 0.812 | 1.948 | 49.416 | 0.047 | 11.792 |
| 15 | ∼0.050 | 0.10 | 0.249 | 0.801 | 2.300 | 49.457 | 0.051 | 13.049 |
| 20 | ∼0.050 | 0.10 | 0.249 | 0.801 | 2.641 | 49.465 | 0.055 | 13.825 |
| 25 | ∼0.050 | 0.10 | 0.250 | 0.799 | 2.419 | 49.475 | 0.054 | 15.155 |
| Gain K [A/(Hz/s)] | Frequency Reporting Time [s] | Alpha | Fall Time [s] | Average RoCoF [Hz/s] | Time nadir [s] | Frequency nadir [Hz] | Overshoot [%] | Settling Time [s] |
|---|---|---|---|---|---|---|---|---|
| 0 | - | - | 0.242 | 0.824 | 1.616 | 49.211 | 0.050 | 5.063 |
| 10 | ∼0.050 | 0.10 | 0.246 | 0.812 | 1.948 | 49.416 | 0.047 | 11.792 |
| 10 | ∼0.050 | 0.25 | 0.251 | 0.797 | 2.285 | 49.386 | 0.054 | 13.526 |
| 10 | 0.100 | 0.10 | 0.244 | 0.817 | 1.496 | 49.393 | 0.047 | 11.785 |
| 10 | 0.100 | 0.25 | 0.246 | 0.812 | 2.100 | 49.410 | 0.047 | 11.663 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bruno, S.; Giannoccaro, G.; Iurlaro, C.; La Scala, M.; Rodio, C. Power Hardware-in-the-Loop Test of a Low-Cost Synthetic Inertia Controller for Battery Energy Storage System. Energies 2022, 15, 3016. https://doi.org/10.3390/en15093016
Bruno S, Giannoccaro G, Iurlaro C, La Scala M, Rodio C. Power Hardware-in-the-Loop Test of a Low-Cost Synthetic Inertia Controller for Battery Energy Storage System. Energies. 2022; 15(9):3016. https://doi.org/10.3390/en15093016
Chicago/Turabian StyleBruno, Sergio, Giovanni Giannoccaro, Cosimo Iurlaro, Massimo La Scala, and Carmine Rodio. 2022. "Power Hardware-in-the-Loop Test of a Low-Cost Synthetic Inertia Controller for Battery Energy Storage System" Energies 15, no. 9: 3016. https://doi.org/10.3390/en15093016
APA StyleBruno, S., Giannoccaro, G., Iurlaro, C., La Scala, M., & Rodio, C. (2022). Power Hardware-in-the-Loop Test of a Low-Cost Synthetic Inertia Controller for Battery Energy Storage System. Energies, 15(9), 3016. https://doi.org/10.3390/en15093016







