Multiobjective Optimization for a Li-Ion Battery and Supercapacitor Hybrid Energy Storage Electric Vehicle

Abstract

The acceptance of hybrid energy storage system (HESS) Electric vehicles (EVs) is increasing rapidly because they produce zero emissions and have a higher energy efficiency. Due to the nonlinear and strong coupling relationships between the sizing parameters of the HESS components and the control strategy parameters and EV’s performances, energy consumption rate, running range and HESS cost, how to design the HESS EVs for different preferences is a key problem. How to get the real time performances from the HESS EV is a difficulty. The multiobjective optimization for the HESS EV considering the real time performances and the HESS cost is a solution. A Li-ion battery (BT) semi-active HESS and optimal energy control strategy were proposed for an EV. The multiobjectives include energy consumption over 100 km, acceleration time from 0–100 km per hour, maximum speed, running range and HESS cost of the EV. According to the degrees of impact on the multiobjectives, the scaled factors of BT capacity, the series number of Li-ion BTs, the series number of super-capacitors (SCs), the parallel number of SCs, and charge power of the SCs were chosen as the optimization variables. Two sets of different weights were used to simulate the multiobjective optimization problem in the ADVISOR software linked with MATLAB software. The simulation results show that some of the multiobjectives are sensitive to their weights. HESS EVs meeting different preferences can be designed through the weights of different objectives. Compared with the direct optimization algorithm, the genetic algorithm (GA) has a stronger optimization ability, and the single objective is more sensitive to its corresponding weight. The proposed optimization method is practical for a Li-ion BT and SC HESS EV design.

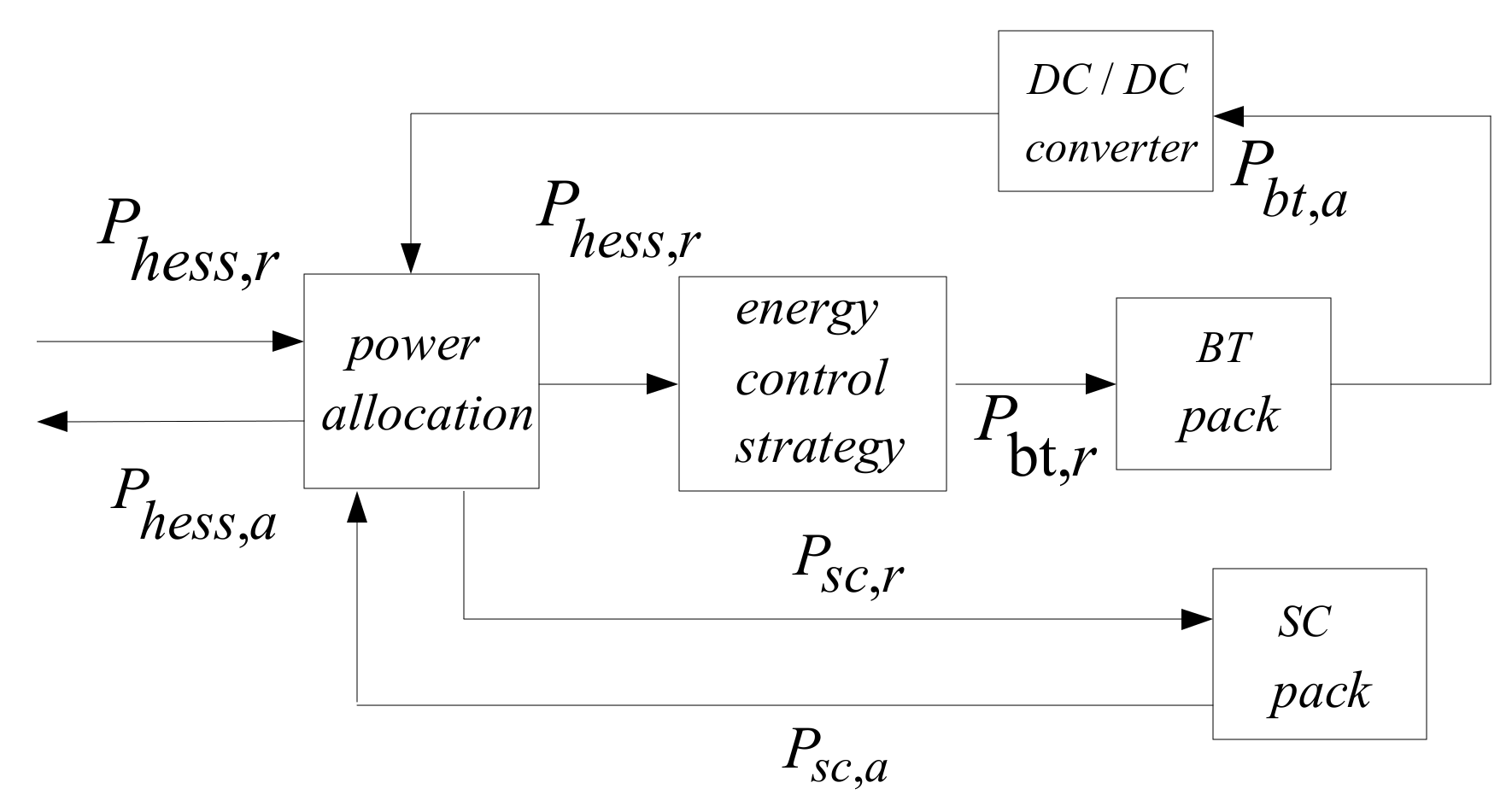
1. Introduction

Due to advantages such as energy conservation, environmental protection, and low charging cost, EVs have been gradually accepted by the market [1,2]. EVs have been considered as a good approach to reduce carbon dioxide emissions, for EVs can overcome the shortcomings of traditional fuel vehicle exhaust pollution. At the same time, EVs can save energy because they can be charged when the power consumption of the power grid is low [3]. The BT is one of the most expensive components of the EV and has a decisive impact on EV’s price and some of their performance [4]. In current EVs, the BTs are always oversized in order to improve power performance and acceleration capability. Such challenges as power performance, running range, lifetime of the BT, and cost of the EV with a sole energy storage system limit the EV’s wider use.

The SC has the advantages of high-power density, short charge and discharge time, and long service life and is less affected by the temperature, but the energy density is small [5]. The Li-ion BT and SC HESS can make up for the advantages of both sides while avoiding their disadvantages [6].

The BT and SC HESS is widely used in different objects and occasions. The BT and SC HESS in smart phones extends the service life of Li-ion BTs [7]. The lead-acid BT and SC HESS in trucks reduces carbon dioxide emissions [8,9,10]. The BT and SC HESS reduces the power fluctuation of fuel cell and wind energy in the HESS with fuel cell and wind energy [11,12,13,14,15,16].

The performance of BT and SC HESS depends on an appropriate energy management strategy. The wavelet analysis method is used to identify the road conditions; then, the neural network is used to learn the conditions data, and the fuzzy energy management strategy is used to distribute the power of the HESS, which improves vehicle performance [17]. The HESS real-time energy management strategy based on SC voltage detection has achieved good results. By improving the topology of HESS, flexible control of lithium BT current is realized, and the effect of energy management is improved. The power performance of HESS is improved by the fuzzy predictive control method [18]. A HESS energy management strategy based on dynamic programming considering lithium BT degradation is proposed [19].

Compared with the BT, the HESS not only improves the performance but also leads to the increase of system complexity and cost. Therefore, the evaluation and optimization of HESS should be carried out with multiple objectives. The purpose of HESS EV is to improve the performances of the EV while taking into account the economy of the EV.

The GA algorithm is widely used in the field of EV optimization [20,21,22,23,24]. The GA algorithm is used to optimize the multi objectives of fuel cell current, lithium BT current, lithium BT’s SOC change, SC’s SOC change, and hydrogen consumption cost by the control of the powers of the BT and SC and the load in the fuel cell, BT, and SC hybrid EV [20]. The multi-objective GA algorithm is used to optimize the automotive electric transmission [21]. The GA algorithm is used to optimize the location and power of EV charging stations [22,23]. The multi-objective GA algorithm is used to optimize the driving paths and powers of multi depot vehicle [24].

The above studies focus on comparing HESS performance with BT or SC performance or, for specific HESS, using an intelligent control method to optimize the energy management strategy and improve the HESS performance, with less consideration of the influence of the sizing parameters of components in HESS and less consideration of the optimal design based on the EV’s specific performance indicators in the optimization. At the same time, how to get the real time performances of the HESS EV is a difficulty. In this paper, a multiobjective optimization on a BT and SC HESS EV using both GA algorithm and ADVISOR software will be studied. The real time performances of the HESS EV are obtained by the ADVISOR software. The EV’s energy consumption over 100 km, acceleration time from 0–100 km per hour, maximum speed, HESS cost, and running range are considered in the objective function. The structure of the paper is as follows: The fundamentals of a BT semi-active HESS EV, the scheme of the multiobjective optimization and an optimal energy management strategy are designed in Section 2. Section 3 focuses on the multiobjective problem analysis. In Section 4 the GA algorithm optimization based on ADVISOR software and MATLAB software is carried out. The study discussion is also presented in Section 4. The conclusions are presented in Section 5.

2. Fundamentals of a BT Semi-Active HESS

2.1. HESS Components

ADVISOR software is a popular advanced vehicle simulation software, which is especially suitable for vehicle performance evaluation, testing, and optimization. A variety of vehicle structures such as traditional fuel vehicles, pure EVs, and fuel cell and Li-ion BT hybrid vehicles are available in the ADVISOR software, but there is no BT and SC HESS EV model available [25]. The new BT’s semi-active HESS EV model is specially developed in the ADVISOR software. The semi-active HESS architecture is reasonable for EVs considering the HESS cost, efficiency, and reliability. The BT’s semi-active HESS structure is easy to lead to unstable motor voltage, but it is still within a range of voltage fluctuation that the motor can withstand. The Li-ion BT pack is connected to the input of the motor controller through a DC/DC converter, and the SC pack is directly connected to the input of the motor controller. The BT semi-active HESS scheme in the ADVISOR software is shown in Figure 1.

The SC pack consists of N_sc,p strings in parallel and N_sc,s SCs in series. The BT pack consists of N_bt,s BTs in series. P_hess,r is the required power of the HESS. P_hess,a is the available output power of the HESS. P_bt,r is the required power of the Li-ion BT pack. P_bt,a is the available output power of the Li-ion BT pack. P_sc,r is the power required of the SC pack. P_sc,a is the available output power of the SC pack.

A midsize EV’s parameters are listed in

Table 1. EV’s model parameters.

Parameters	Value
Cargo mass/kg	200
Glider mass/kg	680
Wheelbase/m	2.7
Frontal area/m2	2.6

. A Saft VL45E LiFePO₄ BT is used, whose parameters are listed in

Table 2. SAFT VL45E Li-ion BT parameters.

Parameters	Value
Capacity/Ah	44
Internal resistance/mΩ	3.6
Stored energy/Wh	140
Mass/kg	0.91

[25]. A Maxwell BACP3000 SC is chosen for the HESS, whose parameters are listed in

Table 3. BACP3000 SC parameters.

Parameters	Value
Rated capacitance/F	3000
Internal resistance/mΩ	0.29
Stored energy/Wh	3.04
Mass/kg	0.51
Usable power/W·kg−1	5900

[25]. A Westinghouse AC75 motor model is used with the parameters listedin

Table 4. Motor parameters.

Parameters	Value
Max. power/kW	75
Max. voltage/V	375
Min. voltage/V	120

[26].

2.2. The Scheme of the Multiobjective Optimization for the HESS EV

The scheme of the multiobjective optimization for the HESS EV is as in Figure 2. The optimal energy control strategy of the HESS will be designed in the HESS EV in the ADVISOR software by secondary development at first. Then, the relationships between the sizing parameters of the HESS components and the control strategy parameters and EV’s real time performances, energy consumption rate, running range and HESS cost, etc., can be obtained by the HESS EV performance simulation in the ADVISOR software. According to the degrees of impacts between them, the optimization variables and multiobjects are selected. Then, a multiobjective optimization in the ADVISOR software linked with the MATLAB software can be carried out with two sets of weights. The conclusion and discussion will be presented at the end.

2.3. The Optimal Energy Control Strategy of the HESS

An optimal energy control strategy is proposed for the BT semi-active HESS. The optimal energy control strategy distributes the output powers of BT and SC according to the required power of the HESS and the SOC of the SC pack. The available output power of the Li-ion BT pack is limited within the rated value of high efficiency to extend the life of the BT, but the available output power of the SC pack can fluctuate greatly for the good performance of the SC pack. The power fluctuation of the EV is large and frequent, and therefore, the SC pack is used as an energy buffer. The SC pack adopts the charge sustaining energy management strategy to meet the power demand of the HESS and maintain the state of charge (SOC) of the SC pack near the target value as far as possible. The optimal control strategy is shown in Figure 3.

SOC_sc is the SOC of the SC pack. SOC_sc,cs,hi is the high SOC of the SC pack. SOC_sc,cs,lo is the low SOC of the SC pack. SOC_sc,goal is the goal value of SOC_sc. The optimal control strategy works on the following rules:

(a)

In normal cases, in order to improve the efficiency and service life of lithium BT,P_bt,r is limited by the minimum control power P_bt,cs,min and the maximum control power P_bt,cs,max.

(b)

When P_hess,r∈[0,P_bt,cs,max] and SOC_sc∈[0,SOC_sc,goal], as the mode 1 in Figure 3, the SC pack is charged by the BT pack, and SOC_sc approaches SOC_sc,goal.

(c)

When P_hess,r ≥ P_bt,cs,max, as the mode 4 in Figure 3, both the BT pack and SC pack provide power to the EV.

(d)

When P_hess, _r∈ [0,P_bt,cs,_max] and SOC_sc∈[SOC_sc,goal, 1], as the mode 2 in Figure 3, the SC pack discharges, and SOC_sc approaches SOC_sc,goal.

(e)

When P_hess,r ≤ 0, as the mode 3 in Figure 3, the SC pack recovers all regenerative braking power.

When P_hess,r ≤ 0, P_bt,r is shown in Equation (1).

P_{bt,r =}P_bt,cs,min

(1)

When P_hess,r > 0, P_bt,r is shown in Equation (2).

P_bt,r = P_hess,r + P_additional

(2)

E_sc,cs,hi is the energy of the SC pack when SOC_sc is SOC_sc,cs,hi. E_sc,cs,lo is the energy of the SC pack when SOC_sc is SOC_sc,cs,lo. E_sc,goal is the energy of the SC pack when SOC_sc is SOC_sc,goal. E_sc,goal is the average value of E_sc,cs,hi and E_sc,cs,lo, as in Equation (3).

E_sc,goal = 0.5×(E_sc,cs,hi + E_sc,cs,lo)

(3)

According to the SC’s energy formula, E_sc,goal and E_sc,cs,hi, E_sc,cs,lo are as in Equations (4)–(6), respectively.

E_sc,goal = 0.5×C×V²_sc,goal = 0.5×C×V²×SOC²_sc,goal

(4)

E_sc,cs,hi = 0.5×C×V²_sc,cs,hi = 0.5×C×V²×SOC²_sc,cs,hi

(5)

E_sc,cs,lo = 0.5×C×V²_sc,cs,lo = 0.5×C×V²×SOC²_sc,cs,lo

(6)

C is the SC’s capacitance; V is the SC’s voltage. SOC_sc,goal is obtained from Equations (3)–(6), which is shown in Equation (7).

$$SO{C}_{\mathrm{sc},\mathrm{goal}}=\sqrt{\frac{SO{C}^2{}_{\mathrm{sc},\mathrm{cs},\mathrm{hi}}+SO{C}^2{}_{\mathrm{sc},\mathrm{cs},\mathrm{lo}}}{2}}$$

(7)

P_additional is the additional power needed to maintain SOC_sc near SOC_sc,goal. P_additional is shown in Equation (8).

$$P_{\mathrm{additional}}=\frac{SO{C}_{\mathrm{sc},\mathrm{goal}}-SO{C}_{\mathrm{sc}}}{0.5\times (SO{C}_{sc,cs,hi}-SO{C}_{\mathrm{sc},\mathrm{cs},\mathrm{lo}})}\cdot P_{\mathrm{charge}}$$

(8)

P_charge is the charge power of the SC pack.

P_sc,r is as shown in Equation (9).

$$P_{\mathrm{sc},\mathrm{r}}=P_{\mathrm{hess},\mathrm{r}}-P_{\mathrm{bt},\mathrm{a}}\cdot {\eta }_{\mathrm{DC}/\mathrm{DC}}$$

(9)

ƞ_DC/DC is energy conversion efficiency of the DC/DC converter.

The parameters of the optimal energy control strategy are in

Table 5. The optimal energy control strategy parameters.

Parameters	Value
Pbt,cs,min/kW	1.5
Pbt,cs,max/kW	12
ηDC/DC	0.95
SOCsc,init	0.9
SOCsc,goal	0.74
SOCsc,cs,hi	0.95
SOCsc,cs,lo	0.45

SOC_sc,init is the initial value of SOC_sc.

.

3. Multiobjective Optimization Analysis

The HESS EV performance simulation results [26] of the HESS EV in the ADVISOR software show that both the sizing parameters of the HESS components and the control strategy parameters have a certain impact on EV’s performances, energy consumption rate, running range, and HESS cost. When k_bt increases, t₁₀₀, Q₁₀₀, l, and C_hess increases, and V_veh,max decreases. When N_bt,s increases, V_veh,max, t_100, l, and C_hess increase, and Q₁₀₀ increases or decreases. When N_sc,s increases, V_veh,max, Q₁₀₀, and C_hess increase, and t₁₀₀ and l decrease. When N_sc,p increases, V_veh,max, l, and C_hess increase, and Q₁₀₀ and t₁₀₀ decrease. When P_charge increases, V_veh,max and Q₁₀₀ increase, and t₁₀₀, l and C_hess decrease. Therefore, the relationships between the sizing parameters of the HESS components and the control strategy parameters and EV’s performances, energy consumption rate, running range, and the HESS cost are nonlinear and strong coupling.

The HESS EV performance simulation results show that, among the sizing parameters of HESS’s components and the control strategy parameters, the scaled factors of BT capacity k_bt, N_bt,s, N_sc,s, N_sc,p, and P_charge have a greater impact on the five objectives, while other parameters have less impact on the five objectives. Therefore, k_bt, N_bt,s, N_sc,s, N_sc,p, and P_charge are selected as the optimization variables.

The semi-active HESS EV evaluation focuses on the energy consumption over 100 km Q₁₀₀, the acceleration time from 0–100 km per hour t₁₀₀, the maximum speed V_veh,max, the running range l, and the HESS cost C_hess, which are essentially contradictory. The variables of the multiobjective optimization problem for the HESS EV contain k_bt, N_bt,s, N_sc,s, N_sc,p, and P_charge, as shown in Equation (10).

$$f(x)=[k_{bt},N_{bt,s},N_{sc,p},N_{\mathrm{sc},\mathrm{s}},P_{\mathrm{charge}}]$$

(10)

The HESS EV performance simulation results and the HESS EV performance constraints reduce the amount of calculations during the optimization. The varied ranges of the variables are described in Equation (11).

$$x_1\in \left[1,4\right],x_2\in \left[50, 150\right],x_3\in \left[1–4\right],x_4\in \left[75, 135\right],x_5\in \left[6000, 9000\right]$$

(11)

The multiobjective function is given by Equation (12). The optimization objective is to maximize the value of F(x).

$$F(x)=w_1·(1-t_{100·}{}_{\mathrm{norm}})+w_2·V_{veh,max,}{}_{\mathrm{norm}}+w_3·l_{\mathrm{norm}}+w_4·(1-Q_{100·\mathrm{norm}})+w_5(1-C_{\mathrm{hess},\mathrm{norm}})$$

(12)

t_100,norm,V_veh,max,norm, l_norm, Q_100,norm, and C_hess,norm are the normalization value of t₁₀₀, V_veh,max, l, Q_100, and C_hess, between zero and one, based on the maximum and minimum values obtained.

t_100,norm is shown in Equation (13).

$$t_{100,norm}=\frac{t_{100}-t_{100,}{}_{min}}{t_{100,max}-t_{100,min}}$$

(13)

t_100,min is the reference minimum value of t₁₀₀, and t_100,max is the reference maximum value of t₁₀₀.

V_veh,max,norm is shown in Equation (14).

$$V_{\mathrm{veh},\max ,}{}_{norm}=\frac{V_{\mathrm{veh},\max }-V_{veh,max,}{}_{min}}{V_{\mathrm{veh},\max }{{}_{,}}_{max}-V_{veh,max,}{}_{min}}$$

(14)

V_veh,max,min is the reference minimum value of V_veh,max, and V_veh,max,max is the maximum value of V_veh,max.

l_norm is shown in Equation (15).

$$l_{\mathrm{norm}}=\frac{l-l_{\min }}{l_{\max }-l_{\min }}$$

(15)

l_min is the reference minimum value of l, and l_max is the reference maximum value of l.

Q_100,norm is shown in Equation (16).

$$Q_{100}{}_{,\mathrm{norm}}=\frac{Q_{100}-Q_{100,}{}_{\min }}{Q_{100,\max }-Q_{100,\min }}$$

(16)

Q_100,min is the reference minimum value of Q₁₀₀, and Q_100,max is the reference maximum value of Q₁₀₀.

C_hess,norm is shown in Equation (17).

$$C_{\mathrm{hess},}{}_{\mathrm{norm}}=\frac{C_{\mathrm{hess}}-C_{\mathrm{hess},}{}_{\min }}{C_{\mathrm{hess},}{}_{\max }-C_{\mathrm{hess},}{}_{\min }}$$

(17)

C_hess,min is the reference minimum value of C_hess. C_hess,max is the reference maximum value of C_hess.

The optimization constraints parameters are shown in

Table 6. The optimization constraints parameters.

Parameters	Value
t100(s)	<10
Vveh,max/(kmph)	>100
l/(km)	>100
mveh/(kg)	<1600

. m_veh is the weight of the HESS EV.

The weights w_1, w_2, w_3, w₄, and w₅ are chosen to indicate the importance of the five objectives. The sum of w_1, w_2, w_3, w₄, and w₅ is 1.

4. Optimization Results

The GA algorithm has been shown to be an effective strategy to solve complex and non-linear engineering optimization problems. The GA algorithm is written in the ADVISOR software in the MATLAB environment. The GA algorithm parameters are as in

Table 7. GA algorithm parameters.

Parameters	Value
Number of termination evolution generations	40
Crossover probability	0.95
Mutation probability	0.08

.

The HESS optimization flowchart diagram based on the ADVISOR software and GA algorithm is as in Figure 4. The optimized variables k_bt, N_bt,s, N_sc,s, N_sc,p, and P_charge are encoded by binary method. w₁, w₂, w_3, w₄, and w₅ are 0.2, 0.2, 0.2, 0.2, and 0.2, respectively. The equivalent fuel economy of the HESS EV under UDDS driving condition is good. Therefore, two consecutive UDDS (Urban Dynamometer Driving Schedule) drive cycles are used in the simulation.

The HESS cost is evaluated by considering a BACP3000 super-capacitor cost as USD 50 and a SAFT VL45E Li-ion BT cost as USD 40. The Li-ion BT packs are replaced once in the cycle lifetime, so the cost of a BT is USD 80. C_hess is presented as Equation (18).

$$C_{\mathrm{hess}}=80\cdot k_{\mathrm{bt}}\cdot N_{\mathrm{bts}}+50\cdot k_{\mathrm{sc}}\cdot N_{\mathrm{scs}}\cdot N_{\mathrm{scp}}$$

(18)

The objection function F(x) convergence process is as in Figure 5, basically stable after nearly 15 generations.

The t₁₀₀ convergence process is as in Figure 6, basically stable after near 20 generations.

The V_veh,max convergence process is as in Figure 7, basically stable after near 25 generations.

The Q₁₀₀ convergence process is as in Figure 8, basically stable after near 25 generations.

The C_hess convergence process is as in Figure 9, basically stable after near 30 generations.

The l convergence process is as in Figure 10, basically stable after near 30 generations.

The simulation results are as in

Table 8. Simulation results.

Generation Number	kbt	Nbt,s	Nsc,s	Nsc,p	Pcharge/W	t100/s	Vveh,max	l/km	Chess (USD)	Q100/(L/100 km)
1	1.59	91	104	1	5015	9.4	108.32	102	16,400	1.9391
5	1.68	93	130	1	6500	9	109.76	110.2	23,400	1.9265
20	1.94	109	114	4	7600	8.4	125.6	150.4	32,100	1.8566
40	2.01	111.2	109	4	8100	8.2	137.5	155.1	30,800	1.7695

. It is clear that the optimization results meet the constraints of the optimization. The GA algorithm can find the optimal value. The optimization results are reasonable taking into account the five objectives, such as t₁₀₀, V_veh,max, l, Q₁₀₀, and C_hess.

Two sets of weights are used to study their influences on the results of multiobjective optimization. The two sets of weights are as in

Table 9. Two sets of weights.

No.	W1	W2	W3	W4	W5
1	0.2	0.2	0.2	0.2	0.2
2	0.15	0.15	0.2	0.2	0.3

. The five weights of the five objectives are the same in the first set of weights. This means that these five objectives are equally important. In the second set of weights, w₁, w₂, and w₅ change, but w₃ and w₄ remain unchanged comparing the first set of weights. The results are shown in

Table 10. The results with two sets of weights.

No.	kbt	Nbt,s	Nsc,s	N sc,p	P charge (W)	t 100(8)	V veh,max (km/h)	L (km)	C hess ($)	Q 100 (L)
1	2.01	111.2	109	4	8100	8.2	155.1	151.8	30800	1.7695
2	2	110.9	109.1	2	8061	9.5	108.85	154.9	19800	1.7708

. It can be seen from Table 9 and Table 10 that when w₁ decreases from 0.2 to 0.15, the corresponding objective t₁₀₀ increases from 8.2 to 9.5. When w₂ decreases from 0.2 to 0.15, the corresponding objective V_veh,max decreases from 133.28 to 108.85. When w₅ increases from 0.2 to 0.3, the corresponding objective C_hess decreases from 30,800 to 19,800. Some of the multi objectives are sensitive to their weights. The weight of each objective can be selected according to the importance of each objective.

The optimization of HESS EV in ADVISOR software is realized by the direct optimization algorithm, which directly uses a large number of simulations and compares the results, so as to obtain the optimal solution or approximate optimal solutions. Compared with GA algorithm optimization, the direct optimization algorithm of the HESS EV takes longer time, but the optimization effect is poor, and it is difficult to find a better solution. Compared with direct optimization algorithm, the GA algorithm has a stronger optimization ability, and the single objective is more sensitive to its corresponding weight.

5. Conclusions

Due to the nonlinear and strong coupling relationship between BT and SC HESS EV sizing parameters and control strategy parameters and the EV’s performances, driving range, and price, as well as the different preferences of different consumers, the GA algorithm is used to study the multiobjective optimization of an HESS EV. A Li-ion semi-active HESS and optimal energy control strategy were presented for the EVs. A multiobjective optimization problem is analyzed based on the ADVISOR software in the MATLAB environment. The multi objectives include energy consumption over 100 km, acceleration time from 0–100 km per hour, maximum speed, running range, and HESS cost of an EV, and the ADVISOR software is used to obtain them. The scaled factors of BT capacity, the series number of Li-ion BTs, the series number of SCs, the parallel number of SCs, and charge power of the SCs are chosen as optimization variables. The optimization results show that the weights are sensitive to their objectives. The proposed optimization method is practical for a Li-ion BT and SC HESS EV.