Two-Stage Energy Management Strategies of Sustainable Wind-PV-Hydrogen-Storage Microgrid Based on Receding Horizon Optimization
Abstract
:1. Introduction
- (1)
- A two-stage energy management model based on receding horizon optimization is proposed to tackle the uncertainties and randomness of renewable energies and loads, as well as to minimize the operation cost.
- (2)
- The day-ahead optimization is performed to minimize the overall operation cost, while the intra-day optimization model is carried out to trace the day-ahead schemes and minimize the deviations of the intra-day and the day-ahead operation strategies.
- (3)
- The roles of battery storage in reducing operation cost and improving the performance of the energy management model have been explored and demonstrated.
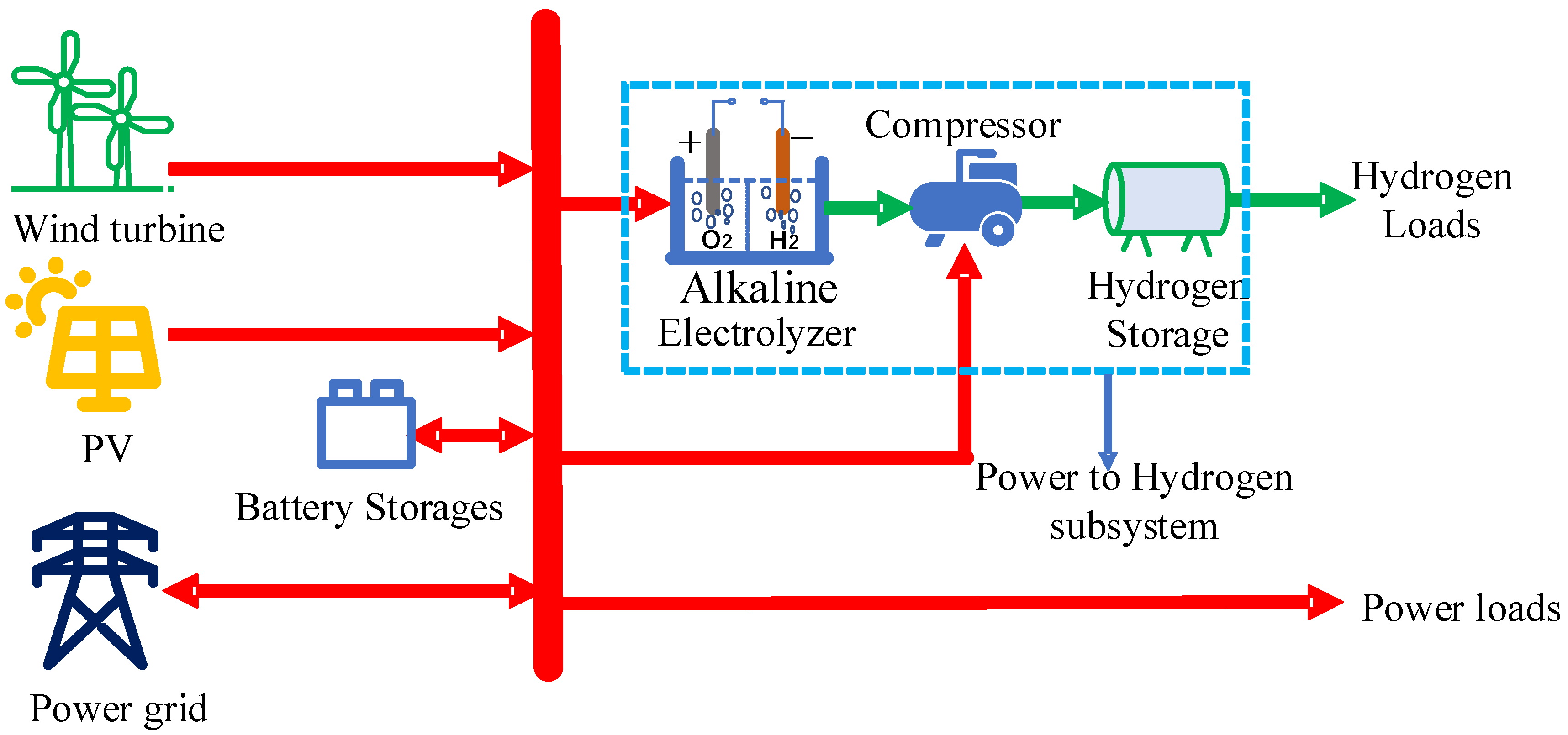
2. The Sustainable Wind-PV-Hydrogen-Storage Microgrid
2.1. The Wind Turbine Model
2.2. The PV Model
2.3. The Battery Storage Model
2.4. The Power-to-Hydrogen Subsystem Model
2.4.1. The Model of Electrolyzer
2.4.2. The Model of Hydrogen Compressor
2.4.3. The Model of Hydrogen Storage Tank
3. The Two-Stage Energy Management Model
3.1. The Day-Ahead Optimization Model
3.2. The Intra-Day Optimization Model
4. Numerical Analysis
4.1. Basic Parameter Settings
4.2. The Analysis and Discussions of the Simulation Results
4.2.1. The Day-Ahead Simulation Results
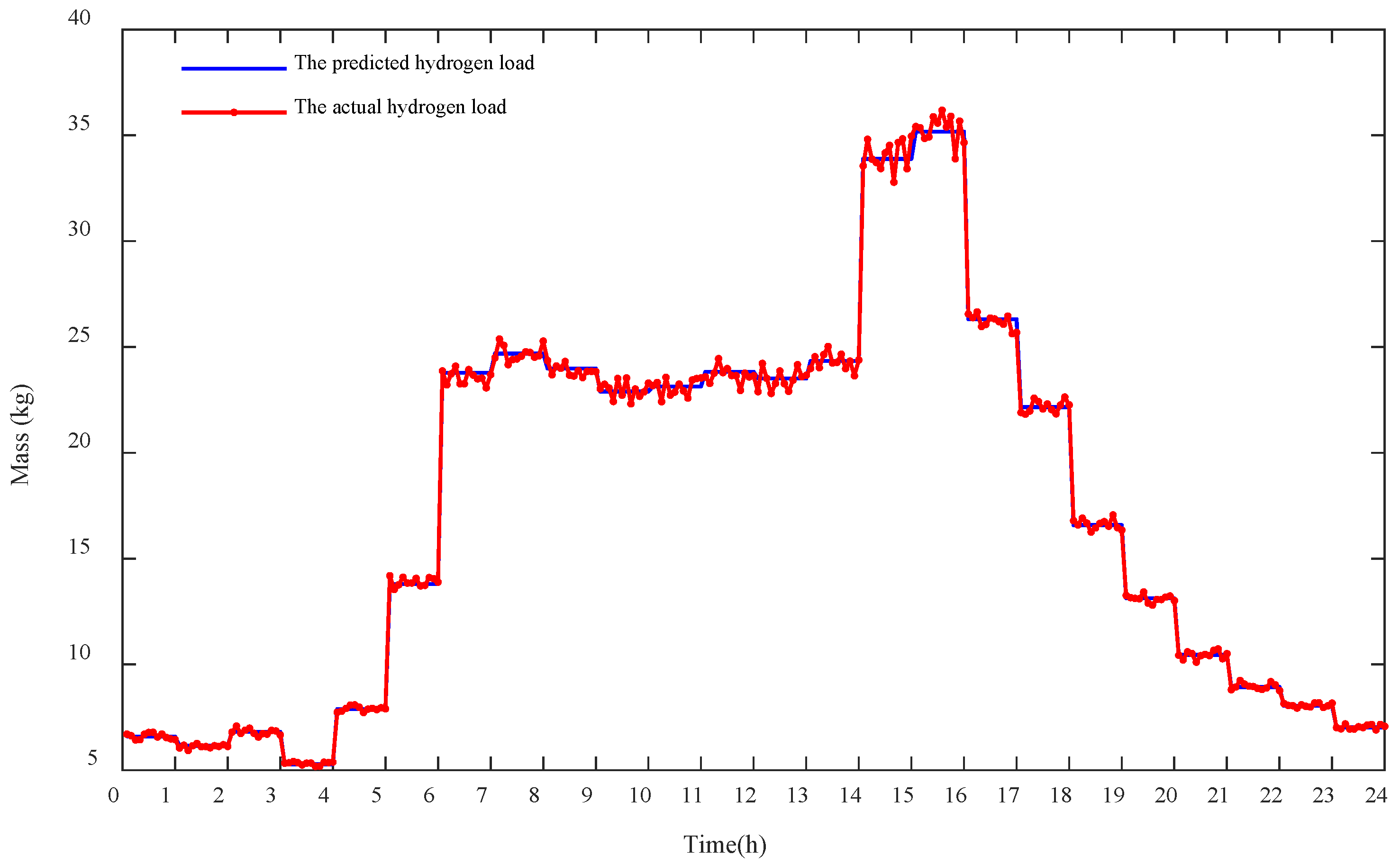
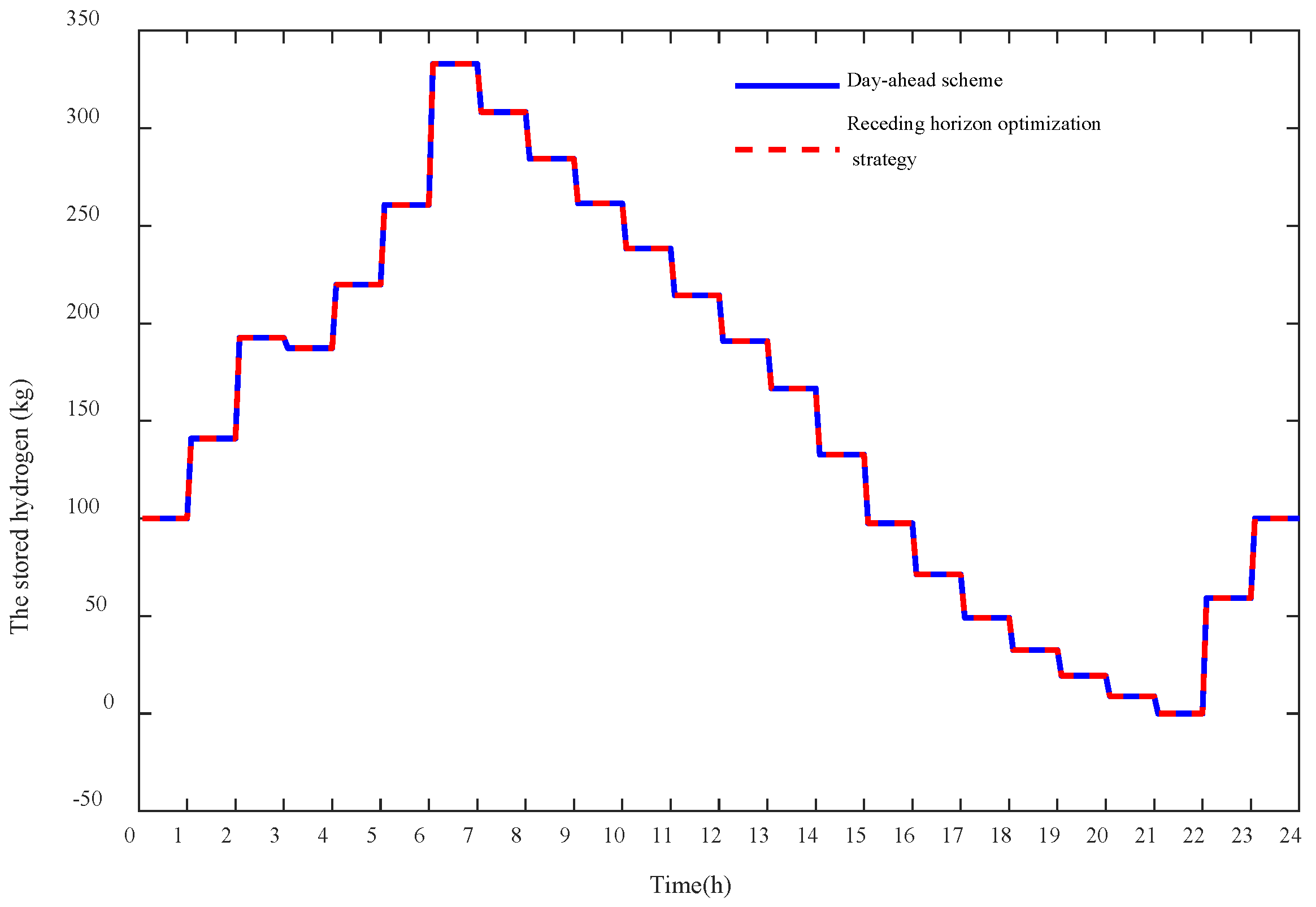
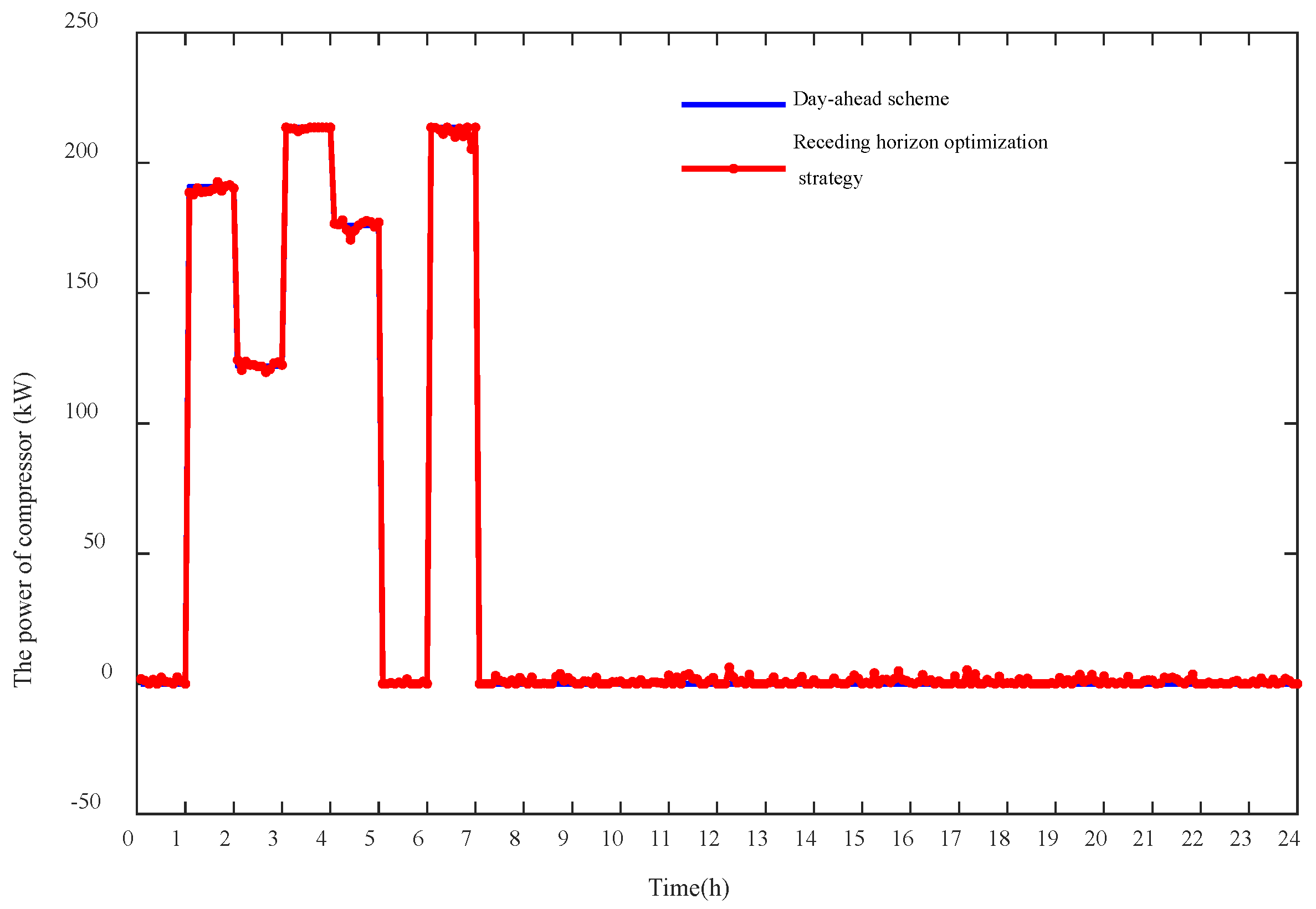
4.2.2. The Intra-Day Simulation Results
4.2.3. The Simulation Results of WPHS Microgrid without Battery Storage
5. Conclusions
- (1)
- The proposed two-stage optimization is effective in managing the operation of the micro and eliminating the uncertainties and fluctuations of WT, PV and loads. The day-ahead optimization can effectively coordinate the operations of the WT, PV, battery storage and power-to-hydrogen subsystems, and realize the high-efficiency operations. The intra-day optimization model is able to improve the operation stability of the WPHS microgrid and eliminate the adverse influence of the fluctuations of WT, PV, power and hydrogen demands.
- (2)
- The proposed two-stage energy management model is robust and effective in coordinating the operation of the sustainable WHP microgrid, and intra-day receding horizon optimization strategies can effectively trace the day-ahead schemes. In addition, the battery storage can reduce the operation cost dramatically by 12.85%, as well as alleviate the fluctuations of the exchanged power with the power grid, and the maximum deviation of the exchanged power between the day-ahead and intra-day strategies is reduced by 12.77% when the battery storage is considered.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Abbreviations
| PV | Photovoltaic | WT | Wind turbine |
| WPHS | Wind-PV-hydrogen-storage | WPH | Wind-PV-hydrogen |
| Parameters and variables of wind turbine model | |||
| Outpower of WT at time slot t | Rated power of WT | ||
| Wind speed at time slot t | Cut-in wind speed | ||
| Cut-out wind speed | Rated wind speed of wind turbine | ||
| Parameters and variables of PV model | |||
| Outpower of PV array | Number of PV panes | ||
| Standard irradiance | Rated power of each PV panel at standard test conditions | ||
| Irradiance at time slot t | Temperature at time slot t | ||
| Parameters and variables of battery storage model | |||
| Energy stored in the batteries at time slot t | Minimum capacity of battery storages | ||
| Maximum capacity of battery storages | Charging power at time slot t | ||
| Discharging power at time slot t | Maximum charging power | ||
| Maximum discharging power | Binary variable | ||
| Parametersand variables of power-to-hydrogen system | |||
| Hydrogen production rate | Maximum power of electrolyzer | ||
| Hydrogen mass-produced at time slot t | Power consumed by electrolyzer at time slot t | ||
| Specific heat of hydrogen at constant pressure | Inlet hydrogen temperature | ||
| Efficiency of compressor | Compression ratio of hydrogen | ||
| Maximum power of compressor | Hydrogen flow rate through compressor at time | ||
| Isentropic exponent of hydrogen | Stored hydrogen mass in the hydrogen tank at time slot t | ||
| Hydrogen load at time slot t | Capacity of hydrogen tank | ||
| Minimum ratio of the rated capacity of hydrogen tank | Maximum ratio of the rated capacity of hydrogen tank | ||
| Variables of the two-stage energy management model | |||
| Day-ahead comprehensive operation cost | Operational and maintenance costs of PV | ||
| Operational and maintenance costs of WT | Degradation costs of battery storage | ||
| Degradation costs of electrolyzer | Net energy cost | ||
| Maintenance cost coefficient of PV | Maintenance cost coefficient of WT | ||
| Degradation cost coefficient of battery storage | Degradation cost coefficient of electrolyzer | ||
| Buying power from the power grid at time slot t | Selling power to the power grid at time slot t | ||
| Predicted power load at time slot t | Binary variable | ||
| Hydrogen production at time slot | Power consumed by electrolyzer device at time slot | ||
Appendix A
References
- Lux, B.; Pfluger, B. A supply curve of electricity-based hydrogen in a decarbonized European energy system in 2050. Appl. Energy 2020, 269, 115011. [Google Scholar] [CrossRef]
- Rabiee, A.; Keane, A.; Soroudi, A. Technical barriers for harnessing the green hydrogen: A power system perspective. Renew. Energy 2021, 163, 1580–1587. [Google Scholar] [CrossRef]
- El-Taweel, N.A.; Khani, H.; Farag, H.E.Z. Hydrogen Storage Optimal Scheduling for Fuel Supply and Capacity-Based Demand Response Program under Dynamic Hydrogen Pricing. IEEE Trans. Smart Grid 2019, 10, 4531–4542. [Google Scholar] [CrossRef]
- Wu, X.; Qi, S.; Wang, Z.; Duan, C.; Wang, X.; Li, F. Optimal scheduling for microgrids with hydrogen fueling stations considering uncertainty using data-driven approach. Appl. Energy 2019, 253, 113568. [Google Scholar] [CrossRef]
- Ulleberg, Ø. Modeling of advanced alkaline electrolyzers: A system simulation approach—ScienceDirect. Int. J. Hydrogen Energy 2003, 28, 21–33. [Google Scholar] [CrossRef]
- Bernal-Agustín, J.L.; Dufo-López, R. Techno-economical optimization of the production of hydrogen from PV-Wind systems connected to the electrical grid. Renew. Energy 2010, 35, 747–758. [Google Scholar] [CrossRef]
- Wu, X.; Li, H.; Wang, X.; Zhao, W. Cooperative Operation for Wind Turbines and Hydrogen Fueling Stations with On-Site Hydrogen Production. IEEE Trans. Sustain Energy 2020, 11, 2775–2789. [Google Scholar] [CrossRef]
- Ma, T.; Pei, W.; Deng, W.; Xiao, H.; Yang, Y.; Tang, C. A Nash bargaining-based cooperative planning and operation method for wind-hydrogen-heat multi-agent energy system. Energy 2022, 239, 122435. [Google Scholar] [CrossRef]
- Mohseni, S.; Brent, A.C.; Burmester, D. A comparison of metaheuristics for the optimal capacity planning of an isolated, battery-less, hydrogen-based micro-grid. Appl. Energy 2020, 259, 114224. [Google Scholar] [CrossRef]
- Petrollese, M.; Valverde, L.; Cocco, D.; Cau, G.; Guerra, J. Real-time integration of optimal generation scheduling with MPC for the energy management of a renewable hydrogen-based microgrid. Appl. Energy 2016, 166, 96–106. [Google Scholar] [CrossRef]
- Appino, R.R.; Wang, H.; Ordiano, J.G.; Faulwasser, T.; Mikut, R.; Hagenmeyer, V.; Mancarella, P. Energy-based stochastic MPC for integrated electricity-hydrogen VPP in real-time markets. Electr. Power Syst. Res. 2021, 195, 106738. [Google Scholar] [CrossRef]
- Shi, M.; Wang, H.; Lyu, C.; Xie, P.; Xu, Z.; Jia, Y. A hybrid model of energy scheduling for integrated multi-energy microgrid with hydrogen and heat storage system. Energy Rep. 2021, 7, 357–368. [Google Scholar] [CrossRef]
- Li, Q.; Member, S.; Zou, X.; Pu, Y.; Member, S.; Chen, W. A real-time energy management method for electric-hydrogen hybrid energy storage microgrid based on DP-MPC. CSEE J. Power Energy Syst. 2020. [Google Scholar] [CrossRef]
- Garcia-Torres, F.; Bordons, C. Optimal Economical Schedule of Hydrogen-Based Microgrids With Hybrid Storage Using Model Predictive Control. IEEE Trans. Ind. Electron. 2015, 62, 5195–5207. [Google Scholar] [CrossRef]
- Zhang, Y.; Campana, P.E.; Lundblad, A.; Yan, J. Comparative study of hydrogen storage and battery storage in grid connected photovoltaic system: Storage sizing and rule-based operation. Appl. Energy 2017, 201, 397–411. [Google Scholar] [CrossRef]
- Möller, M.C.; Krauter, S. Hybrid Energy System Model in Matlab/Simulink Based on Solar Energy, Lithium-Ion Battery and Hydrogen. Energies 2022, 15, 2201. [Google Scholar] [CrossRef]
- Alotaibi, M.A.; Eltamaly, A.M. A Smart Strategy for Sizing of Hybrid Renewable Energy System to Supply Remote Loads in Saudi Arabia. Energies 2021, 14, 7069. [Google Scholar] [CrossRef]
- Tomczewski, A.; Kasprzyk, L. Optimisation of the Structure of a Wind Farm—Kinetic Energy Storage for Improving the Reliability of Electricity Supplies. Appl. Sci. 2018, 8, 1439. [Google Scholar] [CrossRef] [Green Version]
- Tomczewski, A.; Kasprzyk, L.; Nadolny, Z. Reduction of Power Production Costs in a Wind Power Plant–Flywheel Energy Storage System Arrangement. Energies 2019, 12, 1942. [Google Scholar] [CrossRef] [Green Version]
- Kasprzyk, L.; Tomczewski, A.; Pietracho, R.; Mielcarek, A.; Nadolny, Z.; Tomczewski, K.; Trzmiel, G.; Alemany, J. Optimization of a PV-Wind Hybrid Power Supply Structure with Electrochemical Storage Intended for Supplying a Load with Known Characteristics. Energies 2020, 13, 6143. [Google Scholar] [CrossRef]
- Soroudi, A.; Aien, M.; Ehsan, M. A probabilistic modeling of photo voltaic modules and wind power generation impact on distribution networks. IEEE Syst. J. 2012, 6, 254–259. [Google Scholar] [CrossRef] [Green Version]
- Xu, L.; Ruan, X.; Mao, C.; Zhang, B.; Luo, Y. An improved optimal sizing method for wind-solar-battery hybrid power system. IEEE Trans. Sustain. Energy 2013, 4, 774–785. [Google Scholar]
- Korpas, M.; Holen, A.T. Operation planning of hydrogen storage connected to wind power operating in a power market. IEEE Trans. Energy Convers. 2006, 21, 742–749. [Google Scholar] [CrossRef]
- Gökçek, M.; Kale, C. Techno-economical evaluation of a hydrogen refuelling station powered by Wind-PV hybrid power system: A case study for İzmir-Çeşme. Int. J. Hydrogen Energy 2018, 43, 10615–10625. [Google Scholar] [CrossRef]
- El-Taweel, N.A.; Khani, H.; Farag, H.E.Z. Optimal Sizing and Scheduling of LOHC-Based Generation and Storage Plants for Concurrent Services to Transportation Sector and Ancillary Services Market. IEEE Trans. Sustain. Energy 2020, 11, 1381–1393. [Google Scholar] [CrossRef]
- Maleki, A.; Hafeznia, H.; Rosen, M.A.; Pourfayaz, F. Optimization of a grid-connected hybrid solar-wind-hydrogen CHP system for residential applications by efficient metaheuristic approaches. Appl. Therm. Eng. 2017, 123, 1263–1277. [Google Scholar] [CrossRef]
- Han, S.; Han, S.; Aki, H. A practical battery wear model for electric vehicle charging applications. Appl. Energy 2014, 113, 1100–1108. [Google Scholar] [CrossRef]
- Kim, K.; Choi, Y.; Kim, H. Data-driven battery degradation model leveraging average degradation function fitting. Electron. Lett. 2017, 53, 102–104. [Google Scholar] [CrossRef]
- Kim, H.; Lee, J.; Bahrami, S.; Wong, V.W.S. Direct Energy Trading of Microgrids in Distribution Energy Market. IEEE Trans. Power Syst. 2020, 35, 639–651. [Google Scholar] [CrossRef]
- Urgaonkar, R.; Urgaonkar, B.; Neely, M.J.; Sivasubramaniam, A. Optimal power cost management using stored energy in data centers. In Proceedings of the ACM SIGMETRICS, San Jose, CA, USA, 7–11 June 2011; pp. 221–232. [Google Scholar]
- Wang, H.; Huang, J. Incentivizing Energy Trading for Interconnected Microgrids. IEEE Trans. Smart Grid 2018, 9, 2647–2657. [Google Scholar] [CrossRef] [Green Version]
- Eltamaly, A.M.; Alotaibi, M.A.; Elsheikh, W.A.; Alolah, A.I.; Ahmed, M.A. Novel Demand Side-Management Strategy for Smart Grid Concepts Applications in Hybrid Renewable Energy Systems. In Proceedings of the 2022 4th International Youth Conference on Radio Electronics, Electrical and Power Engineering (REEPE), Moscow, Russian, 17–19 March 2022; pp. 1–7. [Google Scholar] [CrossRef]
- Xiao, H.; Pei, W.; Li, K. Multi-time Scale Coordinated Optimal Dispatch of Microgrid Based on Model Predictive Control. Autom. Electr. Power Syst. 2016, 40, 7–14. [Google Scholar]
- Ma, T.; Pei, W.; Xiao, H.; Li, D.; Lyu, X.; Hou, K. Cooperative Operation Method for Wind-solar-hydrogen Multi-agent Energy System Based on Nash Bargaining Theory. Proceeding CSEE 2021, 41, 25–39. [Google Scholar]
- Du, Y.; Pei, W.; Chen, N.; Ge, X.; Xiao, H. Real-time microgrid economic dispatch based on model predictive control strategy. J. Mod. Power Syst. Clean Energy 2017, 5, 787–796. [Google Scholar] [CrossRef]
- Zheng, Q.P.; Wang, J.; Liu, A.L. Stochastic Optimization for Unit Commitment—A Review. IEEE Trans. Power Syst. 2015, 30, 1913–1924. [Google Scholar] [CrossRef]













| Time Slots | Buying Price | Selling Price |
|---|---|---|
| 01:00–07:00, 23:00–24:00 | 0.3376 | 0.4 |
| 12:00–14:00, 19:00–22:00 | 0.8654 | 0.4 |
| 08:00–11:00, 15:00–18:00 | 0.5980 | 0.4 |
| 0.0192 | 0.7 | 5700 kWh | 200 kW | ||||
| 5000 kW | κ | 1.4 | 600 kWh | 100 kW | |||
| 6000 kW | 0 kg | 600 kWh | 10 kW | ||||
| 14.304 | 1000 kg | 2100 kW | 200 kW | ||||
| Tin | 40 °C | 500 kW | 2400 kW |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Li, D.; Lv, X.; Meng, X.; Zhang, J.; Ma, T.; Pei, W.; Xiao, H. Two-Stage Energy Management Strategies of Sustainable Wind-PV-Hydrogen-Storage Microgrid Based on Receding Horizon Optimization. Energies 2022, 15, 2861. https://doi.org/10.3390/en15082861
Wang J, Li D, Lv X, Meng X, Zhang J, Ma T, Pei W, Xiao H. Two-Stage Energy Management Strategies of Sustainable Wind-PV-Hydrogen-Storage Microgrid Based on Receding Horizon Optimization. Energies. 2022; 15(8):2861. https://doi.org/10.3390/en15082861
Chicago/Turabian StyleWang, Jiarui, Dexin Li, Xiangyu Lv, Xiangdong Meng, Jiajun Zhang, Tengfei Ma, Wei Pei, and Hao Xiao. 2022. "Two-Stage Energy Management Strategies of Sustainable Wind-PV-Hydrogen-Storage Microgrid Based on Receding Horizon Optimization" Energies 15, no. 8: 2861. https://doi.org/10.3390/en15082861
APA StyleWang, J., Li, D., Lv, X., Meng, X., Zhang, J., Ma, T., Pei, W., & Xiao, H. (2022). Two-Stage Energy Management Strategies of Sustainable Wind-PV-Hydrogen-Storage Microgrid Based on Receding Horizon Optimization. Energies, 15(8), 2861. https://doi.org/10.3390/en15082861






