Application of Artificial Intelligence in the Unit Commitment System in the Application of Energy Sustainability
Abstract
1. Introduction
- Energy savings (electricity).
- Reduction of CO2 emissions and air pollution.
- Energy efficiency, i.e., decoupling economic growth from energy consumption.
- Increased use of renewable energy sources (RES); which makes it possible to separate energy consumption from greenhouse gas emissions; which should be kept to a minimum.
- Focus on fulfilling energy sustainability and optimizing the performance balance of compact urban neighborhoods (clusters of buildings).
- Unit Commitment (UC) application, which is the process of deciding when and which sources of electricity, for example, in our case the local micro-network of RES, start and stop. This is an important task in the operation of the electricity system and the local island system. This is a system demand in a short period of time. On the other hand, such a restructured system can ensure the supply of electricity, for example, to a city district or city, and can be competitive while allowing consumers to choose an electricity supplier. UC systems are also characterized by sufficient storage and time-consuming calculations. The UC structure has in the past been defined as a schedule of production units to be in operation (on/off) in order to minimize total production costs while meeting all constraints, such as power consumption, minimum on and off time, etc. On the other hand, UC in Deregulatory environments is more complex and competitive than traditional UCs. Such models have been developed by examining the effects of the dynamic growth of electricity produced in the intermittent renewable energy target (RET) system [9]. In a previous study [10], an optimization method was proposed, which addressed the system of dynamic economic management of individual residential loads and charging stations for electric vehicles. In part, our test system has shown that shifting load-bearing loads can significantly flatten the load profile and reduce peaks.
- It is based on the amendment to Directive 2010/31/EU on energy performance in the part of definitions and interpretations of terms. The term “technical building system” includes technical equipment for heating, cooling, ventilation, domestic water heating, built-in lighting, building automation and control, on-site electricity generation, or a combination thereof, including systems using renewable energy from the building or building unit. The definition of a technical system is, therefore, extended to include local electricity generation and automation and control systems, which are further defined as systems consisting of all products, software and engineering services that provide automatic control or facilitate manual operation.
- A major transformation is currently underway to reduce climate change, energy consumption and CO2 emissions. Another important stage of energy infrastructure is to achieve carbon neutrality for the Czech Republic (CR) in electricity generation by 2050. It is about ensuring the replacement of brown coal in the Czech heating industry by 2030 and 2040 at the latest, using alternative energy sources, especially photovoltaic systems. Energy is one of the most affected sectors. The sector now faces many new challenges, including greater use of flexibility from smaller sources, especially RES. As for the flexibility itself, it can be used to ensure energy balance in the system (micro-RES networks), energy trade, or manage its own fluctuations.
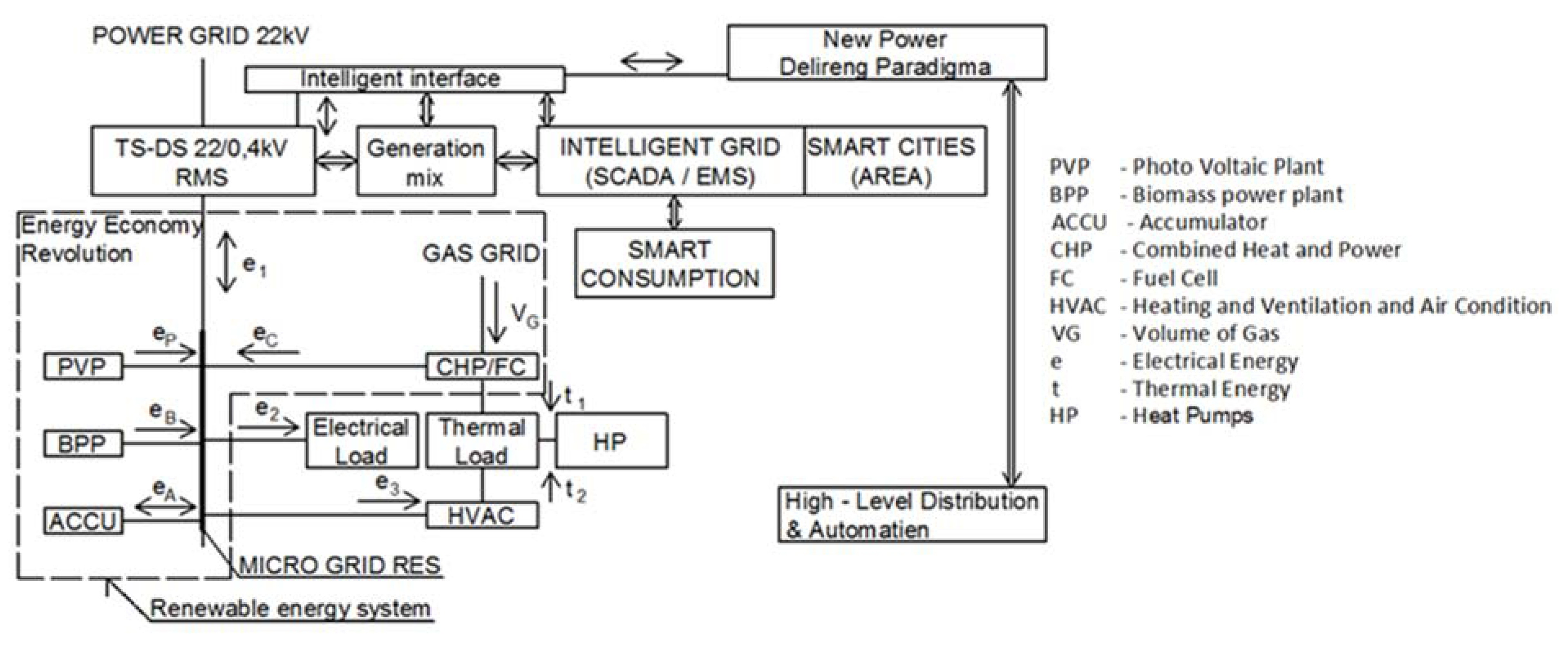
- Design of a micro-network of RES with decentralization of sustainable energy in a defined urban area (cluster of buildings) with the application of an artificial intelligence automated unit commitment (UC) system on the RES platform to optimize power balance (balancing the immediate deviation between production and consumption).
2. Materials and Methods
2.1. RES Unit Commitment to Optimize the Performance Balance
2.1.1. Unit Commitment Problem in the RES Energy System
- Energy balance of the system
- Energy and power exchange
- Backup requirements
- Energy generation limits of given units (RES)
- : Total operating costs of the energy system
- : Output energy from the i-th unit in t hours
- Fuel cost of the i-th unit in t hours
- Power generation ratio and its capability
- Total number of units in the system
- The total time for which UC is performed
- Output of the i-th unit in an hour of t
- Maximum output power of the i-th unit
- Minimum output power of the i-th unit
- Initial cost of the i-th unit in t hours
2.1.2. Teoretika Assumptions for Slovník the Unit Commitment of Our Experiment
- —total output of the RES microgrid
- —total power consumed
- —total power loss
- —power of the i-th source of RES at time t
- —output power of RES microgrid
- —power consumed
- —nominal power of RES, where the variable P is expressed as Pi
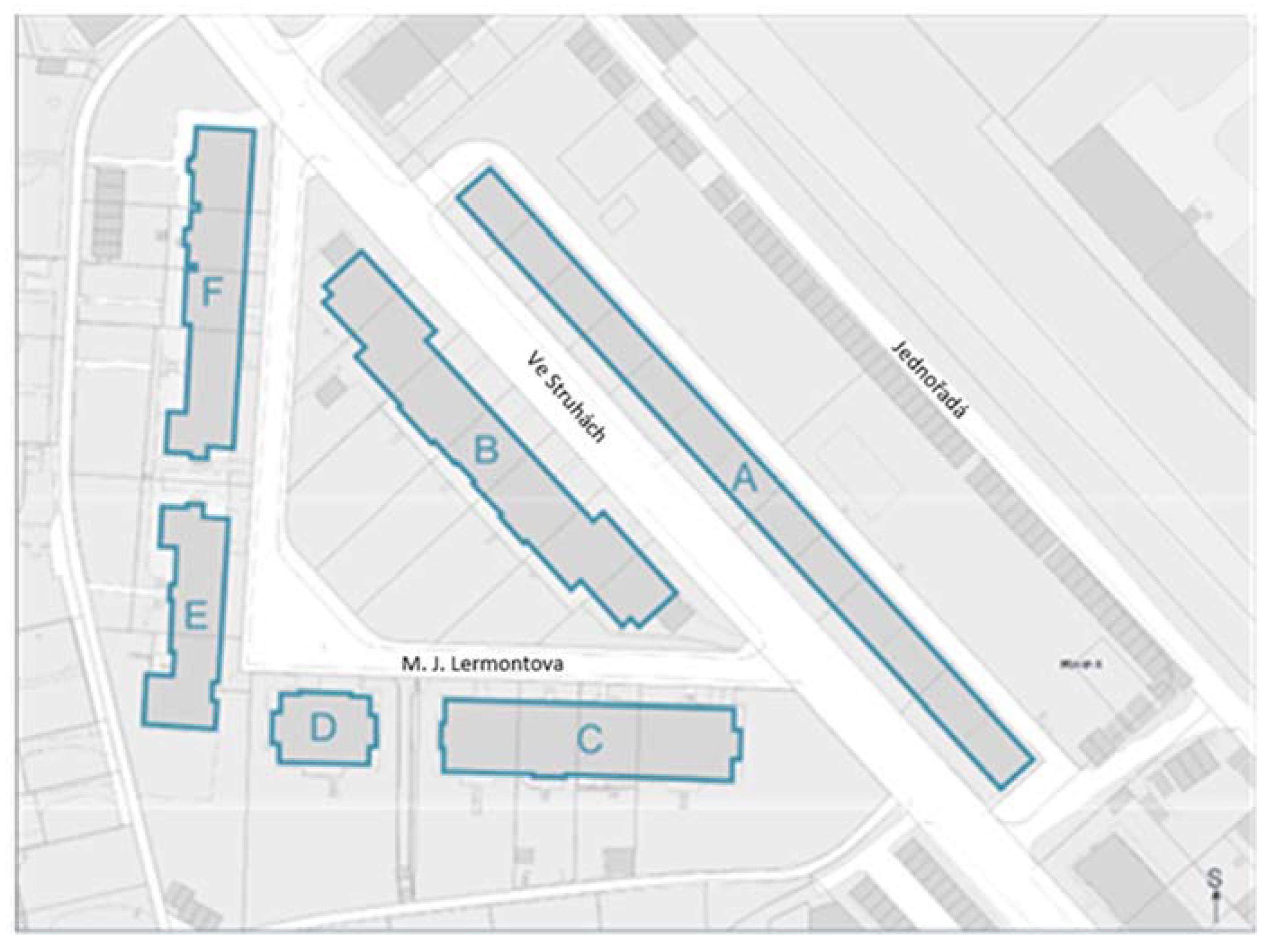
- —is the output power of the i-th RES (i = 1 to 8; we have a total of 6 sources of photovoltaic systems FV1 to FV6 located on the residential units A, B, C, D, E and F, as well as cogeneration and substation TS-DS) in time t
- —power state of the i-th source at time t
- —cost coefficients (downtime) and time constant exp. the increase in the initial costs of the i-th source at time t
- —costs depending on the output produced, —costs dependent on heat loss (Joule heat), a —costs caused by iron losses and friction.
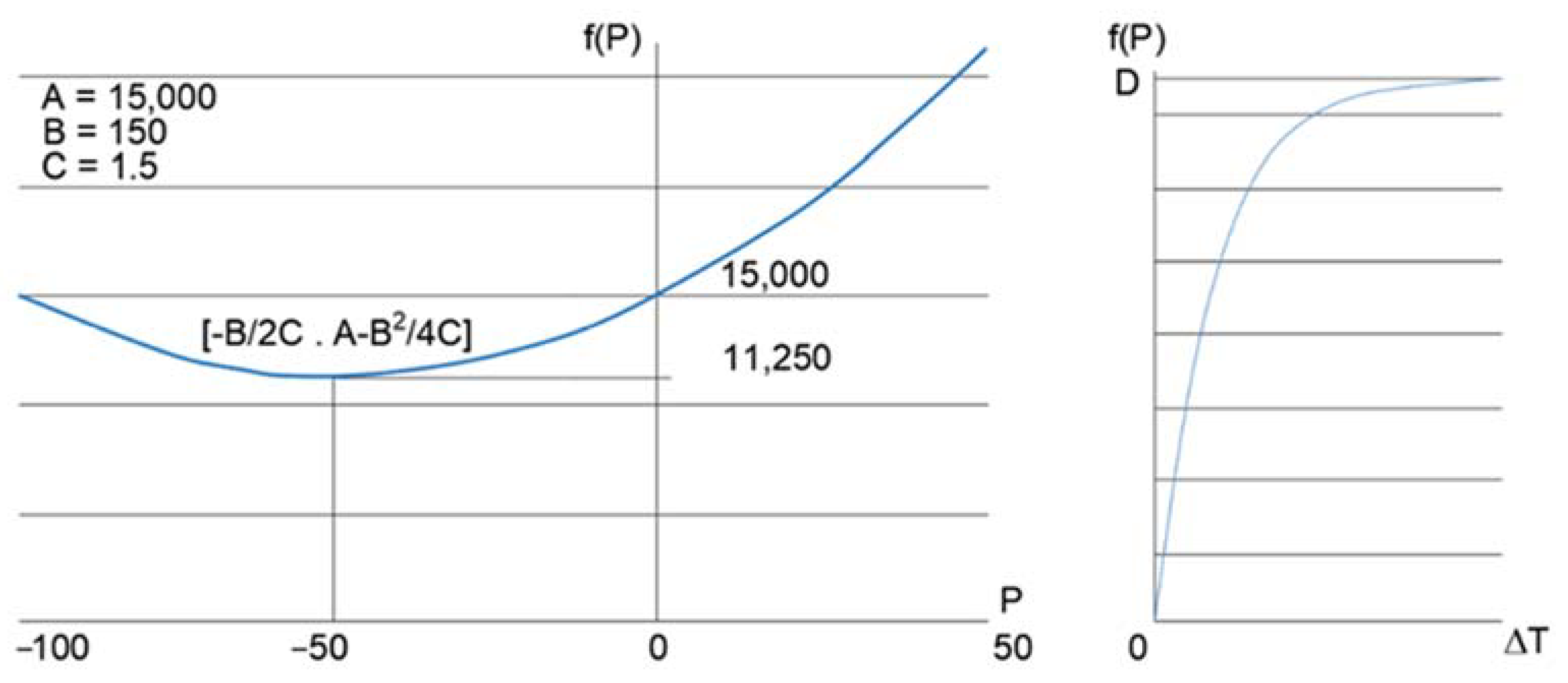
- (a)
- The first sum in relation (14) , expresses operating costs.
- (b)
- The second summand in relation (14) , expresses the so-called start-up costs.
- (a)
- operating costs
- (b)
- start-up costs
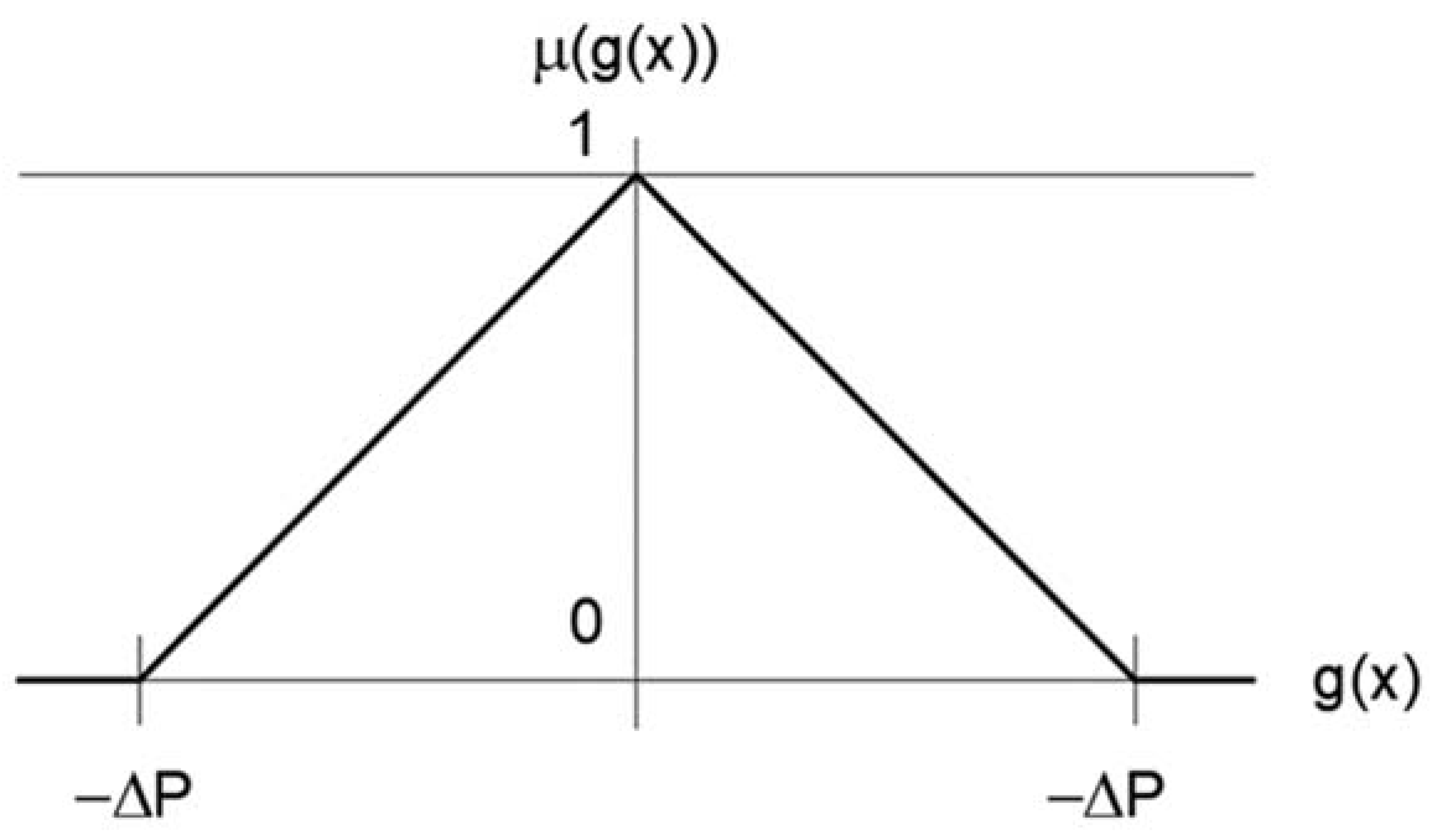
- is the fuzzy number zero Figure 6;
- is the maximum permissible tolerance for the balance.
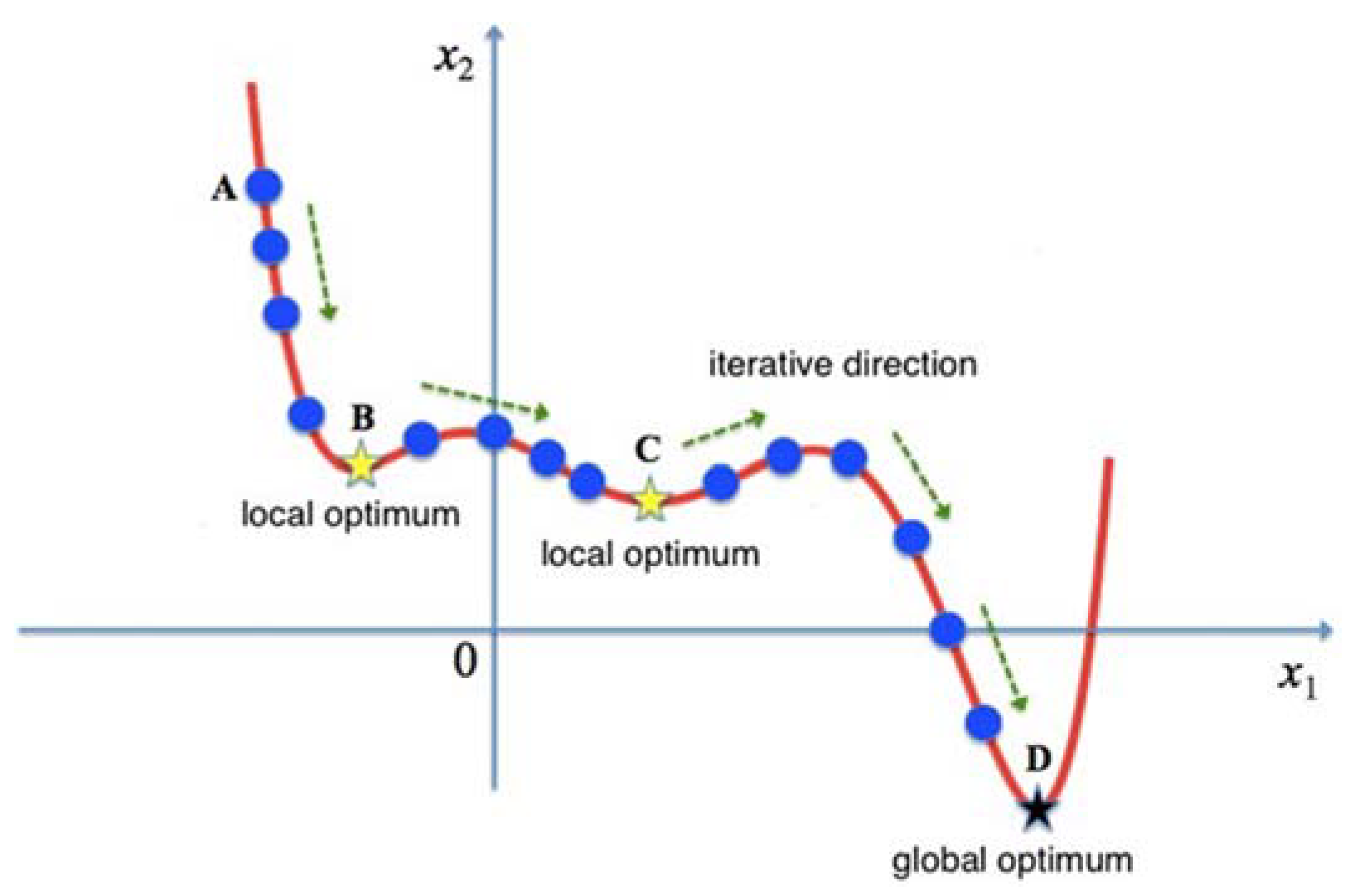
2.2. Application of the Simulated Annealing Algorithm in Our Experiment
| Algorithm 1. Procedure Metropolis algorithm. |
| Input: , |
| #Metropolis Algoritmus |
| def MetropolisAlgorithm(xini, kmax, t): |
| self.k = 0 |
| self.x = xini |
| while self.k < kmax |
| self.k++ |
| self.xt = Opert(self.x) |
| self.pr = min(1, exp(−(f(self.xt) − f(self.x))/t)) |
| if random() < self.pr: |
| self.x = self.xt |
| return self.x |
| Algorithm 2. SA procedure. |
| Input: , , |
| # Simulated annealing |
| def SimulatedAnnealing(tmin, tmax, kmax): |
| self.xout = RandomVegueStated (D) |
| self.T = Tmax |
| while self.T > Tmin: |
| self.xout = MetropolisAlgorithm(self.xout, xout, kmax, T) |
| self.T = change(self.T) |
| return self.xout |
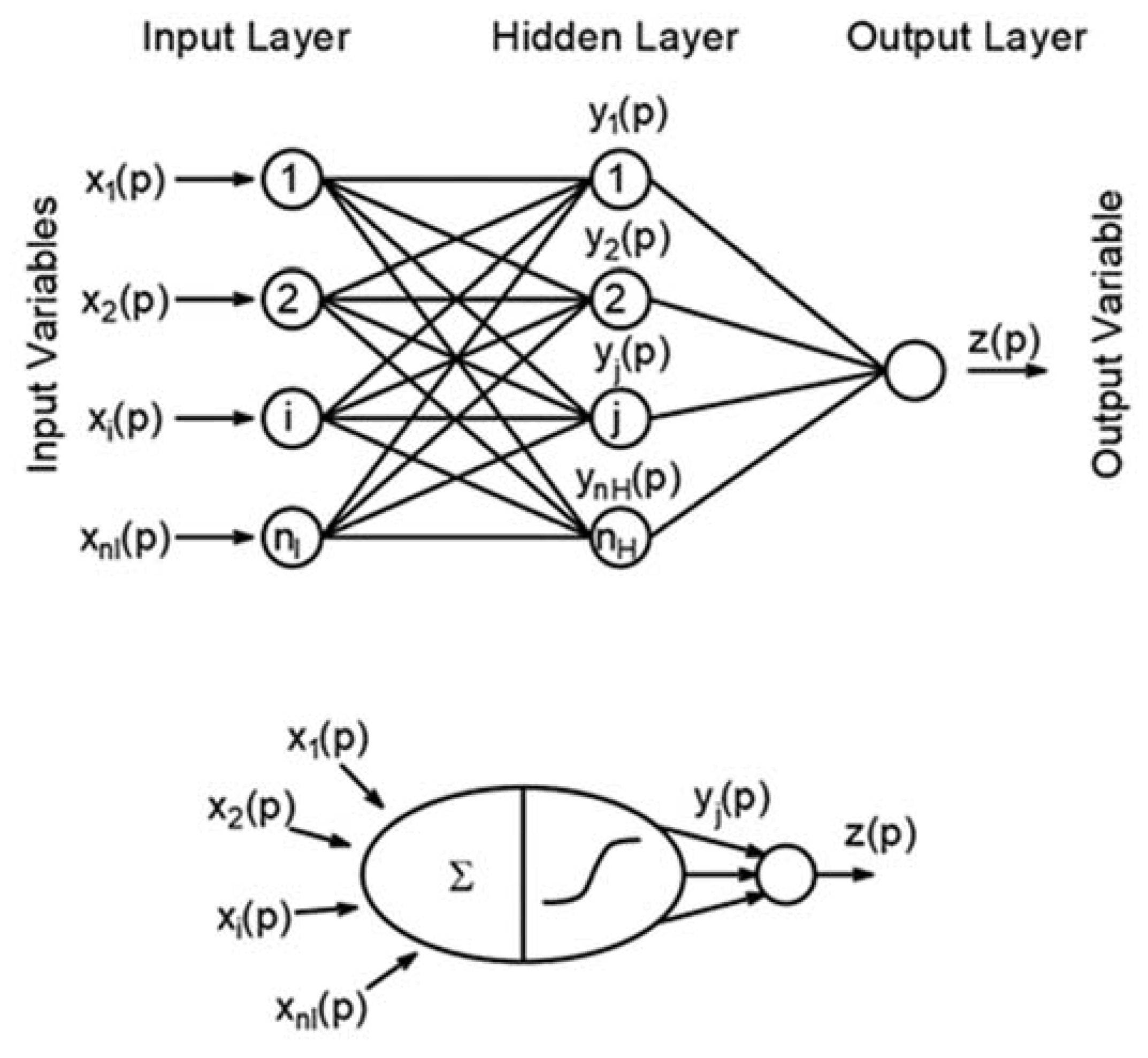
2.3. Artificial Neural Network in the Application of Energy Consumption Diagnostics and Kohonen Maps
- —V-a set of points (neurons), or a population of neurons
- —a group of network edges, called synapses
- —display of edge–vertex incidence
- —dynamic edge evaluation
- —dynamic vertex rating
- The neuron excitation is between and , where the value of means full excitation of the neuron as opposed to a value of “0”, which corresponds to a state of inhibition (damping),
- If the internal potential of the neuron approaches the value , the so-called complete excitation of the neuron will occur, then this will mean
- Conversely, if the internal potential approaches the value of , then full inhibition of the neuron occurs, i.e.,
2.3.1. Competitive Network Model
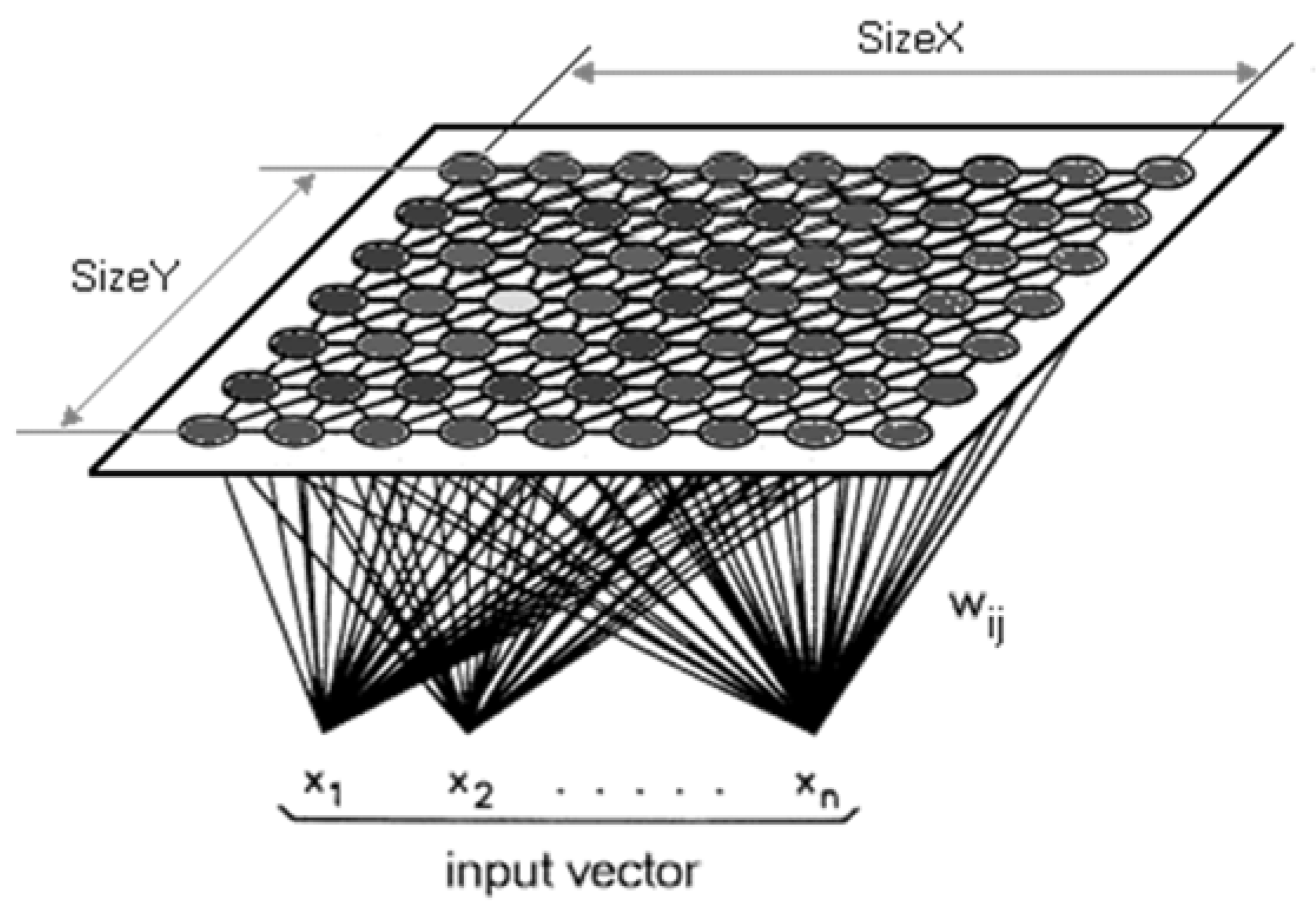
2.3.2. Kohonen Network
3. Results
3.1. Experiment, Interpretation of Problems and Results
3.1.1. Experiment Description and Assignment
3.1.2. Experiment TDD Energy Consumption, Kohonen Map Application
3.1.3. Experiment Proposal for Unit Commitment of the RES Micro-Network in the Given Area
| Algorithm 3. Part of the source code of the purpose function value calculation (20) |
| for (j = 2; j <= nt + 1; j++): |
| for j in range (2, nt + 2): # iterace 2 až nt + 1 |
| for iter in range(1, n+1): |
| i = random(seed) * (ng − 1) + 1 |
| ij = (i − 1)*(nt + 1) + j |
| if x(ij) == 0: |
| if random(seed) < Ponoff: |
| x(ij) = 1 |
| else: |
| if random(seed) < Ponoff: |
| x(ij) = 0 |
| i = random(seed) * (ng − 1) + 1 |
| ij = (i − 1) * (nt + 1) + j |
| p(ij) = random(seed) * (Pmax(i) − Pmin(i)) + Pmin(i) |
3.1.4. Analysis of Experimental Process Results
4. Discussion
- (a)
- Heating: In this case, the energy consumption due to building renovation in the given area decreased by 54.9%, i.e., almost twice for the type of block and by 75.50%, i.e., almost four times for the block of flats.
- (b)
- Hot water preparation: In this case, the energy consumption in the type of block increased by 3.7% even though the buildings in the given area were renovated. So, the energy consumption for hot water preparation was not affected. As for the energy consumption for hot water preparation in blocks of flats of the given area, there was a 6.66% reduction in energy consumption.
- (c)
- As for the reduction in electric power consumption due to building renovations in the given area, the results are as follows:
- Electric power consumption decreased by 7.27% in the type blocks.
- Electric power consumption decreased by 5.96% in the blocks of flats.
5. Conclusions
- Used artificial intelligence methods: cluster analysis, neural networks, Kokonem map and simulated annealing (as an optimization algorithm), in the design of UC solutions of local energy sources, such as RES have established themselves as a very effective chronological method of sustainable energy solutions within NZEB.
- Use in future practice: The fuzzy condition in UC design has been shown to be most effective when a restrictive condition has been adopted (21). UC has significant potential, especially in addressing energy savings and thus reducing emissions, such as CO2.
Funding
Conflicts of Interest
References
- Streimikiene, D.; Balezentiene, L. Assessment of Electricity Generation Technologies Based on GHG Emission Reduction Potential and Costs. Transform. Bus. Econ. 2012, 11, 333–344. [Google Scholar]
- Streimikiene, D.; Mikalauskiene, A. Barakauskaite-Jakubauskiene. Sustainability Assessment of Policy Scenarios. Transform. Bus. Econ. 2011, 10, 165–168. [Google Scholar]
- Streimikienė, D.; Mikalauskienė, A.; Mikalauskas, I. Comparative Assessment of Sustainable Energy Development in the Czech Republic, Lithuania and Slovakia. J. Compet. 2016, 8, 31–41, ISSN 1804-171X (Print), ISSN 1804-1728 (On-line). [Google Scholar] [CrossRef]
- Cicea, C.; Marinescu, C.; Popa, I.; Dobrin, C. Environmental efficiency of investments in renewable energy: Comparative analysis at macroeconomic level. Renew. Sustain. Energy Rev. 2014, 30, 555–564. [Google Scholar] [CrossRef]
- Ibáñez-Forés, V.; Bovea, M.D.; Pérez-Belis, V. A holistic review of applied methodologies for assessing and selecting the optimal technological alternative from a sustainability perspective. J. Clean. Prod. 2014, 70, 259–281. [Google Scholar] [CrossRef]
- Vasauskaite, J.; Streimikiene, D. Review of Energy Efficiency Policies in Lithuania. Transform. Bus. Econ. 2014, 13, 628–643. [Google Scholar]
- Streimikiene, D.; Sarvutyte, M. Impact of renewables on employment in Lithuania. Transform. Bus. Econ. 2013, 11, 167–184. [Google Scholar]
- Banos, R.; Manzano-Agugliaro, F.; Montoya, F.G.; Gil, C.; Alcayde, A.; Gómez, J. Optimization methods applied to renewable and sustainable energy: A review. Renew. Sustain. Energy Rev. 2011, 15, 1753–1766. [Google Scholar] [CrossRef]
- Abujarad, S.Y.; Mustafa, M.W.; Jamian, J.J. Nedávné přístupy jednotkového závazku v přítomnosti občasných obnovitelných zdrojů energie: Přehled (Recent unit commitment approaches in the presence of intermittent renewable energy sources: Overview). Obnovit. Udržet. Energ. Rev. 2017, 70, 215–223. [Google Scholar]
- Rasoul, N.M.; Maigha, M.; Jhi-Young, J.; Crow, M.L. Multi-cílový dynamický ekonomický dispečink s řízením domácích zátěží a elektrických vozidel na straně poptávky (Multi-target dynamic economic dispatching with demand-side control of domestic loads and electric vehicles). Energies 2017, 10, 624. [Google Scholar]
- Zhanga, X.; Lovatib, M.; Vignab, I.; Widénc, J.; Hana, M.; Gala, C.; Fengd, T. A review of urban energy systems at building cluster level incorporating renewable-energy-source (RES) envelope solutions. Appl. Energy 2018, 230, 1034–1056. [Google Scholar] [CrossRef]
- Howell, S.; Rezgui, Y.; Hippolyte, J.-L.; Jayan, B.; Li, H. Towards the next generation of smart grids: Semantic and holonic multiagent management of distributed energy resources. Renew Sustain. Energy Rev. 2017, 77, 193–214. [Google Scholar] [CrossRef]
- Garlík, B. Energy Sustainability of a Cluster of Buildings with the Application of Smart Grids and the Decentralization of Renewable Energy Sources. Energies 2022, 15, 1649. [Google Scholar] [CrossRef]
- Chang, C.; Kuo, C.C. Network reconfiguration in distribution systems using Simulated annealing. Electr. Power Syst. Res. 1994, 29, 227–238. [Google Scholar] [CrossRef]
- GARLÍK, B. The Application of Aetificial Intelligence in the Process of optimizing Energy consuption in intelligent Areas. Neural Netw. World 2017, 27, 415–445. [Google Scholar] [CrossRef]
- Minoux, M. Matematické Programování: Teorie a Algoritmy (Mathematical Programming: Theory and Algorithms) (with a Foreword by Egon Balas); Translated by Steven Vajda from the French Edition (1983 Paris: Dunod.); Wiley-Interscience Publications: Chichester, UK, 1986; p. xxviii + 489. ISBN 978-0-471-90170-9. [Google Scholar]
- Yang, H.; Yang, P.; Huang, C. Evolutionary Programming Based Economic Dispatch with Non-Smooth Fuel Cost Functions. IEEE Trans. Power Syst. 1996, 11, 112–118. [Google Scholar] [CrossRef]
- Wood, A.J.; Wolleberg, B.F. Power Generation, Operation and Control; John Willey & Sons: New York, NY, USA, 1996. [Google Scholar]
- Momoh, J. Smart Grid Fundamentals of Design and Analysis; IEEE Press Series on Power Engineering Appears at the End of This Book; Wiley India Pvt. Ltd.: New Delhy, India, 2018. [Google Scholar]
- Walters, D.C.; Sheble, G.B. Genetic Algorithm Solution of Economic Dispatch with The Valve-point Loading. IEEE Trans. Power Syst. 1993, 8, 1325–1332. [Google Scholar] [CrossRef]
- Lin, W.M.; Cheng, F.S.; Tsay, M.T. An Improved Tabu Search For Economic Dispatch With Multiple Minima. IEEE Trans. Power Syst. 2002, 17, 108–112. [Google Scholar] [CrossRef]
- Lee, K.Y.; Sode-Yome, A.; Park, J.H. Adaptive Hopfield Neural Network For Economic Load Dispatch. IEEE Trans. Power Syst. 1998, 13, 519–526. [Google Scholar] [CrossRef]
- Eberhart, R.E.; Shi, Y. Comparing Inertia Weights and Factors in Particle Swarm Optimization. In Proceedings of the 2000 Congres on Evolutionary Computation, La Jolla, CA, USA, 16–19 July 2000; Volume I, pp. 84–88. [Google Scholar]
- Eberhart, R.E.; Shi, Y. Particle Swarm Optimization: Developments, Applications, and Resources. In Proceedings of the 2001 Congress on Evolutionary Computation, Seoul, Korea, 27–30 May 2001; Volume I, pp. 81–86. [Google Scholar]
- Van Laarhoven, P.J.; Aarts, E.H. Simulated annealing. In Simulated Annealing: Theory and Applications; Springer: Heidelberg/Berlin, Germany, 1987; pp. 7–15. [Google Scholar]
- Yu, H.; Fang, H.; Yao, P.; Yuan, Y. A combined genetic algorithm/simulated annealing algorithm for large scale system energy integration. Comput. Chem. Eng. 2000, 24, 2023–2035. [Google Scholar] [CrossRef]
- Jha, S.; Menon, V. BbmTTP: Beat-based parallel simulated annealing algorithm on GPGPUs for the mirrored traveling tournament problem. In Proceedings of the High-Performance Computing Symposium, Society for Computer Simulation International, Tampa, FL, USA, 13–16 April 2014; p. 3. [Google Scholar]
- Kabova, E.A.; Cole, J.C.; Korb, O.; López-Ibáñez, M.; Williams, A.C.; Shankland, K. Improved performance of crystal structure solution from powder diffraction data through parameter tuning of a simulated annealing algorithm. J. Appl. Crystallogr. 2017, 50, 1411–1420. [Google Scholar] [CrossRef]
- Assad, A.; Deep, K. A Hybrid Harmony search and Simulated Annealing algorithm for continuous optimization. Inf. Sci. 2018, 450, 246–266. [Google Scholar] [CrossRef]
- Zelinka, I.; Oplátková, Z.; Šeda, M.; Ošmera, P.; Včelař, F. Evoluční Výpočetní Techniky (Princip a Aplikace), (Evolutionary Computing (Principle and Application)); BEN-Technická Literature: Praha, Czech, 2009; ISBN 978-80-7300-218-3. [Google Scholar]
- Michalewicz, Z.; Fogel, D.B. How to solve it: Modern Heuritics, 2nd, revised and extended ed.; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Aarts, E.H.L.; Korst, J.H.M.; Michiels, W. Simulované žíhání (Simulated annealing). In Metodiky Vyhledávání (Search Methodology); Burke, E.K., Kendall, G., Eds.; Springer: New York, NY, USA, 2005; pp. 187–210. [Google Scholar]
- Novák, M.; Faber, J.; Kufudaki, O. Neuronové Sítě a Informační Systémy Živych Organism (Neural Networks and Information Systems of Living Organisms); Grada: Prague, Czech Republic, 1993; ISBN 80-58424-95-9. [Google Scholar]
- Grim, J.; Hájek, P.; Horaček, P.; Jiřina, M.; Kléma, J.; Kouba, Z.; Mařík, V.; Štěpánková, O.; Laţanský, J.; Kramosil, I.; et al. Umělá Inteligence (Artificial Intelligence) (3); Academia: Prague, Czech Republic, 2001; ISBN 80-200-0472-6. [Google Scholar]
- Řezanková, H.; Húsek, D.; Snášel, V. Shluková Analýza (Cluster Analysis); Kamil Msřík-Profesional Publishing: Praha, Czech Republic, 2009; ISBN 978-80-86946-81-8. [Google Scholar]
- Catalao, J.P.S.; Mariano, S.J.P.S.; Mendes, V.M.F.; Ferreira, L.A.F.M. Profit based unit commitment with emission limitation: A multi-objective approach. In Proceedings of the IEEE Power Tech, Lausanne, Switzerland, 1–5 July 2007; pp. 1417–1422. [Google Scholar]
- Lu, B.; Shahidehpour, M. Unit commitment with flexible generating units. IEEE Trans. Power Syst. 2005, 20, 1022–1034. [Google Scholar] [CrossRef]
- Wang, Y.; Xia, Q. A novel security stochastic unit commitment for wind thermal system operation. In Proceedings of the 4th International Conference on Electric Utility Deregulation and Restructuring and Power Technologies (DRPT), Weihai, China, 6–9 July 2011; pp. 386–393. [Google Scholar]
- Raglend, I.J.; Kumar, R.; Karthikeyan, S.P.; Palanisamy, K.; Kothari, D.P. Profit based unit commitment problem under deregulated environment. In Proceedings of the 2009 Power Engineering Conference Australasian Universities (AUPEC 2009), Adelaide, Australia, 27–30 September 2009; pp. 1–6. [Google Scholar]
- Zendehdel, N.; Karimpour, A.; Oloomi, M. Optimal Unit Commitment using equivalent linear minimum up and down time constraints. In Proceedings of the 2008 IEEE 2nd International Power and Energy Conference (PECon 2008), Johor Bahru, Malaysia, 1–3 December 2008; pp. 1021–1026. [Google Scholar]
- Ebrahimi, J.; Hosseinian, S.H.; Gharehpetian, G.B. Unit commitment problem solution using shuffled frog leaping algorithm. IEEE Trans. Power Syst. 2011, 26, 573–581. [Google Scholar] [CrossRef]
- Salam, S. Unit commitment solution methods. Proc. World Acad. Sci. Eng. Technol. 2007, 26, 320–325. [Google Scholar]
- Mori, H.; Matsuzaki, O. A parallel tabu search approach to unit commitment in power systems. In Proceedings of the IEEE International Conference on Systems, Man, and Cybernetics, Tokyo, Japan, 12–15 October 1999; pp. 509–514. [Google Scholar]
- Saneifard, S.; Prasad, N.R.; Smolleck, H.A. A fuzzy logic approach to unit commitment. IEEE Trans. Power Syst. 1997, 12, 988–995. [Google Scholar] [CrossRef]
- Zhai, D.; Breipohl, A.M.; Lee, F.N.; Adapa, R. The effect of load uncertainty on unit commitment risk. IEEE Trans. Power Syst. 1994, 9, 510–517. [Google Scholar] [CrossRef]
- Sasaki, H.; Watanabe, M.; Kubokawa, J.; Yorino, N.; Yokoyama, R. A solution method of unit commitment by artificial neural networks. IEEE Trans. Power Syst. 1992, 7, 974–981. [Google Scholar] [CrossRef]
- Kurban, M.; Filik, U.B. Unit commitment scheduling by using the autoregressive and artificial neural network models based short-term load forecasting. In Proceedings of the 10th International Conference on Probabilistic Methods Applied to Power Systems, Rincon, PR, USA, 25–29 May 2008; pp. 1–5. [Google Scholar]
- Abookazemi, K.; Mustafa, M.W. Unit commitment optimization using improved genetic algorithm. In Proceedings of the IEEE Bucharest Power Technology Conference, Bucharest, Romania, 28 June–2 July 2009; pp. 1–6. [Google Scholar]
- Chang, W.P.; Luo, X.J. A solution to the unit commitment using hybrid genetic algorithm. In Proceedings of the 2008 IEEE Region 10 Conference, Hyderabad, India, 19–21 November 2008; pp. 1–6. [Google Scholar]
- Yahya, A.E.M.; Shaban, M.; Yahya, Y. Apply Unit Commitment Method in Power Station to Minimize the Fuel Cost. Open J. Soc. Sci. 2015, 3, 58014. [Google Scholar] [CrossRef][Green Version]
- Kumar, C.; Alwarsamy, T. A novel algorithm unit commitment problem by a fuzzy tuned particle swarm optimization. Eur. J. Sci. Res. 2011, 64, 157–167. [Google Scholar]
- Li, T.; Shahidehpour, M. Price based unit commitment: A case of Langrangian relaxation versus mixed integer programming. IEEE Trans. Power Syst. 2005, 20, 2015–2025. [Google Scholar] [CrossRef]
- Richter, C.W.; Sheble, G.B. A profit-based unit commitment GA for the competitive environment. IEEE Trans. Power Syst. 2000, 15, 715–721. [Google Scholar] [CrossRef]
- Valenzuela, J.; Mazumdar, M. Making unit commitment decisions when electricity is traded at spat market prices. In Proceedings of the IEEE Power Engineering Society Winter Meeting, Columbus, OH, USA, 28 January–1 February 2001; Volume 1, pp. 1509–1512. [Google Scholar]
- Moghimi Hadji, M.; Vahidi, B. A solution to the unit commitment problem using imperialistic competition algorithm. IEEE Trans. Power Syst. 2012, 27, 117–124. [Google Scholar] [CrossRef]
- Daneshi, H.; Srivastava, A.K. Security-constrained unit commitment with wind generation and compressed air energy storage. IET Generation. Transm. Distrib. 2012, 6, 167–175. [Google Scholar] [CrossRef]
- Moussouni, F.; Tran, T.V.; Brisset, S.; Brochet, P. Optimization Methods. Available online: https://l2ep.univ-lille1.fr/come/benchmarktransformer_fichiers/Method_EE.htm (accessed on 30 May 2007).
- Land, A.H.; Doig, A.G. An automatic method of solving discrete programming problems. Econometrica 1960, 28, 497–520. [Google Scholar] [CrossRef]
- Singhal, P.K.; Sharma, R.N. Dynamic programming approach for large scale unit commitment problem. In Proceedings of the International Conference on Communication Systems and Network Technologies, Katra, India, 3–5 June 2011; pp. 714–717. [Google Scholar]
- Chang, G.W.; Tsai, Y.D.; Lai, C.Y.; Chung, J.S. A practical mixed integer linear programming-based approach for unit commitment. In Proceedings of the IEEE Power Engineering Society General Meeting, Denver, CO, USA, 6–10 June 2004; pp. 221–225. [Google Scholar]
- Ouyang, Z.; Shahidehpour, S.M. An intelligent dynamic programming for unit commitment application. IEEE Trans. Power Syst. 1991, 6, 1203–1209. [Google Scholar] [CrossRef]
- Ma, R.; Huang, Y.M.; Li, M.H. Unit commitment optimal research based on the improved genetic algorithm. In Proceedings of the 2011 International Conference on Intelligent Computation Technology and Automation, Shenzhen, China, 28–29 March 2011; pp. 291–294. [Google Scholar]
- Nascimento, F.R.; Silva, I.C.; Oliveira, E.J.; Dias, B.H.; Marcato AL, M. Thermal unit commitment using improved ant colony optimization algorithm via lagrange multipliers. In Proceedings of the 2011 IEEE Conference on Power Technology, Trondheim, Norway, 19–23 June 2011; pp. 1–5. [Google Scholar]
- Ostrowski, J.; Anjos, M.F.; Vannelli, A. Tight mixed integer linear programming formulations for the unit commitment problem. IEEE Trans. Power Syst. 2012, 27, 39–46. [Google Scholar] [CrossRef]
- Withironprasert, K.; Chusanapiputt, S.; Nualhong, D.; Jantarang, S.; Phoomvuthisarn, S. Hybrid ant system/priority list method for unit commitment problem with operating constraints. In Proceedings of the IEEE International Conference on Industrial Technology, Churchill, Australia, 10–13 February 2009; pp. 1–6. [Google Scholar]
- Sum-im, T.; Ongsakul, W. Ant colony search algorithm for unit commitment. In Proceedings of the 2003 IEEE International Conference on Industrial Technology, Maribor, Slovenia, 10–12 December 2003; pp. 72–77. [Google Scholar]
- Yu, D.R.; Wang, Y.Q.; Guo, R. A Hybrid Ant Colony Optimisation Algorithm based lambda iteration method for unit commitment. In Proceedings of the IEEE Second WRI Global Congress on Intelligence Systems, Wuhan, China, 16–17 December 2010; pp. 19–22. [Google Scholar]
- Kazarlis, S.; Bakirtzis, A.; Petridis, V. A genetic algorithm solution to the unit commitment problem. IEEE Trans. Power Syst. 1996, 11, 83–92. [Google Scholar] [CrossRef]
- Zhang, X.H.; Zhao, J.Q.; Chen, X.Y. A hybrid method of lagrangian relaxation and genetic algorithm for solving UC problem. In Proceedings of the International Conference on Sustainable Power Generation and Supply, Nanjing, China, 6–7 April 2009; pp. 1–6. [Google Scholar]
- Kumar, S.S.; Palanisamy, V. A new dynamic programming based hopfield neural network to unit commitment and economic dispatch. In Proceedings of the IEEE International Conference on Industrial Technology, Mumbai, India, 15–17 December 2006; pp. 887–892. [Google Scholar]
- Eusuff, M.M.; Lansey, K.E.; Pasha, F. Shuffled frog-leaping algorithm: A memetic meta-heuristic for discrete optimization. Eng. Optim. 2006, 38, 129–154. [Google Scholar] [CrossRef]
- Wong, S.Y.W. An enhanced simulated annealing approach to unit commitment. Int. J. Electr. Power Energy Syst. 1998, 20, 359–368. [Google Scholar] [CrossRef]
- Purushothama, G.K.; Jenkins, L. Simulated annealing with local search-A hybrid algorithm for unit commitment. IEEE Trans. Power Syst. 2003, 18, 273–278. [Google Scholar] [CrossRef]
- Wang, Q.F.; Guan, Y.P.; Wang, J.H. A chance-constrained two-stage stochastic program for unit commitment with uncertain wind power output. IEEE Trans. Power Syst. 2012, 27, 206–215. [Google Scholar] [CrossRef]


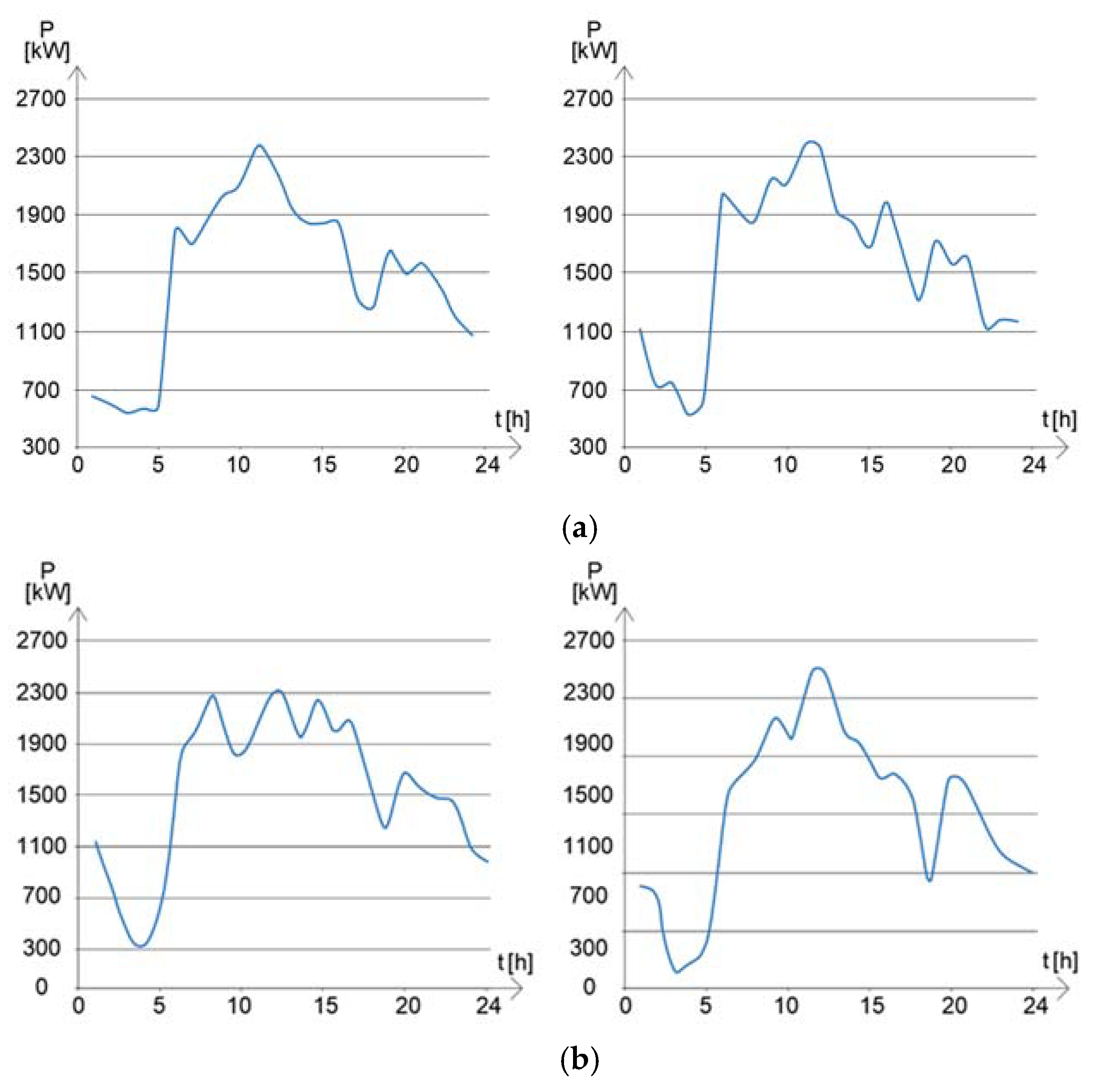
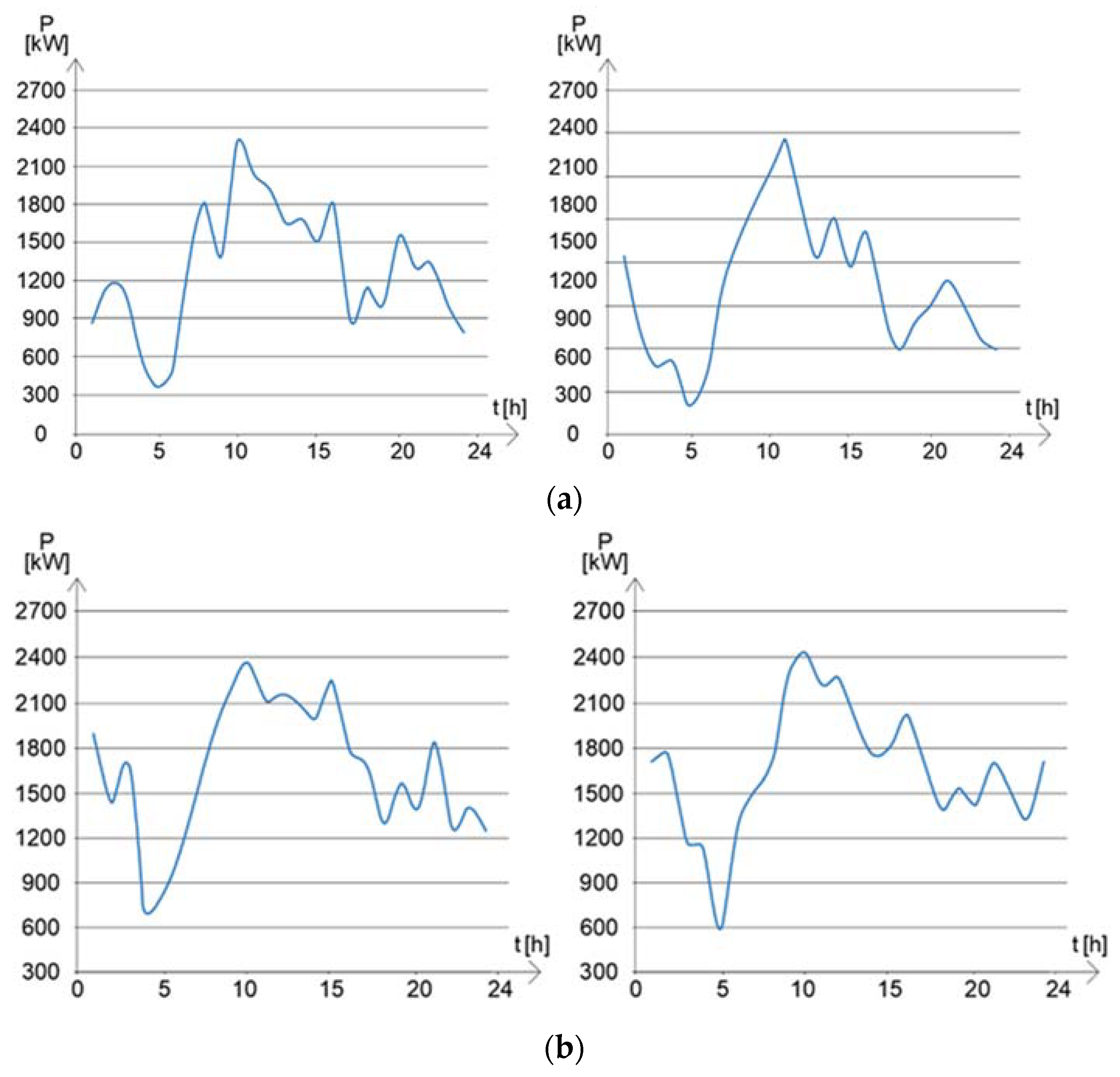
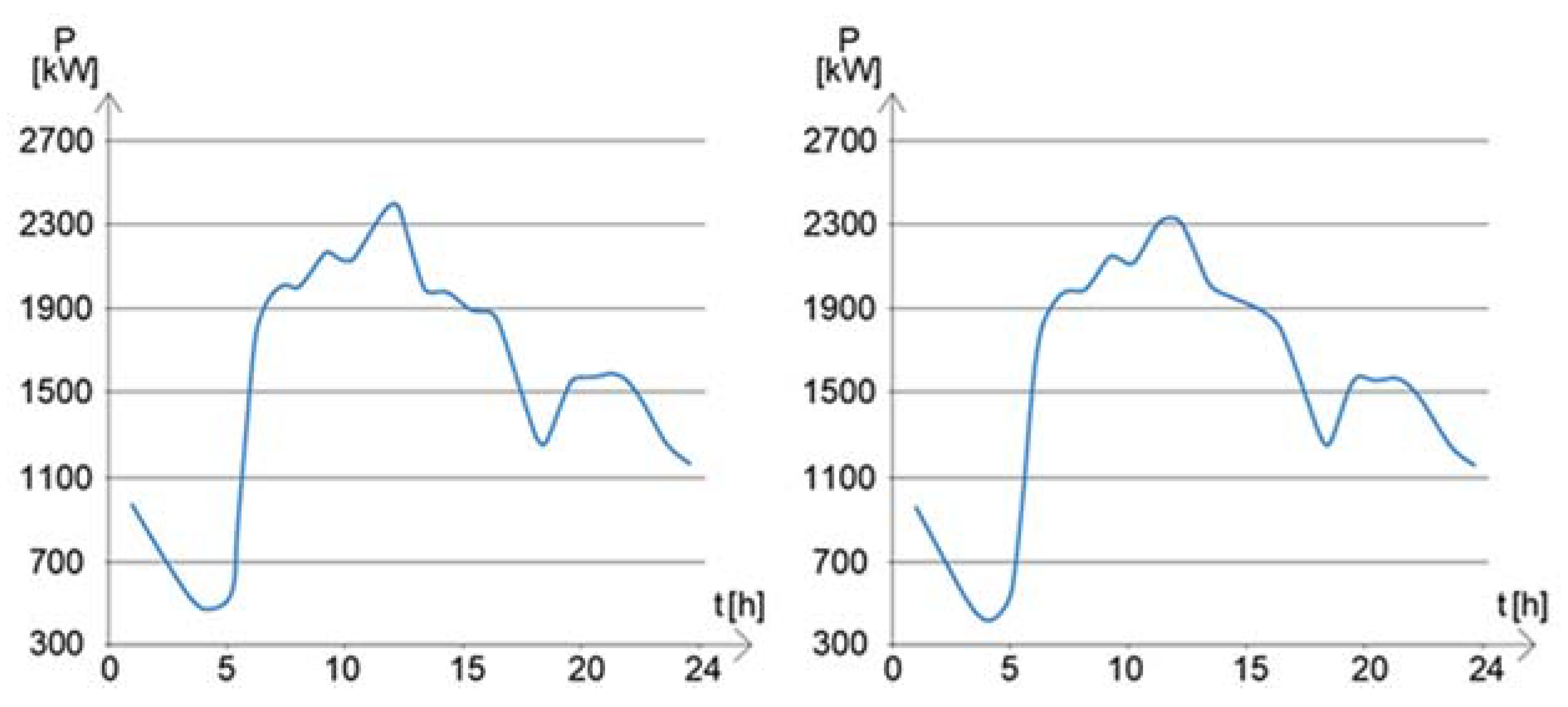
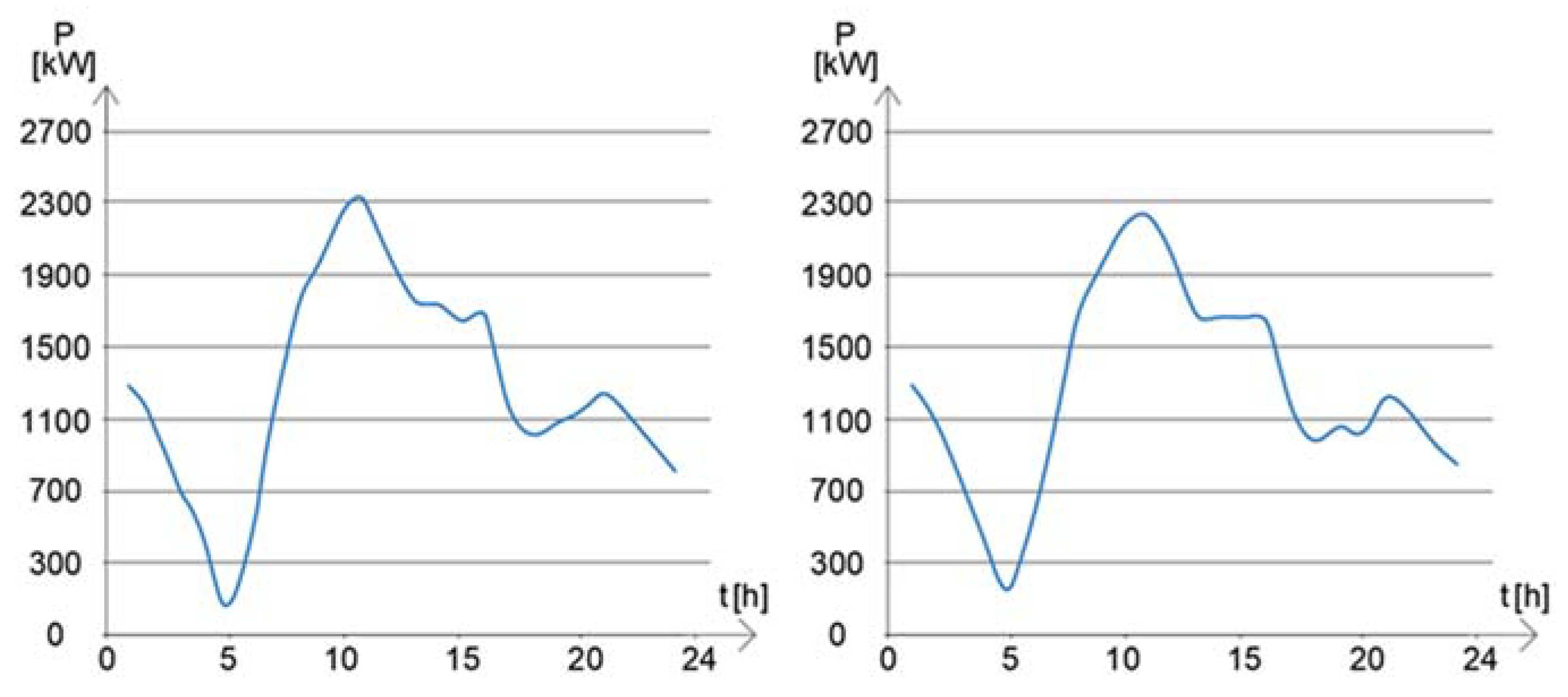
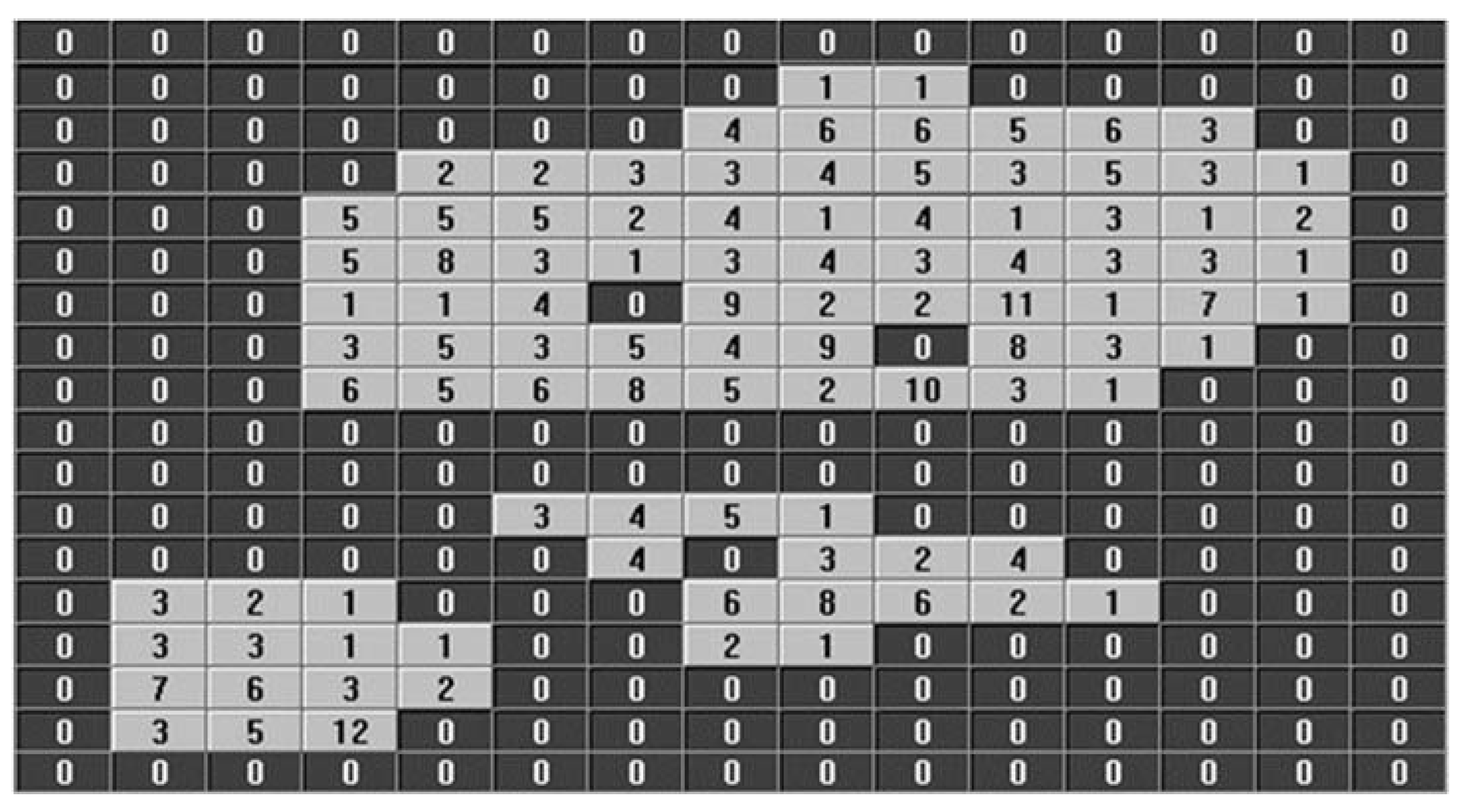
| Climatic Zone | Administrative Buildings | New Houses | ||||
|---|---|---|---|---|---|---|
| Net Primary Energy per Year (kWh/m2) | Primary Energy Consumption per Year (kWh/m2) | Coverage from RES per Year (kWh/m2) | Net Primary Energy per Year (kWh/m2) | Primary Energy Consumption per Year (kWh/m2) | Coverage from RES per Year (kWh/m2) | |
| Mediterranean | 20–30 | 80–90 | 60 | 0–15 | 50–65 | 50 |
| Oceanic | 40–50 | 85–100 | 45 | 15–30 | 50–65 | 35 |
| Continental | 40–55 | 85–100 | 45 | 20–40 | 50–70 | 30 |
| Nordic | 55–70 | 85–100 | 30 | 40–65 | 65–90 | 25 |
| Object | UNIT | Control/State | ||||
|---|---|---|---|---|---|---|
| Building Block | Designation of PV Sources | [off/on] | [MWh/year] | [CZK/MW] | [CZK/MW2] | [CZK] |
| A | PV1 | 1 | 95.000 | 190 | 0.50 | 170 |
| B | PV2 | 0 | 86.700 | 190 | 0.50 | 160 |
| C | PV3 | 0 | 40.375 | 120 | 0.50 | 120 |
| D | PV4 | 1 | 12.588 | 90 | 0.50 | 110 |
| E | PV5 | 1 | 21.375 | 110 | 0.50 | 80 |
| F | PV6 | 0 | 33.725 | 120 | 0.50 | 95 |
| Cogeneration | CO1 | 1 | 1100.95 | 1450 | 0.50 | 1200 |
| Substations TS-DS | 22/0.4 kV | 0 | 11.000 | 80 | 0.2 | 85 |
| Building | Roof Surfaces [m2] | Available Area [m2] | Orientation | Slope [°] | Number of Panels | Power [kWp] | Annual Production [kWh] |
|---|---|---|---|---|---|---|---|
| A | 888 | 800 | South-west | 30 | 400 | 100 | 95,000 |
| F | 1215 | 730 | South-west | 15 | 365 | 91.25 | 86,688 |
| E | 850 | 350 | South | 15 | 170 | 42.5 | 40,375 |
| C | 265 | 100 | South | 15 | 53 | 13.25 | 12,588 |
| D | 617 | 180 | West | 30 | 90 | 22.5 | 21,375 |
| B | 921 | 285 | West | 30 | 142 | 35.5 | 33,725 |
| Σ | 1220 | 318 | 289,751 |
| Electric Power [kWh/year] | Heating [kWh/year] | DHW Preparation [kWh/year] | |
|---|---|---|---|
| Type block: No. 1004 original condition | 13,756.51 | 29,021.70 | 9626.13 |
| Type block: reconstruction | 12,755.96 | 15,932.97 | 9991.59 |
| Block of flats: No. 1020 original condition | 24,226.35 | 106,569.27 | 74,311.63 |
| Block of flats: reconstruction | 22,780.74 | 26,106.61 | 69,361.5 |
| Type Block | Block of Flats | Normative Values 1 | ||||
|---|---|---|---|---|---|---|
| Original Condition [W/m2 K] | Reconstruction [W/m2 K] | Original Condition [W/m2 K] | Reconstruction [W/m2 K] | Required [W/m2 K] | Recommended [W/m2 K] | |
| Uwall | 1.1 | 0.15 | 1.3 | 0.15 | 0.30 | 0.25; 0.20 |
| Ufloor | 1.03 | 0.26 | 1.33 | 0.32 | 0.45 | 0.30 |
| Uroof | 1.1 | 0.12 | 1.2 | 0.13 | 0.24 | 0.16 |
| Uem | 1.4 | 0.19 | 1.2 | 0.25 | 0.35 | 0.30 |
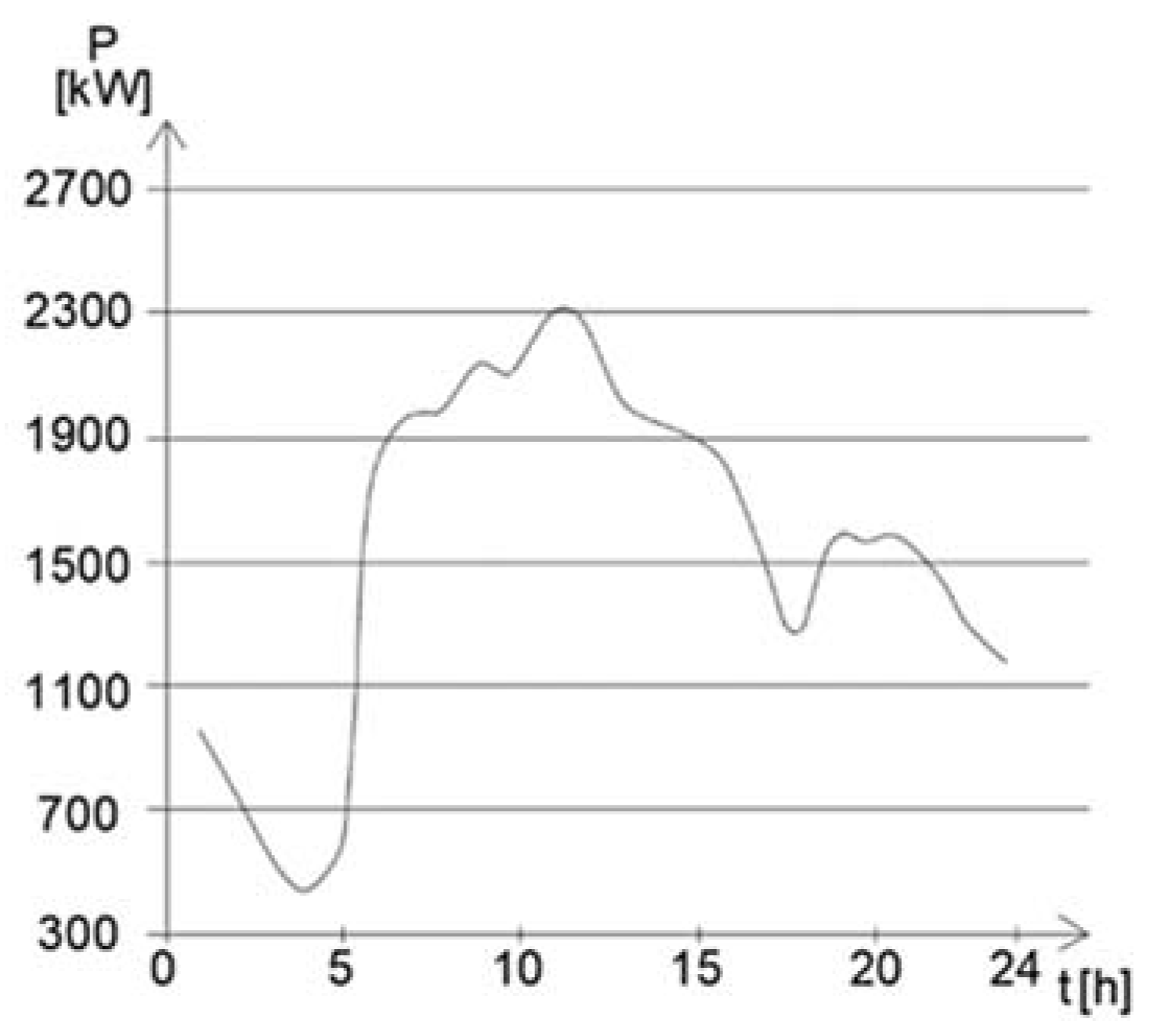
| Thursday | Thursday | ||||||
|---|---|---|---|---|---|---|---|
| Time | TDC | Standard | Diference | Time | TDC | Standard | Diference |
| (Hours Order) | (kW) | (kW) | (%) | (Hours Order) | (kW) | (kW) | (%) |
| 1 | 690 | 690.90 | 0.13 | 13 | 2100 | 2103.00 | 0.14 |
| 2 | 590 | 590.90 | 0.15 | 14 | 2050 | 2058.70 | 0.42 |
| 3 | 550 | 551.55 | 0.28 | 15 | 1850 | 1856.55 | 0.35 |
| 4 | 560 | 561.65 | 0.29 | 16 | 1860 | 1864.65 | 0.25 |
| 5 | 1700 | 1704.80 | 0.28 | 17 | 1500 | 1504.50 | 0.30 |
| 6 | 1690 | 1693.60 | 0.21 | 18 | 1300 | 1304.99 | 0.38 |
| 7 | 1600 | 1601.30 | 0.08 | 19 | 1500 | 1507.85 | 0.52 |
| 8 | 1550 | 1551.30 | 0.08 | 20 | 1480 | 1484.19 | 0.28 |
| 9 | 1900 | 1901.55 | 0.08 | 21 | 1510 | 1513.79 | 0.25 |
| 10 | 2200 | 2204.06 | 0.19 | 22 | 1480 | 1481.10 | 0.07 |
| 11 | 2300 | 2301.90 | 0.08 | 23 | 1200 | 1201.00 | 0.08 |
| 12 | 2320 | 2324.00 | 0.17 | 24 | 1100 | 1102.10 | 0.19 |
| Total | 36,580 | 36,658.40 | 0.214 | ||||
| MEAN= | 0.07 | ||||||
| MAX= | 0.52 | ||||||
| TDD | Standard | MEAN= | |||||
| Unit Commitment of Variant 2 | ||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Total electricity production for 21 September 2021; electricity production in September/number of days in September (30) = 1333 kW | ||||||||||||||||||||||||
| Parameters | ||||||||||||||||||||||||
| Date: 21 September 21 Time: 11:45:28 | ||||||||||||||||||||||||
| Int Temp | Final Temp | Iter Limit | Cost [CZK] | Cost [CZK] | dCost [CZK] | |||||||||||||||||||
| 1 | 0.000001 | 1000 | 4639.343 | 4267.3 | 397.143 | |||||||||||||||||||
| Unit Commitment of Variant 2 | ||||||||||||||||||||||||
| Supply | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| FV1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 200 | 200 | 200 | 200 | 150 | 200 | 200 | 200 | 100 | 80 | 0 | 0 | 0 | 0 | 0 | 0 |
| FV2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 150 | 200 | 200 | 200 | 200 | 200 | 200 | 200 | 200 | 100 | 80 | 0 | 0 | 0 | 0 | 0 | 0 |
| FV3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 150 | 200 | 200 | 200 | 200 | 200 | 200 | 200 | 100 | 100 | 80 | 0 | 0 | 0 | 0 | 0 | 0 |
| FV4 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 150 | 200 | 200 | 200 | 200 | 200 | 200 | 400 | 200 | 150 | 80 | 40 | 0 | 0 | 0 | 0 | 0 |
| FV5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 150 | 200 | 150 | 200 | 200 | 200 | 200 | 250 | 200 | 150 | 80 | 40 | 50 | 0 | 0 | 0 | 0 |
| FV6 | 210 | 140 | 90 | 90 | 250 | 800 | 800 | 400 | 400 | 400 | 200 | 200 | 150 | 100 | 120 | 50 | 100 | 320 | 300 | 400 | 400 | 300 | 400 | 350 |
| Biomasa | 240 | 140 | 90 | 90 | 250 | 800 | 800 | 400 | 300 | 400 | 250 | 250 | 150 | 150 | 120 | 50 | 50 | 300 | 300 | 400 | 300 | 280 | 300 | 200 |
| Cogeneration | 130 | 140 | 90 | 90 | 250 | 400 | 300 | 400 | 100 | 150 | 200 | 250 | 1500 | 150 | 120 | 50 | 50 | 300 | 380 | 380 | 150 | 302 | 320 | 350 |
| Distribution | 22 | 140 | 5 | 0 | 0 | 100 | 200 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 180 | 380 | 250 | 0 | ||
| ACCU | 5 | 30 | 200 | 100 | 10 | 0 | 0 | 20 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 10 | 0 | 0 | 0 | ||
| Total [kW] | 607 | 590 | 295 | 280 | 760 | 2100 | 2100 | 1820 | 1800 | 1900 | 1650 | 1700 | 1400 | 1400 | 1410 | 1050 | 800 | 1320 | 1060 | 1410 | 1240 | 1130 | 1020 | 900 |
| Load [kW] | 616 | 609 | 350 | 299 | 779 | 2109 | 2109 | 1839 | 1809 | 1919 | 1659 | 1709 | 1409 | 1409 | 1419 | 1059 | 809 | 1339 | 1069 | 1401 | 1231 | 1129 | 1016 | 891 |
| Diff [kW] | −9 | −19 | −19 | −19 | −19 | −9 | −9 | −19 | −9 | −19 | −9 | −9 | −9 | −9 | −9 | −9 | −9 | −19 | −9 | 9 | 9 | 1 | 4 | 9 |
| Table Results | Table Results | Table 6 | |
|---|---|---|---|
| Variant | 0 | 1 | 2 |
| Deviation | 55 | 40 | 19 |
| Balance | 950 | −875 | −225 |
| Costs | 4605 | 4145 | 4267 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Garlík, B. Application of Artificial Intelligence in the Unit Commitment System in the Application of Energy Sustainability. Energies 2022, 15, 2981. https://doi.org/10.3390/en15092981
Garlík B. Application of Artificial Intelligence in the Unit Commitment System in the Application of Energy Sustainability. Energies. 2022; 15(9):2981. https://doi.org/10.3390/en15092981
Chicago/Turabian StyleGarlík, Bohumír. 2022. "Application of Artificial Intelligence in the Unit Commitment System in the Application of Energy Sustainability" Energies 15, no. 9: 2981. https://doi.org/10.3390/en15092981
APA StyleGarlík, B. (2022). Application of Artificial Intelligence in the Unit Commitment System in the Application of Energy Sustainability. Energies, 15(9), 2981. https://doi.org/10.3390/en15092981





