Positive Torque Modulation Method and Key Technology of Conventional Beam Pumping Unit
Abstract
:1. Introduction
2. Modulation Principle and Method
2.1. Modulation Method
2.2. Analysis of Working Process and Balancing Effect
3. Kinematic Analysis
3.1. Kinematic Analysis of the Suspension Point
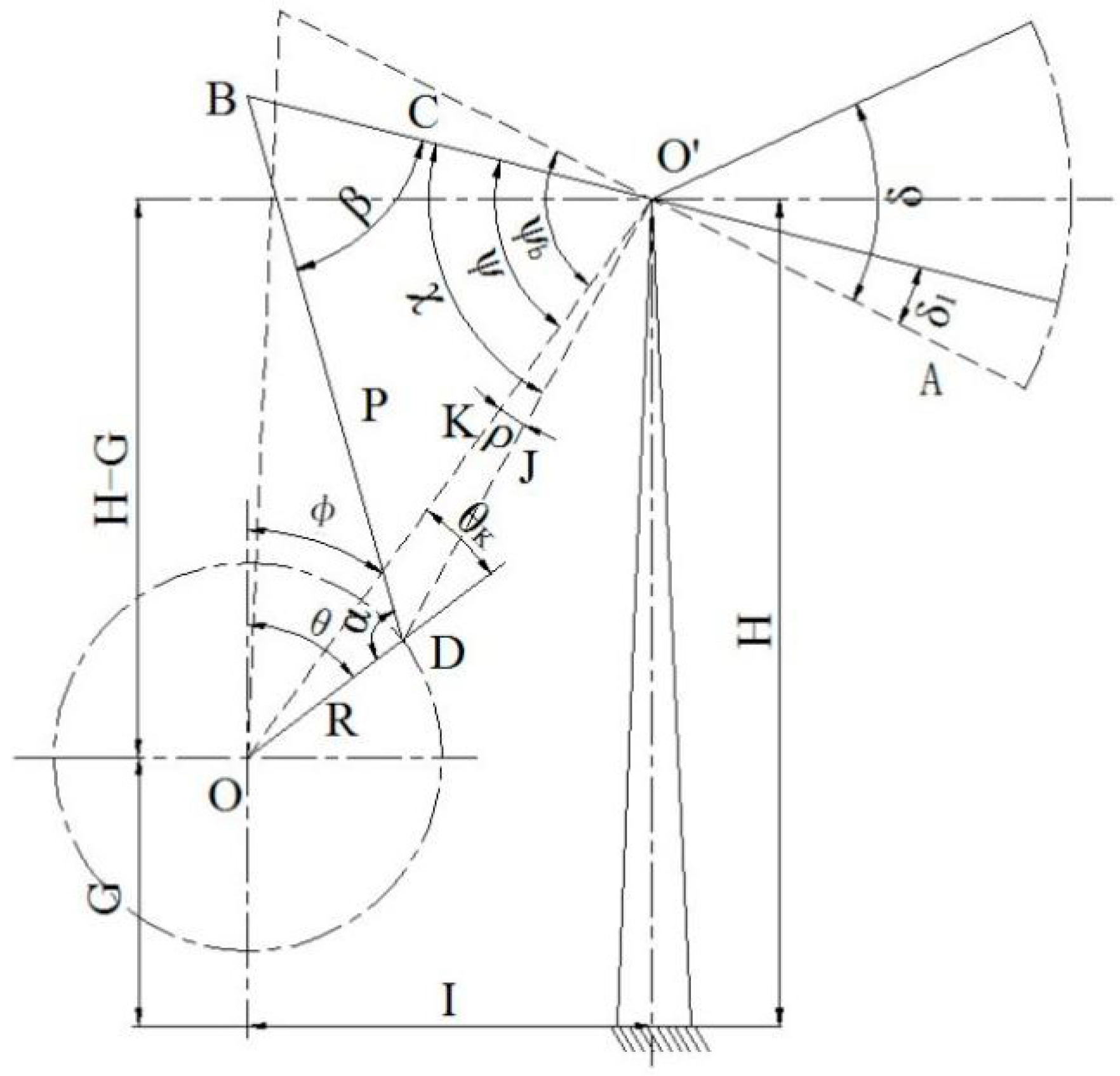
3.2. Kinematic Analysis of Secondary Speed Increasing Mechanism
3.2.1. Angular Velocity Analysis

3.2.2. Analysis of Secondary Balance Acceleration

4. Torque Analysis on the Output Shaft of Gearbox
4.1. Force Analysis of Secondary Balance


4.2. Force Analysis of the Beam
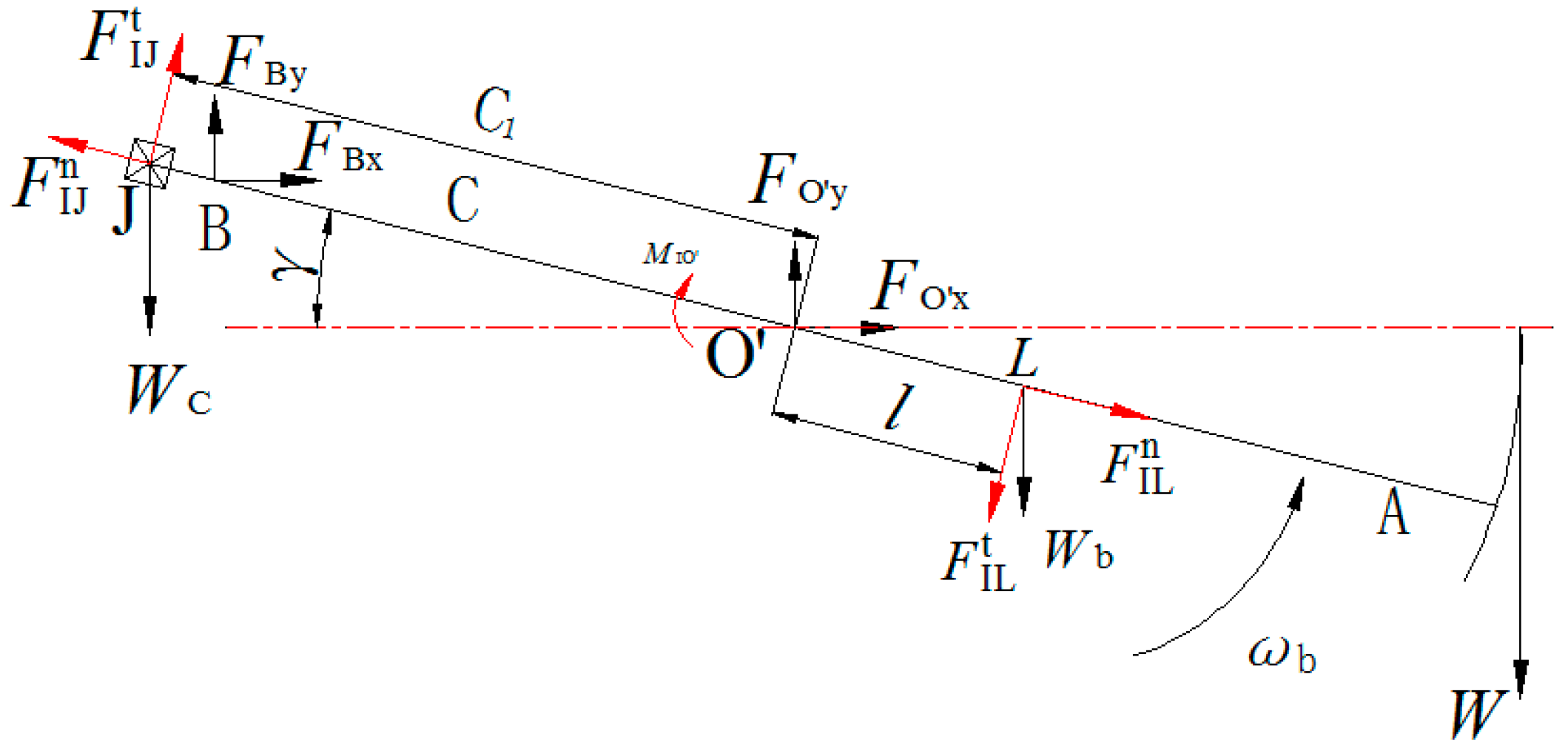
4.3. Force Analysis of the Linkage-Speed Increase Gearbox

4.4. Force Analysis of the Large Crank
4.5. Solving the Force Equations
5. Example Calculation
6. Field Tests
Beam Positive-Torque Pumping Unit Installed on Site
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| A, C, P, R | Length of the beam forearm, length of the beam rear arm, length of the connecting rod, crank radius, m; |
| H | Height of the beam support center to the base bottom, m; |
| I | Horizontal distance from the beam support center to the reducer output shaft center, m; |
| G | Height of reducer output shaft center to base, m; |
| J | Distance between the crank shaft center and the travel beam support center, m; |
| K | Polar distance, that is the distance from the beam support center to the output shaft center of reducer, m; |
| θ | Crank angle, the crank radius R at 12 o’clock position as the zero degree, measured from the zero degree line to the crank along the direction of crank rotation; |
| Φ | The angle between the zero degree line and K, measured from the zero degree line to K along the direction of crank rotation; |
| B, χ, ρ, ψ | The transmission angle between C and P; The angle between C and J; The angle between K and J; The angle between C and K; |
| , | The Angle of the polished rod at its lowest position and the Angle of the polished rod at its highest position; |
| The angle between K and R, measured from K to R along the direction of crank rotation; the angle between P to R; | |
| The swing angle of the beam; | |
| The angular velocity of the beam, rad/s; | |
| Angular velocity of crank rotation, rad/s; | |
| The velocity of the beam suspension, m/s; | |
| a | The acceleration at the suspension point, m/s2; |
| The angular velocity of the connecting rod BD, rad/s; | |
| The angular acceleration of the connecting rod BD, rad/s2; | |
| The velocity at the gear meshing point G, m/s; | |
| The angular velocity of the pinion, rad/s; | |
| r1, r2 | The radii of the reference circle of the large gear and the pinion respectively, m; |
| The angular acceleration of the small crank, rad/s2; | |
| , | The normal and tangential acceleration of point F respectively, m/s2; |
| , | Horizontal and vertical forces of the pinion shaft acting on secondary balance, N; |
| , | The forces of the pinion shaft acting on the secondary balance along the t and n directions respectively, N; |
| The moment of the pinion shaft acting on the secondary balance, N·m; | |
| , | The imaginary added inertia forces corresponding to the acceleration , , N; |
| MII | The imaginary added inertia moment of corresponding to , N·m; |
| Secondary balance mass converted to the center of mass I, kg; | |
| Secondary balance rotational inertia around the axis F, kg·m2; | |
| Secondary balance gravity converted to the center of mass I, N; | |
| The angle between the beam and the horizontal line; | |
| , | Horizontal and vertical binding forces of the connecting rod on the restraint point B of the beam, N; |
| Polished rod load, N; | |
| , | The gravity of the beam (including beam and horsehead) and the balance weight of the beam respectively, N; |
| , | are the virtual inertia forces due to the tangential and normal acceleration attached to the mass center of the beam (including beam and horsehead) respectively, N; |
| , | are the virtual inertia forces due to the tangential and normal acceleration of the mass center of the balance beam respectively, N; |
| Additional virtual inertia moment due to the angular acceleration of the beam (including beam, horsehead and beam balance weight), N·m; | |
| The rotational inertia of the beam (including beam, horsehead and beam balance weight) to the rotation center , N·m; | |
| , | The forces of the large crank acting on the large gear shaft along the x and y axes respectively, N; |
| , | The additional inertia forces corresponding to the tangential and normal acceleration at the mass center F during the rotation of the linkage-speed increase gearbox respectively, N; |
| The additional inertia moment due to angular acceleration during the rotation of the linkage-speed increase gearbox, N·m; | |
| Reaction torque of secondary counterweight acting on pinion shaft, N·m; | |
| Moment of large crank acting on large gear shaft, N·m; | |
| Wf | The total gravity of linkage-speed increase gearbox, N; |
| The rotational inertia of the linkage-speed increase gearbox, kg·m2; | |
| , | The forces at the output shaft of the gearbox on the crank O along the x and y directions respectively, N; |
| Gravity of large crank and balance block, N; | |
| Crank offset angle, rad; | |
| b | Distance from the gravity center of the crank and balance block to the rotating shaft O, m; |
| Inertia force added by radial acceleration during crank rotation, N; | |
| M | the torque of the reduction gearbox output shaft acting on the crank, N·m; |
References
- Ye, Z.W.; Liu, Z.Y.; Cheng, C.; Tan, L.; Feng, K. Efficient evaluation model of beam pumping unit based on principal component regression analysis. Sci. Prog. 2020, 103, 003685041989576. [Google Scholar] [CrossRef] [PubMed]
- Tan, C.D.; Feng, Z.M.; Liu, X.L.; Fan, J.C.; Cui, W.; Sun, R.; Ma, Q.Y. Review of variable speed drive technology in beam pumping units for energy-saving. Energy Rep. 2020, 6, 2676–2688. [Google Scholar] [CrossRef]
- Feng, Z.M.; Guo, C.H.; Zhang, D.S.; Cui, W.; Tan, C.D.; Xu, X.F.; Zhang, Y. Variable speed drive optimization model and analysis of comprehensive performance of beam pumping unit. J. Petrol. Sci. Eng. 2020, 191, 107155. [Google Scholar] [CrossRef]
- Lv, H.Q.; Liu, J.; Han, J.Q.; Jiang, A. An Energy Saving System for a Beam Pumping Unit. Sensors 2016, 16, 685. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Badoiu, D.; Toma, G. Research Concerning the Predictive Evaluation of the Motor Moment at the Crankshaft of the Conventional Sucker Rod Pumping Units. Rev. Chim. 2019, 70, 378–381. [Google Scholar] [CrossRef]
- Feng, Z.M.; Tan, J.J.; Liu, X.L.; Fang, X. Selection method modelling and matching rule for rated power of prime motor used by Beam Pumping Units. J. Petrol. Sci. Eng. 2017, 153, 197–202. [Google Scholar] [CrossRef]
- Cui, J.G.; Xiao, W.S.; Wang, L.H.; Feng, H.; Zhao, J.B.; Wang, H.Y. Optimization design of low-speed surface-mounted PMSM for pumping unit. Int. J. Appl. Electromagn. 2014, 46, 217–228. [Google Scholar] [CrossRef]
- Yang, H.K.; Wang, J.P.; Liu, H. Energy-saving mechanism research on beam-pumping unit driven by hydraulics. PLoS ONE 2021, 16, e0249044. [Google Scholar] [CrossRef]
- Rowlan, O.L.; McCoy, J.N.; Podio, A.L. Best method to balance torque loadings on a pumping unit gearbox. J. Can. Petrol. Technol. 2005, 44, 27–33. [Google Scholar] [CrossRef]
- Kuzmin, S.A.; Melnikov, D.I. Pumping unit for supplying with oil products. Neft. Khoz. 2003, 2, 56–65. [Google Scholar]
- Kazak, A.S. New Type Oil-Field Deep-Well Pumping Units. Neft. Khoz. 1989, 2, 62–63. [Google Scholar]
- Gibbs, S.G. Computing Gearbox Torque and Motor Loading for Beam Pumping Units with Consideration of Inertia Effects. J. Petrol. Technol. 1975, 27, 1153–1159. [Google Scholar] [CrossRef]
- Aliev, T.A.; Rzayev, A.H.; Guluyev, G.A.; Alizada, T.A.; Rzayeva, N.E. Robust technology and system for management of sucker rod pumping units in oil wells. Mech. Syst. Signal Process. 2018, 99, 47–56. [Google Scholar] [CrossRef]
- Zhang, C.Y.; Wang, L.; Li, H.; Wang, L.H. Experimental Research on Parameters of a Late-Model Hydraulic-Electromotor Hybrid Pumping Unit. Math. Probl. Eng. 2020, 2020, 2923154. [Google Scholar] [CrossRef]
- Zhang, C.Y.; Wang, L.; Li, H. Experiments and Simulation on a Late-Model Wind-Motor Hybrid Pumping Unit. Energies 2020, 13, 994. [Google Scholar] [CrossRef] [Green Version]
- Yu, Y.Q.; Chang, Z.Y.; Qi, Y.G.; Xue, X.; Zhao, J.N. Study of a new hydraulic pumping unit based on the offshore platform. Energy Sci. Eng. 2016, 4, 352–360. [Google Scholar] [CrossRef] [Green Version]
- Liang, Y.J.; Wang, T.J.; Wang, X.; Liang, W.Q.; Liu, X.H. Simulation research on hydraulic hybrid assistant beam pumping unit. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2016, 230, 1795–1804. [Google Scholar] [CrossRef]
- Li, Z.H.; Song, J.C.; Huang, Y.J.; Li, Y.G.; Chen, J.W. Design and analysis for a new energy-saving hydraulic pumping unit. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2018, 232, 2119–2131. [Google Scholar] [CrossRef]
- Xing, M.M.; Dong, S.M. A New Simulation Model for a Beam-Pumping System Applied in Energy Saving and Resource-Consumption Reduction. SPE Prod. Oper. 2015, 30, 130–140. [Google Scholar] [CrossRef]
- Bhagavatula, R.; Fashesan, O.A.; Heinze, L.R.; Lea, J.F. A computational method for planar kinematic analysis of beam pumping units. ASME J. Energy Resour. Technol. 2007, 129, 300–306. [Google Scholar] [CrossRef]
- Badoiu, D. Research Concerning the Movement Equation of the Mechanism of the Conventional Sucker Rod Pumping Units. Rev. Chim. 2019, 70, 2477–2480. [Google Scholar] [CrossRef]
- Feng, Z.M.; Ma, Q.Y.; Liu, X.L.; Cui, W.; Tan, C.D.; Liu, Y. Dynamic coupling modelling and application case analysis of high-slip motors and pumping units. PLoS ONE 2020, 15, e0227827. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Byrd, J.P. Mathematical-Model Enhances Pumping-Unit Design. Oil Gas J. 1990, 88, 87–93. [Google Scholar]







| Parameters | Before Transformation | After Transformation |
|---|---|---|
| Motor power/kW | 37 | 37 |
| Maximum upstream current/A | 67.72 | 27.21 |
| Maximum downstream current/A | 32.62 | 29.33 |
| Maximum torque/kN·m | 38.92 | 23.20 |
| Minimum torque/kN·m | −1.89 | 2.05 |
| root mean square torque/kN·m | 14.92 | 14.21 |
| root mean square power/kW | 11.57 | 11.17 |
| Daily power consumption/kWh | 259.71 | 195.5 |
| Liquid production volume/t·d−1 | 110.2 | 108.3 |
| Power consumption per ton liquid/kWh | 2.36 | 1.80 |
| System efficiency/% | 20.6 | 35.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, J.; Meng, S.; Li, W.; Wang, Y. Positive Torque Modulation Method and Key Technology of Conventional Beam Pumping Unit. Energies 2022, 15, 3141. https://doi.org/10.3390/en15093141
Xu J, Meng S, Li W, Wang Y. Positive Torque Modulation Method and Key Technology of Conventional Beam Pumping Unit. Energies. 2022; 15(9):3141. https://doi.org/10.3390/en15093141
Chicago/Turabian StyleXu, Jinchao, Siyuan Meng, Wei Li, and Yan Wang. 2022. "Positive Torque Modulation Method and Key Technology of Conventional Beam Pumping Unit" Energies 15, no. 9: 3141. https://doi.org/10.3390/en15093141







