SST-Based Grid Reinforcement for Electromobility Integration in Distribution Grids

Abstract

Electric Vehicles (EVs) are gaining acceptance due to the advantages they offer in the reduction of nitrogen oxide and carbon dioxide emissions. The need for emission reduction and the potential of EVs for these reductions is reflected in the current sustainable mobility policies of the EU as well as the German government. Increasing the penetration of EVs in the grid requires an expansion of EV charging infrastructure, which in turn requires either grid reinforcement or solutions for more efficient use of existing infrastructure to avoid or postpone grid reinforcement. Distribution transformers face increased loading due to EV charging and need to be protected from overloading during peak load periods to ensure continuity of service. Therefore, transformers are one of the components that are upgraded or replaced as a part of grid reinforcement. In this paper, we propose the connection of a Solid-State Transformers (SST) between two buses operating at the same-voltage level as an alternative to replacement or upgrading of conventional transformer as well as to prevent their overloading. We analyse how the proposed topology can be useful to reduce the impact of EV integration on the overloading of distribution transformers and node voltage violations in the distribution grid.

1. Introduction

Sustainable transport is included in 8 out of the 17 sustainable development goals set by the United Nations [1]. Electrification of the transport sector plays an important role in fulfilling these goals by reducing the dependency on fossil fuels. An additional advantage is also an improvement in air quality in urban environments. At the same time, EVs pose a challenge to planning and operation of distribution grids as sufficient EV charging infrastructure needs to be constructed and operated. Researchers have attempted to evaluate the impact of electric vehicle charging stations (EVCS) on the distribution grids recently. Several issues that are all associated with the increased loading of distribution grids are reported, such as voltage limit violations, overloading of transformers and congestion of distribution lines.

In [2], the impact of EV charging on the bus voltages in selected benchmark grids is analysed. It is found that even a relatively small number of EVs charging at the same time can cause voltage limit violations. An analysis incorporating the California distribution grid is presented in [3], where it is observed that residential EV charging causes an increased peak demand leading to transformer overloading and voltage limit violation issues in the grid. The authors conclude that grid reinforcements are needed for 60% of all feeders. Furthermore, the authors in [4] derive charging profiles of EVs and apply this for analysing the power flow in distribution grids. They conclude that to ensure a reliable operation of distribution grids with an increasing number of EVCS, an intensifying investment in grid reinforcement along with the integration of localised renewable energy resources will be necessary. Similar studies, such as in [5], find that there is a necessity of transformer upgrading to mitigate the impact of concurrent charging of EVs and improve grid supportability. Furthermore, the authors in [6] find that because of the increased loads of EVCS, the lifetime of transformers was reduced by $93\%$ due to overheating.

Controlled charging strategies such as those using Time of Use (ToU) pricing and smart charging strategies that directly control EV charging power and start-time of charging are studied in literature to mitigate the impact of EV charging [7]. In [8], the authors have examined the effect of various charging strategies on the distribution grid. They conclude that without any grid reinforcement, uncontrolled charging leads to increased congestion levels in the distribution lines. Along with [2,3], they conclude that controlled charging strategies can help in reducing transformer overloading and voltage limit violation. Nonetheless, they state that without perfect knowledge of the EV charging behavior and the real-time grid conditions at all times, grid reinforcements are still necessary.

While controlled charging strategies work for residential and workplace charging where the parking duration of the EVs is considerable long, for public and semi-public charging stations the applicability is limited. Especially for public fast-charging stations, controlled charging strategies are not applicable, as it is contrary to the actual purpose to charge immediately and increase the EV range. Furthermore, charging with reduced power or a time-shift in the charging process might not be accepted by the customers. At really high levels of EV penetration even when the charging profiles of the EVs are controlled, transformers are likely to be overloaded and are the most vulnerable component in the distribution grid [9]. Therefore, increasing the size of the transformers is a possible solution that will be able to mitigate the impact of EV penetration on the power grids. However, this is very cost-intensive [10], as many resources are bound and the additional capacity is only needed during peak loading. Hence, planning for the worst case scenarios for EV charging might prove to be expensive in the long run while simultaneously not creating any additional benefit to the grid [11]. Today and in the future, many charging stations will be located in urban areas, where the density of distribution grid transformers is quite high [12]. However, distribution grid transformers tend to be underutilized [13]. According to the study conducted in [14], the annual utilization of these transformers is only in the range of 50%.

In order to meet the high peak loads caused by the charging stations, neighboring transformers or LV grids can be meshed to supply the peak power. Conventional meshing, in the form of, e.g., doubly fed grid segments, can only be realized by the costly modification of the protection equipment in the existing grid. The possibility of coupling by a solid-state transformer, which does not contribute to the short-circuit power of the grid, is presented in this work. In literature, the concept of solid-state transformers is well known, and it is mostly considered as a replacement of conventional transformers with one port acting in the grid-forming mode. A number of significant advantages have already been identified such as the fully controllable bidirectional power flow [15], reactive power compensation [15] and ensuring continued operation in case of asymmetrical faults in the grid [16]. In addition, most topologies make one or multiple DC-links available, which can be used to efficiently integrate storage systems, renewables such as PV [17] or fast-charging stations [18]. Furthermore, SSTs require a smaller footprint, less material and are lighter compared to conventional transformers, which is a big advantage in urban environments where space and weight restrictions are critical. The relatively high cost of power electronics and the complexity of connecting medium-voltage (MV) grids in conjunction with the availability of suitable medium-frequency transformers are currently a hindrance in the way of widespread use. However, economies of scale of modular concepts are expected to lead to a considerable reduction in price. Likewise, the increasing material prices of copper and steel—the main components of a line-frequency transformer—make the SST competitive in the near future.

Until now, SSTs have been studied that always interconnect a higher voltage grid to a lower voltage grid, substituting and extending the functionalities of classical line-frequency transformers, with one side always working in the grid-forming mode. In the context of this work, we propose the SST-Technology to couple already existing grid segments and neighboring transformer substations in order to route the active power flow and compensate reactive power, as shown in Figure 1. In this case, both sides of the SST operate in the grid-following mode. The question whether to what extent the SST can mitigate the impact of integration of EVCS on the distribution grid has not yet been answered in the literature. In order to make a statement about the effectiveness of the proposed solution, we use a power flow simulation for different EV penetration scenarios to investigate the effects the SST has on the overloaded grids. Furthermore, first indicators that are necessary for estimating the required size of the SST will be derived. Therefore, we first present suitable SST topologies for an MV and LV grid coupling operation and further elaborate the control structures needed. Following this, a simplified representation of the SST for power flow calculations is derived. Subsequently, we show two scenarios, one in the MV and one in the LV grid, and analyse the impact on transformer overloading and voltage violations.

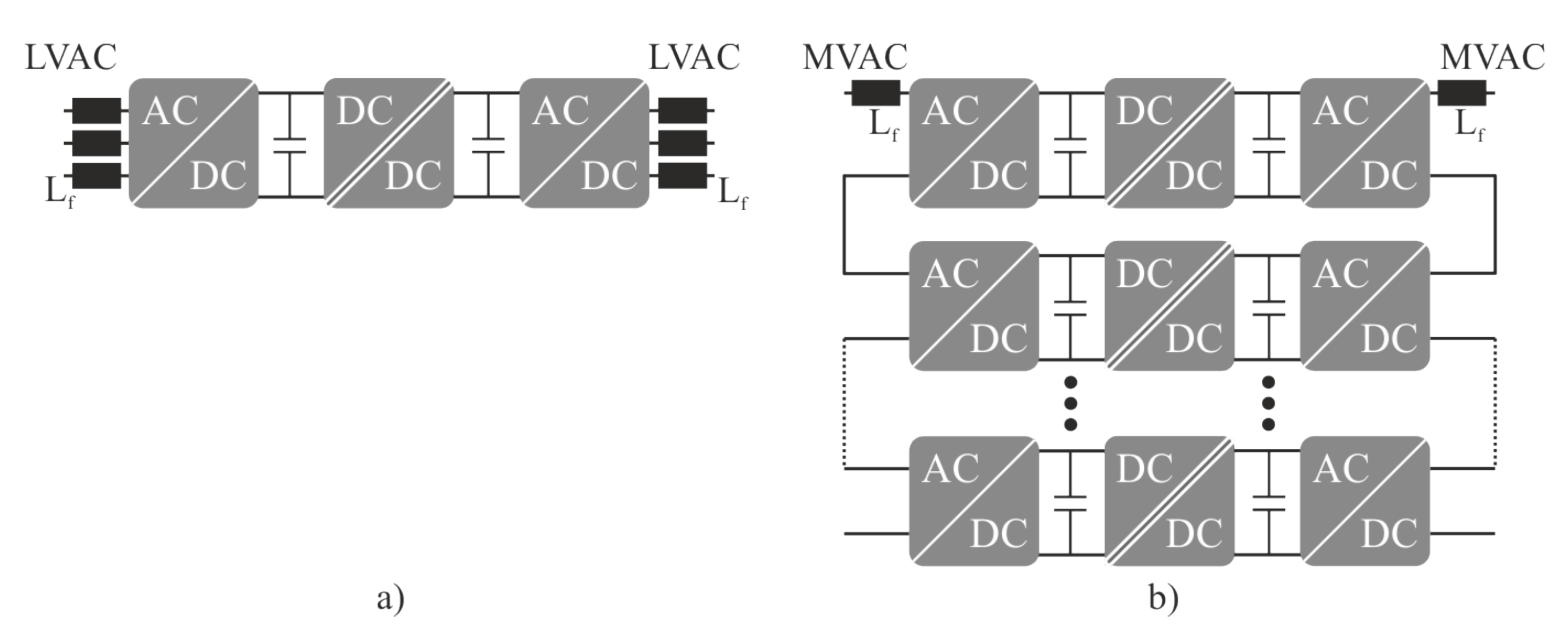
2. Solid-State Transformer

2.1. Topologies

During the early stages of research in power electronics, SST concepts were presented in the literature. To date, numerous topologies have been presented, the most noteworthy of which are reviewed and classified in the following. The different SST topologies are categorized by the number of conversion stages, DC-link availability and galvanic isolation and can be found in [18,19,20]. The LV stage can be realized as a two-level topology, in single or parallel connection depending on the required output power. At the MV stage—due to limited blocking capability of the power electronic switches—multilevel-inverter topologies are a suitable solution, although they add complexity. Multi-level multi-cell inverter topologies [21], however, offer a great cost-reduction potential as LV power-electronics switches can be used. Furthermore, the isolation stage can be directly integrated into so-called power electronics building blocks [22]. The use of medium-frequency transformers within the galvanic isolated DC–DC converters offers an enormous potential in terms of material and size reduction, leading to very compact designs with a low footprint and high efficiency [18]. If an isolation stage is needed or not depends also on the grounding and protection concept of the different grids to be connected [23]. However, adding an isolation stage within the SST facilitates the grid integration, as the necessary grounding and protection of each port can be individually aligned with the needs of the connected grids. Furthermore, in the case of grid faults (e.g., single line-to-ground fault), a galvanic isolated SST is superior to a non-isolated variant, since the fault occurring is limited to the faulty port and does not affect the healthy port [23].

Therefore, we choose two three-stage topologies with galvanic isolation for the horizontal coupling of the low-voltage grids (LVAC) (1) and the medium-voltage grids (MVAC) (2), respectively. This ensures that the grounding schemes of the grid can remain unchanged and grid faults cannot propagate from one grid to another. The selected power converter topologies are presented as follows: (1) The LVAC distribution system in Europe is a three-phase, four-wire system with a solid grounding (TN-S-C) at the transformer star-point. Following this, a three-phase, two-level active front-end (AFE) converter topology is selected at the grid interfaces. Furthermore, a three-phase Dual-Active Bridge (DAB) converter is inserted between the two AFE converters as an additional isolation stage leading to the three-stage topology depicted in Figure 2a. The three-phase DAB is chosen due to its superior power density and higher efficiency compared to its single-phase equivalent [24]. (2) In order to interconnect two MV grids, the multi-level multi-cell topology depicted in Figure 2b is suitable. The AC-stage is realized by a cascaded connection of H-bridge converters with LV power-semiconductor devices (e.g., 1200 V IGBTs/MOSFETs). The isolation stage is realized within every cell with a single- or three-phase DAB converter.

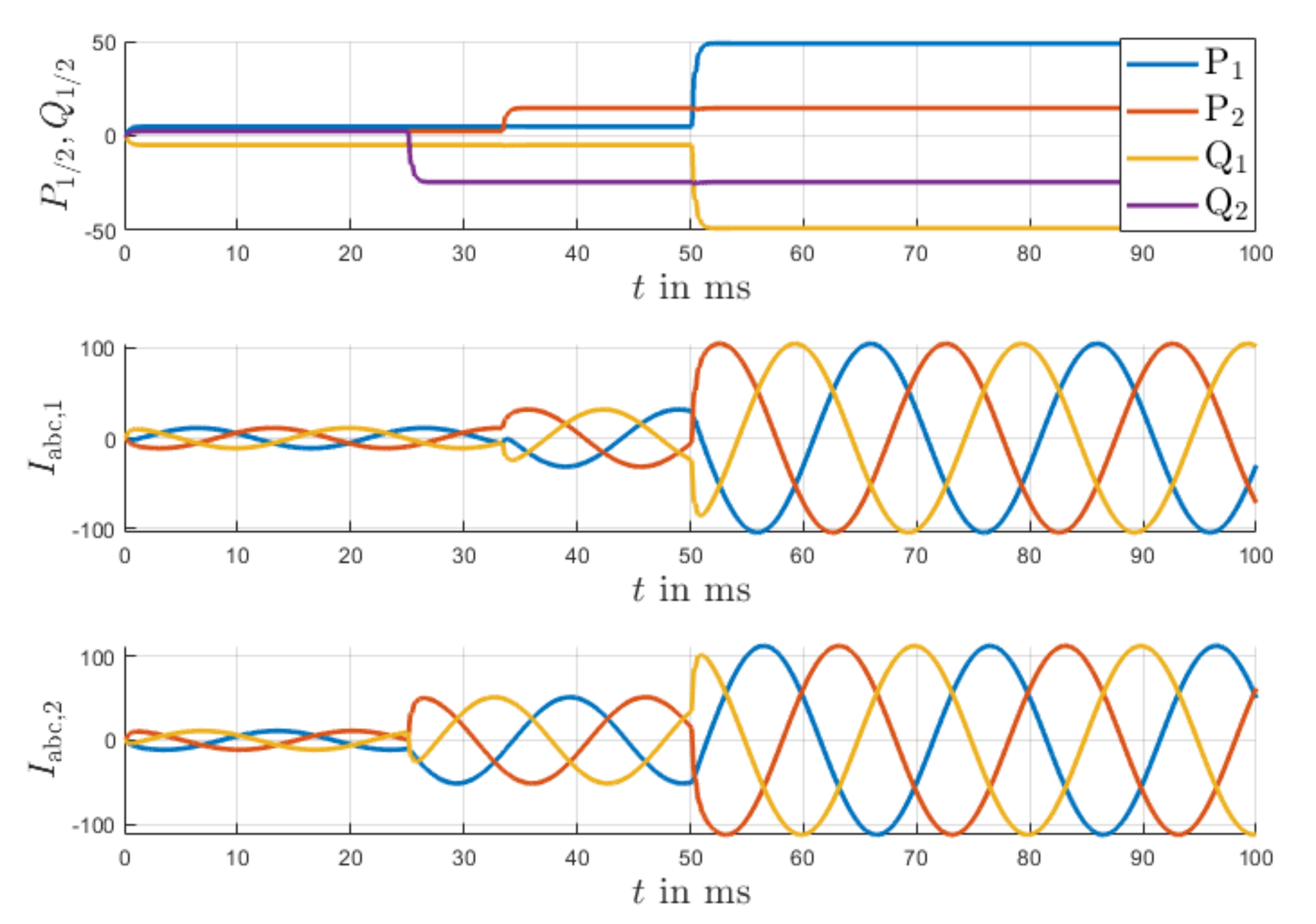
2.2. SST-Control

The converter control of a three-stage SST requires a proper coordination of the individual converter controls to achieve the desired grid operation. For both the MV and LV SST concept, this is ensured by several cascaded control loops, regulating the grid-currents and DC-link voltages of both AFEs. The central stage—the DC–DC converter—features only a power controller, which regulates the active power flow between the two inverter stages. In case of the modular concept additional effort has to be paid to achieve a voltage balancing of the individual sub-module capacitors as presented in [21]. As both AFEs can be operated independently from each other and are responsible for regulating the DC-link voltages, they ensure constant input and output voltages of the DC–DC conversion stage. This is possible since the individual conversion stages are decoupled by the DC-link capacitors. However, if steep power changes are required and the overall capacitance installed should be limited, due to cost or space constraints, the individual conversion-stage controllers can be coupled, e.g., by means of a feed-forward control and load–current decoupling methods, as shown in Figure 3. As a result of these additional measures, the DC-link voltages remain almost constant during load steps, and hence, the dynamic behavior at the AC grid ports is completely determined by the current controller in conjunction with the grid filters [25]. Furthermore, incorporating a Phase-Locked-Loop (PLL), the AFEs regulate the current phase relative to the grid voltage, achieving a unity power factor or arbitrary reactive power set-points. Depending on the maximum designed apparent power as well as the operating point of the AFEs, independent reactive power set-points can be realized at both AC ports. The reactive power can be determined by either a predefined relationship, such as a voltage-dependent set-point and constant or externally set $cos\left(\phi \right)$. Additional functionalities such as active filtering for harmonic mitigation or compensation of unbalanced loads may be desirable.

2.3. Equivalent Steady-State Model

To understand the effectiveness of grid reinforcement using SSTs for improving electromobility integration, a distribution grid power-flow simulation will be conducted in this work. Therefore, an SST model needs to be derived that fulfills the simulation objectives in terms of accurate representation of the active- and reactive-power flow behavior at both AC grid ports. Consequently, the use of detailed switched models of the power electronics circuits is unnecessary since phenomena such as current ripple or THD and the transient behavior are not of primary interest [26]. Therefore, a simplified representation is needed to model this behavior within the power-flow calculation, which is derived in the following. As stated in the control section, the DC-link voltages remain almost constant if the individual conversion stage controllers are coupled. Hence, the current injected or drawn is determined only by the current controller dynamics. This is described by tanking the grid filter inductance transfer function in the complex discrete dq-domain into account [27]:

$${\underline{G}}_{L,\mathrm{filter}}=\frac{T_{\mathrm{s}}}{L_f}·\frac{e^{-j\omega T_{\mathrm{s}}}·z^{-}1}{1-e^{-j\omega T_{\mathrm{s}}}·z^{-}1}$$

(1)

with the time step $T_s=1/f_{sw}$, the grid frequency $\omega$ and the grid filter inductance $L_f$. The current control loop consists of a PI controller of the form:

$${\underline{G}}_{\mathrm{PI}}\left(z\right)=K_{\mathrm{p}}+\frac{K_{\mathrm{i}}}{T_{\mathrm{s}}·(1-z^{-1})},$$

(2)

with the proportional gain $K_{\mathrm{p}}$ and the integral gain $K_{\mathrm{i}}$. The closed-loop transfer function in conjunction with a trajectory filter then describes the transient behavior at the AC ports:

$$\frac{I_{\mathrm{dq}}\left(z\right)}{I_{\mathrm{dq}}^{*}\left(z\right)}=G_{\mathrm{tf}}\left(z\right)·G_{\mathrm{cc}}\left(z\right).$$

(3)

The reference current $I_{\mathrm{dq}}^{*}$ is calculated taking the AC voltage and a perfectly aligned PLL control algorithm into account. The PLL is used to obtain the grid angle that is needed for the dq-transformation. The active and reactive power is computed using the following matrix:

$$\left(\begin{array}{c}{P}_{grid,1/2}\left(z\right)\\ Q_{grid,1}\left(z\right)\\ Q_{grid,2}\left(z\right)\end{array}\right)=\left(\begin{array}{c}3/2U_d\\ 3/2U_d\\ 3/2U_d\end{array}\right)·\left(\begin{array}{c}{I}_{d,1/2}\left(z\right)\\ I_{q,1}\left(z\right)\\ I_{q,2}\left(z\right)\end{array}\right).$$

(4)

The calculated results obtained with Equations (3) and (4) are shown in Figure 4. It is evident, that a smooth output characteristic is achieved and that the active and reactive power set-points are almost instantaneously reached.

Therefore, if a static power-flow calculation is aspired, it is justified that the AC grid behaviour of the SST can be represented in a simplified way by the controller set-points $P^{*}$, $Q_1^{*}$ and $Q_2^{*}$, which is achieved in the course of this work.

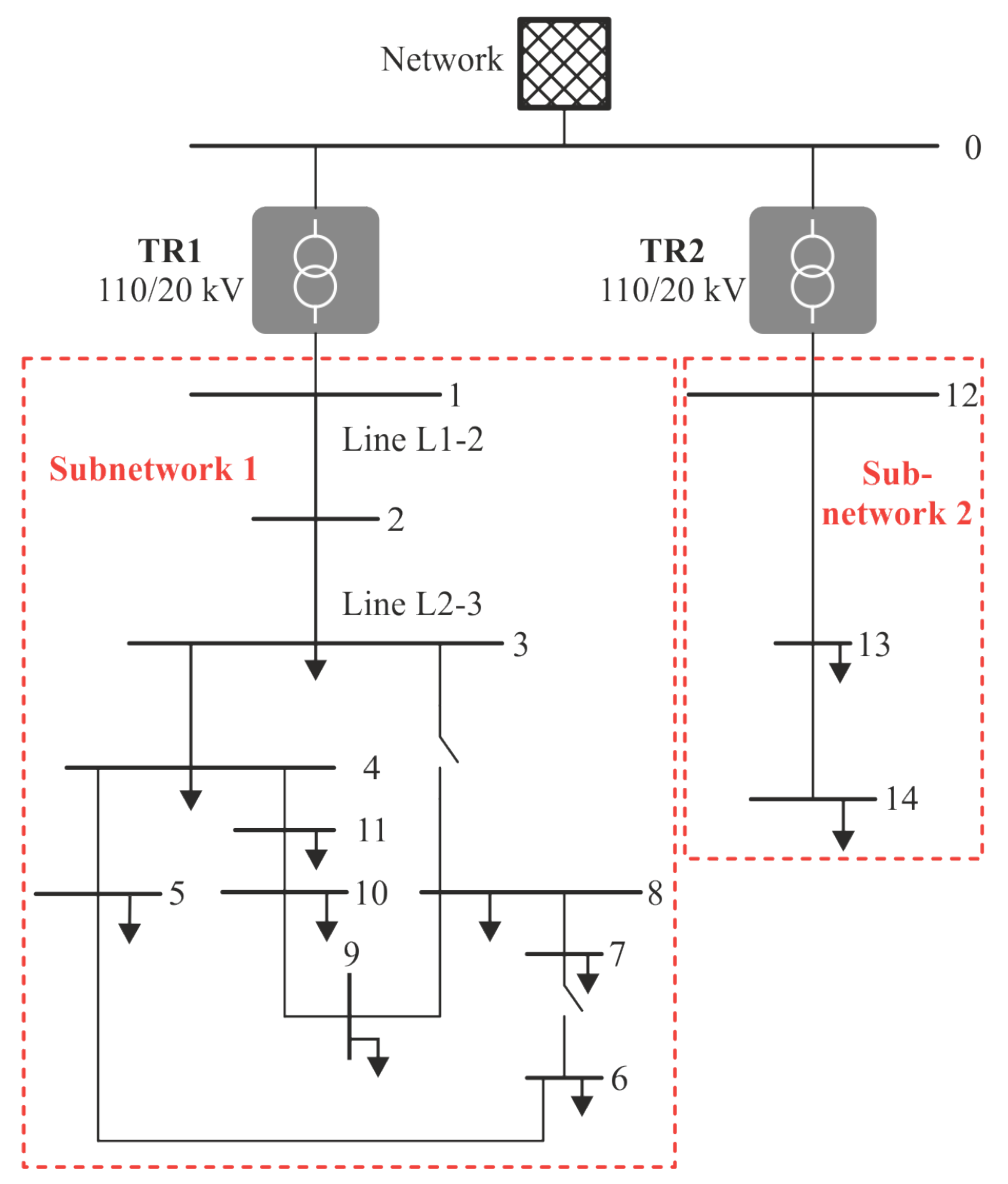
3. Simulation Methodology

The analysis of the impact of increased EVCS integration on the distribution grid considering different levels of EV penetration was carried out via numerical power-flow simulations. The power-flow simulations were performed using the Dynamic Phasor simulator (DPsim) [28]. DPsim is a real-time capable open source simulator that supports dynamic phasor, electromagnetic transient and power flow simulations for electrical networks [29]. DPsim is also integrated with the tool CIMpy [30], which supports the implementation of grid models by importing their Common Information Model (CIM) [31]. This feature facilitates the modelling, simulation and validation of large networks with limited effort and less errors.

The scalability of the proposed SST-based grid-coupling solution was demonstrated by simulating EV penetration scenarios and corresponding SST placement scenarios for the CIGRE MV benchmark distribution grid, as well as for the IEEE EU LV grid. The EV charging scenarios are defined as:

1.

Base case (BC) scenario: Base load profile with 0% EV penetration and without any voltage control;

2.

Uncontrolled charging (UC) scenario: Grid operator does not control EV charging loads nor takes any control actions to prevent the violation of grid stability limits. EV users charge at their convenience;

3.

Controlled charging(CC) scenario: EV users adhere to a charging schedule that is determined based on distribution grid constraints.

We used two different approaches for the modelling of the additional load from EV penetration for the MV and the LV grid. In case of the MV grid, the EV charging load was modelled as an aggregated load at the MV level, while assuming that the EVs were directly connected downstream at the LV level to a single-phase 230 V or a three-phase 400 V charging station. Such an assumption can be justified for charging at home or public and semi-public charging stations [32]. In case of the LV grid, however, the EV charging load is not aggregated. Instead, realistic charging profiles for privately used EVs were generated using empirical data and the tool emobpy [33]. This is due to the fact that modelling EV charging loads in the LV distribution as aggregated loads obscures the actual charging demand coming from EVCSs in the LV distribution grid. The impact of the additional EV charging load on the distribution grid was determined using two indicators, namely, the percentage loading of the transformer and the root mean square (RMS) voltage at the nodes. According to the IEEE Guide for Loading Mineral-Oil Immersed Transformers and Step-Voltage Regulators [34], distribution transformers may not be loaded much higher than their rating in order to preserve their normal life expectancy. We therefore assumed that the maximum permitted percentage loading of the transformer may not exceed 100%. The critical value of RMS voltages was determined using the standard EN 50160 [35], which states that the voltage magnitude in MV or LV grids must remain within $\pm 10\%$ of the nominal voltage value. When the nominal voltage is considered as the base value for per unit calculations, this implies that the voltage must stay within the limits of $0.9\mathrm{pu}-1.1\mathrm{pu}$.

These two metrics were used to quantify the benefit of the SST in mitigating the impact of EV integration on the grid. In doing so, no limitations were placed on the size of the SST. The active-power set point of the SST was determined by analysing the maximum percentage loading of the transformers that are coupled via the SST. Unlike the active power set-point $P_{set}$, the reactive power set-point for each port of the SST can be set independently of each other, as explained in Section 2.2. To determine the reactive power set-point $Q_{set}$, a series of power-flow simulations were performed to determine the threshold reactive power value at which an improvement in node voltages was observed. The set-points for the SST remain constant for the duration of the simulation regardless of the percentage loading of the transformers. A distribution grid control which determines the set-points of the SST based on real-time grid conditions is not in the scope of this work.

4. Results

4.1. Medium-Voltage Distribution Grid

The MV benchmark distribution grid simulated is a modified version of the CIGRE MV benchmark distribution grid [36]. This network is fed by a transmission network via 2 110/20 kV transformers with a rated power of 25 MVA and is shown in Figure 5. We assume that the DC link connected between the nodes 8 and 14 in the original benchmark is open and the network therefore operates radially.

In the base case scenario (BC), the transformers supply 10 household loads and 8 industrial loads with a total peak-load power of 38.895 MW and a minimum of 10.080 MW. The base load profile contains load data for each load for 24 h with a resolution of one second. No distinction is made between weekdays or holidays in the base load profile.

4.1.1. Uncontrolled Charging Scenario

As described in Section 3, the additional load from EV charging is modelled as an aggregated load in the MV grid. In the uncontrolled charging (UC) simulation scenario, the additional load under different levels of penetration of EVs is modelled by modifying the base load profile of each of household by adding 20%, 50% and 80% additional load depending on the time of the day and the start time of the charging processes for the respective penetration levels, similar to the approach used in [32]. This represents a worst-case scenario in which the peak of the additional EV charging load coincides with the peak load of the base case. Power-flow simulations were performed for the base case and each of the three EV penetration scenarios for the UC scenario. The percentage loading of the transformers TR1 and TR2 and the node voltages for each scenario were analysed. As can be seen in Figure 6 and Figure 7 the percentage loading of the transformers increases with increasing levels of EV penetration. It can also been seen in Figure 6 that during peak load hours, for transformer TR1, the percentage loading exceeds 100% of the rated value already at the level of 30% penetration of EVs, whereas for transformer TR2, no overloading is observed.

The additional charging load from the EVs also impacts the node voltages during peak load periods as can be seen in Figure 8 for the case of 80% EV penetration.

The RMS values of the node voltage for eleven nodes are also not within the permissible range of $0.9\mathrm{pu}$ and $1.1\mathrm{pu}$, as defined by the standard EN 50160.

We then connect the SST between node N1 and node N12 to mitigate the impact of EV charging loads on the distribution grid by routing active power from transformer TR2 to reduce the overloading of transformer TR1. No limitations have been placed on the sizing of the SST. In order to determine the active power set-point $\left(P_{set}\right)$ of the SST, we first calculate the maximum percentage loading of transformers TR1 and TR2 for each of the three EV penetration scenarios. For instance, the maximum percentage loading of transformer TR1 for the cases of 30% EV penetration and 80% EV penetration is in the range of 102% and 116%, whereas for transformer TR2, this value is in the range of 83% to 94%. Therefore, the active power set-point for the SST can be set such that it routes a maximum of 10% of the rated power of transformer TR2, i.e., 2.5 MW, assuming a unity power factor.

As the comparison of percentage loading of the transformer presented in

Table 1. EV penetration and the reduction in transformer loading with SST for each case.

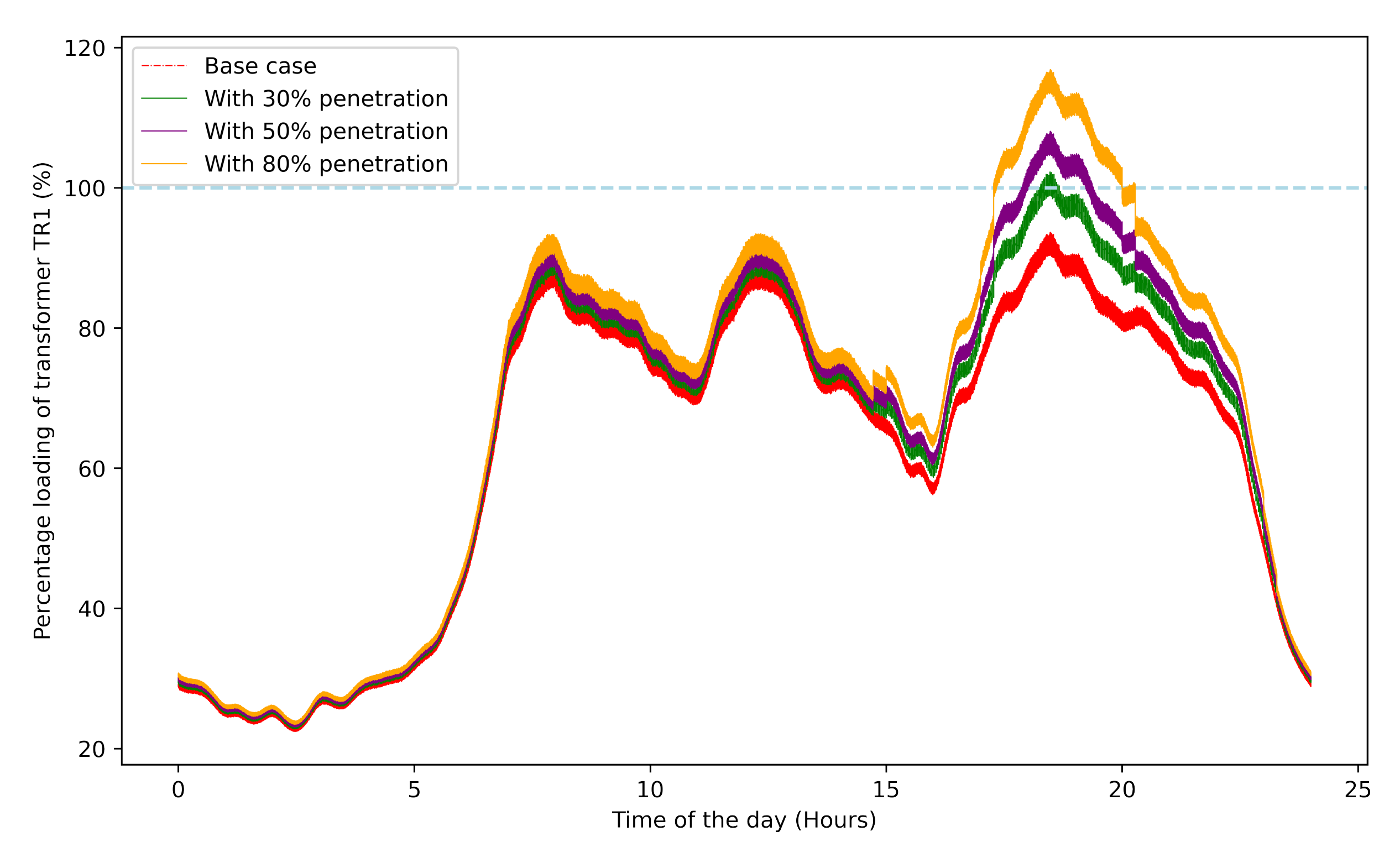
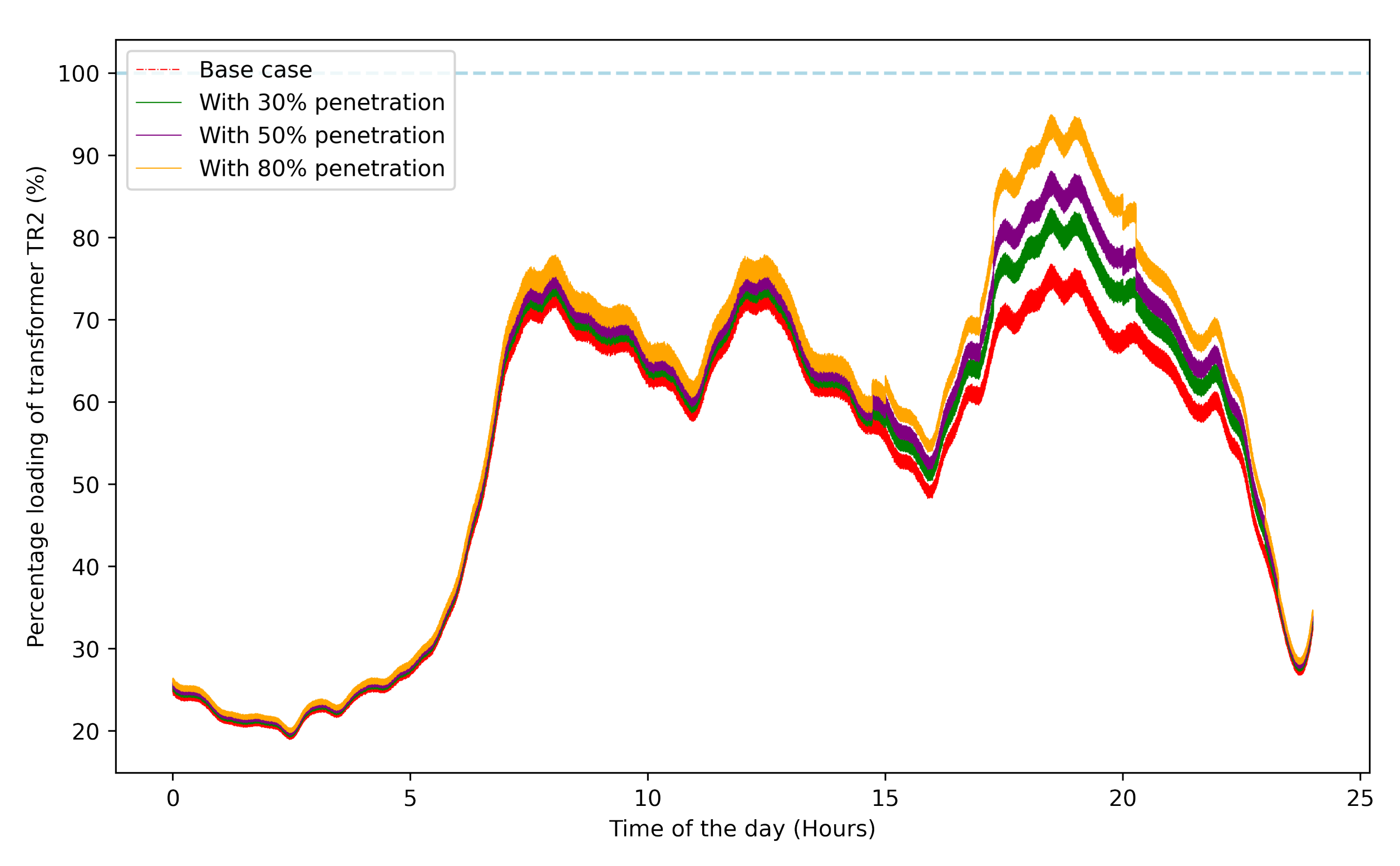
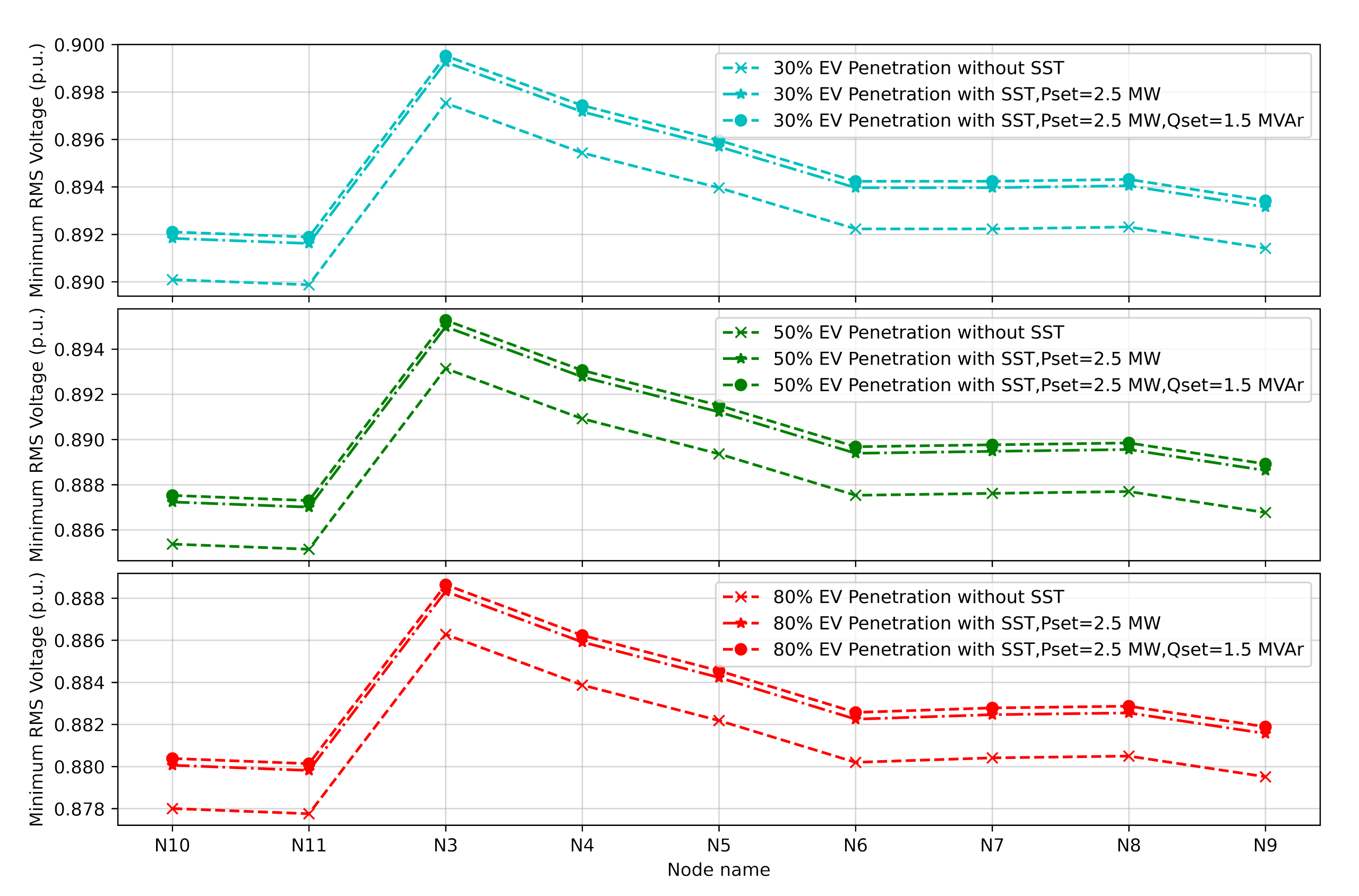
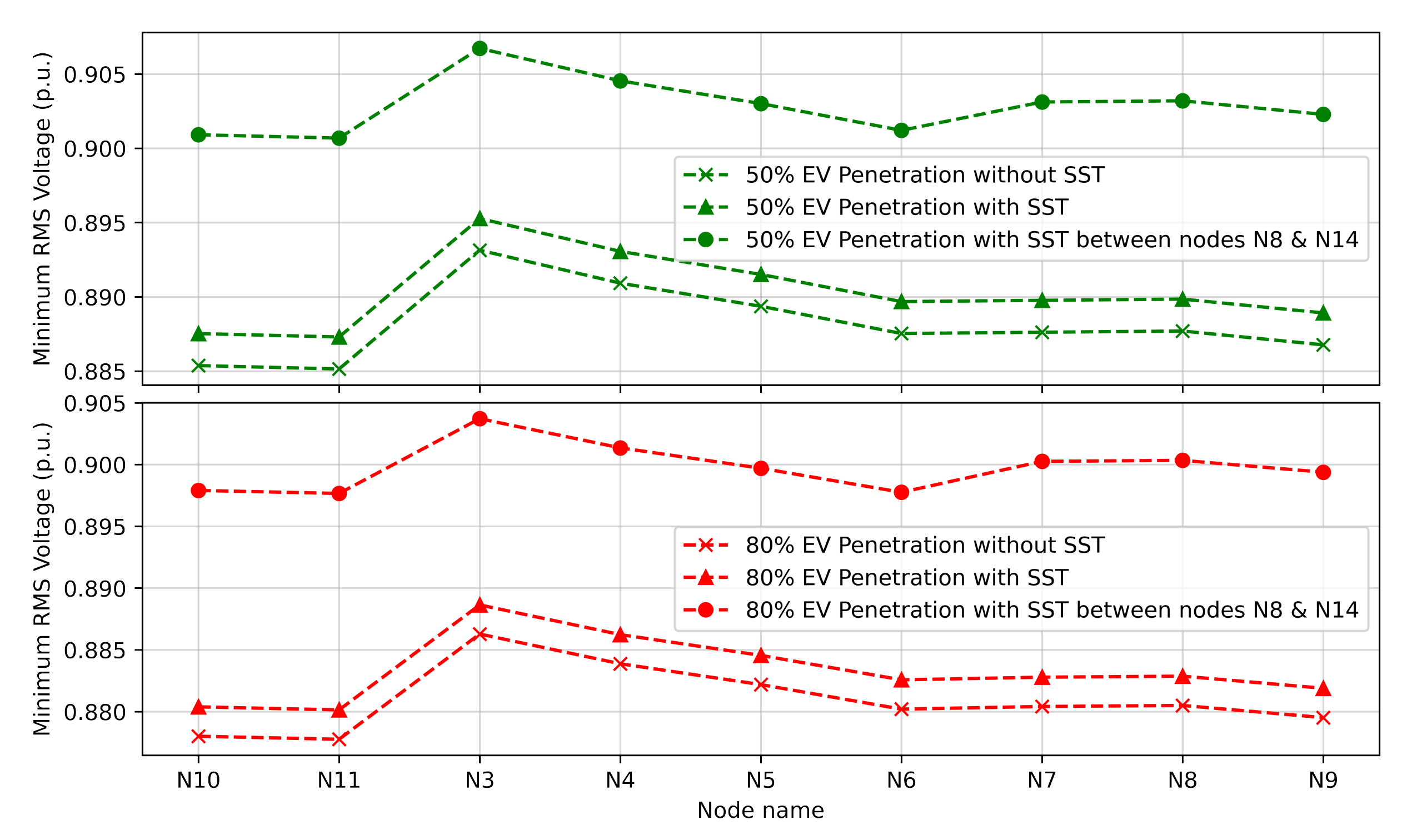
Level of EV Penetration	Max. Loading of the Transformer TR1: Without SST	Max. Loading of the Transformer TR1: With SST	Max. Loading of the Transformer TR2: Without SST	Max. Loading of the Transformer TR2: With SST
30%	102.25%	92.10%	83.53%	93.64%
50%	108.05%	97.83%	88.07%	98.24%
80%	116.86%	106.53%	94.94%	105.19%

shows, a reduction in the percentage loading of transformer TR1 is achieved with this set-point without overloading transformer TR2 for the 30% and 50% penetration cases. However, for the 80% case, this set-point causes both transformers to be overloaded. Consequently, the maximum rating of the SST to be installed depends not only on the forecasted load and maximum rating of transformer TR1 but also of transformer TR2.

In each of these cases, as shown in Figure 9, using the SST only to route active power improves the the minimum voltage at some nodes marginally, although this value for nine nodes still remains below the permissible limit of $0.9\mathrm{pu}$.

We therefore examine in the next step the effect of reactive power compensation from the SST. The reactive power set-point of the SST port connected to node N1 is set to 1.5 MVAr. As can be seen in Figure 9, with this reactive power set-point, a marginal improvement in voltage can be observed. However, the voltages for the case of 80% EV penetration still remain below the acceptable values. It is thus apparent that reactive power injection at the transformer bus is not sufficient to completely resolve voltage violation issues in the grid in case of high levels of EV penetration and uncontrolled charging.

As seen in Figure 9, the minimum voltages occur at the nodes N10 and N11. The placement of the SST is quite far away when compared to these nodes. The placement of the SST at the nodes N8 and N14 (as suggested by the benchmark description) improves the voltages at the critical nodes, as shown in the Figure 10. Thus, it becomes apparent that the position of the SST in the grid determines the overall effectiveness of the reactive power compensation.

4.1.2. Controlled Charging Scenario

As presented in Section 1, controlled charging strategies by Time of Use (ToU) pricing are applied to mitigate the impact of EV charging on the distribution grid and to simultaneously reduce the need for grid reinforcement. The ToU pricing-controlled charging strategy is designed such that the EV charging demand is reduced in peak load hours and increased in off-peak hours. Based on the base load profile, the following probabilities for controlled charging were determined for each of the three penetration cases [37]:

$$P\left(t\right)=\left\{\begin{array}{cc}0.10& t=6^{\mathrm{th}}-{15}^{\mathrm{th}}\mathrm{and}{17}^{\mathrm{th}}-{23}^{\mathrm{rd}}\mathrm{hours}\\ 0.30& t={15}^{\mathrm{th}}-{17}^{\mathrm{th}}\mathrm{hours}\\ 0.60& t=\mathrm{other}\mathrm{times}\end{array}\right.$$

(5)

For example, in the designed controlled charging scenario, peak saving of 25% is achieved as compared to the uncontrolled charging scenario between the 17th and 23rd h.

Table 2. Comparison of transformer loading for the controlled and uncontrolled charging scenarios.

Grid Parameters	30%		50%		80%
	Uncontrolled	Controlled	Uncontrolled	Controlled	Uncontrolled	Controlled
Maximum loading of transformer TR1 (%)	102.25	87.60	108.05	89.00	116.86	91.00
Maximum loading of transformer TR2 (%)	83.53	72.40	88.07	73.50	94.94	75.00

shows the comparison of different grid indicators under controlled and uncontrolled charging conditions. It can be observed that the transformer overloading is mitigated due to the controlled charging scenario. Consequently, the maximum power rating, i.e., the size of the SST used for grid reinforcement, can be reduced for a controlled charging scenario that reduces transformer overloading.

4.2. Low-Voltage Distribution Grid

The LV benchmark distribution grid simulated is the IEEE EU LV test feeder [38]. It is a radial distribution network fed by a 11 kV/416 V transformer (TR1) with the rated power of 0.8 MVA. In the base case scenario (BC), the transformers supply 55 loads. Since the benchmark feeder only has one transformer, an additional feeder with a transformer with a rating of 0.8 MVA (TR2) and load aggregated to emulate the base load profile for the original transformer as shown in Figure 11 was added to the simulation model. Load profiles are provided for the 55 loads with a 1-min time resolution over 24 h for power flow simulation.

As described earlier, the python tool emobpy is used to generate realistic charging profiles for the EV charging loads. The tool uses a combination of empirical mobility data, vehicle data, and a range of customisable inputs to generate profiles for battery electric vehicles. There are four different kinds of profiles that can be generated, out of which one is the most relevant for the purpose of this work, namely, the grid electricity demand profile. A number of assumptions and inputs were provided to the tool to generate the charging profiles. We used mobility data from the German mobility survey Mobilität in Deutschland (Mobility in Germany) [39] and the assumption that each vehicle is a Volkswagen ID.3, which is one of the vehicle models available in emobpy. Furthermore, we assume that charging can take place only at the workplace and at charging stations with a maximum capacity of 22 kW. To simulate a worst-case UC scenario, an immediate full capacity charging strategy, i.e., a charging strategy in which the car starts charging at the full capacity available at the charging station when it arrives, is assumed. Two different levels of penetration of electric vehicle charging stations in the grid were simulated by modifying the load profiles for 22 loads for a 40% EV penetration case and 27 loads for a 50% EV penetration case by adding the additional load caused by the charging of the EVs.

We first performed a BC scenario simulation using the base load profiles, followed by a UC scenario simulation with uncontrolled charging profiles as described previously for the two different penetration cases. Figure 11 and Figure 12 show a comparison of the transformer loading and the node RMS voltages. It can be seen that the simultaneous uncontrolled charging of EVs increases the loading of the transformer TR1 and causes voltage dips at some nodes during the peak load periods. Even though transformer TR1 is not overloaded for the 40% EV penetration, the voltages at some nodes falls below the acceptable limit of $0.9\mathrm{pu}$ during the peak load period. Most of these nodes are located at the end of the feeder.

The mitigation of the impact of the additional EV charging load on the grid is achieved by connecting the SST between the LV buses of transformers TR1 and TR2. The active power set-point $\left(P_{set}\right)$ of the SST is determined for the 50% EV penetration in order to balance the percentage loading of both transformers. Therefore, the active power set-point for the SST is set to 0.46 MW for the 50% EV penetration and to 0.3 MW for the 40% EV penetration.

As summarized in

Table 3. Comparison of grid parameters for different loading conditions and SST configurations.

Grid Parameters	40% EV Penetration without SST	40% EV Penetration with SST	50% EV Penetration without SST	50% EV Penetration with SST
Maximum Transformer TR1 Loading (%)	87.93	64.7	107.57	57.5
Maximum Transformer TR2 Loading (%)	7.70	32.4	7.70	57.5
Number of nodes with Vmin* <= 0.9 p.u. RMS voltage	88	85	116	115

Vmin* : minimum voltage at the node during 24 h.

, the SST reduces the loading of the transformer TR1 by routing active power from transformer TR2. It also reduces the number of nodes for which the minimum value of the RMS voltage is below the acceptable limit. It also improves the magnitude of the voltages at these nodes. However, the minimum voltage at some nodes still remains below the acceptable limit.

Next, we analyse the effect of reactive power compensation from the SST on the node RMS voltages by determining the number of nodes for which the minimum value of the RMS voltage is below the permissible limit with different levels of reactive power injection at the SST bus. Figure 13 shows a trend for the number of nodes for which the node RMS voltages remains below the threshold limit with increasing reactive power compensation from the SST. Although the number of nodes with minimum RMS voltage below the acceptable limit decreases with increasing reactive power injection from the SST, it does not reduce this number to zero, even for higher values of $Q_{set}$. Voltage regulation methods incorporating controlled charging strategies, the integration of renewable energy sources and battery storage systems therefore need to be employed in the LV grid in addition to the SST to resolve the voltage violation issue.

5. Discussion

So far, an analysis of how an SST can be used for grid-coupling in distribution grids to mitigate the impact of EV integration has been presented.

As explained in Section 2.3, the DC bus and losses of the SST are not modelled in this work. Therefore, additional advantages achieved from grid-coupling using the SST such as the integration of renewable energy sources or DC charging stations at the DC bus of the SST remain obscure. Additionally, when renewable energy sources are integrated at the DC bus, they can also route active power from the SST to reduce transformer overloading. The question regarding the determination of the active power set-point and therefore the size of the SST cannot be answered to the full extent due to this assumption. Future work that discusses the sizing and component design of the SST should consider the losses in order to estimate the operational costs arising from them.

The SST reduces transformer overloading by routing active power in the case of both LV and MV distribution grids. Reactive power compensation at the SST bus can be used to improve the voltage at critical nodes to acceptable values in the MV grid. In this case, the placement of the SST is an important factor in determining the extent to which the SST can contribute to voltage improvement. From the perspective of the Distribution System Operator (DSO), the decision regarding placement of the SST should therefore be made by conducting detailed power flow simulations while taking into account the evolution of EV penetration in the future.

To determine the active power and reactive power set-points and therefore the apparent power rating of the SST required, we have used a rule based method in the work. The method used might lead to an overestimation of the sizing of the SST. An accurate estimation of the apparent power rating of the SST required to mitigate the impact of EV integration on transformer overloading can only be obtained by calculating the maximum active and reactive set-points based on a given EV penetration forecast. This in turn requires performing comprehensive simulations that model the distribution-grid-level control to estimate the active and reactive power requirements of the grid based on real-time grid measurements.

In the case of the LV grid, however, when considering a scenario with extensive EV penetration, reactive power compensation from the SST cannot improve the voltage to an acceptable limit at all critical nodes. The SST does not eliminate the need for other, more localised voltage improvement methods such as reactive power injections from battery storage systems or renewable energy sources. Nevertheless, as discussed earlier, the SST offers additional advantages in terms of reducing transformer overloading even in the case of LV grids which localised voltage regulation methods do not offer.

6. Conclusions

This paper presented a novel approach to reduce the impact of EV integration on the distribution grid by coupling neighbouring grid segments using a SST. The simulation studies conducted show that using a SST in the proposed configuration with active power set-points which are in the range of 10% to 50% of the power rating of the conventional transformer reduces the transformer overloading caused by EV charging loads at peak load hours. In addition to this, the SST is also used for reactive power compensation to improve the voltage at critical nodes.

In the MV grid, the proposed solution reduces transformer loading to below 100% in peak load hours via active power routing. Moreover, it ensures that the voltage at all 14 nodes is within the acceptable limits by reactive power injection.

In the LV grid, the proposed solution can reduce the transformer overloading in peak load hours. However, localised measures for voltage improvement can still be necessary in case of high levels of EV penetration under uncontrolled charging conditions.

Our simulation studies thus show that SST-based grid reinforcement mitigates the impact of additional load due to EV charging. As compared to controlled charging scenarios which can be inconvenient for the consumers, the SST uses underutilized capacity in the grid to fulfill EV charging demand and reduces its impact on the grid. The SST also offers additional benefits as described in Section 5, which upgrading of the conventional transformers to accommodate higher loads does not offer.