The Errors of Electronic Energy Meters That Measure Energy Consumed by LED Lighting ^†

Abstract

Various metrological aspects for the correct measurements of electrical energy that is consumed by energy-saving (mainly LED) single phase loads are discussed in this paper. One of the most important problems presented here concerns the question of how strong distortions of the current waveform, introduced by typical LED lighting, affects the operation of electronic energy meters. Measurement results for the energy consumption of different LED lamps used in households in various conditions, alongside comparative results that were obtained by electronic and electromechanical energy meters, were also offered and the appropriate conclusions were then drawn.

1. Introduction

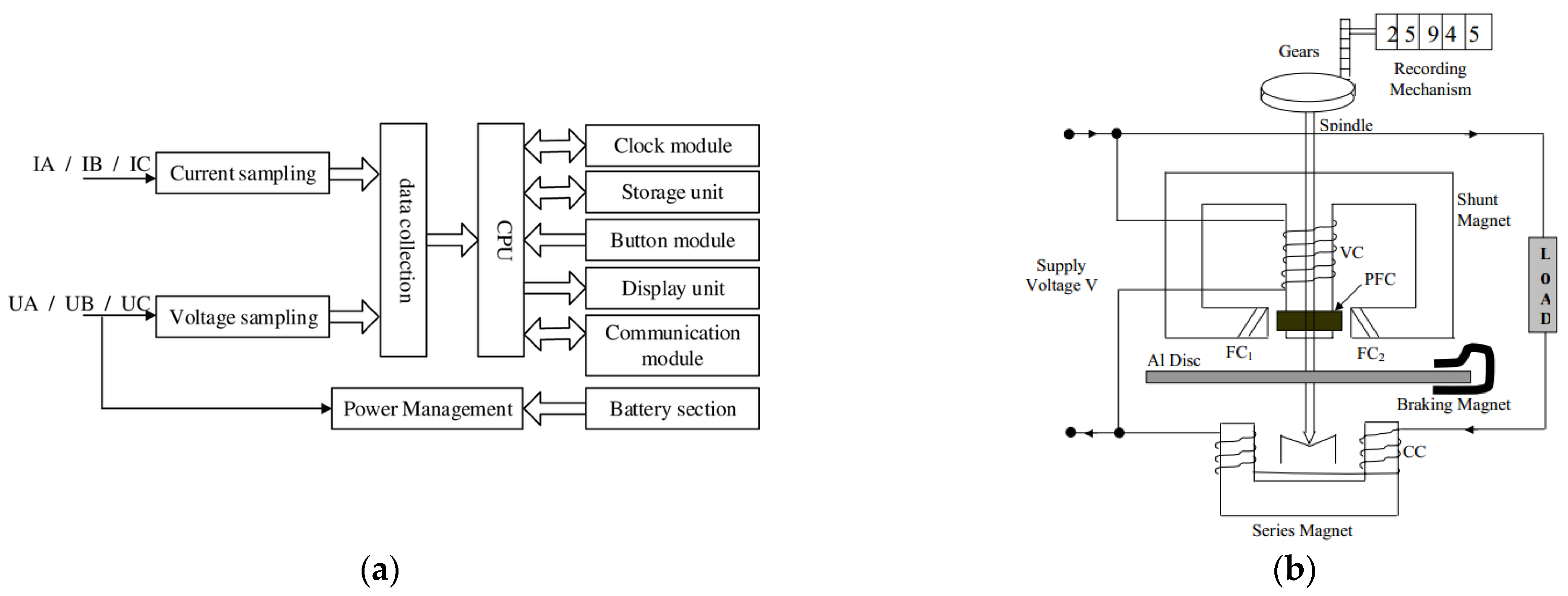
The use of light-emitting diode (LED) lamps in both utility distribution systems and everyday households continues to spread due to the implementation of energy-saving policies [1]. However, LED lamps, and their switching power supplies, can strongly distort the AC current that flows through them [2,3,4,5,6]. Current distortion, in turn, may cause problems with the accurate measure of the electrical energy consumed by a residence, a business, or an electrically powered device. Electric energy is measured using energy meters that are also known as “electricity meters”, “electric meters”, or “kilowatt-hour meters”. Such meters are either the electronic type (Figure 1a) or, less often, the electromechanical type (Figure 1b). For electronic meters, the analog AC signals that are fed into the main inputs of the energy meter are converted, by means of precise analog-to-digital converters, into a digital form, i.e., they are transformed into sequences of quantized samples. Further processing is performed using algorithms that have been developed by the meter manufacturer, which are usually a trade secret that is based on modern achievements in power theory. The instantaneous value of the power is calculated and then integrated over specific time intervals. The processing is performed so that the signal of the energy also reflects the higher harmonics of a specific band, which is present in the input waveform. It is noteworthy that there are many different technical solutions for electronic meters [7,8,9,10], which differ not only in their construction details, but also in their basic signal processing algorithms.

Nowadays, electronic meters are usually equipped with communication interfaces that allow for the use of such instruments in smart grid systems [11,12,13,14]. Moreover, electronic meters are much more resistant to acts of sabotage. Both electromechanical and modern electronic energy meters are adapted to measure the active and the reactive energy consumed by a load. Theoretically, the meters should be designed in a way that enables the correct measure of the energy consumption of various loads, regardless of their type. Among them, there is an ever-growing number of non-linear loads (such as energy-saving LED lamps or switching power supplies), which introduce strong current distortions. However, scientists from the universities of Amsterdam and Enschede highlighted in Ref. [15] that modern, homologated electronic energy meters might incorrectly measure the energy consumed by LED loads. To estimate the losses for electrical energy suppliers and consumers, which depend on the profile of the energy consumption, a great deal of research is now being conducted on the subject [16,17,18,19].

As a result, the authors of this paper performed a thorough study on the issues relating to the determination of how strongly an AC current is distorted by a non-linear LED load, which could affect the operation of the measuring instruments that are used in smart grid systems. The solution of this problem could be sought either via the use of power theory or by performing the relevant experiments. In this paper, which extended the previous work in Ref. [20], following a definition of the basic parameters and the methodology used in the investigation of energy errors, we described the results of measurement errors for electronic energy meters applied to different LED lamps that are available to households and other conditions. Finally, the appropriate conclusions were drawn with respect to the errors in the meters, and their dependence on the type of load and the current value used were discussed.

2. Basic Definitions

For commonly known power theory [21,22], the non-linearity of a load is represented by harmonic components due to the distortion of the current flowing through the load. When the mains voltage is sinusoidal and the load is non-linear, then the current is distorted. The latter can be given by the following formula:

$$I=\sqrt{I_1^2+I_1^2+I_1^2+\dots }=\sqrt{I_1^2+{\displaystyle \sum }_{n=2}^{\infty }{I}_n^2}$$

(1)

where I_n is the root mean square (RMS) value of the n-th harmonic of the current. The instantaneous power p(t) can be expressed as follows:

$$\begin{array}{l}p\left(t\right)=U{I}_1\cos \left({\phi }_1\right)\left(1-\cos \left(2\omega t\right)\right)-U{I}_1\sin \left({\phi }_1\right)\sin \left(2\omega t\right)+\\ +{\displaystyle \sum _{n=2}^{\infty }2U{I}_n\sin \left(\omega t\right)\sin \left(n\omega t-{\phi }_n\right)}\end{array}$$

(2)

Here, φ_n is the phase shift between the n-th harmonic of the voltage and current. The apparent power, S, of a system can be described by the following:

$$S=UI=U\sqrt{I_1^2+{\displaystyle \sum _{n=2}^{\infty }{I}_n^2}}$$

(3)

The following form can be found by squaring the following expression [23]:

$$\begin{array}{l}{S}^2=U^2{I}^2=U^2{I}_1^2+U^2{\displaystyle \sum _{n=2}^{\infty }{I}_n^2=}\\ =S_1^2+H^2=P_1^2+Q_1^2+H^2=P_1^2+D^2\end{array}$$

(4)

where P₁ and Q₁ are the active and the reactive power of the fundamental, H is the deformation power, and $D$ is the distortion power. The relationship between these power vectors is shown in Figure 2.

For the case of a non-linear load, the power factor, PF, is given by the following:

$$PF=\frac{P_1}{S}=\frac{P_1}{\sqrt{S_1^2+H^2}}=\frac{P_1}{\sqrt{P_1^2+Q_1^2+H^2}}$$

(5)

The harmonic content of the distorted AC current can be expressed with respect to the total harmonic distortion (THD) factor:

$$THD=\frac{\sqrt{{\displaystyle \sum _{n=2}^{\infty }{I}_n^2}}}{I_1}$$

(6)

3. Method for Determining Errors in Energy Meters

Energy meters belong to the group of measuring instruments that are subject to legal verification, which is sometimes called “primary verification” or “legalization” [24]. In Europe, all activities that relate to legalization are specified in the international measuring instruments directive (MID) 2014/32/EU. According to European regulations, an examination of the accuracy of the energy meters can be performed by use of the control meter method, or via the power and time method. Meter errors must be checked for different load currents; however, these standards do not mention a necessity to assess meter errors for non-linear loads. However, in non-European countries, other measurement methods and procedures can be used to determine the errors within energy meters [25,26,27,28,29].

To analyze the influence of the distorted current waveforms on the readings from the electricity meters, commonly used LED loads (colloquially called LED lamps) were selected; these are characterized by their different spectral characteristics and the extensive variation in their THD coefficient values. Due to the considerable quantity and variety in LED lighting, and the multitude of devices that can power them, it is perfectly reasonable to replace the analyzed loads in the measuring system with a Calmet C300 power calibrator [30]. The latter, which can simulate any pure or distorted AC voltage and AC current with any phase relation between them, was used to supply the current and voltage to the circuits of the tested electronic energy meters.

The employed measurement procedure to determine the errors in the tested energy meters consisted of the following steps:

• Initially, the harmonic currents of each investigated load were measured using the PQM-710 quality analyzer [31].
• According to the specific LED load, the C300 calibrator generated a suitable distorted current and supply voltage by applying the required amplitude and phase of each harmonic.
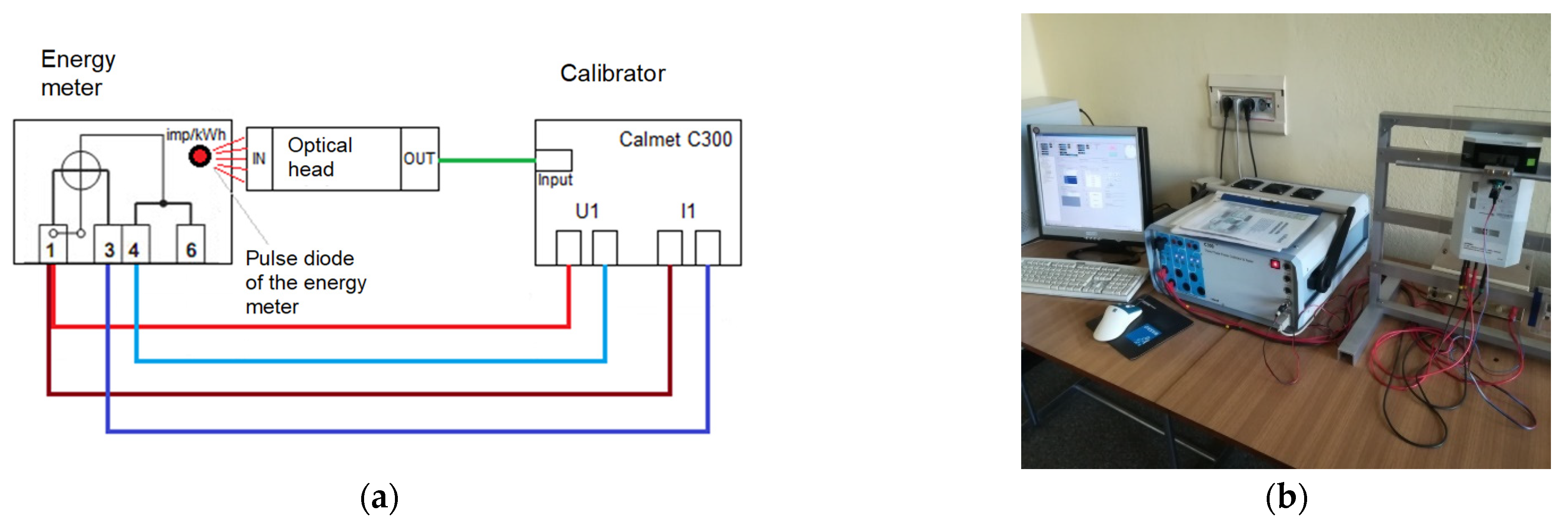
• Previously generated signals were used to supply the current and the voltage to the circuit of the investigated energy meter (see “U1” and “I1” in Figure 3).
• An optical head (see Figure 3) read the measurement from the energy meter under the test and sent the results to the calibrator.
• The software implemented within the C300 calibrator (Figure 4) enabled registration of the energy indicated by the tested meter using the power-time method.
• Finally, the error of the energy measurement was calculated, by use of the CALPRO software, as the difference between the true energy generated by the calibrator and the energy measured by the meter under the test.

The above procedure can be used to test various types of energy meters: both electromechanical and electronic ones, and others that incorporate smart technology. The main advantage of this method centered around the usage of a proper calibrator, as this eliminated the need to perform measurements on real LED loads (but their characteristics must be known). Using this procedure, more than a dozen different electronic energy meters were tested. As seen in the next section, selected measurement results were presented that were typical for such energy meter designs. It is worth emphasizing here that, before the metrological tests, all the electronic energy meters passed the resistance tests in relation to strong magnetic fields and high temperatures, alongside the ESD and EMC tests.

4. Results and Discussion

To analyze the impact of the AC current distortions on the readings from the electronic energy meters, non-linear main powered devices (dedicated to single phase household solutions) were used. The light-emitting diode (LED) bulbs, and the lamps employed in the analysis, had different spectral characteristics and different THDs. The loads selected for the tests are listed in

Table 1. Lighting used in the investigation of the meters.

No.	Load	P	PF	THD
		W	-	%
1.	LED sconce (3 LED lamps, such as load no. 5)	11.0	0.81	34.1
2.	LED stair lighting (8 LED lamps, such as load no. 5)	29.5	0.78	40.1
3.	Household lighting (about 50 LED lamps, such as load no. 5, 6, 7)	236.5	0.74	44.5
4.	One floor of household LED lighting (about 20 LED lamps, such as load no. 5)	58.4	0.67	45.1
5.	1 LED lamp	3.0	0.52	94.0
6.	3 LED lamps	32.1	0.46	134
7.	Smartlight LED (LED lamp with light color adjustment)	5.0	0.43	201

. Position no. 3 from this table should be treated as group lighting, in which the LED lamps accounted for 90% of all the lighting bulbs. The smartlight LED represented a smart LED bulb that was controlled remotely, which could emit light of different colors. Initially, the harmonic currents of each investigated load were measured by use of a power quality analyzer PQM-710 [31] that met the normative requirements of class A, according to EN 61000-4-30 [32]. This instrument was also used to measure the active power P, power factor PF, and total harmonic distortion THD. The results of the measurements are reported in Table 1. As can be seen, the smartlight LED is shown to have the highest THD factor.

The manufacturer of the CALPRO C300 calibrator provided software that enabled the setting up of distorted currents for a load, which was achieved by declaring the magnitudes and phases of each individual harmonic. The software could also calculate the indication error of the tested meter by using the power-time method, taking the calibrator settings as the reference [33]. Different types of LED lighting were tested in various configurations. Among the loads, there were both single LED lamps (positions no. 1, 5, and 7 in Table 1) and groups of LED lamps (positions no. 2, 4, and 6 in Table 1) alongside the mixed loads with a predominant number of LED lamps (position no. 3 in Table 1). Such a diversity of configurations made it possible to determine the impact of group loads on the operation of different electronic energy meters. The accuracy of the meter readings was evaluated according to the current calibration procedure [34], both for sinusoidal AC currents and for distorted current that contained up to 40 harmonics (Figure 5).

The test results that were performed for the selected, relatively high-performance electronic energy meter are presented in

Table 2. Measured errors for a B-class electronic energy meter and a 2.0-class inductive meter.

No.	Load	Error of the Electronic Meter			Error of the Inductive Meter
		ε1	ε2	ε3	ε4
		%			%
1	LED sconce (h)	−0.441	−0.443	−0.439	−0.177
1′	LED sconce	−0.884	−0.892	−0.884	−0.184
2	LED stair lighting (h)	−0.107	−0.111	−0.119	−0.092
2′	LED stair lighting	−0.188	−0.173	−0.184	−0.542
3	home lighting (h)	−0.024	−0.023	−0.024	0.255
3′	home lighting	−0.056	−0.056	−0.056	−0.087
4	LED floor lighting LED (h)	2.659	2.697	2.665	0.930
4′	LED floor lighting LED	−0.116	−0.115	−0.105	0.151
5	1 LED lamp (h)	15.959	15.942	15.951	1.544
5′	1 LED lamp	−0.835	−0.835	−0.843	0.043
6	3 LED lamps (h)	−0.157	−0.153	−0.190	1.660
6′	3 LED lamps	−0.171	−0.168	−0.163	0.107
7	Smartlight LED (h)	2.676	2.664	2.676	1.846
7′	Smartlight LED	−1.016	−1.021	−0.998	0.101

. To confirm their repeatability, three measurements were made and the subsequent meter reading errors were represented as $\epsilon 1$, $\epsilon 2$, and $\epsilon 3$. The marking h in Table 2 indicates the obtained results from the distorted current waveforms. In the final column of this table, the comparative results that were found using an electromechanical 2.0 class meter are reported. Based on the obtained results, it was observed that excessive errors in the electronic energy meter indications only occurred when the distorted current waveform from a load was considered. In addition, a good repeatability (with a maximum deviation, s = 0.02%) was observed and the highest error was obtained for a certain LED lamp. This error exceeded the permissible error (which equated to 2% accuracy for class B) by almost 14%. It is worth emphasizing here that, in each case that exceeded the permissible errors, the obtained errors were positive, i.e., more energy was measured than should have been. This was obviously an unfavorable configuration for the energy consumer. However, when the current was sinusoidal for a given load, the errors of the energy meter were always smaller than the maximum permissible for a given accuracy class. Furthermore, all the results obtained using the electromechanical inductive energy meter were within the permissible error, which was ±2%.

In cases for mixed and group LED loads, the permissible error was never exceeded. In this case the resultant current was less distorted, resulting in smaller total non-linearity of the circuit. During initial investigations on the impact of an LED load on the energy meters errors, it was noted that such errors depended on the power of the load and the level of the current distortion, i.e., the THD. Therefore, a suitable study was performed for different THD values and load currents.

Table 3. Dependence of the electronic energy meter errors on the current value for THD = 34.1.

Load: LED Sconce THD = 34.1
I, A	0.25	0.50	1.00	2.50	5.00	10.00
Error (h), %	−0.211	−0.139	0.133	−0.023	−0.142	−0.096
Error, %	−0.357	−0.303	−0.209	−0.167	−0.181	−0.209

,

Table 4. Dependence of the electronic energy meter errors on the current value for THD = 40.1.

Load: LED Stair Lighting THD = 40.1
I, A	0.25	0.50	1.00	2.50	5.00	10.00
Error (h), %	0.268	0.778	0.648	0.405	0.232	0.518
Error, %	−0.338	−0.259	−0.234	−0.214	−0.165	−0.115

,

Table 5. Dependence of the electronic energy meter errors on the current value for THD = 44.5.

Load: Household Lighting (LED Is Dominated) THD = 44.5
I, A	0.25	0.50	1.00	2.50	5.00	10.00
Error (h), %	0.270	0.785	0.730	0.487	0.130	0.711
Error, %	−0.383	−0.285	−0.261	−0.240	−0.158	−0.040

,

Table 6. Dependence of the electronic energy meter errors on the current value for THD = 45.1.

Load: One floor of Household LED Lighting THD = 45.1
I, A	0.25	0.50	1.00	2.50	5.00	10.00
Error (h), %	0.384	0.959	0.791	0.601	0.426	0.584
Error, %	−0.471	−0.341	−0.297	−0.239	−0.250	0.006

,

Table 7. Dependence of the electronic energy meter errors on the current value for THD = 94.0.

Load: 1 LED Lamp THD = 94.0
I, A	0.25	0.50	1.00	2.50	5.00	10.00
Error (h), %	0.753	34.627	1.045	0.818	−0.896	1.185
Error, %	−0.423	−0.341	−0.310	−0.287	−0.310	−0.264

,

Table 8. Dependence of the electronic energy meter errors on the current value for THD = 134.

Load: 3 LED Lamps THD = 134.0
I, A	0.25	0.50	1.00	2.50	5.00	10.00
Error (h), %	1283	28.694	1.162	0.476	0.244	0.849
Error, %	−0.614	−0.527	−0.487	−0.435	−0.391	−0.098

and

Table 9. Dependence of the electronic energy meter errors on the current value for THD = 201.

Load: Smartlight LED THD = 201
I, A	0.25	0.50	1.00	2.50	5.00	10.00
Error (h), %	0.090	40.148	0.271	0.227	1.032	6.995
Error, %	−0.235	−0.155	−0.120	−0.113	−0.082	−0.145

display, for various loads and load currents, the representative results of these tests.

It was observed that when the THD was higher than approximately 50%, the error indications of the energy meters clearly increased, especially for low-power loads or when a load was tested alone rather than in a group. In special cases, when a load was highly non-linear (i.e., the THD was above 100%), errors for the small load currents might have values that significantly exceed the permissible levels for a certain class of energy meters (for example, 0.5 A in Table 7, Table 8 and Table 9). As determined from the obtained results, there was no visible monotonic dependence between the current value and the measurement error. As seen in the previous tests, the error values for the non-linear loads (the distorted currents) were always positive, which was unfavorable for the consumer. Additional measurements and tests, which were not presented here, have been performed using various energy meters and non-linear loads. These further studies confirm the accuracy of the observations and the results shown in this section. The presented results are typical and they show that measuring the energy power of non-linear loads, using electronic energy meters, could burden electrical systems with substantial measurement errors.

5. Conclusions

In this paper, an analysis on the influence of distorted current waveforms on measurements by smart energy meters was performed. The conducted research concerned the problem of the influence of selected non-linear loads on the measurement results from electronic energy meters used in smart grid systems. The influence of the level of current distortion, represented by the THD factor, for different current values (representing various loads) on the measurement errors of typical electricity meters was determined. In the experiments, special attention was paid to groups of non-linear loads, since they constituted a typical load for current circuits of electricity meters under actual conditions. The sample research results that are presented were representative of a group of several meters tests, which were produced by various manufacturers, that are commonly used in utility distribution systems.

Experimental measurements performed on an LED lamp showed that, for cases when the mains were loaded by a large number of highly non-linear loads (for example, LED bulbs), the errors in the recorded measurements from the electronic energy meter could be significant. In some instances, this might exceed the permissible error for a given accuracy class of the tested meter. It was determined that this situation mainly occurred for low-power loads and devices that are in standby mode. In the case of an analog electromechanical instrument, exceeding the permissible error did not occur. Moreover, the errors in electronic meters that measured the energy consumed by LED loads with THD < 50% were usually within acceptable limits, while errors for electrical loads with a more distorted current (i.e., THD > 50%) were very often seen to significantly exceed permissible values. When loading the current circuits of the meter with non-linear group loads, apart from in rare instances, there were no errors in the measurements from the electronic meters that exceeded the permissible values for a given class. This could be explained, for this case, by the smaller load current distortions that arose compared to individual loads. To conclude, the performed investigations showed that it was advisable to check whether the established calibrating procedures for modern electronic energy meters, assuming sinusoidal current, were providing accurate results, especially in the era of the widespread use of non-linear loads.