1. Introduction
Power quality issues and contingency management techniques have been a constant challenge over the past 30 years for transmission systems and more recently for distribution grids [
1,
2,
3]. Traditional techniques for mitigating contingencies and balancing loads in power systems include grid reconfigurations, new investments in transmission lines, installing new substations, etc., and have promised reduced technical losses and increased distribution reliability and capacity. However, these are practices that require high-cost investments even though nearby lines sometimes are often idle, while others are overloaded.
Instead of installing new infrastructures to increase capacities and power transfer capabilities [
4], power flow manipulation is traditionally achieved using phase-shifting transformers (PSTs) in transmission systems. Modernization using flexible AC transmission systems (FACTS) derived technologies has resulted in changes to traditional methods to improve the capacity of distribution grids. Distribution grid modernization is an essential challenge when seeking to provide more resilient systems as transmission grids are improved. This may include using smart converters, digital protection schemes, or remote operations.
It is known that FACTS allow existing grids to be used closer to their thermal capacities and economic limits, without drawbacks in stability [
5], resulting in better energy use. As explained in [
6], power electronic solutions for distribution grid applications are technologically analogous to modern FACTS with voltage source converters (VSC) and are known as RACDS (resilient AC distribution systems).
The series VSC of this study is considered an active tool, which can be applied to the smart grid concept. The smart grid concept can be defined as the modernization and use of active tools, with control capabilities and telecommunication architectures, in existing power systems [
7]. This allows efficient energy utilization (e.g., in grids with bidirectional power flow as in presence of DGs) when devices are embedded with intelligent algorithms, sometimes controlled autonomously or remotely.
In fully supervised systems, the smart grid philosophy also includes the coordinated use of many types of RACDS devices and ensures improvements in congestion, thus reducing technical losses and the duration and frequency of outages. Furthermore, the authors of [
8] consider a smart grid as the better use of devices and sensors spread throughout the grid.
Distribution grids are traditionally designed using radial topology for unidirectional power flow. Nevertheless, the increasing use of distributed renewable energy resources has drawn the attention of researchers to management solutions for smart load flow behavior, thus guaranteeing increases in the capacity and reliability of these types of power systems for solving voltage and overload problems. Nowadays the compensation approach using series converters has spurred innovations in new technologies while creating challenges for solving many power quality drawbacks associated with the increased investment demands in distribution grids.
Series VSCs have been widely investigated in the power electronics fields, like series active power filters, dynamic voltage restorers (DVRs), and static synchronous series compensators (SSSCs). SSSCs inject an independently controlled voltage in quadrature with the line current and can be used for impedance compensation in long transmission lines, and need only reactive power exchanges with the line without a DC source. On the other hand, to have more degrees of freedom and to control both active and reactive power flow with a series compensator in a meshed grid, either energy storage or a path to receive active power from one of the feeders is required.
The main trends in recent research related to solutions for power flow controllers, or power routers, are listed below. References [
9,
10] present the features and experimental results for meshed grids using unified power flow controllers (UPFCs) applied to distribution systems for reducing technical losses and providing voltage regulation. A study on the benefits of using looping radial distribution systems is discussed in reference [
11], where a multilevel cascaded H-bridge series converter connecting feeders from different substations was used. Furthermore, Ref. [
12] shows the power system behavior when using closed loops in radial systems for distribution and transmission levels, with analysis considering the loop current path for variances in line impedances.
Reference [
13] highlighted challenges and limitations in simulations using additional series converters in short-circuit applications with resonant controllers for medium voltage systems. The drawbacks presented in the study were that the converter needed to impose a voltage at the nominal value in the grid. Furthermore, Ref. [
14] presented a technique for turning off the IGBTs (i.e., using freewheeling diodes) during a short circuit and thus, blocking the current flowing through the interconnection during a fault, and Ref. [
15] presented a simulation for a series converter to substitute the phase shift transformers to control the power flow and mitigate short circuiting.
A multilevel cascaded H-bridge converter called a distribution static synchronous series compensator (DSSSC) was presented in [
16], along with the simulation results for a case study at 20 kV. The study also presented the experimental low-voltage results and offered proposals for control strategies. References [
17,
18] presented topologies for series AC-AC converters, called controllable network transformers (CNTs) and the authors of [
19,
20] presented a compact dynamic phase angle regulator (CD-PAR).
A hybrid solution is presented in [
21,
22], using a series-series VSC topology with a shunt variable capacitor for transmission and distribution systems. These publications present simulations and selectable control modes for each system behavior and propose an optimal dispatch algorithm for power flow control.
References [
23,
24] comment on loop power flow controllers and propose a back-to-back (BTB) converter for a case study for a 6.6 kV level distribution voltage. Additionally, Refs. [
25,
26] present an autonomous control technique for power flow controllers that tracks the best power transfer to minimize losses using information from terminal voltages with a BTB converter.
About the presented AC-AC converters, Ref. [
26] presented drawbacks for a series VSC solution emphasizing fault sensitive problems and the limited lifetime of the DC-link capacitance, and thus propose a buck-type AC-AC converter called a direct power flow controller.
Back-to-back converters interconnected to distribution feeders seem to be the best alternative for this type of application [
27], i.e., this equipment makes use of PQ power transfer between the feeders, resulting in reactive compensation, consequently improving the terminal voltage and in general improving the overall power quality. However, this bulky solution is complex and more costly than series VSCs because full-rated multilevel converters for making the interconnections are needed, e.g., for a 1 MVA power transfer, two 1 MVA DC-AC converters are needed.
One should note that distribution grids do not have a large variation in the phase angle difference between close feeders when they come from the same main source [
28]. Distribution lines are relatively short compared to transmission systems. Instead of using a back-to-back converter, a small-rated series VSC could provide a low-cost approach because only a fraction of the system voltage is needed for loading flow manipulation, even though this approach is not as flexible as the BTB converter [
29].
Furthermore, these solutions can balance power between the future distribution of meshed feeders, and consequently improve power quality, while reducing technical losses. In [
28], their application demonstrates that any changes in the power flow through any grid lead to improvements in the reactive power requirements from the main generators.
The approach allows radial distribution grids to be converted into meshed grids. This results in a controlled and secured way of improving operation in real time and during contingencies. Series devices have fewer commercial applications than shunt devices (not as effective for flow control), and in many cases, the series VSC alone can provide features for effective loading balance management [
6]. Additionally, series VSC is more vulnerable to fault currents [
30,
31]. The biggest challenge when inserting a series converter into an electrical system is that it must be able to make smart decisions or be removed and protected in case of either a short circuit or a power outage.
This work demonstrates a solution of an active tool that contributes to independent control and transfer of active and reactive powers between distribution feeders. Instead of the use of a bulky back-to-back converter, the small-rated series VSC can be a low-cost solution for the same application.
Figure 1 shows the topology of the developed series real-time power flow controller that was built and applied in a 13.8 kV test system. The control system, based on the MSRF (modified synchronous reference frame), was implemented in a TMS320F28335 DSP (digital signal processor).
The power circuit comprises an IGBT-based H-bridge converter connected in series with the distribution lines using a coupling transformer with a diode rectifier supplying the DC-link for each phase. Every phase has its own controller and power circuit, resulting in a modular design that can be arranged for a single or three-phase system. The proposed topology can perform:
Several applications of the proposed system can be mentioned, although not covered completely in this publication due to lack of space. Regarding the embedded protection scheme, the solution can quickly protect the converter in surges (over-voltages and over-currents) using a thyristor-based system that removes the converter during either a fault or an outage, which will be presented and detailed in a future publication.
With respect to the harmonic isolation feature, the proposed series VSC could provide improvements in power quality as shown in [
32]. The converter is also a series active power filter that can harmonically isolate both feeders, keeping the system, from the harmonic point of view, as it was before the interconnection. This is achieved by transferring power between the interconnected feeders exclusively at the fundamental frequency, providing improvements in terminal voltage profiles. Still, this feature is not the main focus of the present article.
In presence of renewable energies or DGs, fluctuations of terminal voltages are commonly caused by the varying active power injected by DGs at the end of long feeders. In this scenario, the equipment can use the power generated by renewables for better active power distribution between feeders, consequently providing mitigation of the voltage fluctuations and over-voltages.
Another application is for reactive power control in situations where there are fixed capacitor banks installed in some of the feeders. The excess of reactive power from existing capacitor banks can be transferred to another branch that is interconnected by the converter, where, at certain times, there is a need for reactive compensation.
Moreover, as distribution systems are unbalanced, the series VSC is composed of three single-phase converters and every phase has its own controller and power circuit (based on the MSRF technique applied in independent single-phase converters), which provides the features for voltage unbalance mitigation.
Thus, focusing on both active and reactive power transfer, this paper provides contributions on modeling fundamentals, control proposals, and the practical results for a series VSC used in 13.8 kV laboratory and field tests.
Furthermore, the next sections show firstly the discussion about the problem formulation and operating challenges regarding the use of series converters application in distribution grids. Finally, it presents the control system and experimental results.
2. Formulation of the Problem
This section will highlight some relevant aspects regarding the strategic changes from a radial to a meshed distribution grid by permanently interconnecting two feeders at the end of their lines, based on reference [
28].
Traditionally, distribution grids do not operate in a permanent loop or ring.
Figure 2 shows a typical distribution system. A well-known operating procedure commonly used in distribution grids is when two feeders are connected in parallel (indicated in
Figure 2 as a normally open switch) for a short time and one of the feeders is removed at the beginning. This is an operating procedure used for maintenance, and it interrupts only a small section of the whole system. This operating procedure is a momentary reconfiguration that prevents many loads from not being supplied for long periods during strategic operations or maintenance.
Distribution systems are commonly radial and overhead. In some cases, the normally open switch (
Figure 2) represents a backup source for reducing interruption times. A strategic rule for ensuring reliability is that at least two feeders at each consumption point are needed [
28]. However, nearby lines are sometimes nearly empty while others are overloaded.
Furthermore, it is common to use reclosers installed at strategical places in distribution systems, sometimes using remote command, to prevent long outages at critical loads when maintenance is needed and/or fault conditions occur. It is well known that distribution lines have a small phase rotation [
28,
33], since it comes from the same main voltage source, and since it has the same configuration as the substation’s step-down transformers, allowing one to permanently operate this system in a meshed configuration. Nevertheless, the impact on the short-circuit level does not allow for a permanent grid reconfiguration this way.
Figure 2 shows the flow of short-circuit currents. Depending on the location of the fault during a phase-to-ground short circuit, the voltage over the converter can reach grid-rated voltage values, which requires an effective protection system for a small-rated topology.
It should be noted that for meshed grids the short-circuit currents flow from both feeders, and this current in the indicated section point can be more damaging (i.e.,
Icc = Icc1 + Icc2) for local protections. Through the interconnected ring (location of the installed converter) the short-circuit currents do not rise like they do in the indicated fault section point. Therefore, in terms of protection, this condition is less damaging to the series converter than at the section point. Regarding the short-circuit behavior, a series converter may be applied with an appropriate protection scheme, as in [
31,
34].
In distribution systems, it is common to use a series of step-up transformers for relatively long distribution lines to compensate for distance voltage drops. In the same way, capacitors are applied for reactive power compensation even knowing that the reactive power flow is less effective in distribution lines than in transmission systems for voltage improvements.
Reactive power flows are effective in transmission due to the high X/R ratio. In distribution systems, the X/R ratio is close to a unity value, and the best place for reactive power injection is close to the loads. Thus, in distribution systems the power factor correction helps alleviate the VAr flow, which increases the ability of circuits to transport more active power.
Furthermore, it is known that the system stability concept is the ability to remain in stable operating conditions (acceptable voltages and power flow) even after a small (dynamic stability) or large disturbance (transient stability). During large disturbances, as explained above, the protection scheme removes the converter from the system and both feeders return to the radial configuration. With respect to the dynamic stability issues, the typical phase difference between the feeders where the proposed solution may be installed is small (about 3 to 5 degrees) and the small-rated low-voltage converter is able to impose a voltage to P&Q manipulation up to 11 degrees i.e., the converter’s power rating is a small fraction of the power transfer capacity which reduces the capacity of operation during large disturbances. This phase angle difference is a value far away from the system stability limit, which is 90 degrees [
35]. Since the purpose of this equipment is to manipulate power only during relatively small disturbances, the converter will always operate in a stable range without reaching the dynamic stability limits. In addition, the results presented show the behavior of the converter during load disturbances, which showed that after load variations (demonstrating amplitude and angle variations during the converter operation), the system returns to stable conditions, proving its behavior within the stability margins.
Finally, the series converter can be installed to replace (or in parallel to) the
normally open switch, indicated in
Figure 2, and can provide real-time active and reactive power flow control, providing load balance between feeders, voltage profile improvements, increased load capacity, and allowing for distribution grids to be automated.
3. Modelling
To analyze the distribution system that will apply a series converter, one must define a coherent dynamic representation. For large systems, it is common to use iterative methods for solving the load flow, especially in meshed grids. In distribution systems, distributed parameters or pi-sections modeling is not needed for short distances less than 80 km. Thus, one approach for this modeling can be achieved with a series impedance (
R + jX), and shunt conductance can be disregarded [
28].
For dynamic representation, the equations that describe the dynamics of the system can be linearized for analysis even if the power system formulation is nonlinear. The next subsections will present the system representation using the impedance method and will emphasize the relationship between the system model and the control blocks of the VSC presented in
Figure 1.
In a hypothetical situation, the analysis starts with two radial feeders that can be interconnected at the ends of the distribution lines, as shown in
Figure 2, with each impedance for each section/node. Terminal voltages
V1 and
V2 represent the loop interconnections.
If we are not interested in the load flow behavior and the values of each voltage node in this system, it is possible to obtain an equivalent representation, as shown in
Figure 3, using Thevenin’s representation for each distribution feeder, where
VA and
VB are the main feeder voltage sources,
TA and
TB are the main step-down transformers,
ZL1 and
ZL2 are the distribution line impedances,
Z1 and
Z2 are load impedances,
LF1 and
LF2 are the converter switching filter inductances,
TS is the coupling transformer, and
Cdc is the series converter DC-link capacitance. V
1,
V2, and
VT are the terminal voltages and the converter’s imposed voltages, respectively.
Since the converter DC-link has a fixed voltage, as it is maintained by a three-phase diode rectifier connected to one of the feeders (
Figure 1), the VSC series can be represented by a controlled AC voltage source, as shown in
Figure 4.
Figure 4 also shows the conversion to equivalent impedances of the main step-down transformers (
ZTA and
ZTB), the filter inductances (
ZF1 and
ZF2), and the coupling transformer equivalent impedances (
ZS1 and
ZS2).
The simplified representation can be derived from
Figure 5 with the loads represented as current sources (
ik1 and
ik2) as a function of the terminal voltages
V1 and
V2 and the load impedances (i.e.,
ik1 =
V1/Z1 and
ik2 =
V2/
Z2). Additionally, the equivalent transformer models can be added to the line parameters for further simplification.
Figure 5 shows the reduced model where
ZA =
ZL1 +
ZTA,
ZB =
ZL2 +
ZTB and
ZT =
ZS1 +
ZF1 +
ZS1 +
ZF2.
The simplified model of the system and the load behavior provides terminal voltage variations where the controllers should track and compensate for the voltage difference. Therefore, modeling depends on the voltages in the feeders, the line parameters, the coupling transformer parameters, and the filter inductances of the series VSC.
Thus, one must know the current IT and the behavior of the terminal voltage difference V1 − V2 under load variance disturbances to model the system as seen by the converter.
From
Figure 5, Equation (1) presents the model for the series converter on the AC side as follows:
Then, the current flowing through loop
IT is derived in (2) as a function of the imposed voltage of the converter. The voltage drop, the loop impedance, or the power transfer between nodes
V1 and
V2 should be adjusted electronically by the converter controllers.
Considering that there is no significant amplitude or phase difference in the main feeders (since they come from the same HV source) their voltage difference can be disregarded, so,
resulting in Equation (4),
which can be rewritten as (5)
From (5) we have three transfer functions. The first represents the imposed voltage influence of the series VSC (a). The second (b) and third (c) terms represent the disturbances in
IT caused by the load variances (
ik1 and
ik2), as shown in
Figure 6.
To model the complete system that will be controlled with the cascaded P.I. controllers from
Figure 1, one must know the behavior of the terminal voltage difference
V1 −
V2. So, Equation (6) can be derived from the converter branch of
Figure 5,
using (4) and (6), we have,
From (7), the block diagram representation is derived in
Figure 6. Equation (7) is the relation (
V1 −
V2)/
IT symbolizing the current flowing through loop (
IT) as a function of the terminal voltage difference (
V1 −
V2) also considering the load variance as disturbances (
Figure 6).
Figure 6 shows the complete system representation seen by the controllers with the load disturbances that include both connected system representations.
Using the Laplace transform, the relationship IT/VT and (V1 − V2)/IT can be derived in (8) and (9) from Equations (4) and (7) (disregarding the load disturbance parameters). Equations (8) and (9) describe the dynamics of the system using the proposed control strategy.
The load impedances are much higher than the line impedances, and in part, the load behavior does not cause influences in the control tuning. Disregarding the disturbances in the load behavior, the main transfer functions that represent the system dynamics using the series converter can be derived.
4. Control
The proposed control strategy uses the
IT current and the voltage difference
V1 −
V2 as feedback variables. The proposed converter controller is based on the MSRF [
36] technique, as presented in
Figure 1, and the AC system variables are converted into continuous variables (
Vd and
Vq for
V1 −
V2) and (
id and
iq for
IT for the feedback, synchronized with
V1 (by the MSRF-PLL [
36]), to be used in the cascaded PI controllers (for
d and
q axis).
When there are load variance disturbances, the voltage above the converter rises, and the controllers track the voltage difference by transferring the current between both feeders to improve the best voltage profile.
Typical distribution line impedances (ZA and ZB) are more than two times the impedance of the L filter of the converter and the coupling transformer equivalent impedance ZT for the proposed small-rated converter. Thus, the control dynamics are strongly dependent on the line parameters. Additionally, the greater the X/R line ratio, the greater the coupling of variables id and iq. In this case, an additional decoupling technique is needed.
It should be noted that (8) and (9) are first-order transfer functions and the system models previously presented must be converted to a DQ-frame to be analyzed in the P.I.-based controllers.
The main control strategy (current control) is shown in
Figure 7, which alone can choose the desired power transfer. Thus,
id and
iq are the active and reactive currents, respectively. The current control (derived from
Figure 1) composed of two P.I. controllers that track the current transfer (
id and
iq) is compared to the reference values (
idref and
iqref) generating the control signals (modulation indexes (
mid and
miq), which are multiplied by unity vectors
sin (
ωt) and
cos (
ωt) that are added to provide the voltage reference signal
Vpwm for the unipolar PWM. Furthermore, the outputs from the P.I. controllers (of the current controllers) have saturation limiters (
miqmin,
miqmax,
midmin, and
midmax) defined between +1 and −1. The current reference values also have limiters (
idrefmin,
idrefmax,
iqrefmin, and
iqrefmax) which are defined based on the converter’s power rating.
The outer control loops (voltage control) of
Figure 7 are used to track the desired terminal voltage difference (
V1 −
V2), also obtained using MSRF by generating the current references (
idref and
iqref) comparing
Vd and
Vq with the desired reference values
Vdref and
Vqref.
This control strategy can be used to maintain either a fixed voltage drop at the interconnection point, a fixed series impedance, or to track a zero impedance using the terminal voltage difference references
Vdref and
Vqref. The current control P.I. gains are set to be faster than the voltage control in
Figure 7.
The modeling method and the MSRF-based control strategy presented in this study can be used as a basis for alternative control purposes, which can be either expanded or changed. For example, one can use impedance compensation, harmonic isolation, voltage restoring, decoupling, SSR mitigation, system identification, techniques, etc., depending on the purpose of each implementation.
When lines of both feeders have similar impedance values, the best choice for the control is to track the zero impedance or the zero voltage drop at the interconnection point provided by the current transfer between them.
6. Experimental and Simulation Results
This section presents the results for two situations:
The laboratory tests were performed twice, first in a radial configuration, without the series VSC, and then in a meshed configuration, with the series VSC manipulating the power flow, as shown in
Figure 11. Additionally, the simulation results will be presented with the same control tuning parameters and the same power system parameters for comparison, using the Matlab
® software (version 2019b, licensed for UNIFEI at Itajuba, Brazil).
Figure 11 shows the performed lab test in which the line impedances on the low-voltage side (
RA,
LA,
RB, and
LB), the step-up transformers (
TA and
TB), and the test loads (
R,
R1,
R2,
C1, and
L2) with the series VSC interconnecting both ends of the feeders using a coupling transformer
TS. As shown in
Figure 1, each phase of the series VSC comprises a three-phase diode rectifier, a DC-link capacitor (
Cdc), a low-voltage IGBT-based H-bridge, and an inductive switching filter (
LF1 and
LF2).
The results will present measurements from the beginning of both feeders (using
VS,
i1, and
i2 from
Figure 11) and from terminal voltages
V1 and
V2. Additionally, the terminal voltage
V1 and the transferred current
IT, will be used to show the P&Q transfer between the feeders. The measurements were made using power quality meters (Fluke 435) and the sampling period was every 0.5 s. Additionally, the load transitions were performed every 3 min.
Table 1 shows the parameters of the converter, the lines, and the loads used in the lab experimental results.
In addition, the simulation results will show the behavior of the system in a meshed configuration with the series VSC operation. Furthermore, for less computational effort, the simulation load transitions were performed every 15 s resulting in a 60 s simulation test.
The data for the transformers used in the test setup are presented in
Table 2. Respectively,
TA,
TB, and
TS are the step-up transformers and the coupling transformer.
Table 3 shows the gains of the P.I. controllers defined by the control strategy.
6.1. Active Power Behavior
The first tests show the system behavior with resistive loads controlling the active power transfer between the feeders. The tests used five resistive load transition stages as follows:
Initial condition;
R1 insertion;
R1 removal;
R2 insertion;
R2 removal.
Figure 12a shows the terminal voltages (
V1 and
V2) for both the radial (without the series VSC) and meshed configurations (with the series VSC manipulating the power flow). One should note that the series converter improves the voltage profile of the overloaded feeder while it decreases the voltage of the less loaded feeder, which converts the interconnected terminal voltages into an intermediate value via power transfer. It also shows that the main feeder
Vs also undergoes smaller voltage variations.
Figure 13a,b show the terminal voltage’s behavior and the transferred power flow in the simulation results which demonstrate equivalence when compared with experimental results.
For the radial configuration, in stage 2 (i.e., R1 insertion) the feeder A terminal voltage V1 drops from 7.4 kV to 6.4 kV and the feeder B terminal voltage V2 also drops but slightly less than the first.
In stage 3, R1 was removed, returning the whole system to the initial voltage conditions. In stage 4, the inserted R2 shows a V2 voltage drop less than in stage 2 because feeder B is stronger than feeder A.
Stage 5 ends the resistive test by removing load R2 that returns the terminal voltages to the initial voltage conditions.
Figure 12b shows the active and reactive power values transferred in the loop. Stage 2 (
R1 insertion) shows the transferred power from feeder B to feeder A, which consequently improves the terminal voltages by an intermediate value via power transfer. Stage 4 (
R2 insertion), shows the power transfer from feeder A to feeder B, also improving the terminal voltages more than in the radial configuration. This shows the power transfer levels achieved from the series converter tracking the best terminal voltage profiles in the interconnected feeders.
Figure 14a shows the phase graph for the stage 2 load transition, which shows that the inserted resistive loads had only voltage magnitude changes without phase angle variation in a radial configuration for these distribution line parameters.
In a meshed configuration,
Figure 14b shows that the phasors in stage 2, with current
IT approximately 180° from both terminal voltages, equal the same values after the power transfer, i.e., the flow from feeder B to Feeder A. It shows that the converter always tracks the best terminal voltage profile, consequently alleviating the overloaded feeder.
Figure 15a,b show the active power delivered by each feeder and the loading balance provided by the converter power flow manipulation.
Figure 16a,b present the active and reactive power delivered by the feeders for the simulation. The reactive power shown in simulation results provides the information that only resistive loads were inserted in this test. To make a clear view, the experimental results do not show the measurement of reactive power in the test with resistive loads.
As shown in
Figure 17a,b, we noted that there is a larger voltage variation (voltage sag and swells) during load transitions in the respective feeder where the load was inserted. Thus, the converter uses slow dynamics to achieve a variable impedance during load insertions, feeding the other branch slowly, and these dynamics can be selected when tuning the voltage controller.
Additionally, instead of the behavior observed for physical interconnections, there are partial voltage sags in the series VSC occurring at the respective feeder where the load was inserted, as shown in
Figure 17a. Regarding the swells shown in
Figure 17b, we noted a predominant swell when load
R1 was removed.
In conclusion, when the series converter transfers power between the feeders, the loading is distributed autonomously, and the emptier feeder always feeds the loaded feeder.
6.2. Reactive Power Behavior
In order to reproduce reactive power manipulation using the series converter, the inductive and capacitive loads were inserted in this test. These results also have five stages, as follows:
Initial condition;
L2 insertion;
C1 insertion;
C1 removal;
L2 removal.
Figure 18a shows the terminal voltage behavior for both meshed and radial converter operations. Although reactive compensation does not significantly improve the voltage profile in the distribution lines, it reduces the current flowing through the lines, thus reducing technical losses. The radial configuration shows that the terminal voltages drop less than in the resistive load test, and the main feeder
VS also experiences small voltage variations because of the impedance
ZS effect (
Figure 11).
Figure 19a,b shows the same simulation results which also demonstrate equivalence when compared with experimental results.
In stage 2 (i.e.,
L2 insertion), the terminal voltage
V2 drops, and the terminal voltage
V1 also drops but slightly less. In stage 3,
C1 was inserted, which slightly improved the terminal voltage profile. In stage 4,
C1 was removed, returning to the voltage condition in stage 2, with only
L2 inserted. Finally, stage 5 showed the initial voltage profile.
Figure 18b presents the active and reactive power transfer from the series converter, which shows predominant reactive power manipulation for the same control strategy. The small active power is provided via losses in the line parameters and via the reactive loads, which are also simultaneously manipulated.
Figure 20a presents the phase graph for stage 3, which shows that, without the radial converter operation for these distribution line parameters, inserted reactive loads show predominant phase angle variations.
Figure 20b shows the state of stage 3 with the series converter transferring power to compensate for the achieved phase angle difference via the reactive loads. Additionally, one should note that in stage 3 capacitor
C1 is inserted into feeder A, and inductance
L2 is inserted into feeder B, to compensate for the inductive reactive power of both feeders using the series converter.
With respect to stage 3,
Figure 20b shows a higher current transfer from feeder A to feeder B to compensate for the higher terminal voltage angular difference provided by inserting loads
L2 and
C1. It also shows current
IT-90° from the equalized terminal voltages.
Figure 21a,b show the behavior of the reactive powers from the feeders for both converter operations. One should note that, when capacitance
C1 was inserted (stage 3), the provided reactive power was reduced in both feeders. Consequently, this results in a reduced reactive power requirement from the main source
VS (
Figure 11) with the converter operation, ZS and V2chuit Boardbances in damentals resulting in technical loss reductions when both radial feeders are interconnected using the series converter power flow manipulation.
Figure 22a,b show the simulation results. The constant active power presented in the simulations shows that only reactive loads were inserted/removed in this test, but a constant load R is maintained in both feeders (
Figure 11) during the reactive load transitions.
Thus, the series VSC, with inserted capacitance C1 in feeder A, compensates for the reactive inductance present in feeder B, provided by L2 with the same control strategy that takes decisions looking at the behavior of the terminal voltages.
In addition, simulations presented together with laboratory tests show comparable and converging results for both active and reactive power behaviors validating the proposed approach.
Finally,
Figure 23 shows the power factor measurements showing reductions in reactive power requirements from both feeders when the radial system is changed to a meshed feeder with a series VSC.
Section 6.1 and
Section 6.2 also showed simulation results that could be analyzed in a comparative way with the experimental results performed in the laboratory. The simulations presented transient voltage and power oscillations shorter than the experimental results, caused by the uncertainties of the actual modeling parameters. However, observing the results as a whole, the agreement between the simulation and experimental tests could validate the equivalence of the computational representation and reality, showing that the proposed converter can effectively improve the voltage profile by properly controlling active and reactive power flow, both in simulation and experimental tests.
6.3. Field Test
The field test was performed using only the current control shown in
Figure 7, by means of manual increments of active and reactive current references (
idref and
iqref).
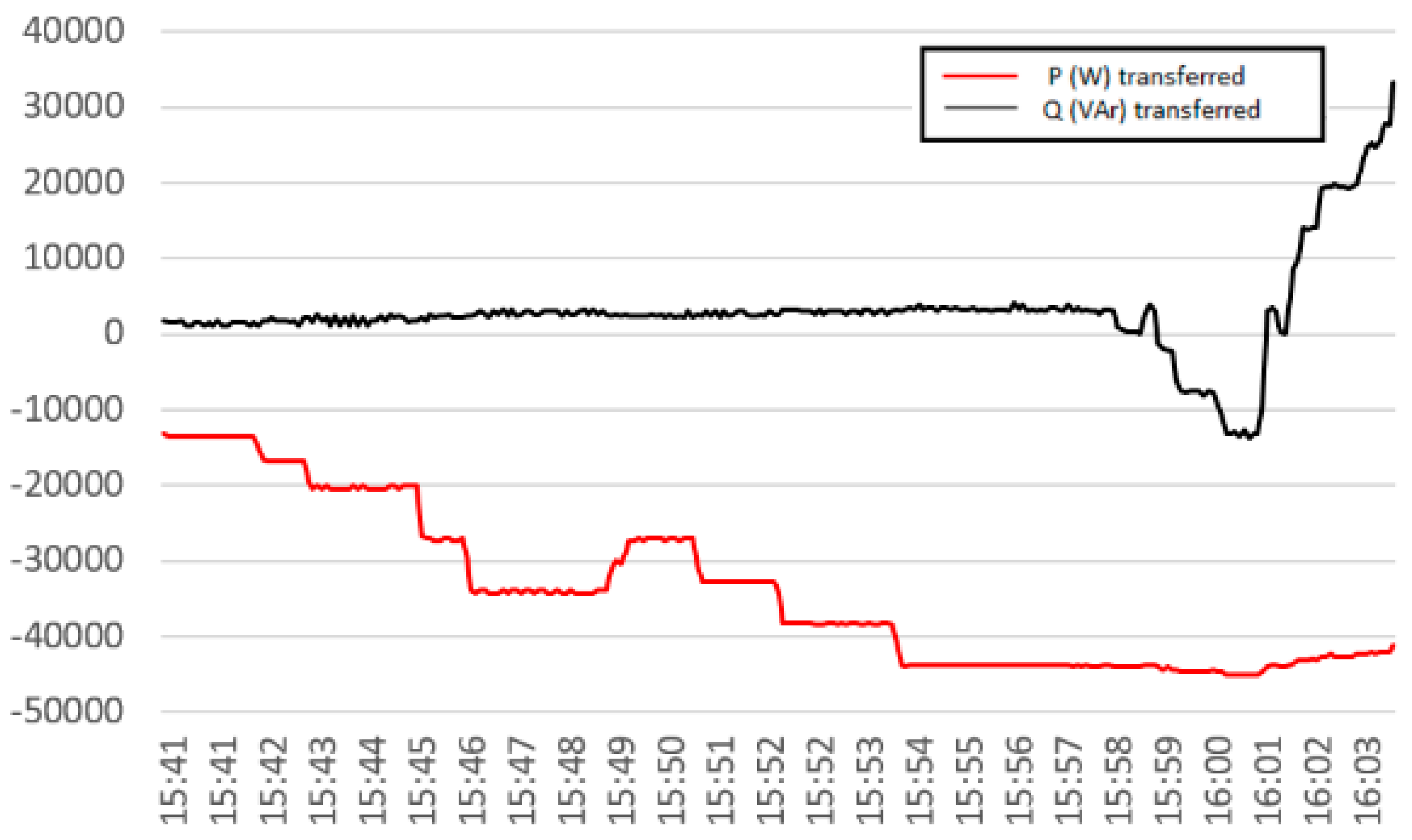
Figure 24 presents the
P and
Q measurements during the field test.
At the beginning, the reactive power reference was maintained at 0 VAr while the active power was changed in small steps. After 15:57 (indicated in
Figure 24), the active power was fixed at approximately 45 kW while the transferred reactive power was manipulated in both directions showing the independent P and Q manipulation for the proposed control strategy, validating the presented formulations of this study also in a real field system.