Low and Ultra-Low Temperature District Heating Equipped by Heat Pumps—An Analysis of the Best Operative Conditions for a Swiss Case Study

Abstract

The manuscript analyses the management of low and ultra-low-temperature district heating systems (DHS) coupled with centralised and decentralised heat pumps. Operative conditions are defined in order to satisfy the heating needs without overloading the electric grid. The results are achieved by dynamic simulations, based on a real DHS located in southern Switzerland. At the building level, the heating needs are estimated considering real data and simultaneous energy simulations. Two DHS configurations, alternatives to the existing one, are simulated and suitable parameters for the management of the DHS are selected. The global performance of the two DHS is evaluated by KPIs also including the flexibility and the impact on the electric peak due to heat pumps. The achieved results are discussed providing suggestions for the stakeholders involved in DHS management for an optimal matching of the electric grid and thermal networks towards a reduction of the peak power. The rule-based control strategies defined allow the expected electric peak shaving and load levelling, conversely, the yearly energy consumptions are lightly increased and have to be further investigated. The outcomes demonstrate a global better performance of the ultra-low temperature DHS in terms of response to the applied control strategies and of energy savings.

1. Introduction

District heating systems (DHS) have increasingly been explored by the technical literature due to their important role in the framework of the evolution of the local energy systems towards the energy and climatic targets for 2050. In this complex path toward the spread of DHS able to adopt the available renewable sources, some technological components such as heat pumps (HP) have a fundamental role, because of their capability to give heat at the desired temperature levels.

The state of the art and the potential evolution in relation to the European context is described in [1], with a deep analysis of DHS for Italy and Switzerland. Two approaches are mentioned and compared: one proposes a classification of DHS based on the levels of supply temperature along the network and technological configurations, with four classes, and the other one proposes a classification of DHS based on different generations, from the first (1GDH, the oldest) to the fifth (5GDHC, the most recent, which intrinsically may include the supply of heating and cooling). The complementarity of the two approaches is clarified and the different technological configurations are deepened. A focus on low-temperature (LT) DHS is then provided, underlining that these systems represent an impressive number in Switzerland, where they are based mainly on Ground Source Heat Pumps (GSHP). In the conclusions, in [1] the importance of further deepening the potentiality of LT DHS by practices is stressed. Indeed, because of the variety and complexity of system configurations and interactions between connected customers (key difference between 4GDH and 5GDHC), these systems pose a challenge in modelling and integrating advanced control systems for optimising electric and thermal energy fluxes and in also evaluating the economic benefits. The work here presented, which also explores the effects of the electric loads due to DHS based on HP, represents an advancement in this issue.

Recent insights are reported also in [2], which identify differences and similarities between 4GDH and 5GDHC regarding aims and abilities. After a very precise description of 4GDH, the Authors explain that the 5GDHC label started to appear in 2015 due to the Flexynets project [3] and that, today, the literature shows a wide range of design specifications for such systems. After a detailed analysis of the recent technical literature, they resume that 5GDHC allows to take advantage of the synergy of combined heating and cooling, minimise the barrier of utilising local waste heat sources, and make central heat supply less critical. They conclude that 5GDHC should not be seen as a sequential or serial development of 4GDH; it is rather a parallel development. This topic is faced also in [4,5] which deeply explore 5GDHC in the European context and provide an advanced model for their control. Another recent research is presented in [6] that mentioned some important issues such as the bidirectional mass flows and energy flows, warm vs. cold networks, decentralised vs. centralised distribution pumps, and different hydronic concepts and connections. In this framework, the role of large-scale electric HP in DHS has already been investigated by [7], verifying the huge potential for using different local thermal sources for the future HP due to their long-term stability, proximity to urban areas, and temperatures. A little later, a very complete analysis of the technical characteristics of HP in DHS has been performed by [8], devoted to exploring the potential to use HP in DHS in EU countries, since it allows an increase in efficiency and flexibility, the decarbonisation of the sector and it could help achieve EU sustainability targets. Investigating typical cases, they conclude that HP can play a pivotal role in the energy infrastructure due to the ability to balance heat and electricity demand, thereby providing flexibility in the district power system. A deep investigation has been already carried out by [9], clarifying the effects of booster HP (decentralised) and central HP in DHS. They conclude that applying booster HP enables the DHS to operate at substantially lower temperature levels, improving the performance of central HP, while simultaneously lowering the heat losses significantly along the thermal network. In brief, the performance for the DHS equipped with HP with the booster combination is considerably better than individual boiler or HP solutions. Afresh a similar approach has been followed in [10], which proposes, as promising DHS, supply temperatures below 45 °C and booster HP at the customers’ substations to provide the appropriate temperature needed for space heating (SH) and domestic hot water (DHW) production. As such, thermal networks allow to abate heat losses and increase the number of usable heat sources. At the same time, the supply temperature from the booster HP can be tailored to the features of each building supplied instead of being based on the most critical user, ensuring also economic competitiveness.

The debate about LT DHS and related optimal configurations is therefore open and the need to support suggestions and considerations by the analysis of exemplary cases of study is universally recognised. In order to provide a research advancement in this framework, an existing Swiss case study of DH is analysed, simulating two different operative scenarios alternative to the real one: a LT and an ultra-low temperature (ULT) DHS respectively, both based on HP. The main features of the two configurations are analysed together with the opportunities for balancing the electric grid thanks to optimised management of the DHS, in a perspective of the interconnection of electrical and thermal loads thanks to the adoption of the HP. Since the work here presented involves the supply of SH and DHW and does not involve space cooling (SC), the approach according to [11] is mainly taken into account to frame the research. Details about this approach are referred to also in [1], while the concept of the two simulated DHS is provided in the following sections. The two district heating networks (DHNs) are based on the real case of Losone (Canton Ticino, Switzerland), an existing high temperature (85 °C as supply temperature) DHS equipped with two biomass boilers (installed thermal power of 3.6 MW) and a back-up oil boiler (installed thermal power of 4 MW), in operation since 2015. The scheme of the plant is reported in Figure 1, while the topology of the network, which supplies 69 buildings of those mapped, is reported in Figure 2. It has to be stressed that the features of the existing biomass DHS are considered in the following only to model the topology of the network, taking into account the current configuration of users, substations, pipes, etc.

1.1. Low-Temperature DHS

According to [11], LT are DHS operating at temperatures below 60 °C. These systems are spreading more and more in the Swiss context, implying new supply concepts and technologies to be considered also for existing traditional DHS that are going to evolve in the future. In the LT category there are three sub-classes (named 2C, 3C, 4C) and the first configuration simulated, presented in this section, belongs to class 2C-LT, characterised by supply temperature from 30 °C to 60 °C; it corresponds to a 4GDH. The system is expected to be equipped with a thermal power station consisting of a large-size HP, while local small-size HPs are distributed to the users for matching the supply temperature needed for: DHW supply of all users and SH supply for users whose heating system requires high-temperature heat (i.e., in case of radiators as emitting systems inside the buildings). In particular, taking into account the real case of Losone, the network serves 69 buildings: 49 are equipped with radiators and therefore need local HP also for SH, while 20 are equipped with radiant panels (LT emitting systems) and therefore need local HP only for DHW. The system is expected to be equipped with HP and storage in the thermal power station and with:

• Heat exchangers users’ side in case of radiant panels as an emitting system in the buildings and local HP devoted only to DHW;
• HP devoted to space heating and DHW users’ side in case of radiators as an emitting system in the buildings.

Simulations were dedicated to the analysis of the contribution of central and local HP to the electrical load. More details of the configuration are available in Section 3.

1.2. Ultra-Low Temperature DHS

The second configuration simulated belongs to the class 4C-LT defined in [11], characterised by a supply temperature lower than 20 °C; it corresponds to a 5GDHC aimed at providing SH and DHW that cannot be supplied directly. In this case, HPs are required for thermal use in the buildings. The supposed system is equipped with a central heat exchanger that uses the thermal energy stored in an aquifer such as a lake or groundwater. SH and DHW at the users are satisfied by local HP at the building level: the substations include HP for meeting the temperature levels needed for SH and DHW according to the existing emitting systems (as already explained in Section 1.1).

Also, in this case, simulations have been dedicated to the analysis of the contribution of central and local HP to the electrical load. More details of the configuration are available in Section 3.

2. Materials and Methods

The two DHS configurations summarised in Section 1.1 and Section 1.2 were modelled dynamically according to the current topology of the network whose features and available data were adopted in the simulation model. The thermal network was modelled by a dynamic tool developed in C++ language by the Authors. The tool allows to accurately simulate the DHN with distributed HP and micro HP for the boost of DHW. More in detail, the capabilities of the tool are:

• An in-depth characterisation of the thermal power station and its storage system (water tank), with a focus on the performance of the HP, especially its electricity consumption at full and partial load at different operating conditions;
• A detailed simulation of DHN focusing on the thermal inertia of the network and the propagation delay of the temperature, based on a pseudo-dynamic model;
• A resistive—capacitive (R-C) model of the buildings connected to the DHN, allowing the dynamic simulation of the thermal demand according to the external climate data (Typical Meteorological Year—TMY file) and to the indoor comfort conditions;
• A completely-mixed model of the DHW tank to include the inertia offered by this storage system.

The HP installed in the thermal power station and different solutions for the heat transfer to the users including conventional heat exchangers, distributed HP, and micro HP to boost DHW are modelled. The overall model refers to the entire system consisting of the main components described in Figure 3.

2.1. Description of Model

The main components of the two simulated configurations (see Section 1.1 and Section 1.2) are described according to the references reported in Table 1 and can be summarised as follows:

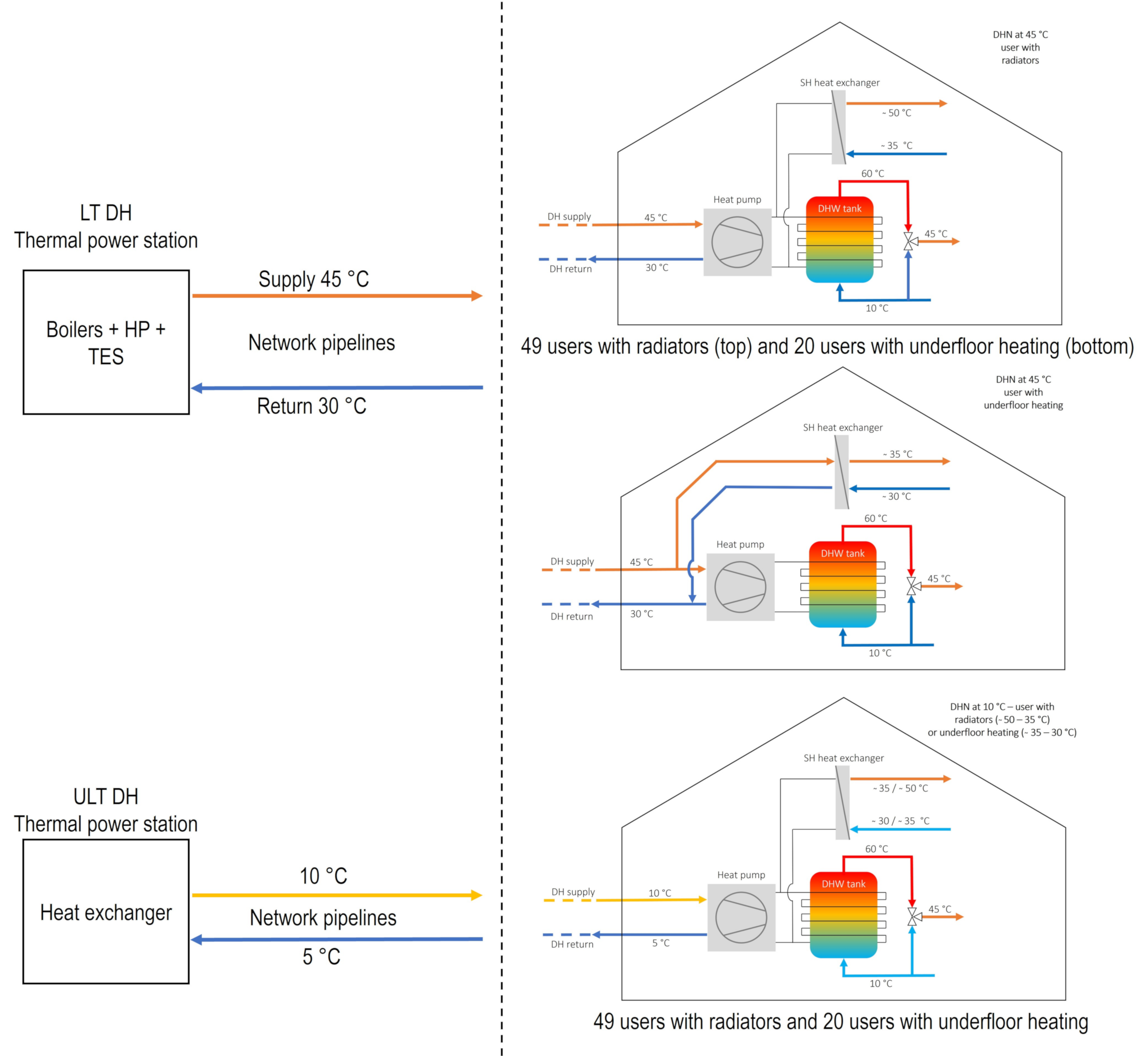
• Thermal power station: Heat Exchanger (HE) for ULT DHS; Heat Pump (HP) for LT DHS;
• Thermal energy storage (TES);
• Distribution network, equipped with a double pipeline, with different diameters of pipes;
• Thermal substations to the users: Heat Exchangers (HE); Heat Pumps (HP) for heating and for DHW purposes; Thermal storage for DHW purposes;
• Management and control system.

The electric power needed for the operation of the hydraulic pumps is evaluated, taking into account the water flow along the network, the pressure losses, and the efficiency of the pumps.

The heat distribution is modelled taking into account the interactions among the various components and, in particular, the different nodes of the network, the temperature and flow in each node, and the thermal and electric power.

Since the model also includes the HE in the thermal power station and on the users’ side, the first one acts as the heat exchange between the local heat source (water in the present case) and the network; the second one acts as the heat exchange between the primary circuit (DHN) and the secondary circuit (building). In the substations, a simple HE allows the transfer of the heat taken from the DHN to the internal distribution system of the building, with the possibility to produce also DHW, if the network temperature is sufficient to meet the requirements of the utilities. If this is not possible, as it is for the two configurations simulated for the present research, the substation includes HP that meets the heating and/or DHW needs, bringing the water to the necessary temperature level, following the method reported in [12].

Considering the mentioned components, the following specific equations are considered in the model:

$$Q_{tps}={{\displaystyle \sum }}_1^n{Q}_i+Q_{loss}$$

(1)

where:

$Q_{tps}$ is the heat demand at the thermal power station.

$Q_i$ is the heat need of each user.

$Q_{loss}$ are the heat losses in the network.

n is the number of users.

$$E_{tps}=E_{HP}+E_P+E_{AUX}$$

(2)

where:

$E_{tps}$ is the electricity demand at the thermal power station.

$E_{HP}$ is the electricity for the centralised HP operation (in the case of LT DHS).

$E_P$ is the electricity for the hydraulic pump.

$E_{AUX}$ is the electricity for the auxiliaries.

Each HP, at the thermal power station or users’ side, can be described by the following equation based on the coefficient of performance (COP) that depends on the temperature levels and on the technical characteristics of the adopted HP:

$$E_{HP}=Q_{HP}/CO{P}_{HP}$$

(3)

where:

$E_{HP}$ is the electricity demand of the HP.

$Q_{HP}$ is the heat delivered by the HP.

The COP is estimated as a function of the condensation and evaporation temperature levels, using manufacturer data and by simulating the thermodynamic cycle of the HP. Further, the value of the COP is also adjusted taking into account the partial load operation.

The operation of the TES has been modelled according to the contributions available in the technical literature in relation to: the hourly storage in the DHN; the daily storage at the thermal power station and for DHW by the users; the thermal inertia of the served buildings. In particular, the equations adopted in the model refer to [13,14,15] and can be summarised as follows:

$$Q_{TES}^t=Q_{TES}^{t-\Delta t}+Q_{ch}^t\times {\eta }_{ch}^{}-\frac{Q_{disch}^t}{{\eta }_{disch}^{}}-Q_{TES\_loss}^t$$

(4)

where:

$Q_{TES}^t$ is the heat stored in the TES at the time t.

$Q_{TES}^{t-\Delta t}$ is the heat stored in the TES at the time previous to t.

$Q_{ch}^t$ is the heat charged in the TES at the time t.

$Q_{disch}^t$ is the heat discharged from the TES at the time t.

${\eta }_{ch}^{}\mathrm{and} {\eta }_{disch}^{}$ are the efficiencies of the charge and discharge of the storage, respectively.

$Q_{TES\_loss}^t$ are the losses to the environment that are evaluated assuming the TES completely mixed by the following equation:

$$Q_{TES\_loss}^t=(T_{TES}^t-T_{out}^t)\times {\mathrm{U}}_{TES}^{}\times {\mathrm{A}}_{TES}^{}$$

(5)

where:

$T_{TES}^t \mathrm{and} T_{out}^t$ are the temperatures of the TES and of the outdoor (external air) at the t time, respectively.

${\mathrm{U}}_{TES}^{}{ \mathrm{and} \mathrm{A}}_{TES}^{}$ are the thermal transmittance and the dispersive surface of the TES, respectively.

The uniform water temperature in the TES is modelled according to the equation:

$$T_{TES}^t=T_{TES}^{t-\Delta t}+(\frac{Q_{disch}^t}{{\eta }_{disch}^{}})/\left(V_{TES}^{}\times {\mathrm{c}}_p^{}\times {\mathsf{\rho }}_{}^{}\right)-\left(Q_{ch}^t\times {\eta }_{ch}^{}\right)/{\left(V_{TES}^{}\times {\mathrm{c}}_p^{}\times {\mathsf{\rho }}_{}^{}\right)}_{}^{}{}_{}^{}$$

(6)

where:

$T_{TES}^t$ is the temperature of the TES at the time t.

$T_{TES}^{t-\Delta t}$ is the temperature of the TES at the time previous to t.

$Q_{ch}^t$ is the heat charged in the TES at the time t.

$Q_{disch}^t$ is the heat discharged from the TES at the time t.

$V_{TES}^{}\times {\mathrm{c}}_p^{}\times {\mathsf{\rho }}_{}^{}$ are the volume of the TES, the specific heat, and the density of the water contained inside the TES, respectively.

In summary, the temperature of the TES is determined by the heat stored in the TES.

Considering the users’ side, the building inertia and the DHW tanks are simulated according to R-C models. The parameters R and C of the building are estimated using publicly available data from the Swiss Federal Register of Buildings and Dwellings (type, age, floor area, number of floors) [16], Swiss SIA regulation, that is, SIA 385/1 [17] and SIA 385/2 [18], and information based on typical Southern Swiss building stock, according to the following equation:

$$C\frac{d{T}_{in}}{dt}=-\frac{T_{in}\left(t\right)-T_{out}\left(t\right)}{R}+Q_{emitter}\left(t\right)$$

(7)

where:

$R$ and $C$ are the thermal resistance and capacity of the building, respectively.

$Q_{emitter}\left(t\right)$ is the thermal power delivered by the emitting system to the final users.

$T_{in}\left(t\right)-T_{out}\left(t\right)$ are the inside and outside temperature, respectively.

For DHW, the storage is simulated analogously to the thermal power station, adding the DHW profile of the buildings and a thermostatic control strategy with hysteresis, as proposed by [19,20]. This results in the following equation:

$$C_{tank}\frac{d{T}_{tank}}{dt} = -\frac{T_{tank}\left(t\right) - T_{out}\left(t\right)}{R_{tank}} + Q_{charge}\left(t\right) - Q_{discharge}\left(t\right)$$

(8)

where:

$R_{tank}$ and $C_{tank}$ are the thermal resistance and capacity of the DHW tank for the storage, respectively.

$T_{tank}\left(t\right) \mathrm{and} T_{out}\left(t\right)$ are the temperature of the TES for DHW and of the outside air, respectively.

$Q_{charge}\left(t\right)$ is the thermal power supplied to the DHW tank.

$Q_{discharge}\left(t\right)$ is thermal power extracted from the tank depending on the DHW need.

2.1.1. Model of the Heat Pumps

The model includes the operation of the HP included in the different DHS configurations. The coefficient of performance (COP) is estimated using manufacturer data and by simulating the thermodynamic cycle of the HP, taking into account the partial load ratio.

For the HP at the thermal power station, the COP is calculated by Equation (9).

$$CO{P}_{th}=a+b\times T_{evap}+c\times T_{evap}^2+d\times T_{cond}+e\times T_{cond}^2+f\times T_{evap}\times T_{cond}$$

(9)

where:

$T_{evap}$ is the evaporation temperature and $T_{cond}$ is the condensation temperature, defined according to [21].

$a \mathrm{to} f$ are the coefficients of the correlation derived by simulating the thermodynamic cycle of an ammonia HP according to [22], while the properties of the fluid are taken from [23].

For single-stage ammonia HP installed in the thermal power station, the coefficients are:

$$a=21.961\to b=0.693\to c=0.00849\to d=-0.7143\to e=0.006914\to f=-0.01232.$$

The full-load COP is derived from [21]:

$$CO{P}_{full-load}=CO{P}_{th}\times {\eta }_{th-to-el}$$

(10)

adopting ${\eta }_{th-to-el}=0.93$ as the thermal-to-electric efficiency from manufacturer data.

The part-load system COP is calculated according to [24,25,26], considering Equations (11)–(13).

$$PLR=Q/Q_{rated}$$

(11)

$$PLF=1.1684+0.01937\times PLR-0.19\times PL{R}^2$$

(12)

$$CO{P}_{part-load}=CO{P}_{full-load}\times \mathrm{PLF}$$

(13)

where:

$Q$ is the thermal power delivered by the HP.

$Q_{rated}$ is the rated (installed) thermal power of the HP.

$PLR$ is the part-load ratio.

$PLF$ is the part-load factor.

The correlation between $PLF$ and $PLR$ and the minimum value of the part-load ratio ($PL{R}_{min}=0.3$) are obtained from manufacturer data [24].

For the HP at the substations (users’ side), the full-load COP is calculated according to [27] as described in Equation (14):

$$CO{P}_{th}=a+b\times T_{cond}+c\times T_{cond}^2+d\times \left(T_{cond}-T_{evap}\right)$$

(14)

The coefficients are derived from HP performance data reported in [24], i.e.,

$$a=14.51421\to b=-0.14735\to c=0.000604\to d=-0.07274$$

Finally, the part-load system COP is calculated following Equations (11)–(13).

2.1.2. Model of the Distribution Networks

In dealing with the DHN, one of the main aspects is the simulation of energy transfer that depends on the mass flow rate of the water and on the temperature level in the network. Changes in flow rate are transferred rapidly to the whole network in the form of pressure waves while temperature changes are transferred at a slightly lower speed due to heat loss to the ground and thermal inertia of the pipelines. As a result, pressure variations reach the whole network in a few seconds while temperature variations within the network are transferred slowly, reaching delays of several hours in networks several kilometres long.

Based on this, the models can be classified into two groups. The first group is represented by completely dynamic models, where both heat transfer and hydraulic phenomena are evaluated dynamically. The second group includes pseudo-dynamic models, where only the heat transfer phenomenon is dynamically simulated. This is the most widely used approach in the literature and it is used also in the present work.

The following assumptions are taken into account in the implementation of thermal and hydraulic models of the DHN:

• As topology a tree network is considered;
• The carrier is water, considered an incompressible fluid with physical characteristics that are constant in time and uniform in space;
• The fluid flow is considered one-dimensional;
• The properties of the materials of the pipe, insulation, and soil are constant in time, uniform in space, and independent of temperature.

The topology of the network is represented according to the graph theory. The joints between pipes are interpreted as nodes and the pipes correspond to branches. The central system and user substations are also treated as nodes. The interconnection of nodes and branches is expressed via the incidence matrix. Rows are equal to the number of nodes and columns equal to the number of branches for the incidence matrix. The generic element (i, j) of the matrix has the value of (+1) if the “i” node is an input for the “j” branch, (−1) if the “i” node is an output for the “j” branch, zero in other cases.

The main variables of the system are the temperatures and the mass flow rate in each node of the network, the thermal power generated by the central system and consumed by the user, and the power consumption of the various components.

2.1.3. Model of the District Thermal Needs

The estimation of the thermal needs has been carried out based on previous research and according to the features of the existing DHS of Losone, selected as a case study.

In particular, SH and DHW needs have been estimated according to the available datasets, materials, and methods described in the main regulations about thermal energy in buildings, that is, SIA 380/1 [28], and in recent contributions related to the same geographic context and approach, for example, [29,30].

Each building has been characterised by the following parameters:

• Thermal resistance of the envelope;
• Thermal capacity;
• SH peak power;
• DHW need in litres per day;
• Thermal resistance and capacity of the DHW storage;
• DHW peak power for the storage recharge.

Starting from these data, the thermal profiles were evaluated at the building level. In particular, considering the DHW need in litres per day and the peak power derived from SIA 380/1, the software DHWCalc [31] was adopted for the definition of the profile of each building all over the year, with a time step of 6 min.

Table 1. Summary of the references considered by the Authors for the development of the model and of the tool.

Thermal Power Station	References
Heat pump	[21,24,25]
Central pump	[22,23,32]
Central hot water tank	[14,15]
Network
Network pipelines	[33,34]
Hydraulic and thermal resolution	[12,32,35,36,37]
Substations
Building model	[25,26,27]
DHW tank model	[19,20,31]
Emitting system	[38,39]
Heat exchanger	[22,23,24,25,26,27,28,29,30,31,32,33,34,38]
Heat pump	[24,25,26,27]

Table 1. Summary of the references considered by the Authors for the development of the model and of the tool.

Thermal Power Station	References
Heat pump	[21,24,25]
Central pump	[22,23,32]
Central hot water tank	[14,15]
Network
Network pipelines	[33,34]
Hydraulic and thermal resolution	[12,32,35,36,37]
Substations
Building model	[25,26,27]
DHW tank model	[19,20,31]
Emitting system	[38,39]
Heat exchanger	[22,23,24,25,26,27,28,29,30,31,32,33,34,38]
Heat pump	[24,25,26,27]

2.2. Definition of the Main Parameters Determining the DHS Features and Management

The model implemented by the authors is aimed at comparing the effects of the operation of the two DHS simulated and finding out the most important parameters for optimising their operation.

To that end, the model includes different stages that involve simulations such as:

• The dynamics of the energy demand for SH and DHW for all the buildings connected to the thermal network, based on the local climatic conditions, the thermo-physic features of the buildings, and the needs for DHW;
• The different TES available, whether they are at the thermal power station or distributed to the users.

The research includes the definition of the effective parameters on the basis of smart management control with the aim of balancing the electric loads. The following parameters were selected to describe the main dimensional and operative characteristics of the DHS:

• Thermal power requested by the users;
• Thermal power requested from the thermal power station;
• Electric power requested by the HP decentralised to the buildings (users);
• Electric power requested by the HP in the thermal power station;
• Electric power requested by pumps and auxiliaries;
• Set point temperature to the users;
• Temperature levels of the thermal storage for the DHW supply.

These parameters represent the main output of the dynamic energy simulations carried out.

Since one aim of the present work is to optimise the matching between the thermal power requested and the load on the electric grid, an indicator for evaluating the load shifting has been defined and calculated. This indicator was defined as the flexibility factor (FF), ranging from −1 to 1 and based on the following equation:

$$FF=\left(E_{stress}-E_{NO-stress}\right)/\left(E_{stress}+E_{NO-stress}\right)$$

(15)

where:

$E_{stress}$ is the electricity consumed by the DHS when the electric grid is in stress condition (overload)

$E_{NO-stress}$ is the electricity consumed by the DHS when the electric grid is not in stress condition (without overload), taking into account that the electric grid is considered under stress when the power load is equal to or greater than the 90° percentile of the peak observed in the Base Case (see Section 2.3.1).

The FF is calculated at the daily level and then at the yearly level in order to compare different operative options for managing the DHS.

In addition, another indicator has been evaluated for describing the effect obtained in terms of peak shaving or load levelling, defined as the load factor (LF), ranging from 0 to 1 and based on the following equation:

$$LF=E_{mean}/E_{max}$$

(16)

where:

$E_{mean}$ is the mean electricity requested by the DHS

$E_{max}$ is the peak electricity requested by the DHS

The FF and the LF are calculated at the daily level and then the annual average is computed in order to compare different operative options for managing the DHS.

The last two indicators (FF and LF) have to be combined in order to define the control strategies for the optimisation of the electricity requested to the grid by the DHS.

According to these data, the model allows the dynamic simulation of the demands for SH and DHW at the building level.

2.3. Definition of Optimised Control Strategies for the Operation of the DHS

As mentioned, the developed model is aimed at defining control strategies able to reduce the load on the electric grid due to the DHS operation, especially in case of overload. To that end, after a deep analysis by the authors, the following parameters were considered the most sensitive:

• Temperature levels of the DHN;
• TES volume at the thermal power station;
• Thermal resistance (R) and capacity (C) of the buildings’ envelope. Compatibly with the features of the existing building stock, in the beginning, different R and C were set in the simulations in order to observe the effects on the electric demand for the operation of the DHS. However, these parameters were not considered in the final results because the definition of scenarios with their improvement implies a general and uniform retrofit of the building stock that is not feasible in a short time;
• Set point temperature inside the buildings and its throttling range. Different set point temperatures and throttling ranges are set in the simulations in order to observe the effects on the electric demand for the operation of the DHS;
• Thermal R and C of the DHW storage, considering that the DHW needs to represent about the 20% of the total thermal needs, on a yearly basis;
• Operation conditions and performance of the HP users’ side, with particular regard to the operation in partial loads and to the shutdown.

These parameters, evaluated in the comparison of the two DHS described in Section 1.1 and Section 1.2 respectively, are resumed and commented on in

Table 2. Parameters adopted in modelling the considered DHS.

Parameters	Features/Issues	Effectiveness in the Control Logics
Network supply temperature	Limited storage capacity (in the network pipes) and stress of the pipes due to fast thermal cycles (pipes were not designed for this kind of operation)	Not effective
Volume of the TES at the central thermal power station	Mature, suitable, and tailored technology; possibility of different timing of storage; Useful to decouple thermal needs and supply. The TES is considered only for the LT DNS; the volume is based on a storage of 6 h and it is kept constant in all the scenarios	Effective
R and C of the buildings	Their improvement implies a deep and wide retrofit, not feasible in the short term	Not effective
Set point temperature inside the buildings	Possible control of the HP power, exploitation of the inertia of the buildings, quick variation of the thermal and electric load at the network level; This parameter is considered in relation to the night operation and to the operation all over the day (Case 1, 2, and 3)	Effective
Throttling range of the set point temperature inside the buildings	Variation of the thermal and electric load at network level is not useful for the balance of the network	Not effective
Control of the TES for DHW	Not relevant effects of the electric loads due to the low heat needs for DHW with respect to the total thermal loads	Not effective
Partial load operation of the HP	Promising option but it requests advanced control strategies of limited feasibility	Not effective
Shut down of the HP	Feasible, it allows the exploitation of the inertia of the buildings and has an immediate effect on the electric loads of the network (Case 2)	Effective

.

The achieved results allow underlining the most effective parameters among those listed. According to [13,40,41], investigating the role of TES in DHS, and to [42], which explores the issue of flexibility in smart DHS and to [14] which compares centralised storage to storage in thermal inertia of buildings in DHS, these parameters are the thermal storage at the thermal power station, the set point temperature inside the buildings and the shutdown of the HP users’ side. These conditions are allowed exploiting the thermal capacity of the buildings and of the network.

The different scenarios and the achieved results are described in the following sections.

2.3.1. Definition of the Scenarios

Taking into account the features of the DHN of Losone and according to Table 2, the following scenarios were simulated for the two configurations described in Section 1.1 and Section 1.2:

• Base case: the LT and ULT DHS are simulated according to the assumptions previously described considering a night set back: inside the buildings, a set point temperature of 19 °C instead of 21 °C is applied to all the users of the DHS, from 10 pm to 6 am. The Base case keeps the operative modality of the existing DHS and is useful to understand the effects of the substitution of the existing biomass systems by the two related to the LT and ULT configuration based on HP;
• Case 1: this case operates on the set point temperature inside the buildings. Case 1 is the same as Base case, but without night set back; in this case, the set point temperature is 21 °C all over the day;
• Case 2: this case operates on the shutdown of the HP and on the set point temperature inside the buildings. Case 2 is the same as Case 1, but with HP switched off for the most impacting consumers when the electric grid is under stress. Indeed seven users of the DHS account for the 41% of the thermal installed power (chosen as the users above the 90th percentile of the installed thermal power), while the electric grid is considered under stress when the power load is greater or equal to the 90th percentile of the electric peak observed in the base case;
• Case 3: this case operates on the set point temperature inside the buildings. Case 3 is the same as Case 1, but with set point temperature inside the buildings at 19 °C instead of 21 °C for the most impacting consumers when the electric grid is under stress.

These scenarios result in eight cases, considering the four control logics and the two DHS configurations.

3. Results

In this section, the results of the simulations of the two analysed DHS are reported. The reference is the existing case of Losone and two different evolutions of the system are imagined:

• Moving from the current HT DHS based on biomass and oil boiler as back up to the LT DHS based on HP, keeping the oil boiler as back up; the existing biomass boilers are substituted by two HP;
• Moving from the current HT DHS based on biomass and the oil boiler as backup to the ULT DHS based only on the possibility to circulate cool water and to supply SH and DHW by local HP; the existing biomass and oil boilers are substituted by the HE.

The main features of the DHS and the operative parameters are described in

Table 3. Main features of the two analysed DHS.

	LT DHS	ULT DHS
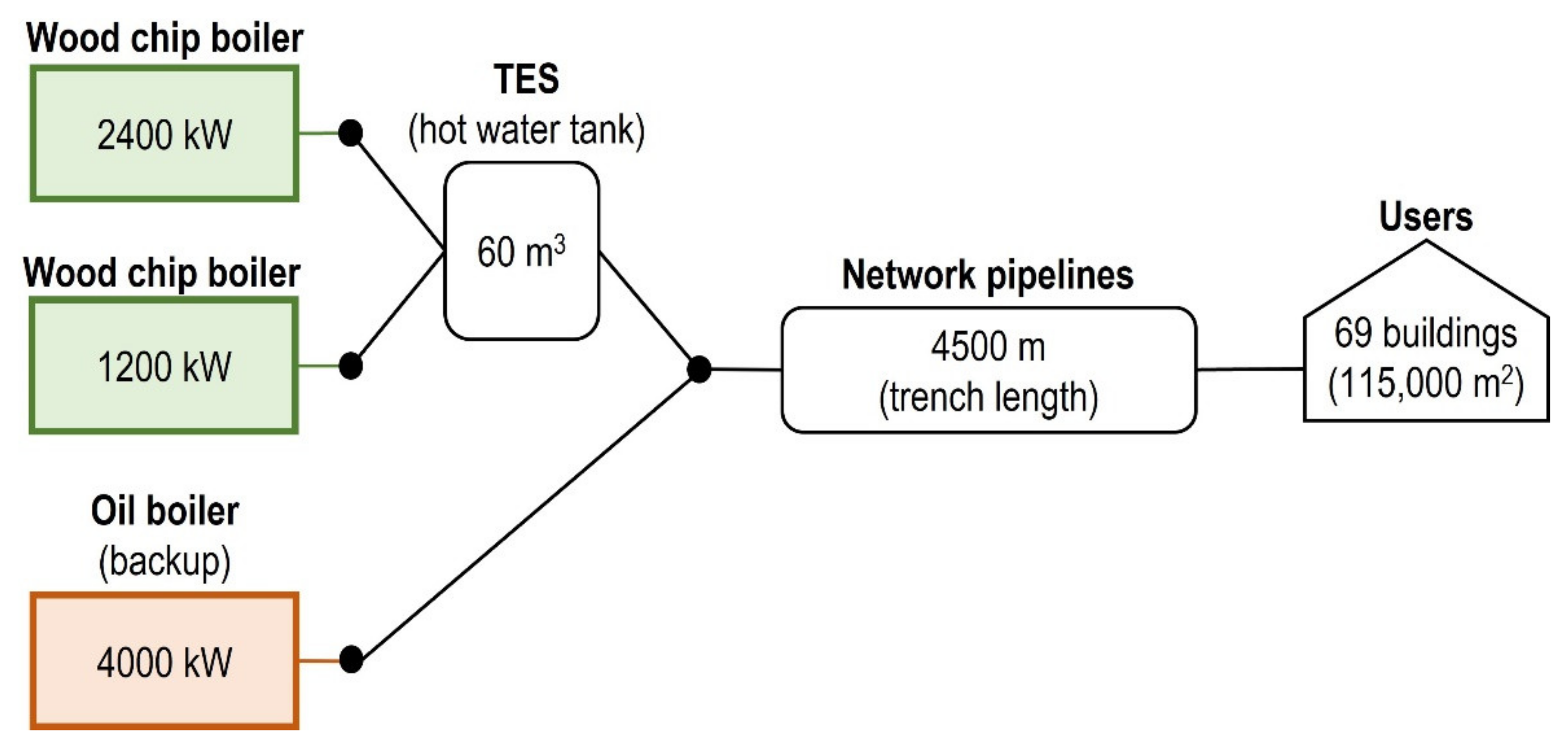
Scheme of operation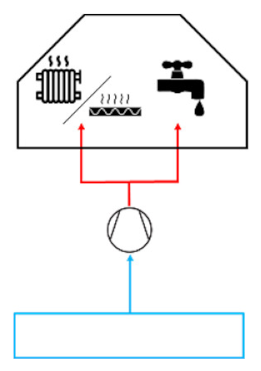
Parameters
Supply temperature of the DHN	45 °C	10 °C
Number of users (buildings connected)	69	69
Local HP for SH	49	69
Local HP to boost DWH	20	-
Thermal power at the local HE	1440 kW	-
Thermal power at the local HP for SH	6370 kW	8300 kW
Thermal power at the local HP for boost DWH	490 kW	-
Thermal power at the thermal power station
Module 1	2400 kW	7600 kW
Module 2	1200 kW	-
Module 3	4000 kW	-
Total	7600 kW	7600 kW
Component types
Module 1	HP	HE
Module 2	HP	-
Module 3	Oil boiler	-
Central heat pump COP @ W10/55	4.30	-
System at users’ side	Heat exchangers in case of radiant panels as emitting system in the buildings and local HP devoted only to DHW HP devoted to space heating and DHW in case of radiators as emitting system	Local HP for space heating and DHW supply
Volume of the TES at the thermal power station	360 m3	-

and

Table 4. Operative parameters users’ side.

Parameters	LT and ULT DHS
Set point temperature for SH	21 °C
Throttling range	0.5 °C
Set point temperature of the TES for the DHW	60 °C
Throttling range of the TES for the DHW	5 °C
Heat pump COP @ W10/W55	4.96

.

Results Achieved for the LT and ULT DHS

The results of the simulations related to the LT and ULT DHS are reported in

Table 5. Results achieved for the Low-Temperature DHS (KPI means Key Performance Indicators).

KPI Energy	Unit	Base Case	Case 1	Case 2	Case 3
Thermal energy production	MWh/year	16,157	16,867	16,813	16,753
Share produced by the HP	MWh/year	14,472	16,107	16,076	15,997
Share produced by the oil boiler	MWh/year	1685	760	737	756
Electricity consumption (breakdown reported below)	MWh/year	7680	8353	8328	8297
KPI Thermal Demand and Losses	Unit	Base Case	Case 1	Case 2	Case 3
Thermal energy demand (buildings side)	MWh/year	17,524	18,339	18,276	18,207
Thermal energy demand (network side)	MWh/year	15,352	16,067	16,013	15,953
Network losses and other effects due to inertia and management	MWh/year	805	800	800	800
KPI Electricity	Unit	Base Case	Case 1	Case 2	Case 3
Electricity consumption of the thermal power station	MWh/year	4234	4764	4752	4734
Share consumed by the HP	MWh/year	4228	4760	4748	4730
Share consumed by the oil boiler	MWh/year	8	4	4	4
Electricity consumption of the hydraulic pump	MWh/year	367	364	364	364
Electricity consumption of the users	MWh/year	3078	3224	3212	3198
Average COP of the central heat pumps	-	3.423	3.384	3.386	3.382
Average COP of the local heat pumps	-	5.987	5.983	5.986	5.989
KPI Peak Power	Unit	Base Case	Case 1	Case 2	Case 3
Peak thermal production	kW	6306	5520	5597	5681
Peak thermal demand	kW	7191	6315	6433	6457
Peak electricity consumption	kW	2476	2337	2374	2379
KPI Flexibility	Unit	Base Case	Case 1	Case 2	Case 3
Flexibility factor	-	0.715	0.796	0.820	0.827
Load factor	-	0.496	0.579	0.580	0.577
Difference (Base Case—Case n)	Unit	Base Case	Case 1	Case 2	Case 3
Thermal energy production	MWh/year	0	−710	−656	−597
Thermal energy demand	MWh/year	0	−815	−752	−682
Electricity consumption	MWh/year	0	−673	−648	−617
Difference (Base Case—Case n)	Unit	Base Case	Case 1	Case 2	Case 3
Peak thermal production	kW	0	786	709	625
Peak thermal demand	kW	0	875	757	734
Peak electricity consumption	kW	0	140	103	97
Percentage Difference [(Base Case—Case n)/(Base Case)]	Unit	Base Case	Case 1	Case 2	Case 3
Thermal energy production	%	0.00	−4.40	−4.06	−3.69
Thermal energy demand	%	0.00	−4.65	−4.29	−3.89
Electricity consumption	%	0.00	−8.76	−8.44	−8.03
Percentage Difference [(Base Case—Case n)/(Base Case)]	Unit	Base Case	Case 1	Case 2	Case 3
Peak thermal production	%	0.00	12.46	11.25	9.91
Peak thermal demand	%	0.00	12.18	10.53	10.21
Peak electricity consumption	%	0.00	5.64	4.14	3.94

and

Table 6. Results achieved for the Ultra-low-temperature DHS (KPI means Key Performance Indicators. In this configuration, Thermal energy production means the heat delivered to the DHN by the HE at the thermal power station).

KPI Energy	Unit	Base Case	Case 1	Case 2	Case 3
Thermal energy production	MWh/year	14,359	15,024	14,975	14,922
Electricity consumption (breakdown reported below)	MWh/year	5279	5355	5336	5317
KPI Thermal Demand and Losses	Unit	Base Case	Case 1	Case 2	Case 3
Thermal energy demand (buildings side)	MWh/year	17,524	18,339	18,279	18,215
Thermal energy demand (network side)	MWh/year	14,401	15,069	15,020	14,968
Network losses and other effects due to inertia and management	MWh/year	negligible	negligible	negligible	negligible
Thermal demand at the thermal power station (demand + losses)	MWh/year	14,359	15,024	14,975	14,922
KPI Electricity	Unit	Base Case	Case 1	Case 2	Case 3
Electricity consumption of the thermal power station	MWh/year	72	75	75	75
Electricity consumption of the hydraulic pump	MWh/year	1652	1552	1546	1540
Electricity consumption of the users	MWh/year	3556	3727	3715	3703
Average COP of the local heat pumps	-	4.928	4.921	4.920	4.919
KPI Peak Power	Unit	Base Case	Case 1	Case 2	Case 3
Peak thermal production	kW	5776	5068	5150	5213
Peak thermal demand	kW	7191	6315	6441	6448
Peak electricity consumption	kW	2621	2184	2178	2203
KPI Peak Power	Unit	Base Case	Case 1	Case 2	Case 3
Peak thermal production	kW	6306	5520	5597	5681
Peak thermal demand	kW	7191	6315	6433	6457
Peak electricity consumption	kW	2476	2337	2374	2379
KPI Flexibility	Unit	Base Case	Case 1	Case 2	Case 3
Flexibility factor	-	0.664	0.800	0.826	0.840
Load factor	-	0.433	0.568	0.564	0.565
Difference (Base Case—Case n)	Unit	Base Case	Case 1	Case 2	Case 3
Thermal energy production	MWh/year	0	−665	−616	−564
Thermal energy demand	MWh/year	0	−815	−754	−690
Electricity consumption	MWh/year	0	−75	−56	−38
Difference (Base Case—Case n)	Unit	Base Case	Case 1	Case 2	Case 3
Peak thermal production	kW	0	708	627	563
Peak thermal demand	kW	0	875	750	743
Peak electricity consumption	kW	0	437	443	418
Percentage Difference [(Base Case—Case n)/(Base Case)]	Unit	Base Case	Case 1	Case 2	Case 3
Thermal energy production	%	0.00	−4.63	−4.29	−3.93
Thermal energy demand	%	0.00	−4.65	−4.30	−3.94
Electricity consumption	%	0.00	−1.43	−1.06	−0.72
Percentage Difference [(Base Case—Case n)/(Base Case)]	Unit	Base Case	Case 1	Case 2	Case 3
Peak thermal production	%	0.00	12.25	10.85	9.75
Peak thermal demand	%	0.00	12.18	10.43	10.33
Peak electricity consumption	%	0.00	16.68	16.92	15.95

with particular regard to the Base case and to Cases 1, 2, and 3 described in Section 2.3.1, taking into account that the TES volume is considered constant in each scenario. Table 5 and Table 6 confirm the assumption reported in [11], where it is assessed that:

• For the LT DHN, the heat losses along the network are in the range of 3–7% of the heat supplied and the energy requested for pumping is around 1–2% of the heat supplied;
• For the ULT DHN network, where temperatures are also adapted to the direct cooling of the building by means of a heat exchanger, heat losses along the network are negligible and energy requested for pumping is around 2–3% of the heat supplied.

In Figure 4 details about the electricity consumption for the two analysed configurations are summarised, with a breakdown of the three contributions.

Results reported in Table 5 and Table 6 show the effects of the application of the different control strategies and of the two configurations. For both the DHS, the scenarios simulated allow the increasing of the flexibility of the system, that is, a load shifting during the moments of high electric load, and the reduction of the thermal and electric peak power.

In particular, for the LT DHS, the maximum reduction of the electric power is reached without the night set back, that is, Case 1, and it is equal to 5.64%.

For the ULT DHS, each scenario allows a reduction of the electric power by around 16–17%, but Case 1 allows also a most appreciable reduction of the thermal consumption. Generally, the ULT DHS seems more sensitive to the application of the selected control logic and, in comparison to the results achieved for the LT DHS, allows a reduction of the electricity consumption with the same boundary conditions.

Instead, the operative conditions related to Case 3 allow the highest values of the flexibility factor for both the DHS simulated.

Looking at the values related to the energy balance at the yearly level, in both the configurations of DHS, the defined scenarios bring pejorative results if compared to the Base case, stressing the need to improve the definition of the control strategies and to better explore the real behaviour of such DHS. However, for the ULT DHS, the thermal energy increases are around 4–5% while the electric ones are around 1% only. In addition, heat losses along the network are negligible in the ULT configuration and there is also the benefit related to the absence of the oil boiler: reduction of fossil fuel usage, the related GHG emissions, and the level of complexity. About this issue, all the defined scenarios for the LT DHS are effective because allow an appreciable reduction of the oil boiler operation.

The details reported in Figure 4 show the slight increase in the electric consumption versus the balancing of the electric load. As mentioned, for the ULT DHS, the difference in the electricity consumed is negligible while the electric peak is reduced by 16–17%. Figure 4 shows also that the ULT DHS allows a lower yearly consumption in comparison to the LT DHS (30–40% less, on average). However, in the ULT case, the electric consumption for the users (for the operation of the distributed HP) is higher than in the LT case.

4. Discussion

The analysis benefits through dynamic simulations able to produce both the thermal and electrical load profile and to evaluate the impact of the HP on the electric grid. The results have shown that management by controlling the set point temperature and switching off the local HP is effective in shifting the electric demand to less critical periods for the electric grid and in reducing the electric peak, due to the lowering of the contemporaneity factor, on a yearly basis. These results can be appreciated in terms of increasing flexibility factor and load factor: The SH profile is more flattered and dependent on the performance of the buildings and on the climatic conditions. However, these control strategies can cause, at least in the simulated case, an increase in the yearly thermal and electric energy demands, justified in the case of the elimination of the night set back but more complex to understand, for example, in Case 3.

Generally, the electric breakdown reveals a light decrease in the consumption for the operation of the hydraulic pumps, while an increase in the operation of the HP, according also to the removal of the night set back. The different breakdowns should be analysed in-depth since the different contributions and their evolution in the various scenarios can affect the perception of such systems by the users.

Definitively, the lesson learned from these simulations is that simple rule-based control strategies are useful in achieving load shifting and peak shaving, but they can create potentially undesirable effects; therefore, rules that consider more factors or smarter rules are needed. Notwithstanding, the analysed cases achieve promising results.

These considerations are in accordance with recent technical contributions such as [43] that are devoted to the study of demand-side management (DSM) techniques for district heating. In their conclusions, the authors underline that DSM allows achieving significant peak reduction (usually between 10 and 30%), the possibility of keeping demand below a certain value and increasing the load factor, while the effects on energy saving and cost are more controversial. Indeed, the energy and economic savings that can be obtained depend on many factors, including heating system schedule, characteristics of the buildings, network dimension and topology, climate conditions, and control strategy, as stressed also in [20]. Focusing on the investment costs, apart from some exceptions and as a general consideration, replacing HT DHS with LT or ULT DHS would provoke a shift in costs from the thermal power station to substations (users’ side), which would become more complex. However, this phenomenon has to be considered together with the different operative costs that could occur depending on the specific contexts.

According to the method and the treated cases, the ULT DHS has better results than the LT DHS in terms of electricity consumption and electricity peak. This effect can most probably be explained by the better COP due to the lower temperature difference between the condenser and the evaporator of the HP and due to the high presence of radiators that penalises the LT DHS. However, the results are case-specific, therefore they might be different with different features of the users and of the heating demand.

5. Conclusions

The research here presented allows understanding the effects of different scenarios of evolution of existing DHS based on innovative paradigms and analysing the opportunities for balancing the electric grid thanks to an optimised management, in a perspective of the interconnection of electrical and thermal networks due to the adoption of the HP as thermal components.

The work takes into account the layout of an existing DHS for which the technical characteristics are known and the real consumption data of the users are available. By means of the available data and the estimates of heating needs for SH and DHW, the thermal features of the DHS have been evaluated.

According to the scientific literature, a set of effective parameters sensitive for the optimisation of the management and control logics have been identified. By several simulations, the most effective variables in reducing the stress of the electric grid, by which the electricity necessary for the operation of the DHS is provided, have been selected. They are the set-point temperature for the SH inside the buildings and the operation of the local HPs devoted to SH (since DHW is considered a priority need, no control logics are applied for DHW supply).

In the framework of bringing new contributions in the field of innovative DHS as models for the evolution of the sector also towards smart solutions for district cooling [44], future developments of this research could include:

• The definition of control logics at the component level, more customised to the performance of the singular building and system (e.g., the shutdown of the HP based on the thermal inertia of each building);
• The implementation of real-time feedback on the impact of the HP on the electric network and with relative instantaneous modification of the management rules;
• An in-depth study of the charge and discharge cycles of the TES with the optimisation of the control system;
• A more in-depth characterisation of the thermal models of buildings;
• The introduction of the space cooling and the study of its impact that, due to the consequences of climate change, will become increasingly relevant even at these latitudes (both to increase users’ comfort and to reduce the load on the electric grid due to increasing use of inefficient refrigeration machines);
• A draft techno-economic evaluation of the feasibility of pertinent scenarios in the real case of Losone.