A 3D Transient CFD Simulation of a Multi-Tubular Reactor for Power to Gas Applications
Abstract
:1. Introduction
2. Materials and Methods
2.1. Reactor Model Description
2.2. Governing Equations
2.3. Numerical Methods
2.4. Physical Models and Boundary Conditions
2.5. Meshing Approach
2.6. CFD Model Validation
2.7. Reactor Dynamic Operation
2.7.1. Start-Up and Shutdown
- Non-reactive steady state: Biogas and coolant under nominal operational conditions are injected until a fully developed flow is attained. A steady-state simulation was conducted to simulate the abovementioned flow and used as an initial condition in further transient studies.
- Reactor start-up: As H2 supply begins, reactor steady state was checked by monitoring the following variables: average CO2 mole fraction, maximum temperature, average temperature and CH4 mole fraction at the tube outlet. A change of less than 1 × 10−4 for all monitored variables in two successive time steps was considered as proof of steady-state condition.
- Reactor shutdown: As a steady state was reached, H2 supply was interrupted. Pure biogas (at 523 K) was fed to the reactor until the average tube temperature matched the coolant temperature (523 K). The average gas composition inside tubes reached that of pure biogas. Biogas is assumed to be continuously recirculated to the bio-digestor under reactor shutdown operation.
2.7.2. Dynamic Disruptions
2.7.3. Stand by Reactor
3. Results and Discussion
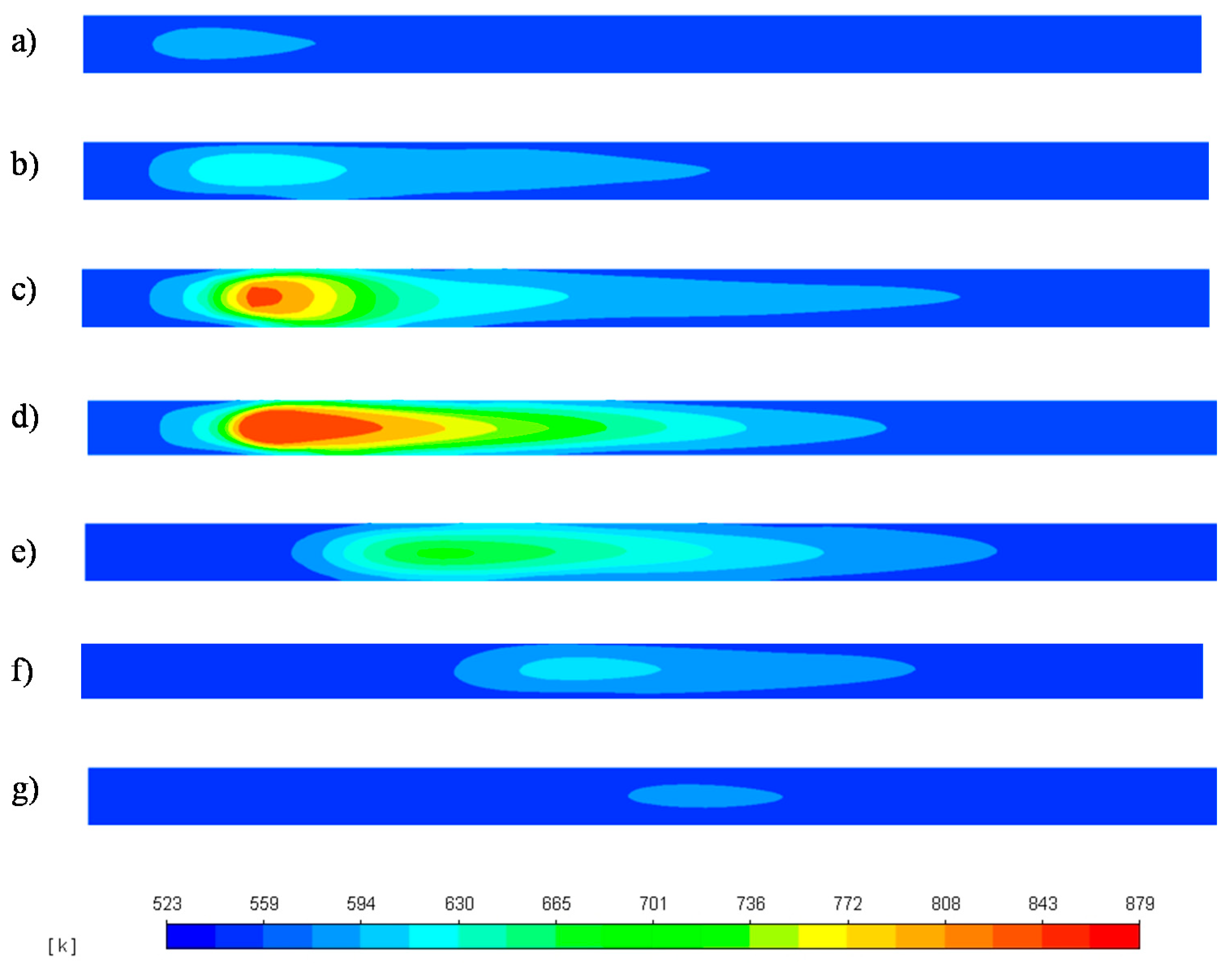
3.1. Reactor Start-Up and Shutdown Simulation
3.2. Reactor Response to H2 Feed Interruption
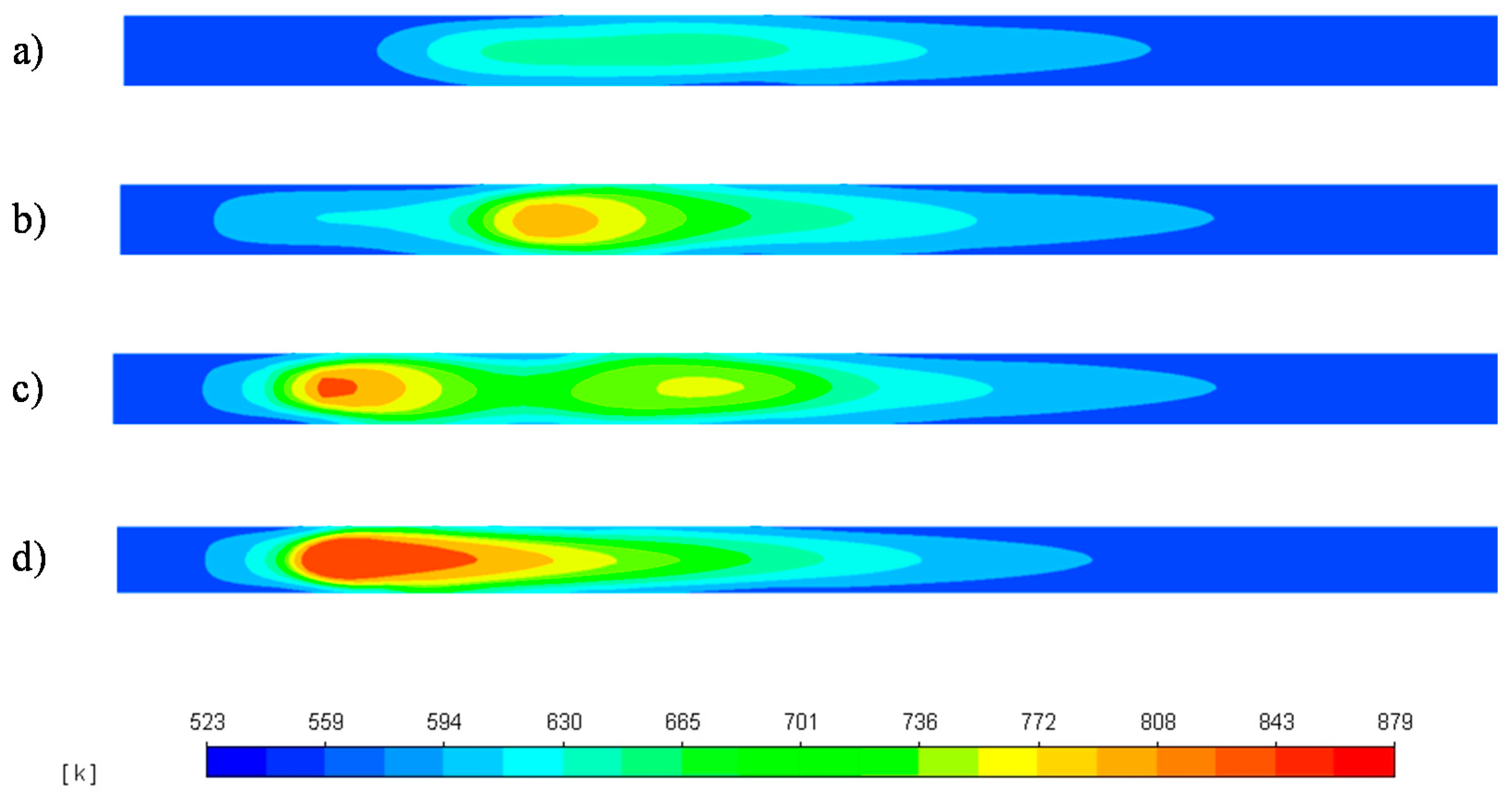
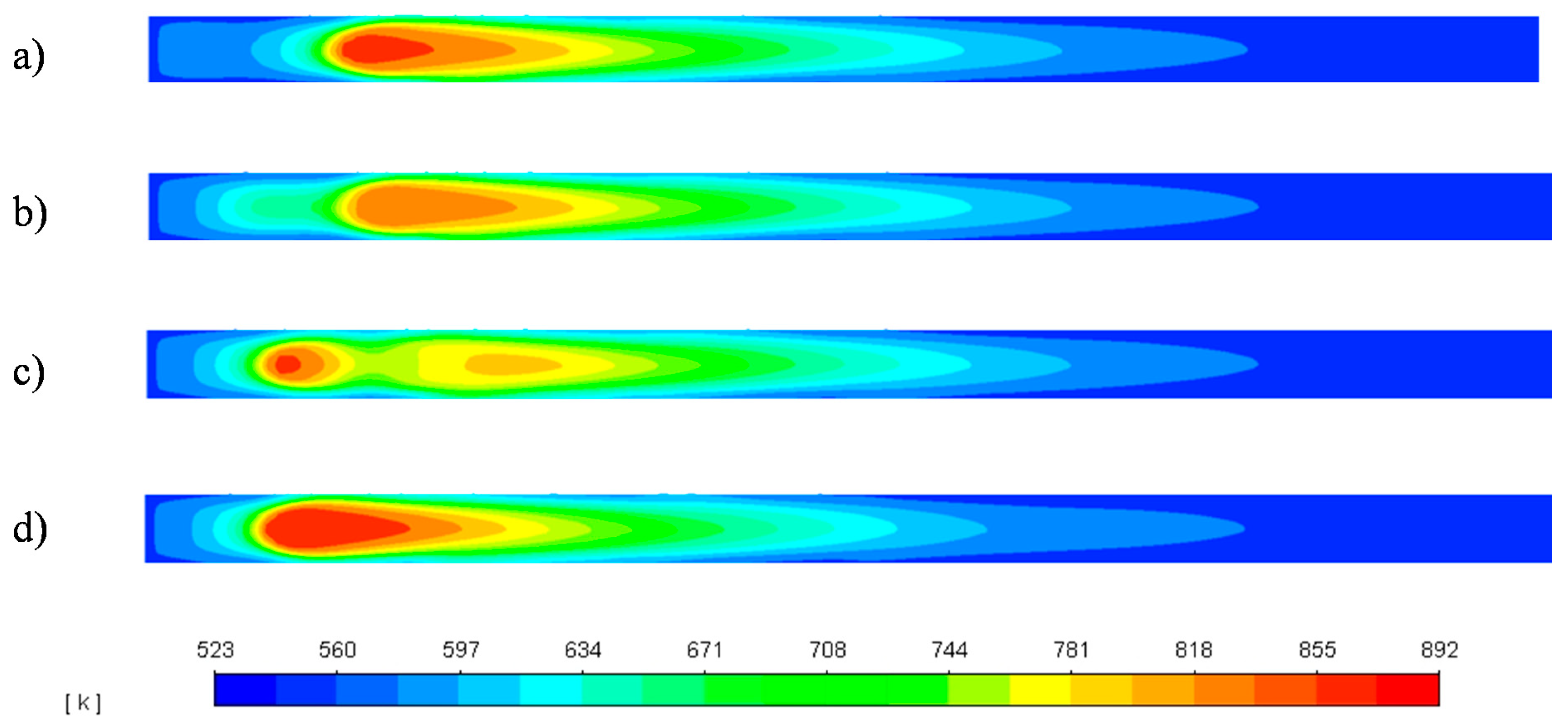
3.3. Reactor Response to Temperature Disruptions
3.3.1. 20 K Feed Temperature Rise
3.3.2. 20 K Feed Temperature Drop
3.4. Stand by Reactor Simulation
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Thermodynamic, Physical Properties and Kinetic Parameters
| Property | Value | Unit | Reference |
|---|---|---|---|
| Gas mixture | |||
| Specific heat | Mixing-law | J kg−1K−1 | [31] |
| Thermal conductivity | Ideal gas mixing law | W m−1 K−1 | [31] |
| Density | Incomp. ideal gas | Kg m−3 | [31] |
| Viscosity | Ideal gas mixing law | Kg m−1 s−1 | [31] |
| Binary molecular diffusion coefficient | Chapman-Enskog | m2 s−1 | [31] |
| Catalyst bed | |||
| Bulk density | 1535 | Kg m−3 | [32] |
| Specific heat | 880 | J kg−1K−1 | [17] |
| Thermal conductivity | 0.67 | W m−1 K−1 | [33] |
| Particle Diameter | 2.6 | mm | [19] |
| Bed porosity | 0.39 | - | [17] |
| Permeability | 1.045 × 10−8 | m2 | [31] |
| Inertial resistance | 12,000 | m−1 | [31] |
| Coolant (thermal oil) | |||
| Density | 867 | Kg m−3 | [34] |
| Specific heat | 2181 | J kg−1K−1 | |
| Viscosity | 2.88 × 10−5 | Kg m−1 s−1 | |
| Thermal conductivity | 0.1055 | W m−1 K−1 | |
| Baffles & tube walls (Steel) | |||
| Density | 8030 | Kg m−3 | [35] |
| Specific heat | 502 | J kg−1K−1 | |
| Thermal conductivity | 16 | W m−1 K−1 | |
| Kinetic parameters | |||
| 3.46 × 10−4 | kmol bar−1 kgcat−1 s−1 | [5] | |
| 77,500 | J mol−1 | ||
| 0.5 | bar−0.5 | ||
| 22,400 | J mol−1 | ||
| 0.44 | bar−0.5 | ||
| −6200 | J mol−1 | ||
| 0.88 | bar−0.5 | ||
| −10,000 | J mol−1 | ||
| Activity factor | 0.1 | - |
References
- Liu, J.; Sun, W.; Harrison, G.P. The economic and environmental impact of power to hydrogen/power to methane facilities on hybrid power-natural gas energy systems. Int. J. Hydrog. Energy 2020, 45, 20200–20209. [Google Scholar] [CrossRef]
- Dannesboe, C.; Hansen, J.B.; Johannsen, I. Catalytic methanation of CO2 in biogas: Experimental results from a reactor at full scale. React. Chem. Eng. 2019, 5, 183–189. [Google Scholar] [CrossRef] [Green Version]
- Gaikwad, R.; Villadsen, S.N.B.; Rasmussen, J.P.; Grumsen, F.B.; Nielsen, L.P.; Gildert, G.; Møller, P.; Fosbøl, P.L. Container-Sized CO2 to Methane: Design, Construction and Catalytic Tests Using Raw Biogas to Biomethane. Catalysts 2020, 10, 1428. [Google Scholar] [CrossRef]
- Hidalgo, D.; Martín-Marroquín, J.M. Power-to-methane, coupling CO2 capture with fuel production: An overview. Renew. Sustain. Energy Rev. 2020, 132, 110057. [Google Scholar] [CrossRef]
- Matthischke, S.; Roensch, S.; Güttel, R. Start-up Time and Load Range for the Methanation of Carbon Dioxide in a Fixed-Bed Recycle Reactor. Ind. Eng. Chem. Res. 2018, 57, 6391–6400. [Google Scholar] [CrossRef]
- Giglio, E.; Pirone, R.; Bensaid, S. Dynamic modelling of methanation reactors during start-up and regulation in intermittent power-to-gas applications. Renew. Energy 2021, 170, 1040–1051. [Google Scholar] [CrossRef]
- Moon, J.; Gbadago, D.Q.; Hwang, S. 3-D Multi-Tubular Reactor Model Development for the Oxidative Dehydrogenation of Butene to 1,3-Butadiene. ChemEngineering 2020, 4, 46. [Google Scholar] [CrossRef]
- Jiang, B.; Hao, L.; Zhang, L.; Sun, Y.; Xiao, X. Numerical investigation of flow and heat transfer in a novel configuration multi-tubular fixed bed reactor for propylene to acrolein process. Heat Mass Transf. 2015, 51, 67–84. [Google Scholar] [CrossRef]
- Fischer, K.L.; Freund, H. On the optimal design of load flexible fixed bed reactors: Integration of dynamics into the design problem. Chem. Eng. J. 2020, 393, 124722. [Google Scholar] [CrossRef]
- Fache, A.; Marias, F. Dynamic operation of fixed-bed methanation reactors: Yield control by catalyst dilution profile and magnetic induction. Renew. Energy 2020, 151, 865–886. [Google Scholar] [CrossRef]
- Soto, V.; Ulloa, C.; Garcia, X. A CFD Design Approach for Industrial Size Tubular Reactors for SNG Production from Biogas (CO2 Methanation). Energies 2021, 14, 6175. [Google Scholar] [CrossRef]
- Try, R.; Bengaouer, A.; Baurens, P.; Jallut, C. Dynamic modeling and simulations of the behavior of a fixed-bed reactor-exchanger used for CO2 methanation. AIChE J. 2017, 64, 468–480. [Google Scholar] [CrossRef]
- Li, X.; Li, J.; Yang, B.; Zhang, Y. Dynamic analysis on methanation reactor using a double-input–multi-output linearized model. Chin. J. Chem. Eng. 2015, 23, 389–397. [Google Scholar] [CrossRef]
- Kreitz, B.; Wehinger, G.D.; Turek, T. Dynamic simulation of the CO2 methanation in a micro-structured fixed-bed reactor. Chem. Eng. Sci. 2019, 195, 541–552. [Google Scholar] [CrossRef]
- Koschany, F.; Schlereth, D.; Hinrichsen, O. On the kinetics of the methanation of carbon dioxide on coprecipitated NiAl(O). Appl. Catal. B Environ. 2016, 181, 504–516. [Google Scholar] [CrossRef]
- Gruber, M.; Weinbrecht, P.; Biffar, L.; Harth, S.; Trimis, D.; Brabandt, J.; Posdziech, O.; Blumentritt, R. Power-to-Gas through thermal integration of high-temperature steam electrolysis and carbon dioxide methanation-Experimental results. Fuel Process. Technol. 2018, 181, 61–74. [Google Scholar] [CrossRef]
- Rönsch, S.; Ortwein, A.; Dietrich, S. Start-and-Stop Operation of Fixed-Bed Methanation Reactors—Results from Modeling and Simulation. Chem. Eng. Technol. 2017, 40, 2314–2321. [Google Scholar] [CrossRef]
- Jürgensen, L.; Ehimen, E.A.; Born, J.; Holm-Nielsen, J.B. Dynamic biogas upgrading based on the Sabatier process: Thermodynamic and dynamic process simulation. Bioresour. Technol. 2015, 178, 323–329. [Google Scholar] [CrossRef]
- Molina, M.M.; Kern, C.; Jess, A. Catalytic Hydrogenation of Carbon Dioxide to Methane in Wall-Cooled Fixed-Bed Reactors‡. Chem. Eng. Technol. 2016, 39, 2404–2415. [Google Scholar] [CrossRef]
- Sun, D.; Simakov, D.S.A. Thermal management of a Sabatier reactor for CO2 conversion into CH4: Simulation-based analysis. J. CO2 Util. 2017, 21, 368–382. [Google Scholar] [CrossRef]
- El Sibai, A.; Struckmann, L.K.R.; Sundmacher, K. Model-based Optimal Sabatier Reactor Design for Power-to-Gas Applications. Energy Technol. 2017, 5, 911–921. [Google Scholar] [CrossRef]
- Alarcón, A.; Guilera, J.; Andreu, T. CO2 conversion to synthetic natural gas: Reactor design over Ni-Ce/Al2O3 catalyst. Chem. Eng. Res. Des. 2018, 140, 155–165. [Google Scholar] [CrossRef]
- Witte, J.; Settino, J.; Biollaz, S.M.A.; Schildhauer, T.J. Direct catalytic methanation of biogas—Part I: New insights into biomethane production using rate-based modelling and detailed process analysis. Energy Convers. Manag. 2018, 171, 750–768. [Google Scholar] [CrossRef]
- Uebbing, J.; Rihko-Struckmann, L.K.; Sundmacher, K. Exergetic assessment of CO2 methanation processes for the chemical storage of renewable energies. Appl. Energy 2019, 233–234, 271–282. [Google Scholar] [CrossRef]
- Hashemi, S.E.; Lien, K.M.; Hillestad, M.; Schnell, S.K.; Austbø, B. Thermodynamic Insight in Design of Methanation Reactor with Water Removal Considering Nexus between CO2 Conversion and Irreversibilities. Energies 2021, 14, 7861. [Google Scholar] [CrossRef]
- Sun, Q.; Gao, Q.; Zhang, P.; Peng, W.; Chen, S.; Zhao, G.; Wang, J. Numerical study of heat transfer and sulfuric acid decomposition in the process of hydrogen production. Int. J. Energy Res. 2019, 43, 5969–5982. [Google Scholar] [CrossRef]
- Gnielinski, V. G7 Heat Transfer in Cross-flow Around Single Rows of Tubes and Through Tube Bundles. In VDI Heat Atlas; Springer: Berlin/Heidelberg, Germany, 2010; pp. 725–730. [Google Scholar] [CrossRef]
- Commission Regulation (EU) 2017/1485 of 2 August 2017 Establishing a Guideline on Electricity Transmission System Operation (Text with EEA Relevance). 2017, Volume 220. Available online: http://data.europa.eu/eli/reg/2017/1485/oj/eng (accessed on 2 February 2022).
- Bremer, J.; Rätze, K.H.G.; Sundmacher, K. CO2 methanation: Optimal start-up control of a fixed-bed reactor for power-to-gas applications. AIChE J. 2016, 63, 23–31. [Google Scholar] [CrossRef] [Green Version]
- Fache, A.; Marias, F.; Guerré, V.; Palmade, S. Optimization of fixed-bed methanation reactors: Safe and efficient operation under transient and steady-state conditions. Chem. Eng. Sci. 2018, 192, 1124–1137. [Google Scholar] [CrossRef]
- ANSYS, Inc. ANSYS Fluent Theory Guide, 15th ed.; ANSYS, Inc.: Canonsburg, PA, USA, 2013. [Google Scholar]
- Scharl, V.; Fischer, F.; Herrmann, S.; Fendt, S.; Spliethoff, H. Applying Reaction Kinetics to Pseudohomogeneous Methanation Modeling in Fixed-Bed Reactors. Chem. Eng. Technol. 2020, 43, 1224–1233. [Google Scholar] [CrossRef] [Green Version]
- Ducamp, J.; Bengaouer, A.; Baurens, P. Modelling and experimental validation of a CO2 methanation annular cooled fixed-bed reactor exchanger. Can. J. Chem. Eng. 2016, 95, 241–252. [Google Scholar] [CrossRef]
- Therminol VP-1 Heat Transfer Fluid. Available online: https://www.therminol.com/product/71093459 (accessed on 25 April 2021).
- Kreith, F.; Manglik, R.M.; Bohn, M.S. Principles of Heat Transfer; Cengage Learning: Boston, MA, USA, 2011. [Google Scholar]


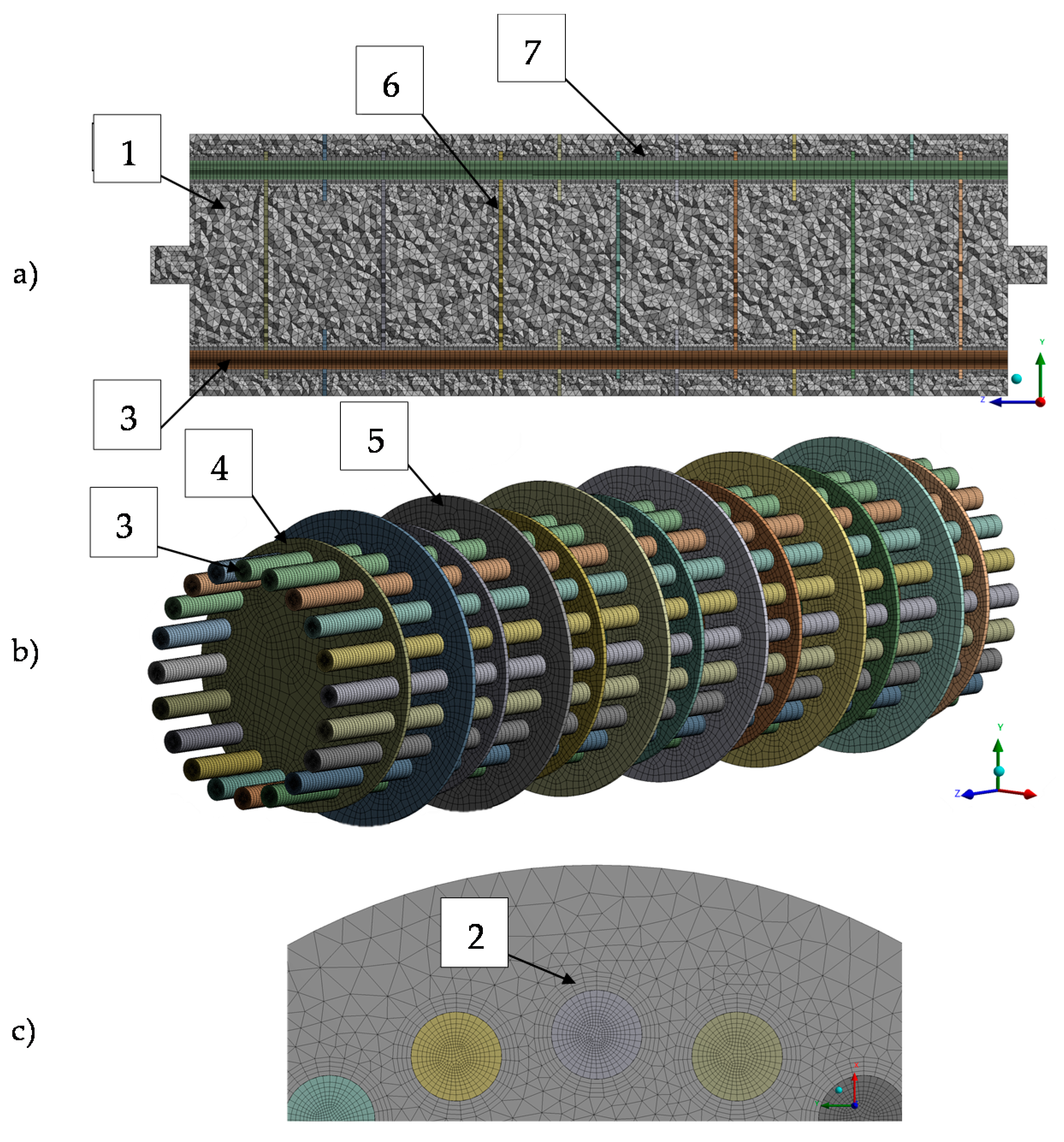



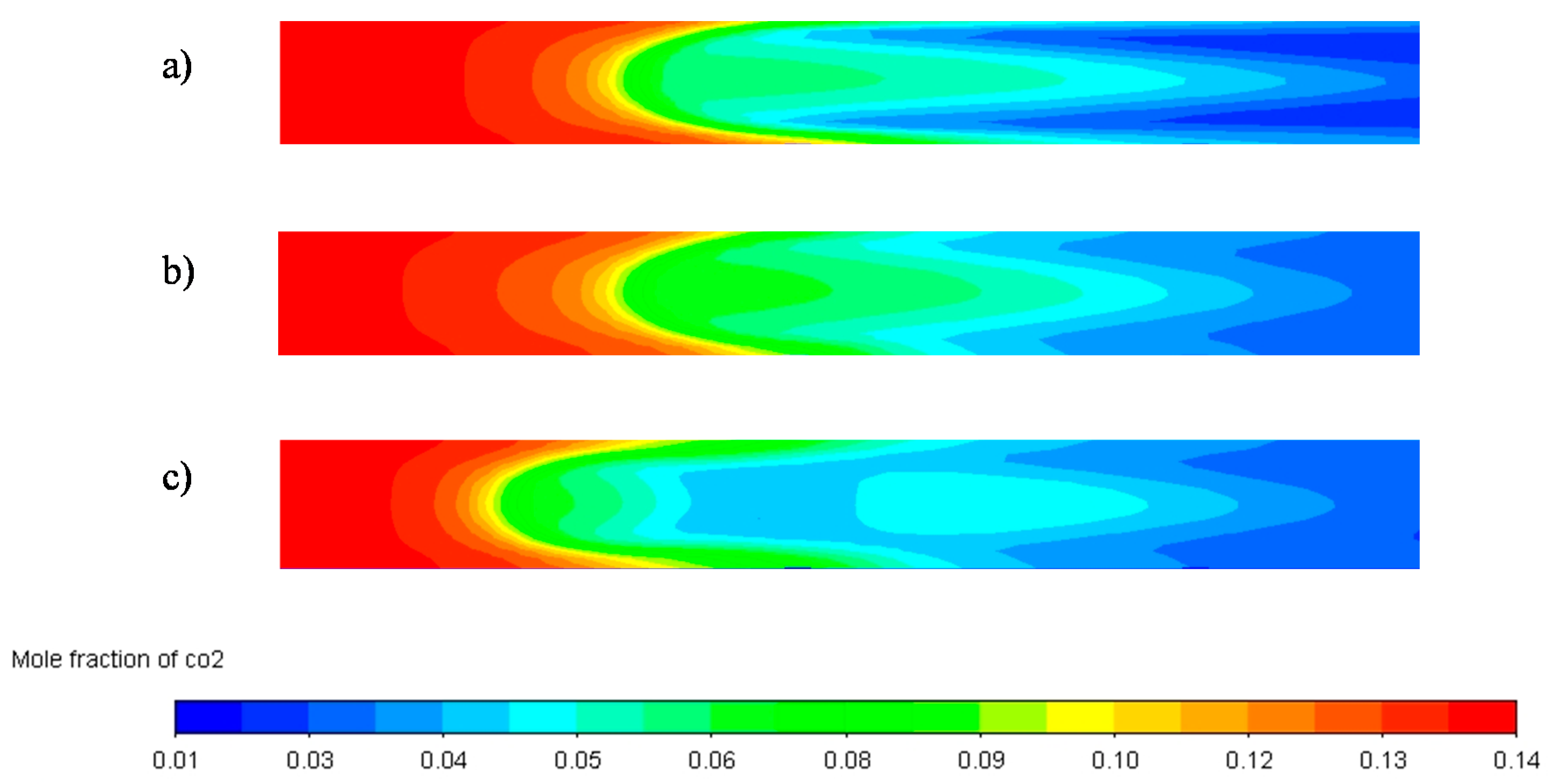
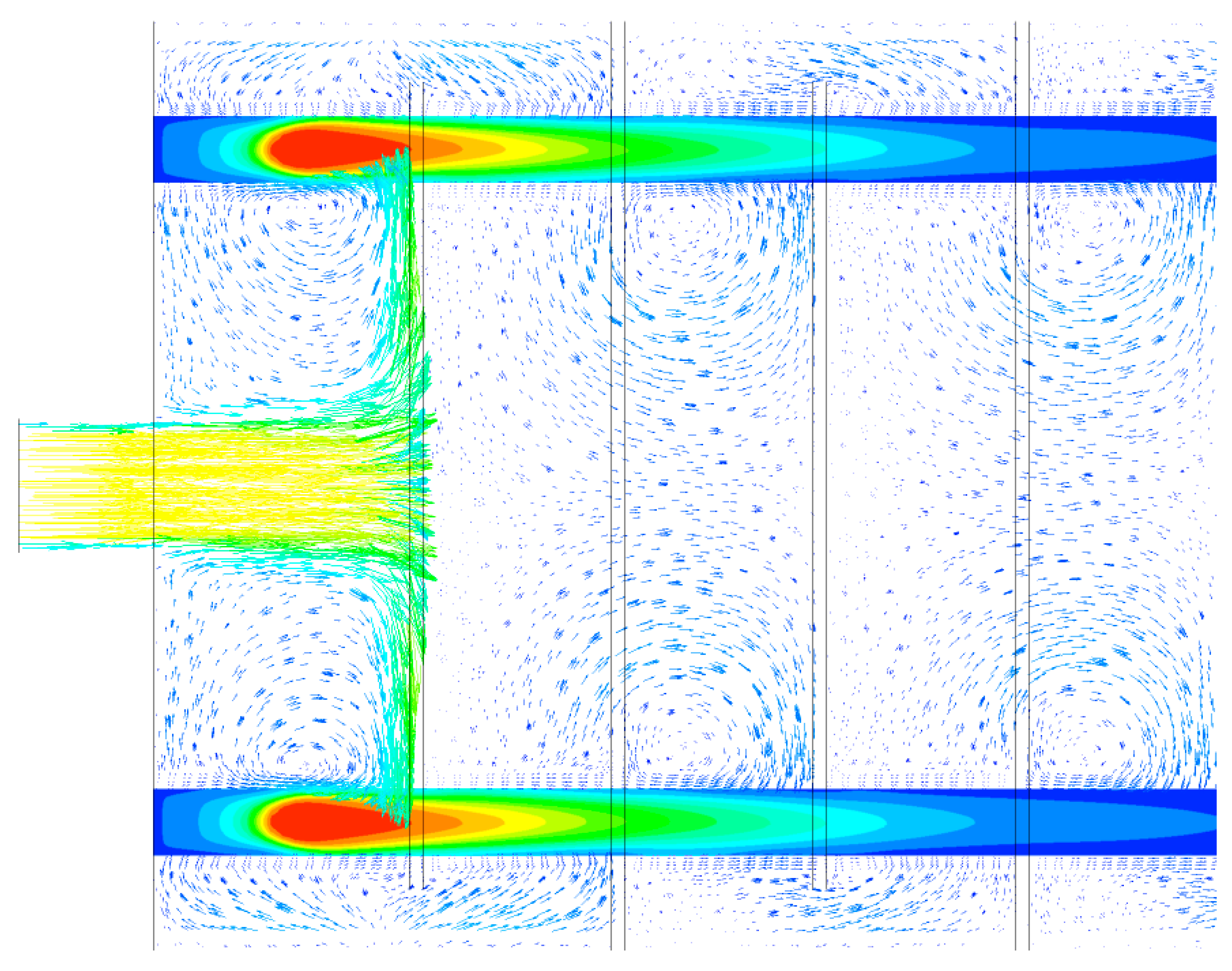
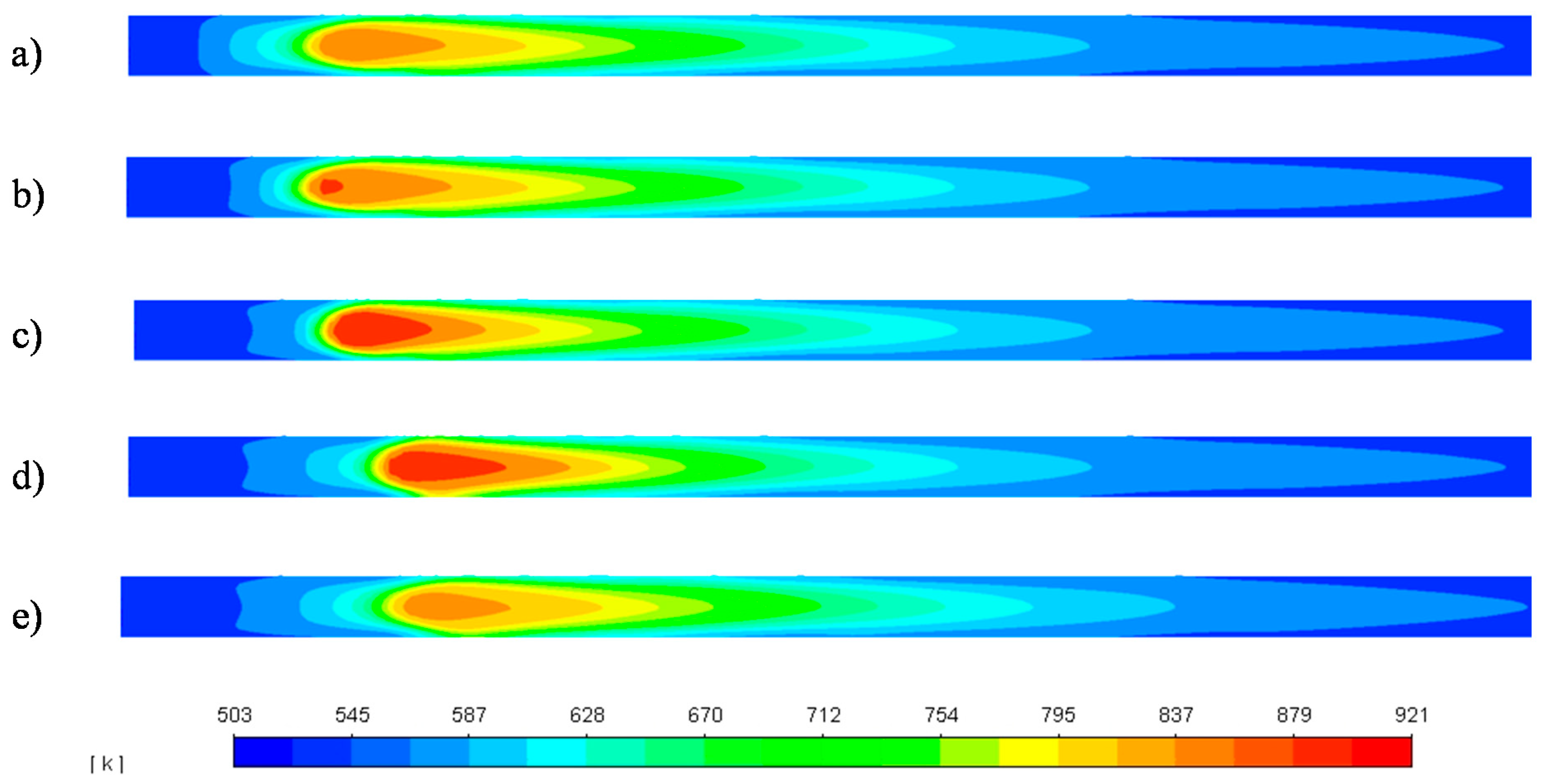
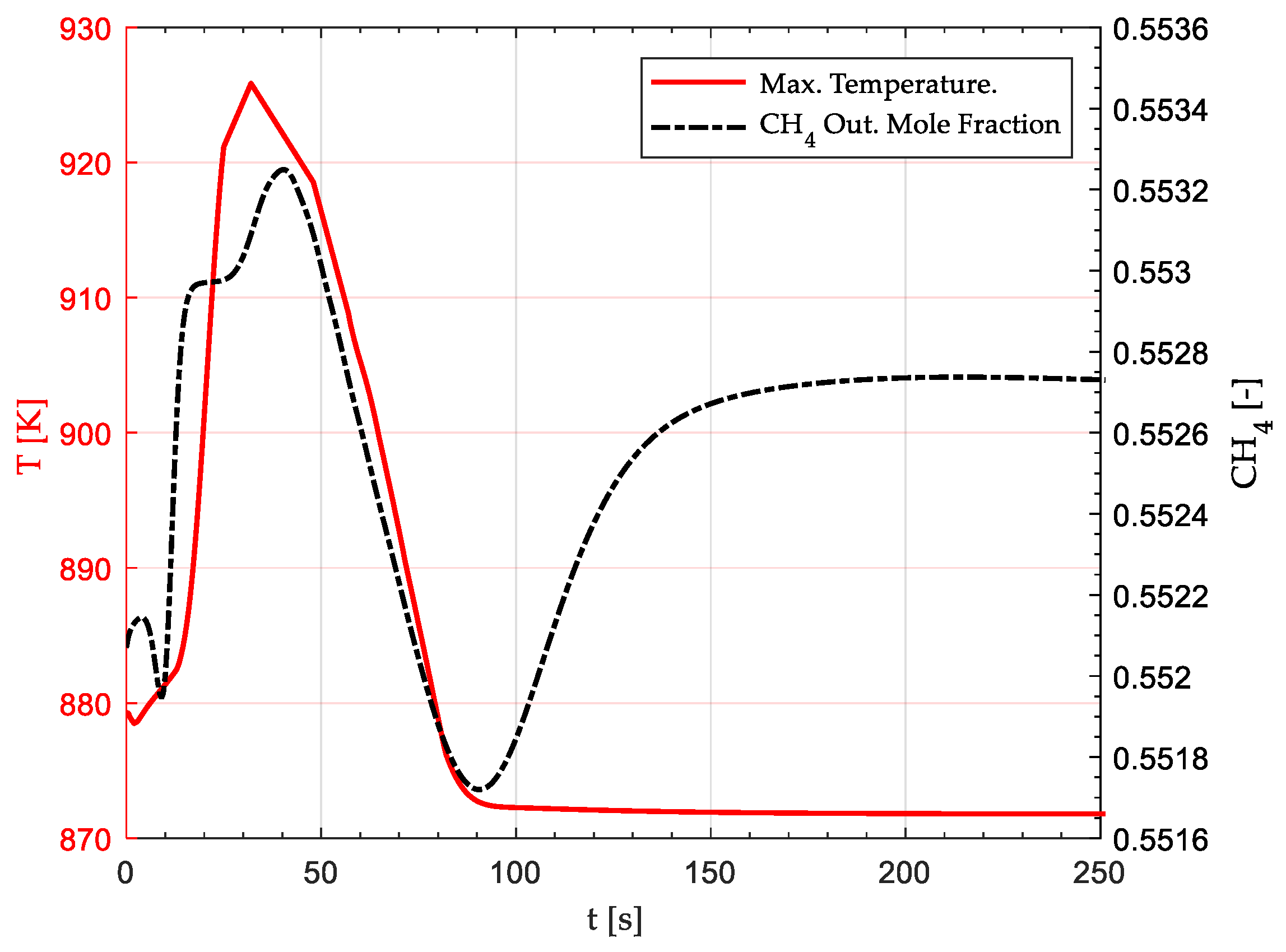
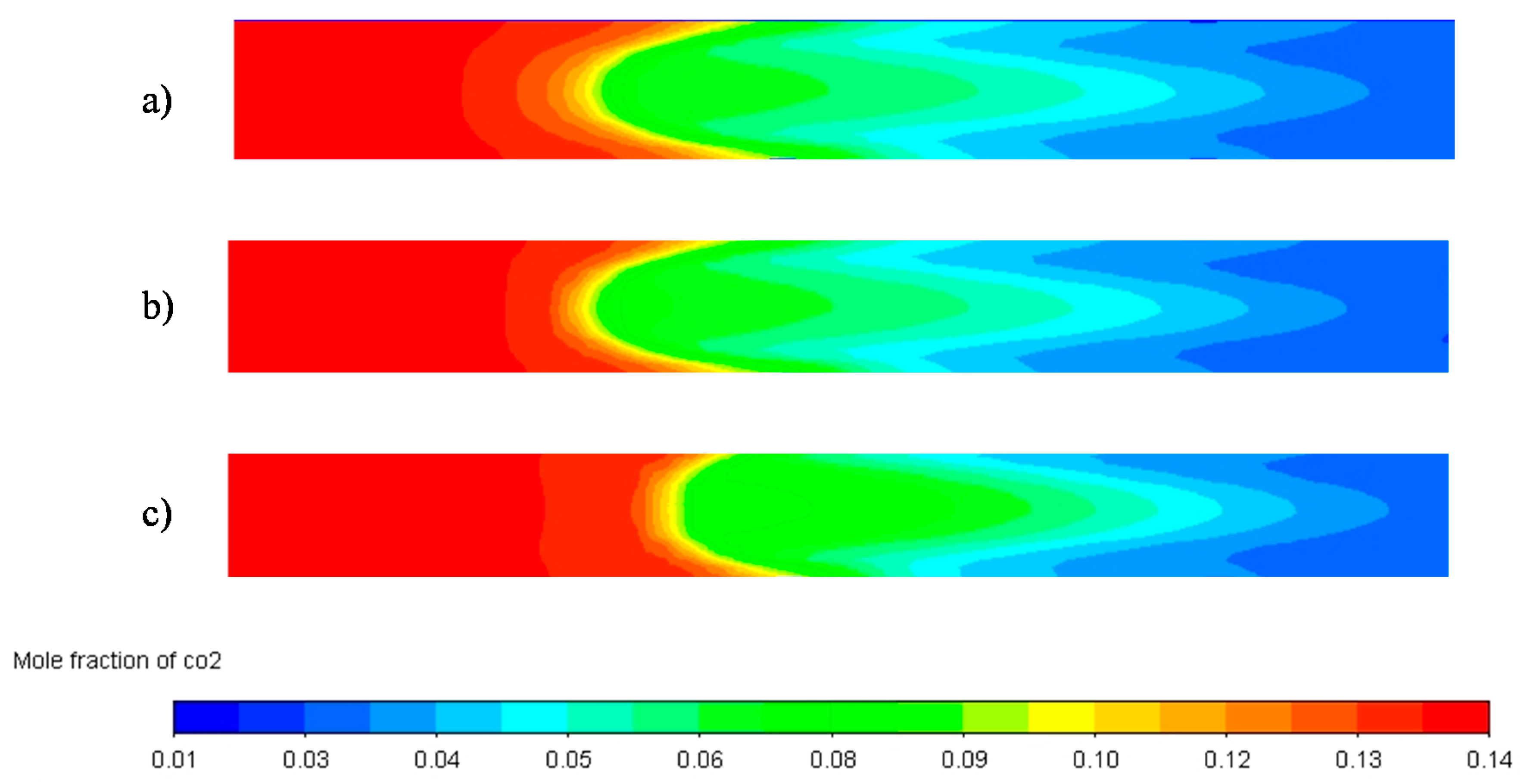
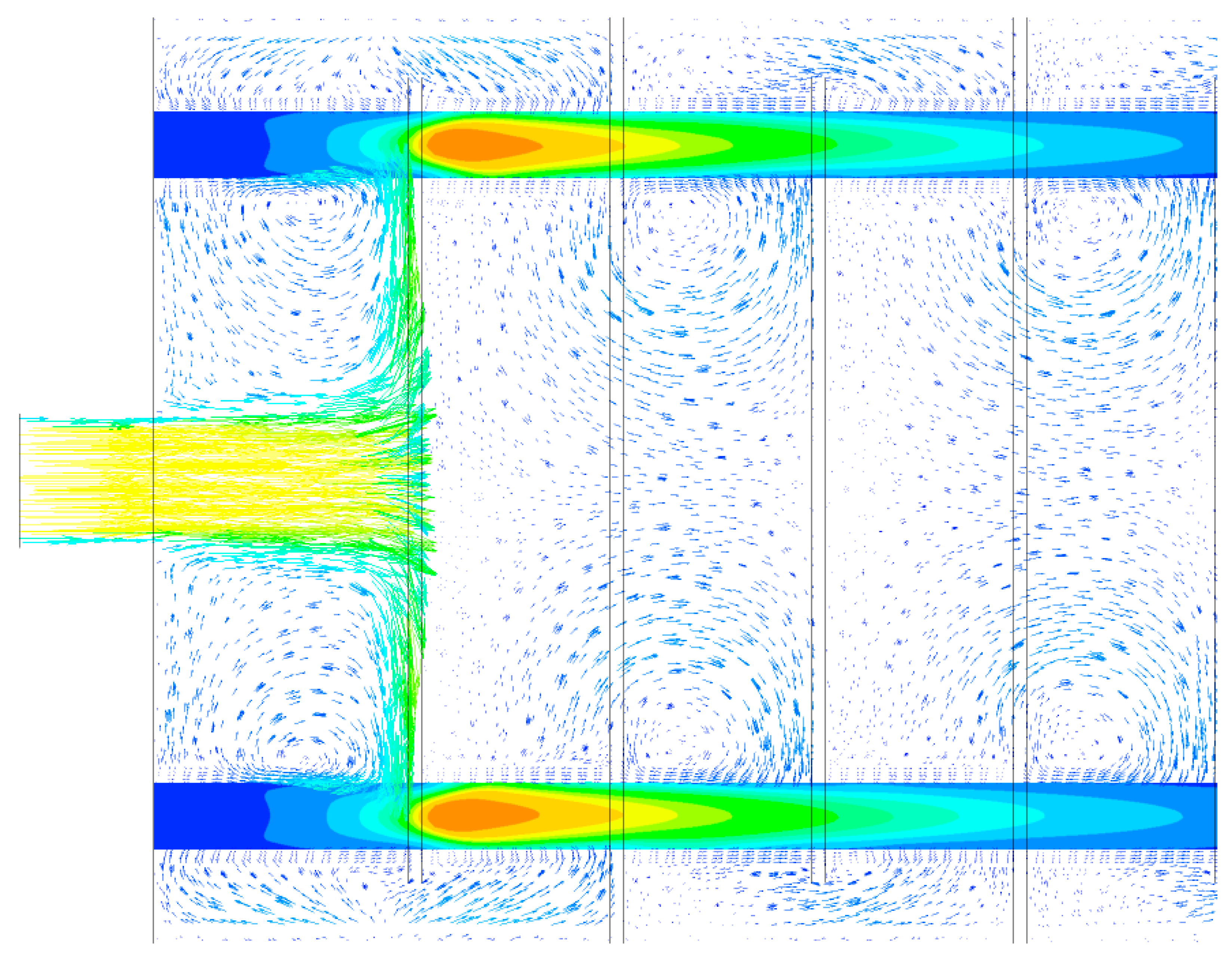
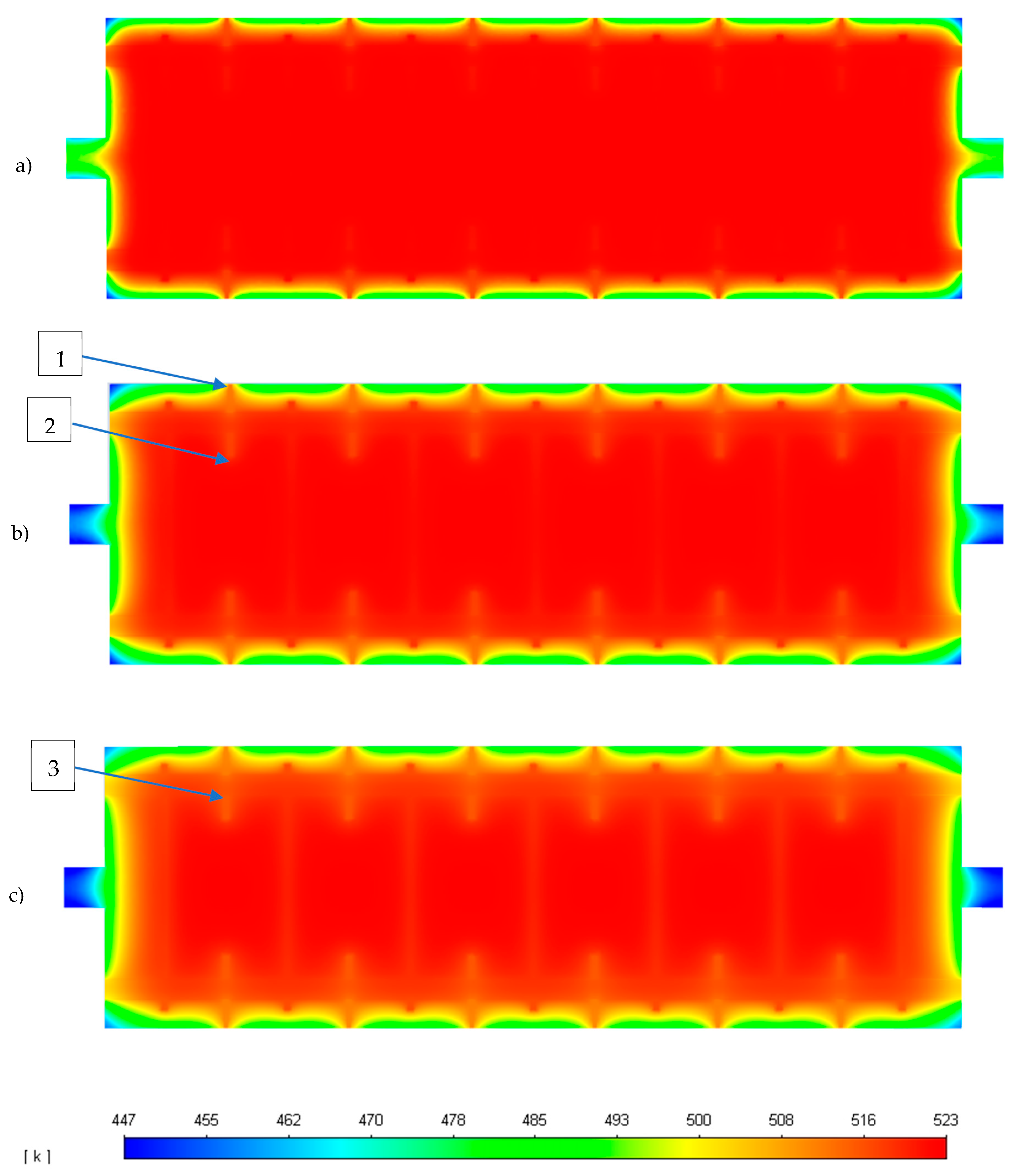
| Parameter | Unit | Value |
|---|---|---|
| Reactor dimensions | ||
| Tube outside diameter | mm | 25 |
| Tube length (First module) | mm | 975 |
| Tube length (Second module) | mm | 500 |
| Number of tubes | - | 20 |
| Insulation [17] | ||
| Material | - | Mineral wool |
| Thickness | mm | 50 |
| Density | kg/m3 | 700 |
| Specific Heat | j/kg∙K | 2310 |
| Thermal conductivity | W/m∙K | 0.05 |
| Operational parameters | ||
| Biogas flow | Nm3/h | 20 |
| Reaction pressure | bar | 10 |
| Gas feed temperature | K | 523 |
| Cooling temperature | K | 523 |
| Catalyst maximum temperature [16] | K | 923 |
| Coolant flow | m3/h | 3.5 |
| GHSV | h−1 | 3200 |
| Gas flow per tube | Nm3/h | 1.5 |
| Feed gas composition | ||
| CH4 inlet mole fraction | mol/mol | 0.280 |
| CO2 inlet mole fraction | mol/mol | 0.146 |
| H2 inlet mole fraction | mol/mol | 0.550 |
| H2O inlet mole fraction | mol/mol | 0.015 |
| O2 inlet mole fraction | mol/mol | 0.004 |
| Reactor Type | Reactor Tubes Dimensions [DxL] | Biogas/Total Flow [Nm3/h] | Inlet Temperature [K] | Pressure [bar] | XCO2 [%] | Cooling System | Study Type | Comments | Reference |
|---|---|---|---|---|---|---|---|---|---|
| Two stage multi tube packed bed | 25 mm × 1 m 25 mm × 0.5 m | 20 | 523 | 10 | 91 ≈99 | Shell side thermal oil 523 K | Numerical CFD | 20 tubes | This work |
| Multi tube packed bed | 45 mm × 4 m | 100 | 473–573 | 8–40 | 94–98 | Shell side thermal oil 519 K | Numerical | 60 tubes | [18] |
| Multi tube packed bed | 20 mm × 8 m | 450 | 476 | 1 | 96 | Shell side Boiling Water | Numerical | 1950 tubes | [19] |
| Single tube packed bed | 200 mm × 1 m | - 382.5 | 550 | 5 | ≈80 | Shell-side Molten Salt tubes 600 K | Numerical | 13 cooling tubes | [20] |
| Three step multi tube packed bed with interstage condensation | 10 mm × 1.13 m 10 mm × 0.95 m 10 mm × 0.36 m | 1612 | 526 515 513 | 13.6–13.9 | 62 91 99.5 | Shell side Molten Salt | Optimisation | 588 tubes | [21] |
| Multi tube packed bed | 9.25 mm × 250 mm | 100 | 473 | 5 | 99 | Tube wall set at T = 373 K | Numerical CFD | 1000 tubes | [22] |
| Two stage multi tube packed bed | 25 mm × 3.5 m 25 mm × 5 m | 200 | 613–673 | 7–45 | >90 | Shell side cooled | Process design | N/A | [23] |
| Multi tube packed bed | Same as [21] | Same as [21] | 442–526 | 13.4–13.9 | Same as [21] | Shell side cooled 500–515 | Exergetic analysis | Same as [21] | [24] |
| Two stage multi tube packed bed | 2.3 m length | 10 | 553.15 | 20 | ≈100 | Boiling water 280 °C-65 bar | Experimental | 2 tubes in series | [2] |
| Four stage multi tube packed bed | 50 mm × 4 m | 8–16 | 473.15 | 15 | 90 | Thermal oil 370 °C | Experimental | 4 tubes in series | [3] |
| Two stage multi tube packed bed | 25.4 mm × 3 m | 0.4–0.64 | 500–600 | 1–15 | 90–99 | - | Numerical thermodynamic | 20–24–28 | [25] |
| Reactive Flow (Tubes) |
|---|
| Gas phase continuity: |
| Gas phase momentum: |
| Gas phase Energy: |
| Species: |
| Coolant flow (shell-side): |
| Fluid phase continuity: |
| Fluid phase momentum: |
| Fluid phase energy: |
| Baffles & tube walls: |
| Solid phase energy: |
| Condition | Unit | Value | Cell Zone |
|---|---|---|---|
| Velocity inlet | m/s | 0.5 | Coolant |
| Pressure (static) outlet | Pa | 0 | Coolant |
| Convective heat transfer coefficient | W·m2·K−1 | 5 | Coolant |
| Free stream temperature | K | 300 | Coolant |
| Thermal coupled wall | - | - | Interface Coolant/Tubes |
| Mass flow inlet | kg/s | 2.15 × 10−4 | Tubes |
| Pressure outlet | Pa | 0 | Tubes |
| Operating pressure (coolant) | Pa | 1.013 × 105 | Coolant |
| Operating pressure (tubes) | Pa | 1.013 × 106 | Tubes |
| Symmetry (tubes inlet/outlet) | - | - | Tubes (stand by simulation) |
| Symmetry (coolant inlet/outlet) | - | - | Coolant (stand by simulation) |
| Sub-Domain | Nodes | Elements | Average Skewness | Average Aspect Ratio | Average Orthogonal Quality |
|---|---|---|---|---|---|
| Fluid | 750,818 | 2,406,886 | 0.34141 | 3.0043 | 0.65751 |
| Tubes (×20) | 1,262,360 | 1,191,000 | 0.11051 | 8.3040 | 0.98924 |
| Doughnut Baffles (×6) | 21,564 | 9150 | 0.18852 | 1.5399 | 0.96949 |
| Disk Baffles (×6) | 21,168 | 9054 | 0.18358 | 1.5027 | 0.97285 |
| Total | 2,055,910 | 3,616,090 | 0.27069 | 4.4693 | 0.76151 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Soto, V.; Ulloa, C.; Garcia, X. A 3D Transient CFD Simulation of a Multi-Tubular Reactor for Power to Gas Applications. Energies 2022, 15, 3383. https://doi.org/10.3390/en15093383
Soto V, Ulloa C, Garcia X. A 3D Transient CFD Simulation of a Multi-Tubular Reactor for Power to Gas Applications. Energies. 2022; 15(9):3383. https://doi.org/10.3390/en15093383
Chicago/Turabian StyleSoto, Victor, Claudia Ulloa, and Ximena Garcia. 2022. "A 3D Transient CFD Simulation of a Multi-Tubular Reactor for Power to Gas Applications" Energies 15, no. 9: 3383. https://doi.org/10.3390/en15093383
APA StyleSoto, V., Ulloa, C., & Garcia, X. (2022). A 3D Transient CFD Simulation of a Multi-Tubular Reactor for Power to Gas Applications. Energies, 15(9), 3383. https://doi.org/10.3390/en15093383






