Creation of a Hydrodynamic Digital Model of a Laboratory Core Experiment of Surfactant Polymer Impact on Oil Recovery, in Order to Determine Parameters for Further Full-Scale Simulation
Abstract
:1. Introduction
2. Materials and Methods
- -
- Temperature in the oven: ±0.5 °C;
- -
- Pressure: 0.1% of the maximum value;
- -
- Effluent fluid volumes: 0.1 cm3.
3. Results
4. Discussion
5. Conclusions
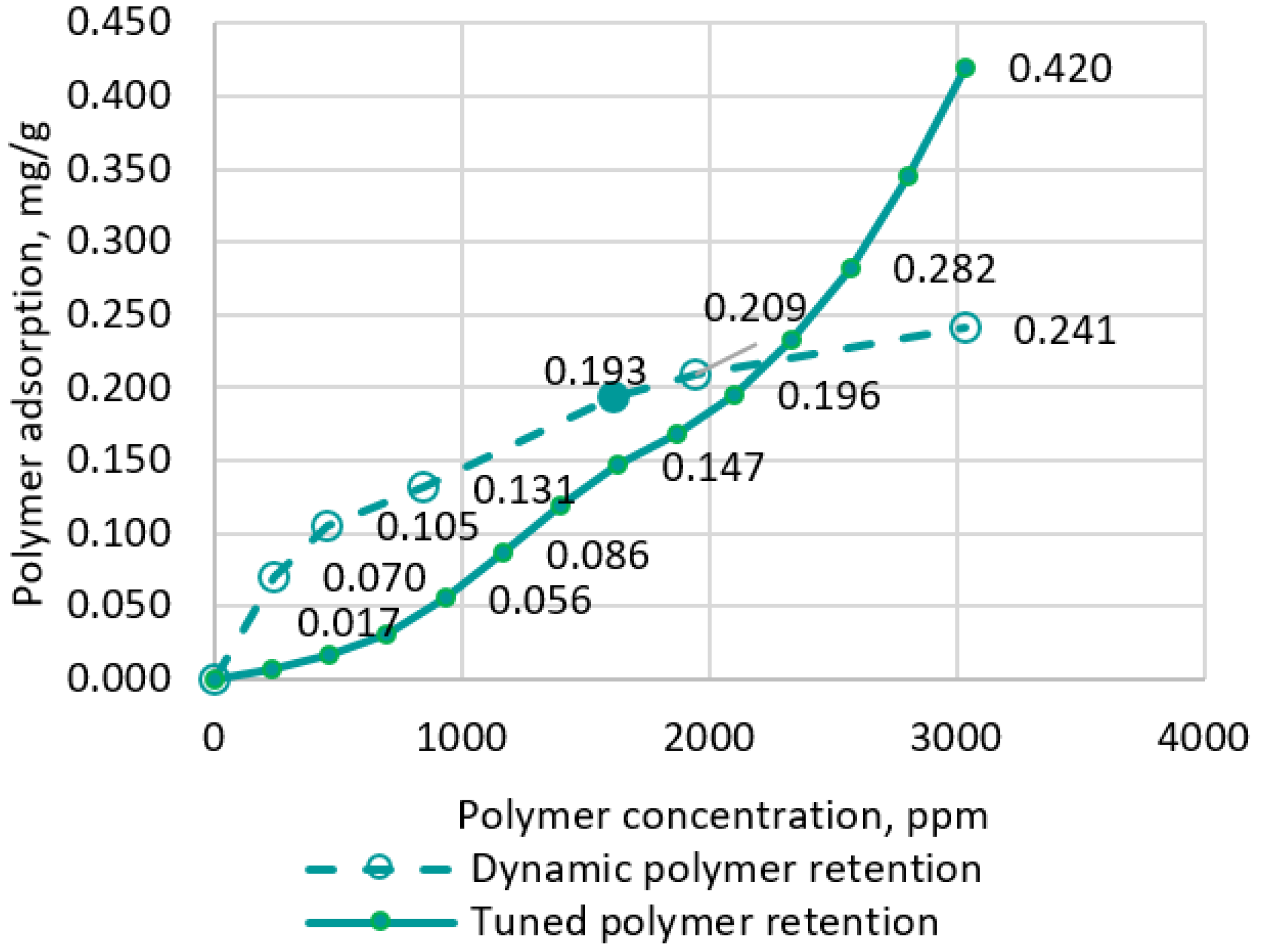
- While performing digital simulations of the laboratory surfactant–polymer oil displacement process, the surfactant and polymer properties that were not directly determined in the laboratory were clarified. These include the polymer residual resistance factor (value—3.5), inaccessible pore volume (for polymer the value was 0.35; for surfactants the value was 0.25), the type of surface tension dependence on surfactant concentration (originally assumed to be linear; in the process of adaptation to the results of the experiment the logarithmic dependence was obtained), and the share of desorption value from adsorption value for surfactant and polymer (0.375).
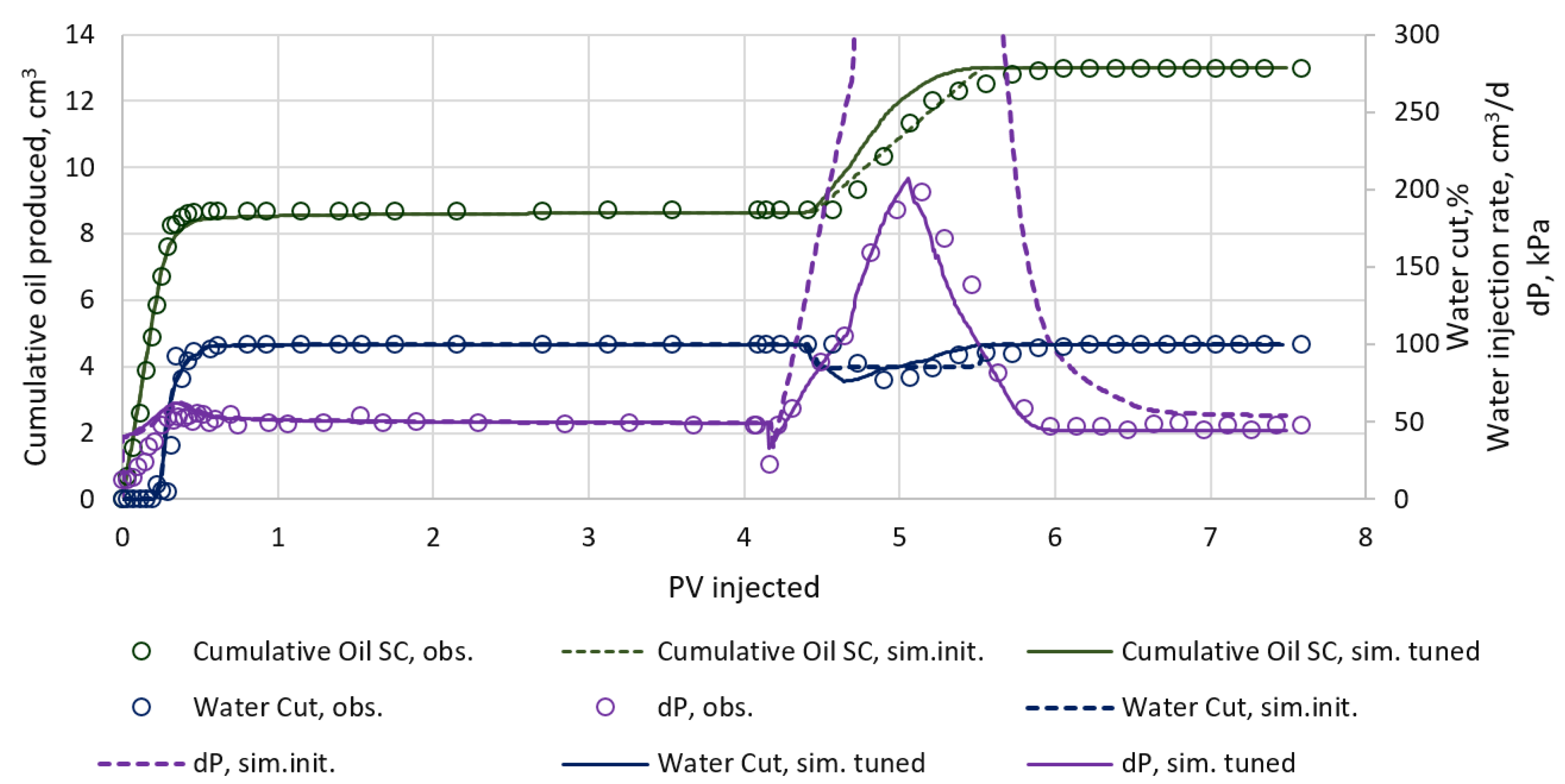
- Since the digital core hydrodynamic model satisfactorily described the behavior in the experiment, the predictive ability of the model with these parameters and at the field scale was enhanced. The error on all model settings did not exceed 5%.
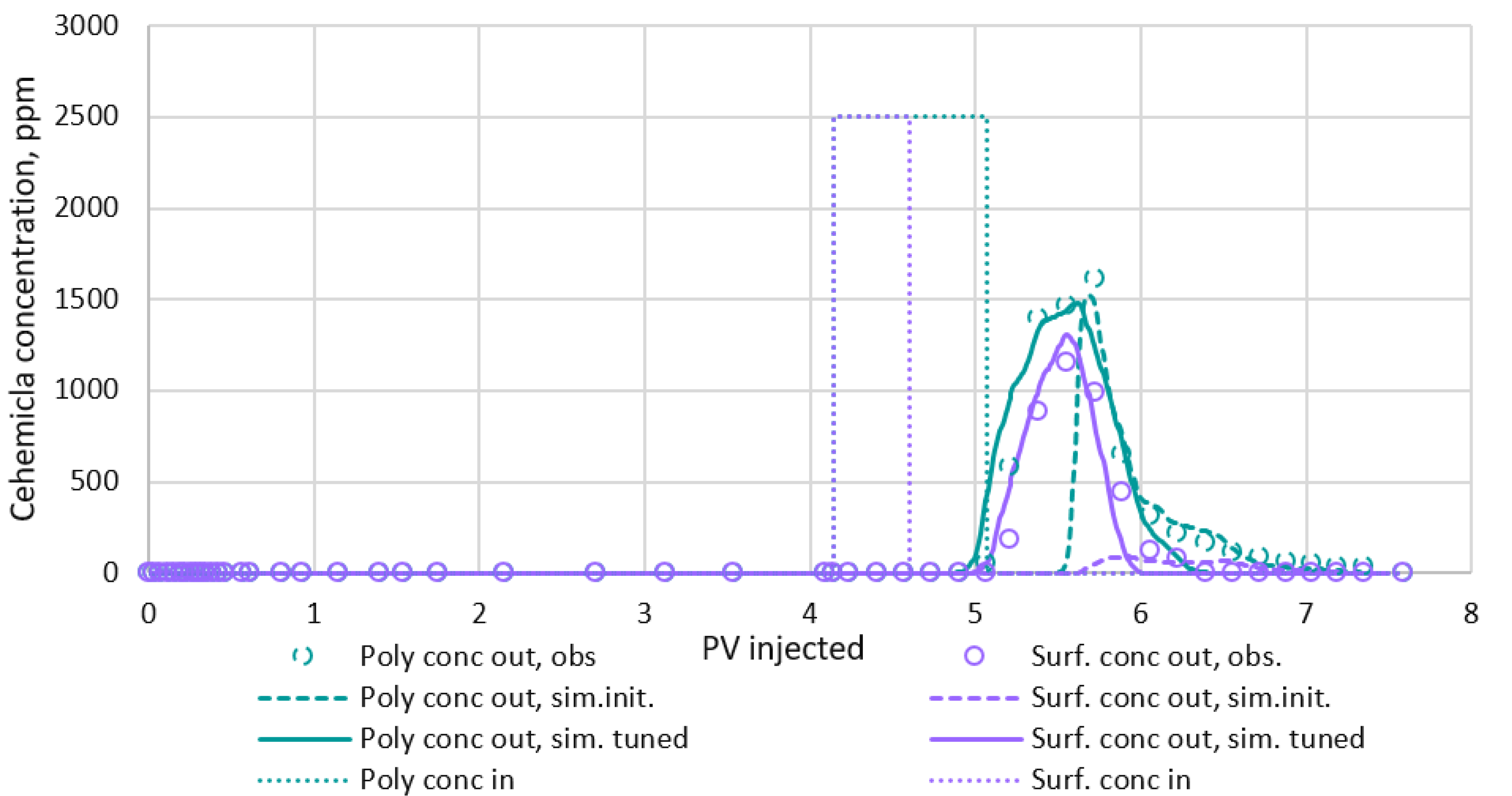
- Reproduction of the experiment on oil displacement by surfactant and polymer with the help of the model allowed attention to be drawn to some imperfections of laboratory experiments, in particular the determination of polymer concentration by viscosity at the output.
- In order to more correctly model the process of oil displacement by surfactant and polymer on the core, it was necessary to inject chemical solutions until the accumulated oil production and concentration of polymer and surfactant at the outlet were stabilized, i.e., until full saturation of the pore space with agents. In this case, the error was reduced in determining the dynamic adsorption of the surfactant and polymer at equilibrium concentration as well as the residual oil saturation factor.
- In the process of tuning the experiment described in this work, the carrying capacity of the polymer when co-filtration with it accelerated the passage of the surfactant through the core (effect of inaccessible pore space for polymer and surfactant) was established, which requires further study, possibly on a digital core, using tomography methods.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| SC | Standard conditions |
| cP | Centipoise (mP s) |
| mD | miliDarcy (10−15 m2) |
| PV | Pore Volume |
| Poly. | Polymer |
| Surf. | Surfactant |
| Sim. | Simulated |
| Conc. | Concentration |
| Init. | Initial |
| Obs. | Observed |
| dP | Differential pressure |
| ITF | Interfacial tension |
References
- Chatzis, I.; Morrow, N.R. Correlation of Capillary Number Relationships for Sandstone. Soc. Pet. Eng. J. 1984, 24, 555–562. [Google Scholar] [CrossRef]
- Druetta, P.; Picchioni, F. Surfactant flooding: The influence of the physical properties on the recovery efficiency. Petroleum 2020, 6, 149–162. [Google Scholar] [CrossRef]
- Wilson, D.; Poindexter, L.; Nguyen, T. Role of surfactant structures on surfactant-rock adsorption in various rock types. In Proceedings of the SPE International Conference on Oilfield Chemistry, Galveston, TX, USA, 8–9 April 2019. [Google Scholar]
- Davarpanah, A.; Mirshekari, B. Numerical simulation and laboratory evaluation of alkali–surfactant–polymer and foam flooding. Int. J. Environ. Sci. Technol. 2020, 17, 1123–1136. [Google Scholar] [CrossRef]
- Mohammadi, H.; Delshad, M.; Pope, G.A. Mechanistic modeling of alkaline/surfactant/polymer floods. SPE Reserv. Eval. Eng. 2009, 12, 518–527. [Google Scholar] [CrossRef]
- Yeh, H.-S.; Juárez, J.J. Waterflooding of Surfactant and Polymer Solutions in a Porous Media Micromodel. Colloids Interfaces 2018, 2, 23. [Google Scholar] [CrossRef] [Green Version]
- Hakiki, F.; Maharsi, D.A.; Marhaendrajana, T. Surfactant-Polymer Coreflood Simulation and Uncertainty Analysis Derived from Laboratory Study. J. Eng. Technol. Sci. 2015, 47, 706–725. [Google Scholar] [CrossRef]
- Zhou, H.; Davarpanah, A. Hybrid Cemical Enhanced Oil Recovery Techniques: A Simulation Study. Symmetry 2020, 12, 86. [Google Scholar] [CrossRef]
- Davarpanah, A.; Mirshekari, B. A mathematical model to evaluate the polymer flooding performances. Energy Rep. 2019, 5, 1651–1657. [Google Scholar] [CrossRef]
- Kuo, C.W. Effect of Gravity, Flow Rate, and Small Scale Heterogenity on Multiphase Flow of CO2 and Brine; SPE: Anaheim, CA, USA, 2010. [Google Scholar]
- Rabinovich, A. Determining Characteristic Relative Permeability from Coreflooding Experiments: A Simplified Model Approach; American Geophysical Union: Washington, DC, USA, 2019. [Google Scholar]
- Krause, M.H. Modeling Sub-Core Scale Permeability in Sandstone for Use in Studying Multiphase Flow of CO2 And Brine in Core Flooding Experiments; Stanford University: Stanford, CA, USA, 2009. [Google Scholar]
- Krause, M.H. Modeling and Investigation of the Influence of Capillary Heterogeneity on Multiphase Flow Heterogeneity on Multiphase Flow; Stanford University: Stanford, CA, USA, 2012. [Google Scholar]
- Wang, K.-L.; Zhang, L.-L.; Li, X.; Ming, Y.-Y. Experimental Study on the Properties and Displacement Effects of Polymer Surfactant Solution. J. Chem. 2013, 2013, 956027. [Google Scholar] [CrossRef] [Green Version]
- Krause, M.H. Modeling Permeability Distributions in a Sandstone Core for History Matching Coreflood Experiments; SPE: Anaheim, CA, USA, 2011. [Google Scholar]
- Krause, B. Accurate Determination of Characteristic Relative Permeability Curves. Adv. Water Resour. 2015, 83, 376–388. [Google Scholar] [CrossRef]
- Kumar, A.; Mandal, A. Core-scale modelling and numerical simulation of zwitterionic surfactant flooding: Designing of chemical slug for enhanced oil recovery. J. Pet. Sci. Eng. 2020, 192, 107333. [Google Scholar] [CrossRef]
- Kechut, N.I.; Jamiolahmady, M.; Sohrabi, M. Numerical Simulation of Experimental Carbonated Water Injection (CWI) for Improved Oil Recovery and CO2 Storage; Elseiver: Amsterdam, The Netherlands, 2011. [Google Scholar]
- Chen, F.; Gu, J.; Jiang, H.; Yao, X.; Li, Y. Laboratory evaluation and numerical simulation of the alkali–surfactant–polymer synergistic mechanism in chemical flooding. RSC Adv. 2018, 8, 26476–26487. [Google Scholar] [CrossRef] [Green Version]
- Pal, N.; Mandal, A. Numerical Simulation of Enhanced Oil Recovery (EOR) studies for aqueous Gemini Surfactant-Polymer-Nanoparticle systems. AIChE J. 2020, 66, e17020. [Google Scholar] [CrossRef]
- Alsofi, A.; Liu, J.S.; Han, M. Numerical Simulation of Surfactant-Polymer Coreflooding Experiments for Carbonates. J. Petrol. Sci. Eng. 2013, 111, 184–196. [Google Scholar] [CrossRef]
- Rai, S.K.; Bera, A.; Mandal, A. Modeling of surfactant and surfactant–polymer flooding for enhanced oil recovery using STARS (CMG) software. J. Pet. Explor. Prod. Technol. 2015, 5, 1–11. [Google Scholar] [CrossRef] [Green Version]
- HosseiniNasab, S.M.; Chahardowli, M.; Zitha, P.L.J. Simplified Numerical Model for Simulation of Surfactant/Polymer (SP) Flooding Process for Enhanced Oil Recovery. In Proceedings of the Conference Proceedings, 78th EAGE Conference and Exhibition 2016, Online, 30 May–2 June 2016; European Association of Geoscientists & Engineers: Bunnik, The Netherlands, 2016; Volume 2016, pp. 1–5. [Google Scholar] [CrossRef]
- Abbas, A.H.; Elhag, H.H.; Sulaiman, W.R.W.; Gbadamosi, A.; Pourafshary, P.; Ebrahimi, S.S.; Alqohaly, O.Y.; Agi, A. Modelling of continuous surfactant flooding application for marginal oilfields: A case study of Bentiu reservoir. J. Petrol. Explor. Prod. 2021, 11, 989–1006. [Google Scholar] [CrossRef]
- Alzayer, H.A.; Jahanbakhsh, A.; Sohrabi, M. New Methodology for Numerical Simulation of Water-Alternating-Gas (WAG) Injection; EAGE: Stavenger, Norway, 2017. [Google Scholar]
- Fulcher, R.A., Jr.; Ertekin, T.; Stahl, C.D. Effect of Capillary Number and Its Constituents on Two-Phase Relative Permeability Curves; SPE: Anaheim, CA, USA, 1985. [Google Scholar]
- Guo, H.; Dou, M.; Wang, H.; Wang, F.; Gu, Y.; Yu, Z.; Wang, Y.; Li, Y. Review of Capillary Number in Chemical Enhanced Oil Recovery; SPE: Anaheim, CA, USA, 2015. [Google Scholar]


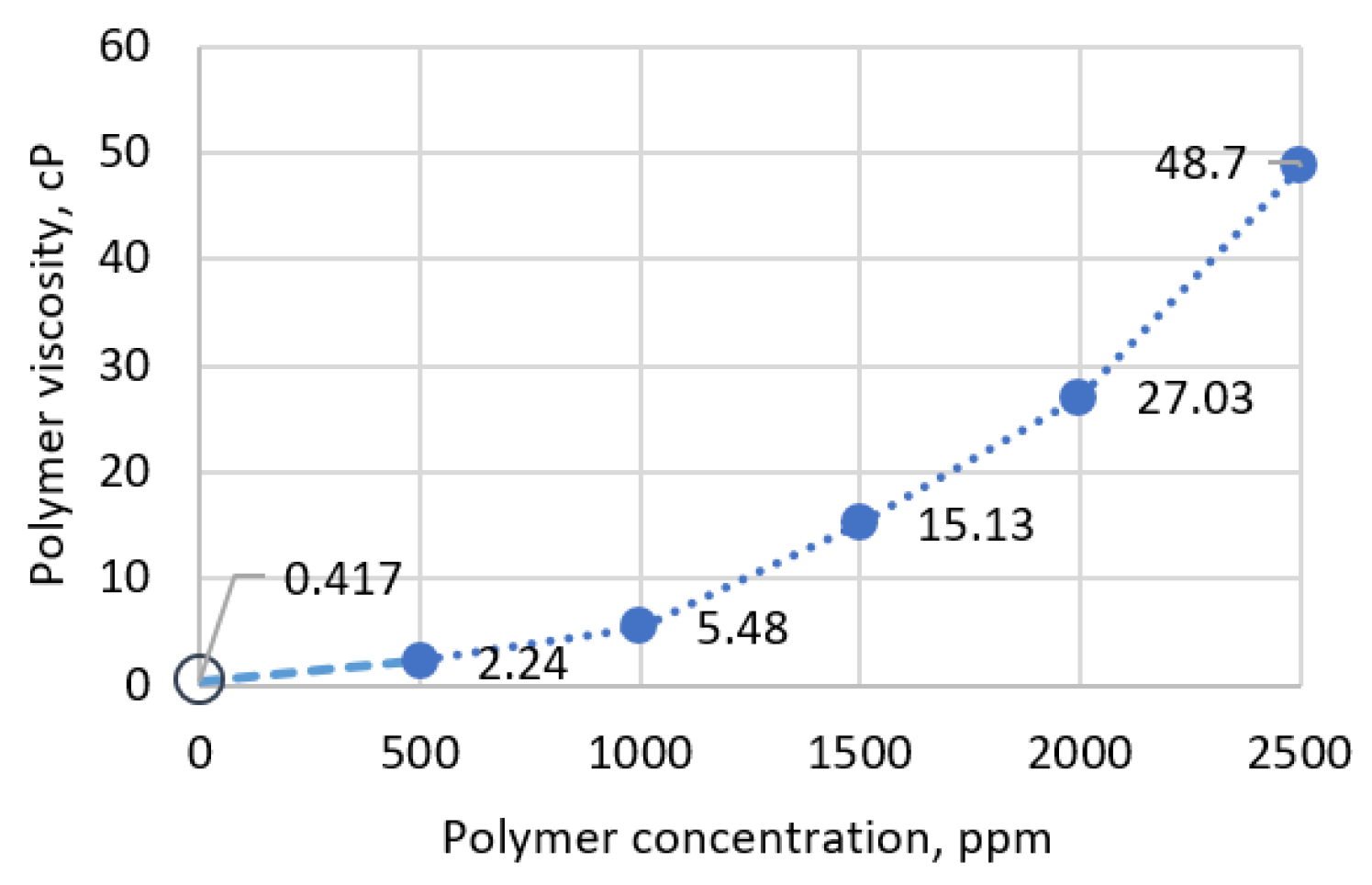

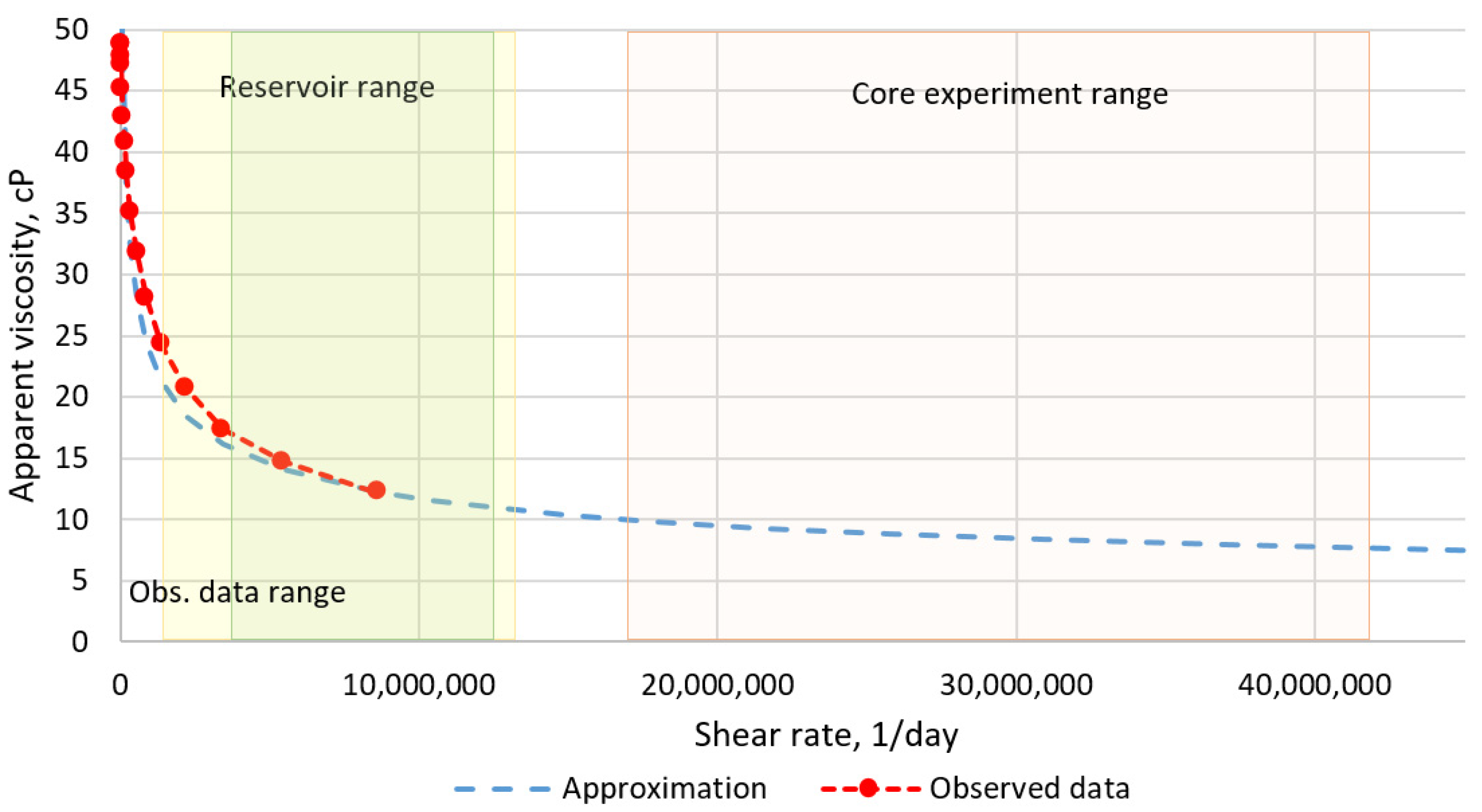

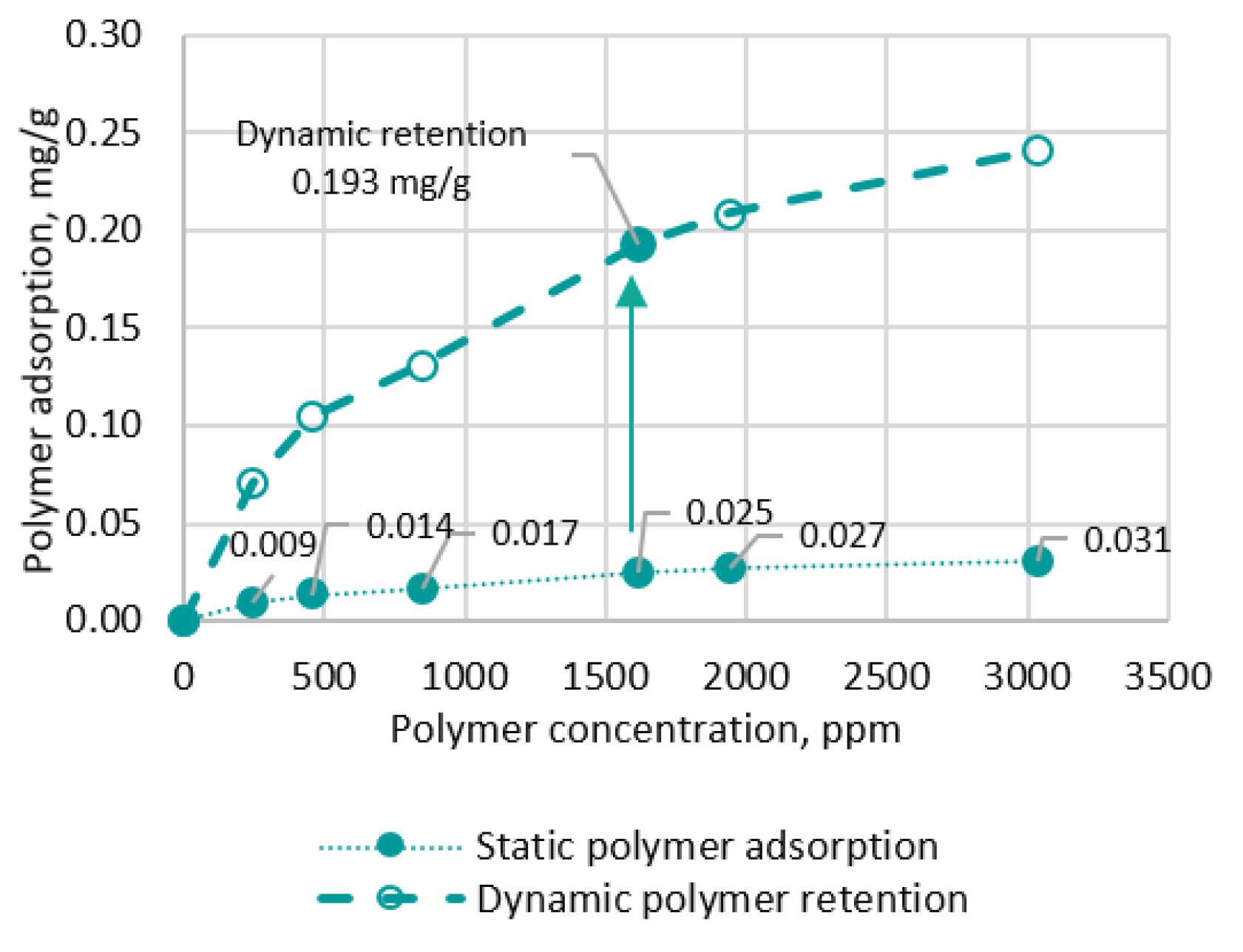
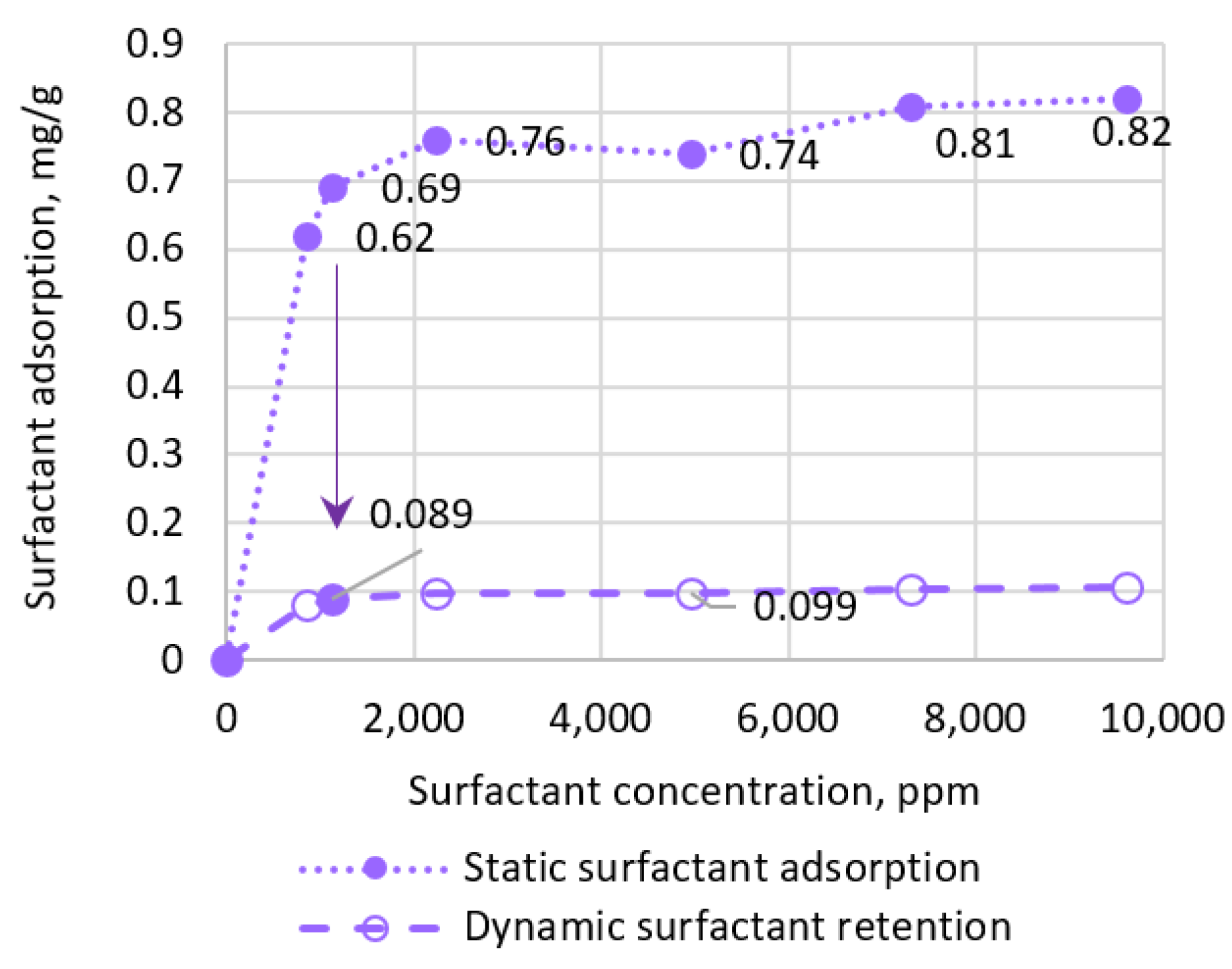
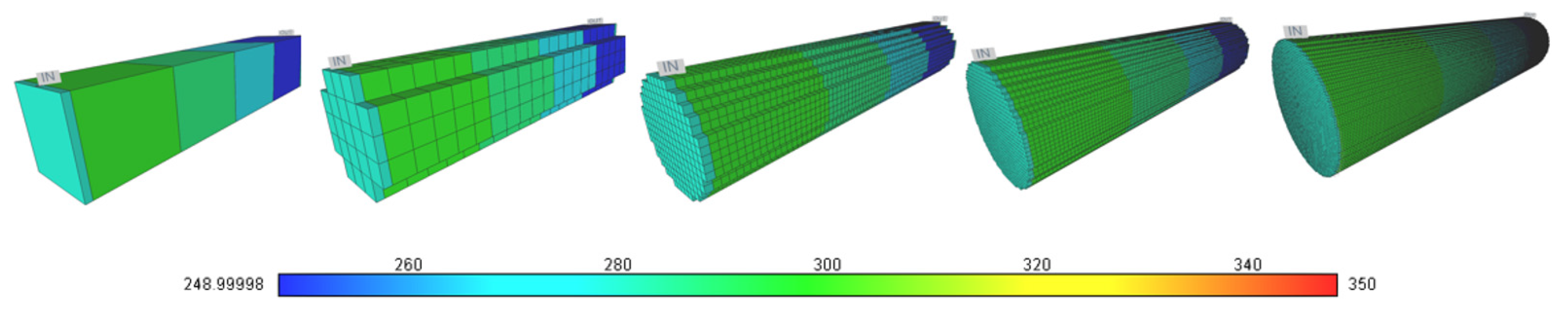
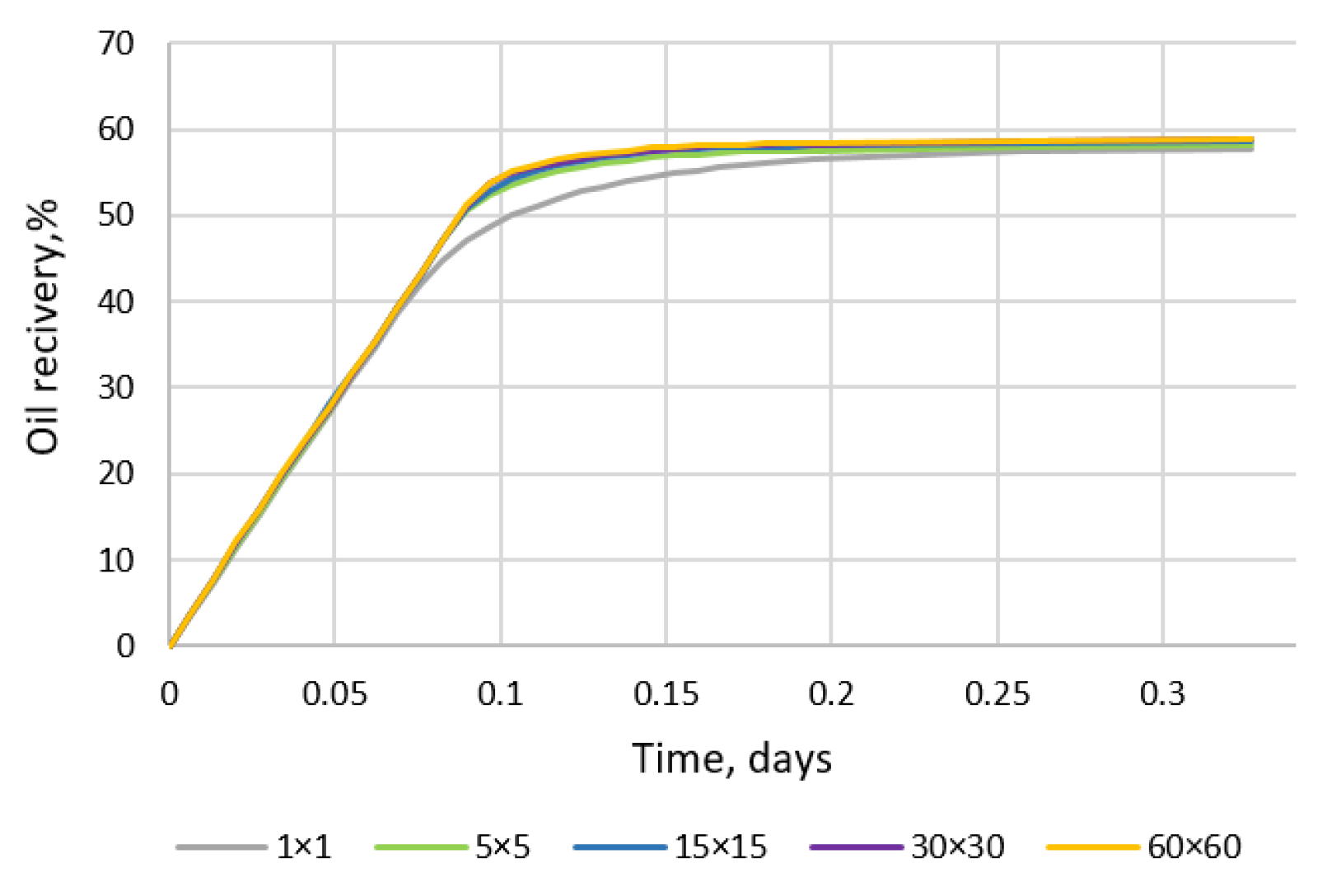
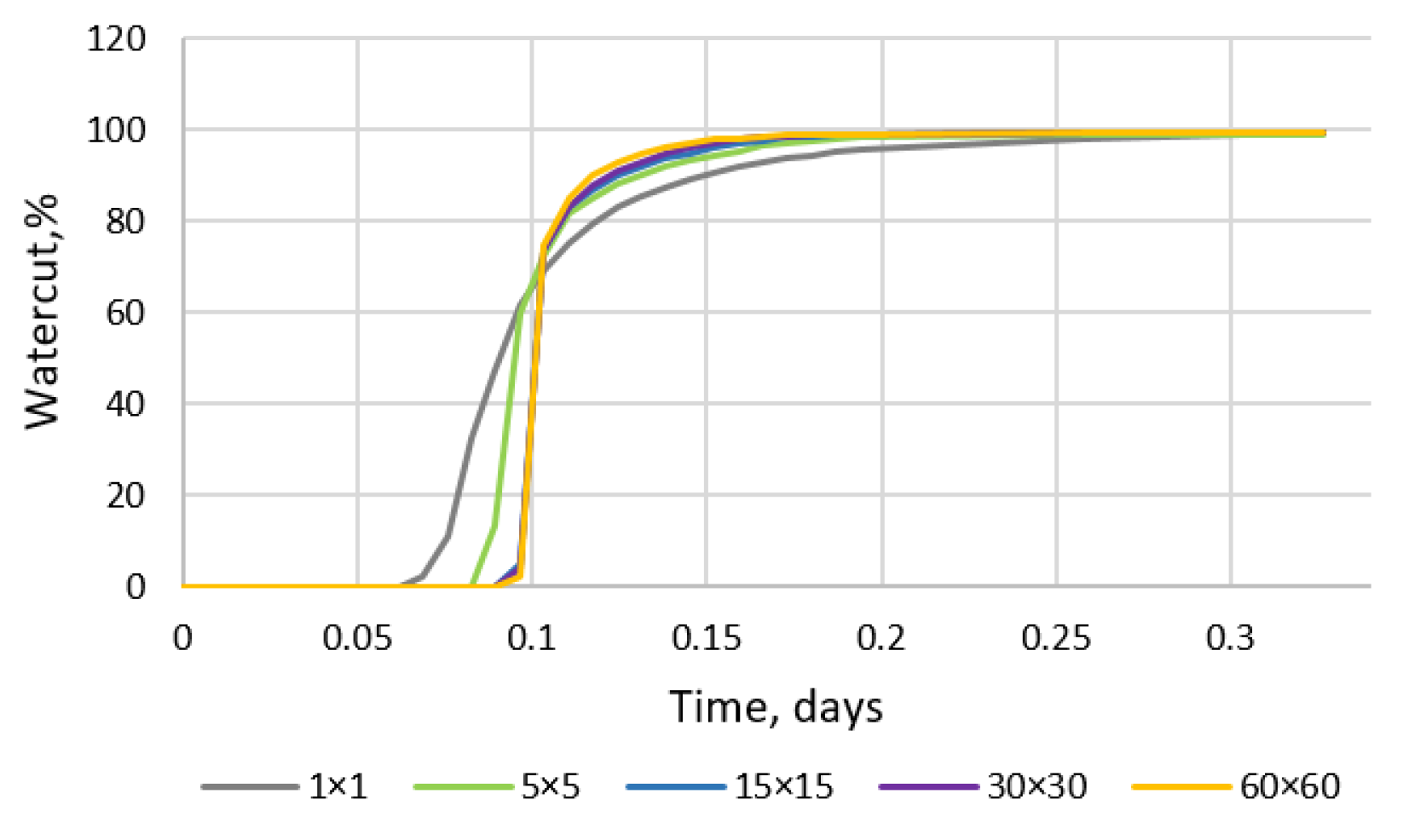

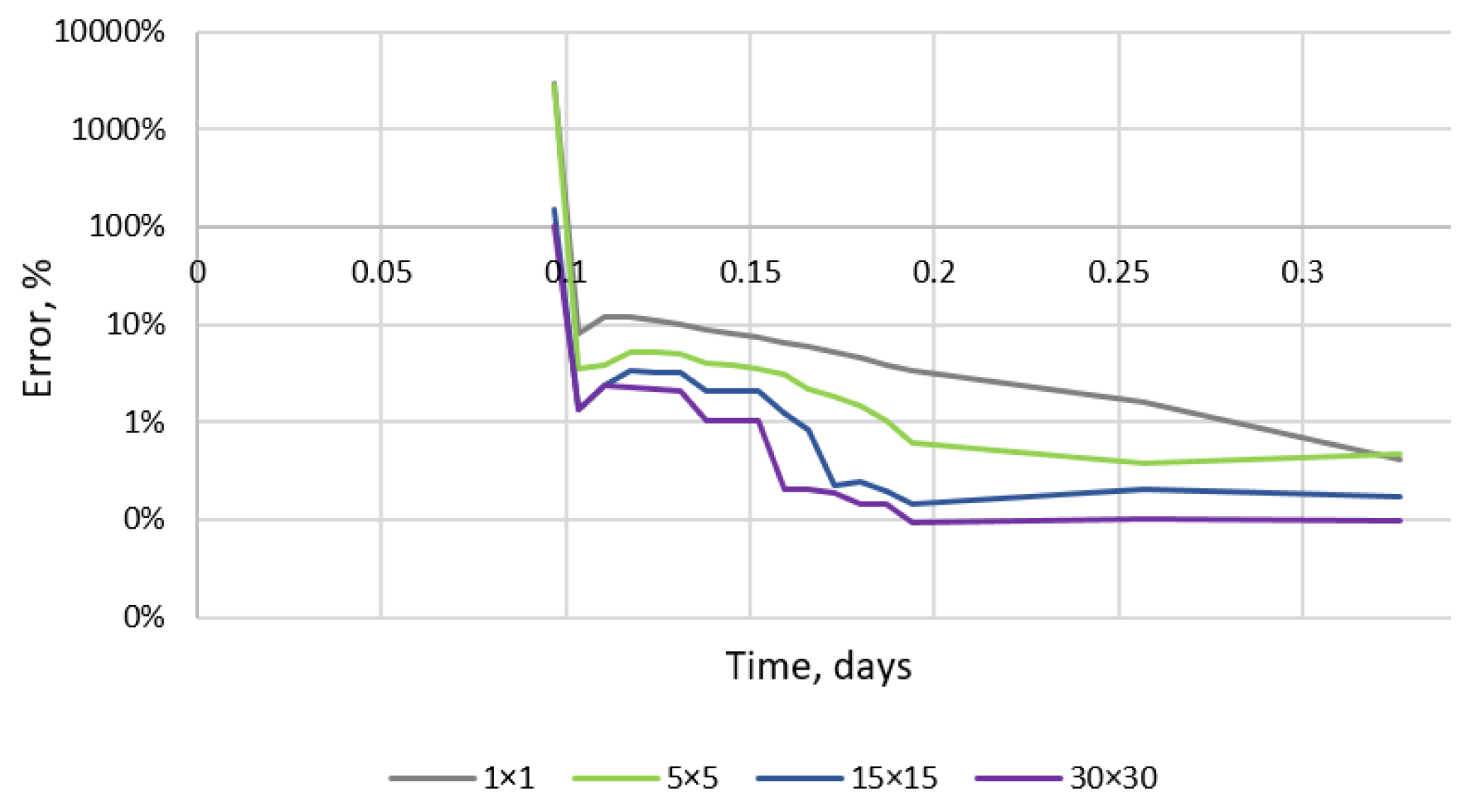
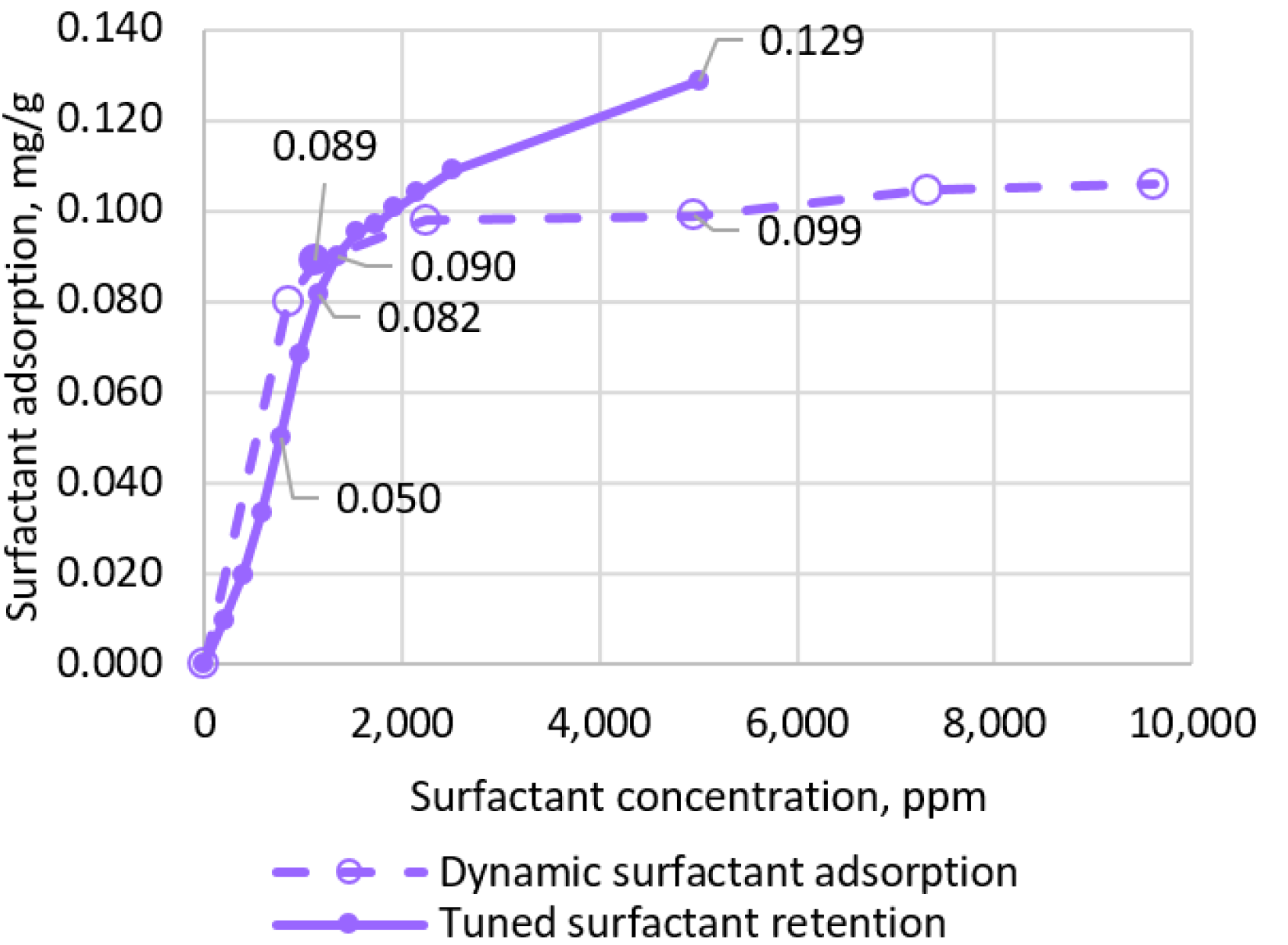
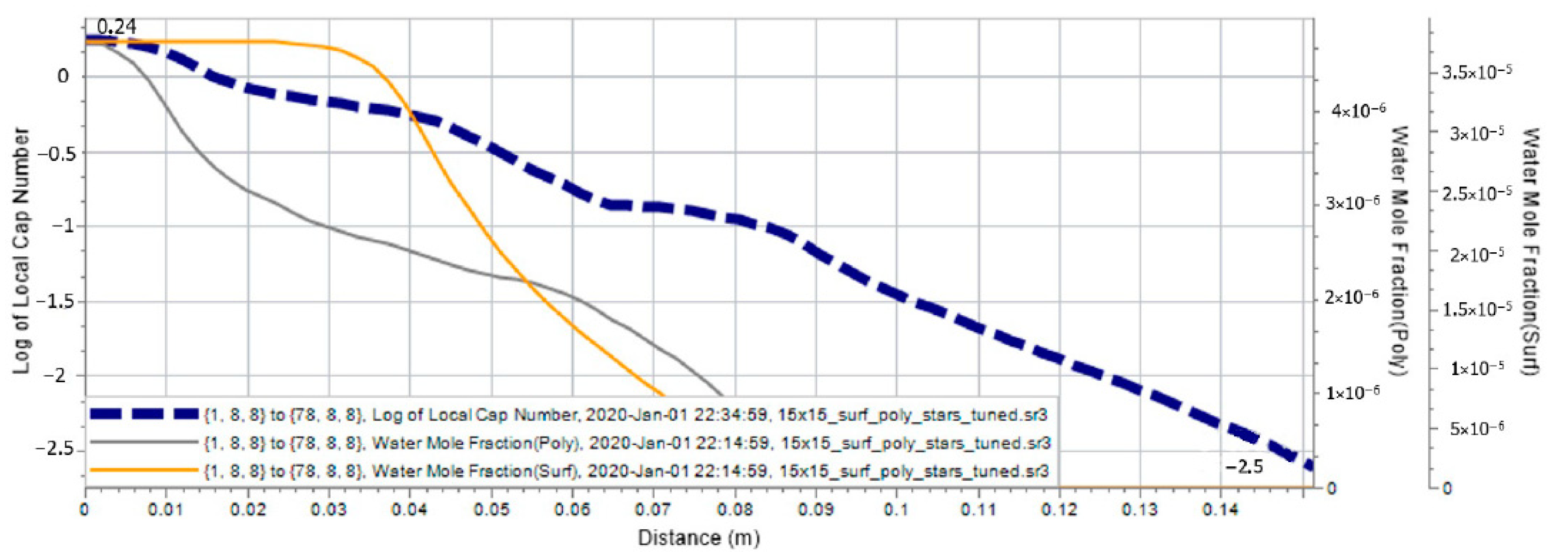
| Slug | Parameter | Value |
|---|---|---|
| Surfactant | Surfactant | Surf |
| Csurf, ppm | 2500 | |
| CNaCl, ppm | 1000 | |
| Polymer | POL | |
| Cpol, ppm | 2500 | |
| Slug size, PV | 0.5 | |
| Polymer | Polymer | Poly |
| Cpol, ppm | 2500 | |
| Slug size, PV | 0.5 | |
| Water | Slug size, PV | 2 |
| Parameter | Polymer | Surfactant |
|---|---|---|
| Unavailable pore volume | 0.25 | 0 |
| Residual resistance factor | 2 | 1 |
| Desorption | No | No |
| Type of interpolation used when doing a table lookup for IFT values | - | Linear |
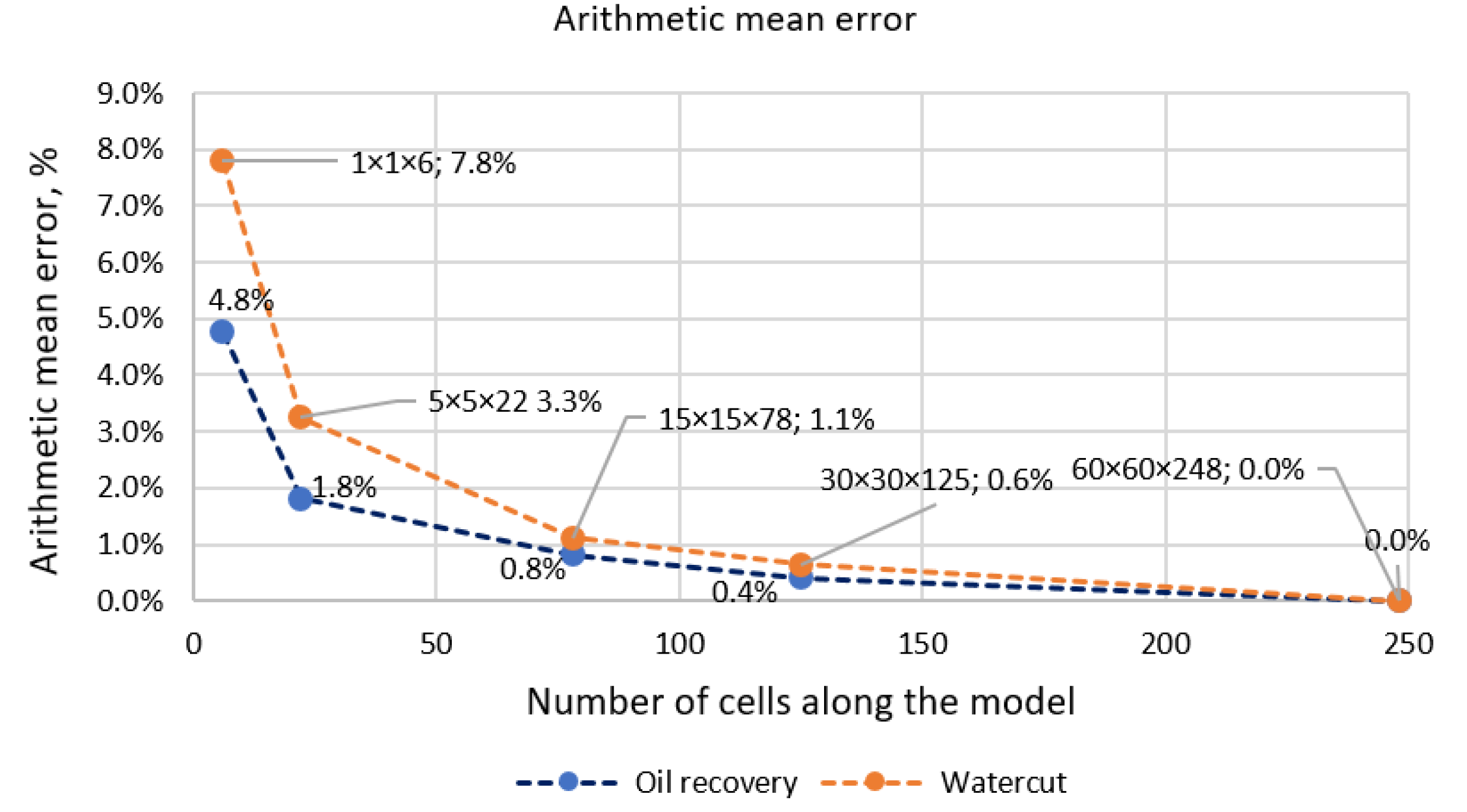
| Model and Cell Size | 1 × 1 × 6 | 5 × 5 × 22 | 15 × 15 × 78 | 30 × 30 × 125 | 60 × 60 × 248 |
|---|---|---|---|---|---|
| Number of active cells | 6 | 462 | 13,806 | 89,750 | 701,344 |
| Cell sizes in X and Y directions (Z—direction along core sample), mm | ~38 | 7.04 | 1.99 | 1.24 | 0.63 |
| Parameter | Value |
|---|---|
| Oil viscosity, cP | 1.6 |
| Water viscosity, cP | 0.417 |
| Pore volume, cm3 | 28.16 |
| Oil in reservoir conditions, cm3 | 15.00 |
| Moveable oil, cm3 | 8.7 |
| Bound water, cm3 | 13.16 |
| Average permeability on 4 samples, mD | 277.3 |
| Average porosity on 4 samples, % | 26.4 |
| Model length, mm | 153.6 |
| Parameter | Polymer | Surfactant |
|---|---|---|
| Unavailable pore volume | 0.35 | 0.25 |
| Residual resistance factor | 3.5 | 1 |
| Fraction of desorbable agent | 0.375 | 0.375 |
| Type of interpolation used when doing a table lookup for IFT values | - | Logarithmetic |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheremisin, A.; Lompik, V.; Spivakova, M.; Kudryashov, A.; Karseka, K.; Mityurich, D.; Podnebesnykh, A. Creation of a Hydrodynamic Digital Model of a Laboratory Core Experiment of Surfactant Polymer Impact on Oil Recovery, in Order to Determine Parameters for Further Full-Scale Simulation. Energies 2022, 15, 3440. https://doi.org/10.3390/en15093440
Cheremisin A, Lompik V, Spivakova M, Kudryashov A, Karseka K, Mityurich D, Podnebesnykh A. Creation of a Hydrodynamic Digital Model of a Laboratory Core Experiment of Surfactant Polymer Impact on Oil Recovery, in Order to Determine Parameters for Further Full-Scale Simulation. Energies. 2022; 15(9):3440. https://doi.org/10.3390/en15093440
Chicago/Turabian StyleCheremisin, Alexander, Vasiliy Lompik, Margarita Spivakova, Alexey Kudryashov, Kiryl Karseka, Denis Mityurich, and Alexander Podnebesnykh. 2022. "Creation of a Hydrodynamic Digital Model of a Laboratory Core Experiment of Surfactant Polymer Impact on Oil Recovery, in Order to Determine Parameters for Further Full-Scale Simulation" Energies 15, no. 9: 3440. https://doi.org/10.3390/en15093440
APA StyleCheremisin, A., Lompik, V., Spivakova, M., Kudryashov, A., Karseka, K., Mityurich, D., & Podnebesnykh, A. (2022). Creation of a Hydrodynamic Digital Model of a Laboratory Core Experiment of Surfactant Polymer Impact on Oil Recovery, in Order to Determine Parameters for Further Full-Scale Simulation. Energies, 15(9), 3440. https://doi.org/10.3390/en15093440






