Eliminating the Influence of Support Conditions on Geometric Shape Measurements of Large Crankshafts of Marine Engines
Abstract
:1. Introduction
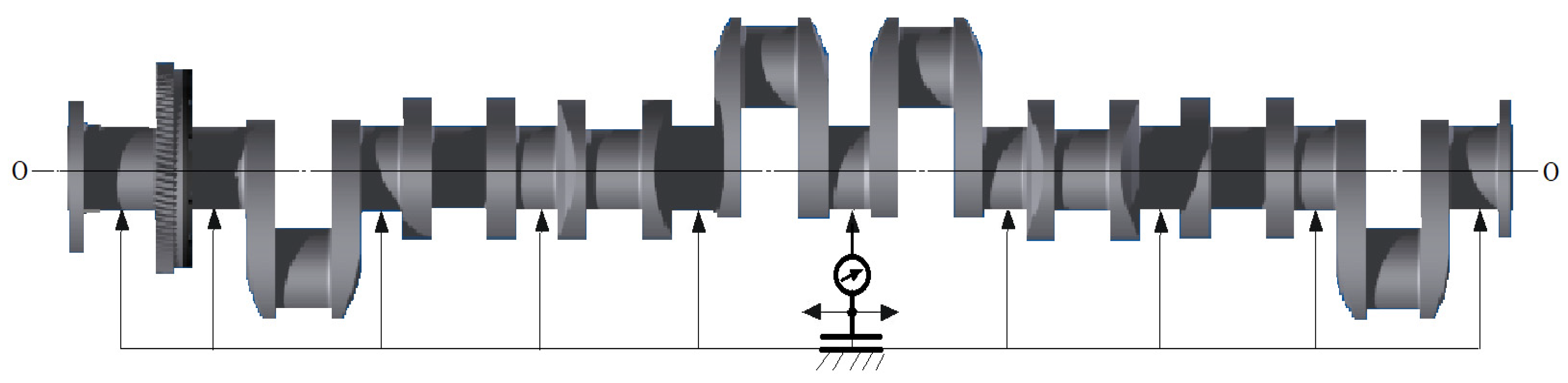
2. Research Problem
3. Solution to the Problem
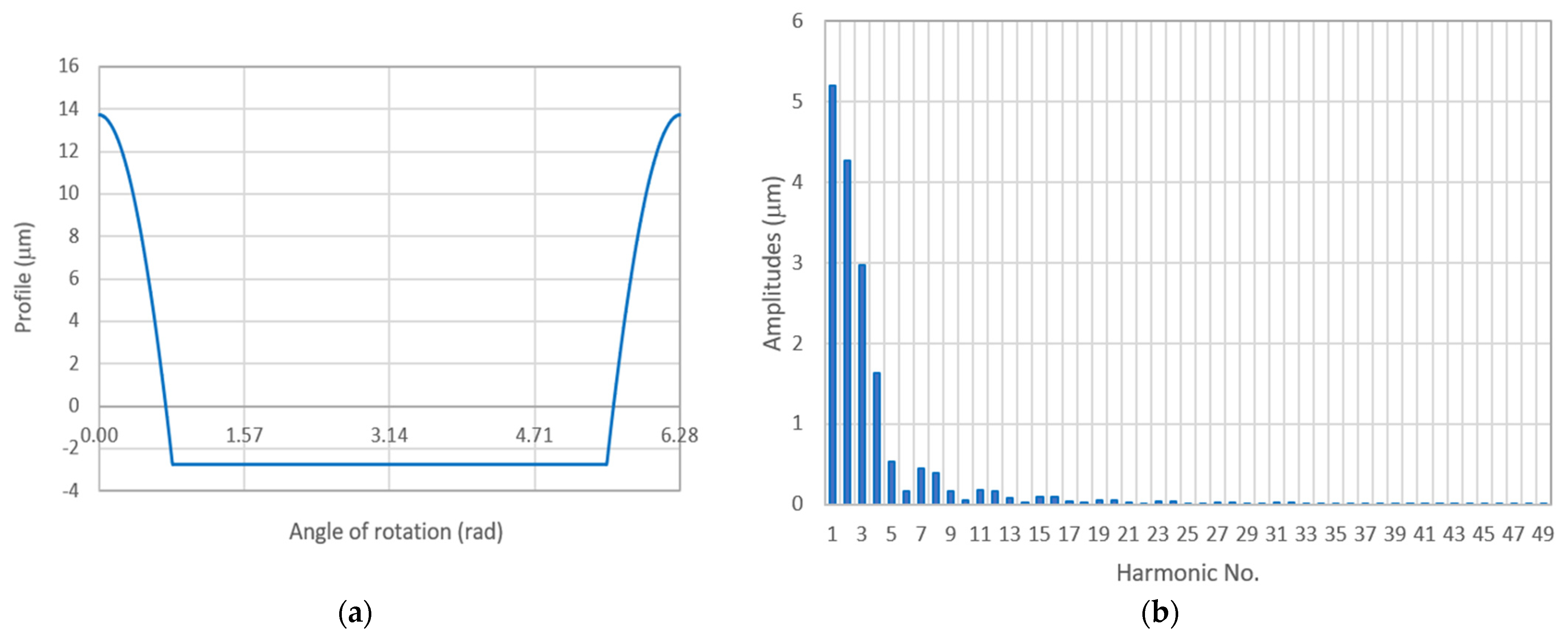
3.1. Determination of Geometric Deviations of Crankshafts with Limited Possibilities of Their Detection Resulting from the Adopted Support Conditions
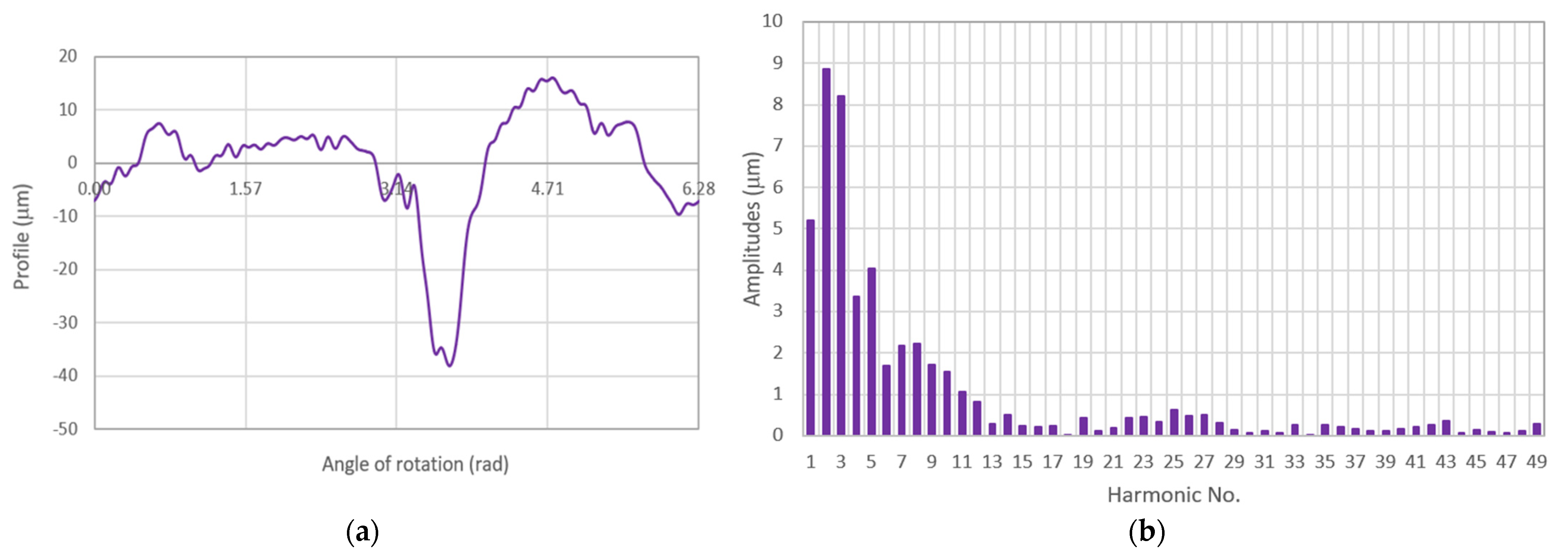
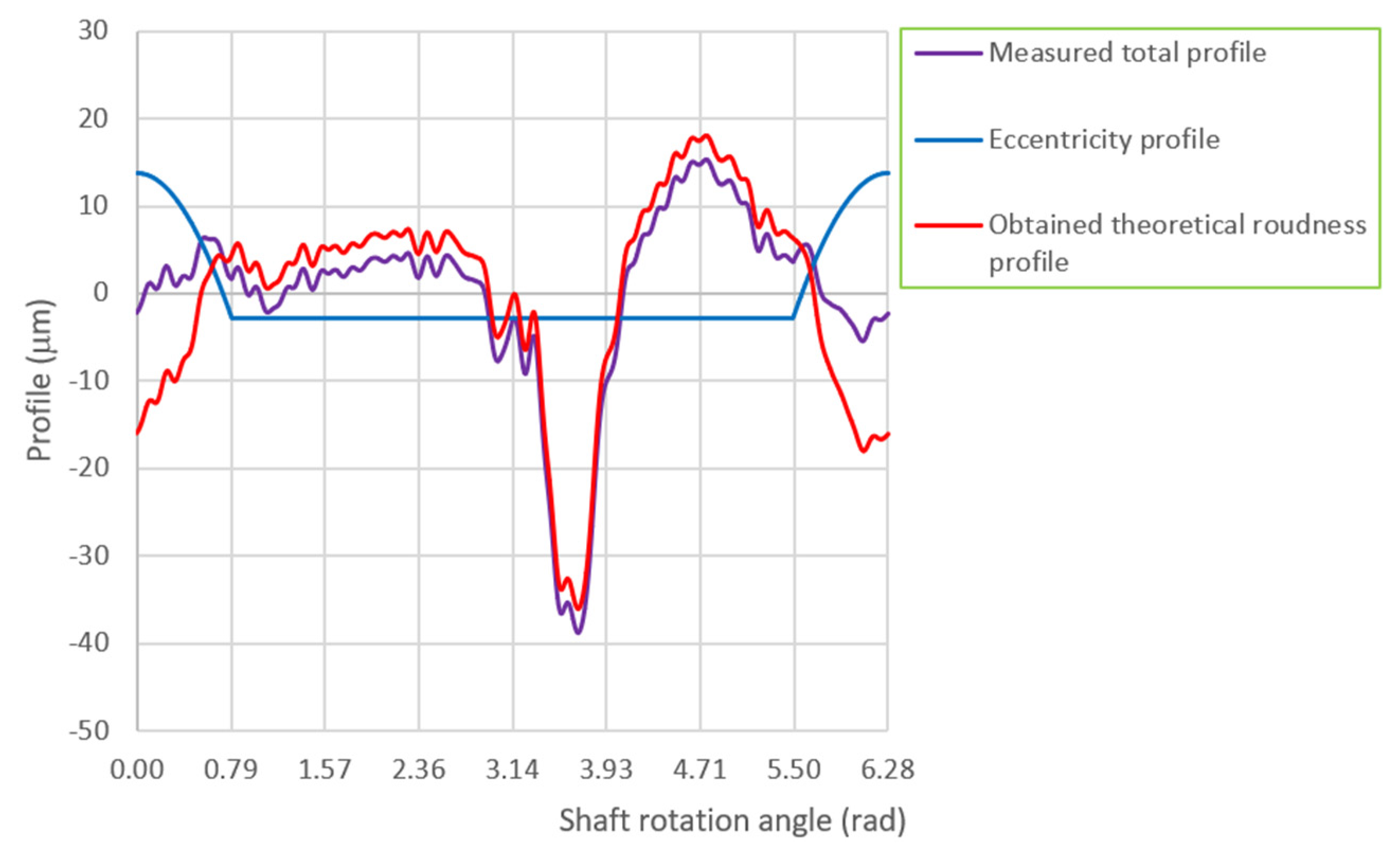
3.2. Exemplary Procedures for Determining the Theoretical Roundness Profile on the Basis of the Measured Summary Profile
3.3. Comparative Assessment of Test Results and Their Validation
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Adamczak, S. Measurements of Geometrical Surfaces, Outlines of Shape, Waviness, and Roughness; WNT: Warsaw, Poland, 2008. (In Polish) [Google Scholar]
- Mekid, S.; Vacharanukul, K. In-process out-of-roundness measurement probe for turned workpieces. Measurement 2011, 44, 762–766. [Google Scholar] [CrossRef]
- Janusiewicz, A.; Adamczak, S.; Makieła, W.; Stępień, K. Determining the theoretical method error during an on-machine roundness measurement. Measurement 2011, 44, 1761–1767. [Google Scholar] [CrossRef]
- Stępień, K.; Janecki, D.; Adamczak, S. Fundamentals of adaptive strategy of cylindricity measurements with the use of longitudinal measurements. Meas. Sens. 2021, 18, 100146. [Google Scholar] [CrossRef]
- Liu, Y.; Mei, Y.; Sun, C.; Li, R.; Wang, X.; Wang, H.; Tan, J.; Lu, Q. A novel cylindrical profile measurement model and errors separation method applied to stepped shafts precision model engineering. Measurement 2022, 188, 110486. [Google Scholar] [CrossRef]
- Li, X.; Xu, K.; Wang, S. Precision measurement method of large shaft diameter based on dual camera system. Sensors 2022, 22, 3982. [Google Scholar] [CrossRef]
- Clader, N. Marine Diesel Engines: Maintenance, Troubleshooting, and Repair, 3rd ed.; International Marine/Ragged Mountain Press: Camden, UK, 2006. [Google Scholar]
- Shen, N.; Li, J.; Qian, X.; Huang, H. Precise alignment method of the large-scale crankshaft during non-circular grinding. Int. J. Adv. Manuf. Technol. 2015, 80, 921–930. [Google Scholar] [CrossRef]
- Nguyen, D.V.; Duy, V.N. Numerical analysis of the forces on the components of a direct diesel engine. Appl. Sci. 2018, 8, 761. [Google Scholar] [CrossRef] [Green Version]
- Kamiński, W. Marine slow-speed engines’ cylinder oil lubrication feed rate optimization in real operational conditions. Energies 2022, 15, 8378. [Google Scholar] [CrossRef]
- Łukomski, Z. Rail and Marine Internal Combustion Engine Technology; Transport and Communication Publishers: Warsaw, Poland, 1972. (In Polish) [Google Scholar]
- Chen, M.; Takahashi, S.; Takamasu, K. Development of high-precision micro-roundness measuring machine using a high-sensitivity and compact multi-beam angle sensor. Precis. Eng. 2015, 42, 276–282. [Google Scholar] [CrossRef]
- Grzejda, R. Finite element modeling of the contact of elements preloaded with a bolt and externally loaded with any force. J. Comput. Appl. Math. 2021, 393, 113534. [Google Scholar] [CrossRef]
- Shape and Position Tolerances of Crankshafts—Engine Technology, Specification; MAN B&W, H. Cegielski, S.A.: Poznan, Poland, 2010. (In Polish)
- IMO. Marine Engine IMO Tier II Programme; IMO: London, UK, 2013. [Google Scholar]
- MAN B&W 50-90 MC/MCE Engines Instruction Manual; MAN B&W Diesel A/S: Copenhagen, Denmark, 2013.
- Nozdrzykowski, K.; Adamczak, S.; Grządziel, Z.; Dunaj, P. The effect of deflections and elastic deformations on geometrical deviation and shape profile measurements of large crankshafts with uncontrolled supports. Sensors 2020, 20, 5714. [Google Scholar] [CrossRef] [PubMed]
- Nozdrzykowski, K.; Grządziel, Z.; Dunaj, P. Determining geometrical deviations of crankshafts with limited detection possibilities due to support conditions. Measurement 2022, 189, 110430. [Google Scholar] [CrossRef]
- Nozdrzykowski, K. Conditions and Criteria of the Correct Assessment of the Geometric Condition of Large Crankshaft; Maritime University of Szczecin Press: Szczecin, Poland, 2022. (In Polish) [Google Scholar]
- Chybowski, L.; Nozdrzykowski, K.; Grządziel, Z.; Jakubowski, A.; Przetakiewicz, W. Method to increase the accuracy of large crankshaft geometry measurements using counterweights to minimize elastic deformations. Appl. Sci. 2020, 10, 4722. [Google Scholar] [CrossRef]
- Vizentin, G.; Vukelic, G.; Murawski, L.; Recho, N.; Orovic, J. Marine propulsion system failures—A review. J. Mar. Sci. Eng. 2020, 8, 662. [Google Scholar] [CrossRef]
- Chen, L.; Xue, D.; Song, X.; He, Z.; Huang, D. A study on anti-shock performance of marine diesel engine based on multi-body dynamics and elastohydrodynamic lubrication. Appl. Sci. 2021, 11, 11259. [Google Scholar] [CrossRef]
- Midas Engineering Software. Available online: https://www.midasoft.com (accessed on 24 October 2022).
- Whitehouse, D.J. Handbook of Surface Metrology, 1st ed.; Institute of Physics Publishing: Bristol, England, 1994. [Google Scholar]
- Mohlenkamp, M.J. A fast transform for spherical harmonics. J. Fourier Anal. Appl. 1999, 5, 159–184. [Google Scholar] [CrossRef]
- Capello, E.; Semeraro, Q. The harmonic fitting method for the assessment of the substitute geometry estimate error. Part I: 2D and 3D theory. Int. J. Mach. Tools Manuf. 2001, 41, 1071–1102. [Google Scholar] [CrossRef]
- Kunis, S.; Potts, D. Fast spherical Fourier algorithms. J. Comput. Appl. Math. 2003, 161, 75–98. [Google Scholar] [CrossRef] [Green Version]
- Nozdrzykowski, K. Applying harmonic analysis in the measurements of geometrical deviations of crankshafts—Roundness shapes analysis. Multidiscip. Asp. Prod. Eng. 2018, 1, 185–189. [Google Scholar] [CrossRef] [Green Version]
- Muhammad, A.; Ali, M.A.H.; Shanono, I.H. Fatigue and harmonic analysis of a diesel engine crankshaft using ANSYS. In iMEC-APCOMS 2019; Osman Zahid, M.N., Abd Aziz, R., Yusoff, A.R., Mat Yahya, N., Abdul Aziz, F., Yazid Abu, M., Eds.; Lecture Notes in Mechanical Engineering; Springer: Singapore, 2020; pp. 371–376. [Google Scholar]
- Nozdrzykowski, K. Method and Device for Measuring the Deviation of Axis Shape and Position of the Crankshaft Pivot Set, PAT.218653, 10.06.2014; Polish Patent Office: Warsaw, Poland, 2014. [Google Scholar]
- Nozdrzykowski, K. Methodology of Geometric Measurements of Deviations of Cylindrical Surfaces of Large-Size Machine Elements Based on the Example of Ship Engine Crankshafts; Maritime University of Szczecin Press: Szczecin, Poland, 2013. (In Polish) [Google Scholar]
- Nozdrzykowski, K. Prevention of elastic strains in flexible large size machine parts with the use of elastic support. Mach. Dyn. Res. 2015, 39, 111–122. [Google Scholar]
- Adamczak, S. Reference Methods for Measuring the Roundness Profiles of Machine Parts; Kielce University of Technology: Kielce, Poland, 1998. (In Polish) [Google Scholar]
- Adamczak, S.; Janecki, D. Reference methods and their wider applicability to measurements of roundness profiles. Elektrotech. Inftech. 1998, 115, 197–202. [Google Scholar] [CrossRef]
- Adamczak, S.; Janecki, D.; Świderski, J.; Dobrowolski, T. Verification of Outlines of Crankshaft Pins Roundness Based on the MUK 25-600 Measuring System with SAJD Software, Research commissioned by the Maritime University of Szczecin; Kielce University of Technology: Kielce, Poland, 2011. (In Polish) [Google Scholar]
- Whitehouse, D.J. Handbook of Surface and Nanometrology, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar]
- PN-EN ISO 12181-2, 2012; Geometrical Product Specifications (GPS), Roundness, Part 2: Specification Operators. Polish Committee for Standardization: Warsaw, Poland, 2012.
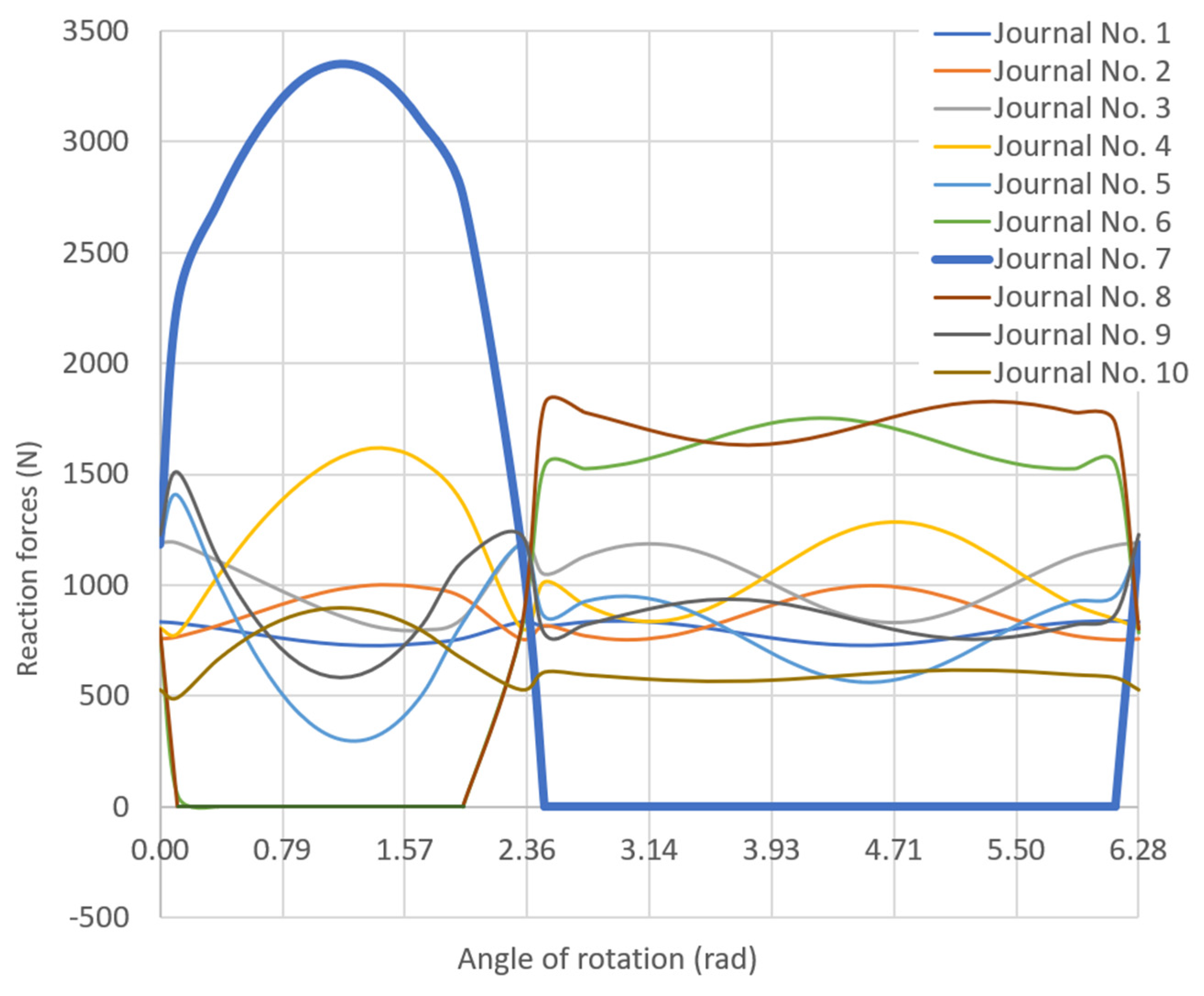
- Nozdrzykowski, K.; Grządziel, Z.; Grzejda, R.; Warzecha, M.; Stępień, M. An analysis of reaction forces in crankshaft support systems. Lubricants 2022, 10, 151. [Google Scholar] [CrossRef]
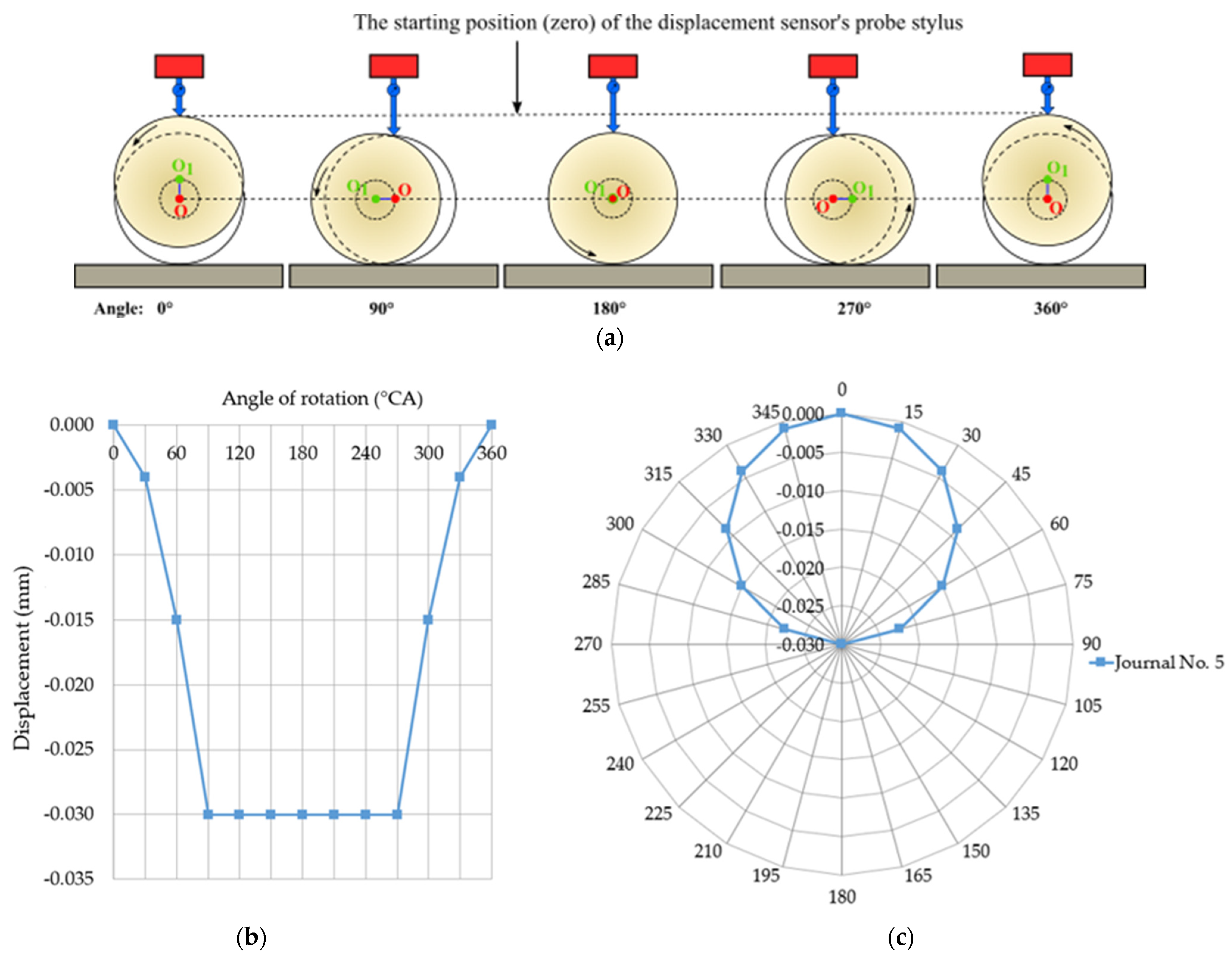

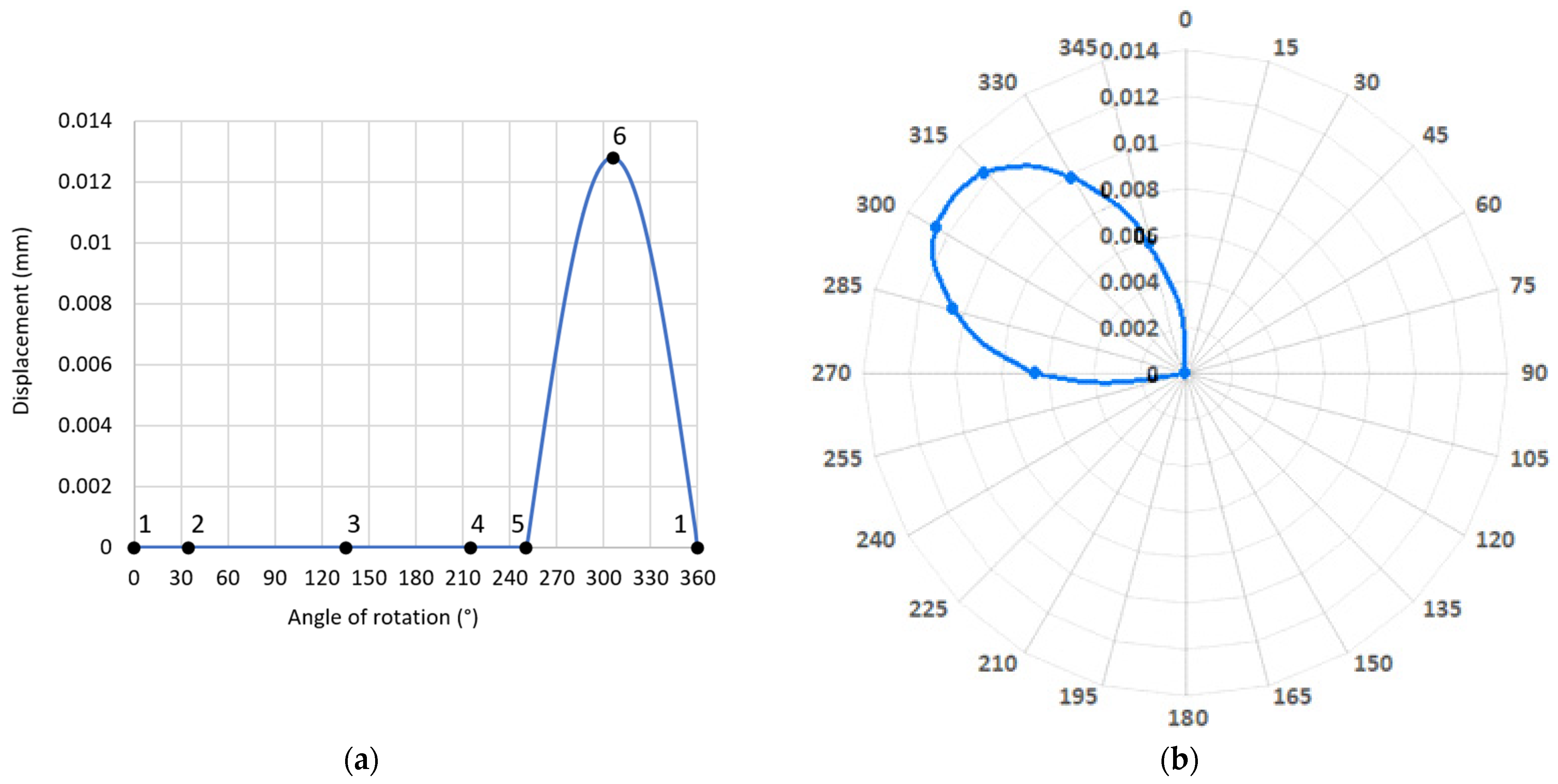


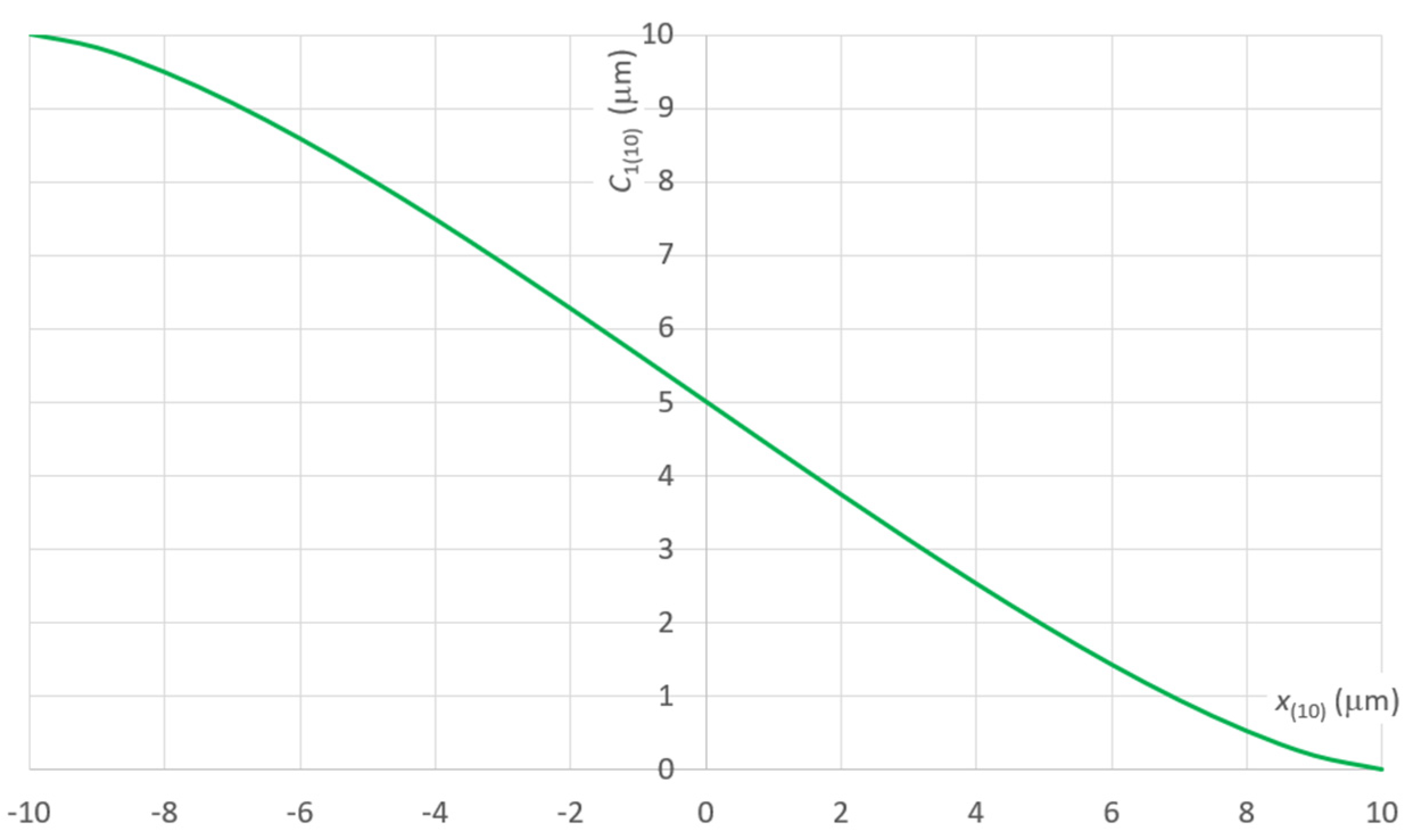

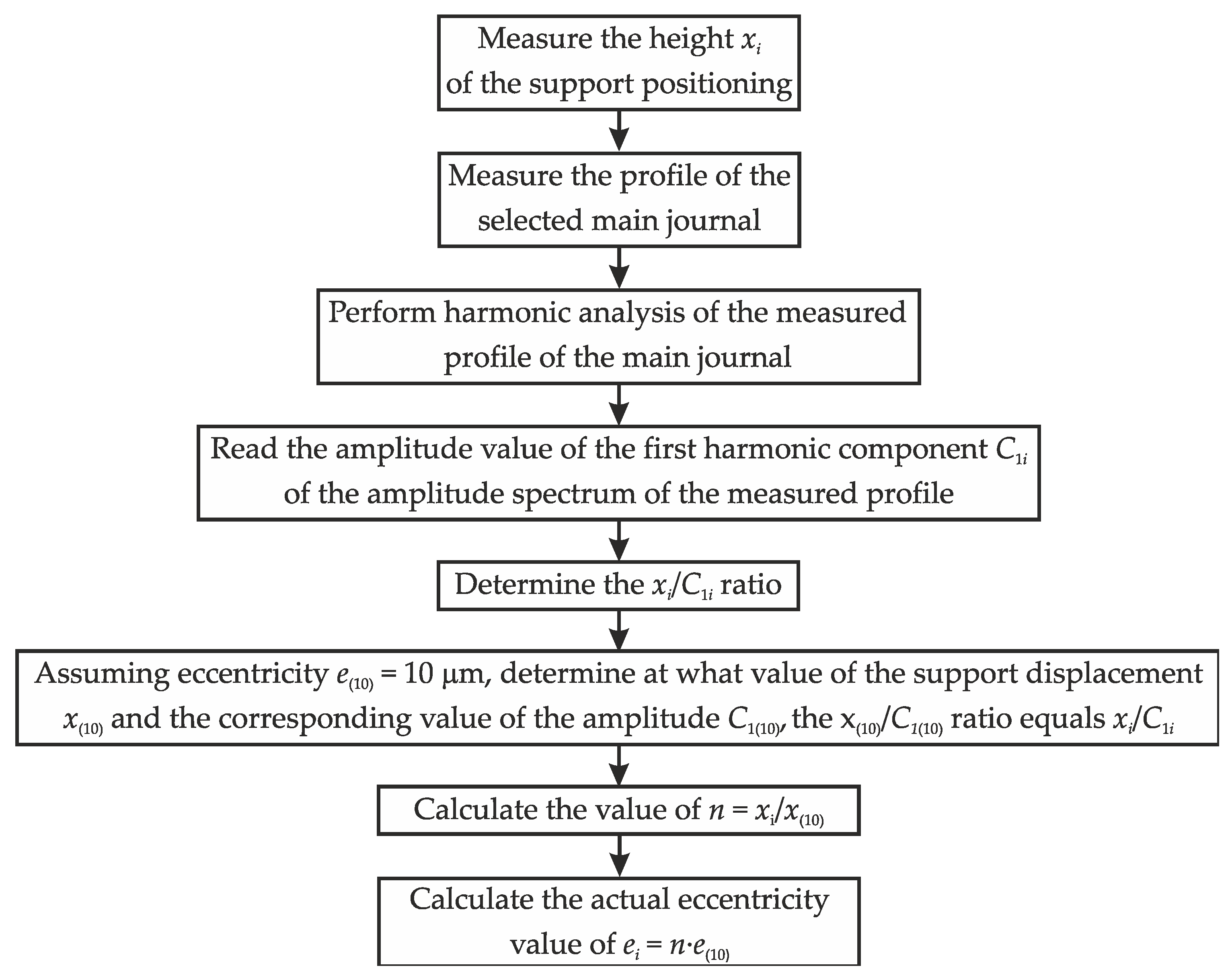



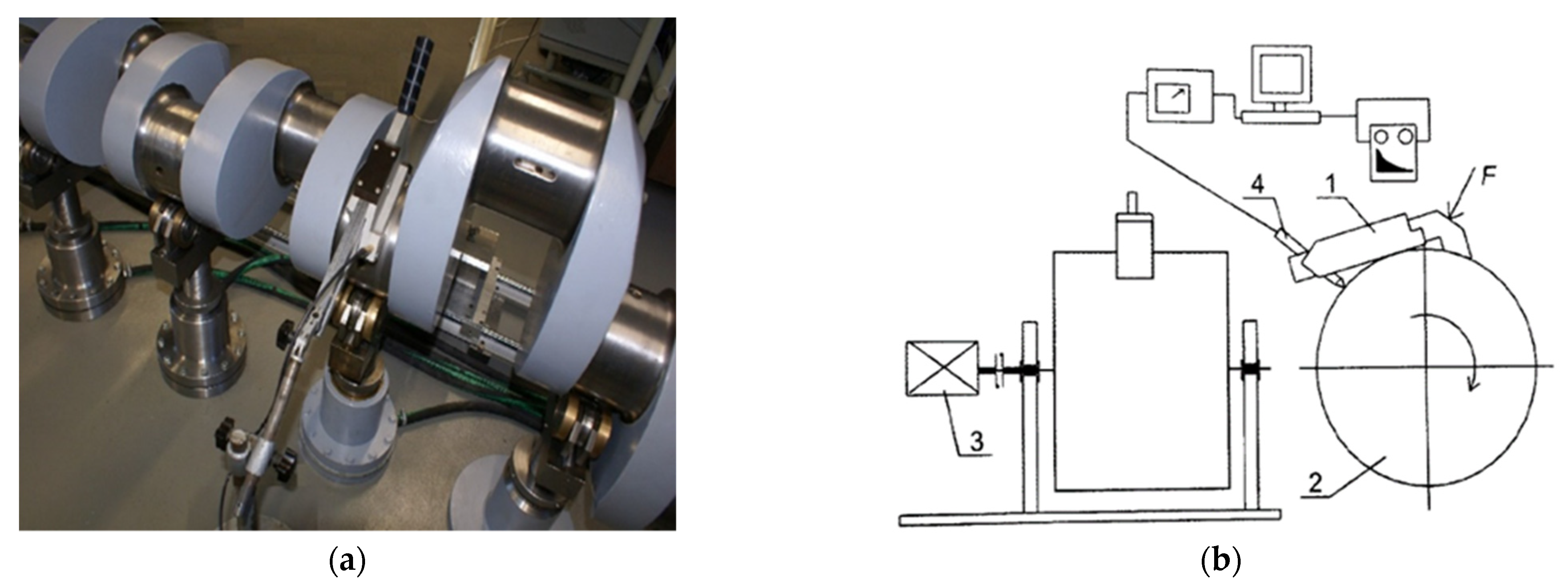
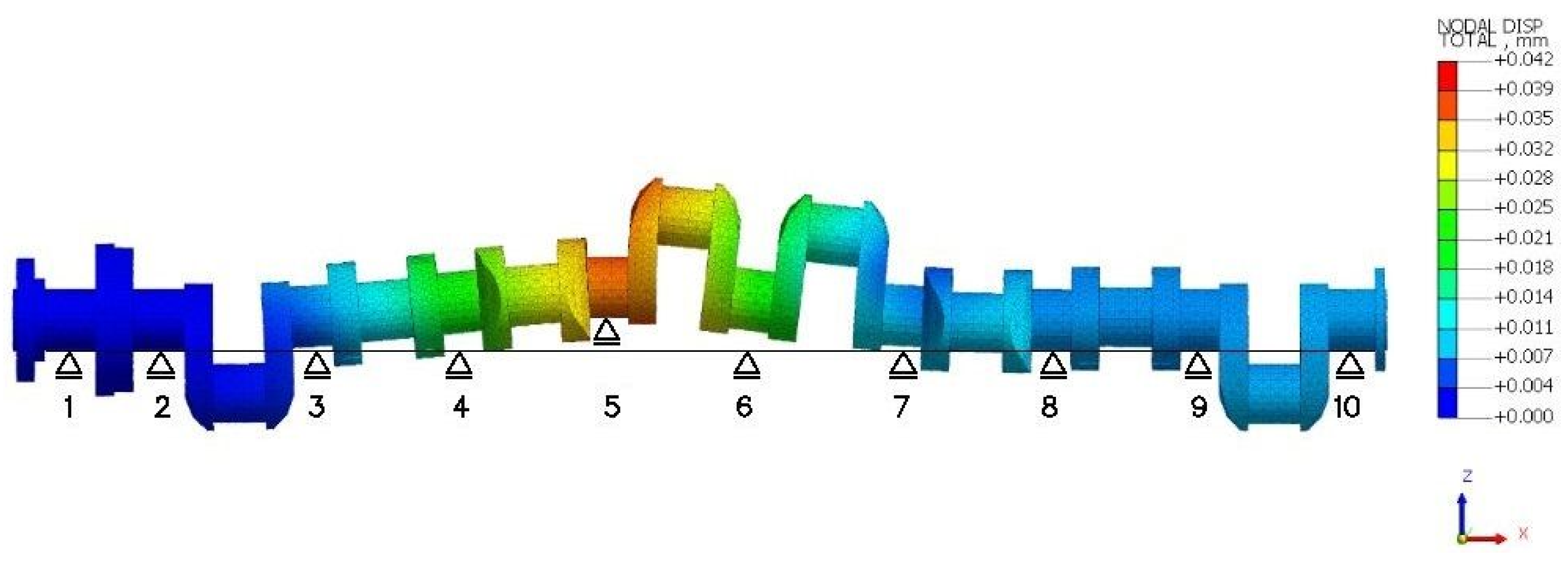
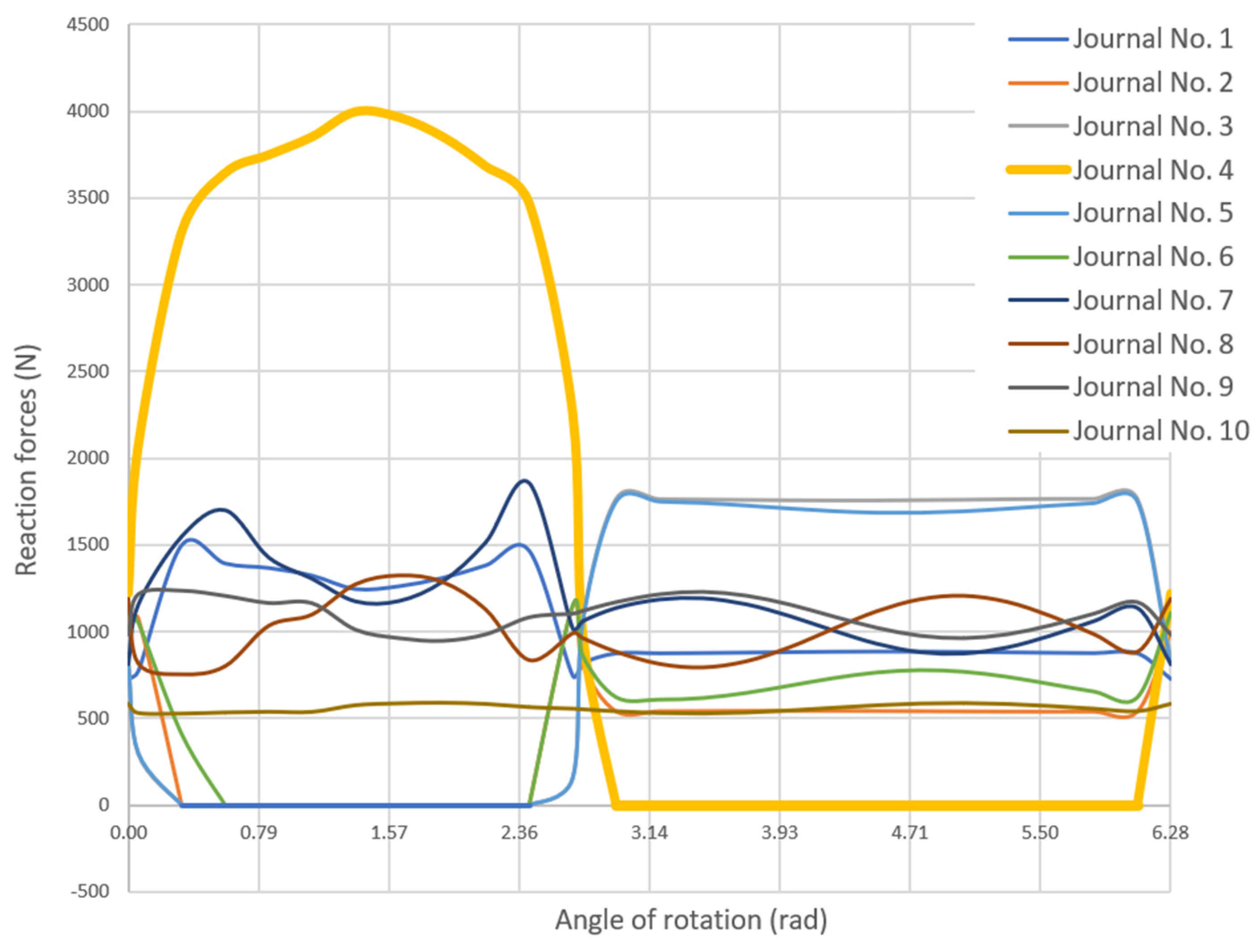
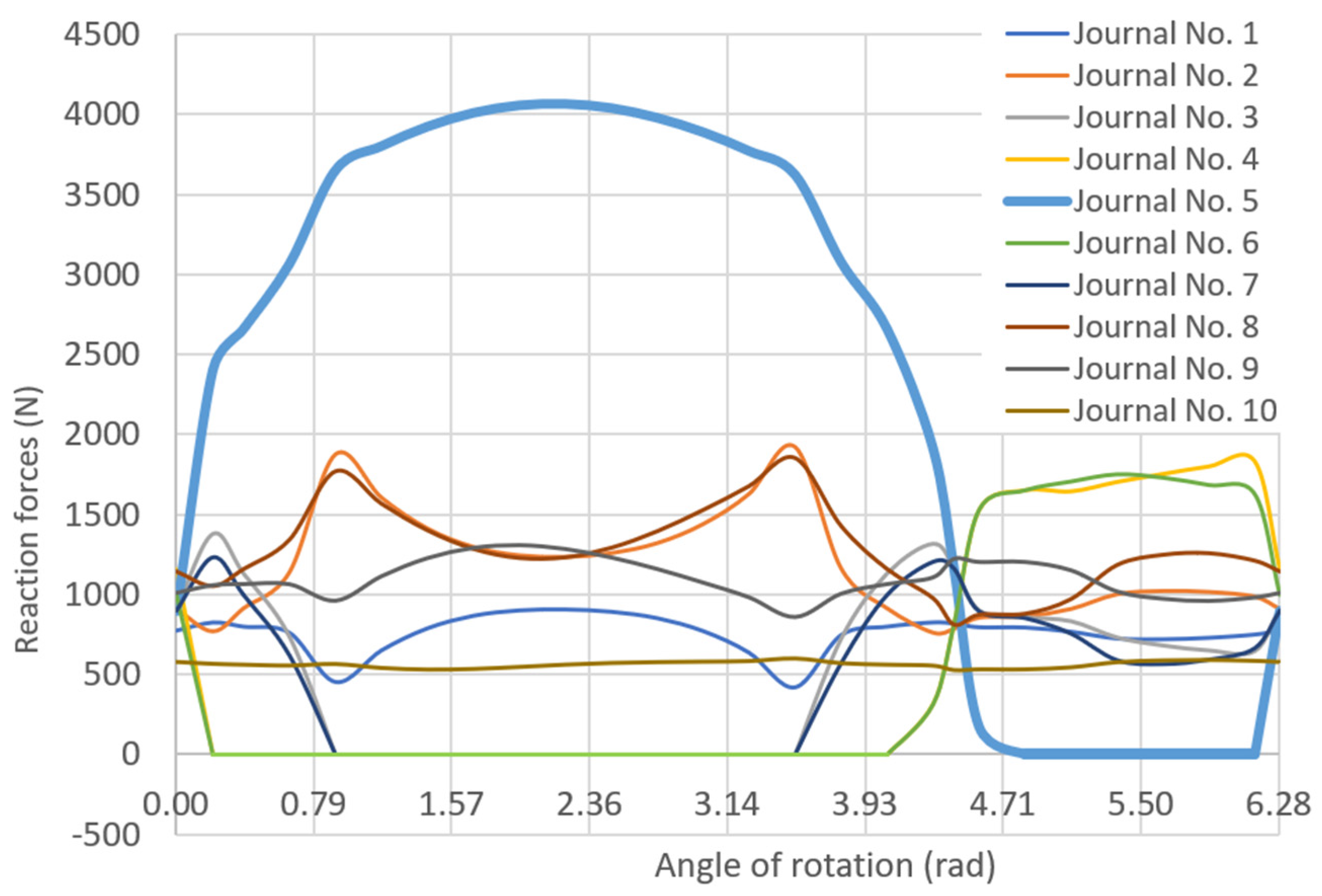
| Number of n-Harmonic | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |||
| Cosine truncation value w (μm) | 0 | Amplitude of harmonic Cn (μm) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0.1886 | 0.1772 | 0.1592 | 0.1363 | 0.1102 | 0.0831 | 0.0568 | 0.0333 | 0.0137 | ||
| 2 | 0.5235 | 0.4605 | 0.3676 | 0.2600 | 0.1541 | 0.0643 | 0.0002 | 0.0361 | 0.0461 | ||
| 3 | 0.9448 | 0.7752 | 0.5411 | 0.2981 | 0.0969 | 0.0313 | 0.0815 | 0.0713 | 0.0309 | ||
| 4 | 1.4289 | 1.0886 | 0.6508 | 0.2490 | 0.0188 | 0.1232 | 0.1015 | 0.0262 | 0.0356 | ||
| 5 | 1.9608 | 1.3799 | 0.6867 | 0.1338 | 0.1407 | 0.1580 | 0.0482 | 0.0501 | 0.0686 | ||
| 6 | 2.5296 | 1.6346 | 0.6498 | 0.0175 | 0.2268 | 0.1222 | 0.0399 | 0.0922 | 0.0345 | ||
| 7 | 3.1260 | 1.8421 | 0.5479 | 0.1737 | 0.2528 | 0.0341 | 0.1106 | 0.0698 | 0.0334 | ||
| 8 | 3.7424 | 1.9950 | 0.3937 | 0.3070 | 0.2137 | 0.0701 | 0.1271 | 0.0002 | 0.0767 | ||
| 9 | 4.3717 | 2.0882 | 0.2031 | 0.3957 | 0.1211 | 0.1515 | 0.0822 | 0.0722 | 0.0611 | ||
| 10 | 5.0073 | 2.1190 | 0.0061 | 0.4262 | 0.0012 | 0.1815 | 0.0018 | 0.1015 | 0.0009 | ||
| 11 | 5.6428 | 2.0863 | 0.2150 | 0.3938 | 0.1231 | 0.1497 | 0.0852 | 0.0704 | 0.0620 | ||
| 12 | 6.2718 | 1.9912 | 0.4048 | 0.3035 | 0.2144 | 0.0671 | 0.1284 | 0.0022 | 0.0757 | ||
| 13 | 6.8877 | 1.8366 | 0.5577 | 0.1692 | 0.2516 | 0.0372 | 0.1101 | 0.0714 | 0.0310 | ||
| 14 | 7.4835 | 1.6276 | 0.6579 | 0.0127 | 0.2237 | 0.1243 | 0.0382 | 0.0920 | 0.0368 | ||
| 15 | 8.0514 | 1.3718 | 0.6929 | 0.1381 | 0.1362 | 0.1584 | 0.0496 | 0.0484 | 0.0693 | ||
| 16 | 8.5822 | 1.0797 | 0.6550 | 0.2519 | 0.0139 | 0.1217 | 0.1014 | 0.0281 | 0.0346 | ||
| 17 | 9.0651 | 0.7660 | 0.5437 | 0.2992 | 0.1011 | 0.0290 | 0.0796 | 0.0717 | 0.0318 | ||
| 18 | 9.4849 | 0.4515 | 0.3691 | 0.2592 | 0.1566 | 0.0659 | 0.0023 | 0.0348 | 0.0451 | ||
| 19 | 9.8181 | 0.1691 | 0.1605 | 0.1343 | 0.1109 | 0.0829 | 0.0581 | 0.0341 | 0.0151 | ||
| 20 | 10.0049 | 0.0065 | 0.0024 | 0.0013 | 0.0008 | 0.0006 | 0.0004 | 0.0003 | 0.0002 | ||
| The Amplitude of the n-Harmonic (μm) | |||||
|---|---|---|---|---|---|
| n | 0 | 10 | 20 | 30 | 40 |
| n + 0 | 1.5476 | 0.1186 | 0.0612 | 0.1592 | |
| n + 1 | 5.1963 | 1.0706 | 0.1856 | 0.1198 | 0.2102 |
| n + 2 | 8.8540 | 0.8095 | 0.4414 | 0.0661 | 0.2584 |
| n + 3 | 8.2003 | 0.2753 | 0.4674 | 0.2745 | 0.3599 |
| n + 4 | 3.3588 | 0.5099 | 0.3367 | 0.0089 | 0.0599 |
| n + 5 | 4.0326 | 0.2387 | 0.6263 | 0.2587 | 0.1439 |
| n + 6 | 1.6983 | 0.2107 | 0.4834 | 0.2089 | 0.0877 |
| n + 7 | 2.1834 | 0.2411 | 0.4933 | 0.1694 | 0.0682 |
| n + 8 | 2.2217 | 0.0281 | 0.3031 | 0.1202 | 0.1273 |
| n + 9 | 1.7136 | 0.4415 | 0.1450 | 0.1133 | 0.2811 |
| The Amplitude of the n-Harmonic (μm) | |||||
|---|---|---|---|---|---|
| n | 0 | 10 | 20 | 30 | 40 |
| n + 0 | 0.05 | 0.06 | 0.01 | 0.01 | |
| n + 1 | 5.1963 | 0.18 | 0.03 | 0.02 | 0.00 |
| n + 2 | 4.2637 | 0.17 | 0.02 | 0.02 | 0.01 |
| n + 3 | 2.9760 | 0.08 | 0.04 | 0.01 | 0.01 |
| n + 4 | 1.6395 | 0.03 | 0.04 | 0.01 | 0.01 |
| n + 5 | 0.5330 | 0.10 | 0.02 | 0.02 | 0.00 |
| n + 6 | 0.1724 | 0.10 | 0.01 | 0.02 | 0.01 |
| n + 7 | 0.4483 | 0.04 | 0.03 | 0.01 | 0.01 |
| n + 8 | 0.3923 | 0.02 | 0.03 | 0.01 | 0.01 |
| n + 9 | 0.1701 | 0.06 | 0.01 | 0.02 | 0.00 |
| The Amplitude of the n-Harmonic (μm) | |||||
|---|---|---|---|---|---|
| n | 0 | 10 | 20 | 30 | 40 |
| n + 0 | 1.5539 | 0.0589 | 0.0523 | 0.1456 | |
| n + 1 | 0.9640 | 0.1681 | 0.1305 | 0.2070 | |
| n + 2 | 12.5866 | 0.9480 | 0.4355 | 0.0881 | 0.2570 |
| n + 3 | 8.4944 | 0.2039 | 0.4463 | 0.2668 | 0.3595 |
| n + 4 | 2.8480 | 0.4848 | 0.3692 | 0.0181 | 0.0503 |
| n + 5 | 4.5054 | 0.2788 | 0.6124 | 0.2777 | 0.1419 |
| n + 6 | 1.8694 | 0.1328 | 0.4707 | 0.1944 | 0.0871 |
| n + 7 | 1.7827 | 0.2165 | 0.5245 | 0.1696 | 0.0714 |
| n + 8 | 2.4778 | 0.0077 | 0.2756 | 0.1284 | 0.1194 |
| n + 9 | 1.7798 | 0.4085 | 0.1562 | 0.0977 | 0.0000 |
| Journal No 4 (e = 55 μm) | ||||||
| x (μm) | w (μm) | Theoretical Profile | Reference Profile | ρ (-) | ||
| RONpt | RONvt | RONtt | RONtr | |||
| (μm) | (μm) | (μm) | (μm) | |||
| 55 | 0 | 20.34 | −33.06 | 53.40 | 54.25 | 0.9200 |
| 44 | 11 | 18.83 | −33.03 | 51.86 | 0.9310 | |
| 33 | 22 | 19.34 | −33.08 | 52.42 | 0.9181 | |
| 22 | 33 | 18.88 | −33.09 | 51.96 | 0.8982 | |
| 11 | 44 | 18.75 | −32.99 | 51.74 | 0.8997 | |
| 0 | 55 | 20.34 | −33.06 | 53.40 | 0.9134 | |
| −11 | 66 | 18.61 | −33.17 | 51.79 | 0.9263 | |
| −22 | 77 | 19.23 | −32.96 | 52.18 | 0.9347 | |
| −33 | 88 | 19.07 | −33.02 | 52.08 | 0.9291 | |
| −44 | 99 | 18.99 | −33.25 | 52.24 | 0.9021 | |
| −55 | 110 | 19.03 | −33.06 | 52.09 | 0.9210 | |
| Journal No 5 (e = 25 μm) | ||||||
| x (μm) | w (μm) | Theoretical Profile | Reference Profile | ρ (-) | ||
| RONpt | RONvt | RONtt | RONtr | |||
| (μm) | (μm) | (μm) | (μm) | |||
| 25 | 0 | 12.37 | −16.02 | 28.39 | 29.78 | 0.9498 |
| 20 | 5 | 12.26 | −15.93 | 28.19 | 0.9461 | |
| 15 | 10 | 13.07 | −16.12 | 29.19 | 0.9513 | |
| 10 | 15 | 12.06 | −15.87 | 27.93 | 0.9527 | |
| 5 | 20 | 12.46 | −16.10 | 28.56 | 0.9462 | |
| 0 | 25 | 12.50 | −16.09 | 28.60 | 0.9458 | |
| −5 | 30 | 12.24 | −15.93 | 28.18 | 0.9479 | |
| −10 | 35 | 12.52 | −16.02 | 28.54 | 0.9455 | |
| −15 | 40 | 12.45 | −16.08 | 28.52 | 0.9503 | |
| −20 | 45 | 12.31 | −15.98 | 28.29 | 0.9507 | |
| −25 | 50 | 12.37 | −16.02 | 28.39 | 0.9498 | |
| Journal No 7 (e = 32 μm) | ||||||
| x (μm) | w (μm) | Theoretical Profile | Reference Profile | ρ (-) | ||
| RONpt | RONvt | RONtt | RONtr | |||
| (μm) | (μm) | (μm) | (μm) | |||
| 32.0 | 0.0 | 15.00 | −25.94 | 40.94 | 43.56 | 0.9687 |
| 25.6 | 6.4 | 15.03 | −25.85 | 40.87 | 0.9640 | |
| 19.2 | 12.8 | 14.87 | −26.06 | 40.93 | 0.9678 | |
| 12.8 | 19.2 | 15.12 | −25.92 | 41.04 | 0.9736 | |
| 6.4 | 25.6 | 15.06 | −25.72 | 40.78 | 0.9751 | |
| 0.0 | 32.0 | 14.89 | −26.25 | 41.14 | 0.9655 | |
| −6.4 | 38.4 | 15.06 | −25.93 | 40.99 | 0.9578 | |
| −12.8 | 44.8 | 15.04 | −26.08 | 41.12 | 0.9618 | |
| −19.2 | 51.2 | 14.94 | −26.04 | 40.98 | 0.9720 | |
| −25.6 | 57.6 | 15.04 | −25.86 | 40.91 | 0.9703 | |
| −32.0 | 64.0 | 15.00 | −25.94 | 40.94 | 0.9687 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nozdrzykowski, K.; Grządziel, Z.; Nozdrzykowska, M.; Grzejda, R.; Stępień, M. Eliminating the Influence of Support Conditions on Geometric Shape Measurements of Large Crankshafts of Marine Engines. Energies 2023, 16, 16. https://doi.org/10.3390/en16010016
Nozdrzykowski K, Grządziel Z, Nozdrzykowska M, Grzejda R, Stępień M. Eliminating the Influence of Support Conditions on Geometric Shape Measurements of Large Crankshafts of Marine Engines. Energies. 2023; 16(1):16. https://doi.org/10.3390/en16010016
Chicago/Turabian StyleNozdrzykowski, Krzysztof, Zenon Grządziel, Magdalena Nozdrzykowska, Rafał Grzejda, and Mateusz Stępień. 2023. "Eliminating the Influence of Support Conditions on Geometric Shape Measurements of Large Crankshafts of Marine Engines" Energies 16, no. 1: 16. https://doi.org/10.3390/en16010016
APA StyleNozdrzykowski, K., Grządziel, Z., Nozdrzykowska, M., Grzejda, R., & Stępień, M. (2023). Eliminating the Influence of Support Conditions on Geometric Shape Measurements of Large Crankshafts of Marine Engines. Energies, 16(1), 16. https://doi.org/10.3390/en16010016







