Computational Fluid Dynamics for Protonic Ceramic Fuel Cell Stack Modeling: A Brief Review
Abstract
1. Introduction
2. Structure, Principle, and Working Nature of PCFCs
2.1. Electrolyte
2.2. Cathode
- It should avoid the adsorption of oxygen on the cathode surface.
- It should give the best oxygen reduction reaction performance.
- It should be less expensive with more stability.
- It should be chemically stable under oxidizing atmosphere.
- The electrodes must possess good surface area with high electronic conductivity.
2.3. Anode
- It should offer high catalytic activity at a low cost.
- It should have suitable porosity and electronic conductivity properties.
- It should be more stable and durable.
- It should be more chemically and physically sustainable.
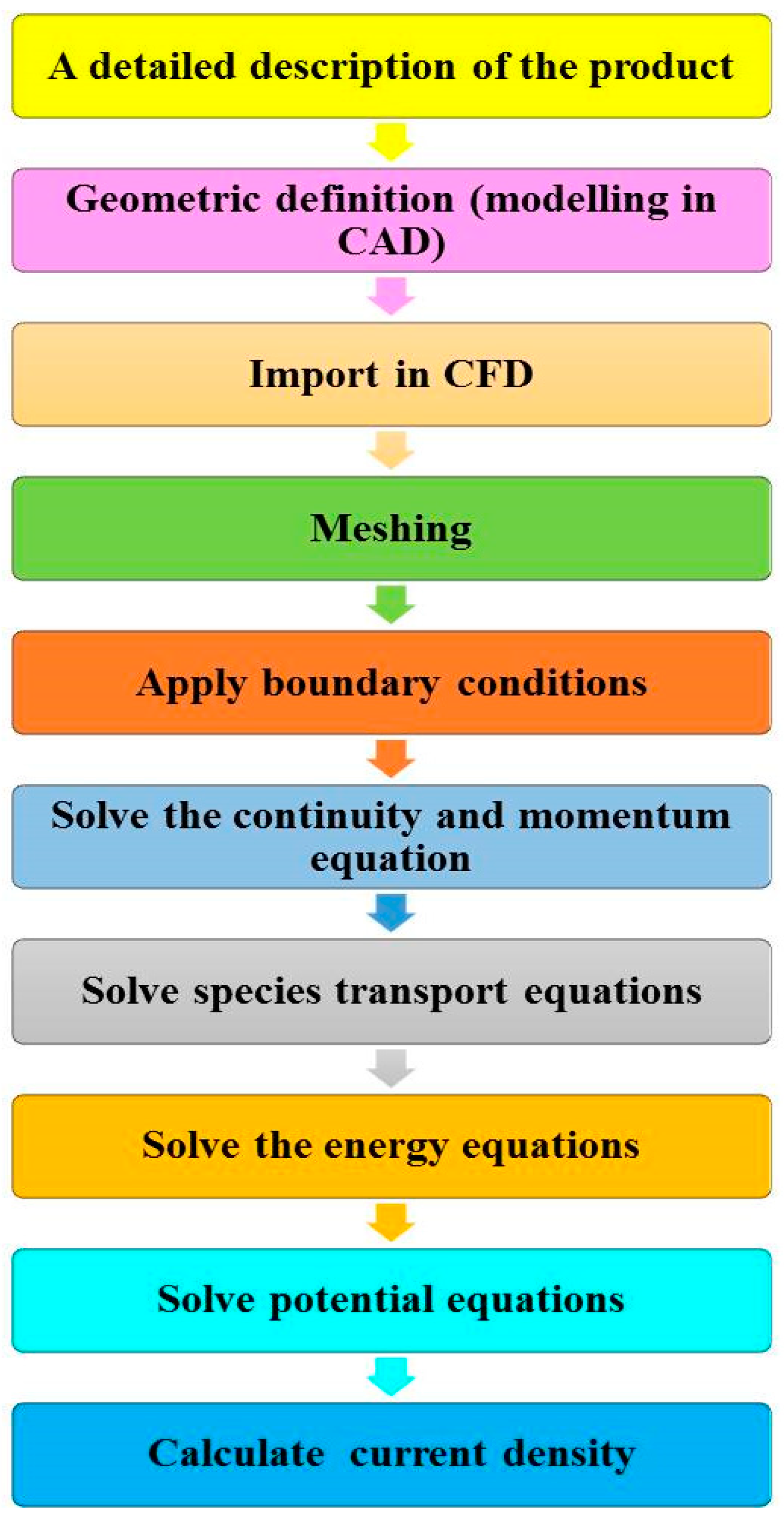
3. Role of Computational Fluid Dynamics
4. Applications of the CFD Modeling in Recent PCFC Models
5. Recent PCFC Models Based on Flow-Channel Design
6. Recent PCFC Models Based on Cathode Layer Thickness
7. Governing Equations Used in PCFC Models
- Mass continuity equations
- Momentum conservation equations
- Proton and electron transport
- Electrochemical reactions
- Energy conservation equations
- = local fluid velocity in the x-direction (m/s)
- = local fluid velocity in the y-direction (m/s)
- = local fluid velocity in the z-direction (m/s)
- = local fluid density (kg/m3)
- Sm = mass source term (kg/m3 s)
- µ = local fluid dynamic viscosity (s/m2)
- P = local fluid pressure (N/m2)
- Sp = source term, momentum (N/m3)
- C = specific heat capacity (s/m2)
- T = local fluid temperature (K)
- k = effective conductivity (W/mK)
- Sh = source term, heat energy (W/m3)
- i = mass diffusion coefficient species at anode and cathode
- = velocity vector (m/s)
- = density (kg/m3)
- J = Diffusion rate of species i depends on mass in various directions (kg m−2 s −1)
- Si = Source term of species i resulting from a chemical process (mol m−2 s −1)
- ipro = protonic current vectors (A)
- iele = electronic current vectors (A)
- 𝜎pro, eff = effective conductivity for proton transport (W/m K)
- 𝜎ele, eff= effective conductivity for electron transport (W/m K)
- φ = potential (V)
- i0 = current density (A/m2)
- = triple phase boundary length per volume (m/m3)
- αan, αca = transfer coefficient for anode and cathode (dimensionless)
- 𝜂act,an, 𝜂act,ca= activation loss for anode and cathode (V) −
- i0,an, i0,ca = exchange current density for anode and cathode (A/m2)
- n = transmitted electrons in the reaction
- F = faraday constant (9.65 × 107 C/k mol)
- R= universal molar gas constant (8.314 J/mol k)
- T = temperature (K)
- = Effective binary diffusion coefficient (m2 s−1)
- = Effective Knudsen diffusion coefficient of species i, (m2 s−1)
- = Porosity
- τ = tortuosity
- = mean pore radius (m)
- T =Temperature (K)
- R = universal molar gas constant (8.314 J/mol k)
- Mi, Mj = molecular mass (g)
- = diffusion volume
- P = pressure (N/m2)
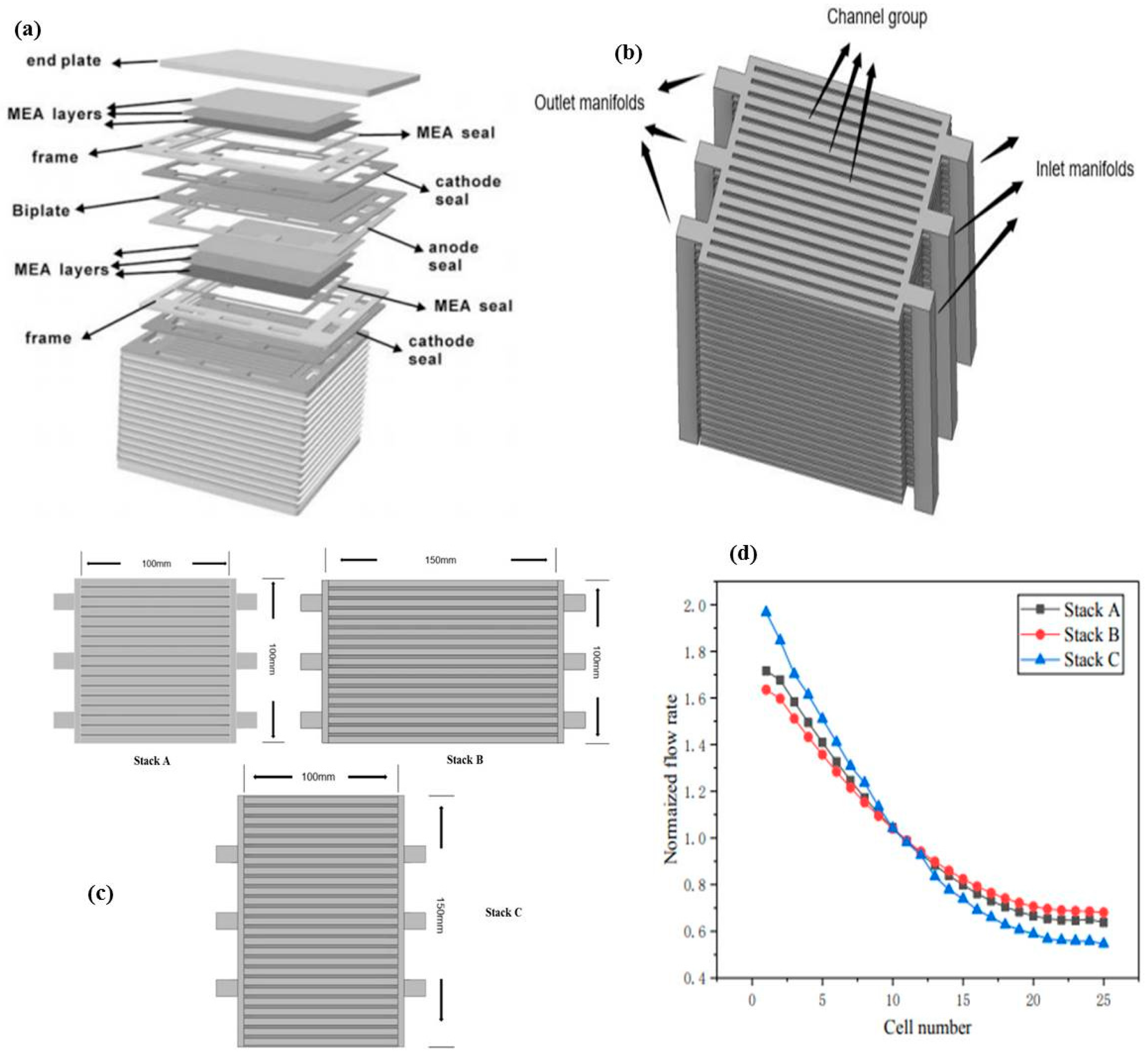
- = minimum value of the normalized air flow rates (kg/s)
- mi = air flow mass rate at the ith layer (kg/s)
- N = number of stacks
- ave (m1:mN) = average air mass flow rate at each cell unit (kg/s).
8. Comparison of Modeling of SOFC with PCFC
9. Research Gap and Future Outlook
- Firstly, the CFD modeling work based on PCFCs is limited and merely a reflection of the modeling work previously utilized for SOFCs. This is because the majority of PCFC electrode and electrolyte components were already used in conventional solid oxide fuel cells. Therefore, extensive research should be conducted to develop new materials and designs for PCFCs in order to advance the protonic ceramic fuel cell modeling process.
- The numerical modeling of water formation and transportation within PCFCs presents a substantial difficulty. Specifically, interactions between water molecules and ions are crucial variables, although they are not yet fully understood; hence, molecular dynamics may be valuable for elucidating the transport of water and its ions in electrolytes and electrodes. In addition, special attention should be made by making specialized and novel submodels to capture the condensation/vaporization and liquid water transport in the GDL and catalyst section.
- To increase the efficiency of the PCFC, it is necessary to comprehend that catalytic electrochemical reactions occur within the PCFC; hence, a unique catalytic CFD modeling analysis should be conducted in addition to the usual electrochemical CFD analysis.
- Most theoretical PCFC models focus on examining steady-state conditions; however, transient transport behaviors must be considered in future designs. In addition, due to the computational demands of PCFCs with complex flow fields, greater emphasis has been placed on simple flow fields and channels, making complex flow field problems challenging to resolve.
- The most crucial obstacle in fuel cell modeling is collecting the necessary data for input into the CFD model and validating it in the form of test results, including the thermal and physical characteristics of the materials. Even though PCFC modeling technology has a lot of promise, it is challenging to create because of the lack of a reliable, all-encompassing modeling technique that correctly represents the fuel cell’s many qualitative and statistical processes. Usually, it can be achieved by comparing the CFD model predictions obtained from the verified input against precise measurement results. However, precise experiment findings from testing fuel cell stacks are extremely restricted at present. In addition, the CFD model necessitates multiple material data, which are exceedingly challenging to attain. It makes fuel cell designing more challenging to conduct accurate measurements. In addition to limiting the general public’s access to a portion of the available data, the major necessity for business concerns significantly restricts the public’s access to other data. Consequently, most fuel cell designs now require experimental data/inputs, specifically thorough measurement data/output, to validate the designed models and their predictions. This circumstance continues to restrict the activity of fuel cell modeling.
10. Summary
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Longo, S.; Cellura, M.; Guarino, F.; Brunaccini, G.; Ferraro, M. Life Cycle Energy and Environmental Impacts of a Solid Oxide Fuel Cell Micro-CHP System for Residential Application. Sci. Total Environ. 2019, 685, 59–73. [Google Scholar] [CrossRef]
- Strazza, C.; del Borghi, A.; Costamagna, P.; Traverso, A.; Santin, M. Comparative LCA of Methanol-Fuelled SOFCs as Auxiliary Power Systems on-Board Ships. Appl. Energy 2010, 87, 1670–1678. [Google Scholar] [CrossRef]
- Radenahmad, N.; Tasfiah, A.; Saghir, M.; Taweekun, J.; Saifullah, M.; Bakar, A.; Reza, S.; Azad, A.K. A Review on Biomass Derived Syngas for SOFC Based Combined Heat and Power Application. Renew. Sustain. Energy Rev. 2020, 119, 109560. [Google Scholar] [CrossRef]
- Mohd Nazrul Aman, N.A.; Muchtar, A.; Somalu, M.R.; Rosli, M.I.; Baharuddin, N.A.; Kalib, N.S. A Short Review on the Modeling of Solid-Oxide Fuel Cells by Using Computational Fluid Dynamics: Assumptions and Boundary Conditions. Int. J. Integr. Eng. 2018, 10, 87–92. [Google Scholar] [CrossRef]
- Anwar, M.; Sa, M.A.; Muchtar, A.; Somalu, M.R. Influence of Strontium Co-Doping on the Structural, Optical, and Electrical Properties of Erbium-Doped Ceria Electrolyte for Intermediate Temperature Solid Oxide Fuel Cells. Ceram. Int. 2019, 45, 5627–5636. [Google Scholar] [CrossRef]
- Kang, E.H.; Choi, H.R.; Park, J.S.; Kim, K.H.; Kim, D.H.; Bae, K.; Prinz, F.B.; Shim, J.H. Protonic Ceramic Fuel Cells with Slurry-Spin Coated BaZr0.2Ce0.6Y0.1Yb0.1O3- δ Thin-Film Electrolytes. J. Power Sources 2020, 465, 228254. [Google Scholar] [CrossRef]
- Radenahmad, N.; Afif, A.; Petra, P.I.; Rahman, S.M.H.; Eriksson, S.G.; Azad, A.K. Proton-Conducting Electrolytes for Direct Methanol and Direct Urea Fuel Cells–A State-of-the-Art Review. Renew. Sustain. Energy Rev. 2016, 57, 1347–1358. [Google Scholar] [CrossRef]
- Hossain, S.; Abdalla, A.M.; Jamain, S.N.B.; Zaini, J.H.; Azad, A.K. A Review on Proton Conducting Electrolytes for Clean Energy and Intermediate Temperature-Solid Oxide Fuel Cells. Renew. Sustain. Energy Rev. 2017, 79, 750–764. [Google Scholar] [CrossRef]
- Akenteng, Y.D.; Yang, X.; Zhao, Y.; Lysyakov, A.; Matveev, A.; Chen, D. Computational Fluid Dynamics Modeling of an Inter-Parallel Flow Field for Proton Ceramic Fuel Cell Stack. Ionics 2022, 28, 3367–3378. [Google Scholar] [CrossRef]
- Klein, J.M.; Bultel, Y.; Georges, S.; Pons, M. Modeling of a SOFC Fuelled by Methane: From Direct Internal Reforming to Gradual Internal Reforming. Chem. Eng. Sci. 2007, 62, 1636–1649. [Google Scholar] [CrossRef]
- Xu, Q.; Guo, Z.; Xia, L.; He, Q.; Li, Z.; Temitope Bello, I.; Zheng, K.; Ni, M. A Comprehensive Review of Solid Oxide Fuel Cells Operating on Various Promising Alternative Fuels. Energy Convers. Manag. 2022, 253, 115175. [Google Scholar] [CrossRef]
- Pan, Y.; Zhang, H.; Xu, K.; Zhou, Y.; Zhao, B.; Yuan, W.; Sasaki, K.; Choi, Y.; Chen, Y.; Liu, M. A High-Performance and Durable Direct NH3 Tubular Protonic Ceramic Fuel Cell Integrated with an Internal Catalyst Layer. Appl. Catal. B 2022, 306, 121071. [Google Scholar] [CrossRef]
- Afif, A.; Radenahmad, N.; Cheok, Q.; Shams, S.; Kim, J.H.; Azad, A.K. Ammonia-Fed Fuel Cells: A Comprehensive Review. Renew. Sustain. Energy Rev. 2016, 60, 822–835. [Google Scholar] [CrossRef]
- Abdalla, A.M.; Hossain, S.; Nisfindy, O.B.; Azad, A.T.; Dawood, M.; Azad, A.K. Hydrogen Production, Storage, Transportation and Key Challenges with Applications: A Review. Energy Convers. Manag. 2018, 165, 602–627. [Google Scholar] [CrossRef]
- Naeem Khan, M.; Azad, A.K.; Savaniu, C.D.; Hing, P.; Irvine, J.T.S. Robust Doped BaCeO3-δ Electrolyte for IT-SOFCs. Ionics 2017, 23, 2387–2396. [Google Scholar] [CrossRef][Green Version]
- Chen, M.; Zhou, M.; Liu, Z.; Liu, J. A Comparative Investigation on Protonic Ceramic Fuel Cell Electrolytes BaZr0.8Y0.2O3-δ and BaZr0.1Ce0.7Y0.2O3-δ with NiO as Sintering Aid. Ceram. Int. 2022, 48, 17208–17216. [Google Scholar] [CrossRef]
- Azim Jais, A.; Muhammed Ali, S.A.; Anwar, M.; Rao Somalu, M.; Muchtar, A.; Wan Isahak, W.N.R.; Yong Tan, C.; Singh, R.; Brandon, N.P. Enhanced Ionic Conductivity of Scandia-Ceria-Stabilized-Zirconia (10Sc1CeSZ) Electrolyte Synthesized by the Microwave-Assisted Glycine Nitrate Process. Ceram. Int. 2017, 43, 8119–8125. [Google Scholar] [CrossRef]
- Anwar, M.; Sa, M.A.; Baharuddin, N.A.; Raduwan, N.F.; Muchtar, A.; Somalu, M.R. Structural, Optical and Electrical Properties of Ce0.8Sm0.2-Er O2- (X=0–0.2) Co-Doped Ceria Electrolytes. Ceram. Int. 2018, 44, 13639–13648. [Google Scholar] [CrossRef]
- Rasaki, S.A.; Liu, C.; Lao, C.; Chen, Z. A Review of Current Performance of Rare Earth Metal-Doped Barium Zirconate Perovskite: The Promising Electrode and Electrolyte Material for the Protonic Ceramic Fuel Cells. Prog. Solid State Chem. 2021, 63, 100325. [Google Scholar] [CrossRef]
- Duan, C.; Tong, J.; Shang, M.; Nikodemski, S.; Sanders, M.; Ricote, S.; Almansoori, A.; O’Hayre, R. Readily Processed Protonic Ceramic Fuel Cells with High Performance at Low Temperatures. Science 2015, 349, 1321–1326. [Google Scholar] [CrossRef]
- Atkinson, A.; Barnett, S.; Gorte, R.J.; Irvine, J.T.S.; McEvoy, A.J.; Mogensen, M.; Singhal, S.C.; Vohs, J. Advanced Anodes for High-Temperature Fuel Cells. Nat. Mater. 2004, 3, 17–27. [Google Scholar] [CrossRef] [PubMed]
- Goodenough, J.B.; Huang, Y.H. Alternative Anode Materials for Solid Oxide Fuel Cells. J. Power Sources 2007, 173, 1–10. [Google Scholar] [CrossRef]
- Minh, N.Q. Solid Oxide Fuel Cell Technology–Features and Applications. Solid. State Ion. 2004, 174, 271–277. [Google Scholar] [CrossRef]
- Ding, K.; Zhu, M.; Han, Z.; Kochetov, V.; Lu, L.; Chen, D. Momentum-Species-Heat-Electrochemistry Distribution Characteristics within Solid Oxide Fuel Cell Stack with Complex Inter-Digital Fuel Channels. Ionics 2020, 26, 4567–4578. [Google Scholar] [CrossRef]
- Afif, A.; Radenahmad, N.; Rahman, S.M.H.; Torino, N.; Saqib, M.; Hossain, S.; Park, J.Y.; Azad, A.K. Ceramic Fuel Cells Using Novel Proton-Conducting BaCe0.5Zr0.3Y0.1Yb0.05Zn0.05O3-δ Electrolyte. J. Solid State Electrochem. 2022, 26, 111–120. [Google Scholar] [CrossRef]
- Hossain, S.; Abdalla, A.M.; Zaini, J.H.; Savaniu, C.D.; Irvine, J.T.S.; Azad, A.K. Highly Dense and Novel Proton Conducting Materials for SOFC Electrolyte. Int. J. Hydrogen Energy. 2017, 42, 27308–27322. [Google Scholar] [CrossRef]
- Afif, A.; Radenahmad, N.; Lim, C.M.; Petra, M.I.; Islam, M.A.; Rahman, S.M.H.; Eriksson, S.; Azad, A.K. Structural Study and Proton Conductivity in BaCe0.7Zr0.25−xYxZn0.05O3 (x = 0.05, 0.1, 0.15, 0.2 & 0.25). Int. J. Hydrogen Energy 2016, 41, 11823–11831. [Google Scholar] [CrossRef]
- Azad, A.K.; Abdalla, A.M.; Afif, A.; Azad, A.; Afroze, S.; Idris, A.C.; Park, J.Y.; Saqib, M.; Radenahmad, N.; Hossain, S.; et al. Improved Mechanical Strength, Proton Conductivity and Power Density in an ‘All-Protonic’ Ceramic Fuel Cell at Intermediate Temperature. Sci. Rep. 2021, 11, 19382. [Google Scholar] [CrossRef]
- Radenahmad, N.; Afif, A.; Abdalla, A.M.; Saqib, M.; Park, J.Y.; Zaini, J.; Irvine, J.; Kim, J.H.; Azad, A.K. A New High-Performance Proton-Conducting Electrolyte for Next-Generation Solid Oxide Fuel Cells. Energy Technol. 2020, 8, 2000486. [Google Scholar] [CrossRef]
- Radenahmad, N.; Afroze, S.; Afif, A.; Azad, A.T.; Shin, J.S.; Park, J.Y.; Zaini, J.H.; Azad, A.K. High Conductivity and High Density SrCe0.5Zr0.35Y0.1A0.05O3-δ (A = Gd, Sm) Proton-Conducting Electrolytes for IT-SOFCs. Ionics 2020, 26, 1297–1305. [Google Scholar] [CrossRef]
- Hossain, S.; Abdalla, A.M.; Radenahmad, N.; Zakaria, A.K.M.; Zaini, J.H.; Rahman, S.M.H.; Eriksson, S.G.; Irvine, J.T.S.; Azad, A.K. Highly Dense and Chemically Stable Proton Conducting Electrolyte Sintered at 1200 °C. Int. J. Hydrogen Energy 2018, 43, 894–907. [Google Scholar] [CrossRef]
- Afif, A.; Radenahmad, N.; Zaini, J.; Abdalla, A.M.; Rahman, S.M.H.; Eriksson, S.; Azad, A.K. Enhancement of Proton Conductivity through Yb and Zn Doping in BaCe0.5Zr0.35Y0.15O3-δ Electrolyte for IT-SOFCs. Process. Appl. Ceram. 2018, 12, 180–188. [Google Scholar] [CrossRef]
- Radenahmad, N.; Afif, A.; Petra, M.I.; Rahman, S.M.H.; Eriksson, S.; Azad, A.K. High Conductivity and High Density Proton Conducting Ba1−xSrxCe0.5Zr0.35Y0.1Sm0.05O3−δ (x = 0.5, 0.7, 0.9, 1.0) Perovskites for IT-SOFC. Int. J. Hydrogen Energy 2016, 41, 11832–11841. [Google Scholar] [CrossRef]
- Khan, M.N.; Savaniu, C.D.; Azad, A.K.; Hing, P.; Irvine, J.T.S. Wet Chemical Synthesis and Characterisation of Ba 0.5 Sr 0.5 Ce 0.6 Zr 0.2 Gd 0.1 Y 0.1 O 3−δ Proton Conductor. Solid State Ion. 2017, 303, 52–57. [Google Scholar] [CrossRef]
- Malik, L.A.; Sina, A.L.; Osmana, N.; Hassanc, O.H.; Jani, A.M. Short Review on the Suitability of CFD Modeling for Proton Conducting Fuel Cell Performance. J. Kejuruter. 2020, 32, 587–590. [Google Scholar]
- Muchtar, A.; Aman, N.A.; Somalu, M.R.; Rosli, M.I.; Kalib, N.S. Overview of Computational Fluid Dynamics Modelling in Solid Oxide Fuel Cell. J. Adv. Res. Fluid Mech. Therm. Sci. 2020, 52, 174–181. [Google Scholar]
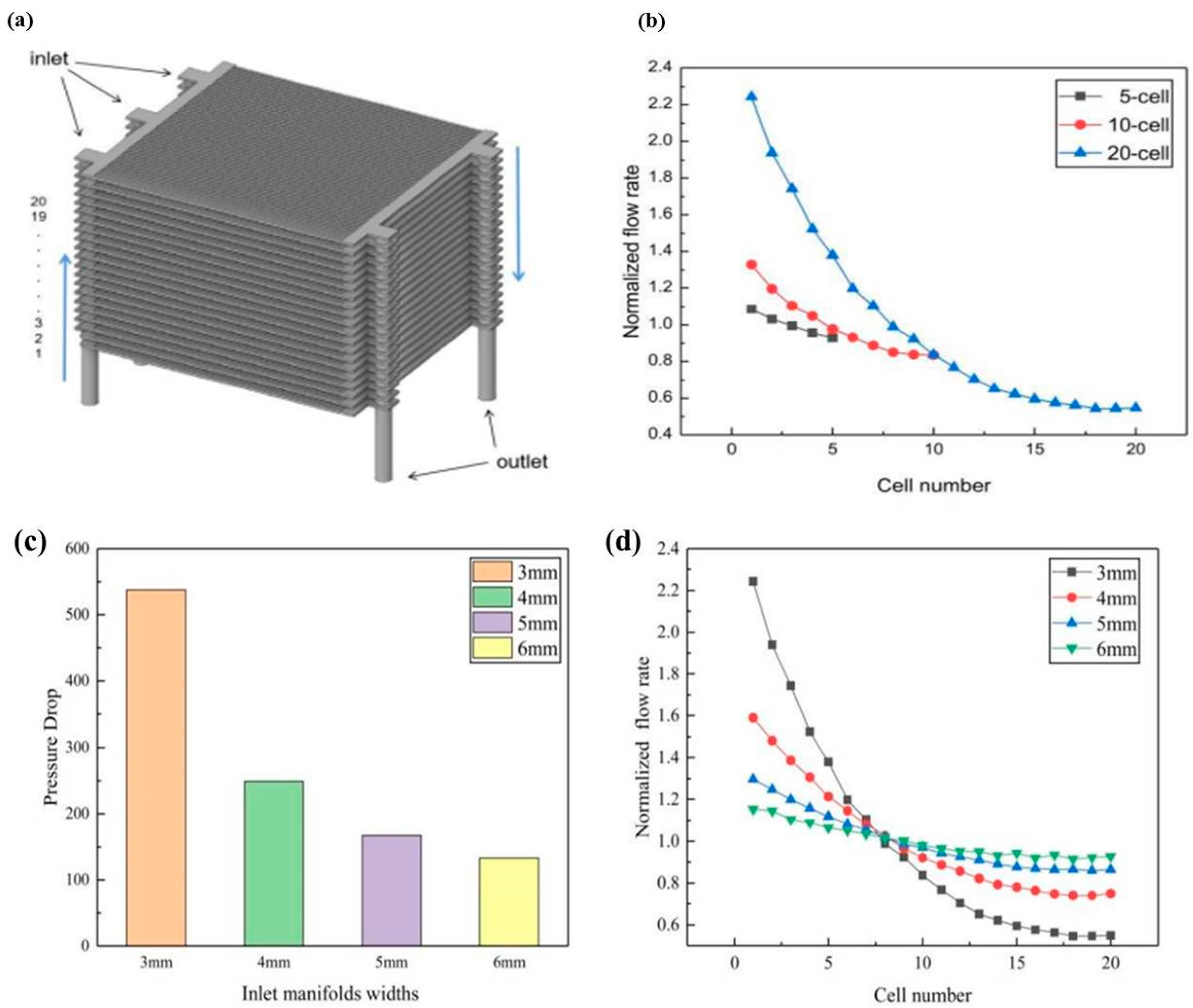
- Dai, J.Q.; Zhu, M.F.; Zhang, H.Z.; Liu, J.P.; Chen, D.F. The Effect of the Geometric Parameters on the Air Flow Distrib Ution Uniformity within the Protonic Ceramic Fuel Cell Stack. Int. J. Electrochem. Sci. 2021, 16, 211052. [Google Scholar] [CrossRef]
- Blum, L.; de Haart, L.G.J.B.; Malzbender, J.; Menzler, N.H.; Remmel, J.; Steinberger-Wilckens, R. Recent Results in Jülich Solid Oxide Fuel Cell Technology Development. J. Power Sources 2013, 241, 477–485. [Google Scholar] [CrossRef]
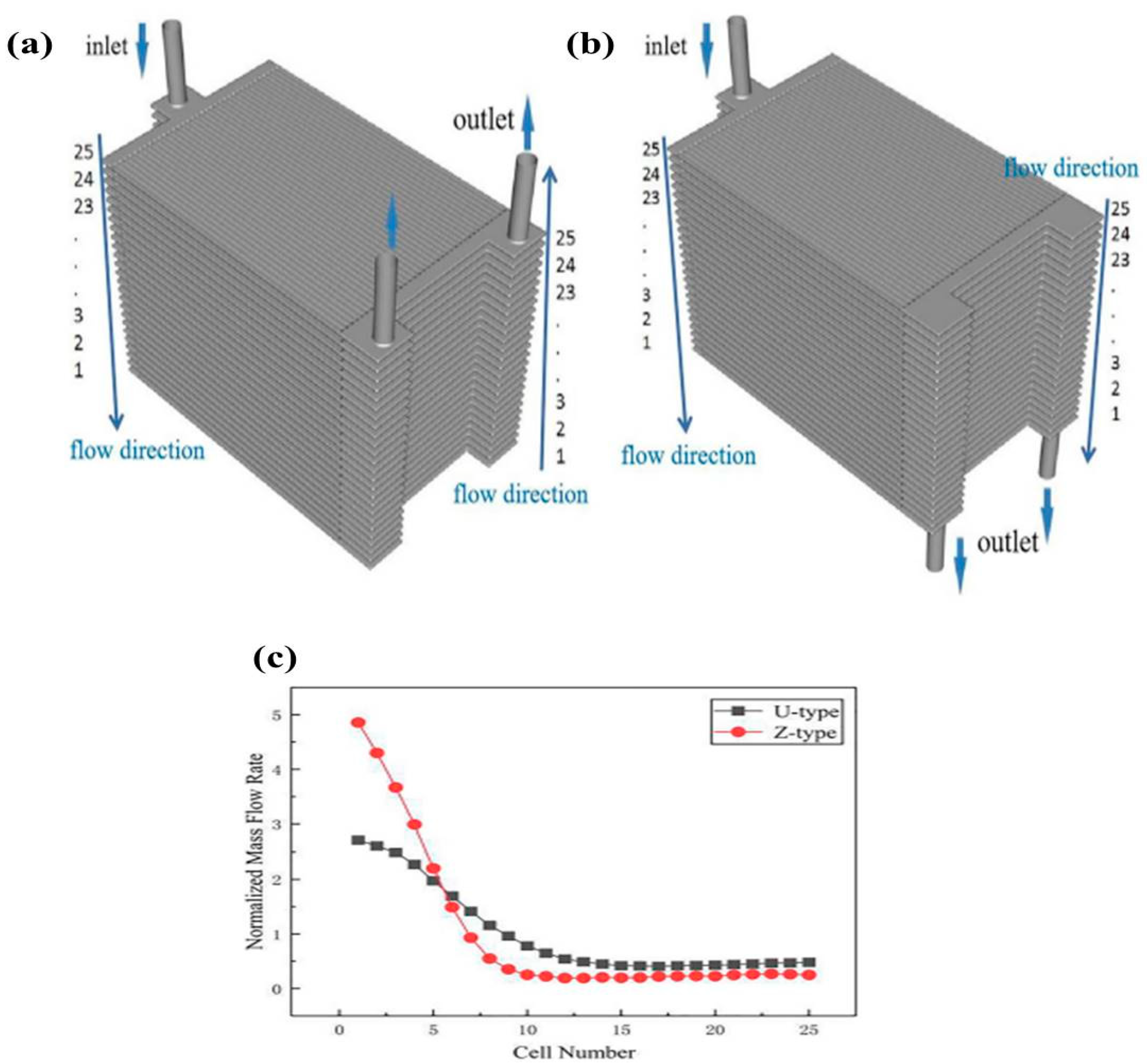
- Dai, J.Q.; Yang, Z.M.; Wang, W.S.; Liu, J.P.; Akenteng, Y.D.; Chen, D.F. Study the Flow and Species Distribution Characteristics in a Typical 25-Cell Proton Ceramic Fuel Cell Stack by 3D Large-Scale Modeling. Ionics 2022, 28, 1863–1872. [Google Scholar] [CrossRef]
- Barbir, F. PEM Fuel Cells: Theory and Practice; Elsevier Academic Press: Burlington, MA, USA, 2005. [Google Scholar]
- Abdalla, A.M.; Dawood, M.K.; Hossain, S.; El-Sabahy, M.; Elnaghi, B.E.; Shaikh, S.P.S.; Azad, A.K. Mathematical Modeling for Fuel Cells; Elsevier: Amsterdam, The Netherlands, 2022. [Google Scholar] [CrossRef]
- Sin, Y.T.; Najmi, W.M.W.A. Industrial and Academic Collaboration Strategies on Hydrogen Fuel Cell Technology Development in Malaysia. Procedia Soc. Behav. Sci. 2013, 90, 879–888. [Google Scholar] [CrossRef]
- Blake, C.W.; Rivkin, C.H. Stationary Fuel Cell Application Codes and Standards: Overview and Gap Analysis; OSTI: Golden, CO, USA, 2010. [Google Scholar] [CrossRef]
- Aloysius Damar Pranadi. Fuel Cell Development for ASEAN: Flawless and Prospective Potential; ASEAN Centre for Energy: Jakarta, Indonesia, 2016. [Google Scholar]
- Wang, M.; Su, C.; Zhu, Z.; Wang, H.; Ge, L. Composite Cathodes for Protonic Ceramic Fuel Cells: Rationales and Materials. Compos. B Eng. 2022, 238, 109881. [Google Scholar] [CrossRef]
- Braun, R.J.; Dubois, A.; Ferguson, K.; Duan, C.; Karakaya, C.; Kee, R.J.; Zhu, H.; Sullivan, N.P.; Tang, E.; Pastula, M.; et al. Development of KW-Scale Protonic Ceramic Fuel Cells and Systems. ECS Trans. 2019, 91, 997–1008. [Google Scholar] [CrossRef]
- Ferguson, K.; Dubois, A.; Albrecht, K.; Braun, R.J. High Performance Protonic Ceramic Fuel Cell Systems for Distributed Power Generation. Energy Convers. Manag. 2021, 248, 114763. [Google Scholar] [CrossRef]
- FuelCellsWorks. SAFCell Completes 50 Watt Fuel Cell Field Trial At Shell Canada Well Site. Available online: https://fuelcellsworks.com/ (accessed on 20 October 2022).
- Gittleman, C.S.; Jia, H.; de Castro, E.S.; Chisholm, C.R.I.; Kim, Y.S. Proton Conductors for Heavy-Duty Vehicle Fuel Cells. Joule 2021, 5, 1660–1677. [Google Scholar] [CrossRef]
- Ma, J.; Pan, Y.; Wang, Y.; Chen, Y. A Sr and Ni Doped Ruddlesden−Popper Perovskite Oxide La1.6Sr0.4Cu0.6Ni0.4O4+δ as a Promising Cathode for Protonic Ceramic Fuel Cells. J. Power Sources 2021, 509, 230369. [Google Scholar] [CrossRef]
- Antonova, E.P.; Osinkin, D.A.; Bogdanovich, N.M. On a Variation of the Kinetics of Hydrogen Oxidation on Ni–BaCe(Y,Gd)O3 Anode for Proton Ceramic Fuel Cells. Int. J. Hydrogen Energy 2021, 46, 22638–22645. [Google Scholar] [CrossRef]
- Robalinho, E.; Cunha, E.F.d.; Zararya, A.; Linardi, M.; Cekinski, E. Advances in PEM Fuel Cells with CFD Techniques. In Proceedings of the 5th International Workshop on Hydrogen and Fuel Cells, Campinas, SP, Brazil, 26–29 October 2010; pp. 44–58. [Google Scholar]
- Zhu, M.; Yang, Z.; Han, Z.; Ishutkin, A.; Raza, A.; Yu, Z.; Chen, D. The Air Flow Distributions within a Typical Planar Protonic Ceramic Fuel Cell Stack. Int. J. Electrochem. Sci. 2022, 17, 220667. [Google Scholar] [CrossRef]
- Bi, W.; Chen, D.; Lin, Z. A Key Geometric Parameter for the Flow Uniformity in Planar Solid Oxide Fuel Cell Stacks. Int. J. Hydrogen Energy 2009, 34, 3873–3884. [Google Scholar] [CrossRef]
- Dai, J.; Uwaneza, D.; Levtsev, A.; Yu, Z.; Chen, D. Effect of the Geometric Parameters of the Rib-Channel and Porous Cathode on the Species Distribution in the Cathodes of Protonic Ceramic Fuel Cell Stack. Int. J. Electrochem. Sci. 2022, 17, 220116. [Google Scholar] [CrossRef]
- Li, Z.; He, Q.; Xia, L.; Xu, Q.; Cheng, C.; Wang, J.; Ni, M. Effects of Cathode Thickness and Microstructural Properties on the Performance of Protonic Ceramic Fuel Cell (PCFC): A 3D Modelling Study. Int. J. Hydrogen Energy 2022, 47, 4047–4061. [Google Scholar] [CrossRef]
- Murphy, A.N. Numerical CFD Analysis of Compact Circular Proton-Conducting Fuel Cell. Master’s Thesis, California State Polytechnic University, Pomona, CA, USA, 2019. [Google Scholar]
- ANSYS Fluent Fuel Cell Modules Manual; Release 15.0; ANSYS, Inc.: Canonsburg, PA, USA, 2013.
- Alhazmi, N.; Almutairi, G.; Alenazey, F.; AlOtaibi, B. Three-Dimensional Computational Fluid Dynamics Modeling of Button Solid Oxide Fuel Cell. Electrochim. Acta 2021, 390, 138838. [Google Scholar] [CrossRef]
- Ahmed, K.I.; Ahmed, M.H. Developing a Novel Design for a Tubular Solid Oxide Fuel Cell Current Collector. Appl. Sci. 2022, 12, 6003. [Google Scholar] [CrossRef]
- Ranasinghe, S.N.; Middleton, P.H. Modelling of Single Cell Solid Oxide Fuel Cells Using COMSOL Multiphysics. In Proceedings of the 2017 IEEE International Conference on Environment and Electrical Engineering and 2017 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Milan, Italy, 6–9 June 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Lakshmi, T.V.V.S.; Geethanjali, P.; Krishna, P.S. Mathematical Modelling of Solid Oxide Fuel Cell Using Matlab/Simulink. In Proceedings of the 2013 Annual International Conference on Emerging Research Areas and 2013 International Conference on Microelectronics, Communications and Renewable Energy, Kanjirapally, India, 4–6 June 2013; pp. 1–5. [Google Scholar] [CrossRef]
- Ghorbani, B. Modelling and Diagnosis of Solid Oxide Fuel Cell (SOFC). Ph.D. Thesis, Simon Fraser University, Burnaby, BC, Canada, 2021. [Google Scholar]
- Goldin, G.M.; Zhu, H.; Kee, R.J.; Bierschenk, D.; Barnett, S.A. Multidimensional Flow, Thermal, and Chemical Behavior in Solid-Oxide Fuel Cell Button Cells. J. Power Sources 2009, 187, 123–135. [Google Scholar] [CrossRef]
- Sembler, W.J.; Kumar, S. Optimization of a Single-Cell Solid-Oxide Fuel Cell Using Computational Fluid Dynamics. J. Fuel Cell Sci. Technol. 2011, 8, 021007. [Google Scholar] [CrossRef]
- Wang, G.; Yang, Y.; Zhang, H.; Xia, W. 3-D Model of Thermo-Fluid and Electrochemical for Planar SOFC. J. Power Sources 2007, 167, 398–405. [Google Scholar] [CrossRef]
- Zhang, Z.; Yue, D.; Yang, G.; Chen, J.; Zheng, Y.; Miao, H.; Wang, W.; Yuan, J.; Huang, N. Three-Dimensional CFD Modeling of Transport Phenomena in Multi-Channel Anode-Supported Planar SOFCs. Int. J. Heat Mass Transf. 2015, 84, 942–954. [Google Scholar] [CrossRef]
- Rashid, K.; Dong, S.K.; Khan, R.A.; Park, S.H. Optimization of Manifold Design for 1 KW-Class Flat-Tubular Solid Oxide Fuel Cell Stack Operating on Reformed Natural Gas. J. Power Sources 2016, 327, 638–652. [Google Scholar] [CrossRef]
- Zinovik, I.; Poulikakos, D. Modeling the Temperature Field in the Reforming Anode of a Button-Shaped Solid Oxide Fuel Cell. Electrochim. Acta. 2009, 54, 6234–6243. [Google Scholar] [CrossRef]
- Campanari, S.; Iora, P. Definition and Sensitivity Analysis of a Finite Volume SOFC Model for a Tubular Cell Geometry. J. Power Sources. 2004, 132, 113–126. [Google Scholar] [CrossRef]
- Wei, S.S.; Wang, T.H.; Wu, J.S. Numerical Modeling of Interconnect Flow Channel Design and Thermal Stress Analysis of a Planar Anode-Supported Solid Oxide Fuel Cell Stack. Energy 2014, 69, 553–561. [Google Scholar] [CrossRef]
- Qu, Z.; Aravind, P.V.; Boksteen, S.Z.; Dekker, N.J.J.; Janssen, A.H.H.; Woudstra, N.; Verkooijen, A.H.M. Three-Dimensional Computational Fluid Dynamics Modeling of Anode-Supported Planar SOFC. Int. J. Hydrogen Energy 2011, 36, 10209–10220. [Google Scholar] [CrossRef]
- Ghorbani, B.; Vijayaraghavan, K. 3D and Simplified Pseudo-2D Modeling of Single Cell of a High Temperature Solid Oxide Fuel Cell to Be Used for Online Control Strategies. Int. J. Hydrogen Energy 2018, 43, 9733–9748. [Google Scholar] [CrossRef]
- Su, S.; He, H.; Chen, D.; Zhu, W.; Wu, Y.; Kong, W.; Wang, B.; Lu, L. Flow Distribution Analyzing for the Solid Oxide Fuel Cell Short Stacks with Rectangular and Discrete Cylindrical Rib Configurations. Int. J. Hydrogen Energy 2015, 40, 577–592. [Google Scholar] [CrossRef]
- Zhao, C.; Yang, J.; Zhang, T.; Yan, D.; Pu, J.; Chi, B.; Li, J. Numerical Simulation of Flow Distribution for External Manifold Design in Solid Oxide Fuel Cell Stack. Int. J. Hydrogen Energy 2017, 42, 7003–7013. [Google Scholar] [CrossRef]
- Liu, H.; Li, P.; Lew, J. van. CFD Study on Flow Distribution Uniformity in Fuel Distributors Having Multiple Structural Bifurcations of Flow Channels. Int. J. Hydrogen Energy 2010, 35, 9186–9198. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, T.; Zhao, C.; Pu, J. Numerical Study of Thermal Stresses in a Planar Solid Oxide Fuel Cell Stack. In ASME 2017 15th International Conference on Fuel Cell Science, Engineering and Technology; American Society of Mechanical Engineers: New York, NY, USA, 2017. [Google Scholar] [CrossRef]
- Wei, J.; Malzbender, J. Steady State Creep of Ni-8YSZ Substrates for Application in Solid Oxide Fuel and Electrolysis Cells. J. Power Sources. 2017, 360, 1–10. [Google Scholar] [CrossRef]
- Fakouri Hasanabadi, M.; Faghihi-Sani, M.A.; Kokabi, A.H.; Malzbender, J. The Analysis of Torsional Shear Strength Test of Sealants for Solid Oxide Fuel Cells. Ceram. Int. 2017, 43, 12546–12550. [Google Scholar] [CrossRef]
- Boccaccini, D.N.; Sevecek, O.; Frandsen, H.L.; Dlouhy, I.; Molin, S.; Charlas, B.; Hjelm, J.; Cannio, M.; Hendriksen, P.V. Determination of the Bonding Strength in Solid Oxide Fuel Cells’ Interfaces by Schwickerath Crack Initiation Test. J. Eur. Ceram. Soc. 2017, 37, 3565–3578. [Google Scholar] [CrossRef]
- Dey, T.; Singdeo, D.; Deshpande, J.; Ghosh, P.C. Structural Analysis of Solid Oxide Fuel Cell under Externally Applied Compressive Pressure. Energy Procedia 2014, 54, 789–795. [Google Scholar] [CrossRef][Green Version]
- Karri, N.K.; Koeppel, B.J.; Nguyen, B.N.; Lai, K. Structural Reliability of Cathode Contact Materials in Planar SOFCs. ECS Trans. 2017, 78, 1701–1712. [Google Scholar] [CrossRef]
- Peksen, M.; Al-Masri, A.; Blum, L.; Stolten, D. 3D Transient Thermomechanical Behaviour of a Full Scale SOFC Short Stack. Int. J. Hydrogen Energy 2013, 38, 4099–4107. [Google Scholar] [CrossRef]
- Peksen, M. 3D Transient Multiphysics Modelling of a Complete High Temperature Fuel Cell System Using Coupled CFD and FEM. Int. J. Hydrogen Energy 2014, 39, 5137–5147. [Google Scholar] [CrossRef]
- Hussain, J.; Ali, R.; Akhtar, M.N.; Jaffery, M.H.; Shakir, I.; Raza, R. Modeling and Simulation of Planar SOFC to Study the Electrochemical Properties. Curr. Appl. Phys. 2020, 20, 660–672. [Google Scholar] [CrossRef]
- Somano, V.; Ferrero, D.; Santarelli, M.; Papurello, D. CFD Model for Tubular SOFC Directly Fed by Biomass. Int. J. Hydrogen Energy 2021, 46, 17421–17434. [Google Scholar] [CrossRef]
- Cimen, F.M.; Kumuk, B.; Ilbas, M. Simulation of Hydrogen and Coal Gas Fueled Flat-Tubular Solid Oxide Fuel Cell (FT-SOFC). Int. J. Hydrogen Energy 2022, 47, 3429–3436. [Google Scholar] [CrossRef]
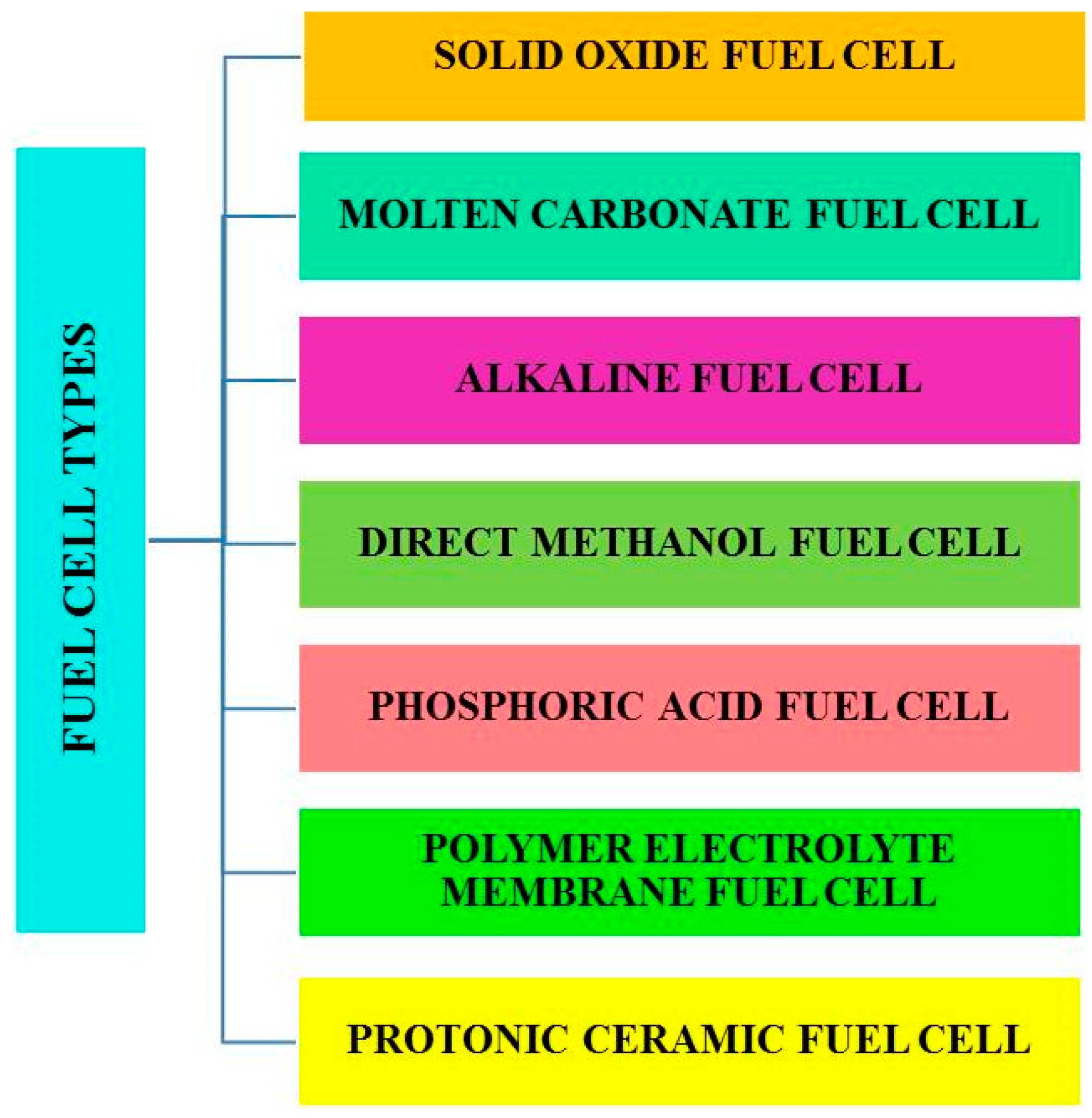


| No | Fuel Cell | Electrolyte | Operating Temperature | Electrical Efficiency | Qualified Power | Advantages | Disadvantages | Applications |
|---|---|---|---|---|---|---|---|---|
| 1 | Direct methanol fuel cell (DMFC) | Polymer membrane (proton exchange membrane) | 60–200 °C | 20–30% | 100 kW–1 mW | Higher power density, less operating temperature. | Less efficiency, the byproduct is more toxic. | Mobiles, laptops, and battery chargers. |
| 2 | Alkaline fuel cell (AFC) | Potassium hydroxide (aqueous alkaline solution) | 60–120 °C | 35–55% | 10–100 kW | Efficiency is high. | Requirement of high removal rate of CO2 from fuel and air. | Aerospace and underwater environments applications. |
| 3 | Phosphoric acid fuel cell (PAFC) | H3PO4 (molten phosphoric acid) | 150–220 °C | 40% | 10 MW | High efficiency, the electrolyte is stable. | Power density is low, corrosion, less power, less current, and more weight. | More energy is needed in hospitals, schools, and offices. |
| 4 | Proton exchange membrane fuel cell (PEMFC) | Nafion (polymer exchange membrane) | 50–100 °C | 35–45% | 100 W–500 kW | Power density is high, less temperature, more safety, and the electrolytes are non-corrosive. | The platinum catalyst is costly, and low efficiency. | House, and vehicles. |
| 5 | Molten carbonate fuel cell (MCFC) | Sodium bicarbonate (alkaline carbonates solution) | 600–650 °C | >50% | 100 MW | Efficiency is high, ability to internally reform and fuel is flexible. | Startup is slow, the electrolyte is corrosive, and managing the electrolyte is more complex. | Large commercial distributed generation. |
| 6 | Solid oxide fuel cell (SOFC) | Yttria-stabilized zirconia (oxygen ion conducting ceramic oxide) | 700–1000 °C | >50% | 100 MW | Efficiency is high, flexible fuel produces waste heat, the electrolyte is solid, and it reduces management problems. | Cost is high, startup is slow, corrosion happens due to higher temperatures. | Factories, residential areas |
| 7 | Protonic ceramic fuel cell | Proton conducting ceramic electrolyte | 450–750 °C [45] | >50% [46] | 25 kW [46] | High conductivity, working temperature is less compared to SOFCs, and lower degradation [20,47]. | Complex fabrication, Required suitable electrolyte and electrode materials. | Remote power applications and heavy-duty trucking [48,49]. |
| Analysis | Configuration | Results | Ref. |
|---|---|---|---|
| CFD |  |
| Zhu et al. [53] |
| CFD |  |
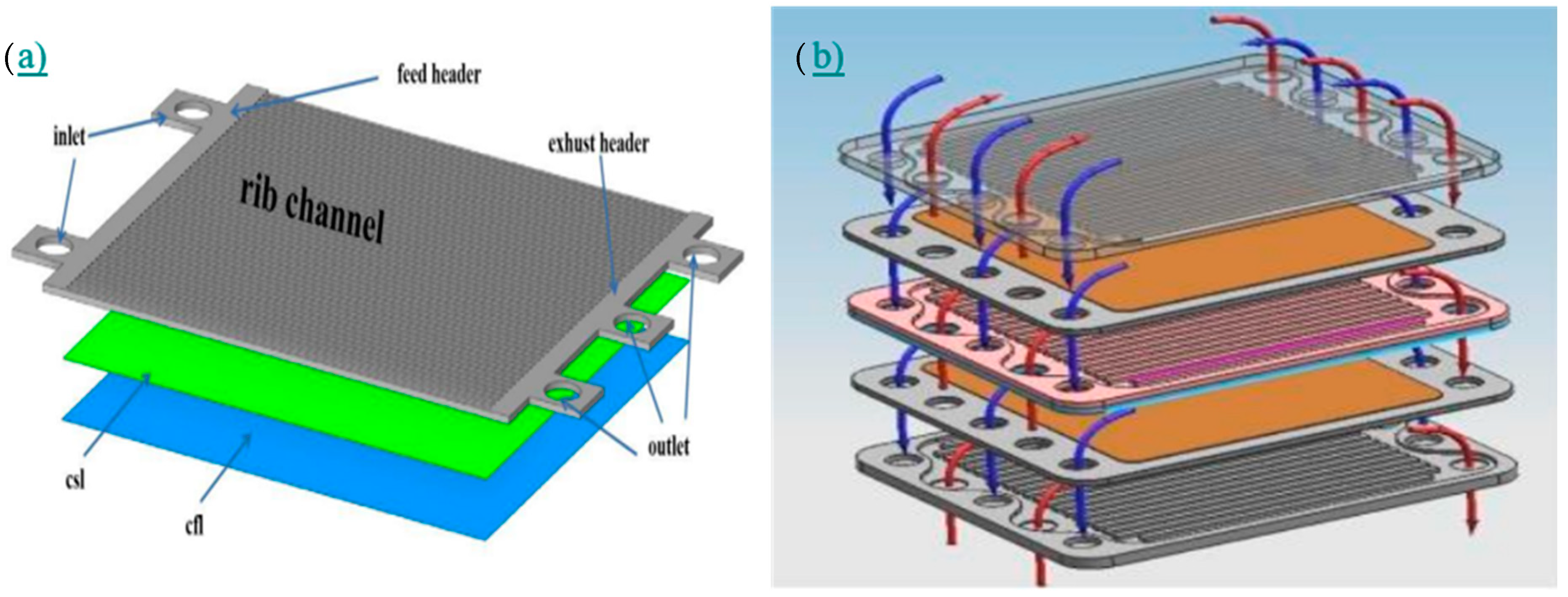
| Dai et al. [37] |
| CFD | 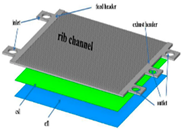 | Rib channel design and inlet/outlet manifold play a key role to know the species distribution over the electrolyte surface. Increasing the cathode layer thickness helps to provide better performance of the PCFC stack. | Dai et al. [55] |
| CFD |  | Inter-parallel structure manages the problem of pressure drop and removes water effectively. | Akenteng et al. [9] |
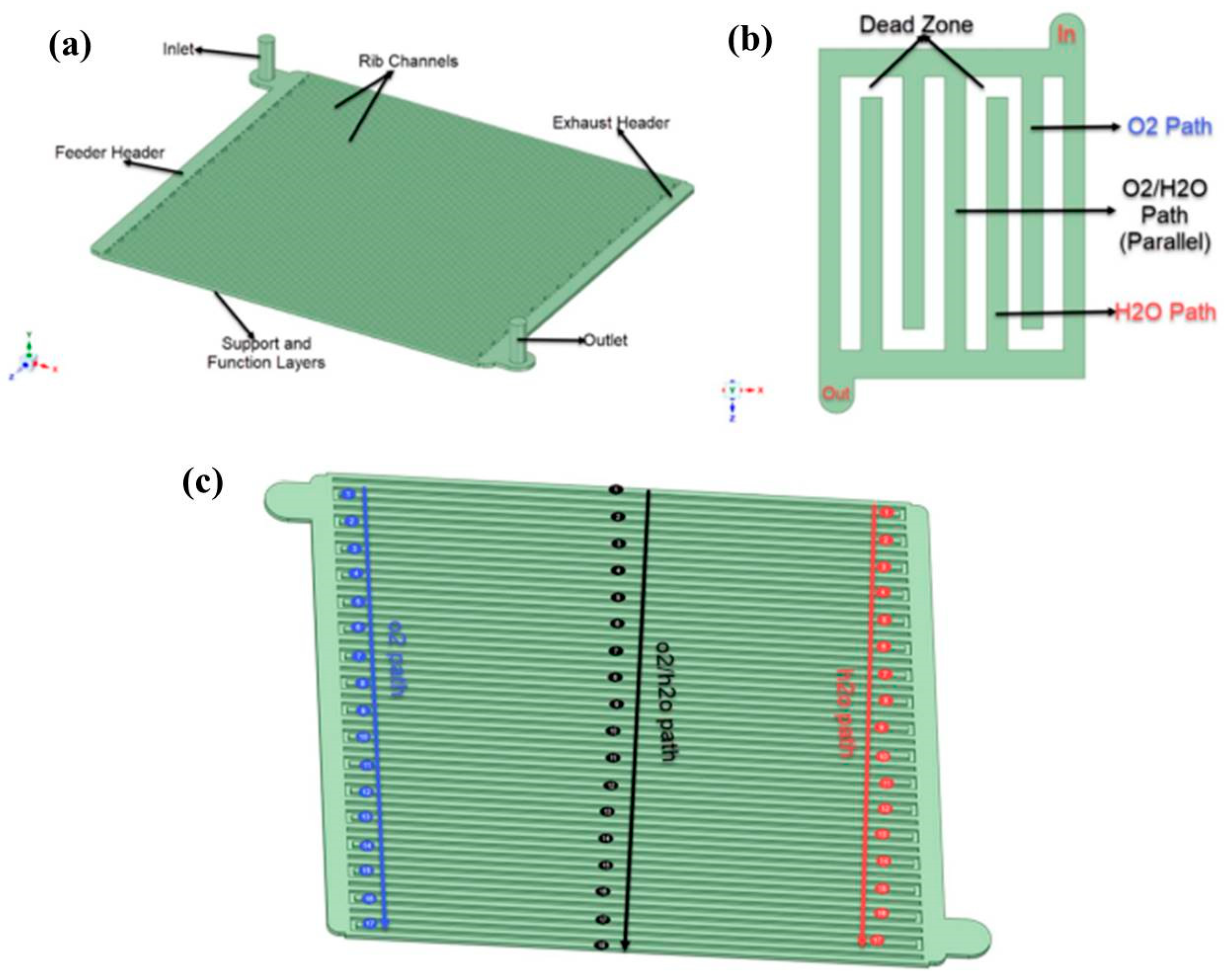
| CFD | 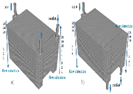 | The U-type air-flow path is the superior option for the PCFC stack to achieve higher air and oxygen distribution characteristics. | Dai et al. [39] |
| Different Types of Modeling and Analysis of SOFCs are Carried out Using Various Types of Software | ||
|---|---|---|
| CFD analysis (ANSYS) | Electrochemistry and flow analysis are carried out using user-defined functions or add-on modules. | |
| Hydrocarbon-fueled SOFCs | Hydrogen-fueled cells | |
| Analysis based on the varying composition of fuels [64] | Variation of fuel/air flow rates [65,66] | |
| Current distribution analysis [65,66] | ||
| Temperature distribution analysis [66,67] | ||
| Research-based on varying cross-section geometries of cells [68] | ||
| Impact of radiative heat transfer [69] | Various flow pattern analysis [66,70] | |
| Research-based on imposing thermal stresses on SOFC [71,72] | Different thermal boundary conditions [71,73] | |
| Flow analysis using ANSYS CFX | By varying manifold designs in SOFC [74,75,76]. | |
| Finite element method Analysis (ANSYS) | Creep behavior analysis [77,78] Torsion test in SOFC [79] Crack initiation test [80] Compression stress test [81,82] | |
| FEM cum CFD Analysis (ANSYS) | Used to analyze thermal stress on the stack [83,84] | |
| MATLAB Simulink | The partial pressures of hydrogen, oxygen, and water were calculated [62] | |
| COMSOL MULTIPHYSICS | The effects of different gas flow patterns in SOFC were analyzed [61] | |
| Electrochemical analysis on planar SOFCs [85] | ||
| Modeling of tubular SOFCs fed by biomass [86] | ||
| Modeling of hydrogen and coal gas-fueled flat-tubular solid oxide fuel cells [87] | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dhanasekaran, A.; Subramanian, Y.; Omeiza, L.A.; Raj, V.; Yassin, H.P.H.M.; SA, M.A.; Azad, A.K. Computational Fluid Dynamics for Protonic Ceramic Fuel Cell Stack Modeling: A Brief Review. Energies 2023, 16, 208. https://doi.org/10.3390/en16010208
Dhanasekaran A, Subramanian Y, Omeiza LA, Raj V, Yassin HPHM, SA MA, Azad AK. Computational Fluid Dynamics for Protonic Ceramic Fuel Cell Stack Modeling: A Brief Review. Energies. 2023; 16(1):208. https://doi.org/10.3390/en16010208
Chicago/Turabian StyleDhanasekaran, Anitha, Yathavan Subramanian, Lukman Ahmed Omeiza, Veena Raj, Hayati Pg Hj Md Yassin, Muhammed Ali SA, and Abul K. Azad. 2023. "Computational Fluid Dynamics for Protonic Ceramic Fuel Cell Stack Modeling: A Brief Review" Energies 16, no. 1: 208. https://doi.org/10.3390/en16010208
APA StyleDhanasekaran, A., Subramanian, Y., Omeiza, L. A., Raj, V., Yassin, H. P. H. M., SA, M. A., & Azad, A. K. (2023). Computational Fluid Dynamics for Protonic Ceramic Fuel Cell Stack Modeling: A Brief Review. Energies, 16(1), 208. https://doi.org/10.3390/en16010208











