Implementation of an ADALINE-Based Adaptive Control Strategy for an LCLC-PV-DSTATCOM in Distribution System for Power Quality Improvement
Abstract
:1. Introduction
- The LCLC-PV-DSTATCOM was designed for the distribution system to enhance the power quality under dynamic load conditions.
- An adaptive ADALINE-based controller was proposed for the suitable control of the considered PV-DSTATCOM. An ADALINE-based controller provides adaptivity regarding power quality issues based on the learning mechanism.
- The performance of the ADALINE-based controller for the PV-DSTATCOM system was analyzed under various dynamic load conditions and compared with the performance of conventional controllers.
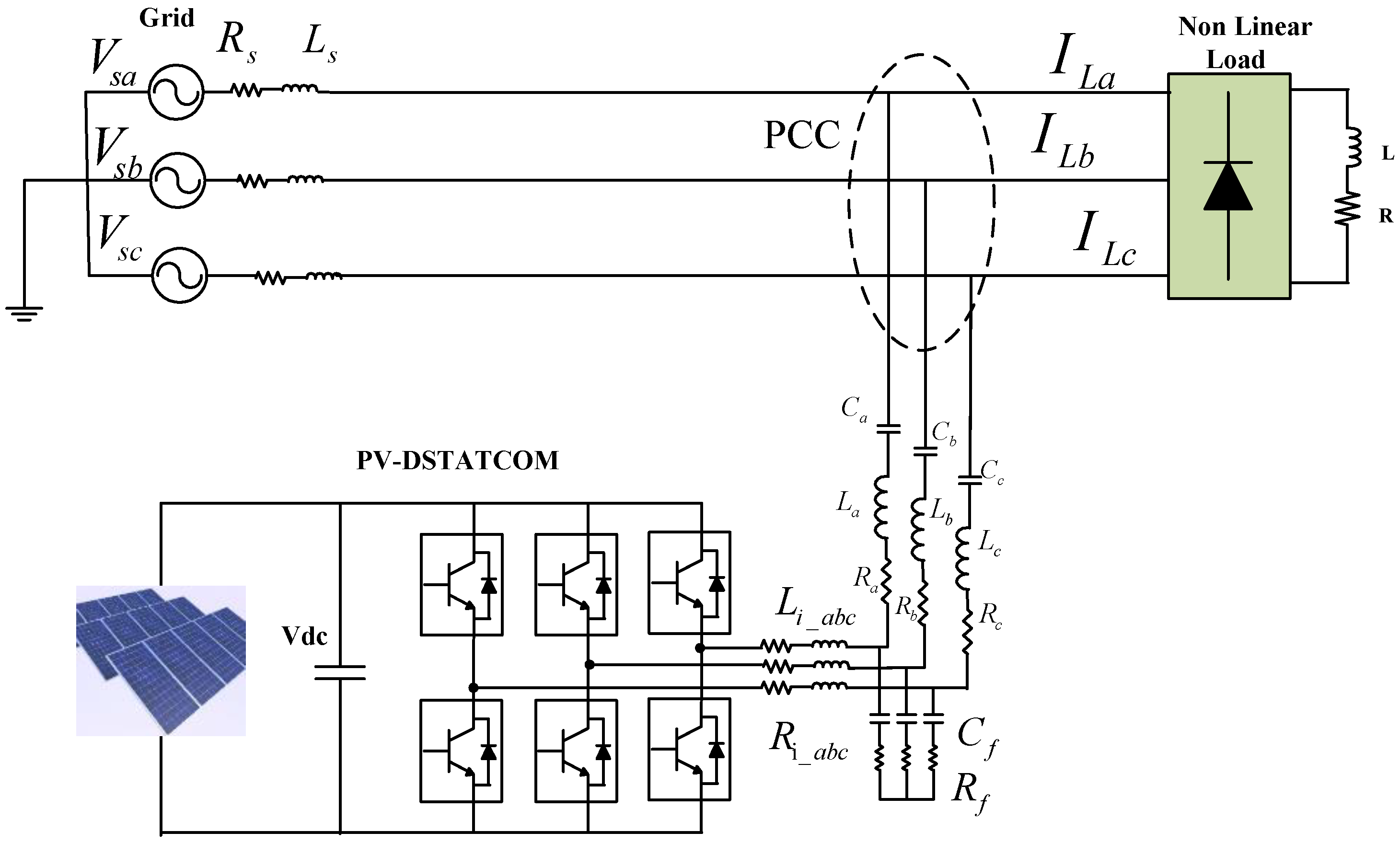
2. System Configuration of the PV-Based DSTATCOM
3. Control Methods Description
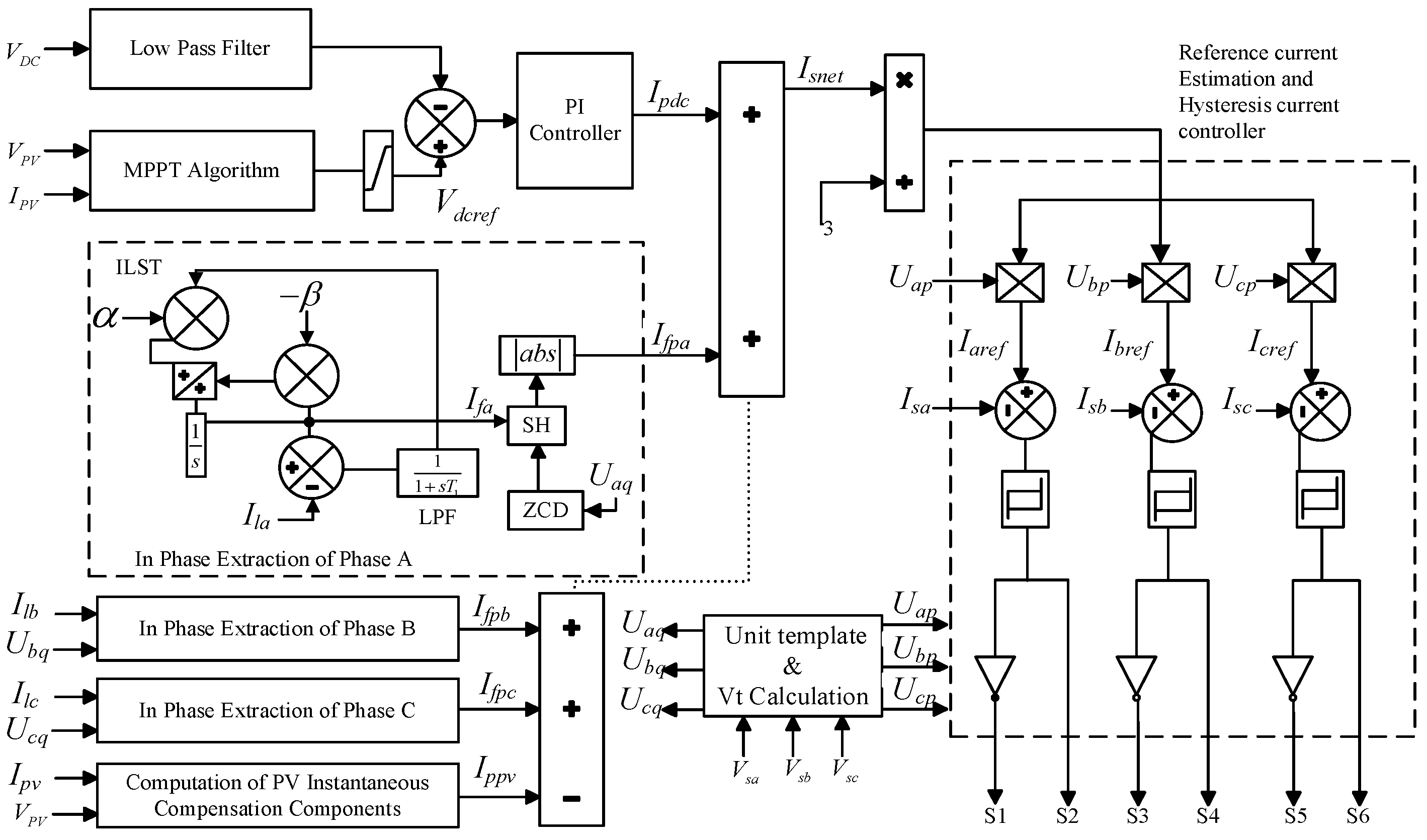
3.1. Synchronous Reference Frame Theory (SRFT)
3.2. Improved Linear Sinusoidal Tracer (ILST)
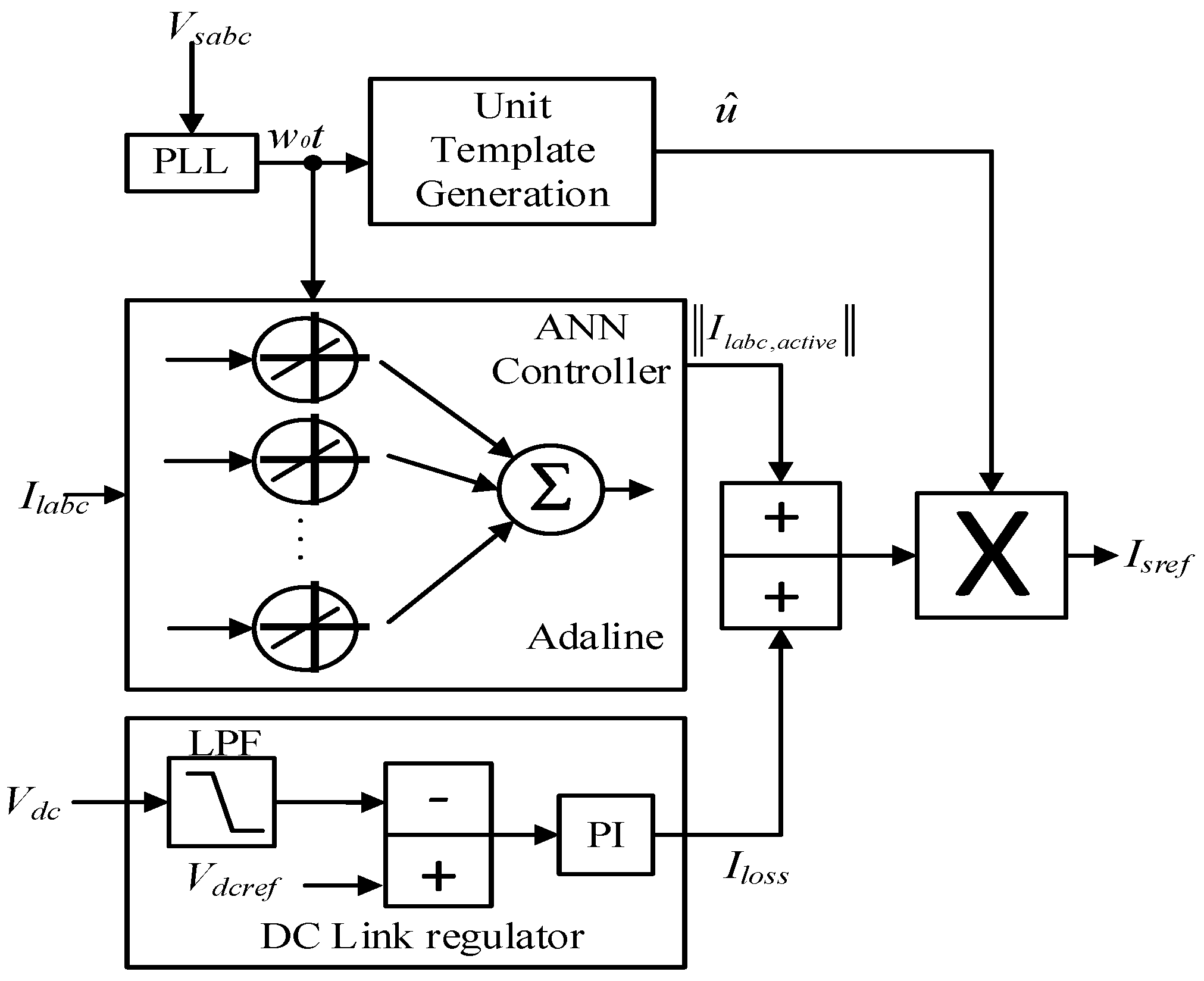
3.3. Backpropagation Algorithm
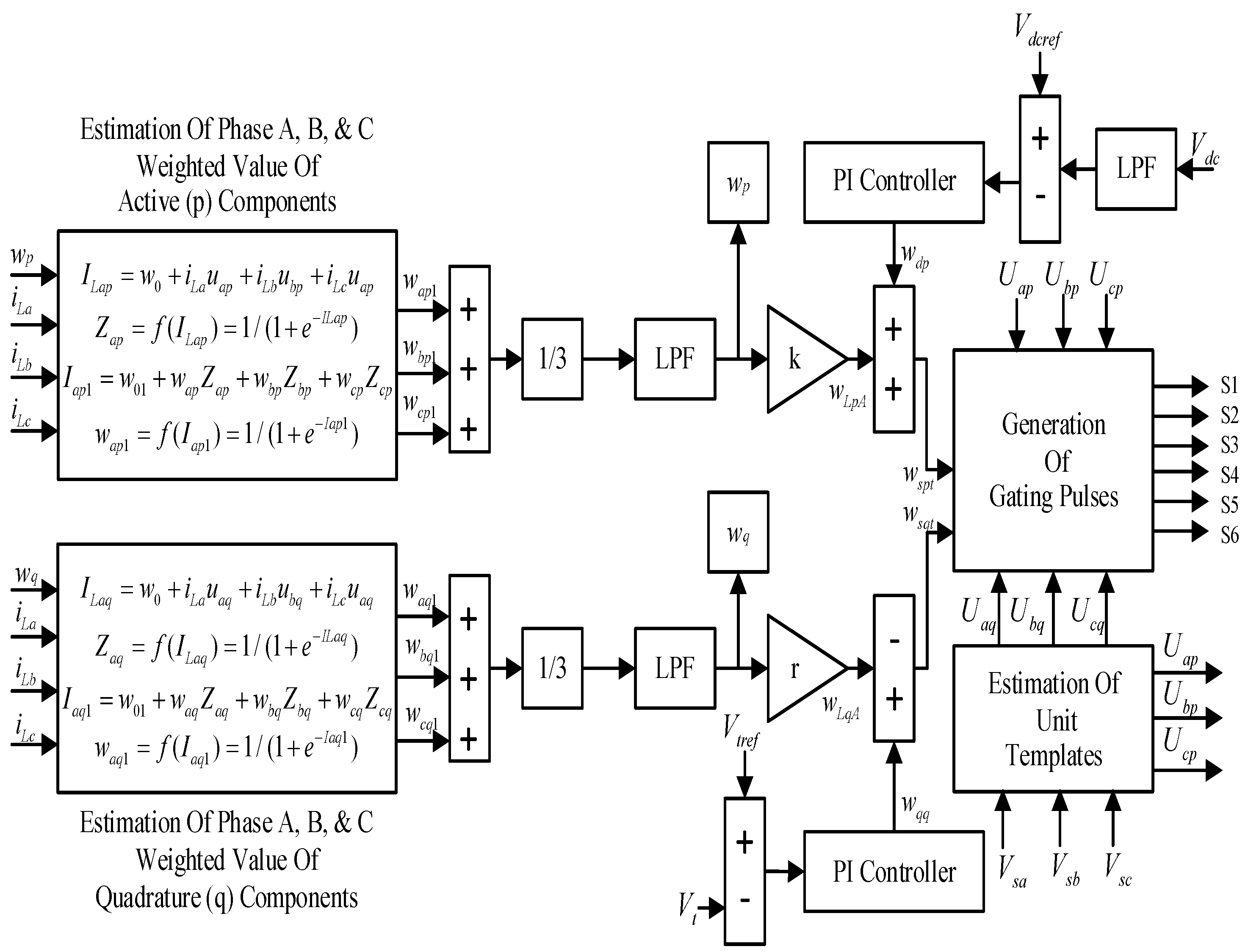
4. The ADALINE-Based Control Method
5. Results and Analysis
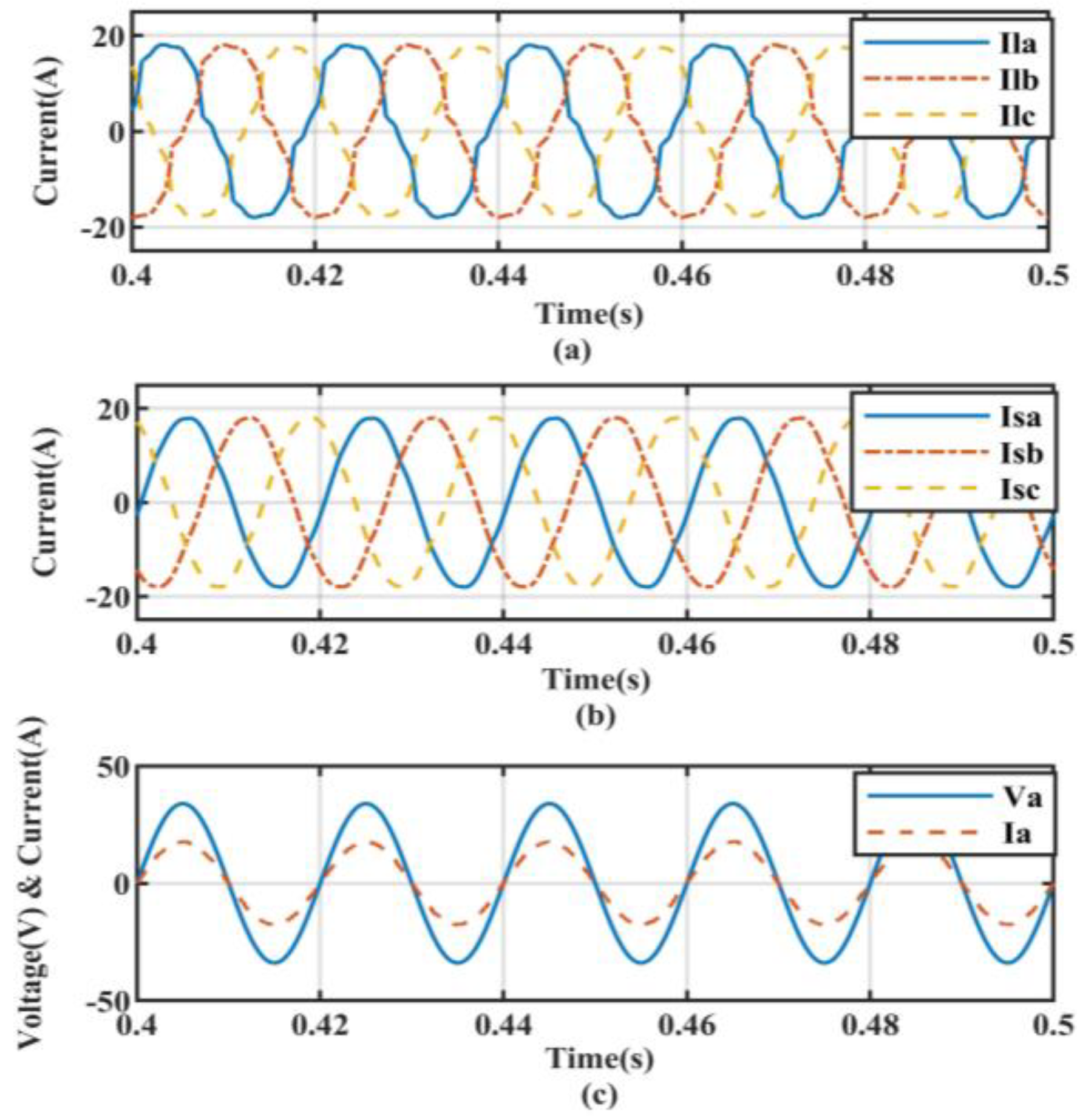
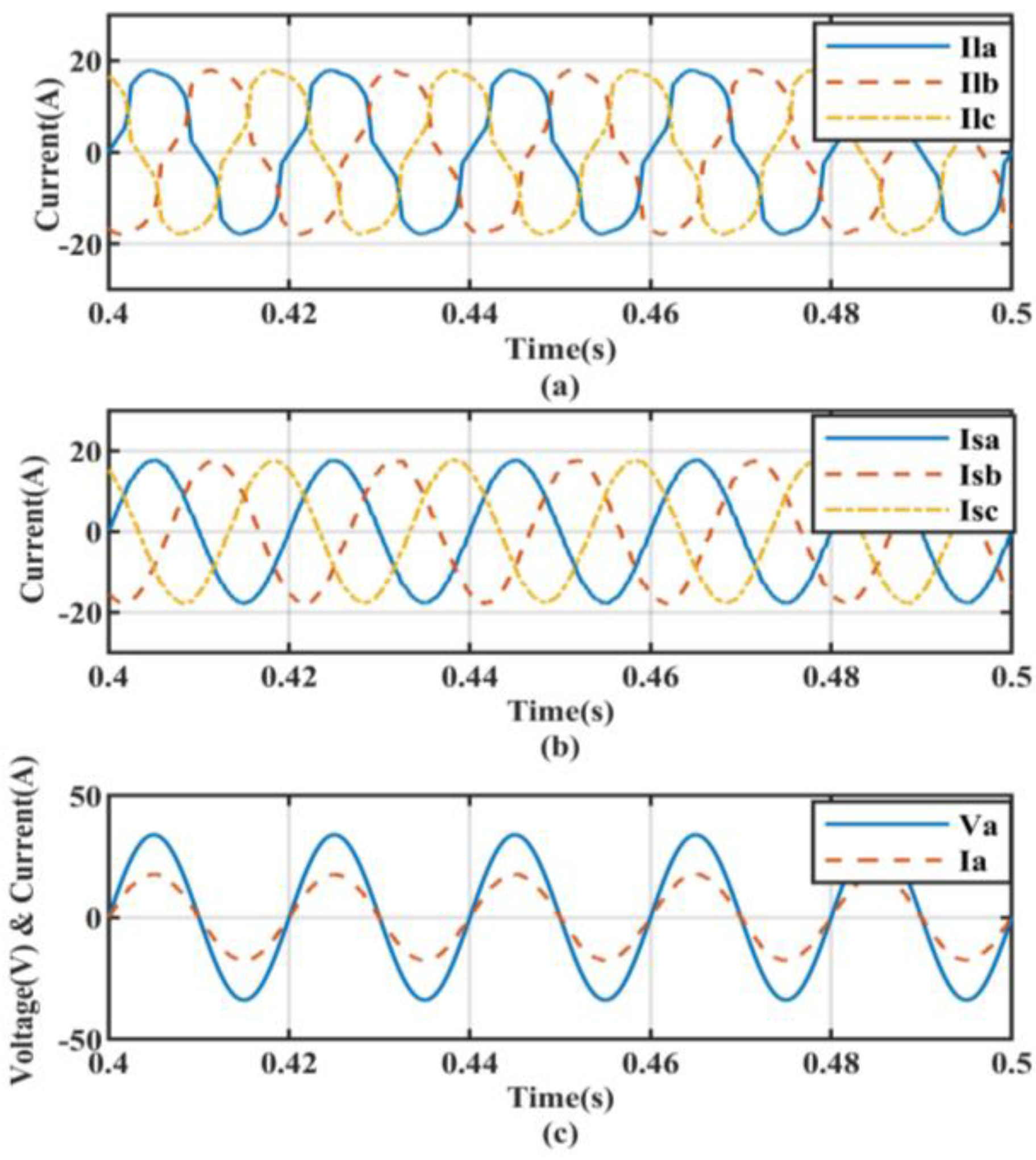
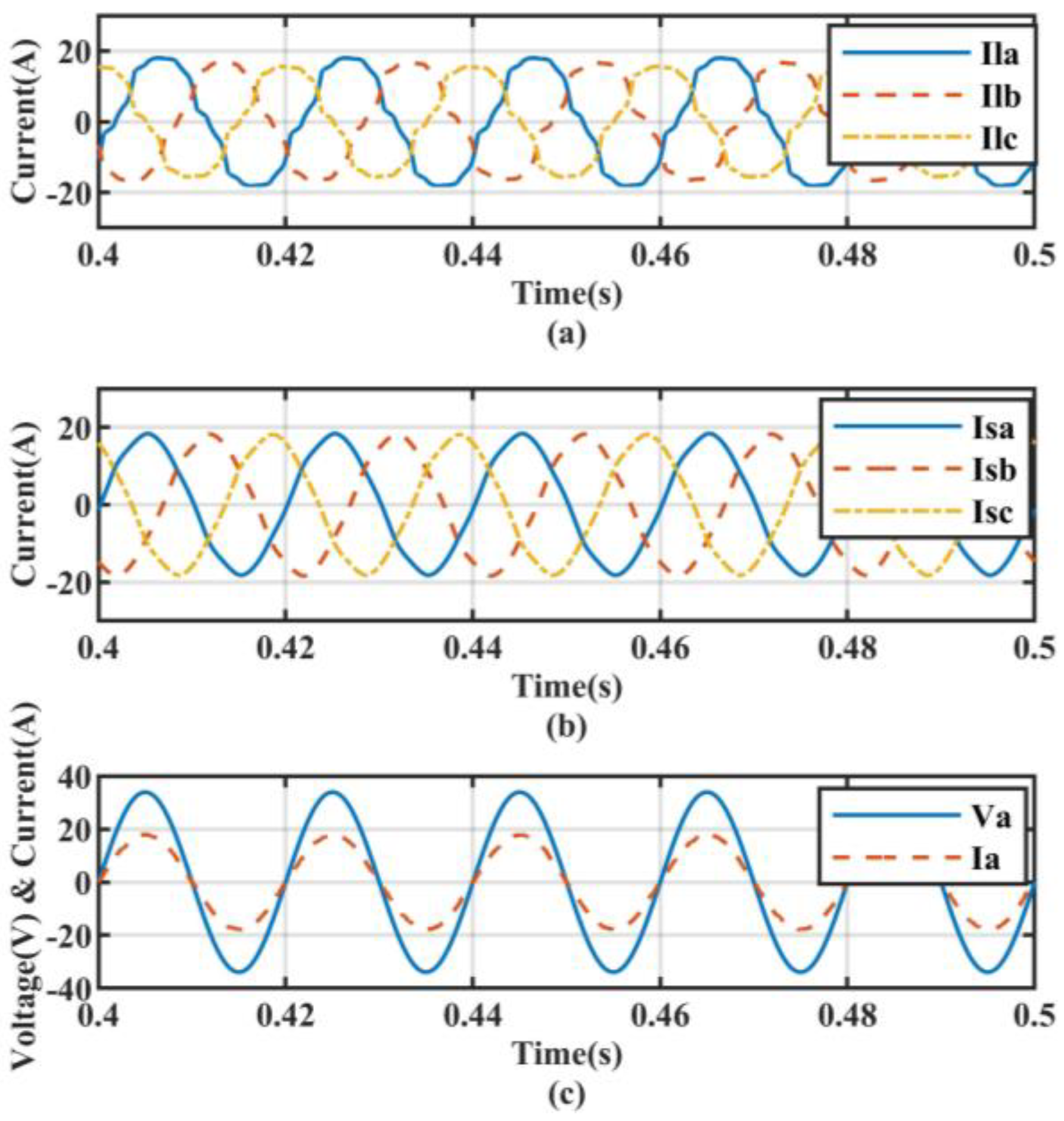
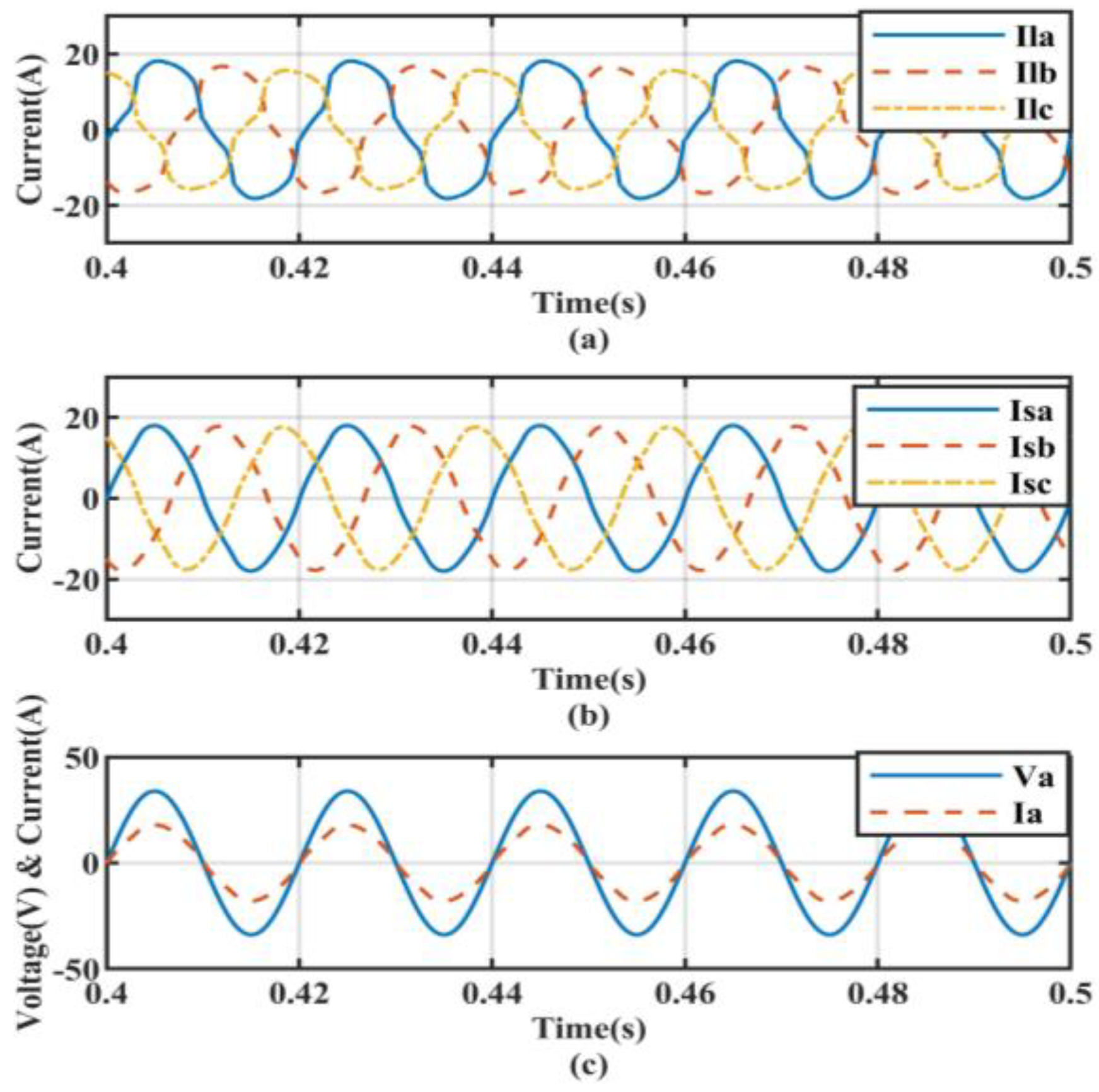
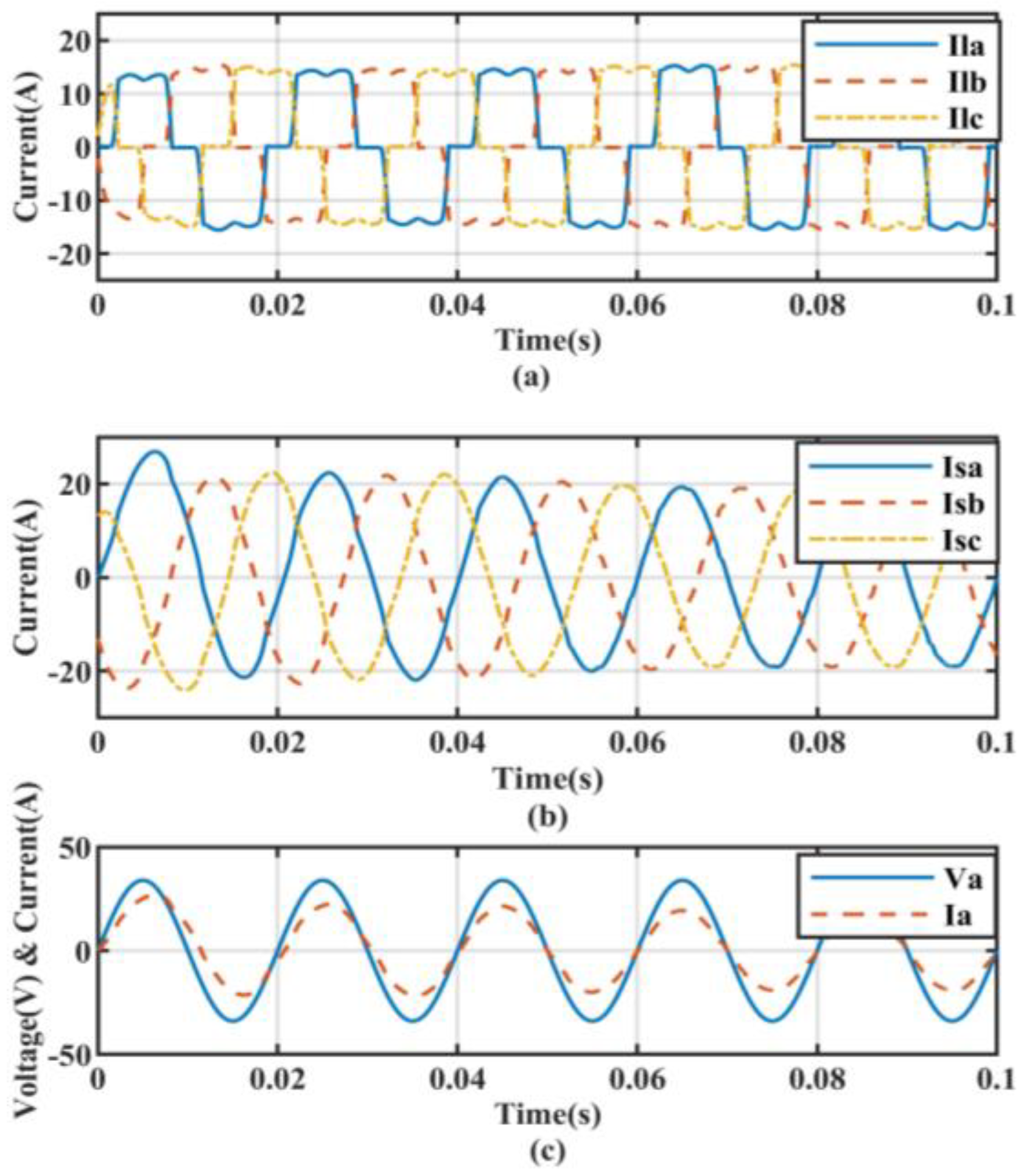
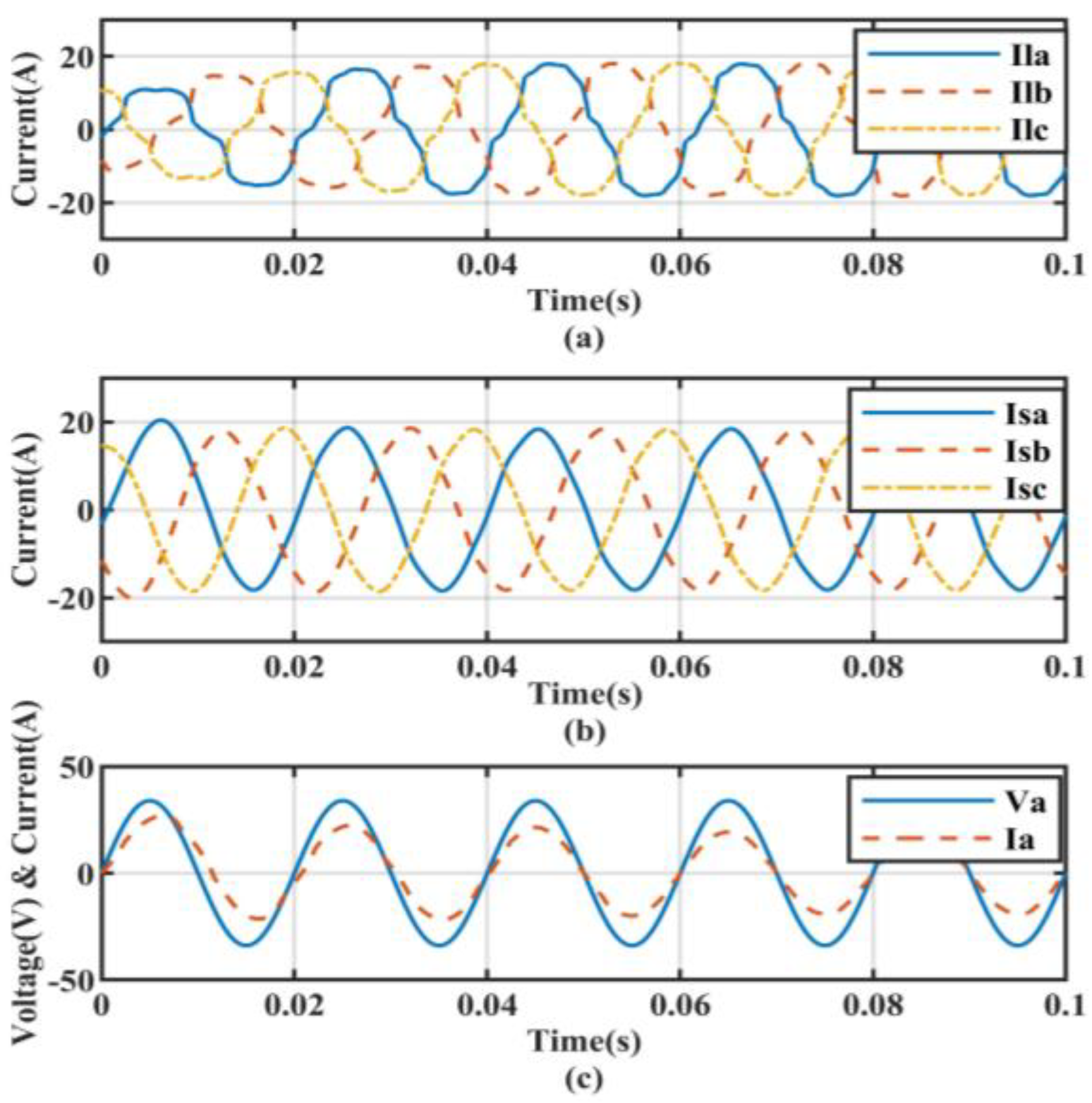
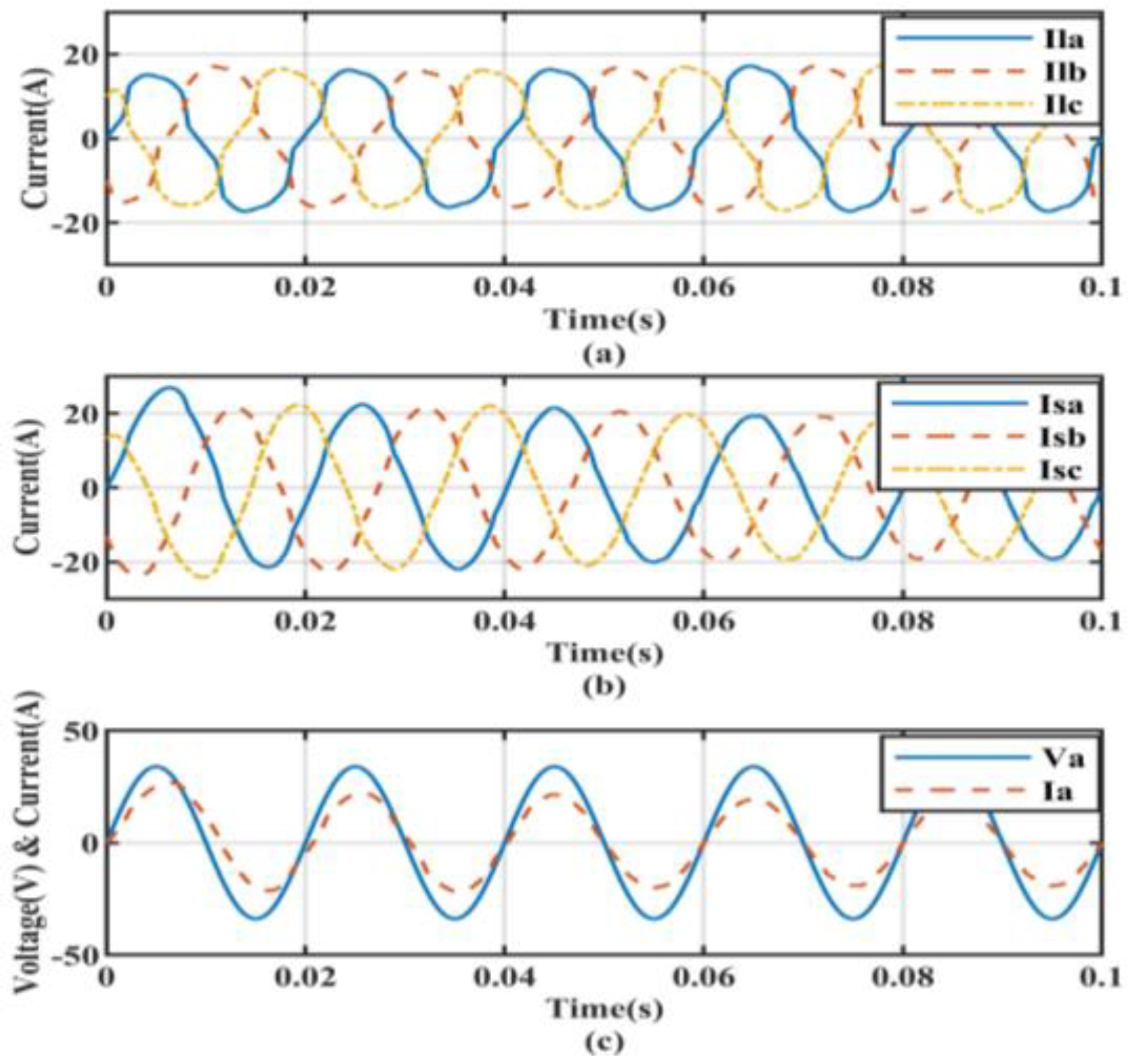
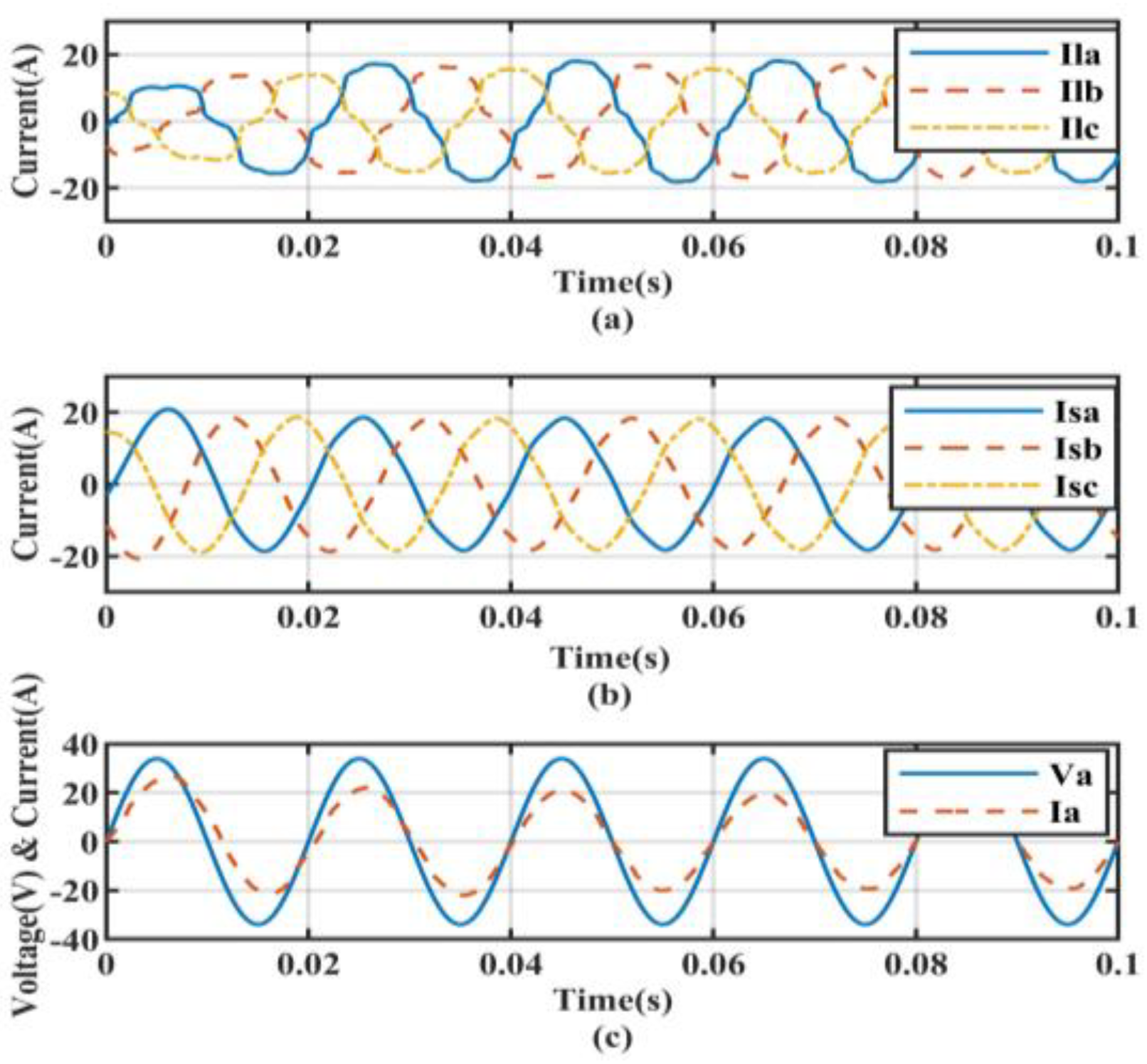
5.1. Performance under Non-Linear Load Conditions
5.2. Non-Linear Load with Linear Balanced Load Conditions
5.3. Non-Linear Load with Linear Unbalanced Load Conditions
5.4. Transient State Analysis for Ideal Source Voltage Condition
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
References
- Singh, B.; Chandra, A.; Al-Haddad, K. Power Quality Problems and Mitigation Techniques; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Singh, B.; Jayaprakash, P.; Kothari, D.P.; Chandra, A.; Al Haddad, K. Comprehensive Study of DSTATCOM Configurations. IEEE Trans. Ind. Inform. 2014, 10, 854–870. [Google Scholar] [CrossRef]
- Pal, Y.; Swarup, A.; Singh, B. A review of compensating type custom power devices for power quality improvement. In Proceedings of the 2008 Joint International Conference on Power System Technology and IEEE Power India Conference, New Delhi, India, 12–15 October 2008. [Google Scholar]
- Mishra, S.; Dash, S.K.; Ray, P.K. Performance analysis of L-type PV-DSTATCOM under ideal and distorted supply voltage. In Proceedings of the 2016 IEEE Students’ Technology Symposium (TechSym), Kharagpur, India, 30 September–2 October 2016; pp. 180–185. [Google Scholar] [CrossRef]
- Mishra, S.; Ray, P.K. Power quality improvement with shunt active filter under various mains voltage using Teaching Learning Based optimization. In Proceedings of the 2015 2nd International Conference on Recent Advances in Engineering & Computational Sciences (RAECS), Chandigarh, India, 21–22 December 2015. [Google Scholar]
- Villalva, M.G.; Gazoli, J.R.; Filho, E.R. Comprehensive approach to modeling and simulation of photovoltaic arrays. IEEE Trans. Power Electron. 2009, 24, 1198–1208. [Google Scholar] [CrossRef]
- Esram, T.; Chapman, P.L. Comparison of Photovoltaic Array Maximum Power Point Tracking Techniques. IEEE Trans. Energy Convers. 2007, 22, 439–449. [Google Scholar] [CrossRef] [Green Version]
- Kouro, S.; Leon, J.I.; Vinnikov, D.; Franquelo, L.G. Grid-Connected Photovoltaic Systems: An Overview of Recent Research and Emerging PV Converter Technology. IEEE Ind. Electron. Mag. 2015, 9, 47–61. [Google Scholar] [CrossRef]
- Patel, N.; Gupta, N.; Babu, B.C. Photovoltaic system operation as DSTATCOM for power quality improvement employing active current control. IET Gener. Transm. Distrib. 2020, 14, 3518–3529. [Google Scholar] [CrossRef]
- Labeeb, M.; Lathika, B. Design and analysis of DSTATCOM using SRFT and ANN-fuzzy based control for power quality improvement. In Proceedings of the 2011 IEEE Recent Advances in Intelligent Computational Systems, Trivandrum, India, 22–24 September 2011; pp. 274–279. [Google Scholar] [CrossRef]
- Singh, B.; Dube, S.K.; Arya, S.R. An improved control algorithm of DSTATCOM for power quality improvement. Int. J. Electr. Power Energy Syst. 2015, 64, 493–504. [Google Scholar] [CrossRef]
- Singh, B.; Solanki, J. A Comparison of Control Algorithms for DSTATCOM. IEEE Trans. Ind. Electron. 2009, 56, 2738–2745. [Google Scholar] [CrossRef]
- Masand, D.; Jain, S.; Agnihotri, G. Control algorithms for distribution static compensator. In Proceedings of the 2006 IEEE International Symposium on Industrial Electronics, Singapore, 24–26 May 2006. [Google Scholar]
- Reddy, M.V.K.; Das’s, D.T.; Pulla, D.S.; Veni, D.K.K. Performance Analysis Of D-Statcom Compensator Using Control Techniques for Load Compensation. Int. J. Electr. Electron. Eng. Res. 2011, 1, 149–171. [Google Scholar]
- Prasad, A.G.; Dheeraj, K.; Kumar, A.N. Comparison of Control Algorithms for Shunt Active Filter for Harmonic Mitigation. Int. J. Eng. Res. Technol. 2012, 1, 5. [Google Scholar]
- Du, S.-W.; Su, J.-M. Analysis of an improved harmonic currents detection method based on LST. In Proceedings of the 2011 2nd International Conference on Artificial Intelligence, Management Science and Electronic Commerce (AIMSEC), Dengfeng, China, 8–10 August 2011; pp. 3755–3759. [Google Scholar] [CrossRef]
- Singh, B.; Arya, S.R. Adaptive Theory-Based Improved Linear Sinusoidal Tracer Control Algorithm for DSTATCOM. IEEE Trans. Power Electron. 2012, 28, 3768–3778. [Google Scholar] [CrossRef]
- Singh, B.; Jain, C.; Goel, S. ILST Control Algorithm of Single-Stage Dual Purpose Grid Connected Solar PV System. IEEE Trans. Power Electron. 2013, 29, 5347–5357. [Google Scholar] [CrossRef]
- Jayachandran, J.; Sachithanadam, R.M. Neural Network-Based Control Algorithm for DSTATCOM Under Nonideal Source Voltage and Varying Load Conditions. Can. J. Electr. Comput. Eng. 2015, 38, 307–317. [Google Scholar] [CrossRef]
- Agarwal, R.K.; Hussain, I.; Singh, B. Application of LMS-based NN structure for power quality enhancement in a distribution network under abnormal conditions. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 1598–1607. [Google Scholar] [CrossRef] [PubMed]
- Singh, B.; Arya, S.R. Back-propagation control algorithm for power quality improvement using DSTATCOM. IEEE Trans. Ind. Electron. 2014, 61, 1204–1212. [Google Scholar] [CrossRef]
- Kumar, P.; Mangaraj, M. DSTATCOM employing hybrid neural network control technique for power quality improvement. IET Power Electron 2017, 10, 480–489. [Google Scholar] [CrossRef]
- Qasim, M.; Khadkikar, V. Application of Artificial Neural Networks for Shunt Active Power Filter Control. IEEE Trans. Ind. Inform. 2014, 10, 1765–1774. [Google Scholar] [CrossRef]
- Chen, C.-I.; Hsu, C.-L.; Chen, C.-H. ADALINE-based shunt active power filter for power quality modification of power system. In Proceedings of the 2018 International Symposium on Computer, Consumer and Control (IS3C), Taichung, Taiwan, 6–8 December 2018. [Google Scholar]
- Mohan, H.M.; Dash, S.K. Performance assessment of a solar-powered three-phase modular multilevel converter with capacitor voltage balancing. In Proceedings of the 2022 Second International Conference on Power, Control and Computing Technologies (ICPC2T), Raipur, India, 1–3 March 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Qasim, M.; Kanjiya, P.; Khadkikar, V. Optimal Current Harmonic Extractor Based on Unified ADALINEs for Shunt Active Power Filters. IEEE Trans. Power Electron. 2014, 29, 6383–6393. [Google Scholar] [CrossRef]
- Dash, S.K.; Garg, P.; Mishra, S.; Chakraborty, S.; Elangovan, D. Investigation of Adaptive Intelligent MPPT Algorithm for a Low-cost IoT Enabled Standalone PV System. Aust. J. Electr. Electron. Eng. 2022, 9, 261–269. [Google Scholar] [CrossRef]
- Ray, P.; Ray, P.K.; Dash, S.K. Power Quality Enhancement and Power Flow Analysis of a PV Integrated UPQC System in a Distribution Network. IEEE Trans. Ind. Appl. 2021, 58, 201–211. [Google Scholar] [CrossRef]
- Dash, S.K.; Roccotelli, M.; Khansama, R.R.; Fanti, M.P.; Mangini, A.M. Long Term Household Electricity Demand Forecasting Based on RNN-GBRT Model and a Novel Energy Theft Detection Method. Appl. Sci. 2021, 11, 8612. [Google Scholar] [CrossRef]
- Mishra, S.; Dash, S.K.; Ray, P.K.; Puhan, P.S. Analysis and experimental evaluation of novel hybrid fuzzy-based sliding mode control strategy for performance enhancement of PV fed DSTATCOM. Int. Trans. Electr. Energy Syst. 2021, 31, e12815. [Google Scholar] [CrossRef]
- Mohan, H.M.; Dash, S.K.; Ram, S.K.; Caesarendra, W. Performance assessment of three-phase PV tied NPC multilevel inverter based UPQC. In Proceedings of the 2022 International Conference on Intelligent Controller and Computing for Smart Power (ICICCSP), Hyderabad, India, 21–23 July 2022; pp. 1–5. [Google Scholar] [CrossRef]
- Dash, S.K.; Chakraborty, S.; Roccotelli, M.; Sahu, U.K. Hydrogen Fuel for Future Mobility: Challenges and Future Aspects. Sustainability 2022, 14, 8285. [Google Scholar] [CrossRef]
- Fanti, M.P.; Mangini, A.M.; Roccotelli, M. A Petri Net model for a building energy management system based on a demand response approach. In Proceedings of the 22nd Mediterranean Conference on Control and Automation (MED), Palermo, Italy, 16–19 June 2014; pp. 816–821. [Google Scholar] [CrossRef]



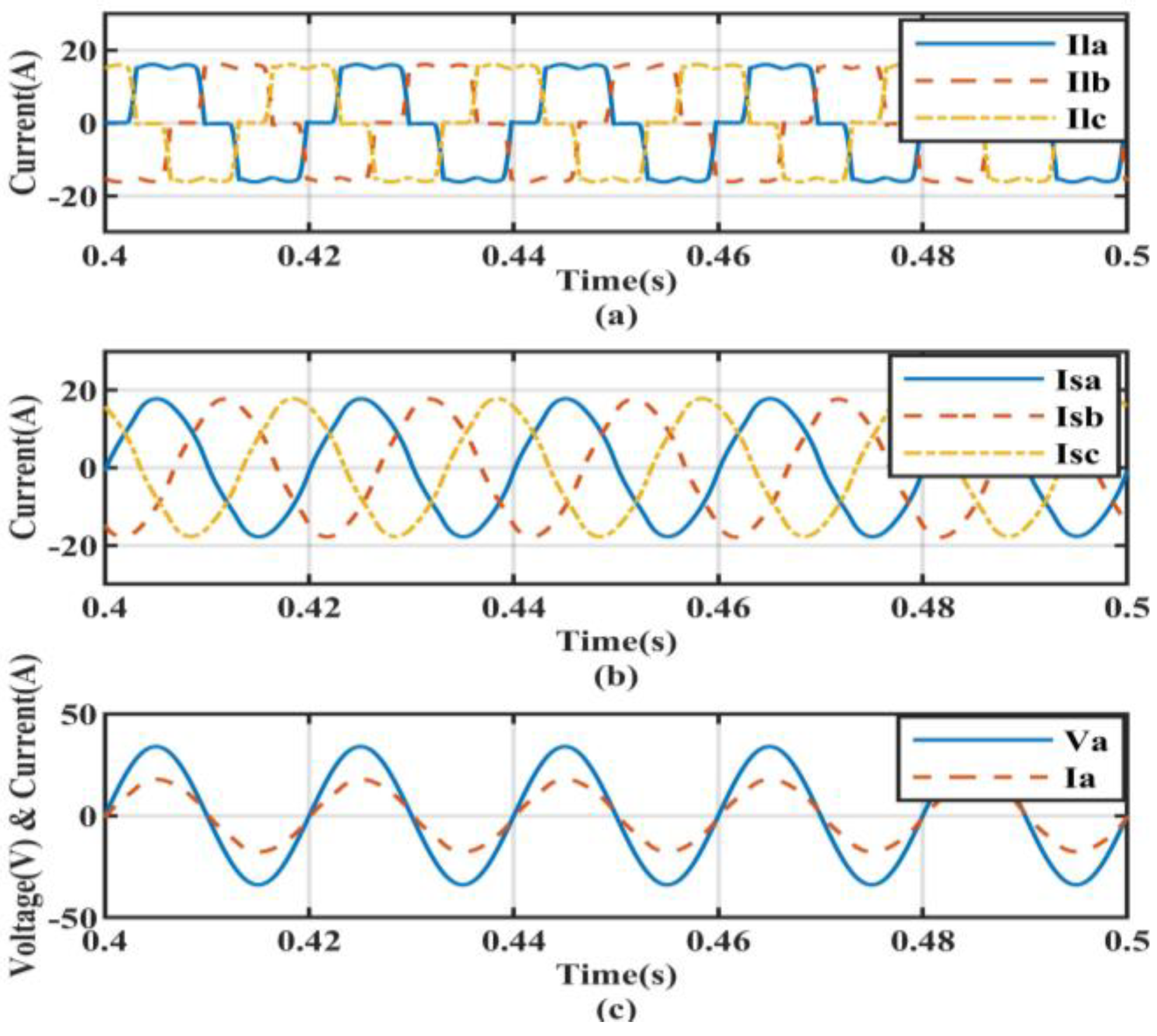
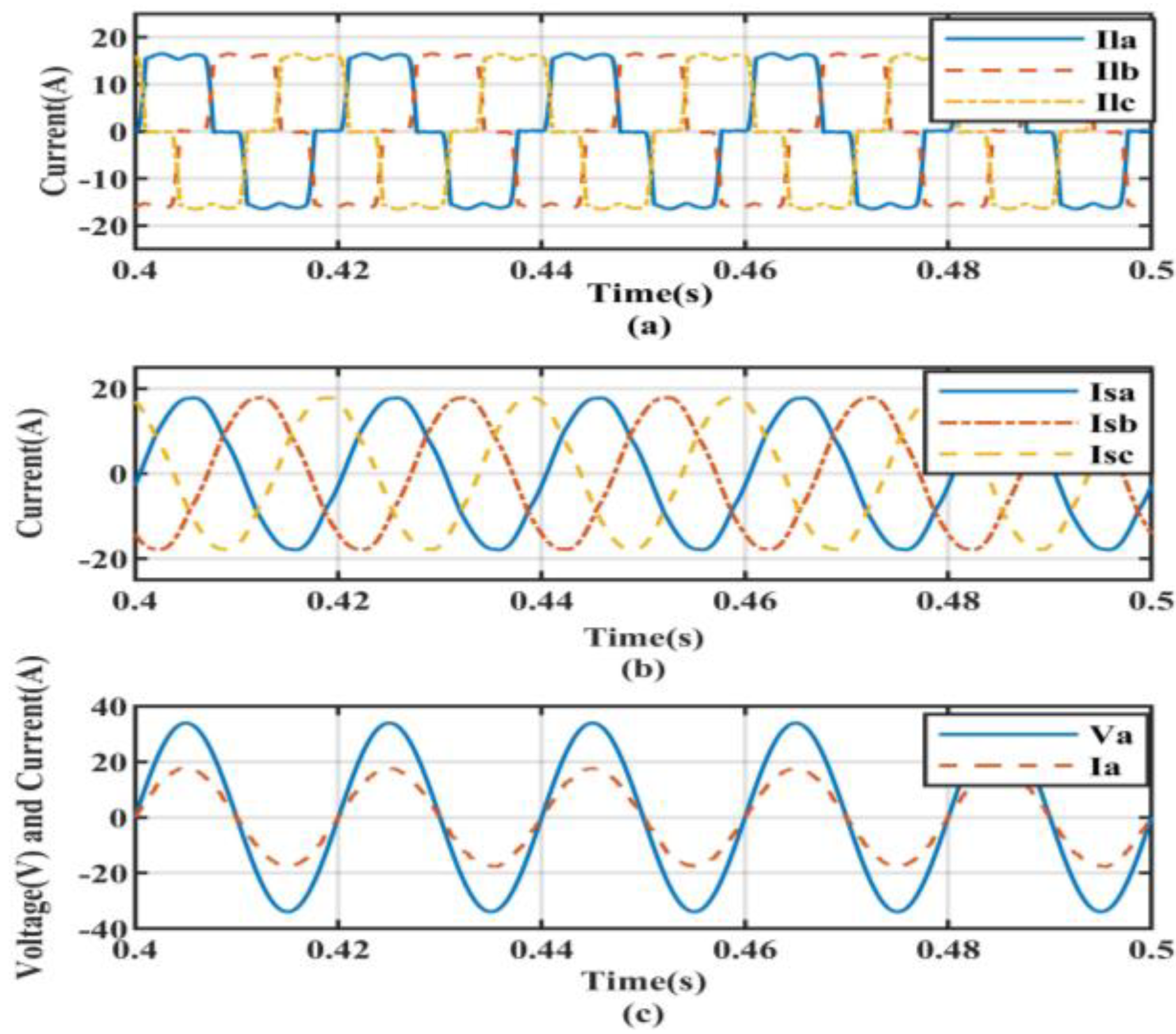
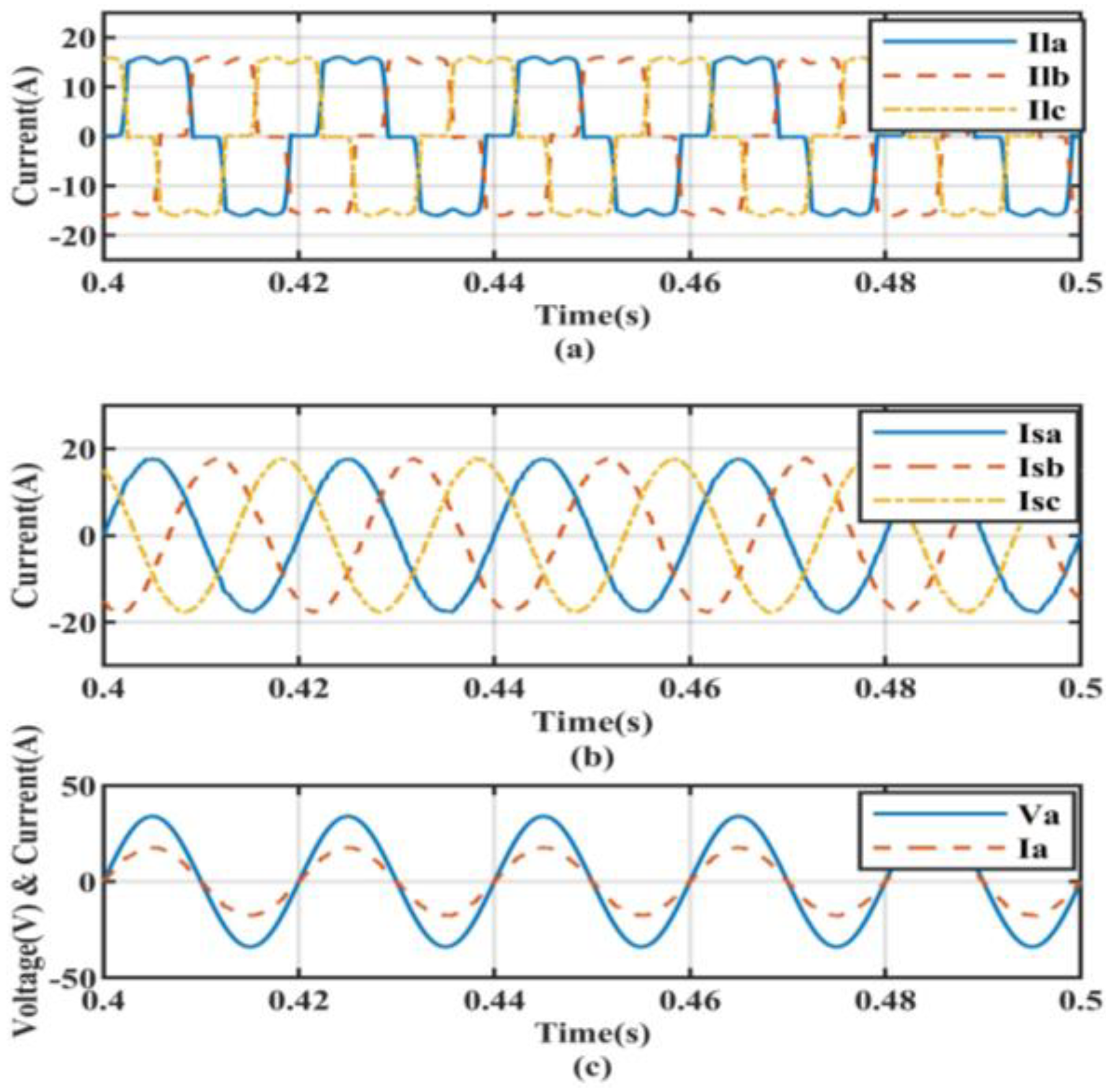
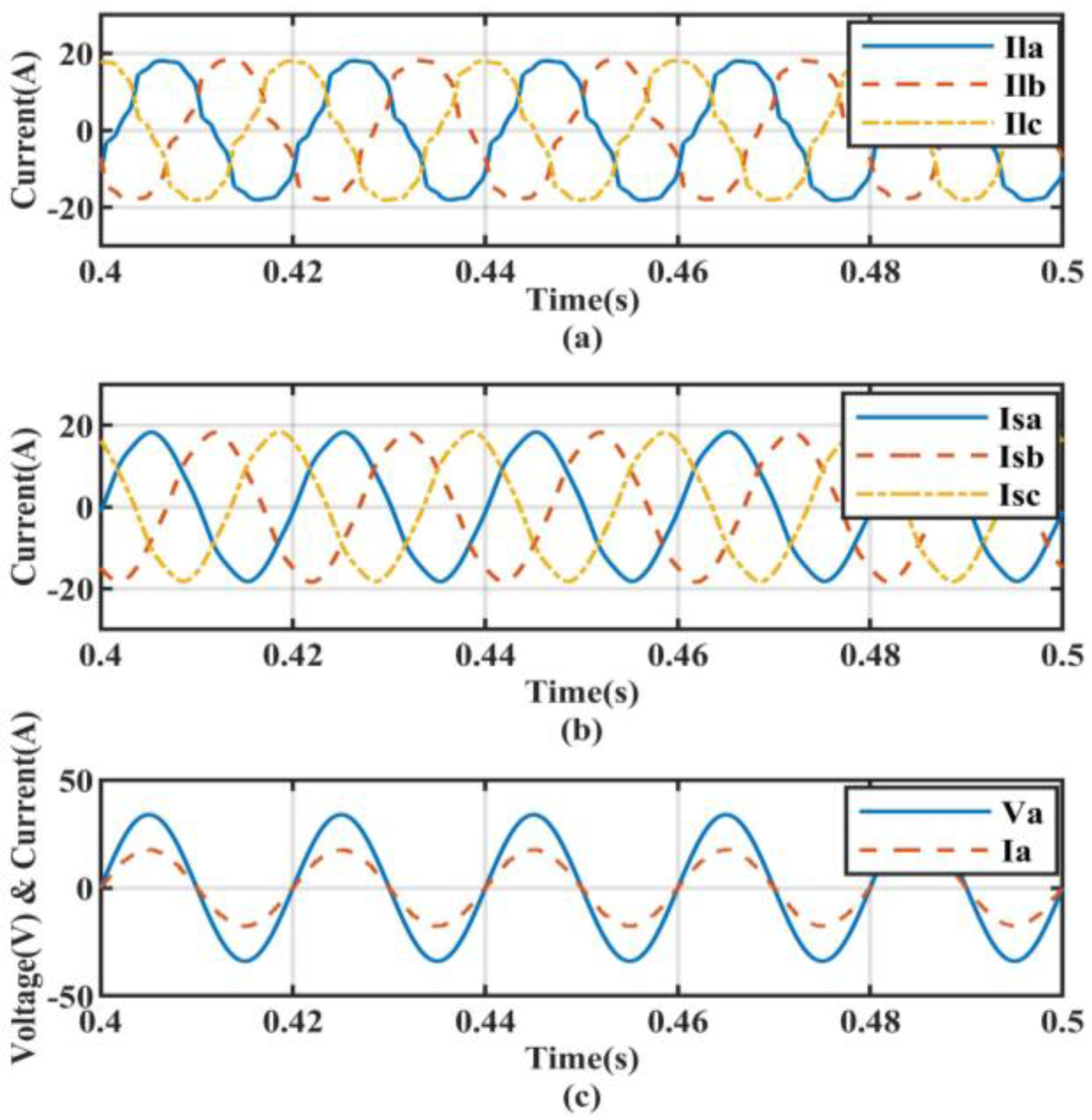

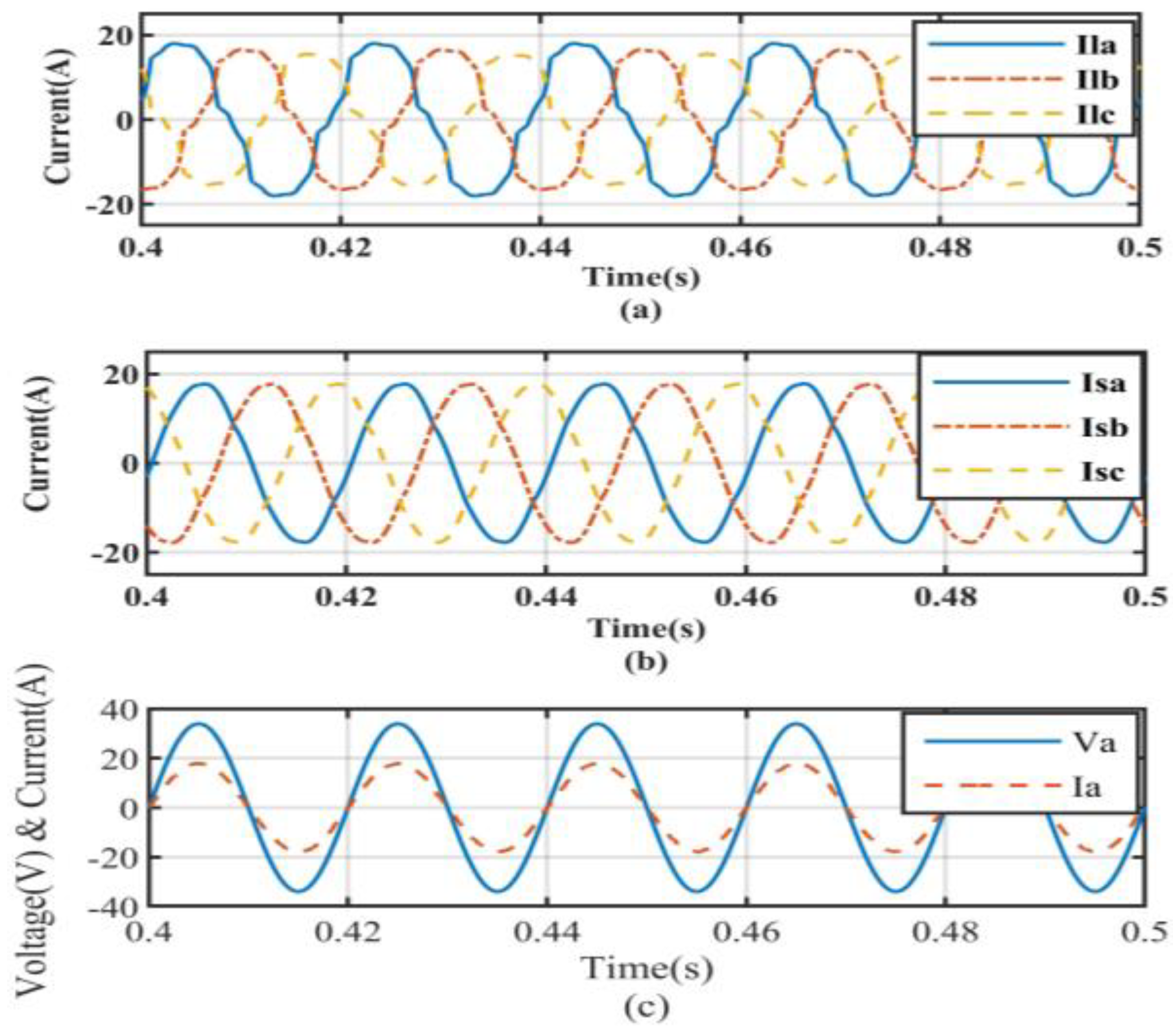
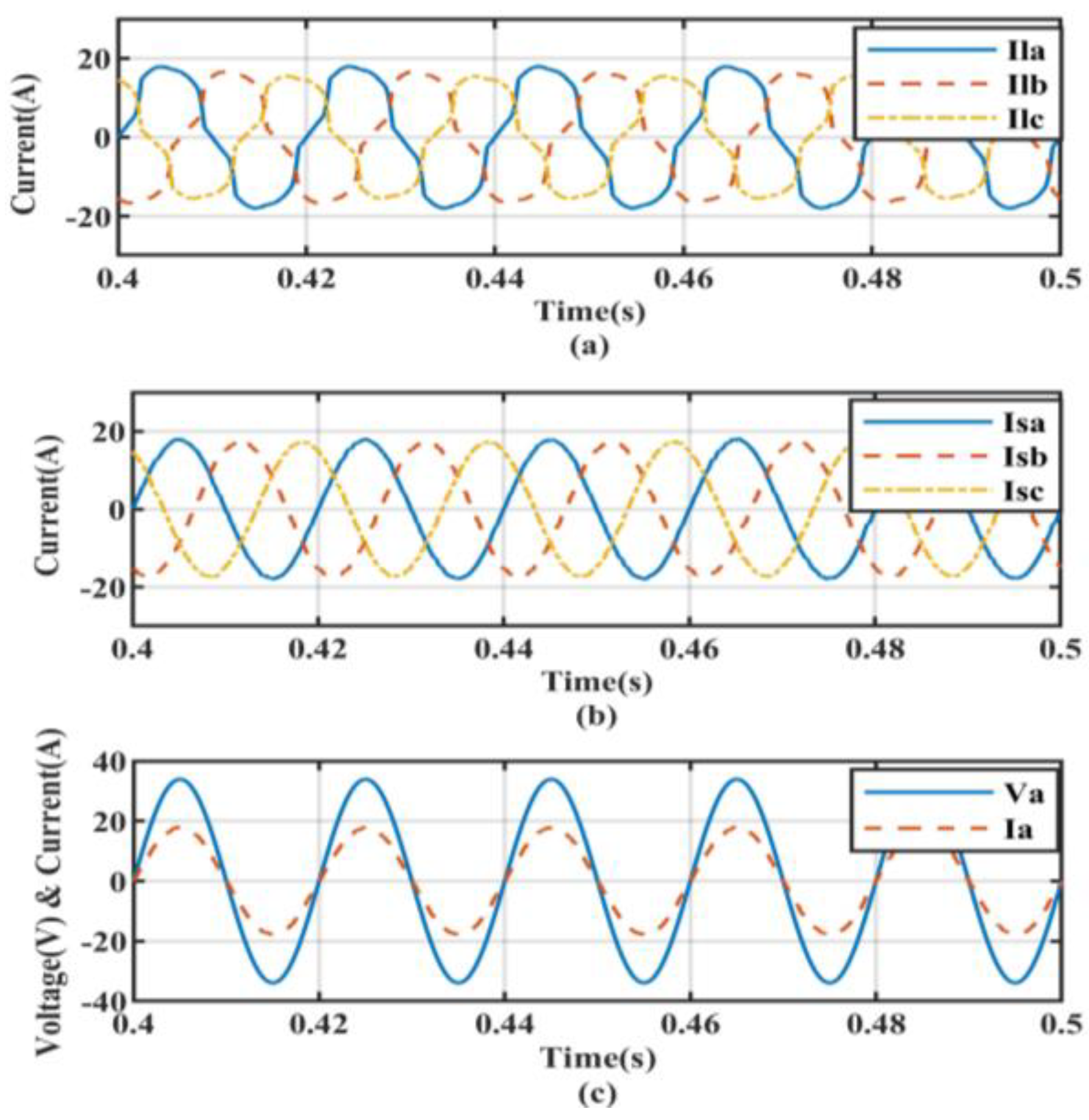
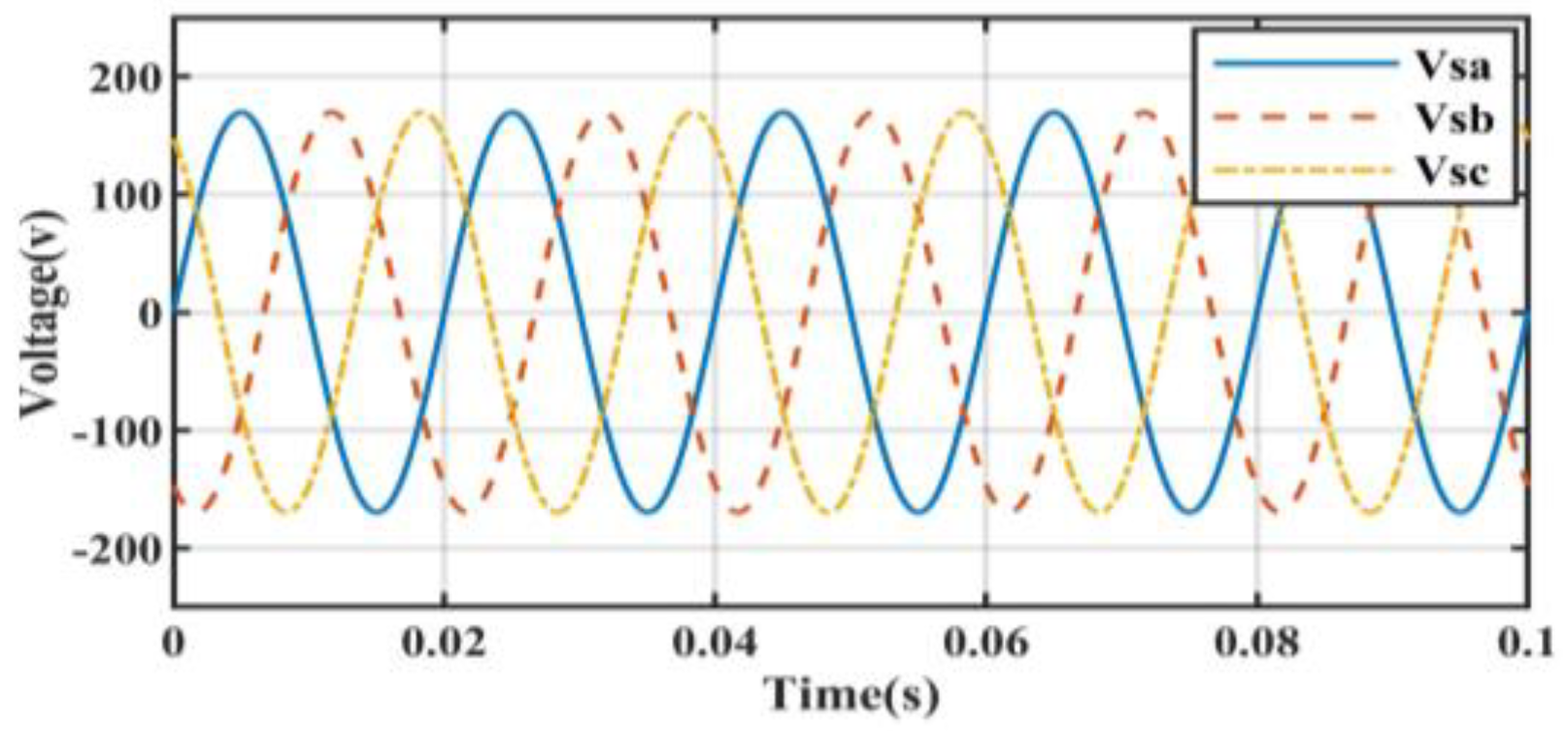

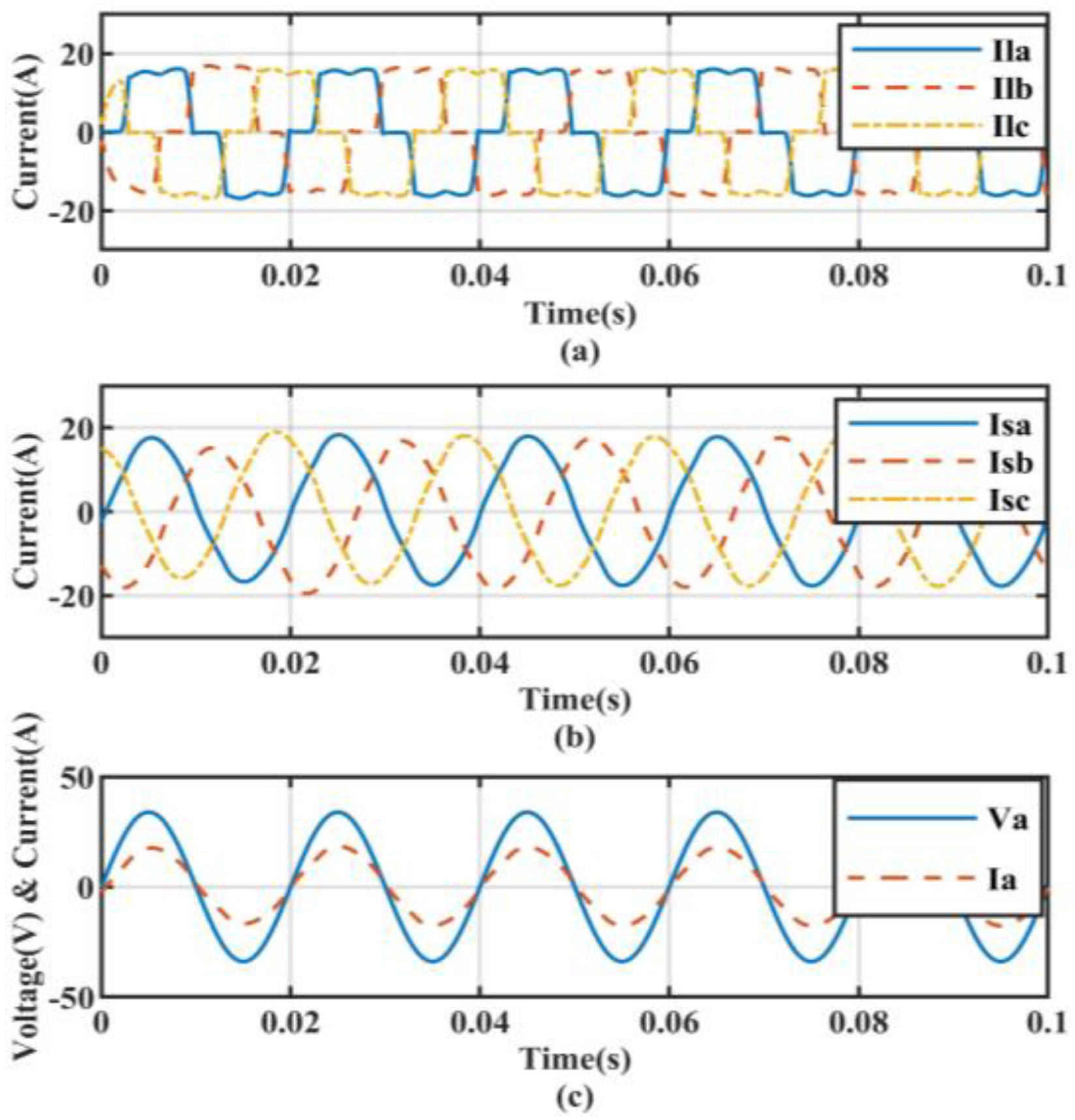



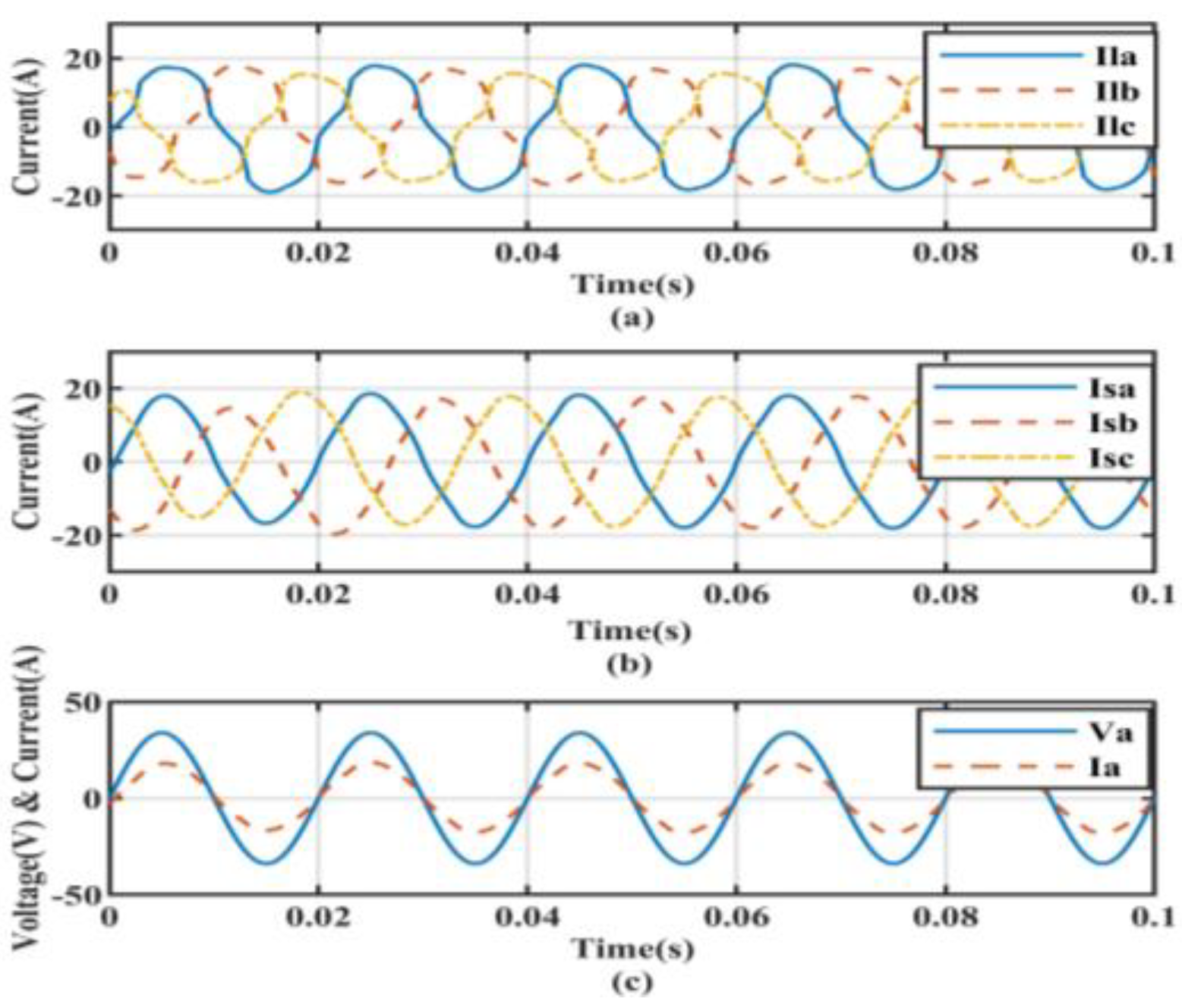
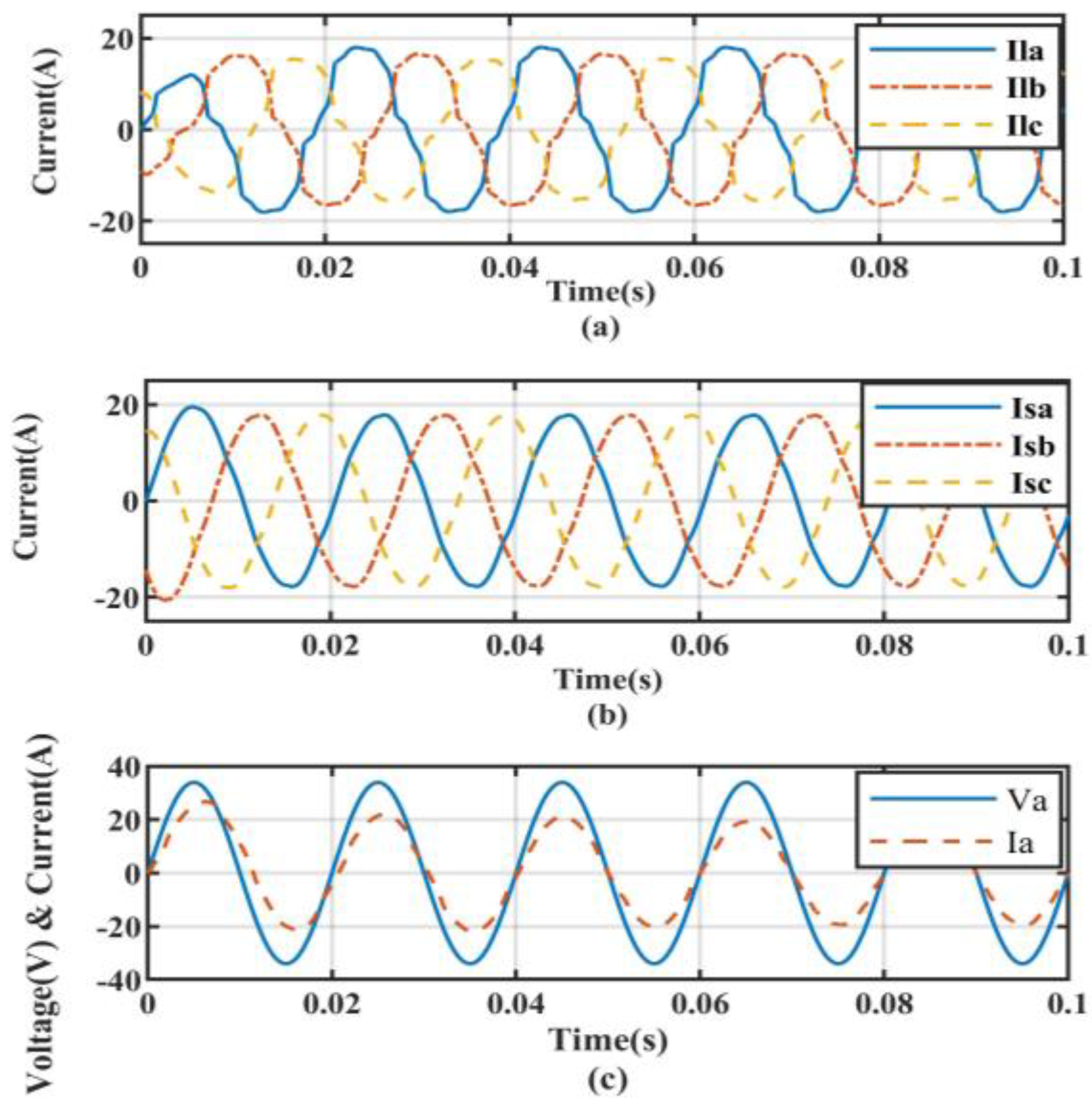
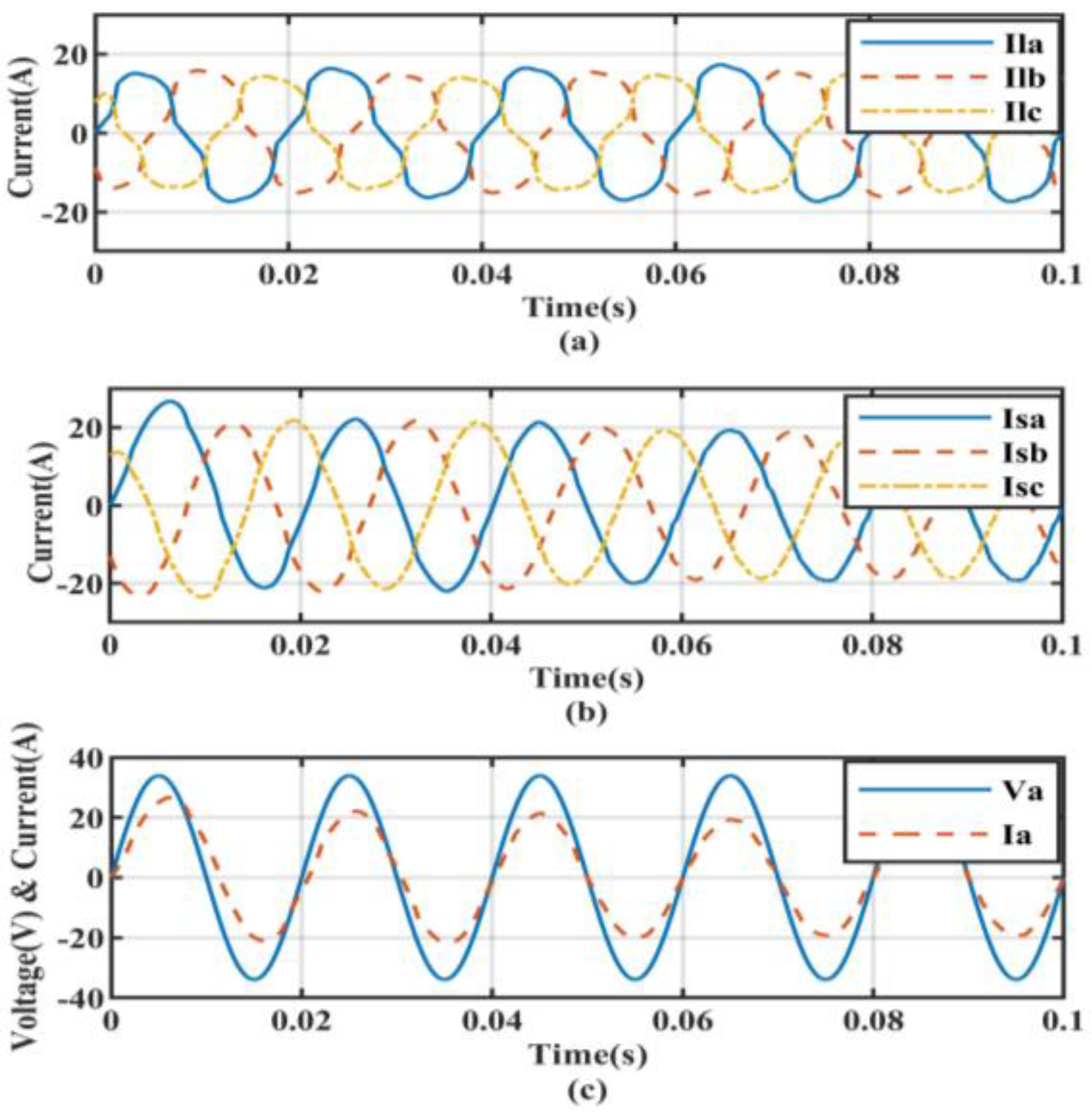
| Controller Type | Non-Linear Load without Compensation | Non-Linear Load Condition | Non-Linear Load with Linear Balanced Load Condition | Non-Linear Load with Linear UnBalanced Load Condition |
|---|---|---|---|---|
| SRFT | 28% | 4.1% | 3.5% | 4.2% |
| ILST | 28% | 2.9% | 2.4% | 2.61% |
| BP | 28% | 2.1% | 2.26% | 2.14% |
| ADALINE | 28% | 1.5% | 1.3% | 1.34% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mishra, S.; Rajashekaran, S.; Mohan, P.K.; Lokesh, S.M.; Ganiga, H.J.; Dash, S.K.; Roccotelli, M. Implementation of an ADALINE-Based Adaptive Control Strategy for an LCLC-PV-DSTATCOM in Distribution System for Power Quality Improvement. Energies 2023, 16, 323. https://doi.org/10.3390/en16010323
Mishra S, Rajashekaran S, Mohan PK, Lokesh SM, Ganiga HJ, Dash SK, Roccotelli M. Implementation of an ADALINE-Based Adaptive Control Strategy for an LCLC-PV-DSTATCOM in Distribution System for Power Quality Improvement. Energies. 2023; 16(1):323. https://doi.org/10.3390/en16010323
Chicago/Turabian StyleMishra, Soumya, Sreejith Rajashekaran, Pavan Kalyan Mohan, Spoorthi Mathad Lokesh, Hemalatha Jyothinagaravaishya Ganiga, Santanu Kumar Dash, and Michele Roccotelli. 2023. "Implementation of an ADALINE-Based Adaptive Control Strategy for an LCLC-PV-DSTATCOM in Distribution System for Power Quality Improvement" Energies 16, no. 1: 323. https://doi.org/10.3390/en16010323
APA StyleMishra, S., Rajashekaran, S., Mohan, P. K., Lokesh, S. M., Ganiga, H. J., Dash, S. K., & Roccotelli, M. (2023). Implementation of an ADALINE-Based Adaptive Control Strategy for an LCLC-PV-DSTATCOM in Distribution System for Power Quality Improvement. Energies, 16(1), 323. https://doi.org/10.3390/en16010323








