Aerodynamic Performance and Wake Characteristics Analysis of Archimedes Spiral Wind Turbine Rotors with Different Blade Angle
Abstract
1. Introduction
2. Numerical Methods
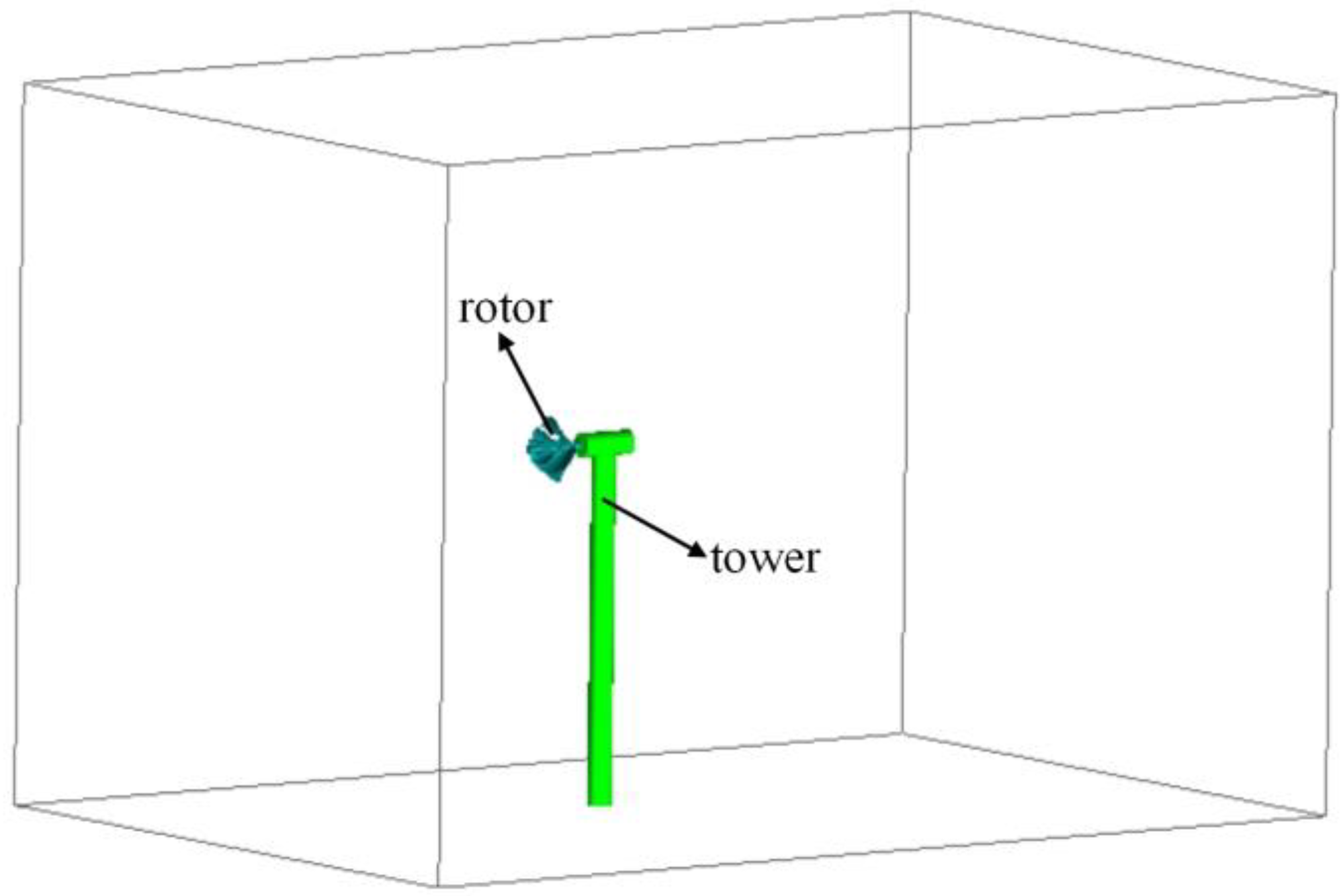
2.1. General Features
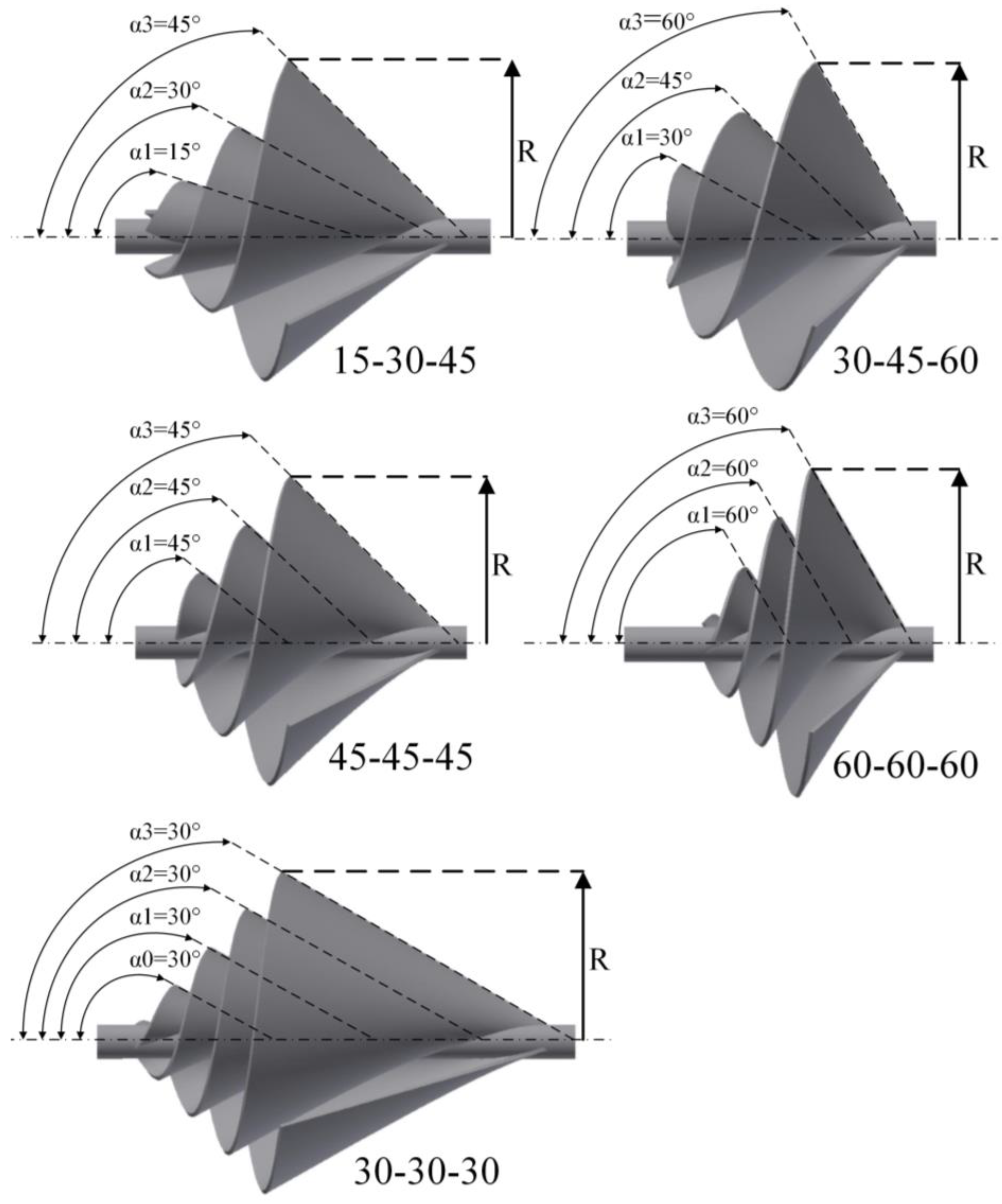
2.2. ASWTRotor Model
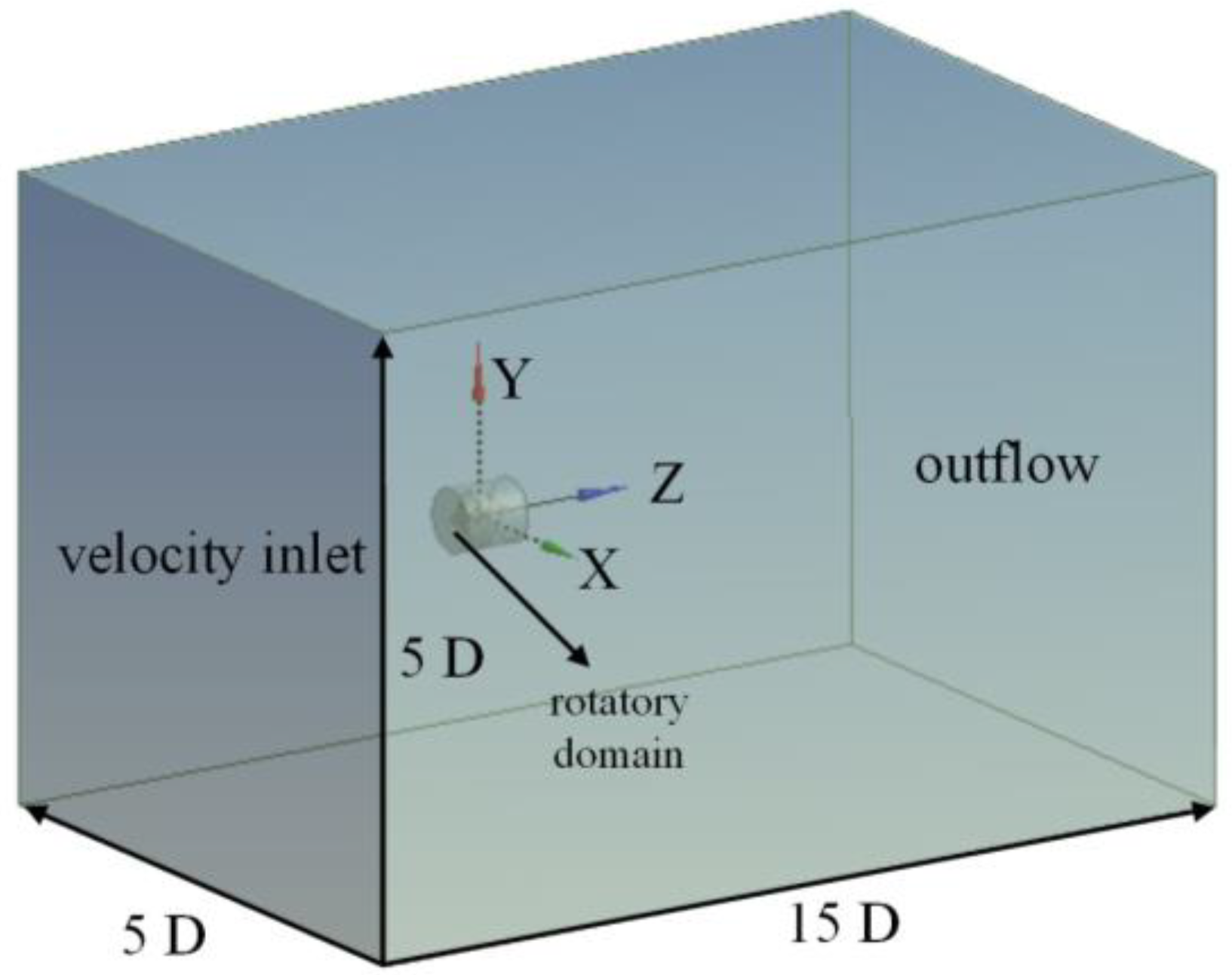
2.3. CFD Approach and Boundary Conditions
2.4. Mesh Generation and Calculation Setups
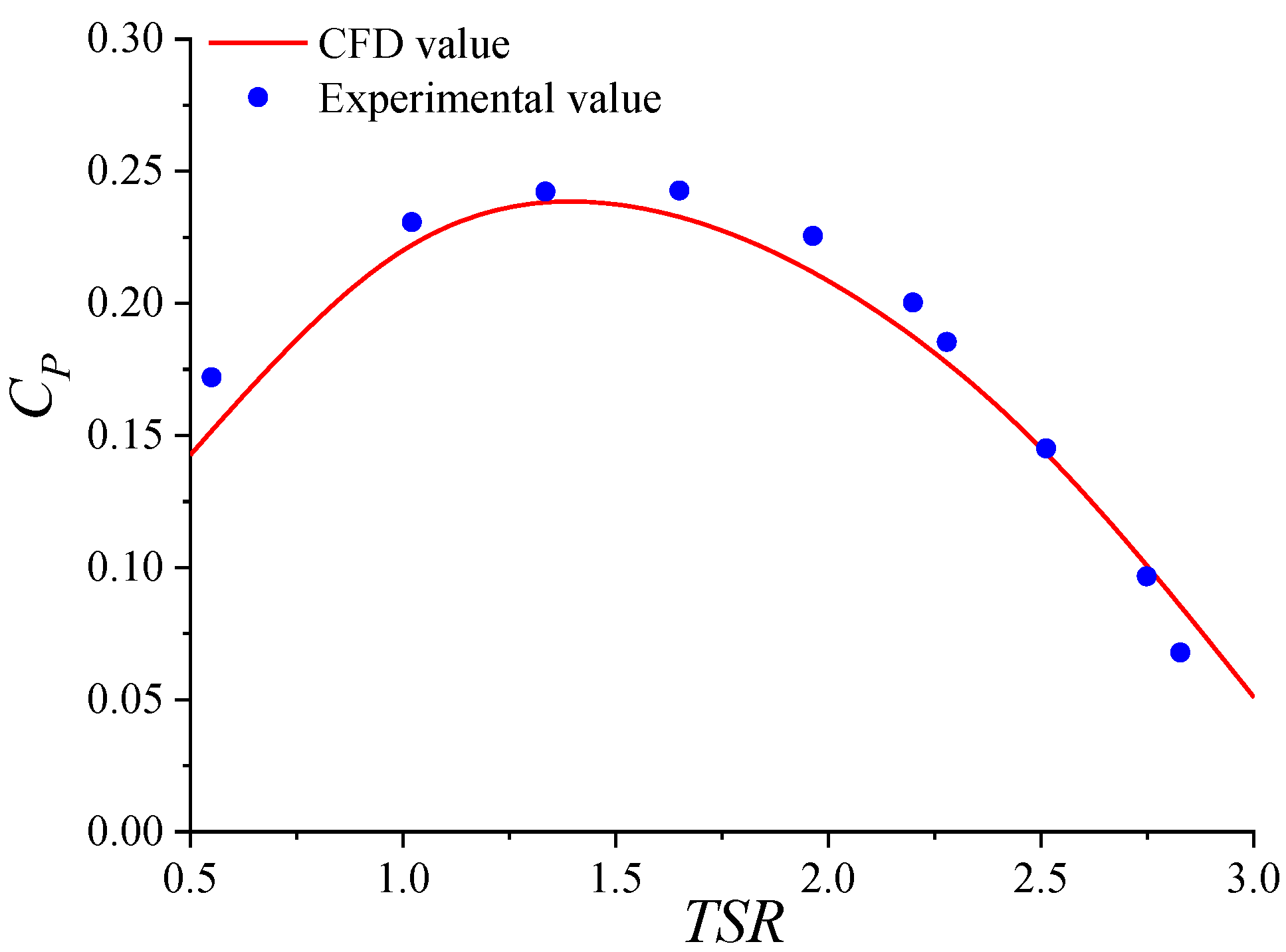
2.5. Numerical Model Validation
3. Results and Discussion
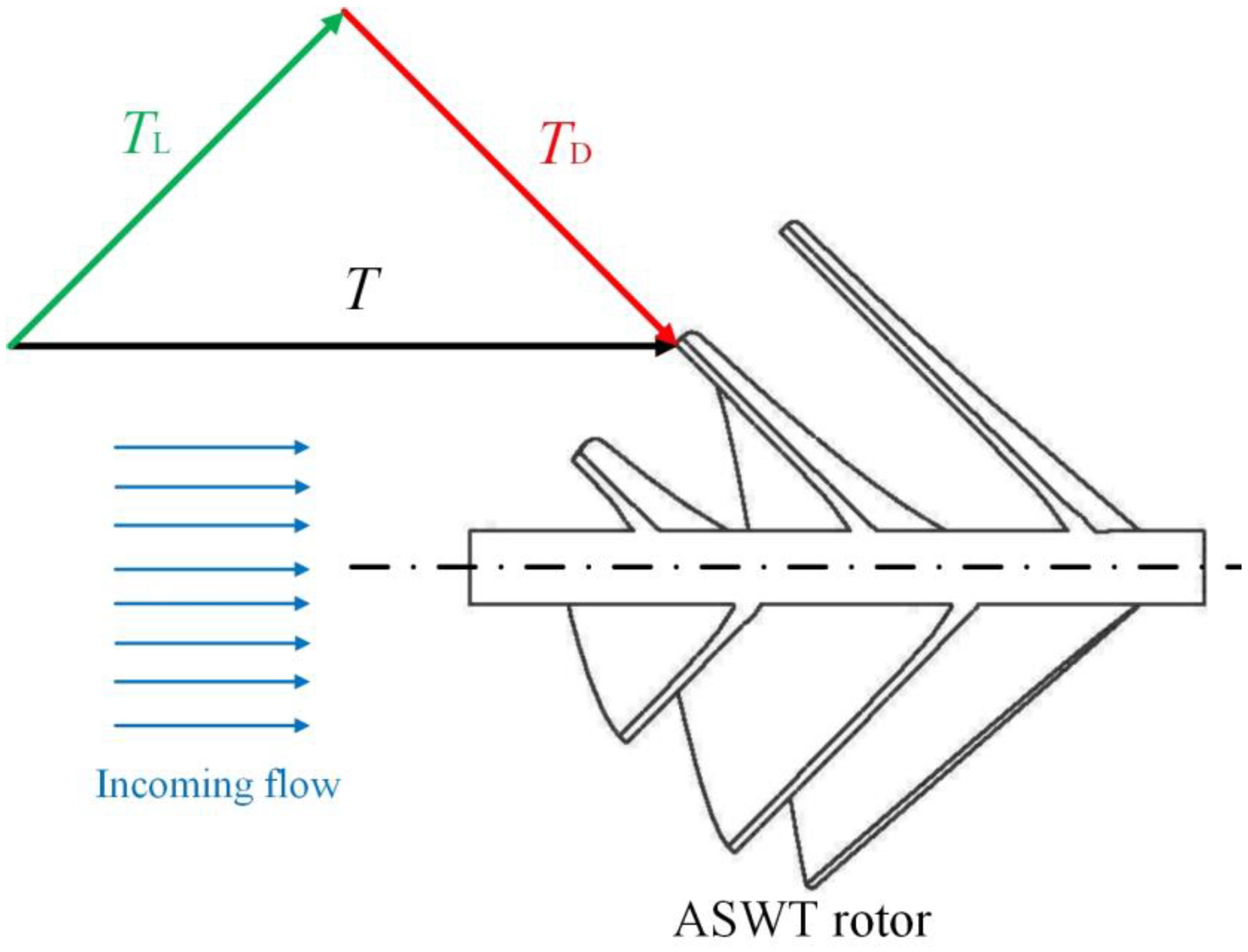
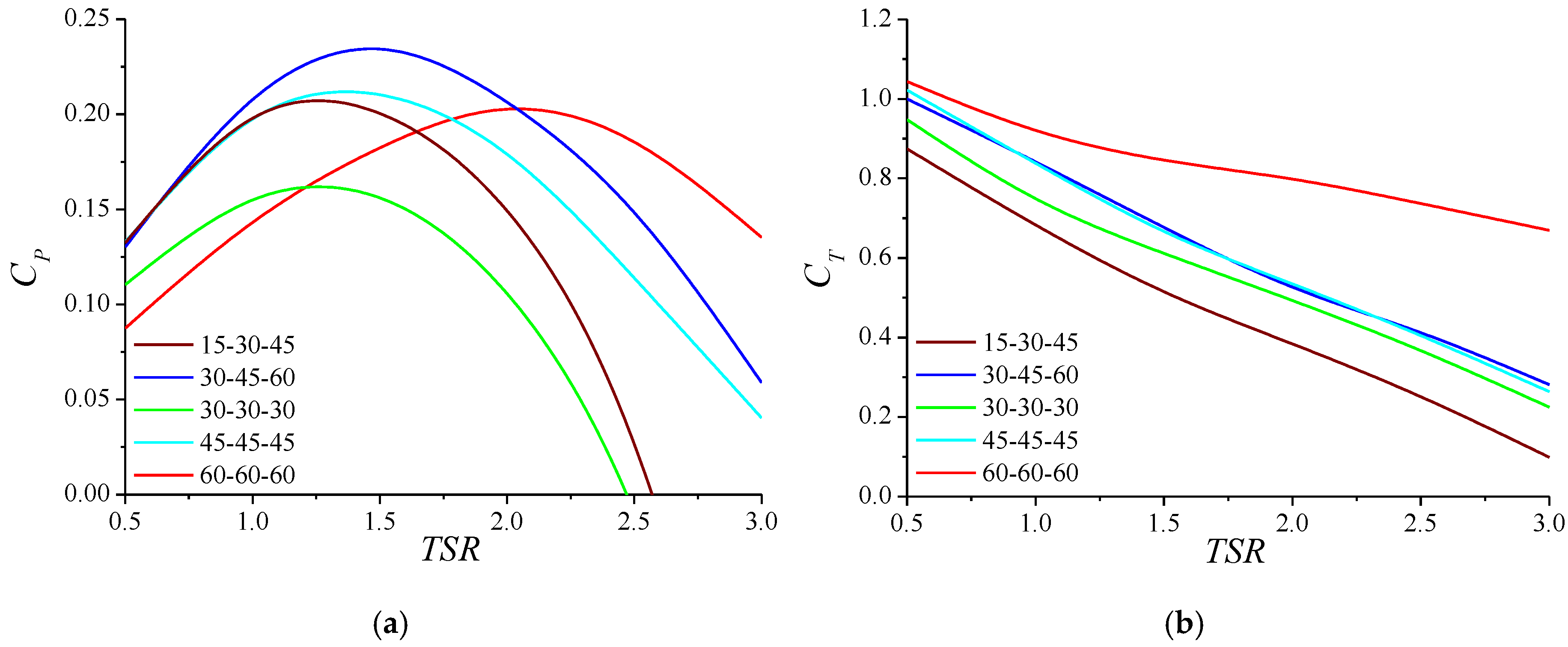
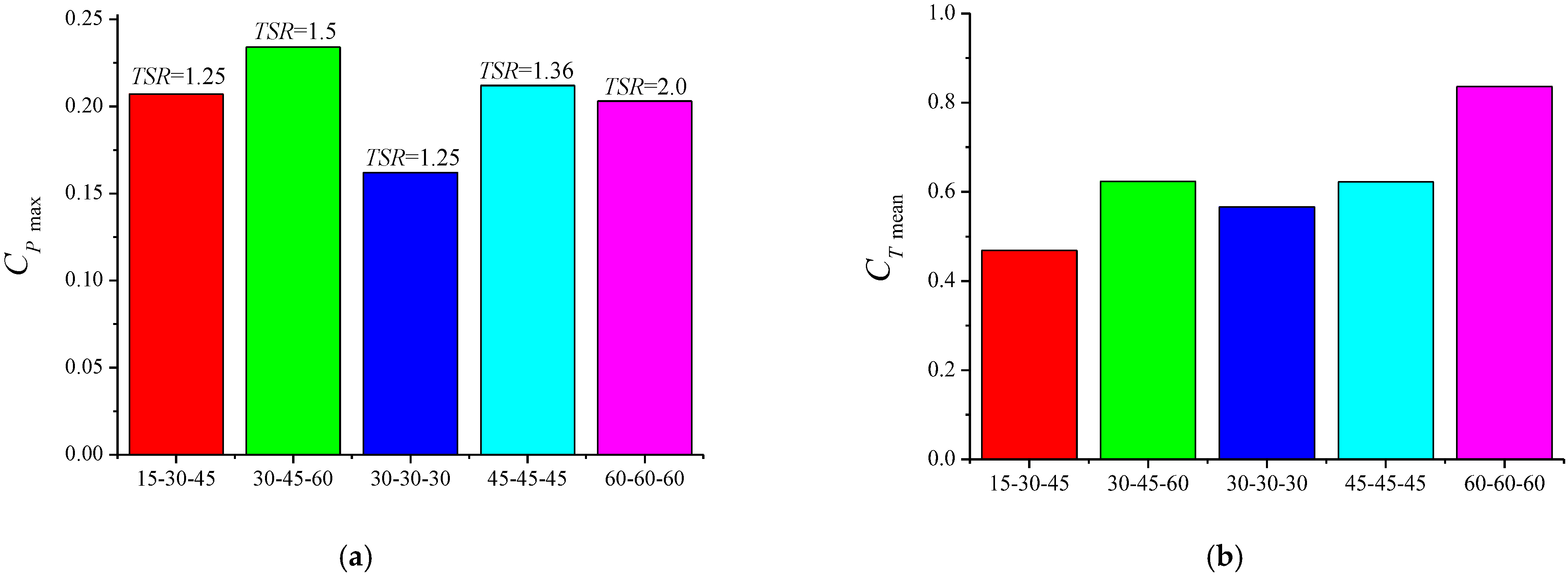
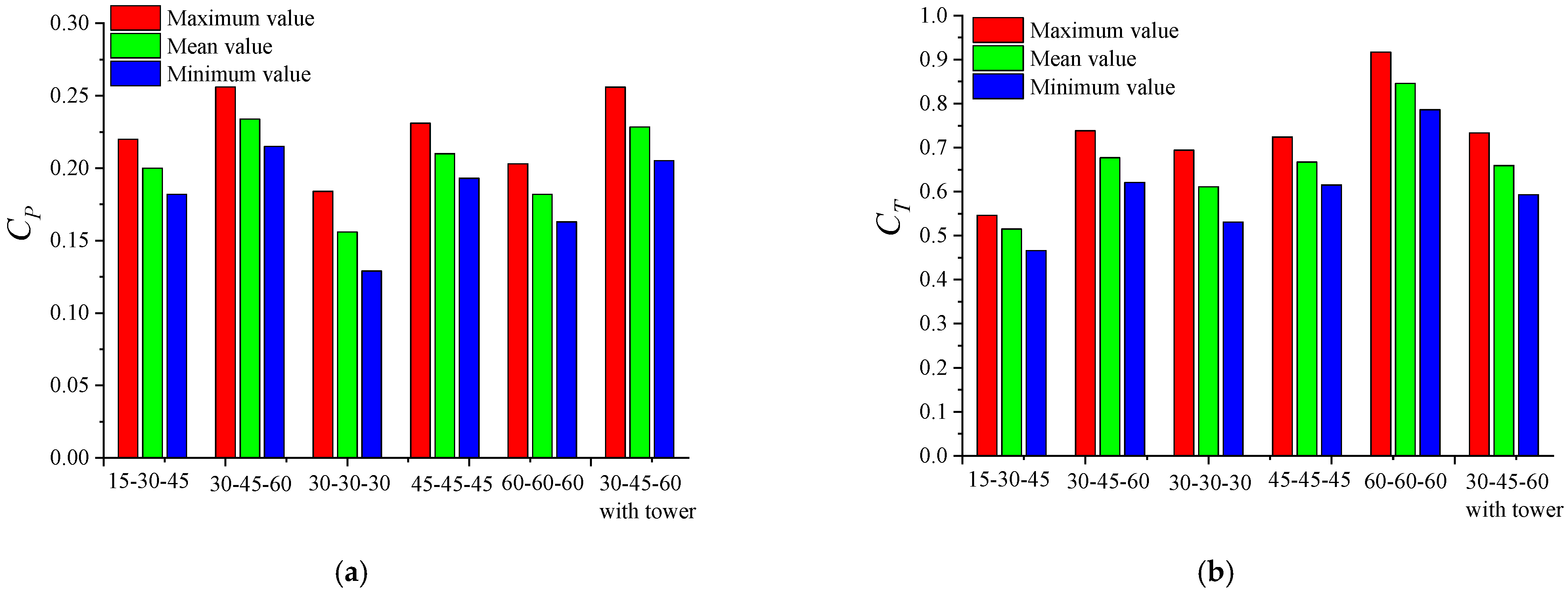
3.1. Power and Thrust
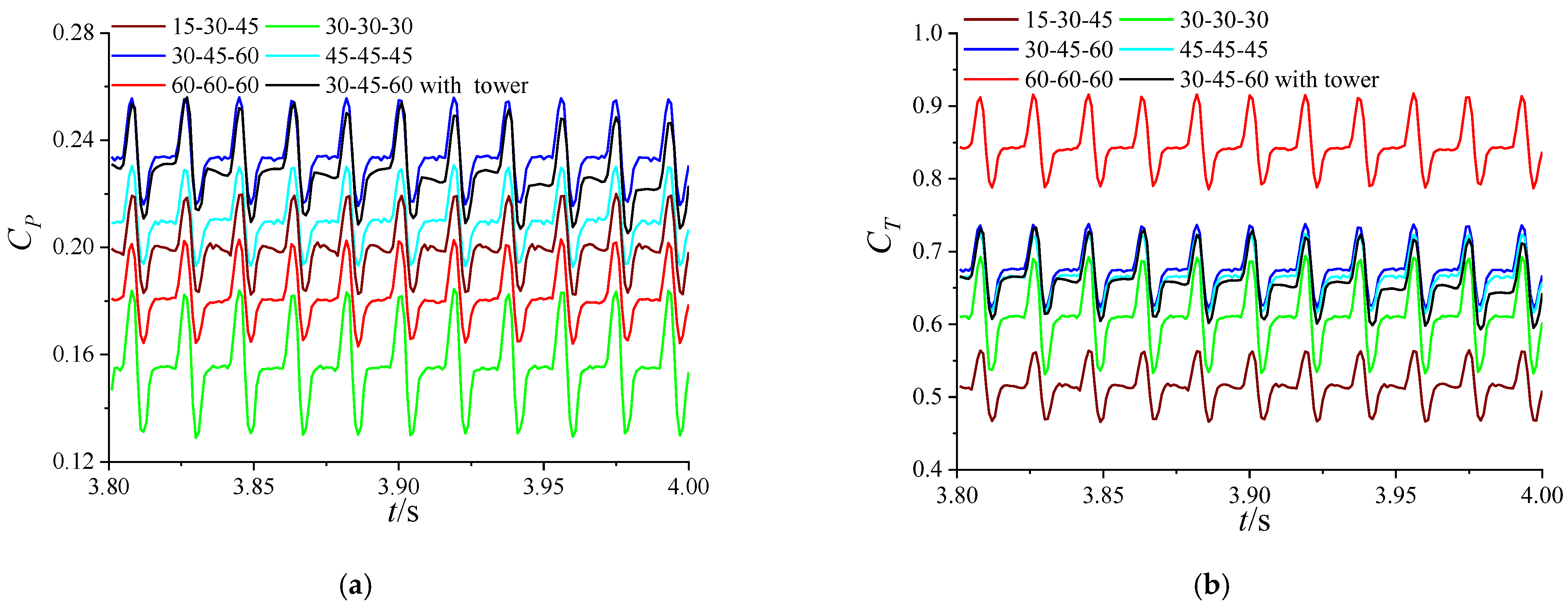
3.2. Performance Fluctuation Characteristics
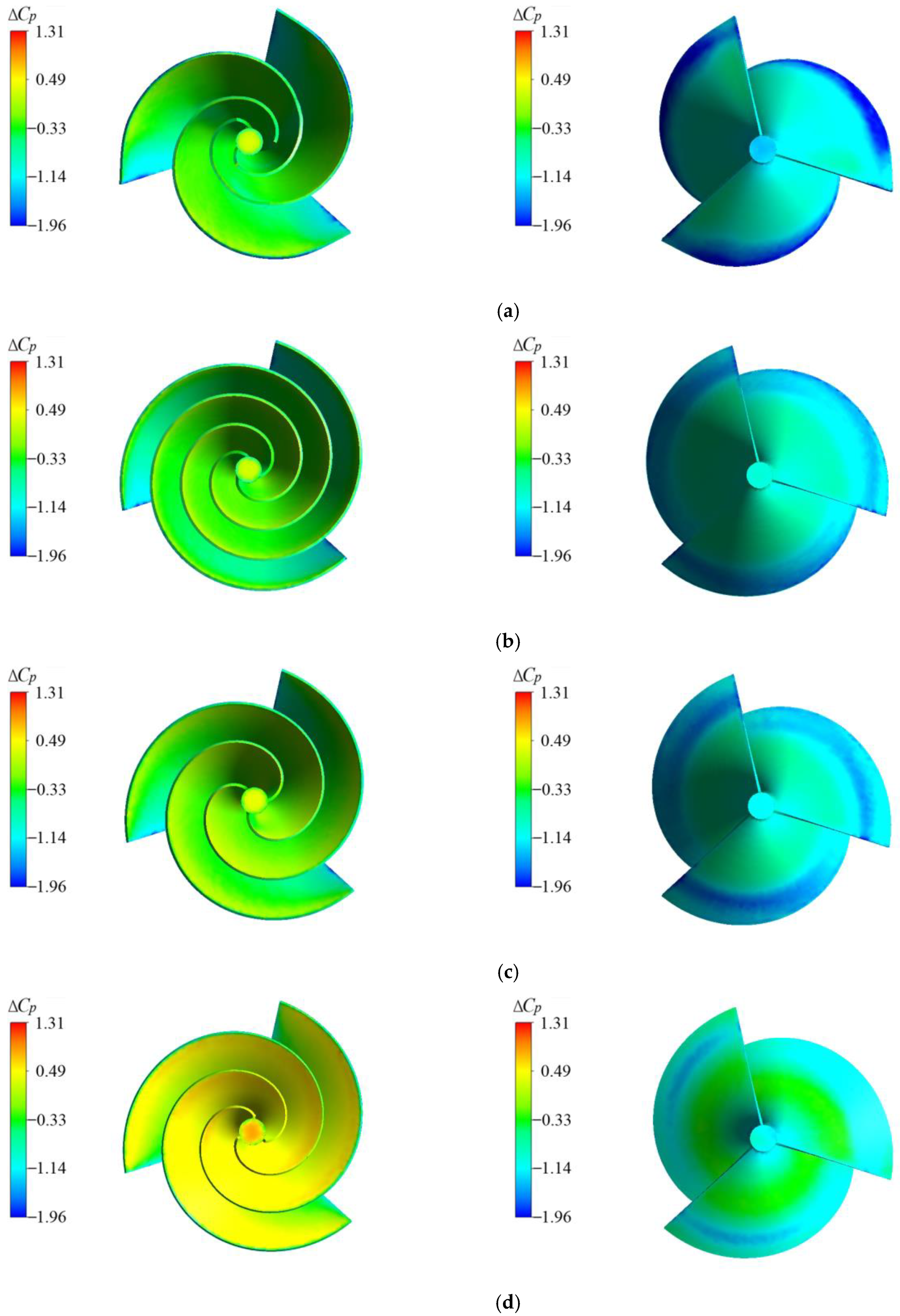
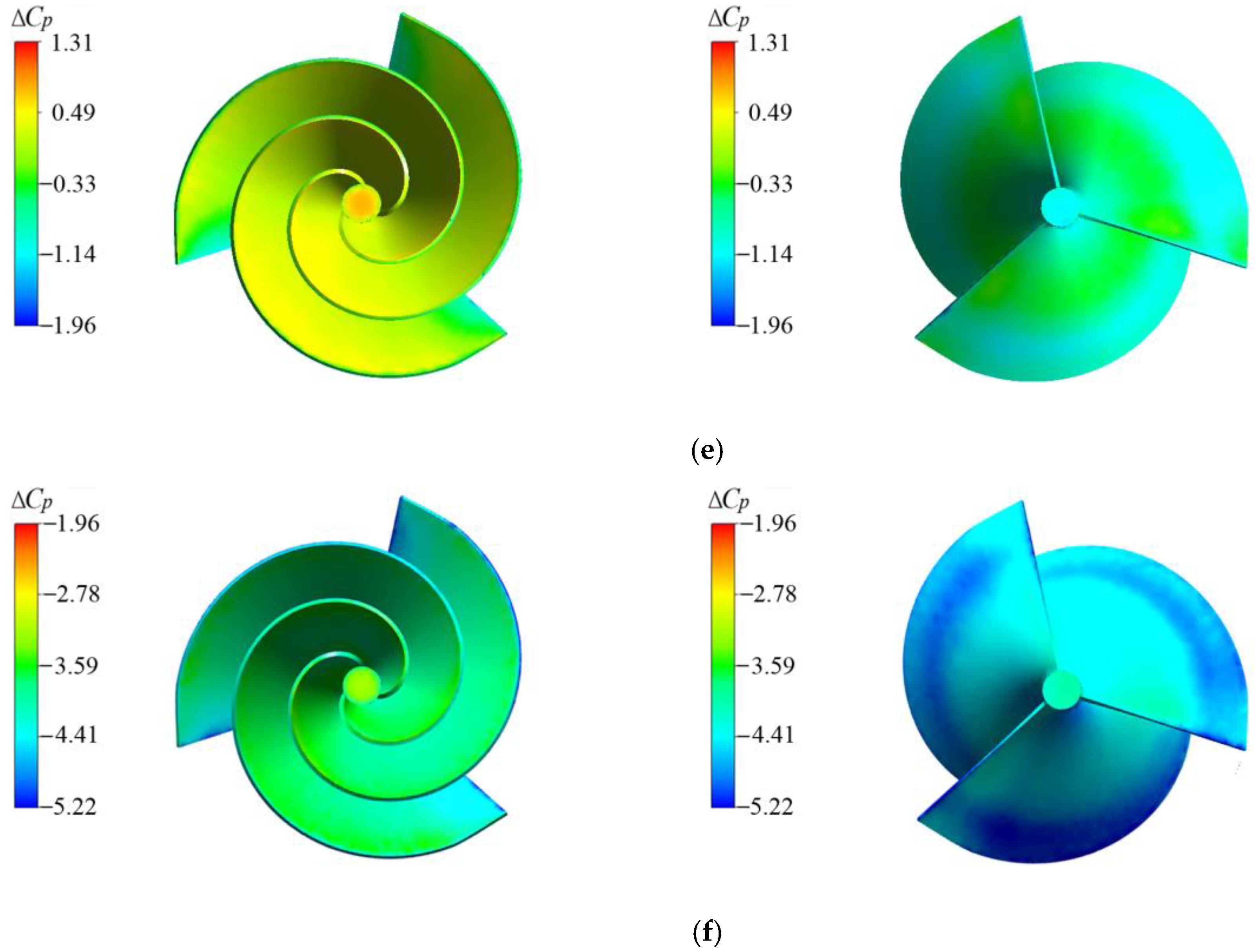
3.3. Pressure Distribution on Blade
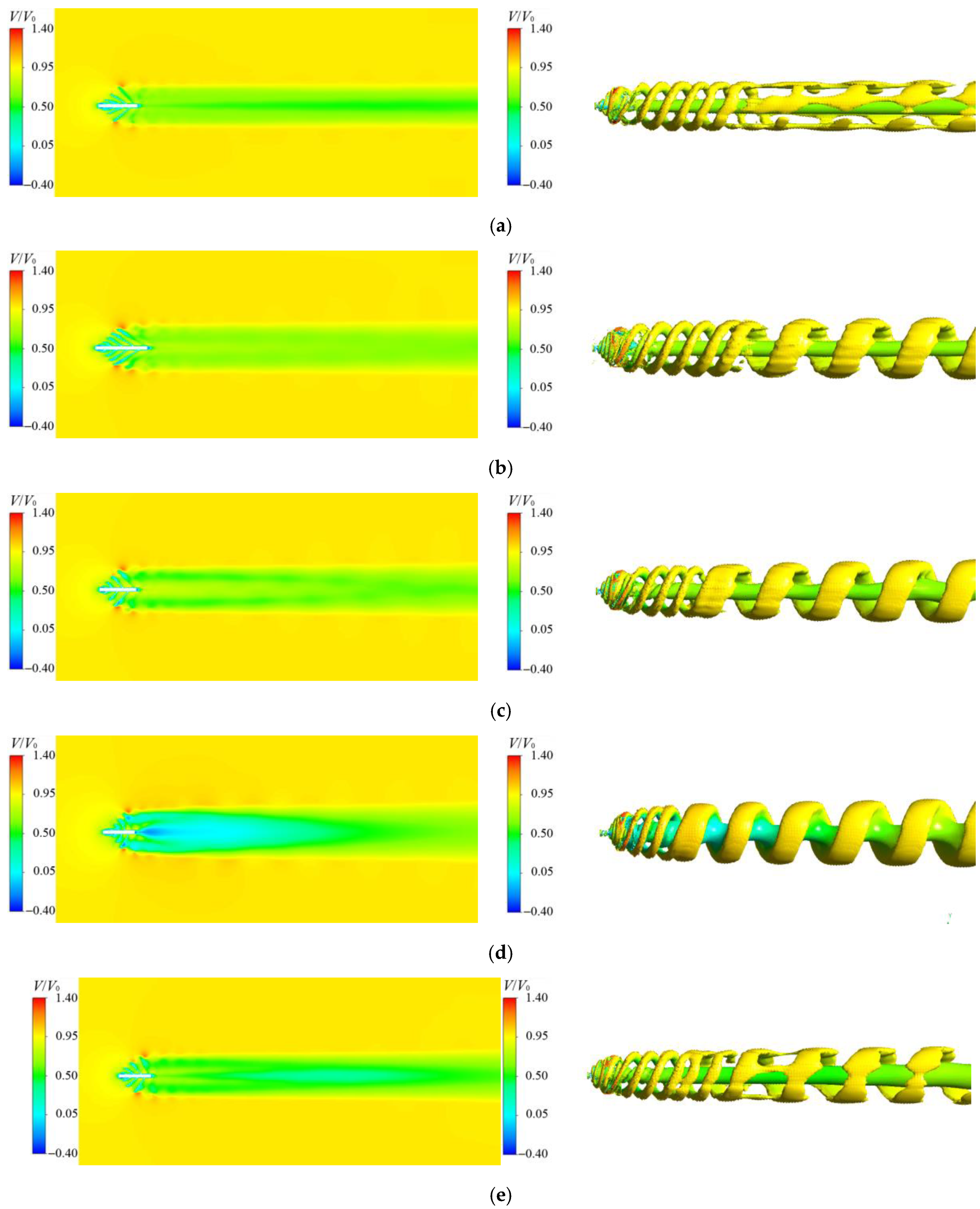
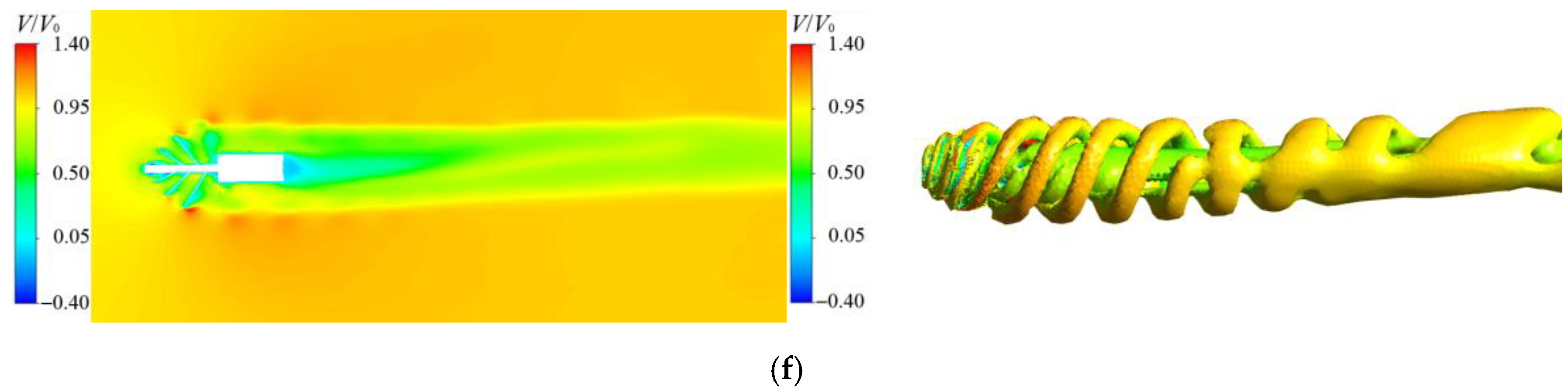
3.4. Velocity Contours and Vortex Structures
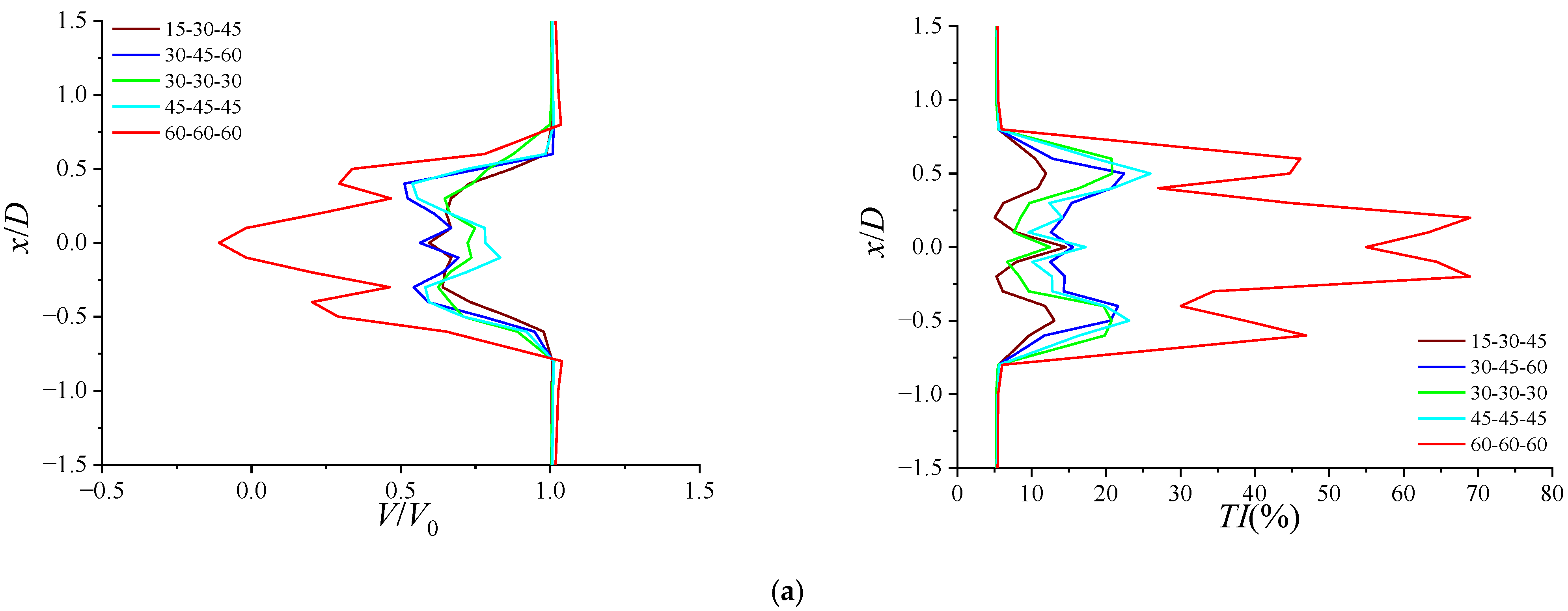
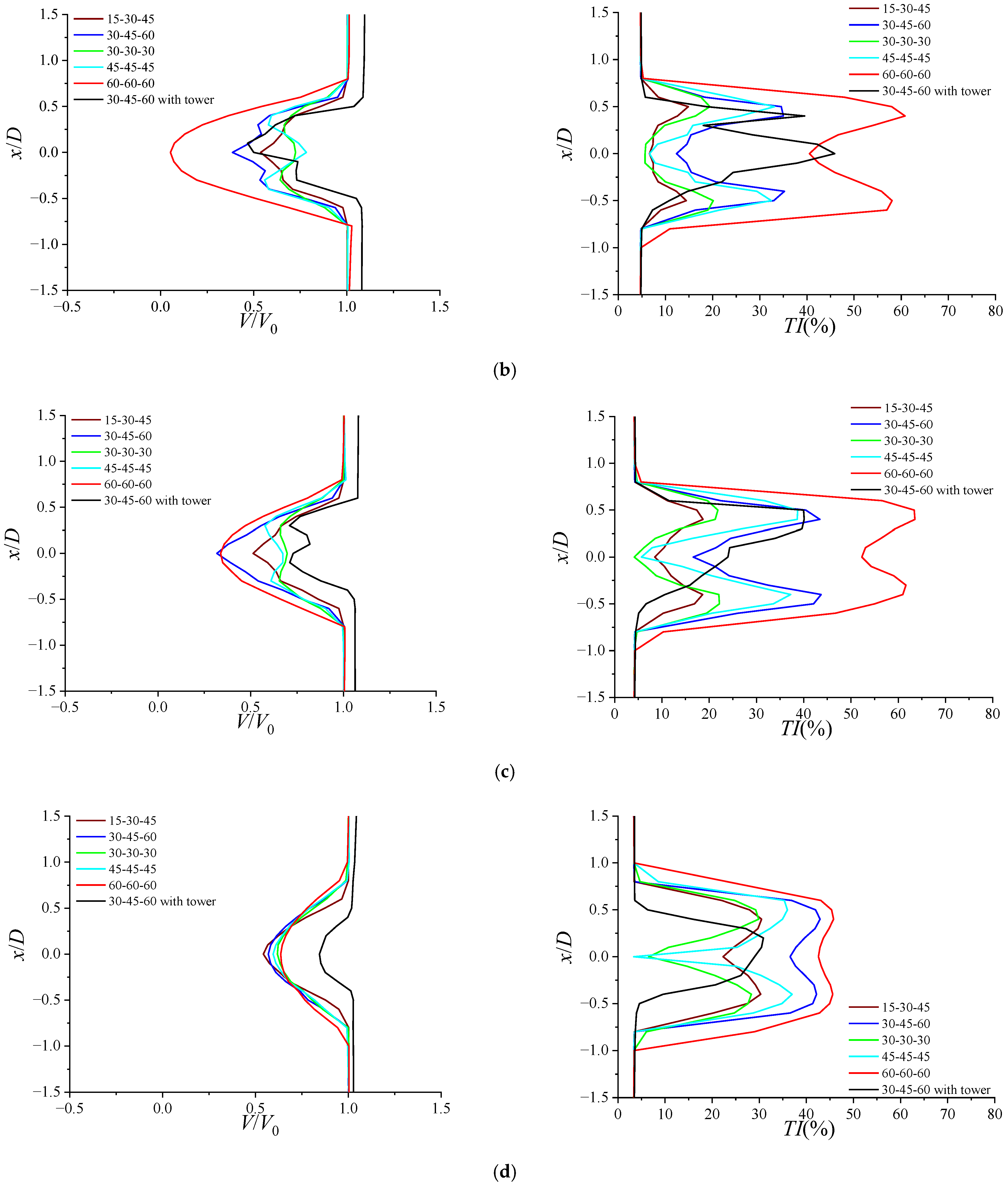
3.5. Velocity Profiles and Turbulence Intensity
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Enevoldsen, P.; Valentine, S.V.; Sovacool, B.K. Insights into wind sites: Critically assessing the innovation, cost, and performance dynamics of global wind energy development. Energy Policy 2018, 120, 1–7. [Google Scholar] [CrossRef]
- Rand, J.; Hoen, B. Thirty years of North American wind energy acceptance research: What have we learned? Energy Res. Soc. Sci. 2017, 29, 135–148. [Google Scholar] [CrossRef]
- Barthelmie, R.J.; Pryor, S.C. The impact of wind direction yaw angle on cliff flows. Wind Energy 2018, 21, 1254–1265. [Google Scholar] [CrossRef]
- Ciri, U.; Rotea, M.A.; Leonardi, S. Effect of the turbine scale on yaw control. Wind Energy 2018, 21, 1395–1405. [Google Scholar] [CrossRef]
- Bader, S.H.; Inguva, V.; Perot, J.B. Improving the efficiency of wind farms via wake manipulation. Wind Energy 2018, 21, 1239–1253. [Google Scholar] [CrossRef]
- Porté-Agel, F.; Bastankhah, M.; Shamsoddin, S. Wind-turbine and wind-farm flows: A review. Bound-Lay Meteorol. 2020, 174, 1–59. [Google Scholar] [CrossRef]
- Johari, M.K.; Jalil, M.; Shariff, M.F.M. Comparison of horizontal axis wind turbine (HAWT) and vertical axis wind turbine (VAWT). Int. J. Eng. Tech. 2018, 7, 74–80. [Google Scholar] [CrossRef]
- Karthikeyan, N.; Murugavel, K.K.; Kumar, S.A.; Rajakumar, S. Review of aerodynamic developments on small horizontal axis wind turbine blade. Renew. Sustain. Energy Rev. 2015, 42, 801–822. [Google Scholar] [CrossRef]
- Rehman, S.; Alam, M.M.; Alhems, L.M.; Rafique, M.M. Horizontal axis wind turbine blade design methodologies for efficiency enhancement—A review. Energies 2018, 11, 506. [Google Scholar] [CrossRef]
- Castellanos Bustamante, R.; Roman Messina, A.; Ramirez Gonzalez, M.; Calderon Guizar, G. Assessment of frequency performance by wind integration in a large-scale power system. Wind Energy 2018, 21, 1359–1371. [Google Scholar] [CrossRef]
- Murali, A.; Rajagopalan, R.G. Numerical simulation of multiple interacting wind turbines on a complex terrain. J. Wind Eng. Ind. Aerod. 2017, 162, 57–72. [Google Scholar] [CrossRef]
- Ji, H.S.; Baek, J.H.; Mieremet, R.; Kim, K.C. The aerodynamic performance study on small wind turbine with 500W class through wind tunnel experiments. Int. J. Renew. Energy Sources 2016, 1, 7–12. [Google Scholar]
- Rao, S.S.; Shanmukesh, K.; Naidu, M.K.; Kalla, P. Design and Analysis of Archimedes Aero-Foil Wind Turbine Blade for Light and Moderate Wind Speeds. Int. J. Recent Technol. Mech. Electr. Eng. 2018, 5, 1–5. [Google Scholar]
- Kim, K.; Ji, K.; Kim, H.Y.; Lu, Q.; Baek, J. Experimental and Numerical Study of the Aerodynamic Characteristics of an Archimedes Spiral Wind Turbine Blade. Energies 2014, 7, 7893–7914. [Google Scholar] [CrossRef]
- Safidari, A.; Kim, K.C. Aerodynamic and Structural Evaluation of Horizontal Archimedes Spiral Wind Turbine. J. Clean Energy Technol. 2015, 3, 34–38. [Google Scholar] [CrossRef]
- Lu, Q.; Li, Q.; Kim, Y.K.; Kim, K.C. A study on design and aerodynamic characteristics of a spiral-type wind turbine blade. J. Korean Soc. Vis. 2012, 10, 27–33. [Google Scholar]
- Jang, H.; Kim, D.; Hwang, Y.; Paek, I.; Kim, S.; Baek, J. Analysis of Archimedes spiral wind turbine performance by simulation and field test. Energies 2019, 12, 4624. [Google Scholar] [CrossRef]
- Nawar, M.A.; Hameed, H.A.; Ramadan, A.; Attai, Y.A.; Mohamed, M.H. Experimental and numerical investigations of the blade design effect on Archimedes Spiral Wind Turbine performance. Energy 2021, 223, 120051. [Google Scholar] [CrossRef]
- Kamal, A.M.; Nawar, M.A.; Attai, Y.A.; Mohamed, M.H. Archimedes Spiral Wind Turbine performance study using different aerofoiled blade profiles: Experimental and numerical analyses. Energy 2023, 262, 125567. [Google Scholar] [CrossRef]
- Kamal, A.M.; Nawar, M.A.; Attai, Y.A.; Mohamed, M.H. Blade design effect on Archimedes Spiral Wind Turbine performance: Experimental and numerical evaluations. Energy 2022, 250, 123892. [Google Scholar] [CrossRef]
- Sapkota, S.; Bhattarai, A.; Bashyal, H.P.; Nepal, U. Design, CFD analysis and modelling of archimedean-spiral type wind turbine. Proc. IOE Grad.Conf. 2019, 6, 563–571. [Google Scholar]
- Mustafa, A.T.; Jaleel, H.A. A comparison study between Archimedes spiral turbine and propeller turbine with wind attack angle effect. AIP Conf. Proc. 2020, 2213, 020058. [Google Scholar]
- Ozeh, M.; Mishra, A.; Wang, X. Mini wind turbine for small scale power generation and storage (Archimedes wind turbine model). In Proceedings of the ASME International Mechanical Engineering Congress and Exposition; American Society of Mechanical Engineers: Pittsburgh, PA, USA, 2018. [Google Scholar]
- Refaie, A.G.; Hameed, H.A.; Nawar, M.A.; Attai, Y.A.; Mohamed, M.H. Comparative investigation of the aerodynamic performance for several Shrouded Archimedes Spiral Wind Turbines. Energy 2022, 239, 122295. [Google Scholar] [CrossRef]
- Hameed, H.S.A.; Hashem, I.; Nawar, M.A.; Attai, Y.A.; Mohamed, M.H. Shape optimization of a shrouded Archimedean-spiral type wind turbine for small-scale applications. Energy 2023, 263, 125809. [Google Scholar] [CrossRef]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Rocha, P.C.; Rocha, H.B.; Carneiro, F.M.; Da Silva, M.V.; Bueno, A.V. k–ω SST (shear stress transport) turbulence model calibration: A case study on a small scale horizontal axis wind turbine. Energy 2014, 65, 412–418. [Google Scholar] [CrossRef]
- Rezaeiha, A.; Montazeri, H.; Blocken, B. On the accuracy of turbulence models for CFD simulations of vertical axis wind turbines. Energy 2019, 180, 838–857. [Google Scholar] [CrossRef]
- Song, K.; Yang, B. A Comparative Study on the Hydrodynamic-Energy Loss Characteristics between a Ducted Turbine and a Shaftless Ducted Turbine. J. Mar. Sci. Eng. 2021, 9, 930. [Google Scholar] [CrossRef]
- Song, K.; Kang, Y. A Numerical Performance Analysis of a Rim-Driven Turbine in Real Flow Conditions. J. Mar. Sci. Eng. 2022, 10, 1185. [Google Scholar] [CrossRef]
- Bai, C.J.; Wang, W.C. Review of computational and experimental approaches to analysis of aerodynamic performance in horizontal-axis wind turbines (HAWTs). Renew. Sustain. Energy Rev. 2016, 63, 506–519. [Google Scholar] [CrossRef]
- Mu, Z.; Tong, G.; Xiao, Z.; Deng, Q.; Feng, F.; Li, Y.; Arne, G.V. Study on aerodynamic characteristics of a Savonius wind turbine with a modified blade. Energies 2022, 15, 6661. [Google Scholar] [CrossRef]
- Howell, R.; Qin, N.; Edwards, J.; Durrani, N. Wind tunnel and numerical study of a small vertical axis wind turbine. Renew. Energy 2010, 35, 412–422. [Google Scholar] [CrossRef]
- Arabgolarcheh, A.; Jannesarahmadi, S.; Benini, E. Modeling of near wake characteristics in floating offshore wind turbines using an actuator line method. Renew. Energy 2022, 185, 871–887. [Google Scholar] [CrossRef]
- Fang, Y.; Li, G.; Duan, L.; Han, Z.; Zhao, Y. Effect of surge motion on rotor aerodynamics and wake characteristics of a floating horizontal-axis wind turbine. Energy 2021, 218, 119519. [Google Scholar] [CrossRef]
- Lee, H.; Lee, D.J. Effects of platform motions on aerodynamic performance and unsteady wake evolution of a floating offshore wind turbine. Renew. Energy 2019, 143, 9–23. [Google Scholar] [CrossRef]
- Kabir, I.F.S.A.; Ng, E.Y.K. Effect of different atmospheric boundary layers on the wake characteristics of NREL phase VI wind turbine. Renew. Energy 2019, 130, 1185–1197. [Google Scholar] [CrossRef]
- Bangga, G.; Lutz, T.; Jost, E.; Krämer, E. CFD studies on rotational augmentation at the inboard sections of a 10 MW wind turbine rotor. J. Renew. Sustain. Energy 2017, 9, 023304. [Google Scholar] [CrossRef]
- Bangga, G. Three-Dimensional Flow in the Root Region of Wind Turbine Rotors; Kassel University Press GmbH: Kassel, Germany, 2018. [Google Scholar]
- Schreck, S.; Robinson, M. Boundary layer state and flow field structure underlying rotational augmentation of blade aerodynamic response. J. Sol. Energy Eng. 2003, 125, 448–456. [Google Scholar] [CrossRef]
- Bangga, G.; Hutomo, G.; Wiranegara, R.; Sasongko, H. Numerical study on a single bladed vertical axis wind turbine under dynamic stall. J. Mech. Sci. Technol. 2017, 31, 261–267. [Google Scholar] [CrossRef]
- Bangga, G. Numerical studies on dynamic stall characteristics of a wind turbine airfoil. J. Mech. Sci. Technol. 2019, 33, 1257–1262. [Google Scholar] [CrossRef]
- Fujisawa, N.; Shibuya, S. Observations of dynamic stall on Darrieus wind turbine blades. J. Wind Eng. Ind. Aerodyn. 2001, 89, 201–214. [Google Scholar] [CrossRef]
- Simão Ferreira, C.; Van Kuik, G.; Van Bussel, G.; Scarano, F. Visualization by PIV of dynamic stall on a vertical axis wind turbine. Exp. Fluids 2009, 46, 97–108. [Google Scholar] [CrossRef]




| Mesh Density | Total Cells | ||
|---|---|---|---|
| Coarse | 3,213,540 | 0.229 | 0.673 |
| Medium | 5,429,876 | 0.234 | 0.677 |
| Fine | 8,327,596 | 0.234 | 0.680 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, K.; Huan, H.; Kang, Y. Aerodynamic Performance and Wake Characteristics Analysis of Archimedes Spiral Wind Turbine Rotors with Different Blade Angle. Energies 2023, 16, 385. https://doi.org/10.3390/en16010385
Song K, Huan H, Kang Y. Aerodynamic Performance and Wake Characteristics Analysis of Archimedes Spiral Wind Turbine Rotors with Different Blade Angle. Energies. 2023; 16(1):385. https://doi.org/10.3390/en16010385
Chicago/Turabian StyleSong, Ke, Huiting Huan, and Yuchi Kang. 2023. "Aerodynamic Performance and Wake Characteristics Analysis of Archimedes Spiral Wind Turbine Rotors with Different Blade Angle" Energies 16, no. 1: 385. https://doi.org/10.3390/en16010385
APA StyleSong, K., Huan, H., & Kang, Y. (2023). Aerodynamic Performance and Wake Characteristics Analysis of Archimedes Spiral Wind Turbine Rotors with Different Blade Angle. Energies, 16(1), 385. https://doi.org/10.3390/en16010385







