High Step-Up Three-Level Soft Switching DC-DC Converter for Photovoltaic Generation Systems
Abstract
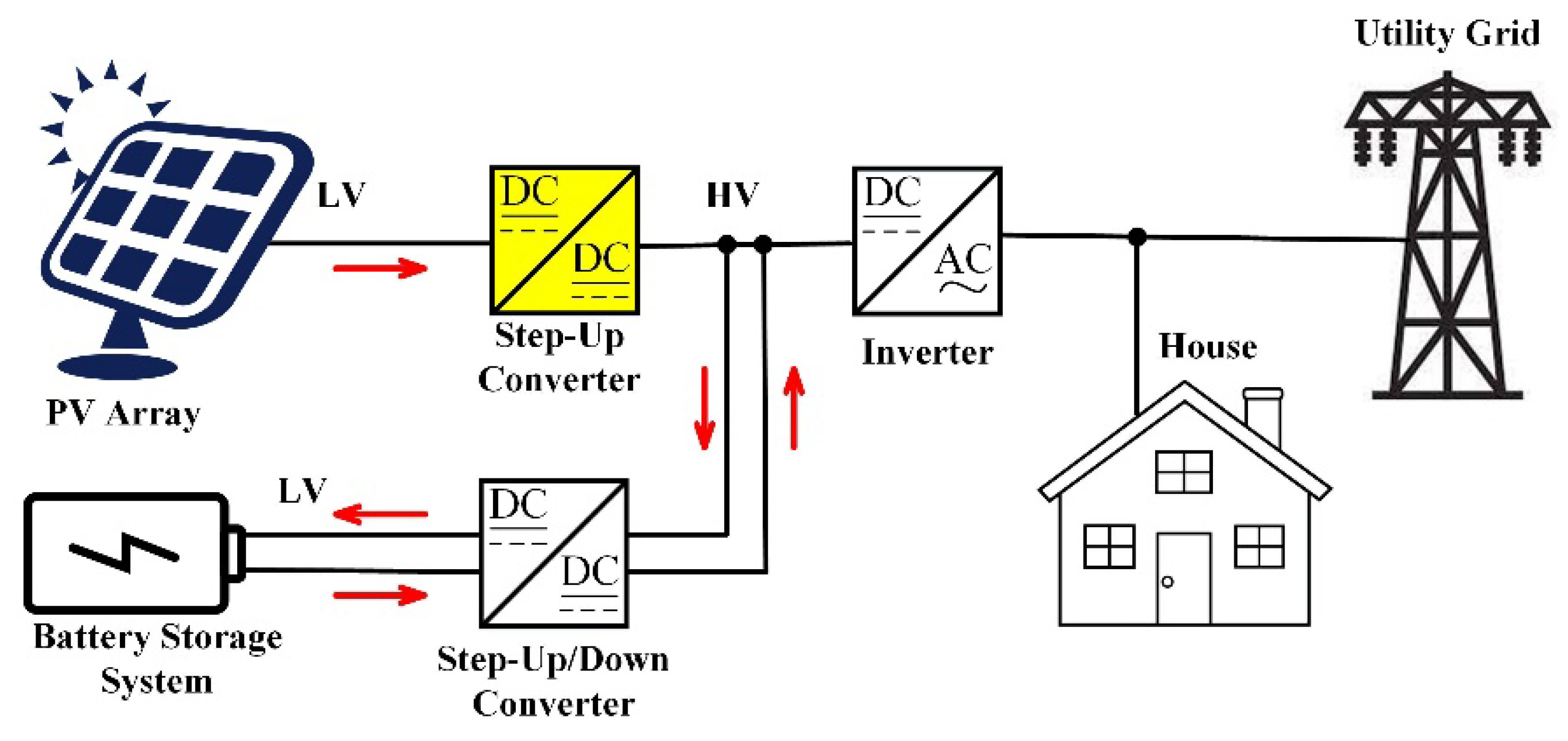
:1. Introduction
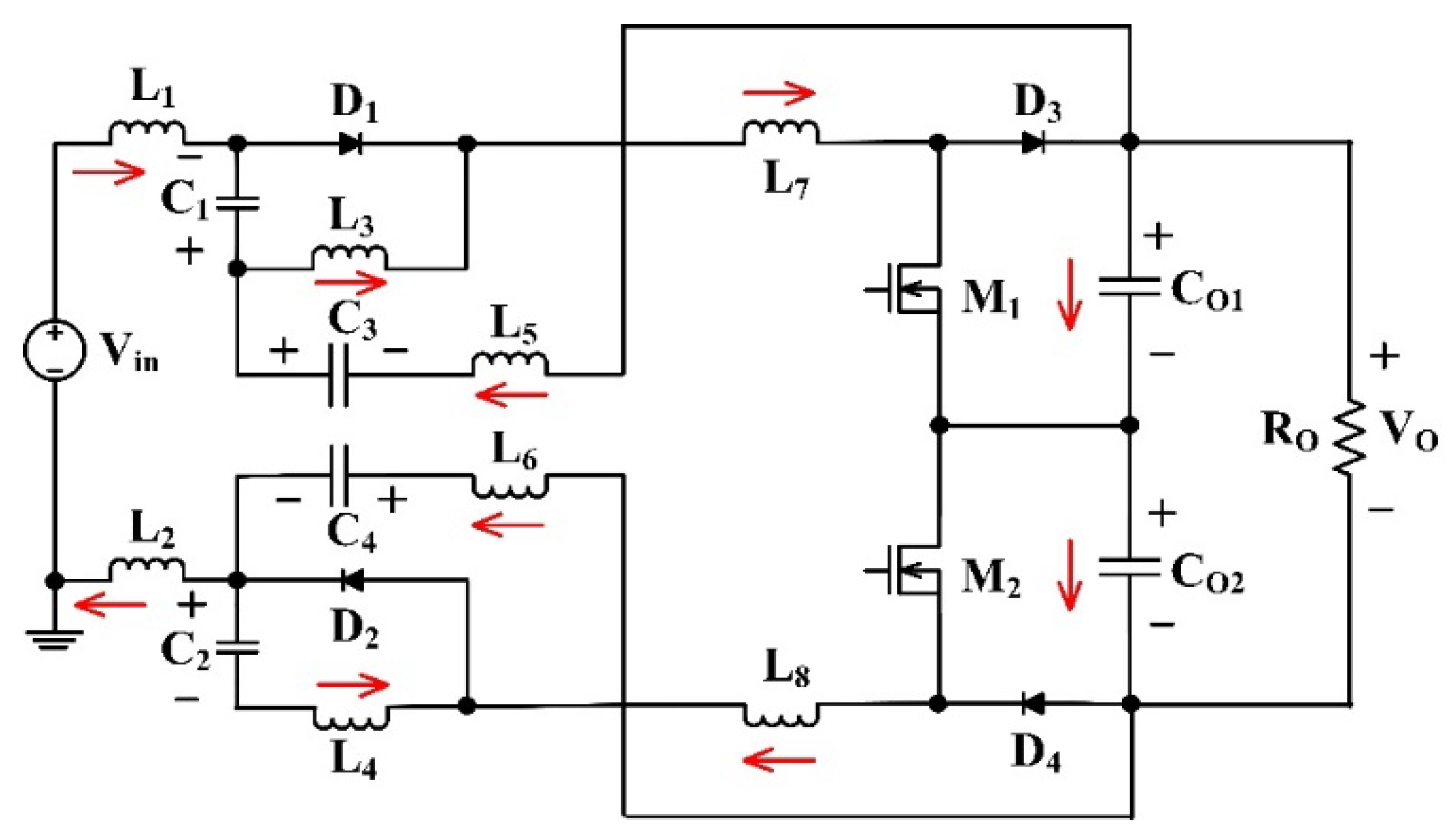
2. Circuit Structure and Its Characteristics
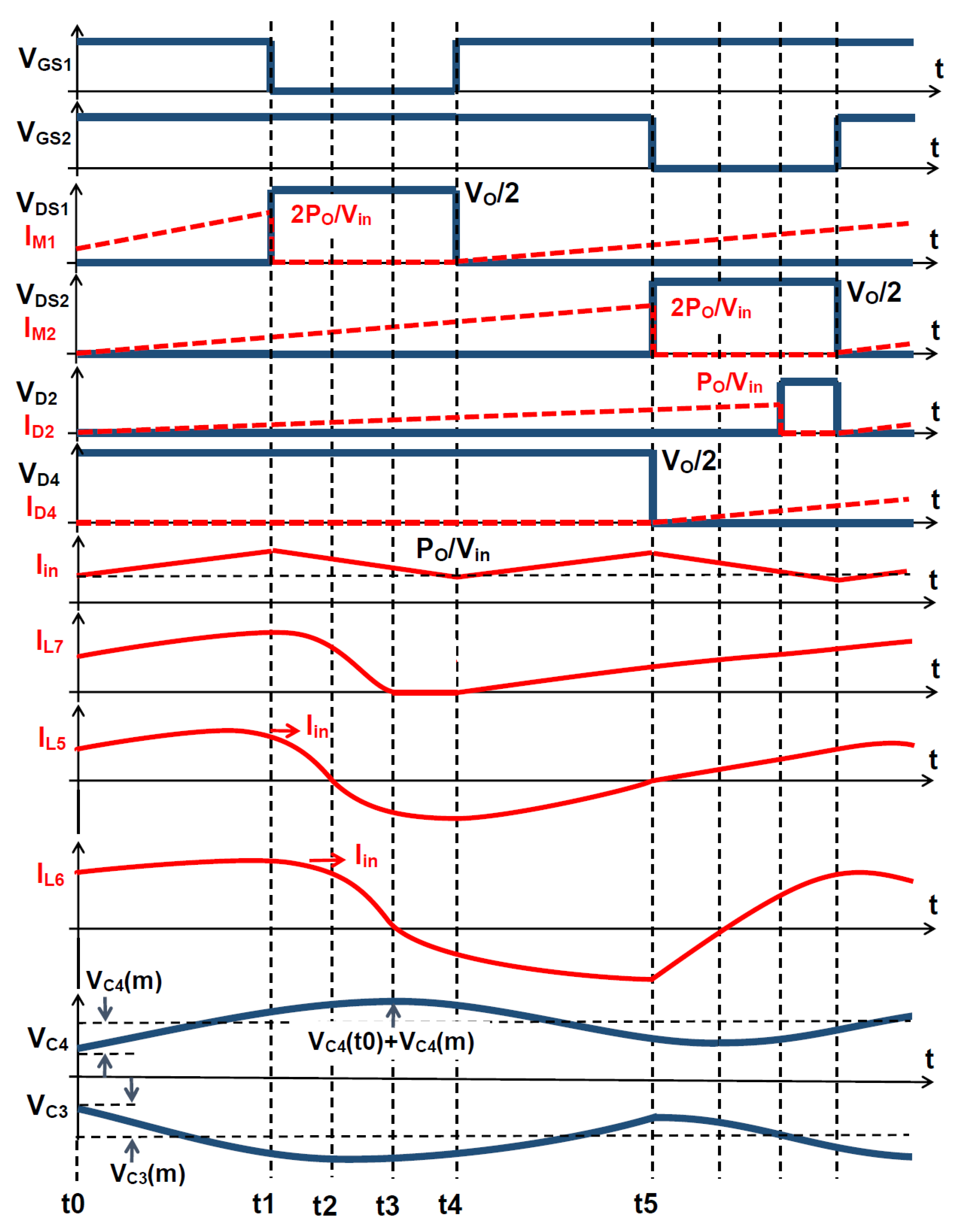
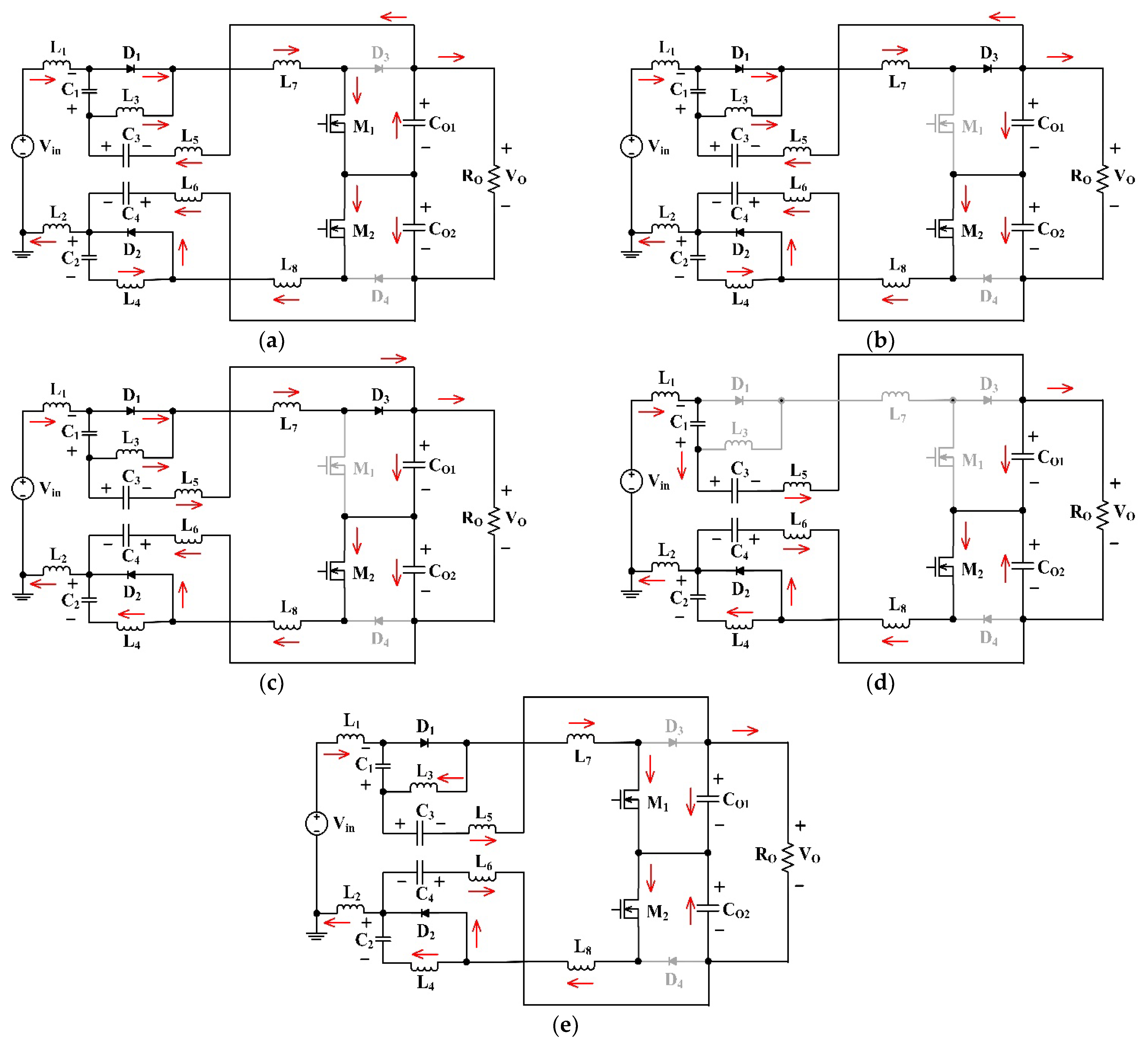
3. Consideration of Operating Modes
4. Small Signal Modelling
5. Design Considerations
5.1. Design of Input Filter Inductors L1, L2
5.2. Design of Output Capacitors Co1, Co2
5.3. Design of Series Inductors L7, L8
5.4. Design of Inductors L3, L4
5.5. Design of Capacitors C1, C2
5.6. Design of Switches M1 and M2
5.7. Design of Output Diodes D3, D4
5.8. Design of Input Diodes D1, D2
5.9. Design of Resonant Elements C3, C4, L5, L6
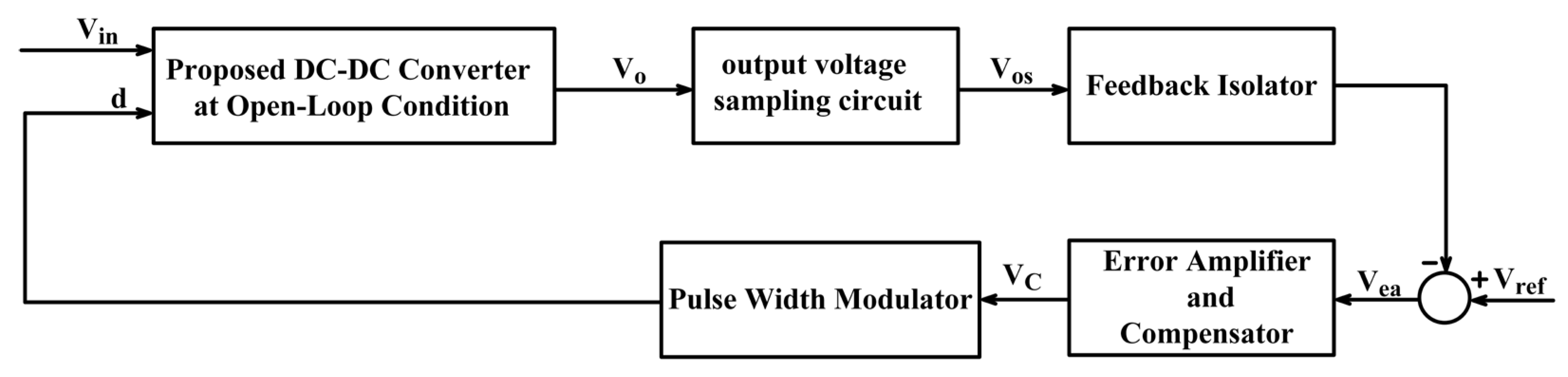
6. Control of the Proposed DC-DC Converter
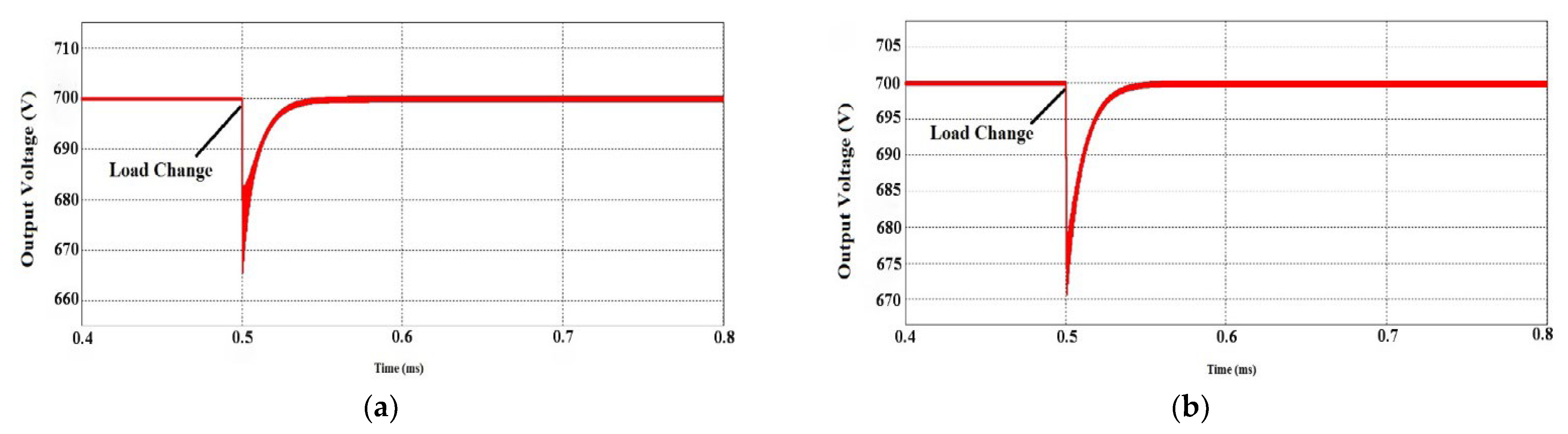
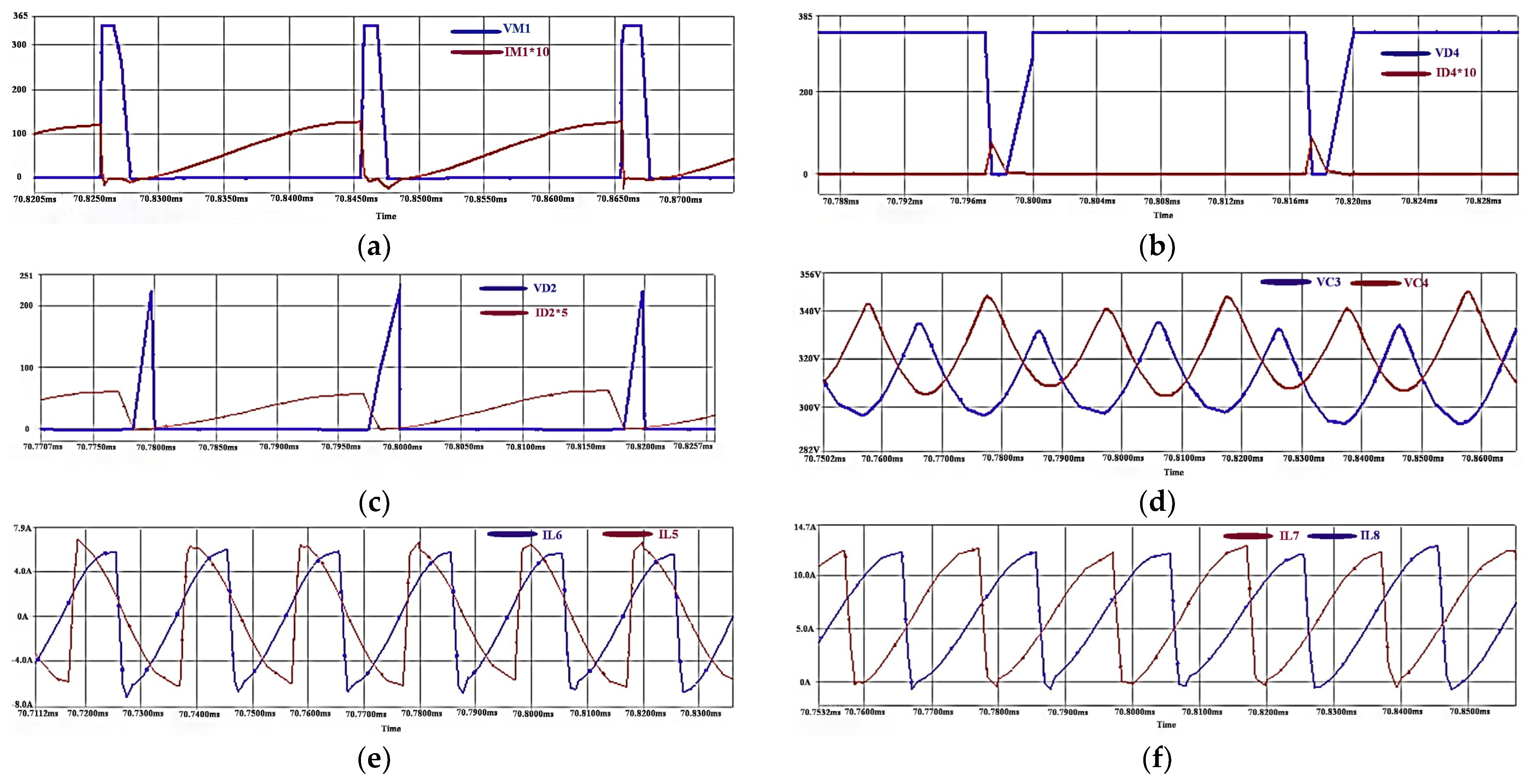
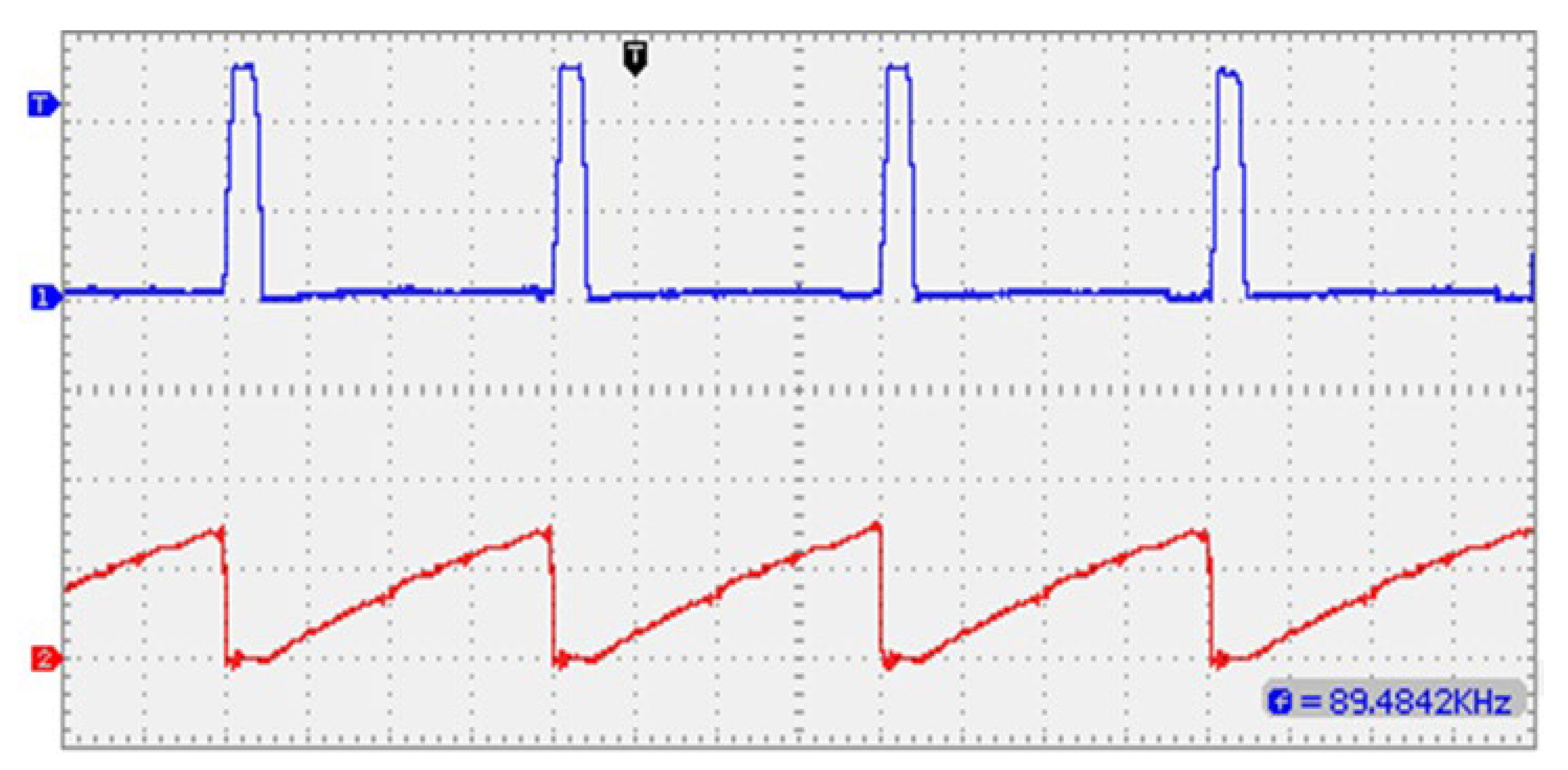
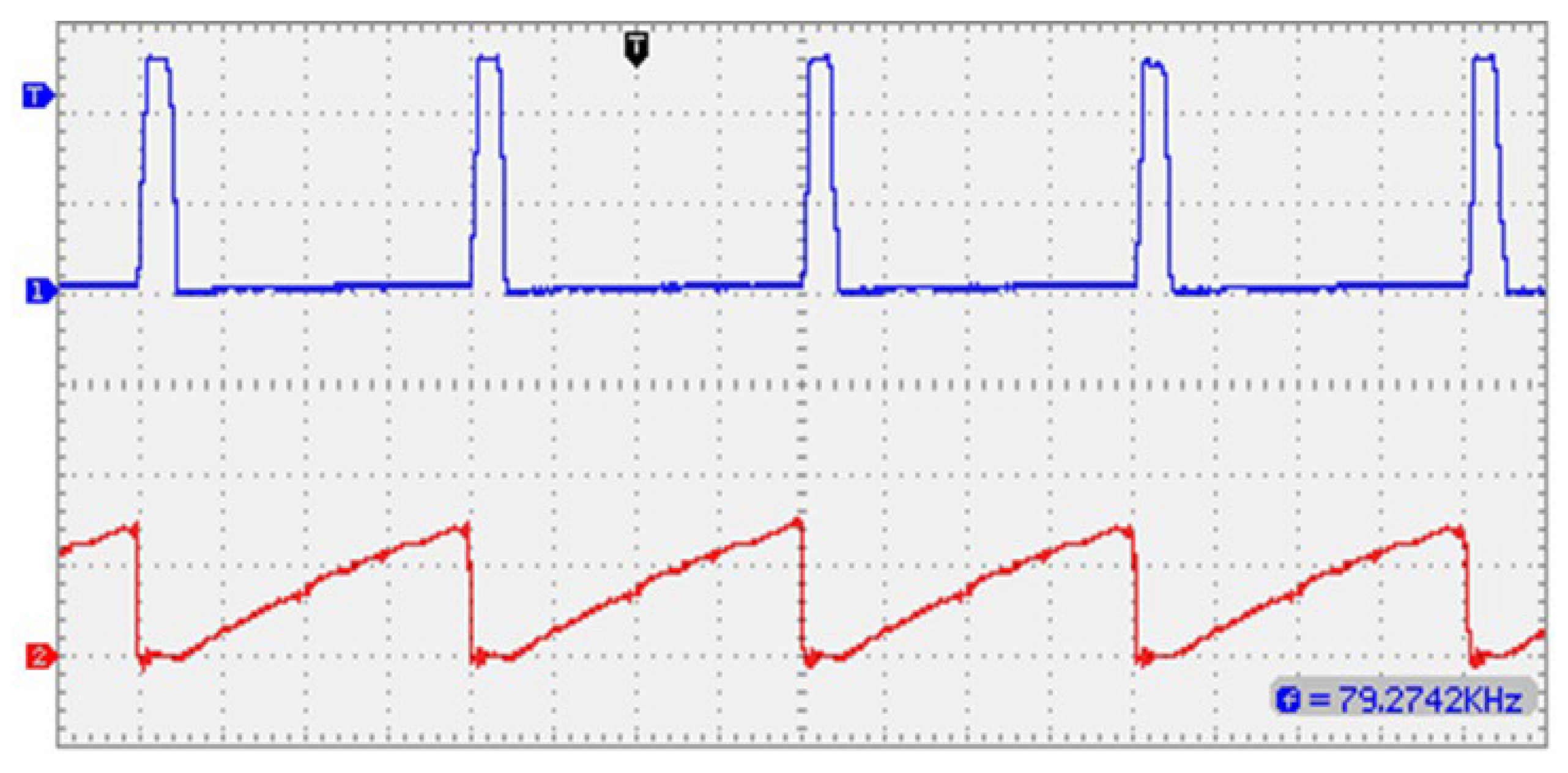
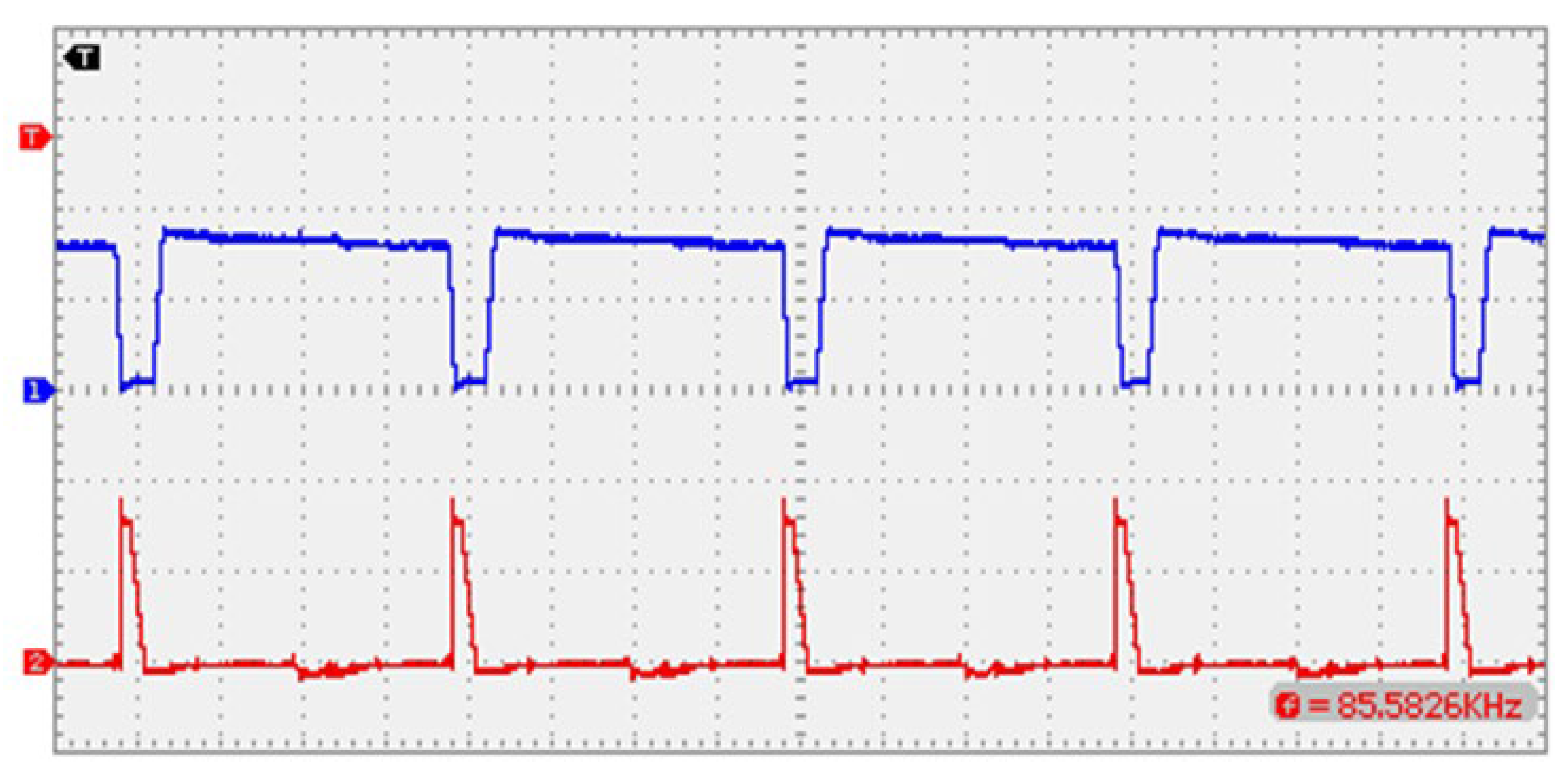
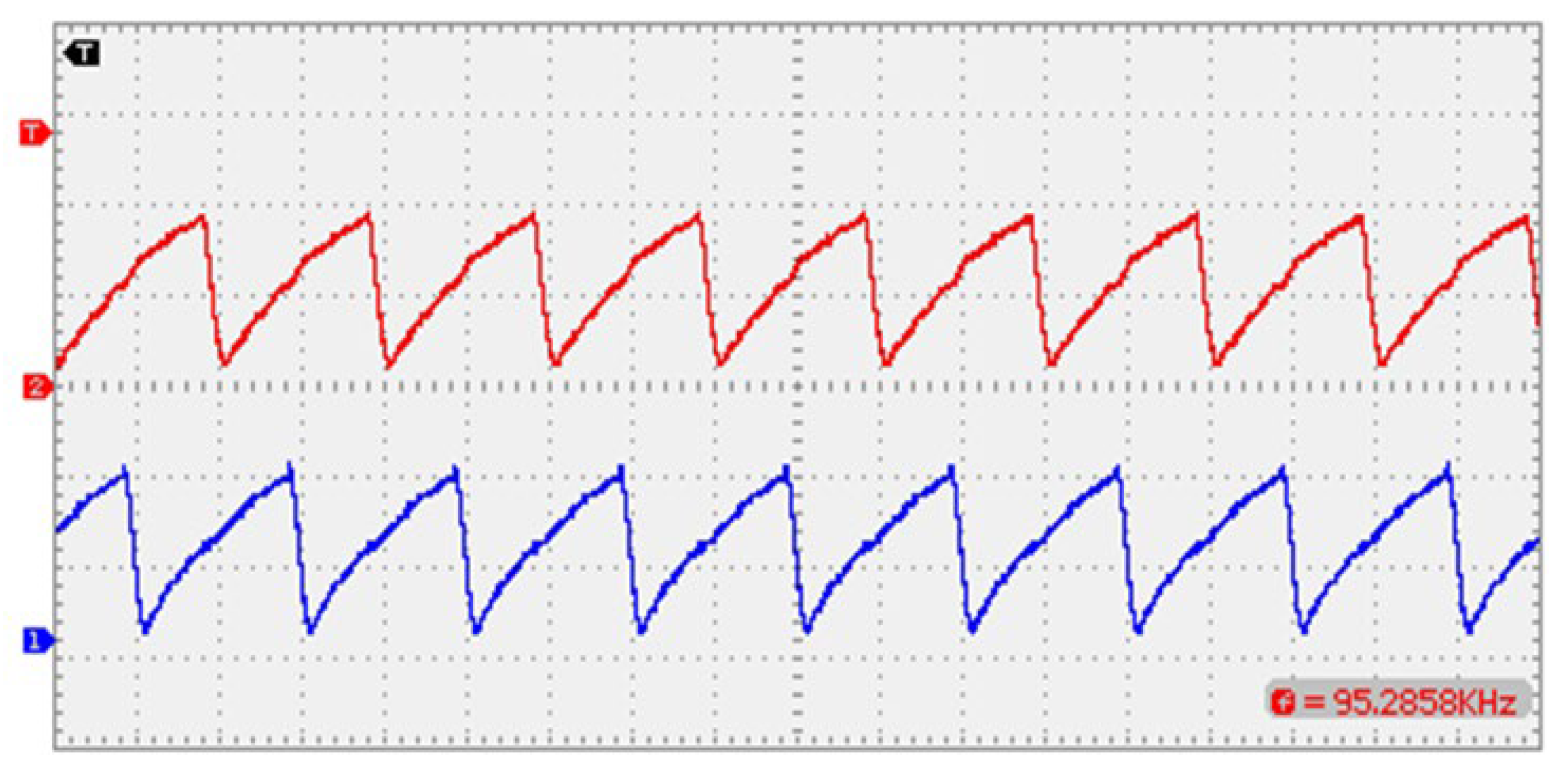
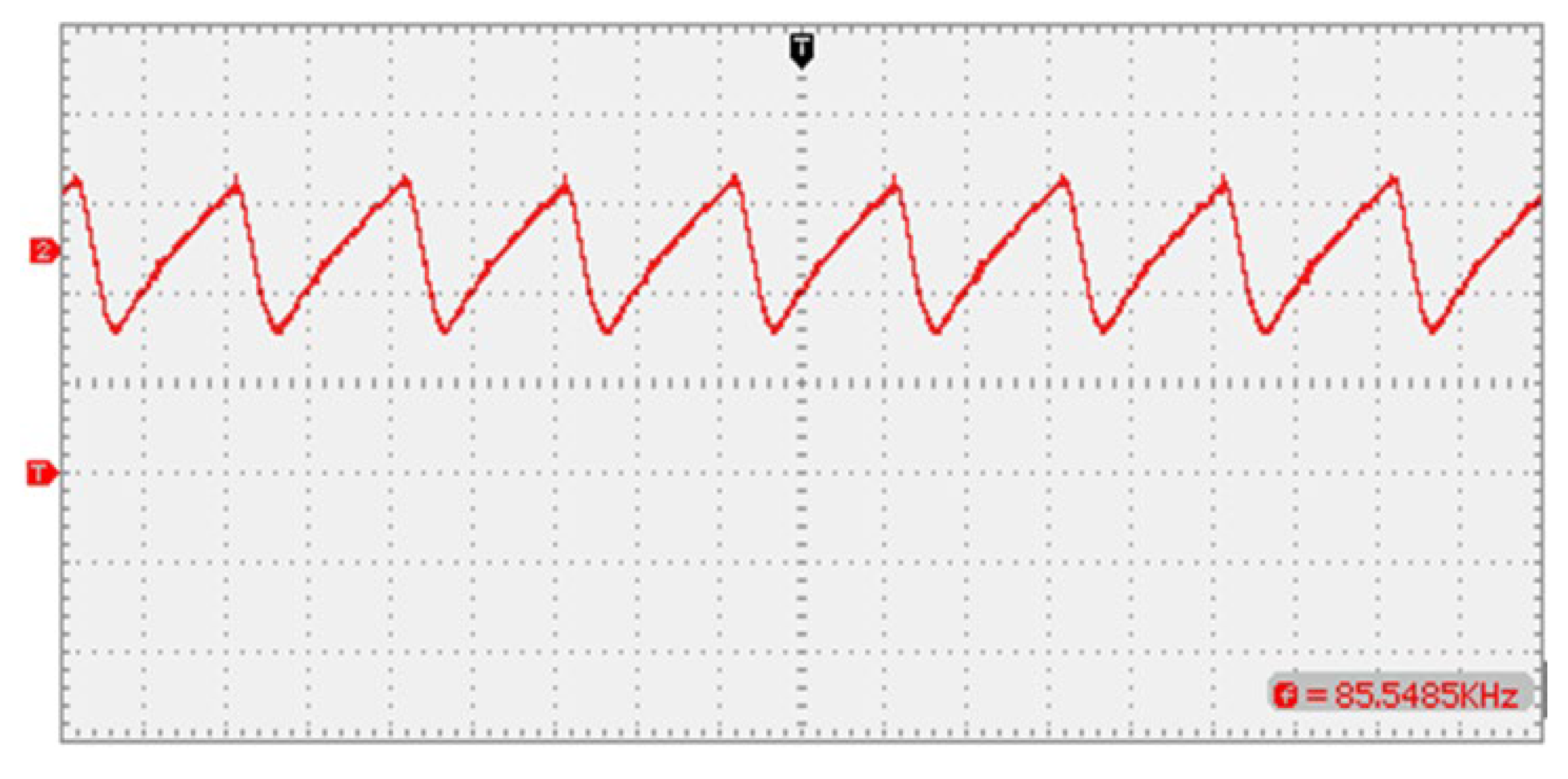
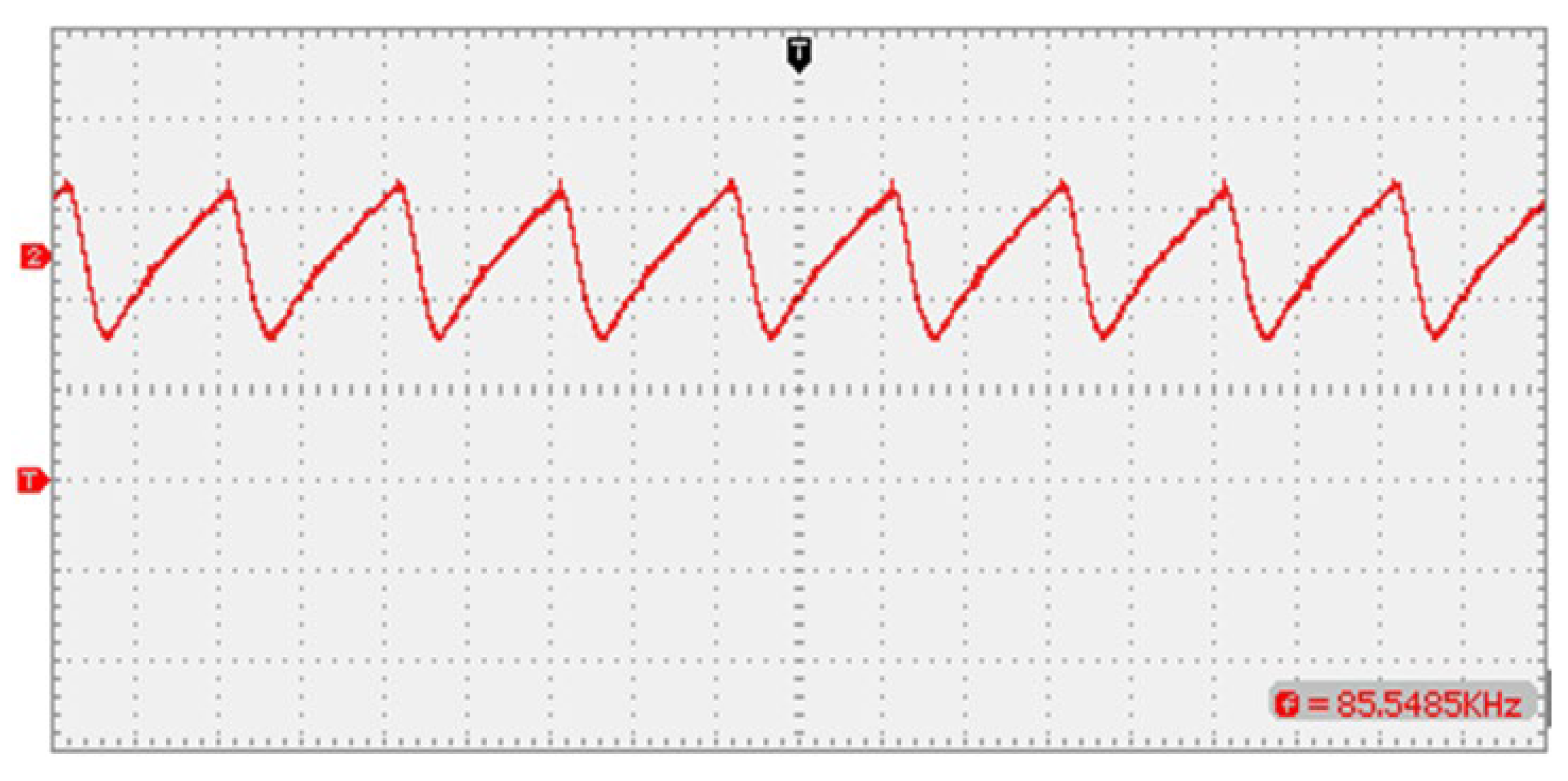
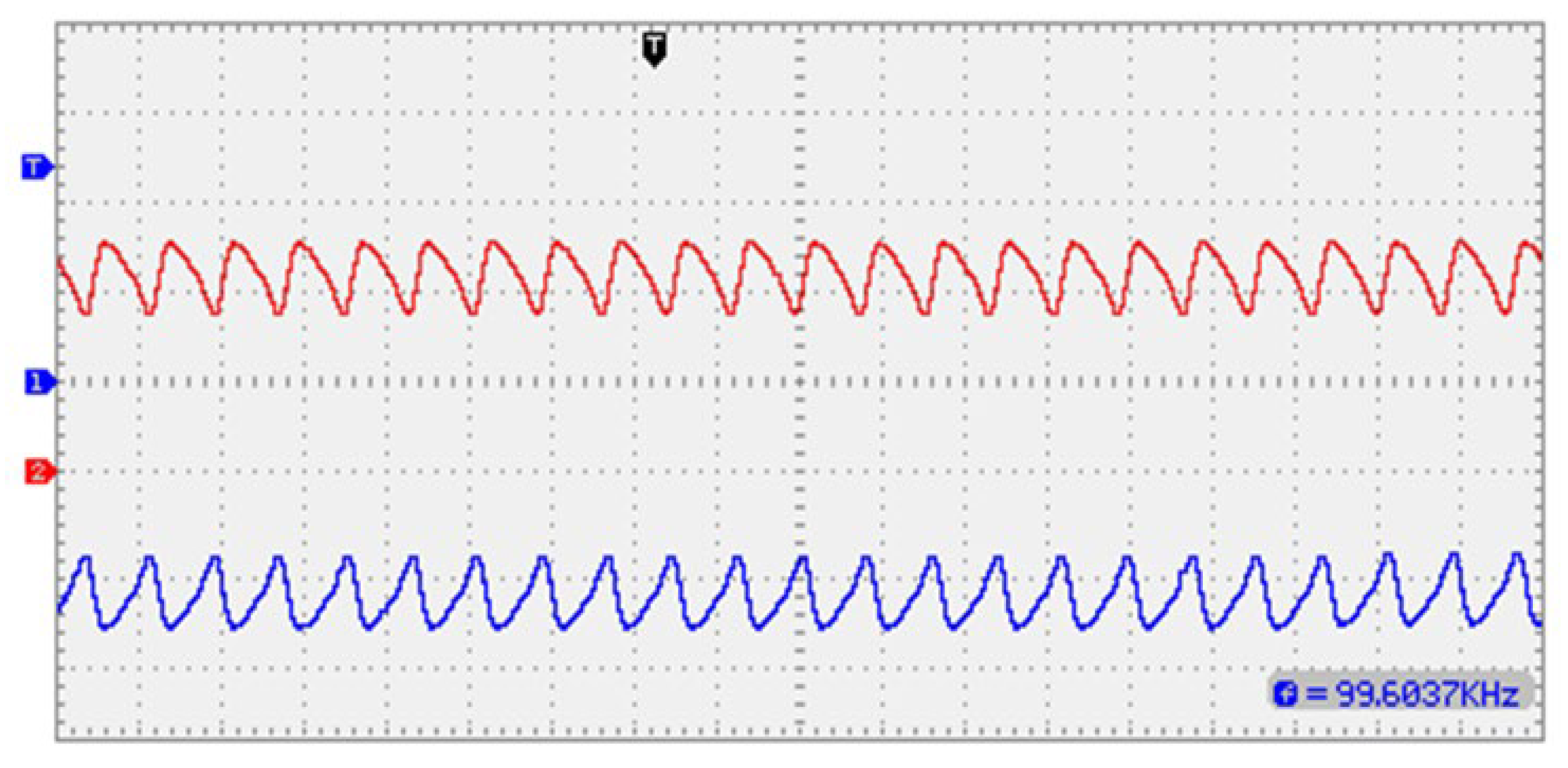
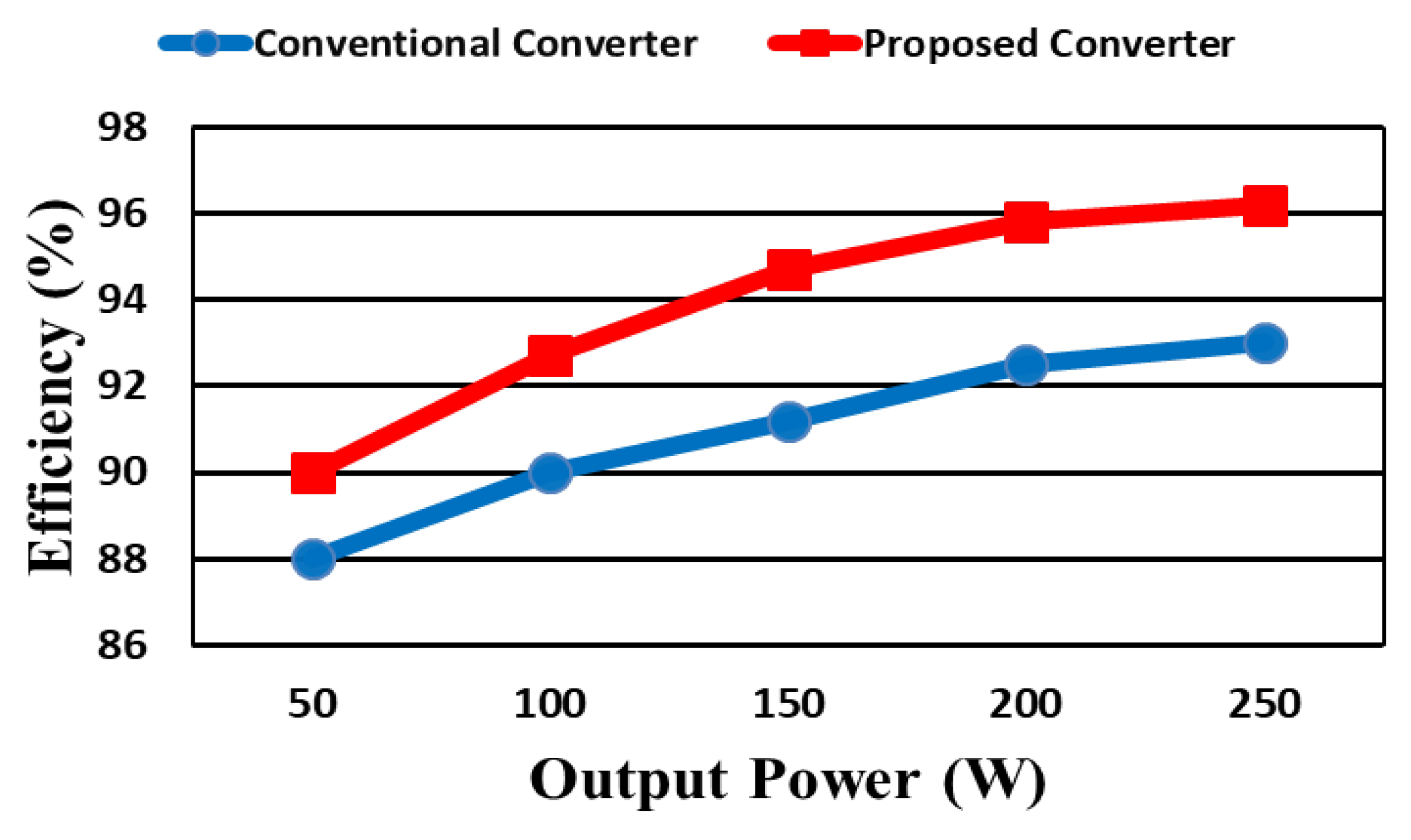
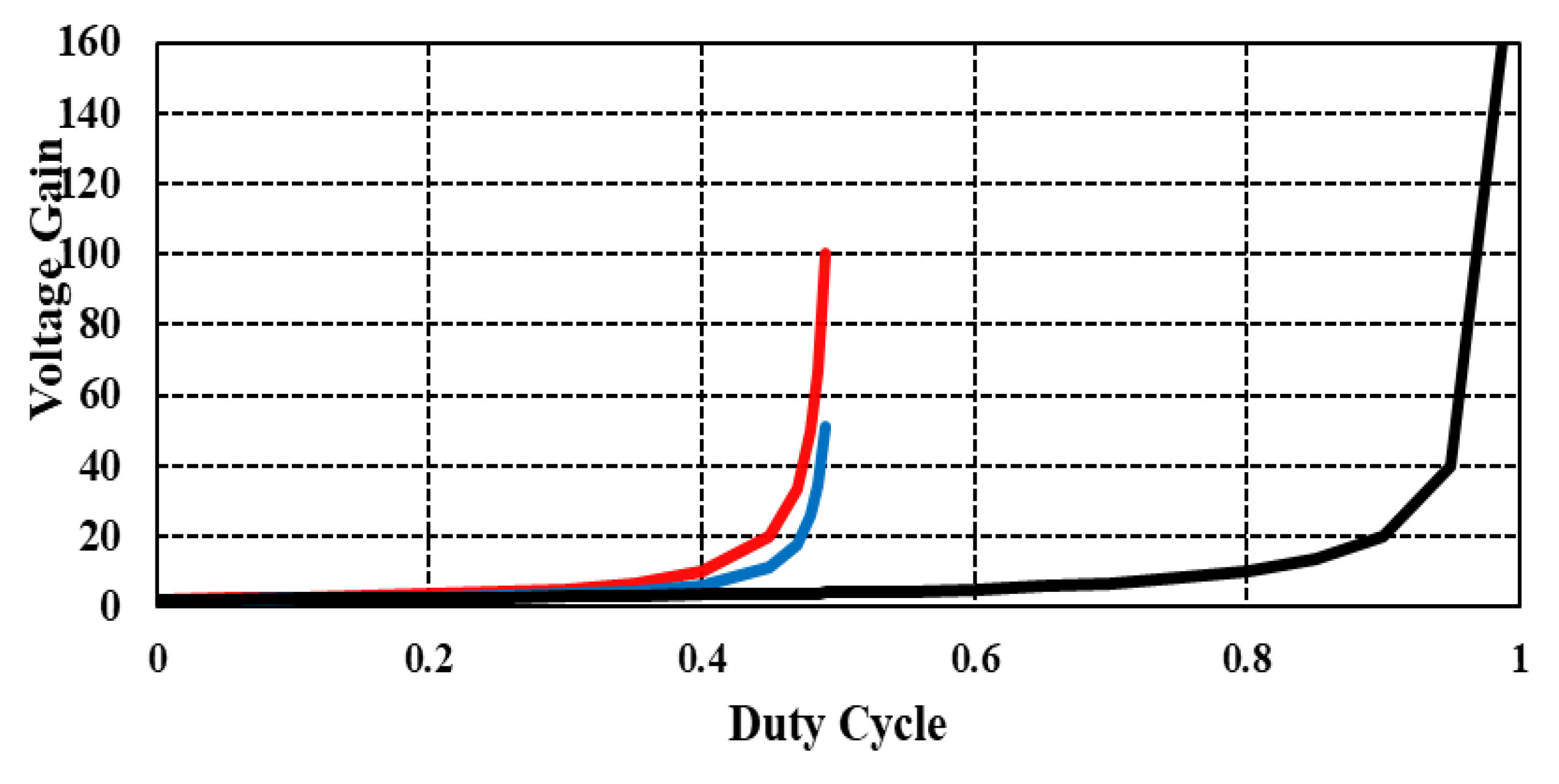
7. Simulation and Experimental Results
8. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Jagadeesh, I.; Indragandhi, V. Comparative Study of DC-DC Converters for Solar PV with Microgrid Applications. Energies 2022, 15, 7569. [Google Scholar] [CrossRef]
- Asghari-Gorji, S.; Ektesabi, M. Input current ripples cancellation in bidirectional switched-inductor quasi-Z-source inverter using coupled inductors. In Proceedings of the 2015 Australasian Universities Power Engineering Conference (AUPEC), Wollongong, NSW, Australia, 27–30 September 2015; pp. 1–6. [Google Scholar]
- Mirzaei, A.; Rezvanyvardom, M. High voltage gain soft switching full bridge interleaved Flyback DC-DC converter for PV applications. Sol. Energy 2020, 196, 217–227. [Google Scholar] [CrossRef]
- Ramirez-Carrillo, M.; Ortega-Cisneros, S.; Rosas-Caro, J.C.; Rivera, J.; Valdez-Resendiz, J.E.; Mayo-Maldonado, J.C.; Valderrabano-Gonzalez, A. A Step-Up Converter with Large Voltage Gain and Low Voltage Rating on Capacitors. Energies 2022, 15, 7944. [Google Scholar] [CrossRef]
- He, X.; Hu, R.; Chen, W. A Hybrid Three-Level ZVZCS Converter for Photovoltaic Power Connecting to MVDC Collection System. Energies 2022, 15, 5365. [Google Scholar] [CrossRef]
- Tsang, K.M.; Chan, W.L. A single switch DC/DC converter with galvanic isolation and input current regulation for photovoltaic systems. Sol. Energy 2015, 119, 203–211. [Google Scholar] [CrossRef]
- Liu, L.; Bala, S.; Canales, F. Stacked DC-DC Converter with Wide Voltage Range. In Proceedings of the 2019 IEEE Energy Conversion Congress and Exposition (ECCE), Baltimore, MD, USA, 29 September–3 October 2019; pp. 1401–1407. [Google Scholar]
- Folmer, S.; Stala, R. DC-DC High Voltage Gain Switched Capacitor Converter With Multilevel Output Voltage and Zero-Voltage Switching. IEEE Access 2021, 9, 129692–129705. [Google Scholar] [CrossRef]
- Sadaf, S.; Bhaskar, M.S.; Meraj, M.; Iqbal, A.; Al-Emadi, N. A Novel Modified Switched Inductor Boost Converter With Reduced Switch Voltage Stress. IEEE Trans. Ind. Electron. 2021, 68, 1275–1289. [Google Scholar] [CrossRef]
- Li, B.; Wang, P.; Wang, Z.; Ma, X.; Bi, H. A New Coupled-Inductor-Based High-Gain Interleaved DC-DC Converter With Sustained Soft Switching. IEEE Trans. Veh. Technol. 2021, 70, 6527–6541. [Google Scholar] [CrossRef]
- Matsuda, A.; Koizumi, H.; Sato, T. Two-Stage Interleaved DC-DC Converter with Input-Parallel Output-Series Connection. In Proceedings of the 2019 IEEE International Symposium on Circuits and Systems (ISCAS), Sapporo, Japan, 26–29 May 2019; pp. 1–5. [Google Scholar]
- Gorji, S.A. Reconfigurable Quadratic Converters for Electrolyzers Utilized in DC Microgrids. IEEE Access 2022, 10, 109677–109687. [Google Scholar] [CrossRef]
- Gorji, S.A.; Sahebi, H.G.; Movahed, M.; Ektesabi, M. Multi-Input Boost DC-DC Converter with Continuous Input-Output Current for Renewable Energy Systems. In Proceedings of the 2019 IEEE 4th International Future Energy Electronics Conference (IFEEC), Singapore, 25–28 November 2019; pp. 1–5. [Google Scholar]
- Rodrigues, J.P.; Mussa, S.A.; Barbi, I.; Perin, A.J. Three-level zero-voltage switching pulse-width modulation DC-DC boost converter with active clamping. IET Power Electron. 2010, 3, 345–354. [Google Scholar] [CrossRef]
- Yang, L.; Liang, T.; Lee, H.; Chen, J. Novel High Step-Up DC–DC Converter With Coupled-Inductor and Voltage-Doubler Circuits. IEEE Trans. Ind. Electron. 2011, 58, 4196–4206. [Google Scholar] [CrossRef]
- Zhang, Y.; Sun, J.T.; Wang, Y.F. Hybrid Boost Three-Level DC–DC Converter With High Voltage Gain for Photovoltaic Generation Systems. IEEE Trans. Power Electron. 2013, 28, 3659–3664. [Google Scholar] [CrossRef]
- Macellari, M.; Schirone, L. Design of high-efficiency non-insulated step-up converters. IET Power Electron. 2015, 8, 743–749. [Google Scholar]
- Poorali, B.; Jazi, H.M.; Adib, E. Single-core soft-switching high step-up three-level boost converter with active clamp. IET Power Electron. 2016, 9, 2692–2699. [Google Scholar] [CrossRef]
- Moradisizkoohi, H.; Elsayad, N.; Mohammed, O.A. Experimental Verification of a Double-Input Soft-Switched DC–DC Converter for Fuel Cell Electric Vehicle With Hybrid Energy Storage System. IEEE Trans. Ind. Appl. 2019, 55, 6451–6465. [Google Scholar] [CrossRef]
- Cordeiro, A.; Pires, V.F.; Foito, D.; Pires, A.J.; Martins, J.F. Three-level quadratic boost DC-DC converter associated to a SRM drive for water pumping photovoltaic powered systems. Sol. Energy 2020, 209, 42–56. [Google Scholar] [CrossRef]
- Ding, X.; Zhao, D.; Liu, Y.; Li, K.; Hao, Y. High step-up three-level DC–DC converter with three-winding coupled-inductor. J. Power Electron. 2020, 20, 53–64. [Google Scholar] [CrossRef]
- Wang, P.; Zhou, L.; Zhang, Y.; Li, J.; Sumner, M. Input-Parallel Output-Series DC-DC Boost Converter With a Wide Input Voltage Range For Fuel Cell Vehicles. IEEE Trans. Veh. Technol. 2017, 66, 7771–7781. [Google Scholar] [CrossRef]
- Zhang, Y.; Sumner, L.Z.M.; Wang, P. Single-Switch, Wide Voltage-Gain Range, Boost DC–DC Converter for Fuel Cell Vehicles. IEEE Trans. Veh. Technol. 2018, 67, 134–145. [Google Scholar] [CrossRef]
- Zhang, Y.; Shi, J.; Zhou, L.; Li, J. Wide Input-Voltage Range Boost Three-Level DC–DC Converter With Quasi-Z Source for Fuel Cell Vehicles. IEEE Trans. Power Electron. 2017, 32, 6728–6738. [Google Scholar] [CrossRef]
- Wu, X.; Yang, M.; Zhou, M.; Zhang, Y.; Fu, J. A Novel High-Gain DC-DC Converter Applied in Fuel Cell Vehicles. IEEE Trans. Veh. Technol. 2020, 69, 12763–12774. [Google Scholar] [CrossRef]




| Parameter | Value | Type | Number |
|---|---|---|---|
| Input Voltage | 48 V | -- | -- |
| Output Voltage | 700 V | -- | -- |
| Switching Frequency | 50 kHz | -- | -- |
| Output Power | 250 W | -- | -- |
| Inductors L1, L2, L3, L4 | 300 µH | -- | 4 |
| Resonant Inductors L5, L6 | 20 µH | -- | 2 |
| Series Inductors L7, L8 | 15 µH | -- | 2 |
| Capacitors C1, C2 | 200 µF | Electrolytic | 2 |
| Resonant Capacitors C3, C4 | 1 µF | Electrolytic | 2 |
| Output Capacitors CO1, CO2 | 80 µF | Electrolytic | 2 |
| Power Switches M1, M2 | -- | IRFP242 | 2 |
| Output Diodes D3, D4 | -- | MUR840 | 2 |
| Power Diodes D1, D2 | -- | BYV27-200 | 2 |
| Ref. | Voltage Gain | Switch Voltage Stress | Diode Voltage Stress | Soft Switching | Efficiency | Switching Frequency | No. of Active Elements | |||
|---|---|---|---|---|---|---|---|---|---|---|
| S | D | L | C | |||||||
| [18] | Yes | 94% | 100 kHz | 3 | 4 | 3 | 8 | |||
| [14] | Load Dependent | Yes | 95.7% | 20 kHz | 4 | 7 | 1 | 4 | ||
| [15] | No | 91.1% | 25 kHz | 2 | 4 | 2 | 2 | |||
| [16] | No | 90.3% | 11.5 kHz | 4 | 8 | 2 | 4 | |||
| [17] | -- | No | 98% | 50 kHz | 4 | 0 | 1 | 2 | ||
| [22] | No | 94.14% | 20 kHz | 2 | 3 | 2 | 3 | |||
| [23] | No | 90.53% | 20 kHz | 1 | 3 | 1 | 3 | |||
| [24] | No | 95.66% | 10 kHz | 3 | 4 | 2 | 4 | |||
| [25] | No | 93.1% | 20 kHz | 2 | 5 | 1 | 4 | |||
| Proposed | Yes | 96.2% | 50 kHz | 2 | 4 | 8 | 6 | |||
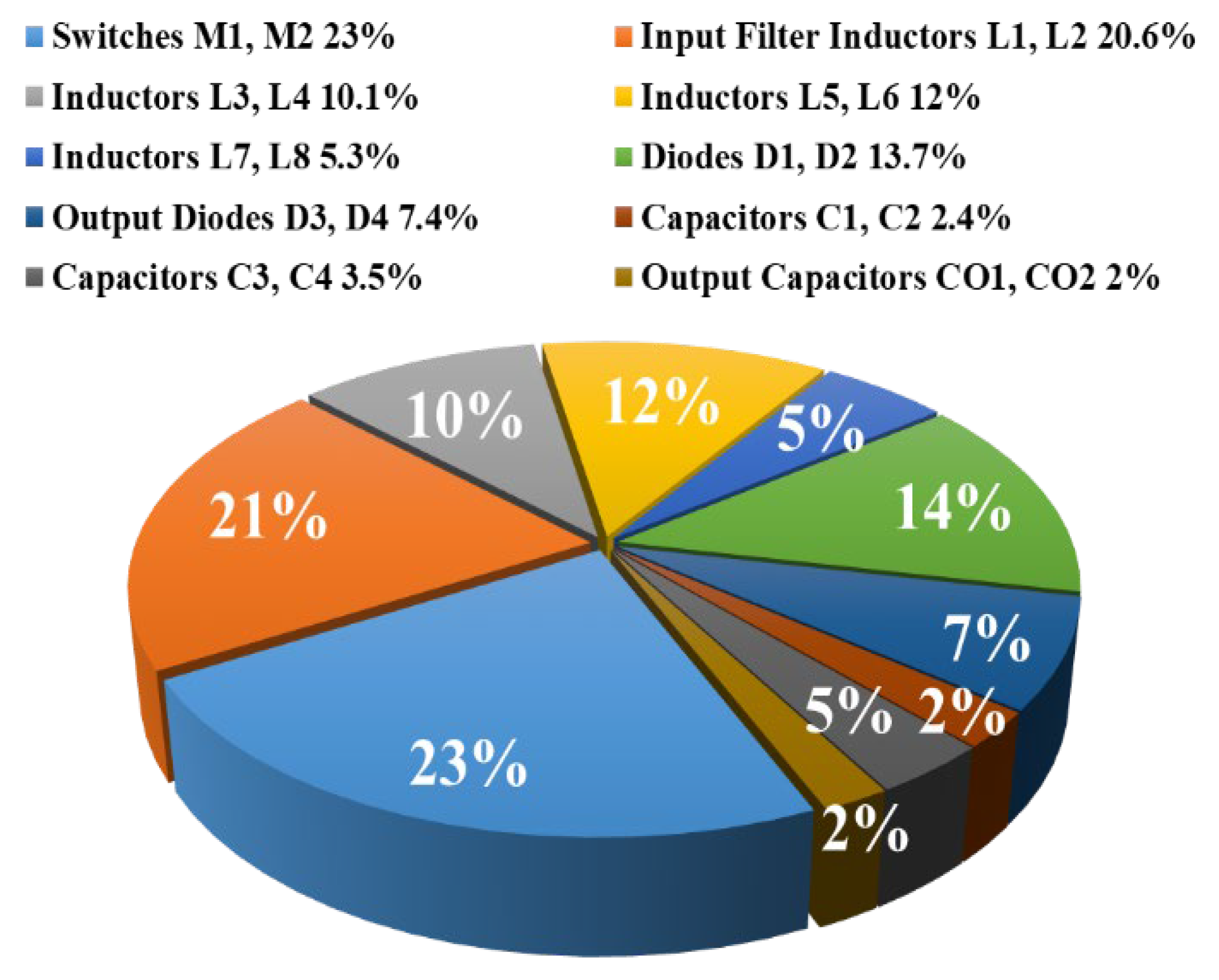
| Type of Loss | Formula | Proposed Converter |
|---|---|---|
| Switching Loss in Switches | (0.5 × 48 × 0.36 × (100 + 100) × 10−9 + 48 × (0.36 + 0.1) × 100 × 10−9) × 50 × 103 | |
| Parasitic Capacitance Loss in Switches | 0.5 × 20 × 10−6 × 442 × 50 × 103 | |
| Conduction Loss in Switches | 0.18 × (50 × 103 × 24.6 × 2 × 10−5)0.5 | |
| Conduction Loss in the Input Diodes (D1 and D2) | 4.64 × 0.5 | |
| Conduction Loss in the Output Diodes (D3 and D4) | 0.24 × 0.5 | |
| The Loss of Inductors | 4.55 | |
| The Loss of Capacitors | 0.75 | |
| Total Losses | - | PLoss = 9.2 W |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Taghavi, S.S.; Rezvanyvardom, M.; Mirzaei, A.; A. Gorji, S. High Step-Up Three-Level Soft Switching DC-DC Converter for Photovoltaic Generation Systems. Energies 2023, 16, 41. https://doi.org/10.3390/en16010041
Taghavi SS, Rezvanyvardom M, Mirzaei A, A. Gorji S. High Step-Up Three-Level Soft Switching DC-DC Converter for Photovoltaic Generation Systems. Energies. 2023; 16(1):41. https://doi.org/10.3390/en16010041
Chicago/Turabian StyleTaghavi, Seyed Shahriyar, Mahdi Rezvanyvardom, Amin Mirzaei, and Saman A. Gorji. 2023. "High Step-Up Three-Level Soft Switching DC-DC Converter for Photovoltaic Generation Systems" Energies 16, no. 1: 41. https://doi.org/10.3390/en16010041
APA StyleTaghavi, S. S., Rezvanyvardom, M., Mirzaei, A., & A. Gorji, S. (2023). High Step-Up Three-Level Soft Switching DC-DC Converter for Photovoltaic Generation Systems. Energies, 16(1), 41. https://doi.org/10.3390/en16010041







