Study on Shear Velocity Profile Inversion Using an Improved High Frequency Constrained Algorithm
Abstract
1. Introduction
2. High-Frequency Constrained Inversion Method of Formation Shear-Velocity Radial Profile
2.1. Basic Method Principle
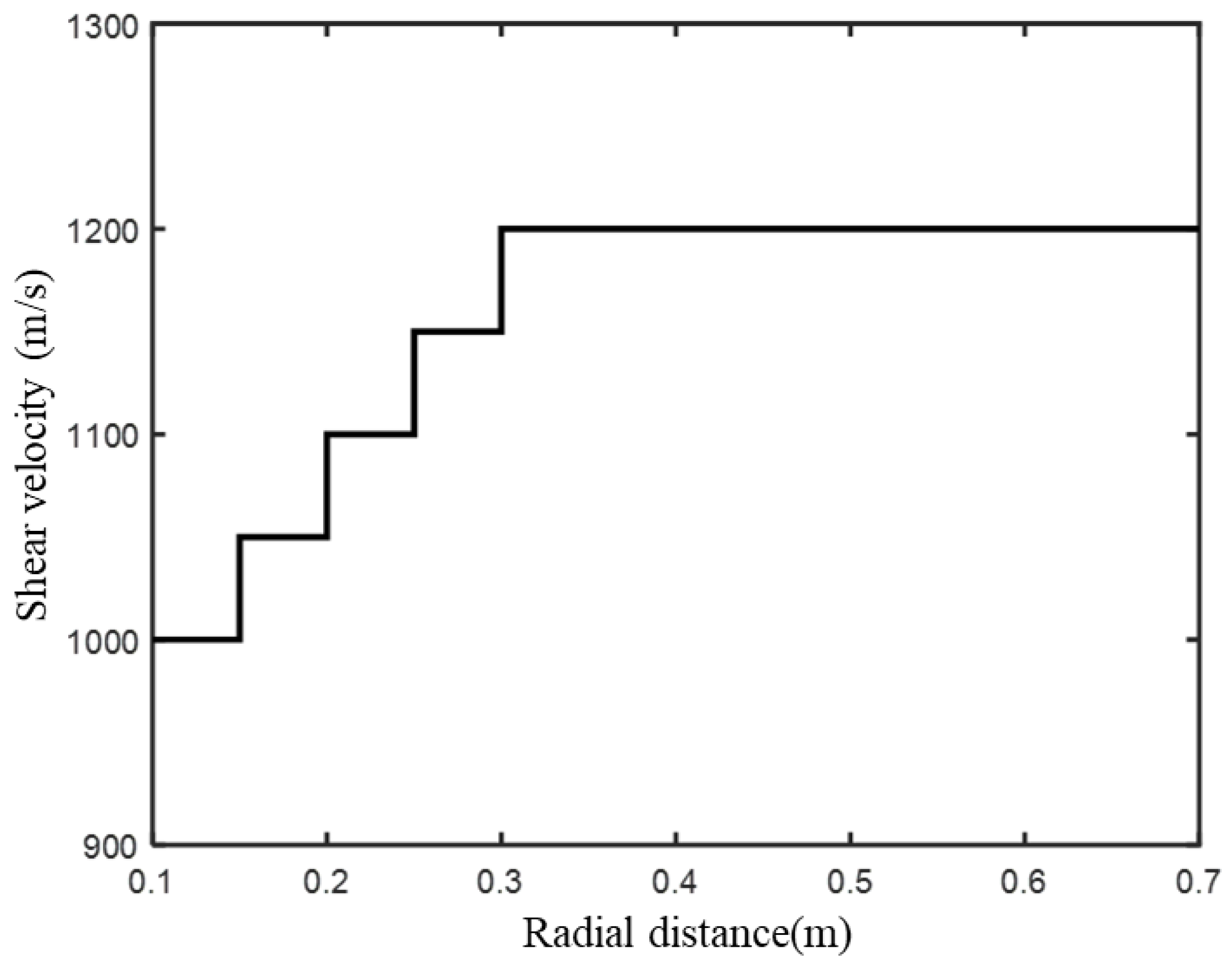
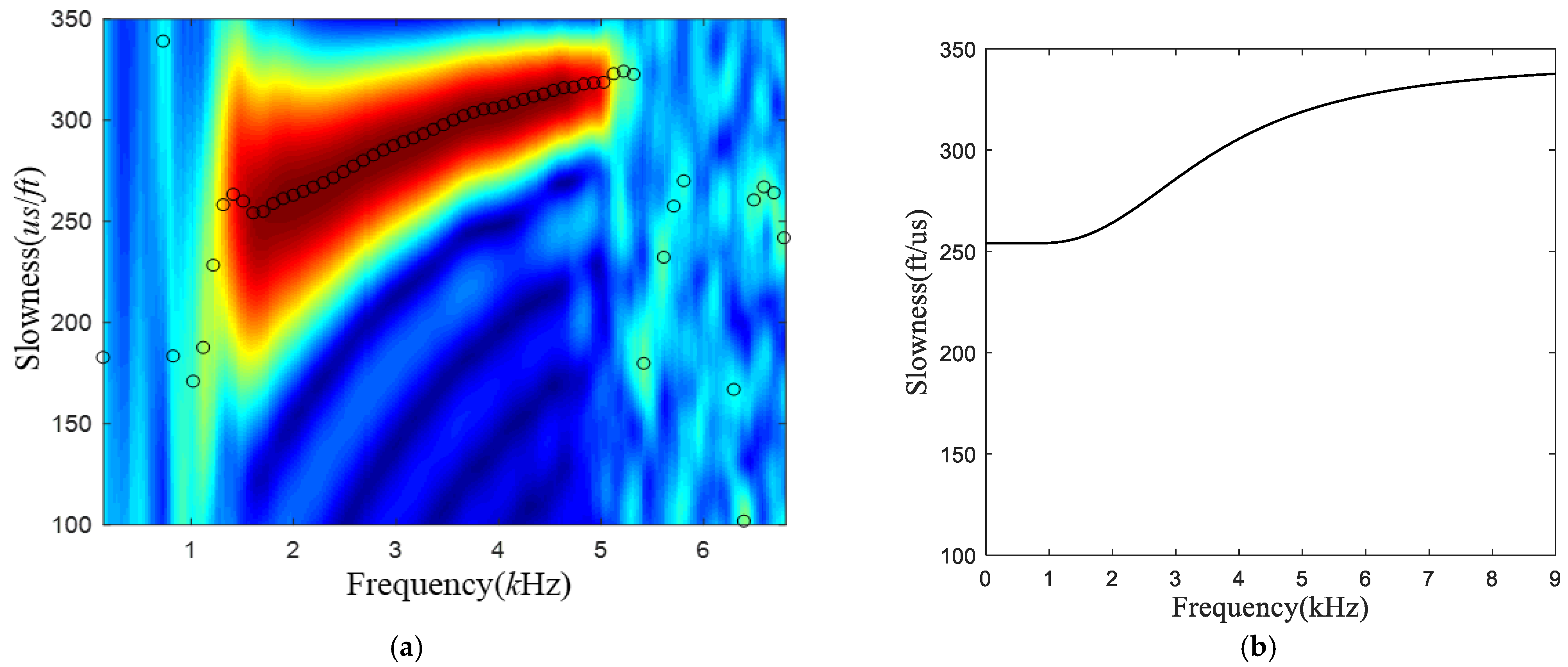
2.2. Theoretical Model Validation
3. Application of Equivalent-Tool Theory in Constrained Inversion
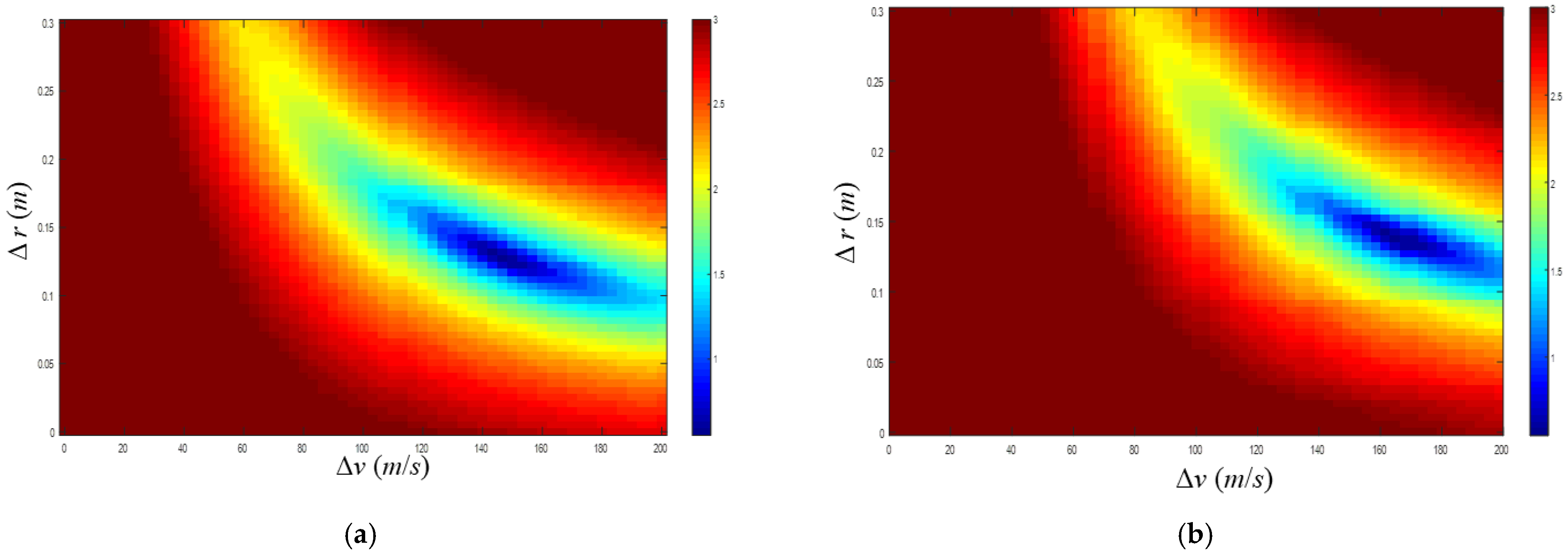
3.1. Equivalent-Tool Theory
3.2. Application of Equivalent-Tool Theory in Constrained Inversion Method
4. Real Data Processing
- Step 1, select the impermeable and tight interval, extract the dispersion curve of the measured dipole waveform, and compute the theoretical dispersion curve using the known formation velocity, density, and borehole parameters.
- Step 2, invert the tool parameters MT and a by matching the real data and the synthetic curve based on the equivalent-tool theory in the impermeable and tight intervals.
- Step 3, implement the formation’s S-wave velocity radial profile inversion algorithm corrected by the equivalent-tool theory in other intervals. The tool equivalent parameters MT and a in this step use the value from Step 2.
5. Conclusions
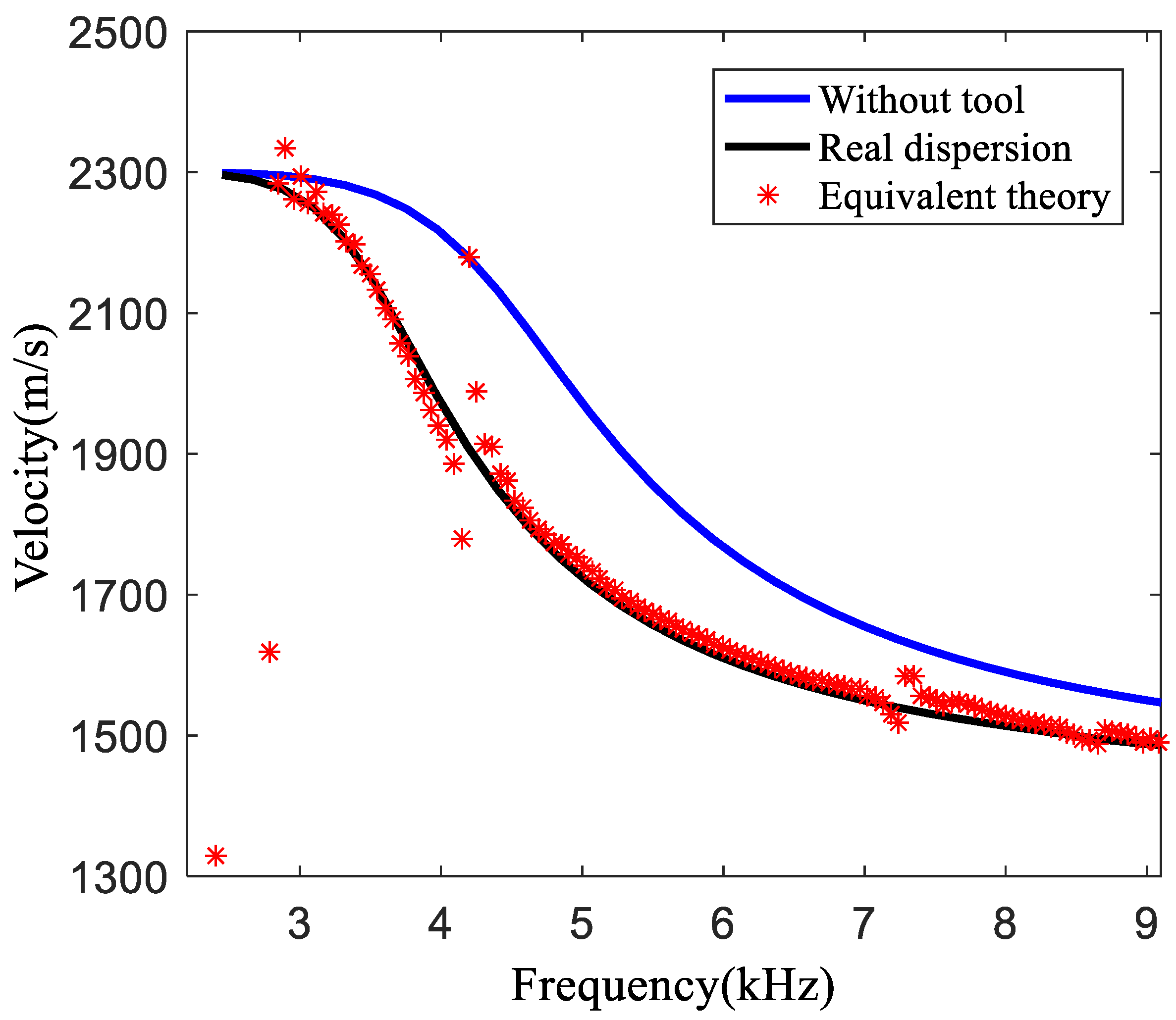
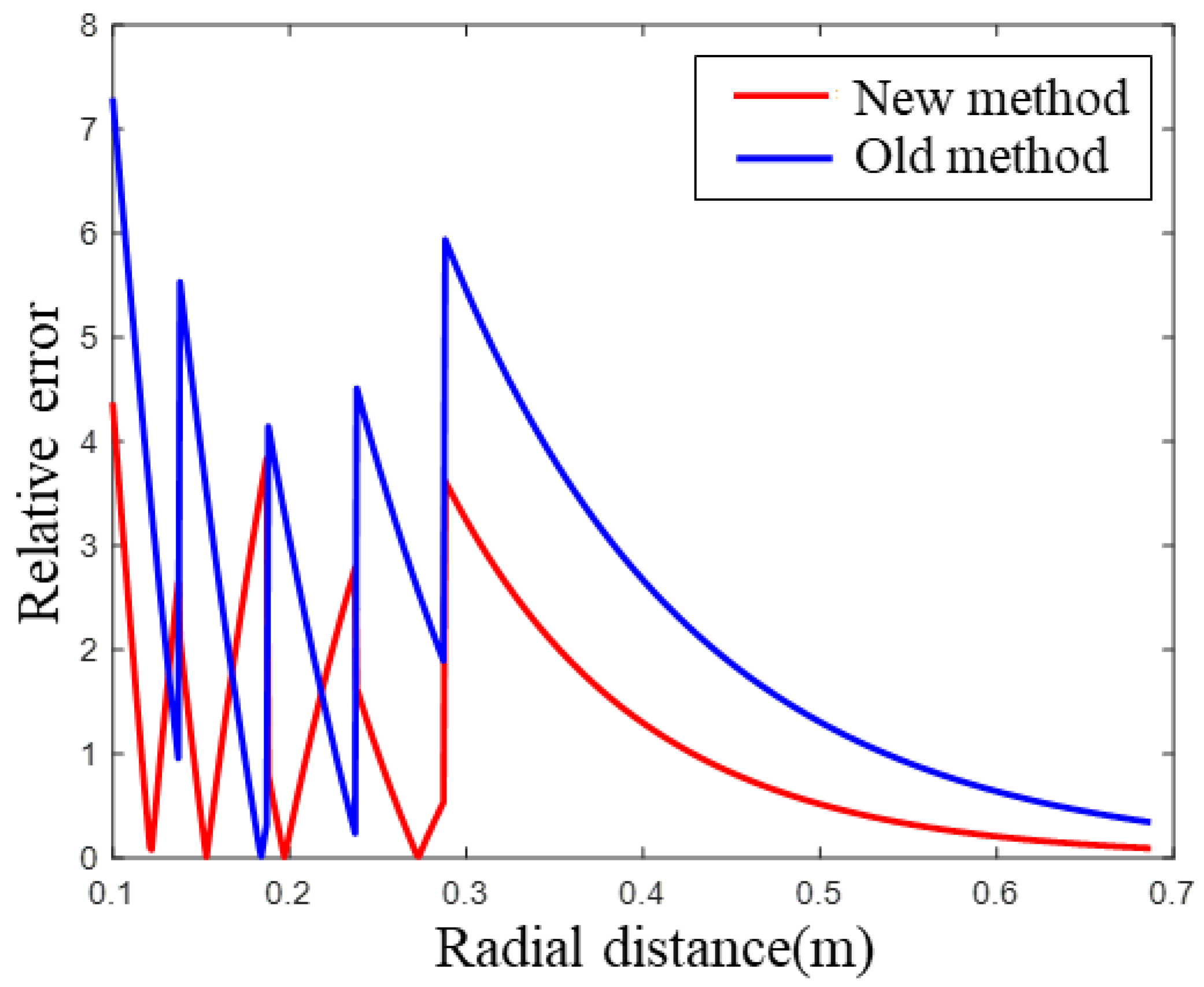
- The existence of the tool makes the dispersion curve of the dipole acoustic logging move to a low frequency. If the inversion calculation is carried out directly without considering the impacts of the tool, the velocity change and the equivalent thickness obtained by this inversion method will be larger, thereby increasing the error. The equivalent-tool theory can be used to calculate the dispersion curve of the theoretical model by considering the tool, thereby eliminating the impacts of the tool and reducing the inversion error.
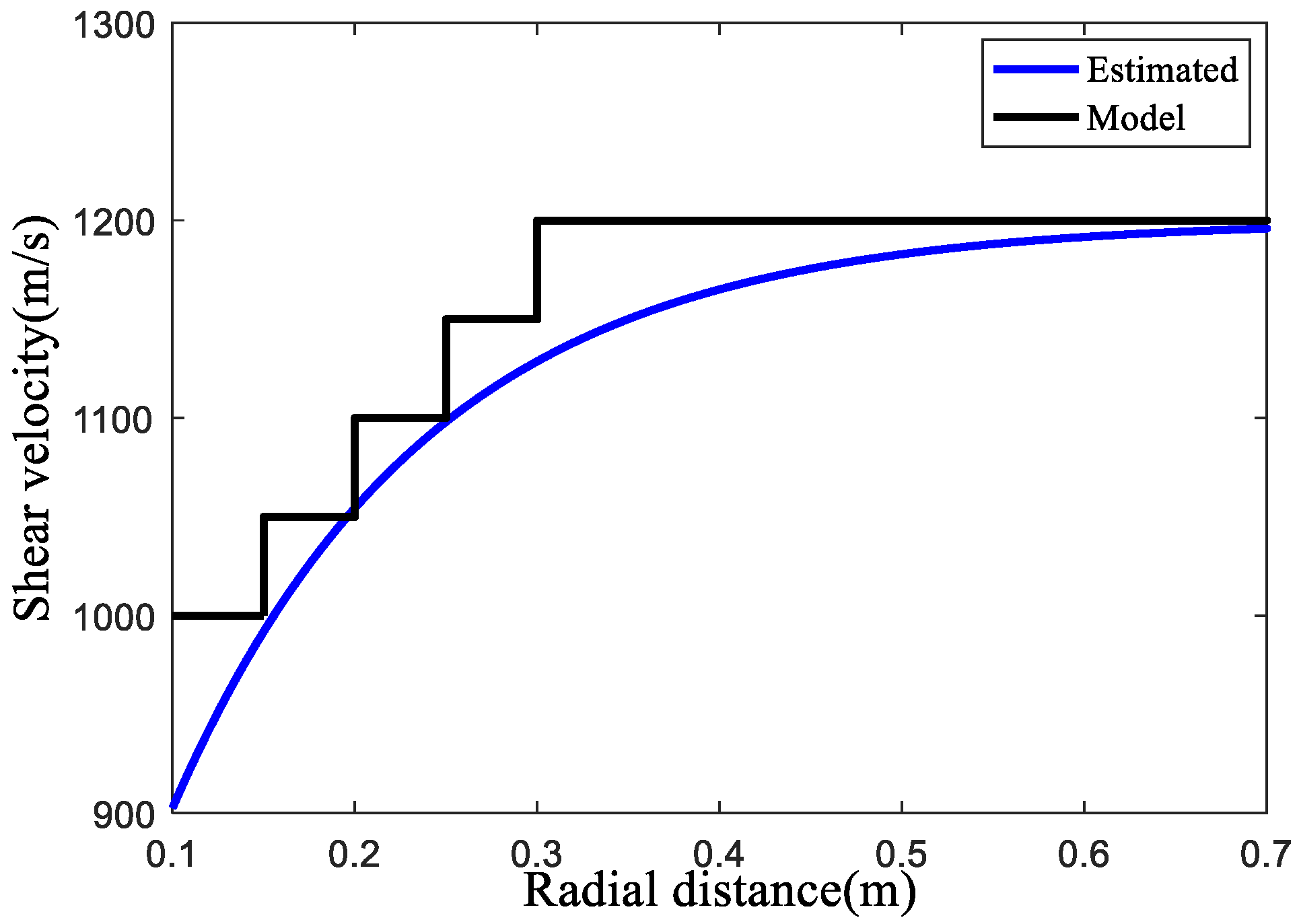
- The results obtained using the improved high-frequency constrained inversion method show that the radial velocity changes in the entire interval of the formation’s S-wave velocity radial profile without using the equivalent-tool theory are not in line with the actual situation, and the formation’s S-wave velocity radial profile using the equivalent-tool theory is in good agreement with other curves. This proves the effectiveness of the improved high-frequency constrained formation’s S-wave velocity radial profile-inversion method.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Baker, L.J. The effect of the invaded zone on full wavetrain acoustic logging. Geophysics 1984, 49, 686–847. [Google Scholar] [CrossRef]
- Sinha, B.K.; Asvadurov, S. Dispersion and radial depth of investigation of borehole modes. Geophys. Prospect. 2004, 52, 271–286. [Google Scholar] [CrossRef]
- Sinha, B.K.; Valero, H.; Ikegami, T.; Pabon, J. Borehole flexural waves in formations with radially varying properties. In Proceedings of the IEEE Ultrasonics Symposium, Rotterdam, The Netherlands, 18–21 September 2005; pp. 556–559. [Google Scholar] [CrossRef]
- Su, Y.-D.; Tang, X.-M.; Zhuang, C.-X.; Xu, S.; Zhao, L. Mapping formation shear-velocity variation by inverting logging-while-drilling quadrupole-wave dispersion data. Geophysics 2013, 78, D491–D498. [Google Scholar] [CrossRef]
- Tang, X.-M.; Xu, S.; Zhuang, C.-X.; Su, Y.-D.; Chen, X.-L. Assessing rock brittleness and fracability from radial variation of elastic wave velocities from borehole acoustic logging. Geophys. Prospect. 2016, 64, 958–966. [Google Scholar] [CrossRef]
- Li, J.; Innanen, K.A.; Tao, G.; Zhang, K.; Lines, L. Wavefield simulation of 3D borehole dipole radiation. Geophysics 2017, 82, D155–D169. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, H.; Li, C.; He, X.; Wang, X.; Habibi, D.; Chai, D. Radial profiling of near-borehole formation velocities by a stepwise inversion of acoustic well logging data. J. Pet. Sci. Eng. 2021, 196, 107648. [Google Scholar] [CrossRef]
- Backus, G.; Gilbert, F. Uniqueness in the inversion of inaccurate gross Earth data. Philos. Trans. R. Soc. Lond., Math. Phys. Sci. 1970, 266, 123–192. [Google Scholar] [CrossRef]
- Burridge, R.; Sinha, B.K. Inversion for formation shear modulus and radial depth of investigation using borehole flexural waves. In Proceedings of the SEG Technical Program Expanded Abstracts 1996, Denver, CO, USA, 10–15 November 1996; pp. 158–161. [Google Scholar] [CrossRef]
- Sinha, B.K.; Burridge, R. Radial Profiling of Formation Shear Velocity from Borehole Flexural Dispersions. In Proceedings of the 2001 IEEE Ultrasonics Symposium, Atlanta, GA, USA, 7–10 October 2001; pp. 391–396. [Google Scholar] [CrossRef]
- Sinha, B.K.; Vissapragada, B.; Renlie, L.; Tysse, S. Radial profiling of the three formation shear moduli and its application to well completions. Geophysics 2006, 71, E65–E77. [Google Scholar] [CrossRef]
- Sinha, B.; Bratton, T.; Cryer, J.; Nieting, S.; Ugueto, G.; Bakulin, A.; Hauser, M. Estimation of near-wellbore alteration and formation stress parameters from borehole sonic data. SPE Reserv. Eval. Eng. 2008, 11, 478–486. [Google Scholar] [CrossRef]
- Sunaga, S.; Sinha, B.K.; Endo, T.; Walsh, J. Radial Profiling of Shear Slowness in TIV Formations. In Proceedings of the SEG Technical Program Expanded Abstracts 2009, Houston, TX, USA, 25–30 October 2009; pp. 3481–3485. [Google Scholar] [CrossRef]
- Yang, J.; Sinha, B.K.; Habashy, T.M. A theoretical study on formation shear radial profiling in well-bonded cased boreholes using sonic dispersion data based on a parameterized perturbation model. Geophysics 2012, 77, WA197–WA210. [Google Scholar] [CrossRef]
- Wang, B.; Ma, M.-M.; Liu, H.; Liu, Z.-J. Inversion of the shear velocity radial profile in a cased borehole. Chin. J. Geophys. 2016, 59, 4782–4790. [Google Scholar] [CrossRef]
- Tang, X.-M.; Patterson, D.J. Mapping formation radial shear-wave velocity variation by a constrained inversion of borehole flexural-wave dispersion data. Geophysics 2010, 75, E183–E190. [Google Scholar] [CrossRef]
- Su, Y.-D.; Tang, X.-M.; Hei, C.; Zhuang, C.-X. An equivalent-tool theory for acoustic logging and applications. Appl. Geophys. 2011, 8, 69–78. [Google Scholar] [CrossRef]
- Xu, S.; Tang, X.-M.; Su, Y.; Zhuang, C. Determining formation shear wave transverse isotropy jointly from borehole Stoneley- and flexural-wave data. Chin. J. Geophys. 2018, 61, 5105–5114. [Google Scholar] [CrossRef]
- Tang, X.M.; Cheng, A. Quantitative Borehole Acoustic Methods; Elsevier: Amsterdam, The Netherlands, 2004; pp. 120–125. [Google Scholar]
- Norris, A.N. The speed of a tube wave. J. Acoust. Soc. Am. 1990, 87, 414. [Google Scholar] [CrossRef]




| Formation Properties | Radial Depth (m) | P-Wave Velocity (m/s) | S-Wave Velocity (m/s) | Density (kg/m3) |
|---|---|---|---|---|
| Borehole fluid | r < 0.1 | 1500 | - | 1000 |
| TZ1 | 0.10 < r < 0.15 | 2400 | 1000 | 2500 |
| TZ2 | 0.15 < r < 0.20 | 2400 | 1050 | 2500 |
| TZ3 | 0.20 < r < 0.25 | 2400 | 1100 | 2500 |
| TZ4 | 0.25 < r < 0.30 | 2400 | 1150 | 2500 |
| Undisturbed Formation | r > 0.30 | 2400 | 1200 | 2500 |
| Formation Parameters | Tool Parameters | ||
|---|---|---|---|
| P-wave velocity (m/s) | 3200 | Density (kg/m3) | 7850 |
| S-wave velocity (m/s) | 2300 | Inner radius (m) | 0.01 |
| Density (kg/m3) | 2500 | Outer radius (m) | 0.045 |
| Radius (m) | 0.1 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ye, Q.; Sun, H.; Jin, Z.; Wang, B. Study on Shear Velocity Profile Inversion Using an Improved High Frequency Constrained Algorithm. Energies 2023, 16, 59. https://doi.org/10.3390/en16010059
Ye Q, Sun H, Jin Z, Wang B. Study on Shear Velocity Profile Inversion Using an Improved High Frequency Constrained Algorithm. Energies. 2023; 16(1):59. https://doi.org/10.3390/en16010059
Chicago/Turabian StyleYe, Qing, Huafeng Sun, Zhiqiang Jin, and Bing Wang. 2023. "Study on Shear Velocity Profile Inversion Using an Improved High Frequency Constrained Algorithm" Energies 16, no. 1: 59. https://doi.org/10.3390/en16010059
APA StyleYe, Q., Sun, H., Jin, Z., & Wang, B. (2023). Study on Shear Velocity Profile Inversion Using an Improved High Frequency Constrained Algorithm. Energies, 16(1), 59. https://doi.org/10.3390/en16010059






