Framework of Transactive Energy Market Strategies for Lucrative Peer-to-Peer Energy Transactions
Abstract
:1. Introduction
- A transactive energy market operator (TEMO) framework is developed to facilitate power trading between residential buildings through a peer-to-peer energy market.
- A new local energy market with different market-clearing strategies is presented to ensure profitable power transaction between the neighboring end-users.
- The proposed trading strategies are extended to increase the market reliability by penalizing the participants for their abnormal activities in energy trading.
2. Framework of TEMO
3. P2P Energy Market Strategies
3.1. Mid-Pricing Strategy (MPS)
3.1.1. Higher Locality Demand ()
3.1.2. Higher Locality Generation ()
3.2. GDR Strategy (GDRS)
3.2.1. Higher Locality Demand ()
3.2.2. Higher Locality Generation ()
3.3. Double Auction Strategy (DAS)
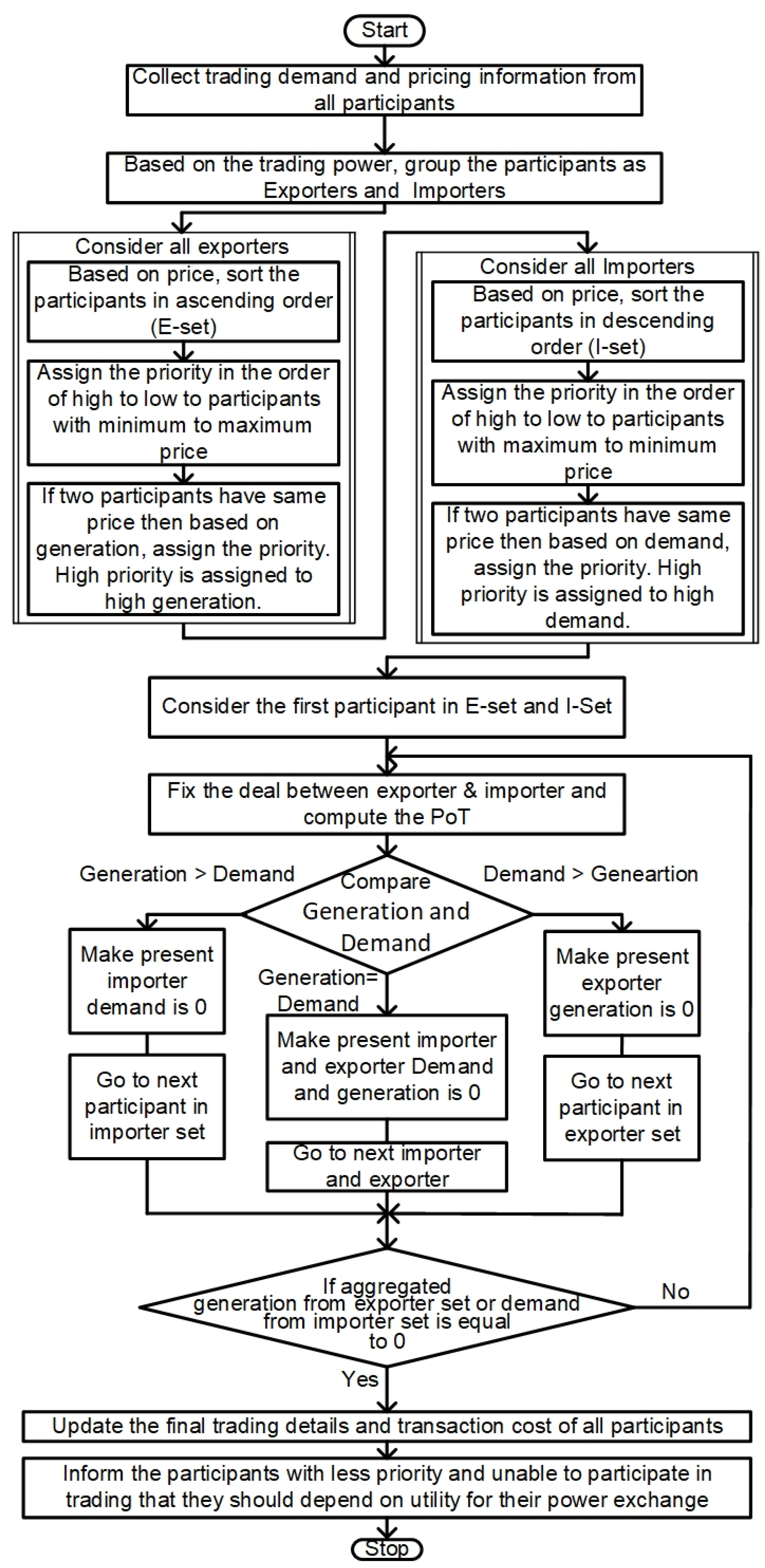
3.4. Priority-Based Auction Strategy (PAS)
4. Simulation Study
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fang, X.; Misra, S.; Xue, G.; Yang, D. Smart Grid—The New and Improved Power Grid: A Survey. IEEE Commun. Surv. Tutor. 2012, 14, 944–980. [Google Scholar] [CrossRef]
- Esther, B.P.; Kumar, K.S. A survey on residential Demand Side Management architecture, approaches, optimization models and methods. Renew. Sustain. Energy Rev. 2016, 59, 342–351. [Google Scholar] [CrossRef]
- Arun, S.L.; Selvan, M.P. Intelligent residential energy management system for dynamic demand response in smart buildings. IEEE Syst. J. 2018, 12, 1329–1340. [Google Scholar] [CrossRef]
- Solar Bonus Report, Queensland Government. Department of Natural Resources, Mines and Energy, October 2018, Policy Guide. 2018. Available online: https://www.dnrm.qld.gov.au/__data/assets/pdf_file/0005/1379678/solar-bonus-scheme.pdf (accessed on 20 July 2019).
- Liu, N.; Yu, X.; Wang, C.; Li, C.; Ma, L.; Lei, J. Energy-Sharing Model with Price-Based Demand Response for Microgrids of Peer-to-Peer Prosumers. IEEE Trans. Power Syst. 2017, 32, 3569–3583. [Google Scholar] [CrossRef]
- Rao, B.H.; Arun, S.L.; Selvan, M.P. Framework of locality electricity trading system for profitable peer-to-peer power transaction in locality electricity market. IET Smart Grid 2020, 3, 318–330. [Google Scholar] [CrossRef]
- Palensky, P.; Dietrich, D. Demand Side Management: Demand Response, Intelligent Energy Systems, and Smart Loads. IEEE Trans. Ind. Inform. 2011, 7, 381–388. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Zhang, C.; Xu, Z.; Wang, J.; Zhao, J.; Zhang, Y.-J.A. Distributed transactive energy trading framework in distribution networks. IEEE Trans. Power Syst. 2018, 33, 7215–7227. [Google Scholar] [CrossRef]
- Ramachandran, V.; Perumal, A.S.; Lakshmaiya, N.; Paramasivam, P.; Dhanasekaran, S. Unified Power Control of Permanent Magnet Synchronous Generator Based Wind Power System with Ancillary Support during Grid Faults. Energies 2022, 15, 7385. [Google Scholar] [CrossRef]
- Wang, Y.; Saad, W.; Han, Z.; Poor, H.V.; Basar, T. A Game-Theoretic Approach to Energy Trading in the Smart Grid. IEEE Trans. Smart Grid 2014, 5, 1439–1450. [Google Scholar] [CrossRef] [Green Version]
- Kang, J.; Yu, R.; Huang, X.; Maharjan, S.; Zhang, Y.; Hossain, E. Enabling Localized Peer-to-Peer Electricity Trading Among Plug-in Hybrid Electric Vehicles Using Consortium Blockchains. IEEE Trans. Ind. Inform. 2017, 13, 3154–3164. [Google Scholar] [CrossRef]
- Rajagopalan, A.; Nagarajan, K.; Montoya, O.D.; Dhanasekaran, S.; Kareem, I.A.; Perumal, A.S.; Lakshmaiya, N.; Paramasivam, P. Multi-Objective Optimal Scheduling of a Microgrid Using Oppositional Gradient-Based Grey Wolf Optimizer. Energies 2022, 15, 9024. [Google Scholar] [CrossRef]
- Lezama, F.; Soares, J.; Hernandez-Leal, P.; Kaisers, M.; Pinto, T.; Vale, Z.M.A.D. Local Energy Markets: Paving the Path Toward Fully Transactive Energy Systems. IEEE Trans. Power Syst. 2018, 34, 4081–4088. [Google Scholar] [CrossRef] [Green Version]
- Nicolaisen, J.; Petrov, V.; Tesfatsion, L. Market power and efficiency in a computational electricity market with discriminatory double-auction pricing. IEEE Trans. Evol. Comput. 2001, 5, 504–523. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.; Yu, X.; Mu, Y.; Jia, H. A distributed Peer-to-Peer energy transaction method for diversified prosumers in Urban Community Microgrid System. Appl. Energy 2019, 260, 114327. [Google Scholar] [CrossRef]
- Zhang, C.; Wu, J.; Cheng, M.; Zhou, Y.; Long, C. A Bidding System for Peer-to-Peer Energy Trading in a Grid-connected Microgrid. Energy Procedia 2016, 103, 147–152. [Google Scholar] [CrossRef]
- Abdella, J.; Shuaib, K. Peer to Peer Distributed Energy Trading in Smart Grids: A Survey. Energies 2018, 11, 1560. [Google Scholar] [CrossRef] [Green Version]
- Huang, Q.; Amin, W.; Umer, K.; Gooi, H.B.; Eddy, F.Y.S.; Afzal, M.; Shahzadi, M.; Khan, A.A.; Ahmad, S.A. A review of transactive energy systems: Concept and implementation. Energy Rep. 2021, 7, 7804–7824. [Google Scholar] [CrossRef]
- Chen, S.; Liu, C.C. From demand response to transactive energy: State of the art. J. Mod. Power Syst. Clean Energy 2017, 5, 10–19. [Google Scholar] [CrossRef] [Green Version]
- Kabiri-Renani, Y.; Daneshvar, M.; Mohammadi-Ivatloo, B. Transactive energy revolution: Innovative leverage for reliable operation of modern energy networks—A critical review. IET Renew. Power Gener. 2022, 16, 3368–3383. [Google Scholar] [CrossRef]
- Xia, Y.; Xu, Q.; Li, S.; Tang, R.; Du, P. Reviewing the peer-to-peer transactive energy market: Trading environment, optimization methodology, and relevant resources. J. Clean. Prod. 2023, 383, 135441. [Google Scholar] [CrossRef]
- Amin, W.; Huang, Q.; Umer, K.; Zhang, Z.; Afzal, M.; Khan, A.A.; Ahmed, S.A. A motivational game-theoretic approach for peer-to-peer energy trading in islanded and grid-connected microgrid. Int. J. Electr. Power Energy Syst. 2020, 123, 106307. [Google Scholar] [CrossRef]
- Arun, S.L.; Selvan, M.P. Dynamic demand response in smart buildings using an intelligent residential load management system. IET Gener. Transm. Distrib. 2017, 11, 4348–4357. [Google Scholar] [CrossRef]
- Singaravel, M.M.R.; Daniel, S.A. Sizing of hybrid PMSG-PV system for battery charging of electric vehicles. Front. Energy 2015, 9, 68–74. [Google Scholar] [CrossRef]
- Kanimozhi, G.; Natrayan, L.; Angalaeswari, S.; Paramasivam, P. An Effective Charger for Plug-In Hybrid Electric Vehicles (PHEV) with an Enhanced PFC Rectifier and ZVS-ZCS DC/DC High-Frequency Converter. J. Adv. Transp. 2022, 2022, 7840102. [Google Scholar] [CrossRef]
- Bokkisam, H.R.; Acharya, R.M.; Selvan, M.P. Framework of transactive energy market pool for community energy trading and demand response management using an auction-theoretic approach. Int. J. Electr. Power Energy Syst. 2021, 137, 107719. [Google Scholar] [CrossRef]








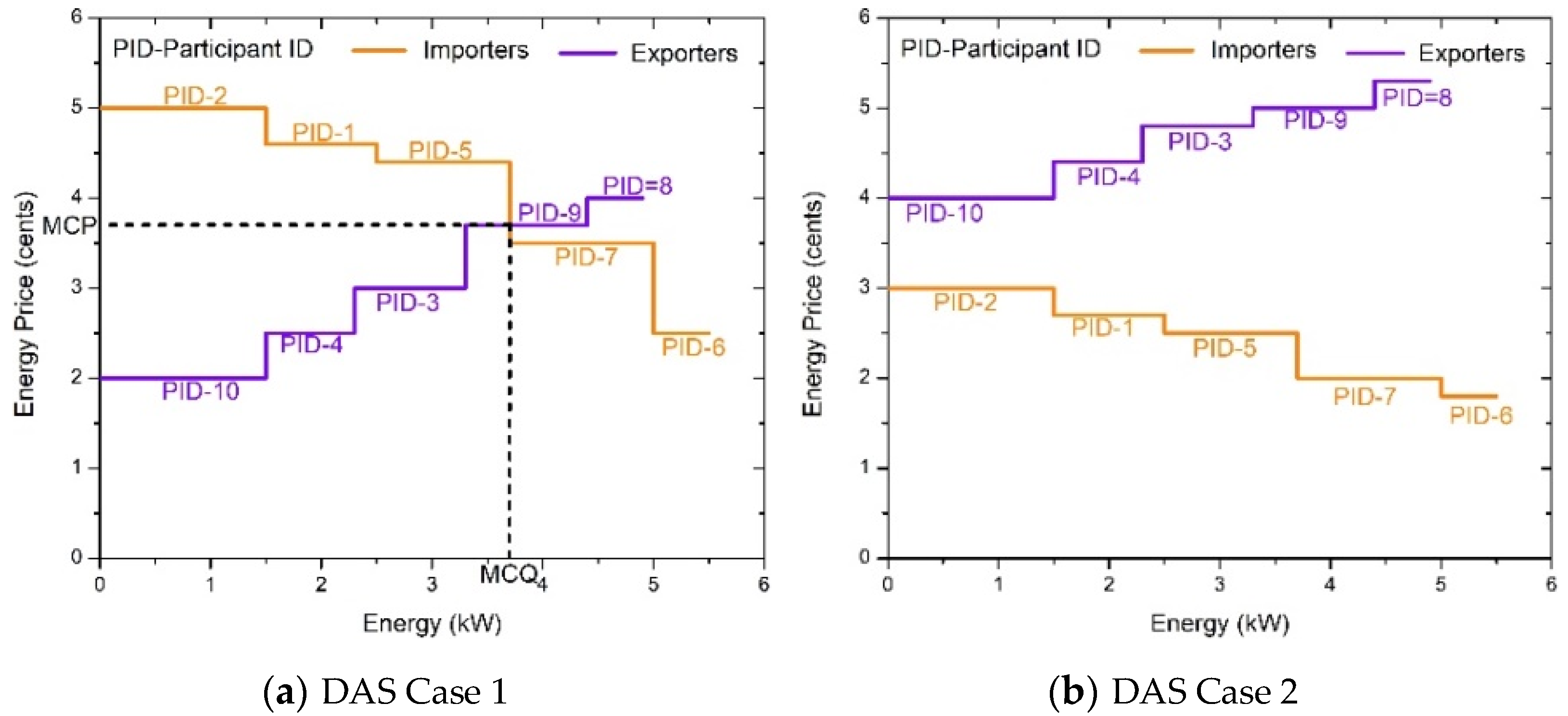
| Participant ID (PID) | (kW) | Case 1 | Case 2 |
|---|---|---|---|
| 1 | 1 | 4.6 | 2.7 |
| 2 | 1.5 | 5 | 3 |
| 3 | −1 | 3 | 4.8 |
| 4 | −0.8 | 2.5 | 4.4 |
| 5 | 1.2 | 4.4 | 2.5 |
| 6 | 0.5 | 2.5 | 1.8 |
| 7 | 1.3 | 3.5 | 2 |
| 8 | −0.5 | 4 | 5.3 |
| 9 | −1.1 | 3.5 | 5 |
| 10 | −1.5 | 2 | 4 |
| Participant | P2G | MPS | GDRS | DAS | PAS | ||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 108.8 | 104.25 | 4.19 | 100.49 | 7.64 | 96.93 | 10.91 | 96.21 | 11.58 |
| 2 | 110.2 | 105.48 | 4.29 | 101.93 | 7.51 | 98 | 11.08 | 97.13 | 11.87 |
| 3 | 93.69 | 84.32 | 10.01 | 87.1 | 7.04 | 83.13 | 11.28 | 80.73 | 13.84 |
| 4 | 95.95 | 88.12 | 8.17 | 89.27 | 6.97 | 85.92 | 10.46 | 81.59 | 14.97 |
| 5 | 95.83 | 86.36 | 9.89 | 88.34 | 7.82 | 84.14 | 12.2 | 82.82 | 13.58 |
| 6 | 96.24 | 90.77 | 5.69 | 87.94 | 8.63 | 85.29 | 11.38 | 81.61 | 15.21 |
| 7 | 112.04 | 107.86 | 3.74 | 102.18 | 8.81 | 97.21 | 13.24 | 94.23 | 15.9 |
| 8 | 99.23 | 92.51 | 6.78 | 92.36 | 6.93 | 88.42 | 10.9 | 86.93 | 12.4 |
| 9 | 94.64 | 89.91 | 5 | 85.61 | 9.55 | 83.86 | 11.4 | 81.27 | 14.13 |
| 10 | 111.77 | 107.07 | 4.21 | 103.12 | 7.74 | 100.3 | 10.27 | 96.47 | 13.69 |
| Participant | (kW) | (kW) | (c) | MPS (Cents) | GDRS (Cents) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1.5 | 1.7 | 0.21 | 6.6 | 1.08 | 0 | 7.89 | 6.3 | 1.08 | 0 | 7.59 |
| 2 | −1 | −0.8 | 0.21 | −3.5 | 0 | 0 | −3.29 | −3.1 | 0 | 0 | −2.89 |
| 3 | 1.5 | 1.5 | 0 | 6.6 | 0 | 0 | 6.6 | 6.3 | 0 | 0 | 6.3 |
| 4 | 2 | 2.5 | 0.53 | 8.8 | 2.7 | 0 | 12.03 | 8.4 | 2.7 | 0 | 11.63 |
| 5 | −1.5 | 0.5 | 2.1 | −5.25 | 2.7 | 5.25 | 4.8 | −4.65 | 2.7 | 4.35 | 4.5 |
| 6 | 2.5 | 1.5 | 1.05 | 11 | 0 | −4.4 | 7.65 | 10.5 | 0 | −4.2 | 7.35 |
| 7 | 0.5 | 0.8 | 0.32 | 2.2 | 1.62 | 0 | 4.14 | 2.1 | 1.62 | 0 | 4.04 |
| 8 | −2 | −2 | 0 | −7 | 0 | 0 | −7 | −6.2 | 0 | 0 | −6.2 |
| 9 | −0.5 | −1.8 | 1.37 | −1.75 | −2.08 | 0 | −2.46 | −1.55 | −2.08 | 0 | −2.26 |
| 10 | 1 | 1 | 0 | 4.4 | 0 | 0 | 4.4 | 4.2 | 0 | 0 | 4.2 |
| Participant | (kW) | (c) | (kW) | (c) | DAS (Cents) | PAS (Cents) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1.5 | 3.2 | 1.7 | 0.21 | 4.8 | 1.08 | 0 | 6.09 | 1.6 | 1.08 | 0 | 2.89 |
| 2 | −1 | 3.2 | −0.8 | 0.21 | −3.2 | 0 | 0 | −2.99 | −3.45 | 0 | 0 | −3.24 |
| 3 | 1.5 | 2.9 | 1.5 | 0 | 0 | 8.1 | 0 | 8.1 | 0 | 8.1 | 0 | 8.1 |
| 4 | 2 | 4.5 | 2.5 | 0.53 | 6.4 | 2.7 | 0 | 9.63 | 6.66 | 2.7 | 0 | 9.89 |
| 5 | −1.5 | 2.7 | 0.5 | 2.1 | −4.8 | 2.7 | 4.8 | 4.8 | −5.175 | 2.7 | 5.175 | 4.8 |
| 6 | 2.5 | 4.2 | 1.5 | 1.05 | 8 | 0 | −3.2 | 5.85 | 8.675 | 0 | −3.7 | 6.025 |
| 7 | 0.5 | 2.5 | 0.8 | 0.32 | 0 | 4.32 | 0 | 4.64 | 0 | 4.32 | 0 | 4.64 |
| 8 | −2 | 2.1 | −2 | 0 | −6.4 | 0 | 0 | −6.4 | −6.66 | 0 | 0 | −6.66 |
| 9 | −0.5 | 2.4 | −1.8 | 1.37 | −1.6 | −2.88 | 0 | −3.11 | −1.65 | −2.88 | 0 | −3.16 |
| 10 | 1 | 2 | 1 | 0 | 0 | 5.4 | 0 | 5.4 | 0 | 5.4 | 0 | 5.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Loganathan, A.S.; Ramachandran, V.; Perumal, A.S.; Dhanasekaran, S.; Lakshmaiya, N.; Paramasivam, P. Framework of Transactive Energy Market Strategies for Lucrative Peer-to-Peer Energy Transactions. Energies 2023, 16, 6. https://doi.org/10.3390/en16010006
Loganathan AS, Ramachandran V, Perumal AS, Dhanasekaran S, Lakshmaiya N, Paramasivam P. Framework of Transactive Energy Market Strategies for Lucrative Peer-to-Peer Energy Transactions. Energies. 2023; 16(1):6. https://doi.org/10.3390/en16010006
Chicago/Turabian StyleLoganathan, Arun S., Vijayapriya Ramachandran, Angalaeswari Sendraya Perumal, Seshathiri Dhanasekaran, Natrayan Lakshmaiya, and Prabhu Paramasivam. 2023. "Framework of Transactive Energy Market Strategies for Lucrative Peer-to-Peer Energy Transactions" Energies 16, no. 1: 6. https://doi.org/10.3390/en16010006
APA StyleLoganathan, A. S., Ramachandran, V., Perumal, A. S., Dhanasekaran, S., Lakshmaiya, N., & Paramasivam, P. (2023). Framework of Transactive Energy Market Strategies for Lucrative Peer-to-Peer Energy Transactions. Energies, 16(1), 6. https://doi.org/10.3390/en16010006









