Sizing of Hybrid Power Systems for Off-Grid Applications Using Airborne Wind Energy
Abstract
1. Introduction
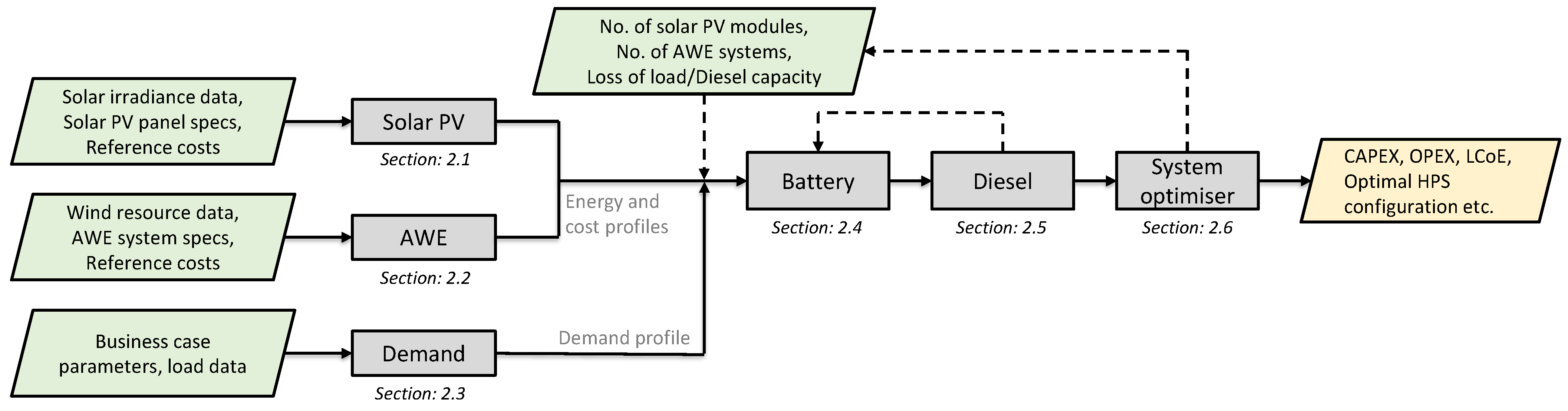
2. Modelling Framework
2.1. Solar Panel Performance, Generated Energy and Costs
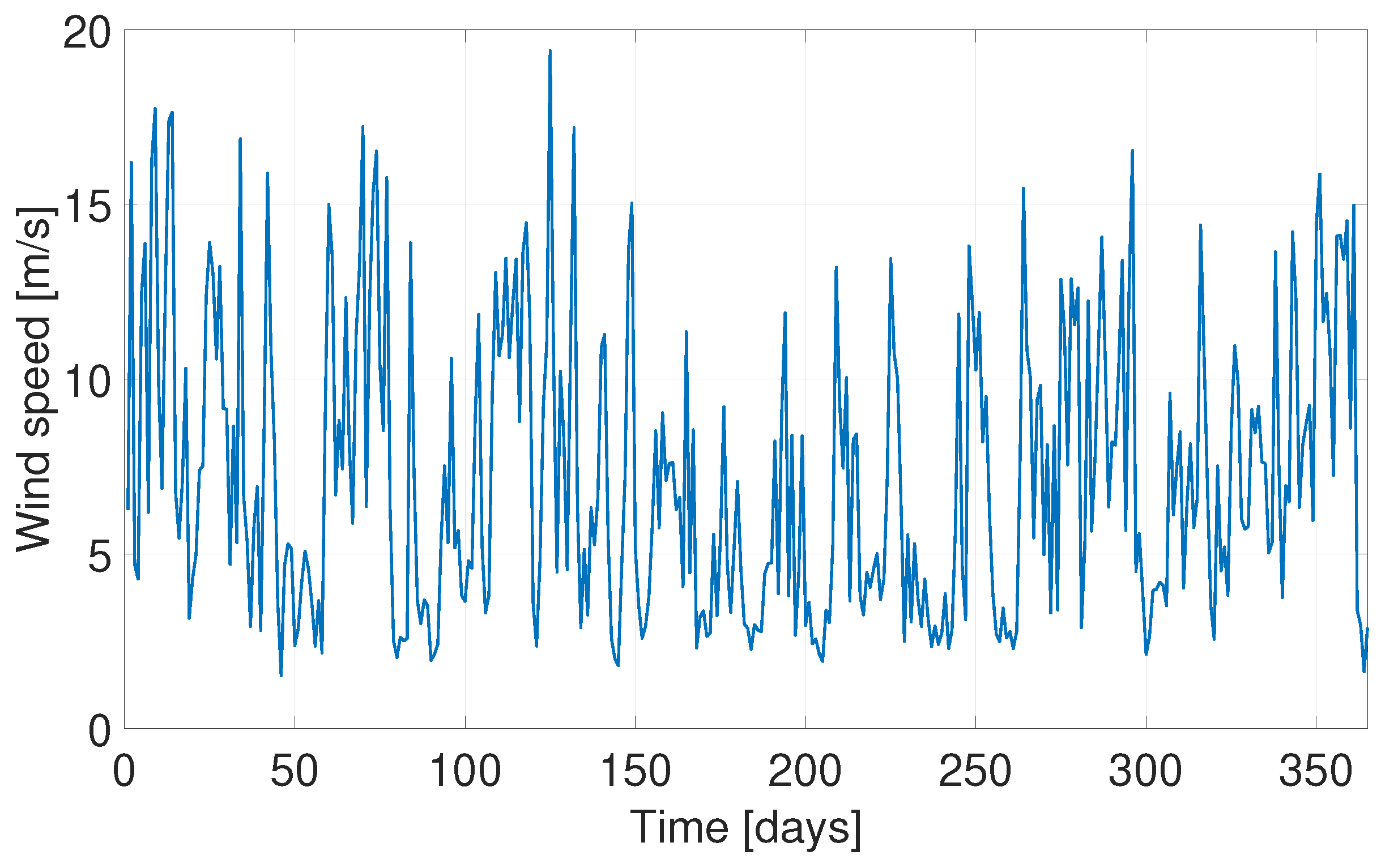
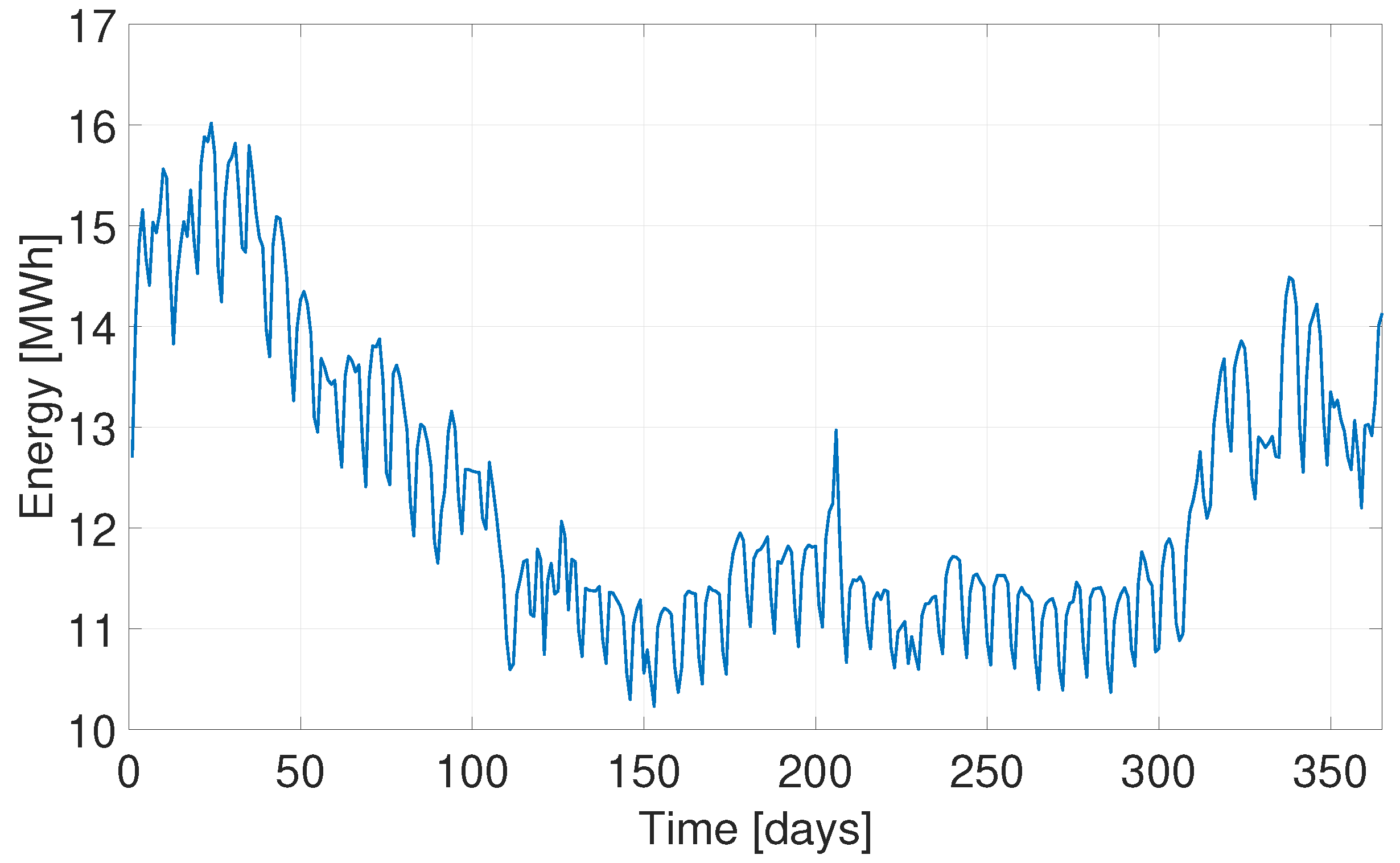
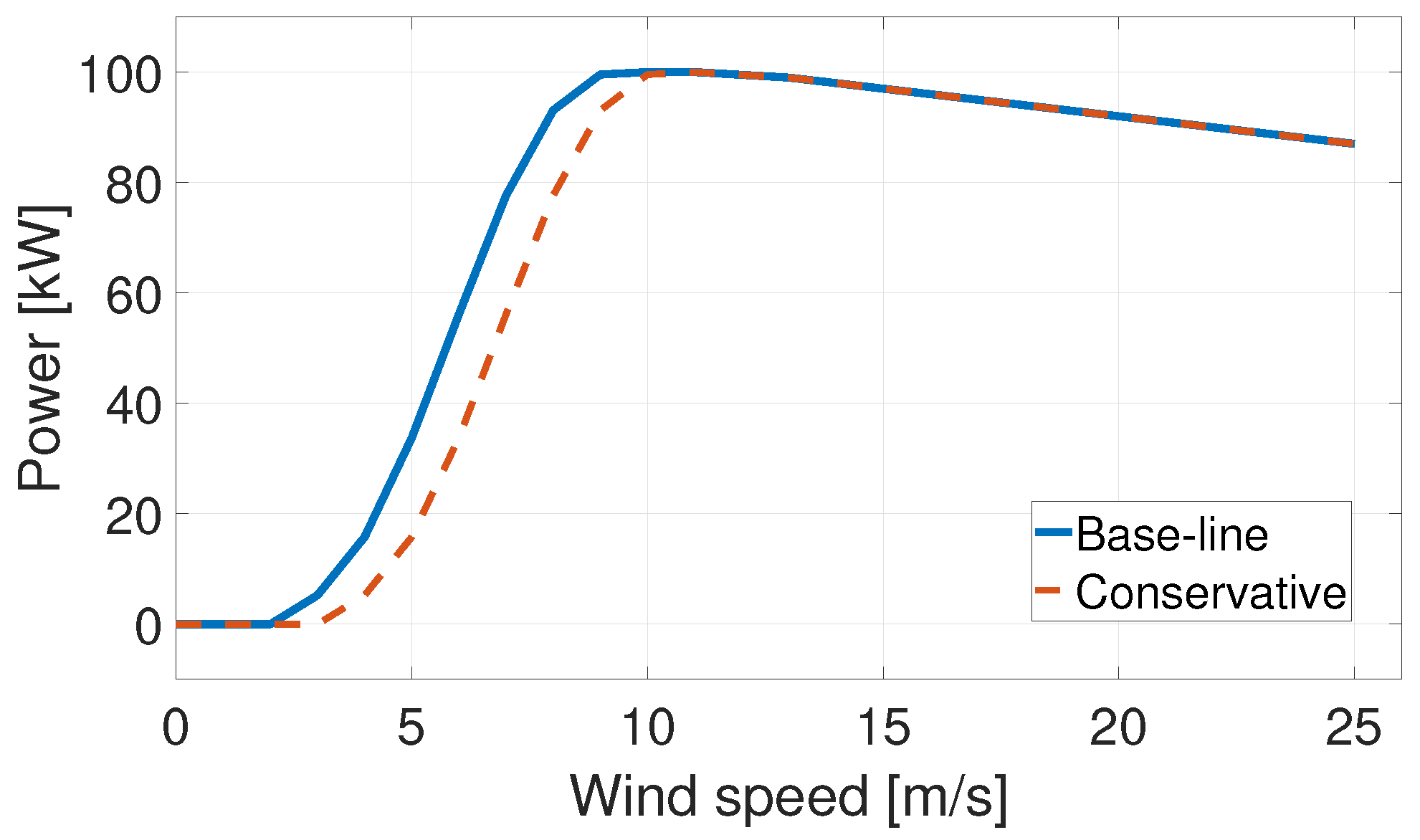
2.2. AWE System Performance, Generated Energy and Costs
2.3. Demand- and Case-Specific Parameters
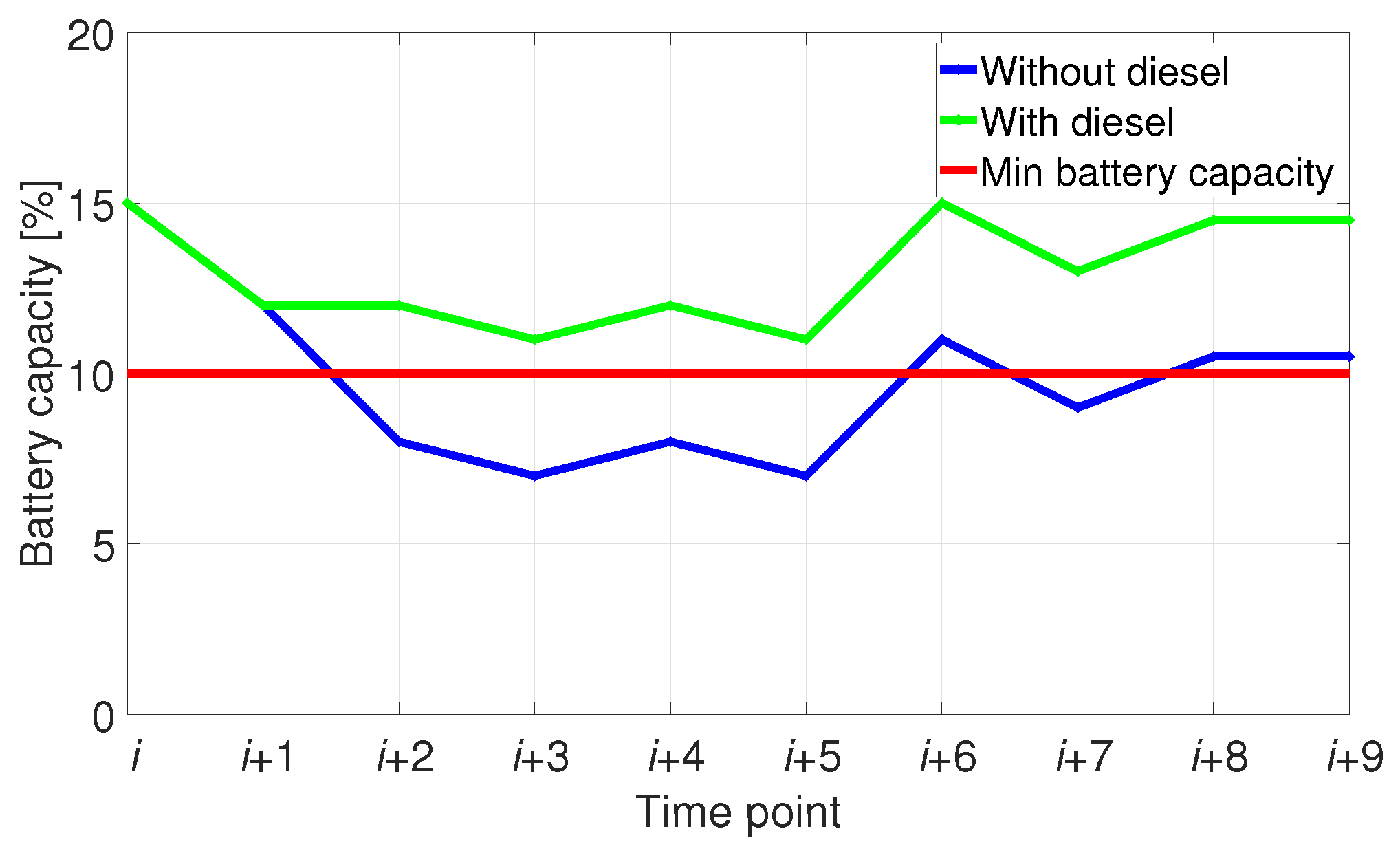
2.4. Battery Capacity and Costs
2.5. Diesel Generator Capacity and Costs
2.6. System Optimiser
3. Results and Discussion
3.1. Case Study Description
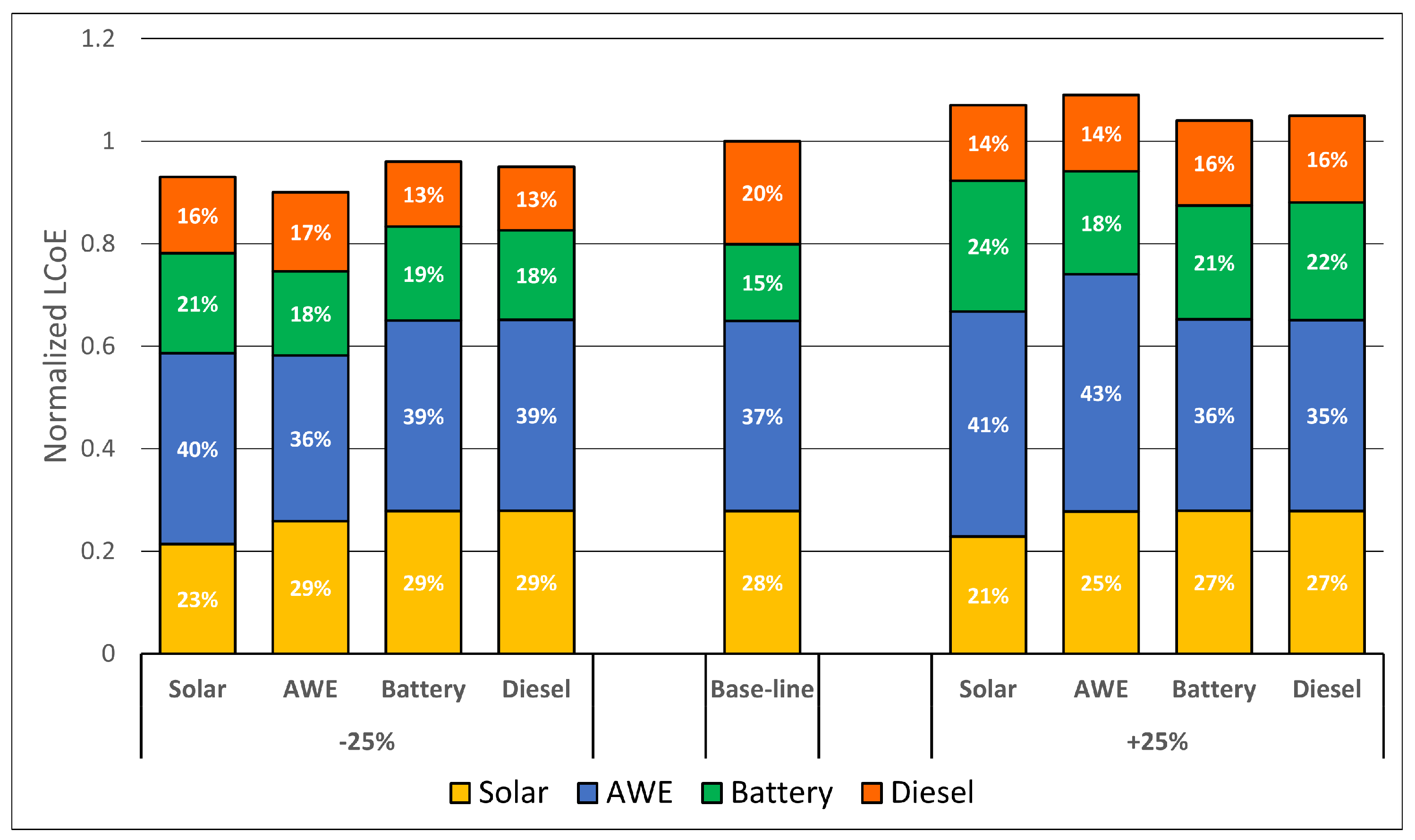
3.2. HPS Configurations
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AWE | Airborne wind energy |
| HPS | Hybrid power system |
| PV | Photovoltaic |
| GHI | Global horizontal irradiance |
| DNI | Direct normal irradiance |
| DHI | Diffuse horizontal irradiance |
| LCoE | Levelised cost of electricity |
| AOI | Angle of incidence |
| SF | Shading factor |
| SVF | Sky view factor |
References
- Paska, J.; Biczel, P.; Kłos, M. Hybrid power systems—An effective way of utilising primary energy sources. Renew. Energy 2009, 34, 2414–2421. [Google Scholar] [CrossRef]
- Dykes, K.; King, J.; Diorio, N.; King, R.; Gevorgian, V.; Corbus, D.; Blair, N.; Anderson, K.; Stark, G.; Turchi, C.; et al. Opportunities for Research and Development of Hybrid Power Plants. Technical Report, National Renewable Energy Laboratory (NREL), Golden, CO, 2020. Available online: https://www.nrel.gov/docs/fy20osti/75026.pdf (accessed on 30 January 2023).
- WindEurope. Database for Wind + Storage Co-Located Projects. Available online: https://windeurope.org/about-wind/database-for-wind-and-storage-colocated-projects/ (accessed on 3 June 2022).
- Bett, P.E.; Thornton, H.E. The climatological relationships between wind and solar energy supply in Britain. Renew. Energy 2016, 87, 96–110. [Google Scholar] [CrossRef]
- Das, K.; Grapperon, A.L.T.P.; Sørensen, P.E.; Hansen, A.D. Optimal battery operation for revenue maximization of wind-storage hybrid power plant. Electr. Power Syst. Res. 2020, 189. [Google Scholar] [CrossRef]
- Gorman, W.; Mills, A.; Bolinger, M.; Wiser, R.; Singhal, N.G.; Ela, E.; O’Shaughnessy, E. Motivations and options for deploying hybrid generator-plus-battery projects within the bulk power system. Electr. J. 2020, 33, 106739. [Google Scholar] [CrossRef]
- Fagiano, L.; Quack, M.; Bauer, F.; Carnel, L.; Oland, E. Autonomous Airborne Wind Energy Systems: Accomplishments and Challenges. Annu. Rev. Control Robot. Auton. Syst. 2022, 5, 603–631. [Google Scholar] [CrossRef]
- Bechtle, P.; Schelbergen, M.; Schmehl, R.; Zillmann, U.; Watson, S. Airborne Wind Energy Resource Analysis. Renew. Energy 2019, 141, 1103–1116. [Google Scholar] [CrossRef]
- Noun Project. Icons and Photos for Everything. Available online: https://thenounproject.com/ (accessed on 23 May 2022).
- Khan, Z.H.; Khan, S.A.; Khan, A.H. Prospects of Airborne Wind Energy Systems in Pakistan. In Proceedings of the Fourth International Conference on Aerospace Science and Engineering (ICASE), Islamabad, Pakistan, 2–4 September 2015. [Google Scholar]
- UNFCCC Technology Executive Committee. Emering Climate Technologies in the Energy Supply Sector. Technical Report, United Nations Framework Convention on Climate Change, Bonn, Germany, 2021. Available online: https://unfccc.int/ttclear/tec/energysupplysector.html (accessed on 21 January 2023).
- Enerwhere. What Will It Take for Airborne Wind Energy (AWE) to Be Successful in Remote & Mini-Grid Applications? Available online: https://www.enerwhere.com/AWES-Success-Remote-Mini-Grid (accessed on 27 December 2022).
- Enerkite GmbH. EK200—Airborne Wind Energy and Storage System, Catering to Off-Grid and Mobile End-Uses (AWESOME). Available online: https://cordis.europa.eu/project/id/736399 (accessed on 22 December 2022).
- Nouri, M.; Miansari, M. Airborne wind energy-driven hybrid system for simultaneous production of power, potable water, and liquid carbon dioxide. Energy Convers. Manag. 2021, 233, 113913. [Google Scholar] [CrossRef]
- De la Garza Cuevas, R. Kite Power in a Microgrid. Master’s Thesis, Delft University of Technology, Delft, The Netherlands, 2018. Available online: http://resolver.tudelft.nl/uuid:7653081f-710b-4511-be05-f1df9e6abc31 (accessed on 21 January 2023).
- Ouroumova, L.; Witte, D.; Klootwijk, B.; Terwindt, E.; van Marion, F.; Mordasov, D.; Vargas, F.C.; Heidweiller, S.; Géczi, M.; Kempers, M.; et al. Combined Airborne Wind and Photovoltaic Energy System for Martian Habitats. Spool 2021, 8, 71–85. [Google Scholar] [CrossRef]
- Rodriguez, M. Airborne Wind Energy Systems for Mars Habitats. Master’s Thesis, Delft University of Technology, Delft, The Netherlands, 2022. Available online: http://resolver.tudelft.nl/uuid:52a156ae-c758-4d3a-a403-54ce5fce2e5e (accessed on 21 January 2023).
- Reuchlin, S.P.A. Modelling and Sizing of a Hybrid Power Plant Using Airborne Wind Energy. Master’s Thesis, Delft University of Technology, Delft, The Netherlands, 2022. Available online: http://resolver.tudelft.nl/uuid:041b3cf7-4b10-44c2-9b49-8f58b6f8419c (accessed on 21 January 2023).
- Reuchlin, S. GitHub Repository of the MATLAB Based Source Code of the Hybrid Power System Sizing Framework. 2022. Available online: https://github.com/awegroup/AWE-HPS (accessed on 1 May 2023).
- NREL. NSRDB Data Viewer. Available online: https://maps.nrel.gov/nsrdb-viewer/ (accessed on 21 March 2022).
- Smets, A.; Jäger, K.; Isabella, O.; van Swaaij, R.; Zeman, M. Solar Energy: The Physics and Engineering of Photovoltaic Conversion Technologies and Systems; UIT Cambridge Ltd.: Cambridge, UK, 2016. [Google Scholar]
- ERA5. ERA5 Hourly Data on Pressure Levels from 1979 to Present. Available online: https://cds.climate.copernicus.eu/ (accessed on 2 February 2022).
- Olauson, J. ERA5: The new champion of wind power modelling? Renew. Energy 2018, 126, 322–331. [Google Scholar] [CrossRef]
- Schelbergen, M.; Kalverla, P.C.; Schmehl, R.; Watson, S.J. Clustering Wind Profile Shapes to Estimate Airborne Wind Energy Production. Wind. Energy Sci. 2020, 5, 1097–1120. [Google Scholar] [CrossRef]
- Schelbergen, M.; Schmehl, R. Validation of the Quasi-Steady Performance Model for Pumping Airborne Wind Energy Systems. J. Phys. Conf. Ser. 2020, 1618, 032003. [Google Scholar] [CrossRef]
- Sommerfeld, M.; Dörenkämper, M.; De Schutter, J.; Crawford, C. Offshore and onshore ground-generation airborne wind energy power curve characterization. Wind. Energy Sci. Discuss. 2020, 2020, 1–39. [Google Scholar] [CrossRef]
- ENTSOE-E. Total Load—Day Ahead/Actual. Available online: https://transparency.entsoe.eu/load-domain/r2/totalLoadR2/show (accessed on 12 March 2022).
- Mulder, F. Implications of diurnal and seasonal variations in renewable energy generation for large scale energy storage. J. Renew. Sustain. Energy 2014, 6, 033105-1–033105-13. [Google Scholar] [CrossRef]
- Hanania, J.; Martin, J.; Stenhouse, K.; Donev, J. Energy Education—Diesel Generator. Available online: https://energyeducation.ca/encyclopedia/Diesel_generator (accessed on 6 May 2022).
- Solano-Peralta, M.; Moner-Girona, M.; van Sark, W.G.; Vallvè, X. “Tropicalisation” of Feed-in Tariffs: A custom-made support scheme for hybrid PV/diesel systems in isolated regions. Renew. Sustain. Energy Rev. 2009, 13, 2279–2294. [Google Scholar] [CrossRef]
- PWC. Green Deal Monitor #4—National or European Taxation of CO2 Emissions? Available online: https://www.pwc.nl/en/topics/sustainability/green-deal-monitor/green-deal-monitor-4.html (accessed on 6 May 2022).
- International Renewable Energy Agency (IRENA). Renewable Power Generation Costs in 2019. Available online: https://www.irena.org/publications/2020/Jun/Renewable-Power-Costs-in-2019 (accessed on 2 January 2021).
- Statista. Average Monthly Price of Diesel Fuel in France from January 2018 to November 2022. Available online: https://www.statista.com/statistics/499442/average-price-of-diesel-in-france/ (accessed on 22 February 2023).
- Mutascu, M.I.; Albulescu, C.T.; Apergis, N.; Magazzino, C. Do gasoline and diesel prices co-move? Evidence from the time–frequency domain. Environ. Sci. Pollut. Res. 2022, 29, 68776–68795. [Google Scholar] [CrossRef] [PubMed]
- Panasonic. Photovoltaic Module HIT. Available online: https://www.europe-solarstore.com/download/panasonic/panasonic_VBHN335SJ53_datasheet.pdf (accessed on 13 April 2022).
- Rodriguez, L. Breaking Down Solar Farm Costs. Available online: https://ratedpower.com/blog/solar-farm-costs/ (accessed on 13 April 2022).
- Kitepower, B.V. Kitepower Falcon. Available online: https://thekitepower.com/product/ (accessed on 13 April 2022).
- Thimm, L.; Schelbergen, M.; Bechtle, P.; Schmehl, R. The Airborne Wind Energy Resource Analysis Tool AWERA. In Proceedings of the 9th international Airborne Wind Energy Conference (AWEC 2021), Milano, Italy, 22–24 June 2022; Available online: http://resolver.tudelft.nl/uuid:ba0c7fb2-baff-4110-9a51-c27a8498663b (accessed on 21 January 2023).
- Van der Vlugt, R.; Bley, A.; Noom, M.; Schmehl, R. Quasi-steady model of a pumping kite power system. Renew. Energy 2019, 131, 83–99. [Google Scholar] [CrossRef]
- European Centre for Medium-Range Weather Forecasts (ECMWF). ERA5 Dataset. Available online: https://www.ecmwf.int/en/forecasts/dataset/ecmwf-reanalysis-v5 (accessed on 2 May 2021).
- Cole, W.; Frazier, A.W.; Augustine, C. Cost Projections for Utility-Scale Battery Storage: 2021 Update. Technical Report, National Renewable Energy Laboratory (NREL), Golden, CO, 2021. Available online: https://www.nrel.gov/docs/fy21osti/79236.pdf (accessed on 21 January 2023).
- Lane, C. Are Lithium Ion Solar Batteries the Best Energy Storage Option? Available online: https://www.solarreviews.com/blog/are-lithium-ion-the-best-solar-batteries-for-energy-storage (accessed on 6 May 2022).
- Lazard. Lazard’s Levelized Cost of Energy Analysis—Version 8.0. Available online: https://www.seia.org/research-resources/lazards-levelized-cost-energy-analysis-v80 (accessed on 12 May 2022).
- Zebra, E.I.C.; van der Windt, H.J.; Nhumaio, G.; Faaij, A.P. A review of hybrid renewable energy systems in mini-grids for off-grid electrification in developing countries. Renew. Sustain. Energy Rev. 2021, 144, 111036. [Google Scholar] [CrossRef]



| Property | Value | Unit | Source |
|---|---|---|---|
| Average hourly demand | 0.5 | MW | [27] |
| Peak hourly demand | 0.7 | MW | [27] |
| Average wind speed at 320 m | 7.2 | m/s | [22] |
| Equivalent sun hours | 4.0 | kWh/m2/day | [20] |
| Diesel price | 1.37 | €/L | [33,34] |
| Carbon tax | 0.125 | €/kg | [31] |
| Property | Value | Unit |
|---|---|---|
| Energy storage cost | 182 | €/kWh |
| Round-trip efficiency | 90 | % |
| State-of-charge limits | 10–100 | % |
| Life cycle | 10,000 | cycles |
| Lifetime | 10 | years |
| HPS Configuration | Solar PV (MWp) | AWE (MW) | Battery (MWh) | Diesel (%) | LCoE (€/MWh) |
|---|---|---|---|---|---|
| Diesel | 0 | 0 | 0 | 100 | 720 |
| AWE + Battery | 0 | 2 | 92 | 0 | 900 |
| AWE + Battery + Diesel | 0 | 0.7 | 0 | 40 | 410 |
| Solar + Battery | 30 | 0 | 36 | 0 | 670 |
| Solar + Battery + Diesel | 10 | 0 | 8.3 | 27 | 410 |
| Solar + AWE + Battery | 10 | 0.5 | 25 | 0 | 390 |
| Solar + AWE + Diesel | 2.7 | 0.6 | 0 | 24 | 330 |
| Solar + AWE + Battery + Diesel | 5 | 0.6 | 7.2 | 7 | 280 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Reuchlin, S.; Joshi, R.; Schmehl, R. Sizing of Hybrid Power Systems for Off-Grid Applications Using Airborne Wind Energy. Energies 2023, 16, 4036. https://doi.org/10.3390/en16104036
Reuchlin S, Joshi R, Schmehl R. Sizing of Hybrid Power Systems for Off-Grid Applications Using Airborne Wind Energy. Energies. 2023; 16(10):4036. https://doi.org/10.3390/en16104036
Chicago/Turabian StyleReuchlin, Sweder, Rishikesh Joshi, and Roland Schmehl. 2023. "Sizing of Hybrid Power Systems for Off-Grid Applications Using Airborne Wind Energy" Energies 16, no. 10: 4036. https://doi.org/10.3390/en16104036
APA StyleReuchlin, S., Joshi, R., & Schmehl, R. (2023). Sizing of Hybrid Power Systems for Off-Grid Applications Using Airborne Wind Energy. Energies, 16(10), 4036. https://doi.org/10.3390/en16104036









