Modelling Aero-Structural Deformation of Flexible Membrane Kites
Abstract
:1. Introduction
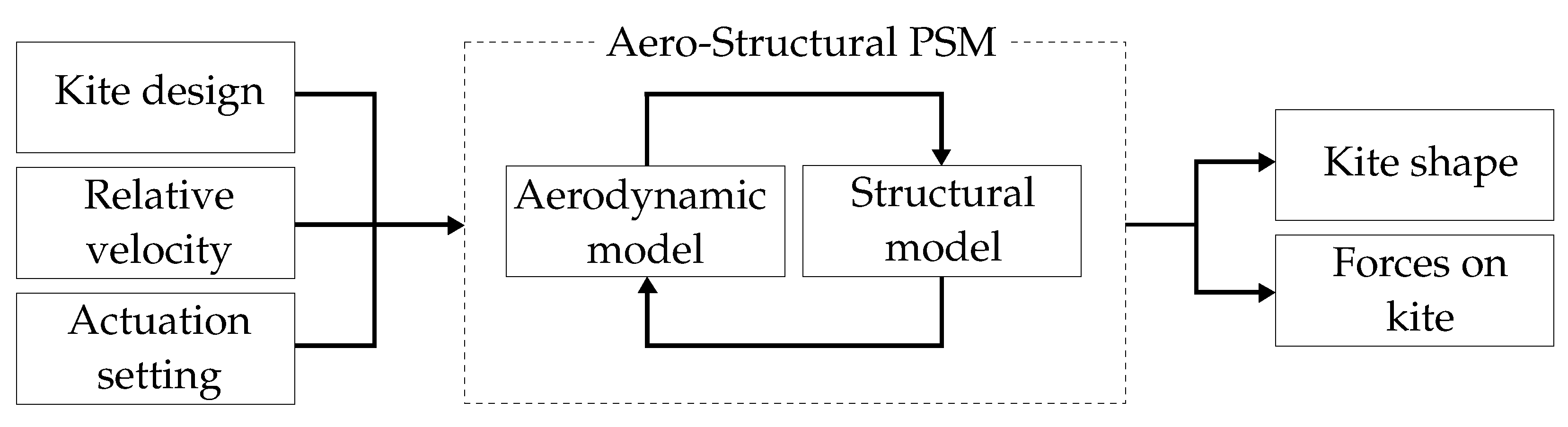
2. Method
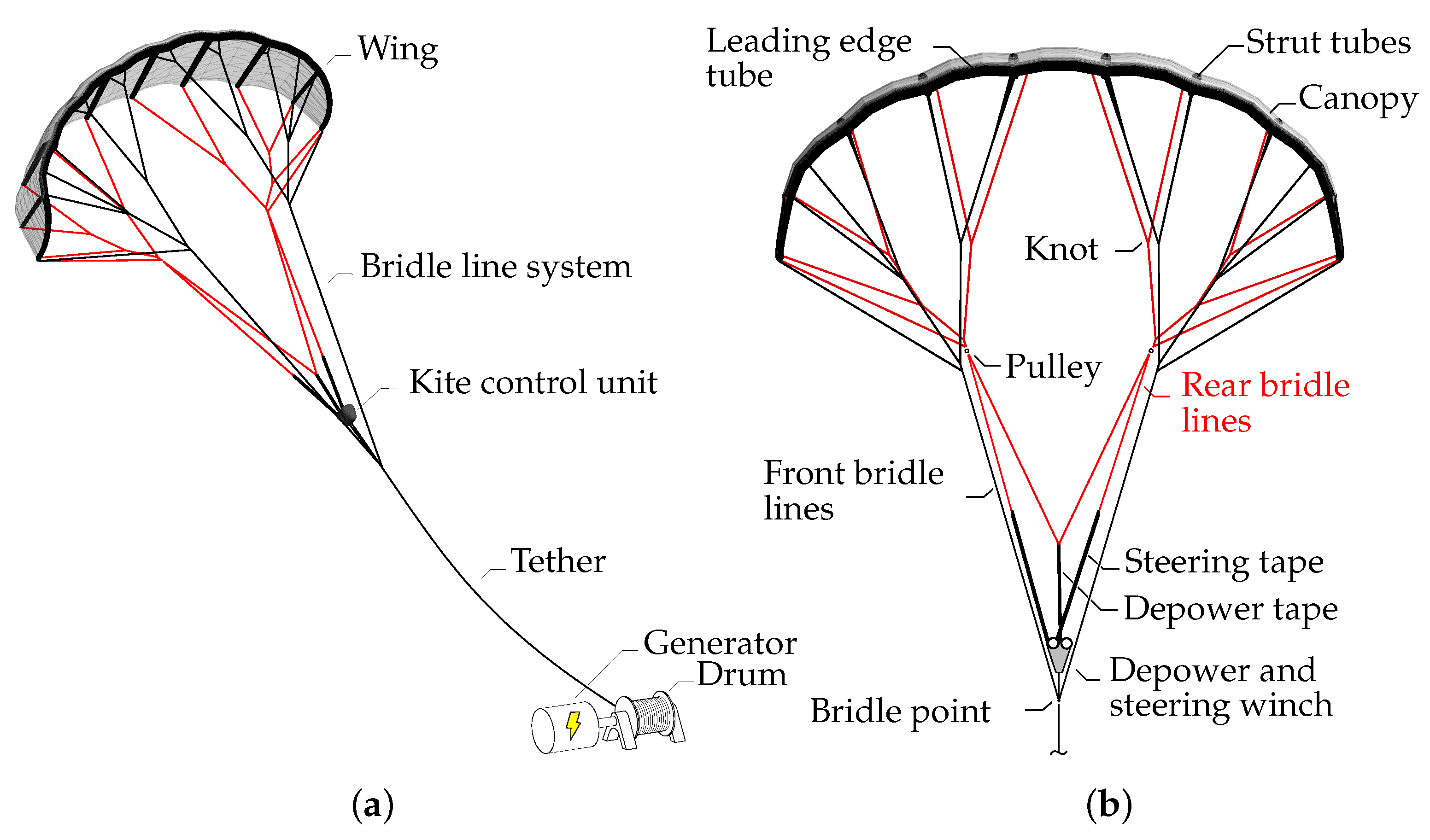
2.1. Kite Specification
2.2. Depowering and Steering Kinematics
2.3. Triangular Two-Plate Wing Model
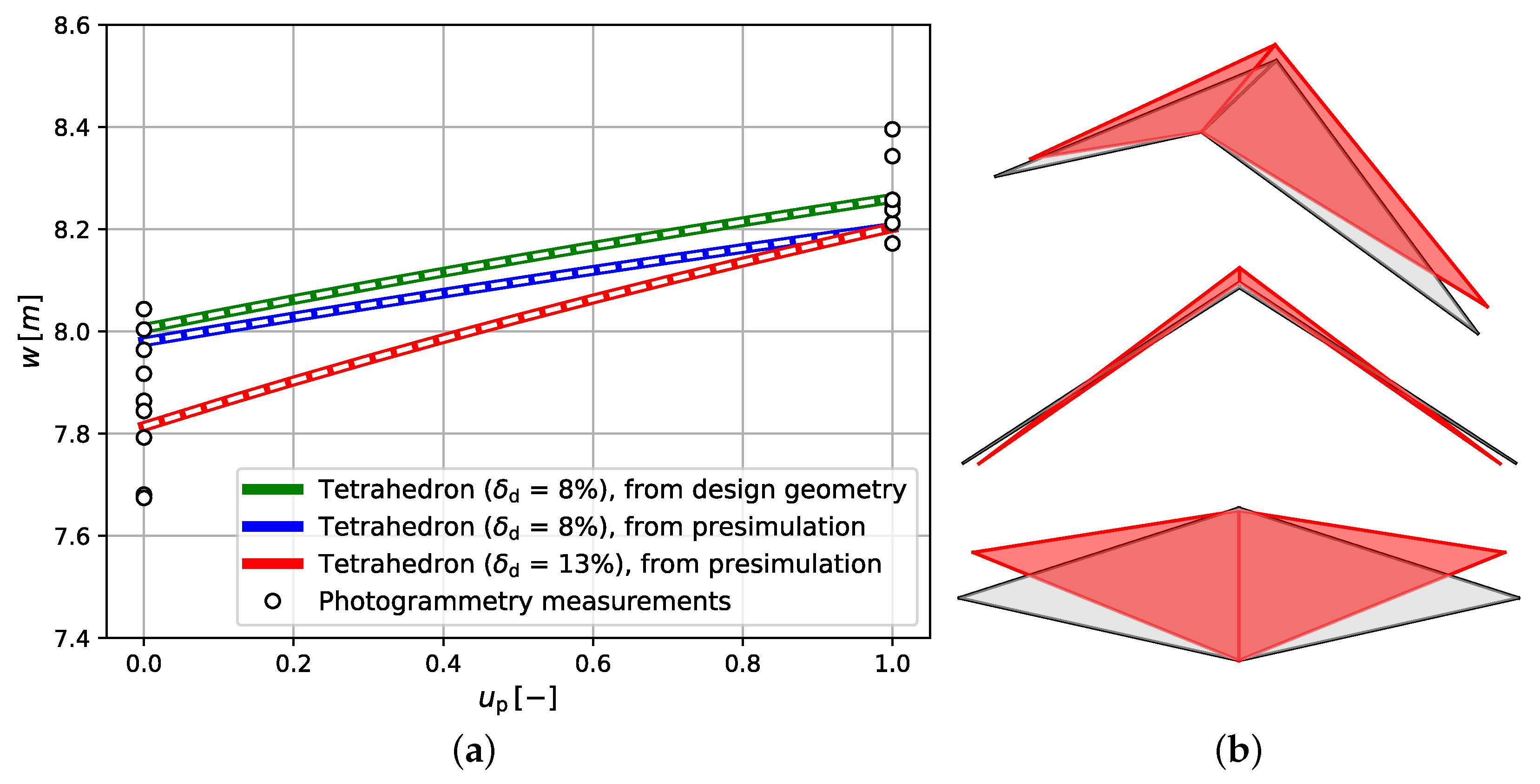
2.3.1. Tetrahedon Algorithm
2.3.2. Trilateration Algorithm
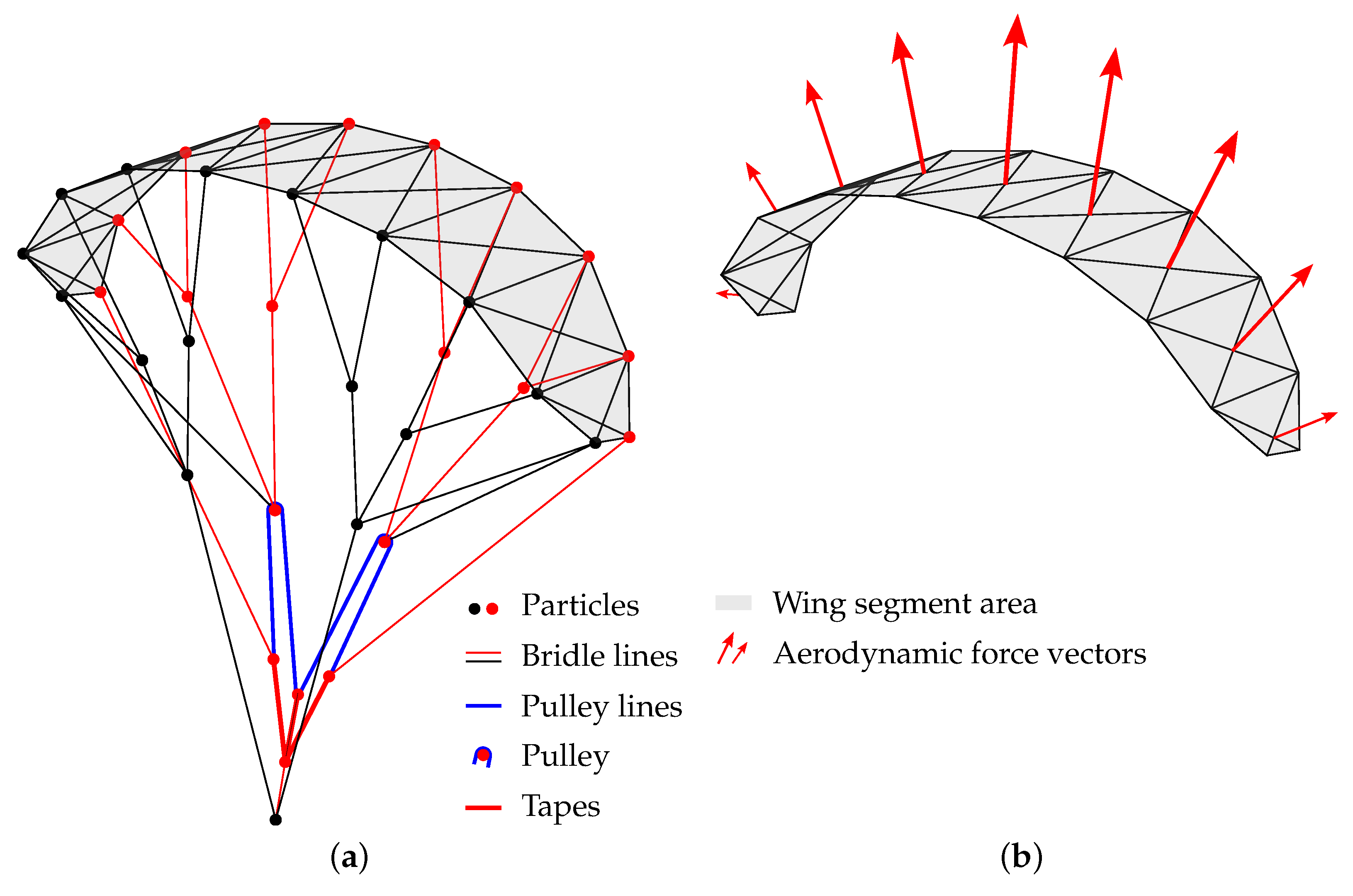
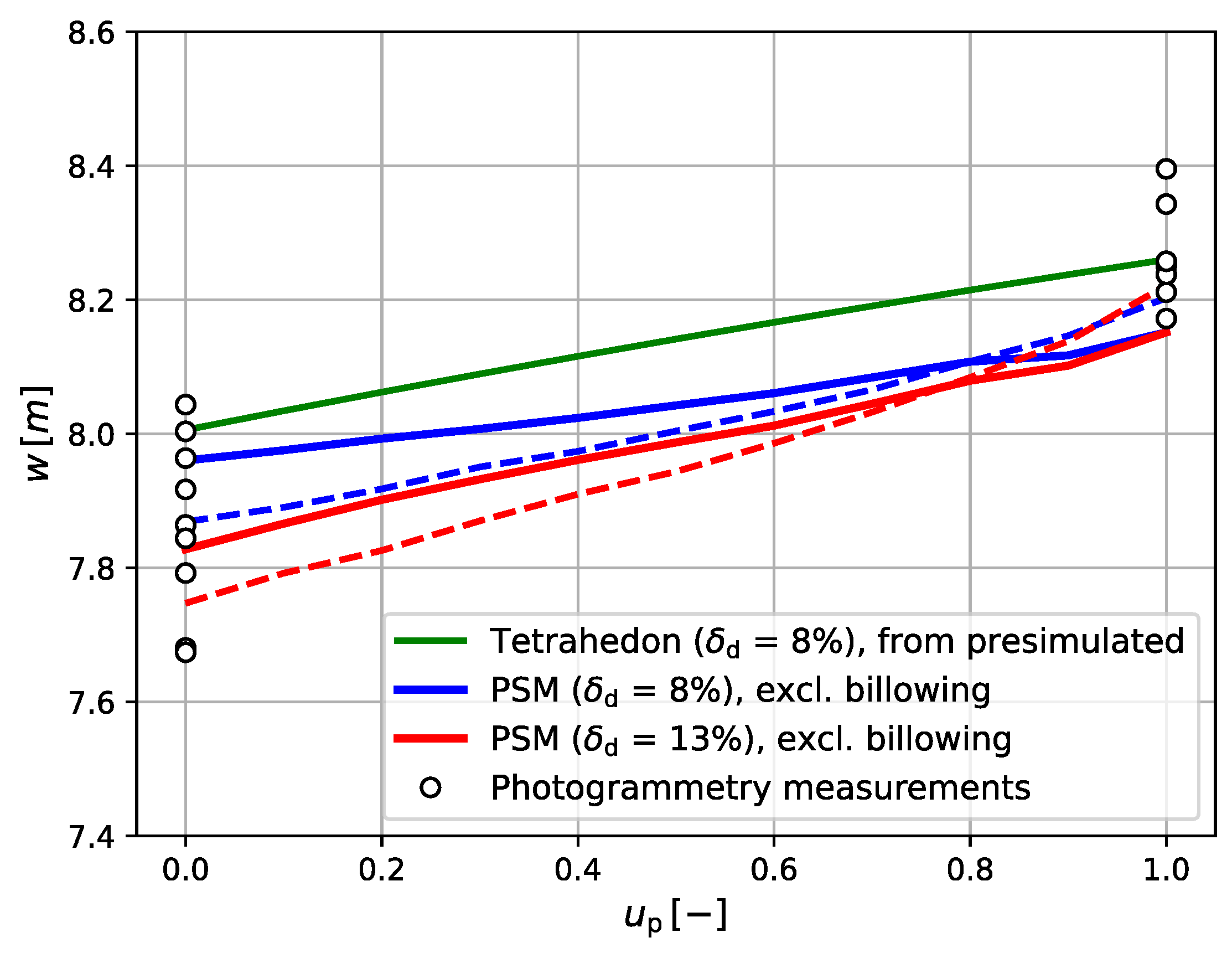
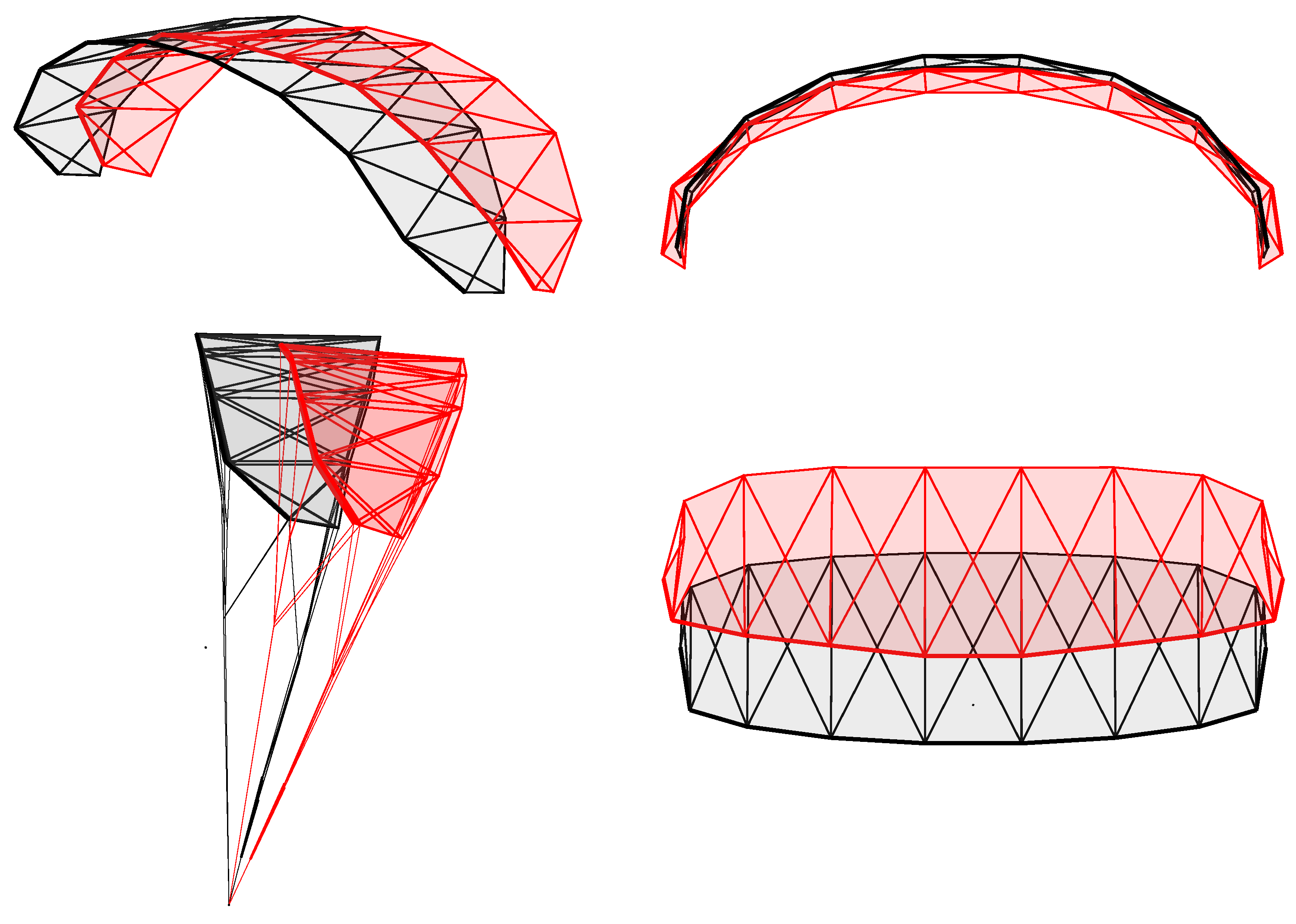
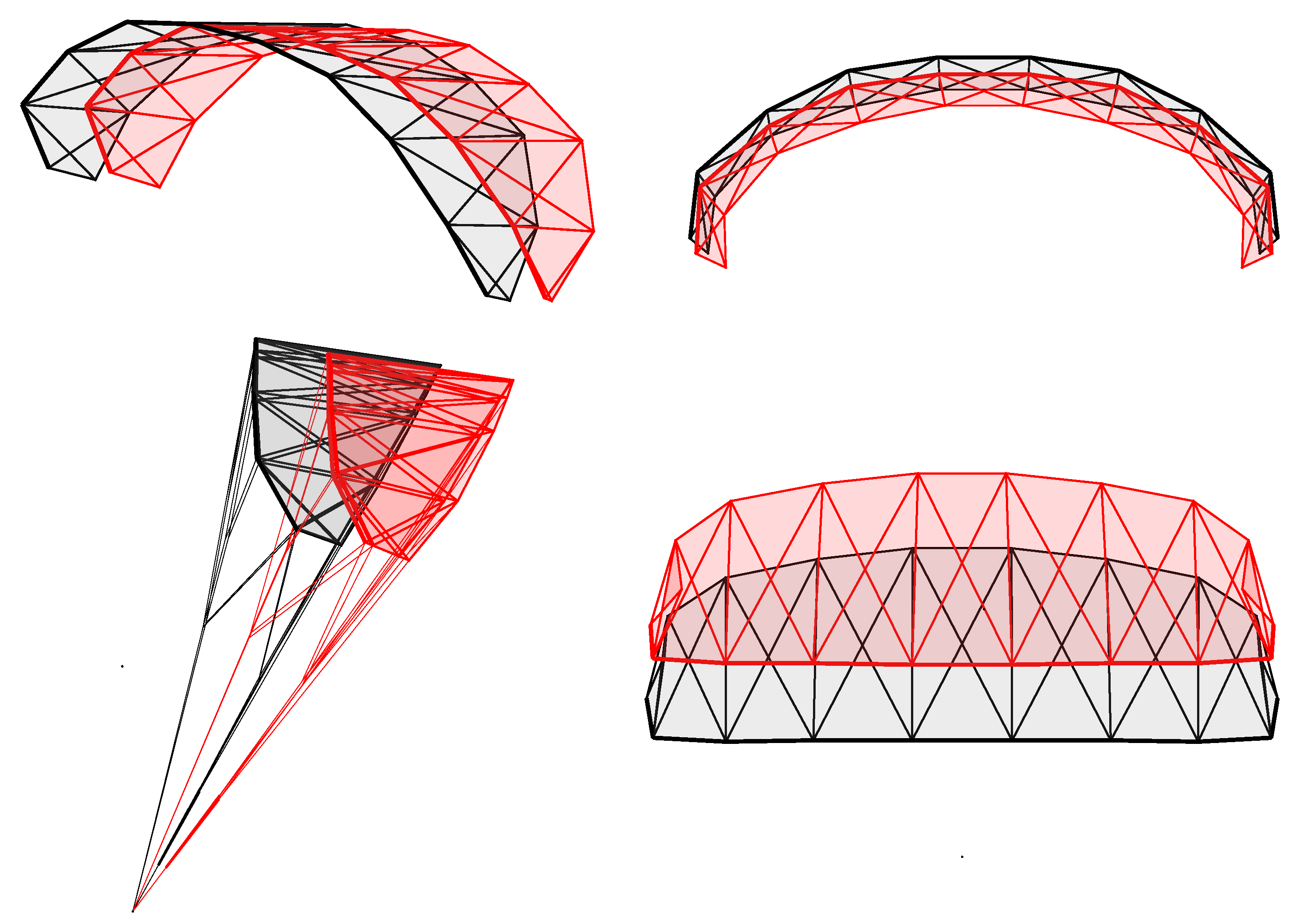
2.4. Multi-Segment Wing Model
2.4.1. Equations of Motion
2.4.2. Aerodynamic Force
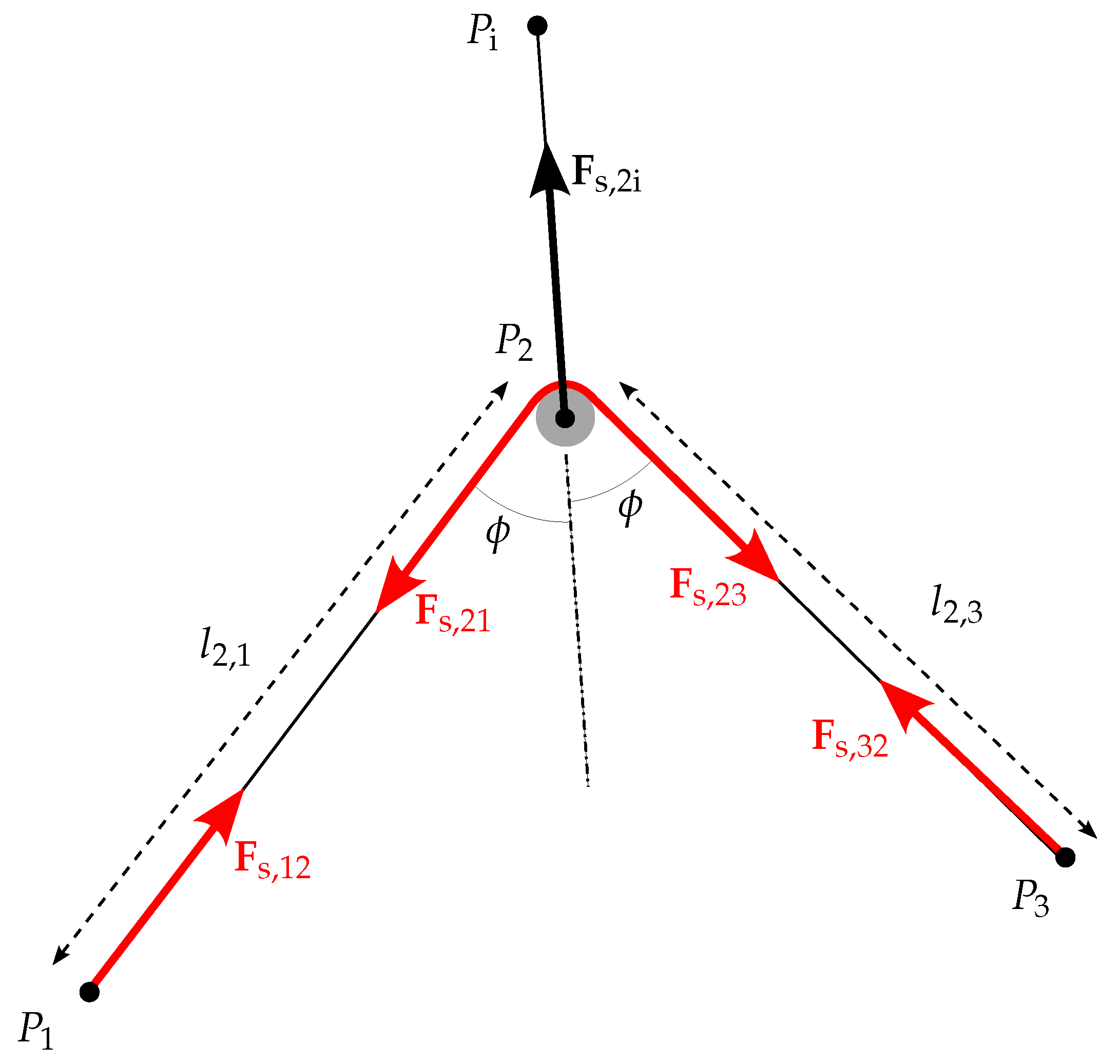
2.4.3. Structural Spring-Damper Elements
2.4.4. Numerical Solver
2.4.5. Static Equilibrium
2.5. Photogrammetry
3. Results
3.1. Triangular Two-Plate Wing Model
3.2. Multi-Segment Wing Model
4. Conclusions and Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AWE | Airborne wind energy |
| CAD | Computer-aided design |
| CFD | Computational fluid dynamics |
| FE | Finite element |
| FSI | Fluid–structure interaction |
| GPS | Global positioning system |
| IMU | Inertial measurement unit |
| KCU | Kite control unit |
| LE | Leading edge |
| PSM | Particle system model |
| TE | Trailing edge |
Appendix A. Multi-Segment Wing Model Bridle Plan
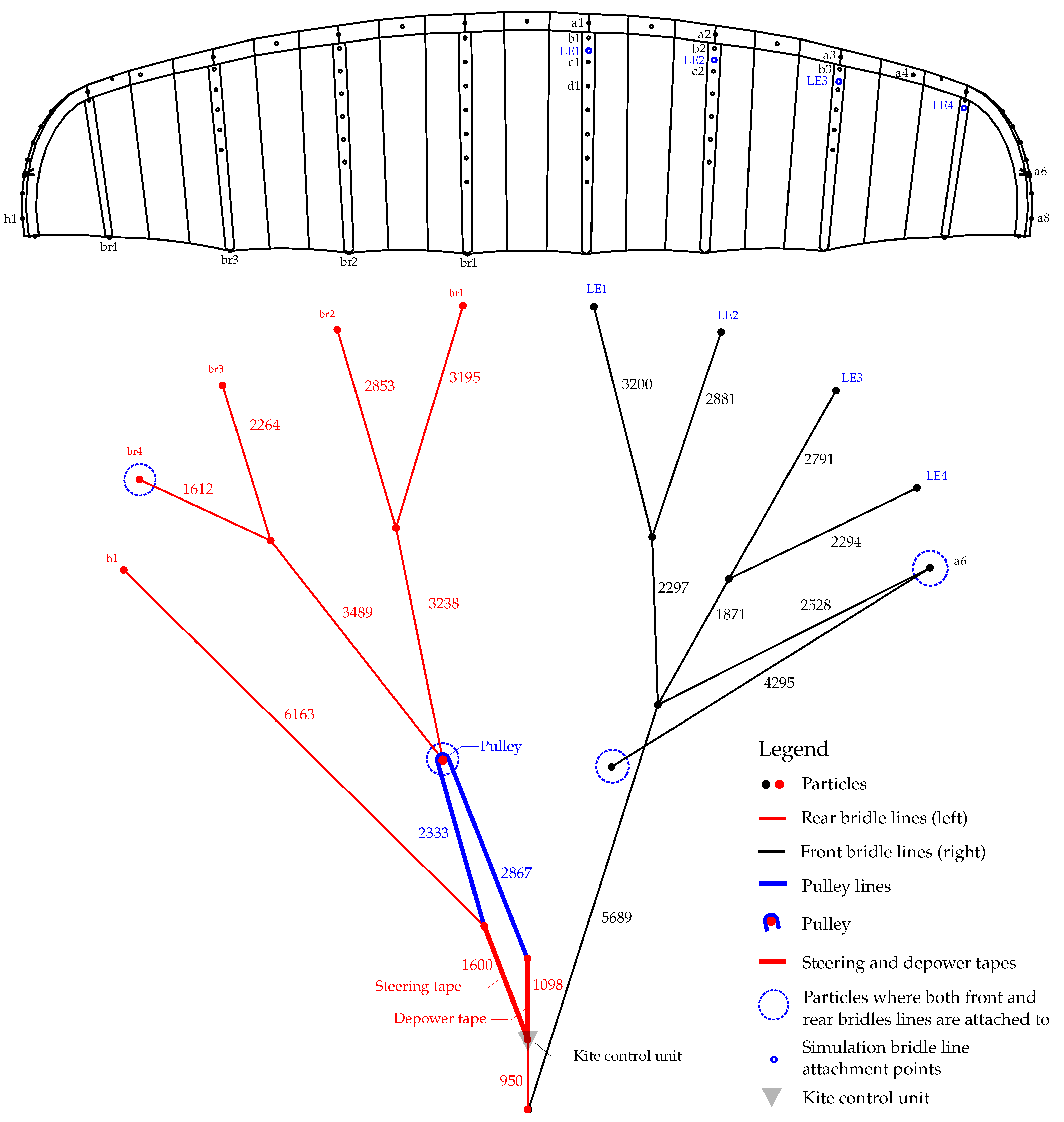
References
- Watson, S.; Moro, A.; Reis, V.; Baniotopoulos, C.; Barth, S.; Bartoli, G.; Bauer, F.; Boelman, E.; Bosse, D.; Cherubini, A.; et al. Future emerging technologies in the wind power sector: A European perspective. Renew. Sustain. Energy Rev. 2019, 113, 109–270. [Google Scholar] [CrossRef]
- Van Hagen, L.; Petrick, K.; Wilhelm, S.; Schmehl, R. Life-Cycle Assessment of a Multi-Megawatt Airborne Wind Energy System. Energies 2023, 16, 1750. [Google Scholar] [CrossRef]
- Bechtle, P.; Schelbergen, M.; Schmehl, R.; Zillmann, U.; Watson, S. Airborne wind energy resource analysis. Renew. Energy 2019, 141, 1103–1116. [Google Scholar] [CrossRef]
- Kleidon, A. Physical limits of wind energy within the atmosphere and its use as renewable energy: From the theoretical basis to practical implications. Meteorol. Z. 2021, 30, 203–225. [Google Scholar] [CrossRef]
- Oehler, J.; Schmehl, R. Aerodynamic characterization of a soft kite by in situ flow measurement. Wind Energy Sci. 2019, 4, 1–21. [Google Scholar] [CrossRef] [Green Version]
- Kitepower Airborne Wind Energy-Plug & Play, Mobile Wind Energy. Available online: https://thekitepower.com/ (accessed on 12 July 2022).
- Van den Heuvel, J. Kitesailing: Improving System Performance and Safety. Master’s Thesis, Delft University of Technology, Delft, The Netherlands, 2010. Available online: http://resolver.tudelft.nl/uuid:cee4dcf5-e2a8-49d0-b731-92db25b44a17 (accessed on 1 October 2021).
- Oehler, J.; van Reijen, M.; Schmehl, R. Experimental Investigation of Soft Kite Performance During Turning Maneuvers. J. Physics: Conf. Ser. 2018, 1037, 052004. [Google Scholar] [CrossRef]
- Breukels, J. An Engineering Methodology for Kite Design. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2011. Available online: http://resolver.tudelft.nl/uuid:cdece38a-1f13-47cc-b277-ed64fdda7cdf (accessed on 1 July 2023).
- Roullier, A. Experimental Analysis of a Kite System’s Dynamics. Master’s Thesis, EPFL, Lausanne, Switzerland, 2020. [Google Scholar] [CrossRef]
- Baayen, J.; Ockels, W. Tracking control with adaption of kites. IET Control Theory Appl. 2011, 4, 182–191. [Google Scholar] [CrossRef] [Green Version]
- Van der Vlugt, R.; Bley, A.; Noom, M.; Schmehl, R. Quasi-steady model of a pumping kite power system. Renew. Energy 2019, 131, 83–99. [Google Scholar] [CrossRef]
- De Groot, S.G.C.; Breukels, J.; Schmehl, R.; Ockels, W.J. Modeling Kite Flight Dynamics Using a Multibody Reduction Approach. J. Guid. Control. Dyn. 2011, 34, 1671–1682. [Google Scholar] [CrossRef]
- Jehle, C.; Schmehl, R. Applied Tracking Control for Kite Power Systems. J. Guid. Control. Dyn. 2014, 37, 1211–1222. [Google Scholar] [CrossRef] [Green Version]
- Schelbergen, M.; Schmehl, R. Validation of the quasi-steady performance model for pumping airborne wind energy systems. J. Phys. Conf. Ser. 2020, 1618, 032003. [Google Scholar] [CrossRef]
- Vermillion, C.; Cobb, M.; Fagiano, L.; Leuthold, R.; Diehl, M.; Smith, R.S.; Wood, T.A.; Rapp, S.; Schmehl, R.; Olinger, D.; et al. Electricity in the Air: Insights From Two Decades of Advanced Control Research and Experimental Flight Testing of Airborne Wind Energy Systems. Annu. Rev. Control 2021, 52, 330–357. [Google Scholar] [CrossRef]
- Gohl, F.; Luchsinger, R.H. Simulation Based Wing Design for Kite Power. In Airborne Wind Energy; Ahrens, U., Diehl, M., Schmehl, R., Eds.; Green Energy and Technology; Springer: Berlin/Heidelberg, Germany, 2013; Chapter 18; pp. 325–338. [Google Scholar] [CrossRef]
- Erhard, M.; Strauch, H. Control of Towing Kites for Seagoing Vessels. IEEE Trans. Control. Syst. Technol. 2013, 21, 1629–1640. [Google Scholar] [CrossRef] [Green Version]
- Fagiano, L.; Zgraggen, A.; Morari, M.; Khammash, M. Automatic crosswind flight of tethered wings for airborne wind energy: Modeling, control design and experimental results. IEEE Trans. Control. Syst. Technol. 2014, 22, 1433–1447. [Google Scholar] [CrossRef] [Green Version]
- Fechner, U.; Van der Vlugt, R.; Schreuder, E.; Schmehl, R. Dynamic Model of a Pumping Kite Power System. Renew. Energy 2015, 83, 705–716. [Google Scholar] [CrossRef] [Green Version]
- Breukels, J.; Schmehl, R.; Ockels, W. Aeroelastic Simulation of Flexible Membrane Wings based on Multibody System Dynamics. In Airborne Wind Energy; Ahrens, U., Diehl, M., Schmehl, R., Eds.; Green Energy and Technology; Springer: Berlin/Heidelberg, Germany, 2013; Chapter 16; pp. 287–305. [Google Scholar] [CrossRef]
- Bosch, A.; Schmehl, R.; Tiso, P.; Rixen, D. Dynamic nonlinear aeroelastic model of a kite for power generation. J. Guid. Control. Dyn. 2014, 37, 1426–1436. [Google Scholar] [CrossRef] [Green Version]
- Geschiere, N. Dynamic Modelling of a Flexible Kite for Power Generation: Coupling a Fluid-Structure Solver to a Dynamic Particle System. Master’s Thesis, Delft University of Technology, Delft, The Netherlands, 2014. Available online: http://resolver.tudelft.nl/uuid:6478003a-3c77-40ce-862e-24579dcd1eab (accessed on 18 May 2021).
- Leloup, R.; Roncin, K.; Bles, G.; Leroux, J.B.; Jochum, C.; Parlier, Y. Estimation of the lift-to-drag ratio using the lifting line method: Application to a leading edge inflatable kite. In Airborne Wind Energy; Ahrens, U., Schmehl, R., Diehl, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; Chapter 19; pp. 339–355. [Google Scholar] [CrossRef]
- Drela, M. XFOIL Subsonic Airfoil Development. Available online: https://web.mit.edu/drela/Public/web/xfoil/ (accessed on 18 May 2021).
- De Solminihac, A.; Alain Nême, C.D.; Leroux, J.B.; Roncin, K.; Jochum, C.; Parlier, Y. Kite as a Beam: A fast Method to get the Flying Shape. In Airborne Wind Energy—Advances in Technology Development and Research; Schmehl, R., Ed.; Green Energy and Technology; Springer: Singapore, 2018; Chapter 4; pp. 79–97. [Google Scholar] [CrossRef]
- Duport, C. Modeling with Consideration of the Fluid-Structure Interaction of the Behavior under Load of a Kite for Auxiliary TRACTION of Ships. Ph.D. Thesis, University of Bretagne, Brest, France, 2018. Available online: https://theses.hal.science/tel-02383312 (accessed on 1 September 2022).
- Van Til, J.; De Lellis, M.; Saraiva, R.; Trofino, A. Dynamic model of a C-shaped bridled kite using a few rigid plates. In Airborne Wind Energy—Advances in Technology Development and Research; Schmehl, R., Ed.; Green Energy and Technology; Springer: Singapore, 2018; Chapter 5; pp. 99–115. [Google Scholar] [CrossRef]
- Poland, J.A.W. Modelling Aeroelastic Deformation of Soft Wing Membrane Kites. Master’s Thesis, Delft University of Technology, Delft, The Netherlands, 2022. Available online: http://resolver.tudelft.nl/uuid:39d67249-53c9-47b4-84c0-ddac948413a5 (accessed on 1 April 2023).
- Cayon, O. Fast Aeroelastic Model of a Leading-Edge Inflatable Kite. Master’s Thesis, Delft University of Technology, Delft, The Netherlands, 2022. Available online: http://resolver.tudelft.nl/uuid:aede2a25-4776-473a-8a75-fb6b17b1a690 (accessed on 1 June 2023).
- Coenen, R. Single Skin Kite Airfoil Optimization for Airborne Wind Energy Systems. Master’s Thesis, Delft University of Technology, Delft, The Netherlands, 2018. Available online: http://resolver.tudelft.nl/uuid:fdcf8423-11f0-4b33-956e-3e761635ac41 (accessed on 1 April 2023).
- Schmehl, R. Successful Mast-Based Launch of the V3 Kite; Delft University of Technology: Delft, The Netherlands, 2020. [Google Scholar] [CrossRef]
- Salma, V.; Friedl, F.; Schmehl, R. Improving Reliability and Safety of Airborne Wind Energy Systems. Wind Energy 2019, 23, 340–356. [Google Scholar] [CrossRef] [Green Version]
- Schmehl, R.; Oehler, J. 25 m2 LEI V3 Tube Kite Transitioning to Traction Phase, Flying Figure Eight Manoeuvres; Copernicus Publications: Göttingen, Germany, 2018. [Google Scholar] [CrossRef]
- Fechner, U. A Methodology for the Design of Kite-Power Control Systems. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2016. [Google Scholar] [CrossRef]
- Oehler, J.; Schmehl, R.; Peschel, J.; Faggiani, P.; Buchholz, B. Kite Power Flight Data Acquired on 24 March 2017; Dataset, 4TU; Centre for Research Data, TU Delft Library: Delft, The Netherlands, 2018. [Google Scholar] [CrossRef]
- Richards, D.; Amos, M. Shape Optimization With Surface-Mapped CPPNs. IEEE Trans. Evol. Comput. 2017, 21, 391–407. [Google Scholar] [CrossRef]
- Fang, B. Trilateration and extension to global positioning system navigation. J. Guid. Control. Dyn. 1986, 9, 715–717. [Google Scholar] [CrossRef]
- Williams, P. Cable Modeling Approximations for Rapid Simulation. J. Guid. Control. Dyn. 2017, 40, 7. [Google Scholar] [CrossRef]
- Schwoll, J. Finite Element Analysis of Inflatable Structures Using Uniform Pressure. Master’s Thesis, Delft University of Technology, Delft, The Netherlands, 2012. Available online: http://resolver.tudelft.nl/uuid:f92da57f-55df-4109-9f8a-8c7c2b220c6a (accessed on 1 July 2021).
- Leuthold, R. Multiple-Wake Vortex Lattice Method for Membrane Wing Kites. Master’s Thesis, Delft University of Technology, Delft, The Netherlands, 2015. Available online: http://resolver.tudelft.nl/uuid:4c2f34c2-d465-491a-aa64-d991978fedf4 (accessed on 1 November 2021).
- Anderson, J.D. Fundamentals of Aerodynamics, 5th ed.; McGraw-Hill Inc.: New York, NY, USA, 2016; pp. 346–352. [Google Scholar]
- Folkersma, M.; Viré, A. Flow transition modeling on two-dimensional circular leading edge airfoils. Wind Energy 2019, 22, 908–921. [Google Scholar] [CrossRef] [PubMed]
- Hairer, E.; Wanner, G. Stiff differential equations solved by Radau methods. J. Comput. Appl. Math. 1998, 111, 93–111. [Google Scholar] [CrossRef]
- Karadayi, M.C. Particle System Modelling and Dynamic Simulation of a Tethered Rigid Wing Kite for Power Generation. Master’s Thesis, Delft University of Technology, Delft, The Netherlands, 2016. Available online: http://resolver.tudelft.nl/uuid:d6a2fcf8-7fce-4eb8-857b-209b9faac755 (accessed on 1 April 2023).
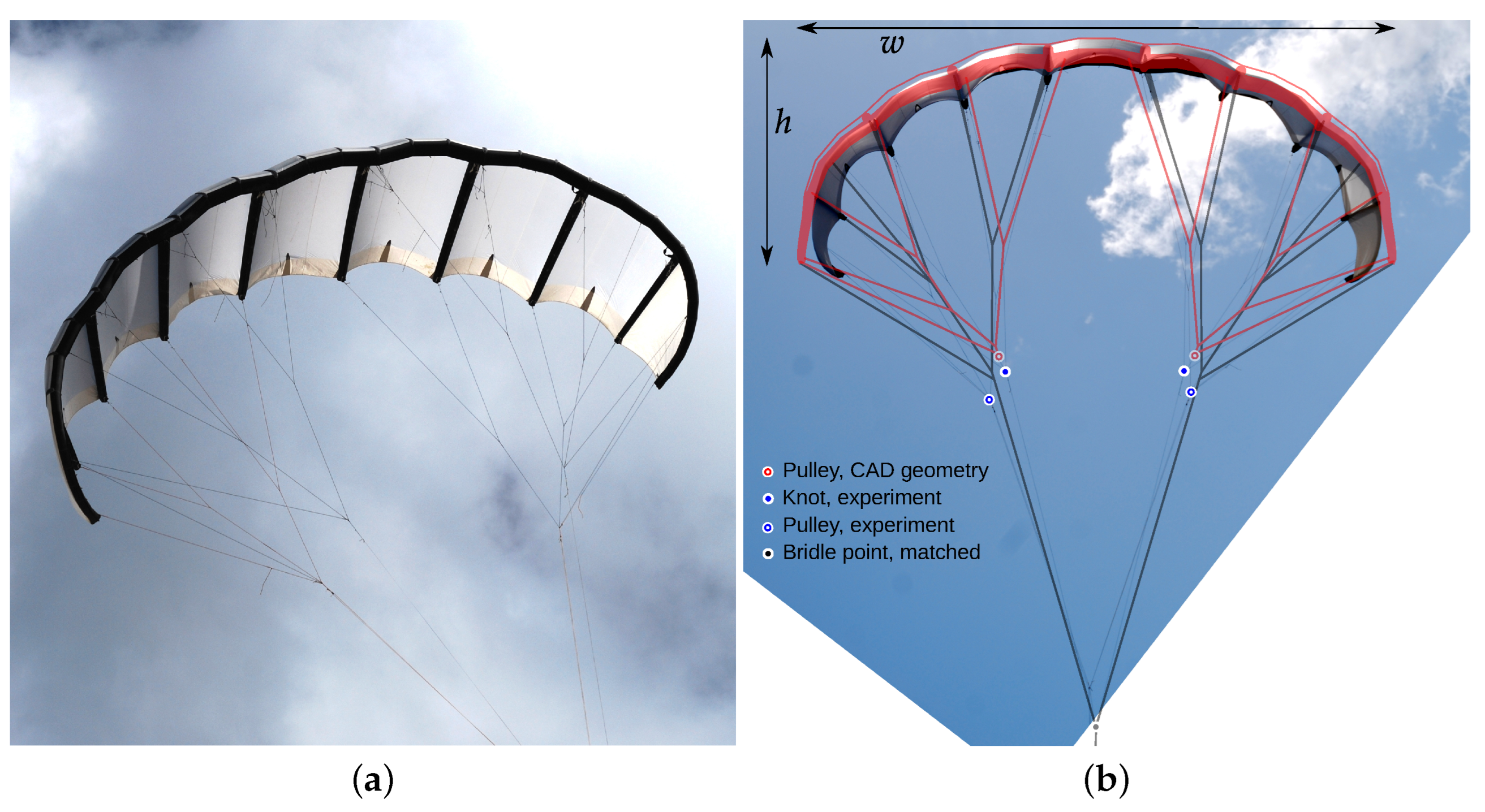
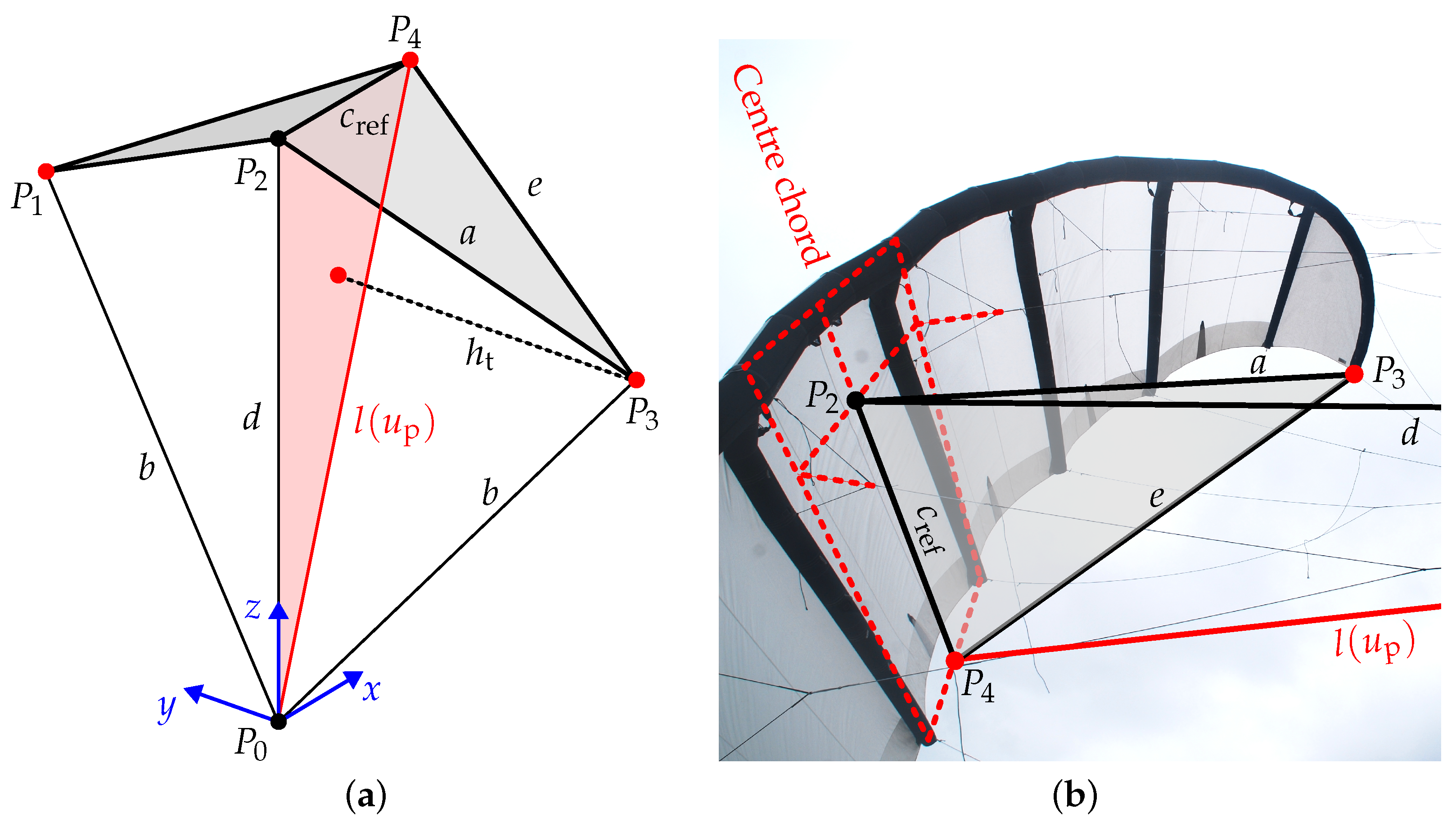
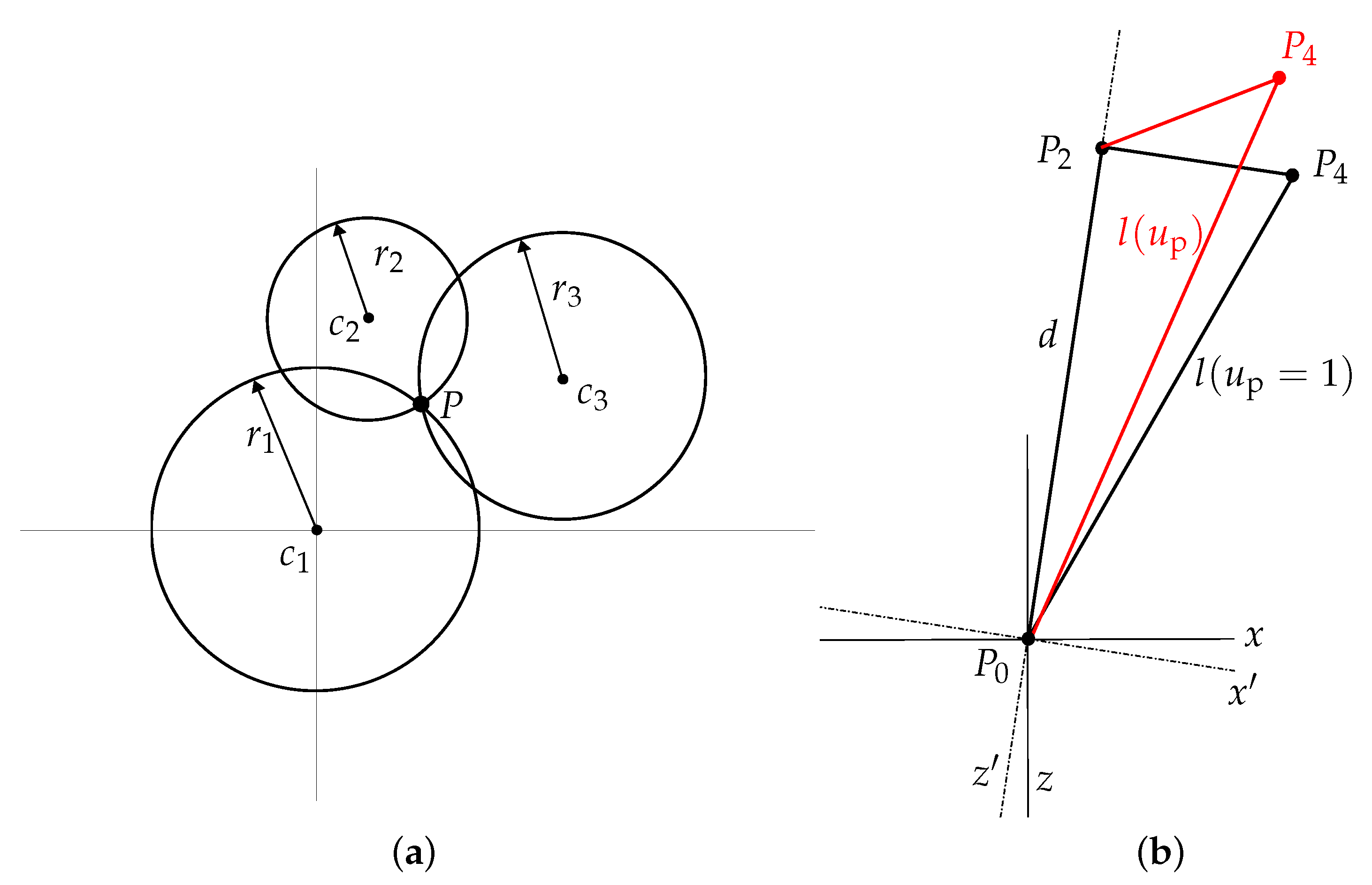


| (a) | (b) | |||
|---|---|---|---|---|
| Property | Symbol | Value | Component | Mass |
| Wing height | h | m | Wing + bridles | 11 kg |
| Wing width (projected wing span) | w | m | KCU | kg |
| Wing chord, maximum | c | m | IMU + GPS | kg |
| Wing surface area, flattened | S | 25 m2 | Flow sensor | 1 kg |
| Wing area, projected | A | m2 | Kite total | kg |
| (a) | ||
|---|---|---|
| Length | Symbol | Value (m) |
| Maximum possible length change | 4.8 | |
| Deployed tape length, powered kite | 1.098 | |
| Deployed tape length, depowered kite | 1.482 | |
| Deployed tape length, depowered kite | 1.722 | |
| (b) | ||
| Length | Symbol | Value (m) |
| Maximum possible length change | 1.4 | |
| Deployed tape length, neutral flight | 1.6 | |
| 1.6 | ||
| Deployed tape length, right turn | 3.0 | |
| 0.2 | ||
| Deployed tape length, left turn | 1.01 | |
| 2.16 | ||
| Length Symbol | a | b | d | e | ||
|---|---|---|---|---|---|---|
| Design Geometry (m) | 5.78 | 8.50 | 2.20 | 11.00 | 5.61 | 11.22 |
| Presimulated (m) | 5.55 | 8.56 | 2.20 | 11.00 | 5.64 | 11.22 |
| (a) | (b) | |||
|---|---|---|---|---|
| Parameters | Symbol | Value | Computational Setting | Value |
| Wind speed | 20 m/s | Absolute error | 1 × 10−4 | |
| Spring stiffness | K | 2 × 105 N/m | Relative error | 1 × 10−2 |
| Damping | c | Maximum step size | 5 × 10−3 | |
| Gravitational constant | g | m/s2 | ||
| Air density | kg/m | |||
| Mass | m | kg | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Poland, J.A.W.; Schmehl, R. Modelling Aero-Structural Deformation of Flexible Membrane Kites. Energies 2023, 16, 5264. https://doi.org/10.3390/en16145264
Poland JAW, Schmehl R. Modelling Aero-Structural Deformation of Flexible Membrane Kites. Energies. 2023; 16(14):5264. https://doi.org/10.3390/en16145264
Chicago/Turabian StylePoland, Jelle A. W., and Roland Schmehl. 2023. "Modelling Aero-Structural Deformation of Flexible Membrane Kites" Energies 16, no. 14: 5264. https://doi.org/10.3390/en16145264
APA StylePoland, J. A. W., & Schmehl, R. (2023). Modelling Aero-Structural Deformation of Flexible Membrane Kites. Energies, 16(14), 5264. https://doi.org/10.3390/en16145264







