Three-Dimensional Surrogate Model Based on Back-Propagation Neural Network for Key Neutronics Parameters Prediction in Molten Salt Reactor
Abstract
:1. Introduction
2. Materials and Methods
2.1. Surrogate Model Based on BPNN
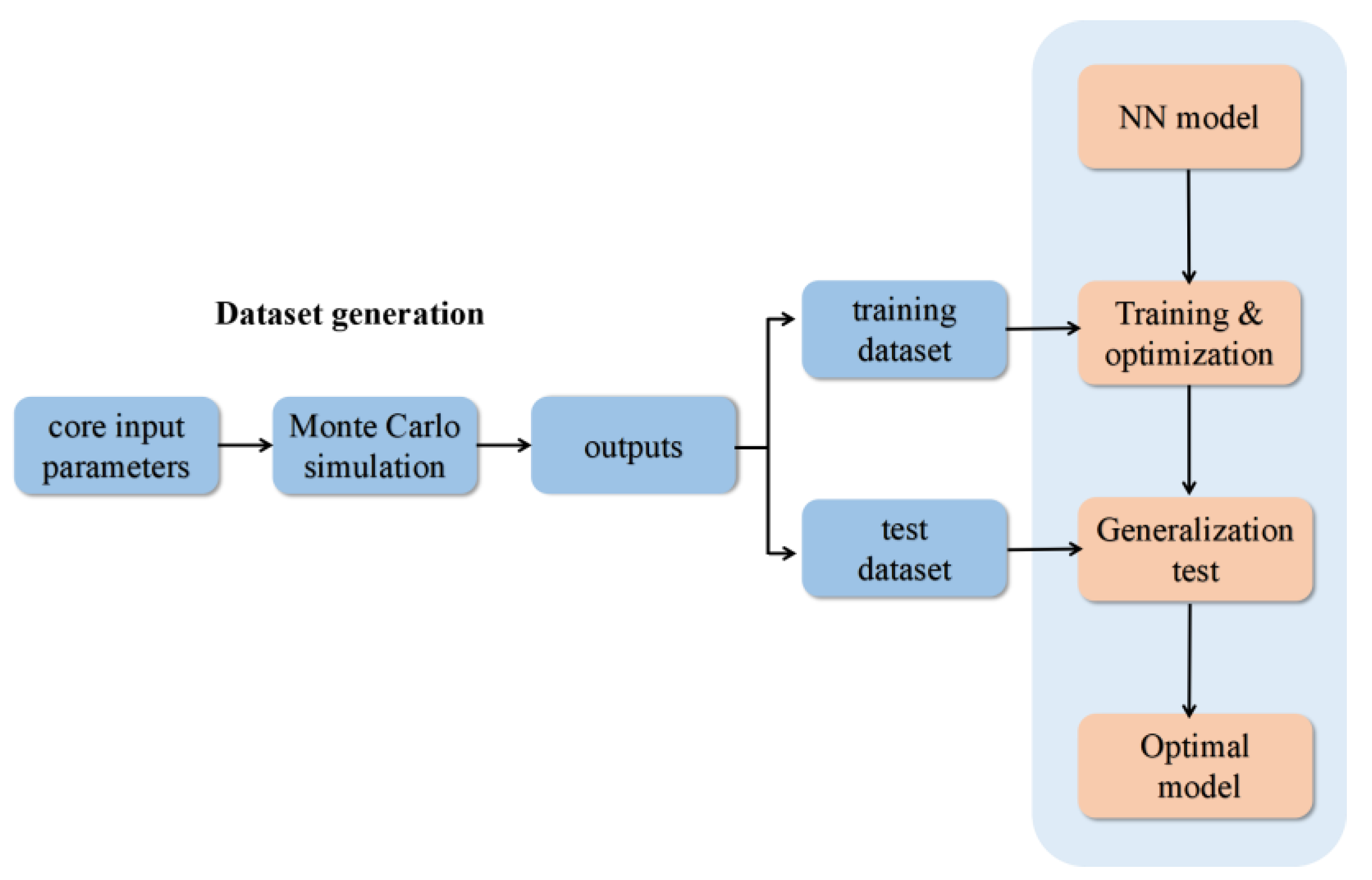
2.2. Dataset Generation
2.3. Hyper-Parameters Optimization
3. Results
3.1. Surrogate Model Optimization
3.2. Prediction
3.3. 3D Neutron Flux Distribution Prediction
3.4. Computational Efficiency
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Serp, J.; Allibert, M.; Beneš, O.; Delpech, S.; Feynberg, O.; Ghetta, V.; Heuer, D.; Holcomb, D.; Ignatiev, V.; Kloosterman, J.L.; et al. The molten salt reactor (MSR) in generation IV: Overview and perspectives. Prog. Nucl. Energy 2014, 77, 308–319. [Google Scholar] [CrossRef]
- Zuo, X.D.; Cheng, M.S.; Dai, Y.Q.; Yu, K.C.; Dai, Z.M. Flow field effect of delayed neutron precursors in liquid-fueled molten salt reactors. Nucl. Sci. Tech. 2022, 33, 96. [Google Scholar] [CrossRef]
- Yu, K.; Cheng, M.; Zuo, X.; Dai, Z. Transmutation and Breeding Performance Analysis of Molten Chloride Salt Fast Reactor Using a Fuel Management Code with Nodal Expansion Method. Energies 2022, 15, 6299. [Google Scholar] [CrossRef]
- Bostelmann, F.; Skutnik, S.E.; Walker, E.D.; Ilas, G.; Wieselquist, W.A. Modeling of the Molten Salt Reactor Experiment with SCALE. Nucl. Technol. 2022, 208, 603–624. [Google Scholar] [CrossRef]
- Boyd, W.; Shaner, S.; Li, L.; Forget, B.; Smith, K. The OpenMOC method of characteristics neutral particle transport code. Ann. Nucl. Energy 2014, 68, 43–52. [Google Scholar] [CrossRef]
- Dai, M.; Zhang, A.; Cheng, M. Improvement of the 3D MOC/DD neutron transport method with thin axial meshes. Ann. Nucl. Energy 2023, 185, 109731. [Google Scholar] [CrossRef]
- Hansen, K.F.; Kang, C.M. Finite element methods in reactor physics analysis. Adv. Nucl. Sci. Technol. Acad. Press 1975, 8, 173–253. [Google Scholar]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Zhang, J.; Zhou, Y.; Zhang, Q.; Wang, X.; Zhao, Q. Surrogate Model of Predicting Eigenvalue and Power Distribution by Convolutional Neural Network. Front. Energy Res. 2022, 10, 919. [Google Scholar] [CrossRef]
- Schlünz, E.B.; Bokov, P.M.; Van Vuuren, J.H. Application of artificial neural networks for predicting core parameters for the SAFARI-1 nuclear research reactor. In Proceedings of the 44th Annual Conference of the Operations Research Society of South Africa, Pecan Manor, Hartbeespoort, South Africa, 13–16 September 2015; pp. 12–22. [Google Scholar]
- Jang, H.; Lee, H. Prediction of pressurized water reactor core design parameters using artificial neural network for loading pattern optimization. In Proceedings of the Transactions of the Korean Nuclear Society Virtual Spring Meeting, Online, 9–10 July 2020; pp. 9–10. [Google Scholar]
- Chen, Y.; Wang, D.; Kai, C.; Pan, C.; Yu, Y.; Hou, M. Prediction of safety parameters of pressurized water reactor based on feature fusion neural network. Ann. Nucl. Energy 2021, 166, 108803. [Google Scholar] [CrossRef]
- Mazrou, H. Performance improvement of artificial neural networks designed for safety key parameters prediction in nuclear research reactors. Nucl. Eng. Des. 2009, 239, 1901–1910. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhang, J.; Liang, L.; Li, Z.; Zhang, T. A deep learning based surrogate model for estimating the flux and power distribution solved by diffusion equation. EPJ Web Conf. 2021, 247, 8. [Google Scholar] [CrossRef]
- Zhang, Q. A deep learning model for solving the eigenvalue of the diffusion problem of 2-D reactor core. In Proceedings of the Reactor Physics Asia 2019 (RPHA19) Conference, Osaka, Japan, 2–3 December 2019. [Google Scholar]
- Wang, Z.; Huo, X.; Zhang, J.; Hu, Y. Geometry Optimization of Monte Carlo Model of Fast Reactor Core. At. Energy Sci. Technol. 2021, 55, 258. [Google Scholar]
- Chen, S.; Ding, P.; Hu, S.; Xia, W.; Liu, M.; Yu, F.; Li, W. Optimization of Core Parameters Based on Artificial Neural Network Surrogate Model. In Proceedings of the International Conference on Nuclear Engineering, Shenzhen, China, 8–12 August 2022. [Google Scholar]
- Cadenas, J.M.; Ortiz-Servin, J.J.; Pelta, D.A.; Montes-Tadeo, J.L.; Castillo, A.; Perusquía, R. Prediction of 3D nuclear reactor's operational parameters from 2D fuel lattice design information: A data mining approach. Prog. Nucl. Energy 2016, 91, 97–106. [Google Scholar] [CrossRef]
- Cai, W.; Xia, H.; Yang, B. Research on 3D Power Reconstruction of Reactor Core Based on BP Neural Network. At. Energy Sci. Technol. 2018, 52, 2130. [Google Scholar]
- Duderstadt, J.J.; Hamilton, L.J. Nuclear Reactor Analysis; Wiley: Hoboken, NJ, USA, 1976. [Google Scholar]
- Oktavian, M.; Nistor, J.; Gruenwald, J.; Xu, Y. Preliminary development of machine learning-based error correction model for low-fidelity reactor physics simulation. Ann. Nucl. Energy 2023, 187, 109788. [Google Scholar] [CrossRef]
- Ayodeji, A.; Amidu, M.A.; Olatubosun, S.A.; Addad, Y.; Ahmed, H. Deep learning for safety assessment of nuclear power reactors: Reliability, explainability, and research opportunities. Prog. Nucl. Energy 2022, 151, 104339. [Google Scholar] [CrossRef]
- Li, J.; Cheng, J.; Shi, J.; Huang, F. Brief Introduction of Back Propagation (BP) Neural Network Algorithm and Its Improvement; Advances in Computer Science and Information Engineering; Springer: Berlin/Heidelberg, Gremany, 2012; Volume 2, pp. 553–558. [Google Scholar]
- Haubenreich, P.N.; Engel, J.R. Experience with the Molten-Salt Reactor Experiment. Nucl. Appl. Technol. 1970, 8, 118–136. [Google Scholar] [CrossRef]
- Robertson, R.C. MSRE Design and Operations Report Part I: Description of Reactor Design (ORNL-TM-728). Retrieved from US Department of Energy Office of Scientific and Technical Information. 1965. Available online: https://www.https://www.osti.gov/biblio/4654707 (accessed on 26 March 2023).
- Fratoni, M.; Shen, D.; Ilas, G.; Powers, J. Molten Salt Reactor Experiment Benchmark Evaluation; University of California: Berkeley, CA, USA; Oak Ridge National Lab (ORNL): Oak Ridge, TN, USA, 2020. [Google Scholar]
- Romano, P.K.; Horelik, N.E.; Herman, B.R.; Nelson, A.G.; Forget, B.; Smith, K. OpenMC: A state-of-the-art Monte Carlo code for research and development. Ann. Nucl. Energy 2015, 82, 90–97. [Google Scholar] [CrossRef]
- Romano, P.K.; Forget, B. The Open MC Monte Carlo particle transport code. Ann. Nucl. Energy 2013, 51, 274–281. [Google Scholar] [CrossRef]
- Bell, M.J. Calculated radioactivity of MSRE fuel salt. Oak Ridge Natl. Lab. 1970. [Google Scholar] [CrossRef]
- Bei, X.; Cheng, M.; Zuo, X.; Yu, K.; Dai, Y. Surrogate models based on Back-propagation neural network for parameters prediction of the PWR core. In Proceedings of the 23rd Pacific Basin Nuclear Conference (PBNC), Chengdu, China, 1–4 November 2022. [Google Scholar]






















| Main Materials | |
|---|---|
| Fuel (mol%) | LiF-BeF2-ZrF4-UF4 (65-29.1-5-0.9) |
| Fuel salt density (g/cm3) | 2.3275 |
| Graphite density (g/cm3) | 1.86 |
| Inor-8 steel density (g/cm3) | 8.77453 |
| Hastelloy density (g/cm3) | 8.86 |
| Temperature for all materials (K) | 911 |
| Core main dimension | |
| Inner core container radius (cm) | 70.485 |
| Outer core container radius (cm) | 71.12 |
| Inner reactor vessel radius (cm) | 73.66 |
| Outer reactor vessel radius (cm) | 75.08875 |
| Height of the up plenum (cm) | 25.4 |
| Height of the low plenum (cm) | 25.4 |
| Height of the vessel (cm) | 236.474 |
| Graphite stringer | |
| Axial length of the graphite (cm) | 160.02 |
| Side length of the graphite (cm) | 5.08 |
| Fuel channel thickness (cm) | 3.048 |
| Fuel channel width (cm) | 1.016 |
| Nuclide | Min/g | Max/g |
|---|---|---|
| U-234 | 676 | 887 |
| U-235 | 70,900 | 74,700 |
| U-236 | 337 | 1030 |
| U-238 | 148 | 149 |
| Pu-239 | 0 | 613 |
| Pu-240 | 0 | 27.7 |
| La-139 | 0 | 117 |
| Ce-140 | 0 | 131 |
| Pr-141 | 0 | 109 |
| Ce-142 | 0 | 114 |
| Nd-143 | 0 | 108 |
| Hyper-Parameters | Values Range |
|---|---|
| Number of hidden layers | [3–5] |
| Number of hidden neurons | [20–1936] |
| Activation function | [relu, sigmoid, tanh] |
| Optimizer | Adam |
| Learning rate | [0.1, 0.01, 0.001] |
| Hyper- Parameters | Number of Hidden Layers | Optimizer | Learning Rate | Activation Function |
|---|---|---|---|---|
| values | 4 | Adam | 0.01 | relu |
| Error for Instance #1 | Error for Instance #2 | Error for Instance #3 | ||
|---|---|---|---|---|
| full-core | MinRE | 0% | 0% | 0% |
| MeanRE | 0.238% | 0.319% | 0.269% | |
| MaxRE | 3.061% | 6.639% | 4.305% | |
| edge region | MinRE | 0% | 0% | 0% |
| MeanRE | 0.317% | 0.334% | 0.331% | |
| activate region | MinRE | 0% | 0% | 0% |
| MeanRE | 0.219% | 0.315% | 0.254% | |
| OpenMC Code | Optimal Surrogate Model | |
|---|---|---|
| Computational time | 77 min | 0.002 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bei, X.; Dai, Y.; Yu, K.; Cheng, M. Three-Dimensional Surrogate Model Based on Back-Propagation Neural Network for Key Neutronics Parameters Prediction in Molten Salt Reactor. Energies 2023, 16, 4044. https://doi.org/10.3390/en16104044
Bei X, Dai Y, Yu K, Cheng M. Three-Dimensional Surrogate Model Based on Back-Propagation Neural Network for Key Neutronics Parameters Prediction in Molten Salt Reactor. Energies. 2023; 16(10):4044. https://doi.org/10.3390/en16104044
Chicago/Turabian StyleBei, Xinyan, Yuqing Dai, Kaicheng Yu, and Maosong Cheng. 2023. "Three-Dimensional Surrogate Model Based on Back-Propagation Neural Network for Key Neutronics Parameters Prediction in Molten Salt Reactor" Energies 16, no. 10: 4044. https://doi.org/10.3390/en16104044





