Sensitivity Analysis of Mechanical Parameters of Collapse Roof of Carbonate Rock Deep Buried Oilfield
Abstract
:1. Introduction
2. Brief Introduction of Sensitivity Analysis Method
3. Sensitivity Analysis of Physical and Mechanical Parameters of the Karst Cave Collapse
3.1. Project Background
3.2. Numerical Analysis Model and Calculation Conditions
3.3. Criteria for Karst Cave Collapse
3.4. Determination Method of Critical Collapse Depth of Karst Cave
3.5. Deformation and Failure Characteristics of Caves
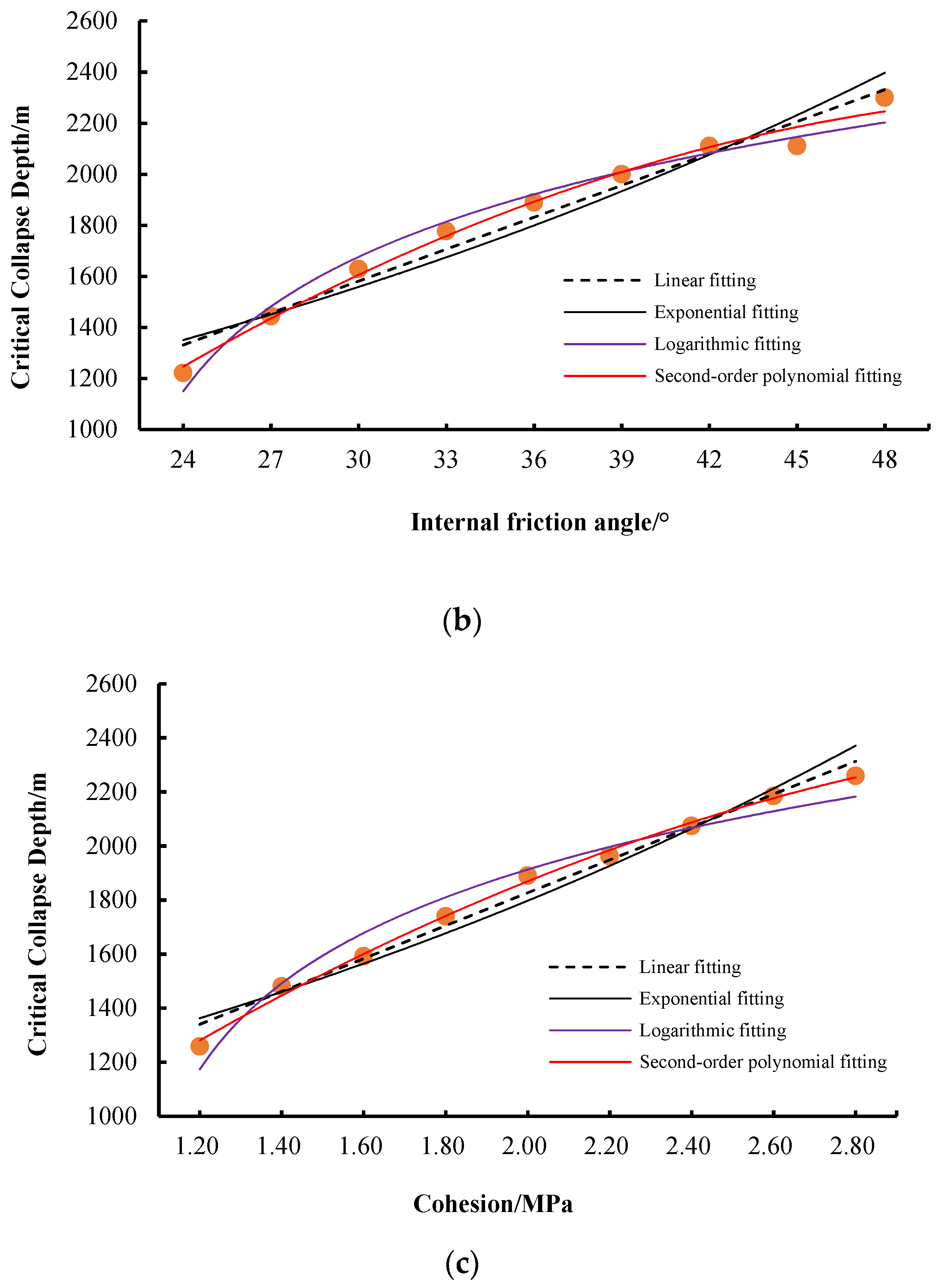
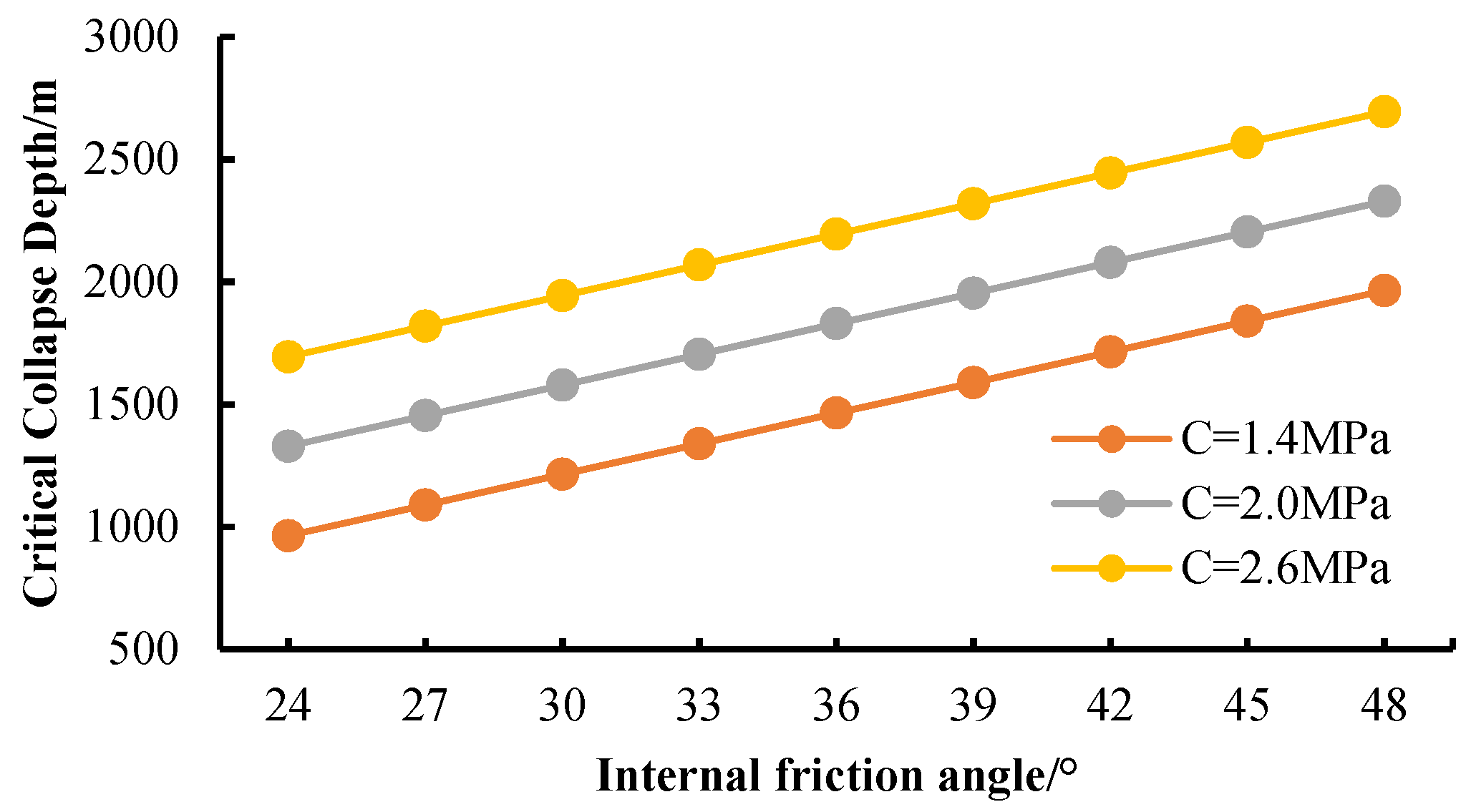
3.6. Critical Collapse Depth of Karst Cave under the Influence of Single Factor
- Four different fitting methods were used, and all of the fitting results reached 0.9 or more. It showed that the critical collapse depth of the cavern had a good correlation with the surrounding rock mechanics parameters.
- When we used these four methods to fit, the correlation coefficient R2 was higher in the critical collapse depth and cohesive force fitting results of the cavern; the largest was the logarithmic fitting where the correlation coefficient was 0.99753, and the smallest was the index fitting where the correlation coefficient was 0.95525.
- Overall, the linear fitting could be used to describe the influence of various factors on the critical collapse depth of the cavern.
3.7. Multi-Factor Sensitivity of Cave Collapse
3.8. Prediction Formula of Critical Collapse Depth of the Karst Cave
4. Engineering Calculation Case
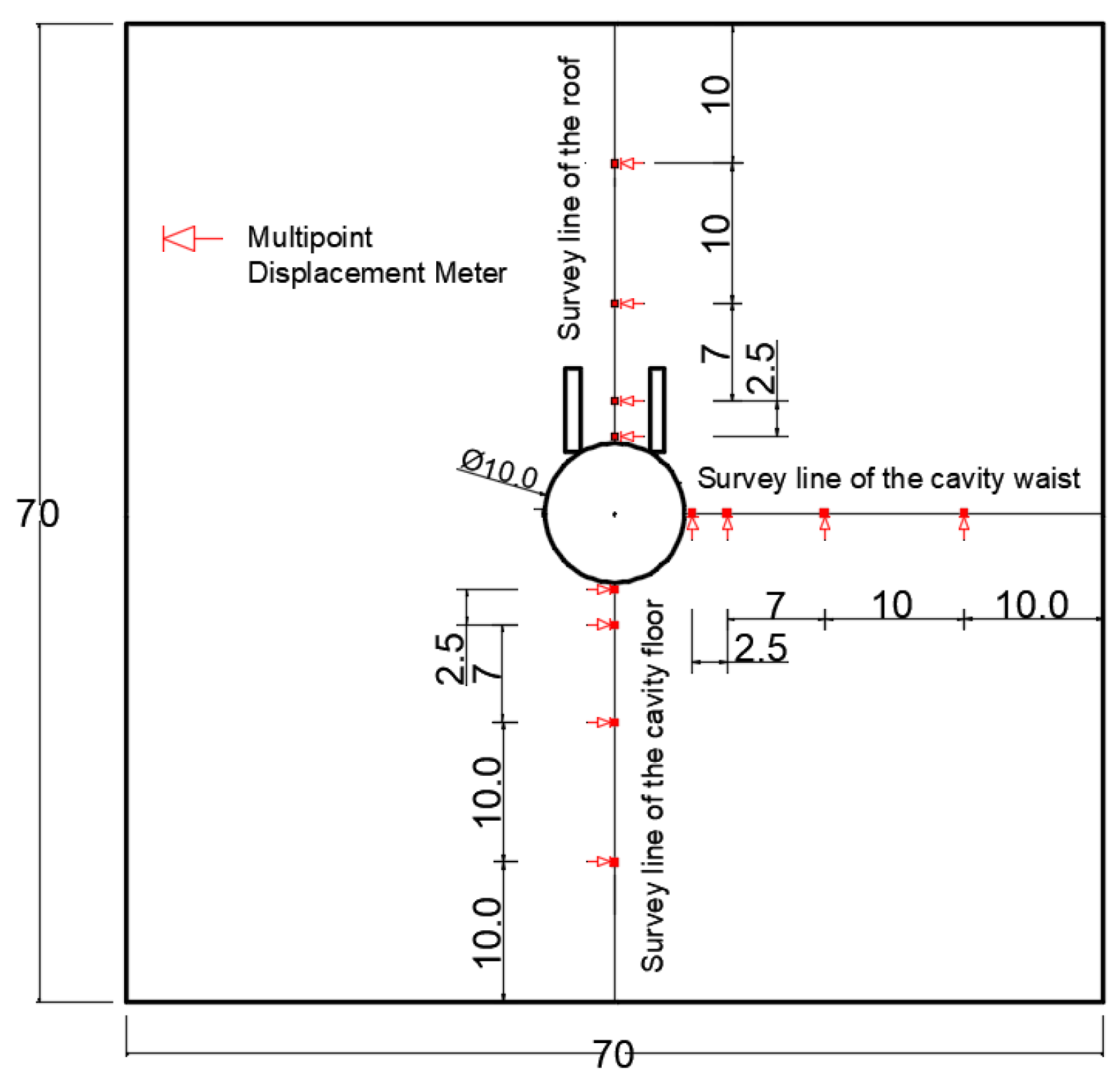
4.1. Geomechanical Model Test
4.2. Test Scheme Design
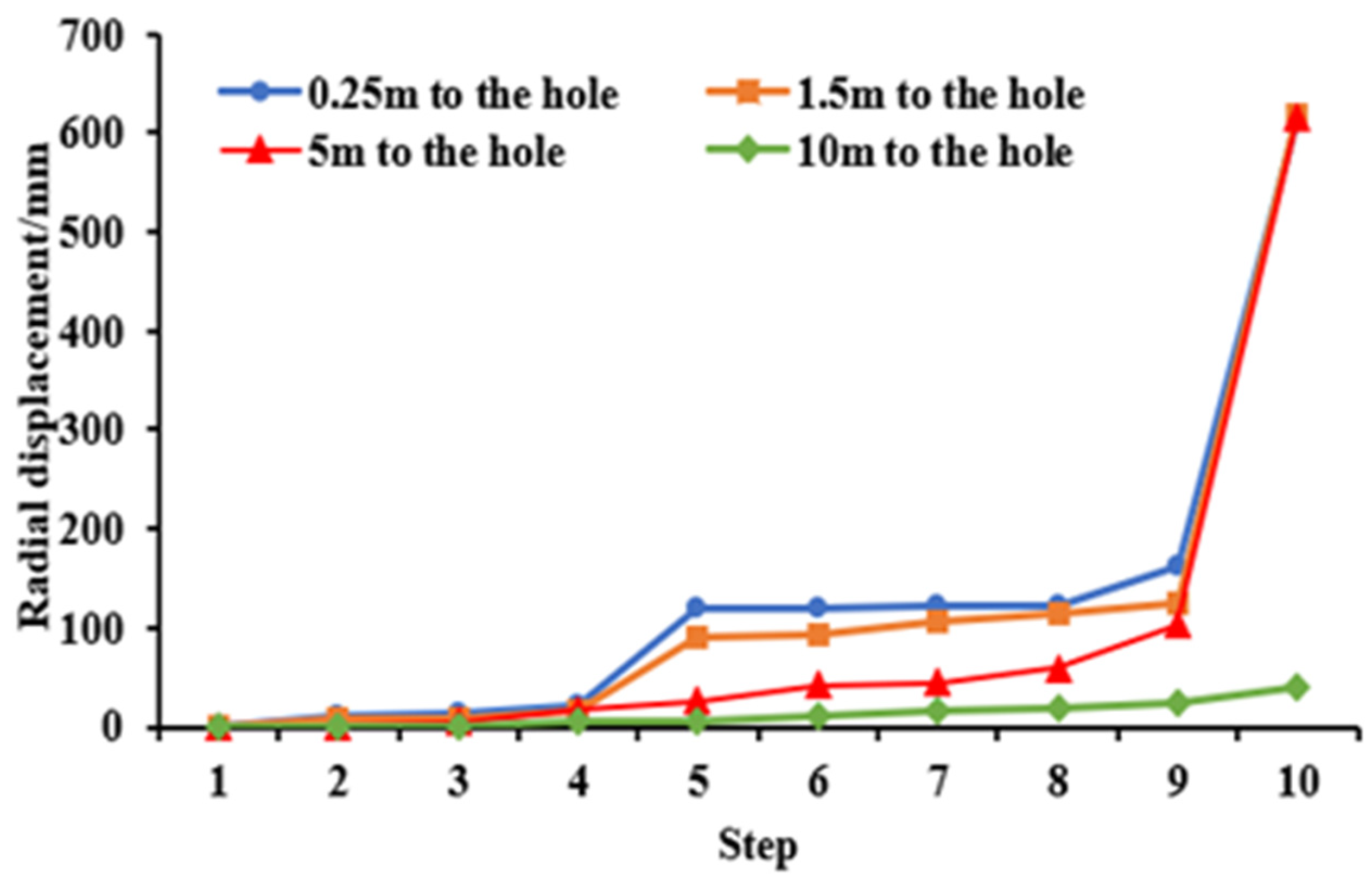
4.3. Analysis of Test Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Huang, Z.Q.; Yao, J.; Wang, Y.Y. An efficient numerical model for immiscible two-phase flow in fractured karst reservoirs. Commun. Comput. Phys. 2013, 13, 540–558. [Google Scholar] [CrossRef]
- Li, S.; Kang, Y.; You, L.; Li, D.; Lian, Z. Experimental and Numerical Investigation of Multiscale Fracture Deformation in Fractured-Vuggy Carbonate Reservoirs. Arab. J. Sci. Eng. 2014, 39, 4241–4249. [Google Scholar] [CrossRef]
- Wang, Z.S.; Yao, J. Study of pressure-transient characteristic for stress-sensitive triple-medium reservoirs with fractures and vugs conveying fluids to wellbore. J. Hydrodyn. Ser. A 2006, 21, 84–89. [Google Scholar]
- Kang, Z.J.; Li, J.; Zhang, D.L.; Wu, Y.C.; Zhang, J. Percolation characteristics of fractured-vuggy carbonate reservoir in Tahe oilfield. Oil Gas Geol. 2005, 5, 635–673. [Google Scholar]
- Kang, Y.Z. Characteristics and distribution laws of paleokarst hydrocarbon reservoirs in palaeozoic carbonate formations in china. Natl. Gas Ind. 2008, 28, 1–12. [Google Scholar]
- Zhao, Z.; Du, J.; Zou, C.; Hu, S. Geological exploration theory for large oil and gas provinces and its significance. Pet. Explor. Dev. 2011, 38, 513–522. [Google Scholar] [CrossRef]
- Ren, Y.; Gong, R.; Feng, Z.; Li, M. Valuable Data Extraction for Resistivity Imaging Logging Interpretation. Tsinghua Sci. Technol. 2020, 25, 281–293. [Google Scholar] [CrossRef]
- Rabbani, A.; Assadi, A.; Kharrat, R.; Dashti, N.; Ayatollahi, S. Estimation of carbonates permeability using pore network parameters extracted from thin section images and comparison with experimental data. J. Nat. Gas Sci. Eng. 2017, 42, 85–98. [Google Scholar] [CrossRef]
- Tang, P.; Wu, S.Q.; Yu, B.S.; Qian, Y.X.; Peng, S.T. Genesis Characteristics and Research Means of Paleokarst Collapse. Geoscience 2015, 29, 675–683. [Google Scholar]
- Zhu, W.; Baud, P.; Wong, T.F. Micromechanics of cataclastic pore collapse in limestone. J. Geophys. Res.-Solid Earth 2010, 115, 1–17. [Google Scholar] [CrossRef]
- Geurey, M.; Dimopoulosb, I.; Lek, S. Two-way interaction of input variables in the sensitivity analysis of neural network models. Ecol. Model. 2006, 195, 43. [Google Scholar]
- Beiki, M.; Bashari, A.; Majdi, A. Genetic programming approach forestimating the deformation modulus of rock mass using sensitivity analysis by neural network. Int. J. Rock Mech. Min. Sci. 2010, 47, 1091–1103. [Google Scholar] [CrossRef]
- Zhu, W.S.; Zhang, G. Susceptibility analyses of parameters of joint to breaking-area-in-surrounding-rock. Underground-Space 1994, 14, 10–15. [Google Scholar]
- Hou, Z.S.; Li, X.; Wang, S.J. Sensitivity analysis of mechanical parameters to deformation of surrounding rocks for a tunnel in Jinchuandeposit I. Chin. J. Rock Mech. Eng. 2005, 24, 406–410. [Google Scholar]
- Li, X.J.; Zhu, W.S.; Xiang, J. System analysis method based on some parameters in underground chambers and its application. Chin. J. Geotech. Eng. 2005, 27, 1207–1210. [Google Scholar]
- Xia, Y.Y.; Xiong, H.F. Sensibility analysis of slope stability based on artificial neural network. Chin. J. Rock Mech. Eng. 2004, 23, 2703–2707. [Google Scholar]
- Nie, W.P.; Xu, W.Y.; Zhou, X.Q. Grey relation analysis of parameter sensitivity of cavern stability based on 3d elastoplastic finite elements. Chin. J. Rock Mech. Eng. 2009, 28, 3885–3893. [Google Scholar]
- Wang, C.; Zhang, Q.Y.; Liu, Z.C. A prediction model for collapse of karst caves in fractured-vuggy oil oilfields and its application. J. China Univ. Pet. 2015, 39, 103–110. [Google Scholar]
- Shen, Y.J.; Xu, G.L. Plastic deformation of surrounding rock mechanics parameters of the sensitivity analysis. People Yangtze River 2013, 44, 85–90. [Google Scholar]
- He, Z.L.; Ma, Y.S.; Zhu, D.Y.; Duan, T.Z.; Geng, J.H.; Zhang, J.T.; Gao, Z.Q. Theoretical and technological progress and research direction of deep and ultra-deep carbonate reservoirs. Oil Gas Geol. 2021, 42, 533–546. [Google Scholar]
- Pang, X.; Lin, H.; Zheng, D.; Li, H.; Zou, H.; Pang, H.; Li, H. Basic characteristics, dynamic mechanism and development direction of the formation and distribution of deep and ultra-deep carbonate reservoirs in China. J. Geomech. 2020, 26, 673–695. [Google Scholar]
- Ma, Y.; Li, M.; Cai, X.; Xu, X.; Hu, D.; Qu, S.; Li, G.; He, D.; Xiao, X.; Zeng, Y.; et al. Advances in basic research on the mechanism of deep marine hydrocarbon enrichment and key exploitation technologies. Pet. Geol. Exp. 2021, 43, 737–748. [Google Scholar]
- Dou, Z. Development Technology of Carbonate Fractured-Vuggy Reservoir in Tahe Oilfield; Beijing Petroleum Industry Press: Beijing, China, 2012; pp. 1–20. [Google Scholar]
- Zhang, X.; Yang, J.; Yang, Q.; Zhang, C. Reservoir description and reserves estimation technique for fracture-cave type carbonate reservoir in Tahe Oilfield. Acta Pet. Sin. 2004, 25, 14–18. [Google Scholar]
- Lyu, X.; Li, H.; Wei, H.; Si, C.; Wu, X.; Bu, C.; Kang, Z.; Sun, J. Classification and characterization method for multi-scale fractured-vuggy reservoir zones in carbonate reservoirs: An example from Ordovician reservoirs in Tahe oilfield S80 unit. Oil Gas Geol. 2017, 38, 813–821. [Google Scholar]
- Jin, Q.; Tian, F.; Lu, X.; Kang, X. Characteristics of collapse breccias filling in caves of runoff zone in the Ordovician karst in Tahe oilfield, Tarim Basin. Oil Gas Geol. 2015, 36, 729–735. [Google Scholar]
- Hu, W. Paleokarst fractured-cavity types and their reconstruction in buried hill area, Tahe oilfield, Tarim Basin. Oil Gas Geol. 2022, 43, 43–53. [Google Scholar]
- Jin, Q.; Tian, F. A study on constructions of fracture-cave in karst carbonates in Tahe Oilfield. J. China Univ. Pet. 2013, 37, 15–21. [Google Scholar]
- Li, Y. Ordovician carbonate fracture-cavity oilfields identification and quantitative characterization in Tahe Oilfield. J. China Univ. Pet. 2012, 36, 1–7. [Google Scholar]
- Zhang, X.D.; Xue, C.J.; Zhang, Y. Research and application of rock mechanical parameters and in-situ stress in Tuofutai area of Tahe Oilfield. J. Oil Gas Technol. 2011, 33, 132–134, 138. [Google Scholar]
- Li, T.; Rutqvist, J.; Hu, M. TOUGH-RFPA: Coupled thermal-hydraulic-mechanical Rock Failure Process Analysis with application to deep geothermal wells. Int. J. Rock Mech. Min. Sci. 2021, 142, 104726. [Google Scholar] [CrossRef]
- Tang, S. Applications of rock failure process analysis (RFPA) method. J. Rock Mech. Geotech. Eng. 2011, 3, 352–372. [Google Scholar] [CrossRef]
- Zhang, Q.; Liu, C.; Duan, K.; Zhang, Z.; Xiang, W. True three-dimensional geomechanical model tests for stability analysis of surrounding rock during the excavation of a deep underground laboratory. Rock Mech. Rock Eng. 2020, 53, 517–537. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, Q.; Xiang, W.; Xue, T.E. Development and application of a three-dimensional geo-mechanical model test system under hydro-mechanical coupling. Geotech. Geol. Eng. 2021, 39, 3147–3160. [Google Scholar] [CrossRef]
- Zhang, Q.Y.; Ren, M.Y.; Duan, K.; Wang, W.S.; Gao, Q.; Lin, H.X.; Xiang, W.; Jiao, Y.Y. Geo-mechanical model test on the collaborative bearing e_ect of rock-support system for deep tunnel in complicated rock strata. Tunn. Undergr. Space Technol. 2019, 91, 103001. [Google Scholar] [CrossRef]
- Niu, Y.J. Study on the Structural and Characteristics of Karst Collapse in Fractured & Cave Carbonate Reservoir; University of Geosciences, China: Beijing, China, 2012. [Google Scholar]
- Deng, X.P.; Shen, A.J.; Shou, J.F. A Quantitative Plate of Collapsed Karst Cave Depth and Its Application in Geological Prediction and Evaluation of Carbonate Reservoir. Mar. Orig. Pet. Geol. 2009, 4, 55–59. [Google Scholar]









| Bulk Density (KN/m3) | Poisson’s Ratio | Elastic Modulus (GPa) | Compressive Strength (MPa) | Tensile Strength (MPa) | Internal Friction Angle (°) | Cohesion (MPa) |
|---|---|---|---|---|---|---|
| 27 | 0.25 | 36.3 | 74.2 | 3.8 | 36 | 2 |
| The Expression of the Fitting Relationship between the Critical Collapse Depth of the Cavity and Various Factors | |||
|---|---|---|---|
| The expression of the fitting relationship between the critical collapse depth H of the cavity and the deformation modulus E | Fitting method | Fitting formula | Correlation coefficient R2 |
| Linear fitting | H = 15.239 E + 1275.4 | 0.95008 | |
| Exponential fitting | H = 1343.8 e0.00842E | 0.94443 | |
| Logarithmic fitting | H = 540.23 ln(E) − 99.039 | 0.96762 | |
| Second-order polynomial fitting | H = −0.33057 E2 + 39.238 E + 859.63 | 0.97073 | |
| The expression of the fitting relationship between the critical collapse depth H of the cavity and the internal friction angle ψ | Fitting method | Fitting formula | Correlation coefficient R2 |
| Linear fitting | H = 41.667 ψ+ 331.56 | 0.96335 | |
| Exponential fitting | H = 760.65 e0.02392ψ | 0.92764 | |
| Logarithmic fitting | H = 1468.2 ln(ψ) − 3394.3 | 0.98668 | |
| Second-order polynomial fitting | H = −1.0135 ψ2 + 114.64 ψ − 921.09 | 0.98968 | |
| The expression of the fitting relationship between the critical collapse depth H of the cavity and the cohesion C | Fitting method | Fitting formula | Correlation coefficient R2 |
| Linear fitting | H = 608.17 C + 610.56 | 0.9829 | |
| Exponential fitting | H = 899.55 e0.34618C | 0.95525 | |
| Logarithmic fitting | H = 1166.5 ln(C) + 1059.8 | 0.99753 | |
| Second-order polynomial fitting | H = −159.52 C2 + 1246.3 C + 15 | 0.99678 | |
| Material | Bulk Density (KN/m3) | Elastic Modulus (GPa) | Compressive Strength (MPa) | Tensile Strength (MPa) | Cohesion (MPa) | Internal Friction Angle (°) | Poisson’s Ratio |
|---|---|---|---|---|---|---|---|
| Carbonate | 27 | 36 | 74 | 3.8 | 12 | 36 | 0.25 |
| Similar Material | Bulk Density (KN/m3) | Elastic Modulus (GPa) | Compressive Strength (MPa) | Tensile Strength (MPa) | Cohesion (MPa) | Internal Friction Angle (°) | Poisson’s Ratio |
|---|---|---|---|---|---|---|---|
| Carbonate | 26.8~27.1 | 710~820 | 1.38~1.61 | 0.71~0.82 | 0.23~0.26 | 35.4~36.5 | 0.23~0.26 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ding, Y.; Zhang, Q.; Xiang, W.; Lyu, X.; Zhang, L. Sensitivity Analysis of Mechanical Parameters of Collapse Roof of Carbonate Rock Deep Buried Oilfield. Energies 2023, 16, 4141. https://doi.org/10.3390/en16104141
Ding Y, Zhang Q, Xiang W, Lyu X, Zhang L. Sensitivity Analysis of Mechanical Parameters of Collapse Roof of Carbonate Rock Deep Buried Oilfield. Energies. 2023; 16(10):4141. https://doi.org/10.3390/en16104141
Chicago/Turabian StyleDing, Yanzhi, Qiangyong Zhang, Wen Xiang, Xinrui Lyu, and Longyun Zhang. 2023. "Sensitivity Analysis of Mechanical Parameters of Collapse Roof of Carbonate Rock Deep Buried Oilfield" Energies 16, no. 10: 4141. https://doi.org/10.3390/en16104141





