Exergy Analysis of a Shell and Tube Energy Storage Unit with Different Inclination Angles
Abstract
:1. Introduction
2. Mathematical Analysis and Operating Conditions
2.1. Mathematical Model
2.2. Operating Conditions
3. Results and Discussion
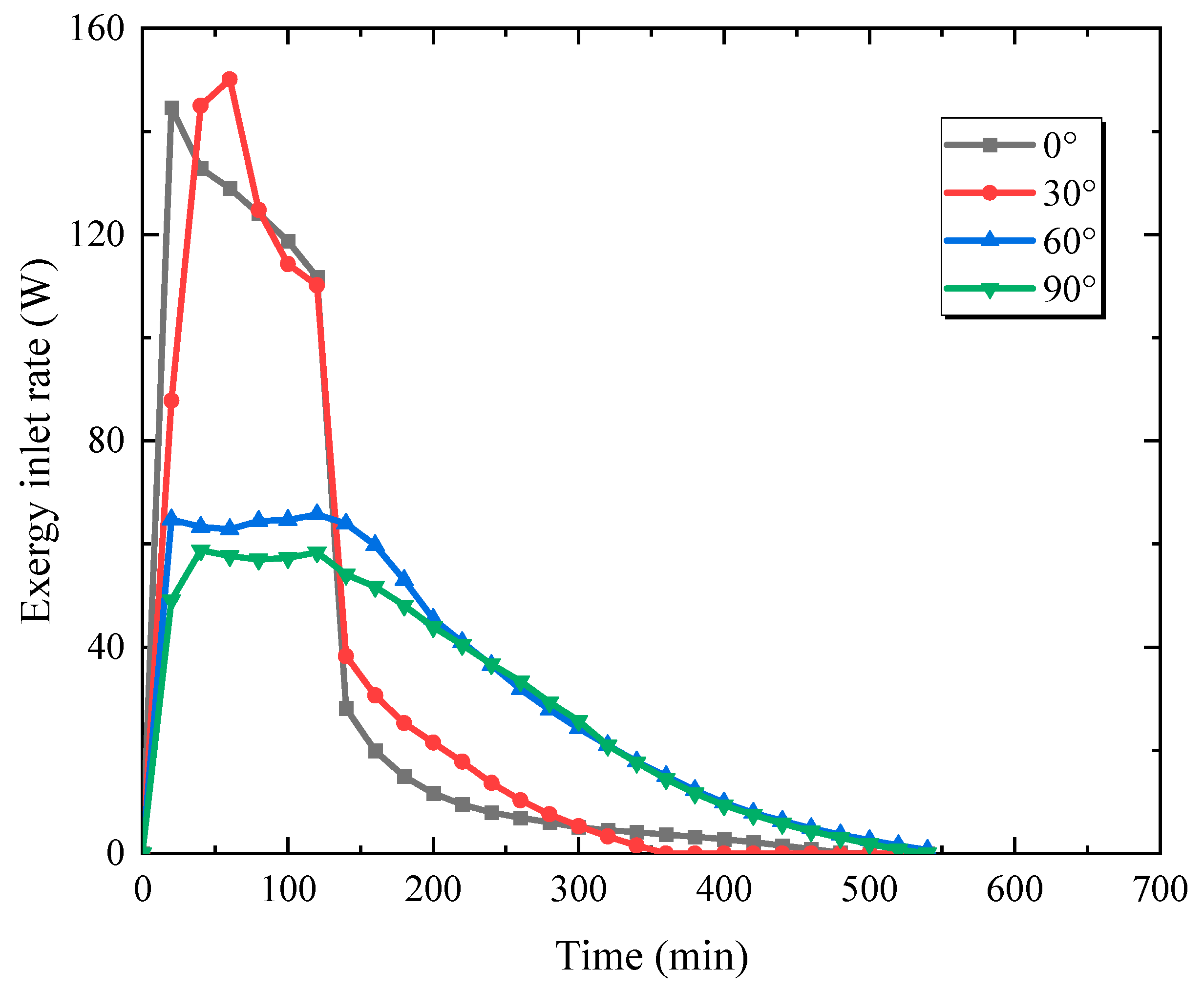
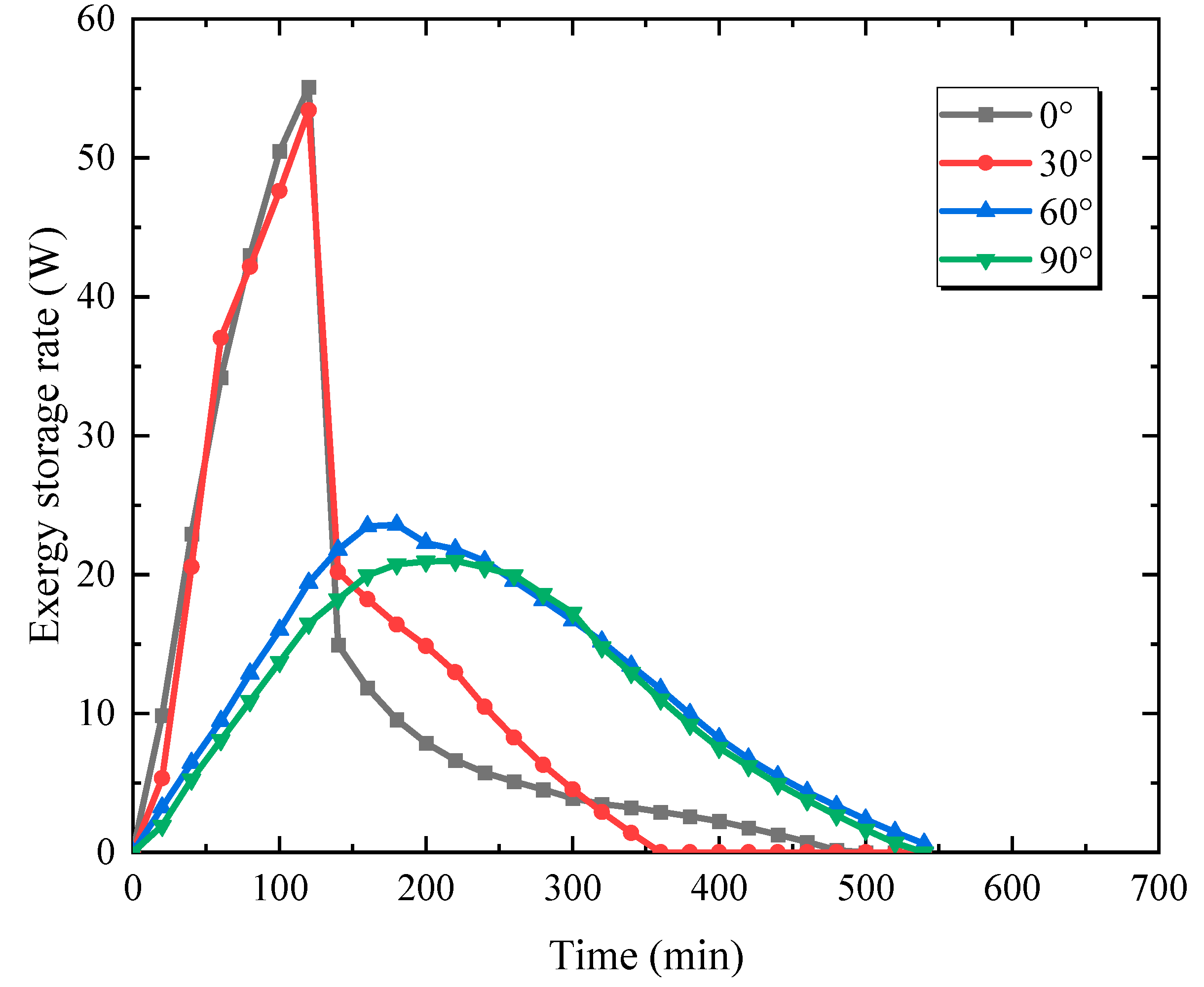
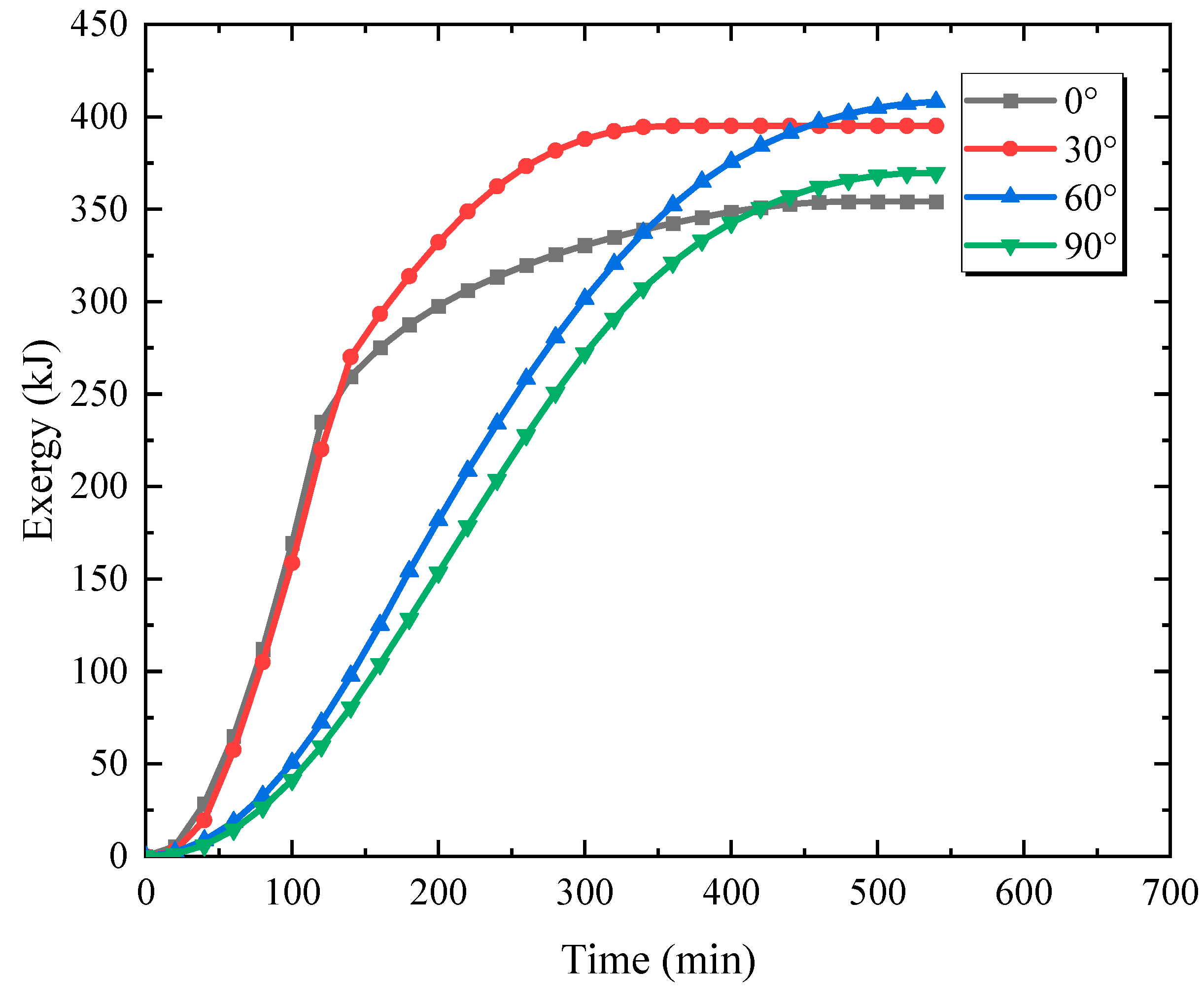
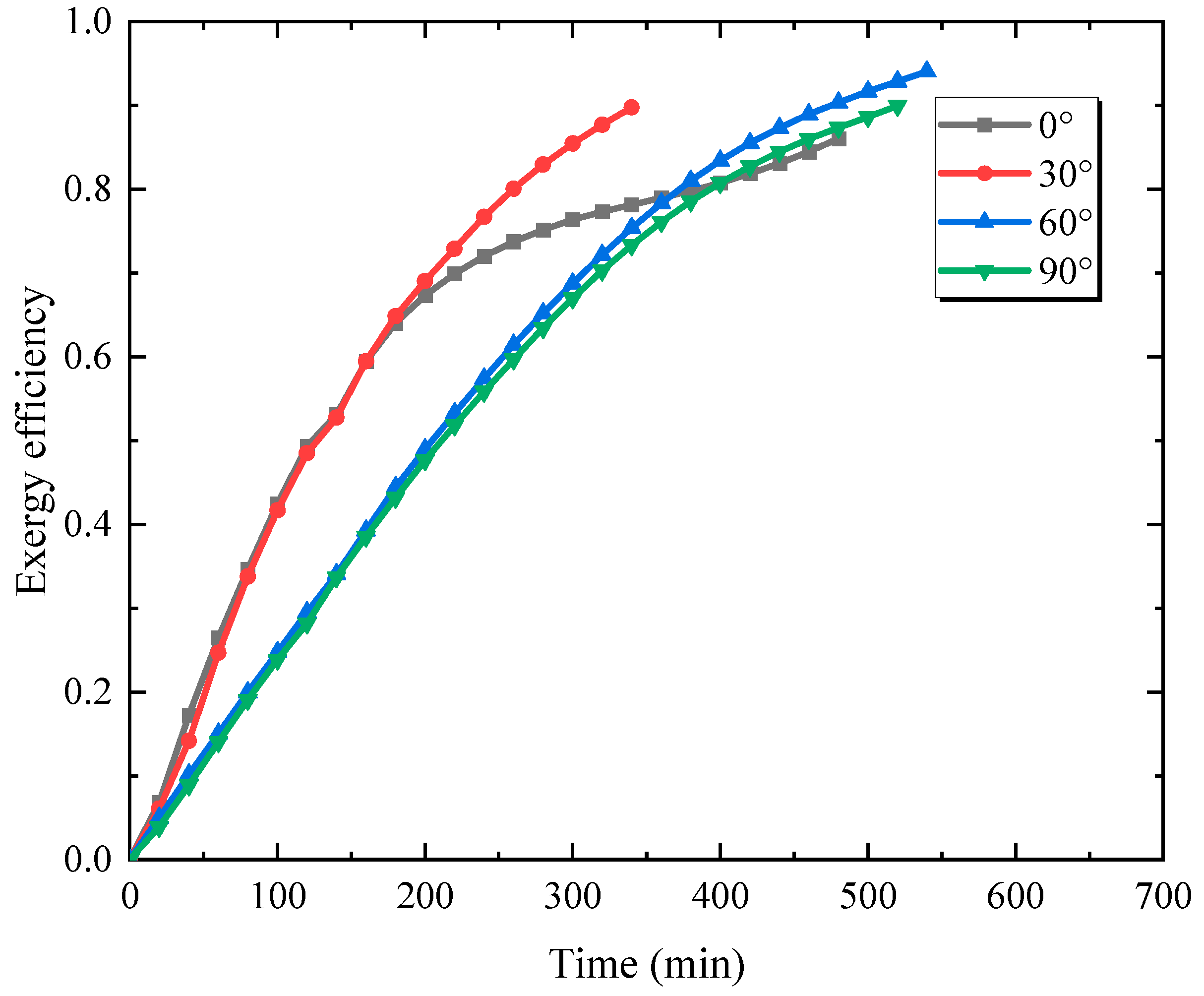
3.1. Effect of Inclination Angle
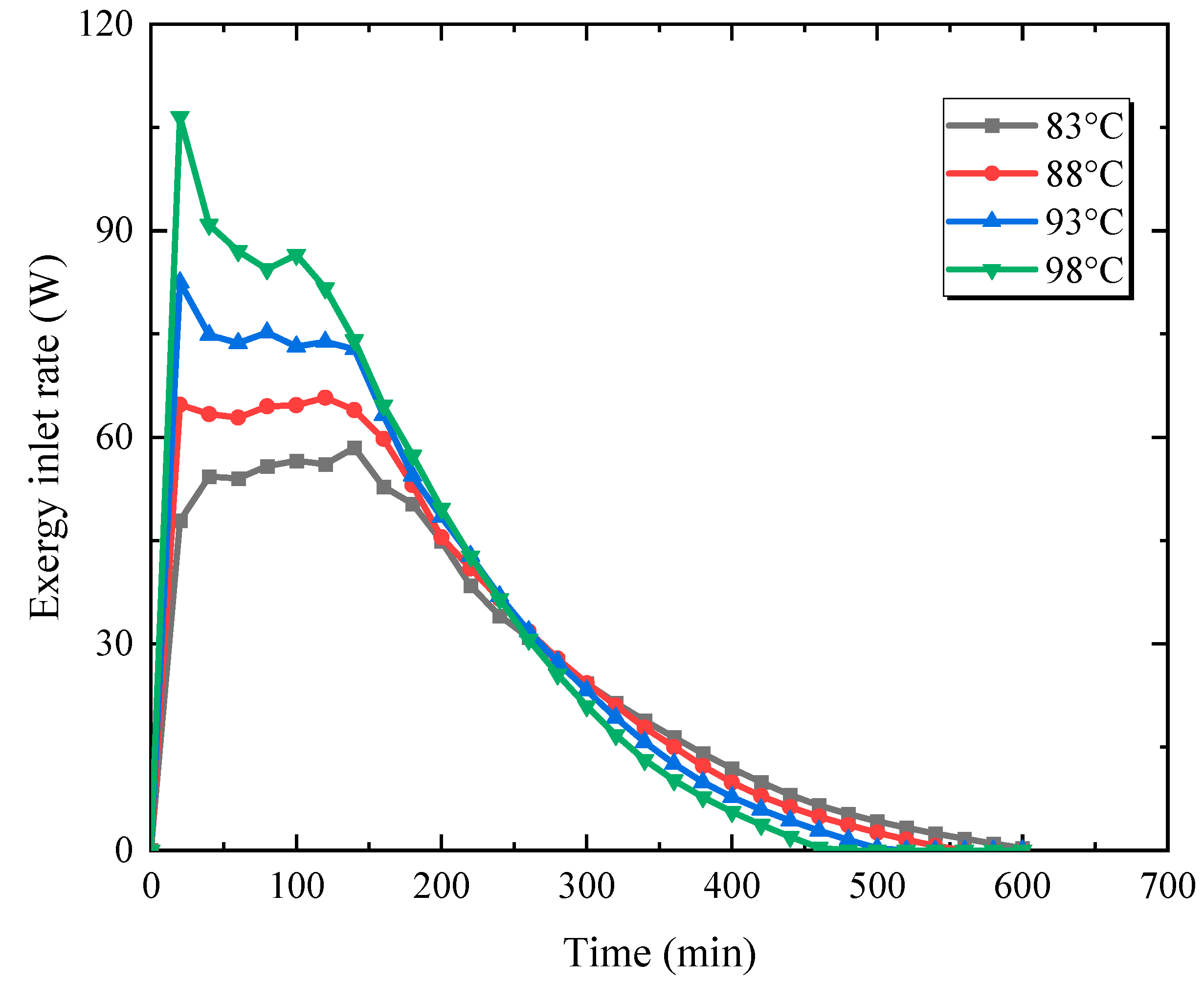
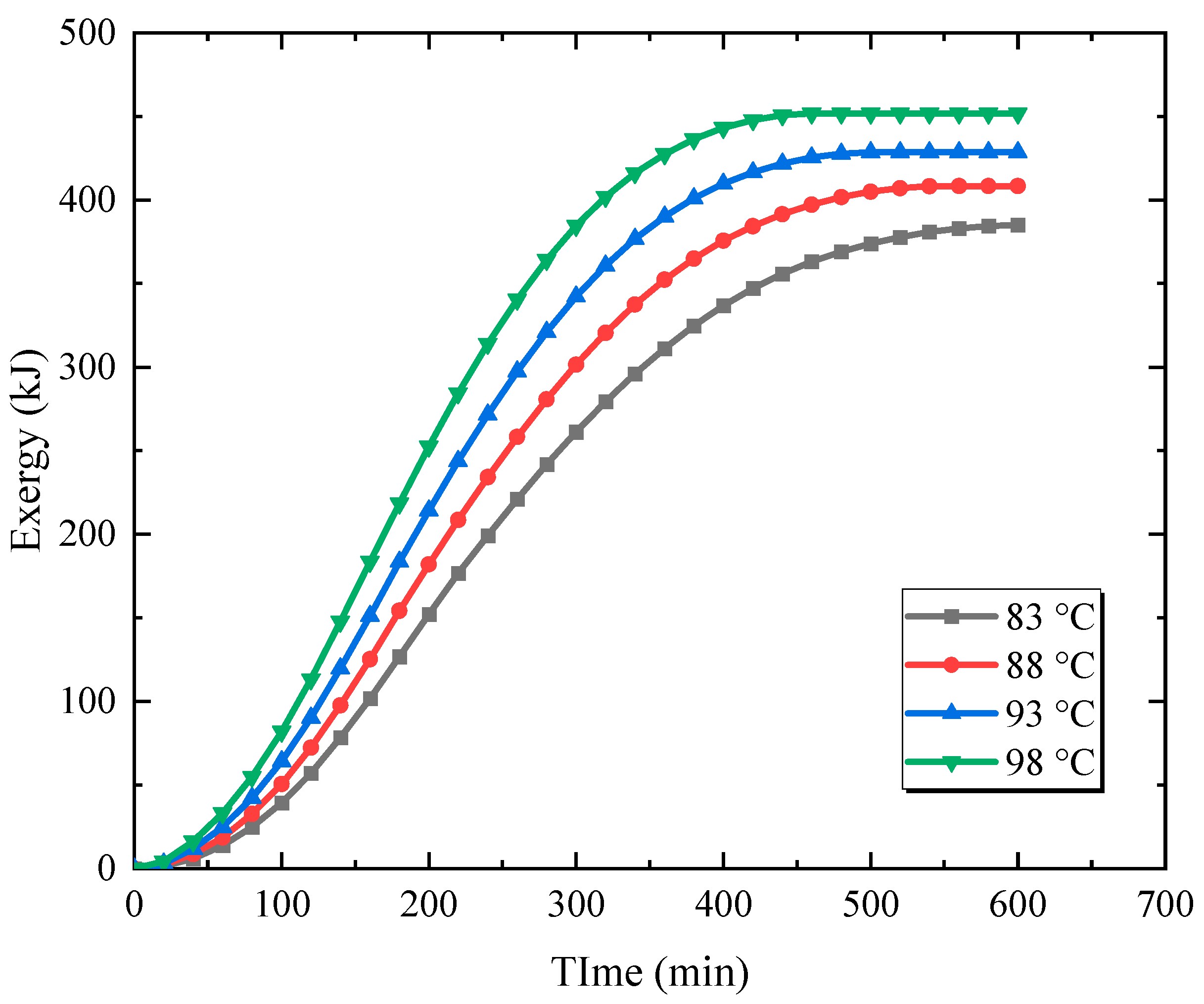
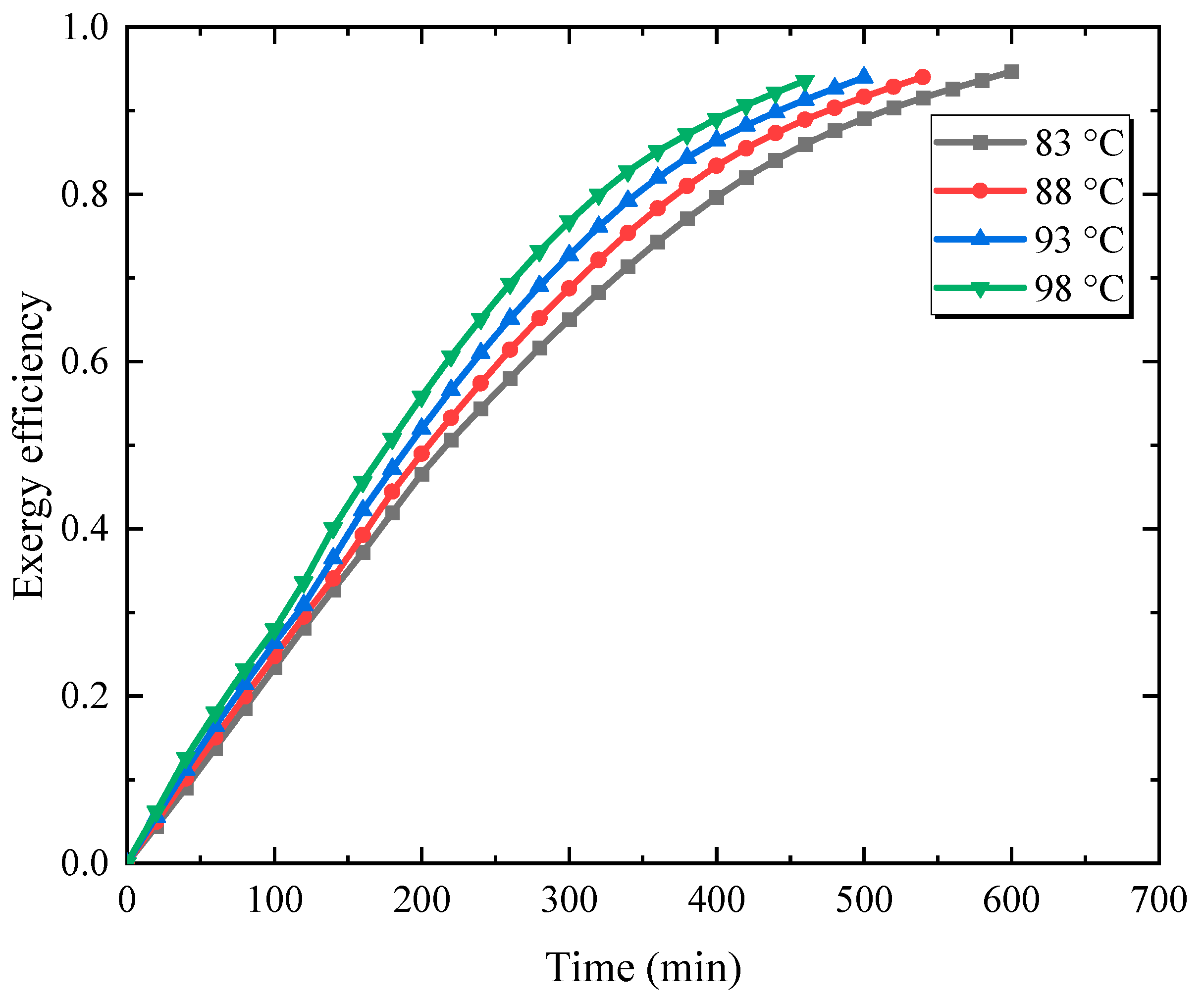
3.2. Effect of Inlet Water Temperature
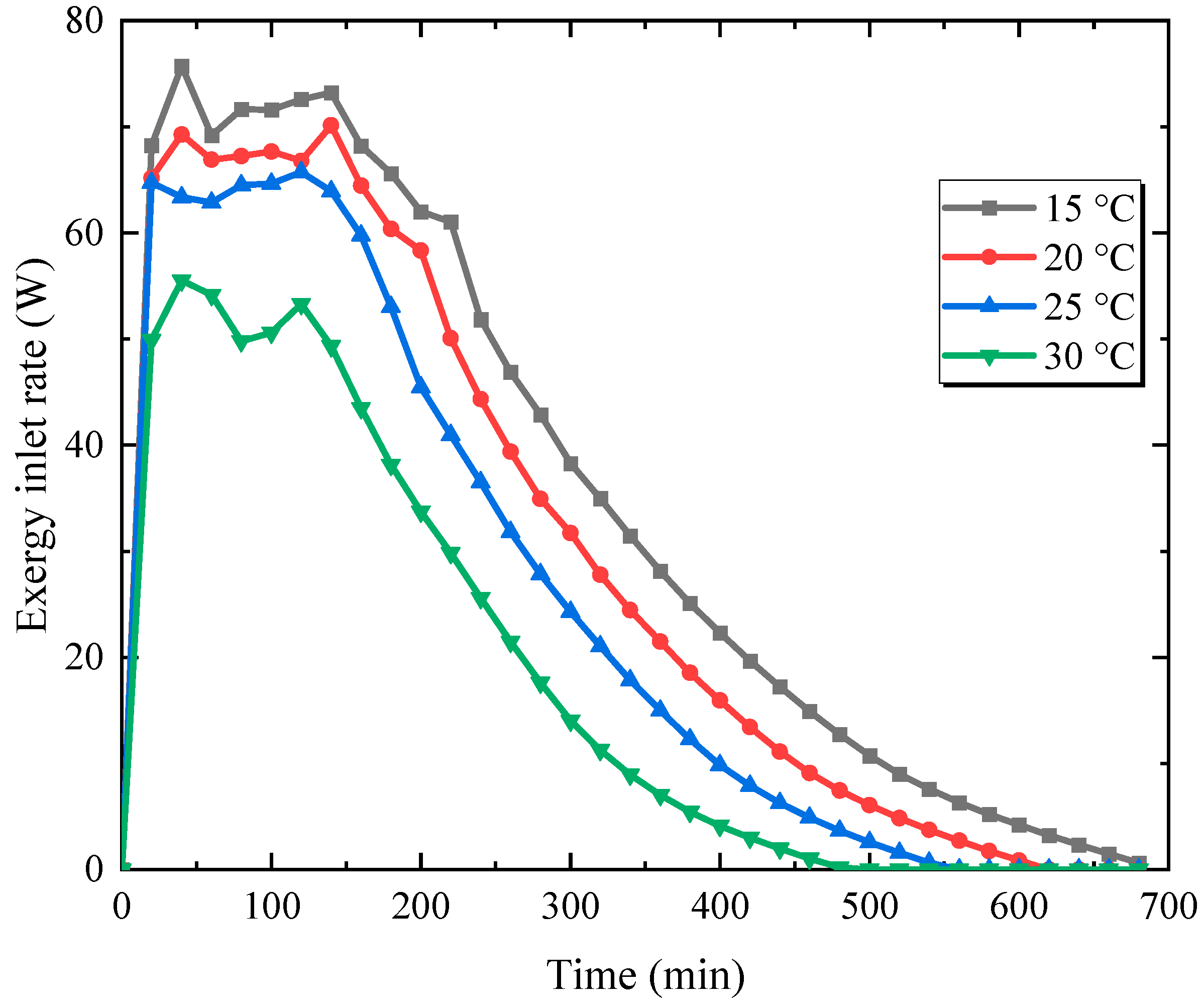
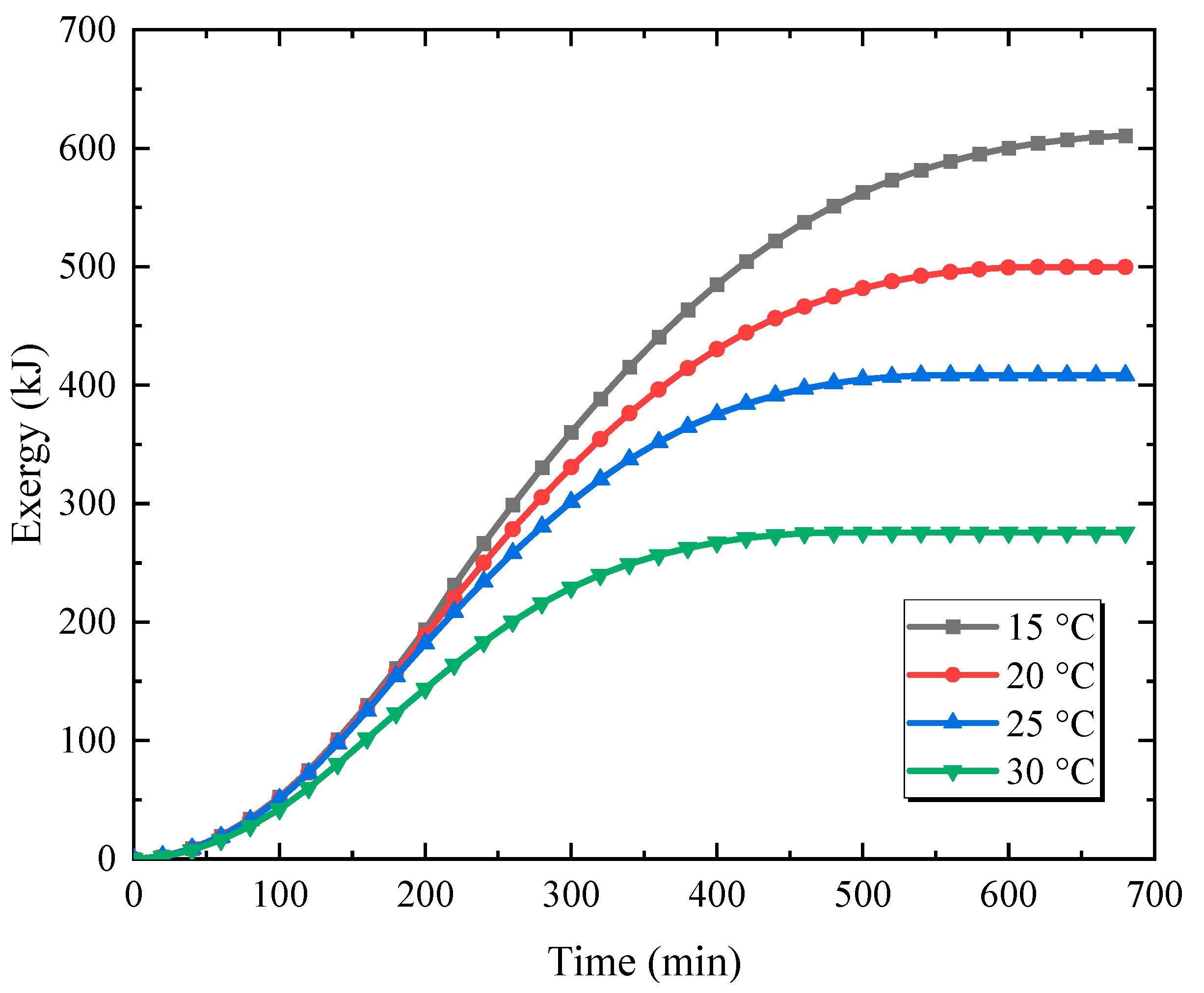
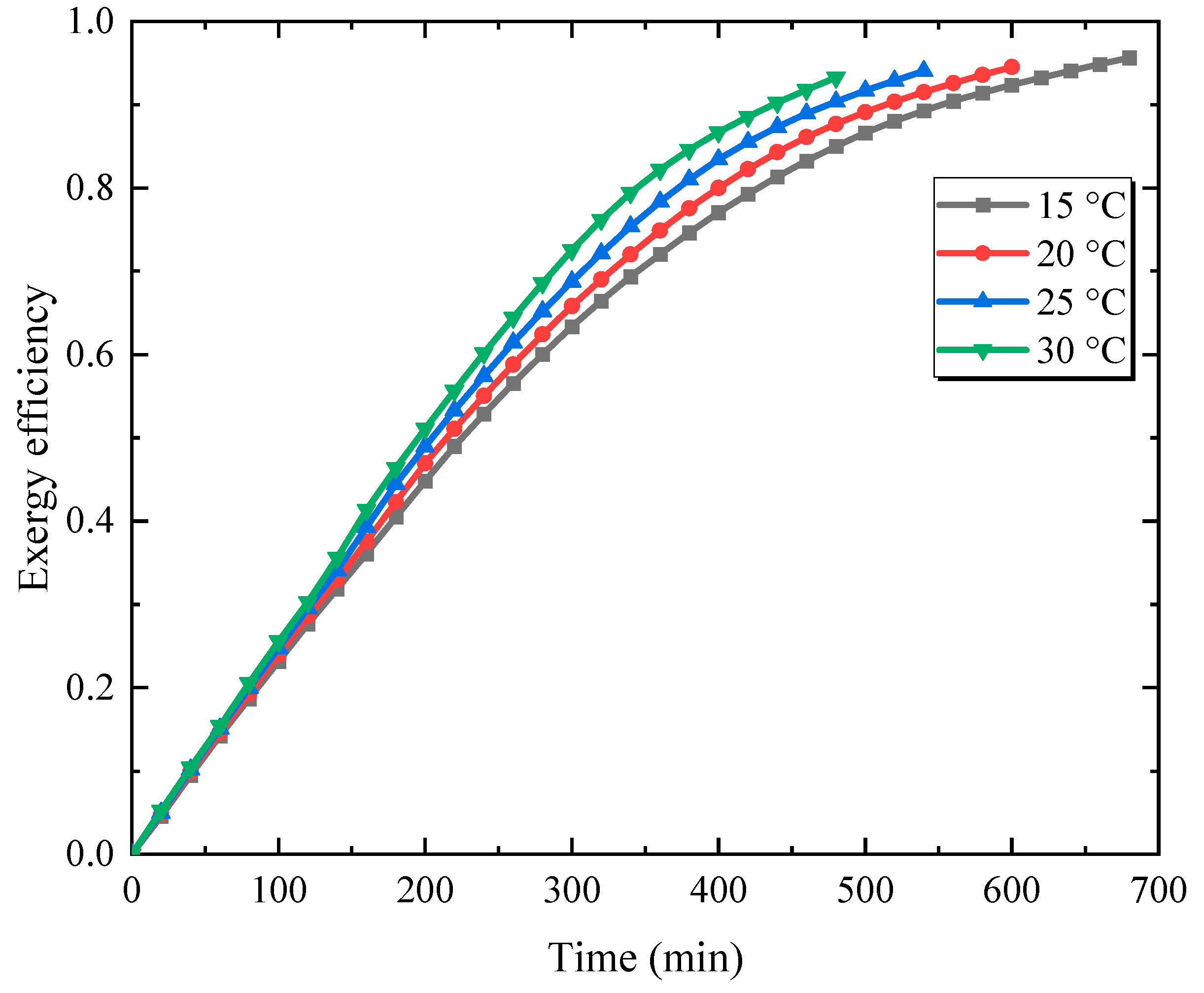
3.3. Effect of Original Temperature
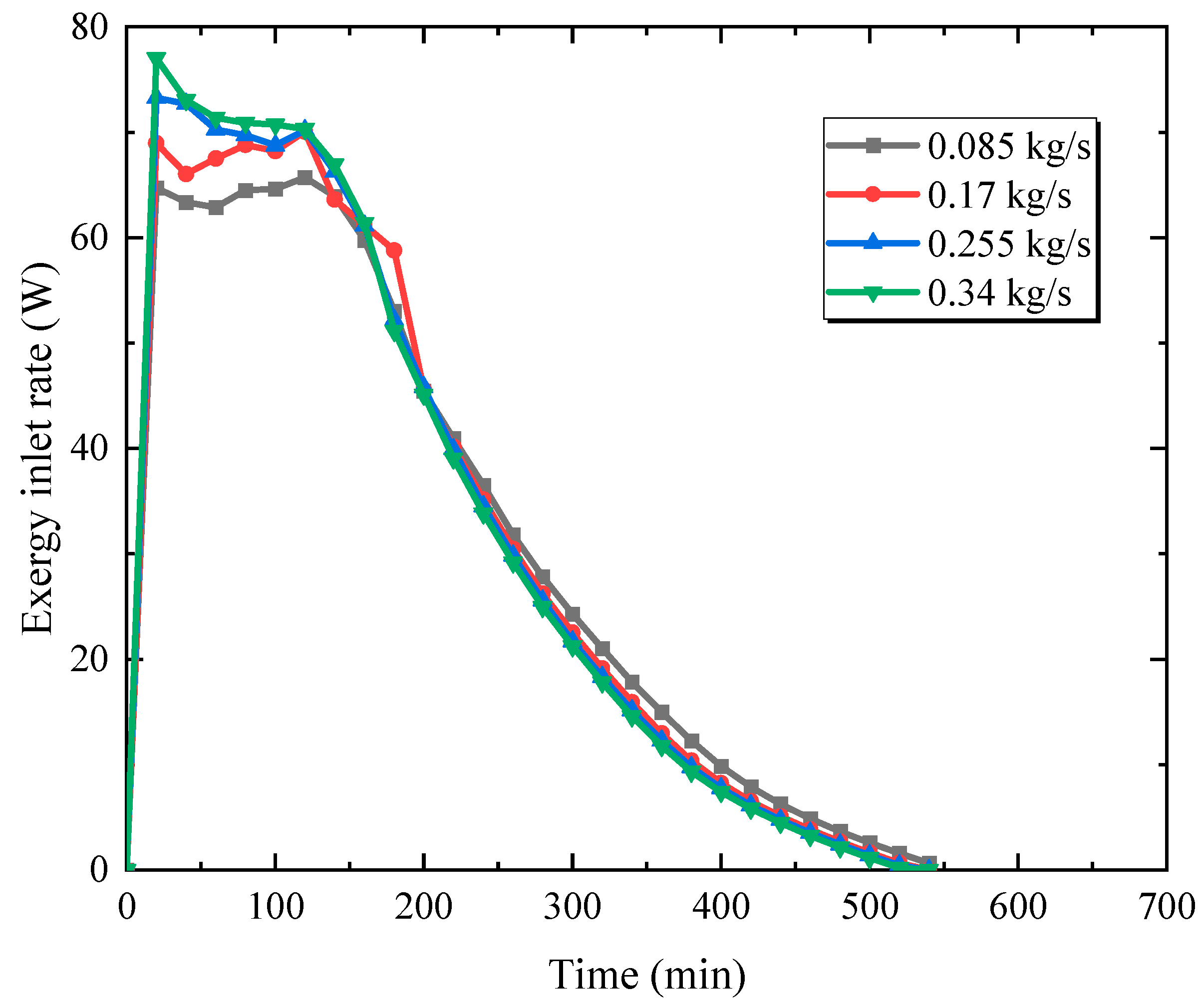
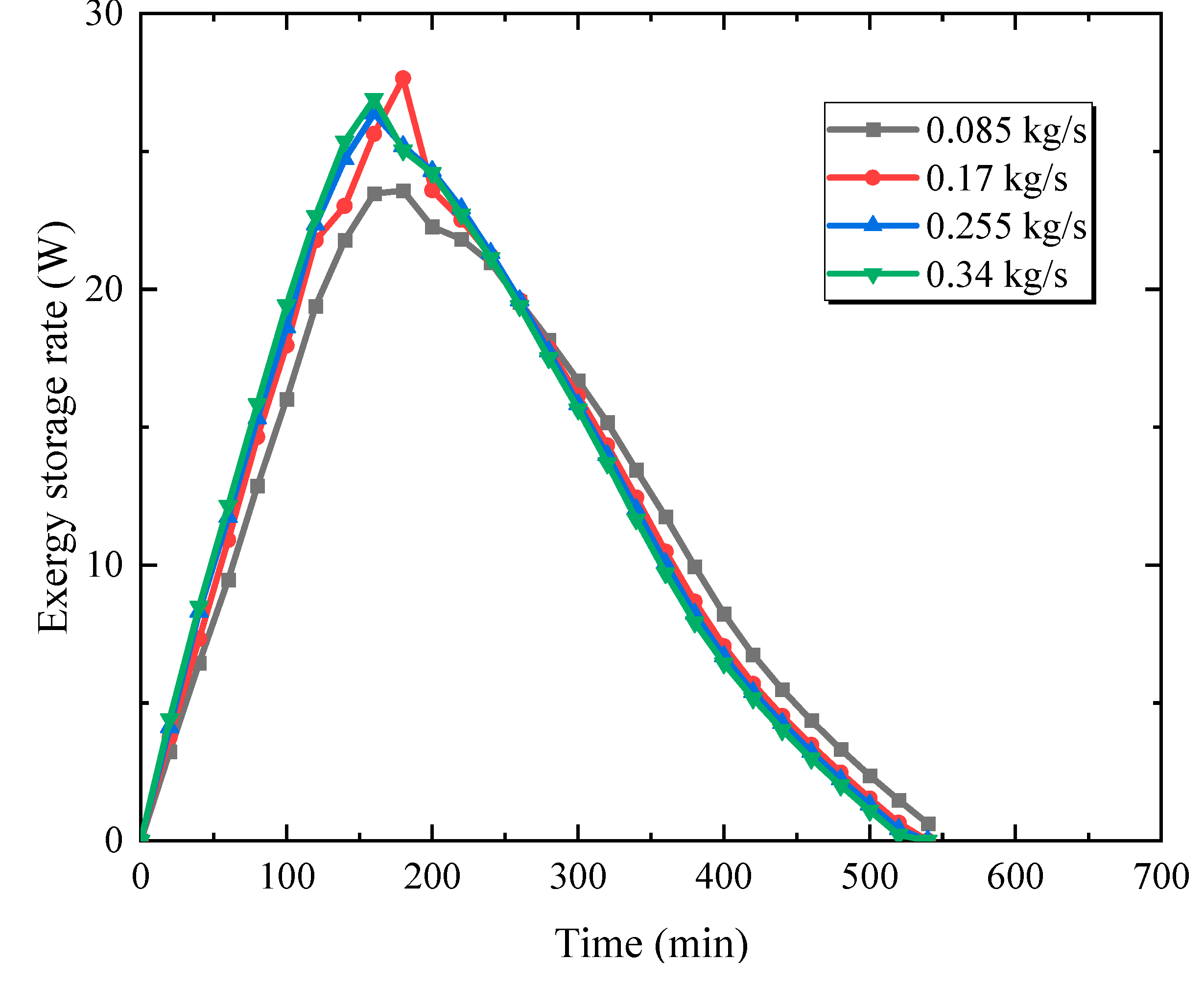
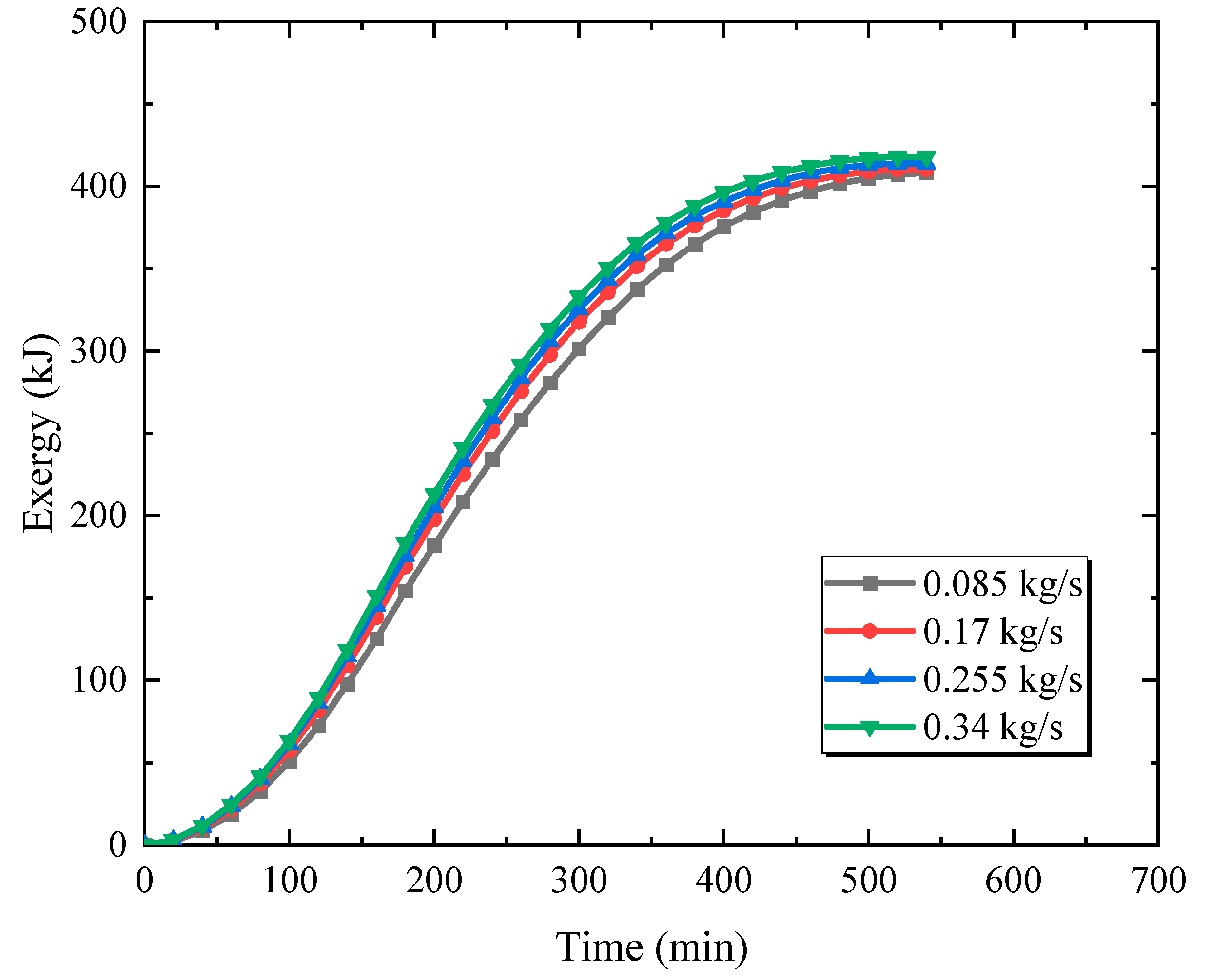
3.4. Effect of Inlet Flow Rate
3.5. Future Work
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| PCM | Phase change material |
| HTF | Heat transfer fluid |
| TES | Thermal energy storage |
| cp | Specific heat capacity (J/kg·K) |
| Mass flow rate (kg/s) | |
| uf | HTF flow rate (m/s) |
| vf | HTF kinematic viscosity (m2/s) |
| Ex | Exergy (J) |
| Q | Energy (J) |
| T | Temperature (°C) |
| To | Original environment temperature (°C) |
| Hm | Latent enthalpy (J/kg) |
| Ns | Entropy generation number |
| t | Time (min) |
| d | Tube diameter (m) |
| ψ | Exergy efficiency |
| in | Inlet |
| sto | Storage |
| loss | Loss |
| f | HTF |
| p | PCM |
| inlet | Inlet |
| outlet | Outlet |
References
- Li, B.; Hong, W.; Li, H.; Lan, J.; Zi, J. Optimized energy distribution management in the nanofluid-assisted photovoltaic/thermal system via exergy efficiency analysis. Energy 2022, 242, 123018. [Google Scholar] [CrossRef]
- Ural, T.; Karaca Dolgun, G.; Güler, O.V.; Keçebaş, A. Performance analysis of a textile based solar assisted air source heat pump with the energy and exergy methodology. Sustain. Energy Technol. Assess. 2021, 47, 101534. [Google Scholar] [CrossRef]
- Wang, Y.; Huang, F.; Tao, S.; Ma, Y.; Ma, Y.; Liu, L.; Dong, F. Multi-objective planning of regional integrated energy system aiming at exergy efficiency and economy. Appl. Energy 2022, 306, 118120. [Google Scholar] [CrossRef]
- Mao, Q.; Cao, W. Effect of variable capsule size on energy storage performances in a high-temperature three-layered packed bed system. Energy 2023, 273, 127166. [Google Scholar] [CrossRef]
- Sharma, S.; Kumar Das, R.; Kulkarni, K. Sustainability analysis of solar air heater roughned with baffles based on exergy efficiency. Mater. Today Proc. 2022, 69, 75–81. [Google Scholar] [CrossRef]
- Li, S.; Gu, W.; Liu, X.; Zhou, Y.; Chen, Z.; Zhang, X.; Ma, T. Pavement integrated photovoltaic thermal (PIPVT) system: A temporal and spatial analysis of energy and exergy performance. J. Clean. Prod. 2022, 340, 130782. [Google Scholar] [CrossRef]
- Abdalla, A.N.; Shahsavar, A. An experimental comparative assessment of the energy and exergy efficacy of a ternary nanofluid-based photovoltaic/thermal system equipped with a sheet-and-serpentine tube collector. J. Clean. Prod. 2023, 395, 136460. [Google Scholar] [CrossRef]
- Abdalla, A.N.; Shahsavar, A. Numerical investigation of the effect of rotary propeller type turbulator on the energy and exergy efficiencies of a concentrating photovoltaic/thermal hybrid collector. J. Clean. Prod. 2023, 393, 136225. [Google Scholar] [CrossRef]
- Braimakis, K.; Karellas, S. Exergy efficiency potential of dual-phase expansion trilateral and partial evaporation ORC with zeotropic mixtures. Energy 2023, 262, 125475. [Google Scholar] [CrossRef]
- Wang, Y.; He, G.; Huang, H.; Guo, X.; Xing, K.; Liu, S.; Tu, Z.; Xia, Q. Thermodynamic and exergy analysis of high compression ratio coupled with late intake valve closing to improve thermal efficiency of two-stage turbocharged diesel engines. Energy 2023, 268, 126733. [Google Scholar] [CrossRef]
- Ozcan, H.G.; Hepbasli, A.; Abusoglu, A.; Anvari-Moghaddam, A. Energy, exergy, economic, environmental and sustainability (4ES) analyses of a wastewater source heat pump system for district heating applications based on real operational data. Sustain. Energy Technol. Assess. 2023, 56, 103077. [Google Scholar] [CrossRef]
- Nazari, M.; Jafarmadar, S.; Khalilarya, S. Exergy and thermoeconomic analyses of serpentine tube flat-plate solar water heaters coated with CuO nanostructures. Case Stud. Therm. Eng. 2022, 35, 102072. [Google Scholar] [CrossRef]
- Bouadila, S.; Rehman, T.-U.; Baig, M.A.A.; Skouri, S.; Baddadi, S. Energy, Exergy and Economic (3E) analysis of evacuated tube heat pipe solar collector to promote storage energy under North African climate. Sustain. Energy Technol. Assess. 2023, 55, 102959. [Google Scholar] [CrossRef]
- Cao, Y.; Kasaeian, M.; Abbasspoor, H.; Shamoushaki, M.; Ehyaei, M.A.; Abanades, S. Energy, exergy, and economic analyses of a novel biomass-based multigeneration system integrated with multi-effect distillation, electrodialysis, and LNG tank. Desalination 2022, 526, 115550. [Google Scholar] [CrossRef]
- Castiñeiras-Filho, S.L.P.; Pradelle, F. Modeling of microalgal biodiesel production integrated to a sugarcane ethanol plant: Energy and exergy efficiencies and environmental impacts due to trade-offs in the usage of bagasse in the Brazilian context. J. Clean. Prod. 2023, 395, 136461. [Google Scholar] [CrossRef]
- Salek, F.; Eshghi, H.; Zamen, M.; Ahmadi, M.H. Energy and exergy analysis of an atmospheric water generator integrated with the compound parabolic collector with storage tank in various climates. Energy Rep. 2022, 8, 2401–2412. [Google Scholar] [CrossRef]
- Eltaweel, M.; Abdel-Rehim, A.A.; Attia, A.A.A. A comparison between flat-plate and evacuated tube solar collectors in terms of energy and exergy analysis by using nanofluid. Appl. Therm. Eng. 2021, 186, 116516. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, Z.; Zhang, G.; Wang, D. Energy, exergy, economic and environmental analysis of a novel direct-expansion solar-assisted flash tank vapor injection heat pump for water heater. Energy Convers. Manag. 2022, 254, 115239. [Google Scholar] [CrossRef]
- Alnaqi, A.A.; Al-Rashed, A.A.A.A. Impact of vortex generator and two-phase MWCNT-MgO/water hybrid nanofluid on thermo-hydraulic performance and exergy and energy efficiency of a solar collector under Kuwait climatic conditions. Eng. Anal. Bound. Elem. 2023, 151, 175–186. [Google Scholar] [CrossRef]
- Cui, F.; Liu, F.; Tong, Y.; Wang, S.; Guo, W.; Han, T.; Qiu, X. Energy and exergy assessment of evacuated tube solar collector using water, Fe3O4 nanofluid and Fe3O4/MWCNT hybrid nanofluid. Process Saf. Environ. Prot. 2022, 163, 236–243. [Google Scholar] [CrossRef]
- Nikolic, D.; Skerlic, J.; Radulovic, J.; Miskovic, A.; Tamasauskas, R.; Sadauskienė, J. Exergy efficiency optimization of photovoltaic and solar collectors’ area in buildings with different heating systems. Renew. Energy 2022, 189, 1063–1073. [Google Scholar] [CrossRef]
- Mohammadpour, J.; Lee, A.; Timchenko, V.; Taylor, R. Nano-Enhanced Phase Change Materials for Thermal Energy Storage: A Bibliometric Analysis. Energies 2022, 15, 3426. [Google Scholar] [CrossRef]
- Riahi, S.; Liu, M.; Jacob, R.; Belusko, M.; Bruno, F. Assessment of exergy delivery of thermal energy storage systems for CSP plants: Cascade PCMs, graphite-PCMs and two-tank sensible heat storage systems. Sustain. Energy Technol. Assess. 2020, 42, 100823. [Google Scholar] [CrossRef]
- Cao, H.; Mao, Y.; Wang, W.; Gao, Y.; Zhang, M.; Zhao, X.; Sun, J.; Song, Z. Thermal-exergy efficiency trade-off optimization of pressure retarded membrane distillation based on TOPSIS model. Desalination 2022, 523, 115446. [Google Scholar] [CrossRef]
- Mouli, K.V.V.C.; Sundar, L.S.; Alklaibi, A.M.; Said, Z.; Sharma, K.V.; Punnaiah, V.; Sousa, A.C.M. Exergy efficiency and entropy analysis of MWCNT/Water nanofluid in a thermosyphon flat plate collector. Sustain. Energy Technol. Assess. 2023, 55, 102911. [Google Scholar] [CrossRef]
- Syam Sundar, L. Experimental study on the thermophysical properties, heat transfer, thermal entropy generation and exergy efficiency of turbulent flow of ZrO2-water nanofluids. Alex. Eng. J 2023, 65, 867–885. [Google Scholar] [CrossRef]
- Sundar, L.S.; Shaik, F. Laminar convective heat transfer, entropy generation, and exergy efficiency studies on ethylene glycol based nanofluid containing nanodiamond nanoparticles. Diam. Relat. Mater. 2023, 131, 109599. [Google Scholar] [CrossRef]
- Syam Sundar, L. Heat transfer, friction factor and exergy efficiency analysis of nanodiamond-Fe3O4/water hybrid nanofluids in a tube with twisted tape inserts. Ain Shams Eng. J. 2022, 14, 102068. [Google Scholar] [CrossRef]
- Sundar, L.S.; Shaik, F. Heat transfer and exergy efficiency analysis of 60% water and 40% ethylene glycol mixture diamond nanofluids flow through a shell and helical coil heat exchanger. Int. J. Therm. Sci. 2023, 184, 107901. [Google Scholar] [CrossRef]
- Khetib, Y.; Sait, H.; Habeebullah, B.; Hussain, A. Numerical study of the effect of curved turbulators on the exergy efficiency of solar collector containing two-phase hybrid nanofluid. Sustain. Energy Technol. Assess. 2021, 47, 101436. [Google Scholar] [CrossRef]
- Vahidinia, F.; Khorasanizadeh, H.; Aghaei, A. Energy, exergy, economic and environmental evaluations of a finned absorber tube parabolic trough collector utilizing hybrid and mono nanofluids and comparison. Renew. Energy 2023, 205, 185–199. [Google Scholar] [CrossRef]
- Carmona, M.; Rincón, A.; Gulfo, L. Energy and exergy model with parametric study of a hot water storage tank with PCM for domestic applications and experimental validation for multiple operational scenarios. Energy Convers. Manag. 2020, 222, 113189. [Google Scholar] [CrossRef]
- Ji, S.; Cheng, Q.; Sun, W.; Qi, Y.; Wang, S. Study on optimal operation conditions in the heating process of a crude oil single-disk floating roof tank: Insights from exergy transfer analysis method. Energy Rep. 2023, 9, 3131–3147. [Google Scholar] [CrossRef]
- Ding, S.; Guo, B.; Hu, S.; Gu, J.; Yang, F.; Li, Y.; Dang, J.; Liu, B.; Ma, J. Analysis of the effect of characteristic parameters and operating conditions on exergy efficiency of alkaline water electrolyzer. J. Power Sources 2022, 537, 231532. [Google Scholar] [CrossRef]
- Si, Y.; Brumercik, F.; Yang, C.; Glowacz, A.; Ma, Z.; Siarry, P.; Sulowicz, M.; Gupta, M.K.; Li, Z. Prediction and evaluation of energy and exergy efficiencies of a nanofluid-based photovoltaic-thermal system with a needle finned serpentine channel using random forest machine learning approach. Eng. Anal. Bound. Elem. 2023, 151, 328–343. [Google Scholar] [CrossRef]
- Hu, Z.; He, D.; Zhao, H. Multi-objective optimization of energy distribution in steel enterprises considering both exergy efficiency and energy cost. Energy 2023, 263, 125623. [Google Scholar] [CrossRef]
- Hançer Güleryüz, E.; Özen, D.N. Advanced exergy and exergo-economic analyses of an advanced adiabatic compressed air energy storage system. J. Energy Storage 2022, 55, 105845. [Google Scholar] [CrossRef]
- Mao, Q.; Zhang, Y. Study on the thermal storage performance of a new cascade structure phase change thermal storage tank. J. Energy Storage 2022, 56, 106155. [Google Scholar] [CrossRef]
- Wu, Y.; Li, D.; Jiang, W.; Zhu, S.; Zhao, X.; Arıcı, M.; Tunçbilek, E. Energy storage and exergy efficiency analysis of a shell and tube latent thermal energy storage unit with non-uniform length and distributed fins. Sustain. Energy Technol. Assess. 2022, 53, 102362. [Google Scholar] [CrossRef]
- Peng, L.; Wu, H.; Mao, Q. Numerical and experimental study on the performance of a thermal energy storage in a solar building. J. Energy Storage 2023, 61, 106745. [Google Scholar] [CrossRef]
- Pahamli, Y.; Hosseini, M.J.; Ardahaie, S.S.; Ranjbar, A.A. Improvement of a phase change heat storage system by Blossom-Shaped Fins: Energy analysis. Renew. Energy 2022, 182, 192–215. [Google Scholar] [CrossRef]




| Variable Conditions [40] | Constant Conditions [40] | Re | Ste | |
|---|---|---|---|---|
| Effect of inclination angle | Inclination angles of 0°, 30°, 60°, and 90°. | Inlet water temperature of 83 °C, original temperature of 20 °C, and inlet flow rate of 0.085 kg/s. | 25,278.7 | 0.478 |
| Effect of inlet water temperature | Inlet water temperatures of 83, 88, 93, and 98 °C. | Inlet water temperature of 83 °C, original temperature of 20 °C, and inlet flow rate of 0.085 kg/s. | 25,278.7 | 0.478, 0.55, 0.623, 0.695 |
| Effect of original temperature | Original temperatures of 15, 20, 25, and 30 °C. | Inlet water temperature of 83 °C, original temperature of 20 °C, and inlet flow rate of 0.085 kg/s. | 25,278.7 | 0.478 |
| Effect of inlet flow rate | Inlet flow rates of 0.085, 0.17, 0.255, and 0.34 kg/s. | Inlet water temperature of 83 °C, original temperature of 20 °C, and inlet flow rate of 0.085 kg/s. | 25,278.7, 50,557.5, 75,836.2, 101,115 | 0.478 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, L.; Wu, H.; Cao, W.; Mao, Q. Exergy Analysis of a Shell and Tube Energy Storage Unit with Different Inclination Angles. Energies 2023, 16, 4297. https://doi.org/10.3390/en16114297
Peng L, Wu H, Cao W, Mao Q. Exergy Analysis of a Shell and Tube Energy Storage Unit with Different Inclination Angles. Energies. 2023; 16(11):4297. https://doi.org/10.3390/en16114297
Chicago/Turabian StylePeng, Li, Hongjun Wu, Wenlong Cao, and Qianjun Mao. 2023. "Exergy Analysis of a Shell and Tube Energy Storage Unit with Different Inclination Angles" Energies 16, no. 11: 4297. https://doi.org/10.3390/en16114297
APA StylePeng, L., Wu, H., Cao, W., & Mao, Q. (2023). Exergy Analysis of a Shell and Tube Energy Storage Unit with Different Inclination Angles. Energies, 16(11), 4297. https://doi.org/10.3390/en16114297






