The Influence of Cutting Technology on Magnetic Properties of Non-Oriented Electrical Steel—Review State of the Art
Abstract
1. Introduction
2. Morphology of Grains and Measurements of the Macroscopic Properties of Strips Undergoing the Cutting Process
- -
- testing the presence of elastic and plastic deformations and residual stress distributions inside the cut material. The research results available in the literature indicate a relatively strong influence of internal stresses on changes in macroscopic material properties. As Ossart points out, plastic deformations predominate at a relatively short distance from the cut edge [7]. Research conducted by many researchers on the deterioration of the material’s macroscopic properties caused by the presence of stresses leads to the conclusion that plastic deformation causes a significant deterioration of the magnetic properties of electrical steels. This is particularly evident at low strains (typically from 0 to 5%) and low and medium magnetic field amplitudes (up to a few kA/m) [21,22,23]. Stresses below the elastic limit can either increase or decrease the macroscopic material parameters, such as the magnetic permeability of a material. This conclusion is supported by research results presented by Daem et al. [23]. This generally depends on whether the material exhibits positive or negative magnetostriction, but exceptions have been reported by Allia et al. [24]. Once the stress crosses the elastic limit and plastic flow occurs, magnetic permeability reduces rapidly. As demonstrated by Maeda et al., tensile stresses are generated near the cut edge, whereas compressive stresses are further away from the cut edge [25]. Analyzing the fundamental work [4], we conclude that the more the stress exceeds the elastic limit, the more the initial and maximum permeability decrease. The study of the impact of plastic deformations and residual stresses on changes in material properties must be supplemented with an answer to the question about the distance from the cut edge where deformations and strains occur. The answer to this question can be found, for example, in the work of Xiong et al. [26]. The authors show the dependence of residual stress in the cut edge zone as a function of the distance from the cut edge. At the same time, they determine the increase in stresses about those that occur in the undamaged part of the material. This distance was defined as close to the one in which mechanical hardening of the material occurs (increase in microhardness). Cutting technology is known to affect the size and area of residual stress. Therefore, research has been conducted in the guillotine and laser cutting field. For guillotine-cut material, Cao et al. presented the research results on the width of the area where residual stress occurs [27]. According to them, the range of rapid stress changes can be defined as 100–150 μm, while more minor changes are observed up to 400 μm. In the entire range, the residual stress value changes from about 350 MPa to about 100 MPa. Maeda et al. show that laser cutting also “generates” residual stresses, with values comparable to those occurring during guillotine cutting [25]. Omura et al. conducted extensive research on the impact of material microhardness (in the undamaged zone) and strip thickness on the maximum plastic strain value [28]. They showed that the harder the material, the lower its maximum hardening on the cut edge and the smaller the area of increased microhardness. Examining the influence of the thickness of the strip, they found that the thicker the strip, the greater the maximum value of plastic strain and the wider the area of increased hardness. Fujisaki et al. researched the presence of plastic and elastic stresses in ferromagnetic strips [29]. The authors presented the results of tests and simulations concerning guillotine cutting, indicating the presence of stresses and the size of the zones where plastic and elastic stresses occur. They concluded that the size of the area where plastic stresses occur is comparable to half the thickness of the tested strip.
- -
- microhardness tests (as known, microhardness is the hardness of a material gauged with instruments using small indenters. It linearly correlates with the tensile strength. This allows cost-effective, non-invasive testing). In work by Hofmann et al., tests were performed for three cutting technologies: guillotine, laser, and spark erosion [30]. When examining the maximum hardening in the cutting zone, it was found that the guillotine causes a rise in hardness by 70%, and the laser causes an increase by 15% with regard to spark erosion cutting. The spark erosion technology essentially does not increase the hardness. At the same time, the authors defined the width of the mechanical hardening zone as 120–150 μm. As described by Araujo et al. [31], microhardness changes in a similar range were registered, while Wenmin et al. in [32] state that this size can be even be defined as reaching 2 mm. On the other hand, the work of A. Pulnikov et al. indicates that the width of the area in which the increase in microhardness occurs (guillotine cutting) is about 150 μm [33]. In this area, there is an 80% increase in microhardness compared to undamaged material. At the same time, the authors note that the introduction of additional compression applied to the sample causes a slight increase in the maximum microhardness with a simultaneous almost two-fold increase in the width of the area with increased microhardness. In another paper, Pulnikov presents the results of microhardness measurements executed for various electrical steel sheets [34]. He obtained deterioration depth ranges from 0.4 to 2.8 mm, depending on the type and thickness of the material tested. The work carried out by the team of Kurosaki et al. indicated a possible greater range of microhardness changes during guillotine cutting (even up to 350 μm) as well as the possibility of a microhardness increase by 10% during laser cutting (at a distance of up to 150 μm from the edge) [35,36]. Schoppa noted in his research that the width of the area with increased microhardness depends on the silicon content [37]. From other works, it is known that an increase in the silicon content causes an increase in grain size, so one could generalize Schoppa’s observations. It should therefore be concluded that the width of the zone with increased microhardness depends on the average grain size. This statement is supported by the results of the research conducted by Schmidt, who defined the zone size as 350 μm, examining a material with 1% silicon content [38]. In materials with a relatively low silicon content (relatively small grains), the size of this zone does not exceed 500 μm. In contrast, it can reach as much as 1–2 mm for materials with somewhat higher content. Omura et al. tested materials with a thickness of 0.35 mm, with a microhardness varying from 154 to 217 [28]. They showed that the material with lower microhardness had a 50% wider zone of microhardness changes resulting from guillotine cutting than the harder material. At the same time, the percentage increase in the maximum microhardness (at the cut edge) of the softer material was 20% higher than for the harder material. This work also described the strip thickness’s influence on the zone’s width in which the microhardness increase occurred. For the thinner material (0.2 mm), a zone whose width was half that of the thicker material (0.35 mm) was found. In turn, the work of Saleem et al. did not show a significant increase in microhardness as a function of distance for laser-cut material [39]. Belhadj et al., who analyzed the material cut with a laser, reached other conclusions, noting the dependence of changes in properties on the speed of moving the laser beam [40]. It has been shown that for a laser moving at a rate of 6 m/min, the hardening zone reaches 500 μm (the authors performed Vickers hardness tests, obtaining microhardness changes from 140 to 180 HV). When the laser beam moved at a lower speed, i.e., 3 m/min, the width of the hardened zone increased to 2 mm, and the microhardness reached 200 HV. In the literature, we can find the results of research conducted by Baudouin et al. in which the effect of knife clearance on the change in maximum hardening and its range was analyzed [41]. The authors showed that at the cut edge, an increase in microhardness by about 60% is possible, and the content of these changes can reach up to about 800 μm, strongly dependent on the chemical composition of the material. Wang et al. studied the effect of clearance varying from 3 to 10% for a material with a thickness of 0.3 mm, having small grains (27 μm) [42]. It was noticed that the range of microhardness changes occurring at a distance of up to 200 μm from the edge did not essentially depend on clearance, and the maximum increase in microhardness differed by 10%. The authors showed that there is an optimal clearance value for which the maximum hardening is the smallest (this value depends on the grain size). Wu et al. compared the size of the zone with increased microhardness and its maximum value for non-oriented materials cut with a guillotine and stamped [43]. They found that guillotine cutting increased the area where the higher microhardness was measured by 20% and, at the same time, reduced the maximum microhardness value by 10%. By simultaneously examining the changes in plastic deformation for both cases, the authors confirmed the same proportions as for the microhardness curve. Similar research was conducted by Weiss et al. In [44], the cutting blade wear’s influence on the zone’s width with increased microhardness and maximum microhardness was described. Materials with a thickness of 0.35 and 0.5 mm, with comparable grain sizes and hardness of the undamaged material, were tested. Studies have shown that cutting with a worn tool causes a 10% increase in microhardness compared to that occurring due to cutting with a sharp blade. A similar result was obtained for four times faster cutting. The width of the area where the increase in microhardness occurs was determined as 0.25 mm for sharp tools and slow cuts and 0.3 mm for worn tools and fast cuts. Research by Ossart et al. indicates a more than two-fold increase in the microhardness of the material (at the cut edge), combining the current microhardness with plastic strain [7]. Although the area of increased microhardness was determined to be about 200 μm from the edge, it was also noticed that even small changes in plastic strain drastically change the macroscopic characteristics of the material, such as the B-H curve. As is known, mechanical hardening generates new dislocations of the crystallographic structure, which, among other things, affect the change in the material’s macroscopic properties. The work finds the results of dislocation density and microhardness tests near the cut edge. The range of observed changes was defined as close to 400 μm, which correlates very well with the results of the study conducted by Xiong et al. [45].
- -
- observations of the domain structure. The work by Hofmann et al. contains observations made with the MOKE microscope, indicating that as a result of cutting, a part of the material is magnetically hardened [4]. Spark erosion did not essentially change the domain structure (only a few μm from the edge), and the guillotine cut affected a larger area than the laser cut (even 600 μm for the guillotine), changing the magnetic domain patterns at the same time. For guillotine cutting, patterns were found to form due to plastic deformations and dislocations. The largest deformation occurs in the range of about 150 μm, which correlates well with the size of the zone with increased microhardness. Laser cutting causes a more significant deformation of domain patterns (in an area of similar width) than guillotine cutting, and changes are observed up to 800 μm from the edge. Works by Steentjes et al. [46] and Schoppa et al. [47] analyze the results of macroscopic measurements of material properties. The authors state that spark erosion and water jet cutting are the least invasive cutting technologies, slightly changing the domain structure. As shown in the above works, the choice of cutting technique affects the size of the damaged area. Additionally, Harstick et al. [48] and Regnet et al. [49] indicate that tool wear significantly influences the changes in the crystallographic structure during guillotine cutting. Research conducted by Hubert et al. indicates the impact of plastic deformations on the movement of Bloch walls [50]. The authors emphasize that plastic deformations (due to the increase in the density of dislocations) affect the movement of the walls more intensively than the rotation of the magnetic moments. These locations act as potential barriers that hinder the Bloch wall motion. A similar conclusion was formulated many years earlier, where the author suggested that plastic strains give rise to forces opposing the movement of Bloch walls [51]. Observation with the MOKE microscope allowed Senda et al. to indicate areas containing different formations of magnetic domains than in the part of the material where the effect of cutting is negligible [52]. Reports on the possibility of the appearance of an oxidized layer with a width of several μm having completely different properties were described by Belhadj et al. [40]. They showed that for a 500 μm thick strip, three characteristic areas could be identified: the area up to about 150 μm from the edge, where strip patterns approximately parallel with the sheet plane were observed; an area extending from 150 to 500 μm, where stripe patterns extending in the perpendicular direction with the sheet plane were observed; and an area extending from 500 to 750 μm, where a slight change in the domain patterns in the limited portions was visible. The total width of the place where changes in domain patterns were observed was determined to be 1–1.4 mm from the cut edge. The analysis of the results of observations with the MOKE microscope, described in [53], leads to similar conclusions. Naumoski et al. links the results of observations of areas with changed domain patterns (created as a result of guillotine cutting) with the results of microhardness measurements, concluding that at a distance of about 200–220 μm from the edge, there is a hardened magnetic zone [54]. In addition, they show, based on magnetic contrast measurements, that the set magnetic zone (with varying degrees of hardening) reaches three to four times deeper into the material than the mechanically hardened zone, reaching as much as 1 mm. According to other researchers, the hardened magnetic zone may extend to a distance of 5 mm [55] or even 10 mm [5]. The research conducted by Naumoski’s team presents the results of observations with the MOKE microscope, pointing to an essential aspect regarding the magnetically hardened zone created due to the guillotine and laser cutting [56]. The authors pointed out that the width of this zone (magnetic activity of the material) depends not only on the cutting technology used but also on the intensity of the magnetic field affecting this region. It was noticed that for low external magnetic field strengths (of the order of 100 A/m), the magnetically hardened zone shows relatively weak activity for both cutting techniques in relation to the zones of undamaged material. For somewhat higher magnetic field strengths (of the order of 1600 A/m), in the case of laser cutting, the zone becomes more active (magnetic domains are formed more quickly). For comparison, the authors also showed the same zones after annealing, indicating a very large replication of the domain structure of these zones. An important area of research is exploring the impact of elastic applied tensile stress. A good example is the work carried out by the team of Perevertov et al. [57]. The tests were carried out for tensile stress from 0 to 60 MPa. They showed significant differences in domain patterns and the formation of a complex domain structure at the grain boundary. Cao et al. observed the domain structure at the guillotine-cut edge and at a long distance where the material was not damaged [27]. The undamaged material tested was shown to have 100 μm grains with complicated domain patterns, including 180°-domain and 90°-domain. Most domain patterns are closure domain structures, which can decrease the magnetostatic energy. The change in the domain structure can be observed within the area of 0.3 mm from the edge to the center of the strip. The difference in the domain structure indicates that the residual compressive stress caused by the punching process can change the crystallographic and domain structures near the edge of the sample. Saleem et al. observed grains with slab-like domains near the edge of a laser-cut strip [39]. The authors indicated that at a distance of about 450 μm from the edge, there was a small number of grains with such a structure (this region is treated as magnetically hardened), and from 450 μm to 3000 μm, there was a constant number of grains with such a structure (essentially independent of the distance). At a distance from 3000 μm to 6000 μm, the number of grains with such a structure increased (depending on the distance), while in the zone located over 6000 μm, the number of grains with such a structure stabilized.
- -
- observations of the crystallographic structure. The study conducted by Araujo et al. concerning the material cut with a guillotine and a laser contains the results of the observation of the crystallographic structure in the vicinity of the cut edge [31]. The guillotine cut causes plastic deformation near the cut line to be seen. In contrast, laser cutting does not induce any changes in the grain morphology near the cut line. Similar observations about punching and spark erosion can be found in [32,35,56,58,59]. Comparing the results of the above studies, it was found that punching “generates” plastic deformations much smaller than cutting with a guillotine. At the same time, spark erosion, as with a laser, does not cause plastic deformations. Gmyrek et al. studied material in the form of a 0.5 mm thick strip subjected to guillotine cutting, with grains of an average size of about 100 μm [60]. During the tests, they noticed the presence of grains of a smaller size at a distance of 200–300 μm from the cut edge. The size of this area harmonizes well with the size of the area where the presence of plastic stresses is observed. An in-depth analysis of changes in the crystallographic structure resulting from guillotine cutting can be found in [41]. The authors indicate the existence of four regions with varying degrees of structure changes (rollover, shear zone, ductile fracture zone, and burr), illustrating it with microscopic observations. Based on the measurements carried out for knife clearance in the range of 2 to 8% of the thickness of the cut strip, its influence on the size of the ductile fracture region and the size of the burr was demonstrated. It was also pointed out that these regions’ size depends on the material’s chemical composition. Currently, the research subject is studying crystallographic orientations using EBSD technology. In the works of Xiong et al. [26,44] and Bali et al. [61], the results of misorientation angle distributions in the edge zone of the Fe–Si steel after mechanical cutting were presented. The authors showed that crystals set at an angle of 0 and 45–50 degrees dominate at the cut edge, while those set at an angle of 40–55 degrees dominate at a distance greater than 500 μm. The results of the work by Füzer et al. show changes in the structure of the crystallographic lattice occurring due to guillotine cutting. These changes depend on the tool’s clearance and cause significant misorientation of the crystals in the damaged area [62]. The authors state that clearance (in the range of 1–7%) significantly affects the size of the area where crystal misorientation occurs. The figures show that the microstructural part in the vicinity of the cutting edge presented by the authors is characterized by a high level of misorientation angles in the range of 2–5 degrees and even more. It indicates that these grains are characterized by increased intensity of mechanical strain associated with high dislocation density. Quoting the authors, it should be stated that the results presented show that the depth of the penetration of residual stresses in the cutting surface area was significantly lower when the shear-cutting process was performed with a smaller cutting clearance. On the other hand, according to the authors, the local misorientation maps show that smaller cutting clearances may lead to higher residual stresses immediately next to the cutting surface. The results also show that a smaller cutting clearance reduces the size of the area affected by shearing.
3. Simulation Models of Changes in Electromagnetic Properties Caused by the Cutting Process of Non-Grain Oriented Electrical Steel Sheets
4. Consideration of the Cutting Effect in the FEM Simulation
5. An Example of Determining the Operating Characteristics of an Induction Motor, Taking into Account the Proposed Approximation of the Properties of the Motor Core Material
6. Summary
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- European Commission. Commission Regulation (EU) 2021/341 of 23 February 2021 Amending Regulations (EU) 2019/424, (EU) 2019/1781, (EU) 2019/2019, (EU) 2019/2020, (EU) 2019/2021, (EU) 2019/2022, (EU) 2019/2023 and (EU) 2019/2024 with Regard to Ecodesign Requirements for Servers and Data Storage Products, Electric Motors and Variable Speed Drives, Refrigerating Appliances, Light Sources and Separate Control Gears, Electronic Displays, Household Dishwashers, Household Washing Machines and Household Washer-Dryers and Refrigerating Appliances with a Direct Sales Function; European Union: Brussels, Belgium, 2021. [Google Scholar]
- Dems, M.; Komeza, K.; Majer, K. Core losses of the induction motor operating in a wide frequency range supplied from the inverter. Int. J. Appl. Electromagn. Mech. 2020, 64, 65–82. [Google Scholar] [CrossRef]
- De Almeida, A.T.; Ferreira, F.J.T.E.; Baoming, G. Beyond Induction Motors—Technology Trends to Move Up Efficiency. IEEE Trans. Ind. Appl. 2014, 50, 2103–2114. [Google Scholar] [CrossRef]
- Bozorth, R.M. Ferromagnetism; Wiley-IEEE Press: Hoboken, NJ, USA, 1978. [Google Scholar] [CrossRef]
- Nakata, T.; Nakano, M.; Kawahara, K. Effects of Stress Due to Cutting on Magnetic Characteristics of Silicon Steel. IEEE Transl. J. Magn. Jpn. 1992, 7, 453–457. [Google Scholar] [CrossRef]
- Moses, A.; Derebasi, N.; Loizos, G.; Schoppa, A. Aspects of the cut-edge effect stress on the power loss and flux density distribution in electrical steel sheets. J. Magn. Magn. Mater. 2000, 215–216, 690–692. [Google Scholar] [CrossRef]
- Ossart, F.; Hug, E.; Hubert, O.; Buvat, C.; Billardon, R. Effect of punching on electrical steels: Experimental and numerical coupled analysis. IEEE Trans. Magn. 2000, 36, 3137–3140. [Google Scholar] [CrossRef]
- Darmani, M.A.; Poskovic, E.; Franchini, F.; Ferraris, L.; Cavagnino, A. Manufacturing and Characterization of Novel Multilayer Magnets for Electrical Machine Applications. IEEE Trans. Energy Convers. 2022, 37, 2398–2407. [Google Scholar] [CrossRef]
- Poskovic, E.; Franchini, F.; Ferraris, L. Effect of the Insulating Layer on the Properties of SMC Inductors. Appl. Sci. 2022, 12, 8756. [Google Scholar] [CrossRef]
- Kocsis, B.; Fekete, I.; Varga, L.K. Metallographic and magnetic analysis of direct laser sintered soft magnetic composites. J. Magn. Magn. Mater. 2020, 501, 166425. [Google Scholar] [CrossRef]
- Poskovic, E.; Franchini, F.; Ferraris, L.; Carosio, F.; Grande, M.A. Rapid Characterization Method for SMC Materials for a Preliminary Selection. Appl. Sci. 2021, 11, 12133. [Google Scholar] [CrossRef]
- Gmyrek, Z.; Lefik, M.; Cavagnino, A.; Ferraris, L. Comparison of the fractional power motor with cores made of various magnetic materials. Open Phys. 2017, 5, 827–832. [Google Scholar] [CrossRef]
- Ferraris, L.; Franchini, F.; Poskovic, E.; Grande, M.A.; Bidulsky, R. Effect of the Temperature on the Magnetic and Energetic Properties of Soft Magnetic Composite Materials. Energies 2021, 14, 4400. [Google Scholar] [CrossRef]
- Grande, M.A.; Bidulsky, R.; Cavagnino, A.; Ferraris, L. Investigations on Different Processing Conditions on Soft Magnetic Composite Material Behavior at Low Frequency. IEEE Trans. Ind. Appl. 2012, 48, 1335–1343. [Google Scholar] [CrossRef]
- Poskovic, E.; Franchini, F.; Ferraris, L.; Grande, M.A. The effect of particle size on the core losses of soft magnetic composites. AIP Adv. 2019, 9, 035224. [Google Scholar] [CrossRef]
- Khorasani, M.; Gibson, I.; Ghasemi, A.H.; Hadavi, E.; Rolfe, B. Laser subtractive and laser powder bed fusion of metals: Review of process and production features. Rapid Prototyp. J. 2023, 29, 935–958. [Google Scholar] [CrossRef]
- Slotwinski, J.A.; Garboczi, E.J.; Stutzman, P.E.; Ferraris, C.F.; Watson, S.S.; Peltz, M.A. Characterization of Metal Powders Used for Additive Manufacturing. J. Res. Natl. Inst. Stand. Technol. 2014, 119, 460–493. [Google Scholar] [CrossRef]
- Zhao, X.; Wang, T. Laser Powder Bed Fusion of Powder Material: A Review. 3D Print. Addit. Manuf. 2022. ahead of print. [Google Scholar] [CrossRef]
- Guan, J.; Wang, Q. Laser Powder Bed Fusion of Dissimilar Metal Materials: A Review. Materials 2023, 16, 2757. [Google Scholar] [CrossRef]
- Dems, M.; Komeza, K.; Szulakowski, J. Practical Approximation of Sheet Losses Taking into Account the Guillotine and Laser Cutting Effect. Energies 2023, 16, 2831. [Google Scholar] [CrossRef]
- Hug, E.; Hubert, O.; Clavel, M. Influence of the plastic anisotropy on the magnetic properties of a nonoriented 3% silicon iron. J. Appl. Phys. 1996, 79, 4571–4573. [Google Scholar] [CrossRef]
- Hug, E.; Hubert, O.; Clavel, M. Some aspects of the magnetomechanical coupling in the strengthening of nonoriented and grain-oriented 3% SiFe alloys. IEEE Trans. Magn. 1997, 33, 763–771. [Google Scholar] [CrossRef]
- Daem, A.; Sergeant, P.; Dupré, L.; Chaudhuri, S.; Bliznuk, V.; Kestens, L. Magnetic properties of silicon steel after plastic deformation. Materials 2020, 13, 4361. [Google Scholar] [CrossRef] [PubMed]
- Allia, P.; Celasco, M.; Ferro Milone, A.; Masoero, A.; Stepanescu, A. Theory of the remanence in grain-oriented Si–Fe sheets in presence of external stresses. IEEE Trans. Magn. 1981, 17, 2863–2865. [Google Scholar] [CrossRef]
- Maeda, A.; Jin, Y.; Kuboki, T. Light press of sheet metal edge for reducing residual stress generated by laser cutting considering mechanical properties and intensity of residual stress. J. Mater. Process. Technol. 2015, 225, 178–184. [Google Scholar] [CrossRef]
- Xiong, X.; Hu, S.; Dang, N.; Hu, K. Effect of stress-relief annealing on microstructure, texture and hysteresis curve of mechanically cut non-oriented Fe-Si steel. Mater. Charact. 2017, 132, 239–247. [Google Scholar] [CrossRef]
- Cao, H.; Hao, L.; Yi, J.; Zhang, X.; Luo, Z.; Chen, S.; Li, R. The influence of punching process on residual stress and magnetic domain structure of non-oriented silicon steel. J. Magn. Magn. Mater. 2016, 406, 42–47. [Google Scholar] [CrossRef]
- Omura, T.; Zaizen, Y.; Fukumura, M.; Senda, K.; Toda, H. Effect of hardness and thickness of nonoriented electrical steel sheets on iron loss deterioration by shearing process. IEEE Trans. Magn. 2015, 51, 2005604. [Google Scholar] [CrossRef]
- Fujisaki, K.; Hirayama, R.; Kawachi, T.; Satou, S.; Kaidou, C.; Yabumoto, M.; Kubota, T. Motor core iron loss analysis evaluating shrink fitting and stamping by Finite-Element Method. IEEE Trans. Magn. 2007, 43, 1950–1954. [Google Scholar] [CrossRef]
- Hofmann, M.; Naumoski, H.; Herr, U.; Herzog, H.-G. Magnetic Properties of electrical steel sheets in respect of cutting: Micromagnetic analysis and macromagnetic modeling. IEEE Trans. Magn. 2016, 52, 2000114. [Google Scholar] [CrossRef]
- Araujo, E.G.; Schneider, J.; Verbeken, K.; Pasquarella, G.; Houbaert, Y. Dimensional effects on magnetic properties of Fe–Si steels due to laser and mechanical cutting. IEEE Trans. Magn. 2010, 46, 213–216. [Google Scholar] [CrossRef]
- Wenmin, S.; Jing, L.; Changyi, L. Effect of cutting techniques on the structure and magnetic properties of a high-grade non-oriented electrical steel. J. Wuhan Univ. Technol.-Mater. Sci. Ed. 2014, 29, 1246–1251. [Google Scholar] [CrossRef]
- Pulnikov, A.; Baudouin, P.; Melkebeek, J. Induced stresses due to the mechanical cutting of non-oriented electrical steels. J. Magn. Magn. Mater. 2003, 254–255, 355–357. [Google Scholar] [CrossRef]
- Pulnikov, A. Modification of Magnetic Properties of Non Oriented Electrical Steels by the Production of Electromagnetic Devices. Ph.D. Dissertation, Ghent University, Ghent, Belgium, 2004. [Google Scholar]
- Kurosaki, Y.; Mogi, H.; Fujii, H.; Kubota, T.; Shiozaki, M. Importance of punching and workability in non-oriented electrical steel sheets. J. Magn. Magn. Mater. 2008, 320, 2474–2480. [Google Scholar] [CrossRef]
- Gmyrek, Z.; Kucharska, B. Investigation of local properties of the Fe-Si alloy subjected to mechanical and laser cutting. Arch. Electr. Eng. 2023, in press. [Google Scholar]
- Schoppa, A.P. Einfluss der Be- und Verarbeitung auf Die Magnetischen Eigenschaften von Schlussgeglühtem, Nichtkornorientiertem Elektroband. Ph.D. Dissertation, Rheinisch-Westfalischen Technischen Hochschule, Aachen, Germany, 2001. (In German). [Google Scholar]
- Schmidt, K.H. Influence of punching on the magnetic properties of electric steel with 1% silicon. J. Magn. Magn. Mater. 1976, 2, 136–150. [Google Scholar] [CrossRef]
- Saleem, A.; Alatawneh, N.; Rahman, T.; Lowther, D.A.; Chromik, R.R. Effects of laser cutting on microstructure and magnetic properties of non-orientation electrical steel laminations. IEEE Trans. Magn. 2020, 56, 6100609. [Google Scholar] [CrossRef]
- Belhadj, A.; Baudouin, P.; Breaban, F.; Deffontaine, A.; De Wulf, M.; Houbaert, Y. Effect of laser cutting on microstructure and on magnetic properties of grain non-oriented electrical steels. J. Magn. Magn. Mater. 2003, 256, 20–31. [Google Scholar] [CrossRef]
- Baudouin, P.; De Wulf, M.; Kestens, L.; Houbaert, Y. The effect of the guillotine clearance on the magnetic properties of electrical steels. J. Magn. Magn. Mater. 2003, 256, 32–40. [Google Scholar] [CrossRef]
- Wang, Z.; Li, S.; Cui, R.; Wang, X.; Wang, B. Influence of grain size and blanking clearance on magnetic properties deterioration of non-oriented electrical steel. IEEE Trans. Magn. 2018, 54, 2000607. [Google Scholar] [CrossRef]
- Wu, F.; Zhou, L.; Soulard, J.; Silvester, B.; Davis, C. Quantitative characterisation and modelling of the effect of cut edge damage on the magnetic properties in NGO electrical steel. J. Magn. Magn. Mater. 2022, 551, 169185. [Google Scholar] [CrossRef]
- Weiss, H.A.; Leuning, N.; Steentjes, S.; Hameyer, K.; Andorfer, T.; Jenner, S.; Volk, W. Influence of shear cutting parameters on the electromagnetic properties of non-oriented electrical steel sheets. J. Magn. Magn. Mater. 2017, 421, 250–259. [Google Scholar] [CrossRef]
- Xiong, X.; Hu, S.; Hu, K.; Zeng, S. Texture and magnetic property evolution of non-oriented Fe–Si steel due to mechanical cutting. J. Magn. Magn. Mater. 2016, 401, 982–990. [Google Scholar] [CrossRef]
- Steentjes, S.; Kameyer, K.; Vogt, S.; Bednarz, M.; Volk, W.; Dierdorf, J.; Hirt, G. Influence of material processing steps annealing and cutting on magnetic materials’ properties relevant for electrical machine design. In Proceedings of the Conference Forming Technology Forum, Herrsching, Germany, 19–20 September 2013; pp. 1–6. [Google Scholar]
- Schoppa, A.; Louis, H.; Pude, F.; Von Rad, C. Influence of abrasive waterjet cutting on the magnetic properties of non-oriented electrical steels. J. Magn. Magn. Mater. 2003, 254–255, 370–372. [Google Scholar] [CrossRef]
- Harstick, H.M.S.; Ritter, M.; Riehemann, W. Influence of punching and tool wear on the magnetic properties of nonoriented electrical steel. IEEE Trans. Magn. 2014, 50, 6200304. [Google Scholar] [CrossRef]
- Regnet, M.; Kremser, A.; Reinlein, M.; Szary, P.; Abele, U. Influence of cutting tool wear on core losses and magnetizing demand of electrical steel sheets. In Proceedings of the 9th International Electric Drives Production Conference (EDPC), Esslingen, Germany, 3–4 December 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Hubert, O.; Hug, E. Influence of plastic strain on magnetic behaviour of non-oriented Fe–3Si and application to manufacturing test by punching. Mater. Sci. Technol. 1995, 11, 482–487. [Google Scholar] [CrossRef]
- De Barr, A.E. Soft Magnetic Materials Used in Industry; Chapman & Hall: London, UK, 1959. [Google Scholar]
- Senda, K.; Ishida, M.; Nakasu, Y.; Yagi, M. Influence of shearing process on domain structure and magnetic properties of non-oriented electrical steel. J. Magn. Magn. Mater. 2006, 304, e513–e515. [Google Scholar] [CrossRef]
- Takezawa, M.; Kitajima, K.; Morimoto, Y.; Yamasaki, J.; Kaido, C. Effect of strain by mechanical punching on nonoriented Si–Fe electrical sheets for a nine-slot motor core. IEEE Trans. Magn. 2006, 42, 2790–2792. [Google Scholar] [CrossRef]
- Naumoski, H.; Maucher, A.; Vandenbossche, L.; Jacobs, S.; Herr, U.; Chassang, X. Magneto-optical and field-metric evaluation of the punching effect on magnetic properties of electrical steels with varying alloying content and grain size. In Proceedings of the IEEE 4th International Electric Drives Production Conference (EDPC), Nuremberg, Germany, 30 September–1 October 2014; pp. 1–9. [Google Scholar] [CrossRef]
- Siebert, R.; Wetzig, A.; Beyer, E.; Betz, B.; Gruenzweig, C.; Lehmann, E. Localized investigation of magnetic bulk property deterioration of electrical steel. In Proceedings of the 3rd Electric Drives Production Conference (EDPC), Nuremberg, Germany, 29–30 October 2013; pp. 60–64. [Google Scholar] [CrossRef]
- Naumoski, H.; Riedmüller, B.; Minkow, A.; Herr, U. Investigation of the influence of different cutting procedures on the global and local magnetic properties of non-oriented electrical steel. J. Magn. Magn. Mater. 2015, 392, 126–133. [Google Scholar] [CrossRef]
- Perevertov, O.; Thielsch, J.; Schafer, R. Effect of applied tensile stress on the hysteresis curve and magnetic domain structure of grain-oriented transverse Fe-3%Si steel. IEEE Trans. Magn. 2015, 385, 358–367. [Google Scholar] [CrossRef]
- Emura, M.; Landgraf, F.; Ross, W.; Barreta, J. The influence of cutting technique on the magnetic properties of electrical steels. J. Magn. Magn. Mater. 2003, 254, 358–360. [Google Scholar] [CrossRef]
- Bulín, T.; Švábenská, E.; Hapla, M.; Ondrkšek, E.; Schneeweiss, O. Influence of laser cutting and punching on magnetic properties of electrical steel M470-50A. In Proceedings of the 25th Anniversary International Conference on Metallurgy and Materials, Brno, Czech Republic, 25–27 May 2016; pp. 670–675. [Google Scholar]
- Gmyrek, Z.; Cavagnino, A.; Ferraris, L. Estimation of the Magnetic properties of the damaged area resulting from the punching process: Experimental research and FEM modeling. IEEE Trans. Ind. Appl. 2013, 49, 2069–2077. [Google Scholar] [CrossRef]
- Bali, M.; Muetze, A. Modeling the effect of cutting on the magnetic properties of electrical steel sheets. IEEE Trans. Ind. Electron. 2016, 64, 2547–2556. [Google Scholar] [CrossRef]
- Füzer, J.; Dobák, S.; Petryshynets, I.; Kollar, P.; Kovac, F.; Slota, J. Correlation between cutting clearance, deformation texture, and magnetic loss prediction in non-oriented electrical steels. Materials 2021, 14, 6893. [Google Scholar] [CrossRef]
- Bali, M.; Muetze, A. The Degradation Depth of Non-grain Oriented Electrical Steel Sheets of Electric Machines Due to Mechanical and Laser Cutting: A State-of-the-Art Review. IEEE Trans. Ind. Appl. 2019, 55, 366–375. [Google Scholar] [CrossRef]
- Bali, M.; Muetze, A. The degradation depth of electrical steel sheets due to mechanical and laser cutting. In Proceedings of the of 2017 IEEE 11th International Symposium on Diagnostics for Electrical Machines, Power Electronics and Drives (SDEMPED), Tinos, Greece, 29 August–1 September 2017; pp. 544–549. [Google Scholar] [CrossRef]
- Manescu Paltanea, V.; Paltanea, G.; Gavrila, H.; Nemoianu, I.V. Estimation of the Damaged Zone Width due to Mechanical Cutting on High Quality Non-Oriented Steels. In Proceedings of the 2018 International Symposium on Fundamentals of Electrical Engineering (ISFEE), Bucharest, Romania, 1–3 November 2018; pp. 1–4. [Google Scholar] [CrossRef]
- Lewis, N.; Anderson, P.; Hall, J.; Gao, Y. Power Loss Models in Punched Non-Oriented Electrical Steel Rings. IEEE Trans. Magn. 2016, 52, 7300704. [Google Scholar] [CrossRef]
- Bali, M.; Gersem, H.D.; Muetze, A. Determination of Original Nondegraded and Fully Degraded Magnetic Properties of Material Subjected to Mechanical Cutting. IEEE Trans. Ind. Appl. 2016, 52, 2297–2305. [Google Scholar] [CrossRef]
- Bali, M.; Gersem, H.D.; Muetze, A. Determination of Original Nondegraded and Fully Degraded Magnetic Characteristics of Material Subjected to Laser Cutting. IEEE Trans. Ind. Appl. 2017, 53, 4242–4251. [Google Scholar] [CrossRef]
- Miyagi, D.; Aoki, Y.; Nakano, M.; Takahashi, N. Effect of Compressive Stress in Thickness Direction on Iron Losses of Nonoriented Electrical Steel Sheet. IEEE Trans. Magn. 2010, 46, 2040–2043. [Google Scholar] [CrossRef]
- Manescu Paltanea, V.; Paltanea, G.; Nemoianu, I.V. Degradation of Static and Dynamic Magnetic Properties of Non-Oriented Steel Sheets by Cutting. IEEE Trans. Magn. 2018, 54, 2001705. [Google Scholar] [CrossRef]
- Manescu (Paltanea), V.; Paltanea, G.; Ferrara, E.; Nemoianu, I.V.; Fiorillo, F.; Gavrila, H. Influence of mechanical and water-jet cutting on the dynamic magnetic properties of NO Fe-Si steels. J. Magn. Magn. Mater. 2020, 499, 166257. [Google Scholar] [CrossRef]
- Selema, A.; Ibrahim, M.N.; Sergeant, P. Non-destructive electromagnetic evaluation of material degradation due to steel cutting in a fully stacked electrical machine. Energies 2022, 15, 7862. [Google Scholar] [CrossRef]
- Winter, K.; Liao, Z.; Ramanathan, R.; Axinte, D.; Vakil, G.; Gerada, C. How non-conventional machining affects the surface integrity and magnetic properties of non-oriented electrical steel. Mater. Des. 2021, 210, 110051. [Google Scholar] [CrossRef]
- Kedous-Lebouc, A.; Cornut, B.; Perrier, J.C.; Manfé, P.; Chevalier, T. Punching influence on magnetic properties of the stator teeth of an induction motor. J. Magn. Magn. Mater. 2003, 254–255, 124–126. [Google Scholar] [CrossRef]
- Ahmet, P.; Sezer, E.; Naim, D. Mathematical model for cutting effect on magnetic flux distribution near the cut edge of non-oriented electrical steels. Comput. Mater. Sci. 2008, 43, 1066–1068. [Google Scholar] [CrossRef]
- Vandenbossche, L.; Jacobs, S.; Henrotte, F.; Hameyer, K. Impact of cut edges on magnetization curves and iron losses in e-machines for automotive traction. World Electr. Veh. J. 2010, 4, 587–596. [Google Scholar] [CrossRef]
- Steentjes, S.; Pfingsten, G.; Hameyer, K. An Application-Oriented Approach for Consideration of Material Degradation Effects Due to Cutting on Iron Losses and Magnetizability. IEEE Trans. Magn. 2014, 50, 7027804. [Google Scholar] [CrossRef]
- Vandenbossche, L.; Jacobs, S.; Jannot, X.; McClelland, M.; Saint-Michel, J.; Attrazic, E. Iron loss modelling which includes the impact of punching, applied to high-efficiency induction machines. In Proceedings of the 2013 3rd International Electric Drives Production Conference (EDPC), Nuremberg, Germany, 29–30 October 2013; pp. 1–10. [Google Scholar] [CrossRef]
- Kedous-Lebouc, A.; Messal, O.; Youmssi, A. Joint punching and frequency effects on practical magnetic characteristics of electrical steels for high-speed machines. J. Magn. Magn. Mater. 2017, 426, 658–665. [Google Scholar] [CrossRef]
- Goldbeck, G.; Cossale, M.; Kitzberger, M.; Bramerdorfer, G.; Andessner, D.; Amrhein, W. Numerical Implementation of Local Degradation Profiles in Soft Magnetic Materials. In Proceedings of the 2018 XIII International Conference on Electrical Machines (ICEM), Alexandroupoli, Greece, 3–6 September 2018; pp. 1037–1043. [Google Scholar] [CrossRef]
- Cossale, M.; Kitzberger, M.; Goldbeck, G.; Bramerdorfer, G.; Andessner, D.; Amrhein, W. Local Degradation in Soft Magnetic Materials: A Simplified Modeling Approach. IEEE Trans. Ind. Appl. 2019, 55, 5897–5905. [Google Scholar] [CrossRef]
- Goldbeck, G.; Cossale, M.; Kitzberger, M.; Bramerdorfer, G.; Andessner, D.; Amrhein, W. Incorporating the Soft Magnetic Material Degradation to Numerical Simulations. IEEE Trans. Ind. Appl. 2020, 56, 3584–3593. [Google Scholar] [CrossRef]
- Sundaria, R.; Nair, D.G.; Lehikoinen, A.; Arkkio, A.; Belahcen, A. Loss Model for the Effects of Steel Cutting in Electrical Machines. In Proceedings of the 2018 XIII International Conference on Electrical Machines (ICEM), Alexandroupoli, Greece, 3–6 September 2018; pp. 1260–1266. [Google Scholar] [CrossRef]
- Sundaria, R.; Nair, D.G.; Lehikoinen, A.; Arkkio, A.; Belahcen, A. Effect of Laser Cutting on Core Losses in Electrical Machines—Measurements and Modeling. IEEE Trans. Ind. Electron. 2020, 67, 7354–7363. [Google Scholar] [CrossRef]
- Sundaria, R.; Lehikoinen, A.; Arkkio, A.; Belahcen, A. Effects of Manufacturing Processes on Core Losses of Electrical Machines. IEEE Trans. Energy Convers. 2021, 36, 197–206. [Google Scholar] [CrossRef]
- Seo, U.-J.; Kim, D.-J.; Chun, Y.-D.; Han, P.-W. Mechanical Cutting Effect of Electrical Steel on the Performance of Induction Motors. Energies 2020, 13, 6314. [Google Scholar] [CrossRef]
- Mohammadi, A.A.; Zhang, S.; Pop, A.-C.; Gyselinck, J.J.C. Effect of Electrical Steel Punching on the Performance of Fractional-kW Electrical Machines. IEEE Trans. Energy Convers. 2022, 37, 1854–1863. [Google Scholar] [CrossRef]
- Gürbüz, I.T.; Martin, F.; Billah, M.M.; Belahcen, A.; Rasilo, P. Effective Implementation of the Effect of Electrical Steel Sheet Cutting into Finite-Element Simulation. In Proceedings of the 2022 IEEE 20th Biennial Conference on Electromagnetic Field Computation (CEFC), Denver, CO, USA, 24–26 October 2022; pp. 1–2. [Google Scholar] [CrossRef]
- Leuning, N.; Schauerte, B.; Schweren, S.; Hameyer, K. Loss Parameter Identification After Cutting for Different Non-Oriented Electrical Steel Grades. IEEE Trans. Magn. 2022, 58, 2001005. [Google Scholar] [CrossRef]
- Martin, F.; Aydin, U.; Sundaria, R.; Rasilo, P.; Belahcen, A.; Arkkio, A. Effect of Punching the Electrical Sheets on Optimal Design of a Permanent Magnet Synchronous Motor. IEEE Trans. Magn. 2018, 54, 8102004. [Google Scholar] [CrossRef]
- M’zali, N.; Martin, F.; Sundaria, R.; Henneron, T.; Benabou, A.; Belahcen, A. Finite-Element Modeling of Magnetic Properties Degradation Due to Plastic Deformation. IEEE Trans. Magn. 2020, 56, 7506704. [Google Scholar] [CrossRef]
- M’zali, N.; Henneron, T.; Benabou, A.; Martin, F.; Belahcen, A. Finite Element Analysis of the Magneto-Mechanical Coupling Due to Punching Process in Electrical Steel Sheet. IEEE Trans. Magn. 2021, 57, 7401304. [Google Scholar] [CrossRef]
- Sano, H.; Narita, K.; Zeze, E.; Yamada, T.; Kazuki, U.; Akatsu, K. A practical approach for electromagnetic analysis with the effect of the residual strain due to manufacturing processes. In Proceedings of the 2016 IEEE Energy Conversion Congress and Exposition (ECCE), Milwaukee, WI, USA, 18–22 September 2016; pp. 1–7. [Google Scholar] [CrossRef]
- Elfgen, S.; Steentjes, S.; Böhmer, S.; Franck, D.; Hameyer, K. Influences of Material Degradation Due to Laser Cutting on the Operating Behavior of PMSM Using a Continuous Local Material Model. IEEE Trans. Ind. Appl. 2017, 53, 1978–1984. [Google Scholar] [CrossRef]
- Al-Timimy, A.; Vakil, G.; Degano, M.; Giangrande, P.; Gerada, C.; Galea, M. Considerations on the Effects That Core Material Machining Has on an Electrical Machine’s Performance. IEEE Trans. Energy Convers. 2018, 33, 1154–1163. [Google Scholar] [CrossRef]
- Weiss, H.A.; Tröber, P.; Golle, R.; Steentjes, S.; Leuning, N.; Elfgen, S.; Hameyer, K.; Volk, W. Impact of Punching Parameter Variations on Magnetic Properties of Nongrain-Oriented Electrical Steel. IEEE Trans. Ind. Appl. 2018, 54, 5869–5878. [Google Scholar] [CrossRef]
- Leuning, N.; Elfgen, S.; Groschup, B.; Bavendiek, G.; Steentjes, S.; Hameyer, K. Advanced Soft- and Hard-Magnetic Material Models for the Numerical Simulation of Electrical Machines. IEEE Trans. Magn. 2018, 54, 8107008. [Google Scholar] [CrossRef]
- Boubaker, N.; Matt, D.; Enrici, P.; Nierlich, F.; Durand, G. Measurements of Iron Loss in PMSM Stator Cores Based on CoFe and SiFe Lamination Sheets and Stemmed from Different Manufacturing Processes. IEEE Trans. Magn. 2019, 55, 8100309. [Google Scholar] [CrossRef]
- Goldbeck, G.; Bramerdorfer, G.; Amrhein, W. Impact of Local Degradation in Soft Magnetic Materials on Performance of Permanent Magnet Synchronous Machines. In Proceedings of the 2019 IEEE Energy Conversion Congress and Exposition (ECCE), Baltimore, MD, USA, 29 September–3 October 2019; pp. 3081–3087. [Google Scholar] [CrossRef]
- Bramerdorfer, G. Effect of the Manufacturing Impact on the Optimal Electric Machine Design and Performance. IEEE Trans. Energy Convers. 2020, 35, 1935–1943. [Google Scholar] [CrossRef]
- Xiao, X.; Müller, F.; Bavendiek, G.; Leuning, N.; Zhang, P.; Zou, J.; Hameyer, K. Modeling of Scalar Dependencies of Soft Magnetic Material Magnetization for Electrical Machine Finite-Element Simulation. IEEE Trans. Magn. 2020, 56, 7505704. [Google Scholar] [CrossRef]
- Leitner, S.; Gruebler, H.; Muetze, A. Effect of Manufacturing Influences on Magnetic Performance Parameters of Sub-Fractional Horsepower Motors. IEEE Trans. Magn. 2021, 57, 8205209. [Google Scholar] [CrossRef]
- Abedini Mohammadi, A.; Zhang, S.; Gyselinck, J.; Pop, A.-C.; Zhang, W. Manufacturing-Induced Cogging Torque in Segmented Stator Permanent-Magnet Machines with Respect to Steel Punching. IEEE Trans. Magn. 2022, 58, 8107808. [Google Scholar] [CrossRef]
- Soltanipour, S.; Thiringer, T.; Lindström, J. Battery Electric Vehicle Performance Evaluation by Considering Punching Effect on PMSM Iron Cores. In Proceedings of the 2022 International Conference on Electrical Machines (ICEM), Valencia, Spain, 5–8 September 2022; pp. 2162–2168. [Google Scholar] [CrossRef]
- Alatawneh, N.; Saleem, A.; Rahman, T.; Lowther, D.A.; Chromik, R. Modelling and analysis of the effects of cutting of core laminations in electric machines. IET Electr. Power Appl. 2020, 14, 2355–2361. [Google Scholar] [CrossRef]
- Mach, M.; Hajek, V. Model of a small induction machine with effects of manufacturing. In Proceedings of the 2015 International Conference on Electrical Drives and Power Electronics (EDPE), Tatranska Lomnica, Slovakia, 21–23 September 2015; pp. 319–323. [Google Scholar] [CrossRef]
- Mach, M.; Hajek, V. Impact of punching on a small induction motor. In Proceedings of the 2015 IEEE 15th International Conference on Environment and Electrical Engineering (EEEIC), Rome, Italy, 10–13 June 2015; pp. 895–900. [Google Scholar] [CrossRef]
- Bourchas, K.; Stening, A.; Soulard, J.; Broddefalk, A.; Lindenmo, M.; Dahlén, M.; Gyllensten, F. Quantifying Effects of Cutting and Welding on Magnetic Properties of Electrical Steels. IEEE Trans. Ind. Appl. 2017, 53, 4269–4278. [Google Scholar] [CrossRef]
- Martin, M.; Radoslav, C.; Marek, T.; Vitezslav, H. Impact of manufacturing proces on optimal shape of induction machine slots. In Proceedings of the 2017 IEEE International Conference on Environment and Electrical Engineering and 2017 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Milan, Italy, 6–9 June 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Colombo, L.; Tokat, A.; Bitsi, K.; Márquez-Fernández, F.J.; Alaküla, M. Performance Degradation due to Cut Edge Effect for an Axial-Flux Induction Machine. In Proceedings of the 2022 International Conference on Electrical Machines (ICEM), Valencia, Spain, 5–8 September 2022; pp. 1253–1259. [Google Scholar] [CrossRef]
- Bayraktar, Ş.; Turgut, Y. Experimental and statistical analysis of the effects of punching and laser cutting methods on induction motor efficiency and total magnetic losses in silicon lamination sheets. J. Magn. Magn. Mater. 2023, 572, 170599. [Google Scholar] [CrossRef]
- Credo, A.; Petrov, I.; Pyrhönen, J.; Villani, M. Impact of Manufacturing Stresses on Multiple-Rib Synchronous Reluctance Motor Performance. IEEE Trans. Ind. Appl. 2023, 59, 1253–1262. [Google Scholar] [CrossRef]
- Daniel, L. Advanced constitutive laws for computational magnetics: The case of magneto-mechanical behaviour. In Proceedings of the 2018 IEEE International Magnetics Conference (INTERMAG), Singapore, 23–27 April 2018; pp. 1–2. [Google Scholar] [CrossRef]
- Aydin, U.; Rasilo, P.; Martin, F.; Singh, D.; Daniel, L.; Belahcen, A.; Rekik, M.; Hubert, O.; Kouhia, R.; Arkkio, A. Magneto-mechanical modeling of electrical steel sheets. J. Magn. Magn. Mater. 2017, 439, 82–90. [Google Scholar] [CrossRef]
- Fujisaki, K.; Satoh, S. Numerical calculations of electromagnetic fields in silicon steel under mechanical stress. IEEE Trans. Magn. 2004, 40, 1820–1825. [Google Scholar] [CrossRef]
- Bramerdorfer, G.; Kitzberger, M.; Wöckinger, D.; Koprivica, B.; Zurek, S. State-of-the-art and future trends in soft magnetic materials characterization with focus on electric machine design—Part 2. TM—Tech. Mess. 2019, 86, 553–565. [Google Scholar] [CrossRef]
- Rasilo, P.; Aydin, U.; Holopainen, T.P.; Arkkio, A. Analysis of iron losses on the cutting edges of induction motor core laminations. In Proceedings of the 2016 XXII International Conference on Electrical Machines (ICEM), Lausanne, Switzerland, 4–7 September 2016; pp. 1312–1317. [Google Scholar] [CrossRef]
- Bali, M.; De Gersem, H.; Muetze, A. Finite-Element Modeling of Magnetic Material Degradation Due to Punching. IEEE Trans. Magn. 2014, 50, 745–748. [Google Scholar] [CrossRef]
- Crevecoeur, G.; Sergeant, P.; Dupre, L.; Vandenbossche, L.; Van de Walle, R. Analysis of the Local Material Degradation Near Cutting Edges of Electrical Steel Sheets. IEEE Trans. Magn. 2008, 44, 3173–3176. [Google Scholar] [CrossRef]
- Elfgen, S.; Steentjes, S.; Böhmer, S.; Franck, D.; Hameyer, K. Continuous Local Material Model for Cut Edge Effects in Soft Magnetic Materials. IEEE Trans. Magn. 2016, 52, 2001304. [Google Scholar] [CrossRef]
- Sundaria, R.; Lehikoinen, A.; Hannukainen, A.; Arkkio, A. Higher-order finite element modeling of material degradation due to cutting. In Proceedings of the 2017 IEEE International Electric Machines and Drives Conference (IEMDC), Miami, FL, USA, 21–24 May 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Sundaria, R.; Lehikoinen, A.; Hannukainen, A.; Arkkio, A.; Belahcen, A. Mixed-Order Finite-Element Modeling of Magnetic Material Degradation Due to Cutting. IEEE Trans. Magn. 2018, 54, 7402008. [Google Scholar] [CrossRef]
- Dems, M.; Gmyrek, Z.; Komeza, K. Analytical Model of an Induction Motor Taking into Account the Punching Process Influence on the Material Properties’ Change of Lamination. Energies 2021, 14, 2459. [Google Scholar] [CrossRef]
- Gmyrek, Z.; Cavagnino, A. Analytical method for determining the damaged area width in magnetic materials due to punching process. In Proceedings of the IECON 2011—37th Annual Conference of the IEEE Industrial Electronics Society, Melbourne, Australia, 7–10 November 2011; pp. 1764–1769. [Google Scholar] [CrossRef]
- Dems, M.; Komeza, K.; Gmyrek, Z.; Szulakowski, J. The Effect of Sample’s Dimension and Cutting Technology on Magnetization and Specific Iron Losses of FeSi Laminations. Energies 2022, 15, 2086. [Google Scholar] [CrossRef]
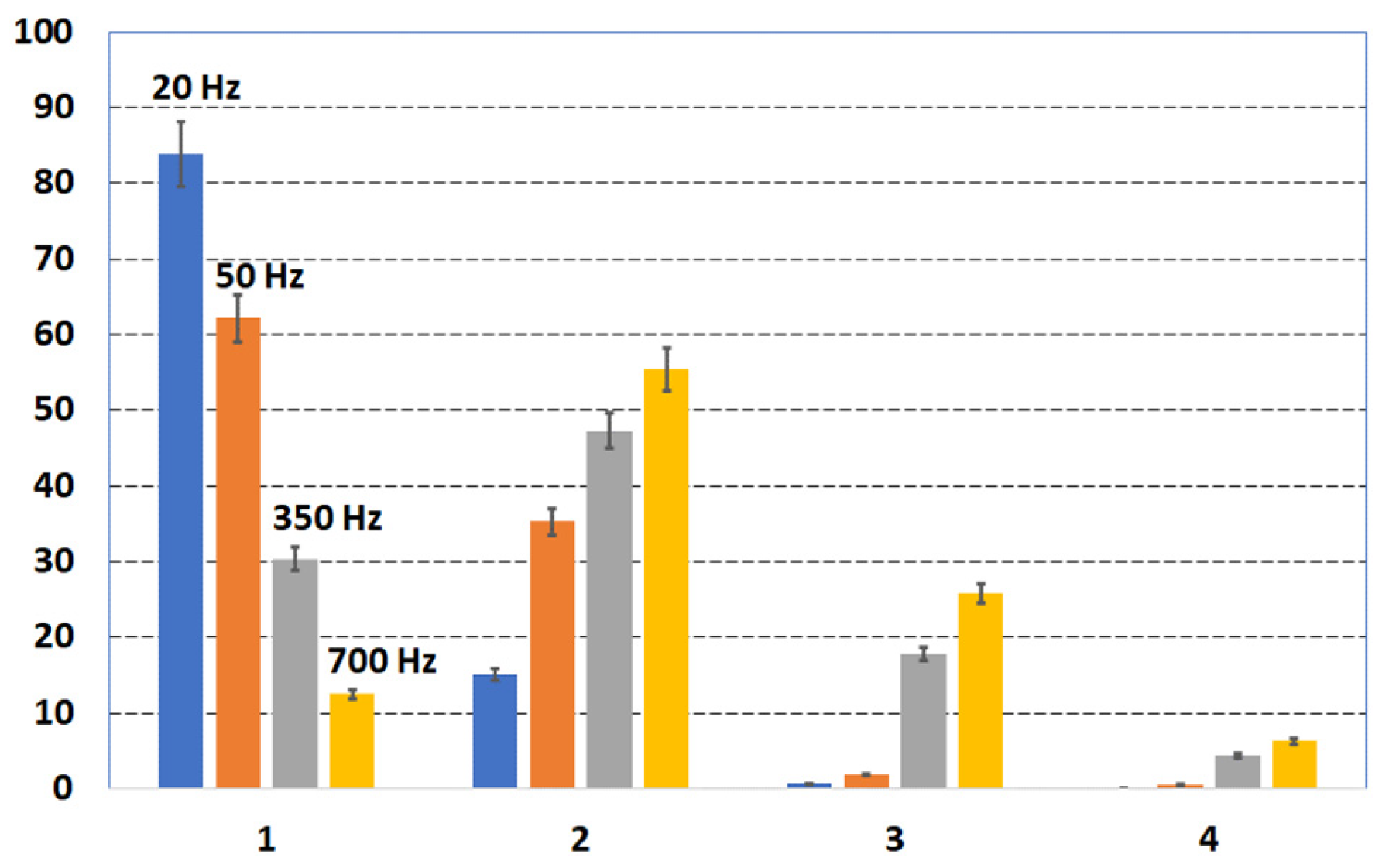
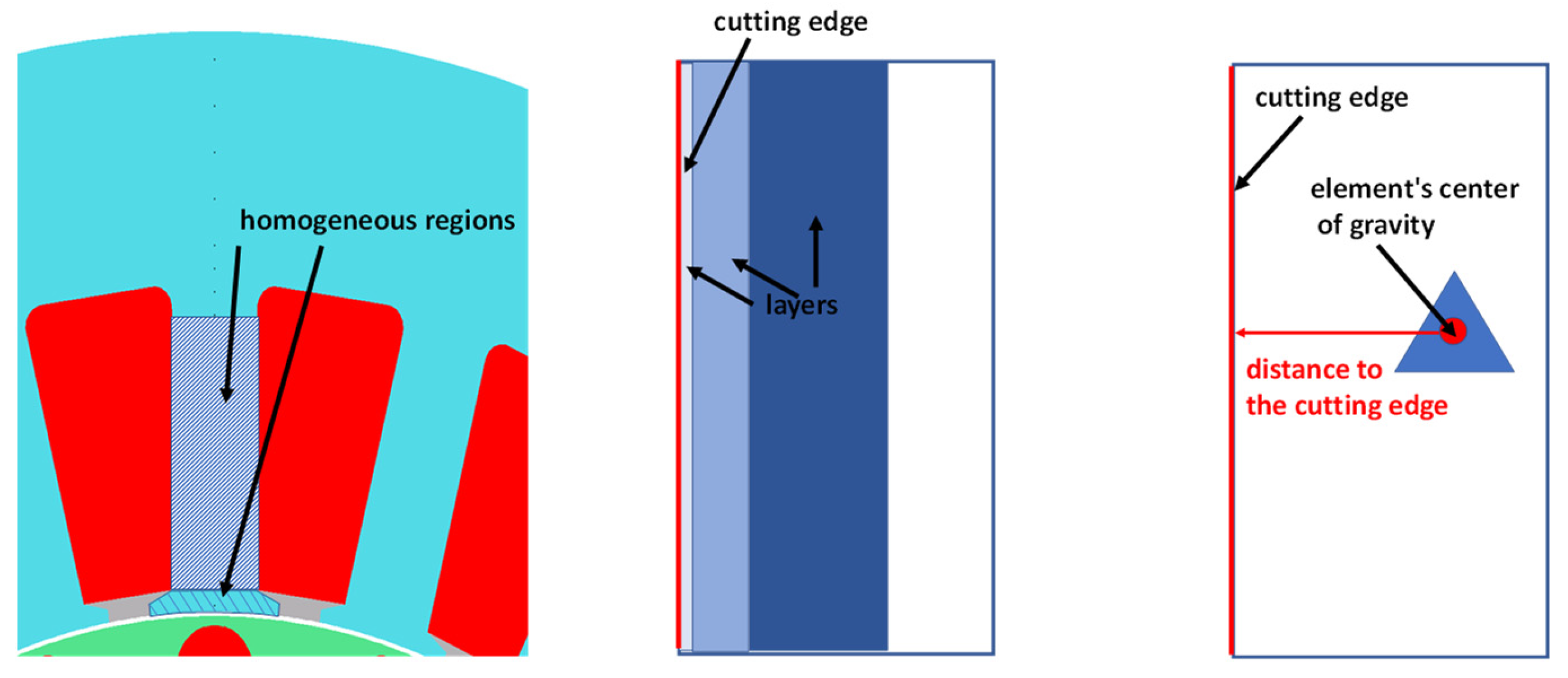
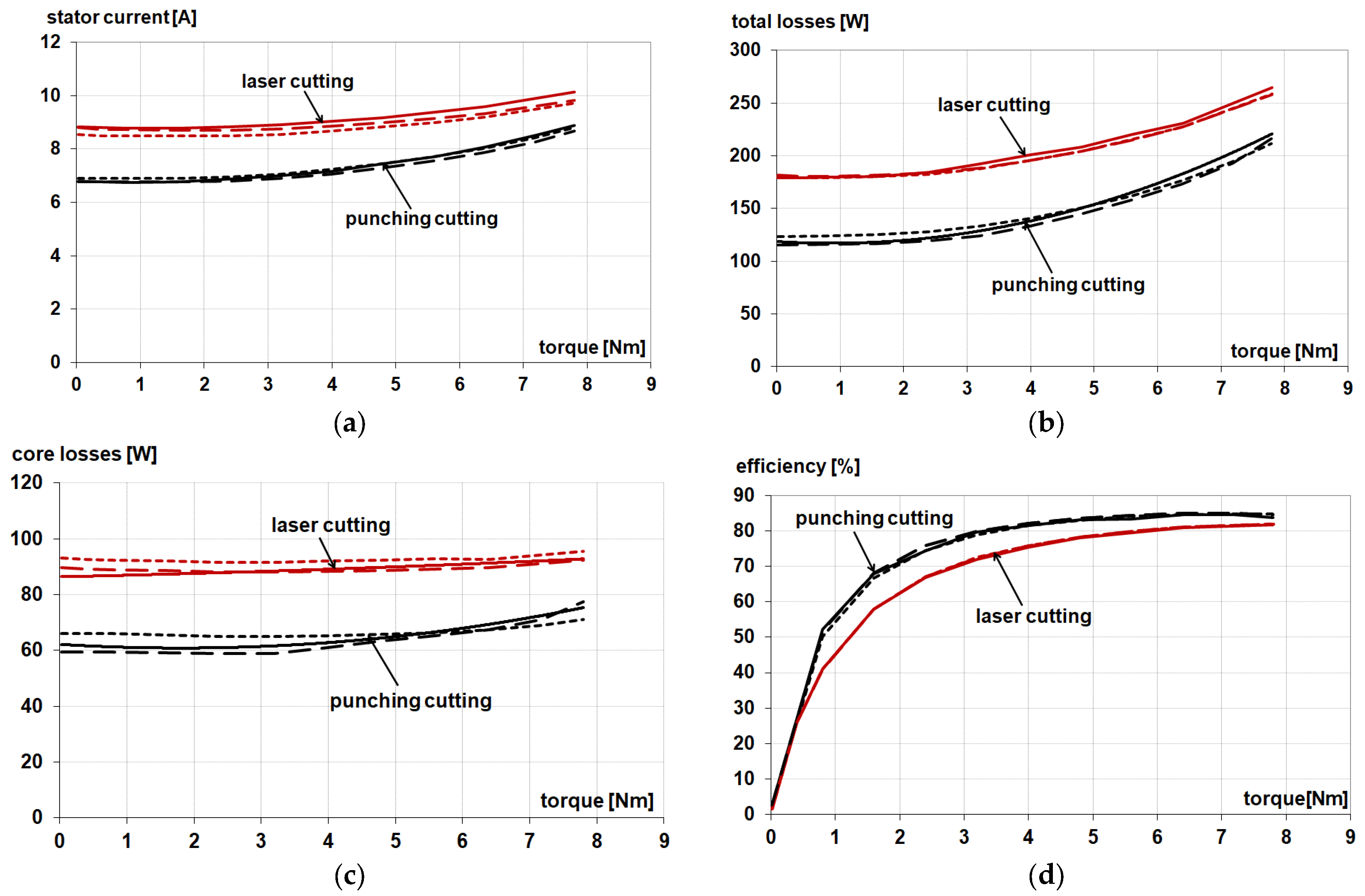
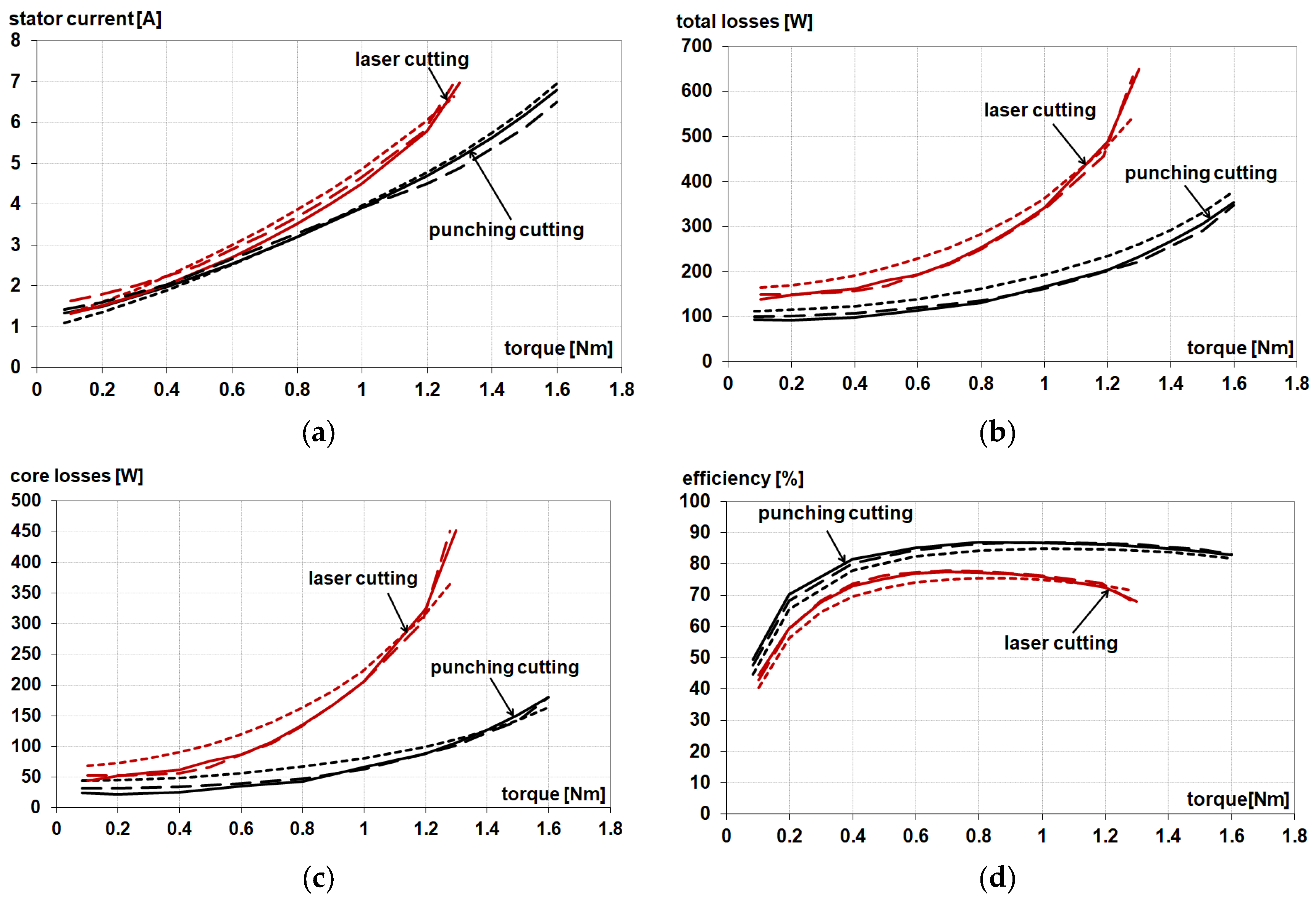
| Paper | Motor Type | Short Description | Contents and Conclusions |
|---|---|---|---|
| [93] | PMSM | Four-pole motor with stator outer diameter of 150 mm, embedded magnets. | Time-stepping finite element analysis of the induced voltage during rotation. The stator sheet at the cut edge was divided into six layers from the edge, and the appropriate identified BH curve was used for each. |
| [94] | PMSM | Analysis of a motor with a rated power of 219 W and an outer stator diameter of 90 mm. | The impact of cutting on the flux distribution was investigated, emphasizing the impact on local distributions. A slight effect of cutting on the electromagnetic torque of the machine was found, but with a significant effect on the efficiency. |
| [95] | PMSM | An 8-pole/9-slot motor with a rated power of 10 kW for a rotational speed of 19,000 rpm and a stator outer diameter of 70 mm. | An increase in core losses was found. A reduction in an overall efficiency of 1% was found, which in high-performance aeronautical applications cannot be overlooked. |
| [96] | PMSM | Four-pole PMSM motor with 90 mm stator outer diameter. | Core losses were studied. A local magnetic material model was used in the FEM simulation. Using a local model of the magnetic material enabled realistic prediction of the magnetic induction distribution and the specific distribution of losses in the tested electrical machine. |
| [97] | PMSM | Six-pole pairs, peak power 85 kW, maximum rotational speed 10,000 rpm. | Accounting for the effects of punching resulted in a 30% increase in rotor and stator losses. The authors also indicate the impact of punching on the mechanical characteristics obtained. |
| [98] | BLDC PM | A brushless DC surface-mounted PM motor with a rated power of 26 kW and a stator outer diameter of 137 mm was tested. | Core losses in the frequency range from 200 to 1400 Hz were investigated. A significant increase in core losses of up to 32% was found due to the cutting and assembly effect. However, this increase in losses could be removed by applying annealing. |
| [99] | PMSM | A permanent magnet synchronous 4-pole machine with a rated power of 150 W and a rotational speed of 6000 rpm. | The simulation results showed that the consideration of material damage at the cut edge in the calculation of the motor size under consideration is of immense importance for accurate result. |
| [100] | PMSM | An interior rotor fractional horsepower permanent magnet synchronous machine featuring 12 stator slots and 2 p = 8 poles was investigated. | The article concerns the optimization of the design of this motor, taking into account the effects of cutting. The stator sheet at the cut edge was divided into four layers from the edge. The authors emphasize that the optimal constructions were very sensitive to changes in the manufacturing process. |
| [101] | PMSM | PMSM motor with a rated power of 30 kW, a rated speed of 2860 rpm, and a maximum speed of 14,000 rpm, embedded magnets, and three pairs of poles. | The influence of the cutting on the magnetization curve was taken into account. The authors emphasize that the significant impact of punching is mainly observed for small-size machines and small-width magnetic circuit elements. |
| [102] | SFHP PM | The analysis of sub-fractional horsepower SFHP machines with a power of about 800 mW. | This paper investigates and compares the three stator lamination stacks’ selected magnetic performance parameters (i.e., cogging torque, hysteresis torque, and iron losses). Due to their small dimensions, such machines are particularly vulnerable to the degradation effects associated with cutting. |
| [103] | SFHP BL PM | SFHP single-phase brushless permanent magnet motor often found in automotive fan applications, 10-pole motor with stator outer diameter of 85 mm. The rotor has surface-mounted bread-loaf-shaped magnets. | The effect of cutting on cogging torque was investigated. It has been found that the change in the magnetic properties of the teeth caused by punching causes the formation of additional ones and low-order harmonics in the machine cogging torque with an amplitude comparable to the fundamental harmonics. |
| [104] | PMSM | The machine under study is a medium-size PMSM with one layer of V-shape magnets and a double-layered aluminum stator winding. Motor rated 100 kW for electric vehicle, 4-pole, outer diameter 213 mm. | The impact of cutting on torque and losses was investigated. Core material degradation can increase losses by up to 35%. Torque reduction can reach 1%. Driving cycle tests show a 21% increase in core loss. |
| [105] | PMSM | PMSM with stator outer diameter of 290 mm, rated speed 2750 rpm. | For the FEM simulation, the authors compared single-layer and multi-layer models. The authors state that cutting has negligible effect on the torque ripple. The calculated core loss difference due to cutting was 8%. |
| [34] | IM | A four-pole induction machine with an external diameter of the stator core of 89 mm and an internal diameter of the rotor core of 20.5 mm is considered. | In addition to examining the impact of cutting on the basic parameters of an induction motor, the work also examined the effects on equivalent inductances used in the circuit modeling of the motor. |
| [106] | IM | The investigated machine is a small squirrel cage induction machine with the following basic parameters: three phases, two poles, wye connection; the output power is 600 W, the rated speed is 2840 rpm, and the supply voltage is 400 V at 50 Hz. | The influence of cutting on the parameters of an induction motor was investigated. The relative difference between measured and simulated parameters was: for efficiency at a nominal load of 0.6%, current at a nominal load of about 2.4%, and total losses at about 1.5%. |
| [107] | IM | Analogous as above. | Additionally, the impact of annealing was investigated, allowing for an increase in efficiency by 1.5% for the rated power load. |
| [108] | IM | An industrial induction motor rated 7.5 kW using 0.5 mm thin sheet, four poles. | FEM simulations indicated an increase of up to 51% in the iron losses and up to 13% in the copper losses at partial load as an effect of cutting. |
| [109] | IM | Two poles induction machine with a rated power of 600 W at 2846 rpm. | Optimization with the genetic algorithm of the induction motor core slot shapes, considering the effects of cutting. The most significant difference between the basic sizes of the optimized flute shapes with and without considering the cutting effects is about 0.3 mm. |
| [110] | DS- AFIM | Double-stator axial-flux induction machine, total active length 103.41 mm, outer torus diameter 220 mm. | The torque capability of the model appeared to decrease by 1.3%, and a significant increase in the core losses was observed. |
| [111] | IM | An induction motor with 5.5 kW power, three phases, four poles, and fan cooling (380 V, 50 Hz, 1500 r/min) was used in the tests. | The study of the impact of punching on the parameters of the induction motor was supported by using an artificial neural network. The measured motor efficiency at 50 Hz and nominal load for punching was 86.81%, while for laser cutting, it was 85%. |
| [112] | SR | A synchronous reluctance motor with a rated power of 230 kW at 6000 rpm and 37.5 kW at a maximal speed of 18,000 rpm. | A comparison of manufacturing effects on two solutions (radial-rib rotor and multi-innerrib one). While in most of the analyzed cases, the cutting effect leads to a decrease in efficiency, in the case of the tested machine, it can work the opposite way thanks to increasing the inductance ratio. |
| [72] | SR | Six-pole reluctance motor with stator outer diameter equal to 120 mm. | Only the stator packages were tested, showing a significant effect of cutting. The additional losses due to cutting decrease with increasing frequency despite the significant increase in total losses. For machine operation at 400 Hz, an additional 50% core loss is expected. |
| Parameter | Value | |
|---|---|---|
| Number of pole pairs | (-) | 2 |
| Stator core outer diameter | (mm) | 134 |
| Stator core inner diameter | (mm) | 77 |
| Core length | (mm) | 120 |
| Number of stator slots | (-) | 24 |
| Number of rotor slots | (-) | 30 |
| Stator tooth mean width | (mm) | 5.5 |
| Rotor tooth mean width | (mm) | 3.5 |
| Stator yoke height | (mm) | 9.5 |
| Rotor yoke height | (mm) | 12.3 |
| Parameter | Punching Cutting | Laser Cutting | ||||
|---|---|---|---|---|---|---|
| Measured | Calculated for Width of 10 mm | Calculated for Actual Width | Measured | Calculated for Width of 10 mm | Calculated for Actual Width | |
| motor shaft power (W) | 1398 | 1398 | 1398 | 1377 | 1377 | 1377 |
| stator winding current (A) | 5.14 | 5.24 | 4.89 | 6.98 | 6.69 | 6.92 |
| stator teeth induction (T) stator yoke induction (T) basic core losses (W) | - - - | 0.377 0.428 28.7 | 0.374 0.424 19.2 | - - - | 0.382 0.436 29.6 | 0.383 0.438 34.0 |
| additional core losses (W) | - | 102.6 | 82.5 | - | 336.9 | 417.4 |
| total core losses (W) | 106.5 | 131.3 | 101.7 | 452.2 | 366.5 | 451.4 |
| total motor losses (W) | 233.4 | 260.4 | 222.9 | 649.3 | 544.4 | 633.1 |
| motor efficiency (%) | 85.7 | 84.3 | 86.2 | 68.0 | 71.7 | 68.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dems, M.; Gmyrek, Z.; Komeza, K. The Influence of Cutting Technology on Magnetic Properties of Non-Oriented Electrical Steel—Review State of the Art. Energies 2023, 16, 4299. https://doi.org/10.3390/en16114299
Dems M, Gmyrek Z, Komeza K. The Influence of Cutting Technology on Magnetic Properties of Non-Oriented Electrical Steel—Review State of the Art. Energies. 2023; 16(11):4299. https://doi.org/10.3390/en16114299
Chicago/Turabian StyleDems, Maria, Zbigniew Gmyrek, and Krzysztof Komeza. 2023. "The Influence of Cutting Technology on Magnetic Properties of Non-Oriented Electrical Steel—Review State of the Art" Energies 16, no. 11: 4299. https://doi.org/10.3390/en16114299
APA StyleDems, M., Gmyrek, Z., & Komeza, K. (2023). The Influence of Cutting Technology on Magnetic Properties of Non-Oriented Electrical Steel—Review State of the Art. Energies, 16(11), 4299. https://doi.org/10.3390/en16114299







