Outlet Pressure and Flow Characteristics of a New Two-Dimensional Piston Pump with an Overlapped Distributor
Abstract
:1. Introduction
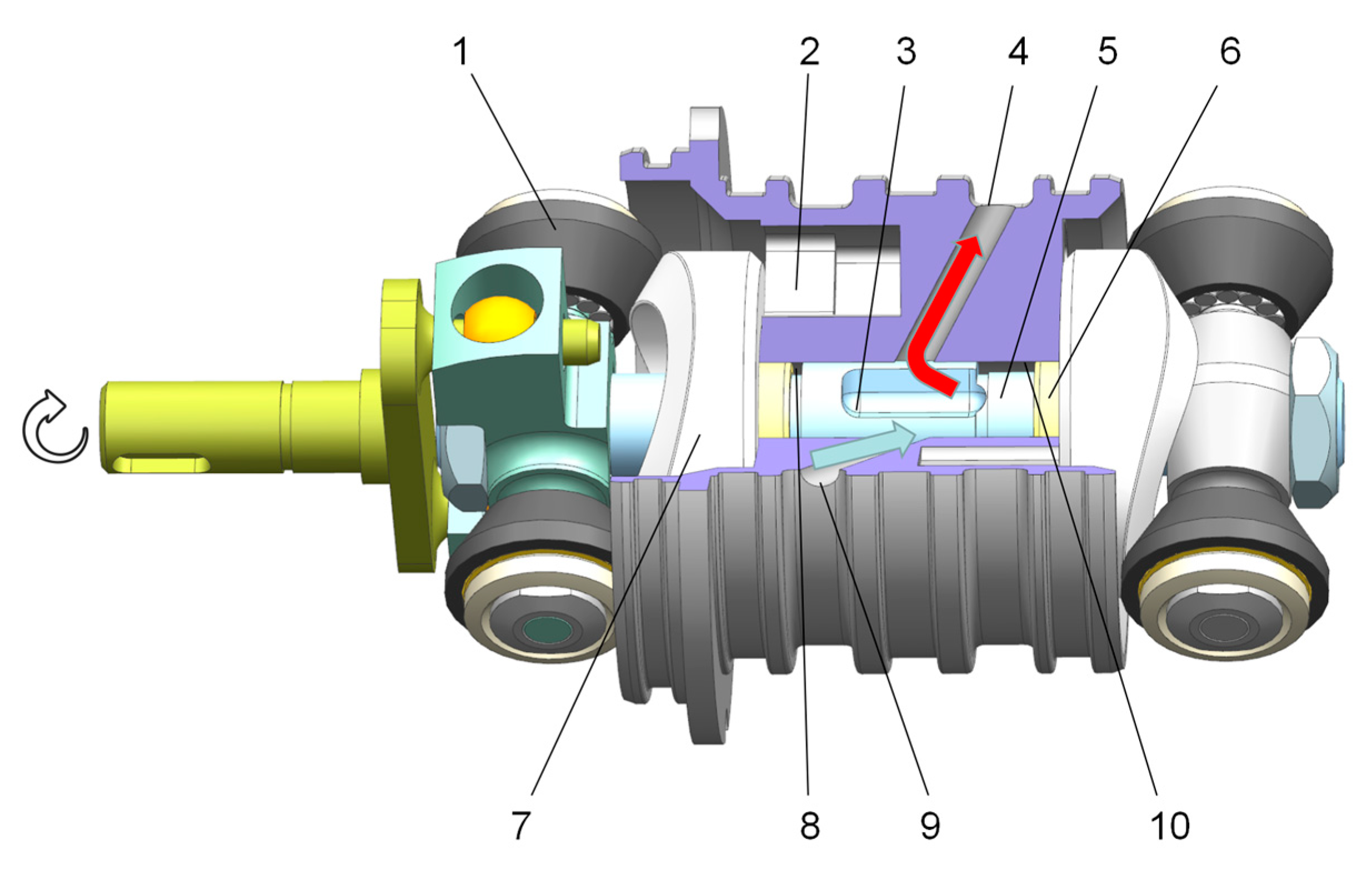
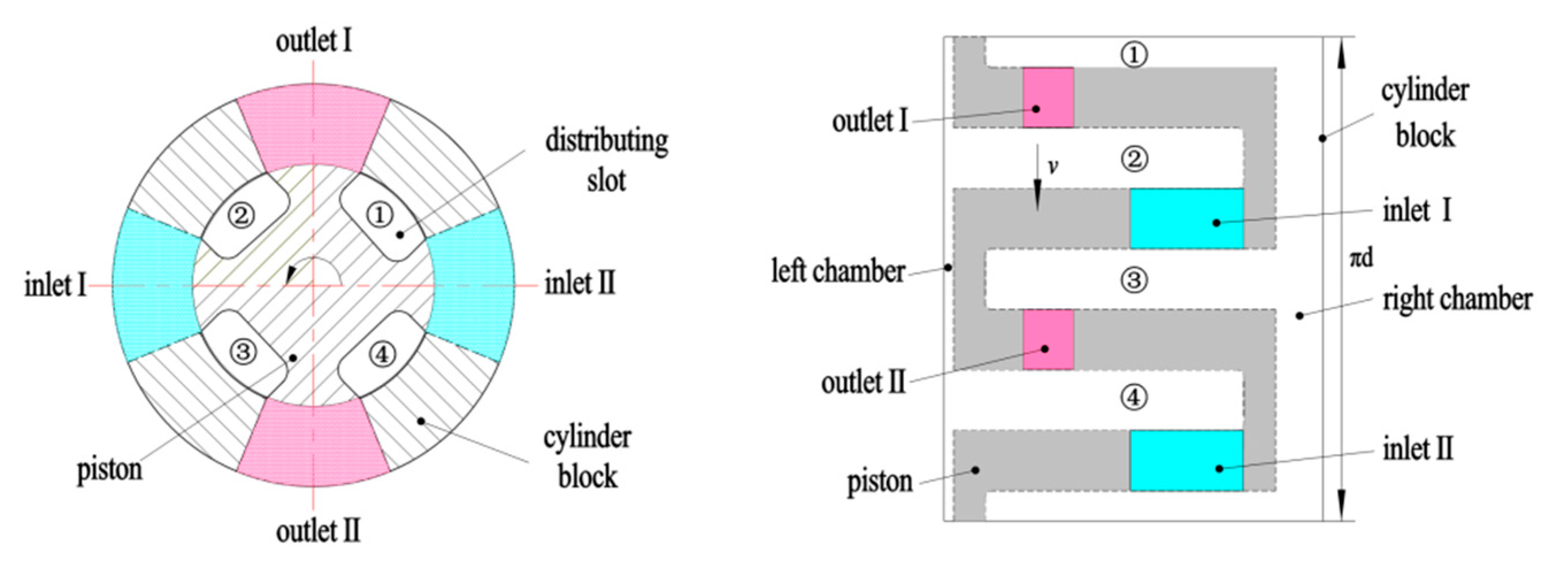
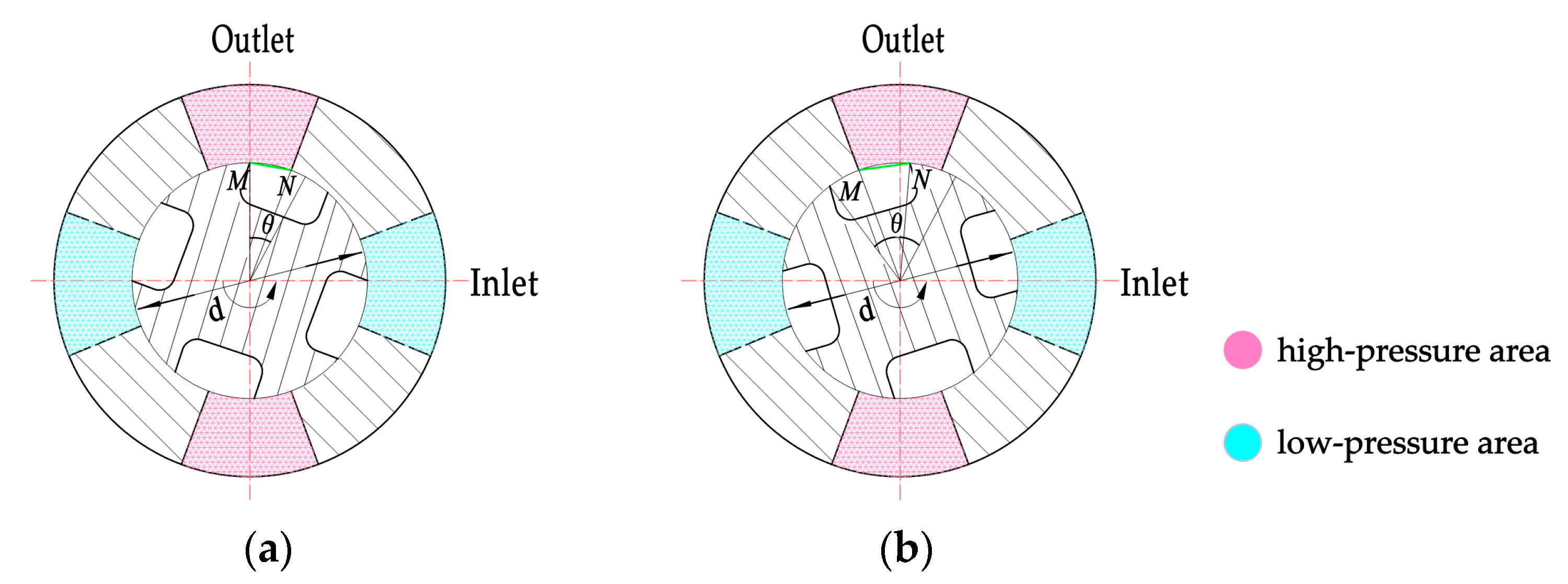
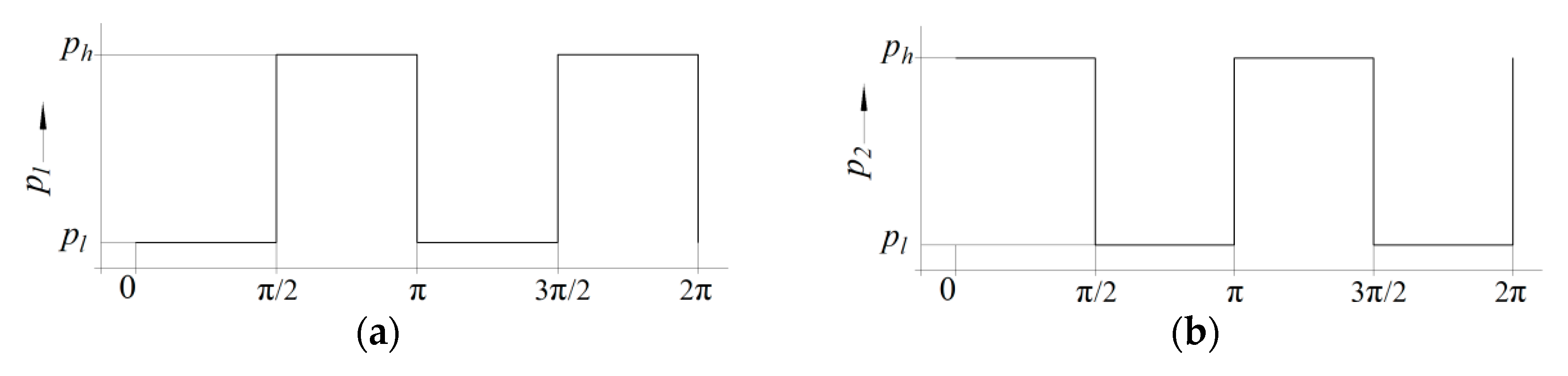
2. Distribution Principle with an Overlapped Distributor
3. Analysis of the Pressure and Flow within the Piston Chambers
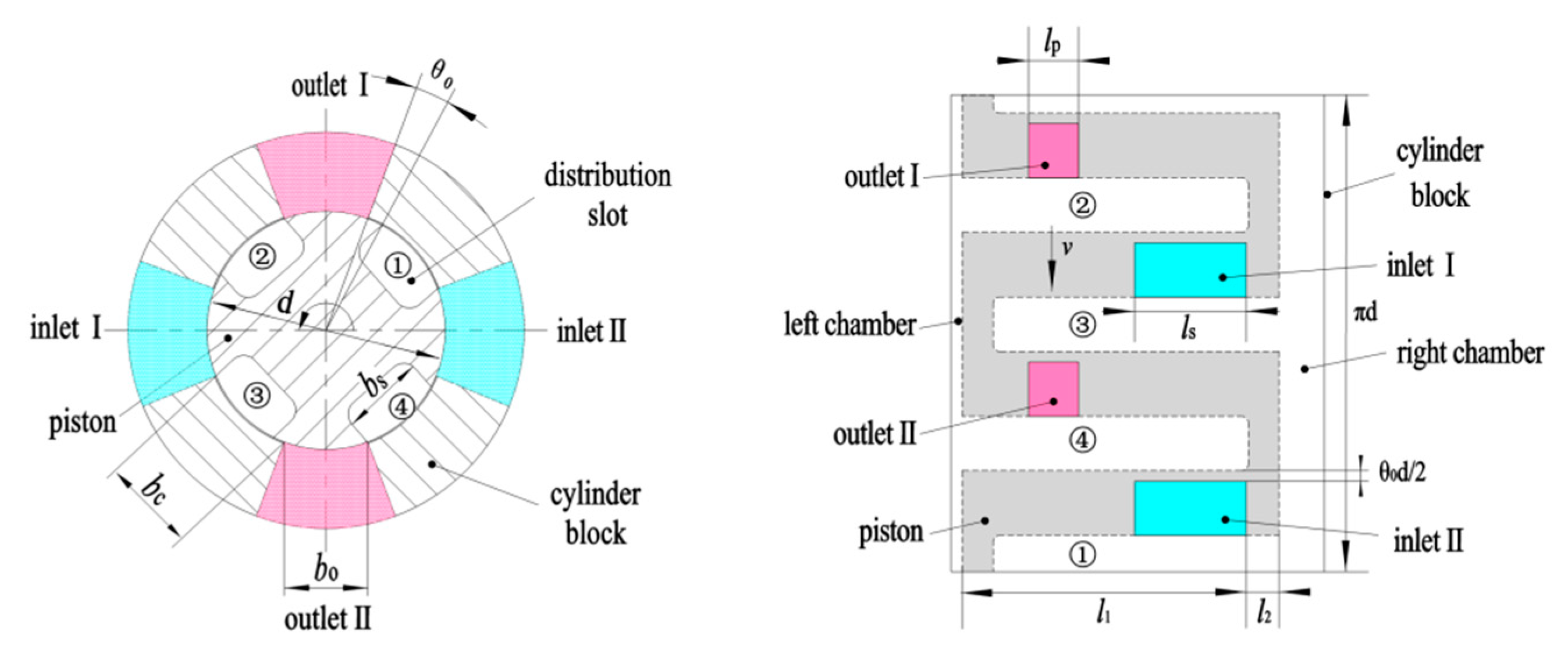
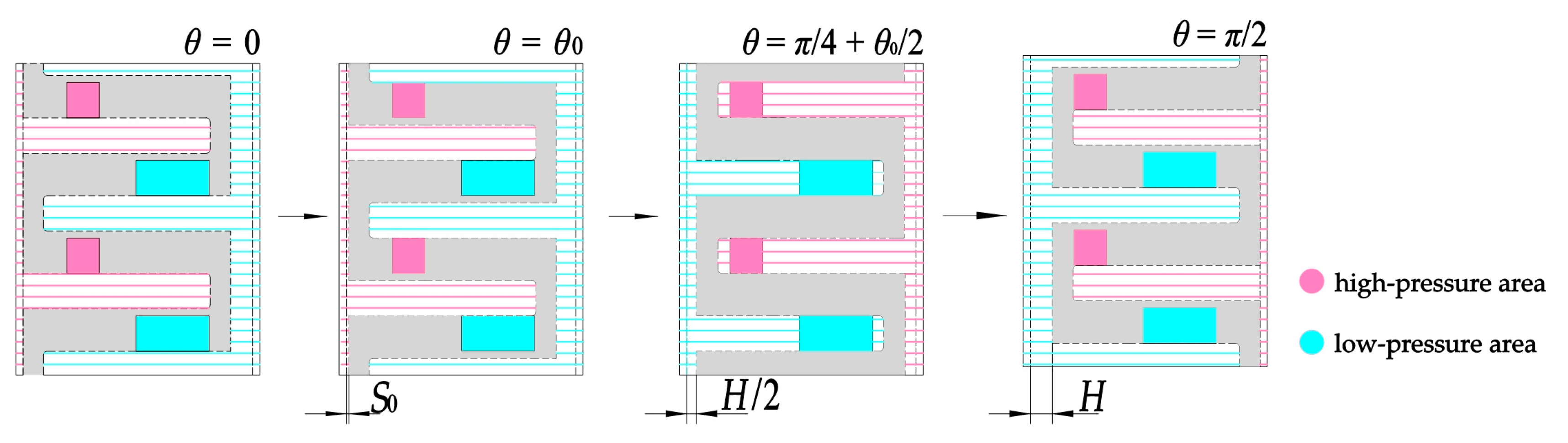
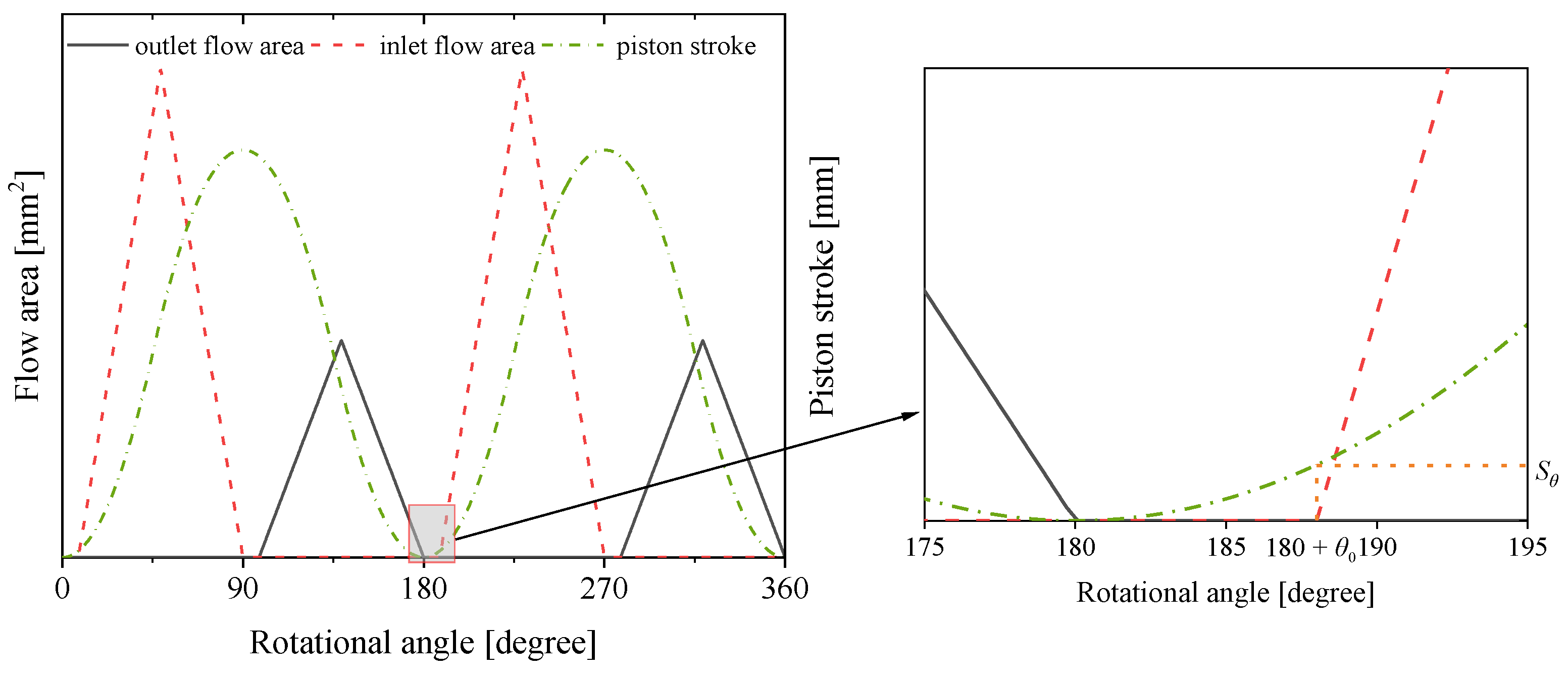
3.1. Flow Area of the Overlapped Distributor
3.2. Volumetric Losses
3.3. Pressure Analysis in a Pump Chamber
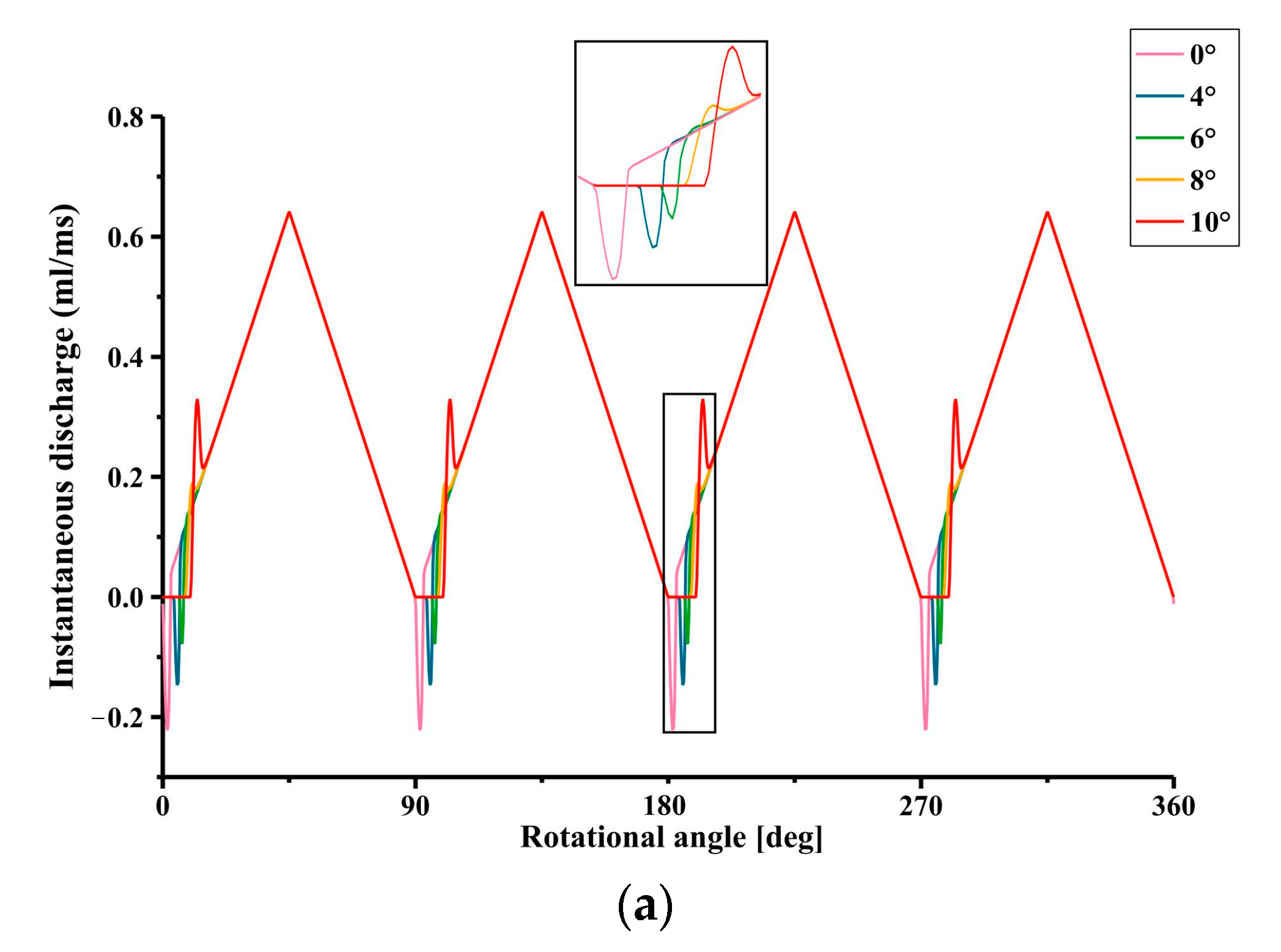
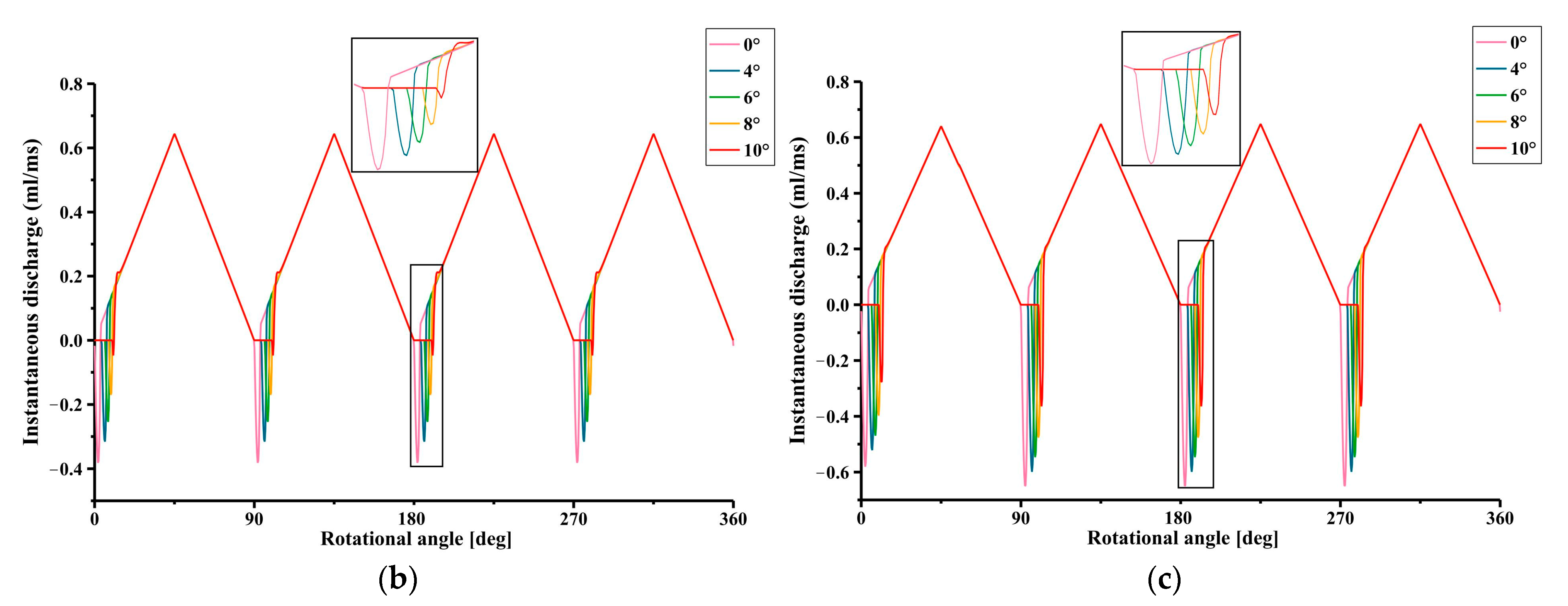
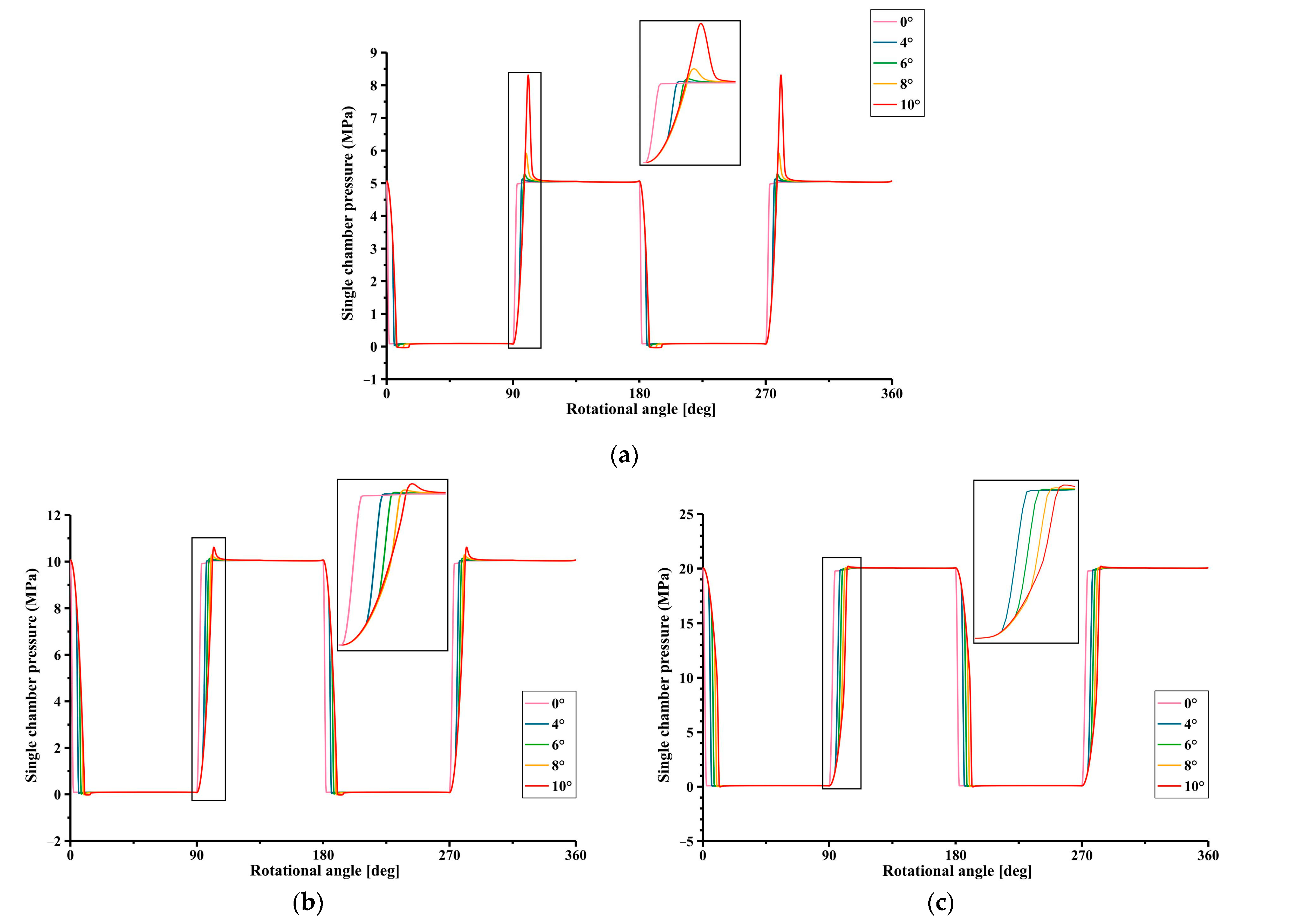
4. Simulation
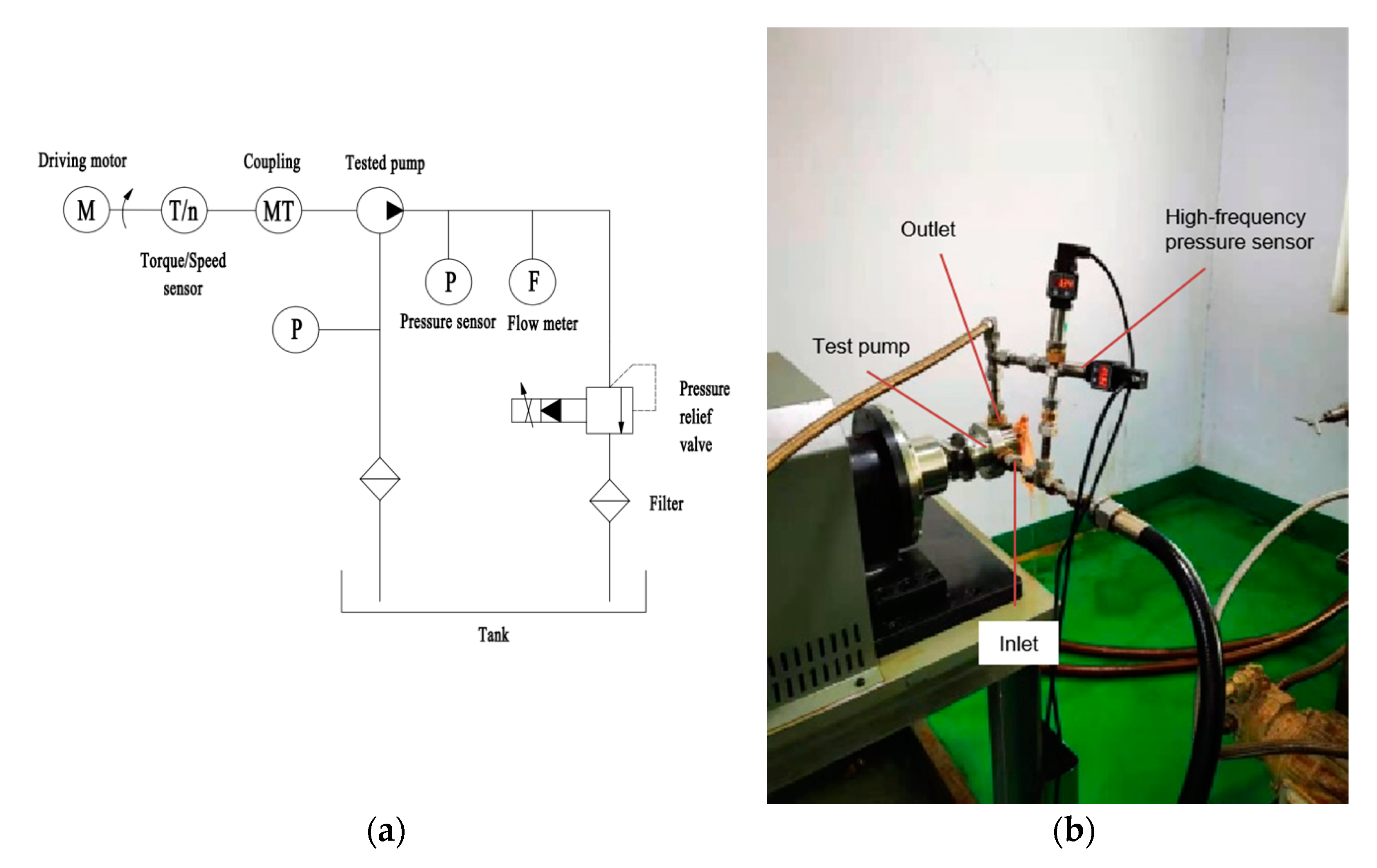
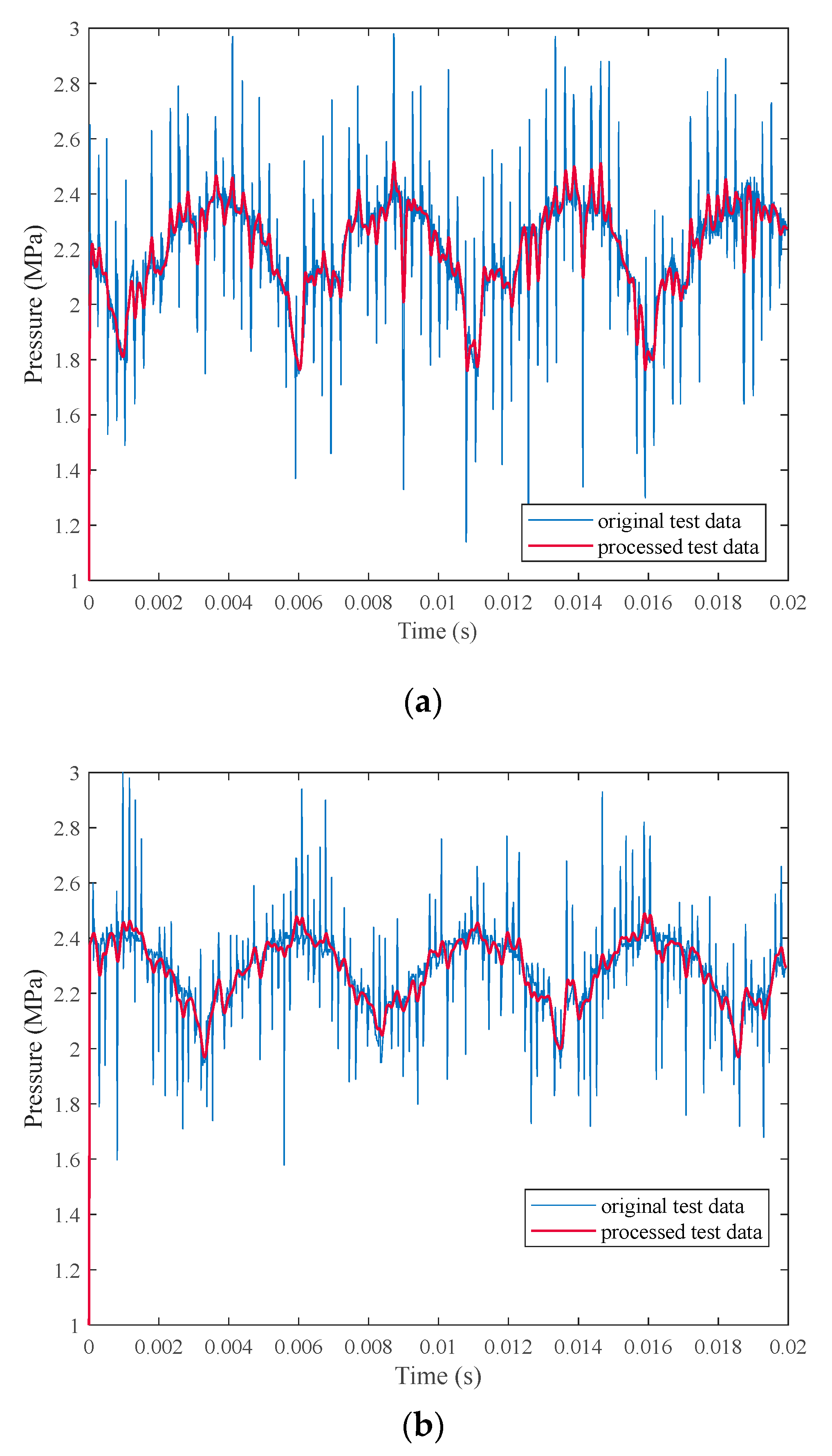
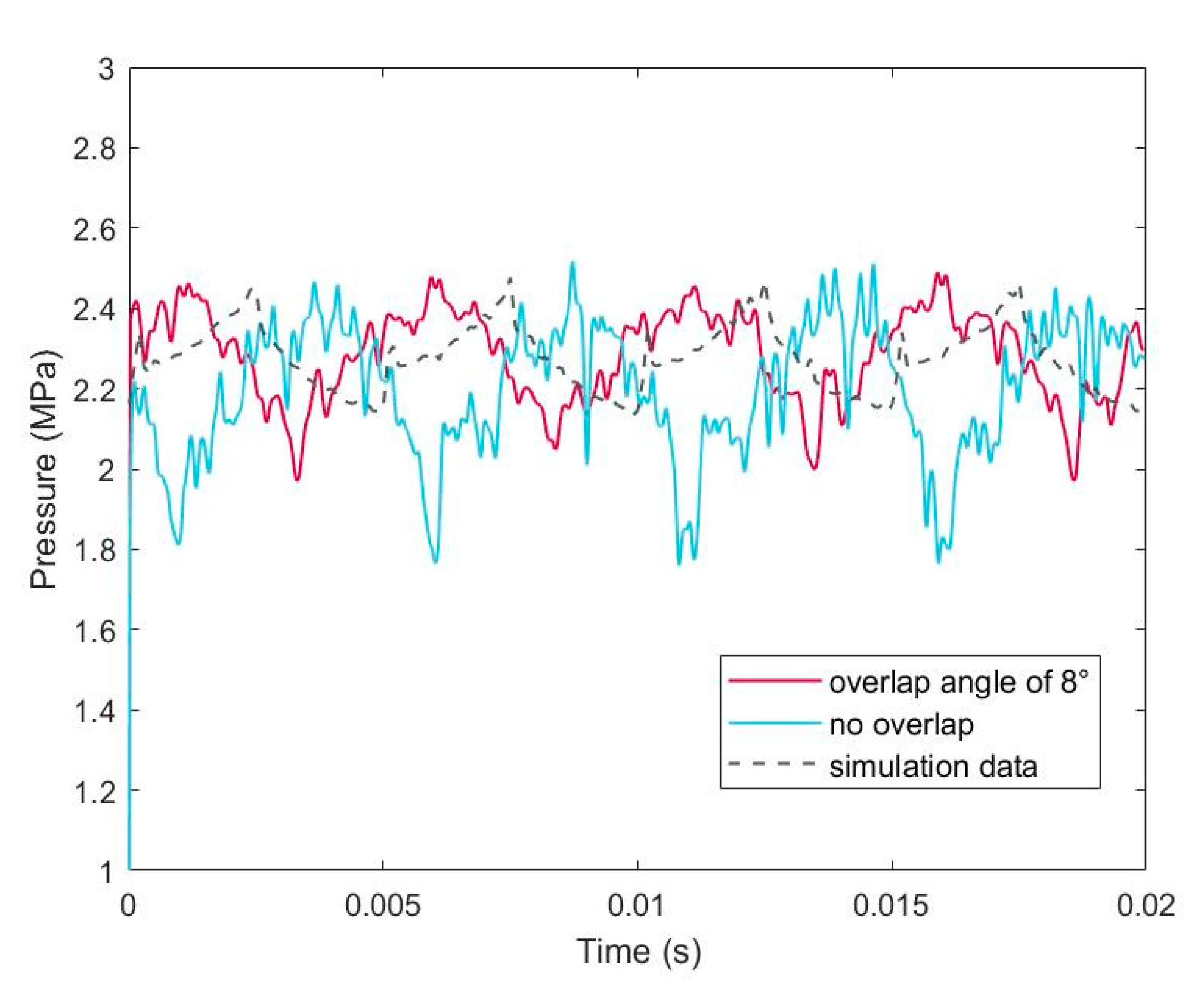
5. Experimental Research
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chao, Q.; Zhang, J.; Xu, B.; Huang, H.; Pan, M. A review of high-speed electro-hydrostatic actuator pumps inaerospace applications: Challenges and solutions. J. Mech. Des. 2019, 141, 050801. [Google Scholar]
- Zhang, T.T. Trends and challenges of high-speed hydraulic pump technology in the era of electricization—According to Xu Bing’s report, an expert of Zhejiang University. Hydraul. Pneum. Seals 2022, 42, 103–107. [Google Scholar]
- Kaminaga, H.; Amari, T.; Niwa, Y.; Nakamura, Y. Development of knee power assist using backdrivable electrohydrostatic actuator. In Proceedings of the 2010 IEEE/RSJ International Conference on Intelligent Robots and Systems, Taipei, Taiwan, 18 October 2010; pp. 5517–5524. [Google Scholar]
- Sun, M.W.; Ouyang, X.P.; Mattila, J.; Yang, H.; Hou, G. One novel hydraulic actuating system for the lower-body exoskeleton one novel hydraulic actuating system for the lower-body exoskeleton. Chin. J. Mech. Eng. 2021, 34, 31. [Google Scholar] [CrossRef]
- Sun, M.W.; Ouyang, X.P.; Wang, Z.Z.; Liu, H.; Yang, H.Y. Cooperative control strategy of pump-controlled exoskeleton robot walking. J. Mech. Eng. 2022, 58, 159–169. [Google Scholar]
- Ko, T.; Kaminaga, H.; Nakamura, Y. Key design parameters of a few types of electro-hydrostatic actuators for humanoid robots. Adv. Robot. 2018, 32, 1241–1252. [Google Scholar] [CrossRef]
- Ruan, J.; Tong, C.W.; Li, S.; Feng, Z.J.; Shentu, S.N.; Jin, D.C.; Meng, B. Two-Dimensional Axial Piston Pump with Equal Acceleration and Equal Deceleration Track. Chinse patent CN 201510151253.3, 1 April 2015. [Google Scholar]
- Ruan, J.; Li, J.Y.; Jin, D.C. Research and feasibility verification of two-dimensional (2D) piston pump. J. Zhejiang Univ. Technol. 2017, 45, 264–269. [Google Scholar]
- He, H.B. Design and Experimental Study of Two Dimensional (2D) Piston Constant Pressure Variable Pump. Master’s Thesis, Zhejiang University of Technology, Hangzhou, China, 2017. [Google Scholar]
- Huang, Y.; Ruan, J.; Zhang, C.; Ding, C.; Li, S. Research on the mechanical efficiency of high-speed 2D piston pumps. Processes 2020, 8, 853. [Google Scholar] [CrossRef]
- Huang, Y.; Ruan, J.; Chen, Y.; Ding, C.; Li, S. Research on the volumetric efficiency of 2D piston pumps with a balanced force. Energies 2020, 13, 4796. [Google Scholar] [CrossRef]
- Wang, H.Y.; Li, S.; Ruan, J. Design and research of two-dimensional fuel pump with balanced inertia force. Acta Aeronaut. E.T. Astronaut. Sin. 2022, 43, 424696. [Google Scholar]
- Zhu, K.; Ruan, C.; Wang, H.; Li, S.; Ruan, J. Analysis of the torque loss of high-speed transmission mechanism with a stacked roller set. Machines 2021, 9, 140. [Google Scholar] [CrossRef]
- Zhang, C.; Ruan, J.; Xing, T.; Li, S.; Meng, B.; Ding, C. Research on the volumetric efficiency of a novel stacked roller 2D piston pump. Machines 2021, 9, 128. [Google Scholar] [CrossRef]
- Shentu, S.N.; Ruan, J.; Qian, J.Y.; Meng, B.; Wang, L.F.; Guo, S.S. Study of flow ripple characteristics in an innovative two-dimensional fuel piston pump. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 1–15. [Google Scholar] [CrossRef]
- Ruan, J.; Jin, D.C.; Shentu, S.N.; Wu, C.S. Research and feasibility verification of two–dimensional (2D) tandem pump. Chin. Hydraul. Pneum. 2017, 11, 1–5. [Google Scholar]
- Jin, D.C. Research on Design Method and Experimental Verification of Two-Dimensional Piston Pump. Ph.D. Thesis, Zhejiang University of Technology, Hangzhou, China, 2019. [Google Scholar]
- Shentu, S.N. Research on Flow Characteristics of Electric Two-Dimensional Piston (2D) Fuel Pump. Ph.D. Thesis, Zhejiang University of Technology, Hangzhou, China, 2020. [Google Scholar]
- Ding, C.; Huang, Y.; Zhang, L.; Ruan, J. Investigation of the churning loss reduction in 2D motion-converting mechanisms. Energies 2021, 14, 1506. [Google Scholar] [CrossRef]
- Jin, D.C.; Ruan, J. Design and research of two-dimensional fuel pump. Acta Aeronaut. E.T. Astronaut. Sin. 2019, 40, 422730. [Google Scholar]
- Qian, J.Y.; Shentu, S.N.; Ruan, J. Volumetric efficiency analysis of two-dimensional piston aviation fuel pump. Acta Aeronaut. E.T. Astronaut. Sin. 2020, 41, 423267. [Google Scholar]
- Xing, T.; Xu, Y.Z.; Ruan, J. Two-dimensional piston pump: Principle, design, and testing for aviation fuel pumps. Chin. J. Aeronaut. 2020, 33, 1349–1360. [Google Scholar] [CrossRef]
- Ding, C.; Zhu, Y.H.; Liu, L.; Tong, C.W. Research on a novel flowmeter with parallel two-dimensional pistons as its metering units. IEEE Access 2019, 7, 110912–110927. [Google Scholar]
- Ding, C.; Zhang, L.C.; Zhu, Y.H.; Ruan, J.; Tong, C.W. Modified mathematic model of a parallel two-dimensional piston flowmeter. Flow Meas. Instrum. 2021, 79, 101929. [Google Scholar]
- Ding, C.; Chen, H.; Zhang, L.; Xia, N.; Ruan, J. An investigation on the dynamic characteristics of a two-dimensional piston flowmeter. Adv. Mech. Eng. 2022, 14. [Google Scholar] [CrossRef]
- Ding, C. Investigation on two-dimensional piston dynamic flowmeter. Trans. Chin. Soc. Agric. Mach. 2022, 53, 450–458. [Google Scholar] [CrossRef]
- Guo, S.R.; Chen, J.H.; Lu, Y.L.; Wang, Y.; Dong, H.K. Hydraulic piston pump in civil aircraft: Current status, future directions and critical technologies. Chin. J. Aeronaut. 2020, 33, 16–30. [Google Scholar] [CrossRef]
- Ma, J.N. Study on Flow Ripple and Valve Plate Optimization of Axial Piston Pump. Ph.D. Thesis, Zhejiang University, Hangzhou, China, 2009. [Google Scholar]
- Shentu, S.N. Optimization analysis of flow characteristic and distribution window of 2D pump. Trans. Chin. Soc. Agric. Mach. 2019, 50, 403–410. [Google Scholar]

| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Bulk modulus of the oil K (MPa) | 1400 | Flow rate coefficient Cd | 0.62 |
| Oil dynamic viscosity μ (Pa·s) | 3.91 × 10−2 | Cylinder block outlet opening length lp (mm) | 8 |
| Oil density ρ (kg/m3) | 850 | Cylinder block inlet opening length ls (mm) | 18 |
| Out-cylinder block pressure pe (MPa) | 0 | Piston slot length l1 (mm) | 46 |
| 2D piston diameter d (mm) | 24.4 | Sealing length on one side of the slot l2 (mm) | 5 |
| Piston rod diameter ds (mm) | 16 | Sealing length of the sealing ring l3 (mm) | 28 |
| Piston working stroke H (mm) | 6 | Gap width δ (mm) | 0.01 |
| Description | Valve | Description | Valve |
|---|---|---|---|
| Pressure range | 10 MPa | Bandwidth (−3 dB) | 200 KHz |
| Combined non-linearity, hysteresis, and repeatability | ±0.1% FS | Operating temperature range | −50 °C to + 120 °C |
| Thermal sensitivity shift | ±0.1%/10 °C | Thermal zero shift | ±0.1% FS/100 °C |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xing, T.; Yan, X.; Huang, Y.; Gao, C.; Ruan, J. Outlet Pressure and Flow Characteristics of a New Two-Dimensional Piston Pump with an Overlapped Distributor. Energies 2023, 16, 4303. https://doi.org/10.3390/en16114303
Xing T, Yan X, Huang Y, Gao C, Ruan J. Outlet Pressure and Flow Characteristics of a New Two-Dimensional Piston Pump with an Overlapped Distributor. Energies. 2023; 16(11):4303. https://doi.org/10.3390/en16114303
Chicago/Turabian StyleXing, Tong, Xinyu Yan, Ying Huang, Cun Gao, and Jian Ruan. 2023. "Outlet Pressure and Flow Characteristics of a New Two-Dimensional Piston Pump with an Overlapped Distributor" Energies 16, no. 11: 4303. https://doi.org/10.3390/en16114303
APA StyleXing, T., Yan, X., Huang, Y., Gao, C., & Ruan, J. (2023). Outlet Pressure and Flow Characteristics of a New Two-Dimensional Piston Pump with an Overlapped Distributor. Energies, 16(11), 4303. https://doi.org/10.3390/en16114303






