A Bi-Level Optimal Operation Model for Small-Scale Active Distribution Networks Considering the Coupling Fluctuation of Spot Electricity Prices and Renewable Energy Sources
Abstract
:1. Introduction
- It can achieve precise control of electricity through intelligent control technology, improve energy utilization efficiency, and reduce energy waste;
- It has energy storage capacity, which can balance the load of power grid effectively and enhance the stability of the power grid;
- Through the use of small-scale power generation units, it can better adapt to the demand for decentralized energy supply and improve the flexibility of energy supply.
- It is difficult to influence the wholesale market price. Small-scale active distribution networks need to import electricity from the electricity wholesale market and distribute it to their customers. As price takers, operators of small-scale active distribution networks passively face price fluctuations;
- Small-scale active distribution networks rely on controllable fossil energy or unpredictable renewable energy to provide part of their electricity internally to increase power supply flexibility. The uncertainty of variational renewable energy generation from internal and external sources can affect profitability;
- There exists a game relationship between operators and internal customers. The strategy determined unilaterally by the operator may deviate from the equilibrium point.
2. Literature Review
3. Conditional Wholesale Power Price Forecast for High VRE Penetration Market
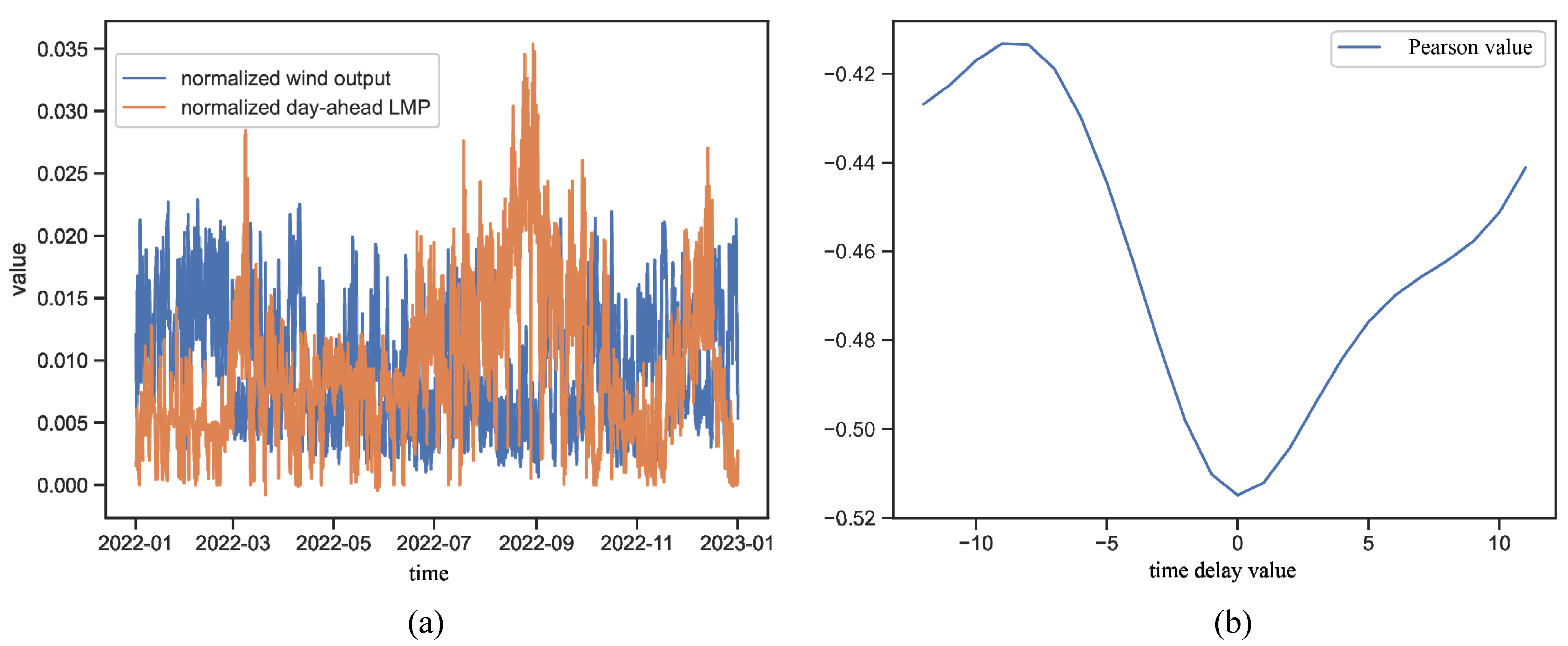
3.1. Correlation between Wind Power Output and Electricity Spot Price in High Penetration Markets
3.2. ADNO Local Wind Power Output and Nodal Price Prediction Based on ISO Wind Power Forecast
3.2.1. Improved Transformer Time Series Conditional Prediction Model
3.2.2. Multi-Head Attention Mechanism
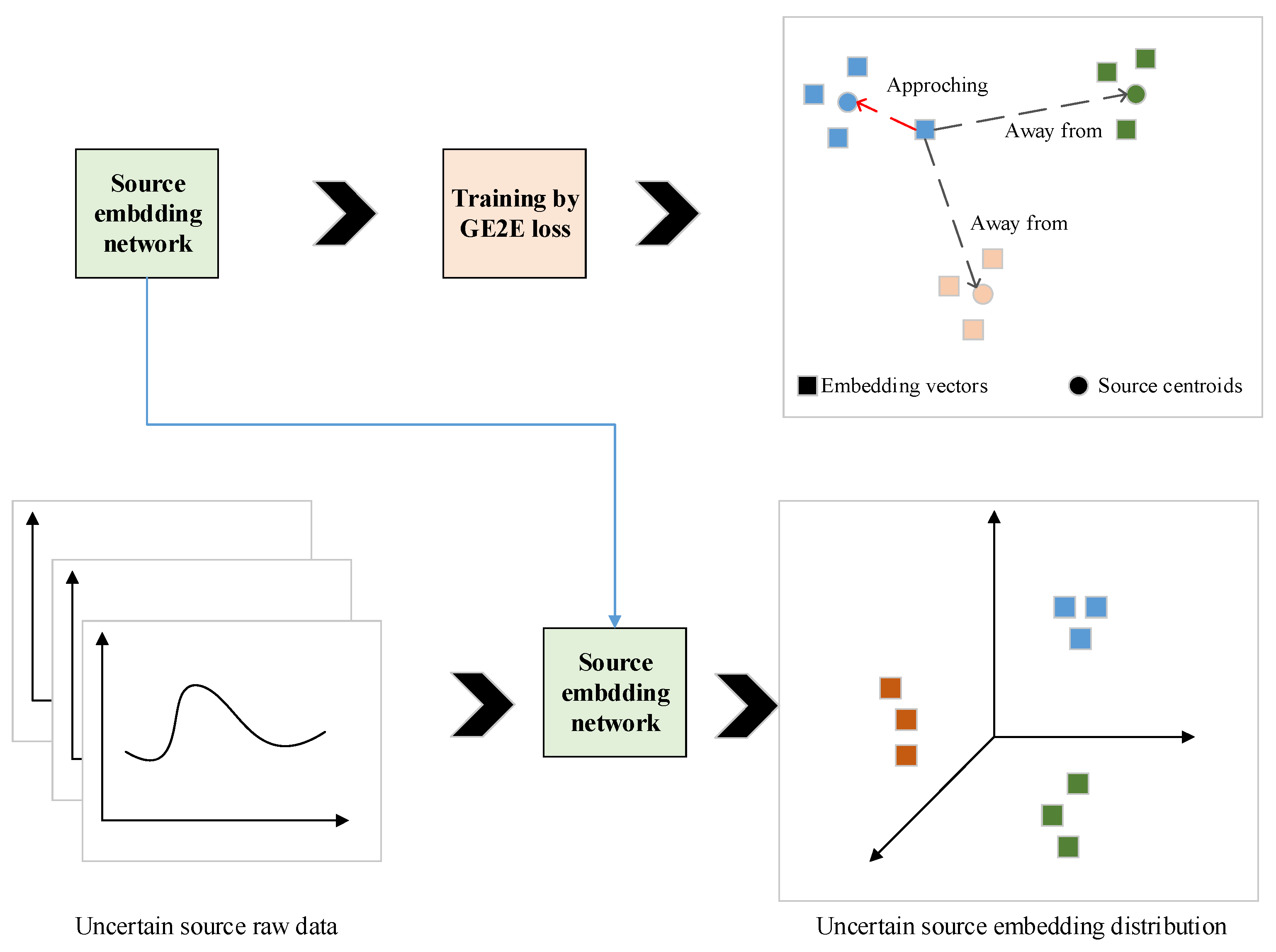
3.2.3. Source Embedding Mechanism
3.3. Evaluation of Prediction Methods
4. Bi-Level Optimization Model for Equilibrium Operation Strategy
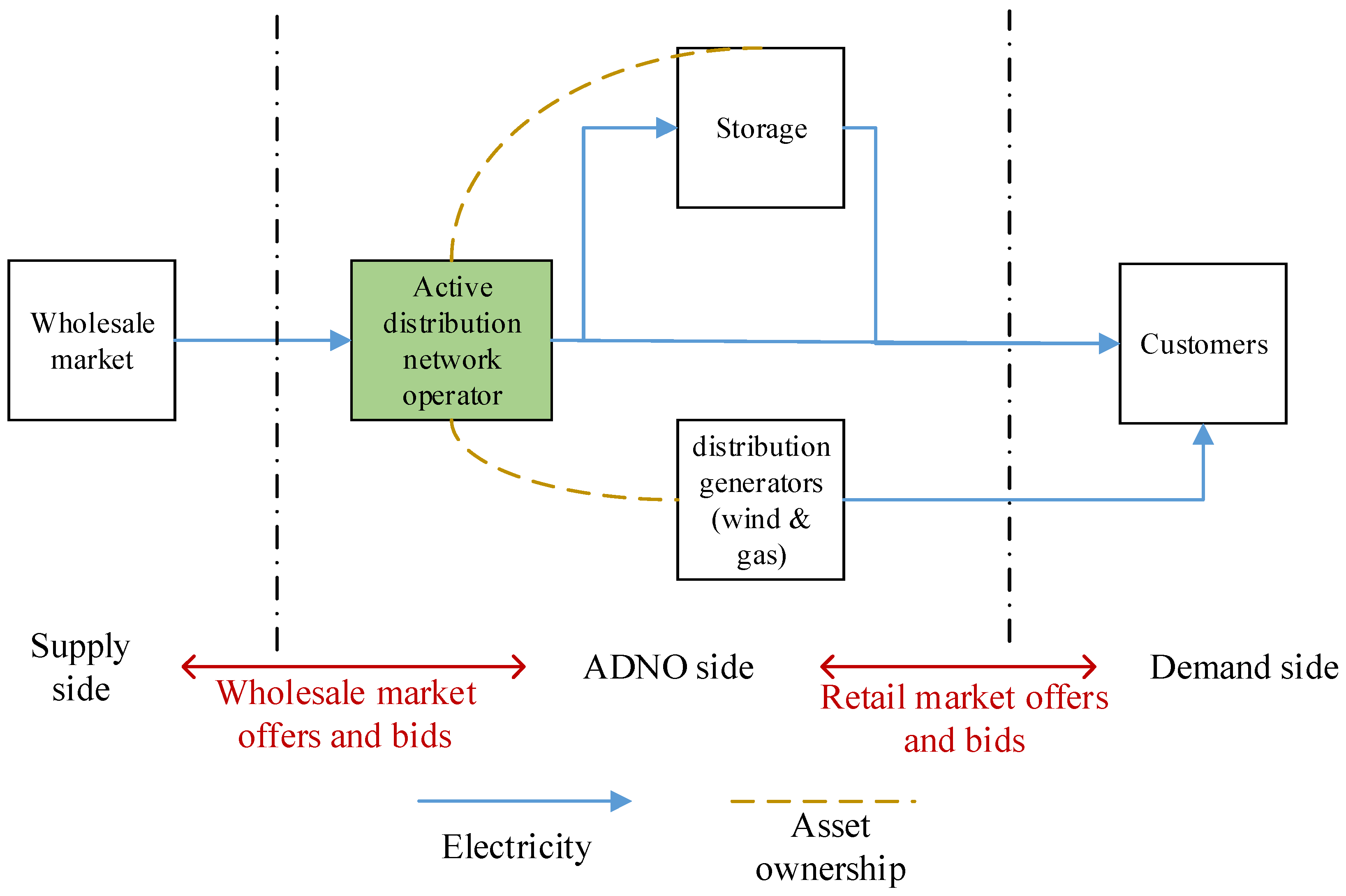
4.1. Short-Term and Long-Term Operational Issues Faced by ADNO
4.2. Hedging Strategies of ADNO for Spot Wholesale Electricity Prices and Renewable Energy Output Fluctuations
4.2.1. Configuring Energy Storage Systems
4.2.2. Configuring Distributed Fossil Energy
4.2.3. Configuring Distributed Wind Power Generation
4.3. Customer Electricity Demand and Network Constraints
4.3.1. Customer Electricity Demand
4.3.2. Network Constraints
4.4. Stackelberg Game and Bi-Level Optimization Model
4.5. Short-Term Equilibrium Solution and Long-Term Optimal Investment Analysis Method
5. Case Study
5.1. IEEE 33 Test System and Main Experimental Parameters
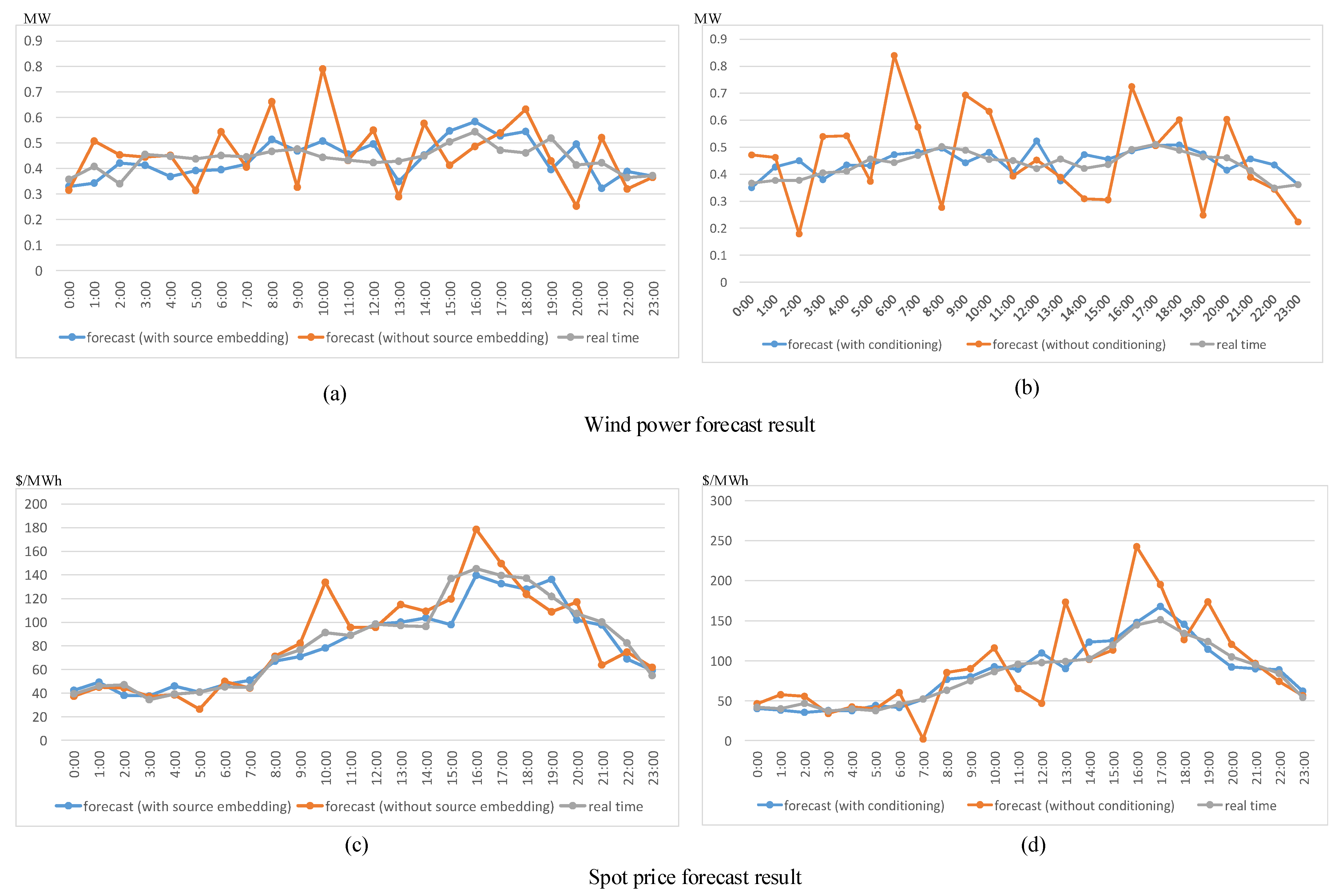
5.2. Ablation Experiment of The Forecast Model
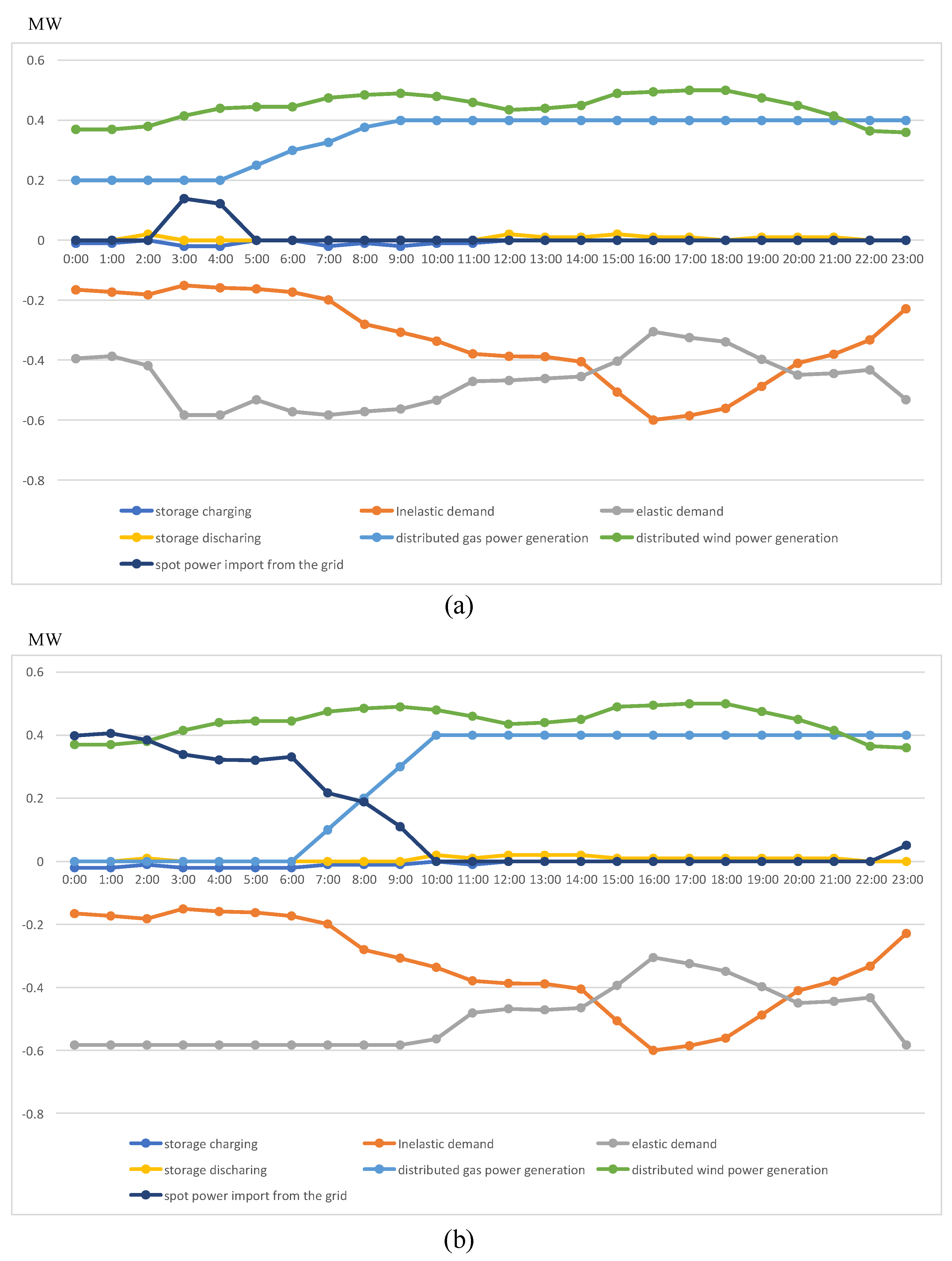
5.3. Equilibrium Scheduling and Short-Term Optimal Strategy
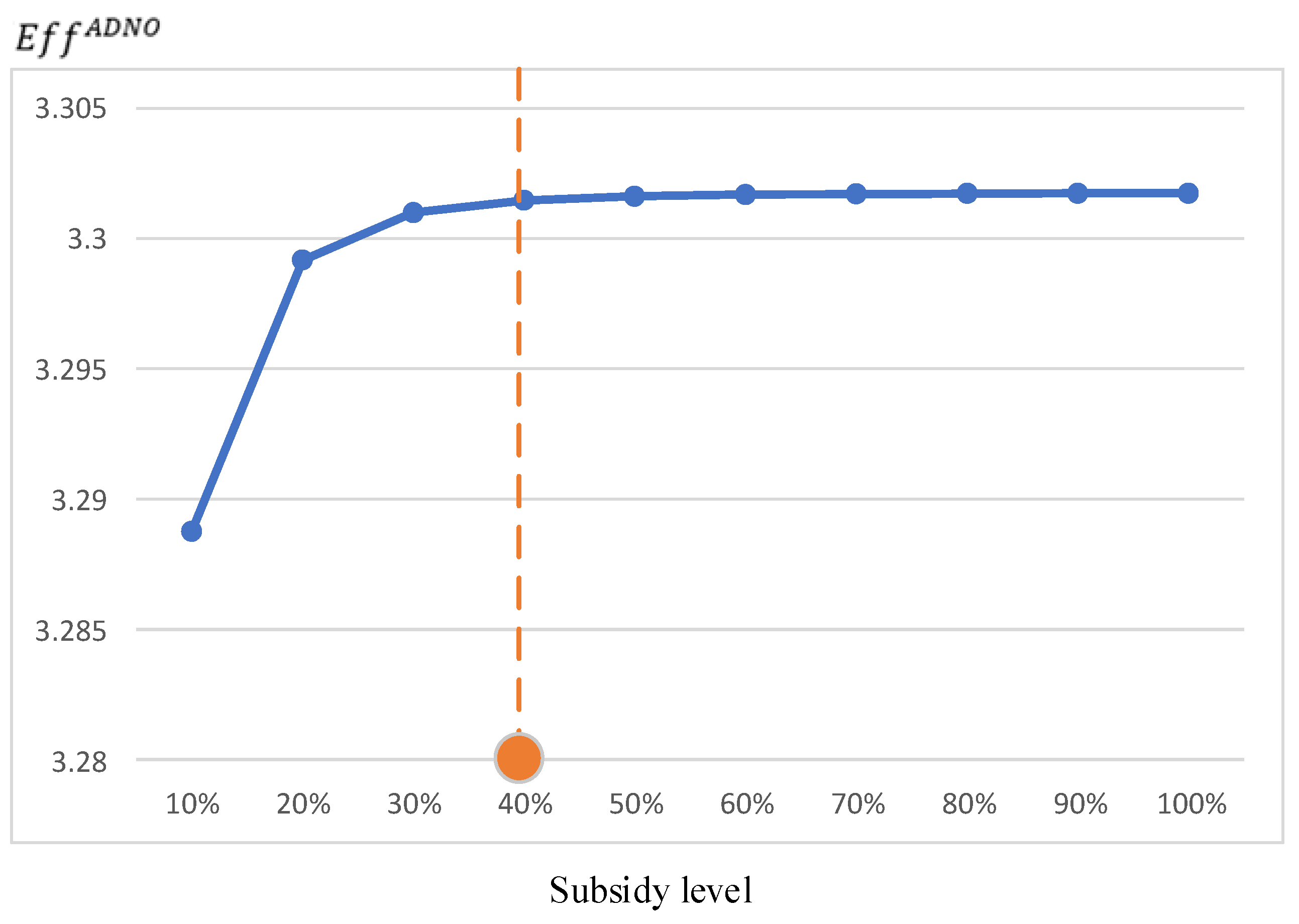
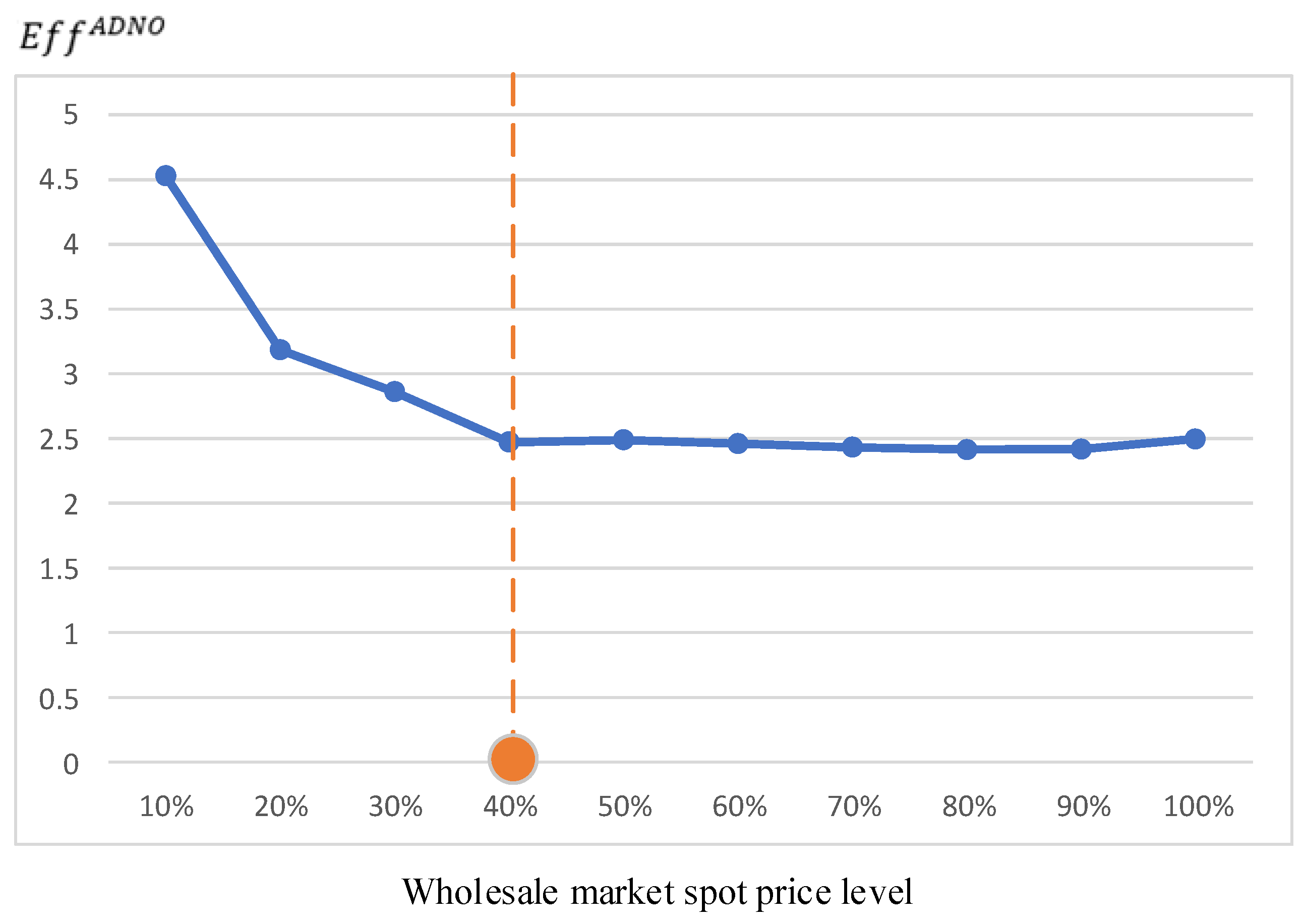
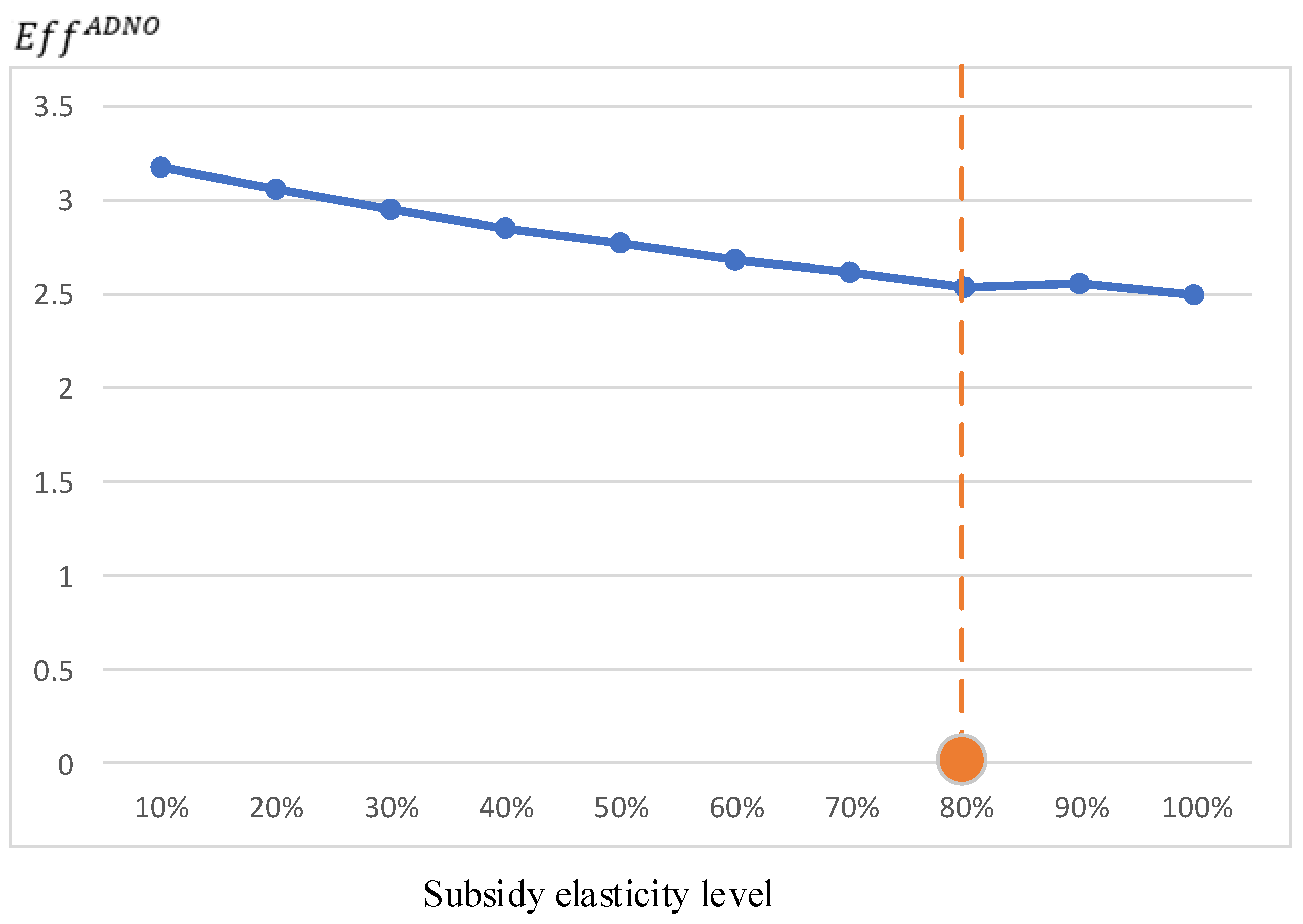
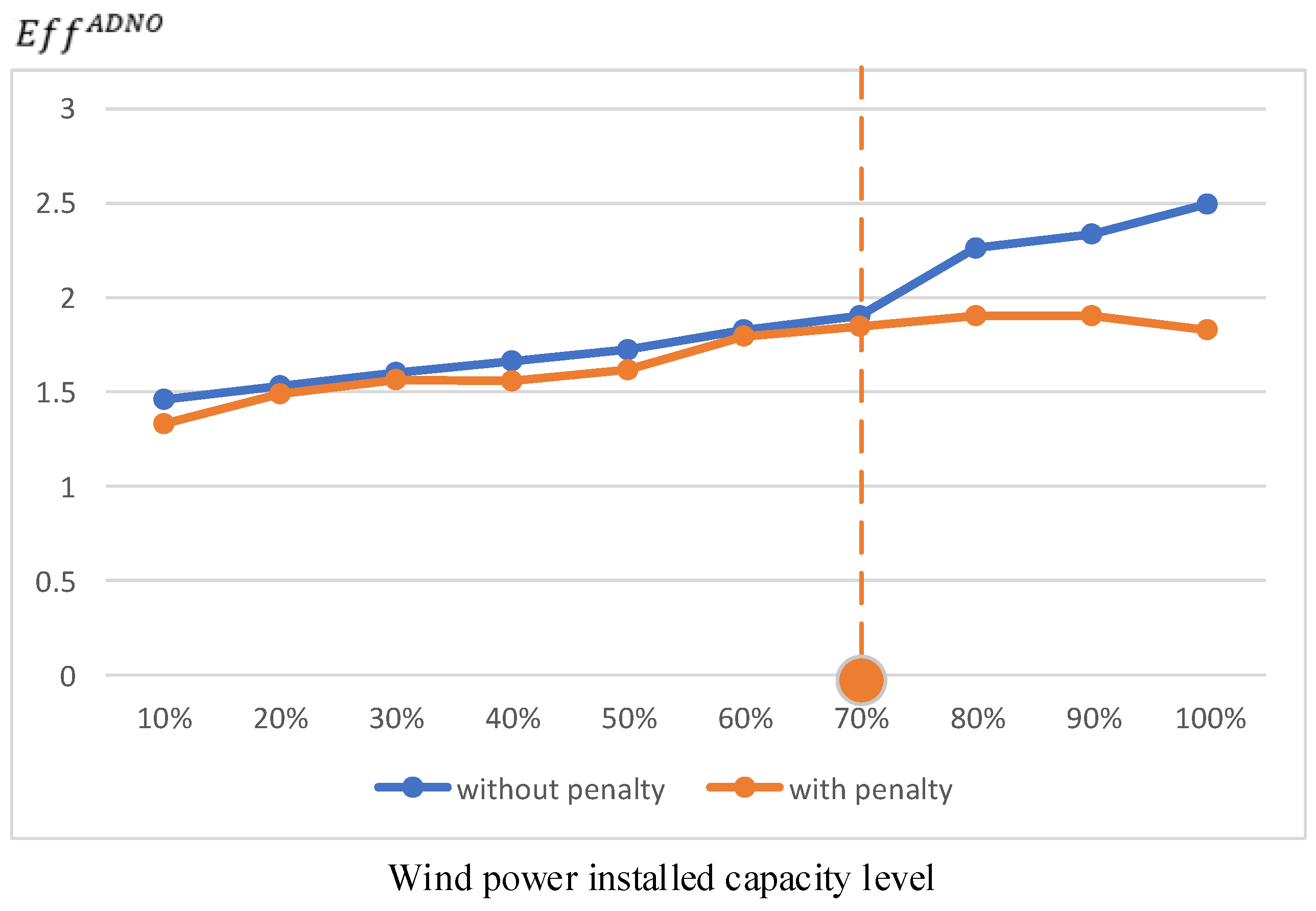
5.4. Sensitivity to Long-Term Factors
6. Conclusions
- The proposed conditional prediction method is effective. By analyzing the spot electricity price and wind power output data under high wind power penetration rate, this paper indicates the significant correlation between the two with zero time lag; therefore, this paper proposes a method based on ISO wind power prediction, which predicts the local wind power output and spot wholesale electricity price conditions. The method combines conditional prediction, transformer deep neural network, and a source embedding method, and improves the prediction accuracy compared with traditional prediction methods. The improvement in prediction accuracy helps to reduce the penalty cost in ADNO operation and improve operational efficiency.
- A subsidy strategy may further improve the profitability of an ADNO. This paper proposes a subsidy strategy that considers the impact of ADNO on user demand. Under this subsidy strategy, a Stackelberg game is formed between the ADNO and users. This paper proposes a game model and its solution method that considers the spot electricity price of the main grid, local wind power output, local gas power generation, local energy storage, and network constraints simultaneously. Through simulation calculations, it is found that the comprehensive predictive method and bi-level optimization method proposed in this paper can indeed further improve the operational efficiency of ADNO compared with traditional methods.
- The proposed model is robust to external long-term factors. This paper compares the impact of long-term factors under the methods proposed in this paper. It is found that the methods proposed in this paper can provide a “guarantee boundary” for the fluctuation of factors such as the spot price of the main grid and the elasticity of user subsidies. When the fluctuation of factors exceeds this “guarantee boundary”, the profitability of ADNO can be guaranteed.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclatures
| Charging and discharging power of energy storage system s at time t | |
| Maximum charging/discharging power of s | |
| Binary value indicate charging or discharging | |
| Total stored electricity of s at time t | |
| Time interval | |
| Active power output of i at time t | |
| Total production cost of i | |
| start-up cost of i | |
| Minimum and Maximum output of unit i | |
| Minimum and Maximum climbing amount of unit i between units | |
| Retail electricity price of customer j at time t | |
| Total active power demand of customer j at time t | |
| Rigid and flexible demand of customer j at time t | |
| Set of demand responses to subsidies | |
| ADNO’s subsidy strategy at time t | |
| Elasticity coefficient of the power demand subsidy for j at time t. | |
| Active and reactive power injected into node n | |
| Active and reactive power flowing from node m to node n | |
| Amplitude of the current flowing from node m to node n | |
| Voltage amplitude of node n | |
| The variable set determined by constraints | |
| Spot price at time t; | |
| ADNO’s profitability indicator | |
| K | Total number of experiments conducted |
| ADNO’s daily generation cost | |
| ADNO’s contract penalty cost caused by forecasting and scheduling deviations | |
| ADNO’s contract penalty cost caused by forecasting and scheduling deviations | |
| Power purchase amount from the wholesale market by ADNO at time t |
Appendix A
References
- Zhao, J.; Wang, C.; Zhao, B.; Lin, F.; Zhou, Q.; Wang, Y. A Review of Active Management for Distribution Networks: Current Status and Future Development Trends. Electr. Mach. Power Syst. 2014, 42, 280–293. [Google Scholar] [CrossRef]
- Xiang, Y.; Han, W.; Zhang, J.; Liu, J.; Liu, Y. Optimal Sizing of Energy Storage System in Active Distribution Networks Using Fourier-Legendre Series based State of Energy Function. IEEE Trans. Power Syst. 2017, 33, 2313–2315. [Google Scholar] [CrossRef]
- Ge, S.; Wang, S.; Lu, Z.; Liu, H. Substation planning method in an active distribution network under low-carbon economy. J. Mod. Power Syst. Clean Energy 2015, 3, 468–474. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.; Wang, H.; Ai, Q.; Zhang, Y. Interactive optimization between active distribution network with multi-microgrids based on distributed algorithm. Energy Rep. 2020, 6, 385–391. [Google Scholar] [CrossRef]
- Xiao, J.; Qibo, H.E.; Guoqiang, Z.U. Distribution management system framework based on security region for future low carbon distribution systems. J. Mod. Power Syst. Clean Energy 2015, 3, 12. [Google Scholar] [CrossRef] [Green Version]
- Usman, M.; Coppo, M.; Bignucolo, F.; Turri, R. Losses management strategies in active distribution networks: A review. Electr. Power Syst. Res. 2018, 163, 116–132. [Google Scholar] [CrossRef]
- Gabash, A.; Li, P. Active-Reactive Optimal Power Flow in Distribution Networks with Embedded Generation and Battery Storage. IEEE Trans. Power Syst. 2012, 27, 2026–2035. [Google Scholar] [CrossRef]
- Cortes, C.A.; Contreras, S.F.; Shahidehpour, M. Microgrid Topology Planning for Enhancing the Reliability of Active Distribution Networks. IEEE Trans. Smart Grid 2017, 9, 6369–6377. [Google Scholar] [CrossRef]
- Kyriakou, D.G.; Kanellos, F.D. Optimal Operation of Microgrids Comprising Large Building Prosumers and Plug-in Electric Vehicles Integrated into Active Distribution Networks. Energies 2022, 15, 6182. [Google Scholar] [CrossRef]
- Sedghi, M.; Ahmadian, A.; Pashajavid, E.; Aliakbar-Golkar, M. Storage scheduling for optimal energy management in active distribution network considering load, wind, and plug-in electric vehicles uncertainties. J. Renew. Sustain. Energy 2015, 7, 033120. [Google Scholar] [CrossRef]
- Jiang, T.; Li, Z.; Jin, X.; Chen, H.; Li, X.; Mu, Y. Flexible operation of active distribution network using integrated smart buildings with heating, ventilation and air-conditioning systems. Appl. Energy 2018, 226, 181–196. [Google Scholar] [CrossRef]
- Chen, F.; Dong, L.; Xiong, X. Research on Stochastic Optimal Operation Strategy of Active Distribution Network Considering Intermittent Energy. Energies 2017, 10, 522. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Zheng, X.; Tai, N.; Wei, W.; Li, L. Resilience-Oriented Optimal Operation Strategy of Active Distribution Network. Energies 2019, 12, 3380. [Google Scholar] [CrossRef] [Green Version]
- Tostado-Véliz, M.; Hasanien, H.M.; Jordehi, A.R.; Turky, R.A.; Gómez-González, M.; Jurado, F. An Interval-based privacy–Aware optimization framework for electricity price setting in isolated microgrid clusters. Appl. Energy 2023, 340, 121041. [Google Scholar] [CrossRef]
- Fan, S.; He, G.; Zhou, X.; Cui, M. Online optimization for networked distributed energy resources with time-coupling constraints. IEEE Trans. Smart Grid 2020, 12, 251–267. [Google Scholar] [CrossRef]
- Saint-Pierre, T.; Mancarella, P. Scheduling model for active distribution system management with renewable energy sources. IETGener. Transm. Distrib. 2017, 11, 1571–1579. [Google Scholar]
- Shen, X.; Shahidehpour, M.; Han, Y.; Zhu, S.; Zheng, J. Expansion planning of active distribution networks with centralized and distributed energy storage systems. IEEE Trans. Sustain. Energy 2016, 8, 126–134. [Google Scholar] [CrossRef]
- Yu, Q.; Li, Z. Correlated load forecasting in active distribution networks using Spatial-Temporal Synchronous Graph Convolutional Networks. IET Energy Syst. Integr. 2021, 3, 355–366. [Google Scholar] [CrossRef]
- Kalantar-Neyestanaki, M.; Sossan, F.; Bozorg, M.; Cherkaoui, R. Characterizing the reserve provision capability area of active distribution networks: A linear robust optimization method. IEEE Trans. Smart Grid 2019, 11, 2464–2475. [Google Scholar] [CrossRef]
- Cheng, G.; Song, S.; Lin, Y.; Huang, Q.; Lin, X.; Wang, F. Enhanced state estimation and bad data identification in active power distribution networks using photovoltaic power forecasting. Electr. Power Syst. Res. 2019, 177, 105974. [Google Scholar] [CrossRef]
- Cong, P.; Tang, W.; Zhang, L.; Zhang, B.; Cai, Y. Day-ahead active power scheduling in active distribution network considering renewable energy generation forecast errors. Energies 2017, 10, 1291. [Google Scholar] [CrossRef] [Green Version]
- Gao, H.; Liu, J.; Wang, L. Robust coordinated optimization of active and reactive power in active distribution systems. IEEE Trans. Smart Grid 2017, 9, 4436–4447. [Google Scholar] [CrossRef]
- Saint-Pierre, A.; Mancarella, P. Active Distribution System Management: A Dual-Horizon Scheduling Framework for DSO/TSO Interface Under Uncertainty. IEEE Trans. Smart Grid 2017, 8, 2186–2197. [Google Scholar] [CrossRef]
- ENTSO-E Transparency Platform. Available online: https://www.entsoe.eu/data/ (accessed on 23 April 2023).
- Hassan, M.A.; Bailek, N.; Bouchouicha, K.; Nwokolo, S.C. Ultra-short-term exogenous forecasting of photovoltaic power production using genetically optimized non-linear auto-regressive recurrent neural networks. Renew. Energy 2021, 171, 191–209. [Google Scholar] [CrossRef]
- Li, G.; Wang, H.; Zhang, S.; Xin, J.; Liu, H. Recurrent neural networks based photovoltaic power forecasting approach. Energies 2019, 12, 2538. [Google Scholar] [CrossRef] [Green Version]
- Alipour, M.; Aghaei, J.; Norouzi, M.; Niknam, T.; Hashemi, S.; Lehtonen, M. A novel electrical net-load forecasting model based on deep neural networks and wavelet transform integration. Energy 2020, 205, 118106. [Google Scholar] [CrossRef]
- Wang, H.; Lei, Z.; Zhang, X.; Zhou, B.; Peng, J. A review of deep learning for renewable energy forecasting. Energy Convers. Manag. 2019, 198, 111799. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30, I. [Google Scholar]
- Wan, L.; Wang, Q.; Papir, A.; Moreno, I.L. Generalized end-to-end loss for speaker verification. In Proceedings of the 2018 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), IEEE, Calgary, AB, Canada, 15–20 April 2018; pp. 4879–4883. [Google Scholar]
- Ruhang, X. Efficient clustering for aggregate loads: An unsupervised pretraining based method. Energy 2020, 210, 118617. [Google Scholar] [CrossRef]
- Wang, Y.; Skerry-Ryan, R.J.; Stanton, D.; Wu, Y.; Weiss, R.J.; Jaitly, N.; Yang, Z.; Xiao, Y.; Chen, Z.; Bengio, S.; et al. Tacotron: Towards end-to-end speech synthesis. arXiv 2017, arXiv:1703.10135, 2017. [Google Scholar]
- Ugurlu, U.; Oksuz, I.; Tas, O. Electricity price forecasting using recurrent neural networks. Energies 2018, 11, 1255. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Zou, R.; Liu, F.; Zhang, L.; Liu, Q. A review of wind speed and wind power forecasting with deep neural networks. Appl. Energy 2021, 304, 117766. [Google Scholar] [CrossRef]
- Zhao, Q.; Shen, Y.; Li, M. Control and bidding strategy for virtual power plants with renewable generation and inelastic demand in electricity markets. IEEE Trans. Sustain. Energy 2015, 7, 562–575. [Google Scholar] [CrossRef]
- Antoniadou-Plytaria, K.E.; Kouveliotis-Lysikatos, I.N.; Georgilakis, P.S.; Hatziargyriou, N.D. Distributed and Decentralized Voltage Control of Smart Distribution Networks: Models, Methods, and Future Research. IEEE Trans. Smart Grid 2017, 8, 2999–3008. [Google Scholar] [CrossRef]
- Li, Y.; Xiao, J.; Chen, C.; Tan, Y.; Cao, Y. Service restoration model with mixed-integer second-order cone programming for distribution network with distributed generations. IEEE Trans. Smart Grid 2018, 10, 4138–4150. [Google Scholar] [CrossRef]
- Baran, M.E.; Wu, F.F. Network reconfiguration in distribution systems for loss reduction and load balancing. IEEE Trans. Power Deliv. 1989, 4, 1401–1407. [Google Scholar] [CrossRef]
- Hu, W.; Guo, Y.; Jing, J.; Chen, L. Dynamic Hosting Capacity Evaluation of DGs in Active Distribution Network. In Proceedings of the 2020 12th IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC), IEEE, Nanjing, China, 20–23 September 2020; pp. 1–6. [Google Scholar]
- Zhang, W.; Liu, K.; Sheng, W.; Du, S.; Jia, D. Critical node identification in active distribution network using resilience and risk theory. IET Gener. Transm. Distrib. 2020, 14, 2771–2778. [Google Scholar] [CrossRef]
- Feroldi, D.; Rullo, P. Day-ahead optimal operation of active distribution networks with distributed generation and energy storage. Int. J. Emerg. Electr. Power Syst. 2022. [Google Scholar] [CrossRef]
- Dolatabadi, S.H.; Ghorbanian, M.; Siano, P.; Hatziargyriou, N.D. An enhanced IEEE 33 bus benchmark test system for distribution system studies. IEEE Trans. Power Syst. 2020, 36, 2565–2572. [Google Scholar] [CrossRef]
- Abdelouadoud, S.Y.; Girard, R.; Neirac, F.P.; Guiot, T. Optimal power flow of a distribution system based on increasingly tight cutting planes added to a second order cone relaxation. Int. J. Electr. Power Energy Syst. 2015, 69, 9–17. [Google Scholar] [CrossRef]



| Parameter Name | Parameter Size |
|---|---|
| Forecasting network batch size | 64 |
| Transformer encoder block number | 2 |
| Transformer decoder block number | 2 |
| Transformer attention head number | 8 |
| Input time series length | 72 |
| Input feature | Short-time Fourier transform (STFT) |
| Output time series length | 24 |
| CBHG | Same as in [32] |
| Source embedding training batch size | 64 |
| optimizer | Adam [32] |
| Learning rate | 0.001 |
| Model | Task1 | Task2 | ||
|---|---|---|---|---|
| RMSE 1 | MAE 2 | RMSE | MAE | |
| LSTM [33] | 1.003 | 0.836 | 0.909 | 0.840 |
| CNN [33] | 0.752 | 0.753 | 0.756 | 0.674 |
| Seq2seq [34] | 0.630 | 0.616 | 0.535 | 0.513 |
| proposed | 0.540 | 0.553 | 0.469 | 0.453 |
| Parameter | Value |
|---|---|
| Encoder input dimension | 72 |
| Decoder input dimension | 24 |
| Decoder output dimension | 24 |
| Multi-head attention head number | 4 |
| Number of encoder blocks | 2 |
| Source embedding dimension | 128 |
| Encoder output dimension | 128 |
| Number of Decoder blocks | 2 |
| Number of training batch | 48 |
| Active function | Tanh |
| Number of training epoch | 200 |
| Training optimizer | Adam |
| Initial learning rate | 5 × 10−5 |
| Parameter | Value |
|---|---|
| Network type | IEEE33 |
| Total wind turbine capacity | 0.5 MW |
| Total energy storage capacity | 0.15 MWh |
| Total gas turbine capacity | 0.6 MW |
| Average variable cost of distributed gas power generation | 91 USD/MWh |
| Average start-up cost of distributed gas power generation | USD 20 |
| Average demand Subsidy | USD 10 |
| Average spot price | USD 81/MWh |
| Comparison Factor | Test Task | RMSE 1 |
|---|---|---|
| Without source embedding | task1 | 0.621 |
| Without conditioning | task1 | 0.594 |
| Without source embedding | task2 | 0.525 |
| Without conditioning | task2 | 0.553 |
| Model Comparison * | Value |
|---|---|
| With LSTM [33] forecast model | 2.209 |
| With CNN [33] forecast model | 2.304 |
| With Seq2seq [34] forecast model | 2.258 |
| With proposed forecast model | 2.496 |
| With single-level (no-subsidy) optimization [43] | 2.433 |
| With proposed bi-level optimization | 2.496 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, Y.; Lv, F.; Gao, X.; Jiang, M.; Luo, H.; Xu, R. A Bi-Level Optimal Operation Model for Small-Scale Active Distribution Networks Considering the Coupling Fluctuation of Spot Electricity Prices and Renewable Energy Sources. Energies 2023, 16, 4507. https://doi.org/10.3390/en16114507
Shi Y, Lv F, Gao X, Jiang M, Luo H, Xu R. A Bi-Level Optimal Operation Model for Small-Scale Active Distribution Networks Considering the Coupling Fluctuation of Spot Electricity Prices and Renewable Energy Sources. Energies. 2023; 16(11):4507. https://doi.org/10.3390/en16114507
Chicago/Turabian StyleShi, Yu, Fei Lv, Xuefeng Gao, Minglei Jiang, Huan Luo, and Ruhang Xu. 2023. "A Bi-Level Optimal Operation Model for Small-Scale Active Distribution Networks Considering the Coupling Fluctuation of Spot Electricity Prices and Renewable Energy Sources" Energies 16, no. 11: 4507. https://doi.org/10.3390/en16114507
APA StyleShi, Y., Lv, F., Gao, X., Jiang, M., Luo, H., & Xu, R. (2023). A Bi-Level Optimal Operation Model for Small-Scale Active Distribution Networks Considering the Coupling Fluctuation of Spot Electricity Prices and Renewable Energy Sources. Energies, 16(11), 4507. https://doi.org/10.3390/en16114507






