Comparison of the Performance of New and Traditional Numerical Methods for Long-Term Simulations of Heat Transfer in Walls with Thermal Bridges
Abstract
:1. Introduction
2. The Studied Cases
2.1. The Equation and Its Discretization
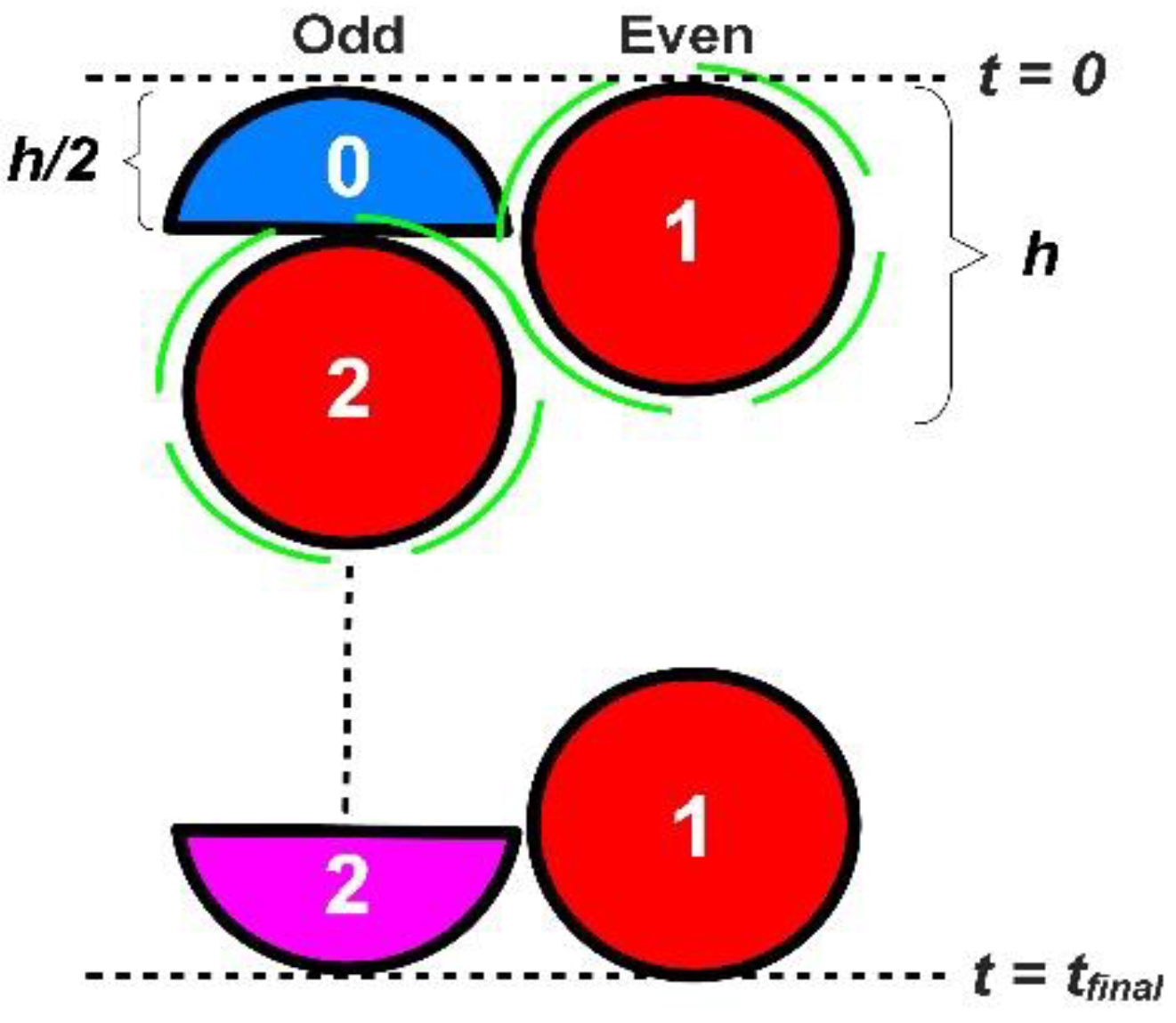
2.2. The Leapfrog–Hopscotch Structure
2.3. The Mathematical Equations We Use
- 1.
- Pseudo-implicit treatment: for the radiation term, which yields:
- 2.
- “Inside” treatment: for the radiation term, which means that it is taken into account explicitly, which yields
- 3.
- Mixed treatment with an equal share of the previous two treatments, that is, for the radiation term, which yields
2.4. Other Explicit and Stable Methods
- 4.
- DF-D: the only place the Sigma and K terms appear is in the denominator:
- 5.
- DF-M: the Sigma and K terms in a mixed way:
- 6.
- DF-KD: the K term appears only in the denominator, and the Sigma term in a mixed way:
- 7.
- DF-SD: the Sigma term appears only in the denominator, and the K term in a mixed way:
- 8.
- Over half a century has passed since the discovery of the original odd–even hopscotch (OOEH) algorithm [47]. Its temporal and spatial organization has been described in [45]. After the first step by the FTCS formula (which is based on explicit Euler time discretization, so ) for the odd cells, the BTCS formula (which is based on implicit Euler time discretization) is used for the even cells. The labels odd and even are interchanged after each time step. We modify this method here to include the convection component, which is always considered at the new time level for enhanced stability. The radiation term is handled first explicitly and then implicitly [29]. These are the equations that are being used:
- 9.
- NS-OOEH algorithm:
2.5. Professional Solvers Used for Comparison Purposes
- (1)
- The direct solver gives the exact solution to the system of equations defining the FE model. For the system represented by the equation , the exact solution is , where is the inverse of the matrix . The high computational cost of finding the inverse of a matrix means that direct solvers do not usually calculate the inverse, but use LU decomposition to solve the equation;
- (2)
- To provide an approximate solution within a certain convergence tolerance, iterative solvers assume an initial solution and iterate until they converge. Therefore, if the convergence tolerance is 0.01%, the solver will repeat until the difference between the current and past estimates of the solution is less than 0.01%.
- (3)
- The programmable solver is controlled by a program and employes a mixture of direct and iterative solvers.
3. Numerical Simulation
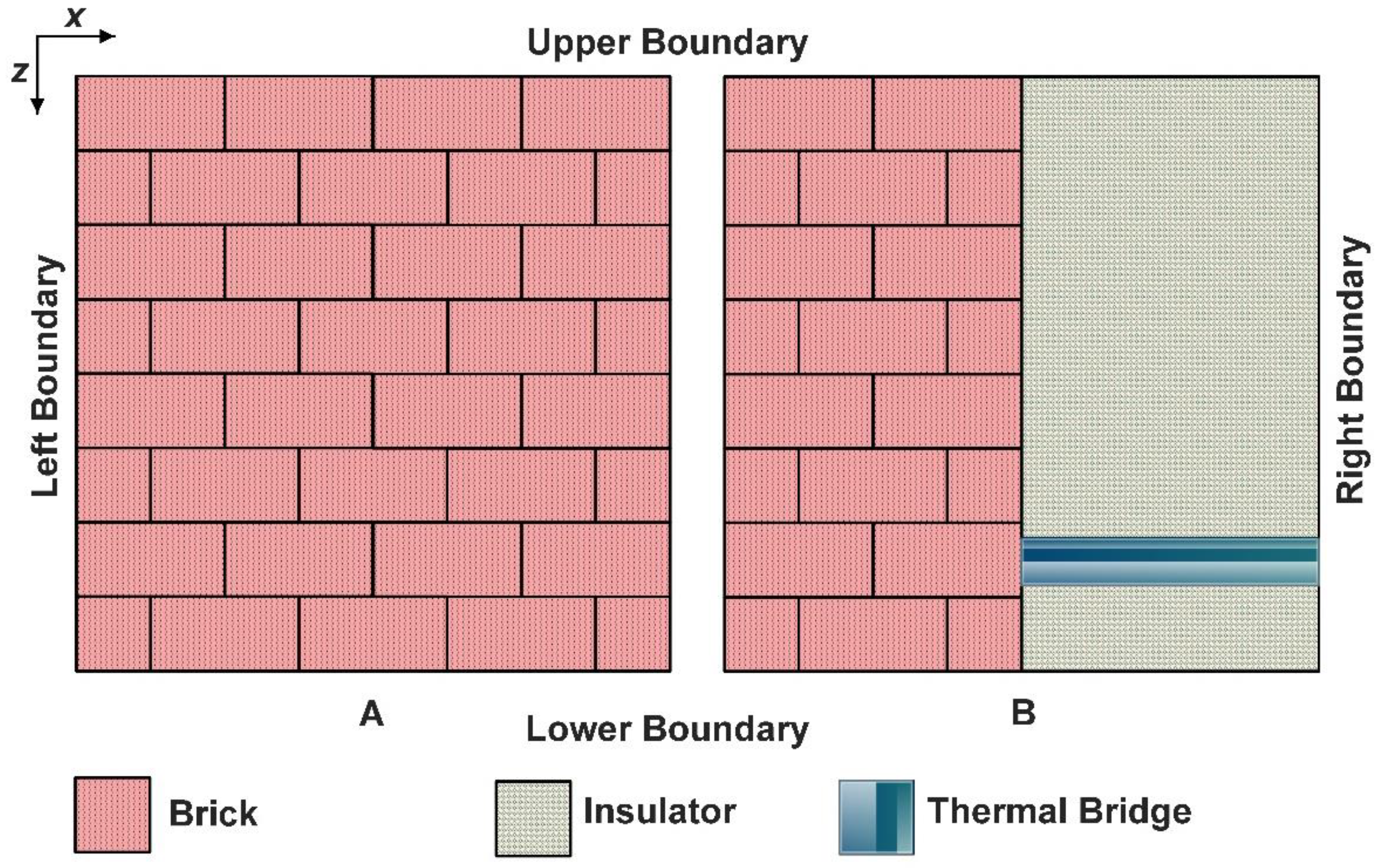
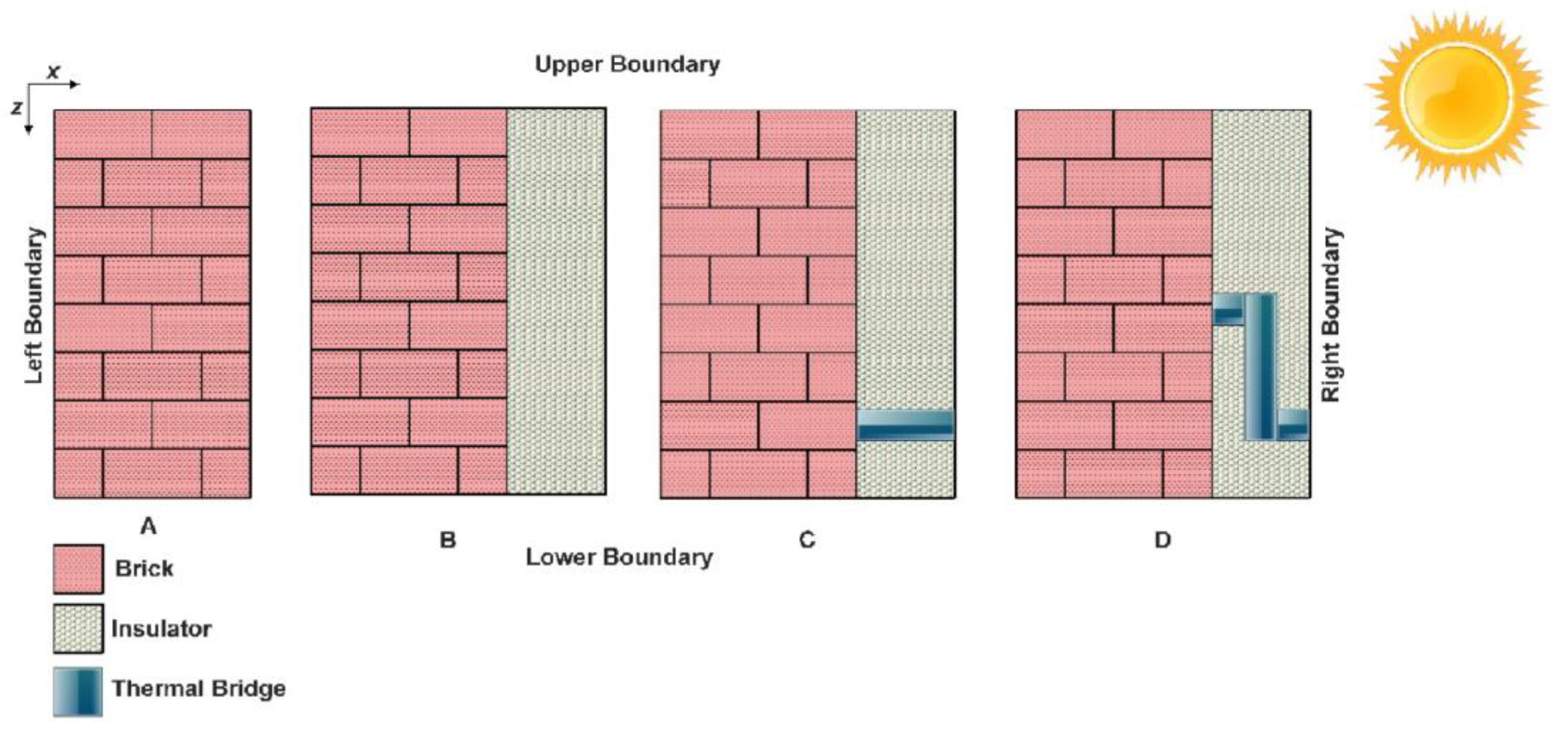
3.1. Geometry and Material Properties
- (a)
- One-layer of brick is examined only for verification case;
- (b)
- Two-layers consisting of brick and rigid polyurethane foam insulation with a straight thermal bridge steel beam for running time measurements.
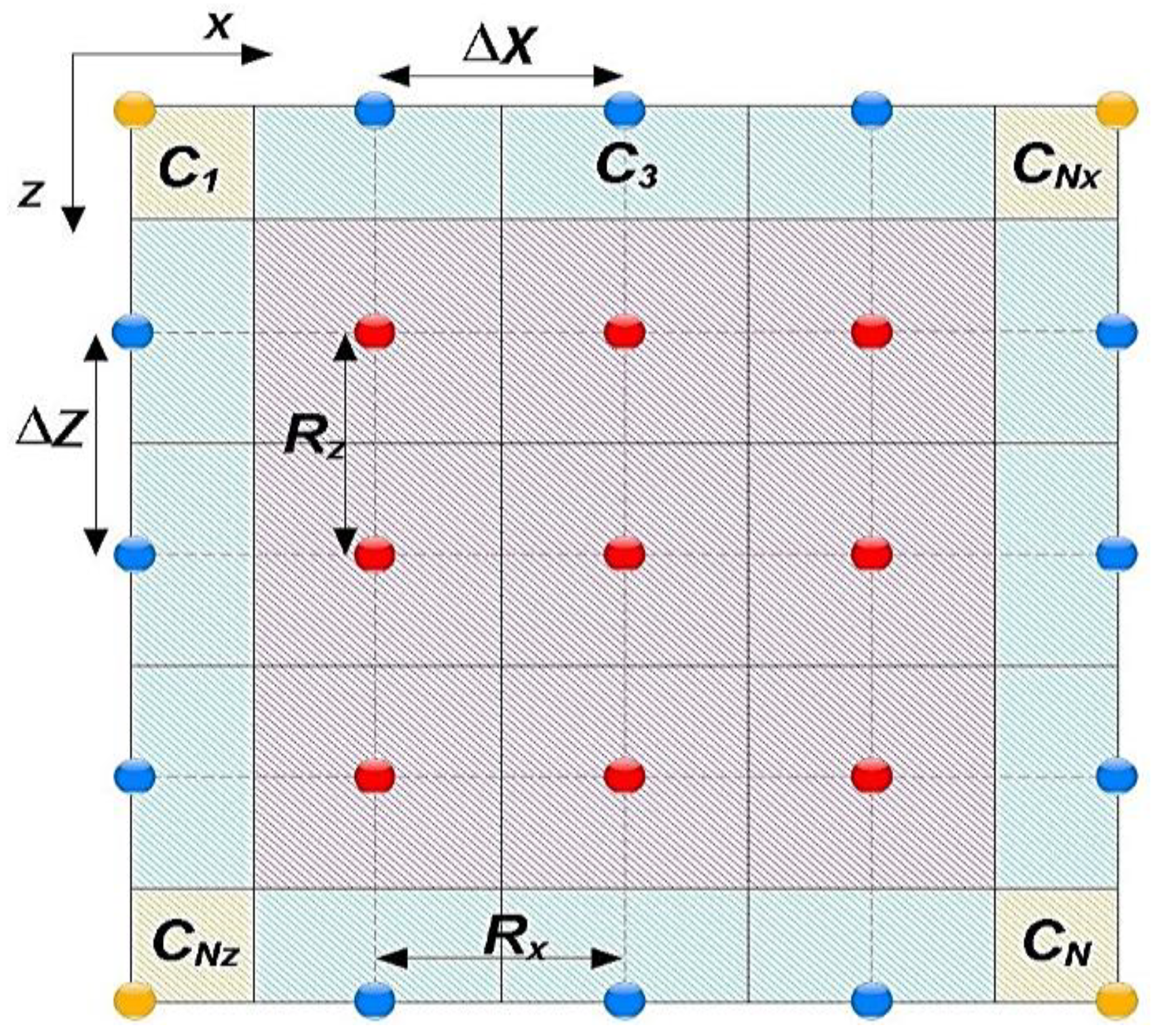
3.2. Mesh Construction
3.3. The Initial and the Boundary Conditions
3.4. Verification Using Analytical Solutions
- First verification (for conduction):
- 1.
- Two sine functions are multiplied to provide the initial condition:
- 2.
- Zero Dirichlet boundary conditions are used:
- 3.
- One can quickly verify that the problem’s analytical solution is
- Second verification (for convection and heat generation)
- Third verification (for radiation)
4. Results: Comparison of Performances by Measuring the Running Times
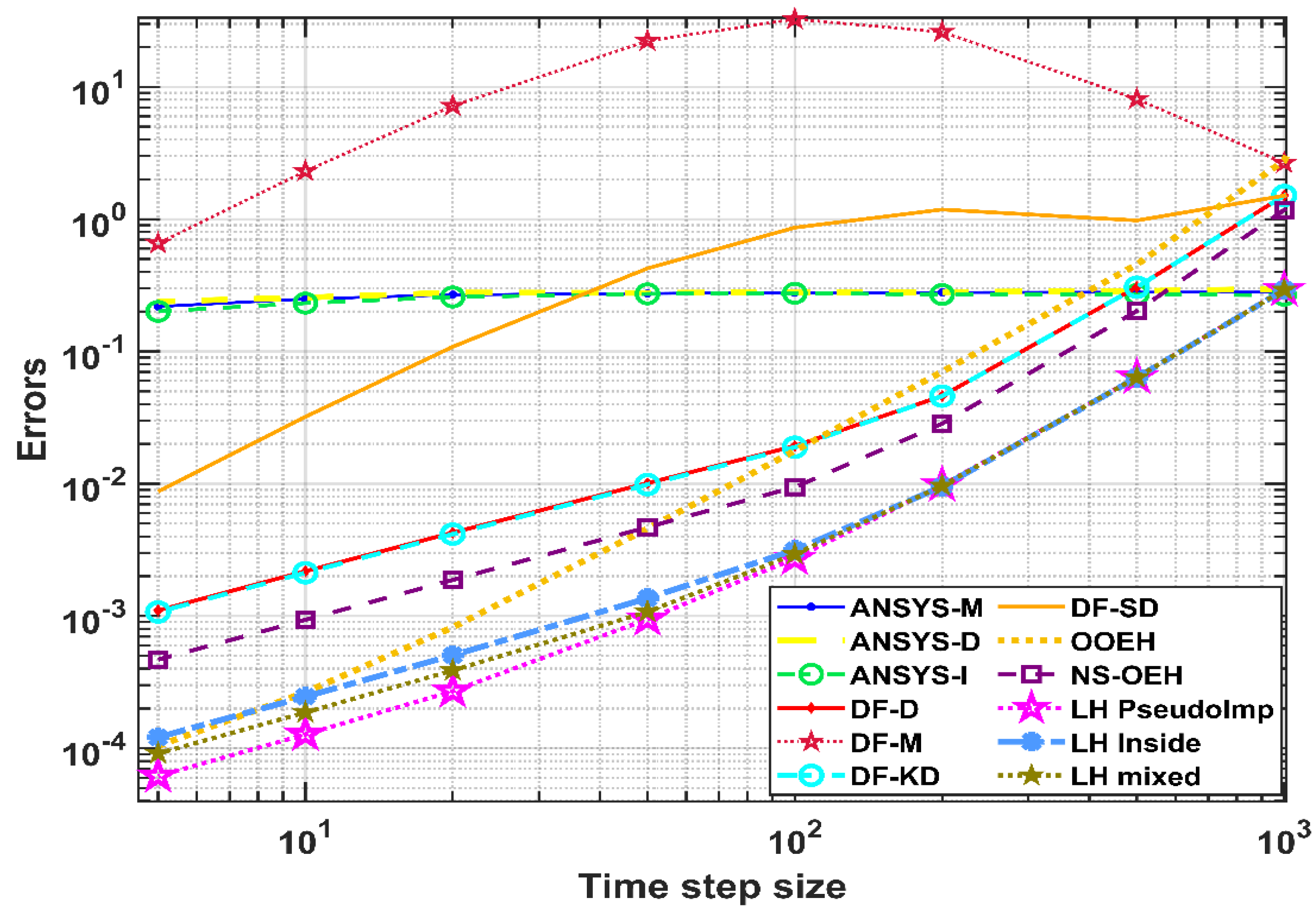
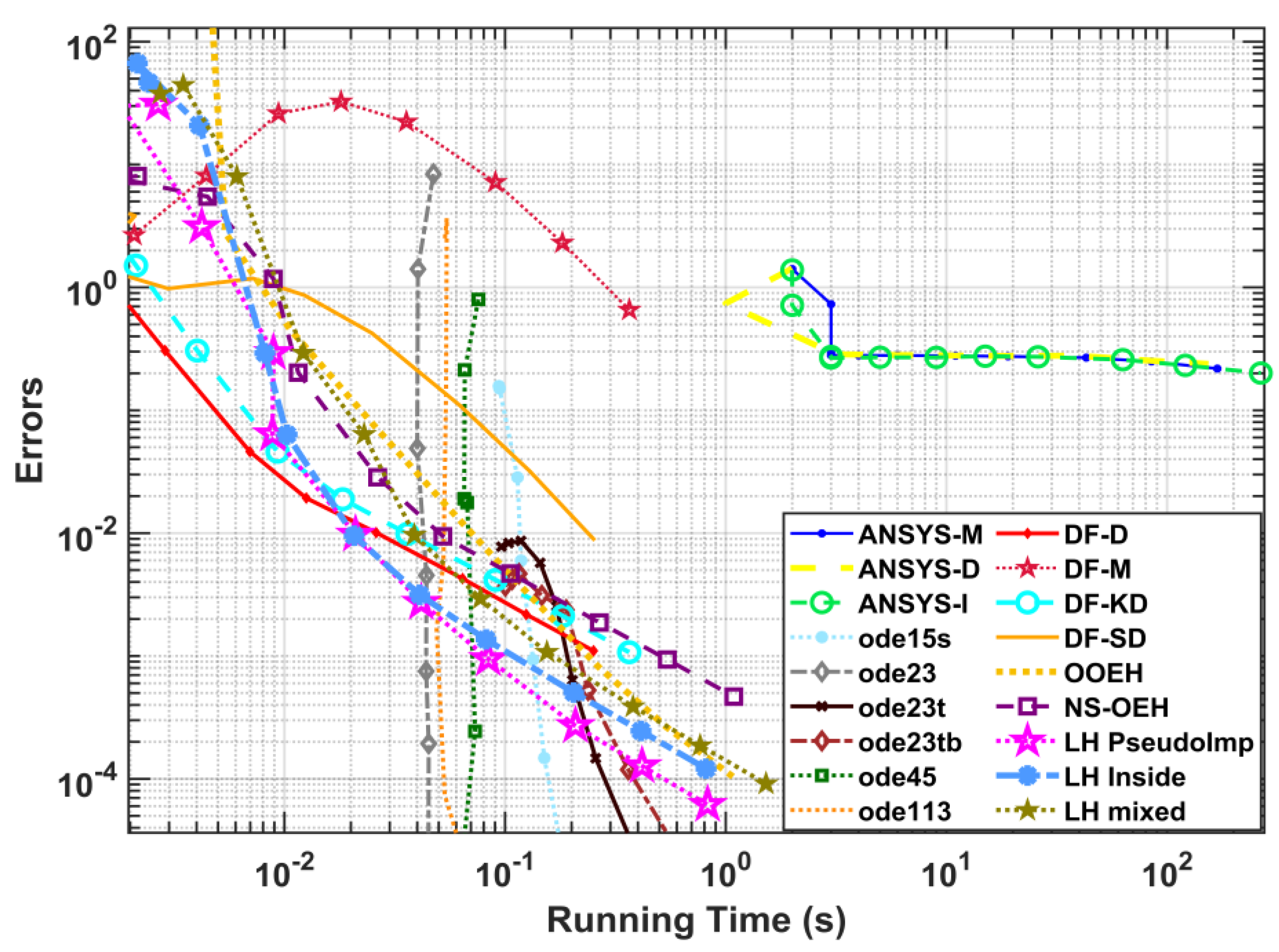
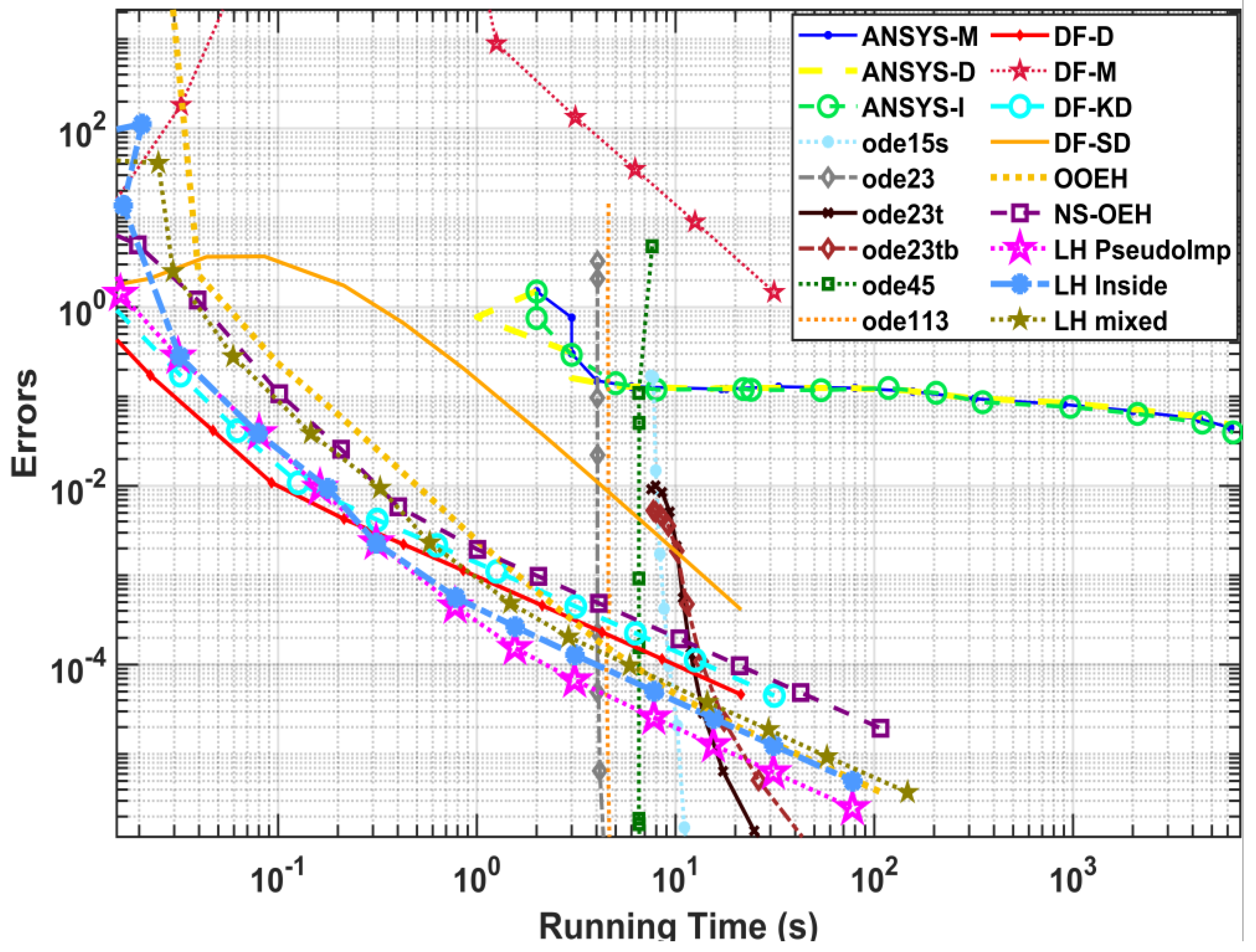
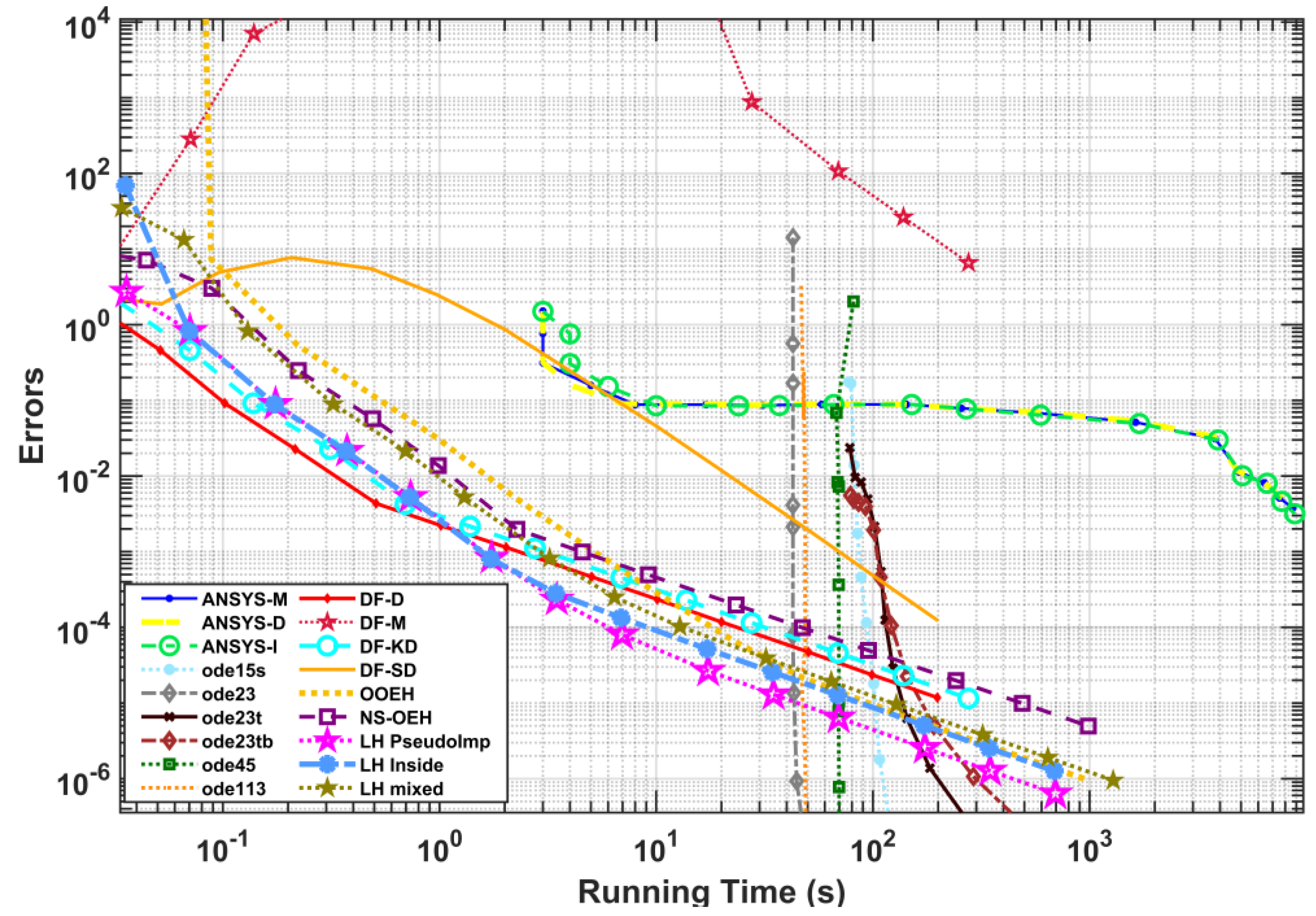
4.1. Comparison with MATLAB Methods and ANSYS Solvers for the Coarse Mesh System
4.2. Comparison with MATLAB Methods and ANSYS Solvers for the Moderate Mesh System
4.3. Comparison with MATLAB Methods and ANSYS Solvers for the Fine Mesh System
5. Long-Term Simulations
5.1. Geometry and Mesh
5.2. Initial and Boundary Conditions
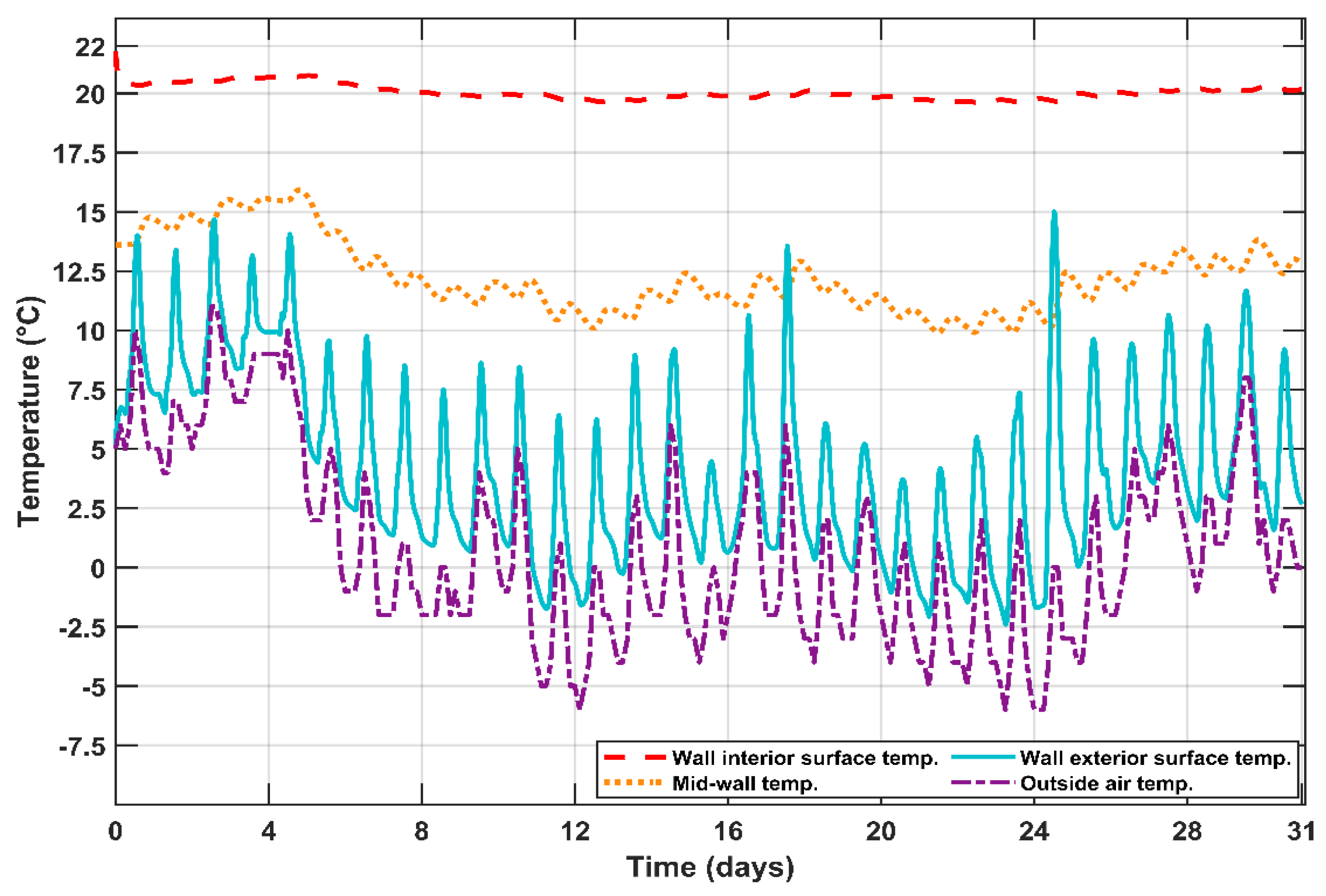
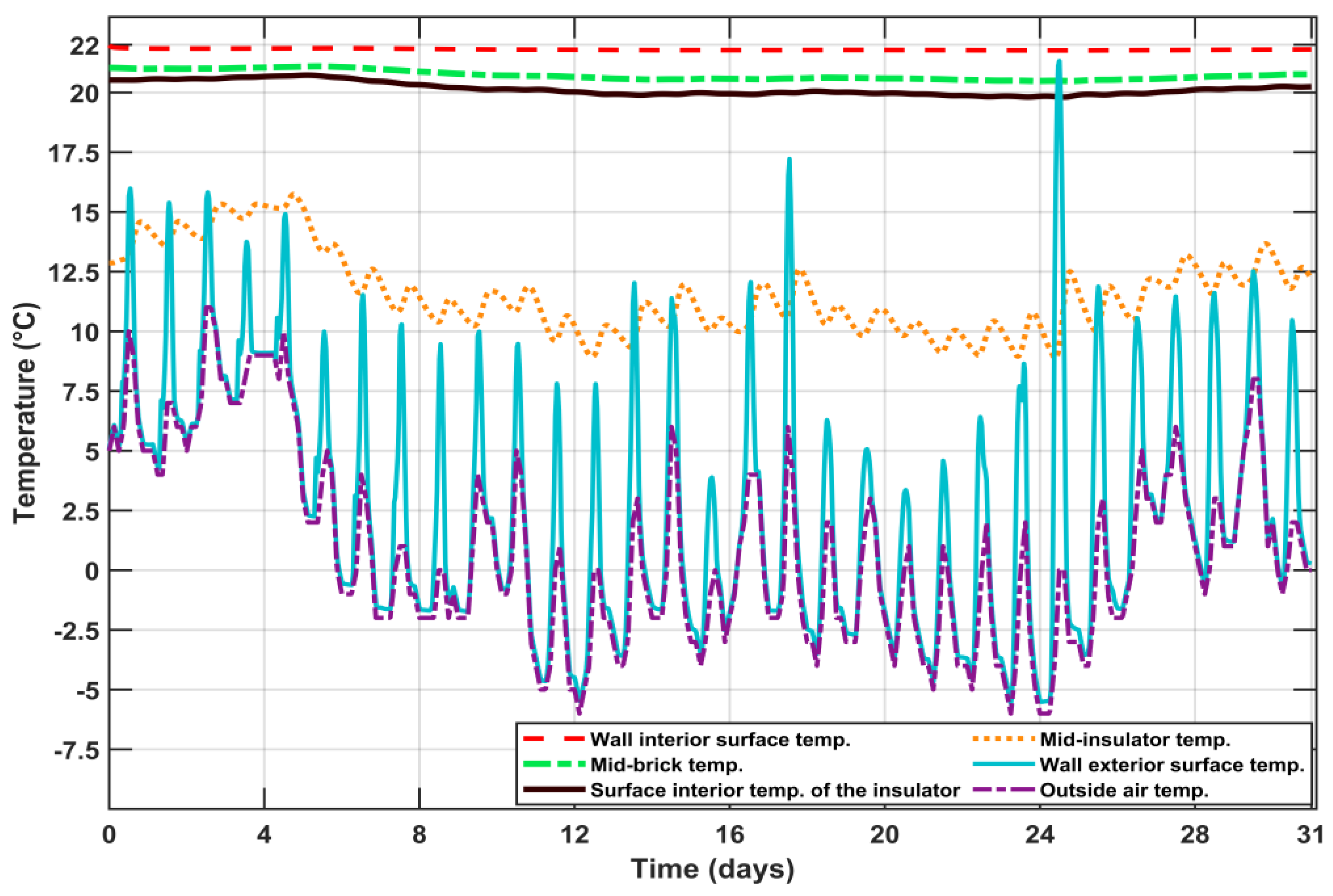
5.3. Result for the Simulation of the Wall
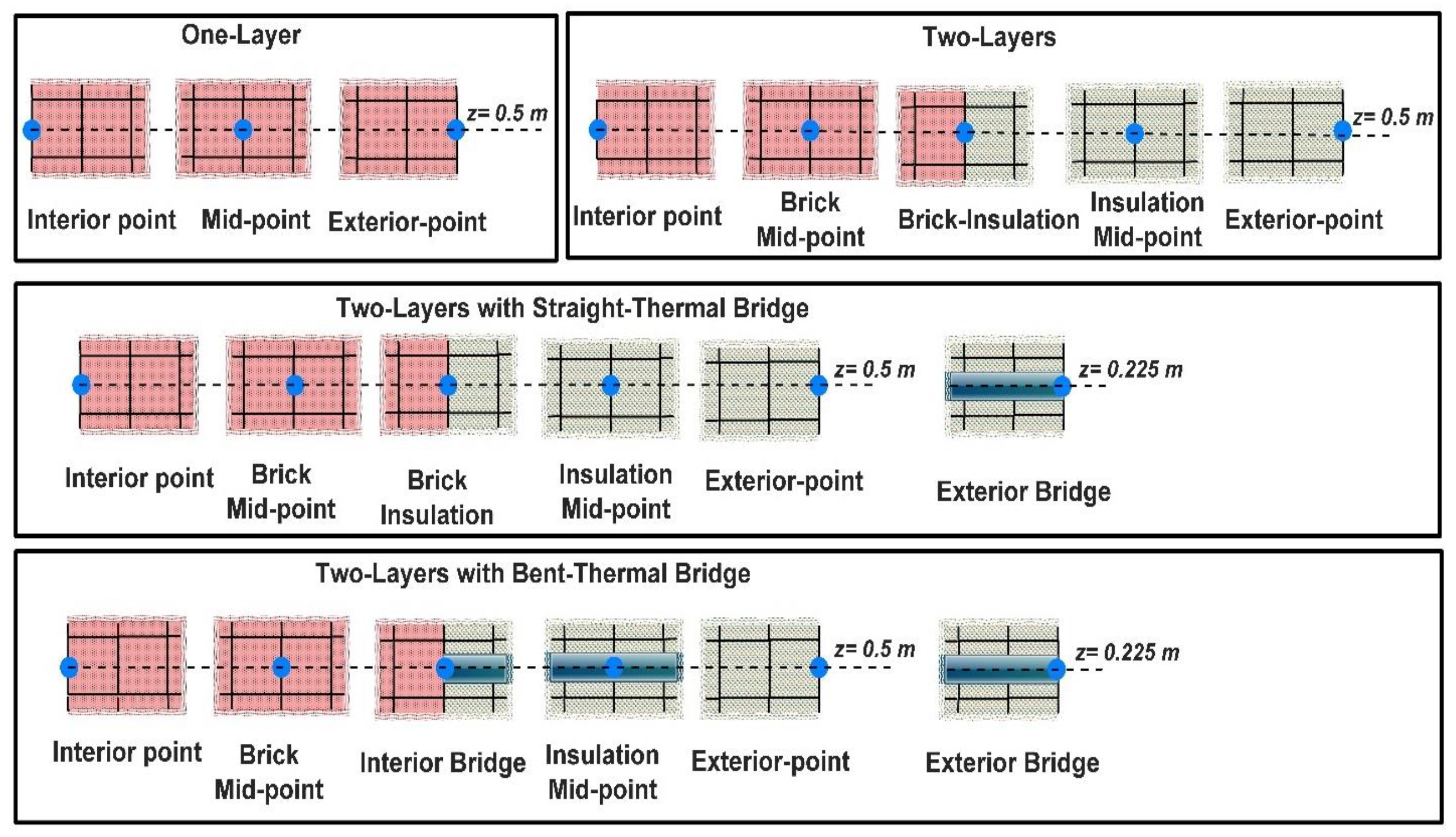
- (A)
- There are 3 points denoted for the one-layer wall: on the interior surface, at the middle of the wall, and on the exterior surface;
- (B)
- Two-layer wall (brick + insulator) with five points on the interior surface, the middle of the brick, the border of the two layers, the middle of the insulation, and the exterior surface;
- (C)
- Two-layers with a straight thermal bridge with 6 points: on the interior surface, the middle of the brick, the border of the two layers, the exterior surface of the straight thermal bridge, the middle of the insulation, and the exterior surface of the insulation;
- (D)
- Two-layers with the bent thermal bridge with six points: on the interior surface, middle of the brick, the border of the two layers with bent thermal bridge, the exterior surface of the bent thermal bridge, the middle of the insulation, and the exterior surface of the insulation.
5.3.1. One Layer (Brick)
5.3.2. Two Layers (Brick and Insulation) without Thermal Bridge
5.3.3. Two Layers with Straight Thermal Bridging
5.3.4. Two Layers with Bent Thermal Bridging
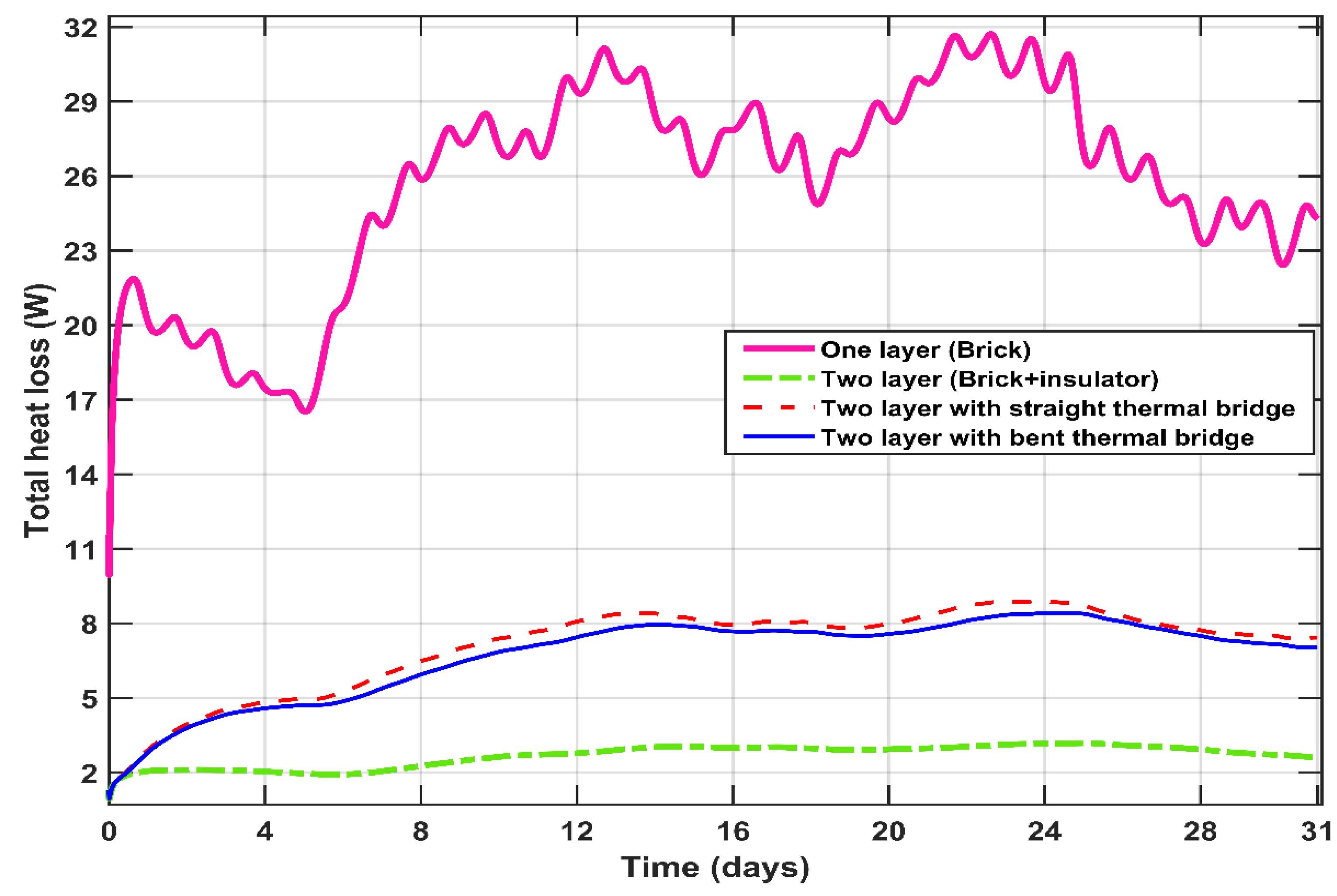
5.3.5. Calculation of Heat Loss
5.4. Simulation of the Coldest Day of the Month
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Symbols | Greek Symbols | ||
| c | Specific heat [J/(kgK)] | α | Thermal diffusivity [m2/s] |
| Time step size [s] | Δ | Difference | |
| hc | Heat transfer coefficient [W/(m2K)] | Ρ | Mass density [kg/m3] |
| K | Convection coefficient [1/s] | Σ | Coefficient of the radiation term [s−1K−3] |
| k | Thermal conductivity [W/(m·K)] | realistic values of the non-black body [W/(m2·K4)] | |
| Q | Heat transfer rate [W] | Subscripts | |
| heat generation [W/m2] | A | Ambient air | |
| q | Heat source rate [K/s] | L | Left side |
| t | time [s] | R | Right side |
| u | Temperature [K] | b, ins | Brick and Insulation |
| L | Thickness [m] | c | convection |
References
- Berggren, B.; Wall, M. State of Knowledge of Thermal Bridges—A Follow up in Sweden and a Review of Recent Research. Buildings 2018, 8, 154. [Google Scholar] [CrossRef] [Green Version]
- Liu, C.; Sharples, S. A Review of Building Energy Retrofit Measures, Passive Design Strategies and Building Regulation for the Low Carbon Development of Existing Dwellings in the Hot Summer—Cold Winter Region of China. Energies 2023, 16, 4115. [Google Scholar] [CrossRef]
- Kusuda, T. Fundamentals of Building Heat Transfer. J. Res. Natl. Bur. Stand. 1977, 82, 97. [Google Scholar] [CrossRef] [PubMed]
- Dai, B.; Qi, H.; Liu, S.; Zhong, Z.; Li, H.; Song, M.; Ma, M.; Sun, Z. Environmental and Economical Analyses of Transcritical CO2 Heat Pump Combined with Direct Dedicated Mechanical Subcooling (DMS) for Space Heating in China. Energy Convers. Manag. 2019, 198, 111317. [Google Scholar] [CrossRef]
- Cao, X.; Dai, X.; Liu, J. Building Energy-Consumption Status Worldwide and the State-of-the-Art Technologies for Zero-Energy Buildings during the Past Decade. Energy Build. 2016, 128, 198–213. [Google Scholar] [CrossRef]
- Li, T.; Xia, J.; Chin, C.S.; Song, P. Investigation of the Thermal Performance of Lightweight Assembled Exterior Wall Panel (LAEWP) with Stud Connections. Buildings 2022, 12, 473. [Google Scholar] [CrossRef]
- Lima, S.A.; Kamrujjaman, M.; Islam, M.S. Numerical Solution of Convection--Diffusion--Reaction Equations by a Finite Element Method with Error Correlation. AIP Adv. 2021, 11, 085225. [Google Scholar] [CrossRef]
- EN ISO 13789:2017; Swedish Standards Institute Thermal Performance of Buildings—Transmission and Ventilation Heat Transfer Coefficients—Calculation Method. International Organization for Standardization: Geneva, Switzerland, 2017. Available online: https://www.iso.org/standard/65713.html (accessed on 20 April 2023).
- EN ISO 10211:2017; Swedish Standards Institute Thermal Bridges in Building Construction—Heat Flows and Surface Temperatures—Detailed Calculations. International Organization for Standardization: Geneva, Switzerland, 2017. Available online: https://www.iso.org/%0Astandard/65710.html (accessed on 20 April 2023).
- EN ISO 14683:2017; Swedish Standards Institute Thermal Bridges in Building Construction—Linear Thermal Transmittance—Simplified Methods and Default Values. International Organization for Standardization: Geneva, Switzerland, 2017. Available online: https://www.iso.org/standard/65706.html (accessed on 20 April 2023).
- Alhawari, A.; Mukhopadhyaya, P. Thermal Bridges in Building Envelopes—An Overview of Impacts and Solutions. Int. Rev. Appl. Sci. Eng. 2018, 9, 31–40. [Google Scholar] [CrossRef]
- Borelli, D.; Cavalletti, P.; Marchitto, A.; Schenone, C. A Comprehensive Study Devoted to Determine Linear Thermal Bridges Transmittance in Existing Buildings. Energy Build. 2020, 224, 110136. [Google Scholar] [CrossRef]
- Karabulut, K.; Buyruk, E.; Fertelli, A. Numerical Investigation of the Effect of Insulation on Heat Transfer of Thermal Bridges with Different Types. Therm. Sci. 2016, 20, 185–195. [Google Scholar] [CrossRef]
- Mátyás, L.; Barna, I.F. General Self-Similar Solutions of Diffusion Equation and Related Constructions. arXiv 2021, arXiv:2104.09128v1. [Google Scholar]
- Amiri, S.; Mazaheri, M.; Bavandpouri Gilan, N. Introducing a New Method for Calculating the Spatial and Temporal Distribution of Pollutants in Rivers. Int. J. Environ. Sci. Technol. 2021, 18, 3777–3794. [Google Scholar] [CrossRef]
- Jejeniwa, O.A.; Gidey, H.H.; Appadu, A.R. Numerical Modeling of Pollutant Transport: Results and Optimal Parameters. Symmetry 2022, 14, 2616. [Google Scholar] [CrossRef]
- Yadav, V.S.; Singh, A.; Maurya, V.; Rajpoot, M.K. New RK Type Time-Integration Methods for Stiff Convection–Diffusion–Reaction Systems. Comput. Fluids 2023, 257, 105865. [Google Scholar] [CrossRef]
- Kumar, V.; Chandan, K.; Nagaraja, K.V.; Reddy, M. V Heat Conduction with Krylov Subspace Method Using FEniCSx. Energies 2022, 15, 8077. [Google Scholar] [CrossRef]
- Mbroh, N.A.; Munyakazi, J.B. A Robust Numerical Scheme for Singularly Perturbed Parabolic Reaction-Diffusion Problems via the Method of Lines. Int. J. Comput. Math. 2022, 99, 1139–1158. [Google Scholar] [CrossRef]
- Essongue, S.; Ledoux, Y.; Ballu, A. Speeding up Mesoscale Thermal Simulations of Powder Bed Additive Manufacturing Thanks to the Forward Euler Time-Integration Scheme: A Critical Assessment. Finite Elem. Anal. Des. 2022, 211, 103825. [Google Scholar] [CrossRef]
- Beuken, L.; Cheffert, O.; Tutueva, A.; Butusov, D.; Legat, V. Numerical Stability and Performance of Semi-Explicit and Semi-Implicit Predictor--Corrector Methods. Mathematics 2022, 10, 2015. [Google Scholar] [CrossRef]
- Fedoseev, P.; Pesterev, D.; Karimov, A.; Butusov, D. New Step Size Control Algorithm for Semi-Implicit Composition ODE Solvers. Algorithms 2022, 15, 275. [Google Scholar] [CrossRef]
- Ndou, N.; Dlamini, P.; Jacobs, B.A. Enhanced Unconditionally Positive Finite Difference Method for Advection--Diffusion--Reaction Equations. Mathematics 2022, 10, 2639. [Google Scholar] [CrossRef]
- Ji, Y.; Xing, Y. Highly Accurate and Efficient Time Integration Methods with Unconditional Stability and Flexible Numerical Dissipation. Mathematics 2023, 11, 593. [Google Scholar] [CrossRef]
- Appadu, A.R. Performance of UPFD Scheme under Some Different Regimes of Advection, Diffusion and Reaction. Int. J. Numer. Methods Heat Fluid Flow 2017, 27, 1412–1429. [Google Scholar] [CrossRef] [Green Version]
- Karahan, H. Unconditional Stable Explicit Finite Difference Technique for the Advection—Diffusion Equation Using Spreadsheets. Adv. Eng. Softw. 2007, 38, 80–86. [Google Scholar] [CrossRef]
- Sanjaya, F.; Mungkasi, S. A Simple but Accurate Explicit Finite Difference Method for the Advection-Diffusion Equation. Proc. J. Phys. Conf. Ser. 2017, 909, 12038. [Google Scholar] [CrossRef]
- Pourghanbar, S.; Manafian, J.; Ranjbar, M.; Aliyeva, A.; Gasimov, Y.S. An Efficient Alternating Direction Explicit Method for Solving a Nonlinear Partial Differential Equation. Math. Probl. Eng. 2020, 2020, 9647416. [Google Scholar] [CrossRef]
- Harley, C. Hopscotch Method: The Numerical Solution of the Frank-Kamenetskii Partial Differential Equation. Appl. Math. Comput. 2010, 217, 4065–4075. [Google Scholar] [CrossRef]
- Al-Bayati, A.Y.; Manaa, S.A.; Al-Rozbayani, A.M. Comparison of Finite Difference Solution Methods for Reaction Diffusion System in Two Dimensions. AL-Rafidain J. Comput. Sci. Math. 2011, 8, 21–36. [Google Scholar] [CrossRef] [Green Version]
- Nwaigwe, C.; An Unconditionally Stable Scheme for Two-Dimensional Convection-Diffusion-Reaction Equations. No. January 2022. Available online: https://www.researchgate.net/publication/357606287_An_Unconditionally_Stable_Scheme_for_Two-Dimensional_Convection-Diffusion-Reaction_Equations (accessed on 5 June 2023).
- Savović, S.; Drljača, B.; Djordjevich, A. A Comparative Study of Two Different Finite Difference Methods for Solving Advection--Diffusion Reaction Equation for Modeling Exponential Traveling Wave in Heat and Mass Transfer Processes. Ric. Mat. 2021, 71, 245–252. [Google Scholar] [CrossRef]
- Nagy, Á.; Omle, I.; Kareem, H.; Kovács, E.; Barna, I.F.; Bognar, G. Stable, Explicit, Leapfrog-Hopscotch Algorithms for the Diffusion Equation. Computation 2021, 9, 92. [Google Scholar] [CrossRef]
- Kovács, E.; Nagy, Á.; Saleh, M. A Set of New Stable, Explicit, Second Order Schemes for the Non-Stationary Heat Conduction Equation. Mathematics 2021, 9, 2284. [Google Scholar] [CrossRef]
- Jalghaf, H.K.; Kovács, E.; Majár, J.; Nagy, Á.; Askar, A.H. Explicit Stable Finite Difference Methods for Diffusion-Reaction Type Equations. Mathematics 2021, 9, 3308. [Google Scholar] [CrossRef]
- Kareem Jalghaf, H.; Omle, I.; Kovács, E. A Comparative Study of Explicit and Stable Time Integration Schemes for Heat Conduction in an Insulated Wall. Buildings 2022, 12, 824. [Google Scholar] [CrossRef]
- Pirasaci, T. Investigation of Phase State and Heat Storage Form of the Phase Change Material (PCM) Layer Integrated into the Exterior Walls of the Residential-Apartment during Heating Season. Energy 2020, 207, 118176. [Google Scholar] [CrossRef]
- Nagy, Á.; Saleh, M.; Omle, I.; Kareem, H.; Kovács, E. New Stable, Explicit, Shifted-Hopscotch Algorithms for the Heat Equation. Math. Comput. Appl. 2021, 26, 61. [Google Scholar] [CrossRef]
- Saleh, M.; Nagy, Á.; Kovács, E. Part 1: Construction and Investigation of New Numerical Algorithms for the Heat Equation. Multidiszcip. Tud. 2020, 10, 323–338. [Google Scholar] [CrossRef]
- Mahmoud, S.; Ádám, N.; Endre, K. Construction and Investigation of New Numerical Algorithms for the Heat Equation: Part III. Multidiszcip. Tud. 2020, 10, 349–360. [Google Scholar]
- Alawadhi, E.M. Finite Element Simulations Using ANSYS; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Holman, J. Heat Transfer, 10th ed.; McGraw-Hill Education: New York, NY, USA, 2010. [Google Scholar]
- Askar, A.H.; Omle, I.; Kovács, E.; Majár, J. Testing Some Different Implementations of Heat Convection and Radiation in the Leapfrog-Hopscotch Algorithm. Algorithms 2022, 15, 400. [Google Scholar] [CrossRef]
- Munka, M.; Pápay, J. 4D Numerical Modeling of Petroleum Reservoir Recovery; Akadémiai Kiadó: Budapest, Hungary, 2001; ISBN 9630578433. [Google Scholar]
- Chen-Charpentier, B.M.; Kojouharov, H.V. An Unconditionally Positivity Preserving Scheme for Advection—Diffusion Reaction Equations. Math. Comput. Model. 2013, 57, 2177–2185. [Google Scholar] [CrossRef]
- Amando, R.S. Numerical Computation of Internal and External Flows, Volume 1: Fundamentals of Numerical Discretization; Hirsch, C., Ed.; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 1989. [Google Scholar]
- Gourlay, A.R.; McGuire, G.R. General Hopscotch Algorithm for the Numerical Solution of Partial Differential Equations. IMA J. Appl. Math. 1971, 7, 216–227. [Google Scholar] [CrossRef]
- Kovács, E. New Stable, Explicit, First Order Method to Solve the Heat Conduction Equation. arXiv 2019, arXiv:1908.09500. [Google Scholar] [CrossRef]
- Weather-Online Website. Available online: https://www.worldweatheronline.com/miskolc-weatherhistory/miskolc/hu.aspx (accessed on 20 November 2022).
- Askar, A.H.; Kovács, E.; Bolló, B. ANN modeling for thermal load estimation in a cabin vehicle. In Vehicle and Automotive Engineering 4: Select Proceedings of the 4th VAE2022, Miskolc, Hungary; Springer: Cham, Switzerland, 2022; pp. 357–373. [Google Scholar]
- Duffie, J.A.; Beckman, W.A. Solar Engineering of Thermal Processes; Wiley: New York, NY, USA, 1980. [Google Scholar]




| Abbreviation | Name/Description of the Method |
|---|---|
| DF-D | Dufort–Frankel, where the Sigma and K terms are only in the denominator |
| DF-M | Dufort–Frankel, where the Sigma and K terms are present in a mixed way |
| DF-KD | Dufort–Frankel, where the K term turns up only in the denominator, and the Sigma term is present in a mixed way |
| DF-SD | Dufort–Frankel, where the Sigma term turns up only in the denominator, and the K term is present in a mixed way |
| OOEH | Original odd–even hopscotch |
| NS-OEH | OOEH with the non-standard treatment of convection and radiation |
| LH Pseudo-Imp | Leapfrog–hopscotch scheme with pseudo-implicit treatment of the Sigma term |
| LH Inside | LH with inside treatment of the Sigma term (it appears in the numerator) |
| LH Mixed | LH with a combination of the pseudo-implicit and inside treatment |
| ANSYS-M | Mixed solver (controlled by ANSYS) |
| ANSYS-D | Direct solver |
| ANSYS-I | Iterative solver |
| ode15s | A 1 to 5-order numerical differentiation formula with variable-step and variable order (VSVO), that was designed for stiff problems |
| ode23t | Applies the trapezoidal rule with a free interpolant |
| ode23tb | Uses trapezoidal rule in the first stage and a backward differentiation formula in the second one |
| ode23 | Second (third) order Runge–Kutta–Bogacki–Shampine method |
| ode45 | A fourth (fifth) order Runge–Kutta–Dormand–Prince solver |
| ode113 | 1-13 order VSVO Adams–Bashforth–Moulton solver |
| Brick | 1900 | 840 | 0.73 |
| Rigid Polyurethane Foam | 320 | 1400 | 0.023 |
| Steel Beam | 7800 | 840 | 16.2 |
| ε | ||||
|---|---|---|---|---|
| Right Elements | 22 | 0.8 | 4.5 | 435.39 |
| Left Elements | 9 | 0.9 | 5.1 | 360.95 |
| The Type of Boundary Condition | Grid Type | The Maximum Error between Analytical Solution | |
|---|---|---|---|
| MATLAB | ANSYS | ||
| Zero Dirichlet | coarse | ||
| medium | |||
| fine | |||
| Only convection on the surface | medium | ||
| Only radiation on the surface | medium | ||
| ε | |||
|---|---|---|---|
| Right Elements | 0.6–22.45 | 0.9 | 5.1 |
| Left Elements | 9 | 0.7 | 3.97 |
| One Layer | Two Layers | Two Layers with a Straight Bridge | Two Layers with Bent Bridge | |
|---|---|---|---|---|
| Heat loss (full month, kWh) | 19.14 | 1.99 | 5.29 | 5.01 |
| The cost in HUF | 717.19 | 74.63 | 198.24 | 187.8 |
| The cost in USD | 1.9 | 0.2 | 0.53 | 0.5 |
| One Layer | Two Layers | Two Layers with a Straight Bridge | Two Layers with Bent Bridge | |
|---|---|---|---|---|
| Heat loss (one day, kWh) | 0.713 | 0.076 | 0.213 | 0.2 |
| The cost in HUF | 26.7 | 2.85 | 7.96 | 7.56 |
| The cost in USD | 0.071 | 0.0076 | 0.022 | 0.02 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Omle, I.; Askar, A.H.; Kovács, E.; Bolló, B. Comparison of the Performance of New and Traditional Numerical Methods for Long-Term Simulations of Heat Transfer in Walls with Thermal Bridges. Energies 2023, 16, 4604. https://doi.org/10.3390/en16124604
Omle I, Askar AH, Kovács E, Bolló B. Comparison of the Performance of New and Traditional Numerical Methods for Long-Term Simulations of Heat Transfer in Walls with Thermal Bridges. Energies. 2023; 16(12):4604. https://doi.org/10.3390/en16124604
Chicago/Turabian StyleOmle, Issa, Ali Habeeb Askar, Endre Kovács, and Betti Bolló. 2023. "Comparison of the Performance of New and Traditional Numerical Methods for Long-Term Simulations of Heat Transfer in Walls with Thermal Bridges" Energies 16, no. 12: 4604. https://doi.org/10.3390/en16124604
APA StyleOmle, I., Askar, A. H., Kovács, E., & Bolló, B. (2023). Comparison of the Performance of New and Traditional Numerical Methods for Long-Term Simulations of Heat Transfer in Walls with Thermal Bridges. Energies, 16(12), 4604. https://doi.org/10.3390/en16124604







