A Family of Zero-Voltage-Transition Magnetic Coupling Bidirectional DC/DC Converters †
Abstract
:1. Introduction
2. Operation Process Analysis
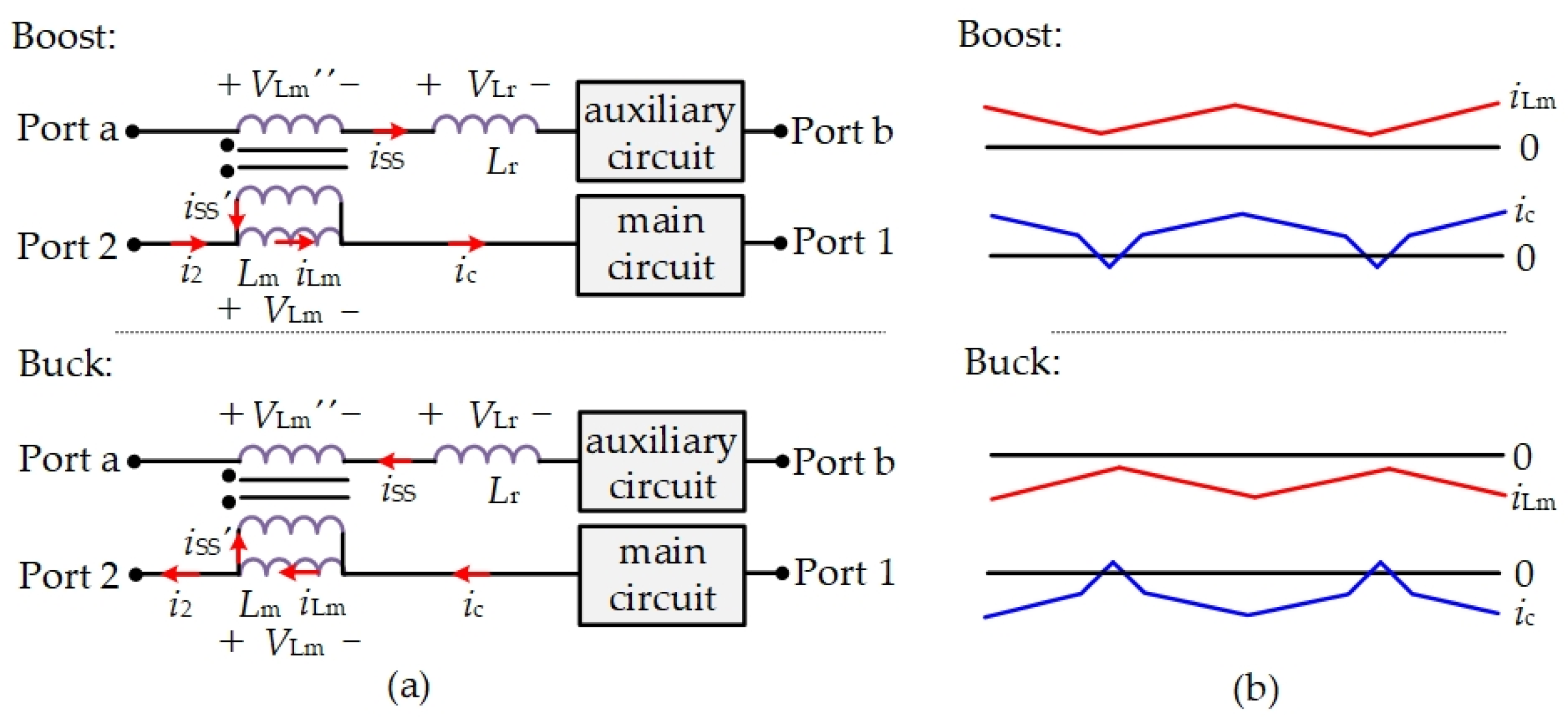
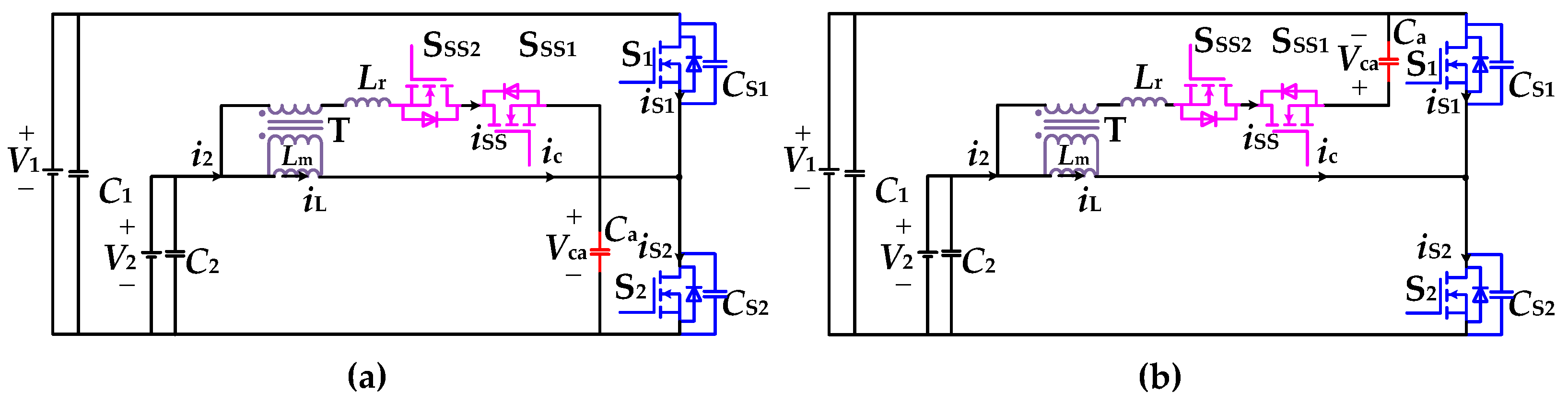
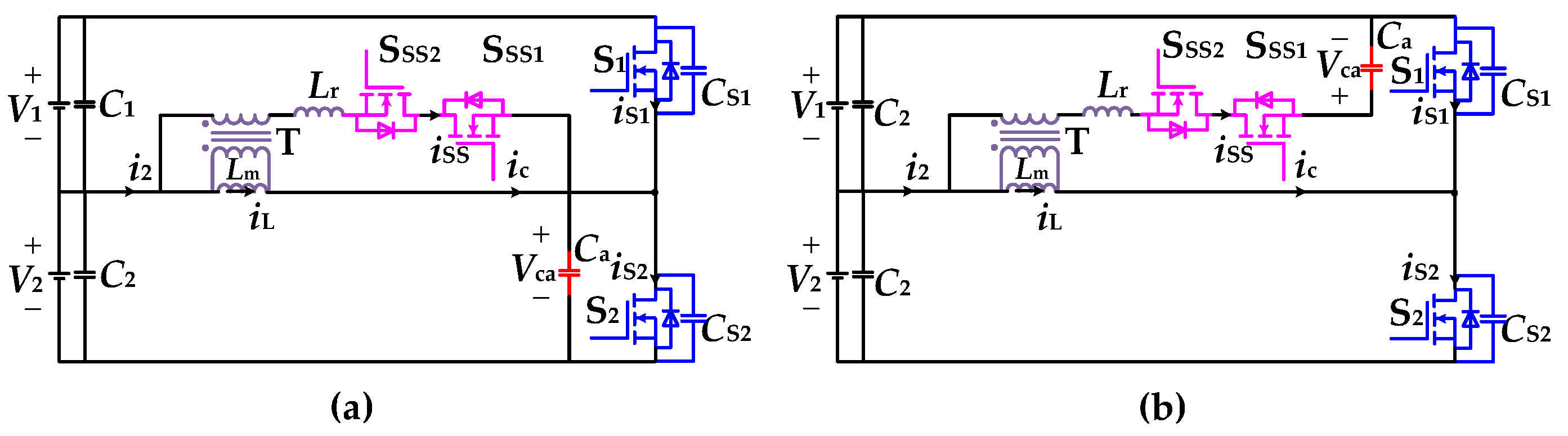
2.1. Proposed ZVT BDCs
2.2. Operation Analysis of the Proposed ZVS BDCs
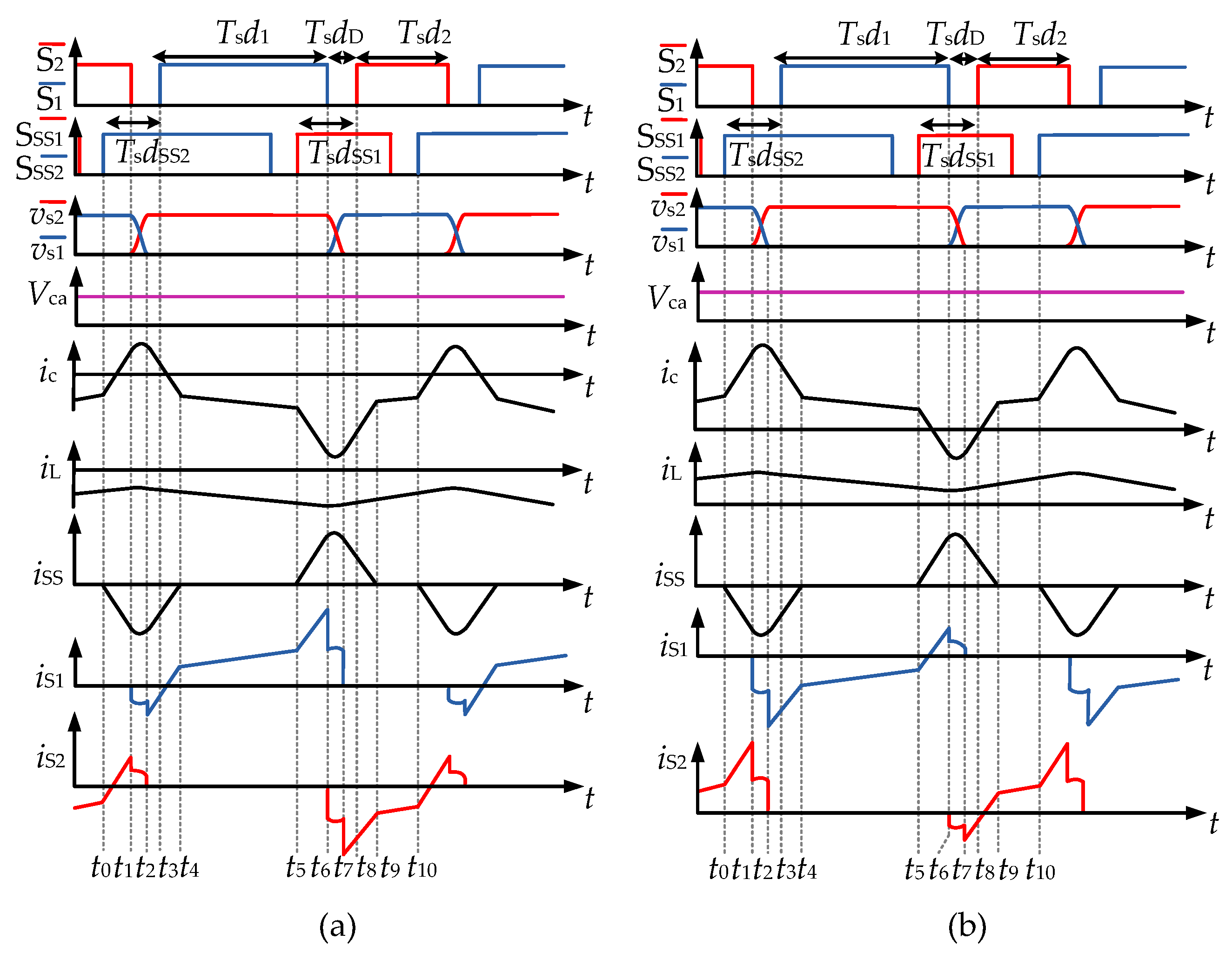
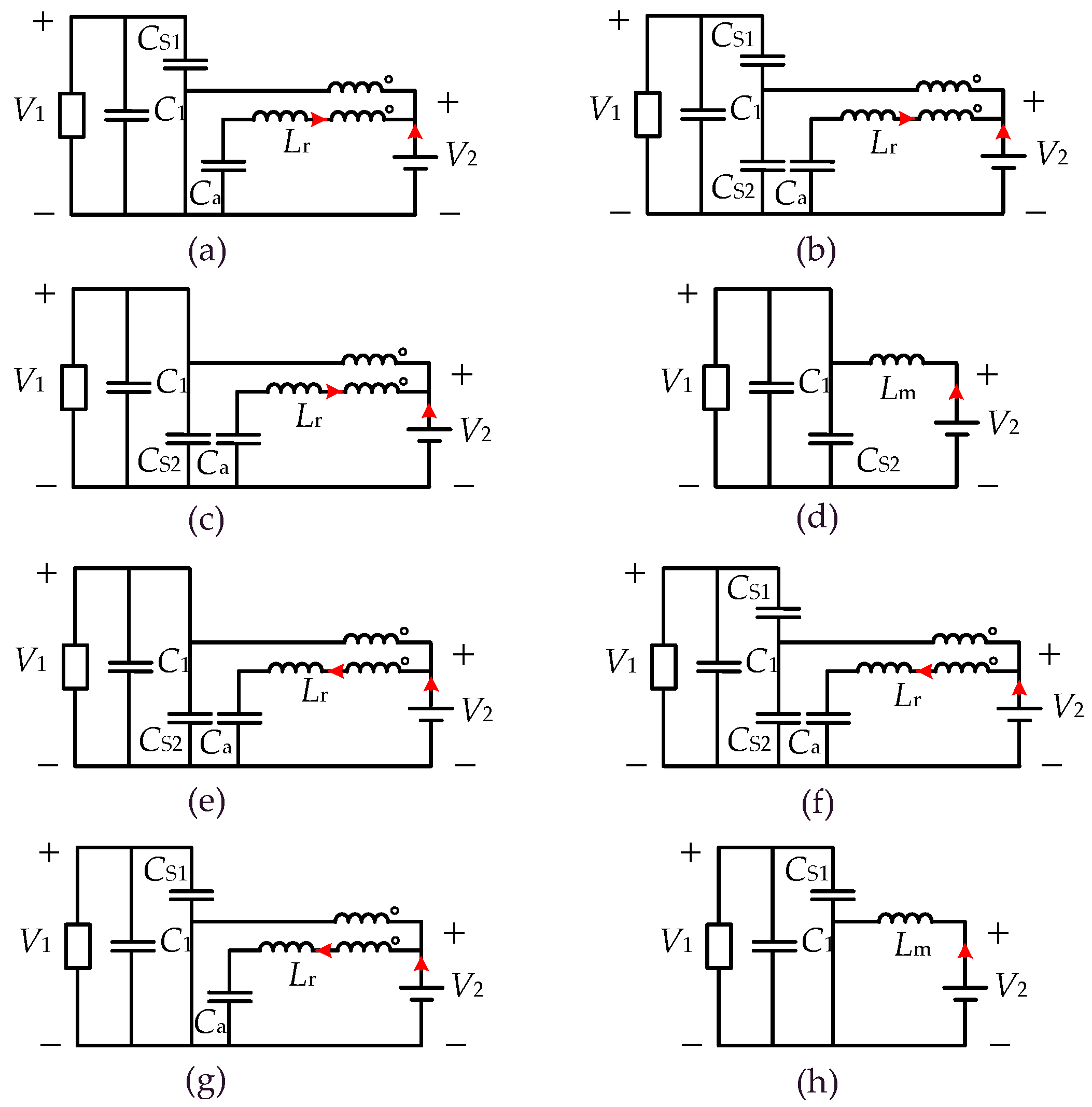
2.2.1. Operation Analysis of Topology 1
2.2.2. Operation Analysis of Topology 2
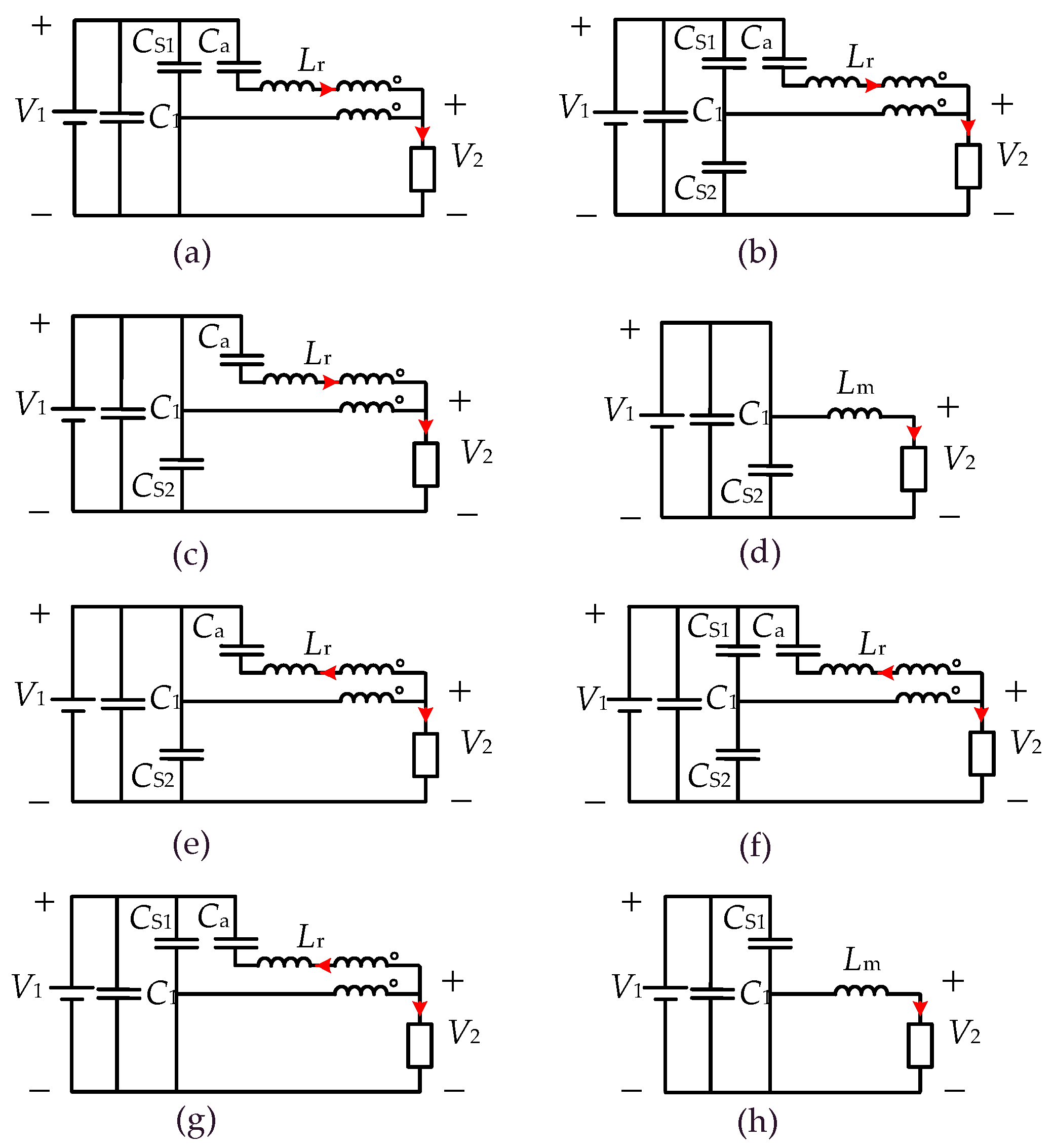
2.3. Other ZVT BDC Topologies
3. Performance Analysis
3.1. Analysis of Input Current Ripple
3.2. Loss Analysis
3.3. Topology Comparison
4. System Design
4.1. Design of Initial Value Vca
4.1.1. Design of Initial Value Vca in Topology 1
4.1.2. Design of Initial Value Vca in Topology 2
4.2. Design of the Coupled Inductor
4.2.1. Design of Lr in Topology 1
4.2.2. Design of Lr in Topology 2
4.3. Design of CS
4.3.1. Design of CS in Topology 1
4.3.2. Design of CS in Topology 2
4.4. Design of Ca
4.4.1. Design of Ca in Topology 1
4.4.2. Design of Ca in Topology 2
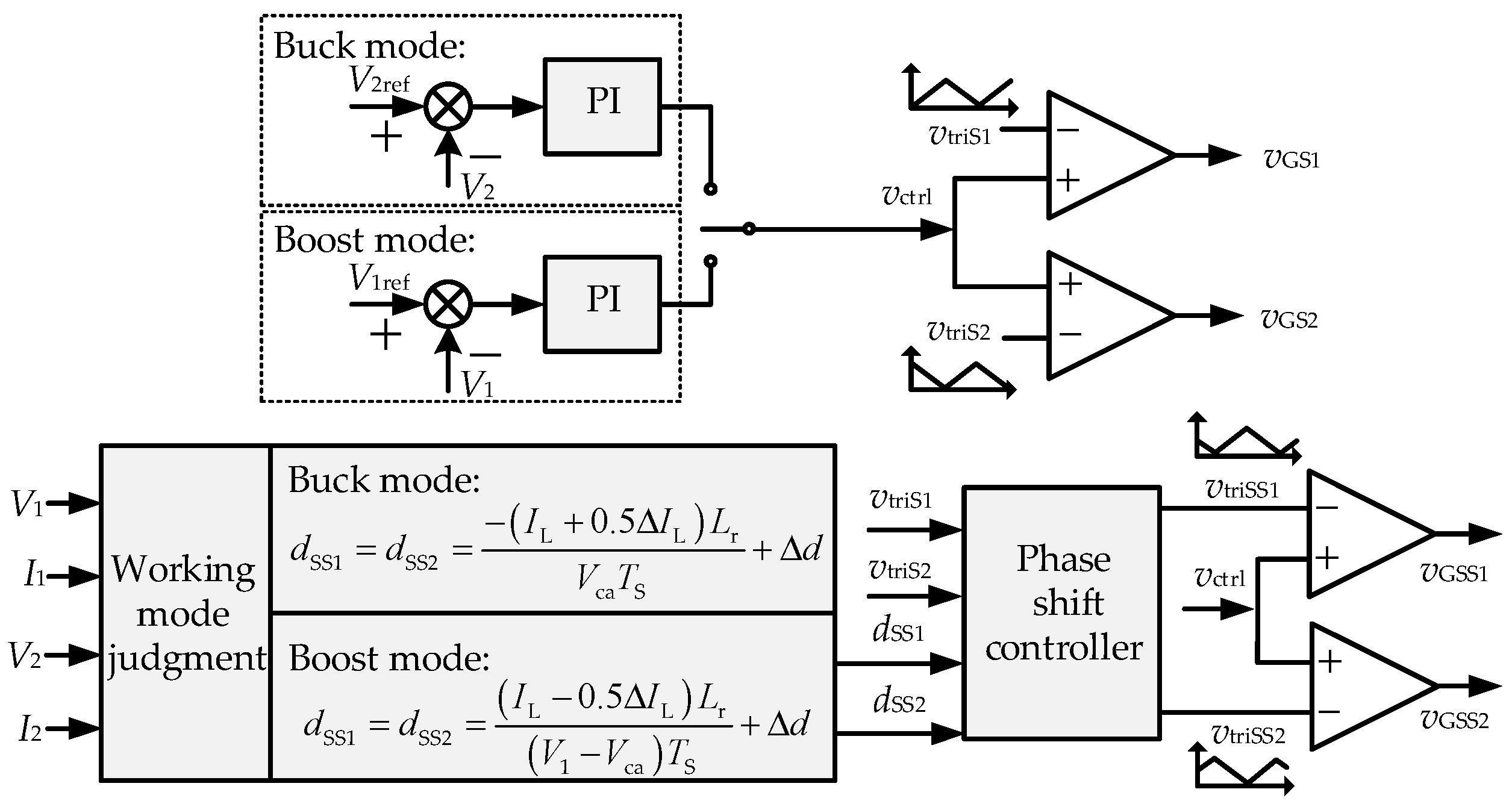
4.5. Design of the Control Method
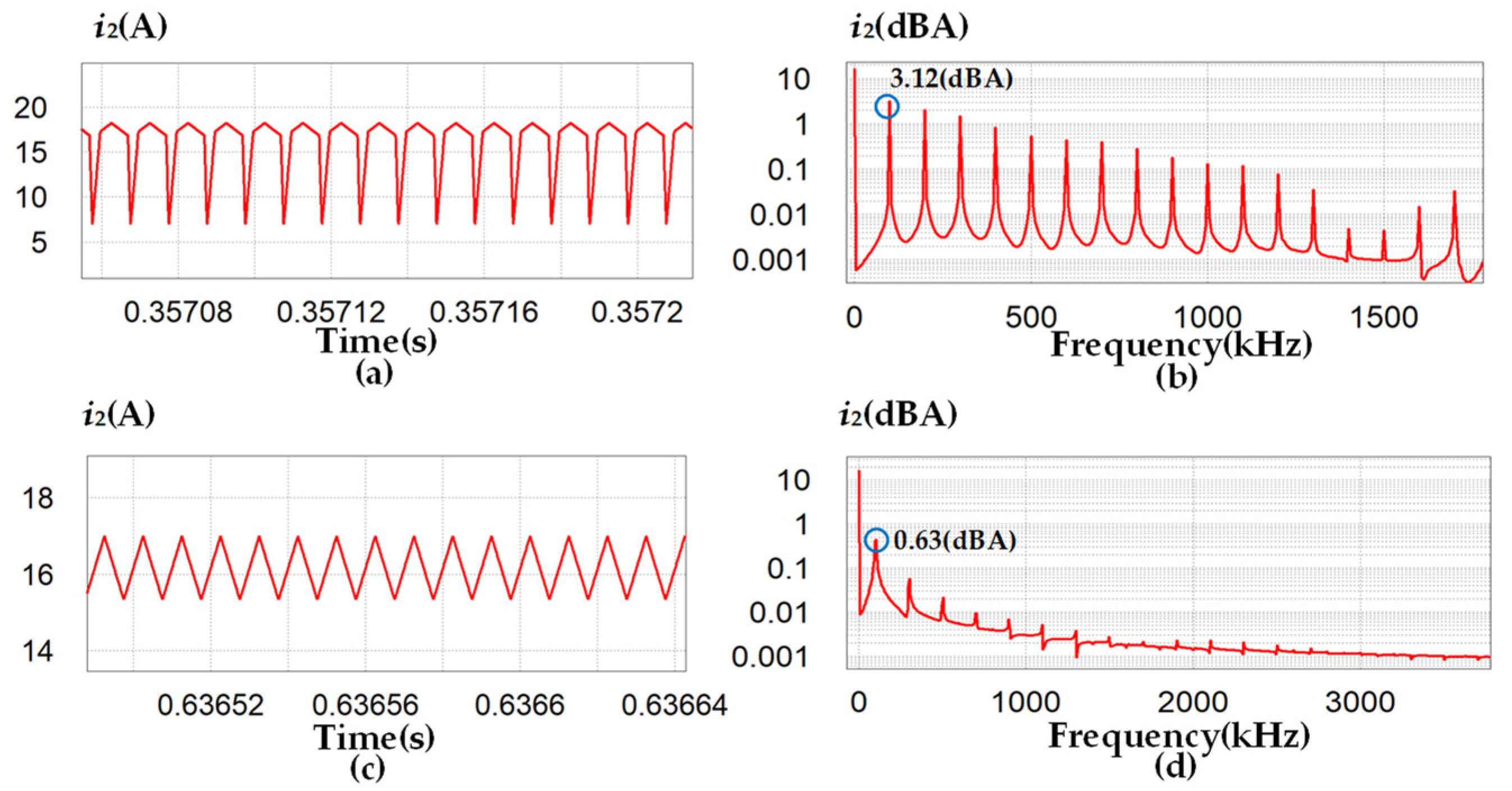
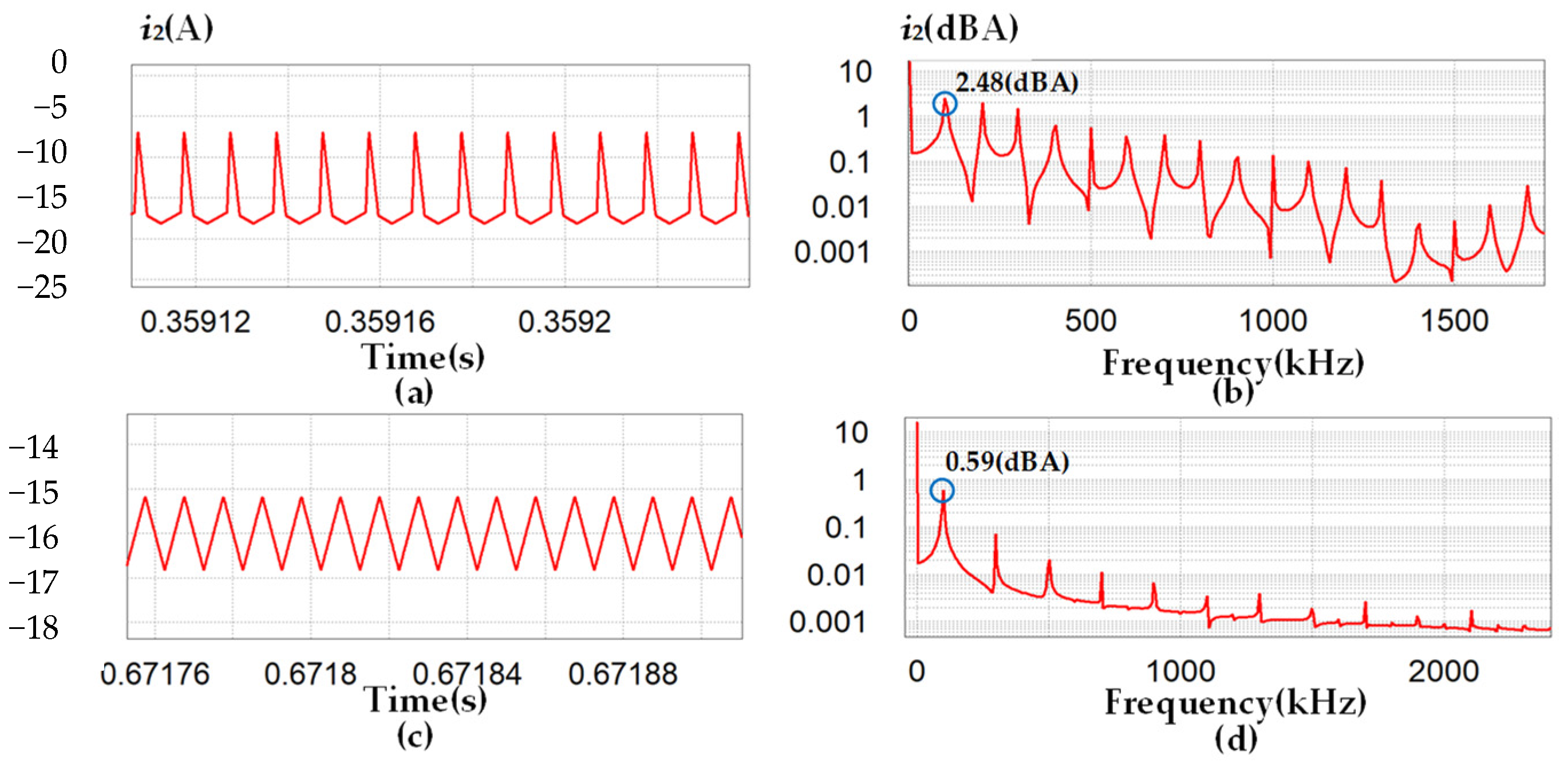
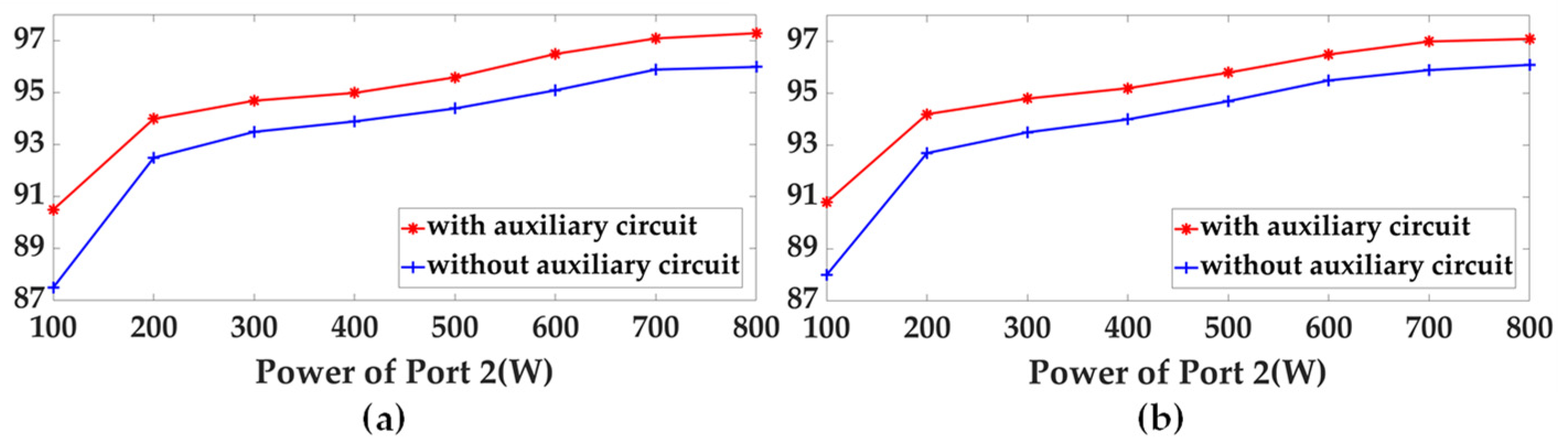
5. Experimental Verification
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lee, H.; Yun, J. High-Efficiency Bidirectional Buck–Boost Converter for Photovoltaic and Energy Storage Systems in a Smart Grid. IEEE Trans. Power Electron. 2019, 34, 4316–4328. [Google Scholar] [CrossRef]
- Mirzaei, A.; Forooghi, M.; Ghadimi, A.A.; Abolmasoumi, A.H.; Riahi, M.R. Design and construction of a charge controller for stand-alone PV/battery hybrid system by using a new control strategy and power management. Sol. Energy 2017, 149, 132–144. [Google Scholar] [CrossRef]
- Dimitrov, B.; Hayatleh, K.; Barker, S.; Collier, G.; Sharkh, S.; Cruden, A. A Buck–Boost Transformerless DC–DC Converter Based on IGBT Modules for Fast Charge of Electric Vehicles. Electronics 2020, 9, 397. [Google Scholar] [CrossRef] [Green Version]
- Park, D.-R.; Kim, Y. Design and Implementation of Improved High Step-Down DC–DC Converter for Electric Vehicles. Energies 2021, 14, 4206. [Google Scholar] [CrossRef]
- Abusara, M.A.; Guerrero, J.M.; Sharkh, S.M. Line-Interactive UPS for Microgrids. IEEE Trans. Ind. Electron. 2013, 61, 1292–1300. [Google Scholar] [CrossRef] [Green Version]
- Wu, J.; Wen, P.; Sun, X.; Yan, X. Reactive Power Optimization Control for Bidirectional Dual-Tank Resonant DC–DC Converters for Fuel Cells Systems. IEEE Trans. Power Electron. 2020, 35, 9202–9214. [Google Scholar] [CrossRef]
- Ramirez-Murillo, H.; Restrepo, C.; Konjedic, T.; Calvente, J.; Romero, A.; Baier, C.R.; Giral, R. An Efficiency Comparison of Fuel-Cell Hybrid Systems Based on the Versatile Buck–Boost Converter. IEEE Trans. Power Electron. 2018, 33, 1237–1246. [Google Scholar] [CrossRef]
- Huang, X.; Lee, F.C.; Li, Q.; Du, W. High-Frequency High-Efficiency GaN-Based Interleaved CRM Bidirectional Buck/Boost Converter with Inverse Coupled Inductor. IEEE Trans. Power Electron. 2016, 31, 4343–4352. [Google Scholar] [CrossRef]
- Yao, Z.; Lu, S. A Simple Approach to Enhance the Effectiveness of Passive Currents Balancing in an Interleaved Multiphase Bidirectional DC–DC Converter. IEEE Trans. Power Electron. 2019, 34, 7242–7255. [Google Scholar] [CrossRef]
- Ahmed, H.F.; Cha, H.; Kim, S.; Kim, D.; Kim, H. Wide Load Range Efficiency Improvement of a High-Power-Density Bidirectional DC–DC Converter Using an MR Fluid-Gap Inductor. IEEE Trans. Ind. Appl. 2015, 51, 3216–3226. [Google Scholar] [CrossRef]
- Jayashree, E.; Uma, G. Design and implementation of zero-voltage switching quasi-resonant positive-output Luo converter using analog resonant controller UC3861. IET Power Electron. 2011, 4, 81–88. [Google Scholar] [CrossRef]
- Moradisizkoohi, H.; Elsayad, N.; Mohammed, O.A. Experimental Demonstration of a Modular, Quasi-Resonant Bidirectional DC-DC Converter Using GaN Switches for Electric Vehicles. IEEE Trans. Ind. Appl. 2019, 55, 7787–7803. [Google Scholar] [CrossRef]
- Liu, S.; Wu, X. A 1-MHz ZVS Boost DC–DC converter with active clamping using GaN power transistors. In Proceedings of the 2016 IEEE 8th International Power Electronics and Motion Control Conference (IPEMC-ECCE Asia), Hefei, China, 22–26 May 2016; pp. 557–562. [Google Scholar]
- Lee, S.S.; Choi, S.W.; Moon, G.W. High efficiency active clamp forward converter with synchronous switch controlled ZVS operation. J. Power Electron. 2006, 6, 131–138. [Google Scholar]
- Lee, I.; Kim, J.; Lee, T.; Jung, Y.; Won, C. A new bidirectional DC–DC converter with ZVT switching. In Proceedings of the 2012 IEEE Vehicle Power and Propulsion Conference (VPPC), Seoul, Republic of Korea, 9–12 October 2012; pp. 684–689. [Google Scholar]
- Yang, J.; Do, H. High-Efficiency Bidirectional DC–DC Converter With Low Circulating Current and ZVS Characteristic Throughout a Full Range of Loads. IEEE Trans. Ind. Electron. 2014, 61, 3248–3256. [Google Scholar] [CrossRef]
- Mohammadi, M.R.; Farzanehfard, H. Analysis of Diode Reverse Recovery Effect on the Improvement of Soft-Switching Range in Zero-Voltage-Transition Bidirectional Converters. IEEE Trans. Ind. Electron. 2015, 62, 1471–1479. [Google Scholar] [CrossRef]
- Lee, J.H.; Yu, D.H.; Kim, J.G.; Kim, Y.H.; Won, C.Y. Auxiliary Switch Control of a Bidirectional Soft-Switching DC/DC Converter. IEEE Trans. Power Electron. 2013, 28, 5446–5457. [Google Scholar] [CrossRef]
- Zhang, Y.; Sen, P.C. A new soft-switching technique for buck, boost, and buck–boost converters. IEEE Trans. Ind. Appl. 2003, 39, 1775–1782. [Google Scholar] [CrossRef]
- Mohammadi, M.R.; Farzanehfard, H. New Family of Zero-Voltage-Transition PWM Bidirectional Converters with Coupled Inductors. IEEE Trans. Ind. Electron. 2012, 59, 912–919. [Google Scholar] [CrossRef]
- Mohammadi, M.R.; Farzanehfard, H. A New Family of Zero-Voltage-Transition Nonisolated Bidirectional Converters with Simple Auxiliary Circuit. IEEE Trans. Ind. Electron. 2016, 63, 1519–1527. [Google Scholar] [CrossRef]
- Chen, G.; Deng, Y.; Tao, Y.; He, X.; Wang, Y.; Hu, Y. Topology Derivation and Generalized Analysis of Zero-Voltage-Switching Synchronous DC–DC Converters With Coupled Inductors. IEEE Trans. Ind. Electron. 2016, 63, 4805–4815. [Google Scholar] [CrossRef]
- Chen, G.; Deng, Y.; Chen, L.; Hu, Y.; Jiang, L.; He, X.; Wang, Y. A Family of Zero-Voltage-Switching Magnetic Coupling Nonisolated Bidirectional DC–DC Converters. IEEE Trans. Ind. Electron. 2017, 64, 6223–6233. [Google Scholar] [CrossRef]
- Mohammadi, M.R.; Farzanehfard, H. Family of Soft-Switching Bidirectional Converters With Extended ZVS Range. IEEE Trans. Ind. Electron. 2017, 64, 7000–7008. [Google Scholar] [CrossRef]
- Mohammadi, M.R.; Peyman, H.; Yazdani, M.R.; Mirtalaei, S.M.M. A ZVT Bidirectional Converter With Coupled-Filter-Inductor and Elimination of Input Current Notches. IEEE Trans. Ind. Electron. 2020, 67, 7461–7469. [Google Scholar] [CrossRef]
- Nan, C.; Ayyanar, R. A 1 MHz Bi-directional Soft-switching DC–DC Converter with Planar Coupled Inductor for Dual Voltage Automotive Systems. In Proceedings of the 2016 IEEE Applied Power Electronics Conference and Exposition (APEC), Long Beach, CA, USA, 20–24 March 2016; pp. 432–439. [Google Scholar]
- Cheng, X.; Zhang, Y.; Yin, C. A Family of Coupled-Inductor-Based Soft-Switching DC–DC Converter With Double Synchronous Rectification. IEEE Trans. Ind. Electron. 2019, 66, 6936–6946. [Google Scholar] [CrossRef]
- Wang, S.; Hu, Y.; Gao, M.; Shi, J. Coupled inductor based zero-voltage-switching buck/boost converter. J. Power Electron. 2022, 22, 1059–1072. [Google Scholar] [CrossRef]
- Rezvanyvardom, M.; Mirzaei, A. Zero-Voltage Transition Nonisolated Bidirectional Buck–Boost DC–DC Converter With Coupled Inductors. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 3266–3275. [Google Scholar] [CrossRef]
- Cheng, X.; Liu, C.; Wang, D.; Zhang, Y. State-of-the-Art Review on Soft-Switching Technologies for Non-Isolated DC-DC Converters. IEEE Access 2021, 9, 119235–119249. [Google Scholar] [CrossRef]











| fS = 100 kHz | fS = 500 kHz | ||||||
|---|---|---|---|---|---|---|---|
| Parameter | Value | Parameter | Value | Parameter | Value | Parameter | Value |
| V2/V | 50 | V1/V | 100 | V2/V | 50 | V1/V | 100 |
| P1max/W | 800 | n | 1 | P1max/W | 800 | n | 1 |
| Lc/μH | 3.8 | Lm/μH | 130 | Lc/μH | 0.85 | Lm/μH | 160 |
| C1/μF | 1000 | C2/μF | 1000 | C1/μF | 1000 | C2/μF | 1000 |
| CS/nF | 2.2 | Ca/μF | 200 | CS/nF | 1 | Ca/μF | 80 |
| Loss Source | fS = 100 kHz | fS = 500 kHz | ||
|---|---|---|---|---|
| Traditional BDC | Proposed BDC | Traditional BDC | Proposed BDC | |
| Pc_S | 2.1 W | 2.5 W | 2.1 W | 3.1 W |
| Pc_SS | --- | 5.4 W | --- | 10.4 W |
| Ps_S | 19.1 W | --- | 95.5 W | --- |
| PRR | --- | 0.8 W | --- | 4.2 W |
| Core loss | 1.9 W | 2.1 W | 0.3 W | 0.4 W |
| Copper loss | 2.7 W | 3.3 W | 2.9 W | 4.3 W |
| Topology | Number of Auxiliary Switches | Number of Auxiliary Diodes | Current Notch | Voltage Stress of Auxiliary Switches |
|---|---|---|---|---|
| ZVT BDC [17] | 2 | 2 | exist | max{DV1, (1 − D)V1} |
| ZVS BDC [18] | 2 | 0 | exist | Buck: V2 Boost: V1 − V2 |
| ZVT BDC [20] | 2 | 2 | exist | (1 + nD)V2 |
| ZVT BDC [21] | 2 | 0 | exist | nDV1 |
| ZVS BDC [23] | 2 | 0 | exist | Sa1: (n + 1)V2 Sa2: (n + 1)( V1 − V2) |
| ZVS BDC [24] | 2 | 2 | exist | Buck: max{|(n − 1)(V1 − V2)|, V2 + n(V1 − V2)} Boost: max{|(n − 1)V2|, V1 + (n − 1)V2} |
| ZVT BDC [25] | 2 | 2 | no | Buck: >0.5 V2 Boost: >0.5 V2 |
| ZVT BDC [26] | 2 | 0 | exist | Sa1: (n + 1)(V1 − V2) Sa2: (n + 1)V2 |
| ZVS BDC [28] | 2 | 2 | no | SSS1: SSS2: |
| Proposed ZVT BDCs | 2 | 0 | no | SSS1: V1 − Vca SSS2: Vca |
| Step 1 | Determine the voltages (V1 and V2) and power level according to the system requirements. |
| Step 2 | Ignore the resonance process and select initial value of Vca, Vca = 0.5V1. |
| Step 3 | Design Lm of T according to the requirements of current ripple, and . |
| Step 4 | Select n = 1. |
| Step 5 | Design Lr of T according to IL − 0.5ΔiL − ΔiSS < 0, in which . |
| Step 6 | Determine value range of (CS, td) according to , and select CS and td. |
| Step 7 | Design Ca according to the requirements of voltage ripple, and . |
| Step 8 | Simulation and experimental verification. |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| V2/V | 40~60 | V1/V | 100 |
| fS/kHz | 100 | n | 1 |
| Lc/μH | 3.8 | Lm/μH | 130 |
| C1 and C2/μF | 1000 | CS/nF | 2.2 |
| P1max and P2max/W | 800 | Ca/μF | 200 |
| Topology | Boost | Buck |
|---|---|---|
| ZVS BDC [17] | 96.7% | 95.2% |
| ZVS BDC [18] | 97.2% | 96.5% |
| ZVT BDC [20] | 95.7% | 95.6% |
| ZVT BDC [21] | 97.7% | 97.2% |
| ZVS BDC [23] | 97.5% | 97.5% |
| ZVS BDC [24] | 96.3% | 96.5% |
| ZVT BDC [25] | 95.3% | 95.4% |
| ZVT BDC [26] | 92.2% | 93.3% |
| ZVS BDC [28] | 96.4% | 96.2% |
| The proposed ZVT BDCs | 96.7% | 96.7% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Gao, M.; Shi, J. A Family of Zero-Voltage-Transition Magnetic Coupling Bidirectional DC/DC Converters. Energies 2023, 16, 4760. https://doi.org/10.3390/en16124760
Wang S, Gao M, Shi J. A Family of Zero-Voltage-Transition Magnetic Coupling Bidirectional DC/DC Converters. Energies. 2023; 16(12):4760. https://doi.org/10.3390/en16124760
Chicago/Turabian StyleWang, Shanshan, Ming Gao, and Jianjiang Shi. 2023. "A Family of Zero-Voltage-Transition Magnetic Coupling Bidirectional DC/DC Converters" Energies 16, no. 12: 4760. https://doi.org/10.3390/en16124760
APA StyleWang, S., Gao, M., & Shi, J. (2023). A Family of Zero-Voltage-Transition Magnetic Coupling Bidirectional DC/DC Converters. Energies, 16(12), 4760. https://doi.org/10.3390/en16124760






