Distributed Intelligence in Autonomous PEM Fuel Cell Control
Abstract
:1. Introduction
2. State-of-the-Art Review
| Control Technique | Control Objective | Improvement Achieved | Comments | C-A-R |
|---|---|---|---|---|
| PID | ||||
|
|
|
| 2-3-2 [16] |
|
|
|
| 2-3-2 [17] |
|
|
|
| 3-4-4 [18] |
| FLC | ||||
|
|
|
| 2-4-5 [20] |
|
|
|
| 2-4-3 [25] |
| Robust control | ||||
|
|
|
| 2-3-3 [26] |
|
|
|
| 3-2-5 [28] |
|
|
|
| 2-3-3 [29] |
|
|
|
| 3-3-4 [30] |
|
|
|
| 3-2-5 [31] |
| Artificial intelligence | ||||
|
|
|
| 2-5-4 [12] |
|
|
|
| 2-4-4 [35] |
|
|
|
| 2-5-4 [36] |
|
|
|
| 3-4-4 [38] |
|
|
|
| 2-4-4 [39] |
|
|
|
| 3-4-4 [40] |
|
|
|
| 3-4-4 [41] |
3. Materials and Methods
3.1. Research Scenario
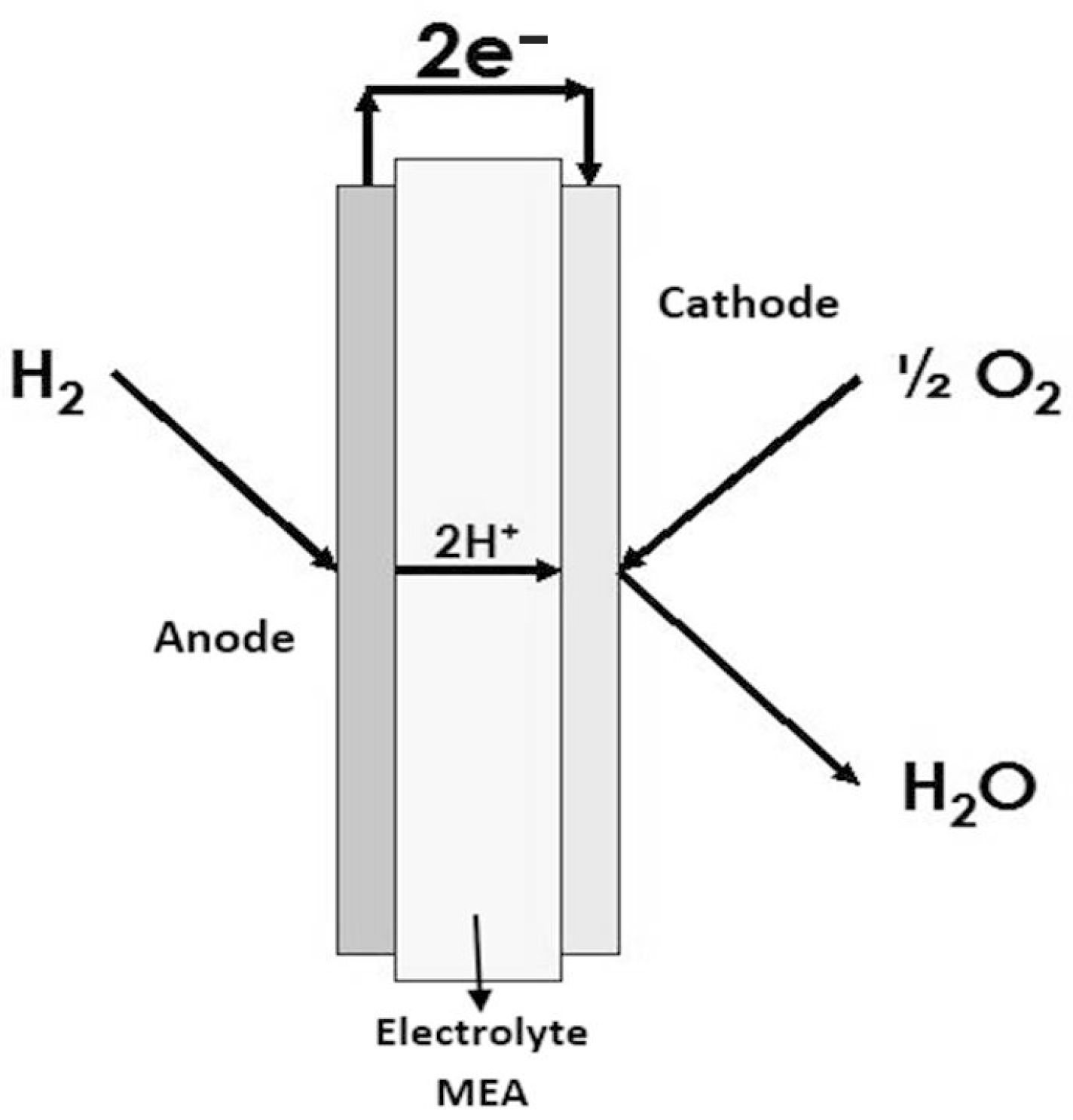
3.1.1. The Proton Exchange Membrane Fuel Cell PEMFC
3.1.2. System Experimentation
- Programmable electronic load AMREL ZVL 100-10-20L that optimizes performance, both for characterization studies and new applications.
- Modular, compact, and economic system that can work for PEM hydrogen fuel cells and direct methanol cells of different powers.
- System with open control architecture, flexible to changes, such as increment of variables to be controlled and incorporation of new control algorithms, such as performance management; this allows for autonomous operation of the PEM stack.
3.1.3. Variation of the Electrical Resistance of the Membrane
3.2. Proposed Control Model
3.2.1. Knowledge Structure
- Computing processes or algorithms based on approximate reasoning that define its competence.
- Variables or parameters required or shared in global memory.
- Inputs and outputs associated with the intelligent agent.
3.2.2. Intelligent Agents for PEMFC Autonomous Control
Agent PERCEIVE ALERT
Agent UPDATE STATE
Agent GENERATE STIMULUS
Agent CONTROL STATE
4. Results and Discussion
4.1. Variation of the Membrane Electrical Resistance, Rm
4.2. Operating State Detection of the PEMFC
4.3. Control of the PEMFC Normal State
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rubio, A.; Agila, W. Sustainable Energy: A Strategic Overview of Fuel Cells. In Proceedings of the 2019 8th International Conference on Renewable Energy Research and Applications (ICRERA), Brasov, Romania, 3–6 November 2019; pp. 239–243. [Google Scholar]
- Rubio, A.; Agila, W. A Novel System-Level Model for a Fuel Cell in a Strategic Context. In Proceedings of the 2018 7th International Conference on Renewable Energy Research and Applications (ICRERA), Paris, France, 14–17 October 2018; pp. 1044–1048. [Google Scholar]
- Munjewar, S.S.; Thombre, S.B.; Mallick, R.K. A comprehensive review on recent material development of passive direct methanol fuel cell. Ionics 2017, 23, 1–18. [Google Scholar] [CrossRef]
- Lin-Kwong-Chon, C.; Grondin-Pérez, B.; Kadjo, J.J.A.; Damour, C.; Benne, M. A review of adaptive neural control applied to proton exchange membrane fuel cell systems. Annu. Rev. Control 2019, 47, 133–154. [Google Scholar] [CrossRef]
- Yang, B.; Li, J.; Li, Y.; Guo, Z.; Zeng, K.; Shu, H.; Cao, P.; Ren, Y. A critical survey of proton exchange membrane fuel cell system control: Summaries, advances, and perspectives. Int. J. Hydrogen Energy 2022, 47, 9986–10020. [Google Scholar] [CrossRef]
- Rubio, G.A.; Agila, W.E. A Fuzzy Model to Manage Water in Polymer Electrolyte Membrane Fuel Cells. Processes 2021, 9, 904. [Google Scholar] [CrossRef]
- Rubio, A.; Agila, W.; Miranda, L.; Lima, B. Real-Time Qualitative Model for Estimate Water Content in PEM Fuel Cell. In Proceedings of the 2019 8th International Conference on Renewable Energy Research and Applications (ICRERA), Brasov, Romania, 3–6 November 2019; pp. 455–459. [Google Scholar]
- Rubio, A.; Agila, W. Dynamic Model of Proton Exchange Membrane Fuel Cells: A Critical Review and a Novel Model. In Proceedings of the IEEE, International Conference on Renewable Energy Research and Applications (ICRERA), Brasov, Rumania, 3–6 November 2019; pp. 353–358. [Google Scholar]
- Chavan, S.L.; Talange, D.B. Modeling and performance evaluation of PEM fuel cell by controlling its input parameters. Energy 2017, 138, 437–445. [Google Scholar] [CrossRef]
- Gomathi, K.; Karthik, M.; Usha, S. An intelligent parametric modeling and identification of a 5 kW ballard PEM fuel cell system based on dynamic recurrent networks with delayed context units. Int. J. Hydrogen Energy 2021, 46, 15912–15927. [Google Scholar]
- He, K.; Zhang, C.; He, Q.; Wu, Q.; Jackson, L.; Mao, L. Effectiveness of PEMFC historical state and operating mode in PEMFC prognosis. Int. J. Hydrogen Energy 2020, 45, 32355–32366. [Google Scholar] [CrossRef]
- Li, J.; Yu, T. Sensors integrated control of PEMFC gas supply system based on large-scale deep reinforcement learning. Sensors 2021, 21, 349. [Google Scholar] [CrossRef]
- Feng, Z.; Huang, J.; Jin, S.; Wang, G.; Chen, Y. Artificial intelligence-based multi-objective optimisation for proton exchange membrane fuel cell: A literature review. J. Power Sources 2022, 520, 230808. [Google Scholar] [CrossRef]
- Yang, B.; Li, D.; Zeng, C.; Chen, Y.; Guo, Z.; Wang, J.; Shu, H.; Yu, T.; Zhu, J. Parameter extraction of PEMFC via Bayesian regularization neural network based meta-heuristic algorithms. Energy 2021, 228, 120592. [Google Scholar] [CrossRef]
- Li, J.; Yu, T. A new adaptive controller based on distributed deep reinforcement learning for PEMFC air supply system. Energy Rep. 2021, 7, 1267–1279. [Google Scholar] [CrossRef]
- Arzaghi, H.; Sedighizadeh, M. A neuro adaptive control strategy for movable power source of proton exchange membrane fuel cell using wavelets. In Proceedings of the International Universities Power Engineering Conference (IUPEC) 2007, Newcastle upon Tyne, UK, 6–8 September 2006; pp. 545–549. [Google Scholar] [CrossRef]
- Zhao, D.; Li, F.; Ma, R.; Zhao, G.; Huangfu, Y. An unknown input nonlinear observer based fractional order PID control of fuel cell air supply system. IEEE Trans. Ind. Appl. 2020, 56, 5523–5532. [Google Scholar] [CrossRef]
- AbouOmar, M.; Zhang, H.; Su, Y.X. Fractional Order Fuzzy PID Control of Automotive PEM Fuel Cell Air Feed System Using Neural Network Optimization Algorithm. Energies 2019, 12, 1435. [Google Scholar] [CrossRef] [Green Version]
- Deng, H.; Li, Q.; Cui, Y.; Zhu, Y.; Chen, W. Nonlinear controller design based on cascade adaptive sliding mode control for PEM fuel cell air supply systems. Int. J. Hydrogen Energy 2019, 44, 19357–19369. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, Y.; Wang, D.; Wang, Y. Adaptive robust control of oxygen excess ratio for PEMFC system based on type-2 fuzzy logic system. Inf. Sci. 2019, 511, 1–17. [Google Scholar] [CrossRef]
- Han, J.; Yu, S.; Yi, S. Oxygen excess ratio control for proton exchange membrane fuel cell using model reference adaptive control. Int. J. Hydrogen Energy 2019, 44, 18425–18437. [Google Scholar] [CrossRef]
- Han, J.; Yu, S.; Yi, S. Adaptive control for robust air flow management in an automotive fuel cell system. Appl. Energy 2017, 190, 73–83. [Google Scholar] [CrossRef]
- Sun, L.; Shen, J.; Hua, Q.; Lee, K.Y. Data-driven oxygen excess ratio control for proton exchange membrane fuel cell. Appl. Energy 2018, 231, 866–875. [Google Scholar] [CrossRef]
- Mammar, K.; Laribi, S. Application of adaptive neuro-fuzzy inference system techniques to predict water activity in proton exchange membrane fuel cell. J. Electrochem. Energy Convers. Storage 2018, 15, 041009. [Google Scholar] [CrossRef]
- Benchouia, N.E.; Derghal, A.; Mahmah, B.; Madi, B.; Khochemane, L.; Aoul, E.H. An adaptive fuzzy logic controller (AFLC) for PEMFC fuel cell. Int. J. Hydrogen Energy 2015, 40, 13806–13819. [Google Scholar] [CrossRef]
- Rigatos, G.; Siano, P.; Wira, P.; Liu, J. A Nonlinear H-Infinity Approach to Optimal Control of PEM Fuel Cells. Intell. Ind. Syst. 2017, 3, 43–58. [Google Scholar] [CrossRef]
- Hammoudi, M.Y.; Kraa, O.; Saadi, R.; Ayad, M.Y.; Bacha, S.; Boukhlouf, A. Nonlinear Control of a Fuel Cell Interleaved Boost Converter Using Weighted Mixed Sensitivity H∞. In Proceedings of the 2018 International Conference on Electrical Sciences and Technologies in Maghreb (CISTEM), Algiers, Algeria, 28–31 October 2018; pp. 1–5. [Google Scholar]
- Afsharinejad, A.; Asemani, M.H.; Dehghani, M. Optimal linear parameter varying controller design for proton exchange membrane fuel cell using LMI techniques. In Proceedings of the 2020 28th Iranian Conference on Electrical Engineering (ICEE), Tabriz, Iran, 4–6 August 2020; pp. 1–5. [Google Scholar]
- Abbaker, A.M.; Wang, H.O.; Tian, Y. Adaptive integral type-terminal sliding mode control for PEMFC air supply system using time delay estimation algorithm. Asian J. Control 2022, 24, 217–226. [Google Scholar] [CrossRef]
- Javaid, U.; Mehmood, A.; Arshad, A.; Imtiaz, F.; Iqbal, J. Operational efficiency improvement of PEM fuel cell—A sliding mode based modern control approach. IEEE Access 2020, 8, 95823–95831. [Google Scholar] [CrossRef]
- Yin, X.; Wang, X.; Wang, L.; Qin, B.; Liu, H.; Jia, L.; Cai, W. Cooperative control of air and fuel feeding for PEM fuel cell with ejector-driven recirculation. Appl. Therm. Eng. 2021, 199, 117590. [Google Scholar] [CrossRef]
- Souissi, A. Adaptive sliding mode control of a PEM fuel cell system based on the super twisting algorithm. Energy Rep. 2021, 7, 3390–3399. [Google Scholar] [CrossRef]
- Li, Y.; Pei, P.; Ma, Z.; Ren, P.; Huang, H. Method for system parameter identification and controller parameter tuning for super-twisting sliding mode control in proton exchange membrane fuel cell system. Energy Convers. Manag. 2021, 243, 114370. [Google Scholar] [CrossRef]
- Legala, A.; Zhao, J.; Li, X. Machine learning modeling for proton exchange membrane fuel cell performance. Energy AI 2022, 10, 100183. [Google Scholar] [CrossRef]
- Li, J.; Li, Y.; Yu, T. Temperature Control of Proton Exchange Membrane Fuel Cell Based on Machine Learning. Front. Energy Res. 2021, 9, 582. [Google Scholar] [CrossRef]
- Cao, Y.; Li, Y.; Zhang, G.; Jermsittiparsert, K.; Nasseri, M. An efficient terminal voltage control for PEMFC based on an improved version of whale optimization algorithm. Energy Rep. 2020, 6, 530–542. [Google Scholar] [CrossRef]
- Yang, B.; Zeng, C.; Wang, L.; Guo, Y.; Chen, G.; Guo, Z.; Chen, Y.; Li, D.; Cao, P.; Shu, H.; et al. Parameter identification of proton exchange membrane fuel cell via Levenberg-Marquardt backpropagation algorithm. Int. J. Hydrogen Energy 2021, 46, 22998–23012. [Google Scholar] [CrossRef]
- Lu, X.; Kanghong, D.; Guo, L.; Wang, P.; Yildizbasi, A. Optimal estimation of the Proton Exchange Membrane Fuel Cell model parameters based on extended version of Crow Search Algorithm. J. Clean. Prod. 2020, 272, 122640. [Google Scholar] [CrossRef]
- Bao, S.; Ebadi, A.; Toughani, M.; Dalle, J.; Maseleno, A.; Yıldızbası, A. A new method for optimal parameters identification of a PEMFC using an improved version of Monarch Butterfly Optimization Algorithm. Int. J. Hydrogen Energy 2020, 45, 17882–17892. [Google Scholar] [CrossRef]
- Hachana, O.; El-Fergany, A.A. Efficient PEM fuel cells parameters identification using hybrid artificial bee colony differential evolution optimizer. Energy 2022, 250, 123830. [Google Scholar] [CrossRef]
- Abaza, A.; El-Sehiemy, R.A.; Mahmoud, K.; Lehtonen, M.; Darwish, M. Optimal estimation of proton exchange membrane fuel cells parameter based on coyote optimization algorithm. Appl. Sci. 2021, 11, 2052. [Google Scholar] [CrossRef]
- Nagulapati, V.M.; Kumar, S.S.; Annadurai, V.; Lim, H. Machine learning based fault detection and state of health estimation of proton exchange membrane fuel cells. Energy AI 2023, 12, 100237. [Google Scholar] [CrossRef]
- Yuan, X.; Chen, F.; Xia, Z.; Zhuang, L.; Jiao, K.; Peng, Z.; Wang, B.; Bucknall, R.; Yearwood, K.; Hou, Z. A Novel Feature Susceptibility Approach for a PEMFC Control System based on an Improved XGBoost-Boruta Algorithm. Energy AI 2023, 12, 100229. [Google Scholar] [CrossRef]
- Ding, R.; Zhang, S.; Chen, Y.; Rui, Z.; Hua, K.; Wu, Y.; Li, X.; Duan, X.; Wang, X.; Li, J.; et al. Application of Machine Learning in Optimizing Proton Exchange Membrane Fuel Cells: A Review. Energy AI 2022, 9, 100170. [Google Scholar] [CrossRef]
- Barbir, F. PEM Fuel Cells: Theory and Practice; Academic Press: Cambridge, MA, USA, 2012; Chapter 2; ISBN 0123877105; 9780123877109. [Google Scholar]
- Sanaguano, D.; Agila, W.; Rubio, G. Open Control Architecture for the Characterization and Control of the PEM Fuel Cell. In Proceedings of the IEEE Fourth Ecuador Technical Chapters Meeting (ETCM), Guayaquil, Ecuador, 11–15 November 2019. [Google Scholar] [CrossRef]
- Equipamientos de Ensayo de Pilas de Combustible de Hydrogenics. Hydrogenics. Available online: http://www.hydrogenics.com/test/ (accessed on 15 August 2019).
- “Testing Equipment” de fuelcell.com, Perteneciente a Electrochem. Available online: http://fuelcell.com/index.asp?PageAction=VIEWCATS&Category=20 (accessed on 15 August 2019).
- Hombrados, A.; González, L.; Rubio, M.; Agila, W.; Guinea, D.; Chinarro, E.; Moreno, B.; Jurado, J. Symmetrical electrode mode for PEMFC characterization by impedance spectroscopy. J. Power Sources 2005, 151, 25–31. [Google Scholar] [CrossRef]
- Tang, Z.; Huang, Q.-A.; Wang, Y.-J.; Zhang, F.; Li, W.; Li, A.; Zhang, L.; Zhang, J. Recent progress in the use of electrochemical impedance spectroscopy for the measurement, monitoring, diagnosis and optimization of proton exchange membrane fuel cell performance. J. Power Sources 2020, 468, 228361. [Google Scholar] [CrossRef]
- Atlam, Ö.; Dündar, G. A practical equivalent electrical circuit model for proton exchange membrane fuel cell (PEMFC) systems. Int. J. Hydrogen Energy 2021, 46, 13230–13239. [Google Scholar] [CrossRef]
- O’Hayre, R.; Cha, S.W.; Colella, W.; Prinz, F.B. Fuel Cell Fundamentals; John Wiley & Son: New York, NY, USA, 2006; ISBN 13 978-0-471-74148-0. [Google Scholar]























| Components | Thickness (mm) | Surface Area (cm × cm) |
|---|---|---|
| Teflon gaskets and thin seals | 1.4 | 7 × 7 |
| Passive-aluminum corrugated bipolar plate | 1.0 | 5 × 5 |
| Electrode | 0.35 | 5 × 5 |
| Nafion-112 membrane | 0.127 | 6 × 6 |
| Electrode | 0.35 | 5 × 5 |
| Passive-aluminum corrugated bipolar plate | 1.0 | 5 × 5 |
| Teflon gaskets and thin seals | 1.4 | 7 × 7 |
| Alert Type | Failure | Conditions |
|---|---|---|
| 1 | Sensor | |
| 2 | Threshold | |
| 3 | Reference | |
| 4 | Emergency stop |
| Applied Stimulus | Extracted Parameter |
|---|---|
| Electrical current change, ΔI | Slope change, ΔP |
| Flow rate change, ΔQ | Voltage amplitude, |
| Current intensity oscillation frequency, fΔI | Voltage change, ΔV |
| Gas Used | Cathode (L/min) | Anode (L/min) | Pressure (bar) | Tstack (°C) |
|---|---|---|---|---|
| Air/air | 0.25 | 0.15 | 0.5 | 40, 50, 60, 70 |
| N2/N2 | 0.25 | 0.15 | 0.5 | 40, 50, 60, 70 |
| O2/O2 | 0.25 | 0.15 | 0.5 | 40, 50, 60, 70 |
| H2/H2 | 0.25 | 0.15 | 0.5 | 40, 50, 60, 70 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rubio, A.; Agila, W.; González, L.; Aviles-Cedeno, J. Distributed Intelligence in Autonomous PEM Fuel Cell Control. Energies 2023, 16, 4830. https://doi.org/10.3390/en16124830
Rubio A, Agila W, González L, Aviles-Cedeno J. Distributed Intelligence in Autonomous PEM Fuel Cell Control. Energies. 2023; 16(12):4830. https://doi.org/10.3390/en16124830
Chicago/Turabian StyleRubio, Abel, Wilton Agila, Leandro González, and Jonathan Aviles-Cedeno. 2023. "Distributed Intelligence in Autonomous PEM Fuel Cell Control" Energies 16, no. 12: 4830. https://doi.org/10.3390/en16124830
APA StyleRubio, A., Agila, W., González, L., & Aviles-Cedeno, J. (2023). Distributed Intelligence in Autonomous PEM Fuel Cell Control. Energies, 16(12), 4830. https://doi.org/10.3390/en16124830





