Modeling and Performance Evaluation of Hybrid Solar Cooling Systems Driven by Photovoltaic and Solar Thermal Collectors—Case Study: Greenhouses of Andalusia
Abstract
:1. Introduction
- Evaluation of hybrid solar refrigeration systems with AWCH and ABCH equipment designed to supply agricultural greenhouses’ heat and cold demand. In that sense, the performance of solar cooling systems will be improved by hybridizing solar photovoltaic and solar thermal systems for the supply of heat and cold, and consequently, the area of the solar field can be reduced.
- Development of a general method for modeling a single-effect lithium bromide ABCH using nominal data supplied by the manufacturer. The performance of the absorption equipment will be predicted based on combining the partial solution of the logarithmic mean temperature difference of the evaporator heat exchanger and a polynomial regression of the performance curves from data supplied by the manufacturer’s catalog.
2. Methodology
2.1. Greenhouse Description: Andalusia as Case Study
2.2. Individual Solar Photovoltaic and Solar Thermal Schemes for Cooling and Heating
2.3. Hybrid Solar Thermal and Photovoltaic System for Heating and Cooling Processes
2.4. Control for Discharge and Charge of the Thermal Energy to Heating and Cooling Processes
3. Description of Solar Technologies and Chiller Simulations
3.1. Photovoltaic Modules and Inverter
3.2. Flat Plate Collectors (FPC)
3.3. Air-Cooled Scroll Compressor Chiller (AWCH)
3.4. Method to Simulate the Performance of Single-Effect Absorption Chiller (SEABC Method)
3.5. Energy Indicators of the Solar Cooling System
4. Results and Discussion
4.1. Validation of SEABC Method
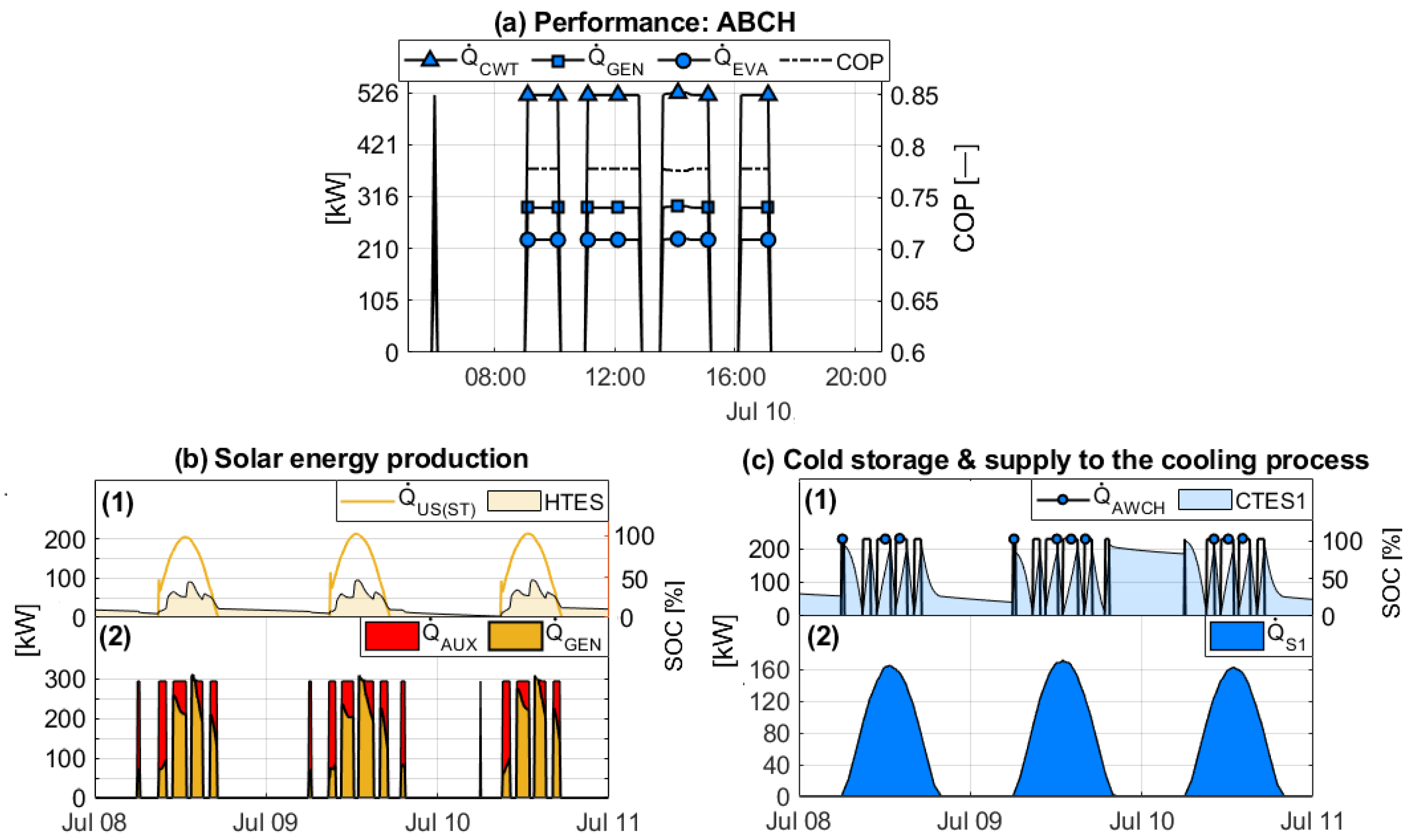
4.2. Performance of the Absorption Chillers
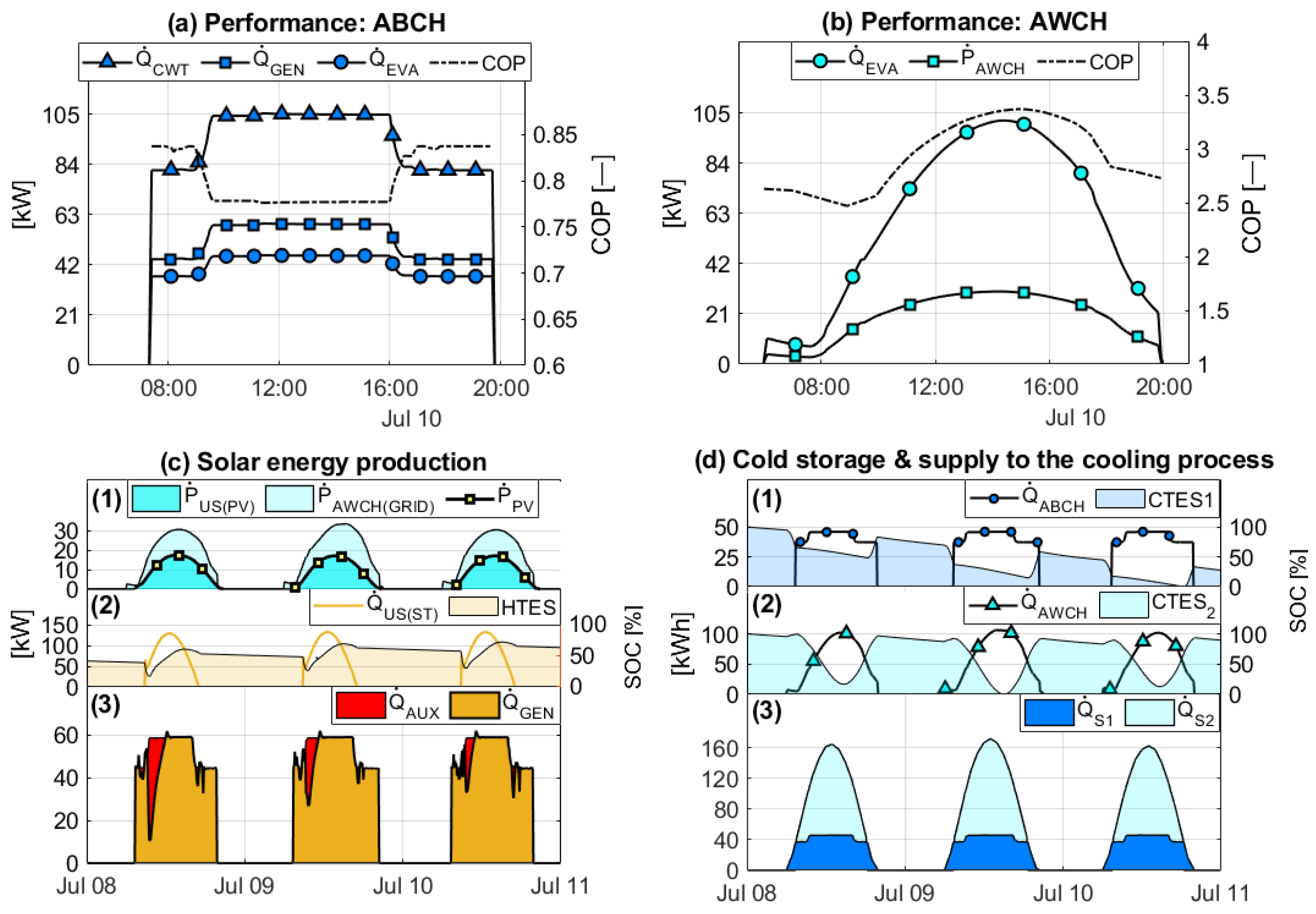
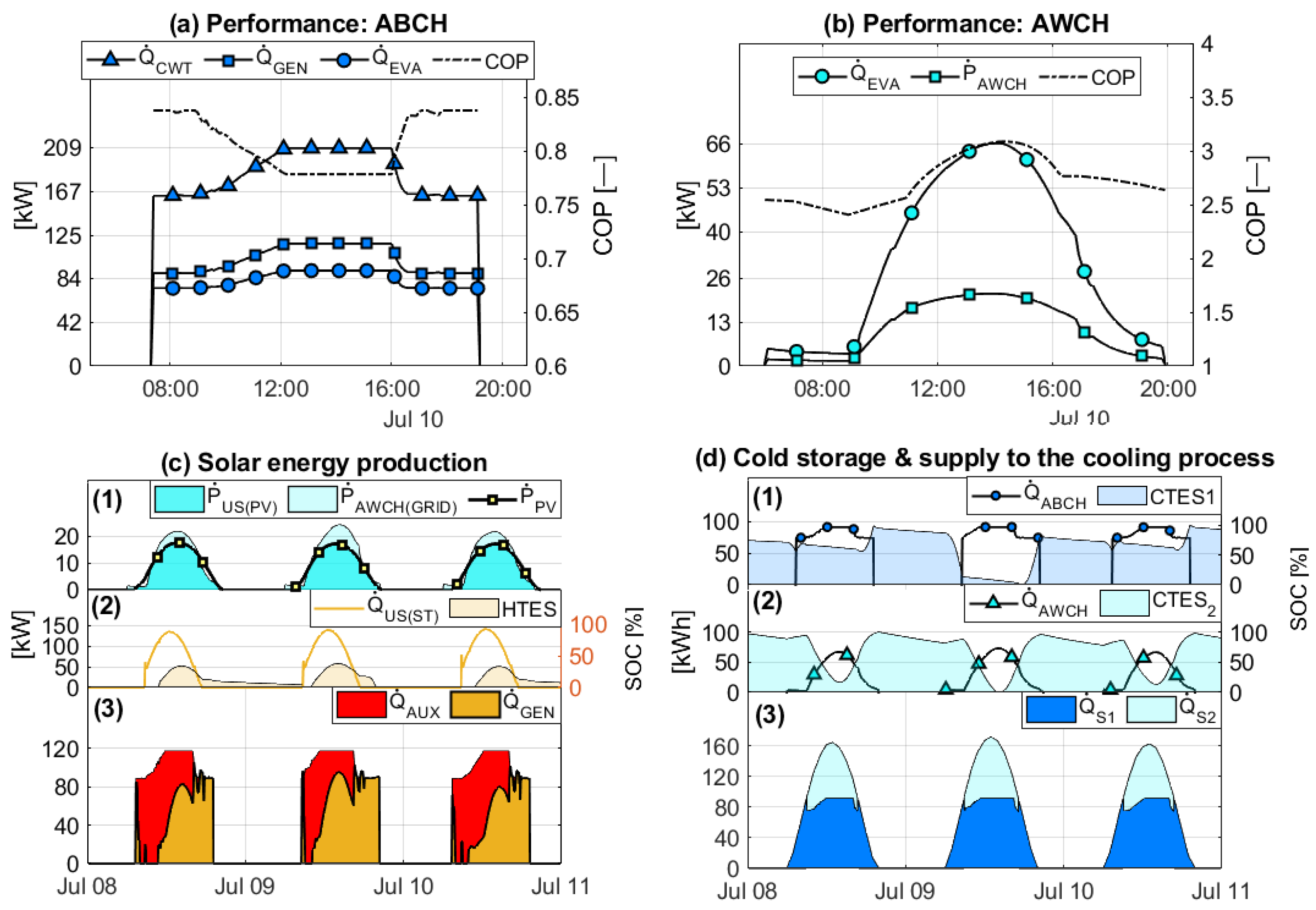
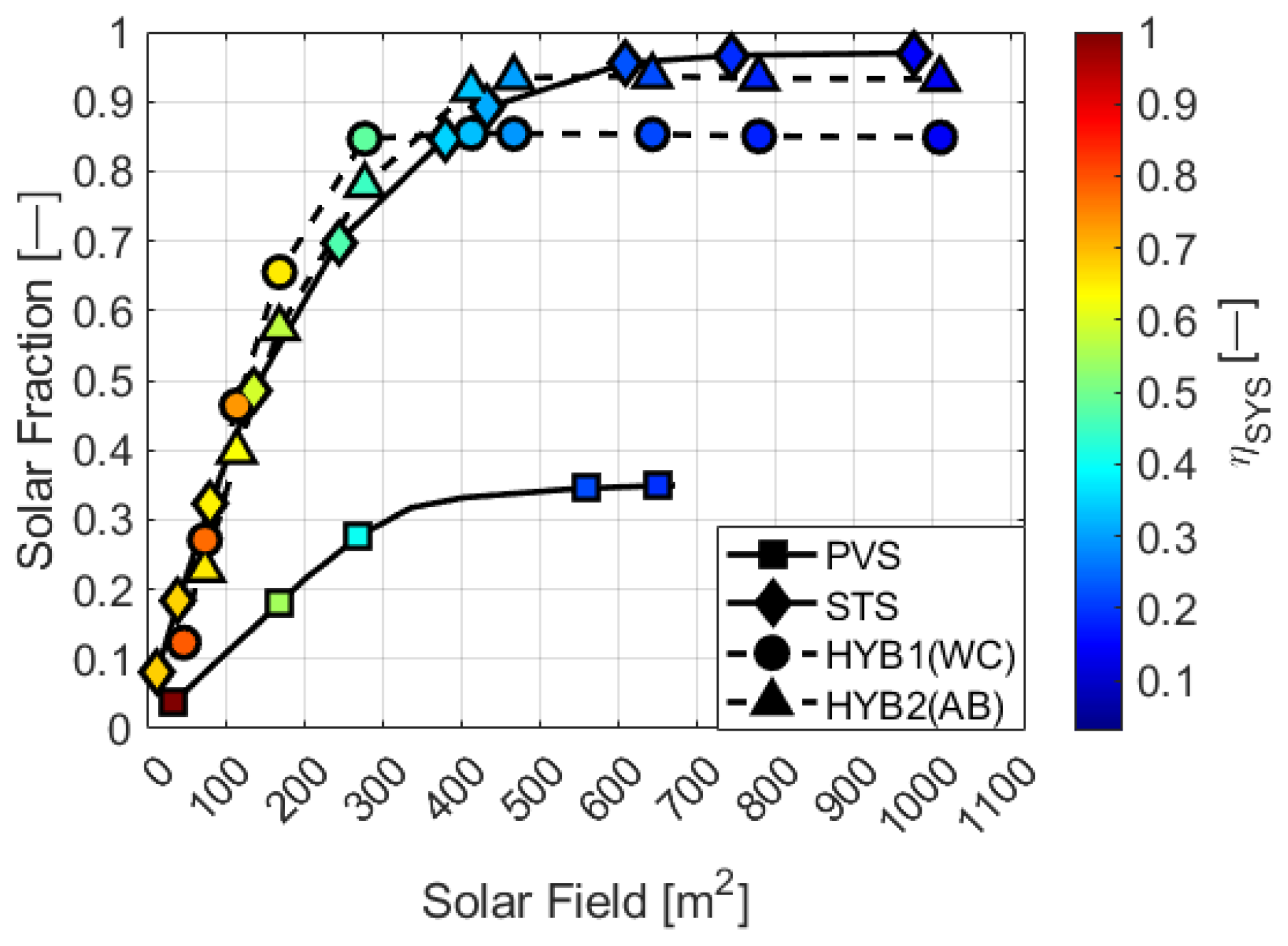
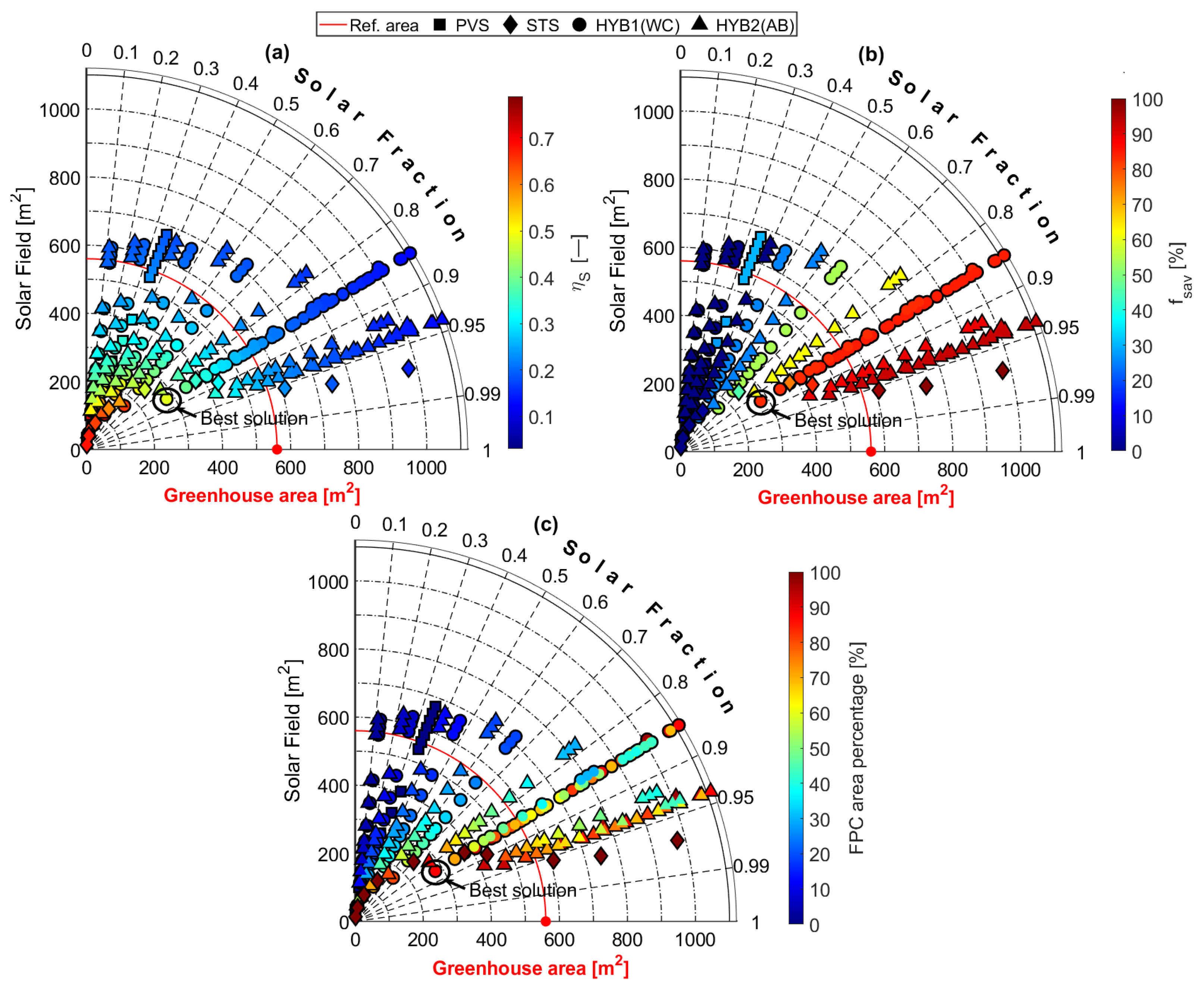
4.3. Performance of the Hybrid Solar Cooling Systems
5. Conclusions
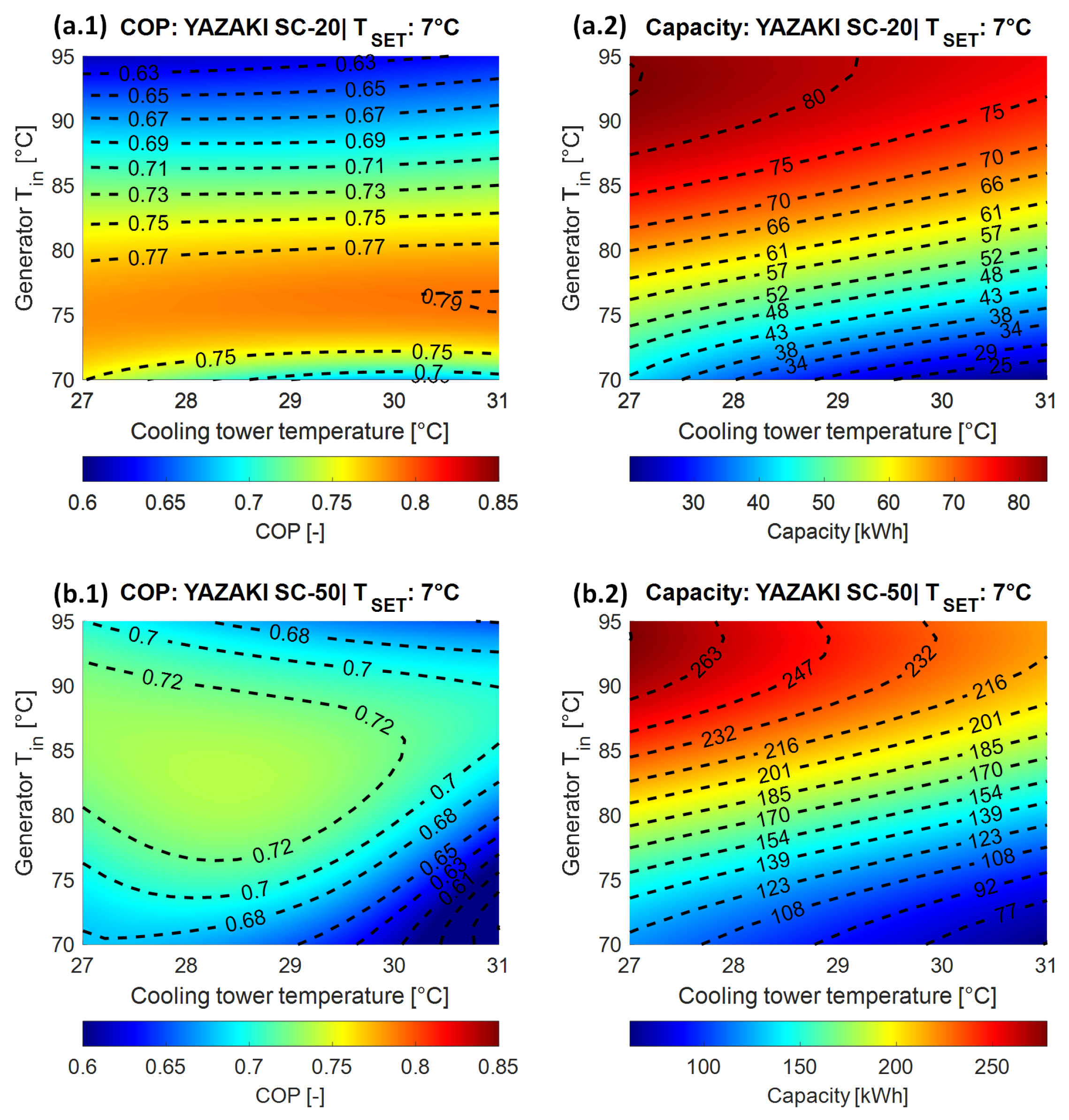
- The SEABC method proposed in this research allows the operation of the ABCH to be replicated, taking as input parameters only six generator inlet temperature points and four cooling tower temperature points, and keeping the fixed.
- The precision of the SEABC method decreases with above 12 C. In contrast, the system’s performance with below 10 C allowed differences of less than 7% to be obtained, demonstrating that the method can predict the behavior of the ABCH with the nominal data and a low number of input temperature data.
- The evaluation of the , , and are necessary to determine the best hybrid configuration. The best results are achieved with the HYB1 configuration with an area of 278 m with a composition of 12% of photovoltaic modules, representing only a quarter of the greenhouse area.
- The increase in the energy efficiency of the HYB1 scheme is due to the AWCH covering most of the cooling demand. This makes it possible to limit the ST field to cover the heating demand and to use the ABCH as a renewable backup. This strategy minimizes the use of auxiliary energy in winter; however, as the capacity of the AWCH compared to the ABCH increases, the efficiency of the system tends to decrease.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Nomenclature: | |
| temperature difference between the module and | |
| flow mass | |
| heat flow rate | |
| efficiency | |
| zero-loss efficiency | |
| A | area |
| absorption chiller | |
| alternative current | |
| maximum AC power rating for the inverter at reference conditions | |
| air-cooled scroll compressor chiller | |
| specific heat capacity | |
| SEABC matrix of coefficients | |
| first order coefficient | |
| second order coefficient | |
| effective thermal capacity | |
| cooling capacity | |
| coefficient of performance | |
| cold thermal energy storage | |
| D | condition |
| direct current | |
| diverger | |
| standard deviation | |
| E | electricity |
| heat energy input | |
| excess of photovoltaic electricity | |
| design energy input fraction | |
| load design factor | |
| nominal capacity fraction | |
| fractional energy saving | |
| flat plate collector | |
| transpiration of sensible heat | |
| I | current | radiation |
| direct radiation on the inclined plane | |
| diffuse radiation on the inclined plane | |
| reflected radiation on the inclined plane | |
| radiation in the inclined plane | |
| k | Boltzmann constant |
| incidence angle modifiers | |
| number of PV cells in series | |
| diode ideality factor | |
| P | electricity power |
| part load ratio | |
| solar photovoltaic | |
| R | electric resistance |
| coefficient of determination | |
| S | effective absorbed solar radiation |
| general method to estimate the performance of simple effect absorption chiller | |
| solar fraction | |
| signal | |
| state of charge | |
| solar thermal | |
| standard conditions | |
| T | temperature |
| internal outlet temperature of the evaporator | |
| internal inlet temperature of the evaporator | |
| heat transfer coefficient value | |
| V | voltage |
| wind speed | |
| coefficients of UA | |
| total mean logarithmic temperature difference | |
| polynomial equation SEABC | |
| matrix reorganized | |
| Subscript: | |
| incidence angle | |
| a | annual |
| absorption | |
| alternating current | |
| ambient temperature | |
| auxiliary | |
| average | |
| boiler | |
| c | load thermals for cooling |
| gas combustion | |
| conduction–convection losses through the covert | |
| condenser | |
| chiller | |
| collector | |
| module | |
| maximum charging | |
| minimum charging | |
| compressor | |
| correction | |
| cooling water tower | |
| direct current | |
| e | electrical consumption |
| evaporator | |
| generator | |
| grid electricity consumption | |
| h | load thermals for heating |
| desorption process heat exchanger | |
| inlet | |
| infiltration losses with closed windows | |
| j | number of coefficients |
| L | light |
| logarithmic mean | |
| module | |
| maximum power | |
| monthly | |
| n | nominal |
| nominal operating cell temperature | |
| o | diode reverse saturation |
| open circuit voltage | |
| outlet | |
| p | number of coefficients of |
| r | reference |
| s | series resistance |
| main chiller of the cooling system | |
| auxiliary cooling system | |
| short circuit current | |
| shunt resistance | |
| radiation interchange through the greenhouse elements and the sky | |
| gain or loss of heat by the soil | |
| useful | |
| v | ventilation losses |
| w | testing |
Appendix A
Appendix A.1. SEABC Method
| SC-20 | SC-50 | ||||
|---|---|---|---|---|---|

References
- United Nations; Framework Convention on Climate Change. Paris Agreement. 2015. Available online: https://unfccc.int/sites/default/files/english_paris_agreement.pdf (accessed on 25 May 2020).
- OECD; IEA. The Future of Cooling. 2018. Available online: https://iea.blob.core.windows.net/assets/0bb45525-277f-4c9c-8d0c-9c0cb5e7d525/The_Future_of_Cooling.pdf (accessed on 13 June 2020).
- Geraldi, M.S.; Ghisi, E. Building-level and stock-level in contrast: A literature review of the energy performance of buildings during the operational stage. Energy Build. 2020, 211, 109810. [Google Scholar] [CrossRef]
- Almasri, R.A.; Abu-Hamdeh, N.H.; Esmaeil, K.K.; Suyambazhahan, S. Thermal solar sorption cooling systems—A review of principle, technology, and applications. Alex. Eng. J. 2022, 61, 367–402. [Google Scholar] [CrossRef]
- Holka, M.; Kowalska, J.; Jakubowska, M. Reducing Carbon Footprint of Agriculture—Can Organic Farming Help to Mitigate Climate Change? Agriculture 2022, 12, 1383. [Google Scholar] [CrossRef]
- Carreño-Ortega, A.; Galdeano-Gómez, E.; Pérez-Mesa, J.C.; Galera-Quiles, M.D.C. Policy and Environmental Implications of Photovoltaic Systems in Farming in Southeast Spain: Can Greenhouses Reduce the Greenhouse Effect? Energies 2017, 10, 761. [Google Scholar] [CrossRef] [Green Version]
- Gil, J.D.; Ramos-Teodoro, J.; Romero-Ramos, J.A.; Escobar, R.; Cardemil, J.M.; Giagnocavo, C.; Pérez, M. Demand-Side Optimal Sizing of a Solar Energy–Biomass Hybrid System for Isolated Greenhouse Environments: Methodology and Application Example. Energies 2021, 14, 3724. [Google Scholar] [CrossRef]
- Cabrera, F.; Sánchez-Molina, J.; Zaragoza, G.; Pérez-García, M.; Rodríguez-Díaz, F. Chapter 8: Renewable energy technologies for greenhouses in semi-arid climates. In Sustainable Energy Developments, 13th ed.; Lovegrove, K., Stein, W., Eds.; CRC Press: Boca Raton, FL, USA, 2017; pp. 153–193. [Google Scholar] [CrossRef]
- Settino, J.; Sant, T.; Micallef, C.; Farrugia, M.; Spiteri Staines, C.; Licari, J.; Micallef, A. Overview of solar technologies for electricity, heating and cooling production. Renew. Sustain. Energy Rev. 2018, 90, 892–909. [Google Scholar] [CrossRef]
- NREL. Best Research-Cell Efficiency Chart. Available online: https://www.nrel.gov/pv/cell-efficiency.html (accessed on 6 April 2023).
- Eicker, U.; Pietruschka, D.; Schmitt, A.; Haag, M. Comparison of photovoltaic and solar thermal cooling systems for office buildings in different climates. Sol. Energy 2015, 118, 243–255. [Google Scholar] [CrossRef]
- Chen, Y.; Liu, Y.; Liu, J.; Luo, X.; Wang, D.; Wang, Y.; Liu, J. Design and adaptability of photovoltaic air conditioning system based on office buildings. Sol. Energy 2020, 202, 17–24. [Google Scholar] [CrossRef]
- Aguilar, F.; Crespí-Llorens, D.; Quiles, P. Techno-economic analysis of an air conditioning heat pump powered by photovoltaic panels and the grid. Sol. Energy 2019, 180, 169–179. [Google Scholar] [CrossRef]
- Aguilar, F.; Aledo, S.; Quiles, P. Experimental analysis of an air conditioner powered by photovoltaic energy and supported by the grid. Appl. Therm. Eng. 2017, 123, 486–497. [Google Scholar] [CrossRef]
- Luerssen, C.; Gandhi, O.; Reindl, T.; Sekhar, C.; Cheong, D. Levelised Cost of Storage (LCOS) for solar-PV-powered cooling in the tropics. Appl. Energy 2019, 242, 640–654. [Google Scholar] [CrossRef]
- Calise, F. Thermoeconomic analysis and optimization of high efficiency solar heating and cooling systems for different Italian school buildings and climates. Energy Build. 2010, 42, 992–1003. [Google Scholar] [CrossRef]
- Hirmiz, R.; Lightstone, M.; Cotton, J. Performance enhancement of solar absorption cooling systems using thermal energy storage with phase change materials. Appl. Energy 2018, 223, 11–29. [Google Scholar] [CrossRef]
- Prieto, J.; Ajnannadhif, R.; Fernández-del Olmo, P.; Coronas, A. Integration of a heating and cooling system driven by solar thermal energy and biomass for a greenhouse in Mediterranean climates. Appl. Therm. Eng. 2023, 221, 119928. [Google Scholar] [CrossRef]
- Villarruel-Jaramillo, A.; Pérez-García, M.; Cardemil, J.M.; Escobar, R.A. Review of Polygeneration Schemes with Solar Cooling Technologies and Potential Industrial Applications. Energies 2021, 14, 6450. [Google Scholar] [CrossRef]
- Rosales-Pérez, J.F.; Villarruel-Jaramillo, A.; Romero-Ramos, J.A.; Pérez-García, M.; Cardemil, J.M.; Escobar, R. Hybrid System of Photovoltaic and Solar Thermal Technologies for Industrial Process Heat. Energies 2023, 16, 2220. [Google Scholar] [CrossRef]
- Labus, J.; Bruno, J.C.; Coronas, A. Performance analysis of small capacity absorption chillers by using different modeling methods. Appl. Therm. Eng. 2013, 58, 305–313. [Google Scholar] [CrossRef]
- Puig-Arnavat, M.; López-Villada, J.; Bruno, J.C.; Coronas, A. Analysis and parameter identification for characteristic equations of single- and double-effect absorption chillers by means of multivariable regression. Int. J. Refrig. 2010, 33, 70–78. [Google Scholar] [CrossRef]
- Tawalbeh, M.; Aljaghoub, H.; Alami, A.H.; Olabi, A.G. Selection criteria of cooling technologies for sustainable greenhouses: A comprehensive review. Therm. Sci. Eng. Prog. 2023, 38, 101666. [Google Scholar] [CrossRef]
- Pérez Neira, D.; Soler Montiel, M.; Delgado Cabeza, M.; Reigada, A. Energy use and carbon footprint of the tomato production in heated multi-tunnel greenhouses in Almeria within an exporting agri-food system context. Sci. Total Environ. 2018, 628–629, 1627–1636. [Google Scholar] [CrossRef]
- ASABE. Heating, Ventilating and Cooling Greenhouses; ASAE EP 406.4; Technical Report; American Society of Agricultural and Biological Engineers: St. Joseph, MI, USA, 2003. [Google Scholar]
- Meteonorm V7.0.22.8. Available online: https://www.meteonorm.com/ (accessed on 20 January 2021).
- Duffie, J.A.; Beckman, W.A. Solar Engineering of Thermal Processes, 4th ed.; John Wiley and Sons, Ltd.: Madison, WI, USA, 2013. [Google Scholar] [CrossRef]
- De Soto, W.; Klein, S.; Beckman, W. Improvement and validation of a model for photovoltaic array performance. Sol. Energy 2006, 80, 78–88. [Google Scholar] [CrossRef]
- King, D.L.; Boyson, W.E.; Kratochvi, J.A. Photovoltaic Array Performance Model; Technical Report; SANDIA National Laboratories: Albuquerque, NM, USA, 2004. Available online: https://www.osti.gov/servlets/purl/919131 (accessed on 23 May 2022).
- Rosiek, S.; Batlles, F.J. Renewable energy solutions for building cooling, heating and power system installed in an institutional building: Case study in southern Spain. Renew. Sustain. Energy Rev. 2013, 26, 147–168. [Google Scholar] [CrossRef]
- Ramos-Teodoro, J. Energy Management Strategies in Production Environments with Support of Solar Energy. Ph.D. Thesis, Departamento de informática, Universidad de Almería, Almería, Spain, 2021. [Google Scholar]
- National Renewable Energy Laboratory; Golden, C. System Advisor Model Version 2020.11.29 (SAM 2020.11.29). Available online: https://sam.nrel.gov/photovoltaic/pv-sub-page-3.html (accessed on 3 June 2022).
- Tian, Z.; Perers, B.; Furbo, S.; Fan, J. Analysis and validation of a quasi-dynamic model for a solar collector field with flat plate collectors and parabolic trough collectors in series for district heating. Energy 2018, 142, 130–138. [Google Scholar] [CrossRef] [Green Version]
- Rosiek, S.; Batlles, F. Integration of the solar thermal energy in the construction: Analysis of the solar-assisted air-conditioning system installed in CIESOL building. Renew. Energy 2009, 34, 1423–1431. [Google Scholar] [CrossRef]
- Millennium®, Y. Model YCAL Style C Air-Cooled Scroll Chiller Engineering Guide. Available online: https://goo.su/fBxG (accessed on 7 July 2022).
- Martínez, J.C.; Martinez, P.; Bujedo, L.A. Development and experimental validation of a simulation model to reproduce the performance of a 17.6 kW LiBr–water absorption chiller. Renew. Energy 2016, 86, 473–482. [Google Scholar] [CrossRef]
- Manu, S.; Chandrashekar, T. A simulation study on performance evaluation of single-stage LiBr–H2O vapor absorption heat pump for chip cooling. Int. J. Sustain. Built Environ. 2016, 5, 370–386. [Google Scholar] [CrossRef] [Green Version]
- YAZAKI Energy Systems. Water-Fired Chiller/Chiller-Heater. Available online: http://jmp.sh/FacJtkG (accessed on 5 November 2021).
- Zenhäusern, D.; Gagliano, A.; Jonas, D.; Marco, G.; Hadorn, J.; Lämmle, M.; Herrando, M. SHC Task 60: Key Performance Indicators for PVT Systems. Technical Report, IEA SHC Task 60. 2020. Available online: https://www.iea-shc.org/Data/Sites/1/publications/IEA-SHC-Task60-D1-Key-Performance-Indicators.pdf (accessed on 2 February 2023).
- Eicher, S.; Bony, J. Definition of Main System Boundaries and Performance Figures for Reporting on SHP Systems. Technical Report, IEA-Solar Heating and Cooling Programme. 2013. Available online: http://www.iea-shc.org/data/sites/1/publications/T44A38_Rep_B1_SHP_Perf_definition%20approved.pdf (accessed on 23 April 2023).
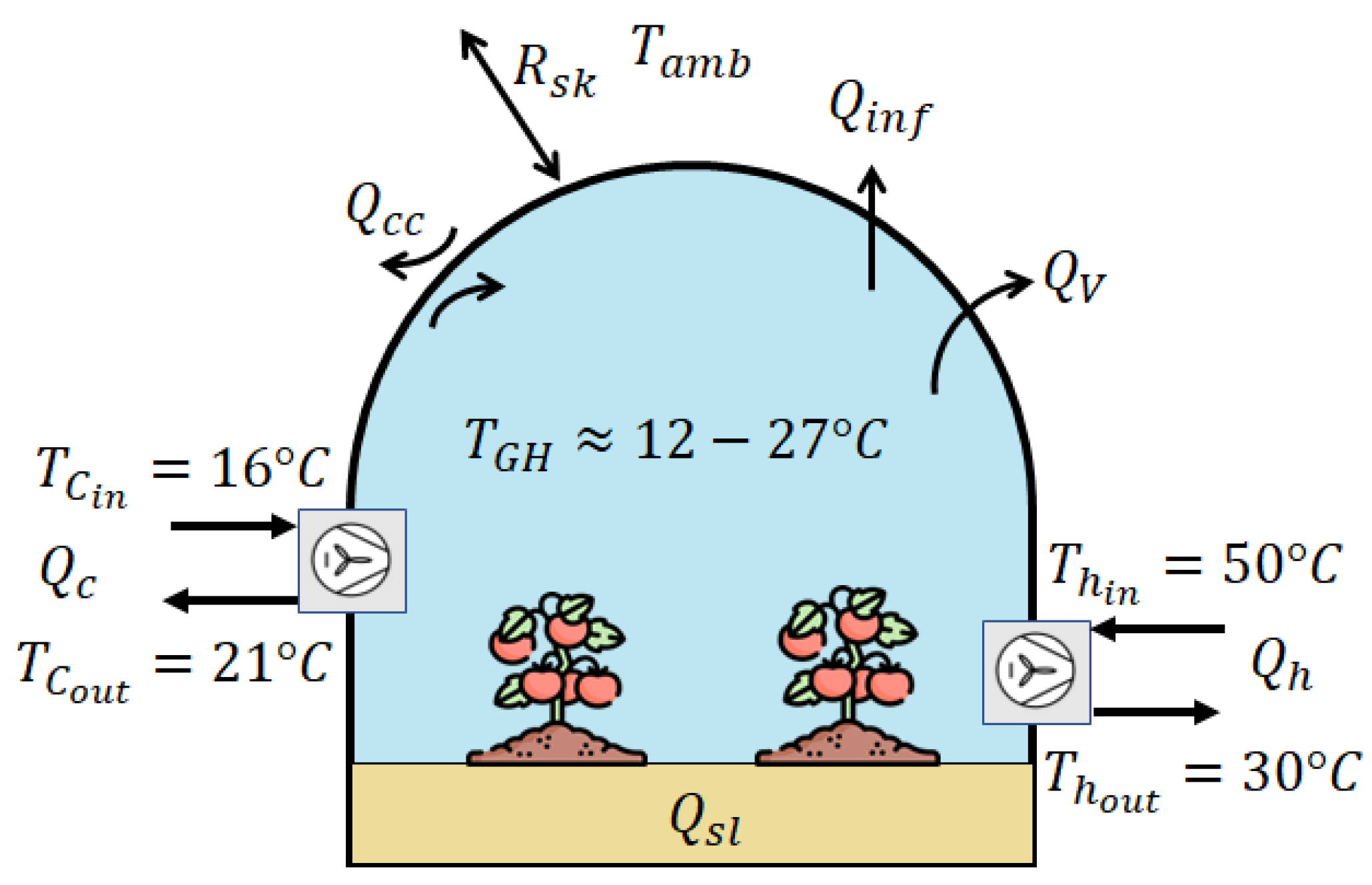
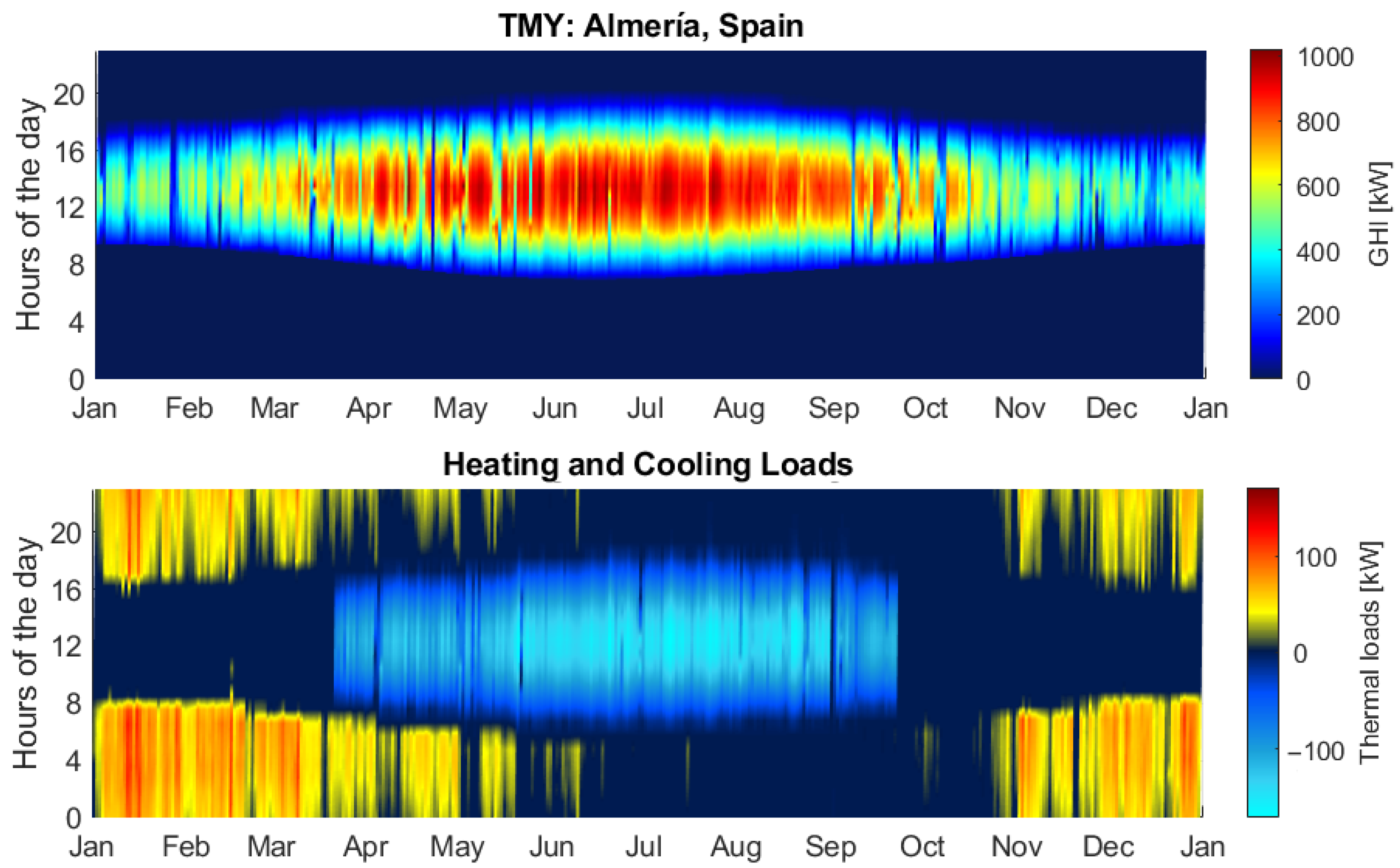

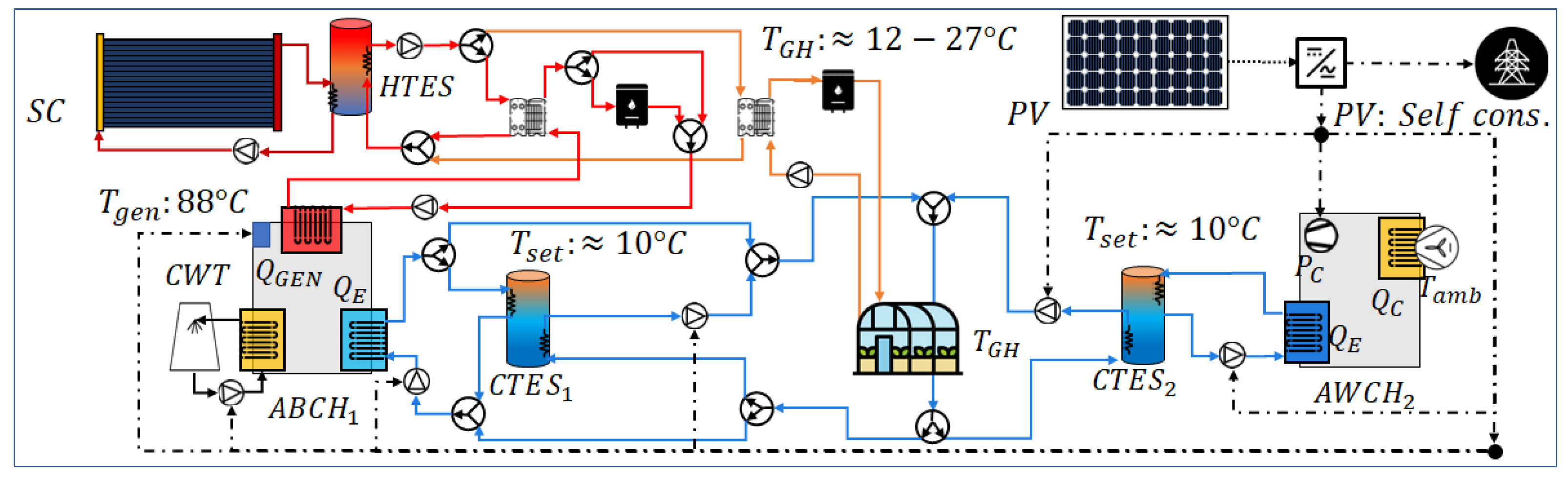
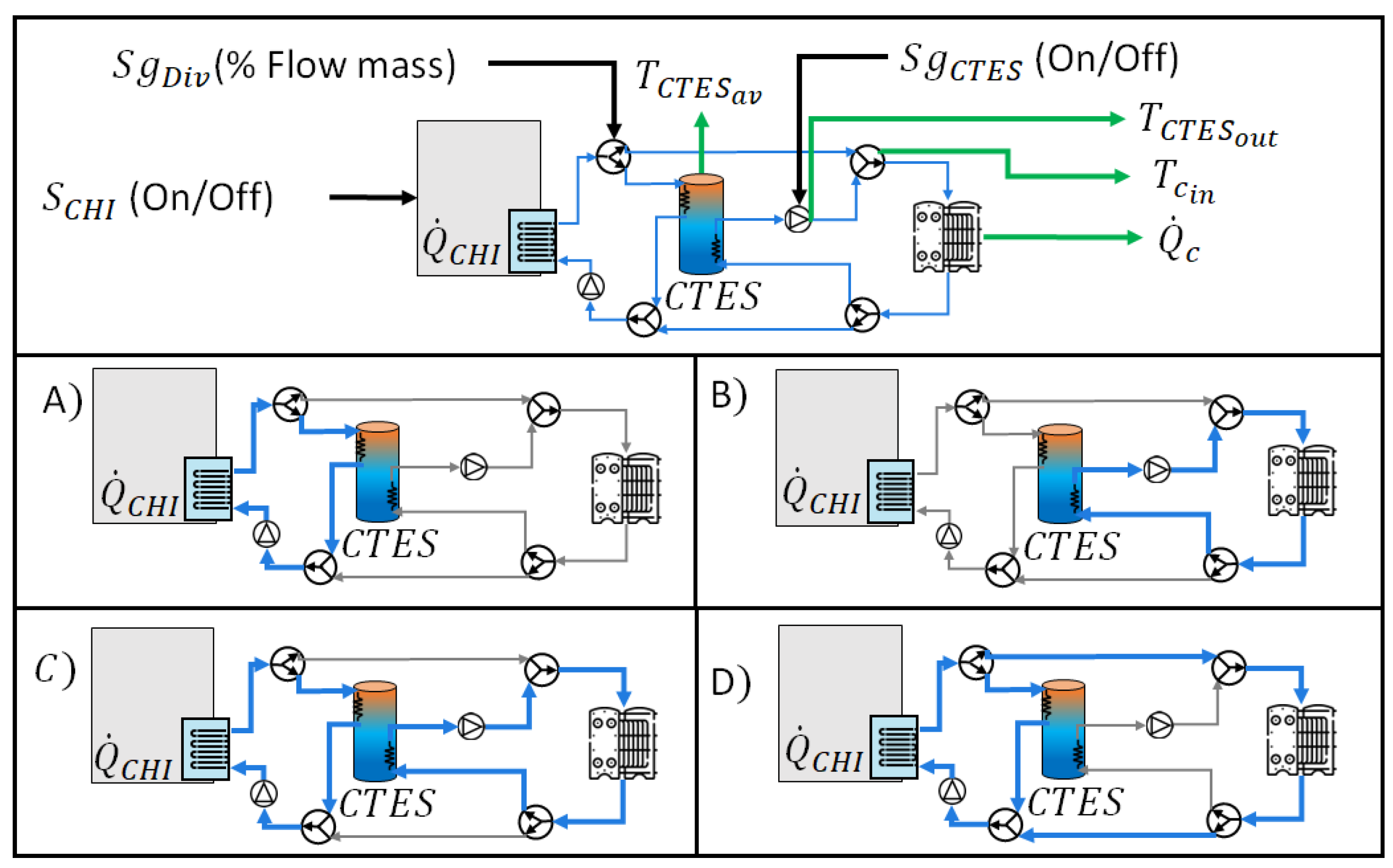
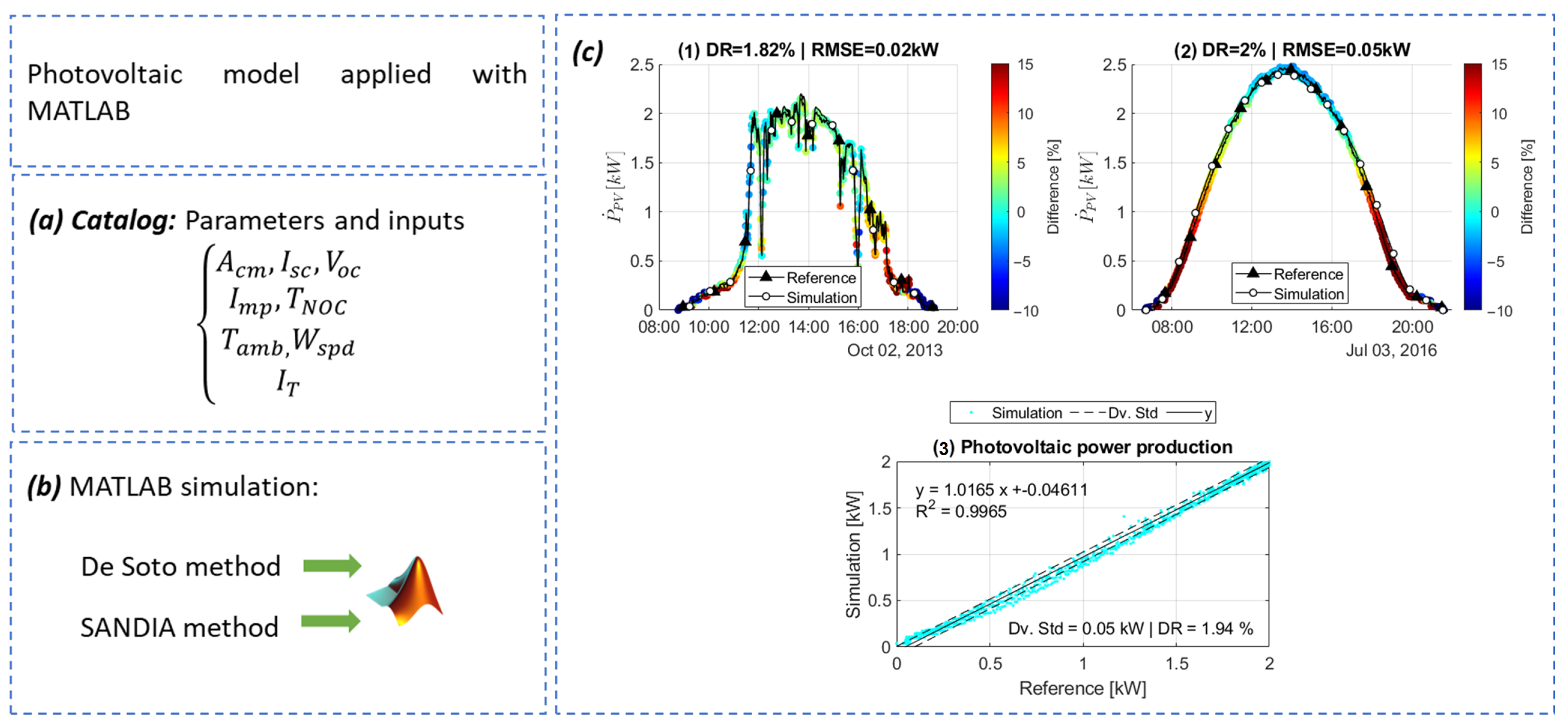


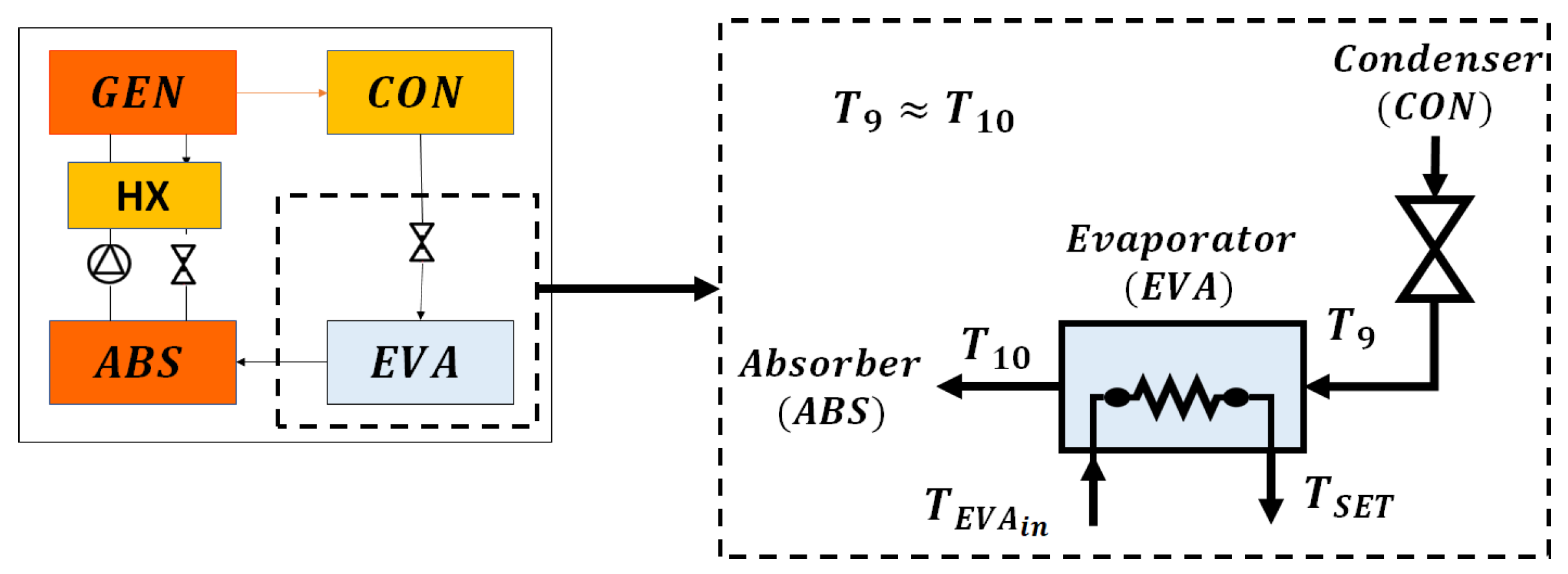
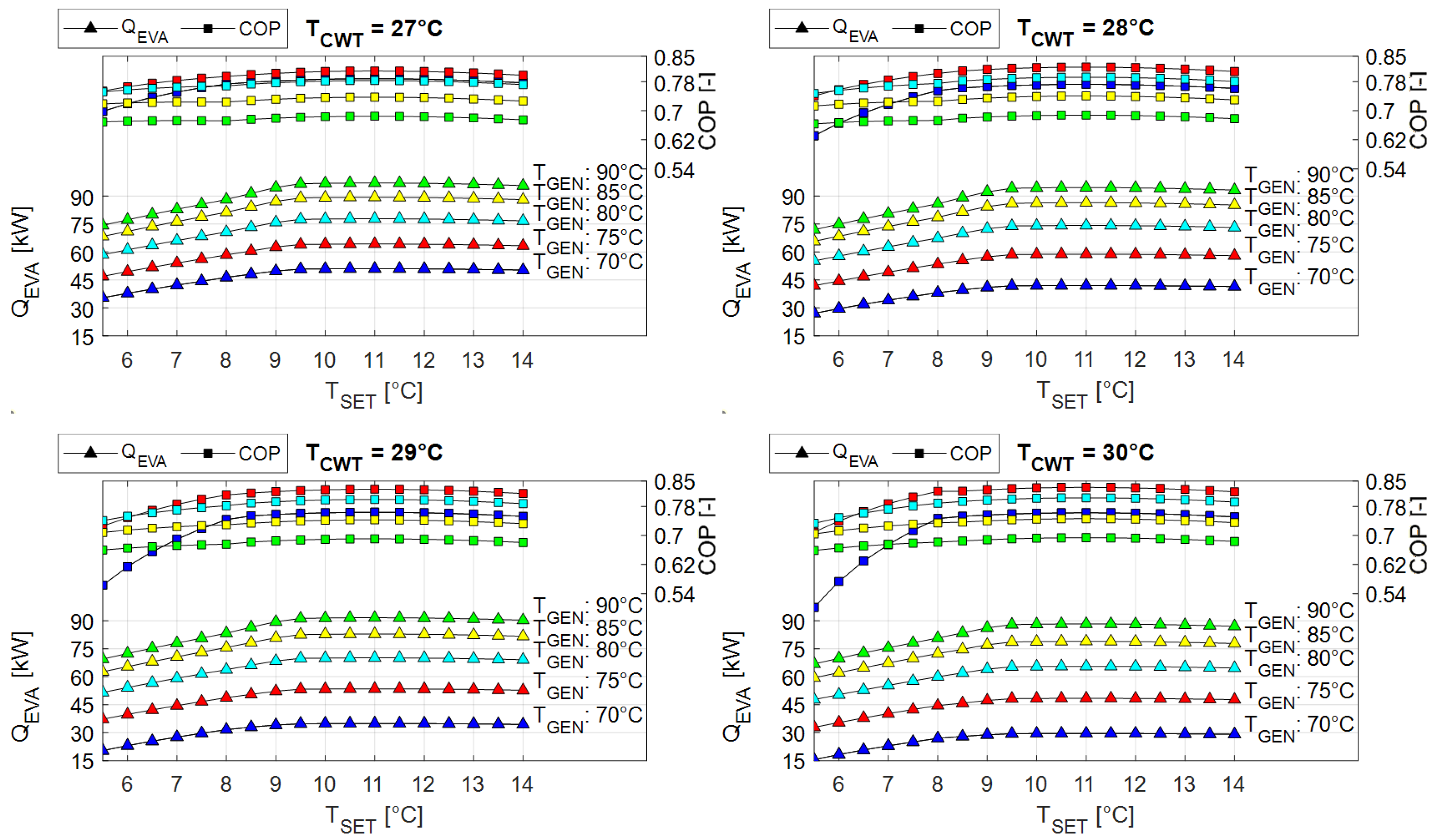
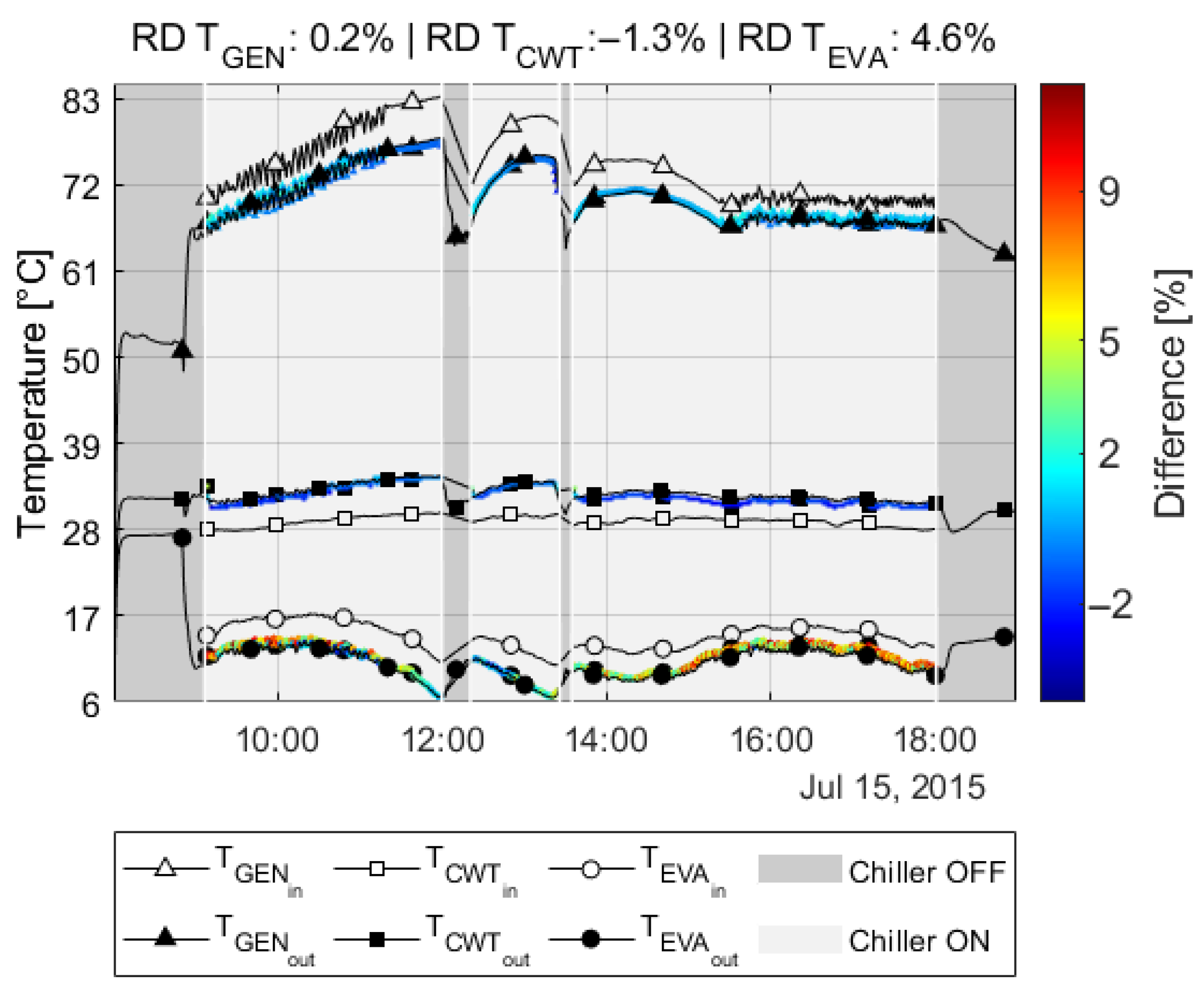
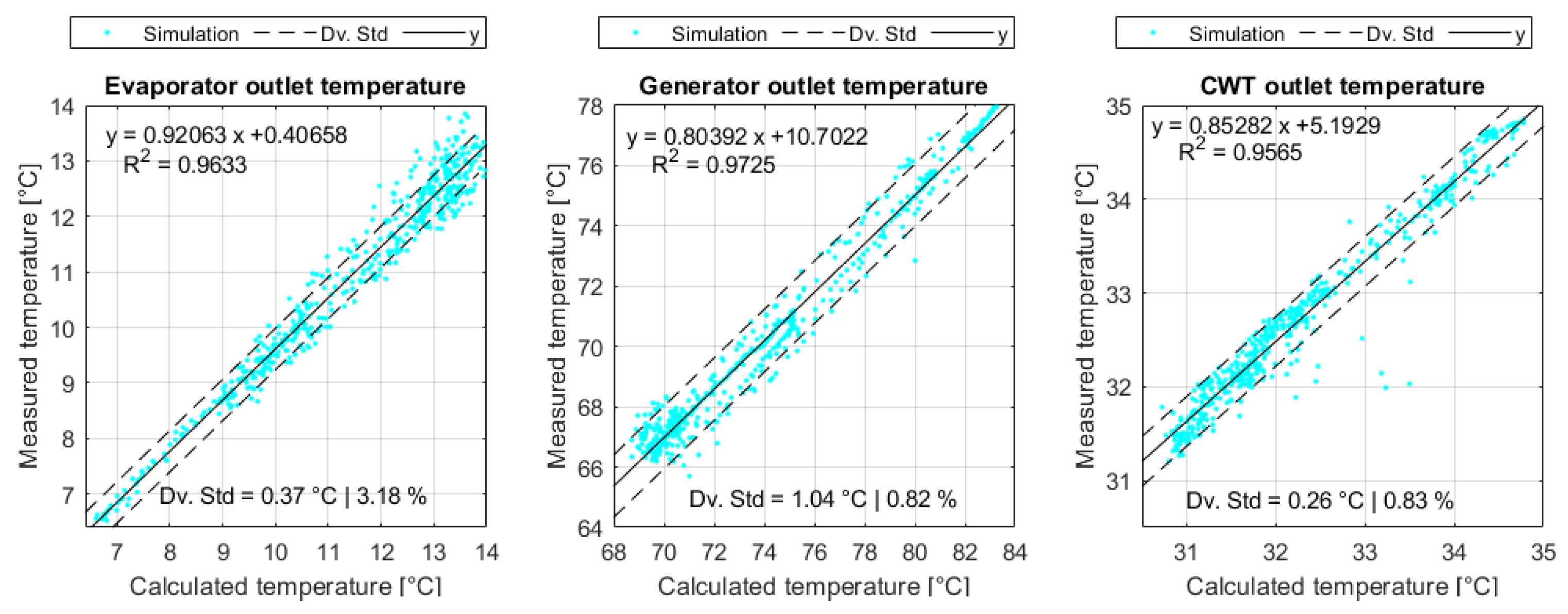
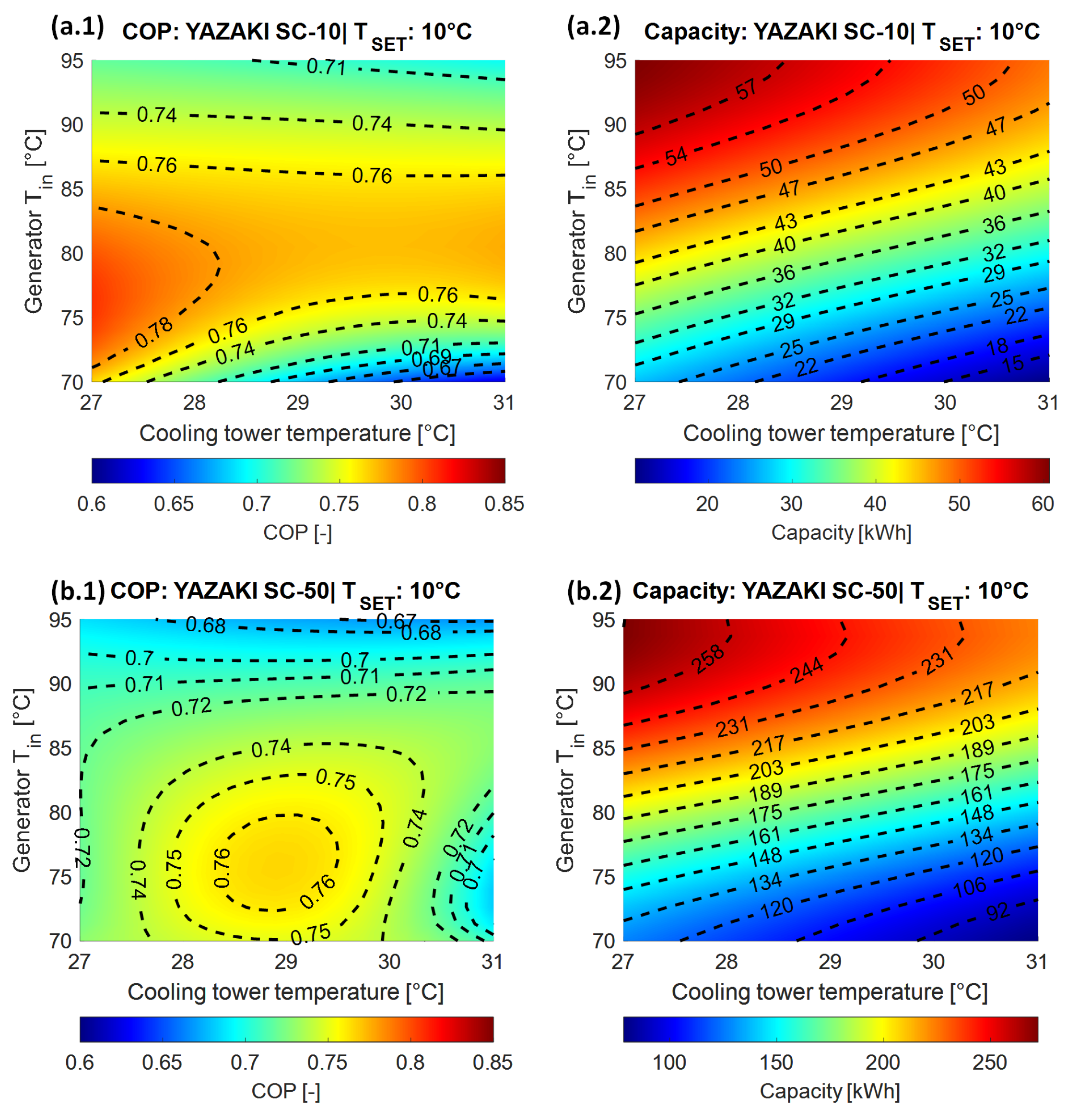
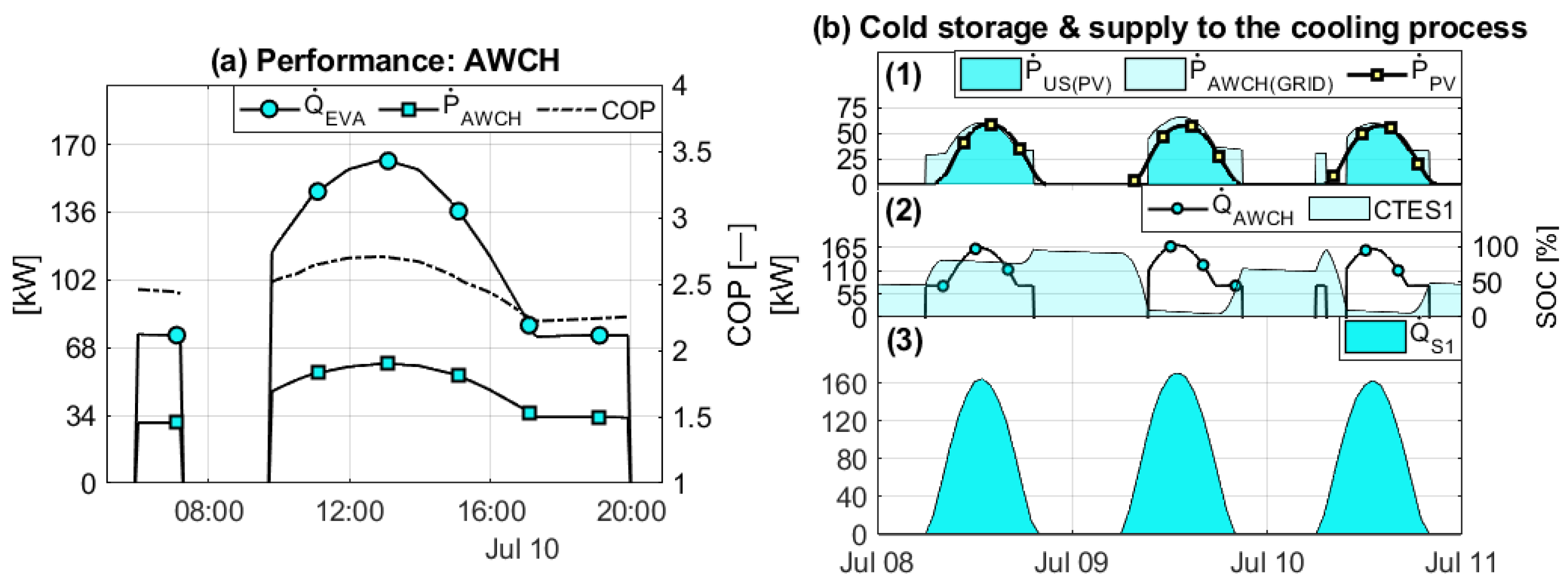


| Type of Greenhouse | Crop | Enclosure Material | [m] | [W/(m K)] | [%] | |
|---|---|---|---|---|---|---|
| Gabled plastic roof | Tomatoes | LDPE | 1120 | 1.34 | 8 | 65 |
| Condition of Control | A | A | B | B | B | C | C | D |
|---|---|---|---|---|---|---|---|---|
| CR1 | No | No | Yes | No | No | Yes | Yes | Yes |
| CR2 | Yes | No | No | No | Yes | Yes | No | Yes |
| CR3 | Yes | Yes | No | No | No | Yes | Yes | No |
| On | On | Off | Off | Off | On | On | On | |
| Off | Off | Off | /Pr | |||||
| Off | Off | On | On | On | On | On | Off |
| Material | Ref. | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| [m] | |||||||||
| Mono-c-Si | 23.8 | 445 | 1.87 | 11.34 | 49.9 | 10.7 | 41.6 | 45.3 | [32] |
| [m] | [−] | [W/mK] | [W/mK] | [kg/mK] | [kJ/sm] | |
|---|---|---|---|---|---|---|
| 13.57 | 0.779 | 2.41 | 0.015 | 6.798 | 0.98 | 0.061 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Villarruel-Jaramillo, A.; Rosales-Pérez, J.F.; Pérez-García, M.; Cardemil, J.M.; Escobar, R. Modeling and Performance Evaluation of Hybrid Solar Cooling Systems Driven by Photovoltaic and Solar Thermal Collectors—Case Study: Greenhouses of Andalusia. Energies 2023, 16, 4888. https://doi.org/10.3390/en16134888
Villarruel-Jaramillo A, Rosales-Pérez JF, Pérez-García M, Cardemil JM, Escobar R. Modeling and Performance Evaluation of Hybrid Solar Cooling Systems Driven by Photovoltaic and Solar Thermal Collectors—Case Study: Greenhouses of Andalusia. Energies. 2023; 16(13):4888. https://doi.org/10.3390/en16134888
Chicago/Turabian StyleVillarruel-Jaramillo, Andrés, Josué F. Rosales-Pérez, Manuel Pérez-García, José M. Cardemil, and Rodrigo Escobar. 2023. "Modeling and Performance Evaluation of Hybrid Solar Cooling Systems Driven by Photovoltaic and Solar Thermal Collectors—Case Study: Greenhouses of Andalusia" Energies 16, no. 13: 4888. https://doi.org/10.3390/en16134888
APA StyleVillarruel-Jaramillo, A., Rosales-Pérez, J. F., Pérez-García, M., Cardemil, J. M., & Escobar, R. (2023). Modeling and Performance Evaluation of Hybrid Solar Cooling Systems Driven by Photovoltaic and Solar Thermal Collectors—Case Study: Greenhouses of Andalusia. Energies, 16(13), 4888. https://doi.org/10.3390/en16134888








