Fault Arc Detection Based on Channel Attention Mechanism and Lightweight Residual Network
Abstract
:1. Introduction
2. Materials and Methods
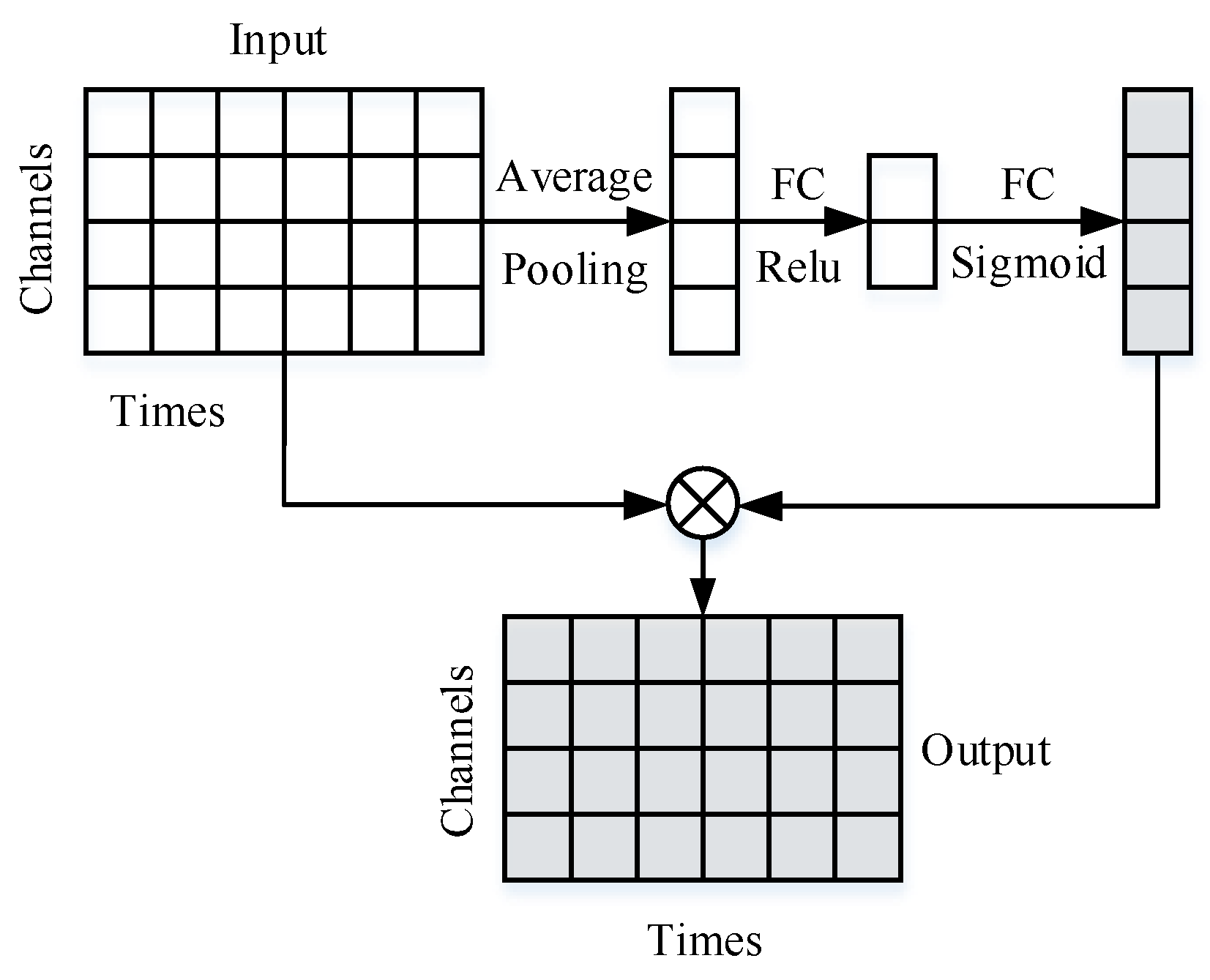
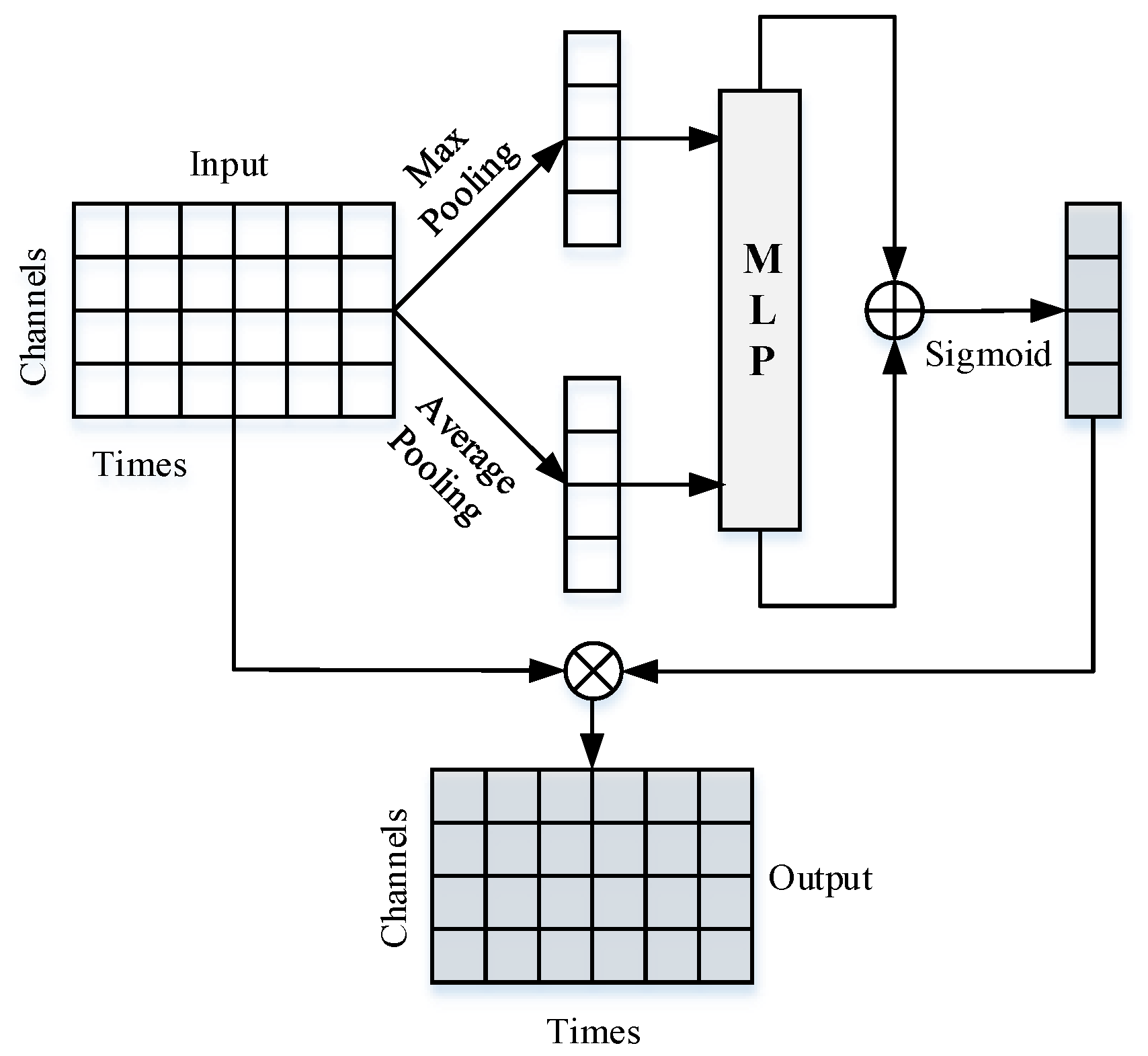
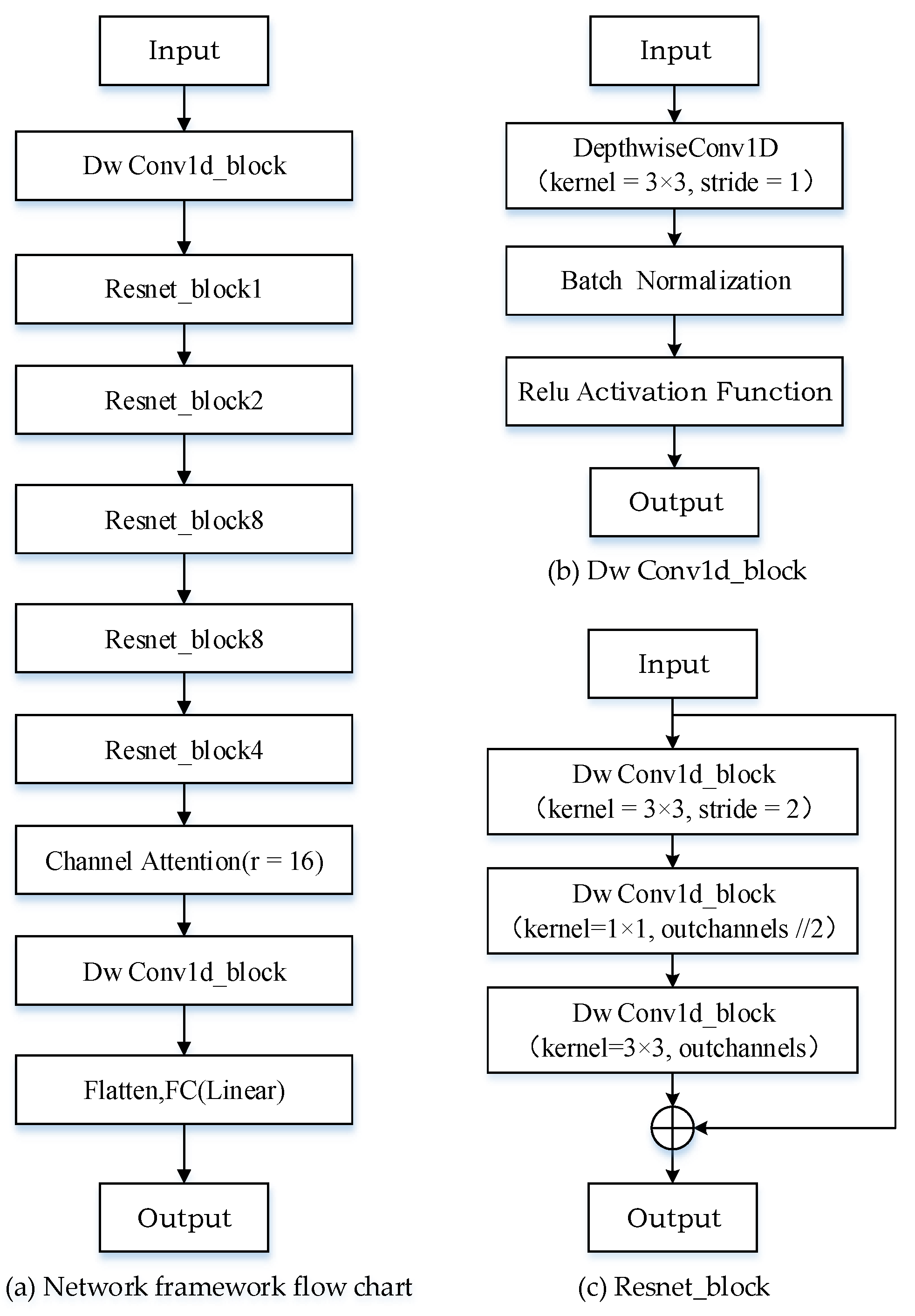
2.1. One-Dimensional Channel Attention Mechanism
2.2. Residual Neural Network Structure
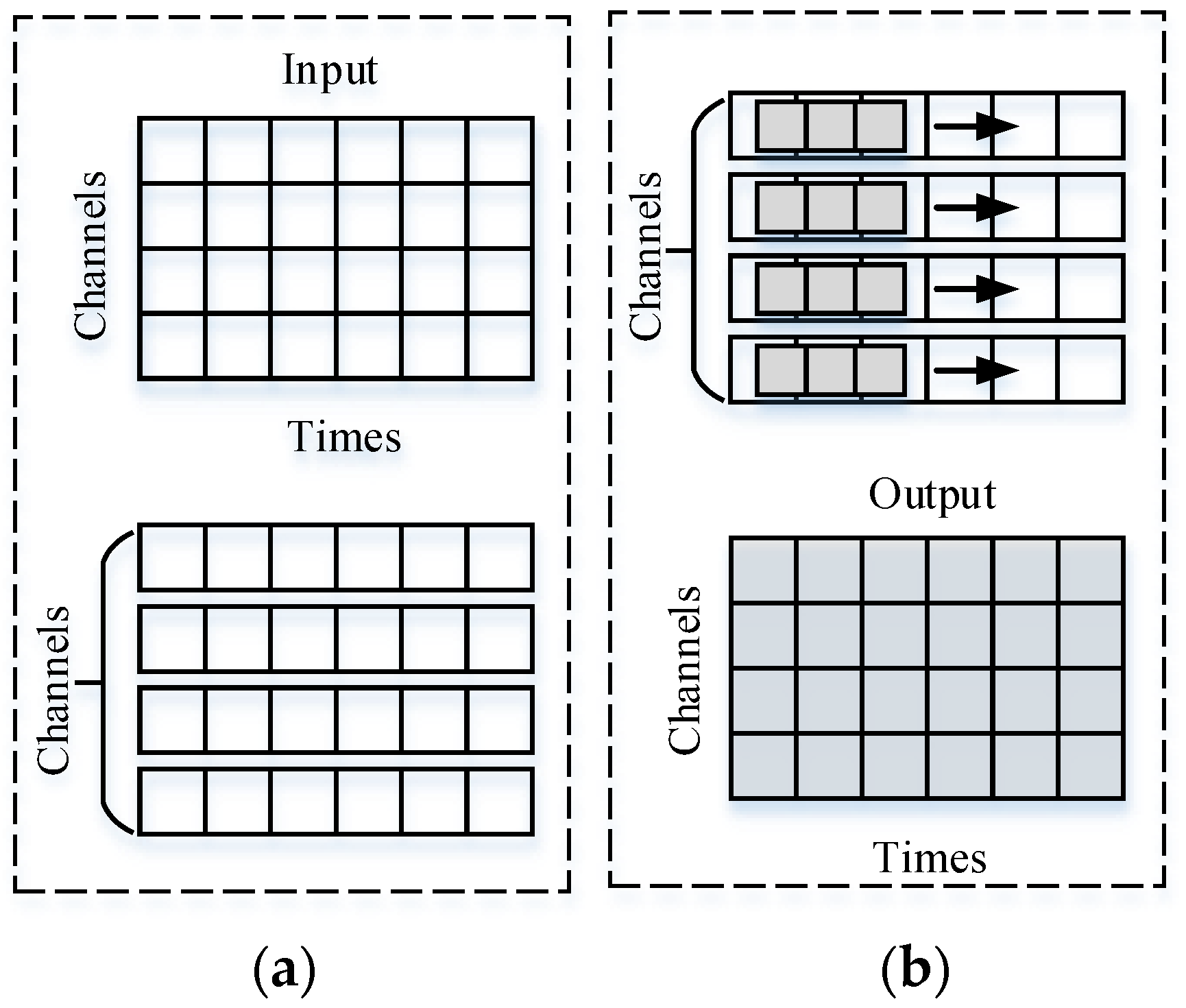
2.3. Depth Separable Convolution
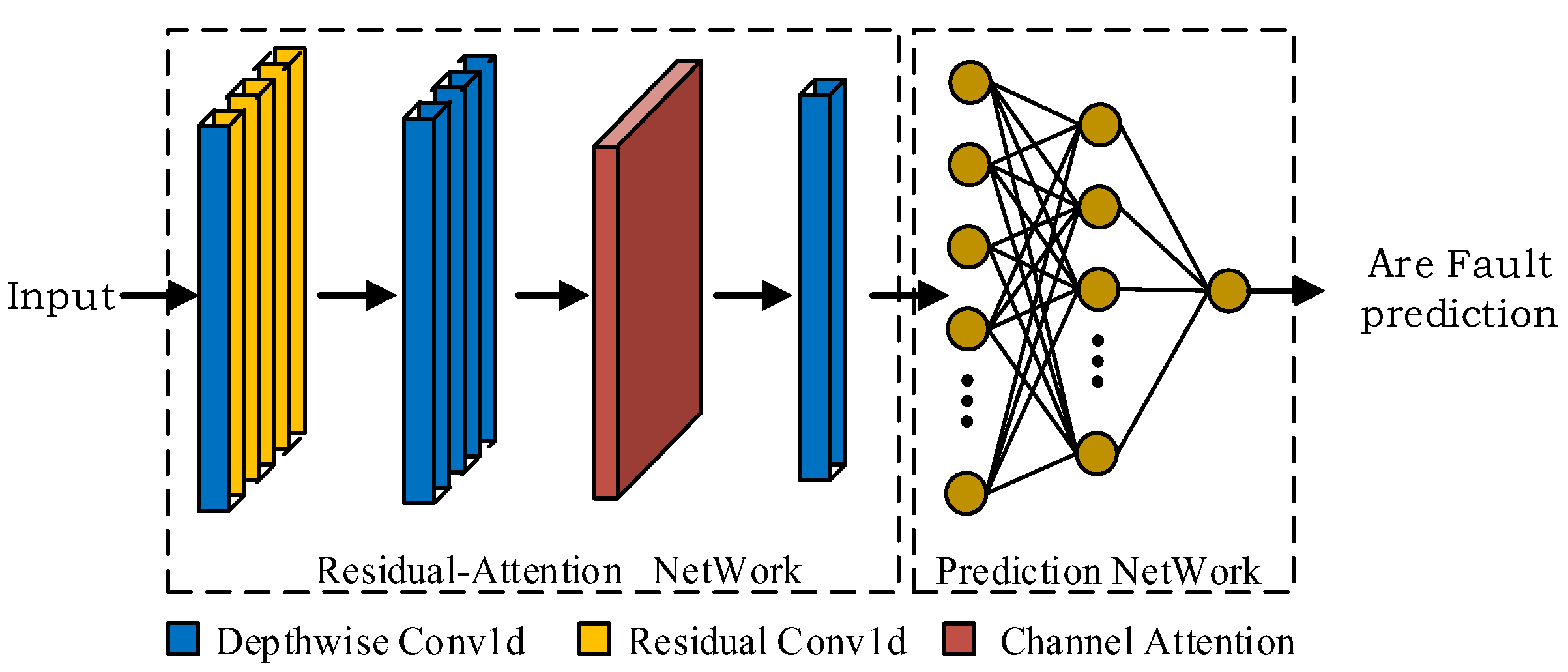
2.4. Arc Fault Detection Network Model Architecture
3. Experiments and Model Validation
3.1. Arc Fault Detection Experiment
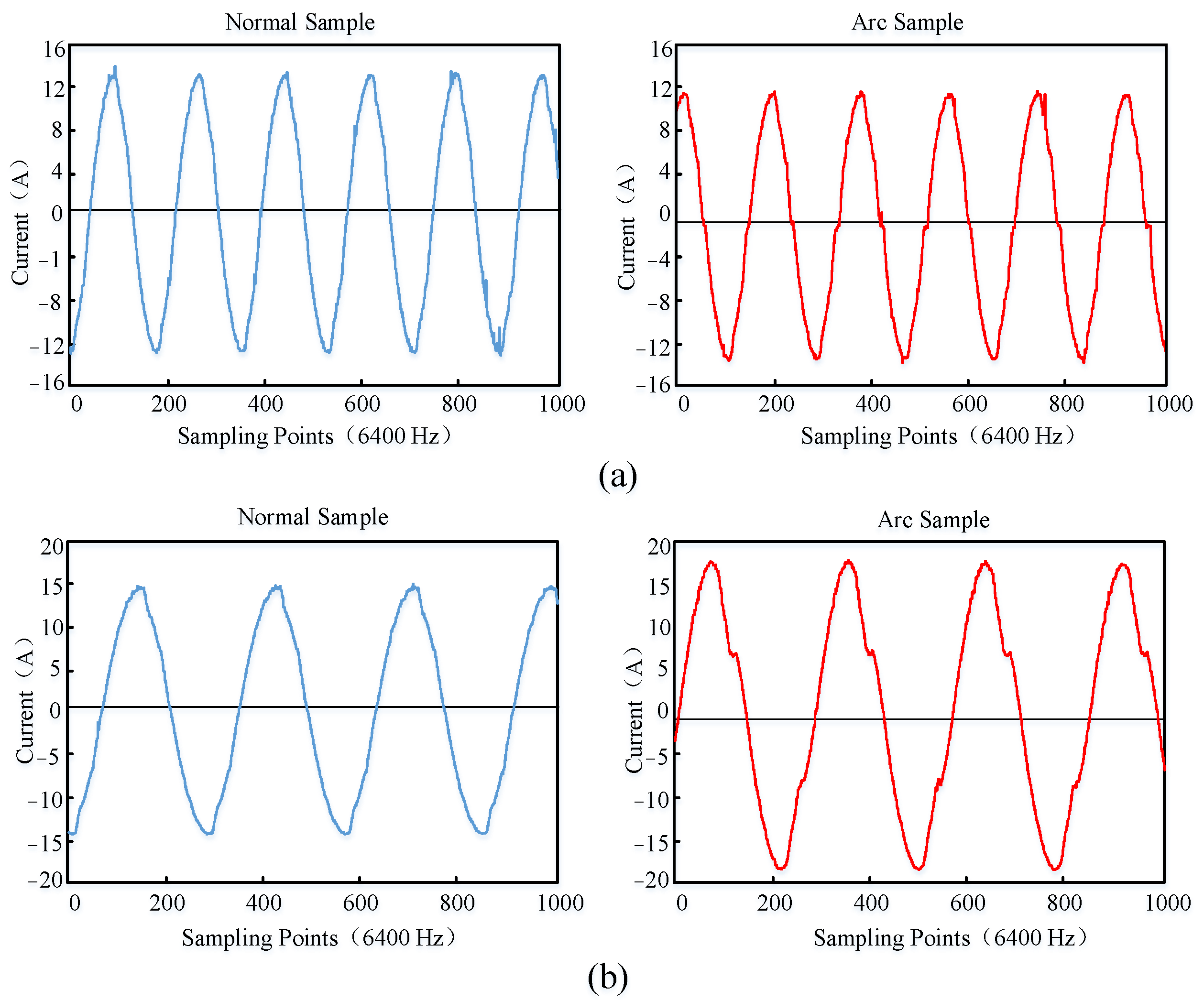
3.1.1. Data Set Establishment
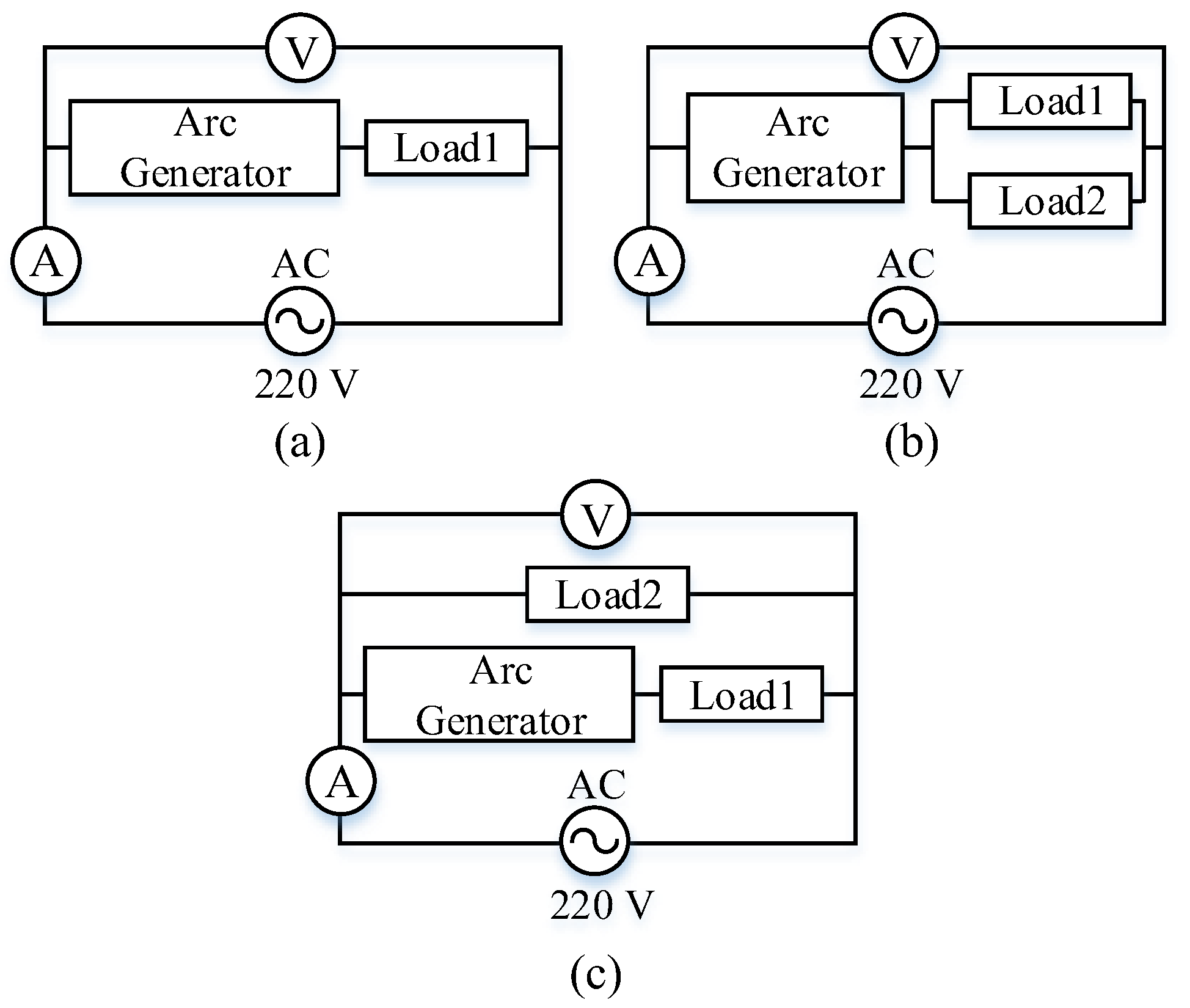
- (a)
- The working condition of the arc generator and the single load in series.
- (b)
- The arc generator in series with two loads in parallel.
- (c)
- The arc generator connected in series with two loads in parallel and the connection mode.
3.1.2. Sample Data Preprocessing and Parameter Optimization
3.1.3. Experimental Parameter Settings
4. Results
4.1. Design of Experimental Hardware Environment
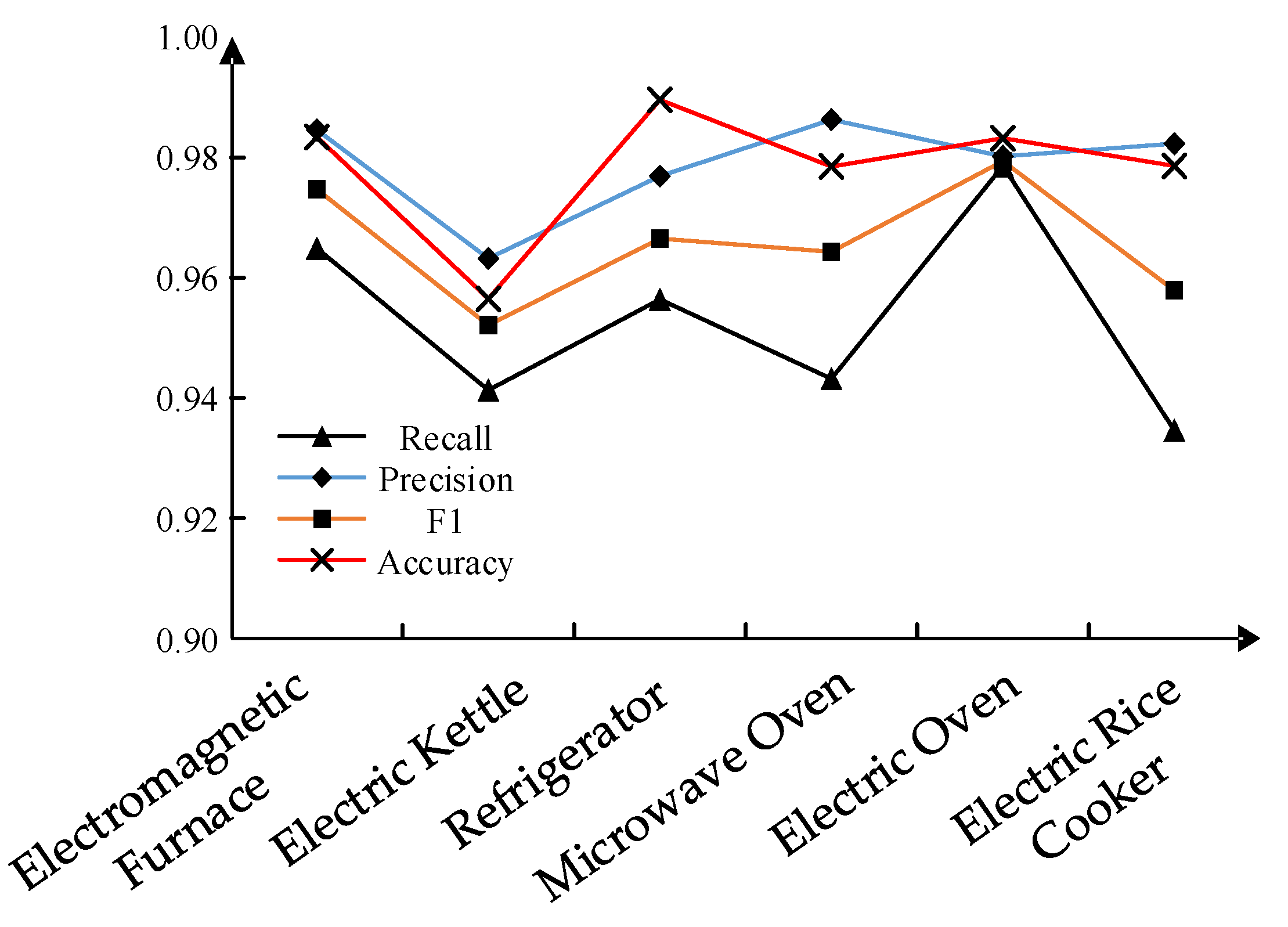
4.2. Analysis of Experimental Results of the Models
4.3. Algorithm Performance and Model Comparison Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hu, A.X. National fire situation in 2020. Fire Prot. 2021, 7, 14–15. [Google Scholar]
- Medora, N.K.; Kusko, A. Arcing faults in low and medium voltage electrical systems: Why do they persist. In Proceedings of the 2011 IEEE Symposium on Product Compliance Engineering Proceedings, San Diego, CA, USA, 10–12 October 2011; IEEE: New York, NY, USA, 2011; pp. 1–6. [Google Scholar]
- Wu, Q.; Zhang, Z.C.; Tu, R.; Yang, K.; Zhou, X.J. Simulation research on steady-state heat transfer characteristics of DC fault arc. J. Electrotech. Technol. 2021, 36, 2697–2709. [Google Scholar]
- Wang, L.D.; Wang, Y. DC fault characteristics of arc and detection methods. China Sci. Technol. Inf. 2021, 06, 86–90. [Google Scholar]
- Zhu, C.; Wang, Y.; Xie, Z.H.; Ban, Y.S.; Fu, B.; Tian, M. Serial arc fault identification method based on improved AlexNet model. J. Jinan Univ. 2021, 35, 605–613. [Google Scholar]
- Zhang, G.Y.; Zhang, X.L.; Liu, H.; Wang, Y.H. On-line detection of series fault arc in low-voltage systems. Electrotech. Sci. 2016, 31, 109–115. [Google Scholar]
- Guo, F.Y.; Gao, H.X.; Tang, A.X.; Wang, Z.Y. Serial fault arc detection and line selection based on local binary mode histogram matching. J. Electrotech. Technol. 2020, 35, 1653–1661. [Google Scholar]
- Saleh, S.A.; Valdes, M.E.; MARDEGAN, C.S.; Alsayid, B. The state-of-the-art methods for digital detection and identification of arcing current faults. IEEE Trans. Ind. Appl. 2019, 55, 4536–4550. [Google Scholar] [CrossRef]
- Garima, G.; Pankaj, K.G. A design analysis and implementation of PI, PID and fuzzy supervised shunt APF at load application to improve power quality and system reliabilit. Int. J. Syst. Assur. Eng. Manag. 2021, 12, 1247–1261. [Google Scholar]
- Dołęgowski, M.; Szmajda, M. A Novel Algorithm for Fast DC Electric Arc Detection. Energies 2021, 14, 288. [Google Scholar] [CrossRef]
- Dolegowski, M.; Szmajda, M. Mechanisms of electric arc detection based on current waveform spectrum and incremental decomposition analysis. Prz. Elektrotechniczny 2016, 92, 59–62. [Google Scholar] [CrossRef]
- Zhang, T.; Wang, H.Q.; Zhang, R.C.; Tu, R.; Yang, K. Arc fault detection method based on self-normalized neural network. J. Instrum. 2021, 42, 141–149. [Google Scholar]
- Yu, Q.F.; Huang, G.L.; Yang, Y.; Sun, Y.Z. A detection method for series arc fault based on AlexNet deep learning network. J. Electron. 2019, 33, 145–152. [Google Scholar]
- Wang, Y.; Hou, L.; Paul, K.C.; Ban, Y.; Zhao, T. ArcNet: Series AC arc fault detection based on raw current and convolutional neural network. IEEE Trans. Ind. Inform. 2021, 18, 77–86. [Google Scholar] [CrossRef]
- Zhu, Z.L.; Rao, Y.; Wu, Y.; Qi, J.N.; Zhang, Y. Research progress of attention mechanism in deep learning. Chin. J. Inf. 2019, 33, 1–11. [Google Scholar]
- Li, Y. Research on Image Super-Resolution Reconstruction Method Based on Deep Learning and Attention Mechanism. Ph.D. Thesis, South China University of Technology, Guangzhou, China, 2019. [Google Scholar]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-excitation networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 7132–7141. [Google Scholar]
- Woo, S.; Park, J.; Lee, J.Y.; Kweon, I.S. Cbam: Convolutional Block Attention Module. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 3–19. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- Sifre, L.; Mallat, S. Rigid-Motion Scattering for Texture Classification. Comput. Sci. 2014, 3559, 501–515. [Google Scholar]
- Chollet, F. Xception: Deep Learning with Depthwise Separable Convolutions. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Howard, A.G.; Zhu, M.; Chen, B.; Kalenichenko, D.; Wang, W.; Weyand, T.; Andreett, M.; Adam, H. Mobile Nets: Efficient Convolutional Neural Networks for Mobile Vision Applications. arXiv 2017, arXiv:1704.04861. [Google Scholar]


| Load Types | Fault Arc Sample(s) | Normal Sample(s) |
|---|---|---|
| Microwave Oven | 68.3 | 194.9 |
| Electromagnetic Furnace | 45.2 | 151.8 |
| Electric Kettle | 72.2 | 143.1 |
| Electric Oven | 59.2 | 131.8 |
| Refrigerator | 53.7 | 102.3 |
| Electric Rice Cooker | 62.3 | 113.6 |
| Load Types | Fault Arc Sample(s) | Normal Sample(s) |
|---|---|---|
| Microwave Oven + Electric Kettle | 67.8 | 125 |
| Electric Rice Cooker + Electric Oven | 87.7 | 178.7 |
| Refrigerator + Electromagnetic Furnace | 72.7 | 247.5 |
| Load Types | Recall | Precision | F1 | Accuracy |
|---|---|---|---|---|
| Microwave Oven | 0.9432 | 0.9863 | 0.9643 | 0.9794 |
| Electromagnetic Furnace | 0.9649 | 0.9632 | 0.9747 | 0.9834 |
| Electric Kettle | 0.9346 | 0.9823 | 0.9579 | 0.9786 |
| Electric Oven | 0.9786 | 0.9802 | 0.9794 | 0.9832 |
| Refrigerator | 0.9564 | 0.9769 | 0.9665 | 0.9896 |
| Electric Rice Cooker | 0.9413 | 0.9632 | 0.9521 | 0.9565 |
| Load Types | Recall | Precision | F1 | Accuracy |
|---|---|---|---|---|
| Microwave Oven + Electric Kettle | 0.8844 | 0.9214 | 0.9026 | 0.9348 |
| Electric Rice Cooker + Electric Oven | 0.9432 | 0.9863 | 0.9643 | 0.9794 |
| Refrigerator + Electromagnetic Furnace | 0.9767 | 0.9843 | 0.9806 | 0.9875 |
| Network Model | Microwave Oven Electric Kettle | Electric Rice Cooker Electric Oven | Refrigerator Electromagnetic Furnace |
|---|---|---|---|
| Basic-Model | 0.9360 | 0.9769 | 0.9543 |
| CA-Model | 0.9807 | 0.9889 | 0.9693 |
| Faster CA-Model | 0.9617 | 0.9805 | 0.9617 |
| Quantitative Index | Basic-Model | CA-Model | Faster CA-Model |
|---|---|---|---|
| Flops (M) | 44.81 | 45.31 | 24.58 |
| Parameters (M) | 23.22 | 22.45 | 12.12 |
| Times (ms) | 18.57 | 16.74 | 13.89 |
| Load Types | Faster CA-Model | CNN | VGG-11 | AlexNet | Yolov3 |
|---|---|---|---|---|---|
| Microwave Oven | 0.9143 | 0.8671 | 0.8896 | 0.8642 | 0.9332 |
| Electromagnetic Furnace | 0.9776 | 0.9026 | 0.8649 | 0.8762 | 0.9456 |
| Electric Kettle | 0.9736 | 0.9145 | 0.9441 | 0.9012 | 0.9351 |
| Electric Oven | 0.9623 | 0.8956 | 0.9123 | 0.9423 | 0.9521 |
| Refrigerator | 0.9457 | 0.8836 | 0.9216 | 0.8612 | 0.9432 |
| Electric Rice Cooker | 0.9633 | 0.8765 | 0.8921 | 0.9063 | 0.9612 |
| Microwave Oven + Electric Kettle | 0.9617 | 0.8469 | 0.8346 | 0.8936 | 0.8963 |
| Electric Rice Cooker + Electric Oven | 0.9805 | 0.8934 | 0.9025 | 0.9321 | 0.9452 |
| Refrigerator + Electromagnetic Furnace | 0.9617 | 0.8701 | 0.8435 | 0.8865 | 0.9601 |
| Network Model | Flops (M) | Parameters (M) | Times (ms) |
|---|---|---|---|
| Faster CA-Model | 24.58 M | 12.12 M | 13.89 |
| CNN | 10.25 M | 6.23 M | 15.93 |
| VGG-11 | 52.63 M | 26.78 M | 26.41 |
| AlexNet | 32.52 M | 16.23 M | 12.36 |
| Yolov3 | 44.85 M | 23.22 M | 18.57 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, X.; Zhou, G.; Zhang, J.; Zeng, Y.; Feng, Y.; Liu, Y. Fault Arc Detection Based on Channel Attention Mechanism and Lightweight Residual Network. Energies 2023, 16, 4954. https://doi.org/10.3390/en16134954
Gao X, Zhou G, Zhang J, Zeng Y, Feng Y, Liu Y. Fault Arc Detection Based on Channel Attention Mechanism and Lightweight Residual Network. Energies. 2023; 16(13):4954. https://doi.org/10.3390/en16134954
Chicago/Turabian StyleGao, Xiang, Gan Zhou, Jian Zhang, Ying Zeng, Yanjun Feng, and Yuyuan Liu. 2023. "Fault Arc Detection Based on Channel Attention Mechanism and Lightweight Residual Network" Energies 16, no. 13: 4954. https://doi.org/10.3390/en16134954
APA StyleGao, X., Zhou, G., Zhang, J., Zeng, Y., Feng, Y., & Liu, Y. (2023). Fault Arc Detection Based on Channel Attention Mechanism and Lightweight Residual Network. Energies, 16(13), 4954. https://doi.org/10.3390/en16134954






