Numerical Study of Flow and Heat Transfer Characteristics in a Simplified Dual Fluid Reactor
Abstract
:1. Introduction
2. Materials and Methods
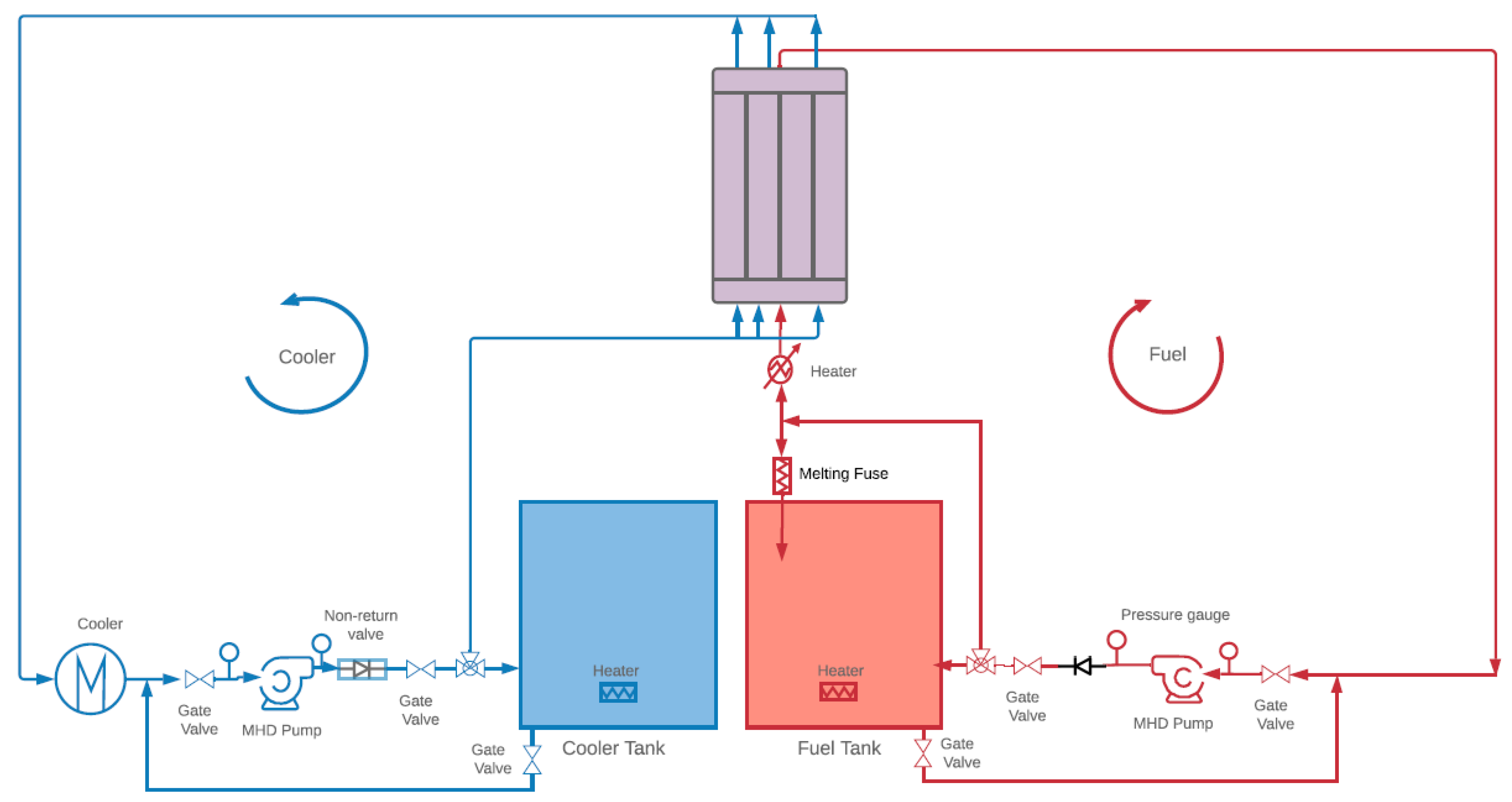
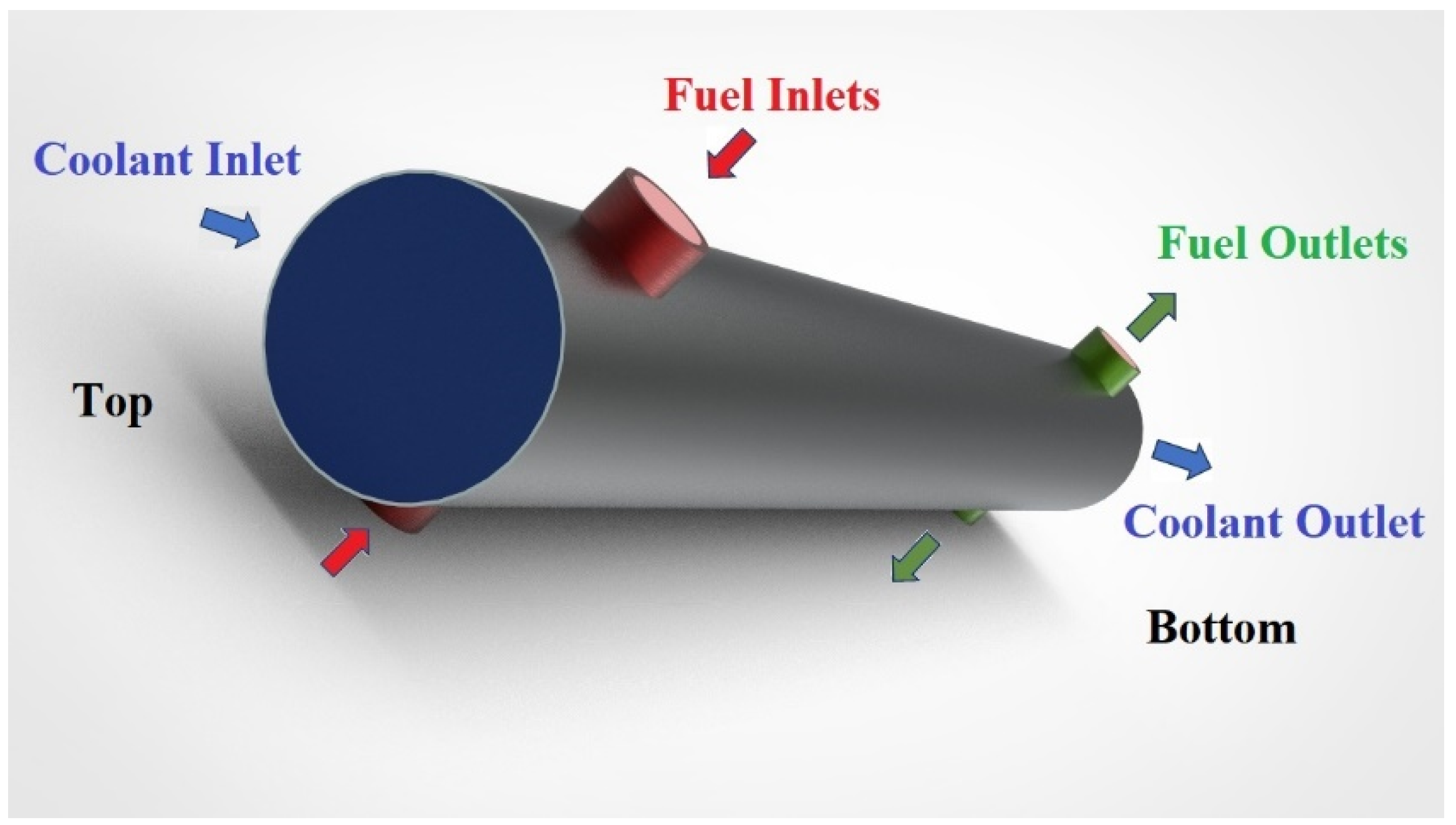
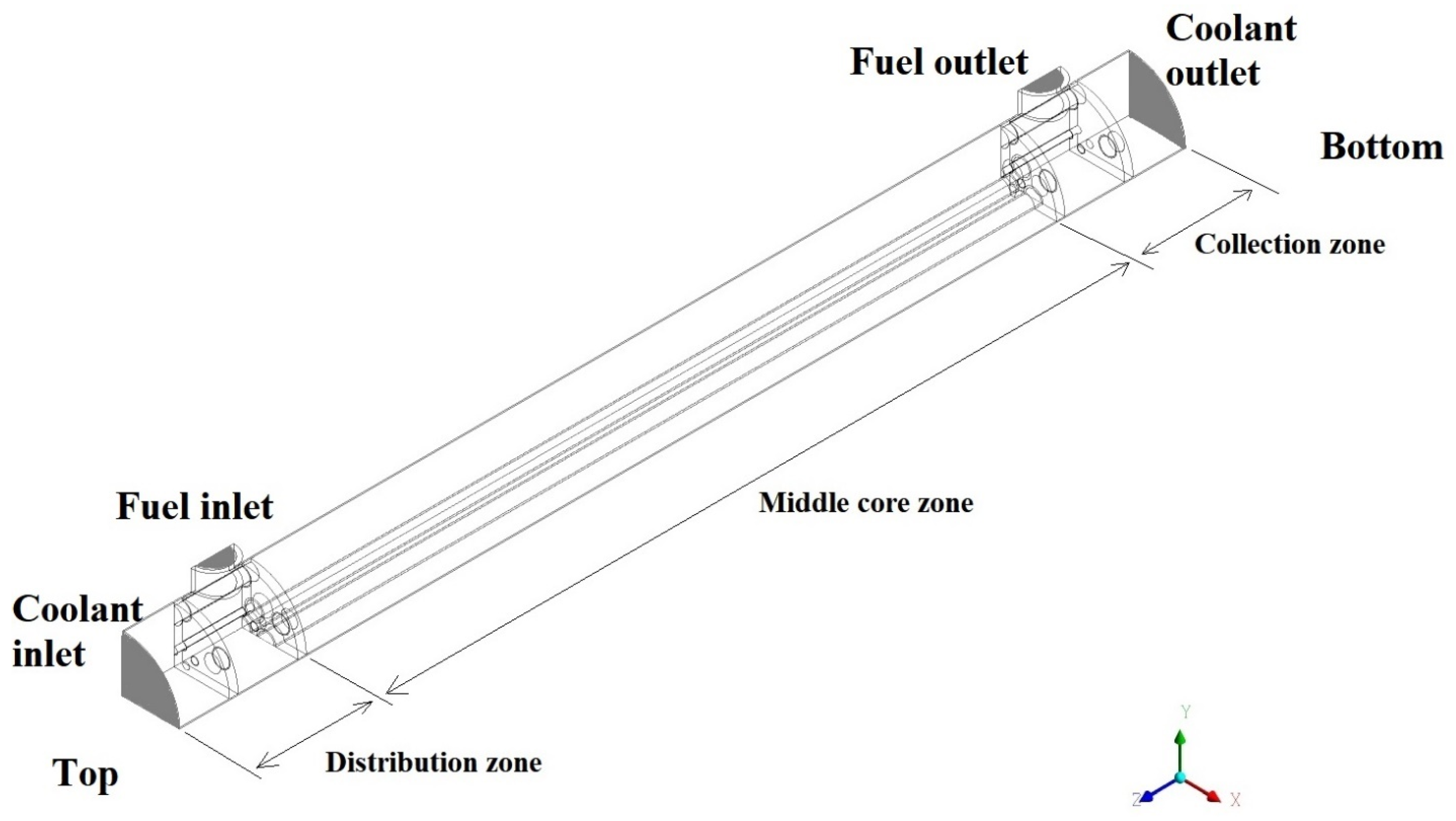
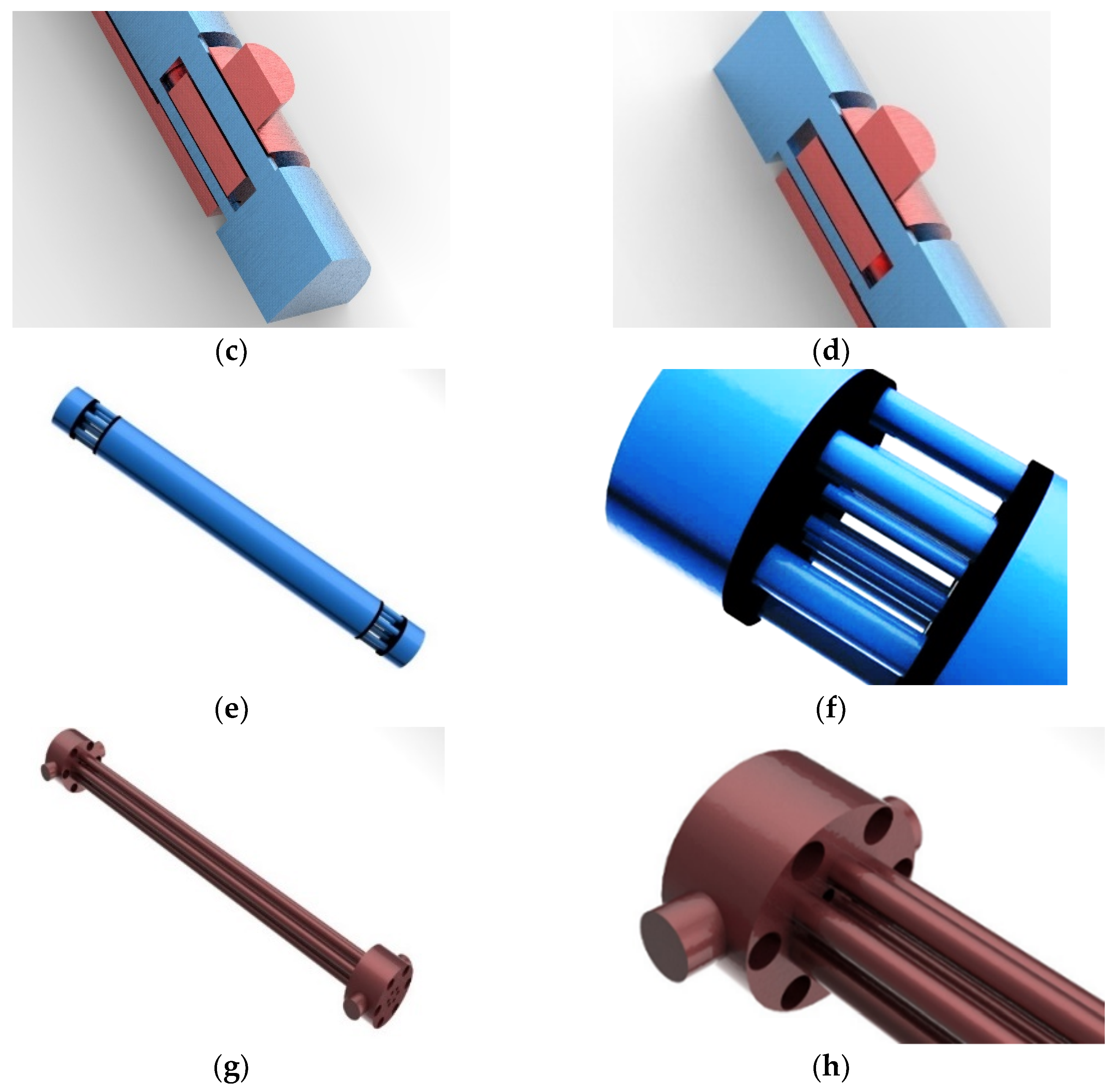
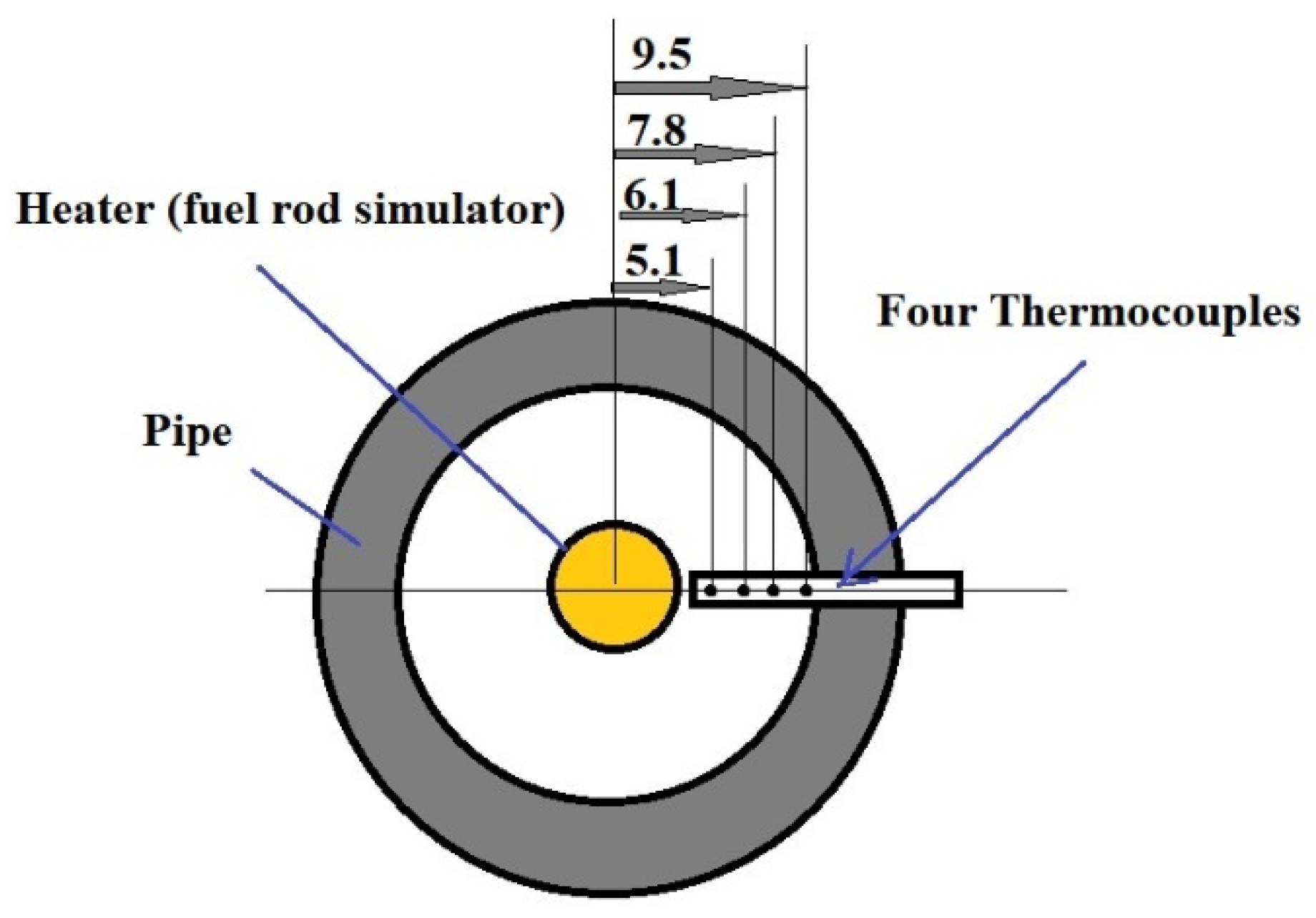
2.1. Description of Test Case
- Distribution zone: This is the zone between the fuel/coolant inlets and the middle core inlets. In this zone, the fuel and coolant enter the MD (from the top), where fuel surrounds the coolant pipes.
- The middle core zone: In this zone, the fuel pipes are surrounded by coolant. The middle core zone is the largest section in the MD, and this is the zone where the major amount of heat transfer is expected to take place.
- The collection zone: This zone lies between the middle core zone outlets and the outlets of the MD in an identical structure to that of distribution zone (bottom).
2.2. Mathematical Background
2.3. Computational Details
2.4. Boundary Conditions and Numerical Scheme
2.5. Meshing
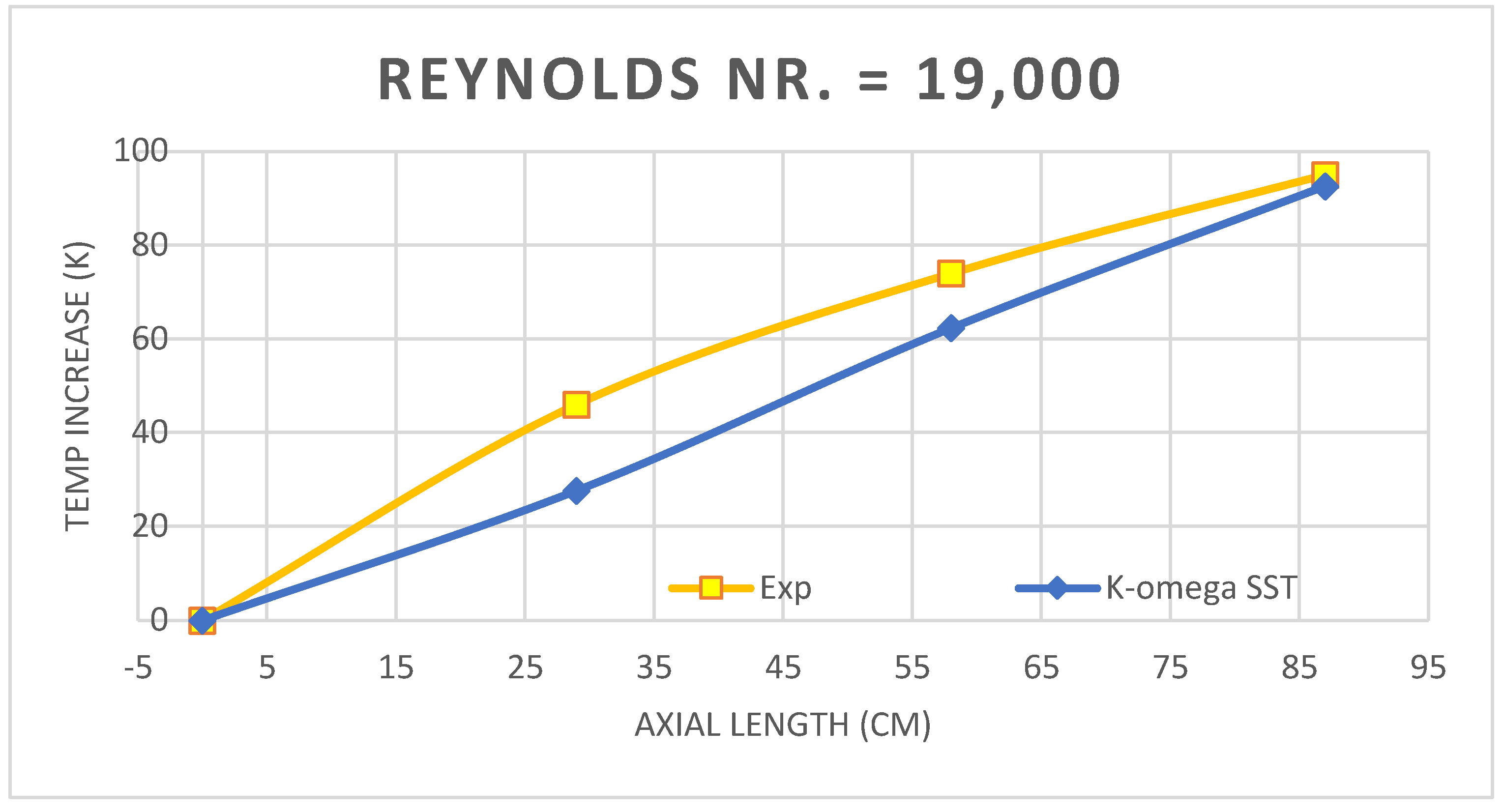
2.6. Validation of RANS Model
3. Results and Discussion
3.1. Global Characteristics
3.2. Local Characteristics
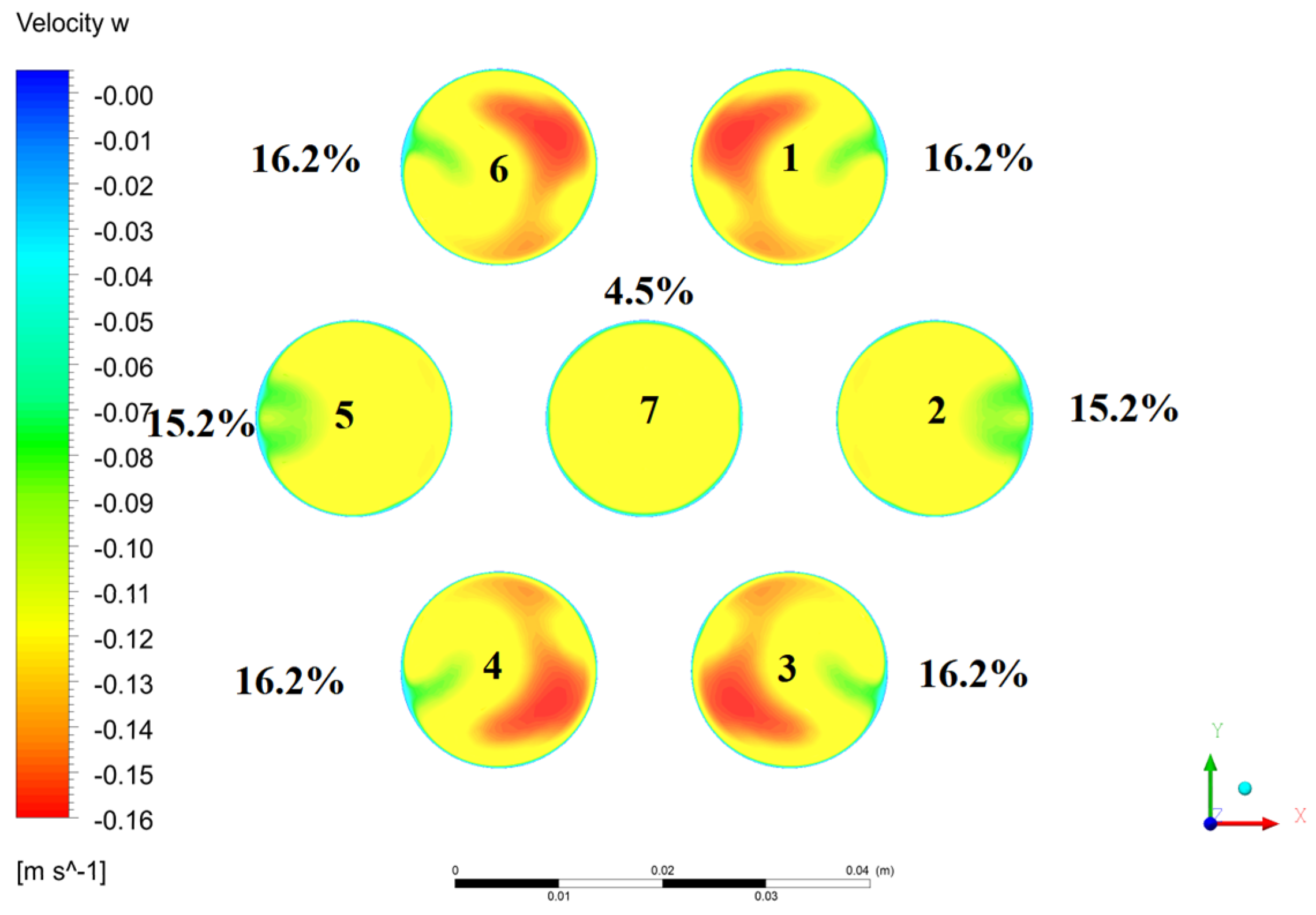
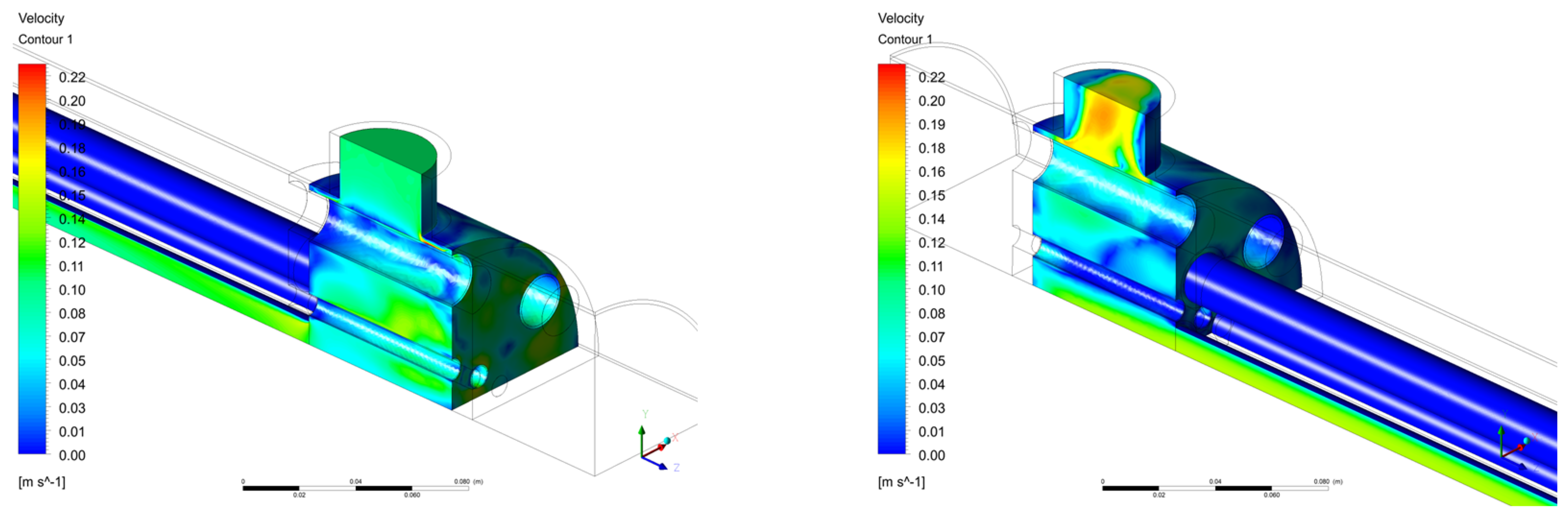
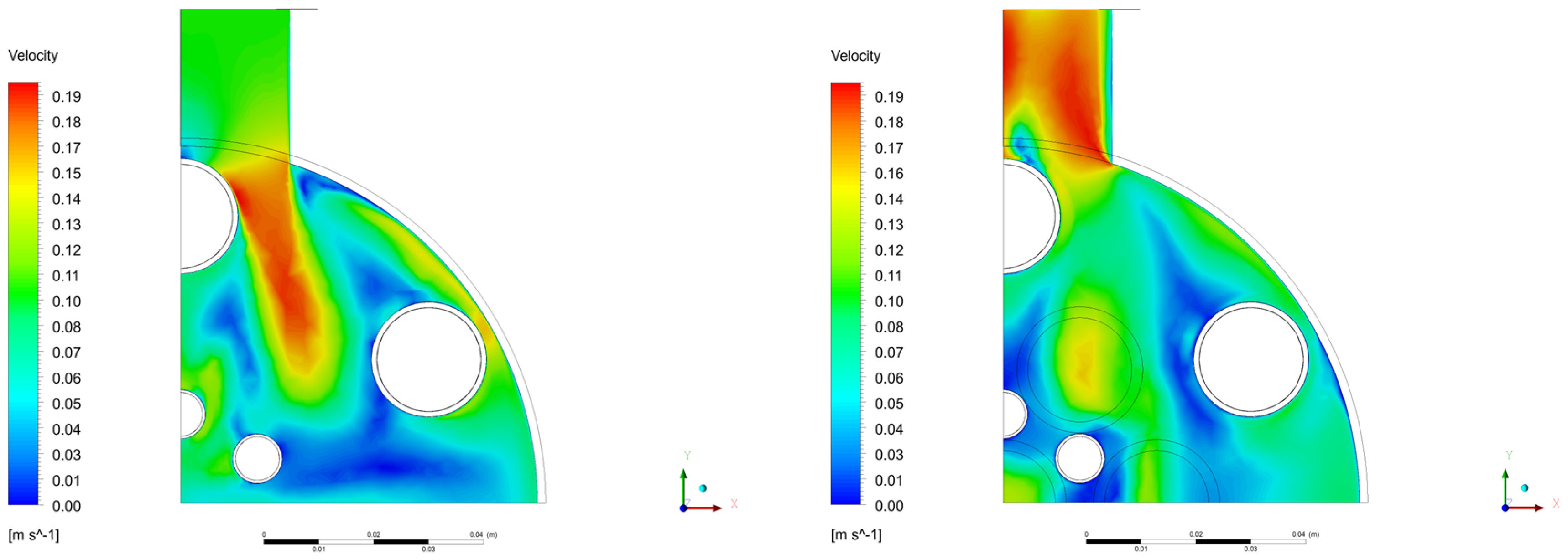
3.2.1. Velocity and Contours Plots
Fuel Contour Plots
Coolant Contours Plots
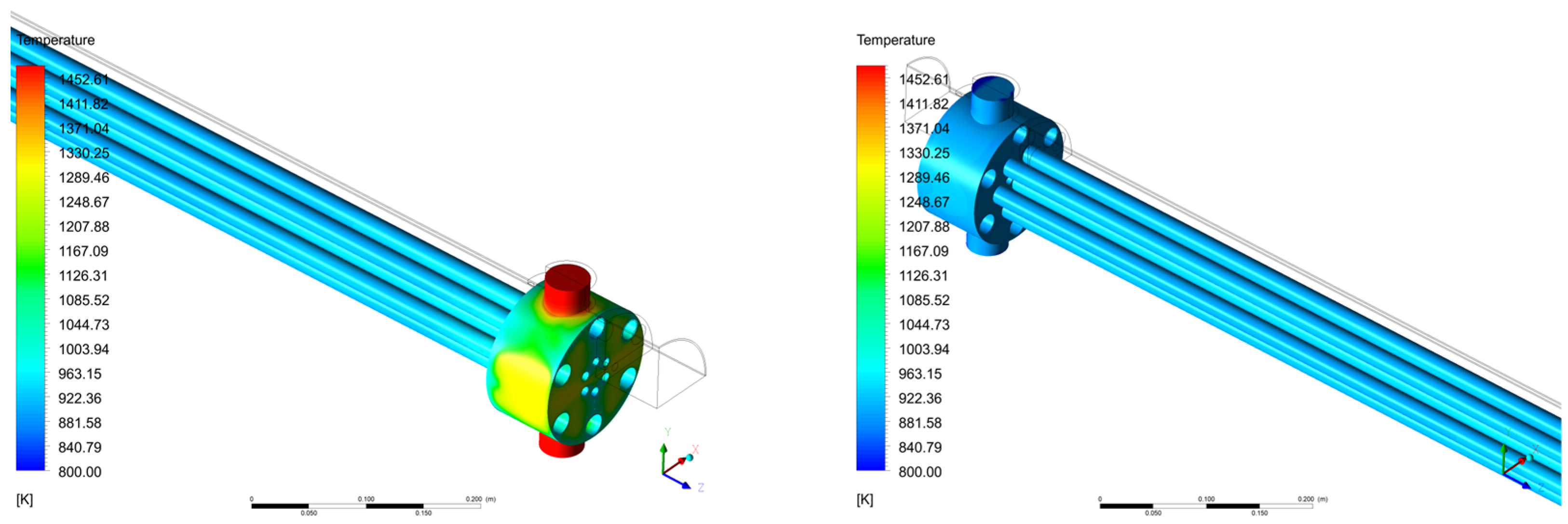
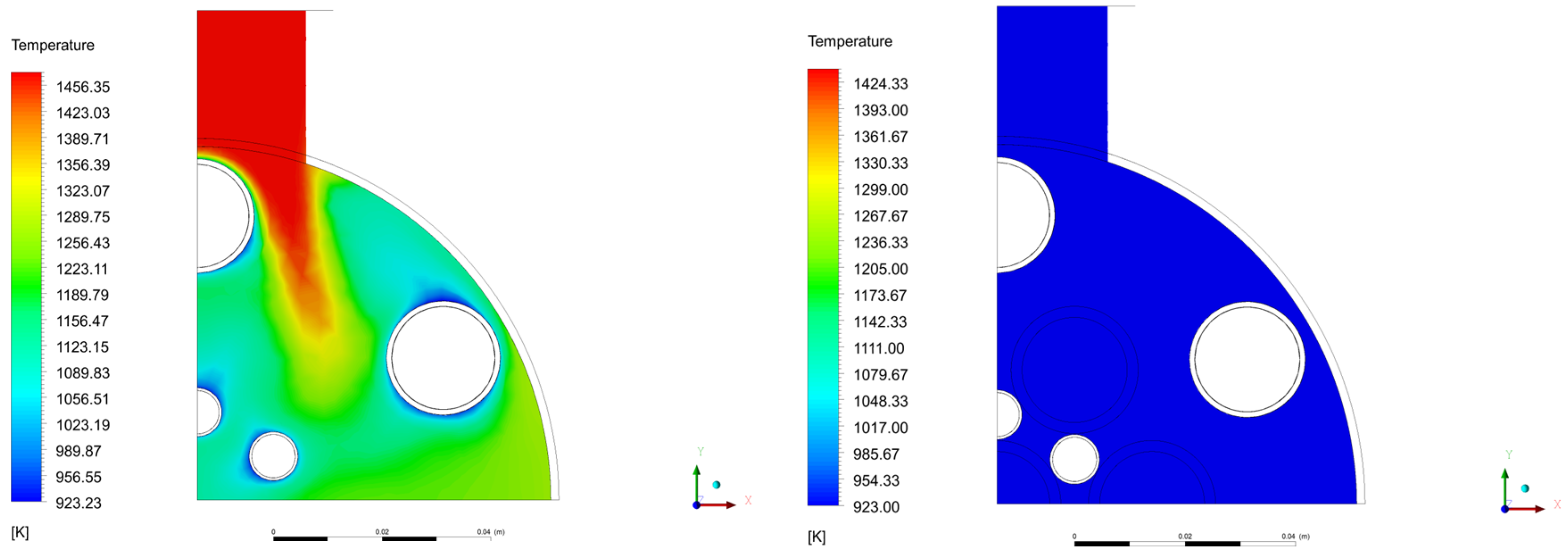
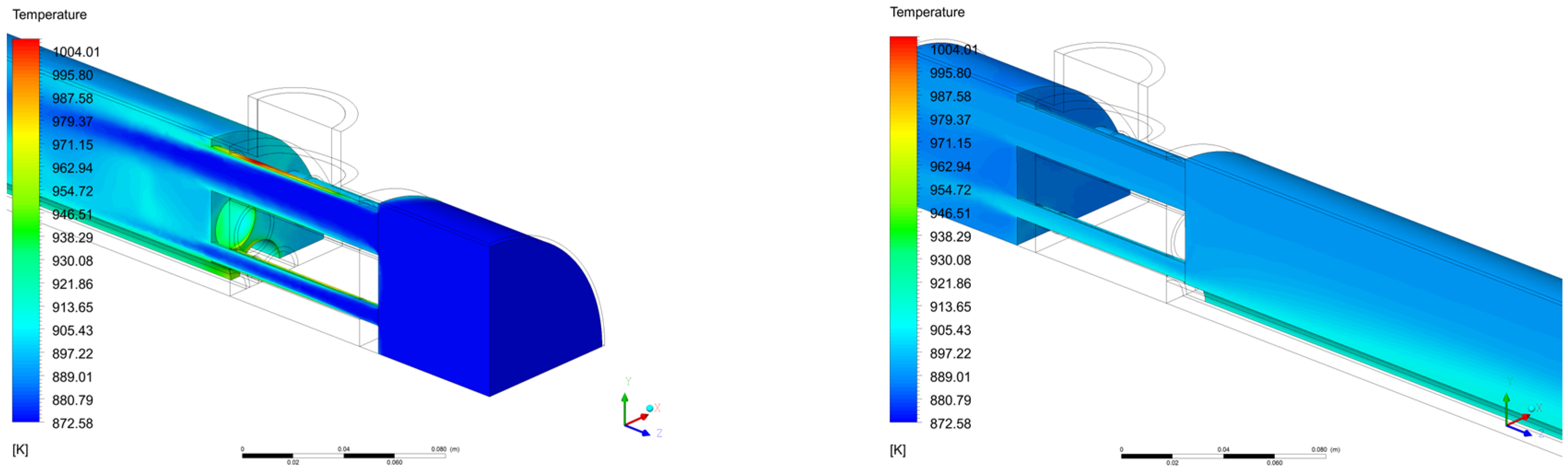
3.2.2. Temperature Contour Plots
Fuel Temperature Contour Plots
Coolant Temperature Contour Plots
3.3. Hot Spots in the Mini Demonstrator
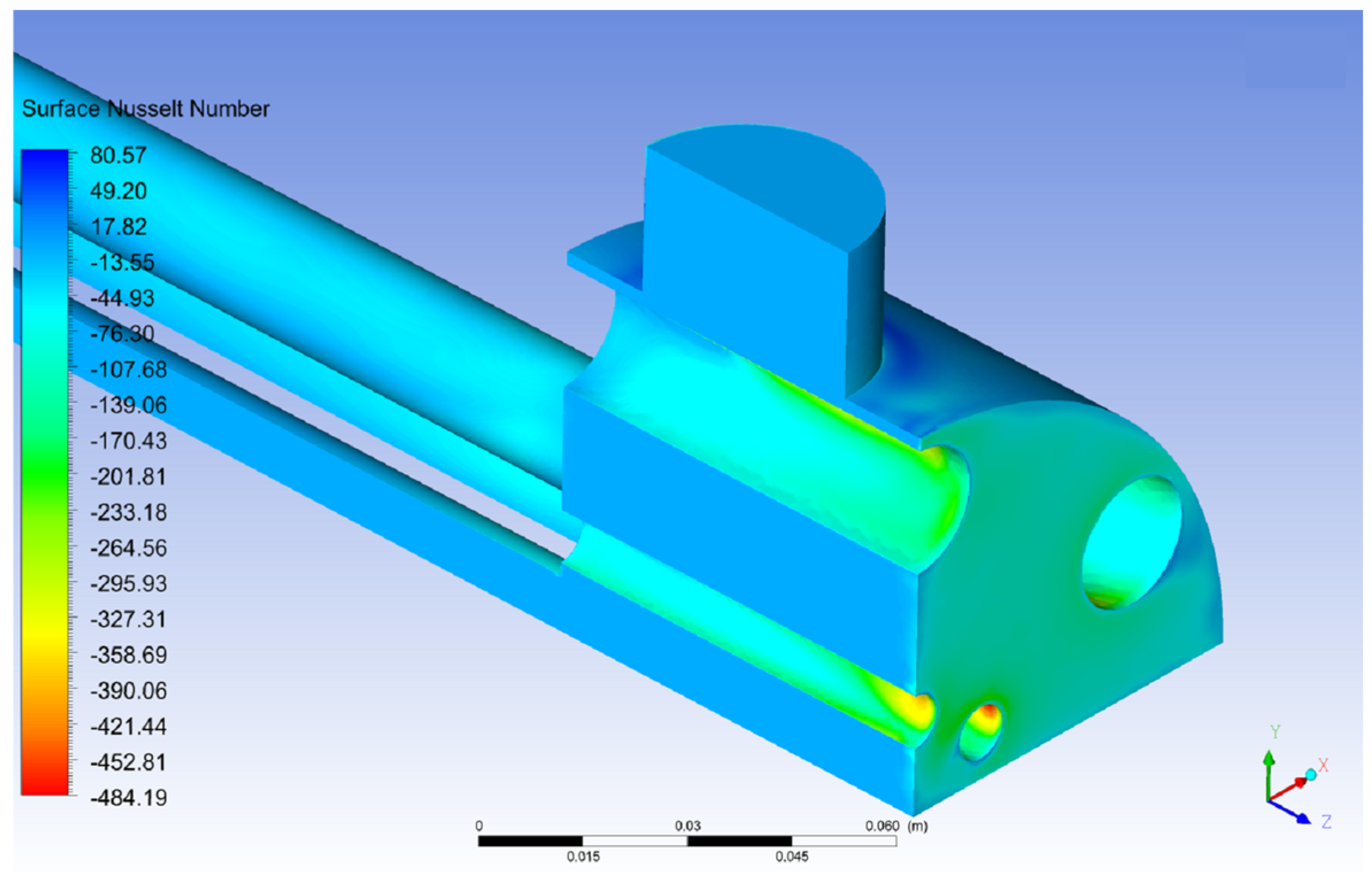
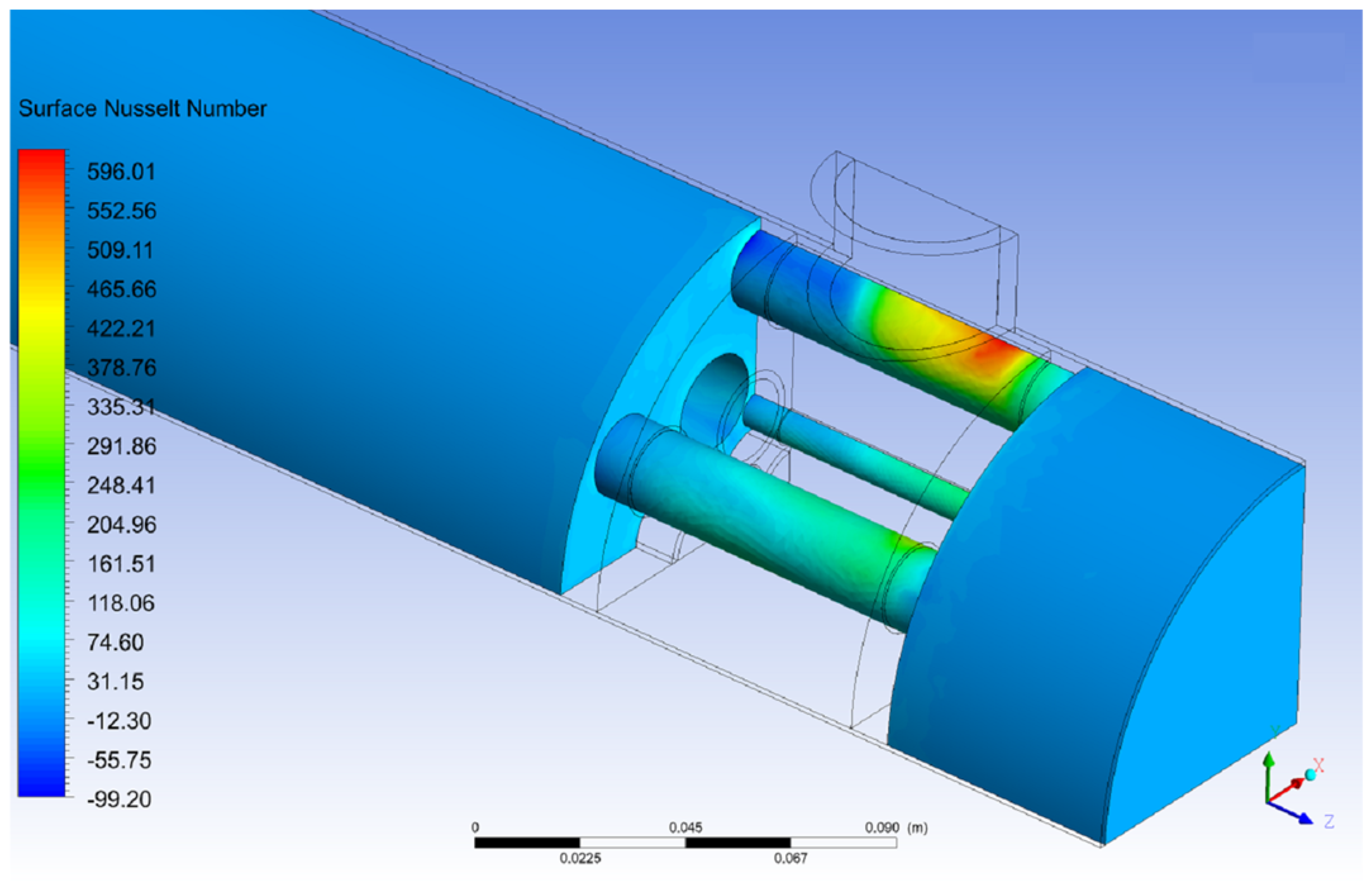
3.3.1. Fuel Nusselt Number Contour Plots and Streamlines
3.3.2. Coolant Nusselt Number Contour Plots and Streamlines
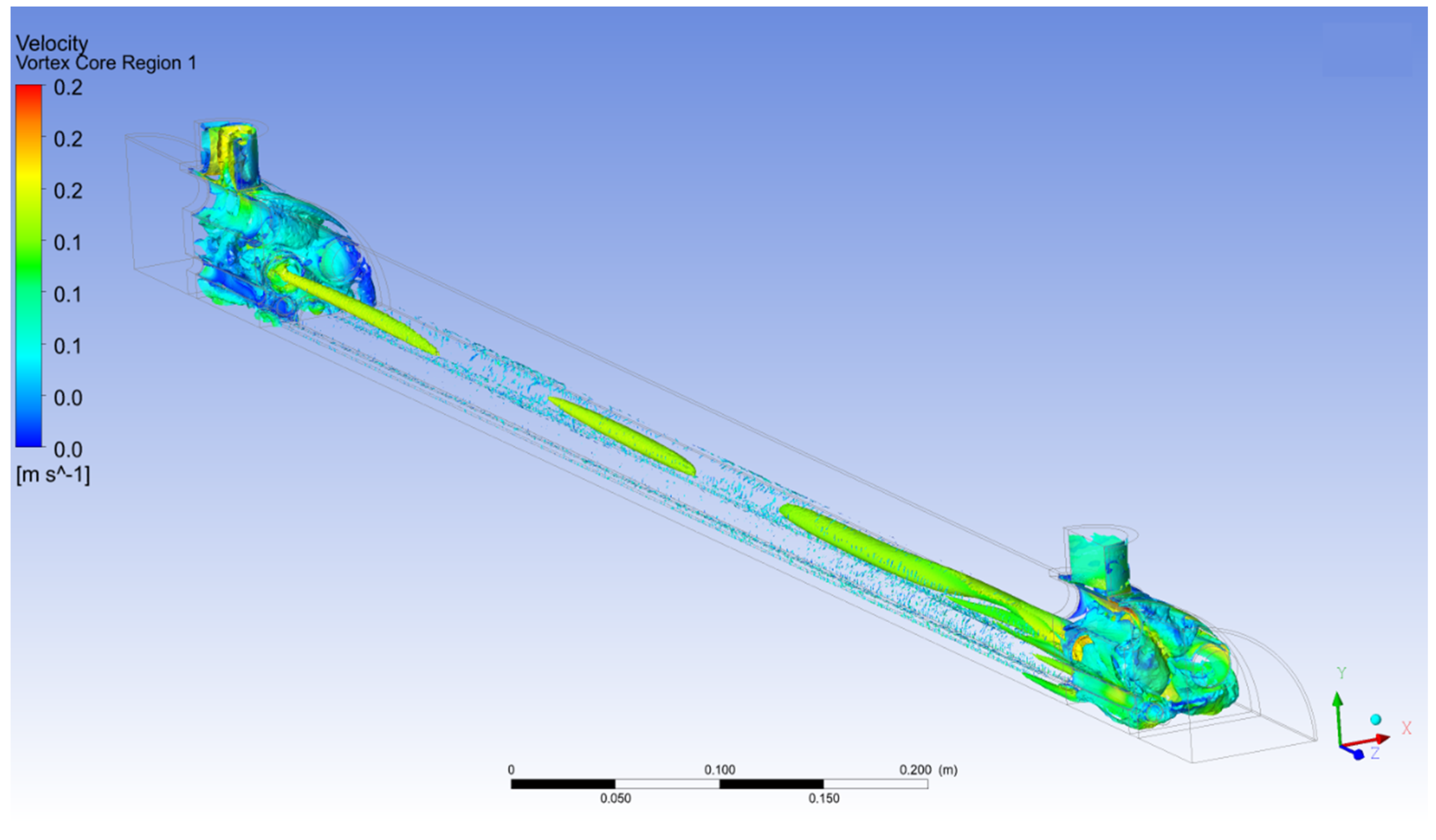
3.3.3. Q-Criterion of Fuel in Core Pipes
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| BC | Boundary Condition | |
| CFD | Computational Fluid Dynamics | |
| DFR | Dual Fluid Reactor | |
| DNS | Direct Numerical Simulation | |
| EROI | Energy Return On Investment | |
| GenIV | Fourth Generation of nuclear reactors | |
| IAEA | International Atomic Energy Agency | |
| LES | Large Eddy Simulation | |
| LFR | Lead-Cooled Fast Reactor | |
| MD | Mini-Demonstrator | |
| MSR | Molten Salt Reactor | |
| PPU | Pyrochemical Processing Unit | |
| RANS | Reynolds Averaged Navier–Stokes | |
| SST | Shear Stress Transport Model | |
| Dimensionless quantities | ||
| Pr | Prandtl number | |
| Prt | Turbulent Prandtl number | |
| Re | Reynolds number | |
| Ri | Richardson number | |
| Nu | Nusselt number | |
| Greek and Latin symbols | ||
| μ | Dynamic viscosity | |
| μt | Turbulent viscosity (eddy viscosity) | |
| ν | Kinematic viscosity | |
| ω | Specific dissipation rate | |
| ρ | Density | |
| τ | Shear stress | |
| τw | Wall shear stress | |
| ε | Dissipation rate | |
| K | Thermal conduction coefficient | |
| m | Mass | |
| v | Velocity | |
| t | Time | |
| k | Turbulence kinetic energy | |
| T | Temperature | |
| u | Characteristic velocity | |
| y | Distance from the wall | |
| Cp | Specific heat capacity | |
References
- International Atomic Energy Agency. Status of Molten Salt Reactor Technology; TRS No 489; International Atomic Energy Agency: Vienna, Austria, 2021. [Google Scholar]
- Thomas, J.D. (Ed.) Molten Salt Reactors and Thorium Energy; Woodhead Publishing Series in Energy; Woodhead Publishing: Sawston, UK, 2017. [Google Scholar]
- Bajorek, S.; Diamond, D.J.; Brown, N.R.; Denning, R. Thermal-Hydraulics Phenomena Important in Modeling and Simulation of Liquid-Fuel Molten Salt Reactors; Brookhaven National Lab. (BNL): Upton, NY, USA, 2018.
- Smith, O.; Cattell, O.; Farcot, E.; O’Dea, R.D.; Hopcraft, K.I. The Effect of Renewable Energy Incorporation on Power Grid Stability and Resilience. Sci. Adv. 2022, 8, eabj6734. [Google Scholar] [CrossRef] [PubMed]
- Huke, A.; Ruprecht, G.; Weißbach, D.; Czerski, K.; Gottlieb, S.; Hussein, A.; Herrmann, F. Dual-Fluid Reactor. In Molten Salt Reactors and Thorium Energy; Elsevier: Amsterdam, The Netherlands, 2017; pp. 619–633. ISBN 9780081012437. [Google Scholar]
- Wang, X.; Macián-Juan, R.; Dabrowski, M. Analysis and Evaluation of the Dual Fluid Reactor Concept; Südwestdeutscher Verlag für Hochschulschriften: London, UK, 2017. [Google Scholar]
- Weißbach, D.; Sierchuła, J.; Dąbrowski, M.P.; Czerski, K.; Ruprecht, G. Dual Fluid Reactor as a Long-term Burner of Actinides in Spent Nuclear Fuel. Int. J. Energy Res. 2021, 45, 11589–11597. [Google Scholar] [CrossRef]
- Weißbach, D.; Ruprecht, G.; Huke, A.; Czerski, K.; Gottlieb, S.; Hussein, A. Energy Intensities, EROIs, and Energy Payback Times of Electricity Generating Power Plants. Energy 2013, 52, 210–221. [Google Scholar] [CrossRef]
- Laidler, J.J.; Battles, J.E.; Miller, W.E.; Ackerman, J.P.; Carls, E.L. Development of Pyroprocessing Technology. Prog. Nucl. Energy 1997, 31, 131–140. [Google Scholar] [CrossRef]
- Dincer, I.; Zamfirescu, C. Other Hydrogen Production Methods. In Sustainable Hydrogen Production; Elsevier: Amsterdam, The Netherlands, 2016; pp. 411–439. [Google Scholar] [CrossRef]
- Vaidya, H.A.; Ertunç, Ö.; Genç, B.; Beyer, F.; Köksoy, Ç.; Delgado, A. Numerical Simulations of Swirling Pipe Flows- Decay of Swirl and Occurrence of Vortex Structures. J. Phys. Conf. Ser. 2011, 318, 062022. [Google Scholar] [CrossRef]
- Hanusek, T.; Macian-Juan, R. Analyses of the Shutdown System and Transients Scenarios for the Dual Fluid Reactor Concept with Metallic Molten Fuel. Int. J. Energy Res. 2022, 46, 17230–17246. [Google Scholar] [CrossRef]
- Nalbandyan, A.; Klinkby, E.; Lauritzen, B.; Groth-Jensen, J.; Steyn, R. Coupled Neutronics/Thermal Hydraulics Assessment of Graphite Moderated Molten Salt Reactors. In Proceedings of the 18th International Topical Meeting on Nuclear Reactor Thermal Hydraulics (NURETH 2019), Portland, OR, USA, 18–23 August 2019. [Google Scholar]
- IAEA. Available online: https://www.Iaea.Org/Topics/Construction-and-Commissioning-of-Nuclear-Power-Plants (accessed on 20 June 2023).
- Liu, C.; Li, X.; Luo, R.; Macian-Juan, R. Thermal Hydraulics Analysis of the Distribution Zone in Small Modular Dual Fluid Reactor. Metals 2020, 10, 1065. [Google Scholar] [CrossRef]
- Wang, X.; Liu, C.; Macian-Juan, R.; Wang, X.; Liu, C.; Macian-Juan, R. Preliminary Hydraulic Analysis of the Distribution Zone in the Dual Fluid Reactor Concept. Prog. Nucl. Energy 2019, 110, 364–373. [Google Scholar] [CrossRef]
- Shams, A.; De Santis, A. Towards the Accurate Prediction of the Turbulent Flow and Heat Transfer in Low-Prandtl Fluids. Int. J. Heat Mass Transf. 2019, 130, 290–303. [Google Scholar] [CrossRef]
- Shams, A.; De Santis, D.; Padee, A.; Wasiuk, P.; Jarosiewicz, T.; Kwiatkowski, T.; Potempski, S. High-Performance Computing for Nuclear Reactor Design and Safety Applications. Nucl. Technol. 2020, 206, 283–295. [Google Scholar] [CrossRef]
- Duponcheel, M.; Bricteux, L.; Manconi, M.; Winckelmans, G.; Bartosiewicz, Y. Assessment of RANS and Improved Near-Wall Modeling for Forced Convection at Low Prandtl Numbers Based on LES up to Re_T = 2000. Int. J. Heat Mass Transf. 2014, 75, 470–482. [Google Scholar] [CrossRef]
- Wei, H.; Bao, H.; Ruan, X. Genetic Algorithm-Driven Discovery of Unexpected Thermal Conductivity Enhancement by Disorder. Nano Energy 2020, 71, 104619. [Google Scholar] [CrossRef]
- Zou, H.; Feng, Y.; Qiu, L. Excellent Heat Transfer Enhancement of CNT-Metal Interface by Loading Carbyne and Metal Nanowire into CNT. Int. J. Heat Mass Transf. 2022, 186, 122533. [Google Scholar] [CrossRef]
- Rostamzadeh, A. Towards Multidimensional Artificially Characteristic-Based Scheme for Incompressible Thermo-Fluid Problems. Mechanics 2018, 23, 826–834. [Google Scholar] [CrossRef] [Green Version]
- Hashemi, M.Y.; Zamzamian, K. A Multidimensional Characteristic-Based Method for Making Incompressible Flow Calculations on Unstructured Grids. J. Comput. Appl. Math. 2014, 259, 752–759. [Google Scholar] [CrossRef] [Green Version]
- Nowak, M.; Spirzewski, M.; Czerski, K. Optimization of the DC Magnetohydrodynamic Pump for the Dual Fluid Reactor. Ann. Nucl. Energy 2022, 174, 109142. [Google Scholar] [CrossRef]
- Al-Habahbeh, O.M.; Al-Saqqa, M.; Safi, M.; Abo Khater, T. Review of Magnetohydrodynamic Pump Applications. Alex. Eng. J. 2016, 55, 1347–1358. [Google Scholar] [CrossRef] [Green Version]
- Smith, C.F.; Halsey, W.G.; Brown, N.W.; Sienicki, J.J.; Moisseytsev, A.; Wade, D.C. SSTAR: The US Lead-Cooled Fast Reactor. J. Nucl. Mater. 2007, 376, 255–259. [Google Scholar] [CrossRef] [Green Version]
- Singh, O.P. Nuclear Reactors of the Future. In Physics of Nuclear Reactors, 1st ed.; Elsevier: Amsterdam, The Netherlands, 2021. [Google Scholar]
- Serp, J.; Allibert, M.; Beneš, O.; Delpech, S.; Feynberg, O.; Ghetta, V.; Heuer, D.; Holcomb, D.; Ignatiev, V.; Kloosterman, J.L.; et al. The Molten Salt Reactor (MSR) in Generation IV: Overview and Perspectives. Prog. Nucl. Energy 2014, 77, 308–319. [Google Scholar] [CrossRef]
- Uhlíř, J. Chemistry and Technology of Molten Salt Reactors–History and Perspectives. J. Nucl. Mater. 2007, 360, 6–11. [Google Scholar] [CrossRef]
- Wilcox, D. Formulation of the k-Omega Turbulence Model Revisited. In Proceedings of the 45th AIAA Aerospace Sciences Meeting and Exhibit, Denver, CO, USA, 2–5 August 2009; American Institute of Aeronautics and Astronautics: Reston, VS, USA, 2007. [Google Scholar]
- Menter, F. Zonal Two Equation k-w Turbulence Models For Aerodynamic Flows. In Proceedings of the 23rd Fluid Dynamics, Plasmadynamics, and Lasers Conference, Orlando, FL, USA, 6–9 July 1993; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 1993. [Google Scholar]
- Sierchuła, J.; Weissbach, D.; Huke, A.; Ruprecht, G.; Czerski, K.; Da¸browskida¸browski, M.P. Determination of the Liquid Eutectic Metal Fuel Dual Fluid Reactor (DFRm) Design-Steady State Calculations. Int. J. Energy Res. 2019, 43, 3692–3701. [Google Scholar] [CrossRef]
- Ma, W.; Karbojian, A.; Hollands, T.; Koch, M.K. Experimental and Numerical Study on Lead-Bismuth Heat Transfer in a Fuel Rod Simulator. J. Nucl. Mater. 2011, 415, 415–424. [Google Scholar] [CrossRef]
- Tong, L.L.; Hou, L.Q.; Cao, X.W. Analysis of the Flow Distribution and Mixing Characteristics in the Reactor Pressure Vessel. Nucl. Eng. Technol. 2021, 53, 93–102. [Google Scholar] [CrossRef]
- Zhao, P.; Shi, K.; Li, S.; Feng, J.; Chen, H. CFD Analysis of the Primary Cooling System for the Small Modular Natural Circulation Lead Cooled Fast Reactor SNRLFR-100. Sci. Technol. Nucl. Install. 2016, 2016, 9612120. [Google Scholar] [CrossRef] [Green Version]
- Feng, J.; Xu, L.; Baglietto, E. Assessing the Applicability of the Structure-Based Turbulence Resolution Approach to Nuclear Safety-Related Issues. Fluids 2021, 6, 61. [Google Scholar] [CrossRef]
- Blazek, J. Computational Fluid Dynamics: Principles and Applications; Elsevier: Amsterdam, The Netherlands, 2005; ISBN 9780080445069. [Google Scholar]
- Zhang, Q.; Ge, J.; Zhang, B.; He, C.; Wu, Z.; Liang, J. Effect of Thermal Residual Stress on the Tensile Properties and Damage Process of C/SiC Composites at High Temperatures. Ceram. Int. 2022, 48, 3109–3124. [Google Scholar] [CrossRef]
- Yingling, J.A.; Gamble, K.A.; Roberts, E.; Freeman, R.A.; Knight, T.W. UPDATED U3SI2 Thermal Creep Model and Sensitivity Analysis of the U3SI2-SIC Accident Tolerant FUEL. J. Nucl. Mater. 2021, 543, 152586. [Google Scholar] [CrossRef]
- Sklenicka, V.; Kral, P.; Kucharova, K.; Kvapilova, M.; Dvorak, J.; Kloc, L. Thermal Creep Fracture of a Zr1%Nb Cladding Alloy in the α and (A + β) Phase Regions. J. Nucl. Mater. 2021, 553, 152950. [Google Scholar] [CrossRef]
- Li, H.; Tomita, Y. Characteristics of Swirling Flow in a Circular Pipe. J. Fluids Eng. 1994, 116, 370–373. [Google Scholar] [CrossRef]
- Amini, Y.; Mokhtari, M.; Haghshenasfard, M.; Barzegar Gerdroodbary, M. Heat Transfer of Swirling Impinging Jets Ejected from Nozzles with Twisted Tapes Utilizing CFD Technique. Case Stud. Therm. Eng. 2015, 6, 104–115. [Google Scholar] [CrossRef] [Green Version]
- Hibara, H.; Sudo, K. Structure and Vibration Phenomenon of Swirling Flow through Conical Diffusers. Trans. Jpn. Soc. Mech. Eng. Ser. B 2002, 68, 3049–3057. [Google Scholar] [CrossRef] [Green Version]
- Takano, T.; Ikarashi, Y.; Uchiyama, K.; Yamagata, T.; Fujisawa, N. Influence of Swirling Flow on Mass and Momentum Transfer Downstream of a Pipe with Elbow and Orifice. Int. J. Heat Mass Transf. 2016, 92, 394–402. [Google Scholar] [CrossRef]
- Ramírez-Arreola, D.E.; Aranda-García, F.J.; Sedano-de la Rosa, C.; Vite-Torres, M.; Gallardo-Hernández, E.A.; Godínez-Salcedo, J.G. Influence of Swirl Number and Incidence Angle on Erosion-Corrosion Behavior of API 5L X-52 Steel under Swirling Jets. Wear 2022, 510–511, 204518. [Google Scholar] [CrossRef]








| Parameter | Values |
|---|---|
| Outer diameter of MD (mm) | 133 |
| Inner diameter of MD (mm) | 130 |
| Length of the domain in axial direction (mm) | 880 |
| Distribution zone height (mm) | 70 |
| Collection zone height (mm) | 70 |
| Number of fuel pipes | 7 |
| Number of large-diameter coolant pipe | 6 |
| Number of small-diameter coolant pipe | 6 |
| Fuel pin pitch (mm) | 28 |
| Outer/inner diameters of fuel pipes (mm) | 23/19 |
| Outer/inner diameters of large-diameter coolant pipes (mm) | 23/19 |
| Outer/inner diameter of small-diameter coolant pipes (mm) | 10/8 |
| Property | Interpolation Function |
|---|---|
| Density (kg/m3) | 11,463 − 1.32 × T |
| Heat Capacity (J/kg.K) | 175.1 − 4.961 × 10−2 × T + 1.985 × 10−5 × T2 2212 2.099 × 10−9 × T3 − 1.524 × 106 × T2 |
| Viscosity (Pa.s) | (1032.2/T) − 7.6354 |
| Fuel boundary conditions | Velocity (m/s) | 0.1 |
| Total pressure (atm) | 1 | |
| Total temp (K) | 1473 | |
| Coolant boundary conditions | Velocity (m/s) | 0.5 |
| Total pressure (atm) | 1 | |
| Total temp (K) | 873 |
| Pipe Group | Mass Flow per Pipe kg/s |
|---|---|
| Pipe group X (pipes 1, 3, 4, 6) | 0.19 |
| Pipe group Y (pipes 2, 5) | 0.18 |
| Pipe group Z (pipe 7) | 0.05 |
| Pipe Group | Heat Transfer Rate/Pipe (Watt) |
|---|---|
| Pipe group X (pipes 1, 3, 4, 6) | −1973 |
| Pipe group Y (pipes 2, 5) | −2001 |
| Pipe group Z (pipe 7) | −1183 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Elgendy, H.; Czerski, K. Numerical Study of Flow and Heat Transfer Characteristics in a Simplified Dual Fluid Reactor. Energies 2023, 16, 4989. https://doi.org/10.3390/en16134989
Elgendy H, Czerski K. Numerical Study of Flow and Heat Transfer Characteristics in a Simplified Dual Fluid Reactor. Energies. 2023; 16(13):4989. https://doi.org/10.3390/en16134989
Chicago/Turabian StyleElgendy, Hisham, and Konrad Czerski. 2023. "Numerical Study of Flow and Heat Transfer Characteristics in a Simplified Dual Fluid Reactor" Energies 16, no. 13: 4989. https://doi.org/10.3390/en16134989
APA StyleElgendy, H., & Czerski, K. (2023). Numerical Study of Flow and Heat Transfer Characteristics in a Simplified Dual Fluid Reactor. Energies, 16(13), 4989. https://doi.org/10.3390/en16134989






