Optimal Scheduling of the Wind-Photovoltaic-Energy Storage Multi-Energy Complementary System Considering Battery Service Life
Abstract
:1. Introduction
2. Multi-Energy Complementary Combined System Composition
2.1. Objective Functions
- (1)
- Minimize the mean squared deviation of “generalized load”:
- (2)
- Minimize the fluctuation of the combined system output:where is the combined system output fluctuation; is the system output at time t.
- (3)
- Minimize the generation cost of the combined system:where is the system’s operating cost, are the fuel cost, fixed cost, environmental cost, wind–solar energy curtailment cost, and ramp-up cost incurred in the time period t of the combined system, respectively.
2.2. Constraint Conditions
- (1)
- Constraints on the system’s power balance:
- (2)
- Constraints on wind and PV output:where and are the output of the wind farms and PV plants at time t; and are the minimum and maximum values of the allowable output of the wind farm and PV plant at time t, respectively.
- (3)
- Constraints on the battery charge\discharge limitations:where are the minimum and maximum values of the allowable output of the battery at time t, respectively; is the capacity of the battery at time t; are the minimum and maximum values of the battery capacity at time t, respectively; are the battery charge and discharge efficiencies.
- (4)
- Constraint on the pumped storage power station:where are the minimum and maximum values of the allowable output of the pumped storage at time t, respectively; is the capacity of the pumped storage at time t; are the minimum and maximum values of the pumped storage capacity at time t, respectively; are the pumped storage charge and discharge efficiency.
- (5)
- Constraint on combined system’s reliability:where is the system’s power supply reliability; is the minimum value of the system’s power supply reliability.
2.3. Combined System Operating Indicators
- (1)
- Reliability indicators for electricity supply
- (2)
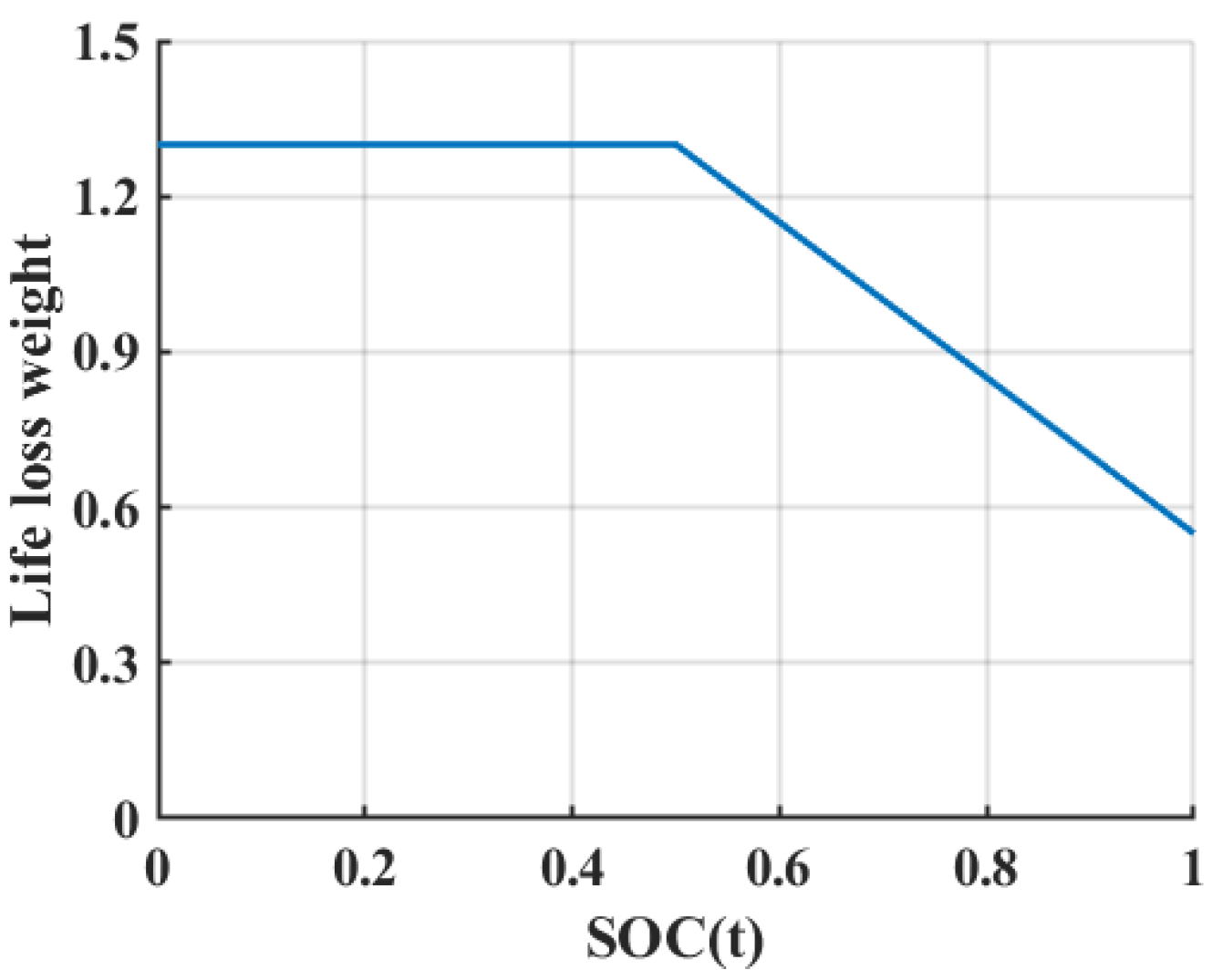
- Evaluation model for battery life
3. Energy Management and Optimization
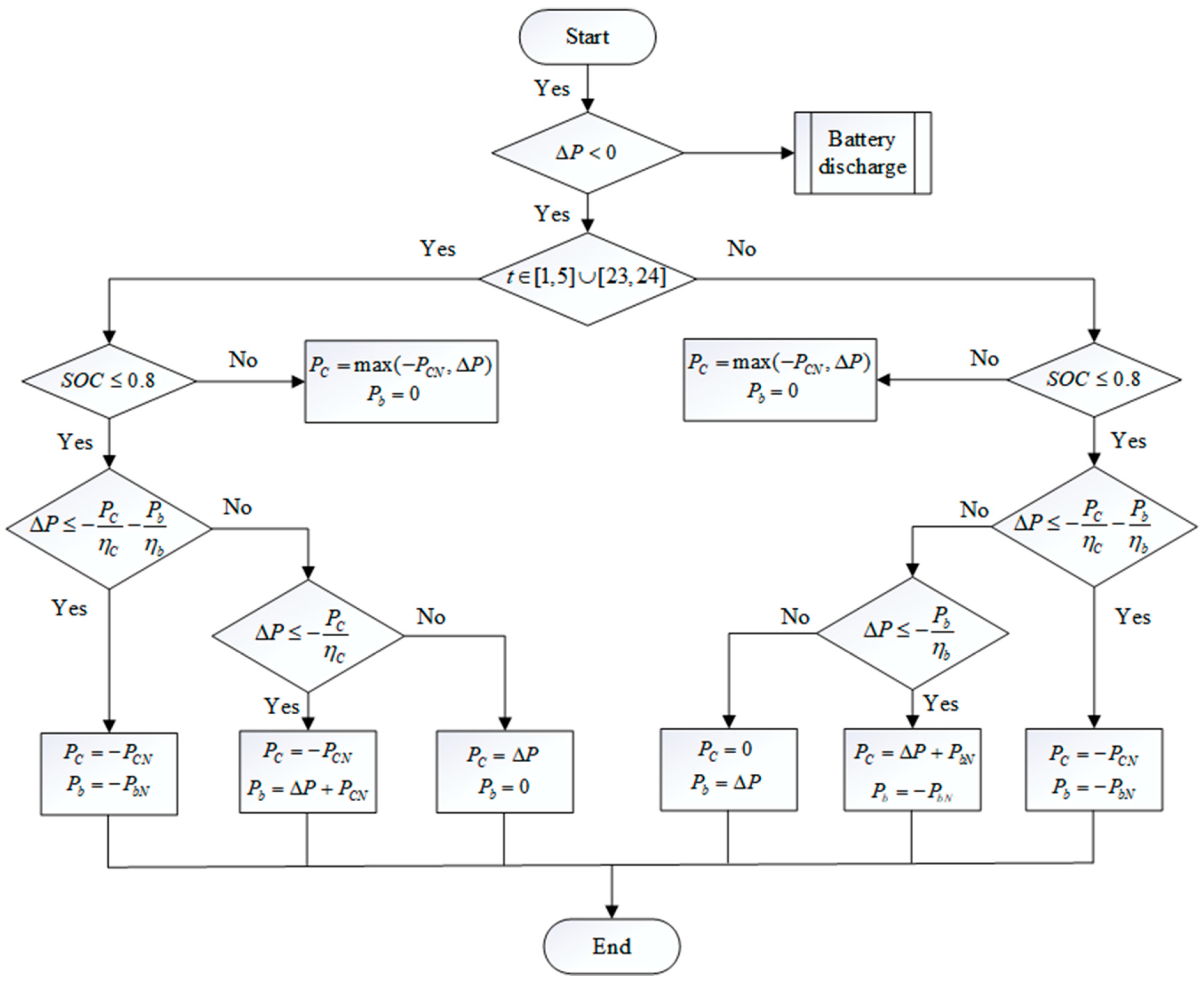
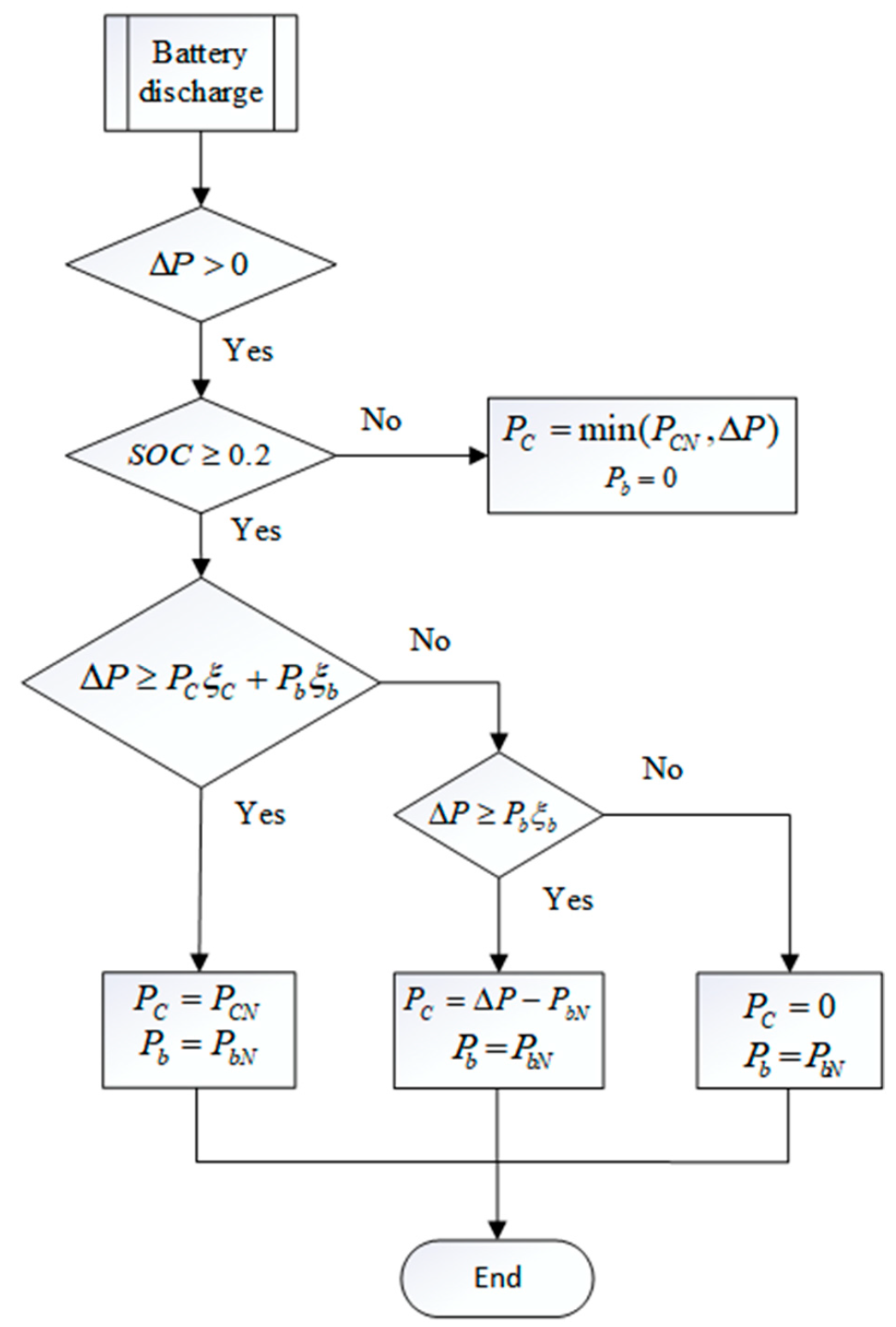
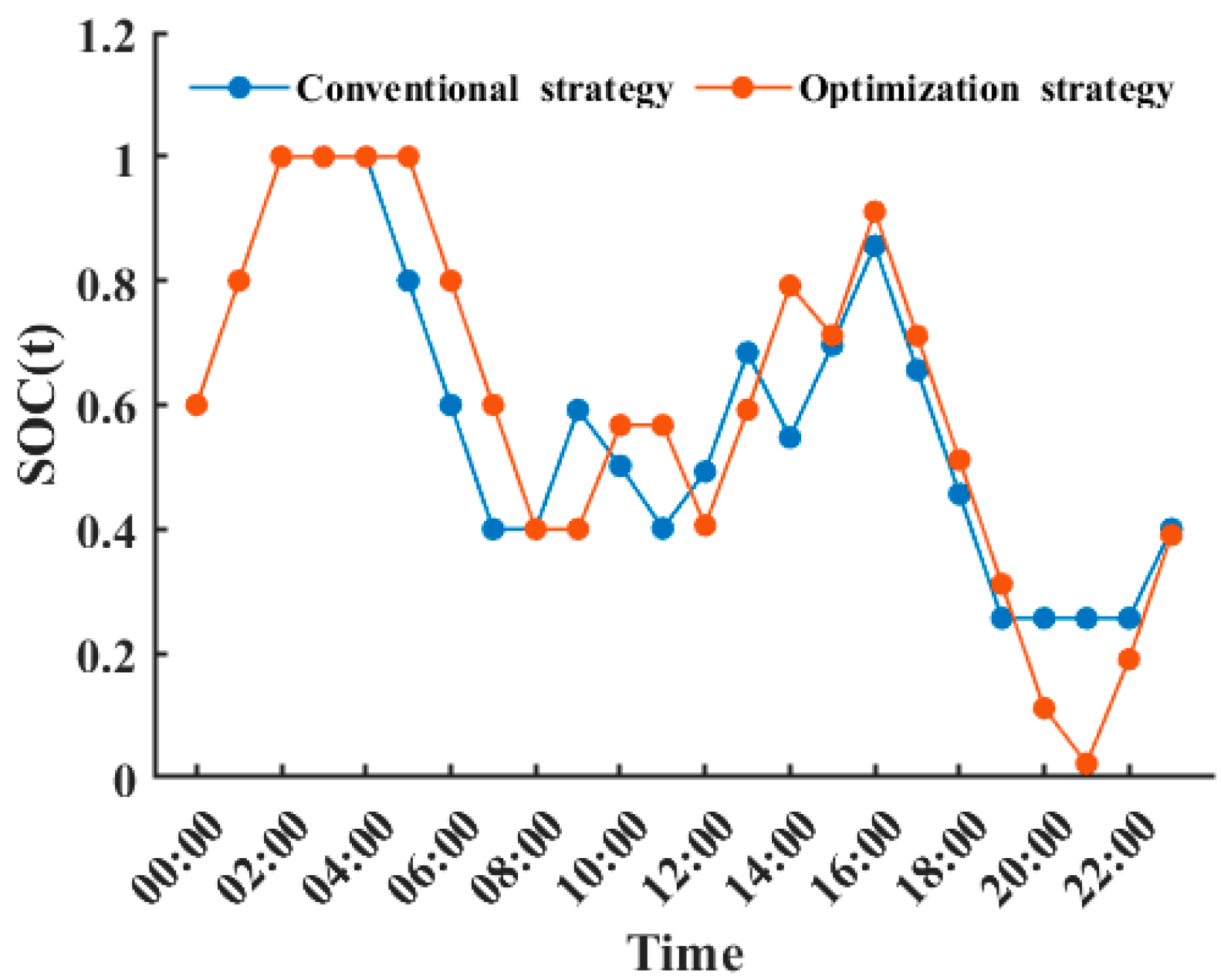
3.1. Hybrid Energy Storage System Operation Strategy
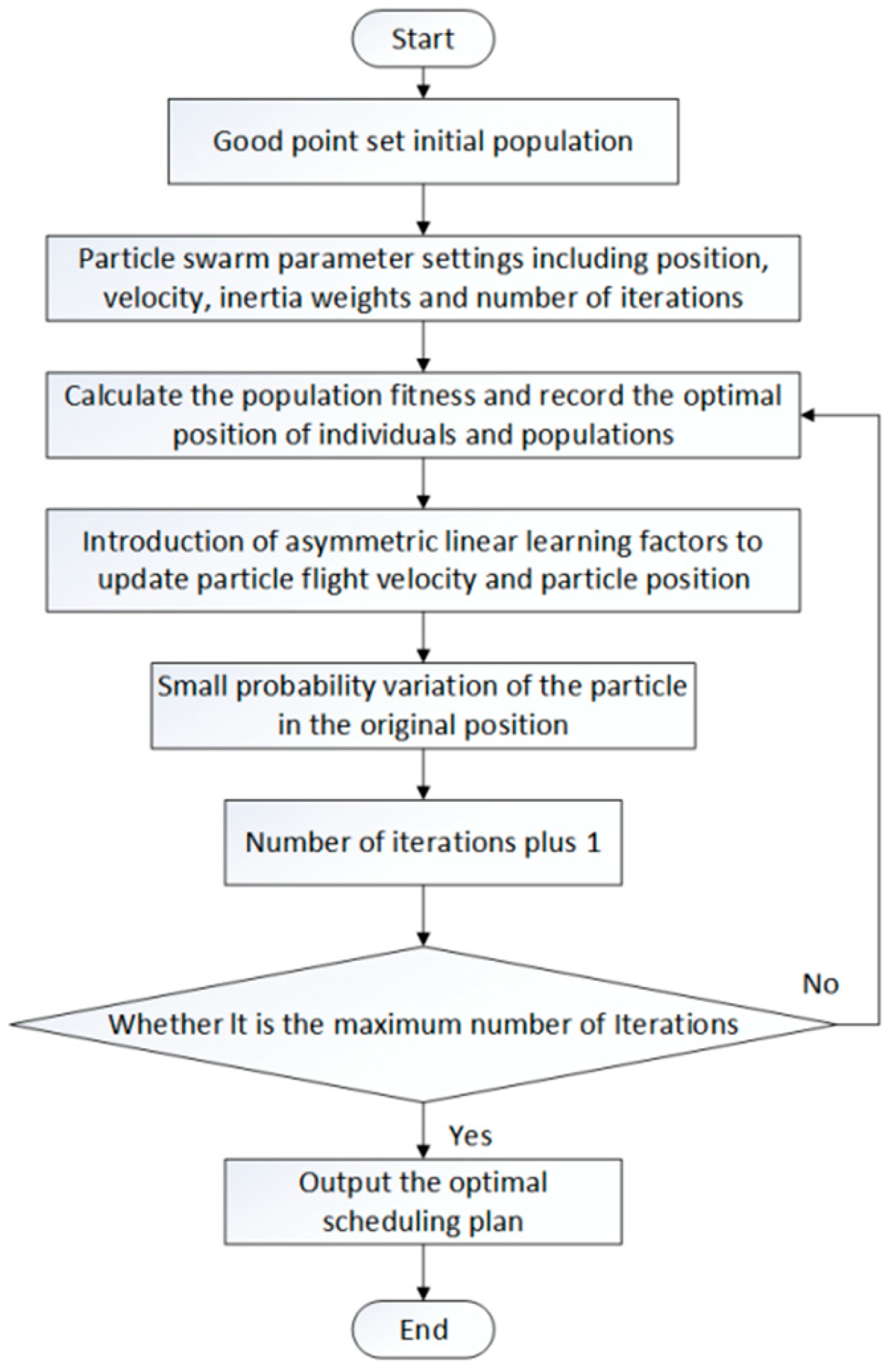
3.2. Improved Particle Swarm Optimization
- (1)
- Linearly decreasing inertia weight
- (2)
- Prime ideal set initialization particle
- (3)
- Learning factors of asynchronous change
4. Results and Analysis
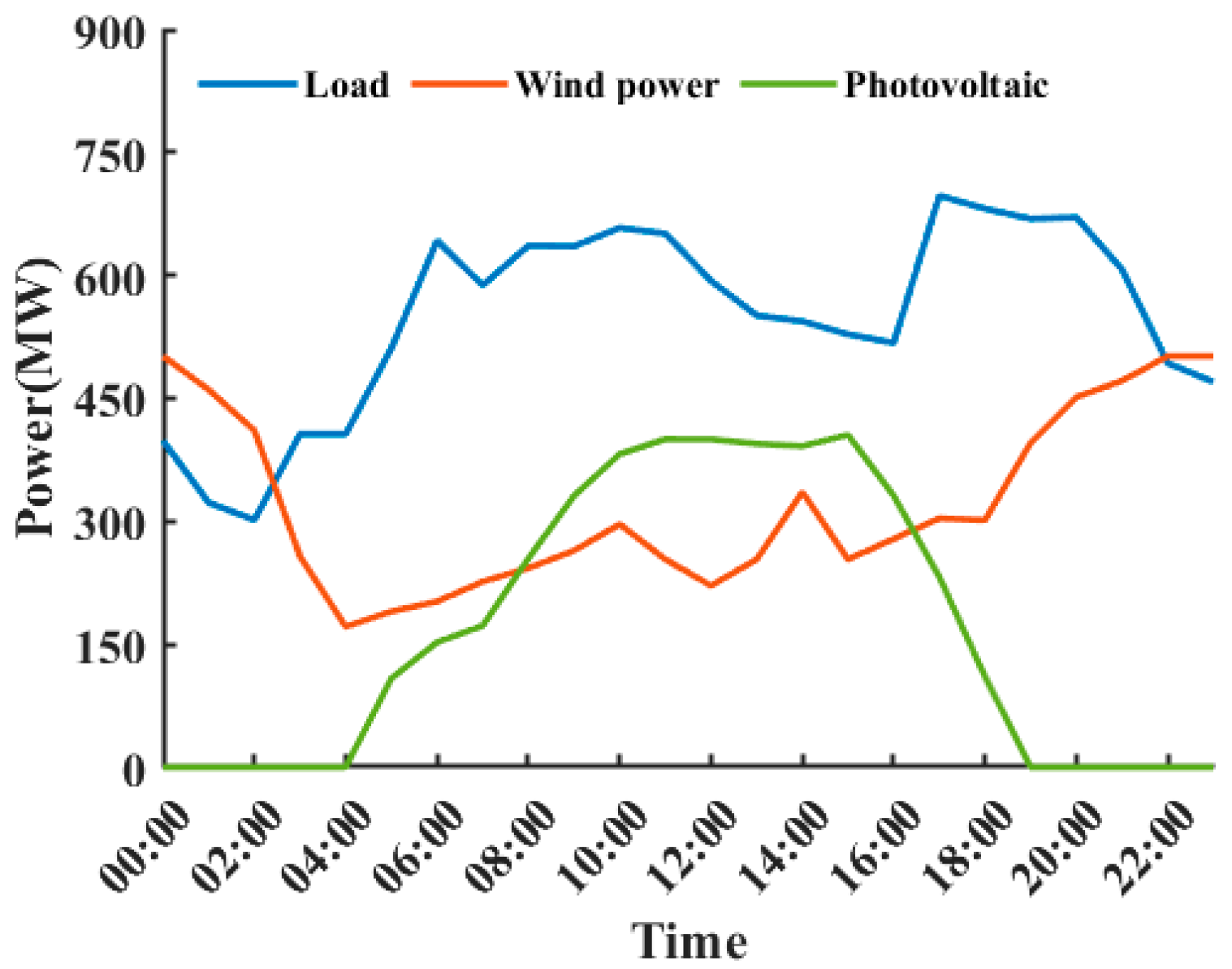
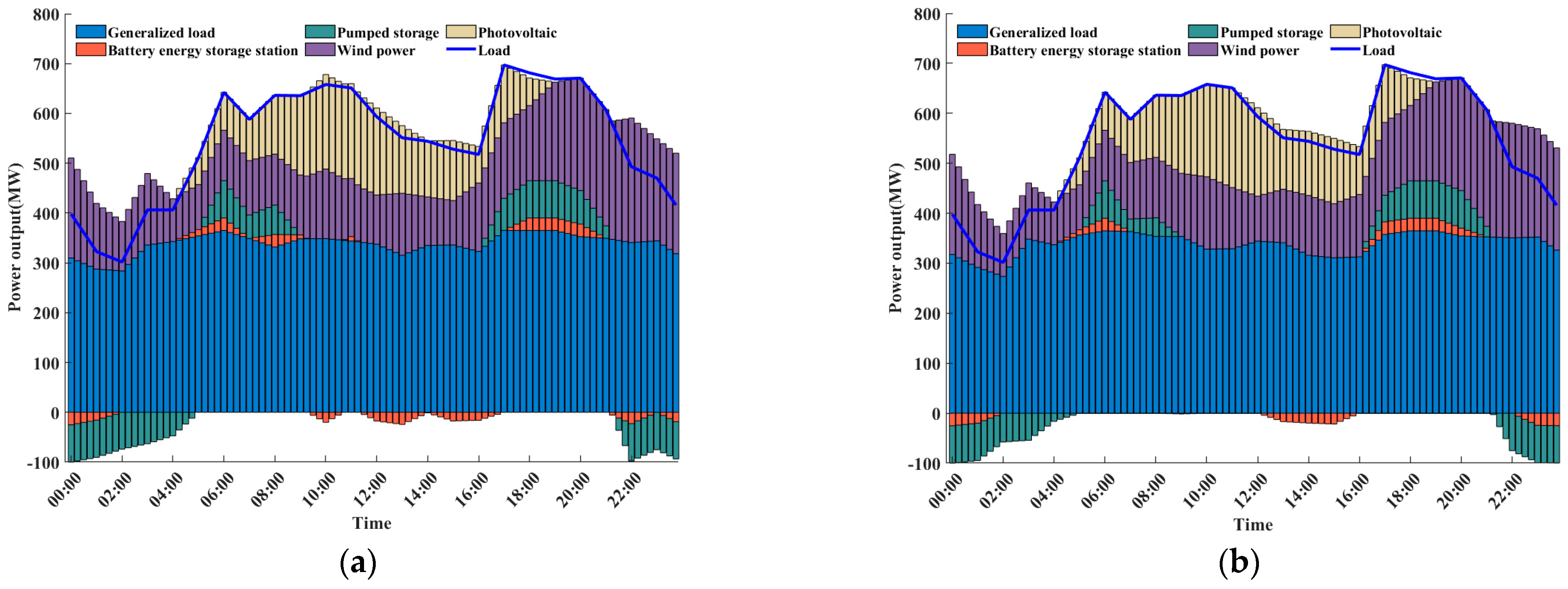
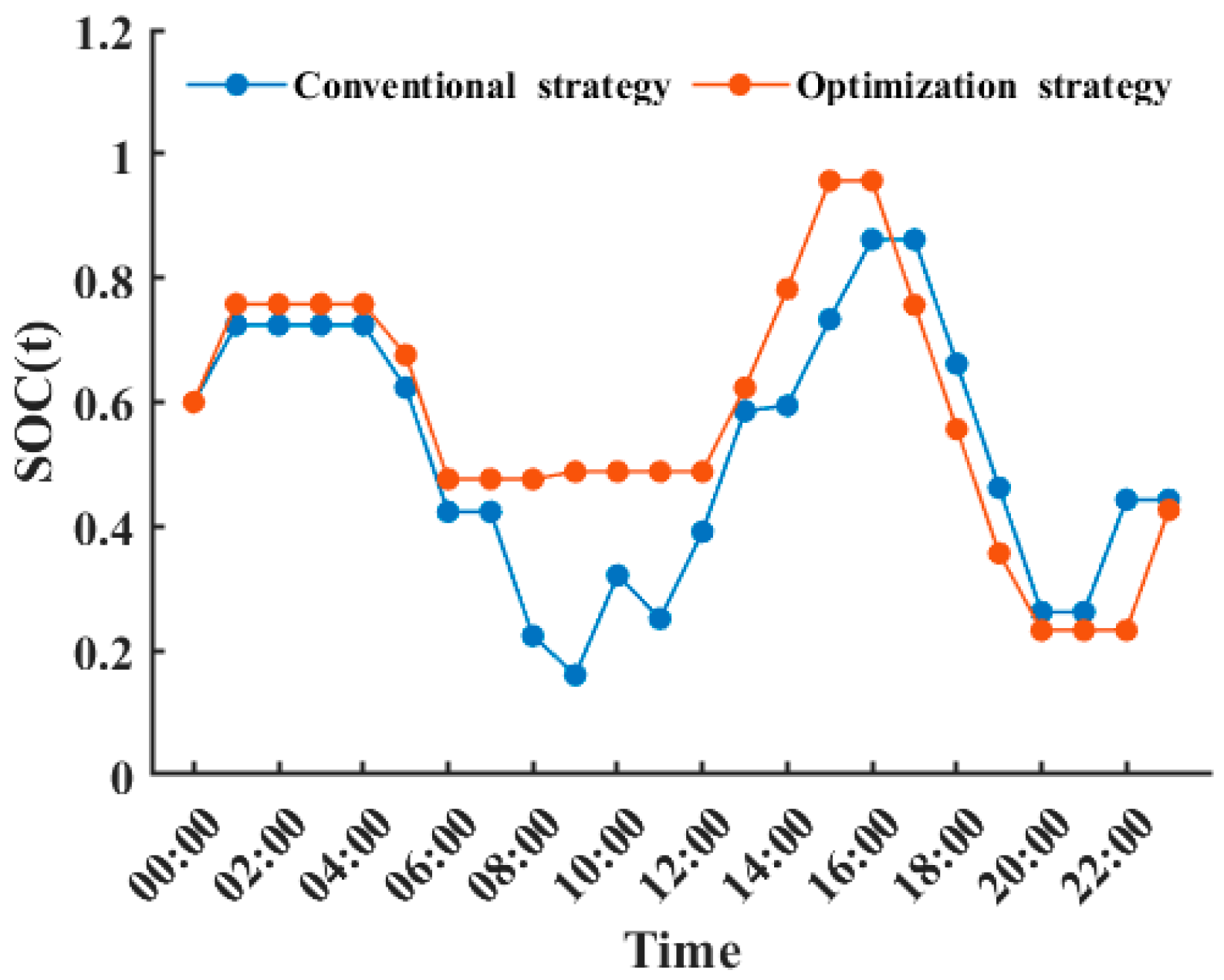
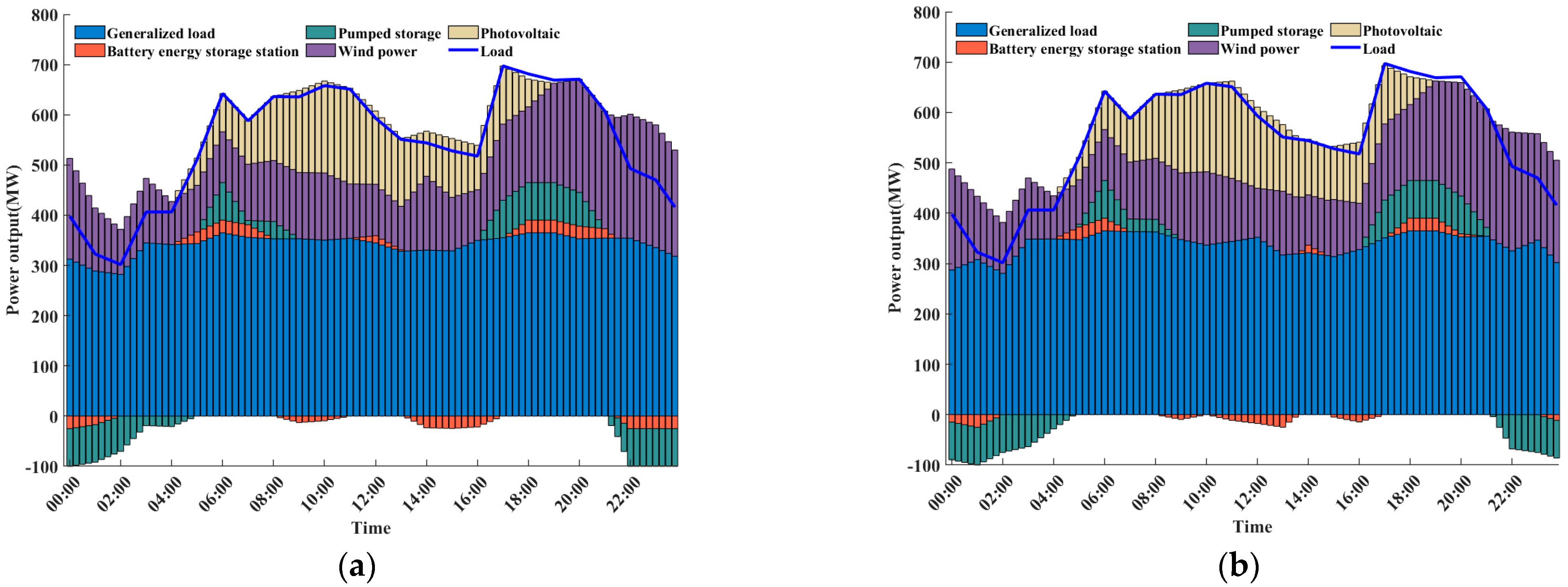
4.1. Analysis of Optimization Scheduling Results
4.2. Analysis of Operating Cost Results
5. Conclusions
- (1)
- By utilizing the hybrid energy storage operation strategy proposed in this article, the scheduling schemes for each objective function were solved. Battery charging and discharging are managed so as to optimize the battery life-loss coefficient, ensuring healthy battery operation while reducing the total combined system’s operating costs.
- (2)
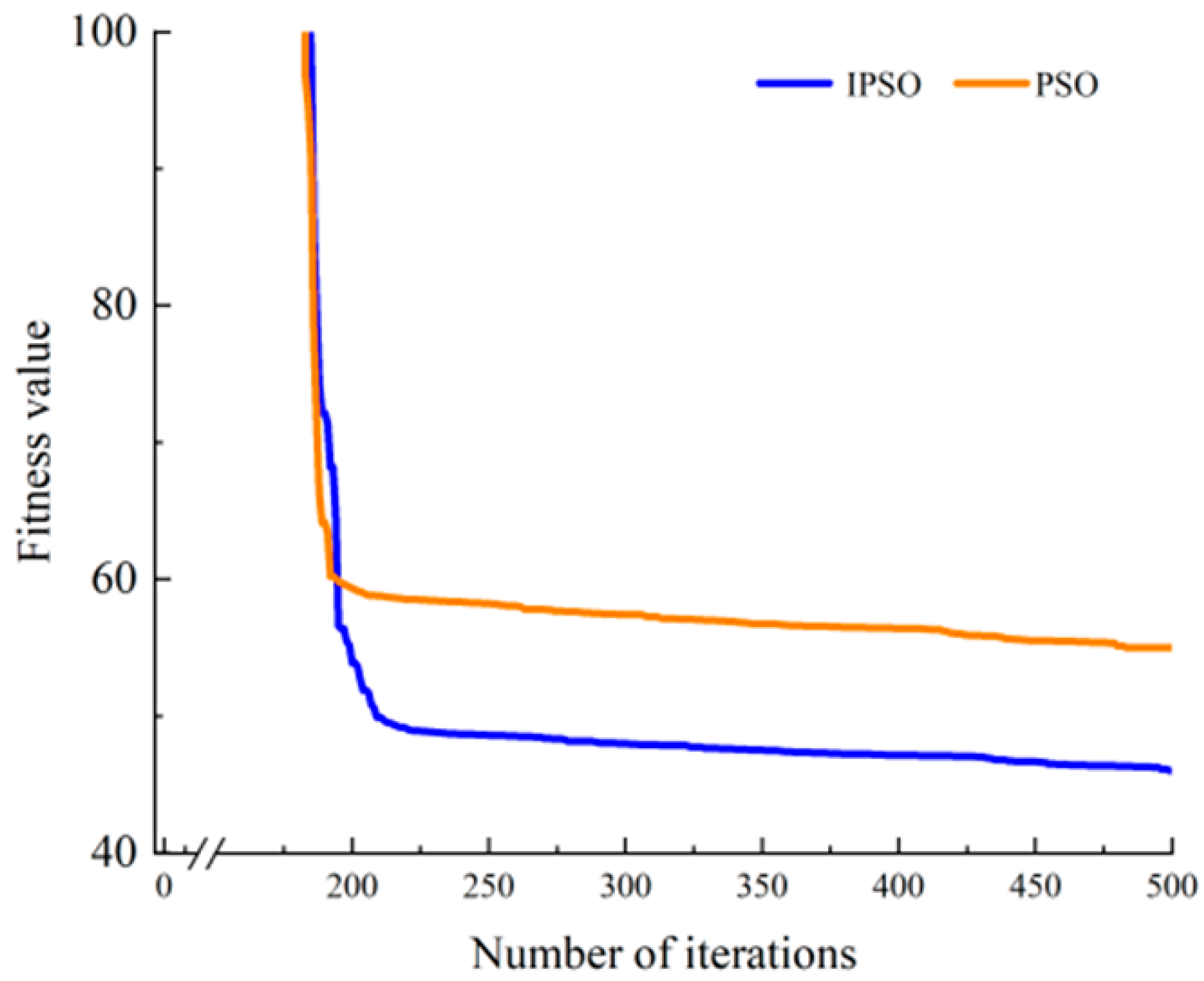
- The improved PSO algorithm introduces a prime ideal set initialization population to improve the quality of the initial population by introducing linear decreasing inertia weights to compensate for its insufficient particle diversity. In order to avoid particles falling into premature convergence, small probability mutation processing was added to the algorithm. The improved PSO algorithm converges to 43. 83MW around the 210th iteration. An improved PSO achieves an optimal scheduling scheme in a more precise manner.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wei, D.; Li, H.; Ren, Y.; Yao, X.; Wang, L.; Jin, K. Modeling of hydrogen production system for photovoltaic power generation and capacity optimization of energy storage system. Front. Energy Res. 2022, 10, 1004277. [Google Scholar] [CrossRef]
- Gaojun, M.; Yanwen, D.; Pau, G.; Linlin, Y.; Wenyi, T. Multi-objective capacity optimization configuration of independent wind-photovoltaichydrogen-battery system based on improved MOSSA algorithm. Front. Energy Res. 2023, 10, 1077462. [Google Scholar] [CrossRef]
- Liu, S.; Lin, Z.; Jiang, Y.; Zhang, T.; Yang, L.; Tan, W.; Lu, F. Modelling and discussion on emission reduction transformation path of China’s electric power industry under "double carbon" goal. Heliyon 2022, 8, e10497. [Google Scholar] [CrossRef] [PubMed]
- Chen, K.; Peng, H.; Zhang, J.; Chen, P.; Ruan, J.; Li, B.; Wang, Y. Optimized Demand-Side Day-Ahead Generation Scheduling Model for a Wind–Photovoltaic–Energy Storage Hydrogen Production System. ACS Omega 2022, 7, 43036–43044. [Google Scholar] [CrossRef] [PubMed]
- Nikolova, S.; Causevski, A.; Al-Salaymeh, A. Optimal operation of conventional power plants in power system with integrated renewable energy sources. Energy Convers. Manag. 2013, 65, 697–703. [Google Scholar] [CrossRef]
- Wang, J.; Huo, J.; Zhang, S.; Teng, Y.; Li, L.; Han, T. Flexibility transformation decision-making evaluation of coal-fired thermal power units deep peak shaving in China. Sustainability 2021, 13, 1882. [Google Scholar] [CrossRef]
- Hou, H.; Xu, T.; Wu, X.; Wang, H.; Tang, A.; Chen, Y. Optimal capacity configuration of the wind-photovoltaic-storage hybrid power system based on gravity energy storage system. Appl. Energy 2020, 271, 115052. [Google Scholar] [CrossRef]
- Lu, M.; Guan, J.; Wu, H.; Chen, H.; Gu, W.; Wu, Y.Z.; Hang, L. Day-ahead optimal dispatching of multi-source power system. Renew. Energy 2022, 183, 435–446. [Google Scholar] [CrossRef]
- Zhang, X.M.; Wang, L.P.; Li, J.W.; Zhang, Y.K. Self-optimization simulation model of short-term cascaded hydroelectric system dispatching based on the daily load curve. Water Resour. Manag. 2013, 27, 5045–5067. [Google Scholar] [CrossRef] [Green Version]
- Wu, X.Y.; Cheng, C.T.; Shen, J.J.; Luo, B.; Liao, S.L.; Li, G. A multi-objective short term hydropower scheduling model for peak shaving. Int. J. Electr. Power Energy Syst. 2015, 68, 278–293. [Google Scholar] [CrossRef]
- Wang, L.; Vo, Q.S.; Prokhorov, A.V. Stability improvement of a multimachine power system connected with a large-scale hybrid wind-photovoltaic farm using a supercapacitor. IEEE Trans. Ind. Appl. 2017, 54, 50–60. [Google Scholar] [CrossRef]
- Al Shereiqi, A.; Al-Hinai, A.; Albadi, M.; Al-Abri, R. Optimal sizing of a hybrid wind-photovoltaic-battery plant to mitigate output fluctuations in a grid-connected system. Energies 2020, 13, 3015. [Google Scholar] [CrossRef]
- Sun, K.; Li, K.J.; Pan, J.; Liu, Y.; Liu, Y. An optimal combined operation scheme for pumped storage and hybrid wind-photovoltaic complementary power generation system. Appl. Energy 2019, 242, 1155–1163. [Google Scholar] [CrossRef]
- Abdelshafy, A.M.; Jurasz, J.; Hassan, H.; Mohamed, A.M. Optimized energy management strategy for grid connected double storage (pumped storage-battery) system powered by renewable energy resources. Energy 2020, 192, 116615. [Google Scholar] [CrossRef]
- Teleke, S.; Baran, M.E.; Huang, A.Q.; Bhattacharya, S.; Anderson, L. Control strategies for battery energy storage for wind farm dispatching. IEEE Trans. Energy Convers. 2009, 24, 725–732. [Google Scholar] [CrossRef]
- He, Y.; Guo, S.; Zhou, J.; Wu, F.; Huang, J.; Pei, H. The quantitative techno-economic comparisons and multi-objective capacity optimization of wind-photovoltaic hybrid power system considering different energy storage technologies. Energy Convers. Manag. 2021, 229, 113779. [Google Scholar] [CrossRef]
- Xu, Y.; Zhao, T.; Zhao, S.; Zhang, J.; Wang, Y. Multi-objective chance-constrained optimal day-ahead scheduling considering BESS degradation. CSEE J. Power Energy Syst. 2018, 4, 316–325. [Google Scholar] [CrossRef]
- Zhang, J.; Cheng, C.; Yu, S.; Wu, H.; Gao, M. Sharing hydropower flexibility in interconnected power systems: A case study for the China Southern power grid. Appl. Energy 2021, 288, 116645. [Google Scholar] [CrossRef]
- Kerdphol, T.; Fuji, K.; Mitani, Y.; Watanabe, M.; Qudaih, Y. Optimization of a battery energy storage system using particle swarm optimization for stand-alone micro-grids. Int. J. Electr. Power Energy Syst. 2016, 81, 32–39. [Google Scholar] [CrossRef]
- Nguyen, T.T. An improved cuckoo search algorithm for the problem of electric distribution network reconfiguration. Appl. Soft Comput. 2019, 84, 105720. [Google Scholar] [CrossRef]
- Mohamed, M.A.; Eltamaly, A.M.; Alolah, A.I. Swarm intelligence-based optimization of grid-dependent hybrid renewable energy systems. Renew. Sustain. Energy Rev. 2017, 77, 515–524. [Google Scholar] [CrossRef]
- Sharifi, M.R.; Akbarifard, S.; Qaderi, K.; Madadi, M.R. Developing MSA algorithm by new fitness-distance-balance selection method to optimize cascade hydropower reservoirs operation. Water Resour. Manag. 2021, 35, 385–406. [Google Scholar] [CrossRef]
- Zhao, M.; Wang, Y.; Wang, X.; Chang, J.; Chen, Y.; Zhou, Y.; Guo, A. Flexibility evaluation of wind-PV-hydro multi-energy complementary base considering the compensation ability of cascade hydropower stations. Appl. Energy 2022, 315, 119024. [Google Scholar] [CrossRef]
- Jenkins, D.P.; Fletcher, J.; Kane, D. Lifetime prediction and sizing of lead–acid batteries for microgeneration storage applications. IET Renew. Power Gener. 2008, 2, 191–200. [Google Scholar] [CrossRef]
- Sun, S.; Zhang, Q.; Sun, J.; Cai, W.; Zhou, Z.; Yang, Z.; Wang, Z. Lead–Acid Battery SOC Prediction Using Improved AdaBoost Algorithm. Energies 2022, 15, 5842. [Google Scholar] [CrossRef]
- Wu, G.; Li, T.; Xu, W.; Xiang, Y.; Su, Y.; Liu, J.; Liu, F. Chance-constrained energy-reserve co-optimization scheduling of wind-photovoltaic-hydrogen integrated energy systems. Int. J. Hydrogen Energy 2023, 48, 6892–6905. [Google Scholar] [CrossRef]
- Yun, J.Y.; Yu, G.; Kook, K.S.; Rho, D.H.; Chang, B.H. SOC-based control strategy of battery energy storage system for power system frequency regulation. Trans. Korean Inst. Electr. Eng. 2014, 63, 622–628. [Google Scholar] [CrossRef] [Green Version]
- Ghorbani, N.; Kasaeian, A.; Toopshekan, A.; Bahrami, L.; Maghami, A. Optimizing a hybrid wind-PV-battery system using GA-PSO and MOPSO for reducing cost and increasing reliability. Energy 2018, 154, 581–591. [Google Scholar] [CrossRef]
- Xing, Y.X.; Wang, J.S.; Zheng, Y.; Wang, Y.C. Partiele Swarm Optimization Algorithm Based on Different Inertia Weights for Solving the P-Hub Allocation Problem. IAENG Int. J. Appl. Math. 2022, 52, 1–15. [Google Scholar]
- Chen, Y.; Liu, Z.; Xu, C.; Zhao, X.; Pang, L.; Li, K.; Shi, Y. Heavy metal content prediction based on Random Forest and Sparrow Search Algorithm. J. Chemom. 2022, 36, e3445. [Google Scholar] [CrossRef]
- Zhang, L.; Xu, J.; Liu, Y.; Zhao, H.; Deng, W. Particle swarm optimization algorithm with multi-strategies for delay scheduling. Neural Process. Lett. 2022, 54, 4563–4592. [Google Scholar] [CrossRef]



| Technical Specifications | ||
|---|---|---|
| Wind farm | Installed capacity (MW) | 500 |
| Investment cost (104 RMB/MW) | 1200 | |
| The operation and maintenance factor | 0.25 | |
| Service life (a) | 25 | |
| PV power station | Installed capacity (MW) | 400 |
| Investment cost (104 RMB/MW) | 2000 | |
| The operation and maintenance factor | 0.125 | |
| Service life (a) | 10 | |
| Pumped storage | Installed capacity (MW) | 75 |
| Pump turbine construction costs (104 RMB/MW) | 210 | |
| Pump turbine operation and maintenance costs (104 RMB/MW) | 2 | |
| 0.8 | ||
| 0.9 | ||
| Battery energy storage station | Installed capacity (MW) | 25 |
| Investment cost (104 RMB/MW) | 502.4 | |
| 0.3 | ||
| 0.8 | ||
| 0.85 | ||
| 0.9 | ||
| Optimization Objectives | Operational Strategies | Generalized Load Mean Square Deviation (MW) | Wind and Solar Curtailment (%) | Battery Life Loss Coefficient (%) | Total System Generation Cost (104 RMB) |
|---|---|---|---|---|---|
| Minimize the mean squared deviation of generalized load | General strategy | 43.83 | 14.32 | 0.073 | 467.91 |
| Optimization strategy | 46.76 | 13.93 | 0.055 | 464.83 | |
| Minimize the fluctuation of combined system output | General strategy | 45.19 | 14.39 | 0.088 | 470.10 |
| Optimization strategy | 47.82 | 14.18 | 0.053 | 465.86 | |
| Minimize the generation cost of the combined system | General strategy | 60.48 | 9.64 | 0.092 | 449.14 |
| Optimization strategy | 54.09 | 9.71 | 0.081 | 448.88 |
| Type of Operating Cost | Daily Operating Cost without Considering Optimization Strategy (104 RMB) | Daily Operating Cost of Considering Optimization Strategy (104 RMB) |
|---|---|---|
| Wind and photovoltaic power | 192.99 | 193.17 |
| Generalized load | 224.58 | 223.03 |
| Pumped storage | 12.12 | 12.84 |
| Battery storage | 10.82 | 11.19 |
| Wind and solar curtailment | 8.63 | 8.65 |
| Total cost | 449.14 | 448.88 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Wang, H.; Zhang, Z.; Li, H.; Wang, X.; Zhang, Q.; Zhou, T.; Zhang, P.; Chang, F. Optimal Scheduling of the Wind-Photovoltaic-Energy Storage Multi-Energy Complementary System Considering Battery Service Life. Energies 2023, 16, 5002. https://doi.org/10.3390/en16135002
Li Y, Wang H, Zhang Z, Li H, Wang X, Zhang Q, Zhou T, Zhang P, Chang F. Optimal Scheduling of the Wind-Photovoltaic-Energy Storage Multi-Energy Complementary System Considering Battery Service Life. Energies. 2023; 16(13):5002. https://doi.org/10.3390/en16135002
Chicago/Turabian StyleLi, Yanpin, Huiliang Wang, Zichao Zhang, Huawei Li, Xiaoli Wang, Qifan Zhang, Tong Zhou, Peng Zhang, and Fengxiang Chang. 2023. "Optimal Scheduling of the Wind-Photovoltaic-Energy Storage Multi-Energy Complementary System Considering Battery Service Life" Energies 16, no. 13: 5002. https://doi.org/10.3390/en16135002
APA StyleLi, Y., Wang, H., Zhang, Z., Li, H., Wang, X., Zhang, Q., Zhou, T., Zhang, P., & Chang, F. (2023). Optimal Scheduling of the Wind-Photovoltaic-Energy Storage Multi-Energy Complementary System Considering Battery Service Life. Energies, 16(13), 5002. https://doi.org/10.3390/en16135002





