Exploring the Impact of Vehicle Lightweighting in Terms of Energy Consumption: Analysis and Simulation
Abstract
1. Introduction
- To use more environmentally sustainable sources of energy such as electric or hybrid traction, alternative fossil fuels, and biofuels [16];
- To improve the aerodynamics of vehicles [17];
- To implement speed control to reduce the fuel or energy consumption and therefore the impacts during vehicle use [10];
- To educate users to have more sustainable driving behaviors [22].
- Adopting solutions with alternative powertrains, for example, a fuel cell/battery pack hybrid electric system, adding the complexity and weight given by the additional components of the system, can allow the total weight of the powertrain to be reduced thanks to the downsizing of the battery pack;
- Implementing suitable regenerative braking logics and range management [29];
- Improving energy dense battery chemistries [29] and, in general, battery weight optimization;
- Improving the battery efficiency, for example, through different and more efficient systems of battery cooling, in such a way as to be able to reduce battery size for the same vehicle range;
- Adopting other, more weight-efficient battery forms and shapes, such as blade batteries and structural battery packs;
- Secondary mass saving and resizes.
- Engine compartment, where the improvement concerns the aesthetic cover of the engine, replacing the traditional one in fiberglass with one made with bio-based fiber materials [35];
- Frame, in particular the substitution of its main constituting parts;
- Bodywork, considering the material substitution, the production processes, and modifying the geometries;
- Wheels, considering different type of tires, brakes, and suspension arms;
- Passenger compartment;
- Electronics and electrical system, considering the introduction of a speed control system [36] (reduction of the maximum speed of the vehicle on motorways from 130 to 120 km/h and reduction of consumption by 6% in a medium-sized gasoline car), and the replacement of traditional copper electrical cables with those in copper-tin (Cu-Sn) of reduced diameter and mass [37]; although, it should be noted that Cu-Sn can only be used in low current or signal applications (e.g., measurement signals of the voltages of the single cells of the battery pack) and not in the power connection cables due to a resistance increase [38].
- Section 2 shows the methodology adopted, in particular the reference vehicles of this study, the driving cycle used for the energy consumption estimation, the simulation tool adopted, the vehicle parameters that are the object of investigation, and a brief explanation of the simulations carried out;
- Section 3 presents the results of the study and the considerations that derive from it;
2. Materials and Methods
2.1. Reference Vehicles
2.2. Driving Cycle
- WLTC (Worldwide Harmonized Light-Duty Vehicles Test Cycle), class 3b, driving cycle described in the WLTP (Worldwide Harmonized Light-Duty Vehicles Test Procedure) procedure [53];
- SFTP-US06, described in the “EPA Supplemental Federal Test Procedure” (SFTP) [54];
- FTP75 (EPA Federal Test Procedure) [55];
- HWFET (EPA Highway Fuel Economy Cycle);
- Japanese JC08 Emission Test Cycle [56];
- Artemis, Urban, Rural Road, and Motorway (130) Cycle [57].
2.3. Simulation Tool
- The possibility to save and use vehicle databases;
- The automation of iterations according to three logics.
- Defining the number of simulations to be performed, where the initial SOC of the next simulation is equal to the final SOC of the previous simulation;
- By defining a minimum SOC, the initial SOC of the next simulation is equal to the final SOC of the previous simulation; the iterations continue until the final SOC falls below the minimum SOC set;
- Iterations by varying the weight of the vehicle, in particular, an iteration is performed with the empty weight of the vehicle, defined in the model variables. A settable number of iterations are also performed, with a constant weight increase to be defined for each simulation with respect to the previous one. The same procedure is conducted for weight reduction, starting from the unladen weight of the vehicle set as the default value.
2.4. Parameters of the Vehicle (and of Its Model) Which Can Affect the Lightweighting Results
- Driving cycle considered: different phases of acceleration and deceleration, different intensities of the latter, different powers involved, and variation of the possibility of regenerative recovery.
- Rolling resistance coefficient: in fact, the latter appears in the mathematical formula of the rolling resistance together with the mass of the vehicle.
- Coefficients of aerodynamic resistance: these realize the aerodynamic resistance force acting on the vehicle. In the mathematical formula of the latter, the mass does not appear, but, for the same driving cycle, this force modifies the proportion between phases in which the electric motor is delivering torque (both in acceleration and deceleration) and those (in deceleration) in which the electric motor does not deliver torque or, alternatively, which acts as a generator recharging the battery pack. In fact, during deceleration, it is possible to have a lower deceleration than that which would occur in the event of an electric motor not delivering torque. Deceleration therefore is due solely to resisting forces, inertia, etc. Therefore, in the event of lower deceleration, the electric motor will still have to deliver torque. The result will therefore not be actual braking but a partial release of the accelerator pedal. Furthermore, aerodynamic resistance is a function of speed, and at different speeds of the driving cycle, it is possible to have different acceleration values, with which the contribution of the vehicle mass is correlated, due to the resulting inertia. The acceleration contribution can therefore have a different influence at different points in the driving cycle, as can the mass contribution but not in a corresponding way.
- Other parameters that may be useful to investigate are listed below:
- Inertias of the electric motor and of the rotating parts of the driveline. The contribution of the inertias appears in the equation of the resisting force, which is a function of the angular acceleration of the considered rotating component.
- Gear ratios and wheel radius: these parameters modify the rotation speed of the various components of the driveline, at the same vehicle speed.
- Type of battery pack, in particular the internal resistance of the cells of the pack itself.
- Efficiencies of the transmission and the rest of the driveline (e.g., efficiency of the motor and inverter in charging and discharging).
2.5. Set of Simulations
- Battery pack parameters (nominal voltage, capacity, and internal resistance);
- Aerodynamics (Af ∙ Cx, where Af is the frontal area of the vehicle, and Cx is the longitudinal aerodynamic coefficient);
- Efficiency of the transmission;
- Rolling resistance (in particular, in the reference models, this resistance is a function of a rolling friction coefficient. The analysis therefore focuses on the value of this coefficient).
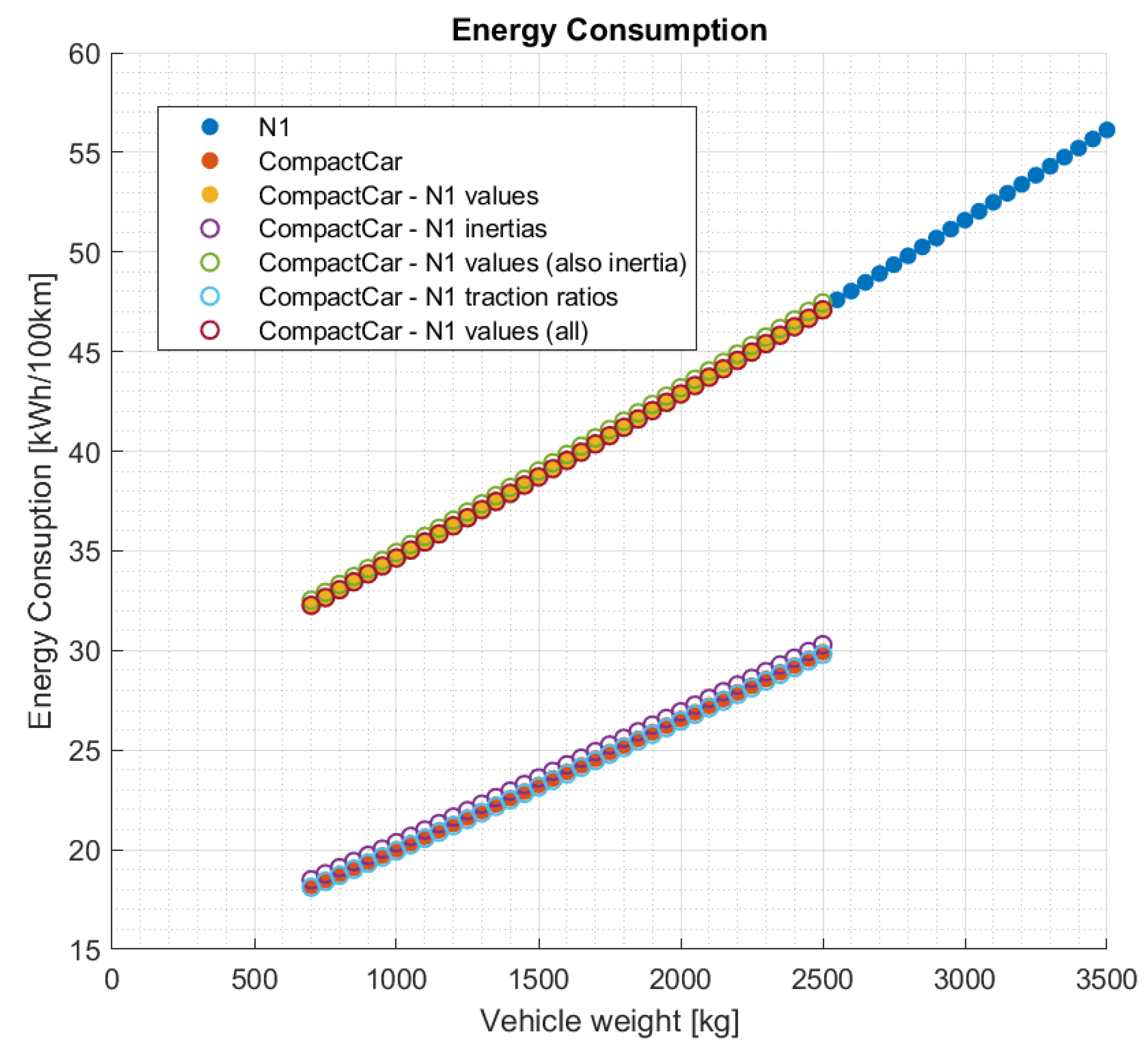
- Compact car with the moments of inertia of the N1 vehicle;
- Compact car with all previously listed parameters and moments of inertia of the N1 vehicle;
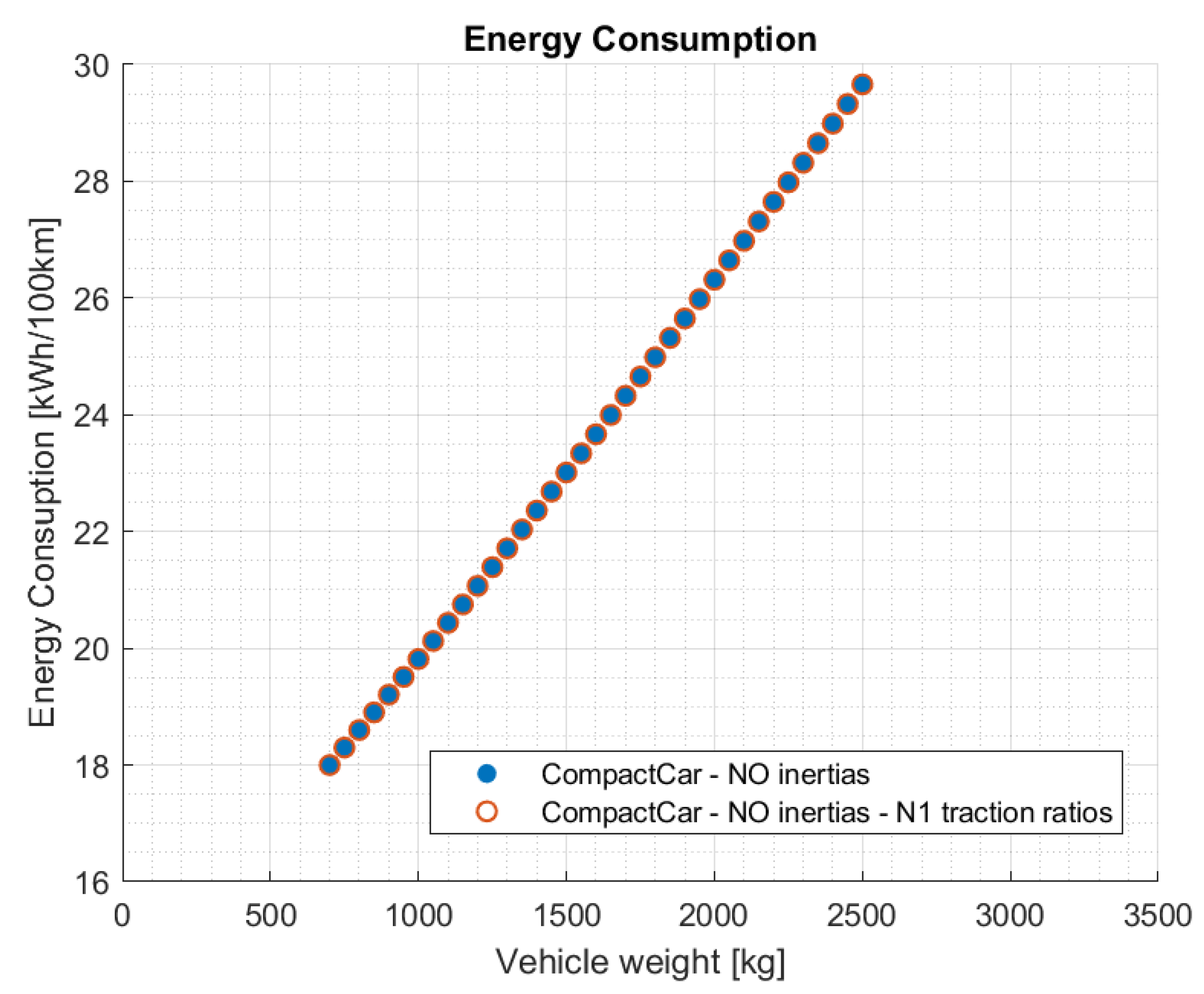
- Compact car with the total traction ratio and wheel radii of the N1 vehicle;
- Compact car with all previously listed parameters, moments of inertia, traction ratio, and wheel radii of the N1 vehicle.
3. Results
3.1. Benchmark Regenerative Braking Logic
3.2. Compact Car and N1 Vehicle in Absence of Regenerative Braking Recovery
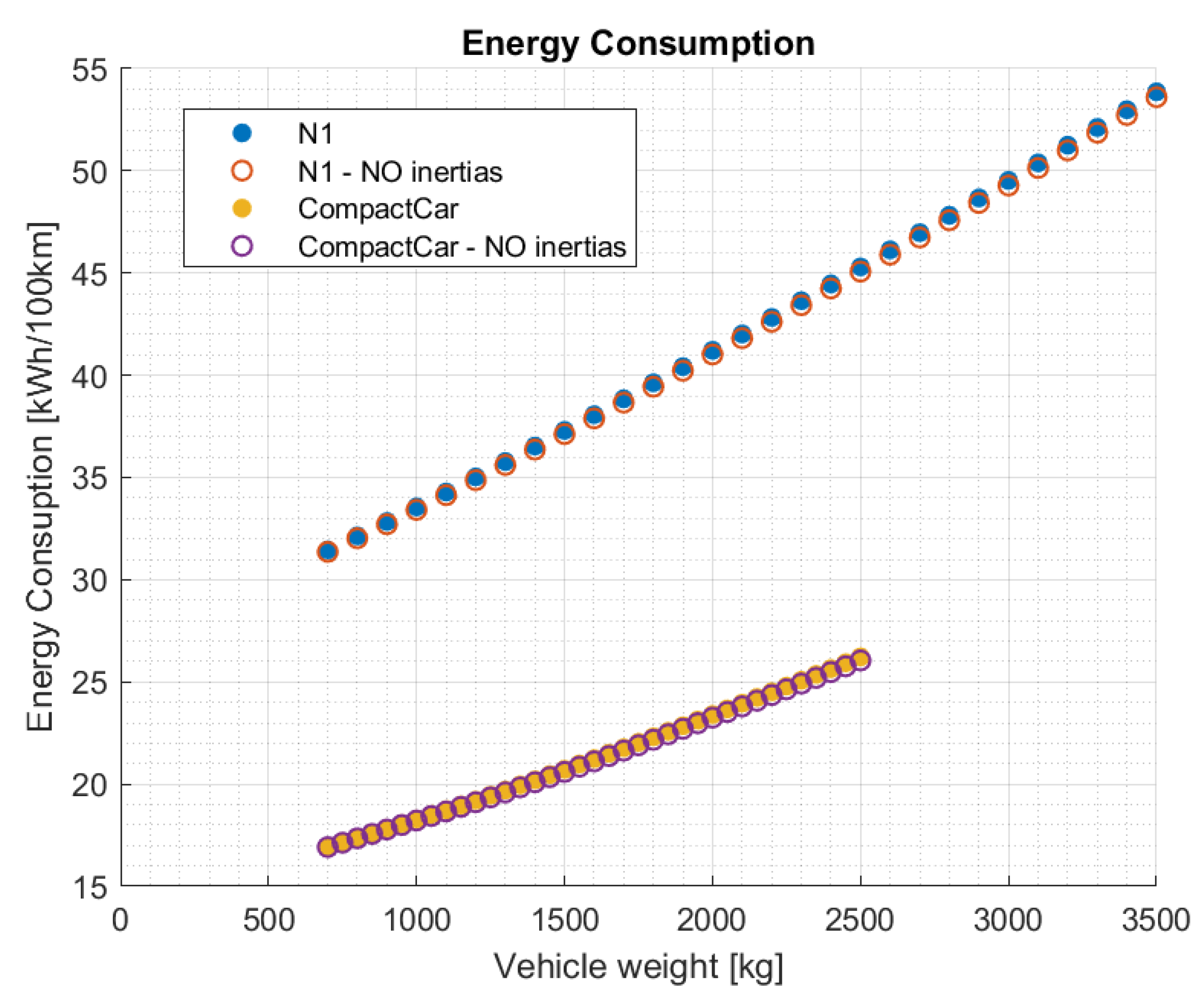
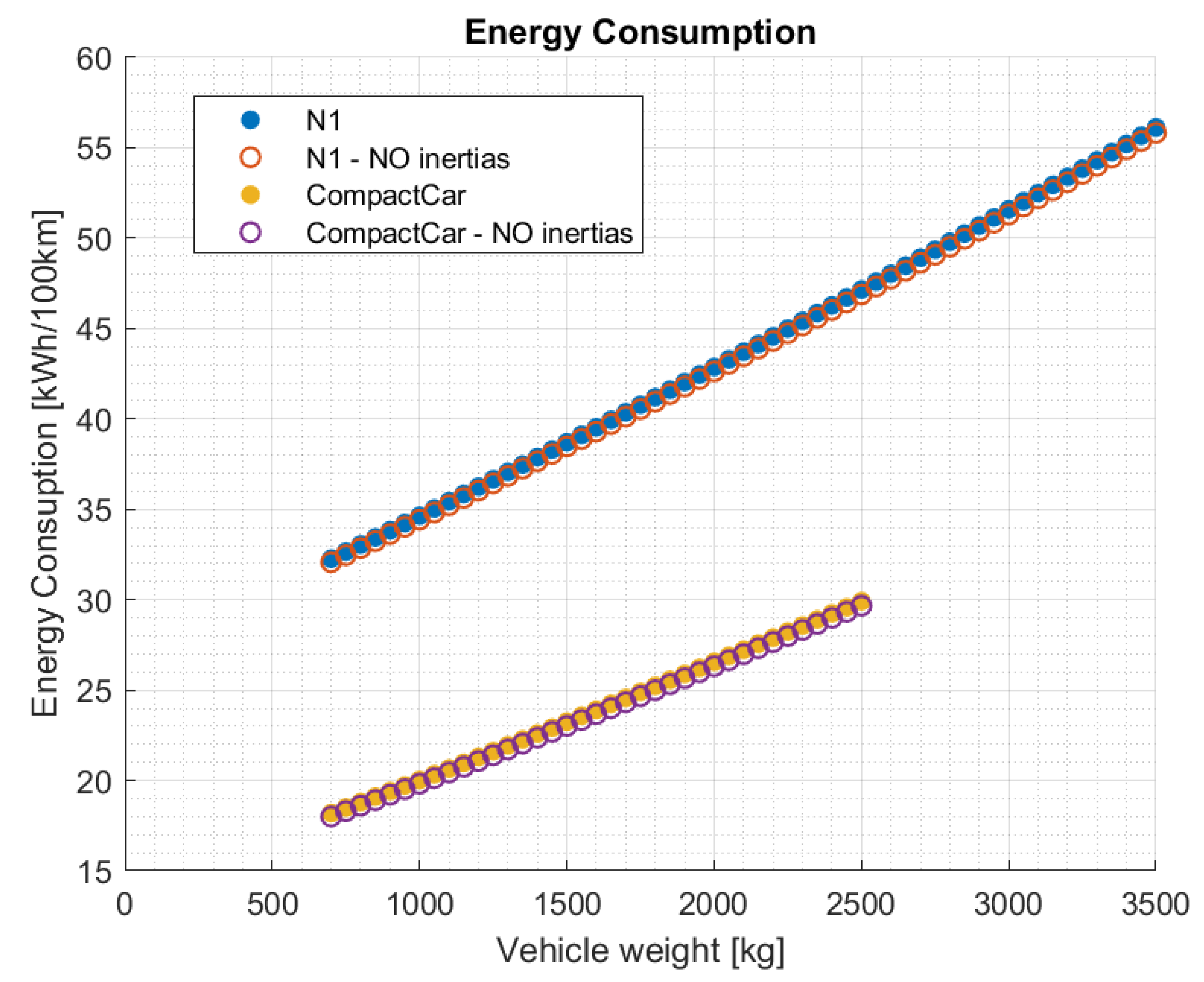
3.2.1. Consumption Analysis
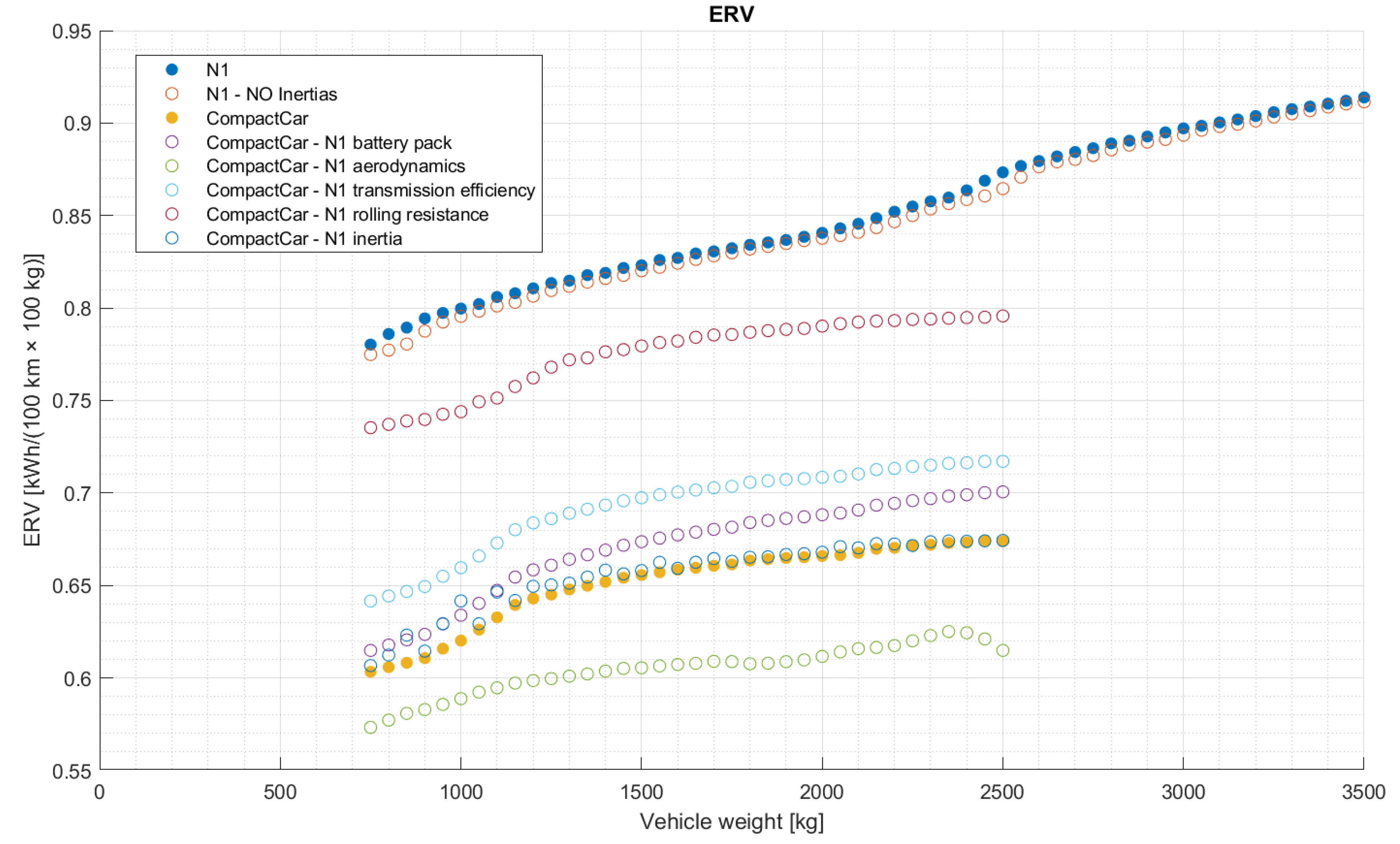
3.2.2. Polynomial Interpolation and ERV Index
3.2.3. Comparison between Different Driving Cycles
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Abbreviation | Description |
| Af | Frontal area of the vehicle |
| polynomial | |
| Cx | Longitudinal aerodynamic coefficient (drag) |
| Average energy consumption of the i-th simulation | |
| Average energy consumption of the simulation with vehicle weight immediately lower than that of the i-th simulation | |
| EPA | U.S. Environmental Protection Agency |
| ERV | Energy Reduction Value |
| ERV index associated with the vehicle weight of the i-th simulation | |
| EV | Electric Vehicle |
| FRV | Fuel Reduction Value |
| FTP75 | Standard driving cycle (FTP75) described in the EPA Federal Test Procedure (FTP) |
| HWFET | EPA Highway Fuel Economy Cycle |
| ICEV | Internal Combustion Engine Vehicle |
| JC08 | Japanese Emission Test Cycle |
| RES | Internal resistance of the battery pack |
| SFTP | EPA Supplemental Federal Test Procedure |
| SFTP-US06 | Standard driving cycle (US06) described in the EPA Supplemental Federal Test Procedure (SFTP) |
| TEST | Target-speed EV Simulation Tool |
| WLTC | Worldwide Harmonized Light-Duty Vehicles Test Cycle |
| WLTP | Worldwide Harmonized Light-Duty Vehicles Test Procedure |
| Vehicle weight (expressed in 100 kg) | |
| Polynomial interpolation function, energy consumption expressed in kWh/(100 km) | |
| Vehicle mass variation between the i-th simulation and the immediately lower mass being simulated |
References
- European Council; Council of the European Union. Stricter CO2 Emission Standards for Cars and Vans Signed Off by the Council. Available online: https://www.consilium.europa.eu/en/press/press-releases/2019/04/15/stricter-co2-emissionstandards-for-cars-and-vans-signed-off-by-the-council/ (accessed on 30 August 2022).
- European Law Brussels. PE-CONS 6/19. Regulation of the European Parliament and of the Council Setting CO2 Emission Performance Standards for New Passenger Cars and for New Light Commercial Vehicles, and Repealing Regulations (EC) No 443/2009 and (EU) No 510/2011 (Recast); 3 April 2019. Available online: https://www.reteambiente.it/repository/normativa/32865_final.pdf (accessed on 18 June 2023).
- Ehsani, M.; Gao, Y.; Longo, S.; Ebrahimi, K. Modern Electric, Hybrid Electric, and Fuel Cell Vehicles; CRC Press, Taylor & Francis Group: Boca Raton, FL, USA, 2018; pp. 1–11. [Google Scholar]
- Lewis, G.M.; Buchanan, C.A.; Jhaveri, K.D.; Sullivan, J.L.; Kelly, J.C.; Das, S.; Taub, A.I.; Keoleian, G.A. Green Principles for Vehicle Lightweighting. Environ. Sci. Technol. 2019, 53, 4063–4077. [Google Scholar] [CrossRef] [PubMed]
- Koffler, C.; Rohde-Brandenburger, K. On the Calculation of Fuel Savings through Lightweight Design in Automotive Life Cycle Assessments. Int. J. Life Cycle Assess. 2010, 15, 128–135. [Google Scholar] [CrossRef]
- Kim, H.C.; Wallington, T.J. Life Cycle Assessment of Vehicle Lightweighting: A Physics-Based Model to Estimate Use-Phase Fuel Consumption of Electrified Vehicles. Environ. Sci. Technol. 2016, 50, 11226–11233. [Google Scholar] [CrossRef]
- Ross, M. Fuel Efficiency and the Physics of Automobiles. Contemp. Phys. 1997, 38, 381–394. [Google Scholar] [CrossRef]
- Sullivan, J.L.; Lewis, G.M.; Keoleian, G.A. Effect of Mass on Multimodal Fuel Consumption in Moving People and Freight in the U.S. Transp. Res. D Transp. Environ. 2018, 63, 786–808. [Google Scholar] [CrossRef]
- Sovran, G.; Blaser, D. Quantifying the Potential Impacts of Regenerative Braking on a Vehicle’s Tractive-Fuel Consumption for the U.S., European, and Japanese Driving Schedules; SAE Technical Paper; SAE International: Warrendale, PA, USA, 2006. [Google Scholar] [CrossRef]
- Spreafico, C. Can Modified Components Make Cars Greener? A Life Cycle Assessment. J. Clean. Prod. 2021, 307, 127190. [Google Scholar] [CrossRef]
- Ford Motor Company. Sustainability Report 2016/2017; Ford Motor Company: Dearborn, MI, USA, 2017. [Google Scholar]
- Cheah, L.; Heywood, J. Meeting U.S. Passenger Vehicle Fuel Economy Standards in 2016 and Beyond. Energy Policy 2011, 39, 454–466. [Google Scholar] [CrossRef]
- Kasseris, E.P.; Heywood, J.B. Comparative Analysis of Automotive Powertrain Choices for the Next 25 Years. J. Mater. Manuf. 2007, 116, 626–647. [Google Scholar]
- Sperling, D.; Cannon, J.S. (Eds.) Reducing Climate Impacts in the Transportation Sector, 2009th ed.; Springer: Dordrecht, The Netherlands, 2009. [Google Scholar]
- Lee, W.; Schubert, E.; Li, Y.; Li, S.; Bobba, D.; Sarlioglu, B. Overview of Electric Turbocharger and Supercharger for Downsized Internal Combustion Engines. IEEE Trans. Transp. Electrif. 2017, 3, 36–47. [Google Scholar] [CrossRef]
- Dhana Raju, V.; Kishore, P.S.; Yamini, K. Experimental Studies on Four Stroke Diesel Engine Fuelled with Tamarind Seed Oil as Potential Alternate Fuel for Sustainable Green Environment. Eur. J. Sustain. Dev. Res. 2018, 2, 10. [Google Scholar] [CrossRef]
- Delogu, M.; Zanchi, L.; Dattilo, C.A.; Pierini, M. Innovative Composites and Hybrid Materials for Electric Vehicles Lightweight Design in a Sustainability Perspective. Mater. Today Commun. 2017, 13, 192–209. [Google Scholar] [CrossRef]
- MacKenzie, D.; Zoepf, S.; Heywood, J. Determinants of US Passenger Car Weight. Int. J. Veh. Des. 2014, 65, 73. [Google Scholar] [CrossRef]
- Kim, H.C.; Wallington, T.J. Life-Cycle Energy and Greenhouse Gas Emission Benefits of Lightweighting in Automobiles: Review and Harmonization. Environ. Sci. Technol. 2013, 47, 6089–6097. [Google Scholar] [CrossRef] [PubMed]
- Helms, H.; Lambrecht, U. The Potential Contribution of Light-Weighting to Reduce Transport Energy Consumption. Int. J. Life Cycle Assess. 2007, 12, 58–64. [Google Scholar]
- Fang, Y. Connected Vehicles Make Transportation Faster, Safer, Smarter, and Greener! IEEE Trans. Veh. Technol. 2015, 64, 5409–5410. [Google Scholar] [CrossRef]
- Raji, R.A.; Mohd Rashid, S.; Mohd Ishak, S. Consumer-Based Brand Equity (CBBE) and the Role of Social Media Communications: Qualitative Findings from the Malaysian Automotive Industry. J. Mark. Commun. 2019, 25, 511–534. [Google Scholar] [CrossRef]
- Iqbal, A.; Rehman, Z.U.; Ali, S.; Ullah, K.; Ghani, U. Road Traffic Accident Analysis and Identification of Black Spot Locations on Highway. Civ. Eng. J. 2020, 6, 2448–2456. [Google Scholar] [CrossRef]
- Legislative Observatory—European Parliament. 2021/0197(COD)-CO2 Emission Standards for Cars and Vans. 2023. Available online: https://oeil.secure.europarl.europa.eu/oeil/popups/printficheglobal.pdf?id=728320&l=en (accessed on 15 June 2023).
- Caffrey, C.; Bolon, K.; Kolwich, G.; Johnston, R.; Shaw, T. Cost-Effectiveness of a Lightweight Design for 2020–2025: An Assessment of a Light-Duty Pickup Truck; SAE Technical Paper; SAE International: Warrendale, PA, USA, 2015. [Google Scholar] [CrossRef]
- Kollamthodi, S.; Kay, D.; Skinner, I.; Dun, C.; Hausberger, S. The Potential for Mass Reduction of Passenger Cars and Light Commercial Vehicles in Relation to Future CO2 Regulatory Requirements. 2015. Available online: https://climate.ec.europa.eu/system/files/2016-11/ldv_downweighting_co2_appendices_en.pdf (accessed on 18 June 2023).
- Lutsey, N. Review of Technical Literature and Trends Related to Automobile Mass-Reduction Technology; UCD-ITS-RR-10-10; Institute of Transportation Studies, University of California: Davis, CA, USA, 2010. [Google Scholar]
- Giordano, G. Plastics Power a New Generation of Electric Vehicles. Plast. Eng. 2019, 75, 24–33. [Google Scholar] [CrossRef]
- Osborne, J.; FEATURE: Light Speed—How Electric Cars Are Driving a New Wave of Lightweighting. Institution of Mechanical Engineers. Available online: https://www.imeche.org/news/news-article/feature-light-speed-how-electric-cars-are-driving-a-new-wave-of-lightweighting (accessed on 14 November 2022).
- Alonso, E.; Lee, T.M.; Bjelkengren, C.; Roth, R.; Kirchain, R.E. Evaluating the Potential for Secondary Mass Savings in Vehicle Lightweighting. Environ. Sci. Technol. 2012, 46, 2893–2901. [Google Scholar] [CrossRef]
- Verbrugge, M.; Lee, T.; Krajewski, P.E.; Sachdev, A.K.; Bjelkengren, C.; Roth, R.; Kirchain, R. Mass Decompounding and Vehicle Lightweighting. Mater. Sci. Forum 2009, 618–619, 411–418. [Google Scholar] [CrossRef]
- Kelly, J.C.; Sullivan, J.L.; Burnham, A.; Elgowainy, A. Impacts of Vehicle Weight Reduction via Material Substitution on Life-Cycle Greenhouse Gas Emissions. Environ. Sci. Technol. 2015, 49, 12535–12542. [Google Scholar] [CrossRef] [PubMed]
- Hottle, T.; Caffrey, C.; McDonald, J.; Dodder, R. Critical Factors Affecting Life Cycle Assessments of Material Choice for Vehicle Mass Reduction. Transp. Res. D Transp. Environ. 2017, 56, 241–257. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.C.; Wallington, T.J.; Sullivan, J.L.; Keoleian, G.A. Life Cycle Assessment of Vehicle Lightweighting: Novel Mathematical Methods to Estimate Use-Phase Fuel Consumption. Environ. Sci. Technol. 2015, 49, 10209–10216. [Google Scholar] [CrossRef]
- Akhshik, M.; Panthapulakkal, S.; Tjong, J.; Sain, M. Life Cycle Assessment and Cost Analysis of Hybrid Fiber-Reinforced Engine Beauty Cover in Comparison with Glass Fiber-Reinforced Counterpart. Environ. Impact. Assess. Rev. 2017, 65, 111–117. [Google Scholar] [CrossRef]
- Leduc, G.; Mongelli, I.; Uihlein, A.; Nemry, F. How Can Our Cars Become Less Polluting? An Assessment of the Environmental Improvement Potential of Cars. Transp. Policy 2010, 17, 409–419. [Google Scholar] [CrossRef]
- Villanueva-Rey, P.; Belo, S.; Quinteiro, P.; Arroja, L.; Dias, A.C. Wiring in the Automobile Industry: Life Cycle Assessment of an Innovative Cable Solution. J. Clean. Prod. 2018, 204, 237–246. [Google Scholar] [CrossRef]
- Copper Tin–CuSn—Innovative Conductor Material for Low Current and Signal Cables. Available online: https://publications.leoni.com/fileadmin/automotive_cables/publications/data_sheet/copper_thin.pdf?1475650458 (accessed on 15 June 2023).
- Czerwinski, F. Current Trends in Automotive Lightweighting Strategies and Materials. Materials 2021, 14, 6631. [Google Scholar] [CrossRef]
- Badino, V.; Baldo, G.L. LCA: Istruzioni per l’uso (LCA: Instructions for Use); Progetto Leonardo, Esculapio Editore: Bologna, Italy, 1998. [Google Scholar]
- van den Berg, N.W.; Dutilh, C.E.; Huppes, G. Beginning LCA—A Guide into Environmental Life Cycle Assessment; Centrum voor Milieukunde, NOH National Reuse of Waste Research Programme: Leiden, The Netherlands, 1995. [Google Scholar]
- Sandrini, G.; Có, B.; Tomasoni, G.; Gadola, M.; Chindamo, D. The Environmental Performance of Traction Batteries for Electric Vehicles from a Life Cycle Perspective. Environ. Clim. Technol. 2021, 25, 700–716. [Google Scholar] [CrossRef]
- Del Pero, F.; Delogu, M.; Pierini, M. The Effect of Lightweighting in Automotive LCA Perspective: Estimation of Mass-Induced Fuel Consumption Reduction for Gasoline Turbocharged Vehicles. J. Clean. Prod. 2017, 154, 566–577. [Google Scholar] [CrossRef]
- Delogu, M.; Del Pero, F.; Pierini, M. Lightweight Design Solutions in the Automotive Field: Environmental Modelling Based on Fuel Reduction Value Applied to Diesel Turbocharged Vehicles. Sustainability 2016, 8, 1167. [Google Scholar] [CrossRef]
- Del Pero, F.; Delogu, M.; Berzi, L.; Dattilo, C.A.; Zonfrillo, G.; Pierini, M. Sustainability Assessment for Different Design Solutions within the Automotive Field. Procedia Struct. Integr. 2019, 24, 906–925. [Google Scholar] [CrossRef]
- Del Pero, F.; Berzi, L.; Antonacci, A.; Delogu, M. Automotive Lightweight Design: Simulation Modeling of Mass-Related Consumption for Electric Vehicles. Machines 2020, 8, 51. [Google Scholar] [CrossRef]
- United Nations. Consolidated Resolution on the Construction of Vehicles (R.E.3); United Nations, Economic and Social Council: New York, NY, USA, 2011; Available online: https://unece.org/fileadmin/DAM/trans/doc/2017/wp29/ECE-TRANS-WP.29-1135e.docx (accessed on 15 June 2023).
- Sandrini, G.; Gadola, M.; Chindamo, D. Longitudinal Dynamics Simulation Tool for Hybrid Apu and Full Electric Vehicle. Energies 2021, 14, 1207. [Google Scholar] [CrossRef]
- Sandrini, G.; Chindamo, D.; Gadola, M. Regenerative Braking Logic That Maximizes Energy Recovery Ensuring the Vehicle Stability. Energies 2022, 15, 5846. [Google Scholar] [CrossRef]
- Zecchi, L.; Sandrini, G.; Gadola, M.; Chindamo, D. Modeling of a Hybrid Fuel Cell Powertrain with Power Split Logic for Onboard Energy Management Using a Longitudinal Dynamics Simulation Tool. Energies 2022, 15, 6228. [Google Scholar] [CrossRef]
- Electric Vehicle Database—Fiat 500e Hatchback 42 KWh. Available online: https://ev-database.org/car/1285/Fiat-500e-Hatchback-42-kWh (accessed on 23 January 2023).
- FleetNews Electric Car and van Data—Fiat 500e Hatchback 42 KWh Price and Specifications. Available online: https://www.fleetnews.co.uk/electric-fleet/electric-car-and-van-data/fiat/500e-1285 (accessed on 23 January 2023).
- COMMISSION REGULATION (EU) 2017/1151. Available online: https://unece.org/DAM/trans/doc/2018/wp29other/EU_2017_1151.pdf (accessed on 15 June 2023).
- EPA—United States Environmental Protection Agency. EPA US06 or Supplemental Federal Test Procedure (SFTP); EPA: Washington, DC, USA, 2023. [Google Scholar]
- EPA—United States Environmental Protection Agency. EPA Federal Test Procedure (FTP). Available online: https://www.epa.gov/emission-standards-reference-guide/epa-federal-test-procedure-ftp (accessed on 2 May 2023).
- Japan Inspection Organization—Certification and Inspection Agency in Japan Japanese JC08 Emission Test Cycle. Available online: https://japaninspection.org/japanese-jc08-emission-test-cycle/ (accessed on 2 May 2023).
- IMEE. Standardized Drive Cycles. Available online: https://imee.pl/pub/drive-cycles (accessed on 2 May 2023).
- Chindamo, D.; Gadola, M.; Romano, M. Simulation Tool for Optimization and Performance Prediction of a Generic Hybrid Electric Series Powertrain. Int. J. Automot. Technol. 2014, 15, 135–144. [Google Scholar] [CrossRef]
- Chindamo, D.; Economou, J.T.; Gadola, M.; Knowles, K. A Neurofuzzy-Controlled Power Management Strategy for a Series Hybrid Electric Vehicle. Proc. Inst. Mech. Eng. Part D: J. Automob. Eng. 2014, 228, 1034–1050. [Google Scholar] [CrossRef]
- Sandrini, G.; Gadola, M.; Chindamo, D.; Zecchi, L. Model of a Hybrid Electric Vehicle Equipped with Solid Oxide Fuel Cells Powered by Biomethane. Energies 2023, 16, 4918. [Google Scholar] [CrossRef]
- Chindamo, D.; Gadola, M. What Is the Most Representative Standard Driving Cycle to Estimate Diesel Emissions of a Light Commercial Vehicle? IFAC-PapersOnLine 2018, 51, 73–78. [Google Scholar] [CrossRef]











| Parameter | Compact Car Value | N1 Value |
|---|---|---|
| Motor power | 87 kW | >160 kW |
| Vehicle weight | 1548.38 kg 1 | 3500 kg 2 |
| Motor efficiency | 98% | 98% 3 |
| Transmission efficiency | 1 | 0.9409 |
| Inverter efficiency in discharge | 0.88 | 0.88 |
| Inverter efficiency in charge | 0.8 | 0.8 |
| Auxiliary power | 1500 W | 1500 W |
| Af ∙ Cx 4 | 1.034 m2 | 2.1 m2 |
| Vertical aerodynamic coefficient | −0.026 m2 | 0 |
| Rolling friction coefficient | 0.01 | 0.015 |
| Total gear ratio | 9.6 | 6.22 |
| Front wheel radius | 0.2987 m | 0.35 m |
| Rear wheel radius | 0.3005 m | 0.35 m |
| Moment of inertia of the wheels | 0.882 kg m2 | 1.09 kg m2 |
| Moment of inertia of the motor | 0.02 kg m2 | 0.086 kg m2 |
| Moment of inertia of the transmission | 0.0001 kg m2 | 0.01 kg m2 |
| Battery capacity | 42 kWh (105 Ah) | 120 Ah |
| Number of battery cells in series | 96 | 108 |
| Number of battery cells in parallel | 2 | 1 |
| Nominal battery pack voltage | 400.0 V | 356.1 V |
| RES 5 | 0.086 Ω | 0.097 Ω |
| Vehicle Model | Polynomial Degree | |||
|---|---|---|---|---|
| N1 | 1st degree | 0 | 0.852 | 25.995 |
| 2nd degree | 0.0024 | 0.750 | 26.903 | |
| N1— NO inertias | 1st degree | 0 | 0.848 | 25.819 |
| 2nd degree | 0.0024 | 0.746 | 26.732 | |
| CompactCar | 1st degree | 0 | 0.654 | 13.488 |
| 2nd degree | 0.0018 | 0.596 | 13.900 | |
| CompactCar— NO inertias | 1st degree | 0 | 0.651 | 13.304 |
| 2nd degree | 0.0020 | 0.586 | 13.766 | |
| CompactCar— N1 battery pack | 1st degree | 0 | 0.673 | 13.514 |
| 2nd degree | 0.0022 | 0.602 | 14.024 | |
| CompactCar— N1 aerodynamics | 1st degree | 0 | 0.606 | 24.564 |
| 2nd degree | 0.0011 | 0.570 | 24.817 | |
| CompactCar— N1 transmission efficiency | 1st degree | 0 | 0.696 | 14.105 |
| 2nd degree | 0.0019 | 0.634 | 14.547 | |
| CompactCar— N1 rolling resistance | 1st degree | 0 | 0.778 | 13.597 |
| 2nd degree | 0.0018 | 0.721 | 14.003 | |
| CompactCar— N1 values | 1st degree | 0 | 0.826 | 26.357 |
| 2nd degree | 0.0019 | 0.766 | 26.779 | |
| CompactCar— N1 inertias | 1st degree | 0 | 0.658 | 13.772 |
| 2nd degree | 0.0015 | 0.610 | 14.117 | |
| CompactCar— N1 values (also inertia) | 1st degree | 0 | 0.830 | 26.607 |
| 2nd degree | 0.0018 | 0.772 | 27.019 | |
| CompactCar— N1 traction ratios | 1st degree | 0 | 0.653 | 13.411 |
| 2nd degree | 0.0019 | 0.592 | 13.841 | |
| CompactCar— N1 inertias and traction ratios | 1st degree | 0 | 0.654 | 13.508 |
| 2nd degree | 0.0018 | 0.598 | 13.912 | |
| CompactCar— N1 values (all) | 1st degree | 0 | 0.825 | 26.380 |
| 2nd degree | 0.0018 | 0.769 | 26.781 |
| Driving Cycle | Polynomial Degree | |||
|---|---|---|---|---|
| WLTC—Class 3b | 1st degree | 0 | 0.852 | 25.995 |
| 2nd degree | 0.0024 | 0.750 | 26.903 | |
| US06 | 1st degree | 0 | 1.077 | 34.562 |
| 2nd degree | 0.0061 | 0.819 | 36.855 | |
| FTP75 | 1st degree | 0 | 0.946 | 15.229 |
| 2nd degree | 0.0016 | 0.874 | 15.972 | |
| HWFET | 1st degree | 0 | 0.630 | 24.647 |
| 2nd degree | 0.0012 | 0.577 | 25.198 | |
| JC08 | 1st degree | 0 | 0.944 | 15.362 |
| 2nd degree | 0.0010 | 0.897 | 15.847 | |
| Artemis—Urban Cycle | 1st degree | 0 | 1.426 | 13.082 |
| 2nd degree | 0.0014 | 1.361 | 13.759 | |
| Artemis— Rural Road Cycle | 1st degree | 0 | 0.929 | 18.344 |
| 2nd degree | 0.0030 | 0.793 | 19.760 | |
| Artemis— Motorway Cycle (130) | 1st degree | 0 | 0.835 | 44.654 |
| 2nd degree | 0.0040 | 0.651 | 46.568 |
| Driving Cycle | Polynomial Degree | |||
|---|---|---|---|---|
| WLTC—Class 3b | 1st degree | 0 | 0.654 | 13.488 |
| 2nd degree | 0.0018 | 0.596 | 13.900 | |
| US06 | 1st degree | 0 | 0.809 | 16.549 |
| 2nd degree | 0.0031 | 0.711 | 17.247 | |
| FTP75 | 1st degree | 0 | 0.746 | 9.742 |
| 2nd degree | 0.0008 | 0.721 | 9.917 | |
| HWFET | 1st degree | 0 | 0.426 | 12.370 |
| 2nd degree | 0.0008 | 0.400 | 12.557 | |
| JC08 | 1st degree | 0 | 0.754 | 10.114 |
| 2nd degree | 0.0008 | 0.729 | 10.292 | |
| Artemis—Urban Cycle | 1st degree | 0 | 1.203 | 11.528 |
| 2nd degree | 0.0004 | 1.189 | 11.628 | |
| Artemis— Rural Road Cycle | 1st degree | 0 | 0.723 | 9.709 |
| 2nd degree | 0.0022 | 0.651 | 10.219 | |
| Artemis— Motorway Cycle (130) | 1st degree | 0 | 0.577 | 20.577 |
| 2nd degree | 0.0030 | 0.482 | 21.253 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sandrini, G.; Gadola, M.; Chindamo, D.; Candela, A.; Magri, P. Exploring the Impact of Vehicle Lightweighting in Terms of Energy Consumption: Analysis and Simulation. Energies 2023, 16, 5157. https://doi.org/10.3390/en16135157
Sandrini G, Gadola M, Chindamo D, Candela A, Magri P. Exploring the Impact of Vehicle Lightweighting in Terms of Energy Consumption: Analysis and Simulation. Energies. 2023; 16(13):5157. https://doi.org/10.3390/en16135157
Chicago/Turabian StyleSandrini, Giulia, Marco Gadola, Daniel Chindamo, Andrea Candela, and Paolo Magri. 2023. "Exploring the Impact of Vehicle Lightweighting in Terms of Energy Consumption: Analysis and Simulation" Energies 16, no. 13: 5157. https://doi.org/10.3390/en16135157
APA StyleSandrini, G., Gadola, M., Chindamo, D., Candela, A., & Magri, P. (2023). Exploring the Impact of Vehicle Lightweighting in Terms of Energy Consumption: Analysis and Simulation. Energies, 16(13), 5157. https://doi.org/10.3390/en16135157









