Robust Optimal Scheduling of Integrated Energy Systems Considering the Uncertainty of Power Supply and Load in the Power Market
Abstract
:1. Introduction
- The electric–gas coupling model of the integrated energy system is established, and the uncertainty model of the supply side and load side of the system is further established based on this model.
- An optimal scheduling model based on robust chance constraints to maximize system profits in the electricity market is presented. The model is solved by converting chance constraints into deterministic constraints.
- The effectiveness of the proposed method is verified by simulations. The proposed method not only guarantees the robustness of the system but also improves the economy of the system. It provides ideas for exploring the survival and development mechanism and strategy of integrated energy systems in the electricity market environment.
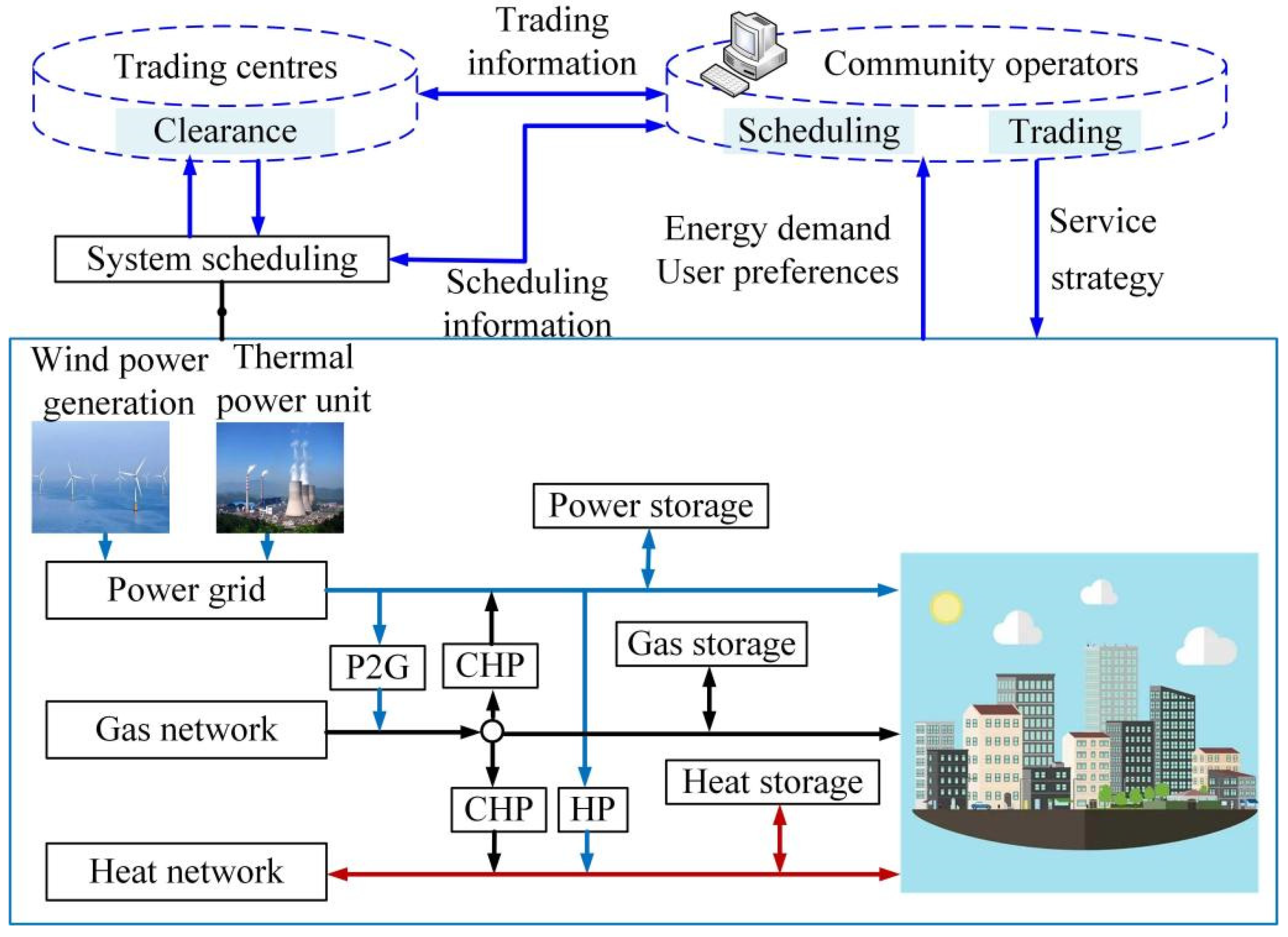
2. Modeling of the Integrated Energy System
2.1. Power Output Equipment
2.1.1. P2G Model
2.1.2. Wind Power Model
2.2. Supply and Demand Uncertainty Analysis of the System
2.2.1. Uncertainty Model of Wind Power Output
2.2.2. Load Uncertainty Model
3. Optimization Scheduling Based on Robust Chance Constraints in Electricity Market
3.1. Objective Function
3.1.1. Operation Cost of Generator Set
3.1.2. Gas Storage Cost of Gas Storage Tank in Natural Gas System
3.1.3. Operation Cost of P2G Conversion Device
3.1.4. Penalty Cost of Wind Abandonment
3.2. Constraints
3.2.1. System Output Constraint
3.2.2. Power and Energy Constraints
3.2.3. Power Balance Constraints of the Power System
3.2.4. Constraints of Gas Storage Tank
3.2.5. Constraints on Node Traffic Balance
3.2.6. Chance Constraints
3.3. Solution Algorithm
4. Example Analysis
4.1. Simulation Parameters
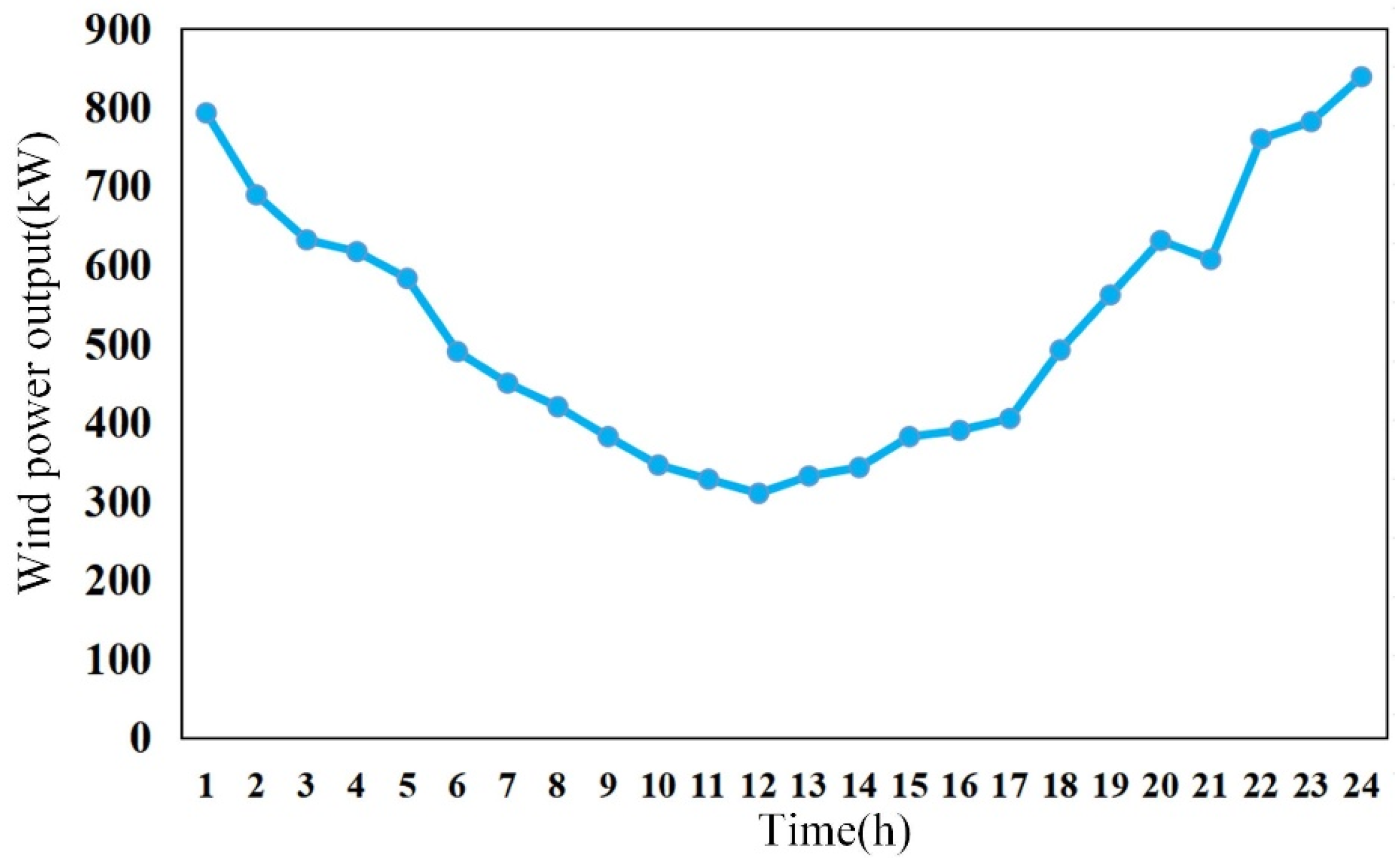
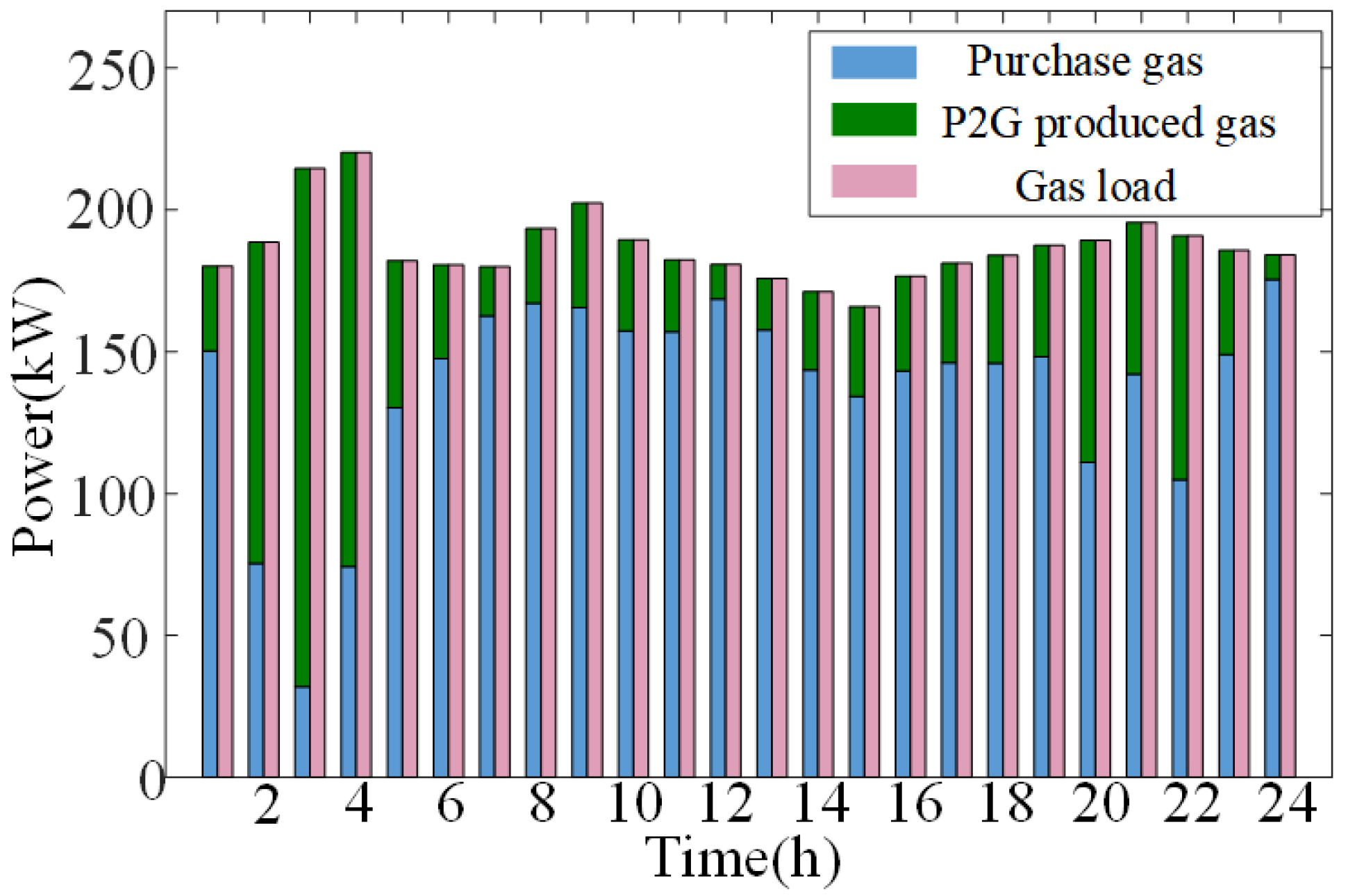
4.2. Analysis of Model Optimization
4.3. Impact of Robust Chance Constraints
4.4. Comparative Analysis of Different Schemes
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Moret, F.; Pinson, P. Energy collectives: A community and fairness based approach to future electricity markets. IEEE Trans. Power Syst. 2019, 34, 3994–4004. [Google Scholar] [CrossRef] [Green Version]
- Bjarghov, S.; Loschenbrand, M.; Saif, A.; Pedrero, R.A.; Farahmand, H. Developments and challenges in local electricity markets: A comprehensive review. IEEE Access 2021, 9, 58910–58943. [Google Scholar] [CrossRef]
- Tao, Y.; Qiu, J.; Lai, S.; Zhao, J.; Xue, Y. Carbon-oriented electricity network planning and transformation. IEEE Trans. Power Syst. 2021, 36, 1034–1048. [Google Scholar] [CrossRef]
- Yang, C.; Cheng, H.; Feng, S. Multi-day unit commitment strategy for linking-up with day-ahead clearing in provincial spot electricity market. Power Syst. Technol. 2020, 44, 982–991. [Google Scholar] [CrossRef]
- Tesfamicael, A.D.; Liu, V.; Mckague, M.; Caelli, W.; Foo, E. A design for a secure energy market trading system in a national wholesale electricity market. IEEE Access 2020, 8, 132424–132445. [Google Scholar] [CrossRef]
- Wu, Y.; Li, B.; Luo, H.; Yuan, Q.; Li, P.; Lai, X.; Sun, Y.; Yin, Z. Conditional section constraints modeling in spot market clearing. Power Syst. Technol. 2020, 44, 2819–2831. [Google Scholar] [CrossRef]
- Scarabaggio, P.; Carli, R.; Dotoli, M. Noncooperative equilibrium-seeking in distributed energy systems under AC power flow nonlinear constraints. IEEE Trans. Cont. Net. Syst. 2022, 9, 1731–1742. [Google Scholar] [CrossRef]
- Yao, M.; Molzahn, D.K.; Mathieu, J.L. An optimal power-flow approach to improve power system voltage stability using demand response. IEEE Trans. Cont. Net. Syst. 2019, 6, 1015–1025. [Google Scholar] [CrossRef]
- Fang, X.; Hodge, B.M.; Du, E.; Kang, C.; Li, F. Introducing uncertainty components in locational marginal prices for pricing wind power and load uncertainties. IEEE Trans. Power Syst. 2019, 34, 2013–2024. [Google Scholar] [CrossRef]
- Wang, Z.; Shen, C.; Liu, F.; Wu, X.; Liu, C.; Gao, F. Chance-constrained economic dispatch with non-gaussian correlated wind power uncertainty. IEEE Trans. Power Syst. 2017, 32, 4880–4893. [Google Scholar] [CrossRef]
- Li, Z.; Wu, W.; Shahidehpour, M.; Zhang, B. Adaptive robust tie-line scheduling considering wind power uncertainty for interconnected power systems. IEEE Trans. Power Syst. 2016, 31, 2701–2713. [Google Scholar] [CrossRef]
- Sperstad, I.B.; Korpås, M. Energy storage scheduling in distribution systems considering wind and photovoltaic generation uncertainties. Energies 2019, 12, 1231. [Google Scholar] [CrossRef] [Green Version]
- Liang, Z.; Chen, H.; Chen, S.; Wang, Y.; Zhang, C.; Kang, C. Robust transmission expansion planning based on adaptive uncertainty set optimization under high-penetration wind power generation. IEEE Trans. Power Syst. 2021, 36, 2798–2814. [Google Scholar] [CrossRef]
- Bai, L.; Li, F.; Jiang, T.; Jia, H. Robust scheduling for wind integrated energy systems considering gas pipeline and power transmission n–1 contingencies. IEEE Trans. Power Syst. 2017, 32, 1582–1584. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, F.; Li, Y.; Wang, Y. An improved two-stage robust optimization model for CCHP-P2G microgrid system considering multi-energy operation under wind power outputs uncertainties. Energy 2021, 223, 120048. [Google Scholar] [CrossRef]
- Carli, R.; Cavone, G.; Pippia, T.; Schutter, B.D.; Dotoli, M. Robust optimal control for demand side management of multi-carrier microgrids. IEEE Trans. Autom. Sci. Eng. 2022, 19, 1338–1351. [Google Scholar] [CrossRef]
- Jiang, T.; Zhang, R.; Li, X.; Chen, H.; Li, G. Integrated energy system security region: Concepts, methods, and implementations. Appl. Energy 2021, 283, 116124. [Google Scholar] [CrossRef]
- Wu, B.; Zhang, S.; Wang, X.; Liu, S. Equilibrium strategy analysis of demand response for integrated energy service provider participating in multi-energy market transaction. Power Syst. Technol. 2022, 46, 1800–1811. [Google Scholar] [CrossRef]
- Ma, T.; Wu, J.; Hao, L.; Yan, H.; Li, D. A real-time pricing scheme for energy management in integrated energy systems: A Stackelberg game approach. Energies 2018, 11, 2858. [Google Scholar] [CrossRef] [Green Version]
- Yavuz, F.G.; Arslan, O. Linear mixed model with Laplace distribution (LLMM). Stat. Papers 2018, 59, 271–289. [Google Scholar] [CrossRef]
- Gupta, R.A.; Gupta, N.K. A robust optimization based approach for microgrid operation in deregulated environment. Energy Convers. Manag. 2015, 93, 121–131. [Google Scholar] [CrossRef]
- Dogru, F.Z.; Arslan, O. Finite mixtures of skew Laplace normal distributions with random skewness. Comput. Stat. 2021, 36, 423–447. [Google Scholar] [CrossRef]
- Roozegar, R.; Balakrishnan, N.; Bekker, A.; Jamalizadeh, A. On multivariate selection scale-mixtures of normal distributions. Braz. J. Prob. Stat. 2021, 35, 351–374. [Google Scholar] [CrossRef]
- Sinha, S.; Hart, J.D. Estimating the mean and variance of a high-dimensional normal distribution using a mixture prior. Comput. Stat. Data Anal. 2019, 138, 201–221. [Google Scholar] [CrossRef]
- Rockafellar, R.T.; Sun, J. Solving Lagrangian variational inequalities with applications to stochastic programming. Math. Program. 2020, 181, 435–451. [Google Scholar] [CrossRef]
- Li, M.; Zhang, C. Two-stage stochastic variational inequality arising from stochastic programming. J. Optim. Theory Appl. 2020, 186, 324–343. [Google Scholar] [CrossRef]
- Tran, N.T.; Staat, M. Direct plastic structural design under lognormally distributed strength by chance constrained programming. Optim. Eng. 2020, 21, 131–157. [Google Scholar] [CrossRef]
- Li, N.; Kolmanovsky, I.; Girard, A. An analytical safe approximation to joint chance-constrained programming with additive gaussian noises. IEEE Trans. Autom. Control 2021, 66, 5490–5497. [Google Scholar] [CrossRef]
- Wei, L.; Wang, Y.; Fan, R.; Hu, Z. A two-stage diversity enhancement differential evolution algorithm for multi-objective optimization problem. J. Intel. Fuzzy Syst. 2022, 43, 3993–4010. [Google Scholar] [CrossRef]
- Wang, P.; Xue, B.; Liang, J.; Zhang, M. Feature selection using diversity-based multi-objective binary differential evolution. Inform. Sci. 2023, 626, 586–606. [Google Scholar] [CrossRef]
- Fan, R.; Wei, L.; Li, X.; Zhang, J.; Fan, Z. Self-adaptive weight vector adjustment strategy for decomposition-based multi-objective differential evolution algorithm. Soft Comput. 2020, 24, 13179–13195. [Google Scholar] [CrossRef]



| Parameter | Value (kW) |
|---|---|
| Power of CHP | 200 |
| Power of GB | 300 |
| Power of P2G | 400 |
| Output of thermal power unit | 3000 |
| Wind farm output | 1000 |
| Wind Speed (m/s) | Error (%) | Standard Deviation | Wind Speed (m/s) | Error (%) | Standard Deviation |
|---|---|---|---|---|---|
| 3–4 | 1.98 | 3.96 | 7–8 | 0.02 | 15.82 |
| 4–5 | 2.01 | 6.27 | 8–9 | −0.71 | 14.25 |
| 5–6 | 1.45 | 15.83 | 10–11 | −0.42 | 12.68 |
| 6–7 | 1.12 | 16.62 | 11–12 | −3.2 | 10.23 |
| E | F (CNY) | ||
|---|---|---|---|
| 0.1 | 43,829 | 19,872 | 198,723 |
| 0.15 | 47,813 | 16,782 | 176,281 |
| 0.2 | 38,921 | 11,982 | 167,268 |
| 0.25 | 32,869 | 8729 | 142,784 |
| Optimization Method | ε | Profit (CNY) |
|---|---|---|
| Optimization of deterministic | 0 | 158,247 |
| Optimization of stochastic | 0 | 167,813 |
| Optimization of robust | 0 | 177,823 |
| Chance constraints of robust optimization | 0.1 | 197,362 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, L.; Zeng, Y.; Wang, Z.; Li, Y.; Peng, D.; Wang, Y.; Wang, X. Robust Optimal Scheduling of Integrated Energy Systems Considering the Uncertainty of Power Supply and Load in the Power Market. Energies 2023, 16, 5292. https://doi.org/10.3390/en16145292
Zhao L, Zeng Y, Wang Z, Li Y, Peng D, Wang Y, Wang X. Robust Optimal Scheduling of Integrated Energy Systems Considering the Uncertainty of Power Supply and Load in the Power Market. Energies. 2023; 16(14):5292. https://doi.org/10.3390/en16145292
Chicago/Turabian StyleZhao, Lang, Yuan Zeng, Zhidong Wang, Yizheng Li, Dong Peng, Yao Wang, and Xueying Wang. 2023. "Robust Optimal Scheduling of Integrated Energy Systems Considering the Uncertainty of Power Supply and Load in the Power Market" Energies 16, no. 14: 5292. https://doi.org/10.3390/en16145292
APA StyleZhao, L., Zeng, Y., Wang, Z., Li, Y., Peng, D., Wang, Y., & Wang, X. (2023). Robust Optimal Scheduling of Integrated Energy Systems Considering the Uncertainty of Power Supply and Load in the Power Market. Energies, 16(14), 5292. https://doi.org/10.3390/en16145292





