Experimental Validation of Damping Adjustment Method with Generator Parameter Study for Wave Energy Conversion
Abstract
1. Introduction
2. Experimental Setup
2.1. Wave Channel
2.2. Electric DC Machines
3. Mathematical Formulation
3.1. Hydrodynamic Model
3.2. Electric Motor Model
3.3. Controllable System Using Variable Resistor
3.4. Coupling Hydrodynamic and Electric
4. Experimental Procedure
- For each tested machine, is varied by using the adjustable resistance system shown in Figure 5b that has been schematically described in Figure 3. The external resistance is adjusted by varying the angular position of the potenciometer connected to the end of the terminals of the DC machine. For a precise adjustment, the angular position is controlled by a step motor that is rigidly attached to the potenciometer. It is important to mention that the linear relation between angular position and resistance load was previously studied. The studied external resistances for this work are 0.8 , 5.0 , and 10.0 .
- Frequency values of 3.20 Hz, 3.30 Hz, and 3.40 Hz are selected on the variable frequency drive (VFD). This VFD controls the velocity of the electric motor shown in Figure 6b, which generates the movement of the wave generator flap. Then, as explained in Section 2, the velocity is reduced by a gear box, generating regular waves with frequencies of 1.28 Hz, 1.32 Hz, and 1.36 Hz, respectively. The experimental wave generation system is shown in Figure 6.
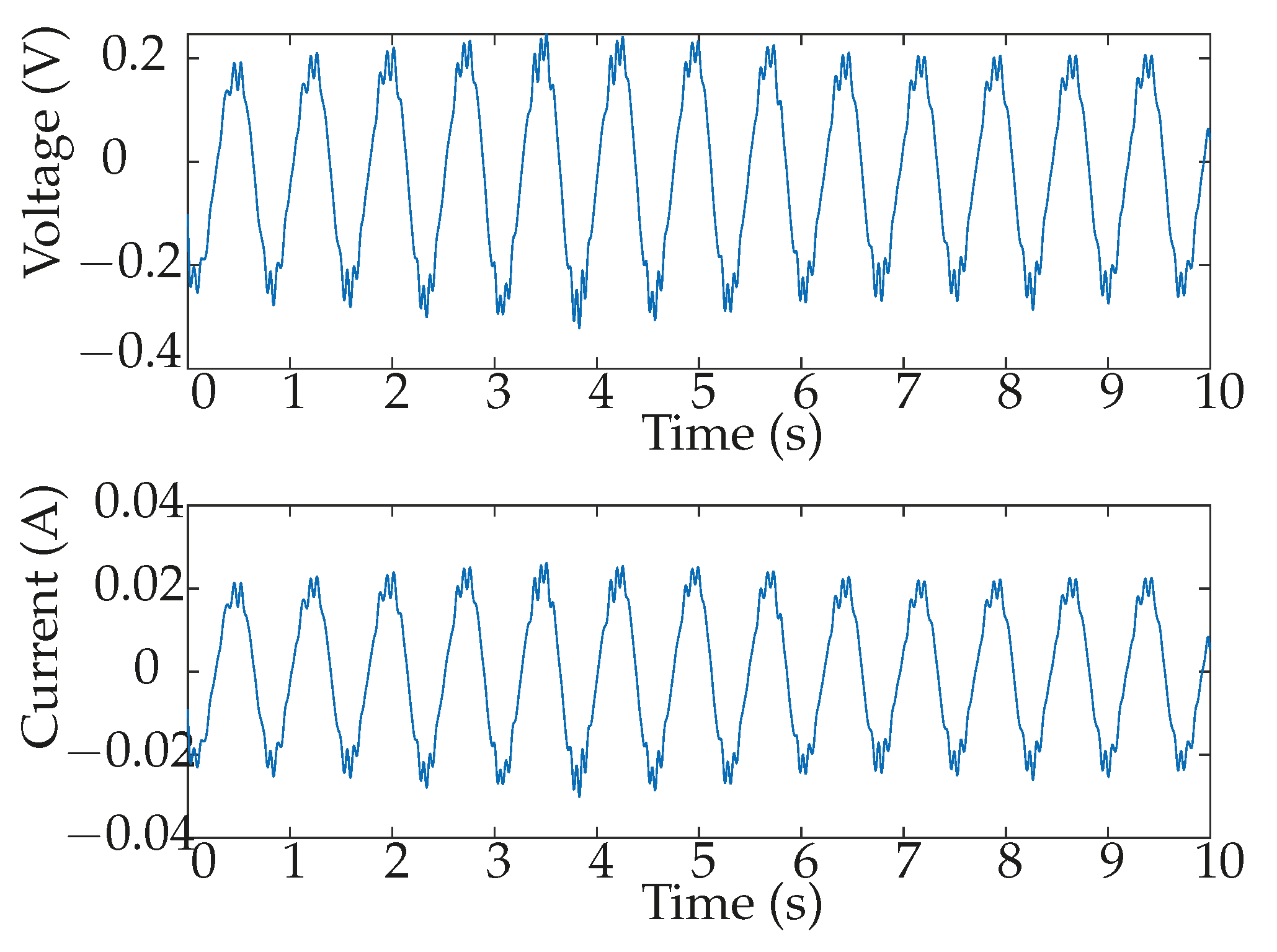
- The generated power is obtained by multiplying the measured voltage and current using the oscilloscope, and the average value of the resulting power is calculated. The measured voltage and current for the case where DC machine G4 is used, with and wave frequency of 1.36 Hz, is depicted in Figure 7 as an example of the procedure. The observed behaviour of the current and voltage in Figure 7 can be explained by the conversion of the sinusoidal linear movement generated by the waves into rotational motion through the rack and pinion system (see Figure 3). This rotational movement closely resembles a sinusoidal pattern, resulting in a sinusoidal rotational speed . According to the relationship , this sinusoidal rotational speed generates a sinusoidal voltage v. Therefore, despite the machine being DC, the voltage and current at the DC machine terminals exhibit a sinusoidal waveform due to the sinusoidal nature of the variable .
5. Results and Analysis
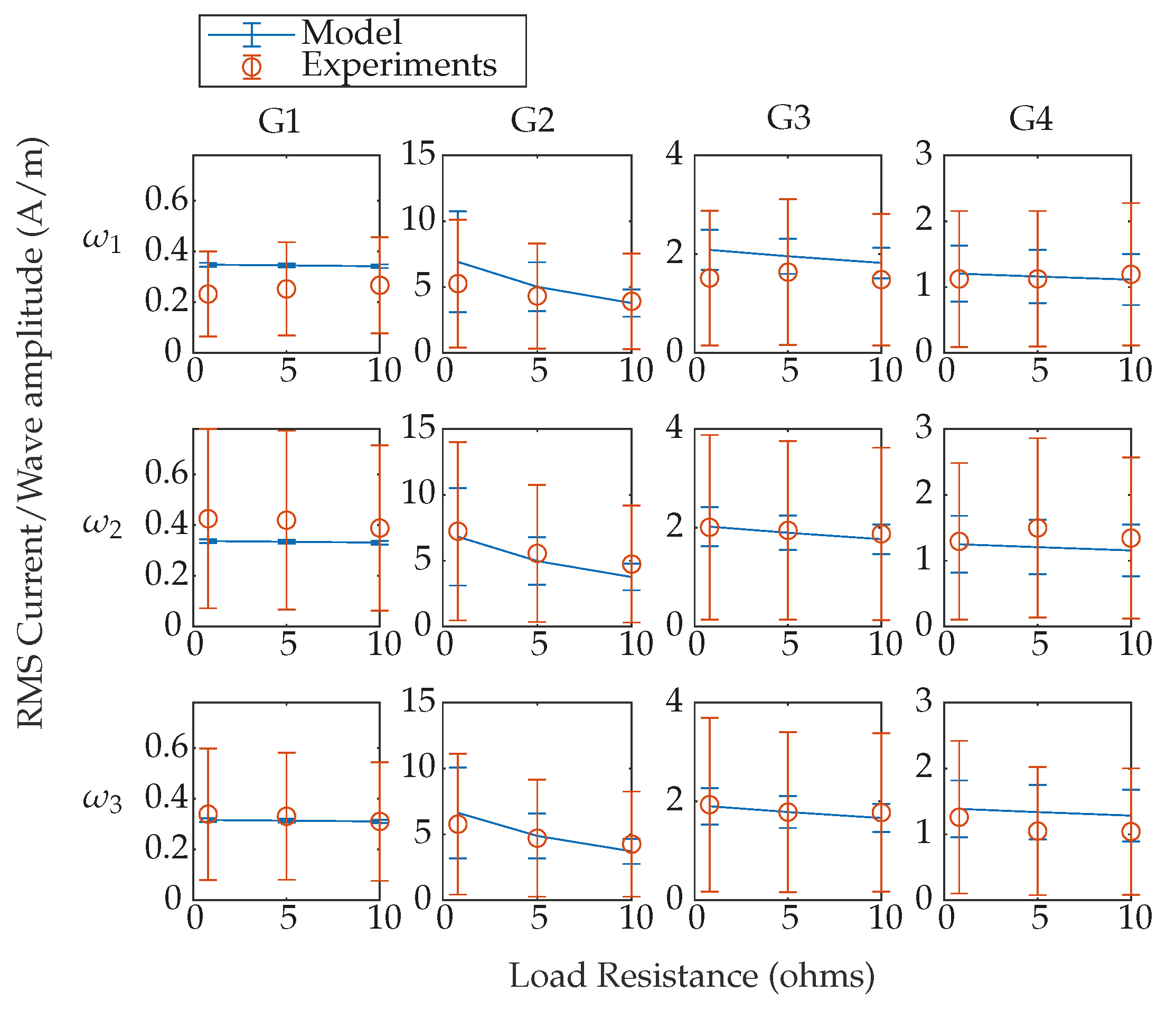
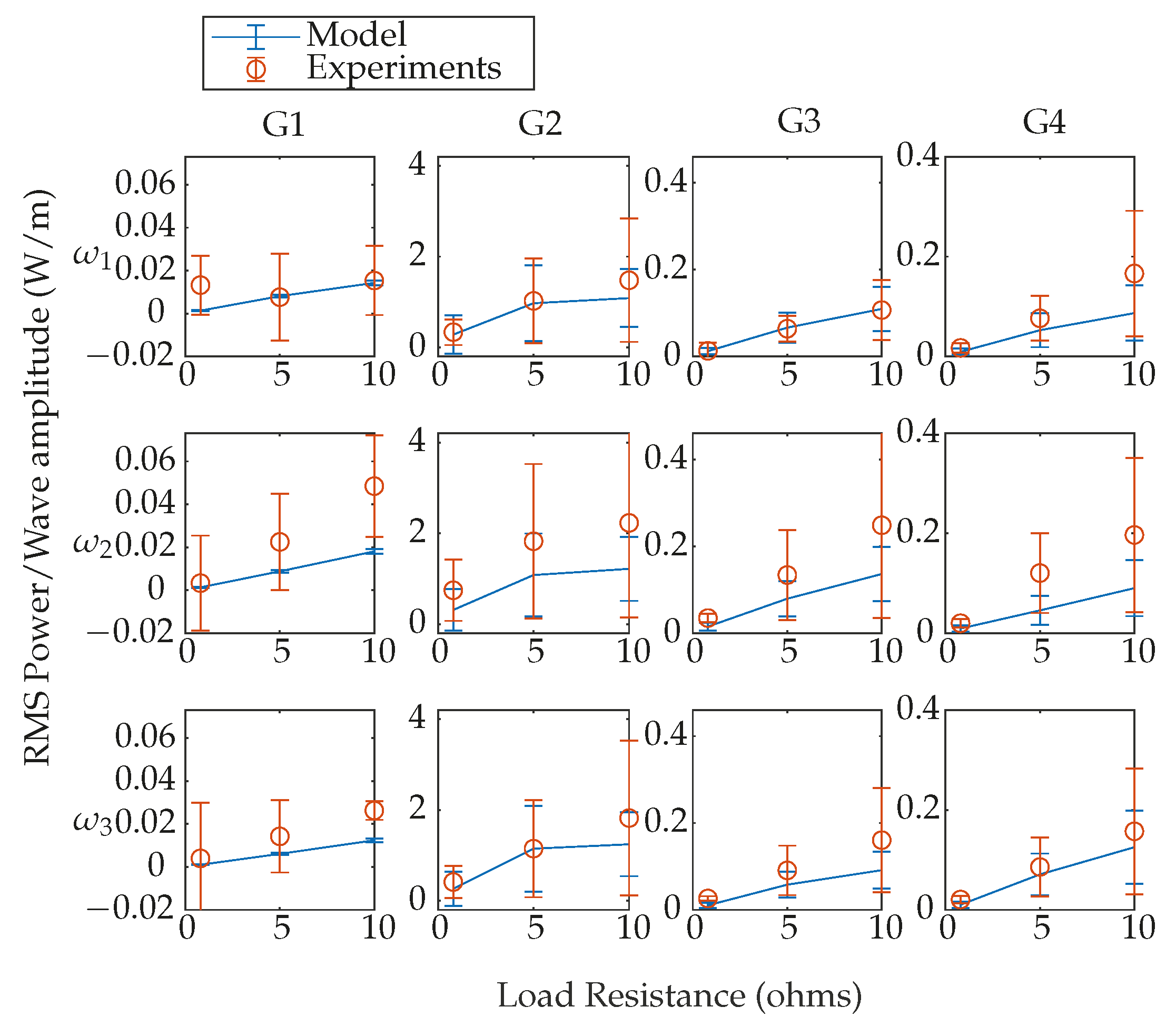
5.1. Experimental Validation
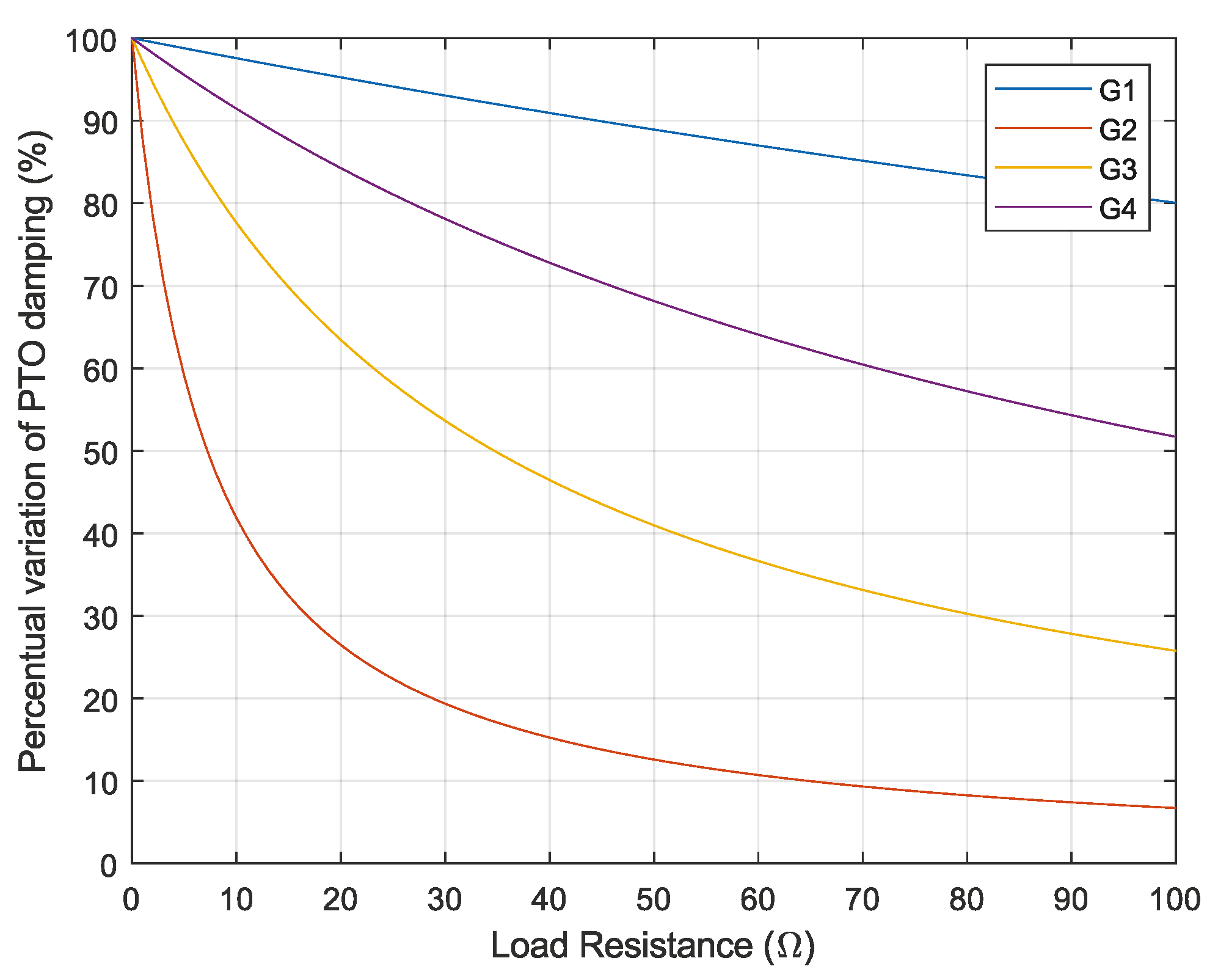
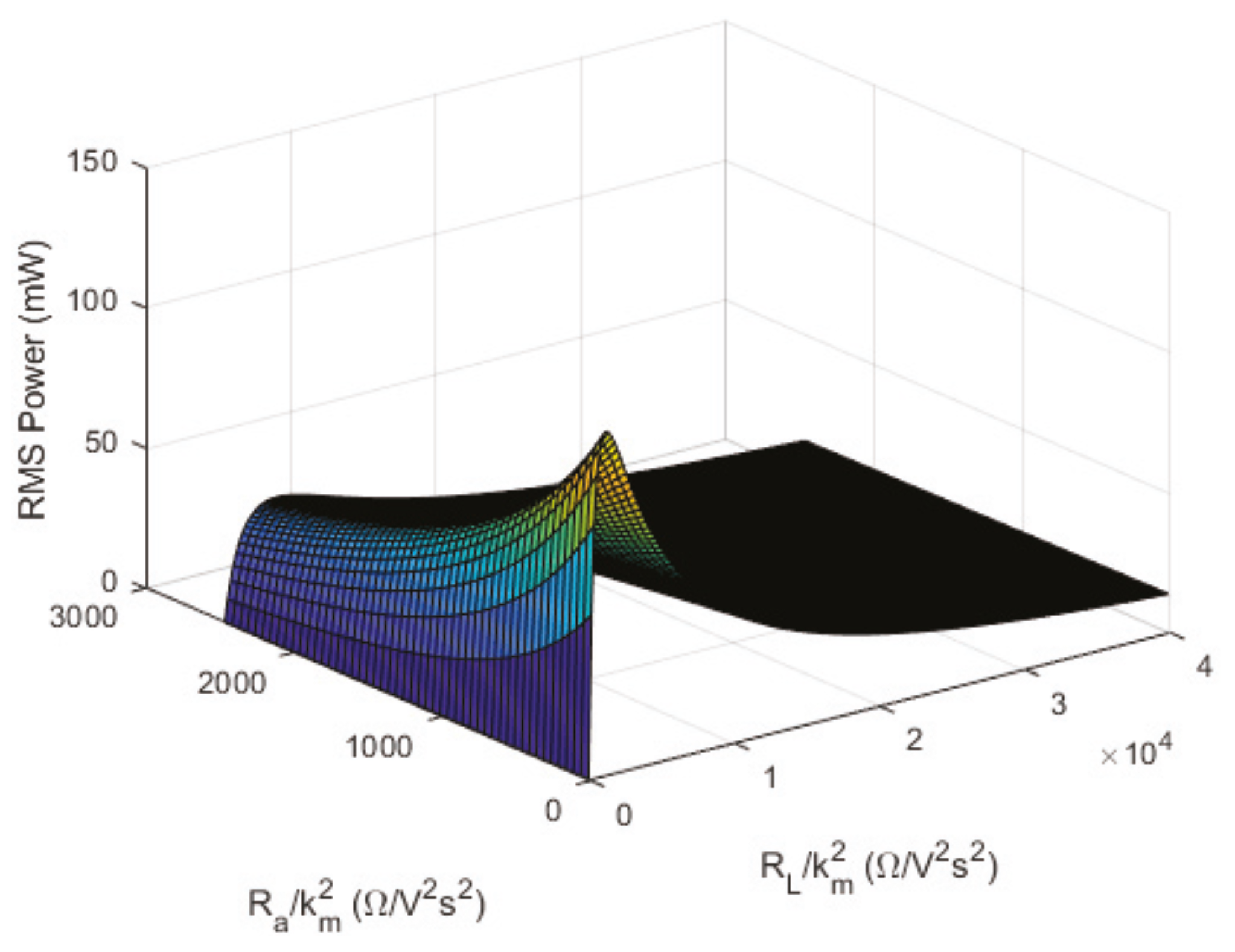
5.2. Theoretical Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| WEC | Wave Energy Converter |
| MPC | Model Predictive Control |
| PTO | Power take-off |
| LPMG | Linear Permanent-Magnet Generator |
| RPMG | Rotating Permanent-Magnet Generator |
| TIM | Tuned Inerter Mass |
| SA | Static Admittance Control |
| PG | Performance Guaranteed |
| NMPC | Nonlineal Model Predictive Control |
| PA-WEC | Point Absorber Wave Energy Converter |
| LPT | Linear Potential Theory |
| BEM | Boundary Element Method |
References
- Boud, R. Status and Research and Development Priorities; DTI Report FES-R-132, AEAT Report AEAT/ENV/1054; UK Department of Trade and Industry (DTI): London, UK, 2003. [Google Scholar]
- Xie, J.; Zuo, L. Dynamics and control of ocean wave energy converters. Int. J. Dyn. Control 2013, 1, 262–276. [Google Scholar] [CrossRef]
- Aderinto, T.; Li, H. Review on Power Perfomance and Efficiency of Wave Energy Converters. Energies 2019, 12, 4329. [Google Scholar] [CrossRef]
- Aderinto, T.; Li, H. Ocean Wave Energy Converters: Status and Challenges. Energies 2018, 11, 1250. [Google Scholar] [CrossRef]
- Garcia-Tuerel, A.; Forehand, D.I.M. A review of geometry optimisation of wave energy converters. Renew. Sustain. Energy Rev. 2021, 139, 110593. [Google Scholar] [CrossRef]
- Guo, B.; Ringwood, J.V.A. A review of wave energy technology from a research and commercial perspective. IET Renew. Power Gener. 2021, 14, 3065–3090. [Google Scholar] [CrossRef]
- Coe, R.; Bacelli, G.; Wilson, D.; Abdelkhalik, O.; Korde, U.; Robinett III, R. A comparison of control strategies for wave energy converters. Int. J. Mar. Energy 2017, 20, 45–63. [Google Scholar] [CrossRef]
- Wang, L.; Isberg, J.; Tedeschi, E. Review of control strategies for wave energy conversion systems and their validation: The wave-to-wire approach. Renew. Sustain. Energy Rev. 2018, 81, 366–379. [Google Scholar] [CrossRef]
- Maria-Arenas, A.; Garrido, A.; Rusu, E.; Garrido, I. Control Strategies Applied to Wave Energy Converters: State of the Art. Energies 2019, 12, 3115. [Google Scholar] [CrossRef]
- Pierart, F.G.; Villegas, C.; Basoalto, C.; Hüsing, M.; Corves, B. Model and Control Analysis for a Point Absorber Wave Energy Converter in Lebu, Chile. In Proceedings of the International Workshop IFToMM for Sustainable Dvelopment Goals, I4SDG Workshop, Bilbao, Spain, 22–23 June 2023; pp. 19–26. [Google Scholar] [CrossRef]
- Montoya, D.; Tedeschi, E.; Castellini, L.; Martins, T. Passive Model Predictive Control on a Two-Body Self-Referenced Point Absorber Wave Energy Converter. Energies 2021, 14, 1731. [Google Scholar] [CrossRef]
- Pierart, F.; Manríquez, C.; Campos, P. Reinforcement learning algorithms applied to reactive and resistive control of a wave energy converter In Proceedings of the IEEE CHILEAN Conference on Electrical, Electronics Egineering, Information and Communication Technologies (CHILECON), Online, 6–9 December 2021. [CrossRef]
- Choi, K.-S.; Yang, D.-S.; Park, S.-Y.; Cho, B.-H. Design and performance test of hydraulic PTO for wave energy converter. Int. J. Precis. Eng. Manuf. 2012, 13, 795–801. [Google Scholar] [CrossRef]
- Falcão, A.F.D.O. Modelling and control of oscillating-body wave energy converters with hydraulic power take-off and gas accumulator. Ocean Eng. 2007, 34, 2021–2032. [Google Scholar] [CrossRef]
- Sarmento, A.J.N.A.; Gato, L.M.C.; Falcao, A.D.O. Turbine-controlled wave energy absorption by oscillating water column devices. Ocean Eng. 1990, 17, 481–497. [Google Scholar] [CrossRef]
- Stalberg, M.; Waters, R.; Danielsson, O.; Leijon, M. Influence of generator damping on peak power and variance of power for a direct drive wave energy converter. In Proceedings of the 26th Internationl Conference on Offshore Mechanincs and Arctic Engineering OMAE, San Diego, CA, USA, 10–15 June 2007. [Google Scholar]
- Haraguchi, R.; Asai, T. Enhanced power absorption of a point absorber wave energy converter using a tuned inertial mass. Energy 2020, 202, 117740. [Google Scholar] [CrossRef]
- Sugiura, K.; Sawada, R.; Nemoto, Y.; Haraguchi, R.; Asai, T. Wave flume testing of an oscillating-body wave energy converter with a tuned inerter. Appl. Ocean Res. 2020, 98, 102127. [Google Scholar] [CrossRef]
- Asai, T.; Sugiura, K. Numerical evaluation of a two-body point absorber wave energy converter with a tuned inerter. Renew. Energy 2021, 171, 217–226. [Google Scholar] [CrossRef]
- Cassidy, I.; Scruggs, J. Nonlinear stochastic controllers for power-flow-constrained vibratory energy harvesters. J. Sound Vib. 2013, 332, 3134–3147. [Google Scholar] [CrossRef]
- Gao, Y.; Shao, S.; Zou, H.; Tnag, M.; Xu, H.; Tian, C. A fully floating system for a wave energy converter with direct-driven linear generator. Energy 2016, 95, 99–109. [Google Scholar] [CrossRef]
- Son, D.; Yeung, R. Real time implementation and validation of optimal damping control for a permanent-magnet linear generator in wave energy extraction. Appl. Energy 2017, 208, 571–579. [Google Scholar] [CrossRef]
- Pierart, F.G.; Fernandez, J.; Olivos, J.; Gabl, R.; Davey, T. Numerical Investigation of the Scaling Effects for a Point Absorber. Water 2022, 14, 2156. [Google Scholar] [CrossRef]
- Folley, M. Numerical Modelling of Wave Energy. Converters, 1st ed.; Joe Hayton: London, UK, 2016; pp. 1–288. [Google Scholar]
- Cummins, W. The impulse response function and ship motions. Schiffstechnik 1962, 9, 101–109. [Google Scholar]
- Anderlini, E.; Forehand, D.; Stansell, P.; Xiao, Q.; Abusara, M. Control of a Point Absorber Using Reinforcement Learning. IEEE Trans. Sustain. Energy 2016, 7, 1681–1690. [Google Scholar] [CrossRef]
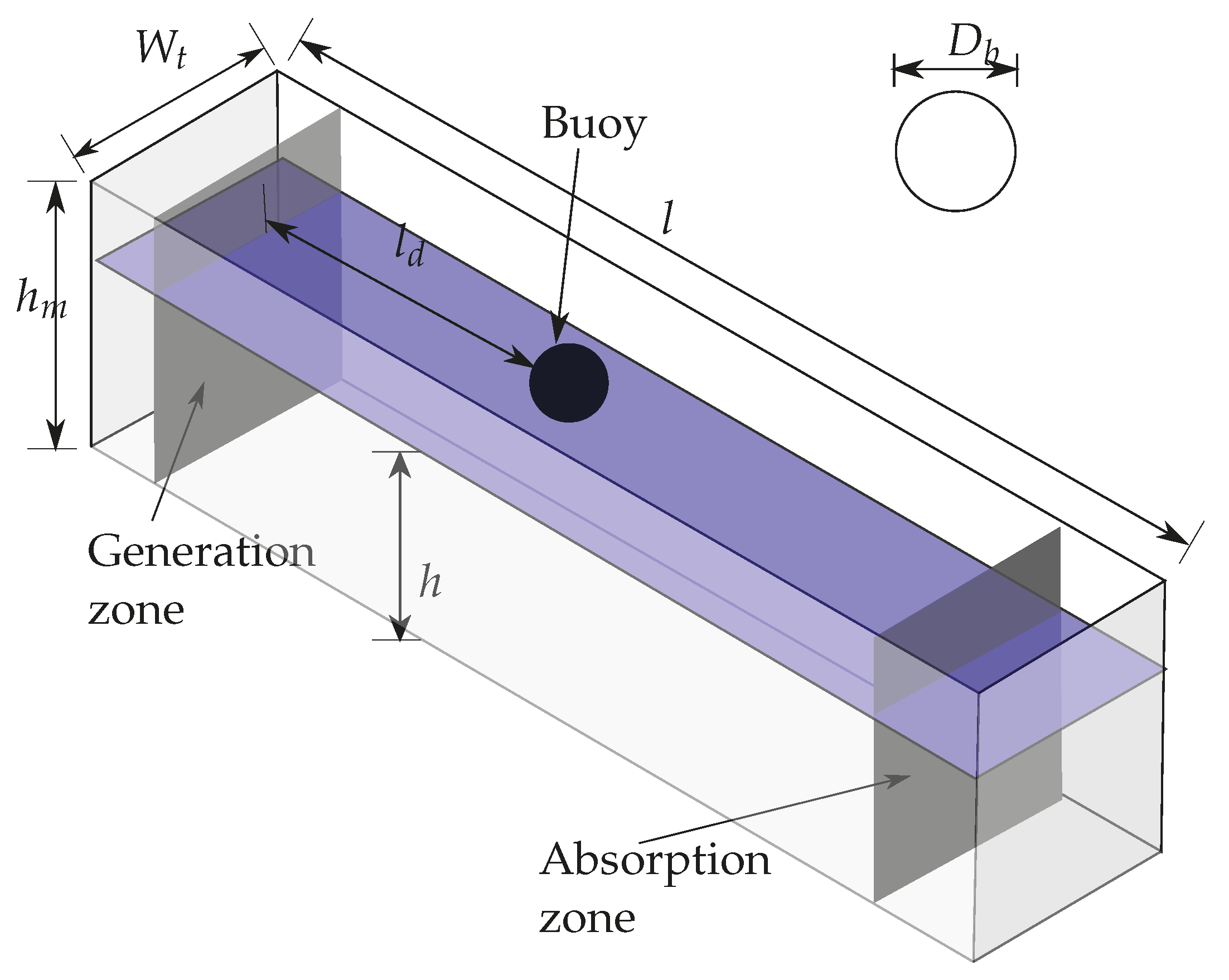

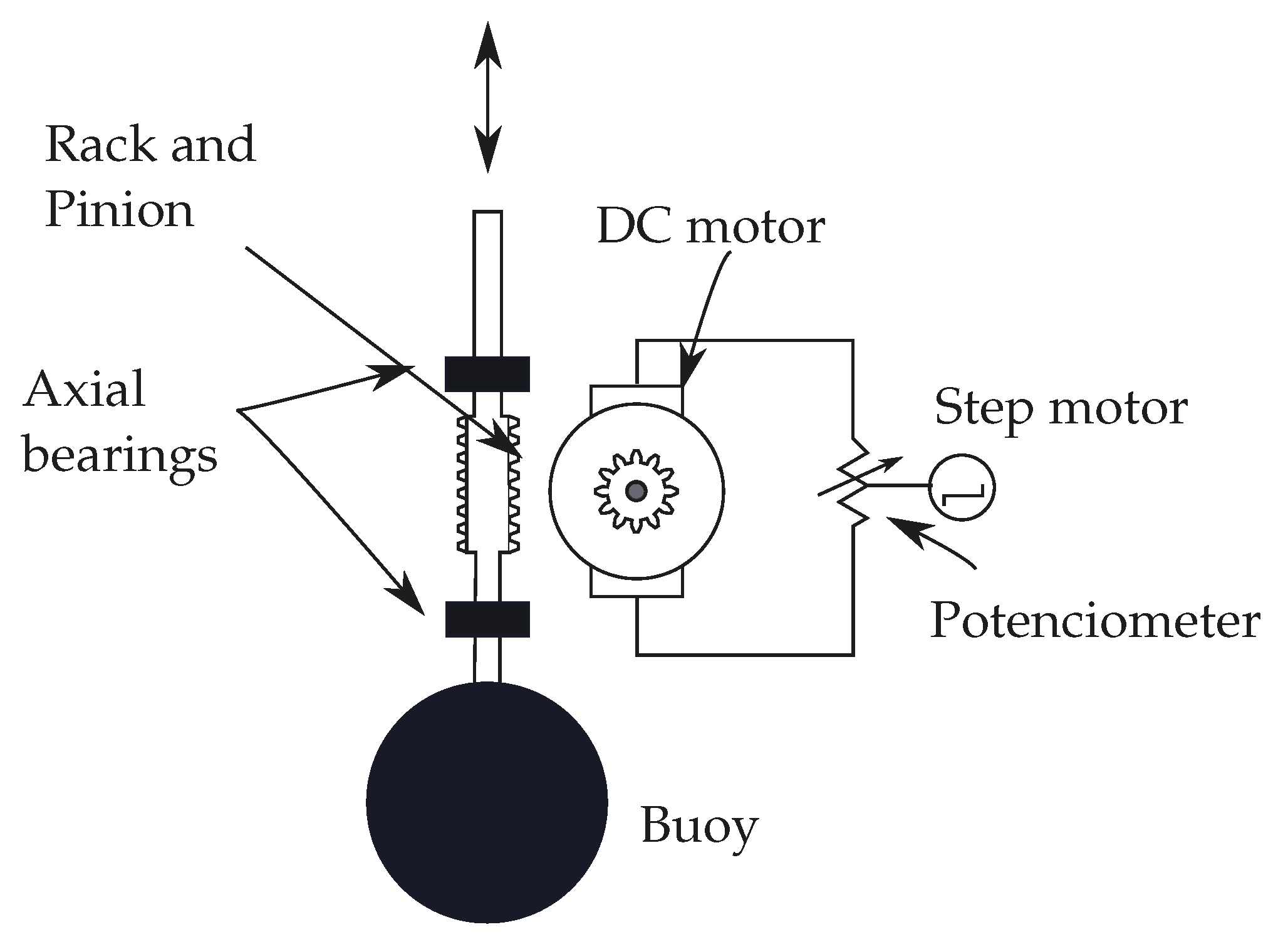
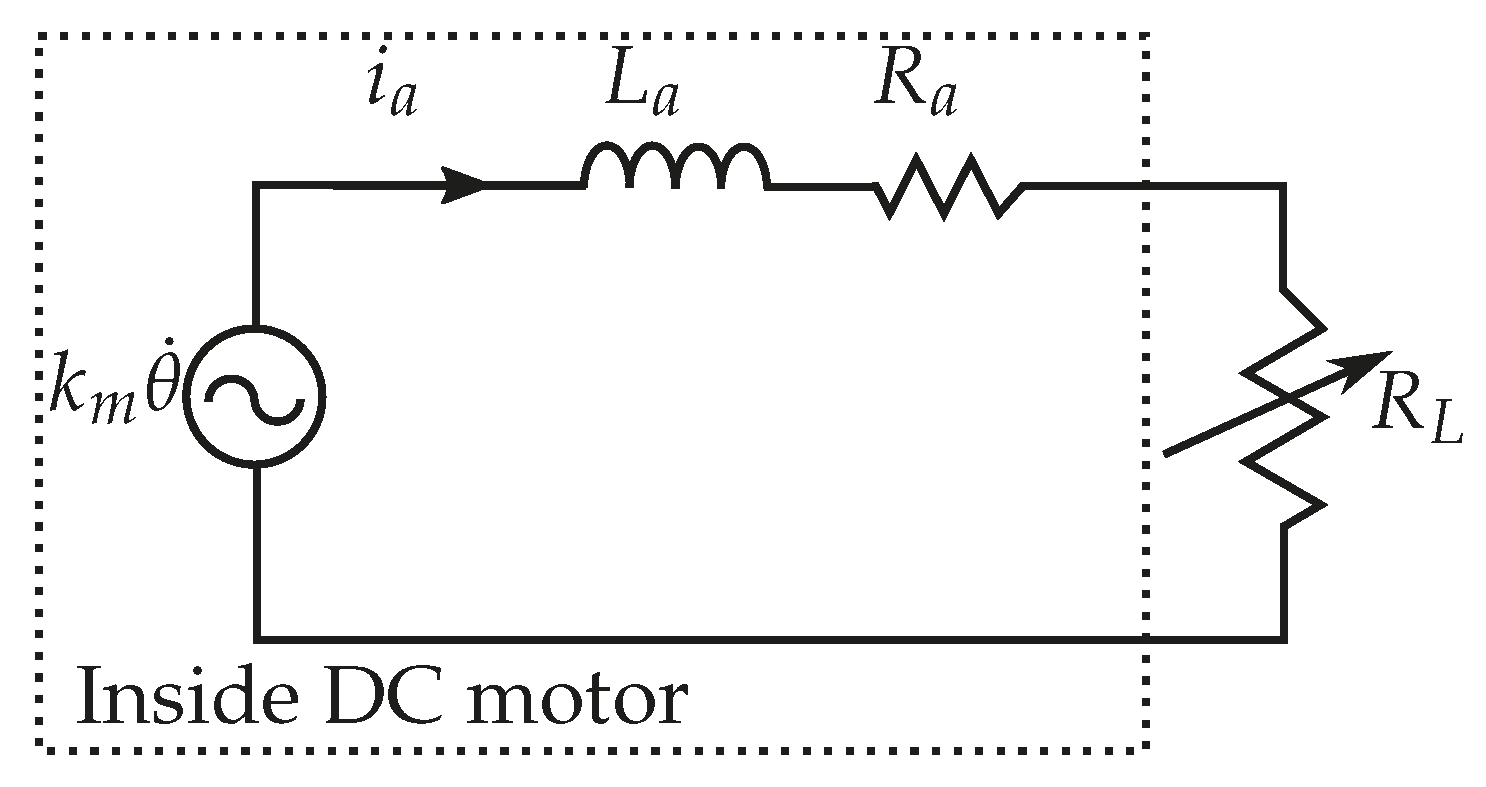




| h | l | ||||
|---|---|---|---|---|---|
| 0.252 | 0.5916 | 0.48 | 1.64 | 1.326 | 0.21 |
| Motor | (V/rad/s) | () | (H) | Nominal Power (W) | Nominal Voltage (V) |
|---|---|---|---|---|---|
| G1 | 0.750 | 401.4 | 0.64 | 35 | 220 |
| G2 | 0.050 | 7.22 | 0.01 | 40 | 18 |
| G3 | 0.235 | 34.78 | 0.08 | 55 | 120 |
| G4 | 0.047 | 107.69 | 0.16 | 0.5 | 12 |
| Wave Frequency () | |||
|---|---|---|---|
| Parameter | 1.28 Hz | 1.32 Hz | 1.36Hz |
| 136.94 N/m | 156.39 N/m | 149.06 N/m | |
| A | 1.23 kg | 1.21 kg | 1.18 kg |
| 6.73 Ns/m | 6.73 Ns/m | 6.71 Ns/m | |
| Electric Machine | External Resistance () | ||
|---|---|---|---|
| 0.8 | 5 | 10 | |
| G1 | 1.90 cm | 1.83 cm | 1.64 cm |
| G2 | 1.53 cm | 1.63 cm | 1.62 cm |
| G3 | 1.63 cm | 1.64 cm | 1.62 cm |
| G4 | 1.91 cm | 1.82 cm | 1.63 cm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pierart, F.G.; Rubilar, M.; Rohten, J. Experimental Validation of Damping Adjustment Method with Generator Parameter Study for Wave Energy Conversion. Energies 2023, 16, 5298. https://doi.org/10.3390/en16145298
Pierart FG, Rubilar M, Rohten J. Experimental Validation of Damping Adjustment Method with Generator Parameter Study for Wave Energy Conversion. Energies. 2023; 16(14):5298. https://doi.org/10.3390/en16145298
Chicago/Turabian StylePierart, Fabian G., Matias Rubilar, and Jaime Rohten. 2023. "Experimental Validation of Damping Adjustment Method with Generator Parameter Study for Wave Energy Conversion" Energies 16, no. 14: 5298. https://doi.org/10.3390/en16145298
APA StylePierart, F. G., Rubilar, M., & Rohten, J. (2023). Experimental Validation of Damping Adjustment Method with Generator Parameter Study for Wave Energy Conversion. Energies, 16(14), 5298. https://doi.org/10.3390/en16145298







