Artificial Intelligence and Mathematical Models of Power Grids Driven by Renewable Energy Sources: A Survey
Abstract
:1. Introduction and Overview
2. The Research Questions Underlying Power Grid Research
- Questions related to the functioning of power grids;
- Questions related to the forecasting of the different properties, variables, and features characterizing the power grids;
- Questions addressed through the exploration of hypothetical scenarios, which are typically implemented in digital representations of the power grid.
2.1. Monitoring the Functioning of Power Grids
- What are the best properties to measure that can function as good precursors of the system’s condition and operating status?
- What is the impact of fluctuating injected power on these properties?
- What are the best control protocols to stabilize the operating status at each control level?
- How can data be stored in an accessible format and best provide documentation with a detailed description of the data?
2.2. Forecasting Dynamical Features of Power Grids
- When assessing the evolution of (fluctuating) geophysical properties that drive one specific RES. One example is the wind speed in front of wind turbines, whose statistical properties are reflected in the highly fluctuating wind power production at wind farms. Another example is the solar irradiance on the earth’s surface.
- When assessing directly the evolution of power and frequency at specific nodes of the grid. Here, the dynamical features are of importance for the monitoring of the overall stability of the grid (see previous subsection).
- When assessing the evolution of external factors that eventually influence the power grid. One important example is the intrinsic demand for energy in cities, following daily, weekly, and seasonal cycles, as well as industry demands in specific locations. Other important examples are demographic and economic transitions, triggered by sudden events, such as climate catastrophes and wars, which change abruptly established patterns of production and consumption.
2.3. Assessing Hypothetical Scenarios with Simulated Topological or Dynamical Features
3. What Data Are Power Grid Data?
3.1. Grid Data: Topological and Electrical Features Underlying the Grid
3.2. Renewable Energy Data: Geophysical and Energy Time-Series
3.3. Finance Data: The Energy Market
3.4. Where to Find Power Grid Data?
Open Power System Data:
IRENA:
Energy Map.info:
Enipedia:
Global Power Plant Database:
OpenGridMap:
Paul-Frederik Bach:
Power grid frequency database:
Renewables.ninja:
SciGRID:
FINO (I, II, and III):
ENTSO-E:
Open-eGo:
React Energy Lab:
Agorameter:
Energy Charts:
EU ETS Dashboard:
SMARD:
Tmrow Electricity Map:
WattTime Explorer:
IAEE EDL:
Open Energy Modeling Initiative:
Yahoo Finance:
4. Modeling Power Grid Functioning and Dynamics
- Models based on dynamical systems and equations, as well as nonlinear methods;
- Models based on stochastic differential equations;
- Models based on Bayesian inference.
- Machine learning algorithms;
- Deep learning algorithms;
- Reinforcement learning algorithms;
- Reservoir computing algorithms.
- Modeling of grid structures;
- Modeling of energy demand and supply;
- Modeling RES, namely wind power, solar power, and biomass power.
- Modeling the energy market, particularly in connection with the power grid functioning and monitoring approaches.
- Towards the end of this survey, we will also examine literature covering some of the present challenges in power grid research, namely in what concerns futuristic scenarios:
- Exploring scenarios of energy storage;
- Exploring scenarios of emission reduction.
4.1. Modeling Different Grid Structures
4.2. Modeling of Energy Demand and Supply
4.3. Modeling Wind Power
4.4. Modeling Solar Power
4.5. Modeling Biomass Power
4.6. Modeling the Energy Market: From Power Grid Data to Energy Prices
5. Future Perspectives
5.1. Exploring Scenarios of Energy Storage
5.2. Exploring Scenarios of Emission Reduction
5.3. Final Remarks and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AI | Artificial Intelligence |
| AEMO | Australian Energy Market Operator |
| ANN | Artificial Neural Network |
| ARMA | Auto Regressive Moving Average |
| ARIMA | Autoregressive Integrated Moving Average |
| CES | Conventional Energy Sources |
| CKLS | Chan–Karolyi–Longstaff–Sanders |
| CNN | Convolutional Neural Network |
| CPI | Climate Policy Initiative |
| DAE | Denoising Autoencoders |
| DL | Deep Learning |
| DEED | Dynamic Economic Emission Dispatch |
| DeepCoin | Deep Learning and Block chain-based Energy Framework for Smart Grids |
| DR | Demand Response |
| ELM | Elaboration Likelihood Model |
| EPEX | European Power Exchange |
| ESS | Energy Storage System |
| EUs | European Unions |
| FCMs | Fuzzy Cognitive Maps |
| GARCH | Generalized Autoregressive Conditional Heteroskedasticity |
| GPU | Graphics Processing Unit |
| HVDC | High-Voltage DC Transmission |
| HEVs | Hybrid Electric Vehicles |
| IEA | International Energy Agency |
| IRENA | International Renewable Energy Agency |
| LUBE | Lower-Upper-Bound-Estimation |
| LSTM | Long Short-Term Memory |
| LiDAR | Light Detection and Ranging |
| MA | Moving Averages |
| MMC | Modular Multilevel Converters |
| ML | Machine Learning |
| MLP | Multilayer Perceptron |
| MPC | Model Predictive Control |
| MPPT | Maximum Power Point Tracking |
| NARX | Nonlinear Autoregressive Model that has eXogenous inputs |
| NILM | Nonintrusive Load Monitoring |
| PV | Photo Voltaic |
| RES | Renewable Energy Sources |
| RL | Reinforcement Learning |
| RMS | Root Mean Square |
| RC | Reservoir Computing |
| R-HFCM | Randomized High-Order Fuzzy Cognitive Maps |
| SIR | Sampling Importance Re-Sampling |
| SCADA | Supervisory Control and Data Acquisition |
| SDAE | Stacked Denoising Autoencoders |
| STC | Star Tracker |
| SVM | Support Vector Machine |
| VAR | Vector Auto-Regression |
| WPP | Wind Power Plant |
| WTG | Wind Turbine Generator |
References
- Demirel, Y. Energy and energy types. In Energy; Springer: Berlin/Heidelberg, Germany, 2012; pp. 27–70. [Google Scholar]
- Maczulak, A. Renewable Energy Sources and Methods: Green Technology; Infobase Publishing: New York, NY, USA, 2010.
- Princen, T.; Manno, J.P.; Martin, P.L. Ending the Fossil Fuel Era; MIT Press: Cambridge, MA, USA, 2015. [Google Scholar]
- Boden, T.A.; Marland, G.; Andres, R.J. Global, Regional, and National Fossil-Fuel CO2 Emissions; Carbon Dioxide Information Analysis Center, Oak Ridge National Laboratory, US Department of Energy: Oak Ridge, TN, USA, 2009; Volume 10.
- Panwar, N.; Kaushik, S.; Kothari, S. Role of renewable energy sources in environmental protection: A review. Renew. Sustain. Energy Rev. 2011, 15, 1513–1524. [Google Scholar] [CrossRef]
- Herzog, A.V.; Lipman, T.E.; Kammen, D.M. Renewable energy sources. In Encyclopedia of Life Support Systems (EOLSS); Forerunner Volume—‘Perspectives and Overview of Life Support Systems and Sustainable Development Eolss Publishers: Paris, France, 2001; Volume 76. [Google Scholar]
- Alrikabi, N. Renewable energy types. J. Clean Energy Technol. 2014, 2, 61–64. [Google Scholar] [CrossRef] [Green Version]
- Barhoumi, E.M.; Ben Belgacem, I.; Khiareddine, A.; Zghaibeh, M.; Tlili, I. A neural-network-based four phases interleaved boost converter for fuel cell system applications. Energies 2018, 11, 3423. [Google Scholar] [CrossRef] [Green Version]
- Barhoumi, E.M.; Okonkwo, P.C.; Farhani, S.; Belgacem, I.B.; Zghaibeh, M.; Mansir, I.B.; Bacha, F. Techno-economic analysis of photovoltaic-hydrogen refueling station case study: A transport company Tunis-Tunisia. Int. J. Hydrogen Energy 2022, 47, 24523–24532. [Google Scholar]
- Barhoumi, E.M.; Okonkwo, P.C.; Belgacem, I.B.; Zghaibeh, M.; Tlili, I. Optimal sizing of photovoltaic systems based green hydrogen refueling stations case study Oman. Int. J. Hydrogen Energy 2022, 47, 31964–31973. [Google Scholar]
- Okonkwo, P.C.; Barhoumi, E.M.; Mansir, I.B.; Emori, W.; Uzoma, P.C. Techno-economic analysis and optimization of solar and wind energy systems for hydrogen production: A case study. Energy Sources Part A Recovery Util. Environ. Eff. 2022, 44, 9119–9134. [Google Scholar] [CrossRef]
- Sánchez, I.J.G. Presentación del informe “ROAD MAP 2050–a practical guide for a prosperous, low-carbon Europe”. Pre-bie3 2010, 1, 4. [Google Scholar]
- Kralova, I.; Sjöblom, J. Biofuels–renewable energy sources: A review. J. Dispers. Sci. Technol. 2010, 31, 409–425. [Google Scholar] [CrossRef]
- Fouquet, D.; Johansson, T.B. European renewable energy policy at crossroads—Focus on electricity support mechanisms. Energy Policy 2008, 36, 4079–4092. [Google Scholar] [CrossRef]
- Knopf, B.; Nahmmacher, P.; Schmid, E. The European renewable energy target for 2030–An impact assessment of the electricity sector. Energy Policy 2015, 85, 50–60. [Google Scholar] [CrossRef]
- USA-RES. Available online: https://www.statista.com/statistics/186818/north-american-investment-in-sustainable-energy-since-2004/ (accessed on 5 July 2023).
- Klass, D.L. A critical assessment of renewable energy usage in the USA. Energy Policy 2003, 31, 353–367. [Google Scholar] [CrossRef]
- Yildirim, E.; Saraç, Ş.; Aslan, A. Energy consumption and economic growth in the USA: Evidence from renewable energy. Renew. Sustain. Energy Rev. 2012, 16, 6770–6774. [Google Scholar] [CrossRef]
- USA-data. Available online: https://www.nature.org/en-us/newsroom/senate-passes-inflation-reduction-act/ (accessed on 5 July 2023).
- Helmke-Long, L.; Carley, S.; Konisky, D.M. Municipal government adaptive capacity programs for vulnerable populations during the US energy transition. Energy Policy 2022, 167, 113058. [Google Scholar] [CrossRef]
- Jiang, R.; Wu, P.; Song, Y.; Wu, C.; Wang, P.; Zhong, Y. Factors influencing the adoption of renewable energy in the US residential sector: An optimal parameters-based geographical detector approach. Renew. Energy 2022, 201, 450–461. [Google Scholar] [CrossRef]
- Zhang, D.; Wang, J.; Lin, Y.; Si, Y.; Huang, C.; Yang, J.; Huang, B.; Li, W. Present situation and future prospect of renewable energy in China. Renew. Sustain. Energy Rev. 2017, 76, 865–871. [Google Scholar] [CrossRef]
- Zhang, P.; Yang, Y.; Shi, j.; Zheng, Y.; Wang, L.; Li, X. Opportunities and challenges for renewable energy policy in China. Renew. Sustain. Energy Rev. 2009, 13, 439–449. [Google Scholar] [CrossRef]
- Kumar, A.; Kumar, K.; Kaushik, N.; Sharma, S.; Mishra, S. Renewable energy in India: Current status and future potentials. Renew. Sustain. Energy Rev. 2010, 14, 2434–2442. [Google Scholar] [CrossRef]
- Pillai, I.R.; Banerjee, R. Renewable energy in India: Status and potential. Energy 2009, 34, 970–980. [Google Scholar] [CrossRef]
- Bhattacharya, S.; Jana, C. Renewable energy in India: Historical developments and prospects. Energy 2009, 34, 981–991. [Google Scholar] [CrossRef]
- Amri, F. Intercourse across economic growth, trade and renewable energy consumption in developing and developed countries. Renew. Sustain. Energy Rev. 2017, 69, 527–534. [Google Scholar] [CrossRef]
- Hammons, T.J.; Boyer, J.C.; Conners, S.R.; Davies, M.; Ellis, M.; Fraser, M.; Holt, E.A.; Markard, J. Renewable energy alternatives for developed countries. IEEE Trans. Energy Convers. 2000, 15, 481–493. [Google Scholar] [CrossRef]
- Martinot, E.; Chaurey, A.; Lew, D.; Moreira, J.R.; Wamukonya, N. Renewable energy markets in developing countries. Annu. Rev. Energy Environ. 2002, 27, 309–348. [Google Scholar] [CrossRef]
- Topcu, M.; Tugcu, C.T. The impact of renewable energy consumption on income inequality: Evidence from developed countries. Renew. Energy 2020, 151, 1134–1140. [Google Scholar] [CrossRef]
- Khatib, H. Renewable energy in developing countries. In Proceedings of the International Conference on Renewable Energy-Clean Power 2001, 1993, IET, London, UK, 17–19 November 1993; pp. 1–6. [Google Scholar]
- Arndt, C.; Arent, D.J.; Hartley, F.; Merven, B.; Mondal, A.H. Faster than you think: Renewable energy and developing countries. Annu. Rev. Resour. Econ. 2019, 11, 149–168. [Google Scholar] [CrossRef] [Green Version]
- Georgilakis, P.S. Technical challenges associated with the integration of wind power into power systems. Renew. Sustain. Energy Rev. 2008, 12, 852–863. [Google Scholar] [CrossRef] [Green Version]
- Heide, D.; Von Bremen, L.; Greiner, M.; Hoffmann, C.; Speckmann, M.; Bofinger, S. Seasonal optimal mix of wind and solar power in a future, highly renewable Europe. Renew. Energy 2010, 35, 2483–2489. [Google Scholar] [CrossRef]
- Aoufi, S.; Derhab, A.; Guerroumi, M. Survey of false data injection in smart power grid: Attacks, countermeasures and challenges. J. Inf. Secur. Appl. 2020, 54, 102518. [Google Scholar] [CrossRef]
- Tan, R.; Nguyen, H.H.; Foo, E.Y.; Dong, X.; Yau, D.K.; Kalbarczyk, Z.; Iyer, R.K.; Gooi, H.B. Optimal false data injection attack against automatic generation control in power grids. In Proceedings of the 2016 ACM/IEEE 7th International Conference on Cyber-Physical Systems (ICCPS), Vienna, Austria, 11–14 April 2016; pp. 1–10. [Google Scholar]
- Landsberg, P.T. A simple model for solar energy economics in the U.K. Energy 1977, 2, 149–159. [Google Scholar] [CrossRef]
- Marchetti, G.; Piccolo, M. Mathematical models for the construction of a renewable energy hybrid plant. In Proceedings of the Tenth EC Photovoltaic Solar Energy Conference, Lisbon, Portugal, 8–14 April 1991; Springer: Berlin/Heidelberg, Germany, 1991; pp. 442–445. [Google Scholar]
- Consoli, A.; Musumeci, S.; Raciti, A.; Leotta, A.; Nocera, U. Hybrid systems long term simulation. In Proceedings of the First International Caracas Conference on Devices, Circuits and Systems, IEEE, Caracas, Venezuela, 12–14 December 1995; pp. 266–270. [Google Scholar]
- Bonanno, F.; Consoli, A.; Lombardo, S.; Raciti, A. A logistical model for performance evaluations of hybrid generation systems. IEEE Trans. Ind. Appl. 1998, 34, 1397–1403. [Google Scholar] [CrossRef]
- Smith, O.; Cattell, O.; Farcot, E.; O’Dea, R.D.; Hopcraft, K.I. The effect of renewable energy incorporation on power grid stability and resilience. Sci. Adv. 2022, 8, eabj6734. [Google Scholar] [CrossRef]
- Barthelemy, M. Spatial networks. Phys. Rep.-Rev. –Phys. Lett. 2011, 499, 1–101. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.; Lei, Z.; Zhang, X.; Zhou, B.; Peng, J. A review of deep learning for renewable energy forecasting. Energy Convers. Manag. 2019, 198, 111799. [Google Scholar] [CrossRef]
- He, Y.; Mendis, G.J.; Wei, J. Real-time detection of false data injection attacks in smart grid: A deep learning-based intelligent mechanism. IEEE Trans. Smart Grid 2017, 8, 2505–2516. [Google Scholar] [CrossRef]
- Vázquez-Canteli, J.R.; Nagy, Z. Reinforcement learning for demand response: A review of algorithms and modeling techniques. Appl. Energy 2019, 235, 1072–1089. [Google Scholar] [CrossRef]
- Herbert, G.J.; Iniyan, S.; Sreevalsan, E.; Rajapandian, S. A review of wind energy technologies. Renew. Sustain. Energy Rev. 2007, 11, 1117–1145. [Google Scholar] [CrossRef]
- Negnevitsky, M.; Mandal, P.; Srivastava, A.K. Machine learning applications for load, price and wind power prediction in power systems. In Proceedings of the 2009 15th International Conference on Intelligent System Applications to Power Systems, IEEE, Curitiba, Brazil, 8–12 November 2009; pp. 1–6. [Google Scholar]
- Foley, A.M.; Leahy, P.G.; Marvuglia, A.; McKeogh, E.J. Current methods and advances in forecasting of wind power generation. Renew. Energy 2012, 37, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Li, G.; Shi, J. Applications of Bayesian methods in wind energy conversion systems. Renew. Energy 2012, 43, 1–8. [Google Scholar] [CrossRef]
- Yesilbudak, M.; Çolak, M.; Bayindir, R. A review of data mining and solar power prediction. In Proceedings of the 2016 IEEE International Conference on Renewable Energy Research and Applications (ICRERA), Oshawa, ON, Canada, 29 August–1 September 2016; pp. 1117–1121. [Google Scholar]
- Ardabili, S.; Mosavi, A.; Várkonyi-Kóczy, A.R. Systematic review of deep learning and machine learning models in biofuels research. In Proceedings of the International Conference on Global Research and Education, Budapest, Hungary, 4–7 September 2019; Springer: Berlin/Heidelberg, Germany, 2019; pp. 19–32. [Google Scholar]
- Ghoddusi, H.; Creamer, G.G.; Rafizadeh, N. Machine learning in energy economics and finance: A review. Energy Econ. 2019, 81, 709–727. [Google Scholar] [CrossRef]
- Jogunola, O.; Adebisi, B.; Ikpehai, A.; Popoola, S.I.; Gui, G.; Gačanin, H.; Ci, S. Consensus algorithms and deep reinforcement learning in energy market: A review. IEEE Internet Things J. 2020, 8, 4211–4227. [Google Scholar] [CrossRef]
- Emereuwa, C.A. Mathematical homogenization and stochastic modeling of energy storage systems. Curr. Opin. Electrochem. 2020, 21, 117–124. [Google Scholar] [CrossRef]
- Witthaut, D.; Hellmann, F.; Kurths, J.; Kettemann, S.; Meyer-Ortmanns, H.; Timme, M. Collective nonlinear dynamics and self-organization in decentralized power grids. Rev. Mod. Phys. 2022, 94, 015005. [Google Scholar] [CrossRef]
- Artrith, N. Machine learning for the modeling of interfaces in energy storage and conversion materials. J. Phys. Energy 2019, 1, 032002. [Google Scholar] [CrossRef]
- Yu, L.; Qin, S.; Zhang, M.; Shen, C.; Jiang, T.; Guan, X. A review of deep reinforcement learning for smart building energy management. IEEE Internet Things J. 2021, 8, 12046–12063. [Google Scholar] [CrossRef]
- The World Plug. Available online: https://www.iec.ch/world-plugs (accessed on 10 July 2022).
- Bengiamin, N.; Chan, W. 3-level load-frequency control of power systems interconnected by asynchronous tie lines. IET Digit. Libr. Proc. Inst. Electr. Eng. 1979, 126, 1198–1200. [Google Scholar] [CrossRef]
- Perujo, A.; Kaiser, R.; Sauer, D.U.; Wenzl, H.; Baring-Gould, I.; Wilmot, N.; Mattera, F.; Tselepis, S.; Nieuwenhout, F.; Rodrigues, C.; et al. Data monitoring and evaluation of renewable energy systems, in particular energy storage systems, and definition of categories of similar use. In Proceedings of the 2003 IEEE Bologna Power Tech Conference Proceedings, IEEE, Bologna, Italy, 23–26 June 2003; Volume 2, p. 6. [Google Scholar]
- Zhuang, M.; Shahidehpour, M.; Li, Z. An overview of non-intrusive load monitoring: Approaches, business applications, and challenges. In Proceedings of the 2018 international conference on power system technology (POWERCON), IEEE, Guangzhou, China, 6–8 November 2018; pp. 4291–4299. [Google Scholar]
- Chauhan, A.; Saini, R. A review on Integrated Renewable Energy System based power generation for stand-alone applications: Configurations, storage options, sizing methodologies and control. Renew. Sustain. Energy Rev. 2014, 38, 99–120. [Google Scholar] [CrossRef]
- Denholm, P.; Arent, D.J.; Baldwin, S.F.; Bilello, D.E.; Brinkman, G.L.; Cochran, J.M.; Cole, W.J.; Frew, B.; Gevorgian, V.; Heeter, J.; et al. The challenges of achieving a 100% renewable electricity system in the United States. Joule 2021, 5, 1331–1352. [Google Scholar] [CrossRef]
- Allegrini, J.; Orehounig, K.; Mavromatidis, G.; Ruesch, F.; Dorer, V.; Evins, R. A review of modelling approaches and tools for the simulation of district-scale energy systems. Renew. Sustain. Energy Rev. 2015, 52, 1391–1404. [Google Scholar] [CrossRef]
- Raischel, F.; Moreira, A.; Lind, P.G. Big DATA sets: An opportunity to study empirically scale phenomena in society and renewable energy. Eur. Phys. J. Spec. Top. 2014, 223, 2107–2118. [Google Scholar] [CrossRef] [Green Version]
- Runze, W.U.; Bao, Z.; Song, X.; Deng, W. Research on Short-term Load Forecasting Method of Power Grid Based on Deep Learning. Mod. Electr. Power 2018, 35, 43–48. [Google Scholar]
- Wei, R.; Gan, Q.; Wang, H.; You, Y.; Dang, X. Short-term multiple power type prediction based on deep learning. Int. J. Syst. Assur. Eng. Manag. 2020, 11, 835–841. [Google Scholar] [CrossRef] [Green Version]
- Khan, P.W.; Byun, Y.C.; Lee, S.J.; Park, N. Machine learning based hybrid system for imputation and efficient energy demand forecasting. Energies 2020, 13, 2681. [Google Scholar]
- MacDougall, P.; Kosek, A.M.; Bindner, H.; Deconinck, G. Applying machine learning techniques for forecasting flexibility of virtual power plants. In Proceedings of the 2016 IEEE Electrical Power and Energy Conference (EPEC), Ottawa, ON, Canada, 12–14 October 2016; pp. 1–6. [Google Scholar]
- Sharma, V.; Cali, Ü.; Sardana, B.; Kuzlu, M.; Banga, D.; Pipattanasomporn, M. Data-driven short-term natural gas demand forecasting with machine learning techniques. J. Pet. Sci. Eng. 2021, 206, 108979. [Google Scholar] [CrossRef]
- Wang, H.z.; Li, G.q.; Wang, G.b.; Peng, J.c.; Jiang, H.; Liu, Y.t. Deep learning based ensemble approach for probabilistic wind power forecasting. Appl. Energy 2017, 188, 56–70. [Google Scholar] [CrossRef]
- Hao, Y.; Tian, C. A novel two-stage forecasting model based on error factor and ensemble method for multi-step wind power forecasting. Appl. Energy 2019, 238, 368–383. [Google Scholar] [CrossRef]
- Wu, W.; Peng, M. A data mining approach combining K-Means clustering with bagging neural network for short-term wind power forecasting. IEEE Internet Things J. 2017, 4, 979–986. [Google Scholar] [CrossRef] [Green Version]
- Tascikaraoglu, A.; Uzunoglu, M. A review of combined approaches for prediction of short-term wind speed and power. Renew. Sustain. Energy Rev. 2014, 34, 243–254. [Google Scholar] [CrossRef]
- Chen, M.R.; Zeng, G.Q.; Lu, K.D.; Weng, J. A two-layer nonlinear combination method for short-term wind speed prediction based on ELM, ENN, and LSTM. IEEE Internet Things J. 2019, 6, 6997–7010. [Google Scholar] [CrossRef]
- Ak, R.; Fink, O.; Zio, E. Two machine learning approaches for short-term wind speed time-series prediction. IEEE Trans. Neural Netw. Learn. Syst. 2015, 27, 1734–1747. [Google Scholar] [CrossRef]
- Soman, S.S.; Zareipour, H.; Malik, O.; Mandal, P. A review of wind power and wind speed forecasting methods with different time horizons. In Proceedings of the North American Power Symposium 2010, IEEE, Arlington, TX, USA, 26–28 September 2010; pp. 1–8. [Google Scholar]
- Li, J.; Dueñas-Osorio, L.; Chen, C.; Berryhill, B.; Yazdani, A. Characterizing the topological and controllability features of US power transmission networks. Phys. A Stat. Mech. Its Appl. 2016, 453, 84–98. [Google Scholar] [CrossRef] [Green Version]
- Azzolin, A.; Dueñas-Osorio, L.; Cadini, F.; Zio, E. Electrical and topological drivers of the cascading failure dynamics in power transmission networks. Reliab. Eng. Syst. Saf. 2018, 175, 196–206. [Google Scholar] [CrossRef]
- Li, J.; Duenas-Osorio, L.; Chen, C.; Shi, C. Connectivity reliability and topological controllability of infrastructure networks: A comparative assessment. Reliab. Eng. Syst. Saf. 2016, 156, 24–33. [Google Scholar] [CrossRef] [Green Version]
- Han, F.; Zio, E.; Kopustinskas, V.; Praks, P. Quantifying the importance of elements of a gas transmission network from topological, reliability and controllability perspectives, considering capacity constraints. In Proceedings of the Risk, Reliability and Safety: Innovating Theory and Practice, Glasgow, Scotland, 25–29 September 2016; pp. 2565–2571. [Google Scholar]
- Gemmell, B.; Dorn, J.; Retzmann, D.; Soerangr, D. Prospects of multilevel VSC technologies for power transmission. In Proceedings of the 2008 IEEE/PES Transmission and Distribution Conference and Exposition, IEEE, Chicago, IL, USA, 21–24 April 2008; pp. 1–16. [Google Scholar]
- Zhou, M.; Yan, J.; Feng, D. Digital twin framework and its application to power grid online analysis. CSEE J. Power Energy Syst. 2019, 5, 391–398. [Google Scholar]
- Pan, H.; Dou, Z.; Cai, Y.; Li, W.; Lei, X.; Han, D. Digital twin and its application in power system. In Proceedings of the 2020 5th International Conference on Power and Renewable Energy (ICPRE), IEEE, Shanghai, China, 12–14 September 2020; pp. 21–26. [Google Scholar]
- Jiang, Z.; Lv, H.; Li, Y.; Guo, Y. A novel application architecture of digital twin in smart grid. J. Ambient. Intell. Humaniz. Comput. 2022, 13, 3819–3835. [Google Scholar] [CrossRef]
- He, X.; Ai, Q.; Qiu, R.C.; Zhang, D. Preliminary exploration on digital twin for power systems: Challenges, framework, and applications. arXiv 2019, arXiv:1909.06977. [Google Scholar]
- Germany Blackout. Available online: https://www.nzz.ch/english/blackout-germany-what-happens-when-millions-lose-power-for-days-ld.1708562 (accessed on 10 July 2022).
- Lai, L.L.; Zhang, H.T.; Mishra, S.; Ramasubramanian, D.; Lai, C.S.; Xu, F.Y. Lessons learned from July 2012 Indian blackout. In Proceedings of the 9th IET International Conference on Advances in Power System Control, Operation and Management (APSCOM 2012), IET, Hong Kong, China, 7–9 November 2012; pp. 1–6. [Google Scholar]
- Ratha, A. Indian blackouts of July 2012: What happened and why? ESI Bull. Energy Trends Dev. 2013, 5, 3–6. [Google Scholar]
- Burlando, A. Power outages, power externalities, and baby booms. Demography 2014, 51, 1477–1500. [Google Scholar] [CrossRef]
- Rand, K.; Kurth, M.; Fleming, C.H.; Linkov, I. A resilience matrix approach for measuring and mitigating disaster-induced population displacement. Int. J. Disaster Risk Reduct. 2020, 42, 101310. [Google Scholar] [CrossRef]
- Andersson, G.; Donalek, P.; Farmer, R.; Hatziargyriou, N.; Kamwa, I.; Kundur, P.; Martins, N.; Paserba, J.; Pourbeik, P.; Sanchez-Gasca, J.; et al. Causes of the 2003 major grid blackouts in North America and Europe, and recommended means to improve system dynamic performance. IEEE Trans. Power Syst. 2005, 20, 1922–1928. [Google Scholar] [CrossRef]
- Pourbeik, P.; Kundur, P.S.; Taylor, C.W. The anatomy of a power grid blackout-root causes and dynamics of recent major blackouts. IEEE Power Energy Mag. 2006, 4, 22–29. [Google Scholar] [CrossRef]
- Tavakoli, M.; Nafar, M. Human reliability analysis in maintenance team of power transmission system protection. Prot. Control. Mod. Power Syst. 2020, 5, 1–13. [Google Scholar] [CrossRef]
- Zhong, S.; Sun, Z. Challenges and opportunities in emergency management of electric power system blackout. In Proceedings of the 2010 International Conference on E-Product E-Service and E-Entertainment, IEEE, Henan, China, 7–9 November 2010; pp. 1–4. [Google Scholar]
- Sullivan, J.E.; Kamensky, D. How cyber-attacks in Ukraine show the vulnerability of the US power grid. T Electr. J. 2017, 30, 30–35. [Google Scholar] [CrossRef]
- Bompard, E.; Huang, T.; Wu, Y.; Cremenescu, M. Classification and trend analysis of threats origins to the security of power systems. Int. J. Electr. Power Energy Syst. 2013, 50, 50–64. [Google Scholar] [CrossRef]
- Hemaida, R.S.; Kwak, N. A linear goal programming model for trans-shipment problems with flexible supply and demand constraints. J. Oper. Res. Soc. 1994, 45, 215–224. [Google Scholar] [CrossRef]
- Hines, P.; Blumsack, S.; Sanchez, E.C.; Barrows, C. The topological and electrical structure of power grids. In Proceedings of the 2010 43rd Hawaii International Conference on System Sciences, IEEE, Kauai, HI, USA, 5–8 January 2010; pp. 1–10. [Google Scholar]
- Ramakrishna, R.; Scaglione, A. Grid-graph signal processing (grid-GSP): A graph signal processing framework for the power grid. IEEE Trans. Signal Process. 2021, 69, 2725–2739. [Google Scholar] [CrossRef]
- Pagani, G.A.; Aiello, M. The power grid as a complex network: A survey. Phys. A Stat. Mech. Its Appl. 2013, 392, 2688–2700. [Google Scholar] [CrossRef] [Green Version]
- Cavraro, G.; Kekatos, V. Graph algorithms for topology identification using power grid probing. IEEE Control. Syst. Lett. 2018, 2, 689–694. [Google Scholar] [CrossRef] [Green Version]
- Barabási, A.L.; Albert, R. Emergence of scaling in random networks. Science 1999, 286, 509–512. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Watts, D.J.; Strogatz, S.H. Collective dynamics of ‘small-world’networks. Nature 1998, 393, 440–442. [Google Scholar] [CrossRef]
- Albert, R.; Barabási, A.L. Statistical mechanics of complex networks. Rev. Mod. Phys. 2002, 74, 47. [Google Scholar] [CrossRef] [Green Version]
- Zhou, C.; Motter, A.E.; Kurths, J. Universality in the synchronization of weighted random networks. Phys. Rev. Lett. 2006, 96, 034101. [Google Scholar] [CrossRef] [Green Version]
- Motter, A.E.; Zhou, C.; Kurths, J. Network synchronization, diffusion, and the paradox of heterogeneity. Phys. Rev. E 2005, 71, 016116. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, S.; Yan, Y.; Bao, W.; Guo, S.; Jiang, J.; Ma, M. Network topology identification algorithm based on adjacency matrix. In Proceedings of the 2017 IEEE Innovative Smart Grid Technologies-Asia (ISGT-Asia), IEEE, Auckland, New Zealand, 4–7 December 2017; pp. 1–5. [Google Scholar]
- Omer, A.M. Energy, environment and sustainable development. Renew. Sustain. Energy Rev. 2008, 12, 2265–2300. [Google Scholar] [CrossRef]
- Lu, X.; McElroy, M.B. Global potential for wind-generated electricity. In Wind Energy Engineering; Elsevier: Amsterdam, The Netherlands, 2017; pp. 51–73. [Google Scholar]
- Strbac, G.; Shakoor, A.; Black, M.; Pudjianto, D.; Bopp, T. Impact of wind generation on the operation and development of the UK electricity systems. Electr. Power Syst. Res. 2007, 77, 1214–1227. [Google Scholar] [CrossRef]
- Kota, S.; Bayne, S.B.; Nimmagadda, S. Offshore wind energy: A comparative analysis of UK, USA and India. Renew. Sustain. Energy Rev. 2015, 41, 685–694. [Google Scholar] [CrossRef]
- Rubin, E.S.; Chen, C.; Rao, A.B. Cost and performance of fossil fuel power plants with CO2 capture and storage. Energy Policy 2007, 35, 4444–4454. [Google Scholar] [CrossRef]
- Akai, M.; Nomura, N.; Waku, H.; Inoue, M. Life-cycle analysis of a fossil-fuel power plant with CO2 recovery and a sequestering system. Energy 1997, 22, 249–255. [Google Scholar] [CrossRef]
- Abbasi, T.; Abbasi, S. Decarbonization of fossil fuels as a strategy to control global warming. Renew. Sustain. Energy Rev. 2011, 15, 1828–1834. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, Z. A review on tidal power utilization and operation optimization. In Proceedings of the IOP Conference Series: Earth and Environmental Science, Voronezh, Russia, 23–24 October 2019; IOP Publishing: Bristol, UK, 2019; Volume 240, p. 052015. [Google Scholar]
- Charlier, R.H. Re-invention or aggorniamento? Tidal power at 30 years. Renew. Sustain. Energy Rev. 1997, 1, 271–289. [Google Scholar] [CrossRef]
- Sleiti, A. Overview of tidal power technology. Energy Sources Part B Econ. Plan. Policy 2015, 10, 8–13. [Google Scholar] [CrossRef]
- International Geothermal Association. Available online: https://www.lovegeothermal.org/ (accessed on 1 January 2023).
- IRENA. Available online: https://www.irena.org/Statistics (accessed on 10 July 2022).
- The Open Power System Data. Available online: https://data.open-power-system-data.org/ (accessed on 10 July 2022).
- Energymap. Available online: http://www.energymap.info (accessed on 10 July 2022).
- Enipedia. Available online: https://datahub.io/dataset/enipedia (accessed on 10 July 2022).
- Global Power. Available online: https://datasets.wri.org/dataset/globalpowerplantdatabase (accessed on 10 July 2022).
- Open-Grid-Map. Available online: https://github.com/OpenGridMap (accessed on 10 July 2022).
- Paul-Frederik Bach. Available online: http://www.pfbach.dk/ (accessed on 10 July 2022).
- Power Grid Freq. Database. Available online: https://power-grid-frequency.org/database/ (accessed on 10 July 2022).
- Renewables-Ninja. Available online: https://www.renewables.ninja/ (accessed on 10 July 2022).
- SciGrid. Available online: https://www.scigrid.de/ (accessed on 10 July 2022).
- Fino: I. Available online: https://www.fino3.de/en/ (accessed on 10 July 2022).
- Fino: II. Available online: https://www.fino2.de/en/fino2.html (accessed on 10 July 2022).
- Fino: III. Available online: https://www.fino1.de/en/ (accessed on 10 July 2022).
- ENTSOE. Available online: https://www.entsoe.eu/ (accessed on 10 July 2022).
- Open Ego. Available online: https://openegoproject.wordpress.com/ (accessed on 10 July 2022).
- Visualization. Available online: https://data.open-power-system-data.org/renewable_power_plants/ (accessed on 10 July 2022).
- Agorameter. Available online: https://www.agora-energiewende.de/en/publications/agorameter-documentation/ (accessed on 10 July 2022).
- Energy-Charts. Available online: https://www.energy-charts.info/index.html?l=de&c=DE (accessed on 10 July 2022).
- EU ETS Dashboard. Available online: https://www.eea.europa.eu/data-and-maps/dashboards/emissions-trading-viewer-1 (accessed on 10 July 2022).
- SMARD. Available online: https://www.smard.de/home (accessed on 10 July 2022).
- Tmrow Electricity Map. Available online: https://electricitymaps.com/ (accessed on 10 July 2022).
- WattTime Explorer. Available online: https://www.watttime.org/explorer/#3/41.23/-97.64 (accessed on 10 July 2022).
- IAEE EDL. Available online: http://www.iaee.org/en/EnergyDataLinks/ (accessed on 10 July 2022).
- Open Energy Modelling Initiative. Available online: https://wiki.openmod-initiative.org/wiki/Data (accessed on 10 July 2022).
- Yahoo Finance. Available online: https://finance.yahoo.com/ (accessed on 10 July 2022).
- Milano, F. Power System Modelling and Scripting; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Mei, S.; Zhang, X.; Cao, M. Power Grid Complexity; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Mao, X.; Yuan, C. Stochastic Differential Equations with Markovian Switching; World Scientific Publishing: Singapore, 2006. [Google Scholar]
- Milstein, G.N. Numerical Integration of Stochastic Differential Equations; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1994; Volume 313. [Google Scholar]
- Martin, O. Bayesian Analysis with Python; Packt Publishing Ltd.: Birmingham, UK, 2016. [Google Scholar]
- Neal, R.M. Bayesian Learning for Neural Networks; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; Volume 118. [Google Scholar]
- Robert, C. Machine Learning, a Probabilistic Perspective; The MIT Press: Cambridge, MA, USA, 2014. [Google Scholar]
- Harrington, P. Machine Learning in Action; Simon and Schuster: New York, NY, USA, 2012. [Google Scholar]
- Bonaccorso, G. Machine Learning Algorithms; Packt Publishing Ltd.: Birmingham, UK, 2017. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Stevens, E.; Antiga, L.; Viehmann, T. Deep Learning with PyTorch; Manning Publications: New York, NY, USA, 2020. [Google Scholar]
- Dayhoff, J.E. Neural Network Architectures: An Introduction; Van Nostrand Reinhold Co.: New York, NY, USA, 1990. [Google Scholar]
- Grossi, C. Algorithms for Reinforcement Learning; Springer Nature: Berlin/Heidelberg, Germany, 2022. [Google Scholar]
- Nakajima, K.; Fischer, I. Reservoir Computing; Springer: Berlin/Heidelberg, Germany, 2021. [Google Scholar]
- Caliskan, S.Y.; Tabuada, P. Uses and abuses of the swing equation model. In Proceedings of the 2015 54th IEEE Conference on Decision and Control (CDC), IEEE, Osaka, Japan, 15–18 December 2015; pp. 6662–6667. [Google Scholar]
- Zhou, J.; Ohsawa, Y. Improved swing equation and its properties in synchronous generators. IEEE Trans. Circuits Syst. I Regul. Pap. 2008, 56, 200–209. [Google Scholar] [CrossRef]
- Anahua, E.; Barth, S.; Peinke, J. Markovian power curves for wind turbines. Wind. Energy Int. J. Prog. Appl. Wind. Power Convers. Technol. 2008, 11, 219–232. [Google Scholar] [CrossRef]
- Marino, E.; Lugni, C.; Borri, C. A novel numerical strategy for the simulation of irregular nonlinear waves and their effects on the dynamic response of offshore wind turbines. Comput. Methods Appl. Mech. Eng. 2013, 255, 275–288. [Google Scholar] [CrossRef]
- PyPi. Available online: https://pypi.org/project/power-grid-model/ (accessed on 28 April 2023).
- Renpow. Available online: https://cran.r-project.org/web/packages/renpow/ (accessed on 28 April 2023).
- Lindner, M.; Lincoln, L.; Drauschke, F.; Koulen, J.M.; Würfel, H.; Plietzsch, A.; Hellmann, F. NetworkDynamics.jl—Composing and simulating complex networks in Julia. Chaos Interdiscip. J. Nonlinear Sci. 2021, 31, 063133. [Google Scholar] [CrossRef]
- Plietzsch, A.; Kogler, R.; Auer, S.; Merino, J.; Gil-de Muro, A.; Liße, J.; Vogel, C.; Hellmann, F. PowerDynamics.jl—An experimentally validated open-source package for the dynamical analysis of power grids. SoftwareX 2021, 17, 100861. [Google Scholar] [CrossRef]
- Jacobson, M.Z.; Archer, C.L. Saturation wind power potential and its implications for wind energy. Proc. Natl. Acad. Sci. USA 2012, 109, 15679–15684. [Google Scholar] [CrossRef]
- Yang, T.; Cai, S.; Yan, P.; Li, W.; Zomaya, A.Y. Saturation defense method of a power cyber-physical system based on active cut set. IEEE Trans. Smart Grid 2022, 1–12. [Google Scholar] [CrossRef]
- Chen, G.; Dong, Z.; Hill, D.; Zhang, G.; Hua, K. Attack structural vulnerability of power grids: A hybrid approach based on complex networks. Drug Alcohol Rev. 2010, 389, 595–603. [Google Scholar] [CrossRef]
- Li, Y.W.; Vilathgamuwa, D.M.; Loh, P.C. A Grid-Interfacing Power Quality Compensator for Three-Phase Three-Wire Microgrid Applications. IEEE Trans. Power Electron. 2006, 3, 1–7. [Google Scholar] [CrossRef]
- Lee, B. Multigrid for model reduction of power grid networks. Numer. Linear Algebra Appl. 2018, 25, e2201. [Google Scholar] [CrossRef]
- Nishikawa, T.; Motter, A.E. Comparative analysis of existing models for power-grid synchronization. New J. Phys. 2015, 17, 015012. [Google Scholar] [CrossRef]
- Battista, H.D.; Mantz, R.J. Dynamical variable structure controller for power regulation of wind energy conversion systems. IEEE Trans. Energy Convers. 2004, 19, 756–763. [Google Scholar] [CrossRef]
- Susuki, Y.; Mezic, I. Nonlinear Koopman Modes and Power System Stability Assessment without Models. IEEE Trans. Power Syst. 2014, 29, 899–907. [Google Scholar] [CrossRef] [Green Version]
- Huang, Z.; Wang, C.; Ruj, S.; Stojmenovic, M.; Nayak, A. Modeling cascading failures in smart power grid using interdependent complex networks and percolation theory. In Proceedings of the 2013 IEEE 8th Conference on Industrial Electronics and Applications (ICIEA), IEEE, Melbourne, Australia, 19–21 June 2013; pp. 1023–1028. [Google Scholar]
- van der Schaft, A.; Stegink, T. Perspectives in modeling for control of power networks. Annu. Rev. Control. 2016, 41, 119–132. [Google Scholar] [CrossRef]
- Cuadra, L.; Pino, M.D.; Nieto-Borge, J.C.; Salcedo-Sanz, S. Optimizing the structure of distribution smart grids with renewable generation against abnormal conditions: A complex networks approach with evolutionary algorithms. Energies 2017, 10, 1097. [Google Scholar] [CrossRef] [Green Version]
- Faza, A.Z.; Sedigh, S.; McMillin, B.M. Reliability modeling for the advanced electric power grid: A proposal for doctoral research. In Proceedings of the 2009 33rd Annual IEEE International Computer Software and Applications Conference, IEEE, Seattle, WA, USA, 20–24 July 2009; Volume 1, pp. 672–675. [Google Scholar]
- Rohden, M.; Sorge, A.; Timme, M.; Witthaut, D. Self-organized synchronization in decentralized power grids. Phys. Rev. Lett. 2012, 109, 064101. [Google Scholar] [CrossRef] [Green Version]
- Schäfer, B.; Matthiae, M.; Timme, M.; Witthaut, D. Decentral smart grid control. New J. Phys. 2015, 17, 015002. [Google Scholar] [CrossRef]
- Schäfer, B.; Witthaut, D.; Timme, M.; Latora, V. Dynamically induced cascading failures in power grids. Nat. Commun. 2018, 9, 1975. [Google Scholar] [CrossRef] [Green Version]
- Witthaut, D.; Rohden, M.; Zhang, X.; Hallerberg, S.; Timme, M. Critical links and nonlocal rerouting in complex supply networks. Phys. Rev. Lett. 2016, 116, 138701. [Google Scholar] [CrossRef] [Green Version]
- Haehne, H.; Casadiego, J.; Peinke, J.; Timme, M. Detecting hidden units and network size from perceptible dynamics. Phys. Rev. Lett. 2019, 122, 158301. [Google Scholar] [CrossRef]
- Schiel, C.; Lind, P.G.; Maass, P. Resilience of electricity grids against transmission line overloads under wind power injection at different nodes. Sci. Rep. 2017, 7, 11562. [Google Scholar] [CrossRef] [Green Version]
- Kim, S.K.; Jeon, J.H.; Cho, C.H.; Ahn, J.B.; Kwon, S.H. Dynamic Modeling and Control of a Grid-Connected Hybrid Generation System with Versatile Power Transfer. IEEE Trans. Ind. Electron. 2008, 55, 1677–1688. [Google Scholar] [CrossRef]
- Guan, M.; Xu, Z. Modeling and Control of a Modular Multilevel Converter-Based HVDC System Under Unbalanced Grid Conditions. IEEE Trans. Power Electron. 2012, 27, 4858–4867. [Google Scholar] [CrossRef]
- Ropp, M.E.; Gonzalez, S. Development of a MATLAB/Simulink Model of a Single-Phase Grid-Connected Photovoltaic System. IEEE Trans. Energy Convers. 2009, 24, 195–202. [Google Scholar] [CrossRef]
- Katiraei, F.; Iravani, M.R.; Lehn, P.W. Small-signal dynamic model of a micro-grid including conventional and electronically interfaced distributed resources. Gener. Transm. Distrib. Iet 2007, 1, 369–378. [Google Scholar] [CrossRef] [Green Version]
- Anghel, M.; Werley, K.A.; Motter, A.E. Stochastic model for power grid dynamics. In Proceedings of the 2007 40th Annual Hawaii International Conference on System Sciences (HICSS’07), IEEE, Big Island, HI, USA, 3–6 January 2007; p. 113. [Google Scholar]
- Wang, K.; Low, S.; Lin, C. How stochastic network calculus concepts help green the power grid. In Proceedings of the 2011 IEEE International Conference on Smart Grid Communications (SmartGridComm), IEEE, Brussels, Belgium, 17–20 October 2011; pp. 55–60. [Google Scholar]
- Carrillo, J.A.; Clini, A.; Solem, S. The mean field limit of stochastic differential equation systems modelling grid cells. arXiv 2021, arXiv:2112.06213. [Google Scholar]
- Chau, K.W.; Oosterlee, C.W. Stochastic grid bundling method for backward stochastic differential equations. Int. J. Comput. Math. 2019, 96, 2272–2301. [Google Scholar] [CrossRef]
- Zhan, H.; Lei, X.; Wang, C.; Yue, D.; Xie, X. Adaptive grid based multi-objective Cauchy differential evolution for stochastic dynamic economic emission dispatch with wind power uncertainty. PLoS ONE 2017, 12, 1–25. [Google Scholar] [CrossRef] [Green Version]
- Ren, X.; Yang, N.; Ye, B.; Yao, Y.; Gao, C. Stochastic Planning Model for Incremental Distributio Network Considering CVaR and Wind Power Penetration. In Proceedings of the 2019 IEEE Innovative Smart Grid Technologies-Asia (ISGT Asia), IEEE, Chengdu, China, 21–24 May 2019; pp. 1358–1363. [Google Scholar]
- Wang, K. A Stochastic Power Network Calculus for Integrating Renewable Energy Sources into the Power Grid. IEEE J. Sel. Areas Commun. 2012, 30, 1037–1048. [Google Scholar] [CrossRef]
- Alnowibet, K.A. A strategic bi-level framework for wind power investment considering grid strength index: A stochastic programming approach. Sustain. Energy, Grids Netw. 2022, 31, 100718. [Google Scholar] [CrossRef]
- Schäfer, B.; Beck, C.; Aihara, K.; Witthaut, D.; Timme, M. Non-Gaussian power grid frequency fluctuations characterized by Lévy-stable laws and superstatistics. Nat. Energy 2018, 3, 119–126. [Google Scholar] [CrossRef] [Green Version]
- Haehne, H.; Schmietendorf, K.; Tamrakar, S.; Peinke, J.; Kettemann, S. Propagation of wind-power-induced fluctuations in power grids. Phys. Rev. E 2019, 99, 050301. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Joshi, C.; Wilson, S. Grid Based Bayesian Inference for Stochastic Differential Equation Models; Technical Paper; Trinity College: Dublin, Ireland, 2011. [Google Scholar]
- Chen, W.; Liao, Q. Research on Bayesian network adaptive knowledge construction and inference based on genetic algorithm. In Proceedings of the 2008 Fourth International Conference on Natural Computation, IEEE, Washington, DC, USA, 18–20 October 2008; Volume 6, pp. 315–319. [Google Scholar]
- Ma, H.; Li, H. Analysis of frequency dynamics in power grid: A Bayesian structure learning approach. IEEE Trans. Smart Grid 2013, 4, 457–466. [Google Scholar] [CrossRef]
- Rudin, C.; Waltz, D.; Anderson, R.N.; Boulanger, A.; Salleb-Aouissi, A.; Chow, M.; Dutta, H.; Gross, P.N.; Huang, B.; Ierome, S. Machine Learning for the New York City Power Grid. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 34, 328–345. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Anderson, R.N.; Boulanger, A.; Rudin, C.; Waltz, D.; Salleb-Aouissi, A.; Chow, M.; Dutta, H.; Gross, P.; Bert, H.; Ierome, S.; et al. Machine Learning for Power Grid. U.S. Patent 8,751,421, 10 June 2014. [Google Scholar]
- Vasseur, J.P.; Mota, J.C.; Di Pietro, A. Cross-Validation of a Learning Machine Model Across Network Devices. U.S. Patent 9,503,466, 22 November 2016. [Google Scholar]
- Yu, R.; Zhang, Y.; Gjessing, S.; Yuen, C.; Xie, S.; Guizani, M. Cognitive radio based hierarchical communications infrastructure for smart grid. IEEE Netw. 2011, 25, 6–14. [Google Scholar] [CrossRef]
- Niu, X.; Li, J.; Sun, J.; Tomsovic, K. Dynamic detection of false data injection attack in smart grid using deep learning. In Proceedings of the 2019 IEEE Power & Energy Society Innovative Smart Grid Technologies Conference (ISGT), IEEE, Washington, DC, USA, 17–20 February 2019; pp. 1–6. [Google Scholar]
- Nauck, C.; Lindner, M.; Schürholt, K.; Zhang, H.; Schultz, P.; Kurths, J.; Isenhardt, I.; Hellmann, F. Predicting basin stability of power grids using graph neural networks. New J. Phys. 2022, 24, 043041. [Google Scholar] [CrossRef]
- Mukherjee, S.; He, B.; Chakrabortty, A. Reinforcement Learning Control of Power Systems with Unknown Network Model under Ambient and Forced Oscillations. In Proceedings of the IEEE Conference on Control Technology and Applications (CCTA), Montreal, QC, Canada, 24–26 August 2020. [Google Scholar]
- Du, Y.; Li, F. Intelligent Multi-Microgrid Energy Management Based on Deep Neural Network and Model-Free Reinforcement Learning. IEEE Trans. Smart Grid 2019, 11, 1066–1076. [Google Scholar] [CrossRef]
- Torres, P.J.R.; García, C.G.; Izquierdo, S.K. Reinforcement Learning with Probabilistic Boolean Network Models of Smart Grid Devices. arXiv 2021, arXiv:2102.01297. [Google Scholar]
- Sharma, S.; Gupta, P.; Das, L. Reinforcement Learning for Computing Power Grid Network Operating Functions. In Proceedings of the Third International Conference on Computing, Mathematics and Statistics (iCMS2017); Langkawi: November 2017; Springer Publisher: Singapore, 20 November 2019; Volume 17. [Google Scholar] [CrossRef]
- Pu, T.; Wang, X.; Cao, Y.; Liu, Z.; Qiu, C.; Qiao, J.; Zhang, S. Power flow adjustment for smart microgrid based on edge computing and multi-agent deep reinforcement learning. J. Cloud Comput. 2021, 10, 1–13. [Google Scholar] [CrossRef]
- Ghasemkhani, A.; Darvishi, A.; Niazazari, I.; Darvishi, A.; Livani, H.; Yang, L. Deepgrid: Robust deep reinforcement learning-based contingency management. In Proceedings of the 2020 IEEE Power & Energy Society Innovative Smart Grid Technologies Conference (ISGT), IEEE, Washington, DC, USA, 17–20 February 2020; pp. 1–5. [Google Scholar]
- Li, Y. Deep reinforcement learning: An overview. arXiv 2017, arXiv:1701.07274. [Google Scholar]
- Wu, J.; Xu, X.; Zhang, P.; Liu, C. A novel multi-agent reinforcement learning approach for job scheduling in grid computing. Future Gener. Comput. Syst. 2011, 27, 430–439. [Google Scholar] [CrossRef]
- Galstyan, A.; Czajkowski, K.; Lerman, K. Resource allocation in the grid using reinforcement learning. In Proceedings of the Third International Joint Conference on Autonomous Agents and Multiagent Systems, 2004, AAMAS 2004, IEEE Computer Society, Washington, DC, USA, 23 July 2004; Volume 1, pp. 1314–1315. [Google Scholar]
- Peters, M.; Ketter, W.; Saar-Tsechansky, M.; Collins, J. A reinforcement learning approach to autonomous decision-making in smart electricity markets. Mach. Learn. 2013, 92, 5–39. [Google Scholar] [CrossRef] [Green Version]
- Kuznetsova, E.; Li, Y.F.; Ruiz, C.; Zio, E.; Ault, G.; Bell, K. Reinforcement learning for microgrid energy management. Energy 2013, 59, 133–146. [Google Scholar] [CrossRef]
- Markovic, D.S.; Zivkovic, D.; Branovic, I.; Popovic, R.; Cvetkovic, D. Smart power grid and cloud computing. Renew. Sustain. Energy Rev. 2013, 24, 566–577. [Google Scholar] [CrossRef]
- Lukoševičius, M.; Jaeger, H.; Schrauwen, B. Reservoir computing trends. KI-Künstliche Intell. 2012, 26, 365–371. [Google Scholar] [CrossRef]
- Lei, Z.; Huang, D.; Kulshrestha, A.; Pena, S.; Allen, G.; Li, X.; White, C.; Duff, R.; Smith, J.R.; Kalla, S. Resgrid: A grid-aware toolkit for reservoir uncertainty analysis. In Proceedings of the Sixth IEEE International Symposium on Cluster Computing and the Grid (CCGRID’06), IEEE, Singapore, 16–19 May 2006; Volume 1, pp. 249–252. [Google Scholar]
- Verwiebe, P.A.; Seim, S.; Burges, S.; Schulz, L.; Müller-Kirchenbauer, J. Modeling energy demand—A systematic literature review. Energies 2021, 14, 7859. [Google Scholar] [CrossRef]
- Ochoa, P.; Van Ackere, A. Policy changes and the dynamics of capacity expansion in the Swiss electricity market. Energy Policy 2009, 37, 1983–1998. [Google Scholar] [CrossRef]
- Sun, M.; Tian, L.; Fu, Y. An energy resources demand–supply system and its dynamical analysis. Chaos Solitons Fractals 2007, 32, 168–180. [Google Scholar] [CrossRef]
- Sun, M.; Wang, X.; Chen, Y.; Tian, L. Energy resources demand-supply system analysis and empirical research based on non-linear approach. Energy 2011, 36, 5460–5465. [Google Scholar] [CrossRef]
- Matsypura, D. Dynamics of Global Supply Chain and Electric Power Networks: Models, Pricing Analysis, and Computations; University of Massachusetts: Amherst, MA, USA, 2006. [Google Scholar]
- Song, Y.; Liu, T.; Liang, D.; Li, Y.; Song, X. A fuzzy stochastic model for carbon price prediction under the effect of demand-related policy in China’s carbon market. Ecol. Econ. 2019, 157, 253–265. [Google Scholar] [CrossRef]
- Ouyang, L.Y.; Wu, K.S.; Ho, C.H. Integrated vendor–buyer cooperative models with stochastic demand in controllable lead time. Int. J. Prod. Econ. 2004, 92, 255–266. [Google Scholar] [CrossRef]
- Long, B.; Wang, J.; Zhu, J. Stochastic Inventory Model with Supply and Demand Based on Inventory Level. Wuhan Ligong Daxue Xuebao (Jiaotong Kexue Gongcheng Ban)/J. Wuhan Univ. Technol. (Transp. Sci. Eng.) 2018, 42, 732–737. [Google Scholar]
- Poole, D.; Raftery, A.E. Inference for Deterministic Simulation Models: The Bayesian Melding Approach. Publ. Am. Stat. Assoc. 2000, 95, 1244–1255. [Google Scholar] [CrossRef]
- Gupta, R.; Das, S. Spatial Bayesian methods of forecasting house prices in six metropolitan areas of South Africa. S. Afr. J. Econ. 2008, 76, 298–313. [Google Scholar] [CrossRef] [Green Version]
- Gelman, A.; Carlin, J.B.; Stern, H.S.; Dunson, D.B.; Vehtari, A.; Rubin, D.B. Bayesian Data Analysis; Chapman and Hall/CRC: Hoboken, NJ, USA, 2013. [Google Scholar]
- Jia, L.; Zhao, Q.; Tong, L. Retail pricing for stochastic demand with unknown parameters: An online machine learning approach. In Proceedings of the 2013 51st Annual Allerton Conference on Communication, Control, and Computing (Allerton), IEEE, Monticello, IL, USA, 2–4 October 2013; pp. 1353–1358. [Google Scholar]
- Paterakis, N.G.; Mocanu, E.; Gibescu, M.; Stappers, B.; van Alst, W. Deep learning versus traditional machine learning methods for aggregated energy demand prediction. In Proceedings of the 2017 IEEE PES Innovative Smart Grid Technologies Conference Europe (ISGT-Europe), IEEE, Espoo, Finland, 18–21 October 2017; pp. 1–6. [Google Scholar]
- Coelho, V.N.; Coelho, I.M.; Rios, E.; Alexandre Filho, S.; Reis, A.J.; Coelho, B.N.; Alves, A.; Netto, G.G.; Souza, M.J.; Guimarães, F.G. A hybrid deep learning forecasting model using GPU disaggregated function evaluations applied for household electricity demand forecasting. Energy Procedia 2016, 103, 280–285. [Google Scholar] [CrossRef]
- Polson, M.; Sokolov, V. Deep learning for energy markets. Appl. Stoch. Model. Bus. Ind. 2020, 36, 195–209. [Google Scholar] [CrossRef] [Green Version]
- Paudel, P.; Kim, S.; Park, S.; Choi, K.H. A context-aware IoT and deep-learning-based smart classroom for controlling demand and supply of power load. Electronics 2020, 9, 1039. [Google Scholar] [CrossRef]
- Petkovic, M.; Koch, T.; Zittel, J. Deep learning for spatio-temporal supply and demand forecasting in natural gas transmission networks. Energy Sci. Eng. 2021, 10, 1812–1825. [Google Scholar] [CrossRef]
- Lu, R.; Hong, S.H.; Zhang, X. References 239 and 450 are duplicates. Please remove duplicated ref and update ref list and ref citations in main text accordingly. A dynamic pricing demand response algorithm for smart grid: Reinforcement learning approach. Appl. Energy 2018, 220, 220–230. [Google Scholar] [CrossRef]
- Wan, Y.; Qin, J.; Yu, X.; Yang, T.; Kang, Y. Price-Based Residential Demand Response Management in Smart Grids: A Reinforcement Learning-Based Approach. IEEE/CAA J. Autom. Sin. 2021, 9, 123–134. [Google Scholar] [CrossRef]
- Bao, T.; Zhang, X.; Yu, T.; Liu, X.; Wang, D. A stackelberg game model of real-time supply-demand interaction and the solving method via reinforcement learning. Zhongguo Dianji Gongcheng Xuebao/Proc. Chin. Soc. Electr. Eng. 2018, 38, 2947–2955. [Google Scholar]
- Wen, L.; Zhou, K.; Li, J.; Wang, S. Modified deep learning and reinforcement learning for an incentive-based demand response model. Energy 2020, 205, 118019. [Google Scholar] [CrossRef]
- Munir, M.S.; Abedin, S.F.; Tran, N.H.; Han, Z.; Huh, E.N.; Hong, C.S. Risk-aware energy scheduling for edge computing with microgrid: A multi-agent deep reinforcement learning approach. IEEE Trans. Netw. Serv. Manag. 2021, 18, 3476–3497. [Google Scholar] [CrossRef]
- Hussain, A.; Bui, V.H.; Kim, H.M. Deep reinforcement learning-based operation of fast charging stations coupled with energy storage system. Electr. Power Syst. Res. 2022, 210, 108087. [Google Scholar] [CrossRef]
- Colla, V.; Matino, I.; Dettori, S.; Cateni, S.; Matino, R. Reservoir computing approaches applied to energy management in industry. In Proceedings of the International Conference on Engineering Applications of Neural Networks, Xersonisos, Greece, 24–26 May 2019; Springer: Berlin/Heidelberg, Germany, 2019; pp. 66–79. [Google Scholar]
- Orang, O.; Silva, P.C.d.L.; Guimarães, F.G. Introducing Randomized High Order Fuzzy Cognitive Maps as Reservoir Computing Models: A Case Study in Solar Energy and Load Forecasting. arXiv 2022, arXiv:2201.02158. [Google Scholar]
- Song, Y.D.; Li, P.; Liu, W.; Qin, M. An overview of renewable wind energy conversion system modeling and control. Meas. Control. 2010, 43, 203–208. [Google Scholar] [CrossRef] [Green Version]
- Pulgar-Painemal, H.A.; Sauer, P.W. Dynamic modeling of wind power generation. In Proceedings of the 41st North American Power Symposium, IEEE, Starkville, MI, USA, 4–6 October 2009; pp. 1–6. [Google Scholar]
- Akhmatov, V. Analysis of Dynamic Behavior of Electric Power Systems with Large Amount of Wind Power. Ph.D. Thesis, Technical University of Denmark, Kgs. Lyngby, Denmark, 2003. [Google Scholar]
- Muljadi, E.; Zhang, Y.C.; Gevorgian, V.; Kosterev, D. Understanding dynamic model validation of a wind turbine generator and a wind power plant. In Proceedings of the 2016 IEEE Energy Conversion Congress and Exposition (ECCE), IEEE, Milwaukee, WI, USA, 18–22 September 2016; pp. 1–5. [Google Scholar]
- Guo, Y.; Jiang, J.N.; Tang, C.Y. Nonlinear control of wind power generation systems. In Proceedings of the 2009 IEEE/PES Power Systems Conference and Exposition, IEEE, Seattle, WA, USA, 15–18 March 2009; pp. 1–7. [Google Scholar]
- Li, D.; Chen, C. Wind speed model for dynamic simulation of wind power generation system. Proc. CSEE 2005, 25, 41–44. [Google Scholar]
- Sim, S.K.; Maass, P.; Lind, P.G. Wind Speed Modeling by Nested ARIMA Processes. Energies 2019, 12, 69. [Google Scholar] [CrossRef] [Green Version]
- Møller, J.K.; Zugno, M.; Madsen, H. Probabilistic forecasts of wind power generation by stochastic differential equation models. J. Forecast. 2016, 35, 189–205. [Google Scholar] [CrossRef] [Green Version]
- Iversen, E.B.; Morales, J.M.; Møller, J.K.; Madsen, H. Short-term probabilistic forecasting of wind speed using stochastic differential equations. Int. J. Forecast. 2016, 32, 981–990. [Google Scholar] [CrossRef]
- Wang, X.; Chiang, H.D.; Wang, J.; Liu, H.; Wang, T. Long-term stability analysis of power systems with wind power based on stochastic differential equations: Model development and foundations. IEEE Trans. Sustain. Energy 2015, 6, 1534–1542. [Google Scholar] [CrossRef] [Green Version]
- Olsson, M.; Perninge, M.; Söder, L. Modeling real-time balancing power demands in wind power systems using stochastic differential equations. Electr. Power Syst. Res. 2010, 80, 966–974. [Google Scholar] [CrossRef]
- Sauhatas, A.; Bezrukovs, D. The application of stochastic differential equation models in the assessment of the economic feasibility of wind energy projects in Latvia. In Proceedings of the 2016 57th International Scientific Conference on Power and Electrical Engineering of Riga Technical University (RTUCON). IEEE, Riga, Latvia, 13–14 October 2016; pp. 1–6. [Google Scholar]
- Zárate-Miñano, R.; Anghel, M.; Milano, F. Continuous wind speed models based on stochastic differential equations. Appl. Energy 2013, 104, 42–49. [Google Scholar] [CrossRef]
- Verdejo, H.; Awerkin, A.; Kliemann, W.; Becker, C. Modelling uncertainties in electrical power systems with stochastic differential equations. Int. J. Electr. Power Energy Syst. 2019, 113, 322–332. [Google Scholar] [CrossRef]
- Su, H.; Wang, D.; Duan, X. Condition Maintenance Decision of Wind Turbine Gearbox Based on Stochastic Differential Equation. Energies 2020, 13, 4480. [Google Scholar] [CrossRef]
- Loukatou, A.; Howell, S.; Johnson, P.; Duck, P. Stochastic wind speed modelling for estimation of expected wind power output. Appl. Energy 2018, 228, 1328–1340. [Google Scholar] [CrossRef]
- Jiang, C.; Zhao, W.; Liu, J.; Liang, W.; Masoud, B.; Lu, X.; Luo, T.; Meng, T. A new numerical simulation for stochastic transient stability analysis of power systems integrated wind power. In Proceedings of the 2014 International Conference on Power System Technology, IEEE, Chengdu, China, 20–22 October 2014; pp. 2788–2793. [Google Scholar]
- Friedrich, R.; Peinke, J. Description of a turbulent cascade by a Fokker-Planck equation. Phys. Rev. Lett. 1997, 78, 863–866. [Google Scholar] [CrossRef]
- Siegert, S.; Friedrich, R.; Peinke, J. Analysis of data sets of stochastic systems. Phys. Lett. A 1998, 243, 275–280. [Google Scholar] [CrossRef] [Green Version]
- Friedrich, R.; Peinke, J.; Sahimi, M.; Tabar, M. Approaching complexity by stochastic methods: From biological systems to turbulence. Phys. Rep. 2011, 506, 87–162. [Google Scholar] [CrossRef]
- Wächter, M.; Milan, P.; Mücke, T.; Peinke, J. Power performance of wind energy converters characterized as stochastic process: Applications of the Langevin power curve. Wind Energy 2011, 14, 711–717. [Google Scholar] [CrossRef]
- Milan, P.; Wächter, M.; Peinke, J. Turbulent character of wind energy. Phys. Rev. Lett. 2013, 110, 138701. [Google Scholar] [CrossRef] [Green Version]
- Anvari, M.; Lohmann, G.; Wächter, M.; Milan, P.; Lorenz, E.; Heinemann, D.; Kleinhans, D.; Rahimi Tabar, M.R. Short-term fluctuations of wind and solar power systems. New J. Phys. 2016, 18, 063027. [Google Scholar] [CrossRef]
- Raischel, F.; Scholz, T.; Lopes, V.V.; Lind, P.G. Uncovering wind turbine properties through two-dimensional stochastic modeling of wind dynamics. Phys. Rev. E 2013, 88, 042146. [Google Scholar] [CrossRef] [Green Version]
- Lind, P.G.; Wächter, M.; Peinke, J. Reconstructing the intermittent dynamics of the torque in wind turbines. J. Physics Conf. Ser. 2014, 524, 012179. [Google Scholar] [CrossRef]
- Lind, P.G.; Herráez, I.; Wächter, M.; Peinke, J. Fatigue Loads Estimation Through a Simple Stochastic Model. Energies 2014, 7, 8279–8293. [Google Scholar] [CrossRef] [Green Version]
- Lind, P.G.; Vera-Tudela, L.; Wächter, M.; Kühn, M.; Peinke, J. Normal Behaviour Models for Wind Turbine Vibrations: Comparison of Neural Networks and a Stochastic Approach. Energies 2017, 10, 1944. [Google Scholar] [CrossRef] [Green Version]
- Boettcher, F.; Peinke, J.; Kleinhans, D.; Friedrich, R.; Lind, P.G.; Haase, M. Reconstruction of complex dynamical systems affected by strong measurement noise. Phys. Rev. Lett. 2006, 97, 090603. [Google Scholar] [CrossRef] [Green Version]
- Lind, P.G.; Haase, M.; Boettcher, F.; Peinke, J.; Kleinhans, D.; Friedrich, R. Extracting strong measurement noise from stochastic time series: Applications to empirical data. Phys. Rev. E 2010, 81, 041125. [Google Scholar] [CrossRef] [Green Version]
- Lehle, B. Stochastic Time Series with Strong, Correlated Measurement Noise: Markov Analysis in N Dimensions. J. Stat. Phys. 2013, 152, 1145–1169. [Google Scholar] [CrossRef]
- Lehle, B. Analysis of stochastic time series in the presence of strong measurement noise. Phys. Rev. E 2011, 83, 021113. [Google Scholar] [CrossRef] [Green Version]
- Scholz, T.; Raischel, F.; Lopes, V.V.; Lehle, B.; Wächter, M.; Peinke, J.; Lind, P.G. Parameter-free resolution of the superposition of stochastic signals. Phys. Lett. A 2017, 381, 194–206. [Google Scholar] [CrossRef] [Green Version]
- Rinn, P.; Lind, P.G.; Wächter, M.; Peinke, J. The Langevin Approach: An R Package for Modeling Markov Processes. J. Open Res. Softw. 2016, 4, e34. [Google Scholar] [CrossRef]
- Rydin Gorjão, L.; Witthaut, D.; Lind, P.G. jumpdiff: A Python Library for Statistical Inference of Jump-Diffusion Processes in Observational or Experimental Data Sets. J. Stat. Softw. 2023, 105, 1–22. [Google Scholar] [CrossRef]
- Fuchs, A.; Kharche, S.; Patil, A.; Friedrich, J.; Wächter, M.; Peinke, J. An open source package to perform basic and advanced statistical analysis of turbulence data and other complex systems. Phys. Fluids 2022, 34, 101801. [Google Scholar] [CrossRef]
- Tabar, M.R.R. Analysis and Data-Based Reconstruction of Complex Nonlinear Dynamical Systems; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Chen, P.; Berthelsen, K.K.; Bak-Jensen, B.; Chen, Z. Markov model of wind power time series using Bayesian inference of transition matrix. In Proceedings of the 2009 35th Annual Conference of IEEE Industrial Electronics, IEEE, Porto, Portugal, 3–5 November 2009; pp. 627–632. [Google Scholar]
- Xie, W.; Zhang, P.; Chen, R.; Zhou, Z. A nonparametric Bayesian framework for short-term wind power probabilistic forecast. IEEE Trans. Power Syst. 2018, 34, 371–379. [Google Scholar] [CrossRef]
- Haslett, J.; Raftery, A.E. Space-time modelling with long-memory dependence: Assessing Ireland’s wind power resource. J. R. Stat. Soc. Ser. C (Appl. Stat.) 1989, 38, 1–21. [Google Scholar] [CrossRef]
- Chiodo, E.; Lauria, D. Bayes prediction of wind gusts for wind power plants reliability estimation. In Proceedings of the 2011 International Conference on Clean Electrical Power (ICCEP), IEEE, Ischia, Italy, 14–16 June 2011; pp. 498–506. [Google Scholar]
- Ning, C.; You, F. Data-driven adaptive robust unit commitment under wind power uncertainty: A Bayesian nonparametric approach. IEEE Trans. Power Syst. 2019, 34, 2409–2418. [Google Scholar] [CrossRef]
- Pesch, T.; Schröders, S.; Allelein, H.J.; Hake, J.F. A new Markov-chain-related statistical approach for modelling synthetic wind power time series. New J. Phys. 2015, 17, 055001. [Google Scholar] [CrossRef] [Green Version]
- Mbuvha, R. Bayesian neural networks for short term wind power forecasting. Master’s Thesis, KTH Royal Institute of Technology, Stockholm, Sweden, 2017. [Google Scholar]
- Demolli, H.; Dokuz, A.S.; Ecemis, A.; Gokcek, M. Wind power forecasting based on daily wind speed data using machine learning algorithms. Energy Convers. Manag. 2019, 198, 111823. [Google Scholar] [CrossRef]
- Heinermann, J.; Kramer, O. Machine learning ensembles for wind power prediction. Renew. Energy 2016, 89, 671–679. [Google Scholar] [CrossRef]
- Treiber, N.A.; Heinermann, J.; Kramer, O. Wind power prediction with machine learning. In Computational Sustainability; Springer: Berlin/Heidelberg, Germany, 2016; pp. 13–29. [Google Scholar]
- Sasser, C.; Yu, M.; Delgado, R. Improvement of wind power prediction from meteorological characterization with machine learning models. Renew. Energy 2022, 183, 491–501. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, H. An empirical study on machine learning models for wind power predictions. In Proceedings of the 2016 15th IEEE International Conference on Machine Learning and Applications (ICMLA), IEEE, Anaheim, CA, USA, 18–20 December 2016; pp. 758–763. [Google Scholar]
- Zhang, Y.; Liu, K.; Qin, L.; An, X. Deterministic and probabilistic interval prediction for short-term wind power generation based on variational mode decomposition and machine learning methods. Energy Convers. Manag. 2016, 112, 208–219. [Google Scholar] [CrossRef]
- Zameer, A.; Khan, A.; Javed, S.G. Machine Learning based short term wind power prediction using a hybrid learning model. Comput. Electr. Eng. 2015, 45, 122–133. [Google Scholar]
- Dong, W.; Yang, Q.; Fang, X. Multi-step ahead wind power generation prediction based on hybrid machine learning techniques. Energies 2018, 11, 1975. [Google Scholar] [CrossRef] [Green Version]
- Ahmad, T.; Zhang, D.; Huang, C. Methodological framework for short-and medium-term energy, solar and wind power forecasting with stochastic-based machine learning approach to monetary and energy policy applications. Energy 2021, 231, 120911. [Google Scholar] [CrossRef]
- Chaudhary, A.; Sharma, A.; Kumar, A.; Dikshit, K.; Kumar, N. Short term wind power forecasting using machine learning techniques. J. Stat. Manag. Syst. 2020, 23, 145–156. [Google Scholar] [CrossRef]
- Singh, U.; Rizwan, M.; Alaraj, M.; Alsaidan, I. A Machine Learning-Based Gradient Boosting Regression Approach for Wind Power Production Forecasting: A Step towards Smart Grid Environments. Energies 2021, 14, 5196. [Google Scholar] [CrossRef]
- Mishra, S.; Bordin, C.; Taharaguchi, K.; Palu, I. Comparison of deep learning models for multivariate prediction of time series wind power generation and temperature. Energy Rep. 2020, 6, 273–286. [Google Scholar] [CrossRef]
- Lin, Z.; Liu, X. Wind power forecasting of an offshore wind turbine based on high-frequency SCADA data and deep learning neural network. Energy 2020, 201, 117693. [Google Scholar] [CrossRef]
- Li, C.; Tang, G.; Xue, X.; Chen, X.; Wang, R.; Zhang, C. The short-term interval prediction of wind power using the deep learning model with gradient descend optimization. Renew. Energy 2020, 155, 197–211. [Google Scholar] [CrossRef]
- Tao, Y.; Chen, H.; Qiu, C. Wind power prediction and pattern feature based on deep learning method. In Proceedings of the 2014 IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC), IEEE, Hong Kong, China, 7–10 December 2014; pp. 1–4. [Google Scholar]
- Hossain, M.A.; Chakrabortty, R.K.; Elsawah, S.; Gray, E.M.; Ryan, M.J. Predicting wind power generation using hybrid deep learning with optimization. IEEE Trans. Appl. Supercond. 2021, 31, 1–5. [Google Scholar] [CrossRef]
- Meka, R.; Alaeddini, A.; Bhaganagar, K. A robust deep learning framework for short-term wind power forecast of a full-scale wind farm using atmospheric variables. Energy 2021, 221, 119759. [Google Scholar] [CrossRef]
- Xiaoyun, Q.; Xiaoning, K.; Chao, Z.; Shuai, J.; Xiuda, M. Short-term prediction of wind power based on deep long short-term memory. In Proceedings of the 2016 IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC), IEEE, Xi’an, China, 25–28 October 2016; pp. 1148–1152. [Google Scholar]
- Wang, Y.; Zou, R.; Liu, F.; Zhang, L.; Liu, Q. A review of wind speed and wind power forecasting with deep neural networks. Appl. Energy 2021, 304, 117766. [Google Scholar] [CrossRef]
- Deng, X.; Shao, H.; Hu, C.; Jiang, D.; Jiang, Y. Wind power forecasting methods based on deep learning: A survey. Comput. Model. Eng. Sci. 2020, 122, 273. [Google Scholar] [CrossRef]
- Mujeeb, S.; Alghamdi, T.A.; Ullah, S.; Fatima, A.; Javaid, N.; Saba, T. Exploiting deep learning for wind power forecasting based on big data analytics. Appl. Sci. 2019, 9, 4417. [Google Scholar] [CrossRef] [Green Version]
- Zhang, D.; Zhang, H.; Zhang, X.; Li, X.; Ren, K.; Zhang, Y.; Guo, Y. Research on AGC performance during wind power ramping based on deep reinforcement learning. IEEE Access 2020, 8, 107409–107418. [Google Scholar] [CrossRef]
- Zhang, H.; Yue, D.; Dou, C.; Li, K.; Hancke, G.P. Two-Step Wind Power Prediction Approach with Improved Complementary Ensemble Empirical Mode Decomposition and Reinforcement Learning. IEEE Syst. J. 2021. [Google Scholar] [CrossRef]
- Yin, S.; Liu, H. Wind power prediction based on outlier correction, ensemble reinforcement learning, and residual correction. Energy 2022, 250, 123857. [Google Scholar] [CrossRef]
- Dong, H.; Xie, J.; Zhao, X. Wind farm control technologies: From classical control to reinforcement learning. Prog. Energy 2022, 4, 032006. [Google Scholar] [CrossRef]
- Malik, H.; Yadav, A.K. A novel hybrid approach based on relief algorithm and fuzzy reinforcement learning approach for predicting wind speed. Sustain. Energy Technol. Assessments 2021, 43, 100920. [Google Scholar] [CrossRef]
- Wei, X.; Xiang, Y.; Li, J.; Zhang, X. Self-Dispatch of Wind-Storage Integrated System: A Deep Reinforcement Learning Approach. IEEE Trans. Sustain. Energy 2022, 13, 1861–1864. [Google Scholar] [CrossRef]
- Zhong, S.; Wang, X.; Zhao, J.; Li, W.; Li, H.; Wang, Y.; Deng, S.; Zhu, J. Deep reinforcement learning framework for dynamic pricing demand response of regenerative electric heating. Appl. Energy 2021, 288, 116623. [Google Scholar] [CrossRef]
- Li, G.; Shi, J. Agent-based modeling for trading wind power with uncertainty in the day-ahead wholesale electricity markets of single-sided auctions. Appl. Energy 2012, 99, 13–22. [Google Scholar] [CrossRef]
- Sanayha, M.; Vateekul, P. Model-based deep reinforcement learning for wind energy bidding. Int. J. Electr. Power Energy Syst. 2022, 136, 107625. [Google Scholar] [CrossRef]
- Dorado-Moreno, M.; Cornejo-Bueno, L.; Gutiérrez, P.; Prieto, L.; Hervás-Martínez, C.; Salcedo-Sanz, S. Robust estimation of wind power ramp events with reservoir computing. Renew. Energy 2017, 111, 428–437. [Google Scholar] [CrossRef]
- Dorado-Moreno, M.; Cornejo-Bueno, L.; Gutiérrez, P.A.; Prieto, L.; Salcedo-Sanz, S.; Hervás-Martínez, C. Combining reservoir computing and over-sampling for ordinal wind power ramp prediction. In Proceedings of the International Work-Conference on Artificial Neural Networks, Cadiz, Spain, 14–16 June 2017; Springer: Berlin/Heidelberg, Germany, 2017; pp. 708–719. [Google Scholar]
- Dorado-Moreno, M.; Durán-Rosal, A.M.; Guijo-Rubio, D.; Gutiérrez, P.A.; Prieto, L.; Salcedo-Sanz, S.; Hervás-Martínez, C. Multiclass prediction of wind power ramp events combining reservoir computing and support vector machines. In Proceedings of the Conference of the Spanish Association for Artificial Intelligence, Salamanca, Spain, 14–16 September 2016; Springer: Berlin/Heidelberg, Germany, 2016; pp. 300–309. [Google Scholar]
- Dorado-Moreno, M.; Gutiérrez, P.A.; Cornejo-Bueno, L.; Prieto, L.; Salcedo-Sanz, S.; Hervás-Martínez, C. Ordinal multi-class architecture for predicting wind power ramp events based on reservoir computing. Neural Process. Lett. 2020, 52, 57–74. [Google Scholar] [CrossRef]
- Dorado-Moreno, M.; Navarin, N.; Gutiérrez, P.A.; Prieto, L.; Sperduti, A.; Salcedo-Sanz, S.; Hervás-Martínez, C. Multi-task learning for the prediction of wind power ramp events with deep neural networks. Neural Netw. 2020, 123, 401–411. [Google Scholar] [CrossRef]
- Wang, J.; Niu, T.; Lu, H.; Yang, W.; Du, P. A novel framework of reservoir computing for deterministic and probabilistic wind power forecasting. IEEE Trans. Sustain. Energy 2019, 11, 337–349. [Google Scholar] [CrossRef]
- Hu, J.; Lin, Y.; Tang, J.; Zhao, J. A new wind power interval prediction approach based on reservoir computing and a quality-driven loss function. Appl. Soft Comput. 2020, 92, 106327. [Google Scholar] [CrossRef]
- Mammedov, Y.D.; Olugu, E.U.; Farah, G.A. Weather forecasting based on data-driven and physics-informed reservoir computing models. Environ. Sci. Pollut. Res. 2022, 29, 24131–24144. [Google Scholar] [CrossRef]
- Ferreira, A.A.; Ludermir, T.B.; De Aquino, R.R. An approach to reservoir computing design and training. Expert Syst. Appl. 2013, 40, 4172–4182. [Google Scholar] [CrossRef]
- Hamedani, K.; Liu, L.; Atat, R.; Wu, J.; Yi, Y. Reservoir computing meets smart grids: Attack detection using delayed feedback networks. IEEE Trans. Ind. Informatics 2017, 14, 734–743. [Google Scholar] [CrossRef]
- Chaabene, M.; Annabi, M. A dynamic model for predicting solar plant performance and optimum control. Energy 1997, 22, 567–578. [Google Scholar] [CrossRef]
- Huang, J.; Korolkiewicz, M.; Agrawal, M.; Boland, J. Forecasting solar radiation on an hourly time scale using a Coupled AutoRegressive and Dynamical System (CARDS) model. Sol. Energy 2013, 87, 136–149. [Google Scholar] [CrossRef]
- Antonelli, M.; Baccioli, A.; Francesconi, M.; Desideri, U. Dynamic modelling of a low-concentration solar power plant: A control strategy to improve flexibility. Renew. Energy 2016, 95, 574–585. [Google Scholar] [CrossRef]
- Andrade, G.; Pagano, D.; Alvarez, J.D.; Berenguel, M. A practical NMPC with robustness of stability applied to distributed solar power plants. Sol. Energy 2013, 92, 106–122. [Google Scholar] [CrossRef]
- Manenti, F.; Ravaghi-Ardebili, Z. Dynamic simulation of concentrating solar power plant and two-tanks direct thermal energy storage. Energy 2013, 55, 89–97. [Google Scholar] [CrossRef]
- Gil, P.; Henriques, J.; Carvalho, P.; Duarte-Ramos, H.; Dourado, A. Adaptive neural model-based predictive control of a solar power plant. In Proceedings of the 2002 International Joint Conference on Neural Networks, IJCNN’02 (Cat. No. 02CH37290), IEEE, Honolulu, HI, USA, 12–17 May 2002; Volume 3, pp. 2098–2103. [Google Scholar]
- Bessa, R.J.; Trindade, A.; Miranda, V. Spatial-temporal solar power forecasting for smart grids. IEEE Trans. Ind. Inform. 2014, 11, 232–241. [Google Scholar] [CrossRef]
- Ahmed Mohammed, A.; Aung, Z. Ensemble learning approach for probabilistic forecasting of solar power generation. Energies 2016, 9, 1017. [Google Scholar] [CrossRef]
- Ghiassi-Farrokhfal, Y.; Keshav, S.; Rosenberg, C.; Ciucu, F. Solar power shaping: An analytical approach. IEEE Trans. Sustain. Energy 2014, 6, 162–170. [Google Scholar] [CrossRef] [Green Version]
- Chong, D.; Leung, J.; Bertes, T.; Mardira, L. Validation of Solar Power Plant Dynamic Model Using Commissioning Test Measurements. DIgSILENT Pacific. 2019. Available online: https://digsilent.com.au/en/publications.html?file=files/publications/2019/papers/SIW19-181_paper_Chong.pdf&cid=13832 (accessed on 5 July 2023).
- Panamtash, H.; Zhou, Q.; Hong, T.; Qu, Z.; Davis, K.O. A copula-based Bayesian method for probabilistic solar power forecasting. Sol. Energy 2020, 196, 336–345. [Google Scholar] [CrossRef]
- Doubleday, K.; Jascourt, S.; Kleiber, W.; Hodge, B.M. Probabilistic solar power forecasting using bayesian model averaging. IEEE Trans. Sustain. Energy 2020, 12, 325–337. [Google Scholar] [CrossRef]
- Shedbalkar, K.H.; More, D. Bayesian Regression for Solar Power Forecasting. In Proceedings of the 2022 2nd International Conference on Artificial Intelligence and Signal Processing (AISP), IEEE, Vijayawada, India, 12–14 February 2022; pp. 1–4. [Google Scholar]
- Zhang, X.; Fang, F.; Wang, J. Probabilistic solar irradiation forecasting based on variational Bayesian inference with secure federated learning. IEEE Trans. Ind. Inform. 2020, 17, 7849–7859. [Google Scholar] [CrossRef]
- Buwei, W.; Jianfeng, C.; Bo, W.; Shuanglei, F. A solar power prediction using support vector machines based on multi-source data fusion. In Proceedings of the 2018 International Conference on Power System Technology (POWERCON), IEEE, Guangzhou, China, 6–8 November 2018; pp. 4573–4577. [Google Scholar]
- Sheng, H.; Xiao, J.; Cheng, Y.; Ni, Q.; Wang, S. Short-term solar power forecasting based on weighted Gaussian process regression. IEEE Trans. Ind. Electron. 2017, 65, 300–308. [Google Scholar] [CrossRef]
- Oluwafemi, O.; Olusola, O.S.; Israel, E.; Babatunde, A. Autoregressive neural network models for solar power forecasting over nigeria. J. Sol. Energy Res. 2022, 7, 983–996. [Google Scholar]
- Gondalia, A.; Shah, C. Solar power forecasting analysis of trends in modeling techniques and error minimization mechanism. In Proceedings of the 2017 2nd IEEE International Conference on Recent Trends in Electronics, Information & Communication Technology (RTEICT), IEEE, Bangalore, India, 19–20 May 2017; pp. 1860–1866. [Google Scholar]
- Iversen, E.B.; Morales, J.M.; Møller, J.K.; Madsen, H. Probabilistic forecasts of solar irradiance using stochastic differential equations. Environmetrics 2014, 25, 152–164. [Google Scholar] [CrossRef] [Green Version]
- Badosa, J.; Gobet, E.; Grangereau, M.; Kim, D. Day-ahead probabilistic forecast of solar irradiance: A Stochastic Differential Equation approach. In Proceedings of the Forecasting and Risk Management for Renewable Energy, Paris, France, 7–9 June 2017; Springer: Berlin/Heidelberg, Germany, 2017; pp. 73–93. [Google Scholar]
- Iversen, E.B.; Morales, J.M.; Møller, J.K.; Trombe, P.J.; Madsen, H. Leveraging stochastic differential equations for probabilistic forecasting of wind power using a dynamic power curve. Wind Energy 2017, 20, 33–44. [Google Scholar] [CrossRef]
- Li, W.; Paraschiv, F. Modelling the evolution of wind and solar power in feed forecasts. J. Commod. Mark. 2022, 25, 100189. [Google Scholar] [CrossRef]
- Zhang, Y.; Kong, L. Photovoltaic power prediction based on hybrid modeling of neural network and stochastic differential equation. ISA Trans. 2021, 128, 181–206. [Google Scholar] [CrossRef]
- Qiu, Y.; Lin, J.; Liu, F.; Song, Y.; Chen, G.; Ding, L. Stochastic online generation control of cascaded run-of-the-river hydropower for mitigating solar power volatility. IEEE Trans. Power Syst. 2020, 35, 4709–4722. [Google Scholar] [CrossRef]
- Zhang, H.; Baeyens, J.; Degrève, J.; Cacères, G. Concentrated solar power plants: Review and design methodology. Renew. Sustain. Energy Rev. 2013, 22, 466–481. [Google Scholar] [CrossRef]
- Munawar, U.; Wang, Z. A framework of using machine learning approaches for short-term solar power forecasting. J. Electr. Eng. Technol. 2020, 15, 561–569. [Google Scholar] [CrossRef]
- Amarasinghe, P.; Abeygunawardane, S. Application of machine learning algorithms for solar power forecasting in Sri Lanka. In Proceedings of the 2018 2nd International Conference On Electrical Engineering (EECon), IEEE, Hambantota, Sri Lanka, 28 September 2018; pp. 87–92. [Google Scholar]
- Wang, H.; Liu, Y.; Zhou, B.; Li, C.; Cao, G.; Voropai, N.; Barakhtenko, E. Taxonomy research of artificial intelligence for deterministic solar power forecasting. Energy Convers. Manag. 2020, 214, 112909. [Google Scholar] [CrossRef]
- Hassan, M.Z.; Ali, M.E.K.; Ali, A.S.; Kumar, J. Forecasting day-ahead solar radiation using machine learning approach. In Proceedings of the 2017 4th Asia-Pacific World Congress on Computer Science and Engineering (APWC on CSE), IEEE, Mana Island, Fiji, 11–13 December 2017; pp. 252–258. [Google Scholar]
- Jawaid, F.; NazirJunejo, K. Predicting daily mean solar power using machine learning regression techniques. In Proceedings of the 2016 Sixth International Conference on Innovative Computing Technology (INTECH), IEEE, Coimbatore, India, 2–4 December 2016; pp. 355–360. [Google Scholar]
- Hossain, M.R.; Oo, A.M.T.; Ali, A. The combined effect of applying feature selection and parameter optimization on machine learning techniques for solar Power prediction. Am. J. Energy Res. 2013, 1, 7–16. [Google Scholar] [CrossRef] [Green Version]
- Ramadhan, R.A.; Heatubun, Y.R.; Tan, S.F.; Lee, H.J. Comparison of physical and machine learning models for estimating solar irradiance and photovoltaic power. Renew. Energy 2021, 178, 1006–1019. [Google Scholar] [CrossRef]
- Guher, A.B.; Tasdemir, S. Determining of solar power by using machine learning methods in a specified region. Teh. Vjesn. 2021, 28, 1471–1479. [Google Scholar]
- Ibrahim, M.; Alsheikh, A.; Awaysheh, F.M.; Alshehri, M.D. Machine Learning Schemes for Anomaly Detection in Solar Power Plants. Energies 2022, 15, 1082. [Google Scholar] [CrossRef]
- Voyant, C.; Notton, G.; Kalogirou, S.; Nivet, M.L.; Paoli, C.; Motte, F.; Fouilloy, A. Machine learning methods for solar radiation forecasting: A review. Renew. Energy 2017, 105, 569–582. [Google Scholar] [CrossRef]
- Torres, J.F.; Troncoso, A.; Koprinska, I.; Wang, Z.; Martínez-Álvarez, F. Big data solar power forecasting based on deep learning and multiple data sources. Expert Syst. 2019, 36, e12394. [Google Scholar] [CrossRef]
- AlKandari, M.; Ahmad, I. Solar power generation forecasting using ensemble approach based on deep learning and statistical methods. Appl. Comput. Inform. 2020. [Google Scholar] [CrossRef]
- Elsaraiti, M.; Merabet, A. Solar power forecasting using deep learning techniques. IEEE Access 2022, 10, 31692–31698. [Google Scholar] [CrossRef]
- Gensler, A.; Henze, J.; Sick, B.; Raabe, N. Deep Learning for solar power forecasting—An approach using Auto-Encoder and LSTM Neural Networks. In Proceedings of the 2016 IEEE international conference on systems, man, and cybernetics (SMC), IEEE, Budapest, Hungary, 9–12 October 2016; pp. 2858–2865. [Google Scholar]
- Wang, J.; Guo, L.; Zhang, C.; Song, L.; Duan, J.; Duan, L. Thermal power forecasting of solar power tower system by combining mechanism modeling and deep learning method. Energy 2020, 208, 118403. [Google Scholar] [CrossRef]
- Sun, Y.; Venugopal, V.; Brandt, A.R. Short-term solar power forecast with deep learning: Exploring optimal input and output configuration. Sol. Energy 2019, 188, 730–741. [Google Scholar] [CrossRef]
- Du Plessis, A.; Strauss, J.; Rix, A. Short-term solar power forecasting: Investigating the ability of deep learning models to capture low-level utility-scale Photovoltaic system behaviour. Appl. Energy 2021, 285, 116395. [Google Scholar] [CrossRef]
- Wen, L.; Zhou, K.; Yang, S.; Lu, X. Optimal load dispatch of community microgrid with deep learning based solar power and load forecasting. Energy 2019, 171, 1053–1065. [Google Scholar] [CrossRef]
- Chang, R.; Bai, L.; Hsu, C.H. Solar power generation prediction based on deep Learning. Sustain. Energy Technol. Assessments 2021, 47, 101354. [Google Scholar] [CrossRef]
- Torres, J.F.; Troncoso, A.; Koprinska, I.; Wang, Z.; Martínez-Álvarez, F. Deep learning for big data time series forecasting applied to solar power. In Proceedings of the The 13th International Conference on Soft Computing Models in Industrial and Environmental Applications, San Sebastian, Spain, 6–8 June 2018; Springer: Berlin/Heidelberg, Germany, 2018; pp. 123–133. [Google Scholar]
- Zaouali, K.; Rekik, R.; Bouallegue, R. Deep learning forecasting based on auto-lstm model for home solar power systems. In Proceedings of the 2018 IEEE 20th International Conference on High Performance Computing and Communications; IEEE 16th International Conference on Smart City; IEEE 4th International Conference on Data Science and Systems (hpcc/smartcity/dss), IEEE, Exeter, UK, 28–30 June 2018; pp. 235–242. [Google Scholar] [CrossRef]
- Poudel, P.; Jang, B. Solar power prediction using deep learning. Adv. Sci. Technol. Lett. 2017, 146, 148–151. [Google Scholar]
- Leo, R.; Milton, R.; Sibi, S. Reinforcement learning for optimal energy management of a solar microgrid. In Proceedings of the 2014 IEEE global humanitarian technology conference-south asia satellite (GHTC-SAS), IEEE, Trivandrum, India, 26–27 September 2014; pp. 183–188. [Google Scholar]
- Raju, L.; Sankar, S.; Milton, R. Distributed optimization of solar micro-grid using multi agent reinforcement learning. Procedia Comput. Sci. 2015, 46, 231–239. [Google Scholar] [CrossRef] [Green Version]
- Singh, Y.; Pal, N. Reinforcement learning with fuzzified reward approach for MPPT control of PV systems. Sustain. Energy Technol. Assessments 2021, 48, 101665. [Google Scholar] [CrossRef]
- Heidari, A.; Maréchal, F.; Khovalyg, D. Reinforcement Learning for proactive operation of residential energy systems by learning stochastic occupant behavior and fluctuating solar energy: Balancing comfort, hygiene and energy use. Appl. Energy 2022, 318, 119206. [Google Scholar] [CrossRef]
- Basterrech, S. Geometric particle swarm optimization and reservoir computing for solar power forecasting. In Proceedings of the International Conference on Soft Computing-MENDEL, Brno, Czech Republic, 10–12 July 2016; Springer: Berlin/Heidelberg, Germany, 2016; pp. 88–97. [Google Scholar]
- Macek, K.; Endel, P.; Cauchi, N.; Abate, A. Long-term predictive maintenance: A study of optimal cleaning of biomass boilers. Energy Build. 2017, 150, 111–117. [Google Scholar] [CrossRef]
- Moraes, E.C.; Franchito, S.H.; Brahmananda Rao, V. Effects of biomass burning in Amazonia on climate: A numerical experiment with a statistical-dynamical model. J. Geophys. Res. Atmos. 2004, 109, D05109. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H.; Xu, W.; Lei, Y.; Qiao, Y. Early warning and basin stability in a stochastic vegetation-water dynamical system. Commun. Nonlinear Sci. Numer. Simul. 2019, 77, 258–270. [Google Scholar] [CrossRef]
- Ludovici, G.; Casella, F. Dynamic simulation of a solid biomass power plant, based on EFMGT: Two different approaches. In Proceedings of the 2015 5th International Youth Conference on Energy (IYCE), IEEE, Pisa, Italy, 27–30 May 2015; pp. 1–7. [Google Scholar]
- Jadhav, S.P.; Adik, R.; Chile, R.H.; Singhji, S.G.G.; Hamde, S.T. Reduced-parameter fractional-order modeling of large dynamical system: Application to Gas Turbine. In Proceedings of the 2016 International Conference on Automatic Control and Dynamic Optimization Techniques (ICACDOT), IEEE, Pune, India, 9–10 September 2016; pp. 47–51. [Google Scholar]
- Spinti, J.P.; Smith, P.J.; Smith, S.T. Atikokan Digital Twin: Machine learning in a biomass energy system. Appl. Energy 2022, 310, 118436. [Google Scholar] [CrossRef]
- Nicoulaud-Gouin, V.; Gonze, M.A.; Hurtevent, P.; Calmon, P. Bayesian inference of biomass growth characteristics for sugi (C. japonica) and hinoki (C. obtusa) forests in self-thinned and managed stands. For. Ecosyst. 2021, 8, 1–18. [Google Scholar] [CrossRef]
- Hou, D.; Hassan, I.; Wang, L. Review on building energy model calibration by Bayesian inference. Renew. Sustain. Energy Rev. 2021, 143, 110930. [Google Scholar] [CrossRef]
- Xie, L.; Li, F.; Zhang, L.; Widagdo, F.R.A.; Dong, L. A Bayesian Approach to Estimating Seemingly Unrelated Regression for Tree Biomass Model Systems. Forests 2020, 11, 1302. [Google Scholar] [CrossRef]
- Hilborn, R.; Pikitch, E.K.; McAllister, M.K. A Bayesian estimation and decision analysis for an age-structured model using biomass survey data. Fish. Res. 1994, 19, 17–30. [Google Scholar] [CrossRef]
- Khorri, N.A.S.M.; Sulaiman, N.S. Bayesian Network for Probability Risk Analysis of Biomass Boiler in Renewable Energy Plant. In Proceedings of the E3S Web of Conferences, EDP Sciences, Virtual Conference, 13–15 July 2021; Volume 287, p. 03008. [Google Scholar]
- Chiu, M.C.; Kuo, M.H.; Chang, H.Y.; Lin, H.J. Bayesian modeling of the effects of extreme flooding and the grazer community on algal biomass dynamics in a monsoonal Taiwan stream. Microb. Ecol. 2016, 72, 372–380. [Google Scholar] [CrossRef]
- Shabani, N.; Sowlati, T.; Ouhimmou, M.; Rönnqvist, M. Tactical supply chain planning for a forest biomass power plant under supply uncertainty. Energy 2014, 78, 346–355. [Google Scholar] [CrossRef]
- Nyassoke Titi, G.C.; Sadefo Kamdem, J.; Fono, L.A. Optimal Renewable Resource Harvesting model using price and biomass stochastic variations: A Utility Based Approach. Math. Methods Oper. Res. 2022, 95, 297–326. [Google Scholar] [CrossRef]
- Ozbas, E.E.; Aksu, D.; Ongen, A.; Aydin, M.A.; Ozcan, H.K. Hydrogen production via biomass gasification, and modeling by supervised machine learning algorithms. Int. J. Hydrogron Energy 2019, 44, 17260–17268. [Google Scholar] [CrossRef]
- Umenweke, G.; Afolabi, I.C.; Epelle, E.I.; Okolie, J.A. Machine learning methods for modeling conventional and hydrothermal gasification of waste biomass: A review. Bioresour. Technol. Rep. 2022, 17, 100976. [Google Scholar] [CrossRef]
- Dai, Z.; Chen, Z.; Selmi, A.; Jermsittiparsert, K.; Denić, N.M.; Neš ić, Z. Machine learning prediction of higher heating value of biomass. Biomass Convers. Biorefinery 2023, 13, 3659–3667. [Google Scholar] [CrossRef]
- Xing, J.; Luo, K.; Wang, H.; Gao, Z.; Fan, J. A comprehensive study on estimating higher heating value of biomass from proximate and ultimate analysis with machine learning approaches. Energy 2019, 188, 116077. [Google Scholar] [CrossRef]
- Tao, J.; Liang, R.; Li, J.; Yan, B.; Chen, G.; Cheng, Z.; Li, W.; Lin, F.; Hou, L. Fast characterization of biomass and waste by infrared spectra and machine learning models. J. Hazard. Mater. 2020, 387, 121723. [Google Scholar] [CrossRef]
- Han, L.; Yang, G.; Dai, H.; Xu, B.; Yang, H.; Feng, H.; Li, Z.; Yang, X. Modeling maize above-ground biomass based on machine learning approaches using UAV remote-sensing data. Plant Methods 2019, 15, 1–19. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.; Shao, Z.; Liu, J.; Cheng, Q. Deep learning based retrieval of forest above ground biomass from combined LiDAR and landsat 8 data. Remote Sens. 2019, 11, 1459. [Google Scholar] [CrossRef] [Green Version]
- Li, N.; Lu, G.; Li, X.; Yan, Y. Prediction of NOx emissions from a biomass fired combustion process based on flame radical imaging and deep learning techniques. Combust. Sci. Technol. 2016, 188, 233–246. [Google Scholar] [CrossRef]
- Qin, L.; Lu, G.; Hossain, M.M.; Morris, A.; Yan, Y. A flame imaging based online deep learning model for predicting NOx emissions from an oxy-biomass combustion process. IEEE Trans. Instrum. Meas. 2021. [Google Scholar] [CrossRef]
- Kartal, F.; Özveren, U. A deep learning approach for prediction of syngas lower heating value from CFB gasifier in Aspen plus®. Energy 2020, 209, 118457. [Google Scholar] [CrossRef]
- Nam, K.; Hwangbo, S.; Yoo, C. A deep learning-based forecasting model for renewable energy scenarios to guide sustainable energy policy: A case study of Korea. Renew. Sustain. Energy Rev. 2020, 122, 109725. [Google Scholar] [CrossRef]
- Ferrag, M.A.; Maglaras, L. DeepCoin: A novel deep learning and blockchain-based energy exchange framework for smart grids. IEEE Trans. Eng. Manag. 2019, 67, 1285–1297. [Google Scholar] [CrossRef] [Green Version]
- Kozlov, A.N.; Tomin, N.V.; Sidorov, D.N.; Lora, E.E.; Kurbatsky, V.G. Optimal operation control of PV-biomass gasifier-diesel-hybrid systems using reinforcement learning techniques. Energies 2020, 13, 2632. [Google Scholar] [CrossRef]
- Obafemi, O.; Stephen, A.; Ajayi, O.; Nkosinathi, M. A survey of artificial neural network-based prediction models for thermal properties of biomass. Procedia Manuf. 2019, 33, 184–191. [Google Scholar] [CrossRef]
- Wang, M.; Tian, L. Regulating effect of the energy market—Theoretical and empirical analysis based on a novel energy prices–energy supply–economic growth dynamic system. Appl. Energy 2015, 155, 526–546. [Google Scholar] [CrossRef]
- Duan, H.; Liu, Y.; Wang, G. A novel dynamic time-delay grey model of energy prices and its application in crude oil price forecasting. Energy 2022, 251, 123968. [Google Scholar] [CrossRef]
- Cao, Y.; Wang, C.; Mu, Y.; Jia, H.; Yuan, K.; Song, Y. Risk assessment of park-level integrated energy system considering uncertainty and dynamic correlation of energy prices. Energy Rep. 2021, 7, 451–459. [Google Scholar] [CrossRef]
- Zhou, D.P.; Roozbehani, M.; Dahleh, M.A.; Tomlin, C.J. Stability analysis of wholesale electricity markets under dynamic consumption models and real-time pricing. In Proceedings of the 2017 American Control Conference (ACC), IEEE, Seattle, WA, USA, 24–26 May 2017; pp. 2048–2053. [Google Scholar]
- Roozbehani, M.; Dahleh, M.A.; Mitter, S.K. Volatility of power grids under real-time pricing. IEEE Trans. Power Syst. 2012, 27, 1926–1940. [Google Scholar] [CrossRef] [Green Version]
- An, J.; Kumar, P.; Xie, L. Dynamic modeling of price responsive demand in real-time electricity market: Empirical analysis. arXiv 2016, arXiv:1612.05021. [Google Scholar]
- Jäger, S. Nonlinear and Stochastic Dynamical Systems Modeling Price Dynamics. Ph.D. Thesis, Universitäts-und Landesbibliothek, Bonn, Germany, 2008. [Google Scholar]
- Roozbehanit, M.; Rinehart, M.; Dahleh, M.; Mitter, S.; Obradovic, D.; Mangesius, H. Analysis of competitive electricity markets under a new model of real-time retail pricing. In Proceedings of the 2011 8th International Conference on the European Energy Market (EEM), IEEE, Zagreb, Croatia, 25–27 May 2011; pp. 250–255. [Google Scholar]
- Fleschutz, M.; Murphy, M.D. elmada: Dynamic electricity carbon emission factors and prices for Europe. J. Open Source Softw. 2021, 6, 3625. [Google Scholar] [CrossRef]
- Lopes, V.V.; Scholz, T.; Raischel, F.; Lind, P.G. Principal wind turbines for a conditional portfolio approach to wind farms. J. Phys. Conf. Ser. 2014, 524, 012183. [Google Scholar] [CrossRef]
- Müller, G.; Seibert, A. Bayesian estimation of stable CARMA spot models for electricity prices. Energy Econ. 2019, 78, 267–277. [Google Scholar] [CrossRef]
- Costa Lewis, N.D. Stochastic differential equations for derivative pricing and energy risk management. In Energy Risk Modeling; Springer: Berlin/Heidelberg, Germany, 2005; pp. 213–226. [Google Scholar]
- de Oliveira, A.M.B.; Mandal, A.; Power, G.J. A primer on the pricing of electric energy options in Brazil via mean-reverting stochastic processes. Energy Rep. 2019, 5, 594–601. [Google Scholar] [CrossRef]
- Jäger, S.; Kostina, E. An Inverse Problem for a Nonlinear Stochastic Differential Equation Modeling Price Dynamics; Interdisciplinary Center for Scientific Computing: Heidelberg, Germany, 2006. [Google Scholar] [CrossRef]
- Calvo-Garrido, M.d.C.; Ehrhardt, M.; Vázquez Cendón, C. Pricing swing options in electricity markets with two stochastic factors using a partial differential equation approach. J. Comput. Financ. Forthcom. 2016. [Google Scholar] [CrossRef]
- D’Ecclesia, R.L. Introduction to price models for energy. In Handbook of Risk Management in Energy Production and Trading; Springer: Berlin/Heidelberg, Germany, 2013; pp. 25–45. [Google Scholar]
- Yin, L.; Qiu, Y. Long-term price guidance mechanism of flexible energy service providers based on stochastic differential methods. Energy 2022, 238, 121818. [Google Scholar] [CrossRef]
- Benth, F.E.; Šaltytė-Benth, J. The normal inverse Gaussian distribution and spot price modelling in energy markets. Int. J. Theor. Appl. Financ. 2004, 7, 177–192. [Google Scholar] [CrossRef]
- Herrera, G.P.; Constantino, M.; Tabak, B.M.; Pistori, H.; Su, J.J.; Naranpanawa, A. Data on forecasting energy prices using machine learning. Data Brief 2019, 25, 104122. [Google Scholar] [CrossRef]
- Sheha, M.; Powell, K. Using real-time electricity prices to leverage electrical energy storage and flexible loads in a smart grid environment utilizing machine learning techniques. Processes 2019, 7, 870. [Google Scholar] [CrossRef] [Green Version]
- Castelli, M.; Groznik, A.; Popovič, A. Forecasting Electricity Prices: A machine learning approach. Algorithms 2020, 13, 119. [Google Scholar] [CrossRef]
- Čeperić, E.; Žiković, S.; Čeperić, V. Short-term forecasting of natural gas prices using machine learning and feature selection algorithms. Energy 2017, 140, 893–900. [Google Scholar] [CrossRef]
- Naumzik, C.; Feuerriegel, S. Forecasting electricity prices with machine learning: Predictor sensitivity. Int. J. Energy Sect. Manag. 2021, 15, 157–172. [Google Scholar] [CrossRef]
- Chou, J.S.; Tran, D.S. Forecasting energy consumption time series using machine learning techniques based on usage patterns of residential householders. Energy 2018, 165, 709–726. [Google Scholar] [CrossRef]
- Spiliotis, E.; Doukas, H.; Assimakopoulos, V.; Petropoulos, F. Forecasting week-ahead hourly electricity prices in Belgium with statistical and machine learning methods. In Mathematical Modelling of Contemporary Electricity Markets; Elsevier: Amstedam, The Netherlands, 2021; pp. 59–74. [Google Scholar]
- Mosavi, A.; Salimi, M.; Faizollahzadeh Ardabili, S.; Rabczuk, T.; Shamshirband, S.; Varkonyi-Koczy, A.R. State of the art of machine learning models in energy systems, a systematic review. Energies 2019, 12, 1301. [Google Scholar] [CrossRef] [Green Version]
- Antonopoulos, I.; Robu, V.; Couraud, B.; Kirli, D.; Norbu, S.; Kiprakis, A.; Flynn, D.; Elizondo-Gonzalez, S.; Wattam, S. Artificial intelligence and machine learning approaches to energy demand-side response: A systematic review. Renew. Sustain. Energy Rev. 2020, 130, 109899. [Google Scholar] [CrossRef]
- Lago, J.; De Ridder, F.; De Schutter, B. Forecasting spot electricity prices: Deep learning approaches and empirical comparison of traditional algorithms. Appl. Energy 2018, 221, 386–405. [Google Scholar] [CrossRef]
- Zhang, R.; Li, G.; Ma, Z. A deep learning based hybrid framework for day-ahead electricity price forecasting. IEEE Access 2020, 8, 143423–143436. [Google Scholar] [CrossRef]
- Li, X.; Shang, W.; Wang, S. Text-based crude oil price forecasting: A deep learning approach. Int. J. Forecast. 2019, 35, 1548–1560. [Google Scholar] [CrossRef]
- Alameer, Z.; Fathalla, A.; Li, K.; Ye, H.; Jianhua, Z. Multistep-ahead forecasting of coal prices using a hybrid deep learning model. Resour. Policy 2020, 65, 101588. [Google Scholar] [CrossRef]
- Zhang, W.; Cheema, F.; Srinivasan, D. Forecasting of electricity prices using deep learning networks. In Proceedings of the 2018 IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC), IEEE, Kota Kinabalu, Malaysia, 7–10 October 2018; pp. 451–456. [Google Scholar]
- Brusaferri, A.; Matteucci, M.; Portolani, P.; Vitali, A. Bayesian deep learning based method for probabilistic forecast of day-ahead electricity prices. Appl. Energy 2019, 250, 1158–1175. [Google Scholar] [CrossRef]
- Mari, C.; Mari, E. Deep learning based regime-switching models of energy commodity prices. Energy Syst. 2022, 1–22. [Google Scholar] [CrossRef]
- Scholz, C.; Lehna, M.; Brauns, K.; Baier, A. Towards the prediction of electricity prices at the intraday market using shallow and deep-learning methods. In Proceedings of the Workshop on Mining Data for Financial Applications, Ghent, Belgium, 18 September 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 101–118. [Google Scholar]
- Xu, H.; Sun, H.; Nikovski, D.; Kitamura, S.; Mori, K.; Hashimoto, H. Deep reinforcement learning for joint bidding and pricing of load serving entity. IEEE Trans. Smart Grid 2019, 10, 6366–6375. [Google Scholar] [CrossRef]
- Nanduri, V.; Das, T.K. A reinforcement learning model to assess market power under auction-based energy pricing. IEEE Trans. Power Syst. 2007, 22, 85–95. [Google Scholar] [CrossRef] [Green Version]
- Kim, B.G.; Zhang, Y.; Van Der Schaar, M.; Lee, J.W. Dynamic pricing and energy consumption scheduling with reinforcement learning. IEEE Trans. Smart Grid 2015, 7, 2187–2198. [Google Scholar] [CrossRef]
- Mocanu, E.; Mocanu, D.C.; Nguyen, P.H.; Liotta, A.; Webber, M.E.; Gibescu, M.; Slootweg, J.G. On-line building energy optimization using deep reinforcement learning. IEEE Trans. Smart Grid 2018, 10, 3698–3708. [Google Scholar] [CrossRef] [Green Version]
- Lu, R.; Hong, S.H.; Zhang, X. A dynamic pricing demand response algorithm for smart grid: Reinforcement learning approach. Appl. Energy 2018, 220, 220–230. [Google Scholar] [CrossRef]
- Jiang, Z.; Risbeck, M.J.; Ramamurti, V.; Murugesan, S.; Amores, J.; Zhang, C.; Lee, Y.M.; Drees, K.H. Building HVAC control with reinforcement learning for reduction of energy cost and demand charge. Energy Build. 2021, 239, 110833. [Google Scholar] [CrossRef]
- Ding, Z.; Mukherjee, S. At the Intersection of Deep Sequential Model Framework and State-space Model Framework: Study on Option Pricing. arXiv 2020, arXiv:2012.07784. [Google Scholar]
- Ortega, A.; Milano, F. Generalized model of VSC-based energy storage systems for transient stability analysis. IEEE Trans. Power Syst. 2015, 31, 3369–3380. [Google Scholar] [CrossRef] [Green Version]
- Sidorov, D.; Muftahov, I.; Tomin, N.; Karamov, D.; Panasetsky, D.; Dreglea, A.; Liu, F.; Foley, A. A dynamic analysis of energy storage with renewable and diesel generation using Volterra equations. IEEE Trans. Ind. Inform. 2019, 16, 3451–3459. [Google Scholar] [CrossRef] [Green Version]
- Calero, F.; Cañizares, C.A.; Bhattacharya, K. Dynamic modeling of battery energy storage and applications in transmission systems. IEEE Trans. Smart Grid 2020, 12, 589–598. [Google Scholar] [CrossRef]
- Adrees, A.; Andami, H.; Milanović, J.V. Comparison of dynamic models of battery energy storage for frequency regulation in power system. In Proceedings of the 2016 18th Mediterranean Electrotechnical Conference (MELECON), IEEE, Lemesos, Cyprus, 18–20 April 2016; pp. 1–6. [Google Scholar]
- Gallo, D.; Landi, C.; Luiso, M.; Morello, R. Optimization of experimental model parameter identification for energy storage systems. Energies 2013, 6, 4572–4590. [Google Scholar] [CrossRef]
- Berrada, A.; Loudiyi, K.; Garde, R. Dynamic modeling of gravity energy storage coupled with a PV energy plant. Energy 2017, 134, 323–335. [Google Scholar] [CrossRef]
- Raccanello, J.; Rech, S.; Lazzaretto, A. Simplified dynamic modeling of single-tank thermal energy storage systems. Energy 2019, 182, 1154–1172. [Google Scholar] [CrossRef]
- Yu, Q.; Li, X.; Wang, Z.; Zhang, Q. Modeling and dynamic simulation of thermal energy storage system for concentrating solar power plant. Energy 2020, 198, 117183. [Google Scholar] [CrossRef]
- Maton, J.P.; Zhao, L.; Brouwer, J. Dynamic modeling of compressed gas energy storage to complement renewable wind power intermittency. Int. J. Hydrogen Energy 2013, 38, 7867–7880. [Google Scholar] [CrossRef] [Green Version]
- Bird, T.J.; Jain, N. Dynamic modeling and validation of a micro-combined heat and power system with integrated thermal energy storage. Appl. Energy 2020, 271, 114955. [Google Scholar] [CrossRef]
- Chiodo, E.; Di Noia, L.; Rizzo, R. The application of Bayes inference in multicriteria analysis to design energy storage systems in renewable power generation. In Proceedings of the 2013 International Conference on Clean Electrical Power (ICCEP), IEEE, Alghero, Italy, 11–13 June 2013; pp. 728–733. [Google Scholar]
- Jacob, P.E.; Alavi, S.M.M.; Mahdi, A.; Payne, S.J.; Howey, D.A. Bayesian inference in non-Markovian state-space models with applications to battery fractional-order systems. IEEE Trans. Control. Syst. Technol. 2017, 26, 497–506. [Google Scholar] [CrossRef]
- Suharto, Y. Scenario-based assessment of energy storage technologies for wind power generation using Bayesian causal maps. In Proceedings of the 2013 Proceedings of PICMET’13: Technology Management in the IT-Driven Services (PICMET), IEEE, San Jose, CA, USA, 28 July–1 August 2013; pp. 2033–2044. [Google Scholar]
- Khan, K.; Hossen, T.; Savasci, A.; Gauchia, L.; Paudyal, S. Design of a simplified hierarchical Bayesian network for residential energy storage degradation. In Proceedings of the 2019 IEEE Power & Energy Society General Meeting (PESGM), IEEE, Atlanta, GA, USA, 4–8 August 2019; pp. 1–5. [Google Scholar]
- Ortega, A.; Milano, F. Modeling, simulation, and comparison of control techniques for energy storage systems. IEEE Trans. Power Syst. 2016, 32, 2445–2454. [Google Scholar] [CrossRef] [Green Version]
- Barreiro-Gomez, J.; Duncan, T.E.; Tembine, H. Linear-quadratic mean-field-type games-based stochastic model predictive control: A microgrid energy storage application. In Proceedings of the 2019 American Control Conference (ACC), IEEE, Philadelphia, PA, USA, 10–12 July 2019; pp. 3224–3229. [Google Scholar]
- Johnson, P.; Howell, S.; Duck, P. Partial differential equation methods for stochastic dynamic optimization: An application to wind power generation with energy storage. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2017, 375, 20160301. [Google Scholar] [CrossRef] [Green Version]
- Ortega, A.; Milano, F. Stochastic transient stability analysis of transmission systems with inclusion of energy storage devices. IEEE Trans. Power Syst. 2017, 33, 1077–1079. [Google Scholar] [CrossRef] [Green Version]
- Gobet, E.; Grangereau, M. Federated stochastic control of numerous heterogeneous energy storage systems. HAL Open Sci. 2021, 1, 03108611. [Google Scholar]
- Bayram, I.S.; Abdallah, M.; Tajer, A.; Qaraqe, K.A. A stochastic sizing approach for sharing-based energy storage applications. IEEE Trans. Smart Grid 2015, 8, 1075–1084. [Google Scholar] [CrossRef] [Green Version]
- Durante, J.L.; Nascimento, J.; Powell, W.B. Backward approximate dynamic programming with hidden semi-markov stochastic models in energy storage optimization. arXiv 2017, arXiv:1710.03914. [Google Scholar]
- Chaychizadeh, F.; Dehghandorost, H.; Aliabadi, A.; Taklifi, A. Stochastic dynamic simulation of a novel hybrid thermal-compressed carbon dioxide energy storage system (T-CCES) integrated with a wind farm. Energy Convers. Manag. 2018, 166, 500–511. [Google Scholar] [CrossRef]
- Schmietendorf, K.; Kamps, O.; Wolff, M.; Lind, P.G.; Maass, P.; Peinke, J. Bridging between load-flow and Kuramoto-like power grid models: A flexible approach to integrating electrical storage units. Chaos 2019, 29, 103151. [Google Scholar] [CrossRef] [Green Version]
- Rangel-Martinez, D.; Nigam, K.; Ricardez-Sandoval, L.A. Machine learning on sustainable energy: A review and outlook on renewable energy systems, catalysis, smart grid and energy storage. Chem. Eng. Res. Des. 2021, 174, 414–441. [Google Scholar] [CrossRef]
- Chen, A.; Zhang, X.; Zhou, Z. Machine learning: Accelerating materials development for energy storage and conversion. InfoMat 2020, 2, 553–576. [Google Scholar] [CrossRef]
- Gao, T.; Lu, W. Machine learning toward advanced energy storage devices and systems. Iscience 2021, 24, 101936. [Google Scholar] [CrossRef]
- Zitnick, C.L.; Chanussot, L.; Das, A.; Goyal, S.; Heras-Domingo, J.; Ho, C.; Hu, W.; Lavril, T.; Palizhati, A.; Riviere, M.; et al. An introduction to electrocatalyst design using machine learning for renewable energy storage. arXiv 2020, arXiv:2010.09435. [Google Scholar]
- Henri, G.; Lu, N. A supervised machine learning approach to control energy storage devices. IEEE Trans. Smart Grid 2019, 10, 5910–5919. [Google Scholar] [CrossRef]
- Zsembinszki, G.; Fernández, C.; Vérez, D.; Cabeza, L.F. Deep learning optimal control for a complex hybrid energy storage system. Buildings 2021, 11, 194. [Google Scholar] [CrossRef]
- Hafiz, F.; Awal, M.; de Queiroz, A.R.; Husain, I. Real-time stochastic optimization of energy storage management using deep learning-based forecasts for residential PV applications. IEEE Trans. Ind. Appl. 2020, 56, 2216–2226. [Google Scholar] [CrossRef]
- Jang, H.; Lee, T.; Kim, S.M.; Lee, J.; Park, S. Energy storage system management method based on deep learning for energy-efficient smart home. In Proceedings of the 2020 IEEE International Conference on Consumer Electronics (ICCE), IEEE, Las Vegas, NV, USA, 4–6 January 2020; pp. 1–2. [Google Scholar]
- Miao, L.; Zhang, Y.; Tong, C.; Guo, Q.; Zhang, J.; Yildirim, T. Optimized energy-storage method based on deep-learning adaptive-dynamic programming. J. Energy Eng. 2020, 146, 04020011. [Google Scholar] [CrossRef]
- Chuttar, A.; Shettigar, N.; Thyagrajan, A.; Banerjee, D. Deep Learning to Enhance Transient Thermal Performance and Real-Time Control of an Energy Storage (TES) Platform. In Proceedings of the 2021 20th IEEE Intersociety Conference on Thermal and Thermomechanical Phenomena in Electronic Systems (iTherm), IEEE, San Diego, CA, USA, 1–4 June 2021; pp. 1036–1044. [Google Scholar]
- Kim, S.H.; Lee, G.; Shin, Y.J. Economical energy storage systems scheduling based on load forecasting using deep learning. In Proceedings of the 2019 IEEE International Conference on Big Data and Smart Computing (BigComp), IEEE, Kyoto, Japan, 27 February–2 March 2019; pp. 1–7. [Google Scholar]
- Wang, H.; Zhang, B. Energy storage arbitrage in real-time markets via reinforcement learning. In Proceedings of the 2018 IEEE Power & Energy Society General Meeting (PESGM), IEEE, Portland, OR, USA, 5–10 August 2018; pp. 1–5. [Google Scholar]
- Henze, G.P.; Schoenmann, J. Evaluation of reinforcement learning control for thermal energy storage systems. HVAC Res. 2003, 9, 259–275. [Google Scholar] [CrossRef]
- Cao, J.; Harrold, D.; Fan, Z.; Morstyn, T.; Healey, D.; Li, K. Deep reinforcement learning-based energy storage arbitrage with accurate lithium-ion battery degradation model. IEEE Trans. Smart Grid 2020, 11, 4513–4521. [Google Scholar] [CrossRef]
- Oh, E.; Wang, H. Reinforcement-learning-based energy storage system operation strategies to manage wind power forecast uncertainty. IEEE Access 2020, 8, 20965–20976. [Google Scholar] [CrossRef]
- Gorostiza, F.S.; Gonzalez-Longatt, F.M. Deep reinforcement learning-based controller for SOC management of multi-electrical energy storage system. IEEE Trans. Smart Grid 2020, 11, 5039–5050. [Google Scholar] [CrossRef]
- Shang, Y.; Wu, W.; Guo, J.; Ma, Z.; Sheng, W.; Lv, Z.; Fu, C. Stochastic dispatch of energy storage in microgrids: An augmented reinforcement learning approach. Appl. Energy 2020, 261, 114423. [Google Scholar] [CrossRef]
- Sun, J.; Qi, G.; Mazur, N.; Zhu, Z. Structural scheduling of transient control under energy storage systems by sparse-promoting reinforcement learning. IEEE Trans. Ind. Informatics 2021, 18, 744–756. [Google Scholar] [CrossRef]
- Nyong-Bassey, B.E.; Giaouris, D.; Patsios, C.; Papadopoulou, S.; Papadopoulos, A.I.; Walker, S.; Voutetakis, S.; Seferlis, P.; Gadoue, S. Reinforcement learning based adaptive power pinch analysis for energy management of stand-alone hybrid energy storage systems considering uncertainty. Energy 2020, 193, 116622. [Google Scholar] [CrossRef]
- Yang, Z.; Zhu, F.; Lin, F. Deep-reinforcement-learning-based energy management strategy for supercapacitor energy storage systems in urban rail transit. IEEE Trans. Intell. Transp. Syst. 2020, 22, 1150–1160. [Google Scholar] [CrossRef]
- Zhou, K.; Zhou, K.; Yang, S. Reinforcement learning-based scheduling strategy for energy storage in microgrid. J. Energy Storage 2022, 51, 104379. [Google Scholar] [CrossRef]
- Fang, G.; Tian, L.; Fu, M.; Sun, M.; Du, R.; Lu, L.; He, Y. The effect of energy construction adjustment on the dynamical evolution of energy-saving and emission-reduction system in China. Appl. Energy 2017, 196, 180–189. [Google Scholar] [CrossRef]
- Fang, G.; Tian, L.; Sun, M.; Fu, M. Analysis and application of a novel three-dimensional energy-saving and emission-reduction dynamic evolution system. Energy 2012, 40, 291–299. [Google Scholar] [CrossRef]
- Xu, F.; Xiang, N.; Yan, J.; Chen, L.; Nijkamp, P.; Higano, Y. Dynamic simulation of China’s carbon emission reduction potential by 2020. Lett. Spat. Resour. Sci. 2015, 8, 15–27. [Google Scholar] [CrossRef] [Green Version]
- Song, J.; Yang, W.; Higano, Y. Introducing renewable energy and industrial restructuring to reduce GHG emission: Application of a dynamic simulation model. Energy Convers. Manag. 2015, 96, 625–636. [Google Scholar] [CrossRef]
- Zhou, Y.; Ye, X. Differential game model of joint emission reduction strategies and contract design in a dual-channel supply chain. J. Clean. Prod. 2018, 190, 592–607. [Google Scholar] [CrossRef]
- Barros, V.; Grand, M.C. Implications of a dynamic target of greenhouse gases emission reduction: The case of Argentina. Environ. Dev. Econ. 2002, 7, 547–569. [Google Scholar] [CrossRef]
- Wang, H.; Cao, R.; Zeng, W. Multi-agent based and system dynamics models integrated simulation of urban commuting relevant carbon dioxide emission reduction policy in China. J. Clean. Prod. 2020, 272, 122620. [Google Scholar] [CrossRef]
- Nadimi, R.; Tokimatsu, K. Analyzing of renewable and non-renewable energy consumption via bayesian inference. Energy Procedia 2017, 142, 2773–2778. [Google Scholar] [CrossRef]
- Huang, Y.; Wang, H.; Khajepour, A.; He, H.; Ji, J. Model predictive control power management strategies for HEVs: A review. J. Power Sources 2017, 341, 91–106. [Google Scholar] [CrossRef]
- Qader, M.R.; Khan, S.; Kamal, M.; Usman, M.; Haseeb, M. Forecasting carbon emissions due to electricity power generation in Bahrain. Environ. Sci. Pollut. Res. 2022, 29, 17346–17357. [Google Scholar] [CrossRef]
- Brun, C.; Cook, A.R.; Lee, J.S.H.; Wich, S.A.; Koh, L.P.; Carrasco, L.R. Analysis of deforestation and protected area effectiveness in Indonesia: A comparison of Bayesian spatial models. Glob. Environ. Chang. 2015, 31, 285–295. [Google Scholar] [CrossRef]
- Zhang, Y.; Huang, T.; Bompard, E.F. Big data analytics in smart grids: A review. Energy Inform. 2018, 1, 1–24. [Google Scholar] [CrossRef]
- Heo, Y.; Choudhary, R.; Augenbroe, G. Calibration of building energy models for retrofit analysis under uncertainty. Energy Build. 2012, 47, 550–560. [Google Scholar] [CrossRef]
- Cai, W.; Pan, J. Stochastic differential equation models for the price of European CO2 Emissions Allowances. Sustainability 2017, 9, 207. [Google Scholar] [CrossRef] [Green Version]
- Carmona, R.; Delarue, F.; Espinosa, G.E.; Touzi, N. Singular forward–backward stochastic differential equations and emissions derivatives. Ann. Appl. Probab. 2013, 23, 1086–1128. [Google Scholar] [CrossRef]
- Yu, W.; Xin, B. Governance mechanism for global greenhouse gas emissions: A stochastic differential game approach. Math. Probl. Eng. 2013, 2013. [Google Scholar] [CrossRef] [Green Version]
- Tan, P.; Xia, J.; Zhang, C.; Fang, Q.; Chen, G. Modeling and reduction of NOX emissions for a 700 MW coal-fired boiler with the advanced machine learning method. Energy 2016, 94, 672–679. [Google Scholar] [CrossRef]
- Lacoste, A.; Luccioni, A.; Schmidt, V.; Dandres, T. Quantifying the carbon emissions of machine learning. arXiv 2019, arXiv:1910.09700. [Google Scholar]
- Mardani, A.; Liao, H.; Nilashi, M.; Alrasheedi, M.; Cavallaro, F. A multi-stage method to predict carbon dioxide emissions using dimensionality reduction, clustering, and machine learning techniques. J. Clean. Prod. 2020, 275, 122942. [Google Scholar] [CrossRef]
- Leerbeck, K.; Bacher, P.; Junker, R.G.; Goranović, G.; Corradi, O.; Ebrahimy, R.; Tveit, A.; Madsen, H. Short-term forecasting of CO2 emission intensity in power grids by machine learning. Appl. Energy 2020, 277, 115527. [Google Scholar] [CrossRef]
- Pallonetto, F.; De Rosa, M.; Milano, F.; Finn, D.P. Demand response algorithms for smart-grid ready residential buildings using machine learning models. Appl. Energy 2019, 239, 1265–1282. [Google Scholar] [CrossRef]
- Akhshik, M.; Bilton, A.; Tjong, J.; Singh, C.V.; Faruk, O.; Sain, M. Prediction of greenhouse gas emissions reductions via machine learning algorithms: Toward an artificial intelligence-based life cycle assessment for automotive lightweighting. Sustain. Mater. Technol. 2022, 31, e00370. [Google Scholar] [CrossRef]
- Bakay, M.S.; Ağbulut, Ü. Electricity production based forecasting of greenhouse gas emissions in Turkey with deep learning, support vector machine and artificial neural network algorithms. J. Clean. Prod. 2021, 285, 125324. [Google Scholar] [CrossRef]
- Adams, D.; Oh, D.H.; Kim, D.W.; Lee, C.H.; Oh, M. Deep reinforcement learning optimization framework for a power generation plant considering performance and environmental issues. J. Clean. Prod. 2021, 291, 125915. [Google Scholar] [CrossRef]
- Cheng, Y.; Huang, Y.; Pang, B.; Zhang, W. ThermalNet: A deep reinforcement learning-based combustion optimization system for coal-fired boiler. Eng. Appl. Artif. Intell. 2018, 74, 303–311. [Google Scholar] [CrossRef]
- Fu, J.; Xiao, H.; Wang, H.; Zhou, J. Control strategy for denitrification efficiency of coal-fired power plant based on deep reinforcement learning. IEEE Access 2020, 8, 65127–65136. [Google Scholar] [CrossRef]
- Qi, X.; Luo, Y.; Wu, G.; Boriboonsomsin, K.; Barth, M. Deep reinforcement learning enabled self-learning control for energy efficient driving. Transp. Res. Part C Emerg. Technol. 2019, 99, 67–81. [Google Scholar] [CrossRef]
- Zhang, L.; Gao, Y.; Zhu, H.; Tao, L. Bi-level stochastic real-time pricing model in multi-energy generation system: A reinforcement learning approach. Energy 2022, 239, 121926. [Google Scholar] [CrossRef]
- Tanaka, G.; Yamane, T.; H’eroux, J.B.; Nakane, R.; Kanazawa, N.; Takeda, S.; Numata, H.; Nakano, D.; Hirose, A. Recent advances in physical reservoir computing: A review. Neural Netw. 2019, 115, 100–123. [Google Scholar] [CrossRef] [PubMed]
- Iman, M.; Arabnia, H.R.; Rasheed, K. A Review of Deep Transfer Learning and Recent Advancements. Technologies 2023, 11, 40. [Google Scholar] [CrossRef]
- Upreti, R.; Lind, P.G.; Elmokashfi, A.; Yazidi, A. Trustworthy machine learning in the context of security and privacy. 2023, submitted. Preprint provided by authors. 2023; submitted, Preprint provided by authors. [Google Scholar]
- Banabilah, S.; Aloqaily, M.; Alsayed, E.; Malik, N.; Jararweh, Y. Federated learning review: Fundamentals, enabling technologies, and future applications. Inf. Process. Manag. 2022, 59, 103061. [Google Scholar] [CrossRef]
- Lencastre, P.; Gjersdal, M.; Gorjão, L.R.; Yazidi, A.; Lind, P.G.L. Modern AI versus century-old mathematical models: How far can we go with generative adversarial networks to reproduce stochastic processes? Phys. D Nonlinear Phenom. 2023, 133831. [Google Scholar] [CrossRef]
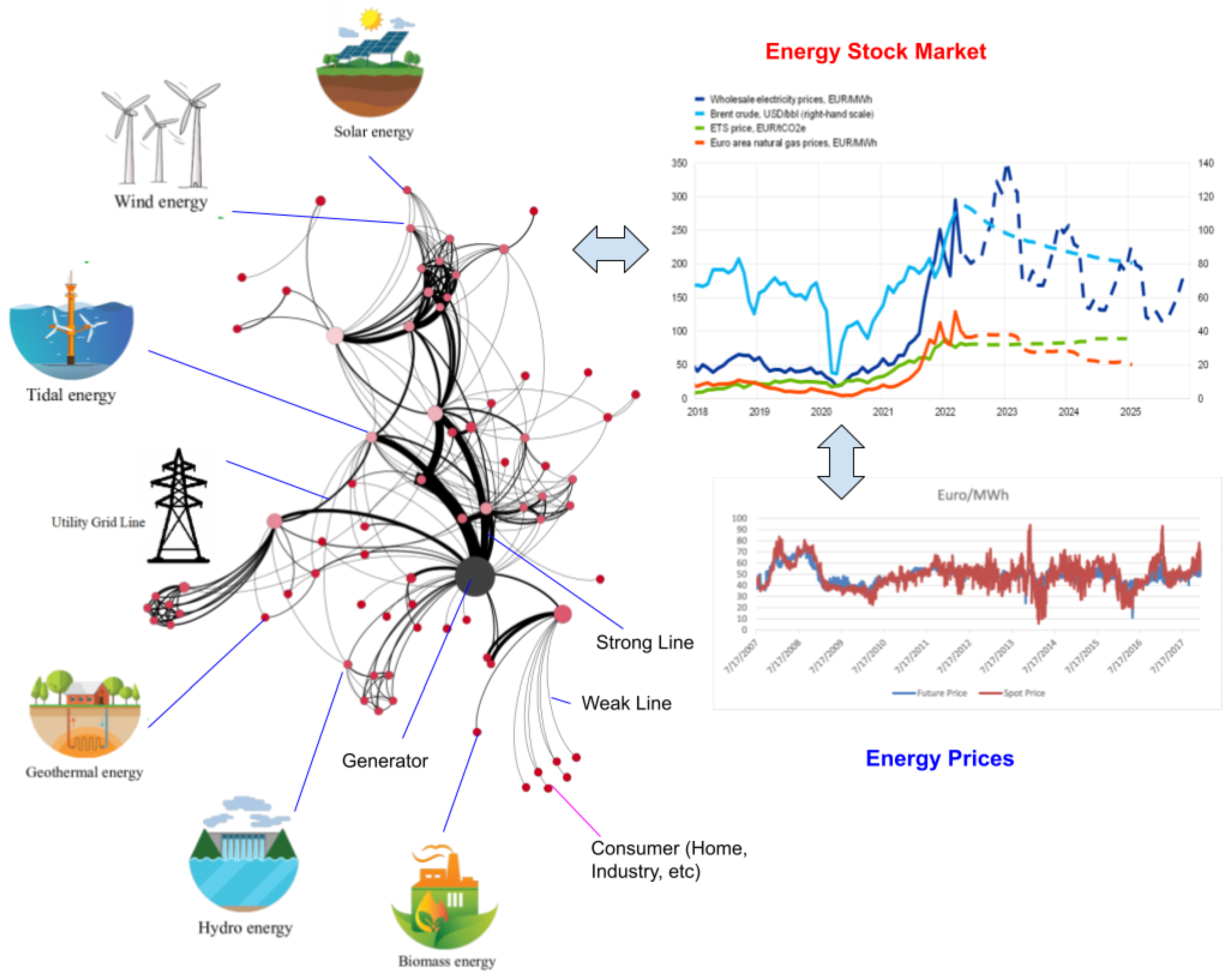



| Year | 2001 | 2010 | 2020 | 2030 | 2040 |
|---|---|---|---|---|---|
| Total consumption (million tons oil equivalent) | 10,038 | 10,549 | 11,425 | 12,352 | 13,310 |
| Biomass | 1080 | 1313 | 1791 | 2483 | 3271 |
| Large hydro | 22.7 | 266 | 309 | 341 | 358 |
| Geothermal | 43.2 | 86 | 186 | 333 | 493 |
| Small hydro | 9.5 | 19 | 49 | 106 | 189 |
| Wind | 4.7 | 44 | 266 | 542 | 688 |
| Solar thermal | 4.1 | 15 | 66 | 244 | 480 |
| Photo-voltaic | 0.1 | 2 | 24 | 221 | 784 |
| Solar thermal electricity | 0.1 | 0.4 | 3 | 16 | 68 |
| Marine (tidal/wave/ocean) | 0.05 | 0.1 | 0.4 | 3 | 20 |
| Total RES | 1365.5 | 1745.5 | 2964.4 | 4289 | 6351 |
| Renewable energy source contribution (in %) | 13.6 | 16.6 | 23.6 | 34.7 | 47.7 |
| Source | Advantages | Disadvantages |
|---|---|---|
| Sun | Unlimited energy source during periods of sunlight. Low level of pollution, at least during energy production. | Produces energy only during sunlight periods, with no energy generation during the night or cloudy weather. More expensive than other RES. Large geographical footprint, in particular for massive energy production. |
| Wind | Wind turbines function with no need for fuel. No-fuel functioning reduces overall costs for massive energy production in large-scale wind farms compared to other RES. One of the cleanest forms of energy. Last turbine generations are already extremely efficient. | Poses danger to some wildlife. Usually, wind turbines are quite noisy, so one has to install them where no people live and also where the wind is good. Produces no energy when wind is not blowing. Construction of massive structures are often hundreds of feet tall and require substantial upfront investment. |
| Water | A clean and abundant RES, at least close to large bodies of water. | Requires construction of dams, which has some environmental impact. In regions or situations that lack water, it has natural limitations. |
| Biomass | Clean, abundant, and can be used without interruption. Energy generation can be almost as controllable as conventional energy sources. Enables an efficient use of waste and reduces methane emissions for biogas. | Generates air pollution. Not very efficient. Can be seasonable and competes with food production activity. Requires large areas of landfill for biogas, at least when compared to conventional power plants, and also generates considerable amounts of pollution. |
| Geothermal Energy | Environmentally very safe and friendly. Lifetime of the source is very large (until earth life) and has huge potential for energy. Very sustainable, nonfluctuating, and reliable compared to other RES. | Implemented geothermal plan has accessible energy. During digging, some gases stored under the earth’s surface may be exploited. Long time investment and very costly. Maintaining sustainability is very tough enough. |
| Energy Storage Systems | Effect on Power Grid Performances |
|---|---|
| Supercapacitors (store electrical energy directly and thus do not need to convert to other energy forms) | Supercapacitors, an alternative form of battery, find application in power grids, particularly microgrids, to stabilize voltages during periods of power peaks. They are well suited for addressing short and medium transient events due to their high specific power. By dampening peaks and ripples in both loads and sources, supercapacitors contribute to voltage stability. Moreover, they enhance the flexibility of microgrids as they enable better adaptation to varying sources and demands across a wider current range, provided effective management is in place. |
| Hydrogen tanks | Hydrogen storage is considered a viable option for mitigating production plant outages and managing demand fluctuations. It serves as an effective energy storage approach and contributes to the balancing of power grids. The utilization of hydrogen presents a promising solution for distributing generated renewable energy. Introducing hydrogen into microgrids can significantly impact their behavior, particularly in terms of the peak electrical energy transfer between the microgrid and utility grid. As the level of hydrogen penetration increases within the microgrid, the peak of electrical energy transfer decreases, indicating the potential for reduced dependency on the utility grid. |
| Flywheels (store energy in the form of mechanical energy) | Stabilizes the frequency and degree of power grids and serves as short-term compensation storage. Flywheel storage power plants are available in the ranges of KWh to tens of MWh, similar to battery storage power plants. |
| Thermal energy storage systems (convert electrical into thermal energy; the storage medium can be solid or liquid) | Thermal energy storage systems find utility in both small-scale applications for heating purposes and large-scale applications for electrical energy generation. In large-scale applications, these systems utilize stored heat energy to generate electricity during periods of high power demand. They exhibit a rapid response capability, making them suitable for meeting short-term high-load demands. Furthermore, thermal energy storage systems offer the advantage of low initial investment and maintenance costs. However, it is important to note that these systems need to be specifically designed according to the intended application area to ensure optimal performance and efficiency. |
| Pumped hydroelectric storage (PHES; makes use of gravitational potential energy to store energy, managing upper and lower reservoirs) | Due to its gravitational potential energy of flow, whenever the power peak demands the elevation reservoirs open the turbines. For low power demand/cheap power, the operations are reversible, i.e., the water is pumped up. PHES allows more electricity sold for peak demand and increases revenue. The applications of PHEs are low operational cost, immediate operations, handling large load variations, high-pressure operations, and compact storage volume. |
| Compressed air energy storage (CAES; electromechanical device that produces electrical energy converted from mechanical energy) | CAES is a technology that involves storing high-pressure air in a tank and then expanding it through a turbine connected to a generator to produce electricity. It serves as an alternative to pumped hydroelectric storage for medium-term energy storage. During the compression process, the air temperature increases, while during the expansion, the pressurized air removes heat from the system. Storing the heat generated during the compression phase significantly enhances the efficiency of the energy storage process. There are two main types of CAES systems: diabatic and adiabatic. Each type employs different approaches to manage the heat produced during compression. Additionally, there is a third type called isothermal CAES that aims to maintain a constant temperature throughout the process. |
| Batteries | The batteries stabilize the microgrid voltage (DC bus) to store large amounts of energy during the narrow voltage operation. It is increasing the cost reduction, improvement in performance, and specific energy in mobile and stationary energy applications. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Srinivasan, S.; Kumarasamy, S.; Andreadakis, Z.E.; Lind, P.G. Artificial Intelligence and Mathematical Models of Power Grids Driven by Renewable Energy Sources: A Survey. Energies 2023, 16, 5383. https://doi.org/10.3390/en16145383
Srinivasan S, Kumarasamy S, Andreadakis ZE, Lind PG. Artificial Intelligence and Mathematical Models of Power Grids Driven by Renewable Energy Sources: A Survey. Energies. 2023; 16(14):5383. https://doi.org/10.3390/en16145383
Chicago/Turabian StyleSrinivasan, Sabarathinam, Suresh Kumarasamy, Zacharias E. Andreadakis, and Pedro G. Lind. 2023. "Artificial Intelligence and Mathematical Models of Power Grids Driven by Renewable Energy Sources: A Survey" Energies 16, no. 14: 5383. https://doi.org/10.3390/en16145383
APA StyleSrinivasan, S., Kumarasamy, S., Andreadakis, Z. E., & Lind, P. G. (2023). Artificial Intelligence and Mathematical Models of Power Grids Driven by Renewable Energy Sources: A Survey. Energies, 16(14), 5383. https://doi.org/10.3390/en16145383







