Minimizing Power Losses for Distributed Generation (DG) Placements by Considering Voltage Profiles on Distribution Lines for Different Loads Using Genetic Algorithm Methods
Abstract
:1. Introduction
2. Materials and Methods
2.1. Power Flow in Radial Distribution Networks
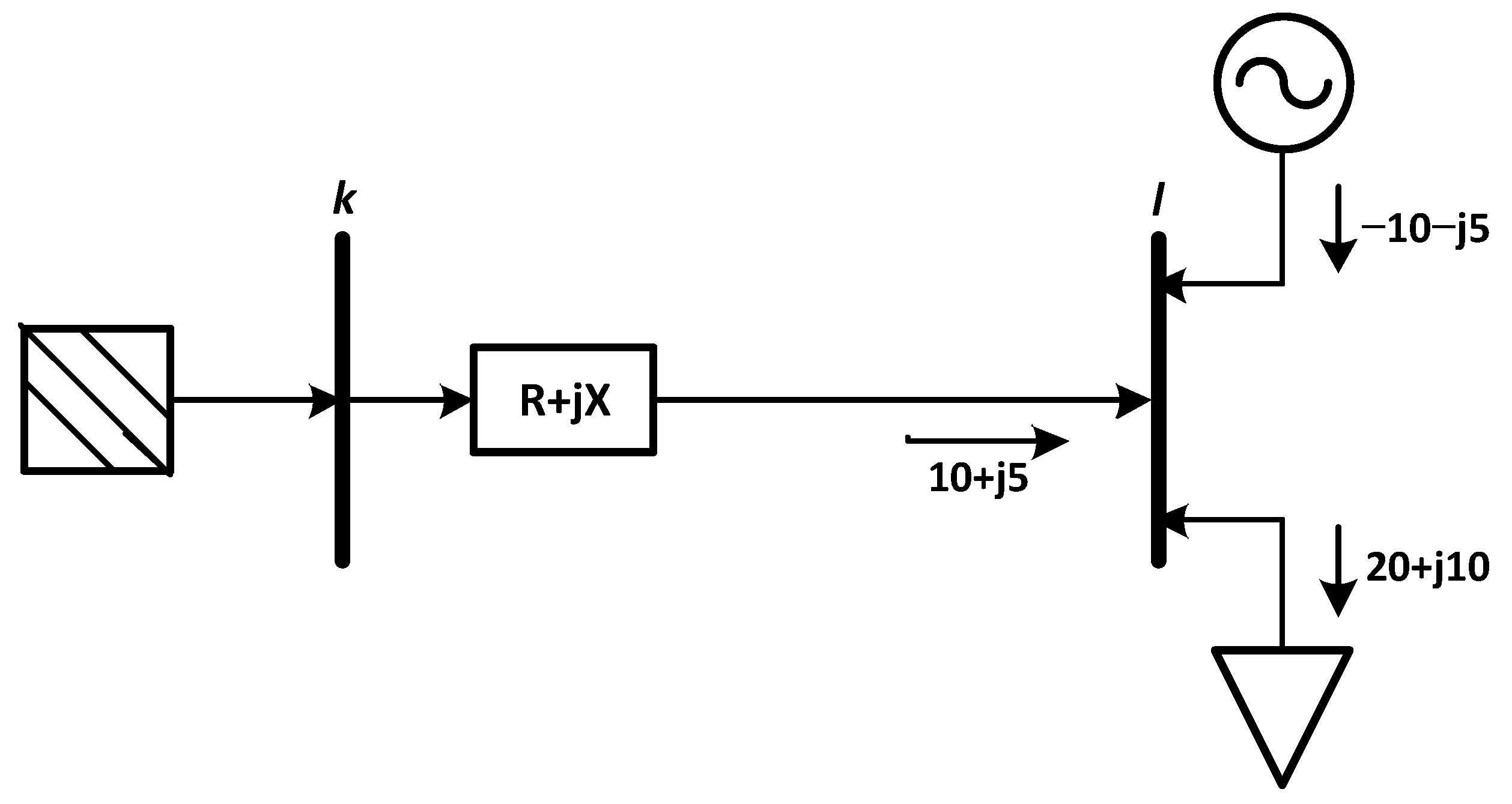
2.1.1. Backward Sweep
2.1.2. Forward Sweep
- Forming the BBIC Matrix
- 2.
- Compiling the BCBV Matrix
2.2. DG Data Reading
2.3. DG as Negative Load
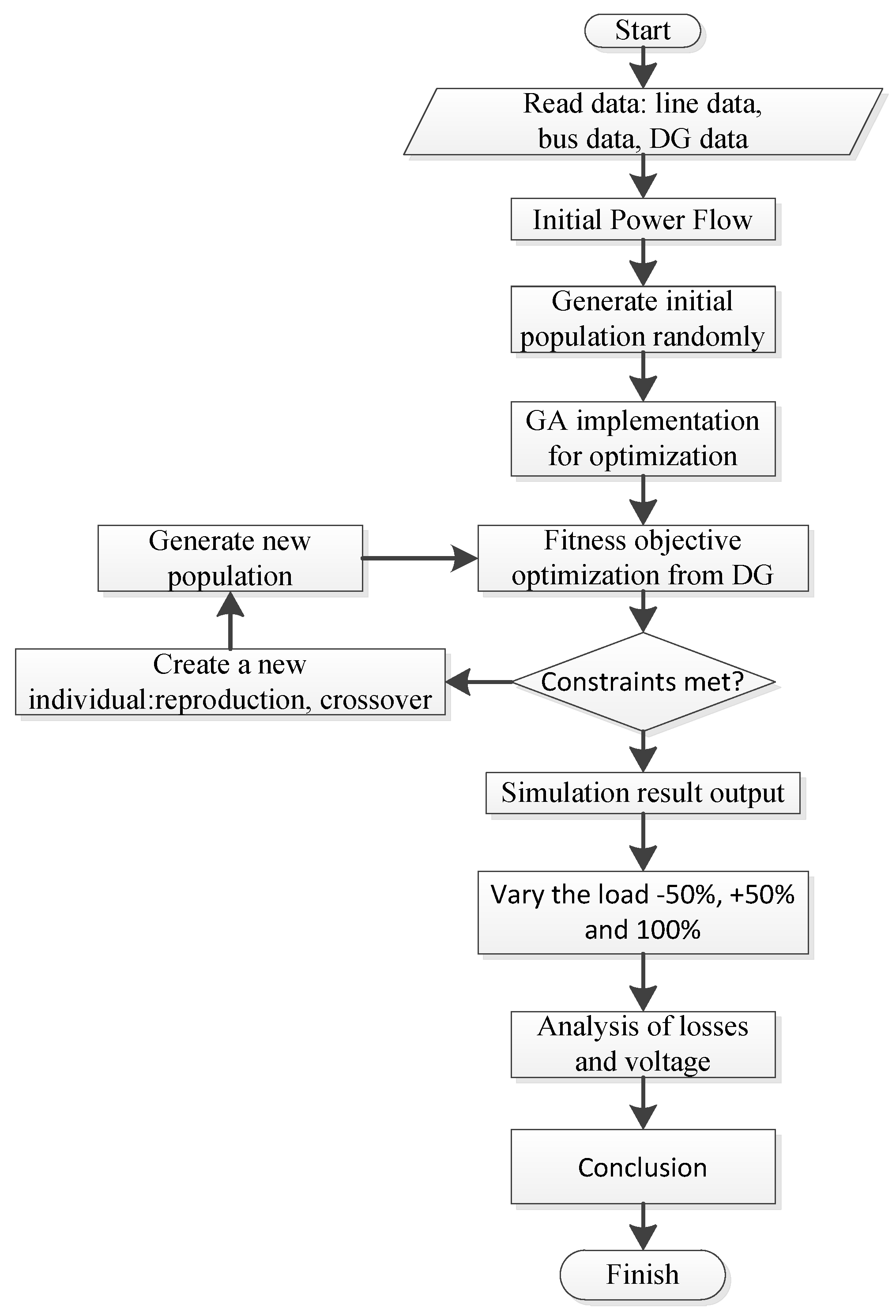
2.4. Raise the Initial Population
2.5. Objective Function
2.6. Create the New Population
2.7. Generate New Population
2.8. Location Determination DG using GA
3. Results
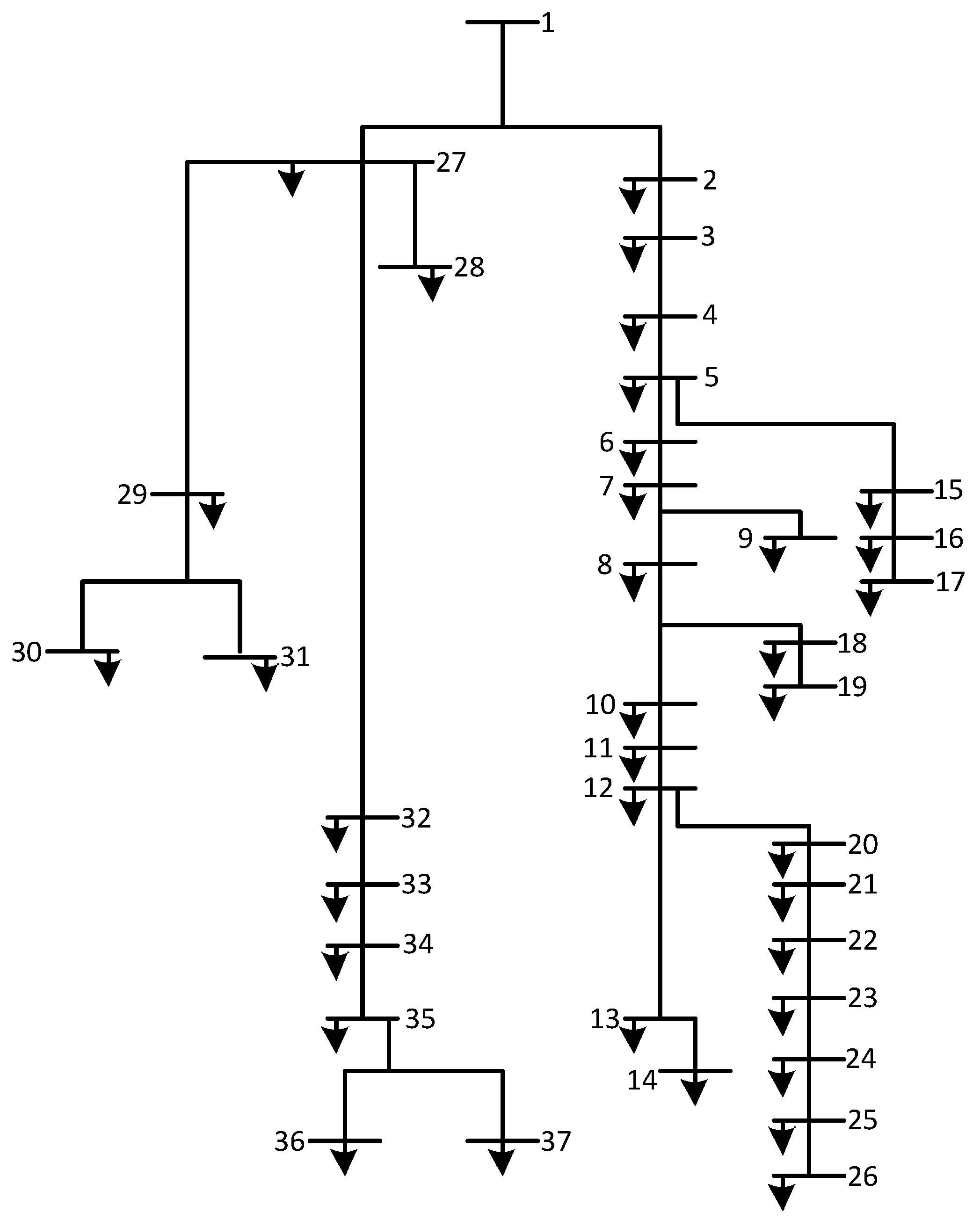
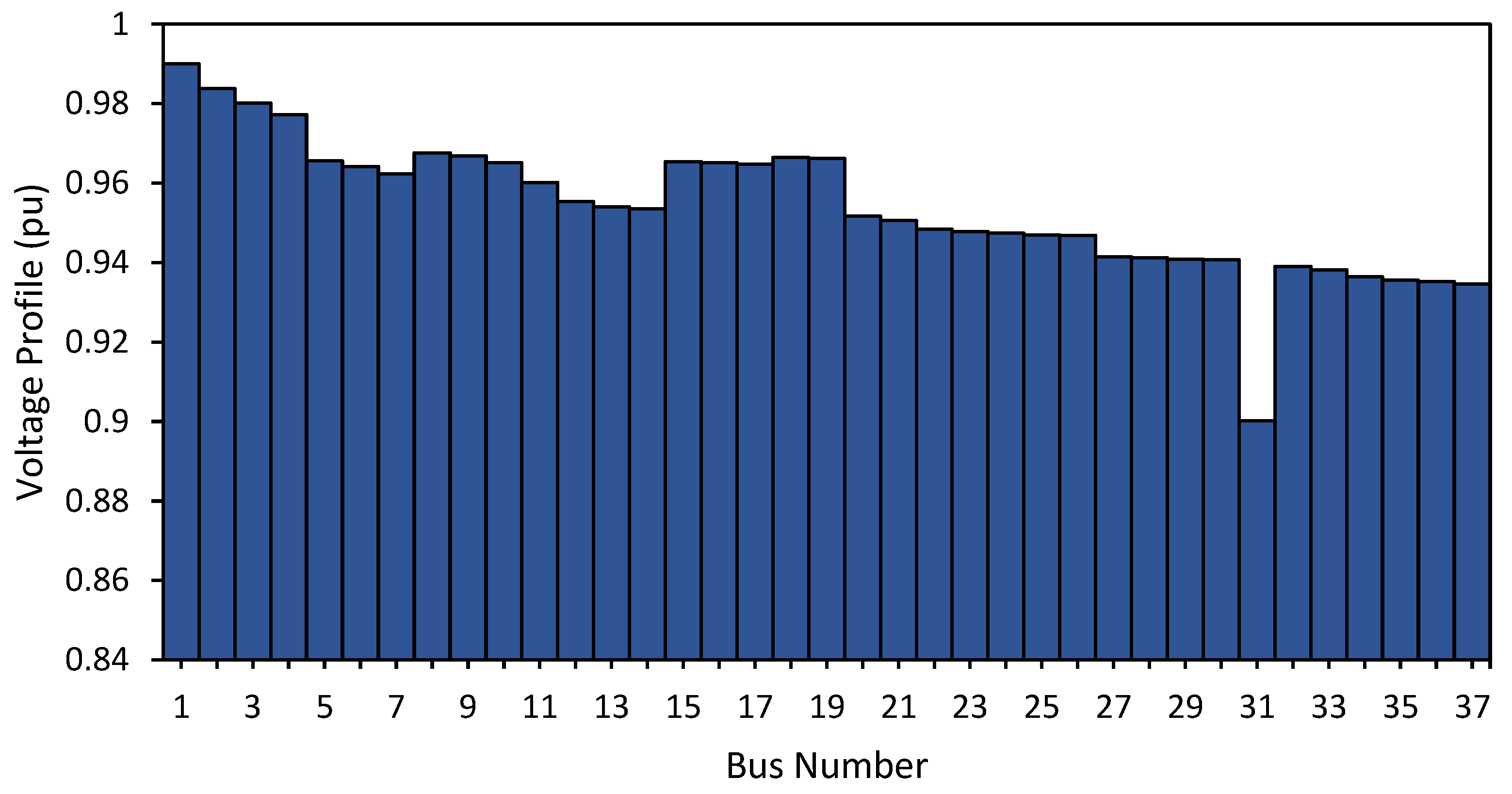
3.1. Data Analysis before DG Placement
3.2. Optimization of DG Placement and Capacity under Normal Load
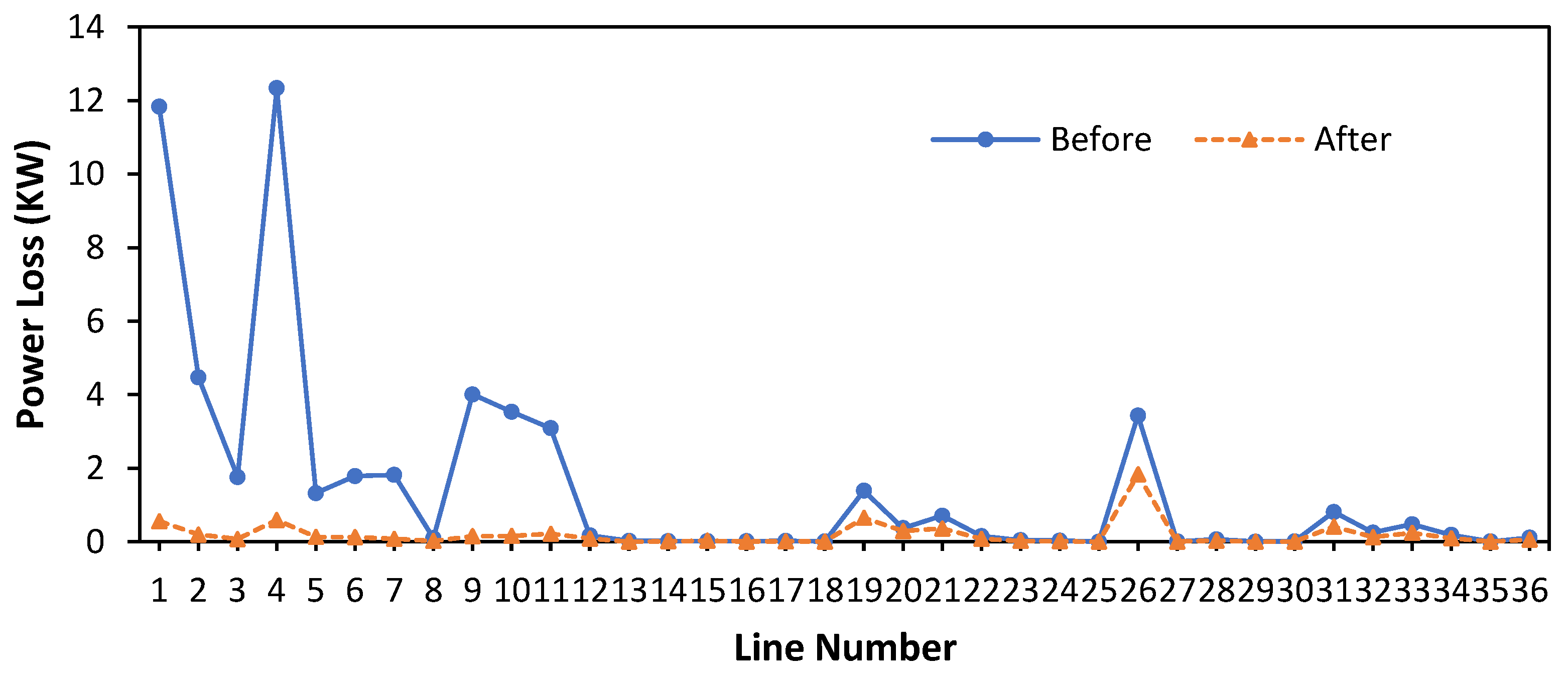
3.3. Comparison of Data Results before and after Optimization of DG Placement
3.4. Comparison of Calculation Results with ETAP and GA as Validation
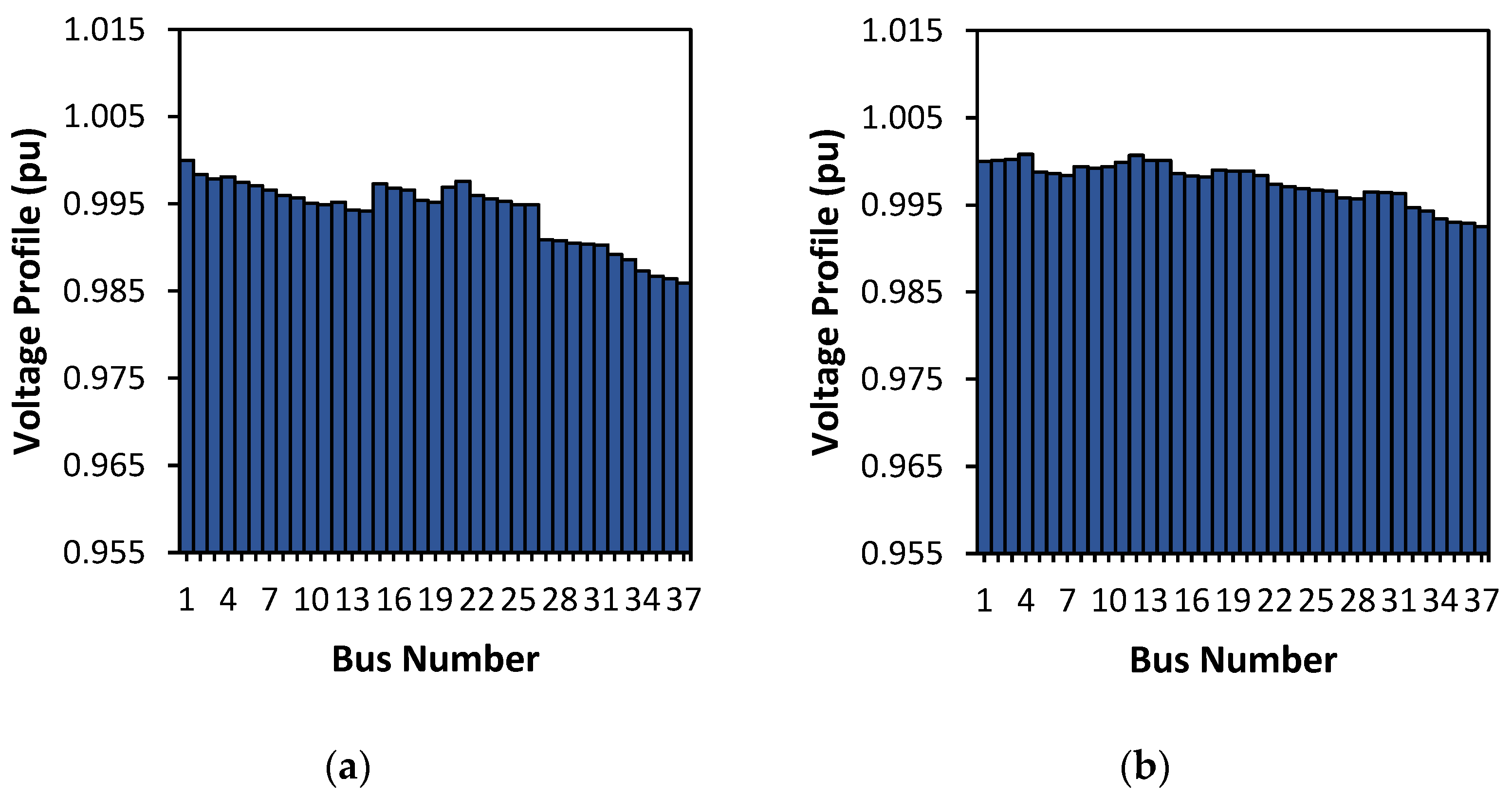
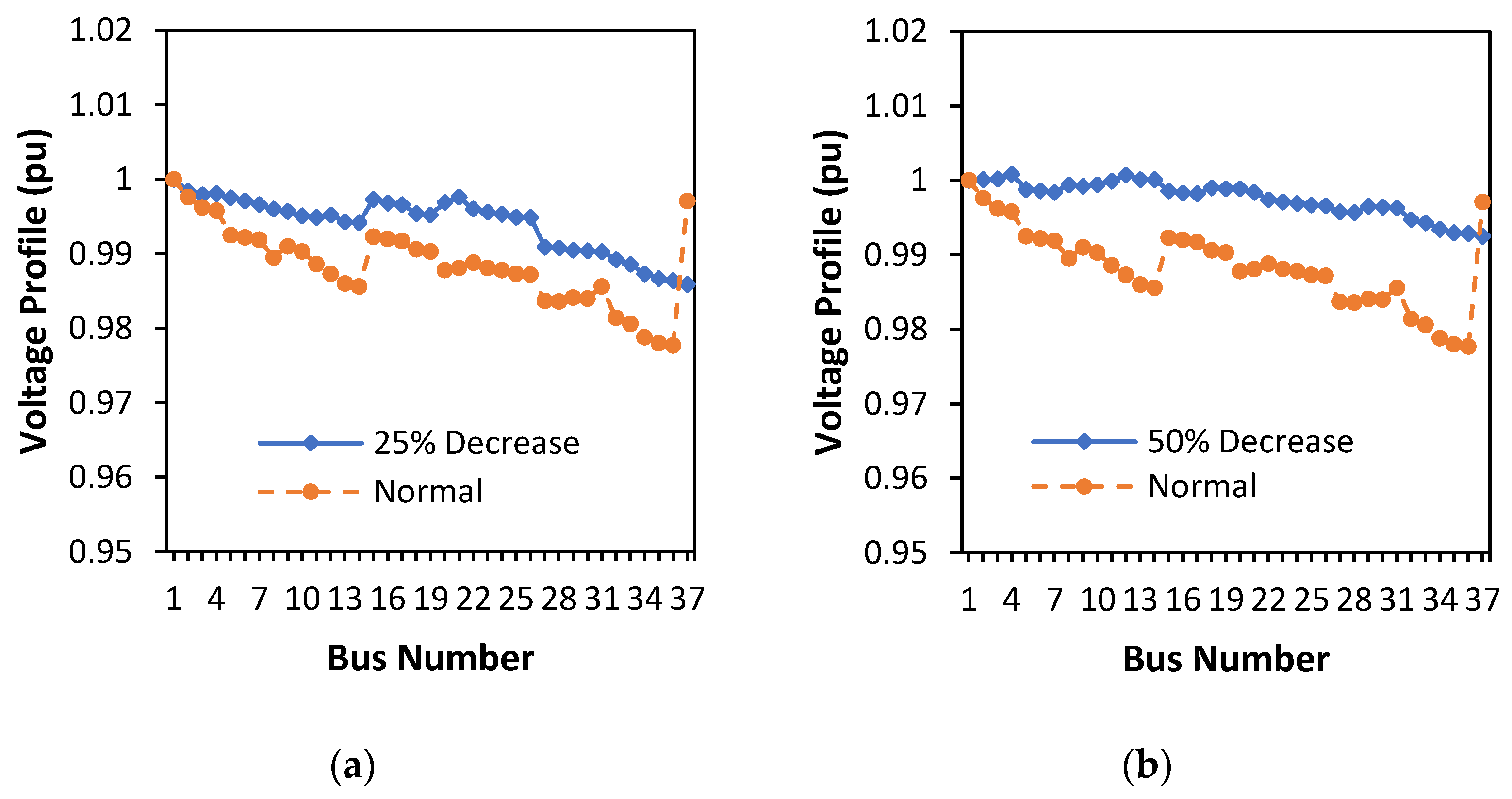
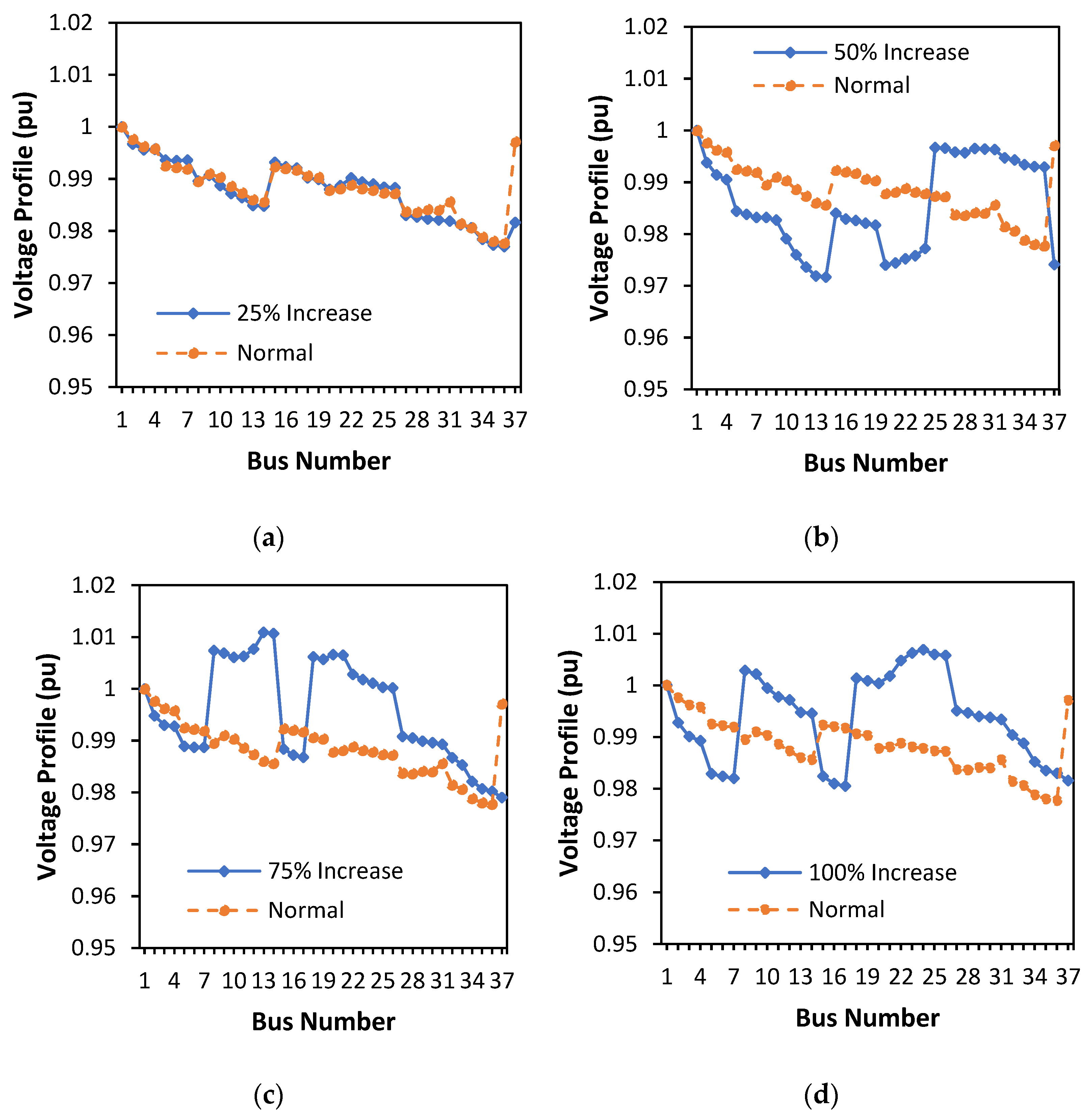
3.5. Optimization of DG Placement and Capacity with Load Decrease and Load Increase for All Percentages
3.6. Comparison of Active Power Losses for Normal Load and 25% Reduction and 50% Reduction
3.7. Comparison of Active Power Losses for Normal Load and for 25%, 50%, 75%, and 100% Increases in Load
4. Discussions
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bahramara, S.; Moghaddam, M.P.; Haghifam, M.R. Optimal planning of hybrid renewable energy systems using HOMER: A review. Renew. Sustain. Energy Rev. 2016, 62, 609–620. [Google Scholar] [CrossRef]
- Holechek, J.L.; Geli, H.M.E.; Sawalhah, M.N.; Valdez, R. A Global Assessment: Can Renewable Energy Replace Fossil Fuels by 2050? Sustainability 2022, 14, 4792. [Google Scholar] [CrossRef]
- Schirone, L.; Pellitteri, F. Energy Policies and Sustainable Management of Energy Sources. Sustainability 2017, 9, 2321. [Google Scholar] [CrossRef] [Green Version]
- Vinichenko, V.; Cherp, A.; Jewell, J. Historical precedents and feasibility of rapid coal and gas decline required for the 1.5°C target. One Earth 2021, 4, 1477–1490. [Google Scholar] [CrossRef]
- Rashedi, A.; Khanam, T.; Jonkman, M. On Reduced Consumption of Fossil Fuels in 2020 and Its Consequences in the Global Environment and Exergy Demand. Energies 2020, 13, 6048. [Google Scholar] [CrossRef]
- Halkos, G.; Gkampoura, E.-C. Assessing Fossil Fuels and Renewables’ Impact on Energy Poverty Conditions in Europe. Energies 2023, 16, 560. [Google Scholar] [CrossRef]
- Zhang, S.; Cheng, H.; Li, K.; Tai, N.; Wang, D.; Li, F. Multi-objective distributed generation planning in distribution network considering correlations among uncertainties. Appl. Energy 2018, 226, 743–755. [Google Scholar] [CrossRef]
- Razavi, S.-E.; Rahimi, E.; Javadi, M.S.; Nezhad, A.E.; Lotfi, M.; Shafie-Khah, M.; Catalão, J.P. Impact of distributed generation on protection and voltage regulation of distribution systems: A review. Renew. Sustain. Energy Rev. 2019, 105, 157–167. [Google Scholar] [CrossRef]
- Sun, P.; Jiao, Z.; Gu, H. Calculation of Short-Circuit Current in DC Distribution System Based on MMC Linearization. Front. Energy Res. 2021, 9, 634232. [Google Scholar] [CrossRef]
- Bevrani, H.; Golpîra, H.; Messina, A.R.; Hatziargyriou, N.; Milano, F.; Ise, T. Power system frequency control: An updated review of current solutions and new challenges. Electr. Power Syst. Res. 2021, 194, 107114. [Google Scholar] [CrossRef]
- Kojovic, L. Impact DG on voltage regulation. In Proceedings of the IEEE Power Engineering Society Summer Meeting, Chicago, IL, USA, 21–25 July 2002. [Google Scholar] [CrossRef]
- Martinez, J.A.; Martin-Arnedo, J. Impact of distributed generation on distribution protection and power quality. In Proceedings of the 2009 IEEE Power & Energy Society General Meeting, Calgary, AB, Canada, 26–30 July 2009; pp. 1–6. [Google Scholar] [CrossRef]
- Ogunsina, A.A.; Petinrin, M.O.; Petinrin, O.O.; Offornedo, E.N.; Petinrin, J.O.; Asaolu, G.O. Optimal distributed generation location and sizing for loss minimization and voltage profile optimization using ant colony algorithm. SN Appl. Sci. 2021, 3, 248. [Google Scholar] [CrossRef]
- Ayodele, T.R.; Ogunjuyigbe, A.S.O.; Akinola, O.O. Optimal Location, Sizing, and Appropriate Technology Selection of Distributed Generators for Minimizing Power Loss Using Genetic Algorithm. J. Renew. Energy 2015, 2015, 832917. [Google Scholar] [CrossRef] [Green Version]
- Dulău, L.I.; Abrudean, M.; Bică, D. Optimal Location of a Distributed Generator for Power Losses Improvement. Procedia Technol. 2016, 22, 734–739. [Google Scholar] [CrossRef] [Green Version]
- Purchala, K.; Belmans, R. Distributed Generation and Grid Integration Issues; Imperial College: London, UK, 2003. [Google Scholar]
- Sari, P.D.; Kumara, I.N.S. The Development of Jatiluwih Micro-Hydro Power Plants to Support Tourism Destinations. In Proceedings of the 2018 International Student Conference on Electrical and Computer Engineering (ISCECE), Bali, Indonesia, 26 October 2018; pp. 9–14, ISBN 978-602-294-346-4.. [Google Scholar]
- Bayat, A.; Bagheri, A. Optimal active and reactive power allocation in distribution networks using a novel heuristic approach. Appl. Energy 2018, 233–234, 71–85. [Google Scholar] [CrossRef]
- Wong, L.A.; Ramachandaramurthy, V.K.; Taylor, P.; Ekanayake, J.; Walker, S.L.; Padmanaban, S. Review on the optimal placement, sizing and control of an energy storage system in the distribution network. J. Energy Storage 2019, 21, 489–504. [Google Scholar] [CrossRef]
- De Jesus, P.M.O. A Simplified Formulation for the Backward/Forward Sweep Power Flow Method. Arxiv Cornell University, United State of America. 2020. Available online: https://arxiv.org/pdf/2010.06389.pdf (accessed on 9 July 2023).
- Rana, A.D.; Darji, J.B.; Pandya, M. Backward/Forward Sweep Load Flow Algorithm for Radial Distribution System. Int. J. Sci. Res. Dev. 2014, 2, 398–400. [Google Scholar]
- Siregar, R.H.; Away, Y. Optimizing the Placement and Capacity of Distributed Generation (DG) on the Krueng Raya Feeder in Banda Aceh Distribution System to Increase Power Flow using Genetic Algorithm Method. In Proceedings of the 2022 International Conference on Electrical Engineering and Informatics (ICELTICs), Banda Aceh, Indonesia, 27–28 September 2022; pp. 184–189. [Google Scholar] [CrossRef]
- Moradi, M.H.; Abedini, M. A combination of genetic algorithm and particle swarm optimization for optimal DG location and sizing in distribution systems. Int. J. Electr. Power Energy Syst. 2012, 34, 66–74. [Google Scholar] [CrossRef]
- Lakshmi, G.V.N.; Jayalaxmi, A.; Veeramsetty, V. Optimal Placement of Distribution Generation in Radial Distribution System Using Hybrid Genetic Dragonfly Algorithm. Technol. Econ. Smart Grids Sustain. Energy 2021, 6, 9. [Google Scholar] [CrossRef]
- C, H.P.; Subbaramaiah, K.; Sujatha, P. Optimal DG unit placement in distribution networks by multi-objective whale optimization algorithm & its techno-economic analysis. Electr. Power Syst. Res. 2023, 214, 108869. [Google Scholar] [CrossRef]
- Khan, M.O.; Wadood, A.; Abid, M.I.; Khurshaid, T.; Rhee, S.B. Minimization of Network Power Losses in the AC-DC Hybrid Distribution Network through Network Reconfiguration Using Soft Open Point. Electronics 2021, 10, 326. [Google Scholar] [CrossRef]
- Abbas, M.; Alshehri, M.A.; Barnawi, A.B. Potential Contribution of the Grey Wolf Optimization Algorithm in Reducing Active Power Losses in Electrical Power Systems. Appl. Sci. 2022, 12, 6177. [Google Scholar] [CrossRef]
- Selim, A.; Kamel, S.; Jurado, F. Efficient optimization technique for multiple DG allocation in distribution networks. Appl. Soft Comput. 2020, 86, 105938. [Google Scholar] [CrossRef]
- Shang, C.; Zhou, T.-T.; Liu, S. Optimization of complex engineering problems using modified sine cosine algorithm. Sci. Rep. 2022, 12, 20528. [Google Scholar] [CrossRef]
- Narayanan, R.C.; Ganesh, N.; Čep, R.; Jangir, P.; Chohan, J.S.; Kalita, K. A Novel Many-Objective Sine–Cosine Algorithm (MaOSCA) for Engineering Applications. Mathematics 2023, 11, 2301. [Google Scholar] [CrossRef]
- Jouhari, H.; Lei, D.; Al-Qaness, M.A.A.; Elaziz, M.A.; Ewees, A.A.; Farouk, O. Sine-Cosine Algorithm to Enhance Simulated Annealing for Unrelated Parallel Machine Scheduling with Setup Times. Mathematics 2019, 7, 1120. [Google Scholar] [CrossRef] [Green Version]
- Das, S.; Abraham, A.; Konar, A. Particle Swarm Optimization and Differential Evolution Algorithms: Technical Analysis, Applications and Hybridization Perspectives. In Advances of Computational Intelligence in Industrial Systems; Springer: Berlin/Heidelberg, Germany, 2008; Volume 116. [Google Scholar] [CrossRef] [Green Version]
- Lim, S.P.; Haron, H. Performance comparison of Genetic Algorithm, Differential Evolution and Particle Swarm Optimization towards benchmark functions. In Proceedings of the 2013 IEEE Conference on Open Systems (ICOS), Kuching, Malaysia, 2–4 December 2013; pp. 41–46. [Google Scholar] [CrossRef]
- Yarat, S.; Senan, S.; Orman, Z. A Comparative Study on PSO with Other Metaheuristic Methods. In Applying Particle Swarm Optimization; Mercangöz, B.A., Ed.; International Series in Operations Research & Management Science; Springer: Berlin/Heidelberg, Germany, 2021; Volume 306, pp. 49–72. [Google Scholar] [CrossRef]
- Jin, Y.; Sun, Y.; Ma, H. A Developed Artificial Bee Colony Algorithm Based on Cloud Model. Mathematics 2018, 6, 61. [Google Scholar] [CrossRef] [Green Version]
- Selim, A.; Kamel, S.; Mohamed, A.A.; Elattar, E.E. Optimal Allocation of Multiple Types of Distributed Generations in Radial Distribution Systems Using a Hybrid Technique. Sustainability 2021, 13, 6644. [Google Scholar] [CrossRef]
- Kartikeya, S.A.; Rafi, K.M. Optimal Capacitor Placement in Radial Distribution Systems using Artificial Bee Colony (ABC) Algorithm. Innov. Syst. Des. Eng. 2011, 2, 177–185. [Google Scholar]
- Ratuhaji, F.; Arief, A.; Nappu, M.B. Determination of optimal location and capacity of distributed generations based on artificial bee colony. J. Phys. Conf. Ser. 2019, 1341, 052012. [Google Scholar] [CrossRef] [Green Version]
- Wicaksana, M.G.S.; Putranto, L.M.; Waskito, F.; Yasirroni, M. Optimal Placement and Sizing of PV as DG for Losses Minimization Using PSO Algorithm: A Case in Purworejo Area. In Proceedings of the 2020 International Conference on Sustainable Energy Engineering and Application (ICSEEA), Tangerang, Indonesia, 18–20 November 2020. [Google Scholar] [CrossRef]
- Essallah, S.; Khedher, A.; Bouallegue, A. Integration of distributed generation in electrical grid: Optimal placement and sizing under different load conditions. Comput. Electr. Eng. 2019, 79, 106461. [Google Scholar] [CrossRef]
- Badran, O.; Mekhilef, S.; Mokhlis, H.; Dahalan, W. Optimal reconfiguration of distribution system connected with distributed generations: A review of different methodologies. Renew. Sustain. Energy Rev. 2017, 73, 854–867. [Google Scholar] [CrossRef]
- Zakaria, Y.Y.; Swief, R.A.; El-Amary, N.H.; Ibrahim, A.M. Optimal Distributed Generation Allocation and Sizing Using Genetic and Ant Colony Algorithms. J. Phys. Conf. Ser. 2020, 1447, 012023. [Google Scholar] [CrossRef]
- Alinejad-Beromi, Y.; Sedighizadeh, M.; Bayat, M.R.; Khodayar, M.E. Using genetic alghoritm for distributed generation allocation to reduce losses and improve voltage profile. In Proceedings of the 2007 42nd International Universities Power Engineering Conference, Brighton, UK, 4–6 September 2007; pp. 954–959. [Google Scholar] [CrossRef]
- Naderipour, A.; Abdul-Malek, Z.; Hajivand, M.; Seifabad, Z.M.; Farsi, M.A.; Nowdeh, S.A.; Davoudkhani, I.F. Spotted hyena optimizer algorithm for capacitor allocation in radial distribution system with distributed generation and microgrid operation considering different load types. Sci. Rep. 2021, 11, 2728. [Google Scholar] [CrossRef]
- Wang, M.; Zhong, J. A novel method for distributed generation and capacitor optimal placement considering voltage profiles. In Proceedings of the 2011 IEEE Power and Energy Society General Meeting, Detroit, MI, USA, 24–28 July 2011; pp. 1–6. [Google Scholar] [CrossRef] [Green Version]
- Srinivasa Rao, R.; Ravindra, K.; Satish, K.; Narasimham, S.V.L. Power Loss Minimization in Distribution System Using Network Reconfiguration in the Presence of Distributed Generation. IEEE Trans. Power Syst. 2013, 28, 317–325. [Google Scholar] [CrossRef]
- Kashyap, M.; Mittal, A.; Kansal, S. Optimal Placement of Distributed Generation Using Genetic Algorithm Approach. In Proceeding of the Second International Conference on Microelectronics, Computing & Communication Systems (MCCS 2017); Nath, V., Mandal, J., Eds.; Lecture Notes in Electrical Engineering; Springer: Singapore, 2019; Volume 476. [Google Scholar]
- Nayeripour, M.; Mahboubi-Moghaddam, E.; Aghaei, J.; Azizi-Vahed, A. Multi-objective placement and sizing of DGs in distribution networks ensuring transient stability using hybrid evolutionary algorithm. Renew. Sustain. Energy Rev. 2013, 25, 759–767. [Google Scholar] [CrossRef]
- Yammani, C.; Maheswarapu, S.; Matam, S.K. A Multi-objective Shuffled Bat algorithm for optimal placement and sizing of multi distributed generations with different load models. Int. J. Electr. Power Energy Syst. 2016, 79, 120–131. [Google Scholar] [CrossRef]
- Imran, A.M.; Kowsalya, M.; Kothari, D. A novel integration technique for optimal network reconfiguration and distributed generation placement in power distribution networks. Int. J. Electr. Power Energy Syst. 2014, 63, 461–472. [Google Scholar] [CrossRef]
- Prabha, D.R.; Jayabarathi, T. Optimal placement and sizing of multiple distributed generating units in distribution networks by invasive weed optimization algorithm. Ain Shams Eng. J. 2016, 7, 683–694. [Google Scholar] [CrossRef] [Green Version]
- Mistry, K.D.; Roy, R. Enhancement of loading capacity of distribution system through distributed generator placement considering techno-economic benefits with load growth. Int. J. Electr. Power Energy Syst. 2014, 54, 505–515. [Google Scholar] [CrossRef]
- Moradi, M.H.; Zeinalzadeh, A.; Mohammadi, Y.; Abedini, M. An efficient hybrid method for solving the optimal sitting and sizing problem of DG and shunt capacitor banks simultaneously based on imperialist competitive algorithm and genetic algorithm. Int. J. Electr. Power Energy Syst. 2014, 54, 101–111. [Google Scholar] [CrossRef]
- Doagou-Mojarrad, H.; Gharehpetian, G.; Rastegar, H.; Olamaei, J. Optimal placement and sizing of DG (distributed generation) units in distribution networks by novel hybrid evolutionary algorithm. Energy 2013, 54, 129–138. [Google Scholar] [CrossRef]
- Biswas, S.; Goswami, S.K.; Chatterjee, A. Optimum distributed generation placement with voltage sag effect minimization. Energy Convers. Manag. 2012, 53, 163–174. [Google Scholar] [CrossRef]
- Esmaili, M.; Firozjaee, E.C.; Shayanfar, H.A. Optimal placement of distributed generations considering voltage stability and power losses with observing voltage-related constraints. Appl. Energy 2014, 113, 1252–1260. [Google Scholar] [CrossRef]
- Gitizadeh, M.; Vahed, A.A.; Aghaei, J. Multistage distribution system expansion planning considering distributed generation using hybrid evolutionary algorithms. Appl. Energy 2013, 101, 655–666. [Google Scholar] [CrossRef]
- El-Zonkoly, A. Optimal placement of multi-distributed generation units including different load models using particle swarm optimisation. IET Gener. Transm. Distrib. 2011, 5, 760–771. [Google Scholar] [CrossRef]
- Biswas, S.; Goswami, S.K.; Chatterjee, A. Optimal distributed generation placement in shunt capacitor compensated distribution systems considering voltage sag and harmonics distortions. IET Gener. Transm. Distrib. 2014, 8, 783–797. [Google Scholar] [CrossRef]
- Kim, K.-H.; Song, K.-B.; Joo, S.-K.; Lee, Y.-J.; Kim, J.-O. Multiobjective distributed generation placement using fuzzy goal programming with genetic algorithm. Eur. Trans. Electr. Power 2008, 18, 217–230. [Google Scholar] [CrossRef]
- Vita, V. Development of a Decision-Making Algorithm for the Optimum Size and Placement of Distributed Generation Units in Distribution Networks. Energies 2017, 10, 1433. [Google Scholar] [CrossRef] [Green Version]
- Kalantari, M.; Kazemi, A. Placement of distributed generation unit and capacitor allocation in distribution systems using genetic algorithm. In Proceedings of the 2011 10th International Conference on Environment and Electrical Engineering, Rome, Italy, 8–11 May 2011; pp. 1–5. [Google Scholar] [CrossRef]
- Parizad, A.; Khazali, A.; Kalantar, M. Optimal placement of distributed generation with sensitivity factors considering voltage stability and losses indices. In Proceedings of the 2010 18th Iranian Conference on Electrical Engineering, Isfahan, Iran, 11–13 May 2010; pp. 848–855. [Google Scholar] [CrossRef]
- Aman, M.; Jasmon, G.; Bakar, A.; Mokhlis, H. A new approach for optimum simultaneous multi-DG distributed generation Units placement and sizing based on maximization of system loadability using HPSO (hybrid particle swarm optimization) algorithm. Energy 2014, 66, 202–215. [Google Scholar] [CrossRef]
- Rath, D.; Dey, S.H.; Goswami, S.K. Optimal Inverter-Based DG Placement considering Energy Loss, Reliability, Voltage Sag, DG, and Substation Power Cost Issues. Electr. Power Compon. Syst. 2023, 51, 409–420. [Google Scholar] [CrossRef]
- El-Zonkoly, A. Optimal placement of multi-distributed generation units including different load models using particle swarm optimization. Swarm Evol. Comput. 2011, 1, 50–59. [Google Scholar] [CrossRef]
- Radosavljevic, J.; Arsic, N.; Milovanovic, M.; Ktena, A. Optimal Placement and Sizing of Renewable Distributed Generation Using Hybrid Metaheuristic Algorithm. J. Mod. Power Syst. Clean Energy 2020, 8, 499–510. [Google Scholar] [CrossRef]
- Karunarathne, E.; Pasupuleti, J.; Ekanayake, J.; Almeida, D. Optimal Placement and Sizing of DGs in Distribution Networks Using MLPSO Algorithm. Energies 2020, 13, 6185. [Google Scholar] [CrossRef]
- Siregar, R.H.; Away, Y.; Tarmizi; Sara, I.D. Planning for Placement of Distributed Generators (DG) in Feeders with the Artificial Intelligent Hybrid GA-ANN Method. In Proceedings of the ICECME 2021: 3rd International Conference on Experimental and Computational Mechanics in Engineering, Banda Aceh, Indonesia, 11–12 October 2021; pp. 161–176. [Google Scholar] [CrossRef]
- Essa, M.B.; Alnabi, L.A.; Dhaher, A.K. Distribution power loss minimization via optimal sizing and placement of shunt capacitor and distributed generator with network reconfiguration. TELKOMNIKA Telecommun. Comput. Electron. Control. 2021, 19, 1039–1049. [Google Scholar] [CrossRef]
- Abbas, A.; Qaisar, S.M.; Waqar, A.; Ullah, N.; Al Ahmadi, A.A. Min-Max Regret-Based Approach for Sizing and Placement of DGs in Distribution System under a 24 h Load Horizon. Energies 2022, 15, 3701. [Google Scholar] [CrossRef]
- Ntombela, M.; Musasa, K.; Leoaneka, M.C. Power Loss Minimization and Voltage Profile Improvement by System Reconfiguration, DG Sizing, and Placement. Computation 2022, 10, 180. [Google Scholar] [CrossRef]
- Alizadeh, S.; Mahdavian, M.; Ganji, E. Optimal placement and sizing of photovoltaic power plants in power grid considering multi-objective optimization using evolutionary algorithms. J. Electr. Syst. Inf. Technol. 2023, 10, 7. [Google Scholar] [CrossRef]
- Sneha, J.A.; Kumar, K.; Victor, V.B.J.; Glenn, J.A. Optimal Placement of Different Types of Dg Sources in Distribution Networks Using Pso Algorithm and Differential Evolution. IOSR J. Electr. Electron. Eng. (IOSR-JEEE) 2014, 9, 41–45. [Google Scholar] [CrossRef]
- Mithulananthan, N.; Oo, T.; Phu, L.V. Distributed Generator Placement in Power Distribution System Using Genetic Algorithm to Reduce Losses. Thammasat Int. J. Sci. Technol. 2004, 9, 55–62. [Google Scholar]

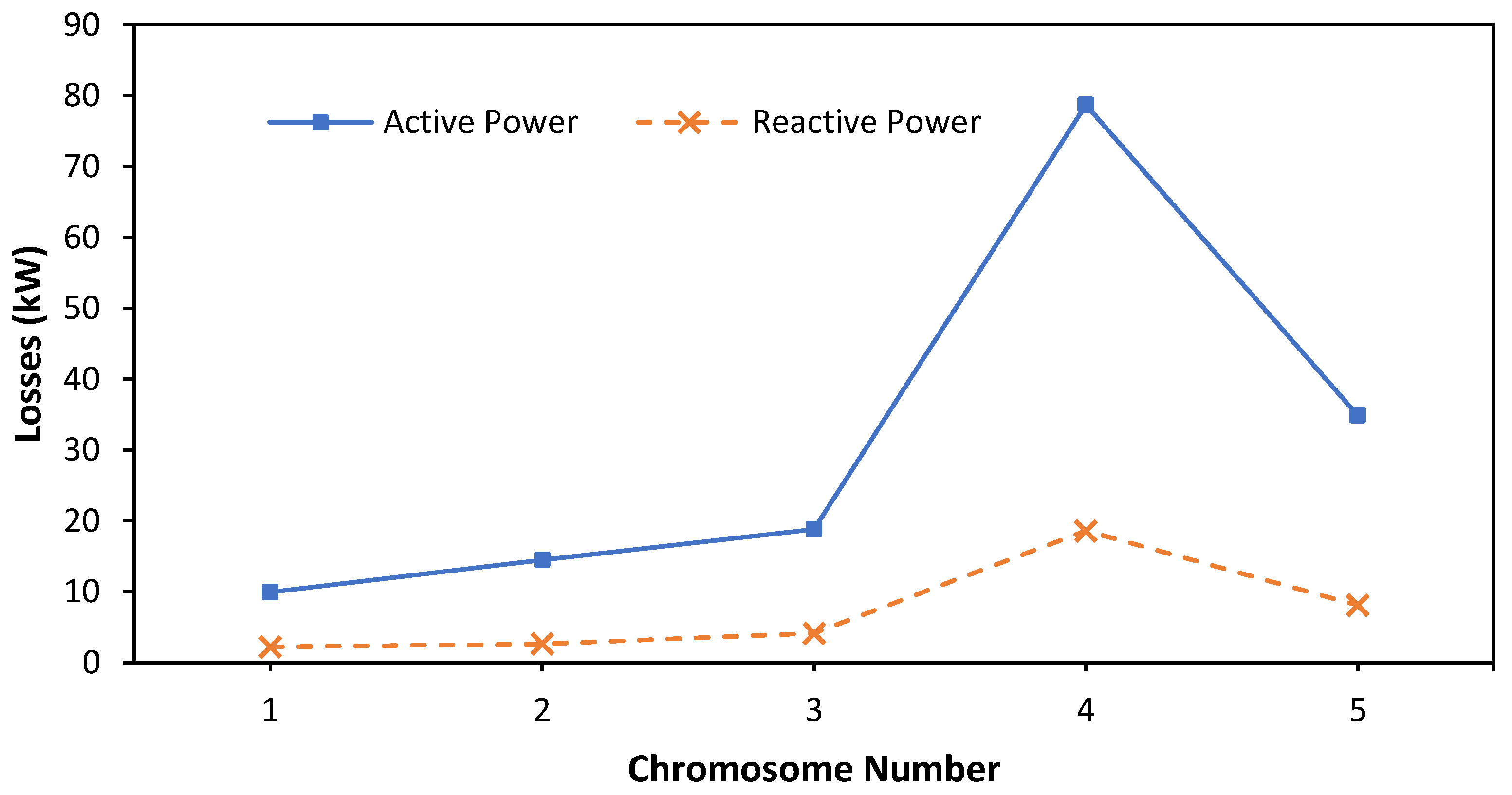
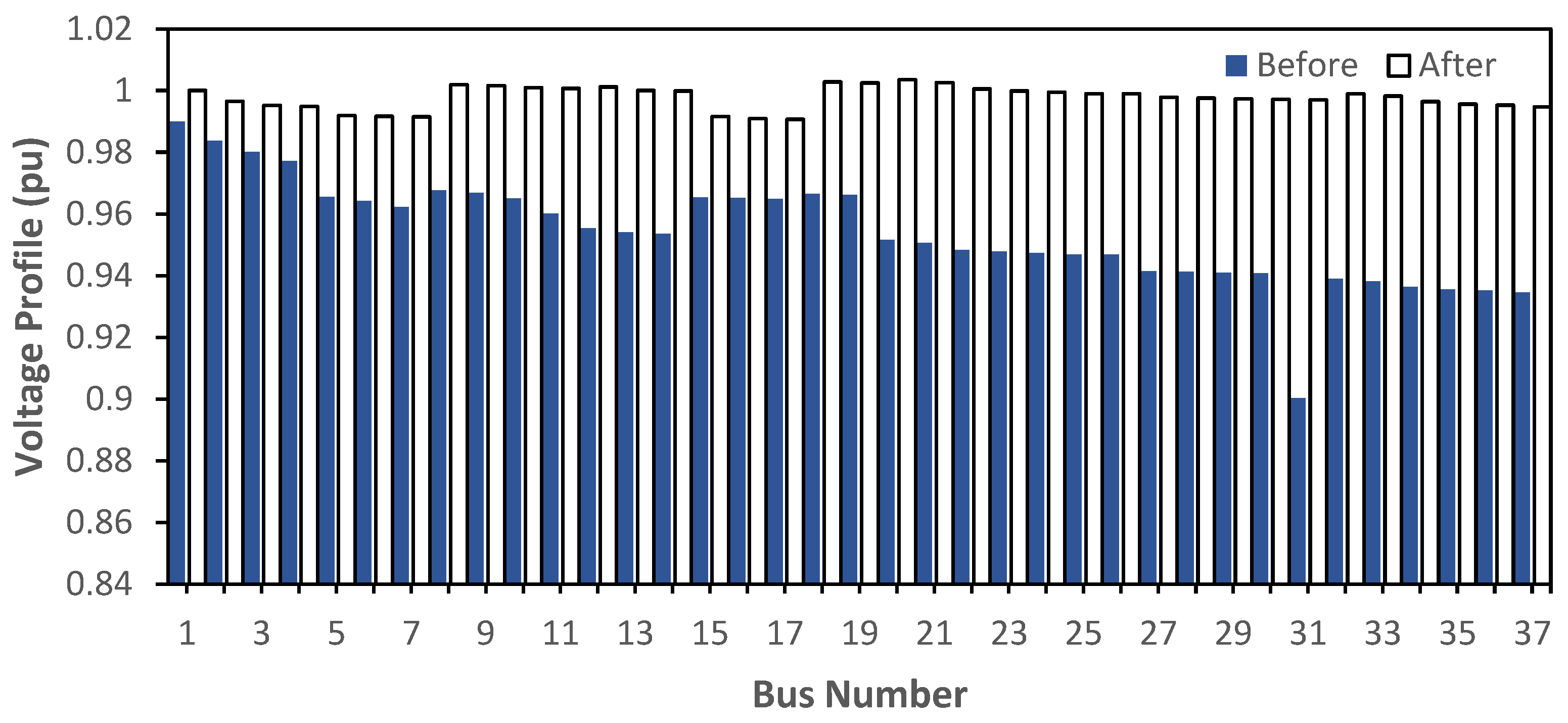
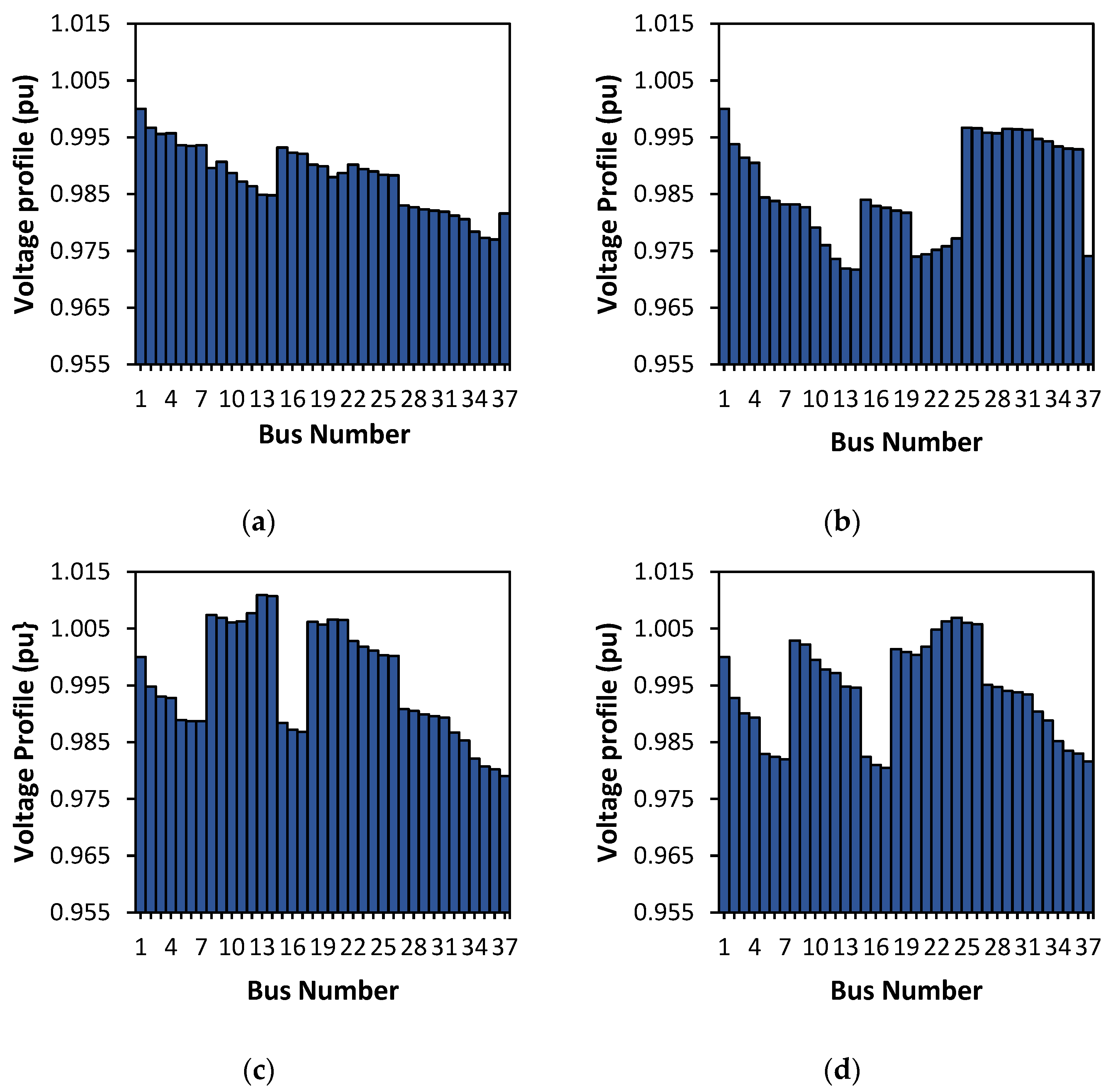
| DG Location (No Bus) | DG Capacity (kW) |
|---|---|
| Bus 18 | 190 |
| Bus 20 | 463 |
| Bus 32 | 370 |
| Active power losses after/before | 9.9443 kW/54.67337875 kW |
| % Loss Reduction | 81.8114% |
| Reactive power losses after/before | 2.2130 kVAr/13.76872173 kVAr |
| From Bus | To Bus | ETAP | GA | ||
|---|---|---|---|---|---|
| P Loss (kW) | Q Loss (kVAr) | P Loss (kW) | Q Loss (kVAr) | ||
| 1 | 2 | 1.2 | 0.4 | 1.7803 | 0.3564 |
| 2 | 3 | 0.6 | 0.1 | 0.5971 | 0.1195 |
| 3 | 4 | 0.2 | 0.4 | 0.2070 | 0.4145 |
| 4 | 5 | 1.0 | 0.2 | 1.1465 | 0.2295 |
| 5 | 6 | 0 | 0 | 0.1027 | 0.0206 |
| 6 | 7 | 0 | 0 | 0.1268 | 0.0254 |
| 7 | 8 | 0.3 | 0.1 | 0.2518 | 0.0504 |
| 7 | 9 | 0.3 | 0.1 | 0.0416 | 0.0083 |
| 8 | 10 | 0.1 | 0 | 0.2710 | 0.0542 |
| 10 | 11 | 0.2 | 0 | 0.2959 | 0.0592 |
| 11 | 12 | 0.1 | 0 | 0.4217 | 0.0844 |
| 12 | 13 | 0.2 | 0 | 0.1560 | 0.0312 |
| 13 | 14 | 0 | 0 | 0.0057 | 0.0011 |
| 5 | 15 | 0 | 0 | 0.0273 | 0.0055 |
| 15 | 16 | 0 | 0 | 0.0563 | 0.0113 |
| 16 | 17 | 0 | 0 | 0.0089 | 0.0018 |
| 8 | 18 | 0 | 0 | 0.3150 | 0.0603 |
| 18 | 19 | 0 | 0 | 0.0080 | 0.0016 |
| 12 | 20 | 0.2 | 0 | 1.2371 | 0.2297 |
| 20 | 21 | 0.1 | 0 | 0.3344 | 0.0413 |
| 21 | 22 | 0.3 | 0 | 0.6403 | 0.0282 |
| 22 | 23 | 0.1 | 0 | 0.1416 | 0.0122 |
| 23 | 24 | 0 | 0 | 0.0391 | 0.0239 |
| 24 | 25 | 0 | 0 | 0.0298 | 0.0013 |
| 25 | 26 | 0 | 0 | 0.0031 | 0.0028 |
| 1 | 27 | 1.5 | 0.2 | 0.2448 | 0.0357 |
| 27 | 28 | 0 | 0 | 0.0091 | 0.0063 |
| 27 | 29 | 0 | 0 | 0.0600 | 0.0190 |
| 29 | 30 | 0 | 0 | 0.0056 | 0.0011 |
| 29 | 31 | 0.2 | 0 | 0.0111 | 0.0022 |
| 27 | 32 | 0.7 | 0.1 | 0.4481 | 0.0897 |
| 32 | 33 | 0.2 | 0 | 0.2250 | 0.0450 |
| 33 | 34 | 0.4 | 0.1 | 0.4225 | 0.0846 |
| 34 | 35 | 0.2 | 0 | 0.1670 | 0.0334 |
| 35 | 36 | 0 | 0 | 0.0075 | 0.0015 |
| 35 | 37 | 0.1 | 0 | 0.0987 | 0.0198 |
| Total | 13.6 | 7.2 | 9.9443 | 2.2130 | |
| Load Condition | DG Location (No Bus) | DG Capacity (kW) | Active Power Losses after/before | Reactive Power Losses | % Loss Reduction |
|---|---|---|---|---|---|
| The 25% of load reduction | Bus 1 | 266 | 6.7279 kW/32.249 kW | 1.2999 kVAr | 79.2771 |
| Bus 5 | 277 | ||||
| Bus 21 | 340 | ||||
| The 50% of load reduction | Bus 11 | 207 | 2.9825 kW/14.064 kW | 0.7113 kVAr | 78.7933 |
| Bus 17 | 207 | ||||
| Bus 22 | 492 | ||||
| Average Loss Reduction (%) | 79.0352% | ||||
| Load Condition | DG Location (No Bus) | DG Capacity (kW) | Active Power Losses after/before | Reactive Power Losses | % Loss Reduction |
|---|---|---|---|---|---|
| The 25% load increase | Bus 9 | 483 | 15.2266 kW/93.172 kW | 3.1142 kVAr | 83.6575% |
| Bus 22 | 465 | ||||
| Bus 33 | 118 | ||||
| The 50% load increase | Bus 7 | 418 | 22.9233 kW/136.94 kW | 5.8553 kVAr | 83.2603% |
| Bus 24 | 445 | ||||
| Bus 34 | 466 | ||||
| The 75% load increase | Bus 8 | 400 | 35.3814 kW/190.34 kW | 7.1415 kVAr | 81.4114% |
| Bus 13 | 456 | ||||
| Bus 21 | 395 | ||||
| The 100% load increase | Bus 8 | 485 | 50.8650 kW/254.02 kW | 10.3729 kVAr | 79.9759% |
| Bus 23 | 489 | ||||
| Bus 24 | 302 | ||||
| Average Loss Reduction (%) | 82.0762% | ||||
| Reference | Basic Objectives | Benefits | Differences with Other Works |
|---|---|---|---|
| Zakaria et al., 2020 [42] | To determine the optimal capacity and location of DG by using genetic algorithm (GA) and ant colony algorithm (ACA). | Optimal DG location and capacity can reduce active power losses. | Its application is not in real systems but in IEEE systems with 57 buses. Otherwise, the load used is a fixed load. |
| Alinejad-Beromi et al., 2007 [43] | Optimal DG allocation to improve the voltage profile and reduce power losses. | The maximum average voltage occurs when DG is placed on bus 13, and the total active power losses occur when DG is placed on bus 9 and bus 13. | The load used in the study is a fixed load. |
| Naderipour et al., 2021 [44] | Allocation of capacitors and DG to minimize energy losses, peak losses, and capacitor costs in grid-connected and islanded modes, considering different load levels. | The total cost, loss costs, and load power losses at fixed loads are lower than other types of loads. |
|
| Wang and Zhong [45] | The allocation of DGs and capacitors takes the voltage profile into account. | DG is more influential in the improvement of the voltage profile. |
|
| Rao et al., 2013 [46] | The use of network reconfiguration in the utilization of DG. | Effect of the number of DG locations in reducing losses for different loads. |
|
| Kashyap et al., 2017 [47] | Optimal allocation of DG using the GA. | The GA provides a higher percentage |
|
| Nayeripour et al., 2013 [48] | Optimal location and capacity of multiple DG objects for transient stability. | Considers different safety and load types. | The system implemented is a Standard IEEE 33 bus system. |
| Yammani et al., 2016 [49] | Multi-objects for optimal DG allocation. | Combination of several functions of the power loss object, voltage profile, and cost. |
|
| Imran et al., 2014 [50] | DG optimal allocation and network reconfiguration. | Power losses and voltage profiles. | Applied for IEEE standard systems, which are not real systems in the field. |
| Prabha and Jayabarathi, 2016 [51] | DG placement and capacity. | Reducing power losses and improving voltage profiles. |
|
| Mistry and Roy, 2014 [52] | Increased loading with DG placement. | Increased loading capacity without violating the voltage range limit. |
|
| Moradi et al., 2014 [53] | Placement of the optimal location and capacity of DG and capacitors with the hybrid method. | Decreased power losses and increased voltage profile. | The system applied is a standard system: 33-bus IEEE. |
| Doagou-Mojarrad et al., 2013 [54] | Optimal DG location and capacity for energy losses, total cost of electricity, and total emissions as a multi-object. | Reducing overall electrical energy waste, overall electrical energy expense, and overall created pollution. | The system applied is a standard system: 33-bus IEEE. |
| Biswas et al., 2012 [55] | Optimal DG placement with technical and economic constraints. | Effect of DG placement on voltage sag disturbance. |
|
| Esmaili, et al. [56] | Placing and sizing of DGs to improve voltage stability and reduce losses. | Multiple DG placements do not always reduce losses. |
|
| Gitizadeh et al., 2012 [57] | Distribution network expansion planning with DG. | Can reduce Investment and Operational (I&O) and Unsupplied Energy (ENS) costs. |
|
| El-Zonkoly, 2011 [58] | DG placement with PSO. | Improved voltage profile and large losses. |
|
| Biswas, 2014 [59] | Placement and location, apart from reducing power losses and improving the voltage profile, are also large harmonics and voltage profiles. | In addition to obtaining the optimal DG location and capacity, total harmonic distortion (THD) results below 5% were also obtained. |
|
| Kim, et al., 2008 [60] | Determine DG location and capacity to obtain minimum power loss and improve voltage profile. | The total energy losses and DG capacity can be reduced if the load voltage characteristics are taken into account. |
|
| Vita, 2017 [61] | Location and DG capacity are needed to reduce power losses and improve the voltage profile. | Shows the effect of two different types of DG, namely photovoltaic (PV) and wind turbines. |
|
| Kalantari and Kazemi, 2011 [62] | Location and capacity of DG and capacitor bank with the GA. | Could reduce power losses and improve the voltage profile. |
|
| Parizad et al., 2010 [63] | Optimal location and capacity with the sensitivity method. | Demonstrates the efficiency of this method for improvement of the voltage profile, reduction in power losses, as well as increasing power transfer capacity, maximum load, and voltage stability margin. |
|
| Aman et al., 2014 [64] | The location and capacity of DGs in improving the loading system without violating the limits. | The penetration of 40% can reduce losses by 60–75%, the maximum loading increases by 15–40%, and, in general, the voltage improvement increases. | Radial distribution test on: Standard IEEE 16 bus systems: 16 bus, 33 bus and 69 bus system. |
| Rath et al., 2023 [65] | Genetic algorithm method for determining the location and size of DG on a radial distribution network. | Reducing power losses results in better results at higher penetrations and without violating the permissible voltage limits. | Starting from a simple radial system to the standard IEEE system. |
| El-Zonkoly, 2011 [66] | With multi-function objects, determine optimal DG location and capacity for different load models. |
| The system applied is the standard IEEE 30 bus system. |
| Moradi and Abedini, 2012 [23] | Determination of the optimal DG location and capacity to reduce power losses with the GA–PSO hybrid method. | Determination of its location using the GA and determination of its capacity using PSO:
| The system applied are the standard IEEE 33 bus and 69 bus system. |
| Radosavljevi et al., 2020 [67] | Placement and DG capacity from combined PV and wind. | Minimizing energy losses and increasing profits. |
|
| Karunarathne et al., 2020 [68] | Refinement of premature convergent algorithms, output accuracy, and complexity. | Reduction in power losses. |
|
| Siregar et al., 2020 [69] | Determining the optimal location and capacity of the DG using the GA and determining the size of the PV with an artificial neural network (ANN). |
| Without considering the increase in load. |
| Essa et al., 2021 [70] | Determine the best conditions for the reconfiguration and combination of DG with shunt capacitors. |
|
|
| Abbas et al., 2022 [71] | Optimal DG allocation for 24 h load variations. |
|
|
| Ntombela et al., 2023 [72] | Reduce computation time in DG optimal allocation and reconfiguration. | Attempting to reduce power loss and correct voltage requires less computation time. |
|
| Alizadeh et al., 2023 [73] | Determine optimal capacity and location in PV applications to reduce power losses and improve voltage profiles. | Improved voltage profile and reduced power losses. |
|
| Proposed approaches: | Minimizing power losses for sitting and sizing on DGs, considering the voltage profile at different loads using a genetic algorithm. | Power losses can be reduced by an average of 81.1695% for each load condition, and the voltage profile is maintained within the allowable range, namely between 0.95 and 1.05 p.u. (better). |
|
| Case | Load Level | |||
|---|---|---|---|---|
| Light (0.5) | Nominal (1.0) | Heavy (1.6) | ||
| Genetic Algorithm (GA) (37-bus Lingke Krueng Cut) | Size of DG in MW (Bus Number) | 0.207 (11) | 0.190 (18) | 0.418 (7) |
| 0.207 (17) | 0.463 (20) | 0.445 (24) | ||
| 0.492 (22) | 0.370 (32) | 0.466 (34) | ||
| Power Loss (kW) | 2.9825 | 9.9443 | 30.9055 | |
| % Loss Reduction | 78.7933 | 81.8114 | 80.3287 (80.3111) | |
| Minimum Voltage (p.u.) | 0.9925 | 0.9907 | 0.9713 | |
| Harmony Search Algorithm (HSA) (33-bus IEEE) [46] | Size of DG in MW (Bus Number) | 0.1303 (18) | 0.1370 (18) | 0.1939 (18) |
| 0.1777 (17) | 0.5724 (17) | 0.9108 (17) | ||
| 0.5029 (33) | 1.0462 (33) | 1.6115 (33) | ||
| Power Loss (kW) | 23.29 | 96.76 | 260.97 | |
| % Loss Reduction | 50.5 | 52.26 | 54.63 (52.4633) | |
| Minimum Voltage (p.u.) | 0.9831 | 0.9670 | 0.9437 | |
| Firework Algorithm (FWA) (33-bus IEEE) [50] | Size of DG in MW (Bus Number) | 0.2948 (14) | 0.5897 (14) | 0.9441 (14) |
| 0.0947 (18) | 0.1895 (18) | 0.3013 (18) | ||
| 0.5072 (32) | 1.0146 (32) | 1.6784 (32) | ||
| Power Loss (kW) | 21.37 | 88.68 | 238.07 | |
| % Loss Reduction | 54.58 | 56.24 | 58.57 (56.4633) | |
| Minimum Voltage (p.u.) | 0.9844 | 0.9680 | 0.9484 | |
| Reference | Parameter | Performance Result |
|---|---|---|
| Genetic Algorithm (GA) (33-bus IEEE) [47] | DG optimum location | 6 |
| DG optimal size (kW) | 2600 kW (2.6 MW) | |
| Power Loss (kW) | 111.03 | |
| % Loss Reduction | 47.39 | |
| Minimum Voltage (p.u.) | 0.9425 | |
| PSO (33-bus IEEE) [74,75] | DG optimum location | 6 |
| DG optimal size (kW) | 3150 kW (3.15 MW) | |
| Power Loss (kW) | 115.29 | |
| % Loss Reduction | 45.36 | |
| Minimum Voltage (p.u.) | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Siregar, R.H.; Away, Y.; Tarmizi; Akhyar. Minimizing Power Losses for Distributed Generation (DG) Placements by Considering Voltage Profiles on Distribution Lines for Different Loads Using Genetic Algorithm Methods. Energies 2023, 16, 5388. https://doi.org/10.3390/en16145388
Siregar RH, Away Y, Tarmizi, Akhyar. Minimizing Power Losses for Distributed Generation (DG) Placements by Considering Voltage Profiles on Distribution Lines for Different Loads Using Genetic Algorithm Methods. Energies. 2023; 16(14):5388. https://doi.org/10.3390/en16145388
Chicago/Turabian StyleSiregar, Ramdhan Halid, Yuwaldi Away, Tarmizi, and Akhyar. 2023. "Minimizing Power Losses for Distributed Generation (DG) Placements by Considering Voltage Profiles on Distribution Lines for Different Loads Using Genetic Algorithm Methods" Energies 16, no. 14: 5388. https://doi.org/10.3390/en16145388
APA StyleSiregar, R. H., Away, Y., Tarmizi, & Akhyar. (2023). Minimizing Power Losses for Distributed Generation (DG) Placements by Considering Voltage Profiles on Distribution Lines for Different Loads Using Genetic Algorithm Methods. Energies, 16(14), 5388. https://doi.org/10.3390/en16145388






