Opportunities to Improve Marine Power Cable Ratings with Ocean Bottom Temperature Models
Abstract
:1. Introduction
1.1. Significance of Marine Power Cables
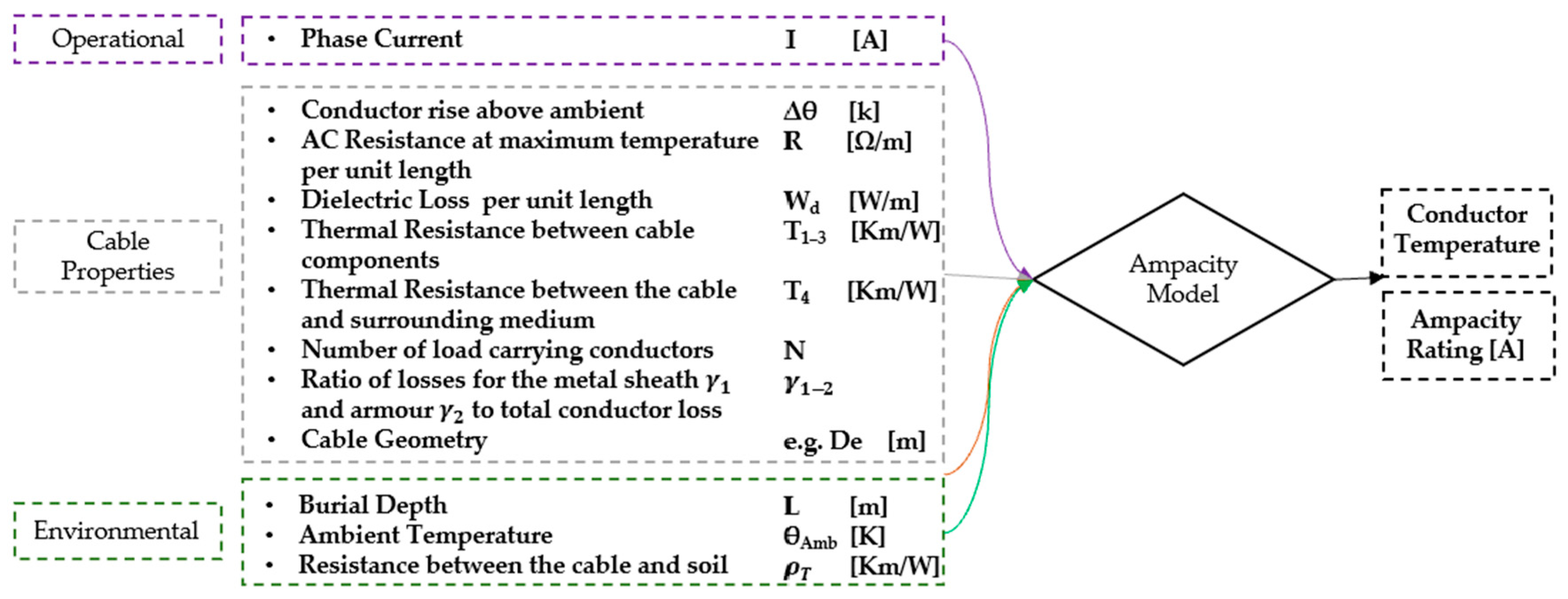
1.2. Cable Ampacity Evaluation Environmental Inputs and Shortcomings
1.3. Ocean Bottom Temperature Models
1.4. Paper Aims
- To devise a transparent method for improving the validation and utilization of publicly accessible OBT models for cable design using the Northwest European shelf AMM7 and AMM15 as exemplars (Section 3).
- To demonstrate the spatial and temporal variation in mean monthly modelled OBTs along “indicative” cable routes across the Northwest European Shelf (Section 4).
- To demonstrate the impact of applying these temporally varying OBT model outputs to IEC-based cable rating algorithms to cable conductor temperature and overall rating (Section 5).
2. Materials
2.1. Ocean Bottom Temperture Models
2.2. In Situ Measured Ocean Bottom Temperature Dataset Construction
- It removed erroneous entries, e.g., corrupted files, deployments with missing measurements, and files with corrupted metadata.
- It retained only those measurements within +/− 5m of the EmodNET bathymetry at each location.
3. Quality Control of In Situ Observations and Validation Methodology
3.1. Quality Controlled (QC) In Situ Database
- Bias Error:BE = modelled OBT − measured OBT
- Square error:SE = (modelled OBT − measured OBT)2
- Extreme positive anomalies > 3rd BE quartile + 3 × BE interquartile range.
- Extreme negative anomalies < 1st BE quartile − 3 × BE interquartile range.
3.2. Validation Methodology
- Mean Bias Error: MBE = (MBE ± σBE is reported).
- Mean Absolute Error: MAE = (MAE ± σMAE is reported).
- Bias Error Standard Deviation:
- Root Mean Square Error:
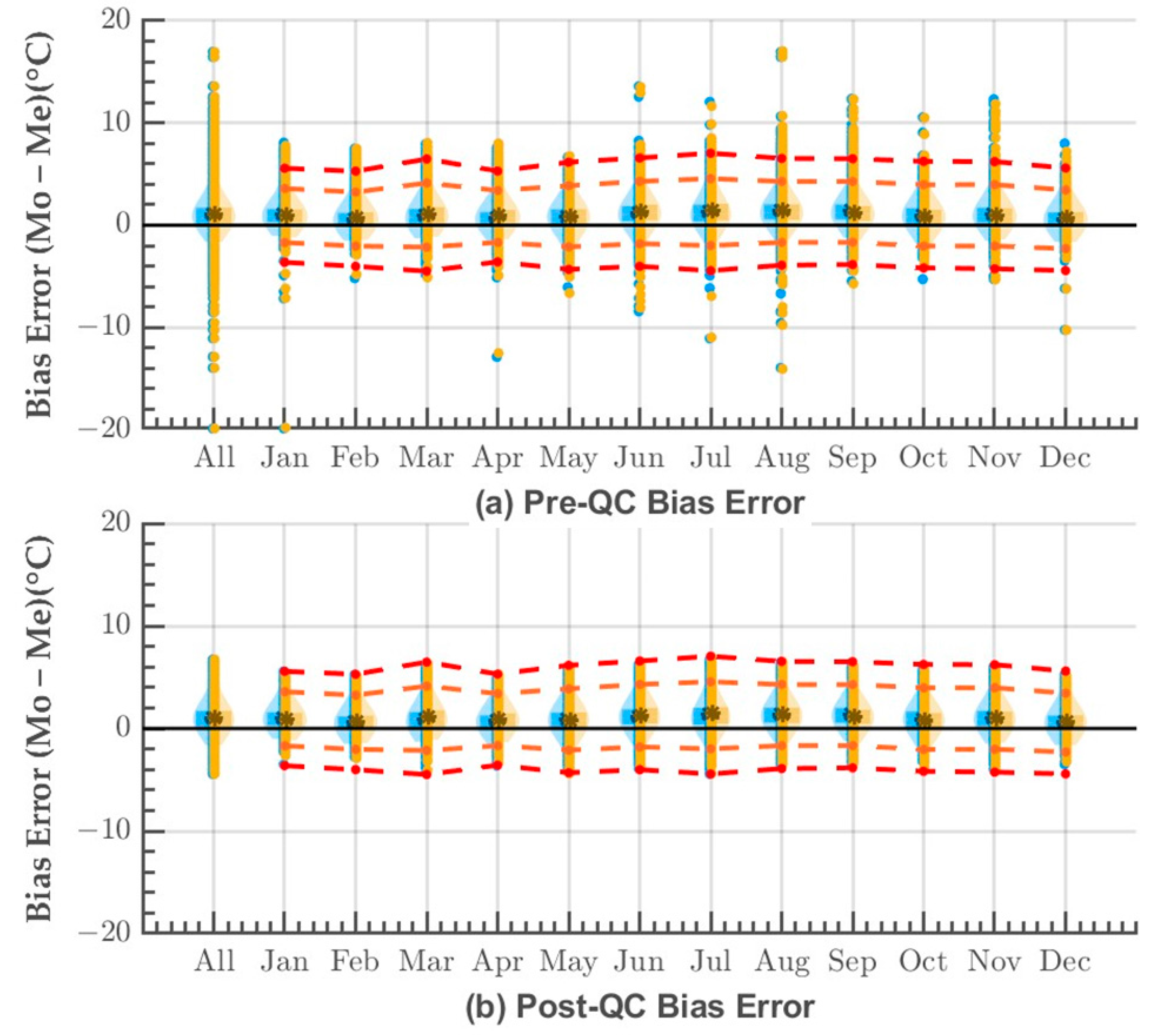
3.3. Quality Control and Validation Results
3.4. Validation Intepretation
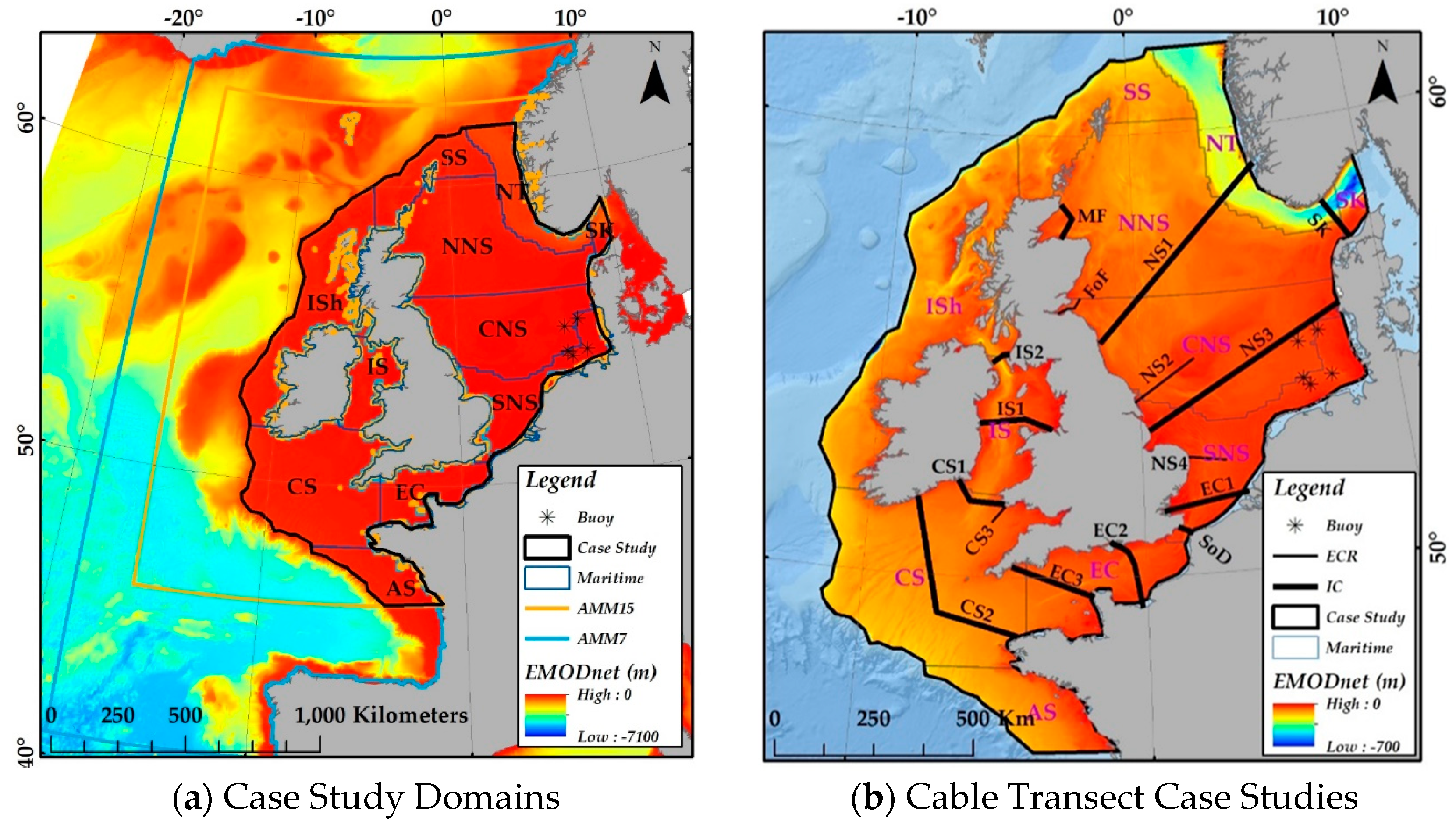
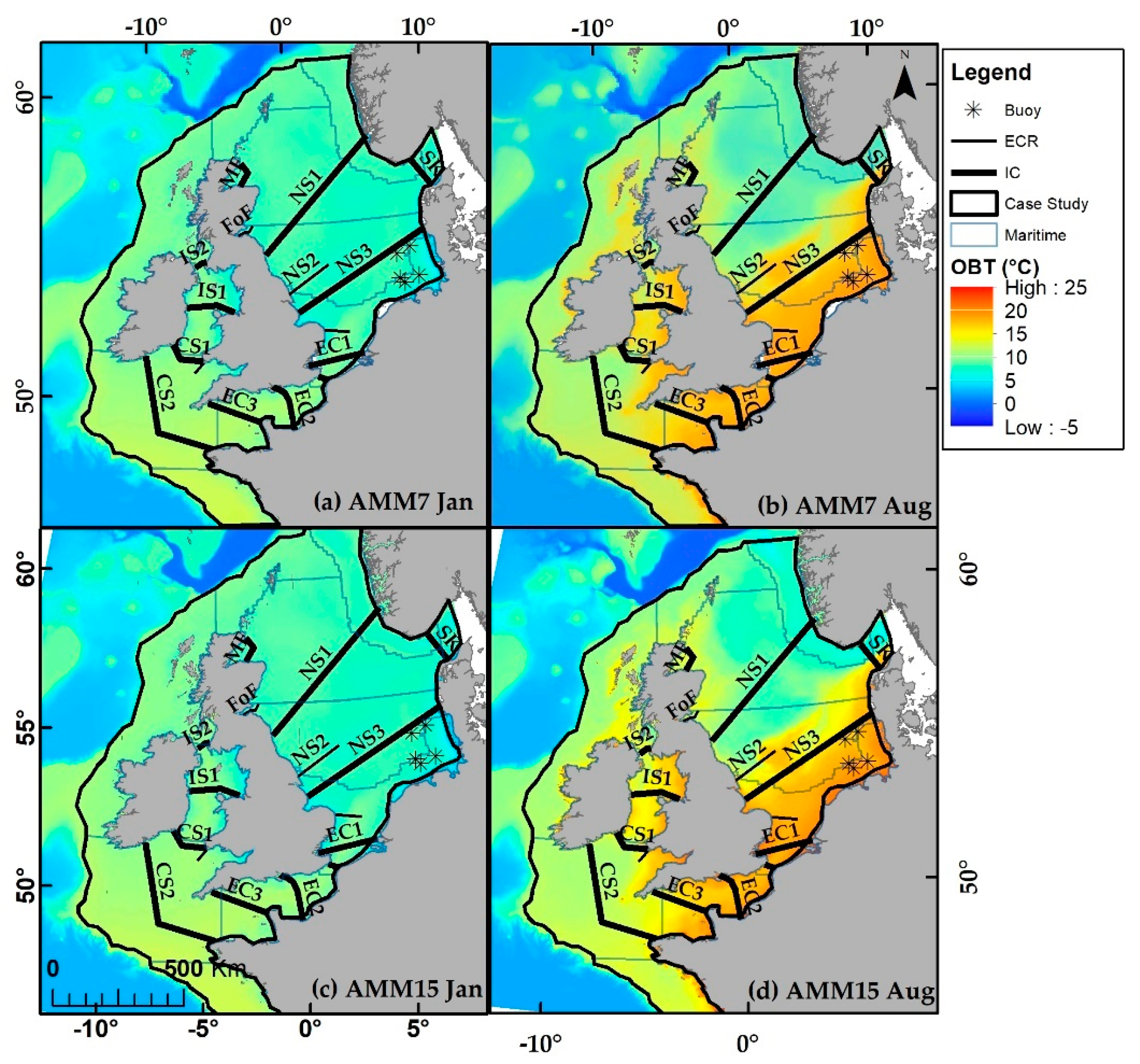
4. Spatial and Temporal Ambient Temperature Variation along Cable Routes
5. Implications for Cable Rating
- A fixed ambient temperature of 15 °C, which is commonly used in commercial projects and used as a base level for comparison.
- A fixed ambient temperature of the maximum OBT.
- A fixed ambient temperature of the mean OBT.
- An OBT time series, which is the most indicative of the true conditions at each site.
6. Discussion
7. Conclusions
- A method is presented for validating publicly available ocean bottom temperature models with equally accessible in situ observations from global databases.
- This validation method has been demonstrated on both the AMM7 and the AMM15 Northwest European Shelf physical models using 181,860, quality controlled, in situ measurements from the World Ocean Database.
- The validation demonstrates that both models perform are similar to the whole shelf and whole year statistics of 1.25 ± 1.06 °C (@ 1 STDEV) MAE for the AMM7 model and 1.27 ± 1.08 °C (@ 1 STDEV) MAE for the AMM15 one. Model performance is temporally and spatially variable, with the models performing better in the winter (October–May: 1.09 °C ≥ MBE ≥ 0.61 °C; and 1.66 °C ≥ RMSE ≥ 1.38 °C) and worse in the summer (June–September: 1.48 °C ≥ MBE ≥ 1.17; 2.2 °C ≥ RMSE ≥ 1.69 °C). Spatially, the model has a positive bias in the East Central North Sea and the German Bight, and it has a negative bias at the outer shelf margins and in the Norwegian Trench.
- Analysis of indicative cable routes across the Northwest European Shelf demonstrates that individual cable routes can experience along-cable temperature variations of >12 °C at single points in time, whilst at single locations, they can experience temperature variations of >15 °C over the course of a year.
- 1-D numerical modelling based on a HVDC bipole at a fixed depth and with fixed thermal soil parameters demonstrates that considering the spatial and temporal variation in OBT can result in a cable rating change of −4.1% and +7.8% across six example case studies.
- The magnitude of these variations demonstrate that a considered approach to OBT within cable models can result in both significant ratings (and hence capital expenditure and operating costs) gains and/or the avoidance of cable overheating. Further consideration of OBT does not require expensive additional in situ survey, but it can be confidently assessed from publicly available datasets with quantified uncertainties.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dix, J.K.; Hughes, T.J.; Emeana, C.J.; Pilgrim, J.A.; Henstock, T.J.; Gernon, T.M.; Thompson, C.E.L. Substrate Controls on the Life-Time Performance of Marine HV Cables. In Offshore Site Investigation Geotechnics 8th International Conference Proceeding; Society for Underwater Technology: London, UK, 2017; Volume 3, pp. 1–8. [Google Scholar]
- Zhao, X.; Liu, Y.; Wu, J.; Xiao, J.; Hou, J.; Gao, J.; Zhong, L. Technical and Economic Demands of HVDC Submarine Cable Technology for Global Energy Interconnection. Glob. Energy Interconnect. 2020, 3, 120–127. [Google Scholar] [CrossRef]
- Department for Business, Energy & Industrial Strategy. DUKES Digest of UK Energy Statistics Annual Data for UK, 2021; About This Release Information on Energy Production, Trade, and Consumption in the UK for Total Energy and by Specific Fuels; Department for Business, Energy & Industrial Strategy: London, UK, 2021; pp. 2–5. [Google Scholar]
- The Crown Estate. The Crown Estate Offshore Wind Report 2021; The Crown Estate: London, UK, 2021; pp. 1–49. [Google Scholar]
- BESS. British Energy Security Strategy. Gov.UK. 2022; pp. 1–33. Available online: https://assets.publishing.service.gov.uk/government/uploads/system/uploads/attachment_data/file/1069969/british-energy-security-strategy-web-accessible.pdf (accessed on 16 July 2023).
- Thomas, B.; McKee, N.J.D.; Kleist, J. Analysis of Standardized Precipitation Index (SPI) Data for Drought Assessment. Water 1993, 26, 1–72. [Google Scholar]
- IEC60287-1-1; Electric Cables—Part 1-1: Current Rating Equations (100% Load Factor) and Calculation of Losses—General. International Electrotechnical Commission: Geneva, Switzerland, 2023.
- Worzyk, T. Submarine Power Cables: Design, Installation, Repair, Environmental Aspects; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar] [CrossRef]
- Brakelmann, H.; Anders, G.J. Current Rating Considerations in Designing HVDC Cable Installations. IEEE Trans. Power Deliv. 2018, 33, 2315–2323. [Google Scholar] [CrossRef]
- de León, F.; Anders, G.J. Effects of Backfilling on Cable Ampacity Analyzed with the Finite Element Method. IEEE Trans. Power Deliv. 2008, 23, 537–543. [Google Scholar] [CrossRef]
- Anders, G.J. Rating of Electric Power Cables in Unfavorable Thermal Environment; Wiley: Hoboken, NJ, USA, 2010; ISBN 9780471718741. [Google Scholar]
- Hanna, M.A.; Chikhani, A.Y.; Salama, M.M.A. Thermal Analysis of Power Cables in Multi-Layered Soil. IEEE Trans. Power Deliv. 1994, 9, 572–578. [Google Scholar] [CrossRef]
- Garrido, C.; Otero, A.F.; Cidrás, J. Theoretical Model to Calculate Steady-State and Transient Ampacity and Temperature in Buried Cables. IEEE Trans. Power Deliv. 2003, 18, 667–678. [Google Scholar] [CrossRef]
- Brakelmann, H.; Stammen, J. Thermal Analysis of Submarine Cable Routes: LSM or FEM? In Proceedings of the National Proceedings Power and Energy Conference (PECon), Putra Jaya, Malaysia, 28–29 November 2006; pp. 560–565. [Google Scholar] [CrossRef]
- De Lieto Vollaro, R.; Fontana, L.; Vallati, A. Thermal Analysis of Underground Electrical Power Cables Buried in Non-Homogeneous Soils. Appl. Therm. Eng. 2011, 31, 772–778. [Google Scholar] [CrossRef]
- Callender, G.; Ellis, D.; Goddard, K.F.; Dix, J.K.; Pilgrim, J.A.; Erdmann, M. Low Computational Cost Model for Convective Heat Transfer from Submarine Cables. IEEE Trans. Power Deliv. 2021, 36, 760–768. [Google Scholar] [CrossRef]
- Duraisamy, N.; Gooi, H.B.; Ukil, A. Ampacity Estimation for Submarine Power Cables Installed in Saturated Seabed-Experimental Studies. IEEE Trans. Ind. Appl. 2020, 56, 6229–6237. [Google Scholar] [CrossRef]
- Hughes, T.J.; Henstock, T.J.; Pilgrim, J.A.; Dix, J.K.; Gernon, T.M.; Thompson, C.E.L. Effect of Sediment Properties on the Thermal Performance of Submarine HV Cables. IEEE Trans. Power Deliv. 2015, 30, 2443–2450. [Google Scholar] [CrossRef]
- Hernandez Colin, M.A.; Dix, J.; Pilgrim, J. Export cable rating optimisation by wind power ramp and thermal risk estimation. IET Renew. Power Gener. 2021, 15, 1564–1581. [Google Scholar] [CrossRef]
- Werle, V.; Rouven, P.; Rathke, C.; Freitag, C.; Kumbartzky, G. Long term temperature measurements compared with transient calculation according to IEC 60853-2. In Proceedings of the JiCable 2019—10th International Conference on Insulated Power Cables, Paris, France, 23–27 June 2019; p. D7-4. [Google Scholar]
- Dix, J.; Rochat, E.; Rizzo, E. How understanding spatial and temporal variation of ocean bottom temperature can significantly enhance the interpretation of DTS data from marine HV cables. In Proceedings of the JiCable 2023, Lyon, France, 18–22 June 2023; p. A7-2. [Google Scholar]
- Müller, C.; Usbeck, R.; Miesner, F. Temperatures in Shallow Marine Sediments: Influence of Thermal Properties, Seasonal Forcing, and Man-Made Heat Sources. Appl. Therm. Eng. 2016, 108, 20–29. [Google Scholar] [CrossRef]
- King, R.R.; While, J.; Martin, M.J.; Lea, D.J.; Lemieux-Dudon, B.; Waters, J.; O’Dea, E. Improving the Initialisation of the Met Office Operational Shelf-Seas Model. Ocean Model. 2018, 130, 1–14. [Google Scholar] [CrossRef]
- Díaz, H.; Guedes Soares, C. Review of the Current Status, Technology and Future Trends of Offshore Wind Farms. Ocean Eng. 2020, 209, 107381. [Google Scholar] [CrossRef]
- Ardelean, M.; Minnebo, P. HVDC Submarine Power Cables in the World; Publications Office of the European Union: Luxembourg, 2015; ISBN 9789279527852. [Google Scholar]
- IEC60287-3-1; Electric Cables—Calculation of the Current Rating, Part 3-1: Operating Conditions—Site Reference Conditions. International Electrotechnical Commission: Geneva, Switzerland, 2017.
- Nielsen, T.V.M.; Jakobsen, S.; Savaghebi, M. Dynamic Rating of Three-Core XLPE Submarine Cables Considering the Impact of Renewable Power Generation. In Proceedings of the 2019 IEEE 13th International Conference on Compatibility, Power Electronics and Power Engineering (CPE-POWERENG), Sonderborg, Denmark, 23–25 April 2019. [Google Scholar] [CrossRef] [Green Version]
- Tonani, M.; Pequignet, C.; King, R.; Sykes, P.; Mcconnell, N.; Siddorn, J. North West European Shelf Production Centre NORTHWESTSHELF_ANALYSIS_FORECAST_PHYS_004_013; Copernicus Marine Service: Toulouse, France, 2021; pp. 1–46. [Google Scholar]
- Tonani, M.; Sykes, P.; King, R.R.; McConnell, N.; Péquignet, A.C.; O’Dea, E.; Graham, J.A.; Polton, J.; Siddorn, J. The Impact of a New High-Resolution Ocean Model on the Met Office North-West European Shelf Forecasting System. Ocean Sci. 2019, 15, 1133–1158. [Google Scholar] [CrossRef] [Green Version]
- Graham, J.A.; O’Dea, E.; Holt, J.; Polton, J.; Hewitt, H.T.; Furner, R.; Guihou, K.; Brereton, A.; Arnold, A.; Wakelin, S.; et al. AMM15: A New High-Resolution NEMO Configuration for Operational Simulation of the European North-West Shelf. Geosci. Model Dev. 2018, 11, 681–696. [Google Scholar] [CrossRef] [Green Version]
- Cowley, R.; Killick, R.E.; Boyer, T.; Gouretski, V.; Reseghetti, F.; Kizu, S.; Palmer, M.D.; Cheng, L.; Storto, A.; Le Menn, M.; et al. International Quality-Controlled Ocean Database (IQuOD) v0.1: The Temperature Uncertainty Specification. Front. Mar. Sci. 2021, 8, 689695. [Google Scholar] [CrossRef]
- Good, S.A.; Martin, M.J.; Rayner, N.A. EN4: Quality Controlled Ocean Temperature and Salinity Profiles and Monthly Objective Analyses with Uncertainty Estimates. J. Geophys. Res. Ocean. 2013, 118, 6704–6716. [Google Scholar] [CrossRef]
- Morris, D.J.; Pinnegar, J.K.; Maxwell, D.L.; Dye, S.R.; Fernand, L.J.; Flatman, S.; Williams, O.J.; Rogers, S.I. Over 10 Million Seawater Temperature Records for the United Kingdom Continental Shelf between 1880 and 2014 from 17 Cefas (United Kingdom Government) Marine Data Systems. Earth Syst. Sci. Data 2018, 10, 27–51. [Google Scholar] [CrossRef] [Green Version]
- Garcia, H.E.; Boyer, T.P.; Locarnini, R.A.; Baranova, O.K.; Zweng, M.M. World Ocean Database 2018: User’s Manual (Prerelease); Mishonov, A.V., Ed.; NOAA: Silver Spring, MD, USA, 2018; Volume 12, pp. 29–34. [Google Scholar]
- Cheng, L.; Abraham, J.; Goni, G.; Boyer, T.; Wijffels, S.; Cowley, R.; Gouretski, V.; Reseghetti, F.; Kizu, S.; Dong, S.; et al. XBT Science: Assessment of Instrumental Biases and Errors. Bull. Am. Meteorol. Soc. 2016, 97, 923–933. [Google Scholar] [CrossRef]
- Moumena, A.; Guessoum, A. Fast Anomaly Detection Using Boxplot Rule for Multivariate Data in Cooperative Wideband Cognitive Radio in the Presence of Jammer. Secur. Commun. Netw. 2015, 8, 212–219. [Google Scholar] [CrossRef]
- Diaz-Aguiló, M.; De León, F.; Jazebi, S.; Terracciano, M. Ladder-type soil model for dynamic thermal rating of underground power cables. IEEE Power Energy Technol. Syst. J. 2014, 1, 21–30. [Google Scholar] [CrossRef]
- Goto, S.; Yamano, M.; Morita, S.; Kanamatsu, T.; Hachikubo, A.; Kataoka, S.; Tanahashi, M.; Matsumoto, R. Physical and thermal properties of mud-dominant sediment from the Joetsu Basin in the eastern margin of the Japan Sea. Mar. Geophys. Res. 2017, 38, 393–407. [Google Scholar] [CrossRef] [Green Version]








| Pre-QC | AMM7 | AMM15 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Month | n | MBE | σMBE | MAE | σMAE | RMSE | MBE | σMBE | MAE | σMAE | RMSE |
| All | 182,637 | 1.08 | 1.35 | 1.29 | 1.15 | 1.72 | 1.05 | 1.33 | 1.28 | 1.12 | 1.70 |
| January | 13,318 | 0.97 | 1.16 | 1.12 | 1.03 | 1.52 | 1.04 | 1.2 | 1.17 | 1.07 | 1.59 |
| February | 18,901 | 0.7 | 1.16 | 0.98 | 0.94 | 1.36 | 0.65 | 1.19 | 0.97 | 0.95 | 1.36 |
| March | 12,421 | 1.1 | 1.28 | 1.26 | 1.12 | 1.68 | 0.92 | 1.29 | 1.16 | 1.07 | 1.58 |
| April | 12,277 | 0.96 | 1.21 | 1.13 | 1.04 | 1.54 | 0.77 | 1.19 | 1.02 | 0.98 | 1.42 |
| May | 18,025 | 0.82 | 1.3 | 1.21 | 0.94 | 1.53 | 0.85 | 1.25 | 1.19 | 0.94 | 1.51 |
| June | 17,340 | 1.31 | 1.33 | 1.48 | 1.13 | 1.86 | 1.18 | 1.28 | 1.37 | 1.08 | 1.74 |
| July | 19,144 | 1.48 | 1.66 | 1.65 | 1.5 | 2.23 | 1.37 | 1.58 | 1.56 | 1.4 | 2.09 |
| August | 20,589 | 1.41 | 1.41 | 1.54 | 1.26 | 1.99 | 1.4 | 1.37 | 1.53 | 1.22 | 1.96 |
| September | 16,881 | 1.27 | 1.38 | 1.42 | 1.23 | 1.88 | 1.41 | 1.4 | 1.53 | 1.27 | 1.99 |
| October | 13,844 | 0.82 | 1.21 | 1.13 | 0.92 | 1.46 | 0.94 | 1.23 | 1.22 | 0.95 | 1.55 |
| November | 12,390 | 0.99 | 1.24 | 1.18 | 1.06 | 1.59 | 1.04 | 1.24 | 1.22 | 1.06 | 1.61 |
| December | 7507 | 0.68 | 1.19 | 1.02 | 0.92 | 1.37 | 0.66 | 1.2 | 1.02 | 0.92 | 1.37 |
| Post-QC | AMM7 | AMM15 | |||||||||
| All | 181,860 | 1.03 | 1.27 | 1.25 | 1.06 | 1.64 | 1.06 | 1.29 | 1.27 | 1.08 | 1.67 |
| January | 13,213 | 1 | 1.09 | 1.13 | 0.95 | 1.48 | 0.94 | 1.05 | 1.08 | 0.91 | 1.41 |
| February | 18,785 | 0.61 | 1.12 | 0.94 | 0.87 | 1.28 | 0.67 | 1.09 | 0.95 | 0.86 | 1.28 |
| March | 12,397 | 0.91 | 1.26 | 1.15 | 1.05 | 1.56 | 1.09 | 1.25 | 1.25 | 1.09 | 1.66 |
| April | 12,202 | 0.75 | 1.11 | 0.99 | 0.91 | 1.34 | 0.93 | 1.13 | 1.1 | 0.97 | 1.47 |
| May | 18,007 | 0.85 | 1.24 | 1.18 | 0.93 | 1.5 | 0.82 | 1.29 | 1.21 | 0.93 | 1.52 |
| June | 17,318 | 1.17 | 1.26 | 1.36 | 1.05 | 1.72 | 1.3 | 1.31 | 1.47 | 1.11 | 1.85 |
| July | 19,108 | 1.36 | 1.56 | 1.55 | 1.37 | 2.07 | 1.48 | 1.64 | 1.64 | 1.47 | 2.2 |
| August | 20,480 | 1.38 | 1.29 | 1.5 | 1.14 | 1.88 | 1.38 | 1.32 | 1.51 | 1.18 | 1.91 |
| September | 16,667 | 1.34 | 1.23 | 1.46 | 1.08 | 1.82 | 1.19 | 1.2 | 1.34 | 1.03 | 1.69 |
| October | 13,828 | 0.93 | 1.21 | 1.21 | 0.94 | 1.53 | 0.82 | 1.19 | 1.13 | 0.91 | 1.45 |
| November | 12,359 | 1.02 | 1.17 | 1.2 | 0.99 | 1.56 | 0.98 | 1.18 | 1.16 | 0.99 | 1.53 |
| December | 7496 | 0.66 | 1.18 | 1.01 | 0.89 | 1.35 | 0.67 | 1.16 | 1.01 | 0.89 | 1.35 |
| Mean Monthly OBT Distribution and Variability (°C) | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Transects | min | max | range | mean | p25 | p50 | p75 | iqr | stdev |
| SK | 3.7 | 18.5 | 14.8 | 8.6 | 6.4 | 7.2 | 9.3 | 2.8 | 3.2 |
| MF | 6.1 | 15.7 | 9.6 | 9.7 | 7.4 | 9.2 | 12.0 | 4.6 | 2.3 |
| FoF | 5.2 | 16.4 | 11.2 | 9.7 | 7.0 | 9.5 | 12.3 | 5.2 | 2.6 |
| NS 1 | 6.3 | 13.3 | 7.0 | 8.2 | 7.3 | 8.0 | 8.8 | 1.5 | 1.1 |
| NS 2 | 5.3 | 17.0 | 11.8 | 10.3 | 7.5 | 9.9 | 12.7 | 5.2 | 3.0 |
| NS 3 | 3.4 | 19.3 | 15.9 | 10.8 | 7.4 | 10.3 | 14.4 | 7.0 | 3.7 |
| NS 4 | 5.3 | 18.4 | 13.1 | 11. 9 | 8.0 | 11.2 | 15.8 | 7.8 | 4.0 |
| SoD | 7.0 | 19.4 | 12.4 | 12.9 | 9.2 | 12.2 | 16.3 | 7.1 | 3.7 |
| EC 1 | 5.3 | 20.6 | 15.3 | 12.6 | 8.8 | 11.6 | 16.6 | 7.9 | 4.3 |
| EC 2 | 6.7 | 20.8 | 14.2 | 13.1 | 9.8 | 12.4 | 16.4 | 6.7 | 3.6 |
| EC 3 | 9.2 | 18.0 | 8.8 | 12.7 | 10.3 | 12.3 | 14.6 | 4.3 | 2.3 |
| CS 1 | 8.2 | 16.5 | 8.2 | 11.4 | 9.5 | 11.1 | 12.8 | 3.3 | 2.1 |
| CS 2 | 8.7 | 15.7 | 7.1 | 11.3 | 10.6 | 11.2 | 11.9 | 1.3 | 1.1 |
| CS 3 | 8.3 | 16.7 | 8.4 | 12.0 | 9.5 | 11.7 | 13.9 | 4.4 | 2.4 |
| IS 1 | 4.9 | 19.1 | 14.2 | 11.5 | 8.7 | 11.3 | 14.1 | 5.4 | 3.0 |
| IS 2 | 7.1 | 15.3 | 8.2 | 10.9 | 8.6 | 10.8 | 13.1 | 4.5 | 2.4 |
| Case Study | Location | Scenario | Ambient OBT | Rating | Rating % Difference from 15 °C |
|---|---|---|---|---|---|
| EC 2 | A: Thermal High | 15 °C fixed | 15.0 | 1844 | - |
| Mean OBT | 12.9 | 1878 | 1.8 | ||
| Max OBT | 19.4 | 1768 | −4.1 | ||
| OBT Time Series | Dynamic | 1869 | 1.4 | ||
| B: Thermal Low | 15 °C fixed | 15.0 | 1844 | - | |
| Mean OBT | 13.1 | 1876 | 1.7 | ||
| Max OBT | 17.7 | 1797 | −2.5 | ||
| OBT Time Series | Dynamic | 1858 | 0.8 | ||
| NS1 | A: Thermal High | 15 °C fixed | 15.0 | 1844 | - |
| Mean OBT | 9.4 | 1937 | 5.0 | ||
| Max OBT | 12.1 | 1892 | 2.6 | ||
| OBT Time Series | Dynamic | 1925 | 4.4 | ||
| B: Thermal Low | 15 °C fixed | 15.0 | 1844 | - | |
| Mean OBT | 7.5 | 1967 | 6.7 | ||
| Max OBT | 7.9 | 1959 | 6.2 | ||
| OBT Time Series | Dynamic | 1964 | 6.5 | ||
| SK4 | A: Thermal High | 15 °C fixed | 15.0 | 1844 | - |
| Mean OBT | 10.7 | 1915 | 3.9 | ||
| Max OBT | 17.7 | 1798 | −2.5 | ||
| OBT Time Series | Dynamic | 1900 | 3.0 | ||
| B: Thermal Low | 15 °C fixed | 15.0 | 1844 | - | |
| Mean OBT | 6.3 | 1985 | 7.6 | ||
| Max OBT | 6.4 | 1983 | 7.5 | ||
| OBT Time Series | Dynamic | 1987 | 7.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Duell, J.; Dix, J.; Callender, G.; Henstock, T.; Porter, H. Opportunities to Improve Marine Power Cable Ratings with Ocean Bottom Temperature Models. Energies 2023, 16, 5454. https://doi.org/10.3390/en16145454
Duell J, Dix J, Callender G, Henstock T, Porter H. Opportunities to Improve Marine Power Cable Ratings with Ocean Bottom Temperature Models. Energies. 2023; 16(14):5454. https://doi.org/10.3390/en16145454
Chicago/Turabian StyleDuell, Jon, Justin Dix, George Callender, Tim Henstock, and Hannah Porter. 2023. "Opportunities to Improve Marine Power Cable Ratings with Ocean Bottom Temperature Models" Energies 16, no. 14: 5454. https://doi.org/10.3390/en16145454
APA StyleDuell, J., Dix, J., Callender, G., Henstock, T., & Porter, H. (2023). Opportunities to Improve Marine Power Cable Ratings with Ocean Bottom Temperature Models. Energies, 16(14), 5454. https://doi.org/10.3390/en16145454






