Hydrogen Spillover in Tungsten Oxide Bronzes as Observed by Broadband Neutron Spectroscopy
Abstract
1. Introduction
2. Materials and Methods
2.1. Catalyst Preparation
2.2. Characterization
2.3. Neutron Scattering Measurements at VESUVIO
2.4. Ab Initio Modelling
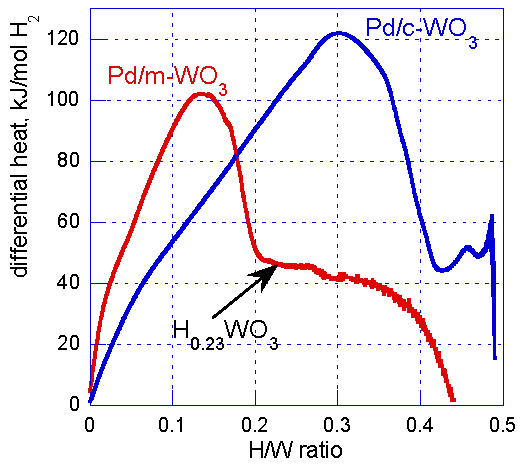
3. Results and Discussion
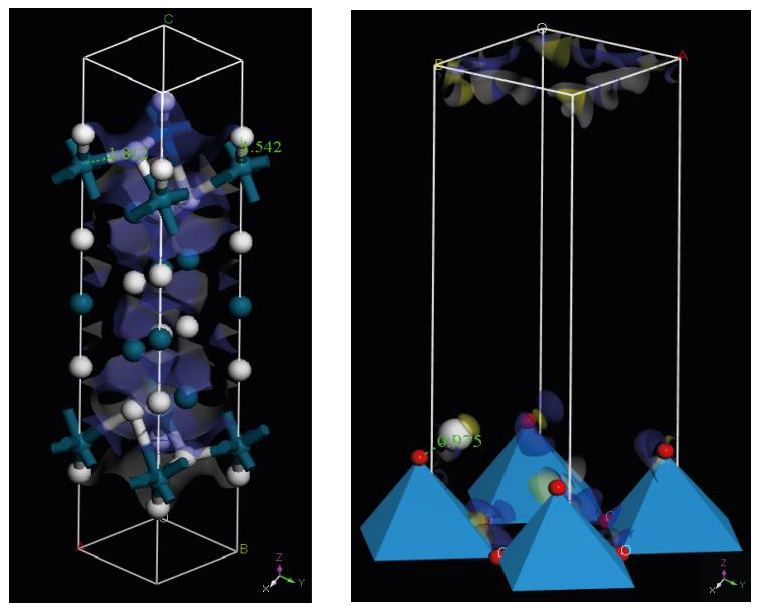
3.1. Ab Initio Modelling
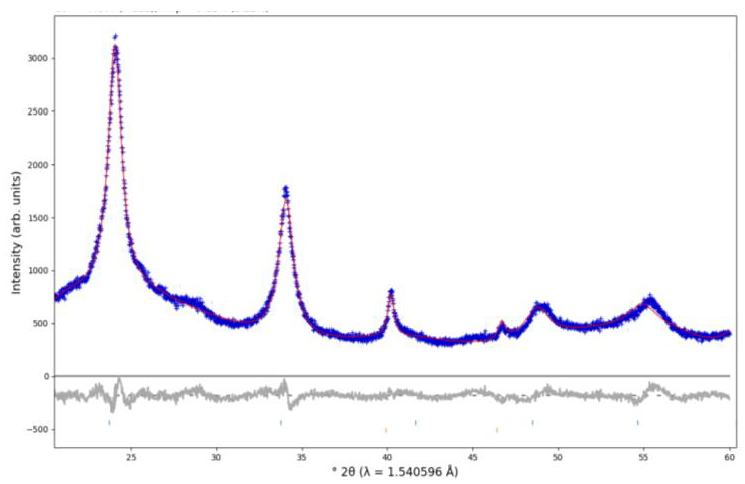
3.2. Characterization
3.3. Neutron Scattering Measurements
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kosydar, R.; Kolodziej, M.; Lalik, E.; Gurgul, J.; Mordarski, G.; Drelinkiewicz, A. The role of hydrogen bronzes in the hydrogenation of polyfunctional reagents: Cinnamaldehyde, furfural and 5-hydroxymethylfurfural over Pd/HxWO3 and Pd/HxMoO3 catalysts. Int. J. Hydrogn Energy 2022, 47, 2347–2365. [Google Scholar] [CrossRef]
- Mobtakeri, S.; Habashyani, S.; Gür, E. Highly Responsive Pd-Decorated MoO3 Nanowall H2 Gas Sensors Obtained from In-Situ-Controlled Thermal Oxidation of Sputtered MoS2 Films. ACS Appl. Mater. Interfaces 2022, 14, 25741–25752. [Google Scholar] [CrossRef]
- Rojas, S.; Roble, M.; Morales-Ferreiro, J.O.; Diaz-Droguett, D.E. Comparative study on the hydrogen storage capacity of crystalline and amorphous nanomaterials of MoO3: Effect of a catalytic Pd capping. Ionics 2018, 24, 3101–3111. [Google Scholar] [CrossRef]
- Xu, K.; Liao, N.; Xue, W.; Zhou, H. First principles investigation on MoO3 as room temperature and high temperature hydrogen gas sensor. Int. J. Hydrogn Energy 2020, 45, 9252–9259. [Google Scholar] [CrossRef]
- Fei, S.X.; Han, B.; Li, L.L.; Mei, P.; Zhu, T.; Yang, M.; Cheng, H.S. A study on the catalytic hydrogenation of N-ethylcarbazole on the mesoporous Pd/MoO3 catalyst. Int. J. Hydrogn Energy 2017, 42, 25942–25950. [Google Scholar] [CrossRef]
- Kolodziej, M.; Drelinkiewicz, A.; Lalik, E.; Gurgul, J.; Duraczynska, D.; Kosydar, R. Activity/selectivity control in Pd/HxMoO3 catalyzed cinnamaldehyde hydrogenation. Appl. Catal. A-Gen. 2016, 515, 60–71. [Google Scholar] [CrossRef]
- Kolodziej, M.; Lalik, E.; Colmenares, J.C.; Lisowski, R.; Gurgul, J.; Duraczynska, D.; Drelinkiewicz, A. Physicochemical and catalytic properties of Pd/MoO3 prepared by the sonophotodeposition method. Mater. Chem. Phys. 2018, 204, 361–372. [Google Scholar] [CrossRef]
- Kuwahara, Y.; Okada, M.; Ge, H.; Yamashita, H. Hydrodeoxygenation of Aromatic Ketones under Mild Conditions over Pd-loaded Hydrogen Molybdenum Bronze with Plasmonic Features. Chem. Lett. 2022, 51, 166–169. [Google Scholar] [CrossRef]
- Matsuda, T.; Ohno, T.; Sakagami, H.; Takahashi, N. Reduction of MoO3 to porous molybdenum oxides and its catalytic properties for alkane isomerization. J. Jpn. Pet. Inst. 2007, 50, 229–239. [Google Scholar] [CrossRef]
- Moberg, D.R.; Thibodeau, T.J.; Amar, F.G.; Frederick, B.G. Mechanism of Hydrodeoxygenation of Acrolein on a Cluster Model of MoO3. J. Phys. Chem. C 2010, 114, 13782–13795. [Google Scholar] [CrossRef]
- Thibodeau, T.J.; Canney, A.S.; DeSisto, W.J.; Wheeler, M.C.; Amar, F.G.; Frederick, B.G. Composition of tungsten oxide bronzes active for hydrodeoxygenation. Appl. Catal. A-Gen. 2010, 388, 86–95. [Google Scholar] [CrossRef]
- Xi, Y.J.; Chen, Z.X.; Kiat, V.G.W.; Huang, L.; Cheng, H.S. On the mechanism of catalytic hydrogenation of thiophene on hydrogen tungsten bronze. Phys. Chem. Chem. Phys. 2015, 17, 9698–9705. [Google Scholar] [CrossRef] [PubMed]
- Shaikh, S.F.; Ghule, B.G.; Shinde, P.V.; Raut, S.D.; Gore, S.K.; Ubaidullah, M.; Mane, R.S.; Al-Enizi, A.M. Continuous hydrothermal flow-inspired synthesis and ultra-fast ammonia and humidity room-temperature sensor activities of WO3 nanobricks. Mater. Res. Express 2020, 7, 015076. [Google Scholar] [CrossRef]
- Loopstra, B.O.; Rietveld, H.M. Further refinement of the structure of WO3. Acta Crystallogr. Sect. B 1969, 25, 1420–1421. [Google Scholar] [CrossRef]
- Shaikh, S.F.; Kalanur, S.S.; Mane, R.S.; Joo, O.S. Monoclinic WO3 nanorods-rutile TiO2 nanoparticles core-shell interface for efficient DSSCs. Dalton Trans. 2013, 42, 10085–10088. [Google Scholar] [CrossRef] [PubMed]
- Urretavizcaya, G.; Tonus, F.; Gaudin, E.; Bobet, J.L.; Castro, F.J. Formation of tetragonal hydrogen tungsten bronze by reactive mechanical alloying. J. Solid State Chem. 2007, 180, 2785–2789. [Google Scholar] [CrossRef]
- Yamaguchi, O.; Tomihisa, D.; Kawabata, H.; Shimizu, K. Formation and Transformation of Wo3 Prepared from Alkoxide. J. Am. Ceram. Soc. 1987, 70, C94–C96. [Google Scholar] [CrossRef]
- Figlarz, M. Soft Chemistry–Thermodynamic and Structural Aspects. Soft Chem. Routes New Mater. Chim. Douce 1994, 152, 55–68. [Google Scholar] [CrossRef]
- Guery, C.; Choquet, C.; Dujeancourt, F.; Tarascon, J.M.; Lassegues, J.C. Infrared and X-ray studies of hydrogen intercalation in different tungsten trioxides and tungsten trioxide hydrates. J. Solid State Electrochem. 1997, 1, 199–207. [Google Scholar] [CrossRef]
- Cao, J.; Luo, B.D.; Lin, H.L.; Xu, B.Y.; Chen, S.F. Thermodecomposition synthesis of WO3/H2WO4 heterostructures with enhanced visible light photocatalytic properties. Appl. Catal. B Environ. 2012, 111, 288–296. [Google Scholar] [CrossRef]
- Drelinkiewicz, A.; Lalik, E.; Kosydar, R.; Pacuła, A.; Góral-Kurbiel, M.; Kołodziej, M.; Szumełda, T. Catalytic Processes Using Bio-Resources. Palladium Catalysts Reactivity Modified by Tungsten Hydrogen Bronzes; Detailed Research Report of Jerzy Haber Institute of Catalysis and Surface Chemistry; Polish Academy of Sciences: Cracow, Poland, 2017; p. 9. [Google Scholar]
- Mayers, J.; Reiter, G. The VESUVIO electron volt neutron spectrometer. Meas. Sci. Technol. 2012, 23, 045902. [Google Scholar] [CrossRef]
- Senesi, R.; Andreani, C.; Bowden, Z.; Colognesi, D.; Degiorgi, E.; Fielding, A.L.; Mayers, J.; Nardone, M.; Norris, J.; Praitano, M.; et al. VESUVIO: A novel instrument for performing spectroscopic studies in condensed matter with eV neutrons at the ISIS facility. Phys. B 2000, 276, 200–201. [Google Scholar] [CrossRef]
- Andreani, C.; Krzystyniak, M.; Romanelli, G.; Senesi, R.; Fernandez-Alonso, F. Electron-volt neutron spectroscopy: Beyond fundamental systems. Adv. Phys. 2017, 66, 1–73. [Google Scholar] [CrossRef]
- Andreani, C.; Senesi, R.; Krzystyniak, M.; Romanelli, G.; Fernandez-Alonso, F. Chapter 7–Atomic Quantum Dynamics in Materials Research. In Experimental Methods in the Physical Sciences; Fernandez-Alonso, F., Price, D.L., Eds.; Academic Press: New York, NY, USA, 2017; Volume 49, pp. 403–457. [Google Scholar]
- Andreani, C.; Senesi, R.; Krzystyniak, M.; Romanelli, G.; Fernandez-Alonso, F.F. Experimental studies of nuclear quantum effects in condensed matter: The case of water. Riv. Nuovo. Cimento. 2018, 41, 291–340. [Google Scholar] [CrossRef]
- Krzystyniak, M.; Romanelli, G.; Fabian, M.; Gutmann, M.; Festa, G.; Arcidiacono, L.; Gigg, M.; Druzbicki, K.; Andreani, C.; Senesi, R.; et al. VESUVIO plus: The Current Testbed for a Next-generation Epithermal Neutron Spectrometer. J. Phys. Conf. Ser. 2018, 1021, 012026. [Google Scholar] [CrossRef]
- Seel, A.G.; Krzystyniak, M.; Fernandez-Alonso, F. The VESUVIO Spectrometer Now and When? J. Phys. Conf. Ser. 2014, 571, 012006. [Google Scholar] [CrossRef]
- Parmentier, A.; Andreani, C.; Romanelli, G.; Shephard, J.J.; Salzmann, C.G.; Senesi, R. Hydrogen mean force and anharmonicity in polycrystalline and amorphous ice. Front. Phys. 2018, 13, 136101. [Google Scholar] [CrossRef]
- Andreani, C.; Colognesi, D.; Mayers, J.; Reiter, G.; Senesi, R. Measurement of momentum distribution of lightatoms and molecules in condensed matter systems using inelastic neutron scattering. Adv. Phys. 2005, 54, 377–469. [Google Scholar] [CrossRef]
- Wallis, J.; Kruth, A.; da Silva, I.; Krzystyniak, M. Nuclear dynamics in BaZr0.7Ce0.2Y0.1O3−δ proton conductor as observed by neutron diffraction and Compton scattering. J. Phys. Commun. 2020, 4, 045004. [Google Scholar] [CrossRef]
- Krzystyniak, M.; Drużbicki, K.; Rudić, S.; Fabian, M. Positional, isotopic mass and force constant disorder in molybdate glasses and their parent metal oxides as observed by neutron diffraction and Compton scattering. J. Phys. Commun. 2020, 4, 095027. [Google Scholar] [CrossRef]
- Druzbicki, K.; Krzystyniak, M.; Hollas, D.; Kapil, V.; Slavicek, P.; Romanelli, G.; Fernandez-Alonso, F. Hydrogen dynamics in solid formic acid: Insights from simulations with quantum colored-noise thermostats. J. Phys. Conf. Ser. 2018, 1055, 012003. [Google Scholar] [CrossRef]
- Krzystyniak, M.; Druzbicki, K.; Romanelli, G.; Gutmann, M.J.; Rudic, S.; Imberti, S.; Fernandez-Alonso, F. Nuclear dynamics and phase polymorphism in solid formic acid. Phys. Chem. Chem. Phys. 2017, 19, 9064–9074. [Google Scholar] [CrossRef] [PubMed]
- Krzystyniak, M.; Druzbicki, K.; Fernandez-Alonso, F. Nuclear dynamics in the metastable phase of the solid acid caesium hydrogen sulfate. Phys. Chem. Chem. Phys. 2015, 17, 31287–31296. [Google Scholar] [CrossRef] [PubMed]
- Krzystyniak, M.; Seel, A.G.; Richards, S.E.; Gutmann, M.J.; Fernandez-Alonso, F. Mass-selective Neutron Spectroscopy Beyond the Proton. J. Phys. Conf. Ser. 2014, 571, 012002. [Google Scholar] [CrossRef]
- Ceriotti, M.; Drechsel-Grau, C.; Fernandez-Alonso, F.; Greaves, N.; Krzystyniak, M.; Major, D.; Parmentier, A.; Salzmann, C.; Senesi, R.; Sturniolo, S.; et al. Discussion: Theoretical Horizons and Calculation. J. Phys. Conf. Ser. 2014, 571, 012013. [Google Scholar] [CrossRef]
- Andreani, C.; Ceriotti, M.; Chass, G.; Drechsel-Grau, C.; Fernandez-Alonso, F.; Greaves, N.; Gidopoous, N.; Krzystyniak, M.; Parmentier, A.; Refson, K.; et al. Discussion: Nuclear Quantum Dynamics–Protons and Beyond. J. Phys. Conf. Ser. 2014, 571, 012004. [Google Scholar] [CrossRef]
- Krzystyniak, M.; Richards, S.E.; Seel, A.G.; Fernandez-Alonso, F. Mass-selective neutron spectroscopy of lithium hydride and deuteride: Experimental assessment of the harmonic and impulse approximations. Phys. Rev. B 2013, 88, 184304. [Google Scholar] [CrossRef]
- Krzystyniak, M.; Fernandez-Alonso, F. Ab initio nuclear momentum distributions in lithium hydride: Assessing nonadiabatic effects. Phys. Rev. B 2011, 83, 134305. [Google Scholar] [CrossRef]
- Krzystyniak, M.; Adams, M.A.; Lovell, A.; Skipper, N.T.; Bennington, S.M.; Mayers, J.; Fernandez-Alonso, F. Probing the binding and spatial arrangement of molecular hydrogen in porous hosts via neutron Compton scattering. Faraday Discuss. 2011, 151, 171–197. [Google Scholar] [CrossRef]
- Krzystyniak, M.; Abdul-Redah, T. Proton momentum distribution in solid and liquid HF. Phys. Rev. B 2010, 82, 064301. [Google Scholar] [CrossRef]
- Krzystyniak, M. Nuclear momentum distribution in solid and liquid HF from ab initio calculation. J. Chem. Phys. 2010, 133, 144505. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.; Yang, T.X.; Lu, H.; Liu, Y.A.; He, Y.F.; Li, Q.; Gao, J.X.; Feng, J.T.; Yan, H.; Miller, J.T.; et al. Increased Hydrogenation Rates in Pd/La-Al2O3 Catalysts by Hydrogen Transfer O(-La) Sites Adjacent to Pd Nanoparticles. Acs. Catal. 2022, 12, 15696–15706. [Google Scholar] [CrossRef]
- Gu, K.X.; Li, C.; Jiang, B.; Lin, S.; Guo, H. Short- and Long-Time Dynamics of Hydrogen Spillover from a Single Atom Platinum Active Site to the Cu(111) Host Surface. J. Phys. Chem. C 2022, 126, 17093–17101. [Google Scholar] [CrossRef]
- Hulsey, M.J.; Fung, V.; Hou, X.D.; Wu, J.S.; Yan, N. Hydrogen Spillover and Its Relation to Hydrogenation: Observations on Structurally Defined Single-Atom Sites. Angew. Chem. Int. Ed. 2022, 61, e202208237. [Google Scholar] [CrossRef]
- Jing, W.T.; Shen, H.; Qin, R.X.; Wu, Q.Y.; Liu, K.L.; Zheng, N.F. Surface and Interface Coordination Chemistry Learned from Model Heterogeneous Metal Nanocatalysts: From Atomically Dispersed Catalysts to Atomically Precise Clusters. Chem. Rev. 2022, 123, 5948–6002. [Google Scholar] [CrossRef] [PubMed]
- Kamada, T.; Ueda, T.; Fukuura, S.; Yumura, T.; Hosokawa, S.; Tanaka, T.; Kan, D.S.K.; Shimakawa, Y. Ultralong Distance Hydrogen Spillover Enabled by Valence Changes in a Metal Oxide Surface. J. Am. Chem. Soc. 2023, 145, 1631–1637. [Google Scholar] [CrossRef]
- Liu, K.R.; Hou, G.J.; Gao, P.; Nie, X.Z.; Bai, S.; Janik, M.J.; Zhang, Z.C. Evolution of multiple spillover hydrogen species on anatase titanium dioxide. Cell Rep. Phys. Sci. 2022, 3, 101190. [Google Scholar] [CrossRef]
- Osada, W.; Tanaka, S.; Mukai, K.; Kawamura, M.; Choi, Y.; Ozaki, F.; Ozaki, T.; Yoshinobu, J. Elucidation of the atomic-scale processes of dissociative adsorption and spillover of hydrogen on the single atom alloy catalyst Pd/Cu(111). Phys. Chem. Chem. Phys. 2022, 24, 21705–21713. [Google Scholar] [CrossRef]
- Shen, H.F.; Li, H.; Yang, Z.S.; Li, C.L. Magic of hydrogen spillover: Understanding and application. Green Energy Environ. 2022, 7, 1161–1198. [Google Scholar] [CrossRef]
- Wang, X.Y.; Li, D.D.; Gao, Z.R.; Guo, Y.; Zhang, H.B.; Ma, D. The Nature of Interfacial Catalysis over Pt/NiAl2O4 for Hydrogen Production from Methanol Reforming Reaction. J. Am. Chem. Soc. 2022, 145, 905–918. [Google Scholar] [CrossRef]
- Wang, Y.L.; Yin, H.B.; Dong, F.; Zhao, X.G.; Qu, Y.K.; Wang, L.X.; Peng, Y.; Wang, D.S.; Fang, W.; Li, J.H. N-Coordinated Cu-Ni Dual-Single-Atom Catalyst for Highly Selective Electrocatalytic Reduction of Nitrate to Ammonia. Small 2023, 19, 2207695. [Google Scholar] [CrossRef]
- Yue, G.C.; Yu, Y.; Li, S.; Li, H.K.; Gao, S.W.; Wang, Y.Q.; Guo, W.; Wang, N.; Li, X.L.; Cui, Z.M.; et al. Boosting Chemoselective Hydrogenation of Nitroaromatic via Synergy of Hydrogen Spillover and Preferential Adsorption on Magnetically Recoverable Pt@Fe2O3. Small 2023, 19, 2207918. [Google Scholar] [CrossRef] [PubMed]
- Vallejo, E. An hydrogen adsorption study on graphene-based surfaces with core-shell type catalysts. Carbon Lett. 2023, 33, 823–832. [Google Scholar] [CrossRef]
- Schmitz, G.; Schnieder, B. Adaptive regularized Gaussian process regression for application in the context of hydrogen adsorption on graphene sheets. J. Comput. Chem. 2023, 44, 732–744. [Google Scholar] [CrossRef]
- Sun, J.K.; Jiang, S.C.; Zhao, Y.L.; Wang, H.L.; Zhai, D.; Deng, W.Q.; Sun, L. First-principles study of CO2 hydrogenation to formic acid on single-atom catalysts supported on SiO2. Phys. Chem. Chem. Phys. 2022, 24, 19938–19947. [Google Scholar] [CrossRef] [PubMed]
- Injongkol, Y.; Khemthong, P.; Yodsin, N.; Wongnongwa, Y.; Sosa, N.; Youngjan, S.; Butburee, T.; Rungtaweevoranit, B.; Kiatphuengporn, S.; Wittayakun, J.; et al. Combined in situ XAS and DFT studies on the role of Pt in zeolite-supported metal catalysts for selective n-hexane isomerization. Fuel 2022, 314, 123099. [Google Scholar] [CrossRef]
- Zhao, G.C.; Qiu, Y.Q.; Liu, C.G. A systematic theoretical study of hydrogen activation, spillover and desorption in single-atom alloys. Appl. Catal. A-Gen. 2021, 610, 117948. [Google Scholar] [CrossRef]
- Dadayan, A.K.; Borisov, Y.A.; Zolotarev, Y.A.; Myasoedov, N.F. Modeling Hydrogen Spillover on Oxide Catalytic Centers. Russ. J. Phys. Chem. A+ 2021, 95, 944–948. [Google Scholar] [CrossRef]
- Lykhach, Y.; Kubat, J.; Neitzel, A.; Tsud, N.; Vorokhta, M.; Skala, T.; Dvorak, F.; Kosto, Y.; Prince, K.C.; Matolin, V.; et al. Charge transfer and spillover phenomena in ceria-supported iridium catalysts: A model study. J. Chem. Phys. 2019, 151, 2204703. [Google Scholar] [CrossRef]
- Guo, J.H.; Li, X.D.; Liu, H.Y.; Li, S.J.; Chen, G. Combined Density Functional Theory and Kinetic Monte Carlo Study of Hydrogen Spillover on Fluorine-Decorating Covalent Organic Frameworks. J. Phys. Chem. C 2019, 123, 15935–15943. [Google Scholar] [CrossRef]
- Doudin, N.; Yuk, S.F.; Marcinkowski, M.D.; Nguyen, M.T.; Liu, J.C.; Wang, Y.; Novotny, Z.; Kay, B.D.; Li, J.; Glezakou, V.A.; et al. Understanding Heterolytic H-2 Cleavage and Water-Assisted Hydrogen Spillover on Fe3O4(001)-Supported Single Palladium Atoms. Acs Catal. 2019, 9, 7876–7887. [Google Scholar] [CrossRef]
- Ren, B.H.; Li, J.D.; Wen, G.B.; Ricardez-Sandoval, L.; Croiset, E. First-Principles Based Microkinetic Modeling of CO2 Reduction at the Ni/SDC Cathode of a Solid Oxide Electrolysis Cell. J. Phys. Chem. C 2018, 122, 21151–21161. [Google Scholar] [CrossRef]
- Guo, J.H.; Liu, D.D.; Li, X.D.; Liu, H.Y.; Chen, G. Pt-4, Pd-4, Ni-4, and Ti-4 catalyzed hydrogen spillover on penta-graphene for hydrogen storage: The first-principles and kinetic Monte Carlo study. Int. J. Hydrogn Energy 2018, 43, 2247–2255. [Google Scholar] [CrossRef]
- Shin, H.; Choi, M.; Kim, H. A mechanistic model for hydrogen activation, spillover, and its chemical reaction in a zeolite-encapsulated Pt catalyst. Phys. Chem. Chem. Phys. 2016, 18, 7035–7041. [Google Scholar] [CrossRef] [PubMed]
- Lucci, F.R.; Darby, M.T.; Mattera, M.F.G.; Ivimey, C.J.; Therrien, A.J.; Michaelides, A.; Stamatakis, M.; Sykes, E.C.H. Controlling Hydrogen Activation, Spillover, and Desorption with Pd-Au Single-Atom Alloys. J. Phys. Chem. Lett. 2016, 7, 480–485. [Google Scholar] [CrossRef]
- Guo, J.H.; Cheng, X.L.; Li, S.J.; Chen, G. Theoretical Study of a Bridging-Spillover Mechanism in Covalent Organic Frameworks on Pt-6 and Pt-4 Cluster Models. J. Phys. Chem. C 2016, 120, 17153–17164. [Google Scholar] [CrossRef]
- Blanco-Rey, M.; Juaristi, J.I.; Alducin, M.; Lopez, M.J.; Alonso, J.A. Is Spillover Relevant for Hydrogen Adsorption and Storage in Porous Carbons Doped with Palladium Nanoparticles? J. Phys. Chem. C 2016, 120, 17357–17364. [Google Scholar] [CrossRef]
- Juarez-Mosqueda, R.; Mavrandonakis, A.; Kuc, A.B.; Pettersson, L.G.M.; Heine, T. Theoretical analysis of hydrogen spillover mechanism on carbon nanotubes. Front. Chem. 2015, 3, 2. [Google Scholar] [CrossRef]
- Choi, S.; Jeong, K.J.; Park, J.Y.; Lee, Y.S. Computational Study of Hydrogen Chemisorption on a Multi-Phenyl Organic Linker as a Model of Hydrogen Spillover on Metal-Organic Frameworks. B Korean Chem. Soc. 2015, 36, 777–783. [Google Scholar] [CrossRef]
- Choi, M.; Yook, S.; Kim, H. Hydrogen Spillover in Encapsulated Metal Catalysts: New Opportunities for Designing Advanced Hydroprocessing Catalysts. ChemCatChem 2015, 7, 1048–1057. [Google Scholar] [CrossRef]
- Nishihara, H.; Ittisanronnachai, S.; Itoi, H.; Li, L.X.; Suzuki, K.; Nagashima, U.; Ogawa, H.; Kyotani, T.; Ito, M. Experimental and Theoretical Studies of Hydrogen/Deuterium Spillover on Pt-Loaded Zeolite-Templated Carbon. J. Phys. Chem. C 2014, 118, 9551–9559. [Google Scholar] [CrossRef]
- Ma, L.; Zhang, J.M.; Xu, K.W. Hydrogen storage on nitrogen induced defects in palladium-decorated graphene: A first-principles study. Appl. Surf. Sci. 2014, 292, 921–927. [Google Scholar] [CrossRef]
- Liu, X.Y.; He, J.; Yu, J.X.; Li, Z.X.; Fan, Z.Q. Theoretical study of molecular hydrogen and spiltover hydrogen storage on two-dimensional covalent-organic frameworks. Chin. Phys. B 2014, 23, 067303. [Google Scholar] [CrossRef]
- Karlicky, F.; Lepetit, B.; Lemoine, D. Quantum modelling of hydrogen chemisorption on graphene and graphite. J. Chem. Phys. 2014, 140, 124702. [Google Scholar] [CrossRef] [PubMed]
- Marcinkowski, M.D.; Jewell, A.D.; Stamatakis, M.; Boucher, M.B.; Lewis, E.A.; Murphy, C.J.; Kyriakou, G.; Sykes, E.C.H. Controlling a spillover pathway with the molecular cork effect. Nat. Mater. 2013, 12, 523–528. [Google Scholar] [CrossRef]
- Hao, S.Q.; Sholl, D.S. First-Principles Models of Facilitating H-2 Transport through Metal Films Using Spillover. J. Phys. Chem. C 2013, 117, 1217–1223. [Google Scholar] [CrossRef]
- Mitchell, P.C.H.; Ramirez-Cuesta, A.J.; Parker, S.F.; Tomkinson, J. Inelastic neutron scattering in spectroscopic studies of hydrogen on carbon-supported catalysts-experimental spectra and computed spectra of model systems. J. Mol. Struct. 2003, 651, 781–785. [Google Scholar] [CrossRef]
- Parker, S.F.; Walker, H.C.; Callear, S.K.; Grunewald, E.; Petzold, T.; Wolf, D.; Mobus, K.; Adam, J.; Wieland, S.D.; Jimenez-Ruiz, M.; et al. The effect of particle size, morphology and support on the formation of palladium hydride in commercial catalysts. Chem. Sci. 2019, 10, 480–489. [Google Scholar] [CrossRef]
- Xi, Y.J.; Zhang, Q.F.; Cheng, H.S. Mechanism of Hydrogen Spillover on WO3(001) and Formation of HxWO3 (x = 0.125, 0.25, 0.375, and 0.5). J. Phys. Chem. C 2014, 118, 494–501. [Google Scholar] [CrossRef]
- Billeter, E.; Sterzi, A.; Sambalova, O.; Wick-Joliat, R.; Grazioli, C.; Coreno, M.; Cheng, Y.Q.; Ramirez-Cuesta, A.J.; Borgschulte, A. Hydrogen in tungsten trioxide by membrane photoemission and density functional theory modeling. Phys. Rev. B 2021, 103, 205304. [Google Scholar] [CrossRef]
- Braun, A.; Chen, Q.L. Experimental neutron scattering evidence for proton polaron in hydrated metal oxide proton conductors. Nat. Commun. 2017, 8, 15830. [Google Scholar] [CrossRef] [PubMed]
- Hjelm, A.; Granqvist, C.G.; Wills, J.M. Electronic structure and optical properties of WO3, LiWO3, NaWO3, and HWO3. Phys. Rev. B 1996, 54, 2436–2445. [Google Scholar] [CrossRef] [PubMed]
- Johansson, M.B.; Kristiansen, P.T.; Duda, L.; Niklasson, G.A.; Osterlund, L. Band gap states in nanocrystalline WO3 thin films studied by soft X-ray spectroscopy and optical spectrophotometry. J. Phys.-Condens. Matter 2016, 28, 475802. [Google Scholar] [CrossRef] [PubMed]
- Leng, X.; Pereiro, J.; Strle, J.; Dubuis, G.; Bollinger, A.T.; Gozar, A.; Wu, J.; Litombe, N.; Panagopoulos, C.; Pavuna, D.; et al. Insulator to metal transition in WO3 induced by electrolyte gating. npj Quantum Mater. 2017, 2, 35. [Google Scholar] [CrossRef]
- Saenger, M.F.; Hoing, T.; Hofmann, T.; Schubert, M. Polaron transitions in charge intercalated amorphous tungsten oxide thin films. Phys. Status Solidi A-Appl. Mater. Sci. 2008, 205, 914–917. [Google Scholar] [CrossRef]
- Saenger, M.F.; Hoing, T.; Robertson, B.W.; Billa, R.B.; Hofmann, T.; Schubert, E.; Schubert, M. Polaron and phonon properties in proton intercalated amorphous tungsten oxide thin films. Phys. Rev. B 2008, 78, 245205. [Google Scholar] [CrossRef]
- Lalik, E.; Mirek, R.; Rakoczy, J.; Groszek, A. Microcalorimetric study of sorption of water and ethanol in zeolites 3A and 5A. Catal. Today 2006, 114, 242–247. [Google Scholar] [CrossRef]
- Irvine, G.J.; Demmel, F.; Playford, H.Y.; Carins, G.; Jones, M.O.; Irvine, J.T.S. Geometric Frustration and Concerted Migration in the Superionic Conductor Barium Hydride. Chem. Mater. 2022, 34, 9934–9944. [Google Scholar] [CrossRef]
- Krzystyniak, M.; Romanelli, G.; Fernandez-Alonso, F. Non-destructive quantitation of hydrogen via mass-resolved neutron spectroscopy. Analyst 2019, 144, 3936–3941. [Google Scholar] [CrossRef]
- Romanelli, G.; Hewer, B.; Krzystyniak, M.; Gigg, M.; Tolchenov, R.; Mukhopadhyay, S.; Fernandez-Alonso, F. Data analysis of neutron Compton scattering experiments using MANTID. J. Phys. Conf. Ser. 2018, 1055, 012016. [Google Scholar] [CrossRef]
- Mayers, J.; Fielding, A.L.; Senesi, R. Multiple scattering in deep inelastic neutron scattering: Monte Carlo simulations and experiments at the ISIS eVS inverse geometry spectrometer. Nucl. Instrum. Meth. A 2002, 481, 454–463. [Google Scholar] [CrossRef]
- Romanelli, G.; Krzystyniak, M.; Senesi, R.; Raspino, D.; Boxall, J.; Pooley, D.; Moorby, S.; Schooneveld, E.; Rhodes, N.; Andreani, C. Characterisation of the incident beam and current diffraction capabilities on the VESUVIO spectrometer. Meas. Sci. Technol. 2017, 28, 095501. [Google Scholar] [CrossRef]
- Capelli, S.C.; Romanelli, G. An effective hydrogen scattering cross section for time-of-flight neutron experiments with simple organic molecules. J. Appl. Crystallogr. 2019, 52, 1233–1237. [Google Scholar] [CrossRef]
- Damian, J.I.M.; Dawidowski, J.; Granada, R.J.; Cantargi, F.; Romanelli, G.; Helman, C.; Krzystyniak, M.; Skoro, G.; Roubtsov, D. Experimental validation of the temperature behavior of the ENDF/B-VIII.0 thermal scattering kernel for light water. Epj Web Conf. 2020, 239, 14001. [Google Scholar] [CrossRef]
- Martellucci, M.; Romanelli, G.; Valeri, S.; Cottone, D.; Andreani, C.; Senesi, R. The neutron cross section of barite-enriched concrete for radioprotection shielding in the range 1 meV-1 keV. Eur. Phys. J. Plus 2021, 136, 259. [Google Scholar] [CrossRef]
- Robledo, J.I.; Dawidowski, J.; Damian, J.I.M.; Skoro, G.; Bovo, C.; Romanelli, G. Measurement of neutron total cross sections at the VESUVIO spectrometer. Nucl. Instrum. Meth. A 2020, 971, 164096. [Google Scholar] [CrossRef]
- Lalik, E.; Druzbicki, K.; Irvine, G.; Gutmann, M.; Rudic, S.; Manuel, P.; Petricek, V.; Krzystyniak, M. Interplay between Local Structure and Nuclear Dynamics in Tungstic Acid: A Neutron Scattering Study. J. Phys. Chem. C 2021, 125, 23864–23879. [Google Scholar] [CrossRef]
- Krzystyniak, M.; Syrykh, G.; Stolyarov, A.; Sadykov, R.A.; Armstrong, J.; da Silva, I.; Romanelli, G.; Fernandez-Alonso, F. Mass-selective neutron spectroscopy of glassy versus polycrystalline structures in binary mixtures of beryllium and zirconium. J. Phys. Conf. Ser. 2018, 1055, 012004. [Google Scholar] [CrossRef]
- Krzystyniak, M.; Syrykh, G.; Stolyarov, A.; Sadykov, R.A.; Romanelli, G. Force constant disorder in the Ni44Nb56 bulk metallic glass as observed by deep inelastic neutron scattering augmented by isotopic substitution. Phys. Scr. 2022, 97, 065702. [Google Scholar] [CrossRef]
- Syrykh, G.F.; Stolyarov, A.A.; Krzystyniak, M.; Romanelli, G.; Sadykov, R.A. Temperature Dependence of the Kinetic Energy in the Zr40Be60 Amorphous Alloy. Jetp. Lett+ 2017, 105, 591–594. [Google Scholar] [CrossRef]
- Fernandez-Alonso, F.; Price, D.L. Neutron Scattering: Applications in Biology, Chemistry and Materials Science; Academic Press, an Imprint of Elsevier: Cambridge, MA, USA, 2017; p. 753. [Google Scholar]
- Jackson, S.; Krzystyniak, M.; Seel, A.G.; Giggi, M.; Richards, S.E.; Fernandez-Alonso, F. VESUVIO Data Analysis Goes MANTID. J. Phys. Conf. Ser. 2014, 571, 012009. [Google Scholar] [CrossRef]
- Krzystyniak, M.; Gutmann, M.J.; Refson, K.; Romanelli, G.; Rudic, S.; Capelli, S.C.; Fortes, D.; Magdysyuk, O.; Damin, J.I.M.; Maciel-Pereira, G. Nuclear quantum dynamics in Hexamethylenetetramine and its deuterated counterpart: A DFT-augmented neutron study. Phys. Scr. 2023, 98, 025707. [Google Scholar] [CrossRef]
- Witek, M.; Krzystyniak, M.; Romanelli, G.; Witczak, T. Glass Transition in Rice Pasta as Observed by Combined Neutron Scattering and Time-Domain NMR. Polymers 2021, 13, 2426. [Google Scholar] [CrossRef] [PubMed]
- Milman, V.; Refson, K.; Clark, S.J.; Pickard, C.J.; Yates, J.R.; Gao, S.P.; Hasnip, P.J.; Probert, M.I.J.; Perlov, A.; Segall, M.D. Electron and vibrational spectroscopies using DFT, plane waves and pseudopotentials: CASTEP implementation. J. Mol. Struc.-Theochem. 2010, 954, 22–35. [Google Scholar] [CrossRef]
- Clark, S.J.; Segall, M.D.; Pickard, C.J.; Hasnip, P.J.; Probert, M.J.; Refson, K.; Payne, M.C. First principles methods using CASTEP. Z. Krist. 2005, 220, 567–570. [Google Scholar] [CrossRef]
- Segall, M.D.; Lindan, P.J.D.; Probert, M.J.; Pickard, C.J.; Hasnip, P.J.; Clark, S.J.; Payne, M.C. First-principles simulation: Ideas, illustrations and the CASTEP code. J. Phys.-Condens. Matter 2002, 14, 2717–2744. [Google Scholar] [CrossRef]
- Peng, H.W.; Perdew, J.P. Rehabilitation of the Perdew-Burke-Ernzerhof generalized gradient approximation for layered materials. Phys. Rev. B 2017, 95, 081105. [Google Scholar] [CrossRef]
- Pedroza, L.S.; da Silva, A.J.R.; Capelle, K. Gradient-dependent density functionals of the Perdew-Burke-Ernzerhof type for atoms, molecules, and solids. Phys. Rev. B 2009, 79, 201106. [Google Scholar] [CrossRef]
- Ropo, M.; Kokko, K.; Vitos, L. Assessing the Perdew-Burke-Ernzerhof exchange-correlation density functional revised for metallic bulk and surface systems. Phys. Rev. B 2008, 77, 195445. [Google Scholar] [CrossRef]
- Xu, X.; Goddard, W.A. The extended Perdew-Burke-Ernzerhof functional with improved accuracy for thermodynamic and electronic properties of molecular systems. J. Chem. Phys. 2004, 121, 4068–4082. [Google Scholar] [CrossRef]
- Ernzerhof, M.; Scuseria, G.E. Assessment of the Perdew-Burke-Ernzerhof exchange-correlation functional. J. Chem. Phys. 1999, 110, 5029–5036. [Google Scholar] [CrossRef]
- Krzystyniak, M.; Druzbicki, K.; Tolnai, I.; Fabian, M. Local structure and dynamics of tungsten oxide-based glasses: Insights from concurrent neutron diffraction and Compton scattering. J. Phys. Commun. 2021, 5, 075013. [Google Scholar] [CrossRef]
- Li, J.Y.; Hu, J.; Zhang, M.K.; Gou, W.Y.; Zhang, S.; Chen, Z.; Qu, Y.Q.; Ma, Y.Y. A fundamental viewpoint on the hydrogen spillover phenomenon of electrocatalytic hydrogen evolution. Nat. Commun. 2021, 12, 3502. [Google Scholar] [CrossRef]
- Wang, J.Q.; Su, Y.C.; Xu, J.; Ye, C.H.; Deng, F. Acid sites and oxidation center in molybdena supported on tin oxide as studied by solid-state NMR spectroscopy and theoretical calculation. Phys. Chem. Chem. Phys. 2006, 8, 2378–2384. [Google Scholar] [CrossRef] [PubMed]
- Sutton, L.E. Tables of Interatomic Distances and Configuration in Molecules and Ions: Supplement 1956–1959; Chemical Society: Cambridge, UK, 1965. [Google Scholar]
- Palomino, L.A.R.; Dawidowski, J.; Helman, C.; Damian, J.I.M.; Romanelli, G.; Krzystyniak, M.; Rudic, S.; Cuello, G.J. Determination of the scattering cross section of calcium using the VESUVIO spectrometer. Nucl. Instrum. Meth. A 2019, 927, 443–450. [Google Scholar] [CrossRef]
- Romanelli, G.; Onorati, D.; Ulpiani, P.; Cancelli, S.; Perelli-Cippo, E.; Damian, J.I.M.; Capelli, S.C.; Croci, G.; Muraro, A.; Tardocchi, M.; et al. Thermal neutron cross sections of amino acids from average contributions of functional groups. J. Phys.-Condens. Matter 2021, 33, 285901. [Google Scholar] [CrossRef] [PubMed]
- Zheng, Y.; Jiao, Y.; Jaroniec, M.; Qiao, S.Z. Advancing the Electrochemistry of the Hydrogen-Evolution Reaction through Combining Experiment and Theory. Angew. Chem. Int. Ed. 2015, 54, 52–65. [Google Scholar] [CrossRef]





| Species | NMD Width [Å−1] | EK [meV] | FC [eV Å−2] |
|---|---|---|---|
| H in PdH | 3.31 | 68.2 | 0.12 |
| Pd | 25.9 | 39.6 | 0.37 |
| H in cWO3 | 4.91 | 149.7 | 0.46 |
| O | 11.6 | 52.8 | 0.93 |
| W | 35.6 | 43.2 | 3.30 |
| Species | Contribution | NMD Width [Å−1] |
|---|---|---|
| H in PdH | 0.0678 +/− 0.004 | 3.31 * |
| H in cWO3 | 0.5638 +/− 0.081 | 4.91 * |
| H in HxWO3 | 0.3684 +/− 0.072 | 3.37 +/− 0.02 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lalik, E.; Parker, S.F.; Irvine, G.; da Silva, I.; Gutmann, M.J.; Romanelli, G.; Drużbicki, K.; Kosydar, R.; Krzystyniak, M. Hydrogen Spillover in Tungsten Oxide Bronzes as Observed by Broadband Neutron Spectroscopy. Energies 2023, 16, 5496. https://doi.org/10.3390/en16145496
Lalik E, Parker SF, Irvine G, da Silva I, Gutmann MJ, Romanelli G, Drużbicki K, Kosydar R, Krzystyniak M. Hydrogen Spillover in Tungsten Oxide Bronzes as Observed by Broadband Neutron Spectroscopy. Energies. 2023; 16(14):5496. https://doi.org/10.3390/en16145496
Chicago/Turabian StyleLalik, Erwin, Stewart F. Parker, Gavin Irvine, Ivan da Silva, Matthias Josef Gutmann, Giovanni Romanelli, Kacper Drużbicki, Robert Kosydar, and Matthew Krzystyniak. 2023. "Hydrogen Spillover in Tungsten Oxide Bronzes as Observed by Broadband Neutron Spectroscopy" Energies 16, no. 14: 5496. https://doi.org/10.3390/en16145496
APA StyleLalik, E., Parker, S. F., Irvine, G., da Silva, I., Gutmann, M. J., Romanelli, G., Drużbicki, K., Kosydar, R., & Krzystyniak, M. (2023). Hydrogen Spillover in Tungsten Oxide Bronzes as Observed by Broadband Neutron Spectroscopy. Energies, 16(14), 5496. https://doi.org/10.3390/en16145496






