Study on Flow and Heat Transfer Characteristics and Anti-Clogging Performance of Tree-Like Branching Microchannels
Abstract
1. Introduction
2. Methodology
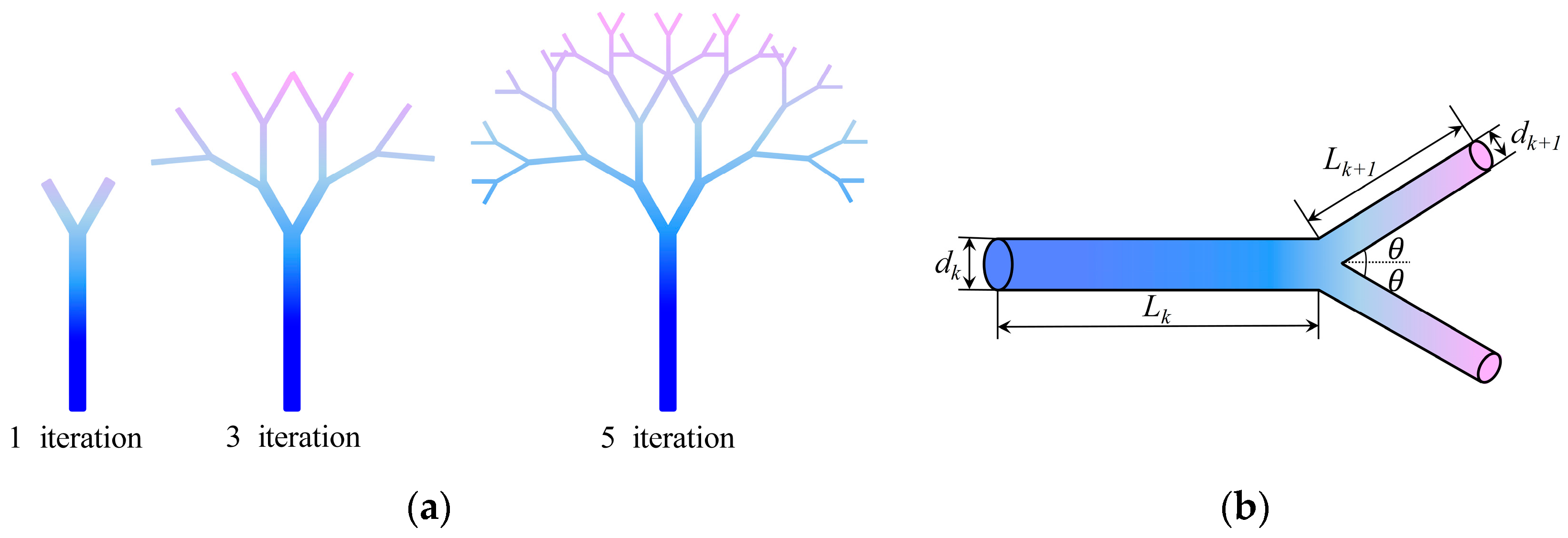
2.1. Physical Model
2.2. Heat Transfer in the Tree-like Branching Networks
2.3. Flow Resistance in the Tree-like Branching Networks
3. Numerical Approach and Experimental Details
3.1. Numerical Approach
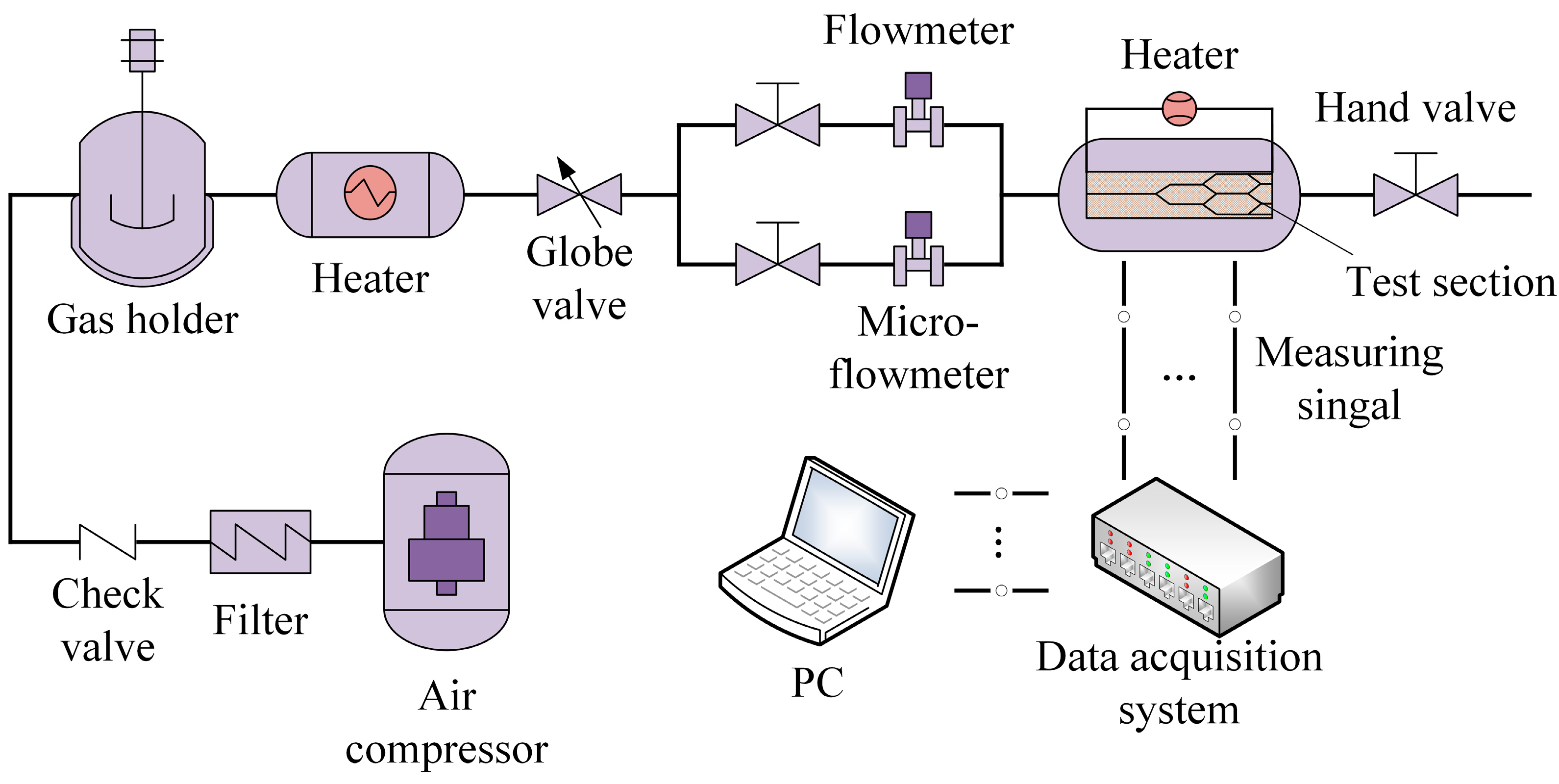
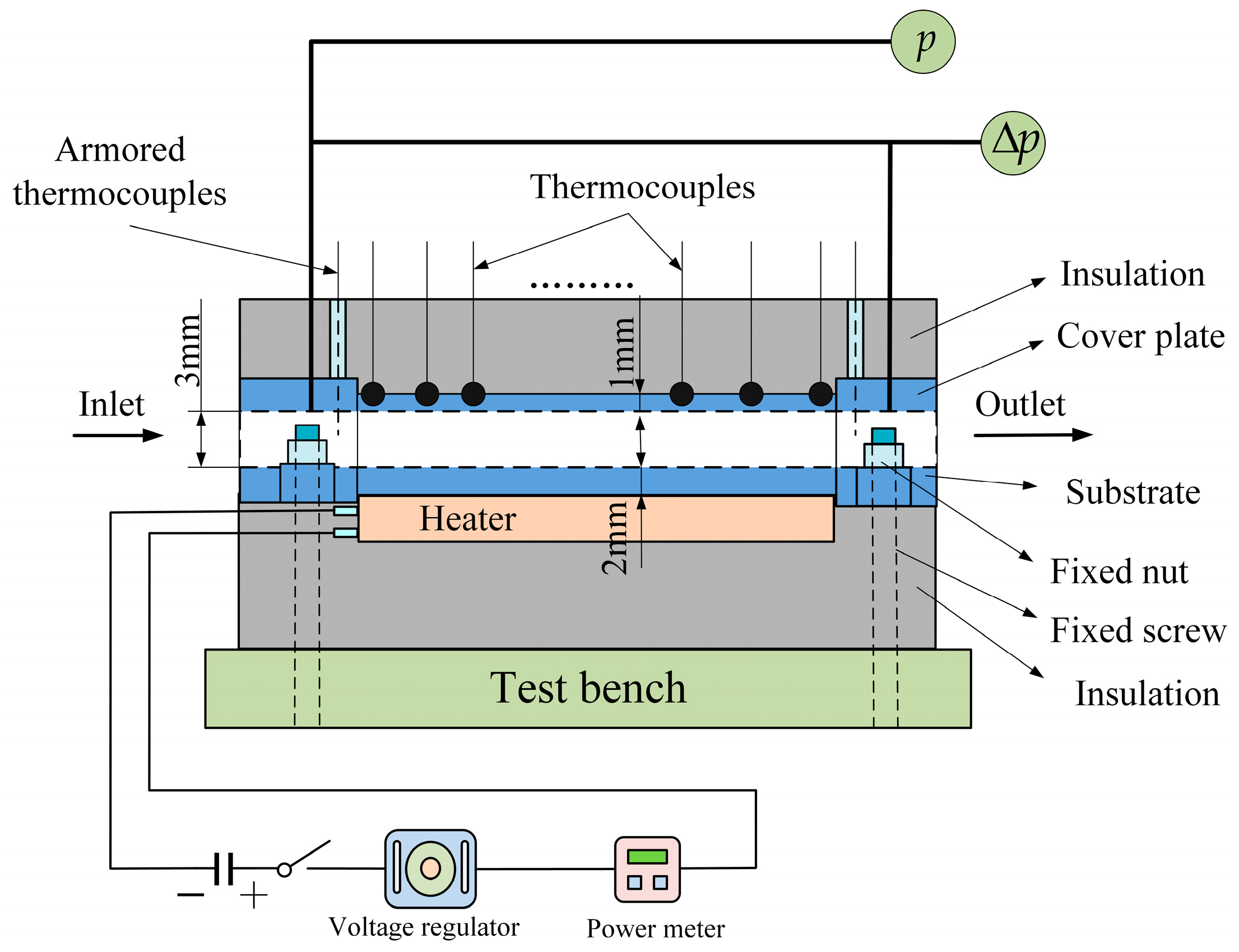
3.2. Experimental Details
3.3. Data Reduction
4. Results
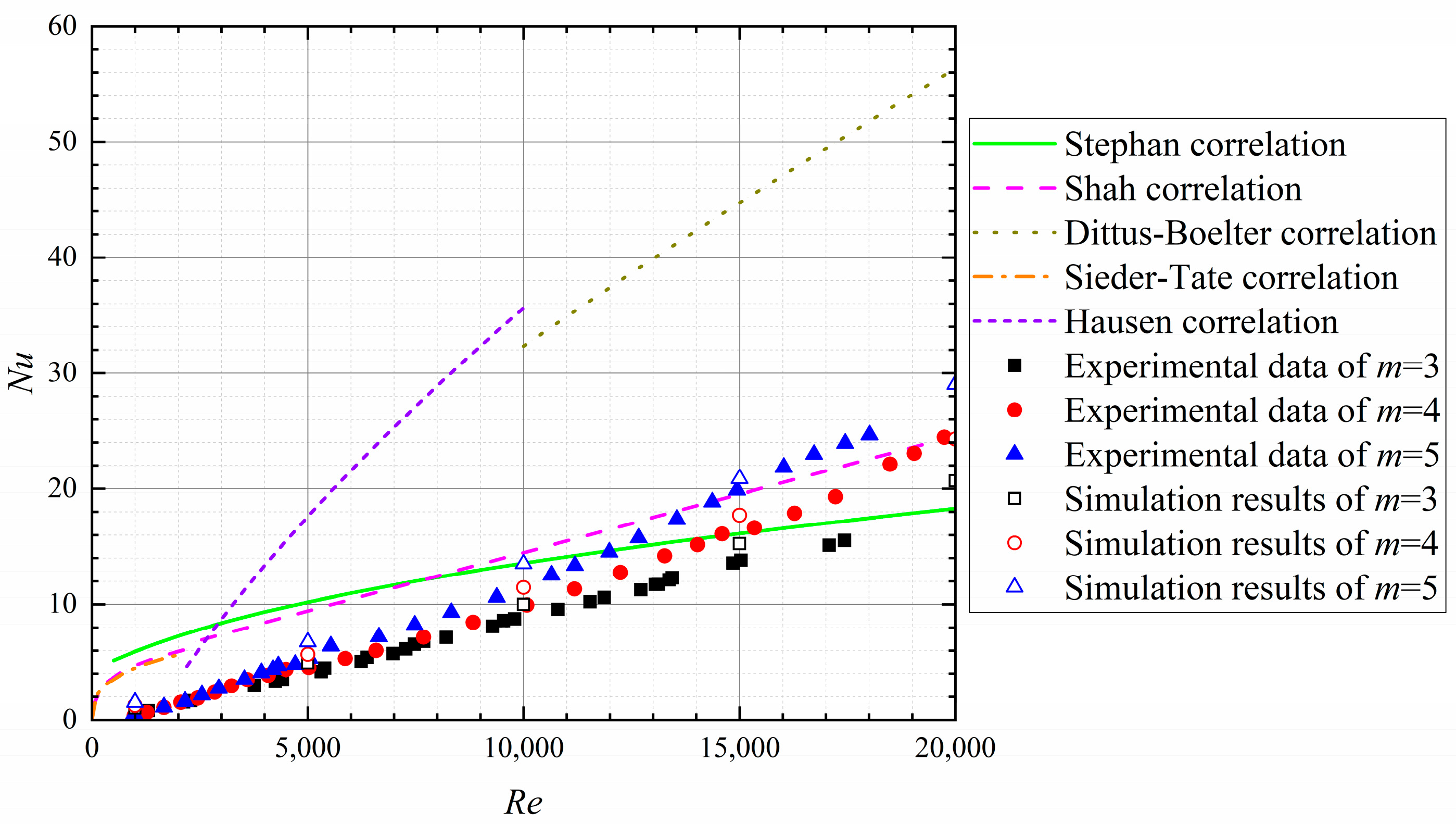
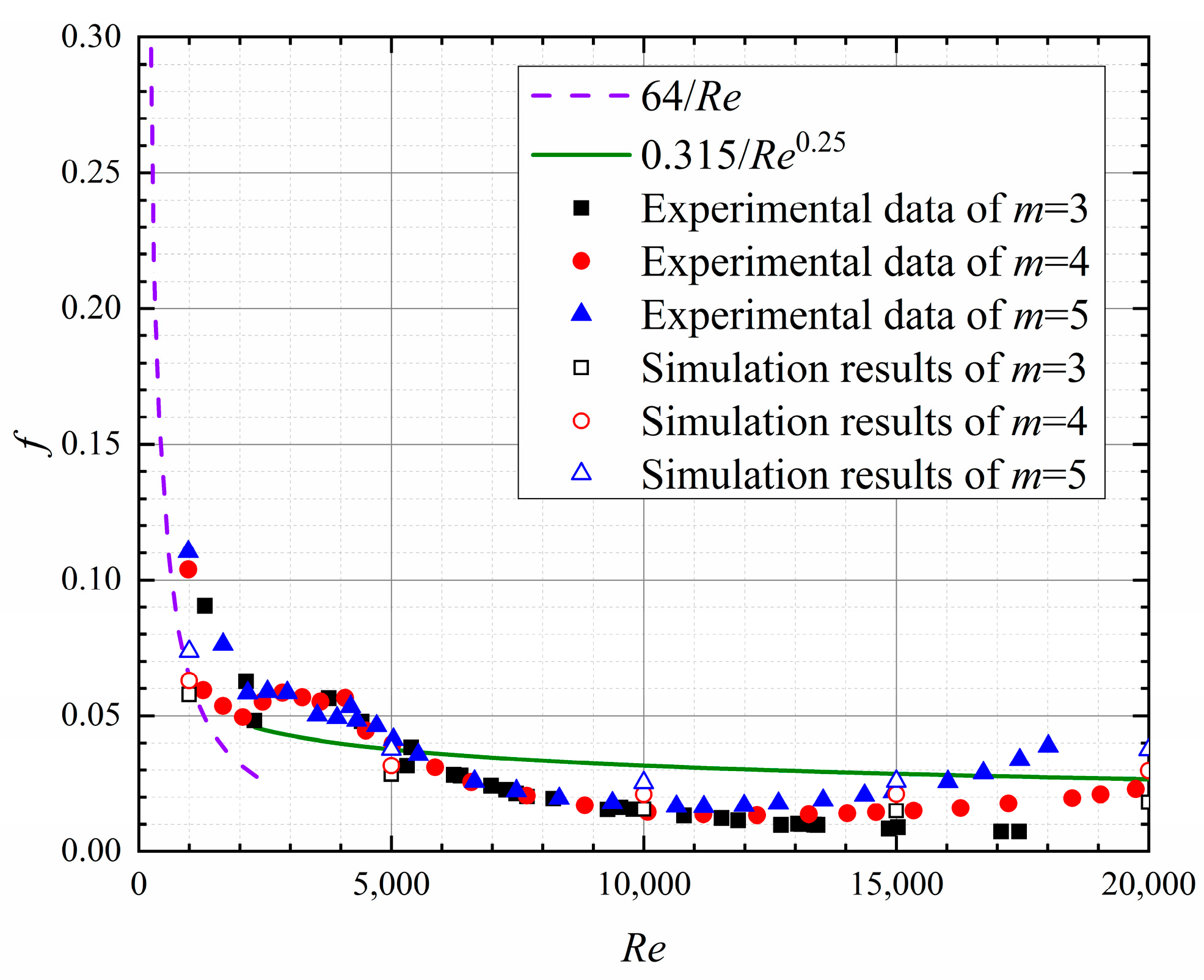
4.1. Experimental Results and Numerical Verification
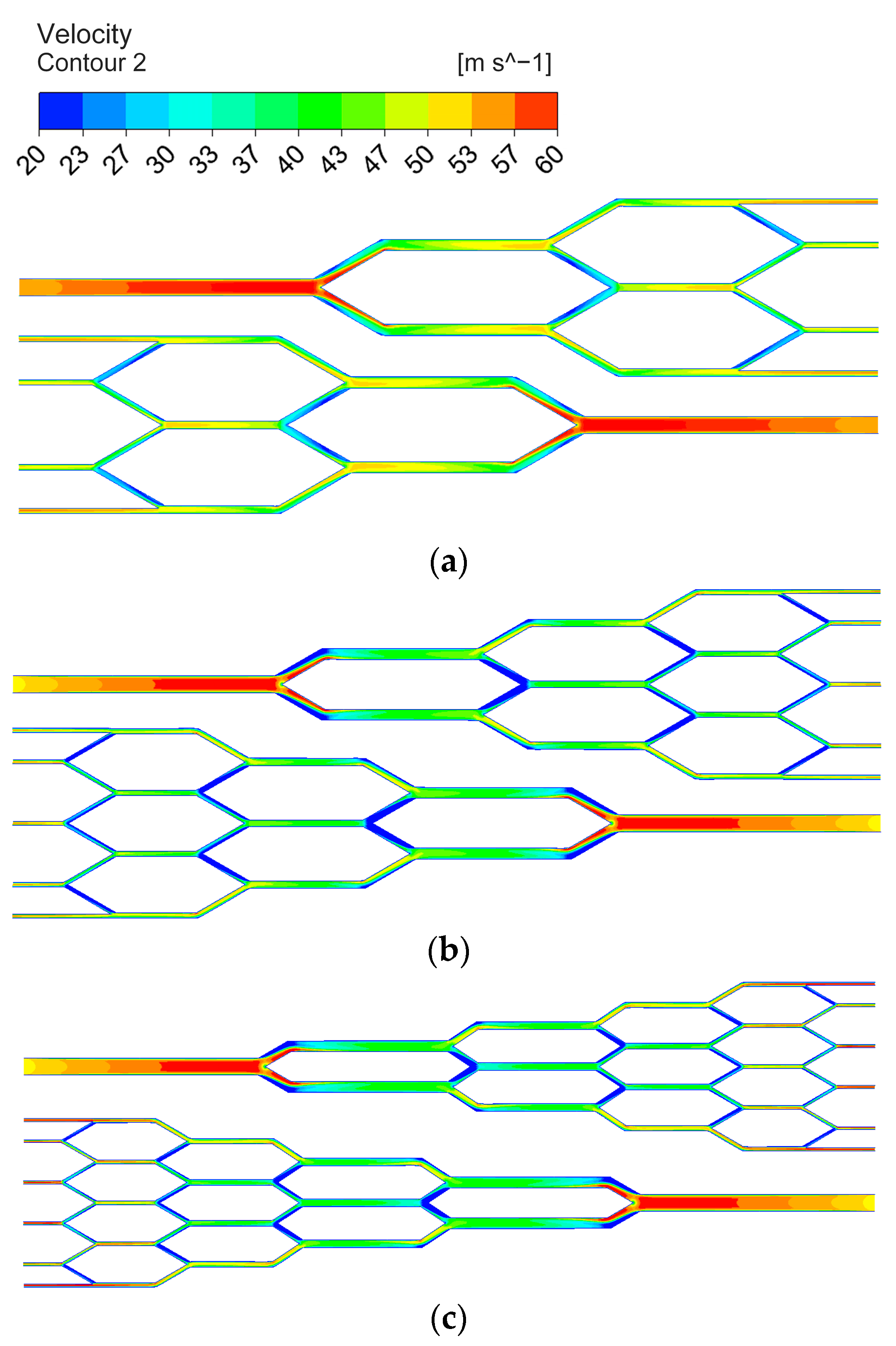
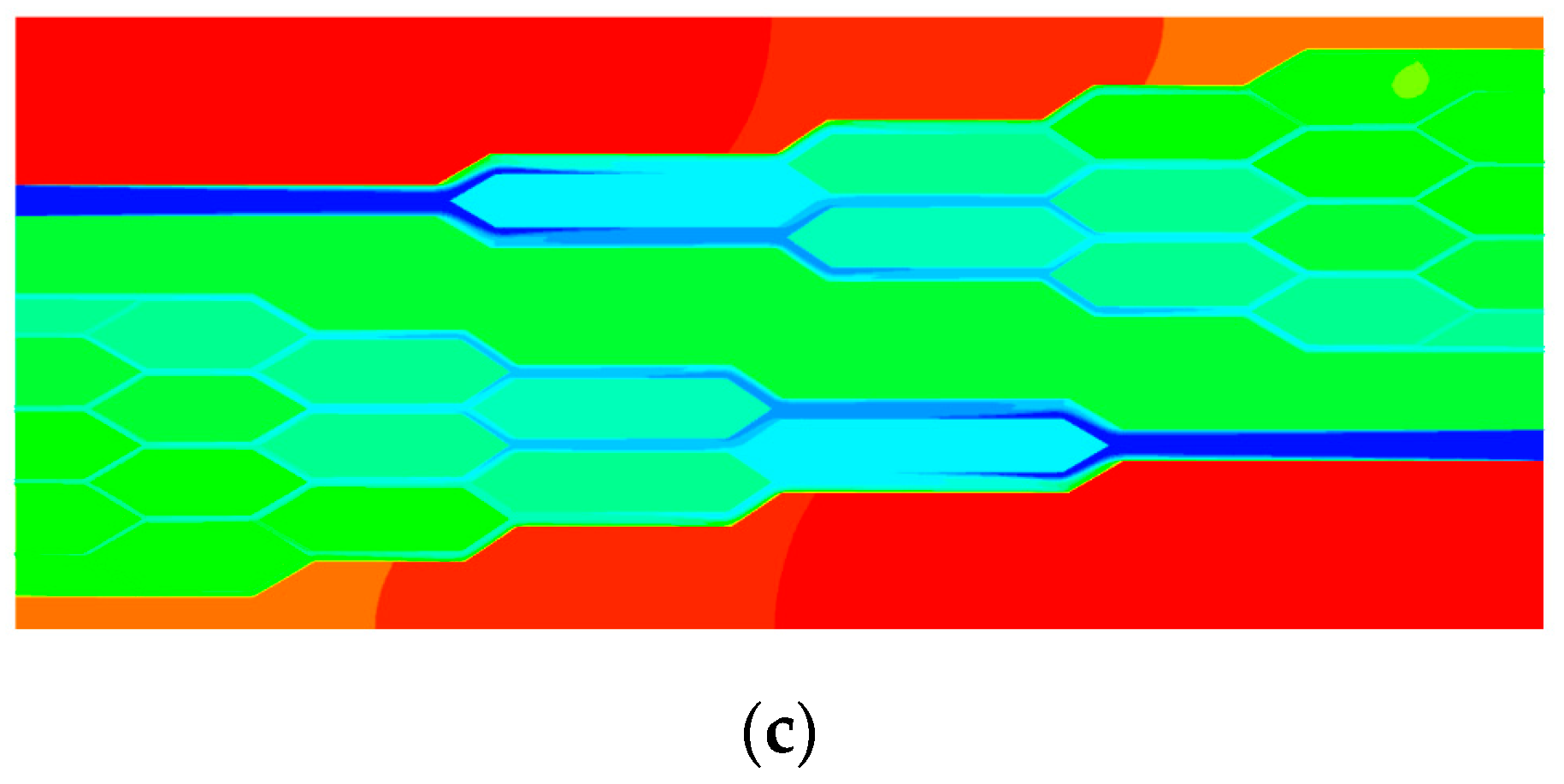
4.2. Flow and Heat Transfer in Tree-like Bifurcating Microchannels
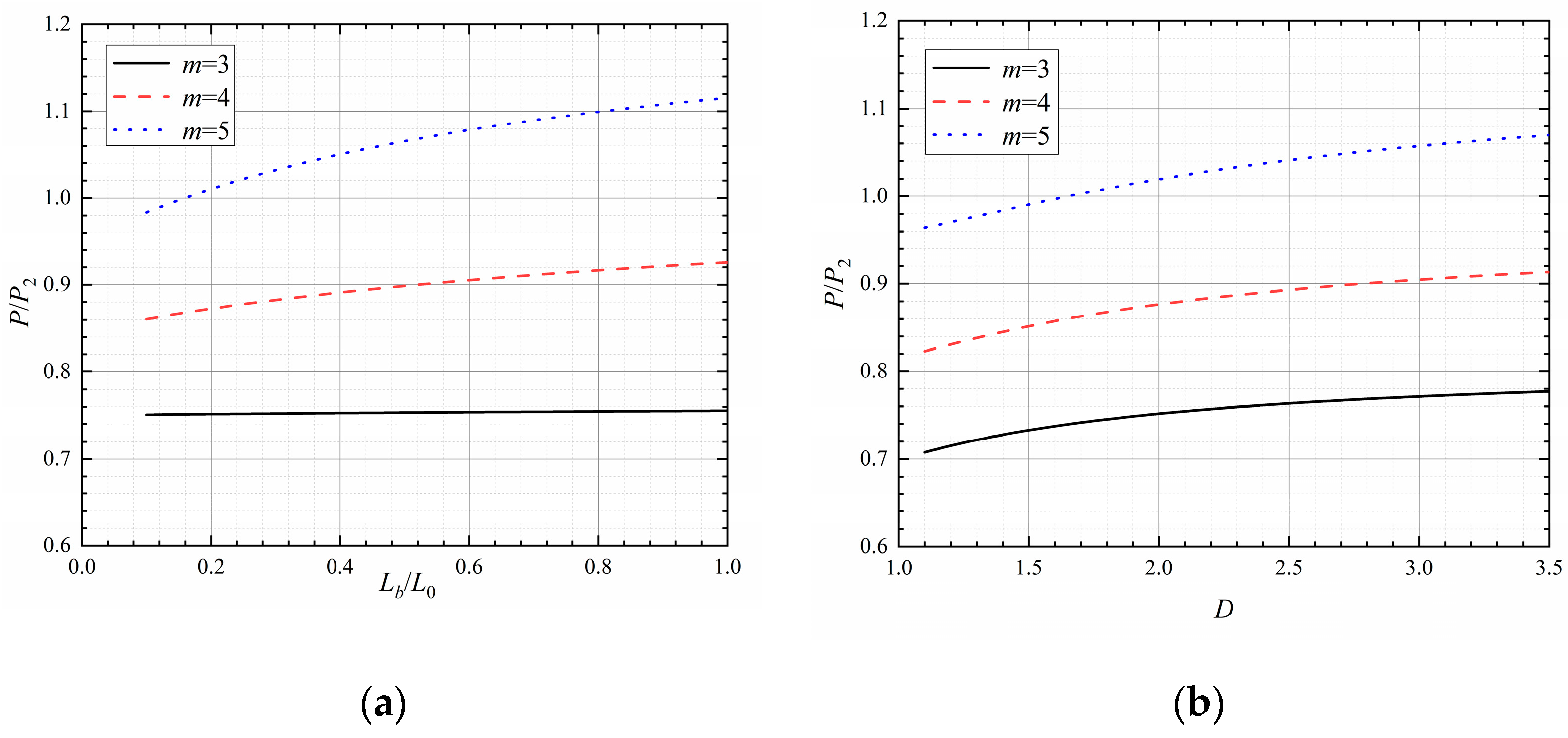
4.3. Thermal Enhancement Performance
4.4. Anti-Clogging Performance
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| c | constant | the total heat removed by air | |
| D | ractal dimension of channel length distribution | Qh | total convective heat transfer of bifurcating channels |
| d0 | the 0th channel hydraulic diameters | Qhp1 | total convective heat transfer of parallel channels with the same heat transfer area as bifurcating channels and diameter of d0 |
| dk | the kth channel hydraulic diameters | ||
| f | the Fanning friction factor | ||
| fs | friction factor in the smooth channel | ||
| hk | heat transfer coefficient of the kth level channel | Qhp2 | convective heat transfer of parallel channels |
| Lb | the channel length of the oblique channel | S | the total heat transfer area of a tree-like net |
| L0 | the channel length of the 0th branching level | Sk | the total heat transfer area of the kth level channel |
| Lk | the channel length of the kth branching level | Sp2 | total heat transfer area of parallel channels |
| L | the centerline length from the channel inlet to the outlet | Tin | the air mean temperature of the inlet in the branching microchannel |
| Lak | the channel length of the straight channel after bifurcation | Tout | the air mean temperature of the outlet in the branching microchannel |
| m | the total number of branching levels | channel volume flow rate of air | |
| Nus | the averaged Nu number in a smooth microchannel for a fully developed flow | v0 | velocity in the initial channel |
| vk | velocity in the kth level channel | ||
| n | number of parallel channels | β | the ratio of the diameter of the channel at the (k + 1)th branch level versus the diameter of the channel at the kth branch level |
| N | number of branches into which a single channel bifurcates | ||
| P | pumping power of the tree-like channels | α | the ratio of the length of the channel at the (k + 1)th branch level versus the length of the channel at the kth branch level |
| Pp2 | pumping power of parallel channels | ||
| Q | flow rate | fractal dimension of the hydraulic diameter distribution | |
| Qp2 | flow rate of parallel channels | ||
| The pressure drop of the tree-like channels | the mass-averaged thermal conductivity of air | ||
| The pressure drop of the parallel channels | temperature difference |
References
- Takeishi, K. Evolution of Turbine Cooled Vanes and Blades Applied for Large Industrial Gas Turbines and Its Trend toward Carbon Neutrality. Energies 2022, 15, 8935. [Google Scholar] [CrossRef]
- Ahn, J. Large Eddy Simulation of Flow and Heat Transfer in a Ribbed Channel for the Internal Cooling Passage of a Gas Turbine Blade: A Review. Energies 2023, 16, 3656. [Google Scholar] [CrossRef]
- Ren, Z.; Yang, X.; Lu, X.; Li, X.; Ren, J. Experimental Investigation of Micro Cooling Units on Impingement Jet Array Flow Pressure Loss and Heat Transfer Characteristics. Energies 2021, 14, 4757. [Google Scholar] [CrossRef]
- Lee, C.-S.; Shih, T.I.-P.; Bryden, K.M.; Dalton, R.P.; Dennis, R.A. Strongly Heated Turbulent Flow in a Channel with Pin Fins. Energies 2023, 16, 1215. [Google Scholar] [CrossRef]
- Yang, Y.; Du, J.; Li, M.; Li, W.; Wang, Q.; Wen, B.; Zhang, C.; Jin, Y.; Wang, W. Embedded microfluidic cooling with compact double H type manifold microchannels for large-area high-power chips. Int. J. Heat Mass Transf. 2022, 197, 123340. [Google Scholar] [CrossRef]
- He, Z.; Yan, Y.; Zhao, T.; Zhang, L.; Zhang, Z. Multi-objective optimization and multi-factors analysis of the thermal/ hydraulic performance of the bionic Y-shaped fractal heat sink. Appl. Therm. Eng. 2021, 195, 117157. [Google Scholar] [CrossRef]
- Kizilova, N.; Sauermoser, M.; Kjelstrup, S.; Pollet, B.G. Fractal-like flow-fields with minimum entropy production for polymer electrolyte membrane fuel cells. Entropy 2020, 22, 176. [Google Scholar] [CrossRef] [PubMed]
- Barnoon, P. Numerical assessment of heat transfer and mixing quality of a hybrid nanofluid in a microchannel equipped with a dual mixer. Int. J. Thermofluid 2021, 12, 100111. [Google Scholar] [CrossRef]
- Jing, D.L.; Zhan, X.K. Cross-sectional dimension dependence of electroosmotic flow in fractal treelike. Micromachines 2020, 11, 266. [Google Scholar] [CrossRef]
- Hu, B.; Wang, J.; Ma, Z.; Sang, S. Permeability and thermal conductivity models of shale matrix with a bundle of tortuous fractal tree-like branching micropore networks. Int. J. Therm. Sci. 2021, 164, 106876. [Google Scholar] [CrossRef]
- Saleh, B.; Sundar, L.S. Experimental study on heat transfer, friction factor, entropy and exergy efficiency analyses of a corrugated plate heat exchanger using Ni/water nanofluids. Int. J. Therm. Sci. 2021, 165, 106935. [Google Scholar] [CrossRef]
- Tian, Y.; Liu, X.; Xu, Q.; Luo, Q.; Zheng, H.; Song, C.; Zhu, Z.; Gao, K.; Dang, C.; Wang, H.; et al. Bionic topology optimization of fins for rapid latent heat thermal energy storage. Appl. Therm. Eng. 2021, 194, 117104. [Google Scholar] [CrossRef]
- Bjan, A. Shape and Structure, from Engineering to Nature; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar] [CrossRef]
- Bejan, A. Constructal Law: Optimization as Design Evolution. J. Heat Trans. 2015, 137, 061003. [Google Scholar] [CrossRef]
- West, G.B.; Brown, J.H.; Enquist, B.J. A General Model for the Origin of Allometric Scaling Laws in Biology Science. Science 1997, 276, 122–126. [Google Scholar] [CrossRef] [PubMed]
- Senn, S.M.; Poulikakos, D. Laminar mixing, heat transfer and pressure drop in tree-like microchannel nets and their application for thermal management in polymer electrolyte fuel cells. J. Power Sources 2004, 130, 178–191. [Google Scholar] [CrossRef]
- Alharbi, A.Y.; Pence, D.V.; Cullion, R.N. Thermal characteristics of microscale fractal-like branching channels. J. Heat Transf. 2004, 126, 744–752. [Google Scholar] [CrossRef]
- Chen, Y.P.; Yao, F.; Huang, X.Y. Mass transfer and reaction in methanol steam reforming reactor with fractal tree-like microchannel network. Int. J. Heat Mass Transf. 2015, 87, 279–283. [Google Scholar] [CrossRef]
- Chen, Y.P.; Cheng, P. Heat transfer and pressure drop in fractal tree-like microchannel nets. Int. J. Heat Mass Transf. 2002, 45, 2643–2648. [Google Scholar] [CrossRef]
- Rubio-Jimenez, C.A.; Hernandez-Guerrero, A.; Cervantes, J.G.; Lorenzini-Gutierrez, D.; Gonzalez-Valle, C.U. CFD study of constructal microchannel networks for liquid-cooling of electronic devices. Appl. Therm. Eng. 2016, 95, 374–381. [Google Scholar] [CrossRef]
- Jing, D.L.; Song, J. Comparison on the hydraulic and thermal performance of two tree-like channel networks with different size constraints. Int. J. Heat Mass Transf. 2019, 130, 1070–1074. [Google Scholar] [CrossRef]
- Lu, Z.H.; Zhang, K.; Liu, J.X.; Li, F. Effect of branching level on the performance of constructal theory based Y-shaped liquid cooling heat sink. Appl. Therm. Eng. 2020, 168, 114824. [Google Scholar] [CrossRef]
- Wang, X.Q.; Yap, C.; Mujumdar, A.S. Laminar Heat Transfer in Constructal Microchannel Networks with Loops. J. Electron. Packag. 2006, 128, 273–280. [Google Scholar] [CrossRef]
- Wang, X.Q.; Mujumdar, A.S.; Yap, C. Thermal characteristics of tree-shaped microchannel nets for cooling of a rectangular heat sink. Int. J. Therm. Sci. 2006, 45, 1103–1112. [Google Scholar] [CrossRef]
- Xu, P.; Wang, X.Q.; Mujumdar, A.S.; Yap, C.; Yu, B.M. Thermal characteristics of tree-shaped microchannel nets with/without loops. Int. J. Therm. Sci. 2009, 48, 2139–2147. [Google Scholar] [CrossRef]
- Miao, T.J.; Chen, A.M.; Xu, Y.; Yang, S.S.; Yu, B.M. Optimal structure of damaged tree-like branching networks for the equivalent thermal conductivity. Int. J. Therm. Sci. 2016, 102, 89–99. [Google Scholar] [CrossRef]
- Devore, M.A.; Kaufman, E.D. Branched Airfoil Core Cooling Arrangement. U.S. Patent 8449254, 28 May 2013. [Google Scholar]
- Ahmad, F.; Burzych, T.; Hummel, E. Arrangement of Cooling Channels in a Turbine Blade. U.S. Patent 15023392, 17 September 2014. [Google Scholar]
- Shui, L.Q.; Huang, B.; Dong, K.K.; Zhang, C.Y. Investigation of Heat Transfer and Flow Characteristics in Fractal Tree-Like Microchannel With Steam Cooling. In Proceedings of the ASME Turbo Expo 2017: Turbomachinery Technical Conference and Exposition, Charlotte, NC, USA, 26–30 June 2017. [Google Scholar] [CrossRef]
- Shui, L.; Huang, B.; Gao, F.; Rui, H. Experimental and numerical investigation on the flow and heat transfer characteristics in a tree-like branching microchannel. J. Mech. Sci. Technol. 2018, 32, 937–946. [Google Scholar] [CrossRef]
- Xu, P.; Yu, B. The scaling laws of transport properties for fractal-like tree networks. J. Appl. Phys. 2006, 100, 104906. [Google Scholar] [CrossRef]
- Hylton, L.D.; Nirmanlan, V.; Sultanian, B.K.; Kaufman, R.M. The Effects of Leading Edge and Downstream Film Cooling on Turbine Vane Heat Transfer; NASA CR-182133. 1988. Available online: https://ntrs.nasa.gov/citations/19890004383 (accessed on 17 July 2023).
- Stephan, K.; Preußer, P. Wärmeübergang und maximale Wärmestromdichte beim Behältersieden binärer und ternärer Flüssigkeitsgemische. Chem-Ing-Tech 1979, 51, 37. [Google Scholar] [CrossRef]
- Kline, S.J.; McClintock, F.A. Describing experimental uncertainties in single-sample experiments. Mech. Eng. 1953, 75, 3–8. [Google Scholar]
- Shah, R.K.; London, A.L. Laminar Flow Forced Convection in Ducts. J. Fluids Eng. 1978, 102, 431–455. [Google Scholar] [CrossRef]
- Incropera, F.P.; De Witt, D.P. Fundamentals of Heat and Mass Transfer, 2nd ed.; John Wiley and Sons: New York, NY, USA, 2007. [Google Scholar]
- Kakac, S.; Shah, R.K.; Aung, W. Handbook of Single-Phase Convective Heat Transfer; John Wiley and Sons: New York, NY, USA, 1987. [Google Scholar]









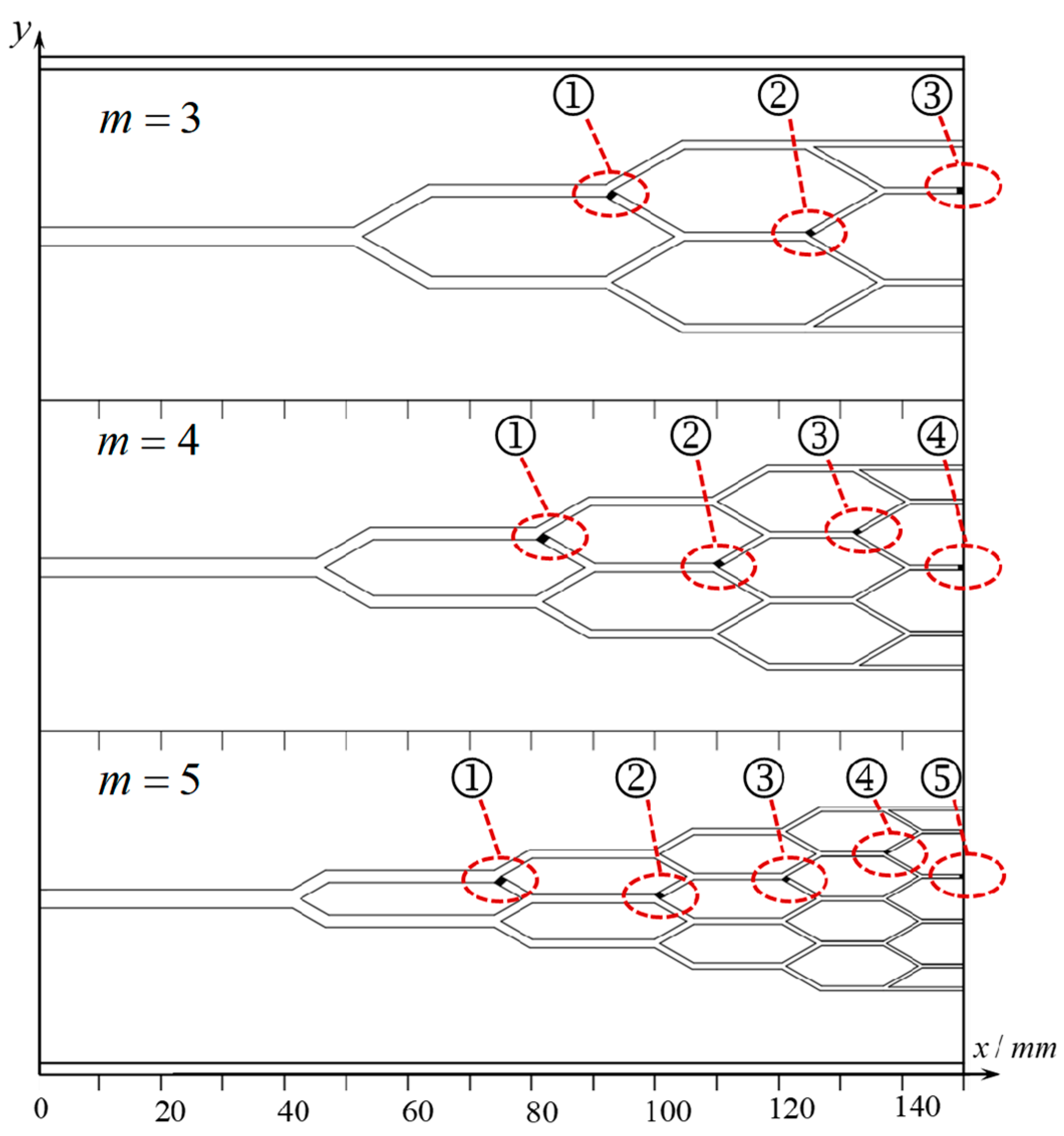



| k | m = 3 | m = 4 | m = 5 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| lk/mm | dk/mm | Wk/mm | lk/mm | dk/mm | Wk/mm | lk/mm | dk/mm | Wk/mm | |
| 0 | 50.67 | 3 | 3 | 44.56 | 3 | 3 | 40.64 | 3 | 3 |
| 1 | 43 | 2.38 | 1.97 | 35.37 | 2.38 | 1.97 | 32.25 | 2.38 | 1.97 |
| 2 | 34.44 | 1.89 | 1.38 | 28.07 | 1.89 | 1.38 | 25.6 | 1.89 | 1.38 |
| 3 | 27.85 | 1.5 | 1 | 22.28 | 1.5 | 1 | 20.31 | 1.5 | 1 |
| 4 | - | - | - | 17.68 | 1.19 | 0.74 | 16.12 | 1.19 | 0.74 |
| 5 | - | - | - | - | - | - | 12.8 | 0.945 | 0.56 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shui, L.; Hu, Z.; Song, H.; Zhai, Z.; Wang, J. Study on Flow and Heat Transfer Characteristics and Anti-Clogging Performance of Tree-Like Branching Microchannels. Energies 2023, 16, 5531. https://doi.org/10.3390/en16145531
Shui L, Hu Z, Song H, Zhai Z, Wang J. Study on Flow and Heat Transfer Characteristics and Anti-Clogging Performance of Tree-Like Branching Microchannels. Energies. 2023; 16(14):5531. https://doi.org/10.3390/en16145531
Chicago/Turabian StyleShui, Linqi, Zhongkai Hu, Hang Song, Zhi Zhai, and Jiatao Wang. 2023. "Study on Flow and Heat Transfer Characteristics and Anti-Clogging Performance of Tree-Like Branching Microchannels" Energies 16, no. 14: 5531. https://doi.org/10.3390/en16145531
APA StyleShui, L., Hu, Z., Song, H., Zhai, Z., & Wang, J. (2023). Study on Flow and Heat Transfer Characteristics and Anti-Clogging Performance of Tree-Like Branching Microchannels. Energies, 16(14), 5531. https://doi.org/10.3390/en16145531












