A Systemic Comparison of Physical Models for Simulating Surfactant–Polymer Flooding

Alhotan, Muhammad M.; Batista Fernandes, Bruno R.; Delshad, Mojdeh; Sepehrnoori, Kamy

doi:10.3390/en16155702

Open AccessArticle

A Systemic Comparison of Physical Models for Simulating Surfactant–Polymer Flooding

by

Muhammad M. Alhotan

¹,

Bruno R. Batista Fernandes

²,

Mojdeh Delshad

^1,*

and

Kamy Sepehrnoori

¹

Hildebrand Department of Petroleum and Geosystems Engineering, The University of Texas at Austin, Austin, TX 78712, USA

²

Center for Subsurface Energy and the Environment, The University of Texas at Austin, Austin, TX 78712, USA

^*

Author to whom correspondence should be addressed.

Energies 2023, 16(15), 5702; https://doi.org/10.3390/en16155702

Submission received: 18 May 2023 / Revised: 22 July 2023 / Accepted: 25 July 2023 / Published: 30 July 2023

(This article belongs to the Special Issue Reservoir Simulation Studies for Enhanced Oil Recovery II)

Download

Browse Figures

Versions Notes

Abstract

:

Three different reservoir simulators that utilize both two-phase and three-phase microemulsion phase behavior models are used to model surfactant–polymer flooding to determine and compare their results. Different models are used in each simulator to describe the physical behavior of injected chemicals into the reservoir, which raises the need to benchmark their results. The physical behavior models of polymer and surfactant were constructed and verified on a 1D scale reservoir model and further verified in a 3D model. Finally, simulations were conducted in a field-scale reservoir containing 680,400 grids, where results were compared and analyzed. The 1D and 3D model results suggest an excellent match between the different simulators in modeling surfactant–polymer floods. In the case of the field-scale model, the simulators matched in terms of oil recovery and total volumes produced and injected, while having similar reservoir pressure profiles but with significant discrepancies in terms of injected and produced chemicals. These results indicate that despite the differences in the calculated injected and produced chemicals due to the different models in the simulators, the effect of surfactant–polymer floods on oil recovery, total injected and produced fluids, and average pressure profiles can be comparably modeled in all of the three simulators.

Keywords:

EOR; microemulsion; reservoir simulation; surfactant; polymer

1. Introduction

Many oil reservoirs start production through primary recovery and transition to secondary oil recovery as the reservoir loses energy to produce alone. These methods, although economically viable, leave behind much untapped potential in oil recovery, with 55% to 75% of the original oil in place (OOIP) remaining in the reservoir after secondary recovery [1]. In addition, steady growth in world energy demand over decades has made oil production increasingly difficult as oil reservoirs became depleted and transitioned to mature fields with declining oil production. Such challenges have led to innovative solutions that can improve oil recovery from existing mature fields, such as enhanced oil recovery (EOR), representing a wide range of advanced oil recovery methods.

When EOR methods are used, injected fluids interact with the reservoir strata and in situ fluids to increase oil production, improving its economic value and lifetime [2]. EOR methods are categorized into chemical, gas/solvent, and thermal [3]. These applications aim to increase oil production by reducing the residual oil saturation (S_or) or reducing oil viscosity. Oil residual saturation is reduced by leveraging two main properties: increasing the capillary number (N_c) and decreasing the mobility ratio (M) [4,5,6,7]. Chemical EOR is characterized by individual or combined injection of polymer, surfactant, cosolvents, and alkali to improve oil recovery [3]. Polymer flooding increases the viscosity of the injected fluid, thereby decreasing the mobility ratio and improving sweep efficiency. Surfactant flooding reduces the interfacial tension between oil and water in the reservoir, changes wettability, and can generate foam in specific cases. Such effects can increase the capillary number and improve the mobility ratio.

The difficulty in producing oil from mature fields comes from several factors, the most important of which are mobility control issues and natural capillary forces that trap the oil in the porous media. Surfactant–polymer flooding is designed to address those issues. Surfactant–polymer flooding increases oil production by decreasing the mobility ratio of the injected fluid and producing a low interfacial tension flood [2,8,9,10,11,12]. These effects aid in moving trapped or bypassed oil to the producer, thereby increasing recovery. However, the physical properties and processes of this type of flooding are complex and require careful investigation. That is, if not properly formulated, designed, or executed, the chemical flood will have an adverse effect on the reservoir. It might even cause permanent damage to the field’s oil production capacities. Therefore, field tests, academic research, and extensive analyses are necessary before executing such a method. Numerical reservoir simulators are tools used to predict the performance of field-scale projects under certain conditions before deployment. Such a tool allows detailed analysis of enhanced oil recovery methods that minimize the risk involved in their development.

Reservoir simulators are computer programs that use reservoir engineering concepts to model the fluid flow and behavior in the reservoir. These models are constructed based on formulations derived from lab data and mathematical derivations that describe various physical behaviors in the field. Chemical EOR methods and physical properties have been studied extensively in recent decades. Subsequently, different simulators have been developed using various solution schemes to describe the reservoir characteristics during chemical EOR. While many approaches have been developed for modeling the fluid flow of black oil and compositional oils [13,14,15,16,17,18,19,20,21,22,23,24], modeling chemical EOR requires special phase behavior and fluid flow concepts, especially in cases where a microemulsion phase is present [25,26,27,28].

Pope and Nelson [29] developed a one-dimensional simulator that modeled the shear-thinning effect in polymer injection and the three-phase oil–brine–microemulsion phase behavior using an Implicit Pressure Explicit Composition (IMPEC) formulation. Delshad et al. [30] presented a three-dimensional, advection–diffusion, multiphase, multicomponent IMPEC reservoir simulator for chemical EOR considering dead crude oil (insignificant solution gas). Tong and Chen [31] developed an isothermal, fully implicit, three-phase, three-dimensional model to simulate polymer flooding with the black oil model. John et al. [32] and Han et al. [33] implemented Winsor Type I [34] microemulsion phase behavior using Hand’s rule [35] in a fully implicit equation of state (EOS) compositional simulator (GPAS), which was further extended by Han et al. [36] to account for the Equivalent Alkane Carbon Number (EACN) and Najafabadi et al. [37] to account for the other Winsor microemulsion types. Another fully implicit four-phase simulator with similar capabilities was developed by Patacchini et al. [38]. Yang et al. [39] presented an adaptive implicit method for surfactant–polymer flooding but considered only Winsor Type I microemulsion when a surfactant was injected. While the polymer’s zero shear rate was assumed to change with the surfactant concentration, the interfacial tension was assumed to be a function of the surfactant concentration rather than the solubilization ratio. Mykkeltvedt et al. [40] implemented a fully implicit scheme using automatic differentiation and high-order discretization schemes for the polymer flooding simulation. Goudarzi et al. [41] conducted a benchmark study comparing various numerical reservoir simulators to assess the strengths and limitations of each simulator for specific chemical EOR processes, aiming to improve chemical design for field-scale studies and optimize field injection projects.

Nghiem et al. [42] presented an adaptive implicit compositional reservoir simulator capable of modeling the surfactant–polymer flooding that approximates the brine/oil/microemulsion three-phase system to a modified brine/oil system [43]. Shi et al. [44] developed a new fully implicit chemical flooding formulation by mixing natural and global concentration variables and using total concentrations as primary unknowns for the components that only partition in the aqueous phase (polymer, anion, cation). The model considered the microemulsion phase and all Winsor phase environments. Such work was further improved by Han et al. [45] with the addition of cosolvents. Jia et al. [46] presented a two-phase, five-component, fully implicit reservoir simulator for polymer-surfactant flooding. Finally, Jia et al. [46] considered a variable substitution method that considered two sets of primary variables, but only the Type II(-) microemulsion type was considered in their work. The five components were water, oil, surfactant, polymer, and salt, and the implementation was performed using perpendicular bisector (PEBI) grid discretization. Their implementation was validated with the UTCHEM simulator [30].

Fernandes [47] and Fernandes et al. [48] presented advanced algorithms for solving partial differential equations in reservoir simulators, focusing on compositional miscible gas flooding and chemical EOR processes. The research develops adaptive implicit (AIM) methods, fully implicit (FI) approaches, and other novel techniques to improve simulation performance. The findings, implemented in the in-house simulators UTCOMPRS and UTCHEMRS, demonstrate increased robustness and computational performance compared to original IMPEC approaches and commercial simulators commonly used in the oil industry. An example of a field simulation case study conducted using different simulators was done by Guzman et al. [49], where different scenarios of polymer flooding and surfactant polymer flooding were evaluated using various simulators as part of a field case study on a Colombian oil field. In their study, a sector model was constructed and validated through history matching with the various simulators to determine the best approach for maximum oil recovery.

In this study, three different chemical EOR reservoir simulators were used to systematically investigate the differences using a three-phase microemulsion phase behavior model versus a two-phase model for SP flooding. Simulators A (UTCHEMRS [47,48]) and B (SLB-INTERSECT [50]) share some similarities, especially in terms of the three-phase microemulsion phase behavior model, but they use different relative permeability and adsorption reversibility models. On the other hand, simulator C (CMG-STARS [51]) can only simulate microemulsion phase behavior in Winsor Type I or Type II, with no capabilities to model Type III phase behavior. Additionally, simulator C uses fundamentally different methods to model polymer rheology, adsorption, and permeability reduction. To the best of our knowledge, this is the first time that commercial-grade reservoir simulators capable of modeling three-phase brine/oil/microemulsion systems for full-field simulation (INTERSECT and UTCHEMRS) are presented against a commercial simulator that models the surfactant flooding with a two-phase brine/oil model (CMG-STARS). It is important to consider that the simulations in this study serve as synthetic cases for comparing the physical models among the reservoir simulators, and the practicalities of real-world scenarios may differ. Notably, there have been significant debates regarding the inclusion of Type III microemulsion phase in the SP models (three phases of water/oil/microemulsion). CMG-STARS can only model Type I or Type II microemulsion systems, whereas UTCHEM-RS and INTERSECT both can model the salinity and phase behavior transition of Type I to Type III to Type II. This paper provides more insights into this aspect of SP modeling, making a valuable contribution to the ongoing discussions in the field.

2. Materials and Methods

Surfactant–polymer flooding was modeled using various simulation cases for three reservoir models. The methodology used to construct and validate the simulation cases is explained here.

2.1. Modeling Approach

In this study, 27 simulation cases are presented based on three reservoir models and three different flooding designs using three simulators. The reservoir models are 1D, 3D, and field reservoir models (Figure 1). The flooding scenarios comprise waterflood, polymer flood, and SP flood. Initially, 1D waterflooding was modeled to validate the physical property models before polymer or SP simulations. Next, a simple 3D model with one injector and one producer and, finally, a field-scale model with 680,400 grids with 12 injectors and six producers were simulated.

2.2. One-Dimensional Model

The reservoir parameters, injection well constraint, production well constraint, and initial conditions are summarized in Table 1. The 1D cases are conducted first to ensure the input parameters among different reservoir simulators are calibrated before conducting the more complex and CPU-intensive 3D cases.

2.3. Three-Dimensional Model

A 3D Cartesian and homogeneous reservoir model is set up, which serves as a precursor to field cases. Sweep efficiency and the changes in species concentrations were more prominent. Table 2 summarizes model parameters.

2.4. Field-Scale Model

The field-scale reservoir model considers a geological model with 680,400 gridblocks based on the publicly available data set of the Volve field in the Norwegian North Sea [52]. This model is constructed using a corner point grid with 215,114 active blocks. The reservoir is highly heterogeneous and faulted.

The reservoir was initialized using the equilibrium model in Simulator B and subsequently applied to the other simulators. The water-oil contact was at a depth of 9800 ft. Figure 2 shows the porosity distribution, permeability in the X direction, the initial reservoir pressure, and the well locations. The model was constructed with 18 wells in a 5-spot pattern, with twelve injectors and six producers (Figure 2d). A summary of the properties of the model is compiled in Table 3.

2.5. Summary of Physical Properties

Physical properties are presented based on the type of flood simulated.

2.6. Waterflood

The first scenario is a waterflood with input parameters summarized in Table 4, and the oil/water relative permeability curves are illustrated in Figure 3.

2.7. Polymer Flood

Polymer is injected after an initial waterflood. Simulating separate cases for polymer and SP is necessary to distinguish between the effects of polymer and surfactant on oil recovery, volumetric and displacement sweep efficiencies, and other results. Table 5 summarizes the polymer property models included, where simulators A and B share the same models (denoted as 1), while simulator C uses different models (denoted as 2). Table 6 summarizes the polymer model input parameters in simulators A and B. The polymer viscosity as a function of polymer concentration is illustrated in Figure 4a. In simulator C, polymer viscosity is modeled using the non-linear mixing function shown in Figure 4b. Polymer adsorption and permeability reduction parameters for simulators A and B are shown in Table 6. Figure 5 illustrates the adsorption model as a function of polymer concentration.

2.8. Surfactant–Polymer Flood

The SP flood was designed in four stages, starting with water, followed by a surfactant–polymer slug; then a polymer drive is injected, and finally, a second waterflood is injected.

Additional physical properties were added to previous water and polymer data to model surfactant–polymer behavior in the reservoir. Table 7 compares the surfactant models in three simulators. First, the presence of a microemulsion phase necessitates an additional viscosity model. Figure 6a displays the microemulsion viscosity behavior as a function of oil concentration in the microemulsion phase for Simulators A and B. A non-linear mixing function is used to model microemulsion viscosity for simulator C.

The surfactant model parameters are detailed in Table 8. Figure 6b shows the adsorption model’s behavior as a function of surfactant concentration. Next, simulators A and B require input parameters to construct the binodal curve for microemulsion phase behavior. Figure 7 shows the solubilization plot for the surfactant formulation used in the simulations. Simulator C lacks this capability and models surfactant as a tracer that can solubilize oil and is provided by a table entry of K-values. The user provides the K-values as a function of temperature, pressure, and surfactant concentration. We generated the K-values using Hand’s rule in Equation (A69) in Appendix A.

The Capillary Desaturation Curve (CDC) parameters are given in Table 8. The CDC describes how residual saturation changes as a function of the capillary/trapping number (Figure 8). These parameters were used in simulators A and B. Simulator C generates residual oil data based on input capillary number for the start and end of the desaturation. Finally, the parameters to model IFT are provided in Table 8. Simulators A and B use Equations (A16)–(A19) in Appendix A and simulator C uses a table of IFT values as a function of oil mole fraction. The oil/microemulsion IFT behavior as a function of oil concentration in the microemulsion phase is given in Figure 9.

3. Results

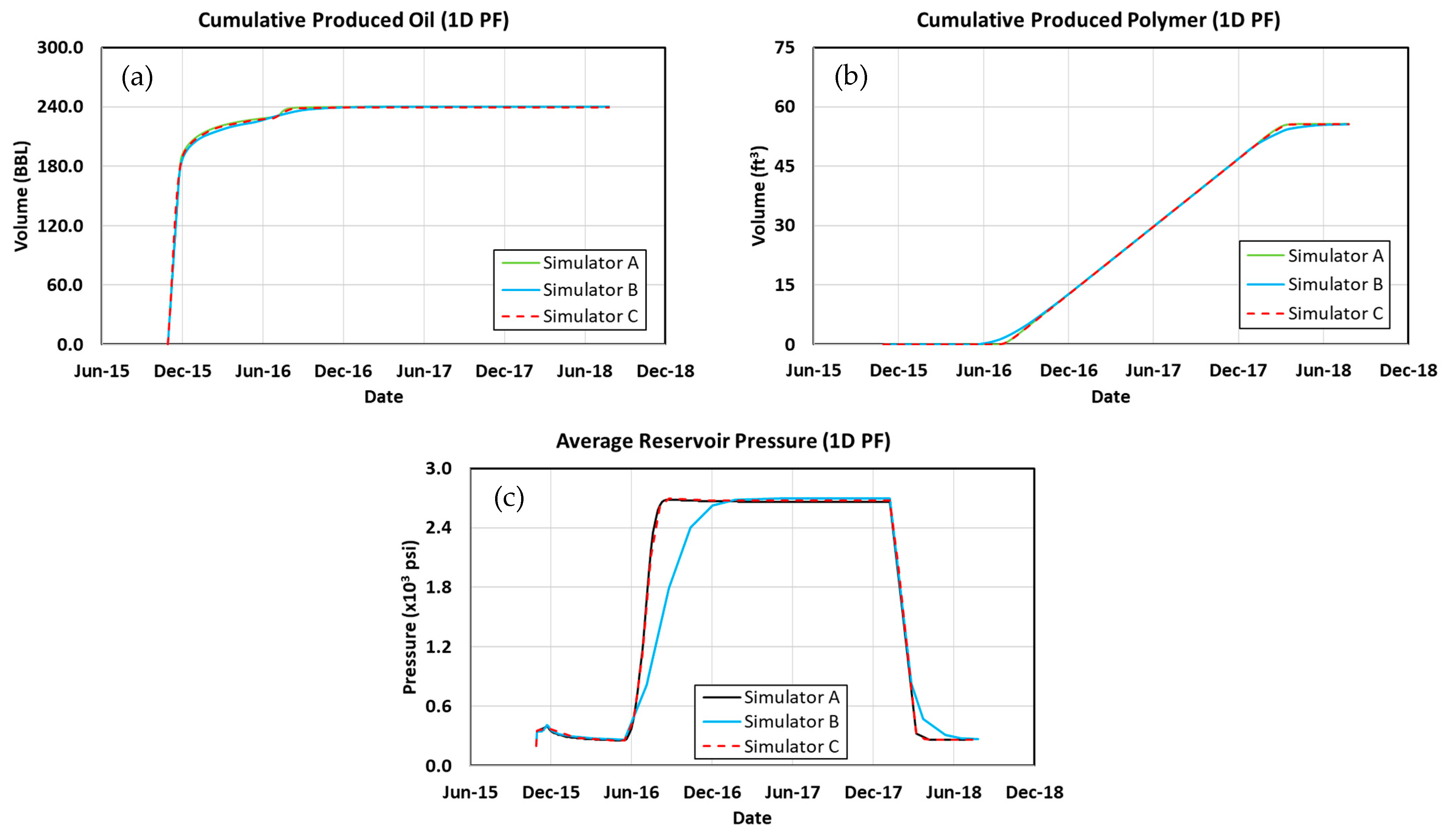
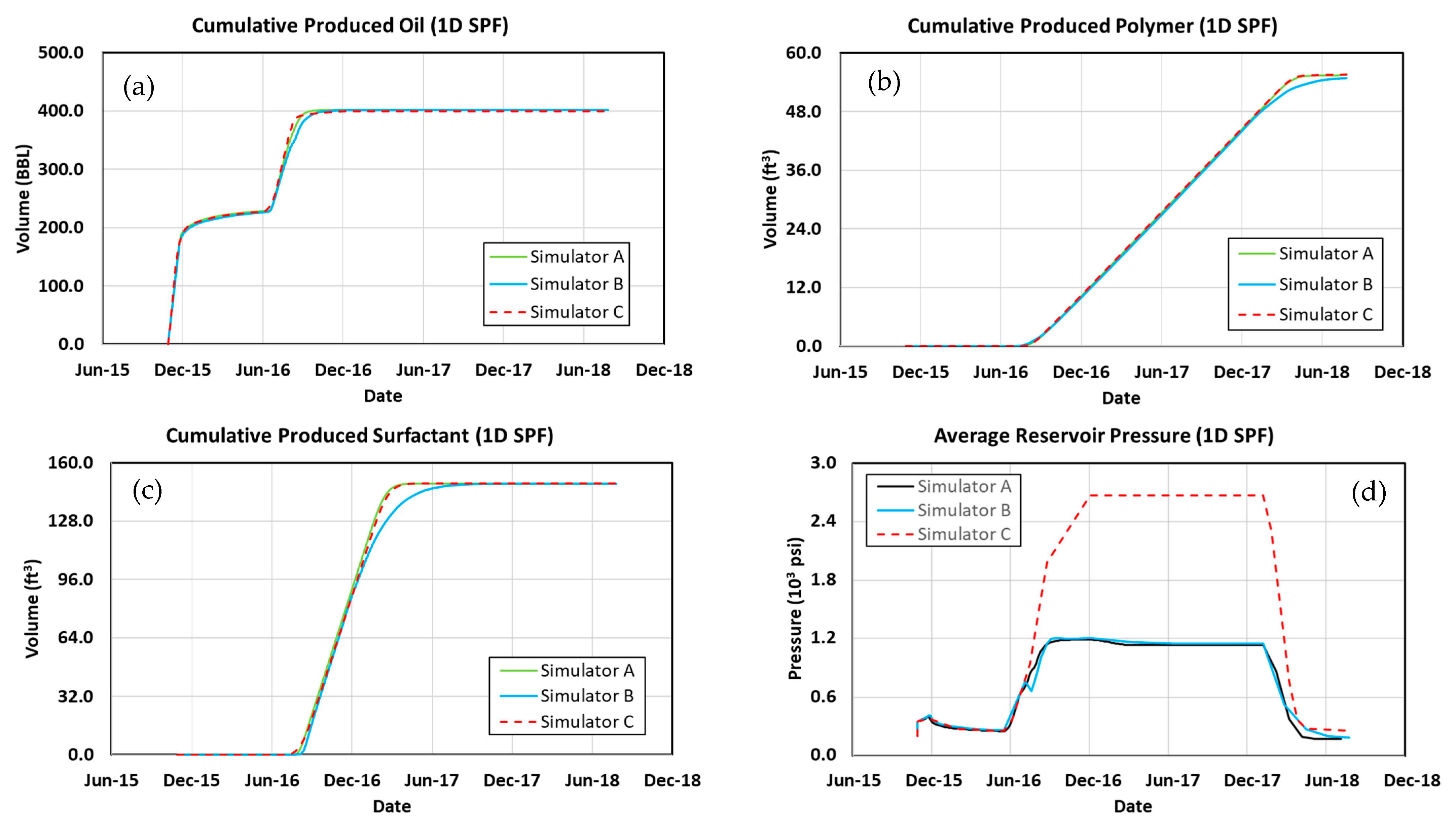
3.1. 1D Model Simulation Cases

In this subsection, simulation results of waterflood, polymer flood, and surfactant–polymer flood in the 1D model are compared among the three simulators.

3.2. Waterflood

This simulation was set to run for 1000 days using waterflooding, with parameters specified in Section 2 (Table 1). Table 9 summarizes the results from these three simulations with very similar results (Figure 10).

3.3. Polymer Flood

Waterflood is conducted for the first 200 days, followed by polymer injection for 600 days with 0.25 wt % polymer concentration, and another waterflood for 200 days. The results in Figure 11 confirm an excellent agreement among the simulators for polymer flood. Further details of the comparison are presented in Table 10, from which can be observed an excellent agreement between the simulators.

3.4. Surfactant–Polymer Flood

For this case, the reservoir was initiated in simulators A and B at a brine salinity of

0.325 \frac{m e q}{m l}

, which is 25% higher than the optimum salinity of

0.26 \frac{m e q}{m l} .

The flood started with a waterflood at

0.325 \frac{m e q}{m l}

, followed by a 200-day SP slug with a 0.25 wt % polymer concentration and 0.02 volume fraction of surfactant concentration at a salinity of

0.26 \frac{m e q}{m l} .

Then, a polymer drive was injected for 400 days at 0.25 wt % concentration at salinity

0.26 \frac{m e q}{m l}

. Finally, a water flush was injected for 200 days at

0.26 \frac{m e q}{m l}

salinity. The salinity profile of this flood enables the surfactant to operate in Type III microemulsion phase behavior, thereby significantly increasing oil production.

Figure 12a–c favorably compare the cumulative produced volumes with a close match across the simulators. Furthermore, Figure 12d indicates similar pressure histories between Simulators A and B but some differences when compared to Simulator C. For Simulator B, the default settings gave a very different pressure history, indicating a different model compared to the other simulators, which is explained in detail in Appendix A. However, the results matched well after modifying the default settings to one similar to Simulator A. However, it showcases a different history match. This is explained by how Simulator C models relative permeability when surfactant is present, as described in Appendix A.

Table 11 summarizes the results with good agreement in the overall results. However, it is important to note that there is a difference of about 1% between simulator C and the other two simulators for produced polymer volumes since it uses a different polymer adsorption model from the other simulators. Nevertheless, this 1D base case establishes that the results from the SP models are comparable for the three simulators.

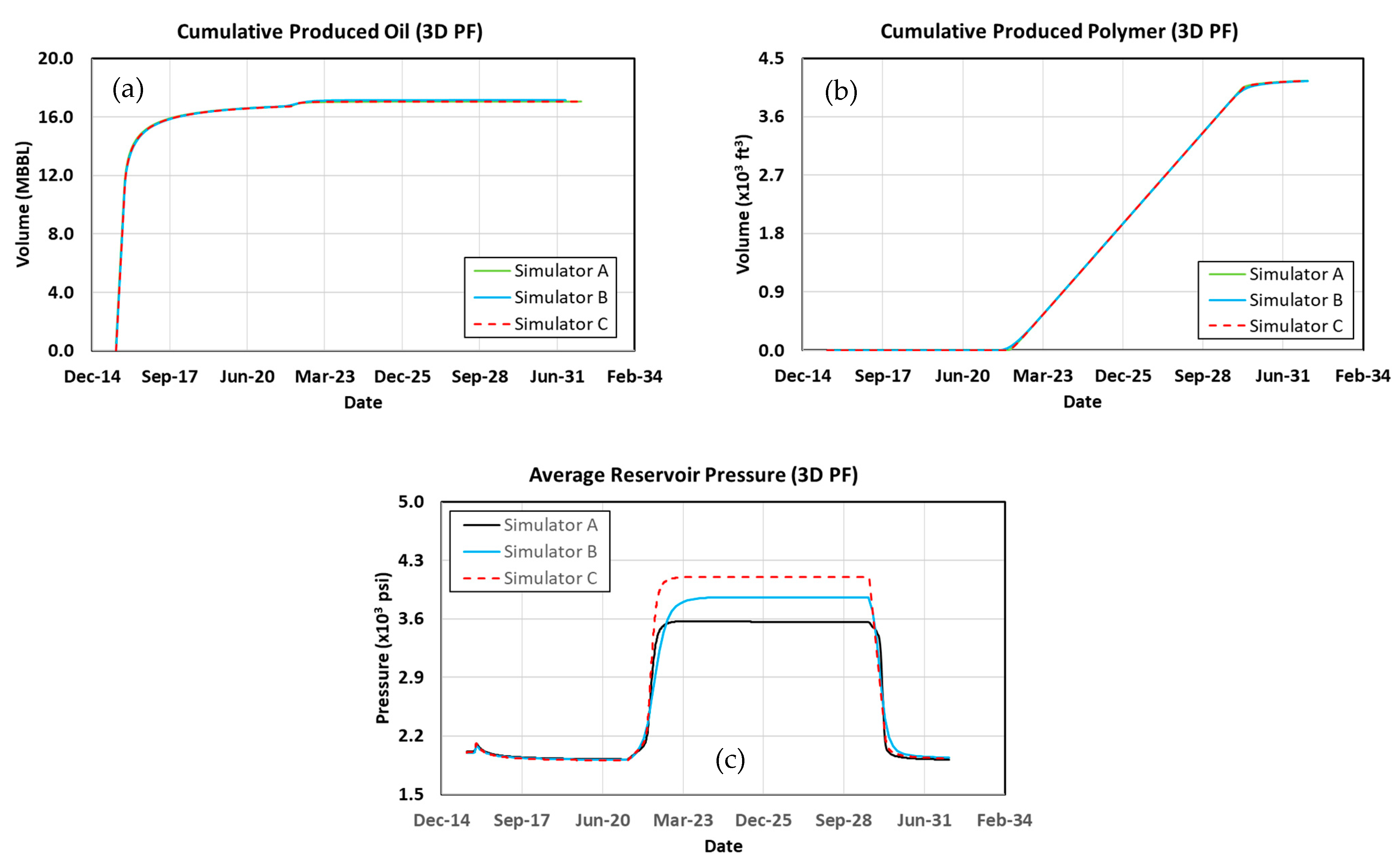
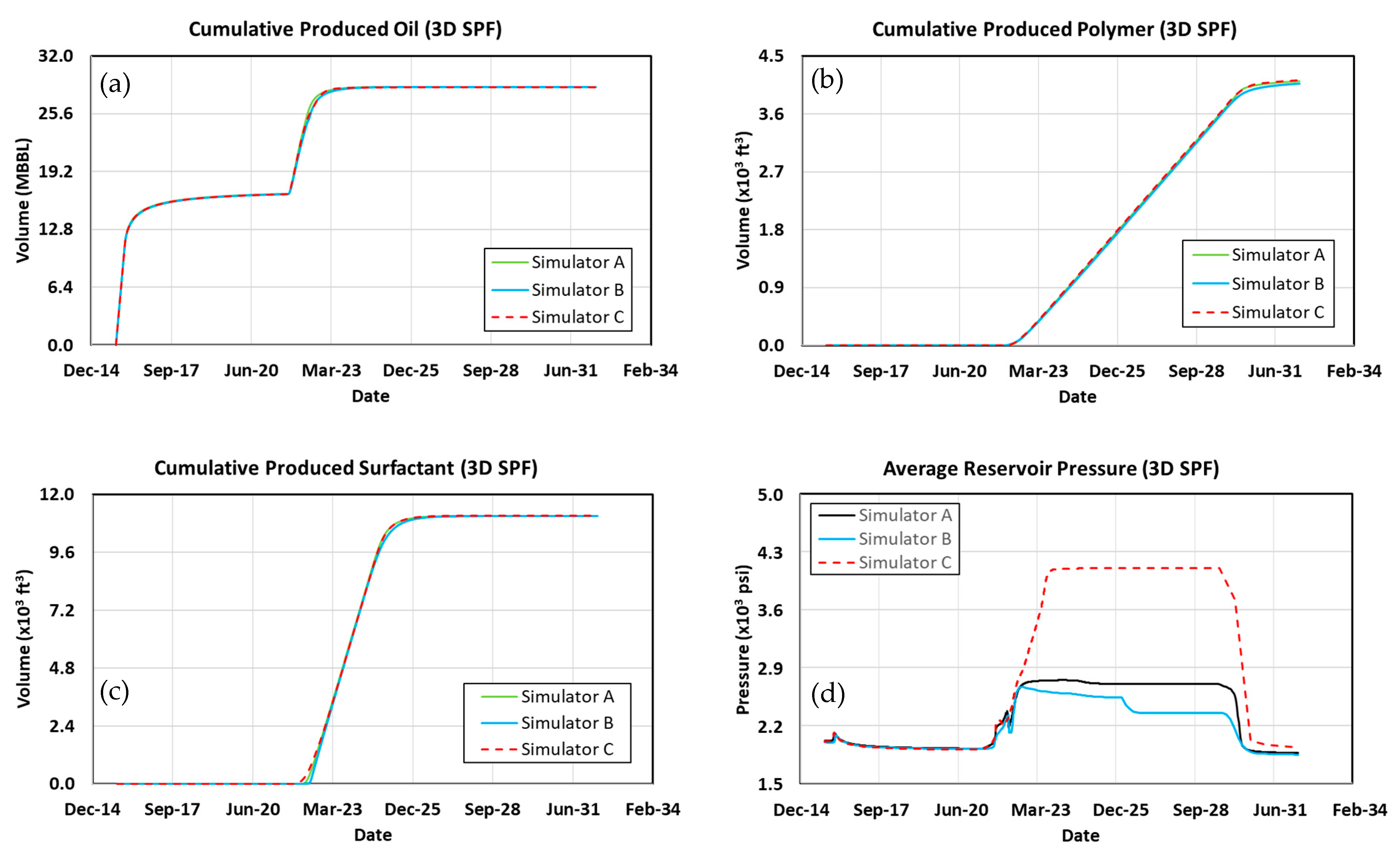
3.5. 3D Simulation Cases

This subsection discusses the 3D simulation results of waterflood, polymer flood, and surfactant–polymer flood.

3.6. Waterflood

Waterflood is conducted for 6000 days. Figure 13 shows good agreements among the simulators. Table 12 summarizes the results and establishes a solid base to model polymer and surfactant flooding.

3.7. Polymer Flood

A waterflood is modeled for the first 1000 days, followed by polymer injection for 5000 days at 0.25 wt % concentration, and finally, a waterflood flush for another 1000 days. Figure 14a,b show a close match of the results for all three simulators. However, there are some discrepancies in reservoir pressure during polymer flood (Figure 14c).

Finally, Table 13 summarizes the results of this simulation case. The results obtained show an agreement between the simulators in this study in terms of polymer flood in the 3D model. However, discrepancies exist in pressure history, as shown in Figure 14c, due to model implementation differences.

3.8. Surfactant–Polymer Flood

The 3D flood design is the same as the 1D SP case, except the waterflood was done for 1000 days, followed by a 1000-day SP slug, a 2000-day polymer drive, and a final water post flush for 1000 days. Similarly to the 1D case, all results agree (Figure 15a–c), except for the average reservoir pressure, which shows significant discrepancies (Figure 15d). The difference in pressure histories is similar to the 1D case, where the source of such differences is the relative permeability models being different between the different simulators. Table 14 summarizes the results presented in this case, which establishes high accuracy in volumetric matches, with discrepancies in pressure results due to relative permeability models when the microemulsion phase is present.

3.9. Field Model Simulations

This subsection discusses the results for water, polymer, and surfactant–polymer flooding simulations based on the Volve field reservoir model.

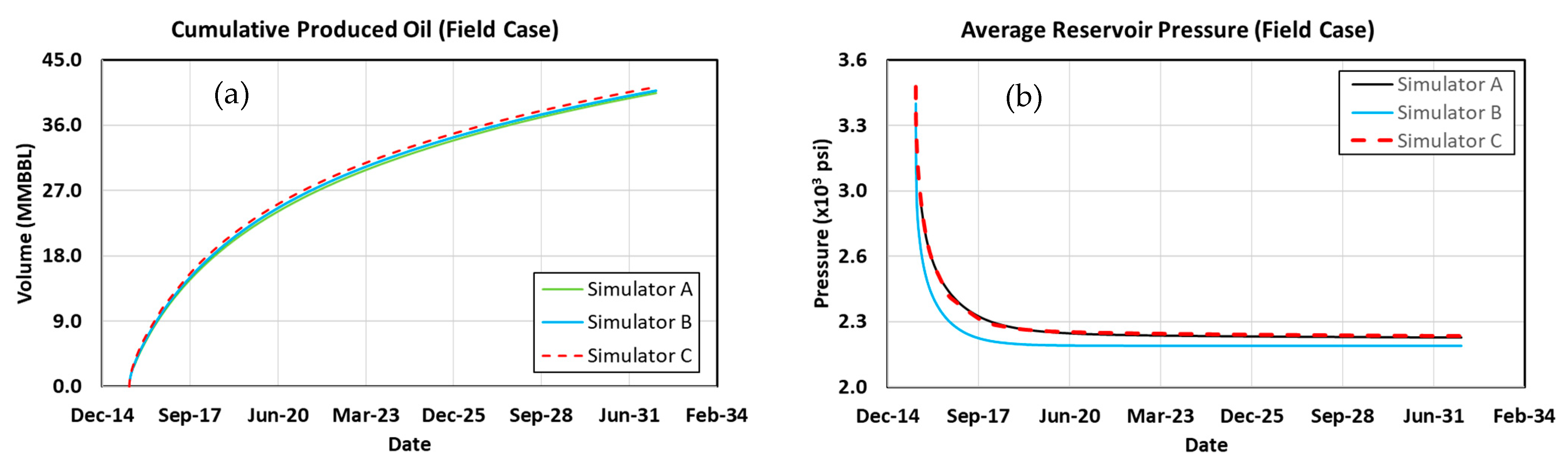
3.10. Waterflood

Waterflooding was simulated for 6000 days using 12 injectors and 6 producers. Figure 16a,b show the three simulators’ total oil production and average reservoir pressure. Table 15 summarizes the quality of the results. All volumetric rates and the pressure history show good agreement among the simulators.

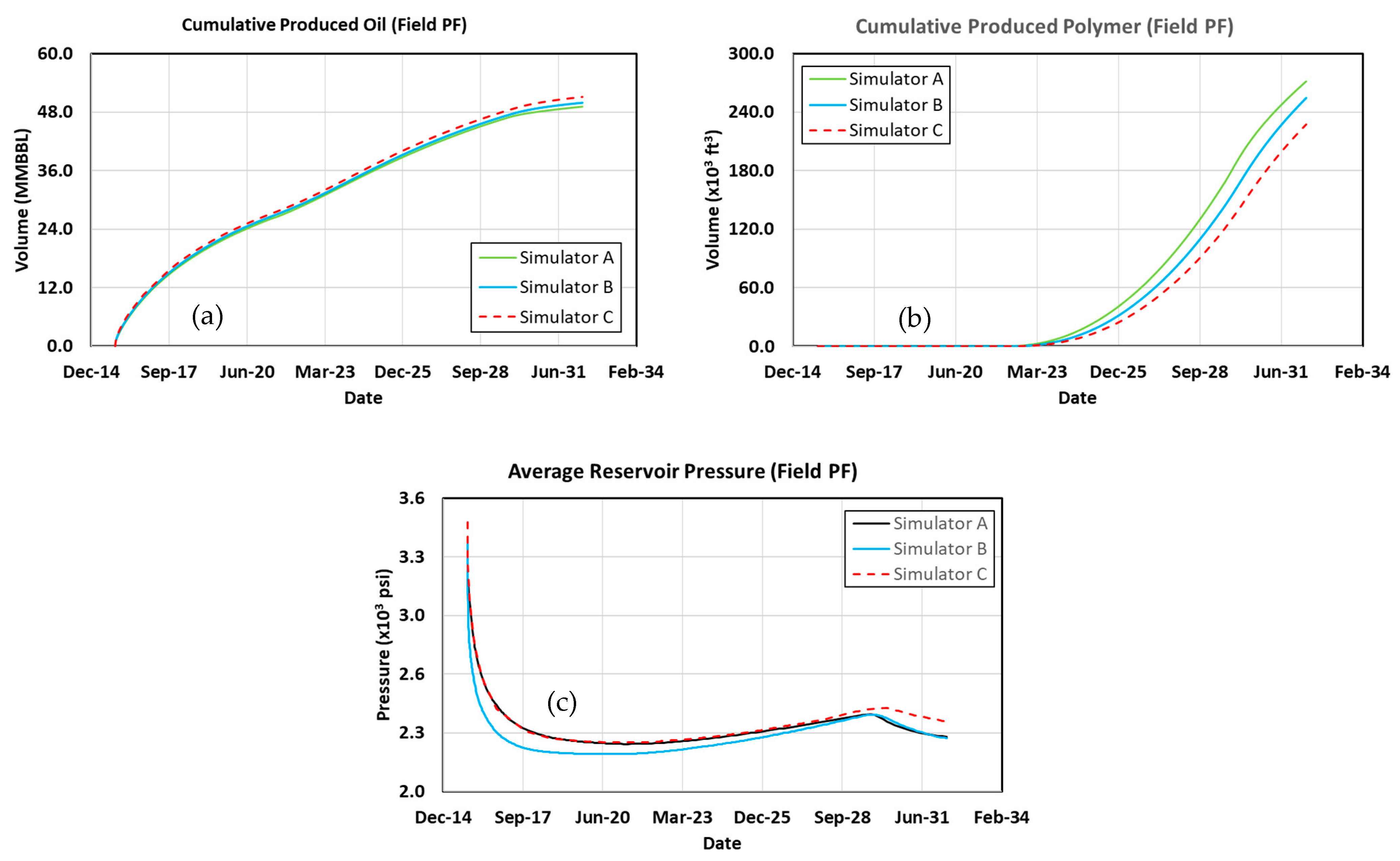
3.11. Polymer Flood

The polymer flood was designed in the same manner as the previously discussed case, with a waterflood for the first 1000 days followed by a polymer injection in all 12 injectors for 5000 days at 0.25 wt % concentration and water salinity of

0.26 \frac{m e q}{m l}

. Finally, water was injected for 1000 days.

The results are illustrated in Figure 17, where the total volumetric rates indicate consistent agreement among the simulators. On the other hand, compared with the previous smaller simulation models, the result for the field simulation has a more significant discrepancy in the produced polymer (Figure 17b). There are several reasons for this difference, the first of which is that Simulator B models irreversible adsorption and can negatively affect the produced quantities of polymer compared with Simulator A. In Simulator C’s case, adsorption and permeability reduction use different models. These were also present in the smaller cases; however, their effect was magnified due to the size and complexity of the reservoir model. Table 16 summarizes the results. Additionally, Figure 17c showcases the average reservoir pressure with good agreement among simulators.

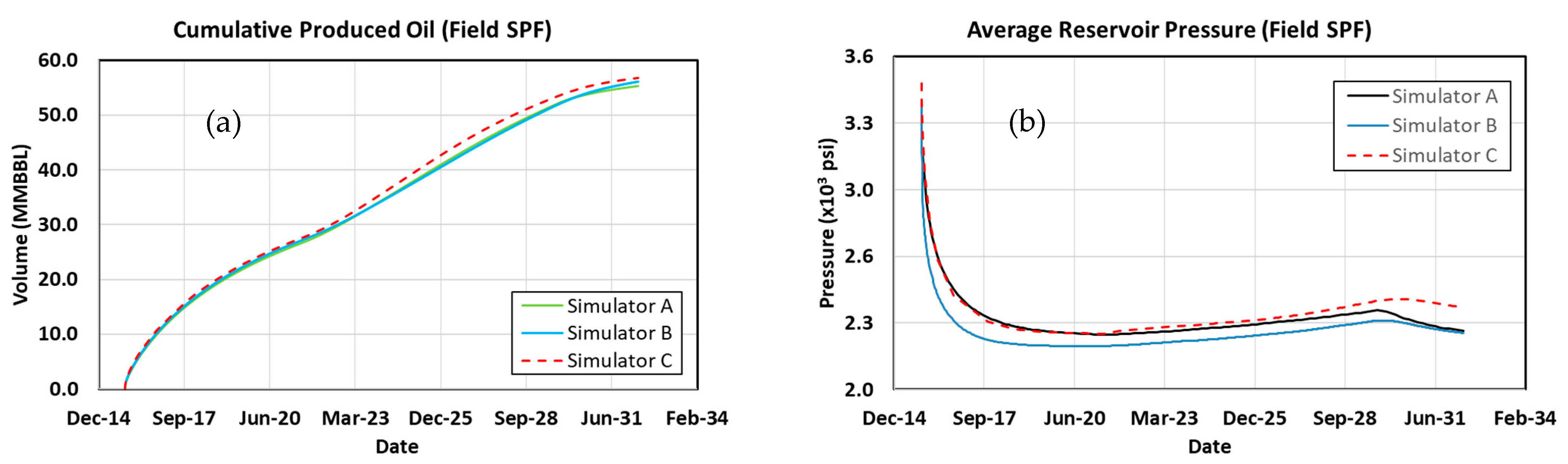
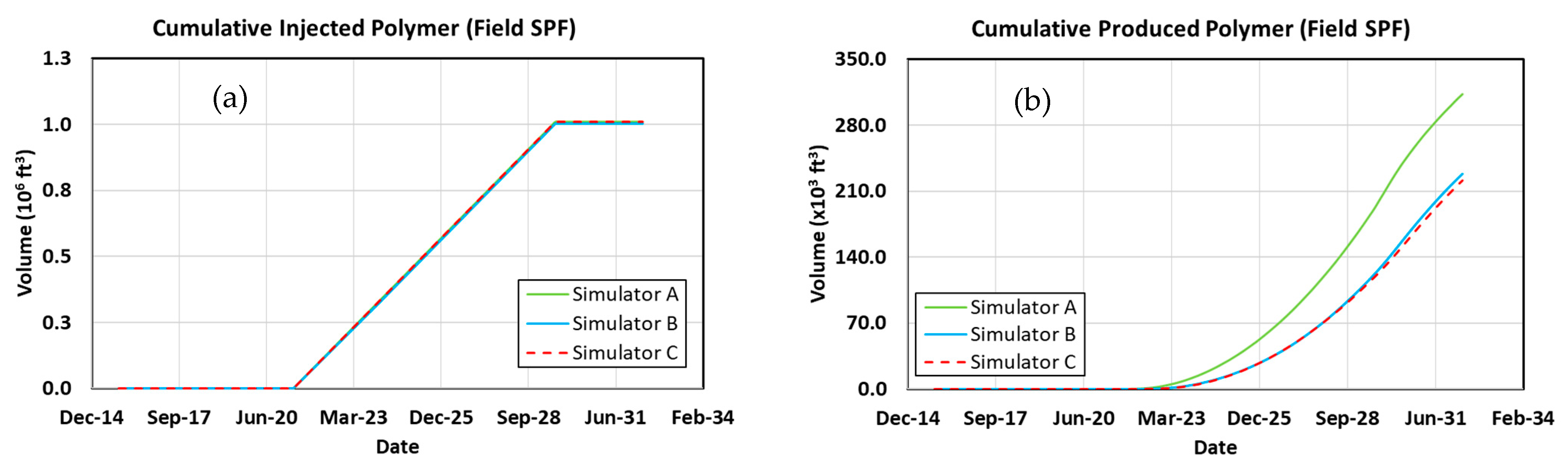
3.12. Surfactant–Polymer Flood

The same chemical injection designed for the previous 3D model is used in this field-scale simulation of a surfactant–polymer flood. Simulators A and B model a salinity gradient design to achieve the Type III microemulsion phase behavior with ultralow interfacial tension.

Figure 18 compares the total volumes of produced oil and average reservoir pressure results, with a good agreement among the three simulators. Figure 19 and Figure 20 show the injected and produced volumes of polymer and surfactant, respectively. Table 17 summarizes the key results indicating that all three simulators can closely match oil recovery, and total injected and produced water. In addition, the average reservoir pressure history has similar trends but with some variations in the range of 100 psi. Finally, the produced surfactant and polymer volumes differ significantly, although the cumulative injected volumes are similar.

3.13. Comparing Results with Previous Work

Despite the prevalence of simulation studies in the existing literature, as highlighted in the introduction, there is a scarcity of research directly analogous to the present study. Such analogues would permit a side-by-side evaluation of outcomes, which can clarify potential similarities and disparities. Nonetheless, a handful of studies do permit a broad level of comparison.

Patacchini et al. [38] compared their new four-fluid-phase, fully implicit in-house research reservoir simulator (IHRRS) with UTCHEM on a 1D, three-fluid-phase (oil/water/microemulsion) synthetic coreflood. They also considered scenarios where it is necessary to account for four phases in equilibrium, such as a scenario where the chemical flood is preceded by a vaporizing gas drive, as well as a case where solution gas is evolved during the flooding. They discussed some aspects of their implementation, such as numerical dispersion vs. timestep length and nonlinear convergence. They showed that numerical performance is not degraded by the four-phase equilibrium. In Figure 6 in their paper, they also showed a close match of oil production and oil recovery factor between the simulators. Khorsandi et al. [27] use 1D and 2D simulations to compare PennSim reservoir simulator to UTCHEM (2000) for surfactant/polymer floods. Their study compared the two simulators in term of compositions and oil, water, and surfactant volumes, which shows a close match. Druetta et al. [53] conducted a similar comparison of UTCHEM to a novel two-dimensional surfactant flooding simulator for a four-component, two-phase system in porous media, where they found the oil recovery to be comparable in Figure 2 of their paper. Additionally, Lashgari et al. [54] compared the UTCHEM four-phase model for oil/water/microemulsion/gas to CMG-IMEX in terms of average pressure, water rate, gas rate, and cumulative oil production (Figure 8 in that paper) with a close match.

A particularly noteworthy example is the work of Goudarzi et al. [41], in which a comparative analysis of UTCHEM, ECLIPSE-E100, and CMG-STARS is conducted in the context of polymer, surfactant/polymer, and alkaline/surfactant/polymer flooding. The pressure results in Figures 7b and 9b in their study reveal similar discrepancies when compared with the results obtained for the 3D polymer simulations in the present paper. It is important to acknowledge that the versions of the simulators utilized are not identical, and one of the simulators is completely different, but the differences are still present. Further agreement is observed when comparing cumulative oil production, as depicted in Figures 16b and 22a, as well as the total surfactant injected (Figure 22) in their study compared to the results of our paper.

In addition to the above comparisons, it is pertinent to note that the present study encompasses a more comprehensive set of data and details that could not be compared against the study by Goudarzi et al. [41]. This is primarily because their study does not delve into certain aspects and parameters that our paper extensively examines. The inclusion of these additional facets in our research not only amplifies the scope but also lends a deeper insight into the complexities and nuances of the simulations. This expanded analysis could be instrumental for researchers and practitioners aiming for a more in-depth understanding and application of these simulations.

4. Summary and Conclusions

This study uses three chemical flooding reservoir simulators to systematically compare the models’ impact on the field scale results, specifically the impact of modeling middle-phase microemulsion in a three-phase (oil, microemulsion, water) system against the two-phase system.

The surfactant–polymer floods were designed in Winsor Type III phase behavior at an optimum salinity in simulators A and B. Simulator C lacks the capabilities to model salinity gradient and the middle-phase microemulsion. However, the effects of surfactant can be approximated by solubilization and IFT tables.

The water, polymer, and SP flood results for the 1D and 3D cases were similar. The results for the field model showed close results for produced water and oil. However, significant discrepancies were observed in injected and produced chemical volumes. These results indicate that despite the different formulations, the effect of surfactant polymer floods on oil recovery, total injected and produced fluids, and average pressure profiles can be comparably modeled in these simulators.

Author Contributions

Methodology, software, validation, analysis, investigation, data curation, writing—original draft preparation, visualization, M.M.A.; Methodology, software, validation, supervision, writing—review and editing, B.R.B.F.; Conceptualization, resources, writing—review and editing, supervision, project administration, M.D.; Conceptualization, resources, writing—review and editing, supervision, project administration, K.S. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

All data generated or analyzed during this study are encompassed within the manuscript. This study is entirely based on modeling and simulation, with sufficient details provided in the paper and the Appendix A to replicate the reported results. These results can be reproduced using any of the commercial reservoir simulators discussed in the manuscript.

Acknowledgments

The first author acknowledges support from Saudi Aramco for sponsoring his studies at the University of Texas at Austin. The authors would like to acknowledge the sponsors of the RSJIP from the University of Texas at Austin for their financial support. The authors thank CMG, SLB, Chevron Corp., and ScienceSoft Inc., for providing the software licenses.

Conflicts of Interest

The authors declare no conflict of interest.

Nomenclature

$\vec{\nabla} Φ_{l^{'}}$	The hydraulic potential gradient of the conjugate phase of phase $l$ ( $l = w a t e r, o i l, m i c r o e m u l s i o n)$
$a$	Interfacial tension model parameter
$A$	Parameter related to the height of the binodal curve for a given salinity
$A_{0}$	Parameter related to the height of the binodal curve at zero salinity
$A_{1}$	Parameter related to the height of the binodal curve at optimal salinity
$A_{2}$	Parameter related to the height of the binodal curve at twice optimal salinity
$a_{p}$	Polymer adsorption
$A_{p 1}$	First fitting parameter for polymer solution viscosity at zero shear rate
$a_{p 1}$	First fitting parameter for $a_{p}$
$A_{p 2}$	Second fitting parameter for polymer solution viscosity at zero shear rate
$a_{p 2}$	Second fitting parameter for $a_{p}$
$A_{p 3}$	Third fitting parameter for polymer solution viscosity at zero shear rate
$A D$	Polymer’s adsorbed concentration obtained from the adsorption isotherm
$a d$	Adsorption of polymer using a Langmuir isotherm
$A D M A X T$	The maximum adsorption capacity of the rock
B	Empirical parameters that define the binodal curves in Equation (A66)
$b_{p}$	Calibration parameter for the isotherm
$b_{r k}$	Permeability reduction input parameter
$C$	Shear correction factor
$c$	Interfacial tension model parameter
${\hat{C}}_{p}$	The adsorbed polymer concentration
${\tilde{C}}_{p}$	The overall concentration of polymer
$C_{a}$	The total anion concentration
$C_{d}$	Total divalent cation concentration
$C_{o m}$	The concentration of oil in the microemulsion phase
$C_{o o}$	The oil concentration in the oleic phase
$C_{o w}$	The oil concentration in the aqueous phase
$C_{p}$	Total polymer concentration
$C_{p w}$	Polymer concentration in the aqueous phase
$C_{p m}$	Polymer concentration in the microemulsion phase
$c_{r k}$	Maximum permeability reduction calibration parameter
$C_{S E}$	The effective salinity
$C_{S E}^{*}$	The optimum effective salinity
$C_{S E L}$	The lower Type III effective salinity window values
$C_{S E P}$	Effective salinity for polymer
$C_{S E U}$	The upper Type III effective salinity window values
$C_{s m}$	The concentration of surfactant in the microemulsion phase
$C_{s o}$	The surfactant concentration in the oleic phase
$C_{s w}$	The surfactant concentration in the aqueous phase
$C_{w}$	The total water concentration
$C_{w m}$	The concentration of water in the microemulsion phase
$C_{w o}$	The water concentration in the oleic phase
$C_{w w}$	The water concentration in the aqueous phase
$c o n_{l}$	Phase term for computing the interfacial tension in Equation (A19)
$D$	Depth
$f (x_{a})$	Mixing function
$F_{l}$	Hirasaki’s correction factor
$f_{m}$	Interpolation parameter used for the microemulsion phase
$g$	The gravity acceleration
$k$	Reservoir permeability
$\bar{k}$	Geometric average of the permeability tensor
$\bar{\bar{K}}$	The permeability tensor
$k_{r e f}$	Reference permeability
$k_{r l}$	The relative permeability of phase $l$ ( $l = w a t e r, o i l, m i c r o e m u l s i o n)$
$k_{r l}^{0}$	The endpoint relative permeability of phase l ( $l = w a t e r, o i l, m i c r o e m u l s i o n)$
$n_{l}$	The exponent of phase $l$ ( $l = w a t e r, o i l, m i c r o e m u l s i o n)$
$n_{o}$	The relative permeability exponents for the aqueous oleic phase
$N_{T l}$	The trapping number of phase $l$ ( $l = w a t e r, o i l, m i c r o e m u l s i o n)$
$n_{w}$	The relative permeability exponents for the aqueous phase
$P_{α}$	Empirical coefficient
$R_{k, c u t}$	Cutoff value for the permeability reduction
$R_{K, l}$	Permeability reduction factor from phase l
$R_{k, m a x}$	Maximum permeability reduction
$R_{k}$	Permeability reduction
$R_{l m}$	The pseudo-phase l (w: water, o: oil) solubilization ratio
$R R F T_{l}$	The residual resistance factor of phase l
$S_{j r}$	The residual saturation of phase j (j $= w a t e r, o i l, m i c r o e m u l s i o n)$
$S_{l}$	The saturation of phase l ( $l = w a t e r, o i l, m i c r o e m u l s i o n)$
$S_{n l}$	The normalized saturation of phase $l$ ( $l = w a t e r, o i l, m i c r o e m u l s i o n)$
$S_{o r w}$	The residual oil saturation
$S_{p}$	Parameter for salinity slope
$S_{r l}$	The residual saturation of phase l ( $l = w a t e r, o i l, m i c r o e m u l s i o n)$
$S_{w}$	The aqueous phase saturation
$S_{w c}$	The connate water saturation
$T_{l}$	The trapping parameter of phase $l$ ( $l = w a t e r, o i l, m i c r o e m u l s i o n)$
$T_{w}$	Function to calculate water relative permeability
$T_{o w}$	Function to calculate oil-water relative permeability
$t a d 1$	First input parameter for $a d$
$t a d 2$	Second input parameter for $a d$
$t a d 3$	Third input parameter for $a d$
$\| u_{w} \|$	Norm of the velocity of the aqueous phase
$w$	Interpolation parameter in Equations (A34)–(A37)
$x_{a}$	Component mole fraction
$x n a c l$	The salinity
$α_{1}$	First microemulsion viscosity from laboratory experiments
$α_{2}$	Second microemulsion viscosity from laboratory experiments
$α_{3}$	Third microemulsion viscosity from laboratory experiments
$α_{4}$	Fourth microemulsion viscosity from laboratory experiments
$α_{5}$	Fifth microemulsion viscosity from laboratory experiments
$β_{P}$	Parameter for accounting for divalent cations
${\dot{γ}}_{1 / 2}$	The shear rate at which the polymer viscosity is equal to the average of $μ_{p}^{0}$ and $μ_{w}$
${\dot{γ}}_{1 / 2}^{0}$	Parameter for computing ${\dot{γ}}_{1 / 2}$ as a function of polymer concentration
${\dot{γ}}_{1 / 2}^{1}$	Parameter for computing ${\dot{γ}}_{1 / 2}$ as a function of polymer concentration
${\dot{γ}}_{c}$	Polymer shear correction
$\dot{γ_{e q}}$	Equivalent shear rate
$μ_{a}$	Component viscosity
$μ_{m}$	The microemulsion viscosity
$μ_{o}$	Polymer viscosity
$μ_{p}$	Polymer viscosity
$μ_{p}^{0}$	Polymer solution viscosity at zero shear rate
$μ_{w}$	Water viscosity
$ρ_{l^{'}}$	The mass density of conjugate phase l ( $l^{'} = w a t e r, o i l, m i c r o e m u l s i o n)$
$ρ_l$	The mass density of phase l ( $l = w a t e r, o i l, m i c r o e m u l s i o n)$
$σ_{l l^{'}}$	The interfacial tension between the phase l ( $l = w a t e r, o i l, m i c r o e m u l s i o n)$ and its conjugate phase
$σ_{l l}$	The interfacial tension between the displacing phase and the displaced phase ( $l = w a t e r, o i l, m i c r o e m u l s i o n)$
$σ_{l m}$	Interfacial tension between the pseudo-phase l (w: water, o: oil) and the microemulsion phase
$σ_{o w}$	The water-oil interfacial tension
$σ_{x}$	Interfacial tension used to calculate the microemulsion trapping number
$ϕ$	Porosity
Superscript
$Ω$	Property at either low or high trapping number
$C$	Critical
$H$	Property at high trapping number
$L$	Property at low trapping number
$o w$	Oil-water
$w$	Water
$T_{o w}$	Oil-water relative permeability
$T_{w}$	water relative permeability
$C_{o w}$	Cell value of the oil-water relative permeability
$C_{w}$	Cell value of the water relative permeability
Subscript
$c r$	Critical
$m a x$	Maximum
$m r$	Residual microemulsion
$w r$	Residual water
$m$	Microemulsion
$w$	Aqueous phase
$o$	Oleic phase
$o r$	Residual oil

Appendix A. Model Description

Models used to describe the physical properties and processes involved in the polymer flood and surfactant–polymer flood for each simulator are discussed in this appendix.

Appendix A.1. Polymer-Related Properties

When the polymer is injected, such as in the polymer flood and surfactant–polymer flood, the viscosity will be altered and the permeability reduction is experienced. However, changes in viscosity and the permeability reduction will be subject to the polymer solution’s rheology and polymer adsorption.

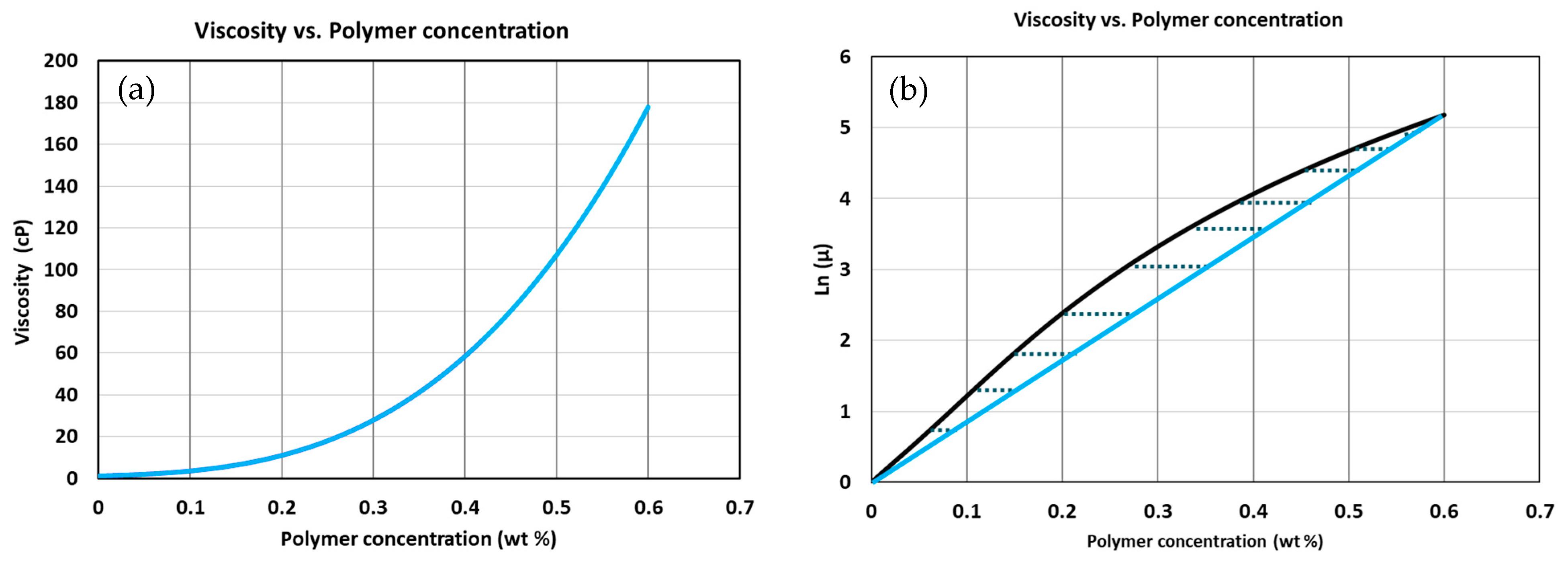
Appendix A.1.1. Viscosity

In Simulators A and B, polymer solution viscosity at zero shear rate is modeled based on the Flory–Huggins equation [55], with modification to account for salinity variation:

μ_{p}^{0} = μ_{w} (1 + (A_{p 1} C_{p w} + A_{p 2} C_{p w}^{2} + A_{p 3} C_{p w}^{3}) C_{S E P}^{S_{p}})

(A1)

where

μ_{w}

is the water viscosity,

C_{p w}

is the polymer concentration in the aqueous phase,

A_{p 1}

,

A_{p 2}

, and

A_{p 3}

are fitting parameters,

C_{S E P}

is the effective salinity for polymer, and

S_{p}

is the parameter for salinity slope, which can be determined by fitting lab data to find the slope of

\frac{μ_{p}^{0} - μ_{w}}{μ_{w}} v s . C_{S E P}

. The effective salinity for polymer,

C_{S E P}

, is calculated as follows:

C_{S E P} = \frac{C_{a} + (β_{P} - 1) C_{d}}{C_{w}}

(A2)

where

C_{a}

is the total anion concentration,

C_{d}

is the total divalent cation concentration,

C_{w}

is the total water concentration, and

β_{P}

is a parameter for accounting for divalent cations.

For Simulator C, the polymer viscosity is calculated by using a non-linear mixing rule as follows:

\ln μ_{p} = f (x_{a}) l n μ_{a} + \frac{1 - f (x_{a})}{1 - x_{a}} \sum_{i \neq a} x_{i} l n μ_{i}

(A3)

where

f (x_{a})

is the mixing function, which depends on

x_{a}

, the component mole fraction, and

μ_{a}

is the component’s viscosity.

Appendix A.1.2. Polymer Rheology

The viscosity of the polymer solution is affected by the shear rate. At a low shear rate, the viscosity of the polymer is independent of the shear rate and follows the previously mentioned equation for viscosity. In contrast, at a high shear rate, the viscosity decreases significantly, reaching values close to water viscosity due to the shear-thinning effect of polymers [56]. In Simulators A and B, the viscosity of the polymer solution can be modeled using various functions, such as the unified viscosity model [57] or the Carreau model [58]. In this work, the relationship to shear rate is modeled with Meter’s equation [59]:

μ_{p} = μ_{w} + \frac{μ_{p}^{0} - μ_{w}}{1 + {(\frac{\dot{γ}}{{\dot{γ}}_{1 / 2}})}^{P_{α} - 1}}

(A4)

where

μ_{p}^{0}

is the viscosity of the polymer solution at zero shear rate,

{\dot{γ}}_{1 / 2}

is the shear rate at which the polymer viscosity is equal to the average between

μ_{p}^{0}

and

μ_{w}

,

P_{α}

is an empirical coefficient, and

μ_{p}

is the polymer solution’s apparent viscosity. In a porous media, the shear rate

(\dot{γ})

is replaced by an equivalent shear rate

({\dot{γ}}_{e q})

. The equivalent shear rate is modeled in Simulators A and B based on the Hirasaki and Pope [60] and Lin [61]:

{\dot{γ}}_{e q} = \frac{{\dot{γ}}_{c} | u_{w} |}{\sqrt{\bar{k} k_{r w} ϕ S_{w}}}

(A5)

where

| u_{w} |

is the norm of the velocity of the aqueous phase,

\bar{k}

is the geometric average of the permeability tensor,

k_{r w}

is the relative permeability of the aqueous phase,

ϕ

is the porosity,

S_{w}

is the saturation of the aqueous phase, and

{\dot{γ}}_{c}

is defined as

{\dot{γ}}_{c} = 3.97 C

(A6)

where C is a shear correction factor.

In simulator A, the value of

{\dot{γ}}_{1 / 2}

can also change with the polymer concentration [62] as

{\dot{γ}}_{1 / 2} = {\dot{γ}}_{1 / 2}^{0} e x p ({\dot{γ}}_{1 / 2}^{1} C_{p w})

(A7)

where

{\dot{γ}}_{1 / 2}^{0}

and

{\dot{γ}}_{1 / 2}^{1}

are model parameters.

In Simulator C, shear-thinning effects are modeled using data tables that relate polymer viscosity to fluid velocity.

Appendix A.1.3. Permeability Reduction

The injection of polymer can reduce both the effective permeability of the reservoir and the mobility of the injection slug. Several factors can affect the permeability reduction of the porous media, such as rock properties, molecular weight, the type of polymer, and shear effects. The permeability reduction is computed from a permeability reduction factor as follows:

R_{k} = \frac{E f f e c t i v e P e r m e a b i l i t y o f W a t e r}{E f f e c t i v e P e r m e a b i l i t y o f P o l y m e r}

(A8)

The permeability reduction factor in Simulator A and B is modeled as follows:

R_{k} = 1 + \frac{(R_{k, m a x} - 1) b_{r k} C_{p l}}{1 + b_{r k} C_{p l}}

(A9)

where

l

refers to the phase with the highest polymer concentration (either aqueous or phase or microemulsion phase),

C_{p l}

is the polymer concentration in phase l,

b_{r k}

is an input parameter, and the maximum permeability reduction (

R_{k, m a x})

is defined as follows:

R_{k, m a x} = m i n {{[1 - \frac{c_{r k} {(A_{p 1} C_{S E P}^{S_{p}})}^{\frac{1}{3}}}{{(\frac{\sqrt{k_{x} k_{y}}}{ϕ})}^{\frac{1}{2}}}]}^{- 4}, R_{k, c u t}}

(A10)

where

c_{r k}

is a calibration parameter and

R_{k, c u t}

is a cutoff value for the permeability reduction defined by the user corresponding to the maximum permeability reduction limit. The permeability reduction is assumed to be irreversible.

For simulator C, permeability reduction is modeled as a function of polymer adsorption. That is, polymer effects on permeability are modeled such that polymer injection can cause blockage in the porous media through adsorption. The permeability reduction is modeled as follows:

R_{K, l} = 1 + \frac{(R R F T_{l} - 1) A D}{A D M A X T}

(A11)

where

R R F T_{l}

is the residual resistance factor of phase l,

A D

is the polymer’s adsorbed concentration obtained from the adsorption isotherm,

R_{K, l}

is the permeability reduction factor from phase l, and

A D M A X T

is the maximum adsorption capacity of the rock.

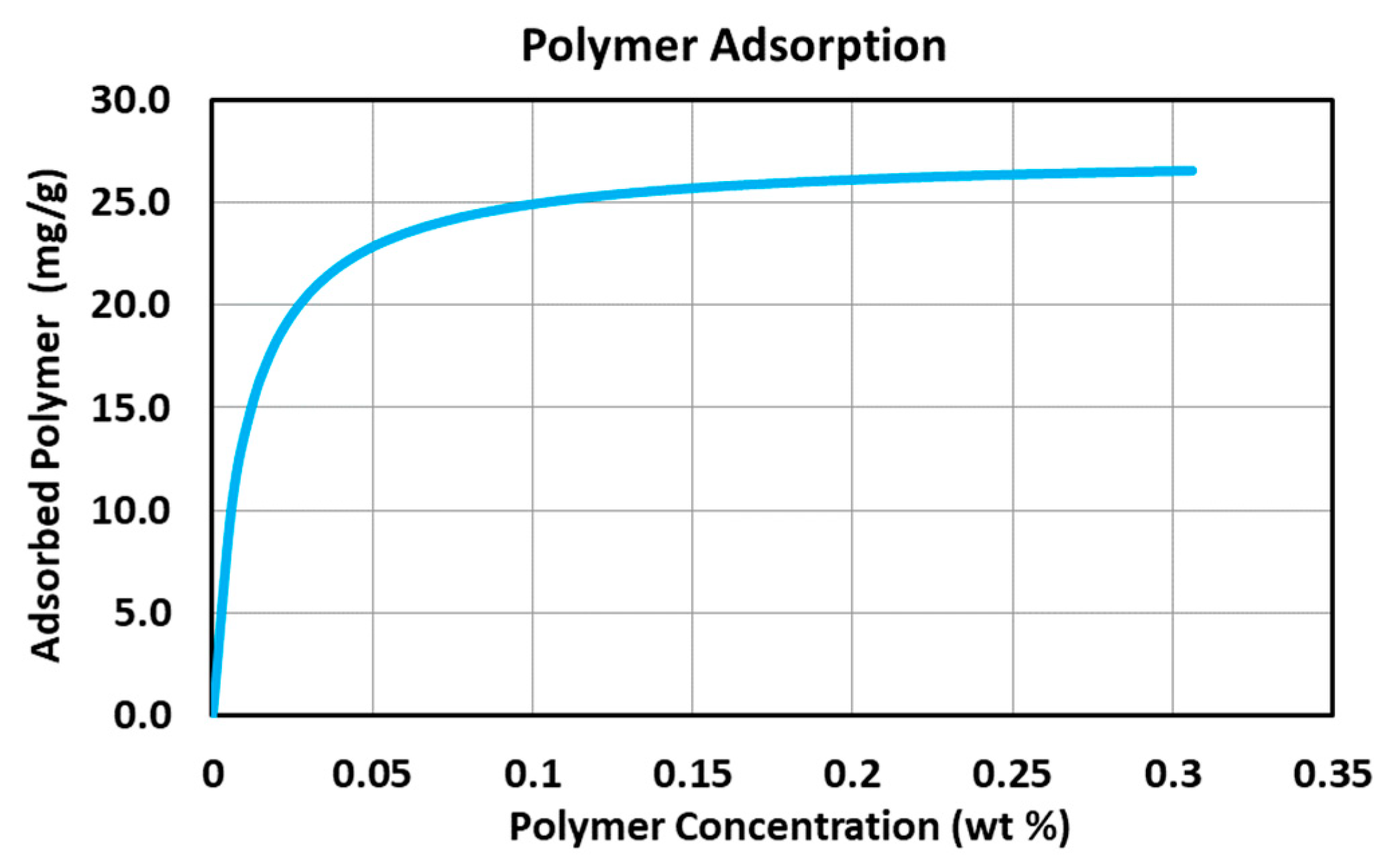
Appendix A.1.4. Adsorption

In simulators A and B, the adsorption is modeled using a Langmuir-type isotherm. The model includes the effects of salinity and polymer concentration:

{\hat{C}}_{p} = m i n ({\tilde{C}}_{p}, \frac{a_{p} ({\tilde{C}}_{p} - {\hat{C}}_{p})}{1 + b_{p} ({\tilde{C}}_{p} - {\hat{C}}_{p})})

(A12)

where

{\hat{C}}_{p}

is the adsorbed polymer concentration,

{\tilde{C}}_{p}

is the overall concentration of polymer,

b_{p}

is a calibration parameter for the isotherm, and the parameter

a_{p}

is defined as

a_{p} = (a_{p 1} + a_{p 2} C_{S E P}) {(\frac{k_{r e f}}{k})}^{0.5}

(A13)

where

a_{p 1}

and

a_{p 2}

are fitting parameters,

k_{r e f}

is a reference permeability, and

k

is the reservoir permeability. Adsorption is reversible in Simulator A and irreversible in Simulator B.

In Simulator C, the adsorption of polymer is also described using a Langmuir isotherm as follows:

a d = \frac{(t a d 1 + t a d 2 \cdot x n a c l) \cdot c a}{(1 + t a d 3 \cdot c a)}

(A14)

where

t a d 1, t a d 2

, and

t a d 3

are input parameters,

c a

is the mole fraction of polymer, and

x n a c l

is the salinity.

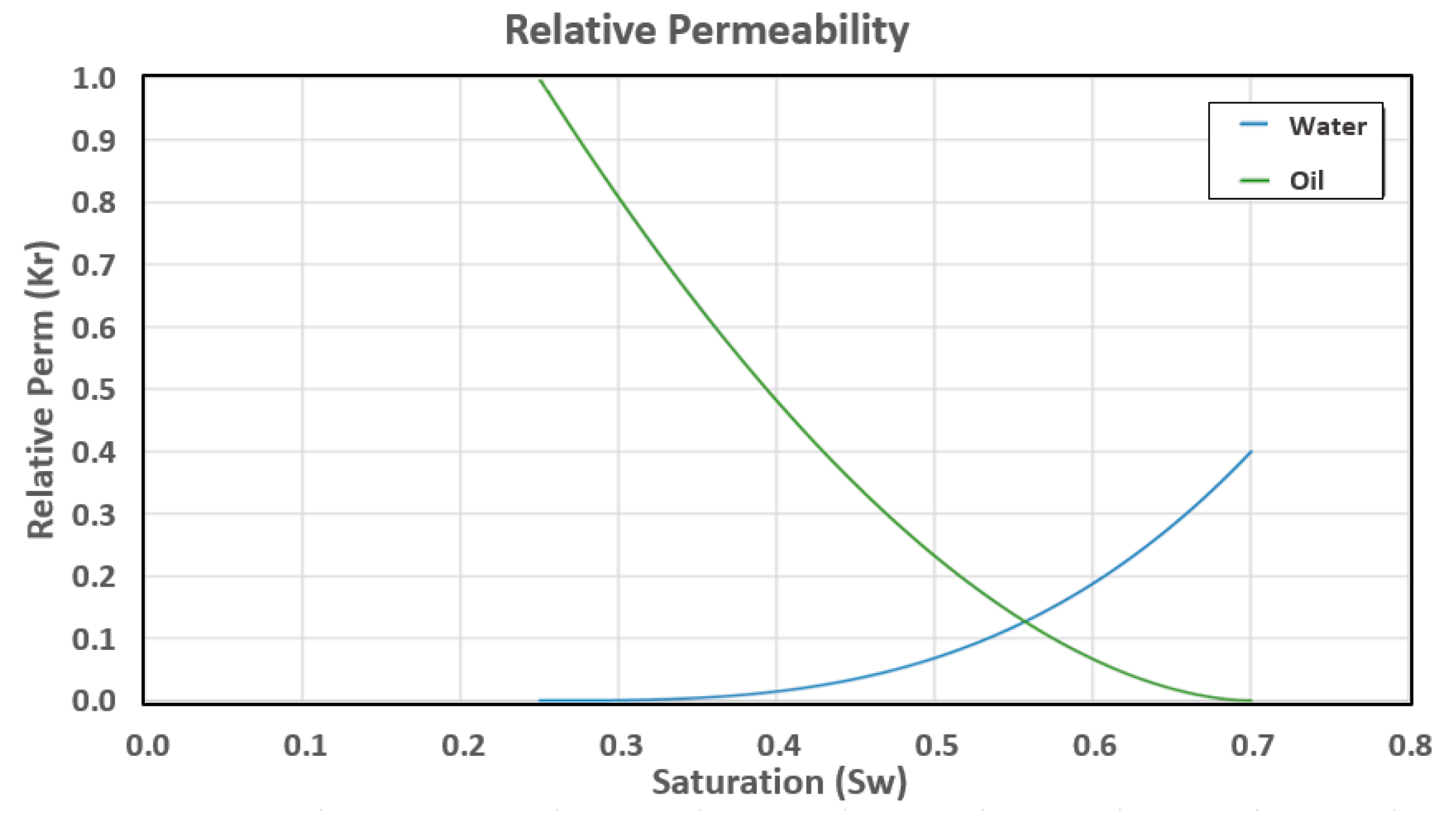
Appendix A.1.5. Oil/Water Relative Permeability

All simulators consider the Corey model to compute the relative permeabilities for oil and brine, as follows:

k_{r w} = k_{r w}^{0} {(\frac{S_{w} - S_{w c}}{1 - S_{w c} - S_{o r w}})}^{n_{w}}, k_{r o} = k_{r o}^{0} {(\frac{1 - S_{o r w} - S_{w}}{1 - S_{w c} - S_{o r w}})}^{n_{o}}

(A15)

where

k_{r w}

is the relative permeability of the aqueous phase,

k_{r o}

is the relative permeability of the oleic phase,

S_{w}

is the aqueous phase saturation,

S_{w c}

is the connate water saturation,

S_{o r w}

is the residual oil saturation, and

n_{w}

and

n_{o}

are the relative permeability exponents for the aqueous and oleic phases, respectively.

Appendix A.2. Surfactant

In this section, the surfactant models are described. Microemulsion viscosity, adsorption, relative permeability, interfacial tension, and phase behavior are the key models that are discussed here.

Appendix A.2.1. Microemulsion Viscosity

One of the key parameters in designing a successful surfactant flood is the microemulsion viscosity. A formulation with a composition that results in an unfavorable microemulsion viscosity can lead to pore plugging, low injectivity, and high surfactant retention. In simulators A and B, microemulsion viscosity is calculated using the microemulsion phase composition as:

μ_{m} = C_{w m} μ_{w} e^{α_{1} (C_{o m} + C_{s m})} + C_{o m} μ_{o} e^{α_{2} (C_{w m} + C_{s m})} + C_{s m} α_{3} e^{α_{4} (C_{w m} + α_{5} C_{o m})}

(A16)

where

α_{1}

,

α_{2}

,

α_{3}

,

α_{4}

, and

α_{5}

are parameters that are determined from laboratory experiments,

C_{w m}

,

C_{o m}

, and

C_{s m}

are the water, oil, and surfactant concentrations in the microemulsion phase, and

μ_{w}

,

μ_{o}

, and

μ_{m}

are the water, oil, and microemulsion viscosities. When polymer is present,

μ_{w}

is replaced by the polymer solution viscosity (

μ_{p}

). Simulator C has no microemulsion phase nor a viscosity model for that phase. Instead, the simulator assumes that either the injected surfactant has the same viscosity as the water or alternatively it can be provided as a constant user input.

Appendix A.2.2. Interfacial Tension

Surfactant type, surfactant concentration, and solution composition all contribute to Interfacial Tension (IFT) reduction [2]. In Simulators A and B, IFT is modeled based on the modified Huh [10,63] correlation, which correlates IFT to the solubilization ratios as follows:

σ_{l m} = σ_{o w} e^{- a R_{l m}} + \frac{c F_{l}}{R_{l m}^{2}} (1 - e^{- a R_{l m}^{3}}), l = w o r o

(A17)

where

R_{l m}

is the pseudo-phase l (w: water, o: oil) solubilization ratio,

a

and

c

are the model parameters,

F_{l}

is Hirasaki’s correction factor,

σ_{o w}

is the water-oil interfacial tension, and

σ_{l m}

is the solubilization ration between excess phase l and the microemulsion phase (m). The solubilization ratio is computed as

R_{l m} = \frac{C_{l m}}{C_{s m}}, l = w o r o

(A18)

Hirasaki’s correction factor is computed as

F_{l} = \frac{1 - e^{\sqrt{- c o n_{l}}}}{1 - e^{\sqrt{2}}}, l = w o r o

(A19)

where

c o n_{l} = \sum_{k = w, o, s} {(C_{k l} - C_{k m})}^{2}, l = w o r o

(A20)

where

C_{w w}

is the water concentration in the aqueous phase,

C_{o w}

is the oil concentration in the aqueous phase,

C_{s w}

is the surfactant concentration in the aqueous phase,

C_{w o}

is the water concentration in the oleic phase,

C_{o o}

is the oil concentration in the oleic phase, and

C_{s o}

is the surfactant concentration in the oleic phase.

For Simulator C, a table of IFT as a function of the mole fraction of oil is used to model the IFT between brine and oil.

Appendix A.2.3. Relative Permeability

In Simulator A, the relative permeability is calculated based on the Corey’s model as follows:

k_{r l} = k_{r l}^{0} {(S_{n l})}^{n_{l}}, l = w, o, m

(A21)

where

l

refers to the aqueous, oleic, or microemulsion phases,

k_{r l}^{0}

is the endpoint relative permeability of phase l,

n_{l}

is the exponent of phase l, and

S_{n l}

is the normalized saturation of phase l. The normalized saturation (

S_{n l}

) is calculated as

S_{n l} = \frac{S_{l} - S_{r l}}{1 - \sum_{j = w, o, m} S_{j r}}, l = w, o, m

(A22)

where

S_{l}

is the saturation of phase l and

S_{l r}

is the residual saturation of phase l. Delshad [64] demonstrated that the trapping number affects the residual saturation according to the Capillary Desaturation Curve (CDC). In simulators A and B, the reduction in residual saturation due to the trapping number was derived by Delshad [64] as follows:

S_{l r} = \min [S_{l}, (S_{l r}^{h i g h} + \frac{S_{l r}^{l o w} - S_{l r}^{h i g h}}{1 + T_{l} N_{T l}})], l = w, o, m

(A23)

where

S_{l r}^{h i g h}

is the residual saturation at high trapping number,

S_{l r}^{l o w}

is the residual saturation at low trapping number,

T_{l}

is the trapping parameter of phase l, and

N_{T l}

is the trapping number of phase l. The trapping number is modeled in the simulator as follows:

N_{T l} = \frac{| - \bar{\bar{K}} \cdot \vec{\nabla} Φ_{l^{'}} - \bar{\bar{K}} \cdot (g (ρ_{l^{'}} - ρ_{l}) g \vec{\nabla} D) |}{σ_{l l^{'}}}, l = w, o, m

(A24)

where

\bar{\bar{K}}

is the permeability tensor,

\vec{\nabla} Φ_{l^{}}

is the hydraulic potential gradient of the conjugate phase of phase l,

g

is the gravity acceleration,

ρ_{l}

is the mass density of phase l,

ρ_{l^{'}}

is the mass density of the conjugate phase of phase l,

σ_{l l^{'}}

is the interfacial tension between the phase l and its conjugate phase, and

D

is the depth. The derivation of the trapping number can be quite complex and can be found in [65]. The interfacial tension for computing the trapping number of the microemulsion phase, to be used in Equation (A24) in the three-phase system (oil/brine/microemulsion) is particularly complex and is computed as

σ_{m m^{'}} = {\begin{matrix} σ_{o m}, f o r S_{w} \leq S_{w r} a n d S_{o} > S_{o r} \\ σ_{w m}, f o r S_{w} > S_{w r} a n d S_{o} \leq S_{o r} \end{matrix}

(A25)

The change in residual saturations will also alter the relative permeability curves. This effect is accounted for by interpolating the endpoints and exponents between low and high trapping number values according to the value of the residual saturation of the conjugate phase [66], as follows:

k_{r l}^{0} = k_{r l}^{0, l o w} + (\frac{S_{l^{'} r}^{l o w} - S_{l^{'} r}}{S_{l^{'} r}^{l o w} - S_{l^{'} r}^{h i g h}}) (k_{r l}^{0, h i g h} - k_{r l}^{0, l o w}), l = w, o, m

(A26)

n_{l} = n_{l}^{l o w} + (\frac{S_{l^{'} r}^{l o w} - S_{l^{'} r}}{S_{l^{'} r}^{l o w} - S_{l^{'} r}^{h i g h}}) (n_{l}^{h i g h} - n_{l}^{l o w}), l = w, o, m

(A27)

where the high and low superscripts refer to values evaluated at high and low trapping numbers.

In Simulator B, the option to model surfactant is only available in the four-phase model (oil, brine, gas, and microemulsion). However, it is possible to initialize our models with no free gas and negligible solution gas in order to initiate the surfactant model. Relative permeability for the three phases (oil, brine, and ME) is modeled using various interpolation functions in Simulator B. The relative permeability of the microemulsion is interpolated based on the functions described next. First, a trapping number interpolation function is defined for the oleic (

f_{o}

) and aqueous (

f_{w}

) phases as follows:

f_{l} = \frac{1}{1 + T_{l} N_{T l}}, l = w, o

(A28)

where

T_{l}

is the trapping parameter for the phase l and

N_{T l}

is the trapping number for phase l. Next, the critical saturations are calculated for the water and oil phases as follows:

S_{l, c r}^{C} = S_{l, c r}^{H} + f_{l} (S_{l, c r}^{L} - S_{l, c r}^{H}), l = w, o

(A29)

where

l

refers to the oleic or aqueous phase,

S_{l, c r}^{H}

is the residual phase saturation at high trapping number, and

S_{l, c r}^{L}

is the phase saturation at low trapping number. Next, the maximum phase saturations at low and high (

Ω

) trapping numbers are calculated as:

S_{l, m a x}^{Ω} = (1 - S_{l, c r}^{Ω}), l = w, o

(A30)

Then, the maximum phase saturation is calculated:

S_{l, m a x}^{C} = S_{l, m a x}^{H} + f_{l} (S_{l, m a x}^{L} - S_{l, m a x}^{H}), l = w, o

(A31)

The critical relative permeability endpoint is interpolated:

k_{r l, m a x}^{C} = k_{r l, m a x}^{H} + f_{w} (k_{r l, m a x}^{L} - k_{r l, m a x}^{H}), l = w, o

(A32)

where

k_{r l, m a x}^{H}

is the phase relative permeability endpoint at high trapping number, and

k_{r l, m a x}^{L}

is the phase relative permeability endpoint at low trapping number.

One can also define an interpolation parameter as

w = \frac{c_{o m}}{c_{o m} + c_{w m}}

(A33)

which is then used to calculate microemulsion trapping number parameters as:

T_{m} = T_{w} + w (T_{o} - T_{w})

(A34)

where

T_{m}

is the trapping parameter for the microemulsion phase. Additionally, microemulsion residual saturations at low and high (

Ω

) trapping numbers are calculated as:

S_{m, c r}^{Ω} = S_{w, c r}^{Ω} + w (S_{o, c r}^{Ω} - S_{w, c r}^{Ω})

(A35)

and the maximum saturation for the microemulsion phase at low and high (

Ω

) trapping number is calculated as:

S_{m, m a x}^{Ω} = S_{w, m a x}^{Ω} + w (S_{o, m a x}^{Ω} - S_{w, m a x}^{Ω})

(A36)

and the endpoint relative permeability for the microemulsion phase at low and high (

Ω

) trapping number is calculated as:

k_{r m, m a x}^{Ω} = k_{r w, m a x}^{Ω} + w (k_{r o, m a x}^{Ω} - k_{r w, m a x}^{Ω})

(A37)

Next, an interpolation parameter is used for the microemulsion phase:

f_{m} = \frac{1}{1 + T_{m} N_{m}}

(A38)

where the interfacial tension is used to calculate the microemulsion trapping number is obtained as

σ_{x} = \frac{c_{o m} σ_{w m} + c_{w m} σ_{o m}}{c_{o m} + c_{w m}}

(A39)

With this, the critical and maximum microemulsion saturation can be computed as follows:

S_{m, c r}^{C} = S_{m, c r}^{H} + f_{m} (S_{m, c r}^{L} - S_{m, c r}^{H})

(A40)

S_{m, m a x}^{C} = S_{m, m a x}^{H} + f_{m} (S_{m, m a x}^{L} - S_{m, m a x}^{H})

(A41)

and the critical endpoint relative permeability is interpolated:

k_{r m, m a x}^{C} = k_{r m, m a x}^{H} + f_{m} (k_{r m, m a x}^{L} - k_{r m, m a x}^{H})

(A42)

Next, horizontal scaling is applied for all phases, with the microemulsion phase being interpolated using the oil-water relative permeability and the water relative permeability saturation functions. For the microemulsion phase horizontal scaling in the oil phase at low and high (

Ω)

trapping numbers, the following equations are used:

S_{m}^{o w, Ω} = S_{o, c r}^{Ω} + \frac{S_{o, m a x}^{Ω} - S_{o, c r}^{Ω}}{S_{m, m a x}^{C} - S_{m, c r}^{C}} (S_{m} - S_{m, c r}^{C})

(A43)

S_{m}^{w, Ω} = S_{w, c r}^{Ω} + \frac{S_{w, m a x}^{Ω} - S_{w, c r}^{Ω}}{S_{m, m a x}^{C} - S_{m, c r}^{C}} (S_{m} - S_{m, c r}^{C})

(A44)

Horizontal scaling is then applied for the water phase at low and high (

Ω)

trapping numbers as follows:

S_{w}^{Ω} = S_{w, c r}^{Ω} + \frac{S_{w, m a x}^{Ω} - S_{w, c r}^{Ω}}{S_{w, m a x}^{C} - S_{w, c r}^{C}} (S_{w} - S_{w, c r}^{C})

(A45)

and the same procedure is applied to the oil phase:

S_{o}^{Ω} = S_{o, c r}^{Ω} + \frac{S_{o, m a x}^{Ω} - S_{o, c r}^{Ω}}{S_{o, m a x}^{C} - S_{o, c r}^{C}} (S_{o} - S_{o, c r}^{C})

(A46)

Next, the scaled saturations are used to calculate the relative permeability of each phase at low and high capillary numbers. For the microemulsion phase, the relative permeability is calculated based on both water and oil relative permeabilities as follows:

k_{r m}^{T_{o w}, Ω} = T_{o w}^{Ω} (S_{m}^{o w, Ω})

(A47)

k_{r m}^{T_{w}, Ω} = T_{w}^{Ω} (S_{m}^{w, Ω})

(A48)

where

T

represents a function (i.e., T(x)) that uses the associated saturation (

S_{m}^{w, Ω} o r S_{m}^{o w, Ω})

for either a relative permeability table look up in the default setting of the simulator, or for a Corey function in another simulator option. A similar procedure is applied to the water phase:

k_{r w}^{T_{w}, Ω} = T_{w}^{Ω} (S_{w}^{Ω})

(A49)

and the oil phase:

k_{r o}^{T_{o w}, Ω} = T_{o w}^{Ω} (S_{o}^{Ω})

(A50)

Afterward, the relative permeabilities are scaled vertically for the three phases. For the microemulsion phase, vertical scaling is described as follows:

k_{r m}^{C_{o w}, Ω} = k_{r m}^{T_{o w}, Ω} \frac{k_{r m, m a x}^{C, Ω}}{k_{r, m a x}^{T_{o w}, Ω}}

(A51)

k_{r m}^{C_{w}, Ω} = k_{r m}^{T_{w}, Ω} \frac{k_{r m, m a x}^{C, Ω}}{k_{r, m a x}^{T_{w}, Ω}}

(A52)

where the same procedure is applied for the oil phase:

k_{r o}^{Ω} = k_{r o}^{T_{o w}, Ω} \frac{k_{r o, m a x}^{C, Ω}}{k_{r, m a x}^{T_{o w}, Ω}}

(A53)

and the water phase:

k_{r w}^{Ω} = k_{r w}^{T_{w}, Ω} \frac{k_{r w, m a x}^{C, Ω}}{k_{r, m a x}^{T_{w}, Ω}}

(A54)

Next, the microemulsions phase interpolated values from the oil and water phases are combined:

k_{r m}^{C, Ω} = {(k_{r m}^{C_{o w}, Ω})}^{w} {(k_{r m}^{C_{w}, Ω})}^{(1 - w)}

(A55)

Additionally, the interpolation between high and low trapping number values is conducted using the following interpolation parameters:

{\tilde{f}}_{w} = \frac{S_{w, c r}^{H} - S_{w, c r}^{C}}{S_{w, c r}^{H} - S_{w, c r}^{L}}

(A56)

{\tilde{f}}_{o} = \frac{S_{o, c r}^{H} - S_{o, c r}^{C}}{S_{o, c r}^{H} - S_{o, c r}^{L}}

(A57)

{\tilde{f}}_{m} = \frac{S_{x, c r}^{H} - S_{x, c r}^{C}}{S_{x, c r}^{H} - S_{x, c r}^{L}}

(A58)

where

S_{x, c r}^{H}

,

S_{x, c r}^{L}

, and

S_{x, c r}^{C}

can be computed from

S_{x, c r}^{Ω} = \frac{c_{o m} S_{w, c r}^{Ω} + c_{w m} S_{o, c r}^{Ω}}{c_{o m} + c_{w m}}

(A59)

In the Simulator B relative permeability model, when the microemulsion phase is present, it becomes the conjugate phase for both the oleic and aqueous phases:

{\tilde{f}}_{w}^{'} = {\tilde{f}}_{m}

(A60)

{\tilde{f}}_{o}^{'} = {\tilde{f}}_{m}

(A61)

This, in turn, allows for the calculation of the relative permeability of the aqueous phase as:

k_{r w} = {(k_{r w}^{C, L})}^{{\tilde{f}}_{w}^{'}} {(k_{r w}^{C, H})}^{(1 - {\tilde{f}}_{w}^{'})}

(A62)

and the relative permeability of the oleic phase as:

k_{r o} = {(k_{r o}^{C, L})}^{{\tilde{f}}_{o}^{'}} {(k_{r o}^{C, H})}^{(1 - {\tilde{f}}_{o}^{'})}

(A63)

For the microemulsion phase, the conjugate phase is the aqueous phase when it is mobile; otherwise the oleic phase is the conjugate phase. Therefore, the microemulsion relative permeability is computed as

k_{r m} = {(k_{r m}^{C, L})}^{{\tilde{f}}_{m}^{'}} {(k_{r m}^{C, H})}^{(1 - {\tilde{f}}_{m}^{'})}

(A64)

In Simulator C, relative permeability is modeled based on two sets of relative permeability curves at low and high capillary numbers, which are user input tables. The microemulsion phase is not modeled.

Appendix A.2.4. Phase Behavior

Microemulsion phase behavior depends on brine salinity [67], with three microemulsion types, as previously discussed. The effective salinity is modeled in Simulators A and B as follows:

C_{S E} = \frac{C_{a}}{C_{w}}

(A65)

where

C_{a}

is the total anion concentration and

C_{w}

is the total water concentration.

The microemulsion phase behavior is based on the extended Hand’s rule [29], with the binodal curve as

\frac{C_{s m}}{C_{o m}} = A {(\frac{C_{s m}}{C_{w m}})}^{B}

(A66)

where A and B are empirical parameters that define the binodal curves and B is assumed here to be −1, since the binodal is assumed to be symmetrical. Furthermore, the phase compositions are constrained as:

C_{w l} + C_{o l} + C_{s l} = 1, l = w, o, m

(A67)

With this,

C_{s m}

can be computed from the binodal curve as function of

C_{o m}

as

C_{s m} = \frac{1}{2} [- A C_{o m} + \sqrt{{(A C_{o m})}^{2} + 4 A C_{o m}) (1 - C_{o m})}]

(A68)

where parameter A determines the height of the binodal curve and is interpolated as

A = {\begin{matrix} (A_{0} - A_{1}) (1 - \frac{C_{S E}}{C_{S E}^{*}}) + A_{1}, i f C_{S E} \leq C_{S E}^{*} \\ (A_{2} - A_{1}) (\frac{C_{S E}}{C_{S E}^{*}} - 1) + A_{1}, i f C_{S E} > C_{S E}^{*} \end{matrix}

(A69)

where

C_{S E}^{*}

is the optimum effective salinity and the values of

A_{0}

,

A_{1}

, and

A_{2}

correspond to the values of

A

at zero, optimal, and twice the optimal effective salinities, respectively. The values of

A_{0}

,

A_{1}

, and

A_{2}

can be computed as follows:

A_{m} = {(\frac{2 C_{s, m a x, m}}{1 - C_{s, m a x, m}})}^{2}, m = 0, 1, 2

(A70)

where the maximum surfactant value in the binodal (

C_{s, m a x, m}

) represents the binodal height. Finally, the optimum effective salinity is obtained as:

C_{S E}^{*} = \frac{C_{S E L} - C_{S E U}}{2}

(A71)

where

C_{S E L}

and

C_{S E U}

are the lower and upper Type III effective salinity window values, respectively.

For Simulator C, there is no microemulsion phase, and the effect of salinity on phase behavior is not modeled. However, Simulator C can model Type I or Type II behavior. Simulator C models surfactant partitioning using K-values. These values are input directly as a function of temperature and pressure in a tabular format.

References

Vishnyakov, V.; Suleimanov, B.; Salmanov, A.; Zeynalov, E. Primer on Enhanced Oil Recovery; Gulf Professional Publishing: Cambridge, MA, USA, 2020; ISBN 978-0-12-817632-0. [Google Scholar]
Green, D.W.; Willhite, G.P. Enhanced Oil Recovery; SPE textbook series; Henry, L., Ed.; Doherty Memorial Fund of AIME, Society of Petroleum Engineers: Richardson, TX, USA, 1998; ISBN 978-1-55563-077-5. [Google Scholar]
Lake, L.W.; Johns, R.; Rossen, B.; Pope, G. Fundamentals of Enhanced Oil Recovery, 2nd ed.; Society of Petroleum Engineers: Richardson, TX, USA, 2014; ISBN 978-1-61399-328-6. [Google Scholar]
Craig, F.F. The Reservoir Engineering Aspects of Waterflooding; Henry, L., Ed.; Doherty series; Doherty Memorial Fund of AIME: Richardson, TX, USA, 1993; ISBN 978-0-89520-202-4. [Google Scholar]
Dake, L.P. Fundamentals of Reservoir Engineering; Developments in petroleum science; Elsevier Scientific Pub. Co.: Amsterdam, The Netherlands; Distributors for the U.S. and Canada Elsevier North-Holland: New York, NY, USA, 1978; ISBN 978-0-444-41667-4. [Google Scholar]
Clifford, P.J.; Sorbie, K.S. The Effects of Chemical Degradation on Polymer Flooding. In Proceedings of the SPE Oilfield and Geothermal Chemistry Symposium, Phoenix, AZ, USA, 9–11 April 1985. [Google Scholar]
Thomas, S. Enhanced Oil Recovery—An Overview. Oil Gas Sci. Technol. Rev. IFP 2008, 63, 9–19. [Google Scholar] [CrossRef] [Green Version]
Griffin, W.C. Classification of Surface-Active Agents by “HLB”. J. Soc. Cosmet. Chem. 1949, 1, 311–326. [Google Scholar]
Bourrel, M.; Schechter, R.S. Microemulsions and Related Systems: Formulation, Solvency, and Physical Properties; Surfactant science series; M. Dekker: New York, NY, USA, 1988; ISBN 978-0-8247-7951-1. [Google Scholar]
Huh, C. Interfacial Tensions and Solubilizing Ability of a Microemulsion Phase That Coexists with Oil and Brine. J. Colloid Interface Sci. 1979, 71, 408–426. [Google Scholar] [CrossRef]
Baran, J.R. Winsor I⇔;III⇔II Microemulsion Phase Behavior of Hydrofluoroethers and Fluorocarbon/Hydrocarbon Catanionic Surfactants. J. Colloid Interface Sci. 2001, 234, 117–121. [Google Scholar] [CrossRef] [PubMed]
Ahmed, S.; Elraies, K.A. Microemulsion in Enhanced Oil Recovery. In Science and Technology Behind Nanoemulsions; Karakuş, S., Ed.; InTech: London, UK, 2018; ISBN 978-1-78923-570-8. [Google Scholar]
Coats, K.H. An Equation of State Compositional Model. SPE J. 1980, 20, 363–376. [Google Scholar] [CrossRef]
Acs, G.; Doleschall, S.; Farkas, E. General Purpose Compositional Model. SPE J. 1985, 25, 543–553. [Google Scholar] [CrossRef]
Young, L.C.; Stephenson, R.E. A Generalized Compositional Approach for Reservoir Simulation. SPE J. 1983, 23, 727–742. [Google Scholar] [CrossRef]
Collins, D.A.; Nghiem, L.X.; Li, Y.-K.; Grabonstotter, J.E. An Efficient Approach to Adaptive- Implicit Compositional Simulation With an Equation of State. SPE Reserv. Eng. 1992, 7, 259–264. [Google Scholar] [CrossRef]
Watts, J.W. A Compositional Formulation of the Pressure and Saturation Equations. SPE Reserv. Eng. 1986, 1, 243–252. [Google Scholar] [CrossRef]
Fernandes, B.R.B.; Marcondes, F.; Sepehrnoori, K. A New Four-Phase Adaptive Implicit Method for Compositional Reservoir Simulation. J. Comput. Phys. 2021, 435, 110263. [Google Scholar] [CrossRef]
Fernandes, B.R.B.; Marcondes, F.; Sepehrnoori, K. Development of a Fully Implicit Approach with Intensive Variables for Compositional Reservoir Simulation. J. Pet. Sci. Eng. 2018, 169, 317–336. [Google Scholar] [CrossRef]
Nogueira, R.L.; Fernandes, B.R.B.; Araújo, A.L.S.; Marcondes, F. Unstructured Grids and an Element Based Conservative Approach for a Black-Oil Reservoir Simulation. In Proceedings of the 13th Brazilian Congress of Thermal Sciences and Engineering, Uberlândia, Brazil, 5–10, December 2010. [Google Scholar]
Haukas, J.; Aavatsmark, I.; Espedal, M.; Aavatsmark, I.; Espedal, M. A Black-Oil and Compositional IMPSAT Simulator with Improved Compositional Convergence. In Proceedings of the Proceedings of the 9th European Conference on the Mathematics of Oil Recovery, Cannes, France, 30 August–2 September 2004. [Google Scholar]
CMG. GEM User Guide; CMG: Calgary, AB, Canada, 2022. [Google Scholar]
CMG. IMEX User Guide; CMG: Calgary, AB, Canada, 2022. [Google Scholar]
Schlumberger. Eclipse Reference Manual; Schlumberger: Houston, TX, USA, 2016. [Google Scholar]
Nelson, R.C.; Pope, G.A. Phase Relationships in Chemical Flooding. SPE J. 1978, 18, 325–338. [Google Scholar] [CrossRef]
Acosta, E.; Szekeres, E.; Sabatini, D.A.; Harwell, J.H. Net-Average Curvature Model for Solubilization and Supersolubilization in Surfactant Microemulsions. Langmuir 2003, 19, 186–195. [Google Scholar] [CrossRef]
Khorsandi, S.; Johns, R.T. Robust Flash Calculation Algorithm for Microemulsion Phase Behavior. J. Surfactants Deterg. 2016, 19, 1273–1287. [Google Scholar] [CrossRef]
Fernandes, B.R.B.; Sepehrnoori, K.; Delshad, M. Challenges in Modeling Microemulsion Phase Behavior. J. Surfact Deterg. 2022, 26, 311–333. [Google Scholar] [CrossRef]
Pope, G.A.; Nelson, R.C. A Chemical Flooding Compositional Simulator. SPE J. 1978, 18, 339–354. [Google Scholar] [CrossRef]
Delshad, M.; Pope, G.A.; Sepehrnoori, K. A Compositional Simulator for Modeling Surfactant Enhanced Aquifer Remediation, 1 Formulation. J. Contam. Hydrol. 1996, 23, 303–327. [Google Scholar] [CrossRef]
Tong, S.; Chen, J. Full Implicit Numerical Simulator for Polymer Flooding and Profile Control. Int. J. Numer. Anal. Model. 2005, 2, 138–142. [Google Scholar]
John, A.; Han, C.; Delshad, M.; Pope, G.A.; Sepehrnoori, K. A New Generation Chemical Flooding Simulator. SPE J. 2005, 10, 206–216. [Google Scholar] [CrossRef] [Green Version]
Han, C.; Delshad, M.; Sepehrnoori, K.; Pope, G.A. A Fully Implicit, Parallel, Compositional Chemical Flooding Simulator. SPE J. 2007, 12, 322–338. [Google Scholar] [CrossRef]
Winsor, P.A. Solvent Properties of Amphiphilic Compounds; Butterworths Scientific Publications: London, UK, 1954. [Google Scholar]
Hand, D.B. Dineric Distribution. J. Phys. Chem. 1929, 34, 1961–2000. [Google Scholar] [CrossRef]
Han, C.; Delshad, M.; Pope, G.A.; Sepehrnoori, K. Coupling Equation-of-State Compositional and Surfactant Models in a Fully Implicit Parallel Reservoir Simulator Using the Equivalent-Alkane-Carbon-Number Concept. SPE J. 2009, 14, 302–310. [Google Scholar] [CrossRef]
Najafabadi, N.F.; Delshad, M.; Han, C.; Sepehrnoori, K. Formulations for a Three-Phase, Fully Implicit, Parallel, EOS Compositional Surfactant–Polymer Flooding Simulator. J. Pet. Sci. Eng. 2012, 86–87, 257–271. [Google Scholar] [CrossRef]
Patacchini, L.; de Loubens, R.; Moncorge, A.; Trouillaud, A. Four-Fluid-Phase, Fully Implicit Simulation of Surfactant Flooding. SPE Reserv. Eval. Eng. 2014, 17, 271–285. [Google Scholar] [CrossRef]
Yang, J.; Jin, B.; Jiang, L.; Liu, F. An Improved Numerical Simulator for Surfactant/Polymer Flooding. In Proceedings of the SPE/IATMI Asia Pacific Oil & Gas Conference and Exhibition, Nusa Dua, Bali, Indonesia, 20–22 October 2015; Society of Petroleum Engineers: Nusa Dua, Bali, Indonesia, 2015. [Google Scholar]
Mykkeltvedt, T.S.; Raynaud, X.; Lie, K.A. Fully Implicit Higher-Order Schemes Applied to Polymer Flooding. Comput. Geosci. 2017, 21, 1245–1266. [Google Scholar] [CrossRef]
Goudarzi, A.; Delshad, M.; Sepehrnoori, K. A Chemical EOR Benchmark Study of Different Reservoir Simulators. Comput. Geosci. 2016, 94, 96–109. [Google Scholar] [CrossRef]
Nghiem, L.; Skoreyko, F.; Gorucu, S.E.; Dang, C.; Shrivastava, V. A Framework for Mechanistic Modeling of Alkali-Surfactant-Polymer Process in an Equation-of-State Compositional Simulator. In Proceedings of the SPE Reservoir Simulation Conference, Montgomery, TX, USA, 20–22 February 2017. [Google Scholar]
Jong, S.; Nguyen, N.M.; Eberle, C.M.; Nghiem, L.X.; Nguyen, Q.P. Low Tension Gas Flooding as a Novel EOR Method: An Experimental and Theoretical Investigation. In Proceedings of the All Days; SPE: Tulsa, OK, USA, 2016; p. SPE-179559-MS. [Google Scholar]
Shi, X.; Han, C.; Wolfsteiner, C.; Chang, Y.-B.; Schrader, M. A Mixed Natural and Concentration Variable Formulation for Chemical Flood Simulation. In Proceedings of the SPE Reservoir Simulation Conference, Montgomery, TX, USA, 20–22 February 2017; Society of Petroleum Engineers: Montgomery, TX, USA, 2017. [Google Scholar]
Han, C.; Shi, X.; Chang, Y.-B.; Wolfsteiner, C.; Guyaguler, B. Modeling of Cosolvents in a Fully-Implicit Surfactant Flood Simulator Using the Three-Level Framework. In Proceedings of the SPE Reservoir Simulation Conference, Galveston, TX, USA, 10–11 April 2019; Society of Petroleum Engineers: Galveston, TX, USA, 2019. [Google Scholar]
Jia, Z.; Li, D.; Xue, Z.; Lu, D. Development of a Fully Implicit Simulator for Surfactant-Polymer Flooding by Applying the Variable Substitution Method. Int. J. Oil Gas Coal Technol. 2019, 21, 1. [Google Scholar] [CrossRef]
Fernandes, B.R.B. Development of Adaptive Implicit Chemical and Compositional Reservoir Simulators. Ph.D. Thesis, The University of Texas at Austin, Austin, TX, USA, 2019. [Google Scholar]
Fernandes, B.R.B.; Sepehrnoori, K.; Delshad, M.; Marcondes, F. New Fully Implicit Formulations for the Multicomponent Surfactant-Polymer Flooding Reservoir Simulation. Appl. Math Model 2022, 105, 751–799. [Google Scholar] [CrossRef]
Guzman, J.A.N.; Fernandes, B.R.B.; Delshad, M.; Sepehrnoori, K.; Zapata, J.F. Evaluation of Polymer Flooding in a Highly Stratified Heterogeneous Reservoir. A Field Case Study. Wseas Trans. Environ. Dev. 2020, 16, 23–33. [Google Scholar] [CrossRef]
Schlumberger. Intersect User Guide; Schlumberger: Houston, TX, USA, 2020. [Google Scholar]
CMG. STARS User Guide; CMG: Calgary, AB, Canada, 2022. [Google Scholar]
Equinor Volve Field Data (CC BY-NC-SA 4.0). Available online: https://www.equinor.com/news/archive/14jun2018-disclosing-volve-data (accessed on 8 April 2023).
Druetta, P.; Picchioni, F. Surfactant flooding: The Influence of the Physical Properties on the Recovery Efficiency. Petroleum 2020, 6, 149–162. [Google Scholar] [CrossRef]
Lashgari, H.R.; Sepehrnoori, K.; Delshad, M.; DeRouffignac, E. Development of a four-phase chemical-gas model in an Impec Reservoir simulator. In Proceedings of the Day 1 Mon, Houston, TX, USA, 23–25 February 2015. SPE Reservoir Simulation Symposium. [Google Scholar] [CrossRef]
Flory, P.J. Principles of Polymer Chemistry; Cornell University Press: Ithaca, NY, USA, 1953; ISBN 978-0-8014-0134-3. [Google Scholar]
Lake, L.W. Enhanced Oil Recovery; Society of Petroleum Engineers: Richardson, TX, USA, 2010; ISBN 978-1-55563-305-9. [Google Scholar]
Delshad, M. A Study of Transport of Micellar Fluids in Porous Media. Ph.D. Dissertation, The University of Texas at Austin, Austin, TX, USA, 1986. [Google Scholar]
Carreau, P.J. Rheological Equations from Molecular Network Theories. Trans. Soc. Rheol. 1972, 16, 99–127. [Google Scholar] [CrossRef]
Meter, D.M.; Bird, R.B. Tube Flow of Non-Newtonian Polymer Solutions: Part I. Laminar Flow and Rheological Models. AIChE J. 1964, 10, 878–881. [Google Scholar] [CrossRef]
Hirasaki, G.J.; Pope, G.A. Analysis of Factors Influencing Mobility and Adsorption in the Flow of Polymer Solution Through Porous Media. Soc. Pet. Eng. J. 1974, 14, 337–346. [Google Scholar] [CrossRef]
Lin, E. A Study of Micellar/Polymer Flooding Using a Compositional Simulator. PhD Thesis, The University of Texas at Austin, Austin, TX, USA, 1981. [Google Scholar]
Al-Rawahi, H.; Delshad, M.; Sepehrnoori, K.; Al-Kindy, A. Modeling Approach and Non-Uniqueness of Polymer Coreflood History Match and Field-Scale Forecasts. In Proceedings of the Day 1 Mon, Abu Dhabi, United Arab Emirates, 9 November 2020; SPE: Abu Dhabi, United Arab Emirates, 2020; p. D012S116R098. [Google Scholar]
Hirasaki, G.J. Application of the Theory of Multicomponent, Multiphase Displacement to Three-Component, Two-Phase Surfactant Flooding. Soc. Pet. Eng. J. 1981, 21, 191–204. [Google Scholar] [CrossRef]
Delshad, M. Trapping of Micellar Fluids in Berea Sandstone. Ph.D. Thesis, The University of Texas at Austin, Austin, TX, USA, 1990. [Google Scholar]
Jin, M. A Study of Nonaqueous Phase Liquid Characterization and Surfactant Remediation. Ph.D. Thesis, The University of Texas at Austin, Austin, TX, USA, 1995. [Google Scholar]
Delshad, M.; Bhuyan, D.; Pope, G.A.; Lake, L.W. Effect of Capillary Number on the Residual Saturation of a Three-Phase Micellar Solution. In Proceedings of the SPE Enhanced Oil Recovery Symposium, Tulsa, Oklahoma, 20–23 April 1986; Society of Petroleum Engineers: Tulsa, Oklahoma, 1986. [Google Scholar]
Healy, R.N.; Reed, R.L.; Stenmark, D.G. Multiphase Microemulsion Systems. SPE J. 1976, 16, 147–160. [Google Scholar] [CrossRef]

Figure 1. Reservoir models. (a) 1D model, (b) 3D model, and (c) Field-scale model.

Figure 2. Volve reservoir model. (a) Porosity distribution, (b) X-direction permeability, (c) Initial pressure, and (d) 5-spot well pattern (blue refers to injectors and green refers to producers).

Figure 3. Two-phase oil and water relative permeability curves.

Figure 4. Polymer viscosity model. (a) Simulators A and B and (b) non-linear mixing rule for simulator C.

Figure 5. Adsorbed polymer concentration vs. polymer concentration.

Figure 6. Surfactant flood properties. (a) Microemulsion viscosity as a function of oil concentration in microemulsion phase, and (b) Langmuir surfactant adsorption as a function of surfactant concentration.

Figure 7. Solubilization ratio plot for the surfactant in Simulators A and B.

Figure 8. Capillary desaturation curves for water, oil, and microemulsion phases.

Figure 9. IFT for oil/microemulsion phases.

Figure 10. Waterflood results in the 1D model. (a) Cumulative produced oil and (b) average reservoir pressure.

Figure 11. Polymer flood results in the 1D model. (a) Cumulative produced oil, (b) Cumulative produced polymer solution volume, and (c) Average reservoir pressure.

Figure 12. Surfactant–Polymer flood in the 1D model results. (a) Cumulative produced oil, (b) Cumulative produced polymer volume, (c) Cumulative produced surfactant volume, (d) Average reservoir pressure.

Figure 13. Waterflood in the 3D model results. (a) Cumulative produced oil and (b) Average reservoir pressure.

Figure 14. Polymer flood in the 3D model results. (a) Cumulative injected fluid, (b) Cumulative produced oil, and (c) Average reservoir pressure.

Figure 15. Surfactant–polymer flood in the 3D model results. (a) Cumulative produced oil, (b) cumulative produced polymer, (c) cumulative produced surfactant, and (d) average reservoir pressure.

Figure 16. Waterflood in the field-scale model results. (a) Cumulative volume of oil produced and (b) average reservoir pressure.

Figure 17. Polymer flood in the field-scale model results. (a) Cumulative produced oil, (b) Cumulative produced polymer solution volume, and (c) Average reservoir pressure.

Figure 18. Surfactant–polymer flood in the field-scale model (a) cumulative produced oil and (b) average reservoir pressure.

Figure 19. Surfactant–polymer flood in the field-scale model (a) cumulative injected polymer and (b) cumulative produced polymer volume.

Figure 20. Surfactant–polymer flood in the field-scale model (a) cumulative volume of surfactant injected and (b) cumulative volume of surfactant produced.

Table 1. Properties for 1D model.

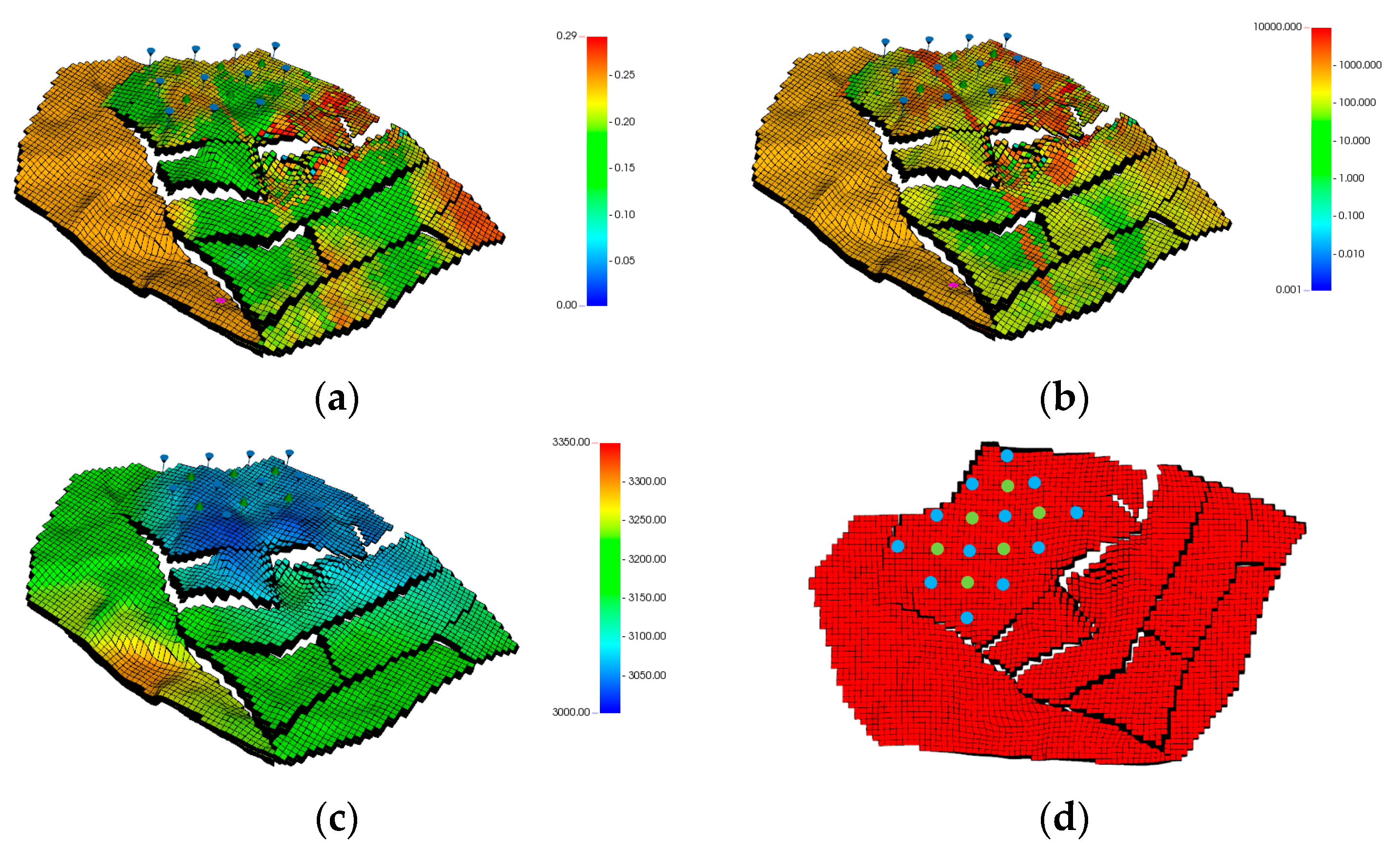
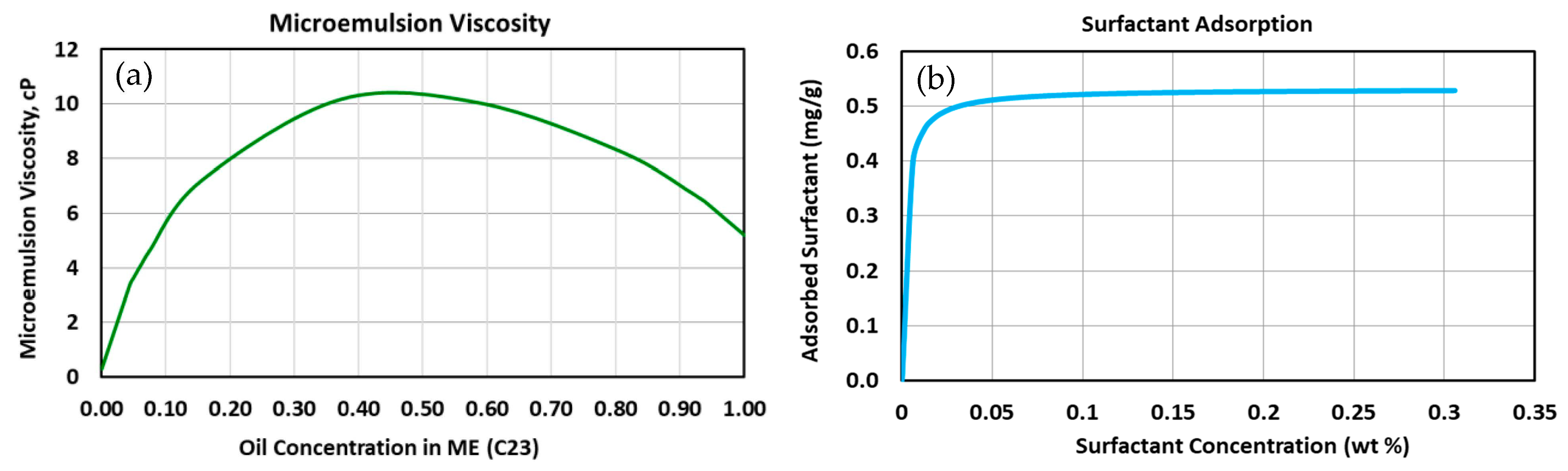
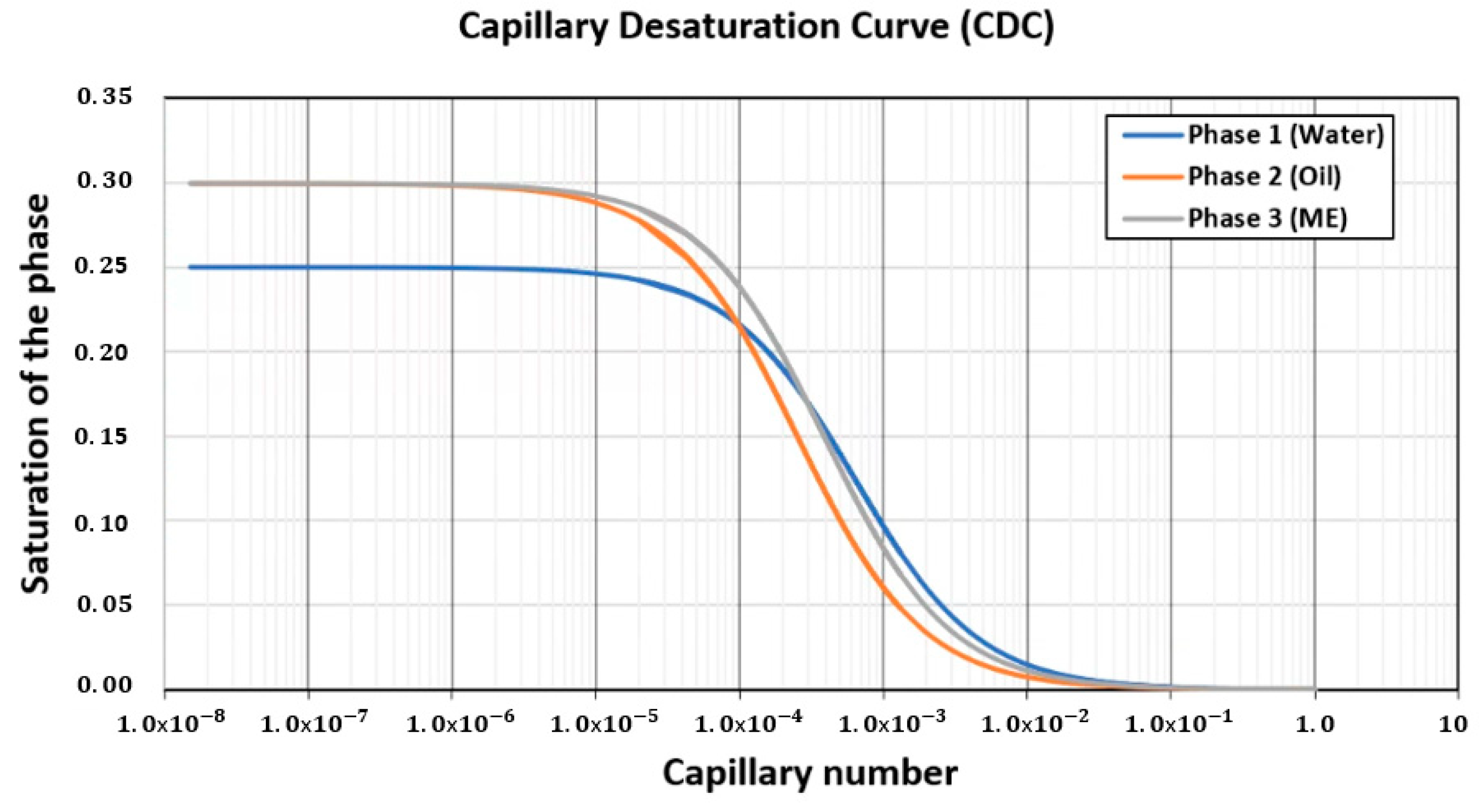
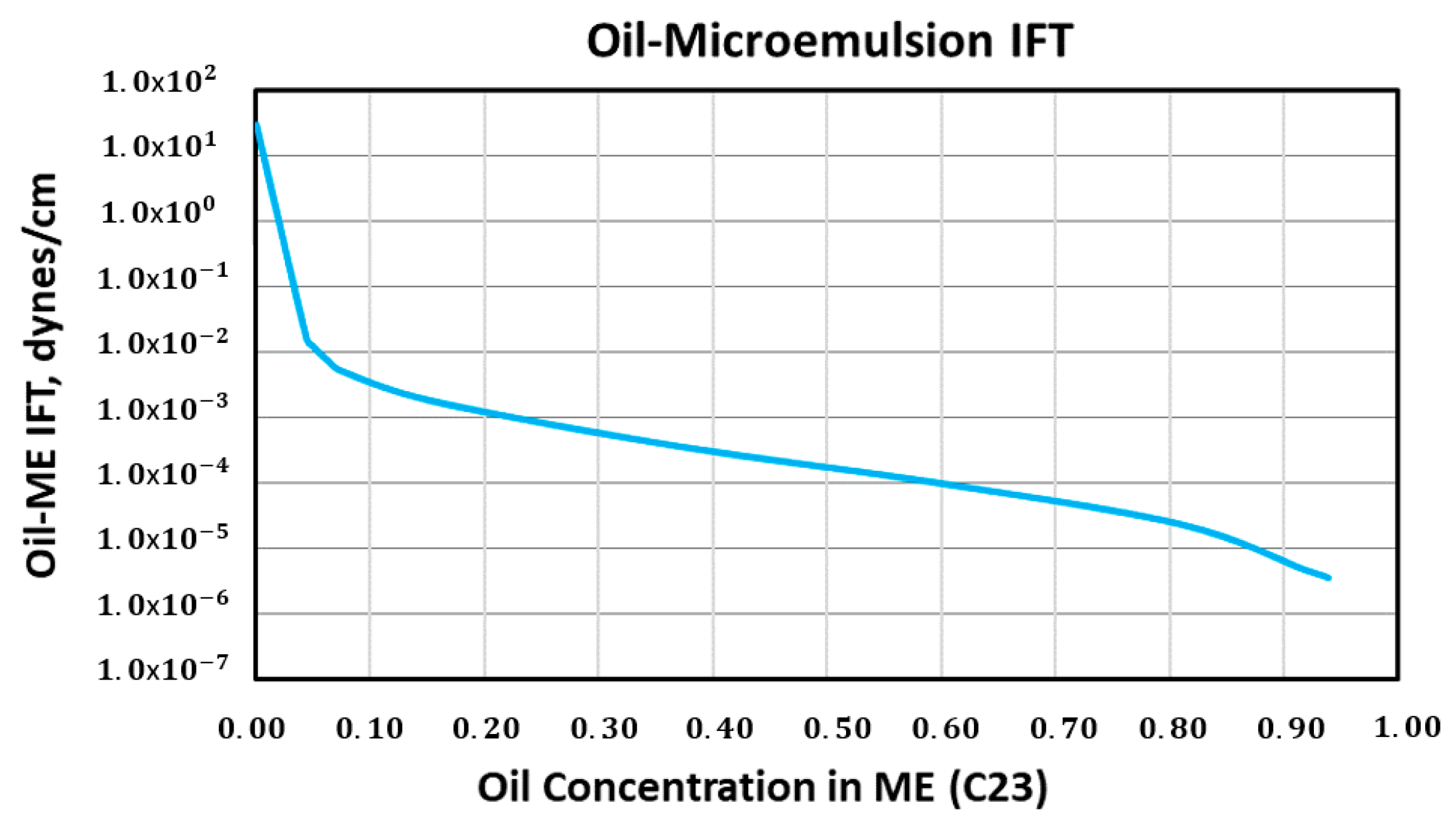
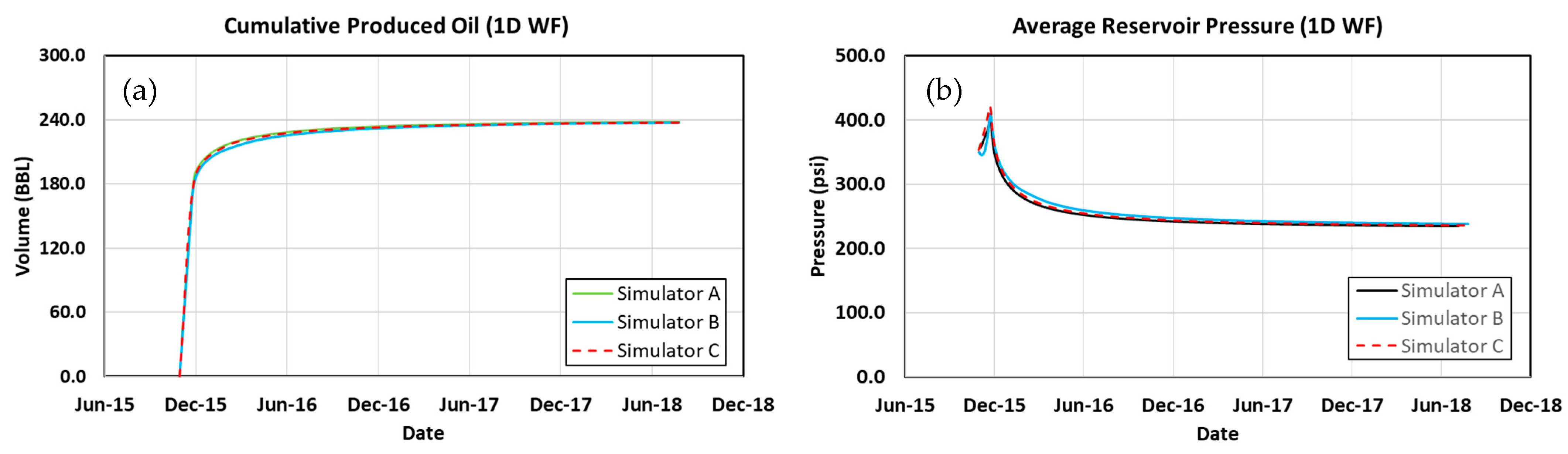
Model	1-Dimensional Cartesian
Grid Size	15 × 1 × 1 Grids
Grid Dimensions	10 × 10 × 10 ft for each grid
Wells	One injector and one producer
Injection Constraint	Rate = 3.75 ft³/day
Production Constraint	BHP = 120 psi
Initial Water Saturation	0.25
Initial Pressure	200 psi
Permeability	100 mD
Porosity	0.2
Rock Compressibility	10⁻⁶ psi⁻¹ @200 psi Ref. Pressure
Reference Pressure	200 psi

Table 2. Properties for the three-dimensional model.

Model	3-Dimensional Cartesian Model
Grid Size	15 × 15 × 10
Grid Dimensions	10 × 10 × 10 ft
Wells	One injector and one producer
Injection Constraint	100 bbls/day
Production Constraint	BHP = 1800 psi
Initial Water Saturation	0.25
Initial Pressure	2000 psi
Permeability	Isotropic 100 mD
Porosity	0.19
Rock Compressibility	$4 \times 10^{- 6}$ 1/psi @ Ref Pressure of 2000 psi

Table 3. Properties for field reservoir model.

Model	3-Dimensional Corner Grid Point Model
No. of Grids	108 × 100 × 63
Wells	12 injectors and 6 producers
Injection Constraint	2000 bbls/day
Production Constraint	BHP = 1800 psi
Average Initial Water Sat.	0.56
Average Initial Pressure	3417 psi
Permeability	X and Y: 0.01 min, 23,381 max, 1348 average mDZ: 0.0001 min, 9352 max, 505 average mD
Porosity	0.01 min, 0.2987 max, 0.2 average
Rock Compressibility	$4 \times 10^{- 6}$ 1/psi @ Ref pressure of 2000 psi

Table 4. Basic physical parameters for waterflood cases.

Parameter	Value
Water Specific Gravity	0.433 psi/ft
Oil Specific Gravity	0.368 psi/ft
Water and Oil Viscosities	1 cP, 5.2 cP
Residual Water Saturation ( $S_{w r}$ )	0.25
Residual Oil Saturation ( $S_{o r}$ )	0.3
Endpoint Water Relative Permeability ( $k_{r w}^{0}$ )	0.4
Endpoint Oil Relative Permeability ( $k_{r o}^{0}$ )	1
Water and Oil Exponents ( $n_{w}, n_{o}$ )	3, 1.8

Table 5. Polymer property model in each simulator.

Polymer Model	Simulator A	Simulator B	Simulator C
Viscosity as a Function of Polymer Concentration	1	1	2
Viscosity as a Function Shear Rate	1	1	2
Effect of Salinity on Polymer Properties	1	1	2
Adsorption	1	1 ¹	2
Permeability Reduction	1	1	2

¹ Simulator B uses the same model as simulator A but with irreversible adsorption.

Table 6. Polymer model parameters.

Parameter	Value
Viscosity Parameter ( $A_{p 1}$ )	12.54
Viscosity Parameter ( $A_{p 2}$ )	41
Viscosity Parameter ( $A_{p 3}$ )	715
Effective Salinity $(C_{s e p})$	0.1 meq/mL
Salinity Parameter $(S_{p})$	0
Adsorption Parameter ( $a_{p 1}$ )	3.1
Adsorption Parameter ( $a_{p 2}$ )	0
Adsorption Parameter ( $b_{p}$ )	100
Perm. Reduction ( $c_{r k}$ )	0.0186
Perm. Reduction ( $b_{r k}$ )	1000
Perm. Reduction Cutoff $(R_{k, c u t})$	10

Table 7. Surfactant model comparison in each reservoir simulator.

Surfactant Model	Simulator A	Simulator B	Simulator C
Microemulsion Viscosity	1	1	Not Included
Adsorption	1	1	2
Binodal Curve for Microemulsion Phase Behavior	1	1	Not Included
Capillary Desaturation Curve	1	1 ¹	Not Included
Interfacial Tension	1	1	2
Relative Permeability	1	2	3

¹ Simulator B uses the same model as simulator A but with irreversible adsorption.

Table 8. Parameters used in microemulsion viscosity model in simulators A and B.

Parameter	Value
Microemulsion Viscosity Parameter ( $α_{1}$ )	2.5
Microemulsion Viscosity Parameter ( $α_{2}$ )	2.3
Microemulsion Viscosity Parameter ( $α_{3}$ ), cP	10
Microemulsion Viscosity Parameter ( $α_{4}$ )	1
Microemulsion Viscosity Parameter ( $α_{5}$ )	1
Surfactant Adsorption Parameter ( $a_{s 1}$ )	0.3
Surfactant Adsorption Parameter ( $a_{s 1}$ )	0
Surfactant Adsorption Parameter ( $b_{s}$ )	500
Lower Limit of Effective Salinity ( $C_{S E L}$ ), meq/mL	0.177
Upper Limit of Effective Salinity ( $C_{S E U}$ ), meq/mL	0.344
Height of Binodal Curve at Zero Effective Salinity	0.131
Height of Binodal Curve at Optimum Effective Salinity	0.026
Height of Binodal Curve at Twice Optimum Effective Salinity	0.028
Water Trapping Parameter ( $T_{w}$ )	1600
Oil Trapping Parameter ( $T_{o}$ )	4000
Microemulsion Trapping Parameter ( $T_{m}$ )	2600
S_wr at High Trapping Number (water phase)	0
S_or at High Trapping Number (oil phase)	0
S_mr at High Trapping Number (microemulsion phase)	0
Huh Interfacial Tension Constant ( $c$ )	0.35
Huh Interfacial Tension Constant ( $a$ )	10

Table 9. Summary of simulation results for 1D waterflood case.

	% Difference
	Simulator B/C	Simulator A/C	Simulator A/B
Cum. Fluid inj.	0.000%	0.000%	0.000%
Prod. Volume of water	−0.006%	−0.012%	−0.005%
Prod. Oil Volume	0.154%	0.299%	0.145%
Total Fluid Produced	−0.001%	0.000%	0.000%

Table 10. Summary of simulation results for 1D polymer flood case.

	% Difference
	Simulator B/C	Simulator A/C	Simulator A/B
Cum. Inj. Fluid	0.000%	0.000%	0.000%
Prod. Water Volume	−0.008%	−0.006%	0.002%
Volume of Oil Prod.	0.293%	0.257%	−0.036%
Polymer Inj.	0.000%	0.000%	0.000%
Polymer Prod.	−0.048%	0.107%	0.156%
Total Fluid Prod.	0.003%	0.004%	0.001%

Table 11. Summary of simulation results for 1D surfactant–polymer flood case.

	% Difference
	Simulator B/C	Simulator A/C	Simulator A/B
Cum. Inj. Fluid	0.000%	0.000%	0.000%
Produced Water Volume	0.011%	−0.011%	−0.023%
Produced Oil Volume	0.323%	0.281%	−0.042%
Polymer Inj.	−0.651%	0.020%	0.667%
Polymer Prod.	−1.299%	0.156%	1.437%
Surfactant Inj.	0.006%	0.006%	0.000%
Surfactant Prod.	−0.098%	−0.053%	0.045%
Total Fluid Prod.	0.030%	0.006%	−0.024%

Table 12. Summary of simulation results for 3D waterflood.

	% Difference
	Simulator B/C	Simulator A/C	Simulator A/B
Cum. Inj. Fluid	0.000%	0.000%	0.000%
Produced Water Volume	−0.005%	0.002%	0.004%
Produced Oil Volume	0.127%	0.065%	−0.061%
Total Fluid Prod.	−0.002%	0.000%	0.002%

Table 13. Summary of simulation results for 3D polymer flood case.

	% Difference
	Simulator B/C	Simulator A/C	Simulator A/B
Cum. Inj. Fluid	0.000%	0.000%	0.000%
Produced Water Volume	−0.022%	0.001%	0.022%
Produced Oil Volume	0.489%	0.025%	−0.466%
Volume of Polymer Inj.	0.000%	0.000%	0.000%
Volume of Polymer Prod.	−0.062%	0.032%	0.093%
Total Fluid Prod.	−0.008%	0.001%	0.009%

Table 14. Summary of simulation results for 3D surfactant–polymer flood case.

	% Difference
	Simulator B/C	Simulator A/C	Simulator A/B
Cum. Inj. Fluid	0.000%	0.000%	0.000%
Produced Water Volume	−0.001%	−0.001%	0.000%
Produced Oil Volume	0.106%	0.117%	0.012%
Volume of Polymer Inj.	−0.651%	0.020%	0.667%
Volume of Polymer Prod.	−1.276%	−0.370%	0.895%
Volume of Surfactant Inj.	0.006%	0.006%	0.000%
Volume of Surfactant Prod.	−0.140%	−0.137%	0.003%
Total Fluid Prod. Volumes	0.004%	0.005%	0.000%

Table 15. Summary of simulation results for field-scale waterflood.

	% Difference
	Simulator B/C	Simulator A/C	Simulator A/B
Cum. Inj. Fluid Volume	0.000%	−0.001%	0.000%
Produced Water Volume	−0.455%	−0.129%	−0.325%
Produced Oil Volume	−1.250%	−2.071%	−0.811%
Total Volume of Fluid Prod.	−0.675%	−0.660%	0.014%

Table 16. Summary of simulation results for field polymer flood.

	% Difference
	Simulator B/C	Simulator A/C	Simulator A/B
Cum. Inj. Fluid	0.000%	0.000%	0.000%
Produced Water Volume	1.028%	1.715%	0.694%
Produced Oil Volume	−2.379%	−4.043%	−1.625%
Polymer Inj.	0.000%	0.000%	0.000%
Polymer Prod.	10.661%	16.243%	6.248%
Total Fluid Prod.	−0.125%	−0.204%	−0.079%

Table 17. Summary of simulation results for field surfactant–polymer flood.

	% Difference
	Simulator B/C	Simulator A/C	Simulator A/B
Cum. Inj. Fluid Volume	0.000%	0.000%	0.000%
Produced Water Volume	0.228%	1.235%	1.010%
Produced Oil Volume	−1.210%	−2.670%	−1.442%
Polymer Inj. Volume	−0.671%	0.000%	0.667%
Polymer Prod. Volume	3.057%	29.28%	27.049%
Surfactant Inj. Volume	2.950%	2.950%	0.000%
Surfactant Prod. Volume	−130.361%	1.357%	57.179%
Total Fluid Prod. Volume	−0.319%	−0.227%	0.092%

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).

Share and Cite

MDPI and ACS Style

Alhotan, M.M.; Batista Fernandes, B.R.; Delshad, M.; Sepehrnoori, K. A Systemic Comparison of Physical Models for Simulating Surfactant–Polymer Flooding. Energies 2023, 16, 5702. https://doi.org/10.3390/en16155702

AMA Style

Alhotan MM, Batista Fernandes BR, Delshad M, Sepehrnoori K. A Systemic Comparison of Physical Models for Simulating Surfactant–Polymer Flooding. Energies. 2023; 16(15):5702. https://doi.org/10.3390/en16155702

Chicago/Turabian Style

Alhotan, Muhammad M., Bruno R. Batista Fernandes, Mojdeh Delshad, and Kamy Sepehrnoori. 2023. "A Systemic Comparison of Physical Models for Simulating Surfactant–Polymer Flooding" Energies 16, no. 15: 5702. https://doi.org/10.3390/en16155702

APA Style

Alhotan, M. M., Batista Fernandes, B. R., Delshad, M., & Sepehrnoori, K. (2023). A Systemic Comparison of Physical Models for Simulating Surfactant–Polymer Flooding. Energies, 16(15), 5702. https://doi.org/10.3390/en16155702

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Menu

A Systemic Comparison of Physical Models for Simulating Surfactant–Polymer Flooding

Abstract

1. Introduction

2. Materials and Methods

2.1. Modeling Approach

2.2. One-Dimensional Model

2.3. Three-Dimensional Model

2.4. Field-Scale Model

2.5. Summary of Physical Properties

2.6. Waterflood

2.7. Polymer Flood

2.8. Surfactant–Polymer Flood

3. Results

3.1. 1D Model Simulation Cases

3.2. Waterflood

3.3. Polymer Flood

3.4. Surfactant–Polymer Flood

3.5. 3D Simulation Cases

3.6. Waterflood

3.7. Polymer Flood

3.8. Surfactant–Polymer Flood

3.9. Field Model Simulations

3.10. Waterflood

3.11. Polymer Flood

3.12. Surfactant–Polymer Flood

3.13. Comparing Results with Previous Work

4. Summary and Conclusions

Author Contributions

Funding

Data Availability Statement

Acknowledgments

Conflicts of Interest

Nomenclature

Appendix A. Model Description

Appendix A.1. Polymer-Related Properties

Appendix A.1.1. Viscosity

Appendix A.1.2. Polymer Rheology

Appendix A.1.3. Permeability Reduction

Appendix A.1.4. Adsorption

Appendix A.1.5. Oil/Water Relative Permeability

Appendix A.2. Surfactant

Appendix A.2.1. Microemulsion Viscosity

Appendix A.2.2. Interfacial Tension

Appendix A.2.3. Relative Permeability

Appendix A.2.4. Phase Behavior

References

Share and Cite

Article Metrics

Article Access Statistics

Further Information

Guidelines

MDPI Initiatives

Follow MDPI