Accurate Modeling and Optimization of Electromagnetic Forces in an Ironless Halbach-Type Permanent Magnet Synchronous Linear Motor
Abstract
1. Introduction
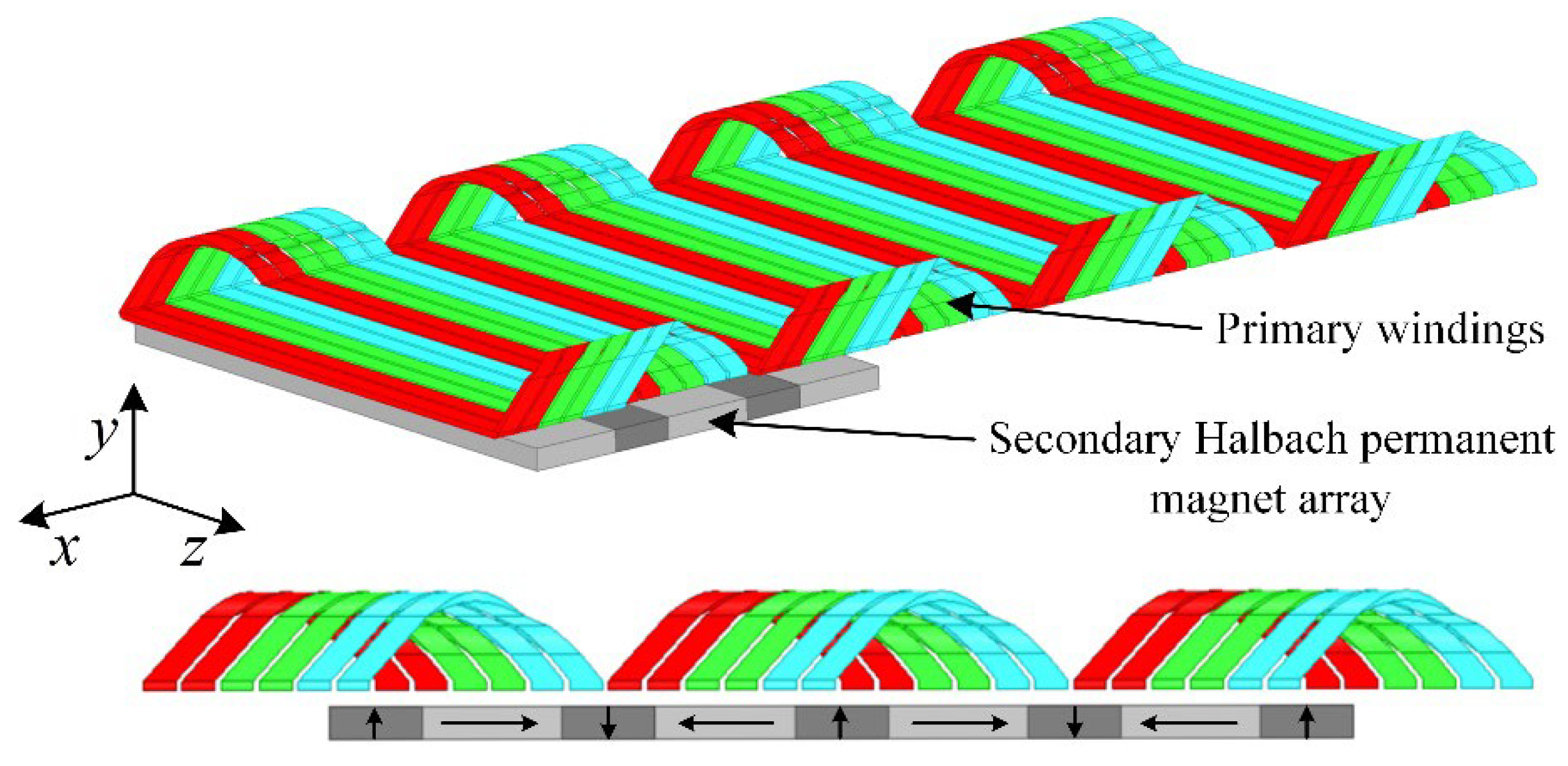
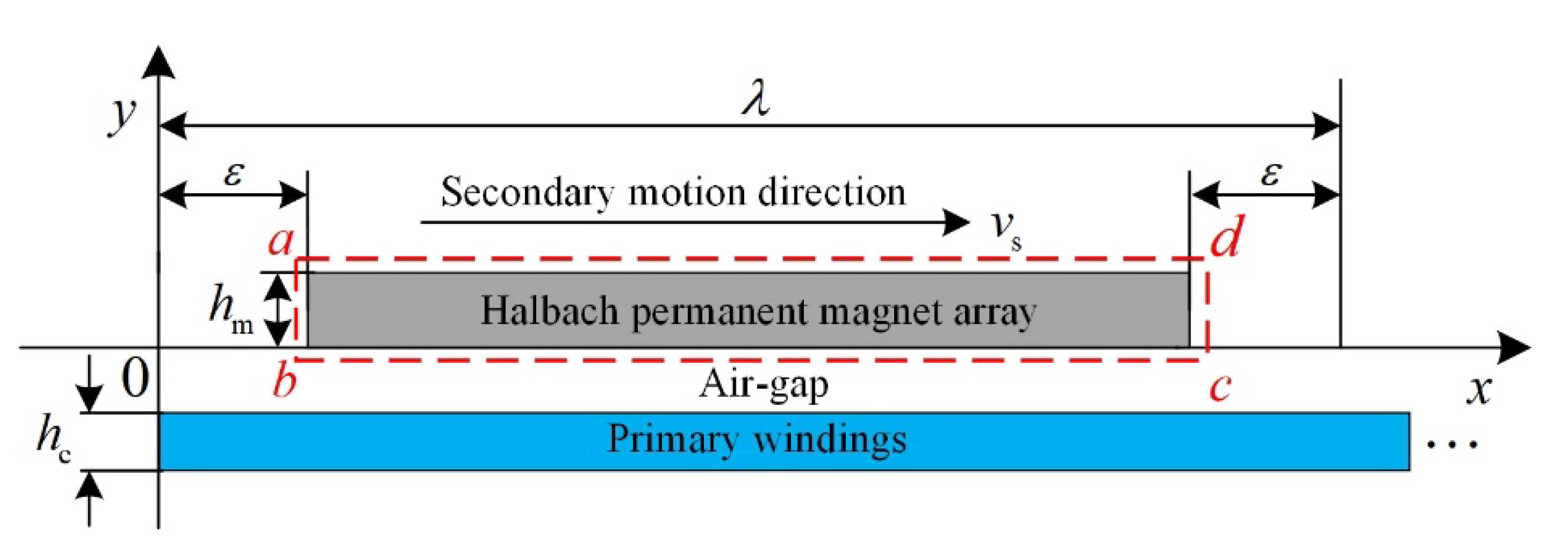
2. Basic Structure of IHPMSLM
3. Magnetic Field Analysis and Finite Element Verification
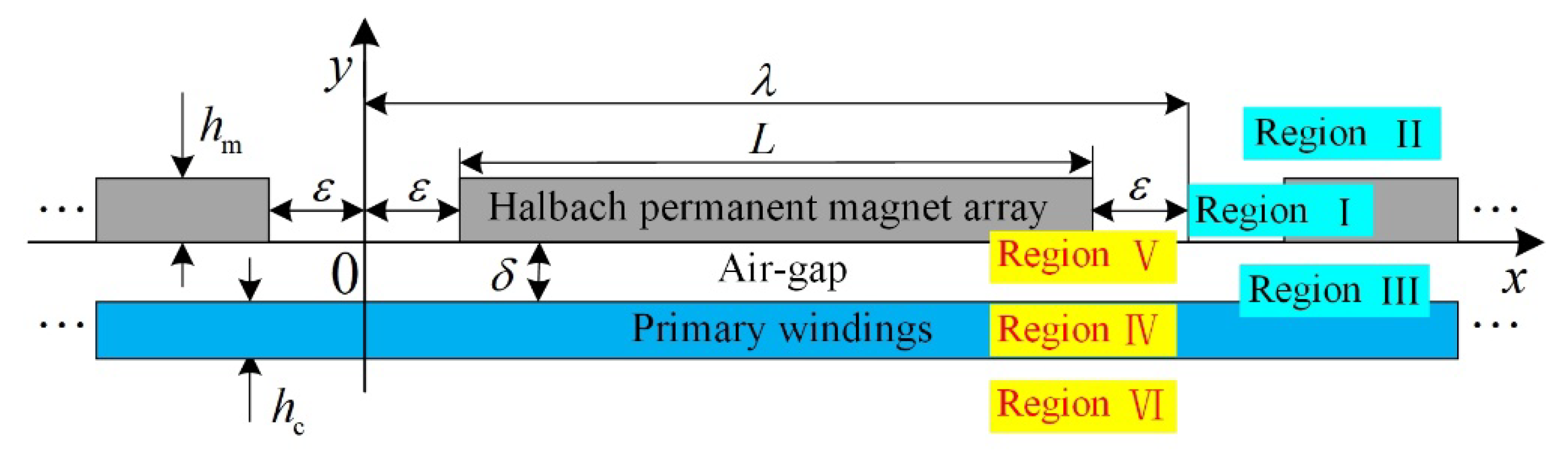
3.1. Unilateral IHPMSLM Magnetic Field Resolution Model
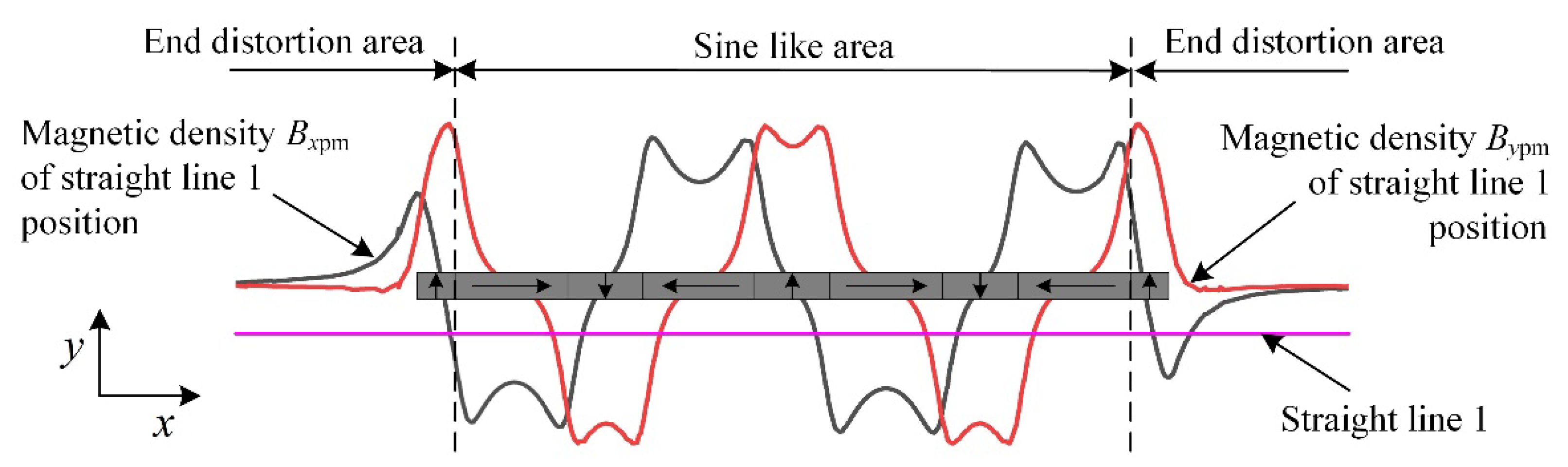
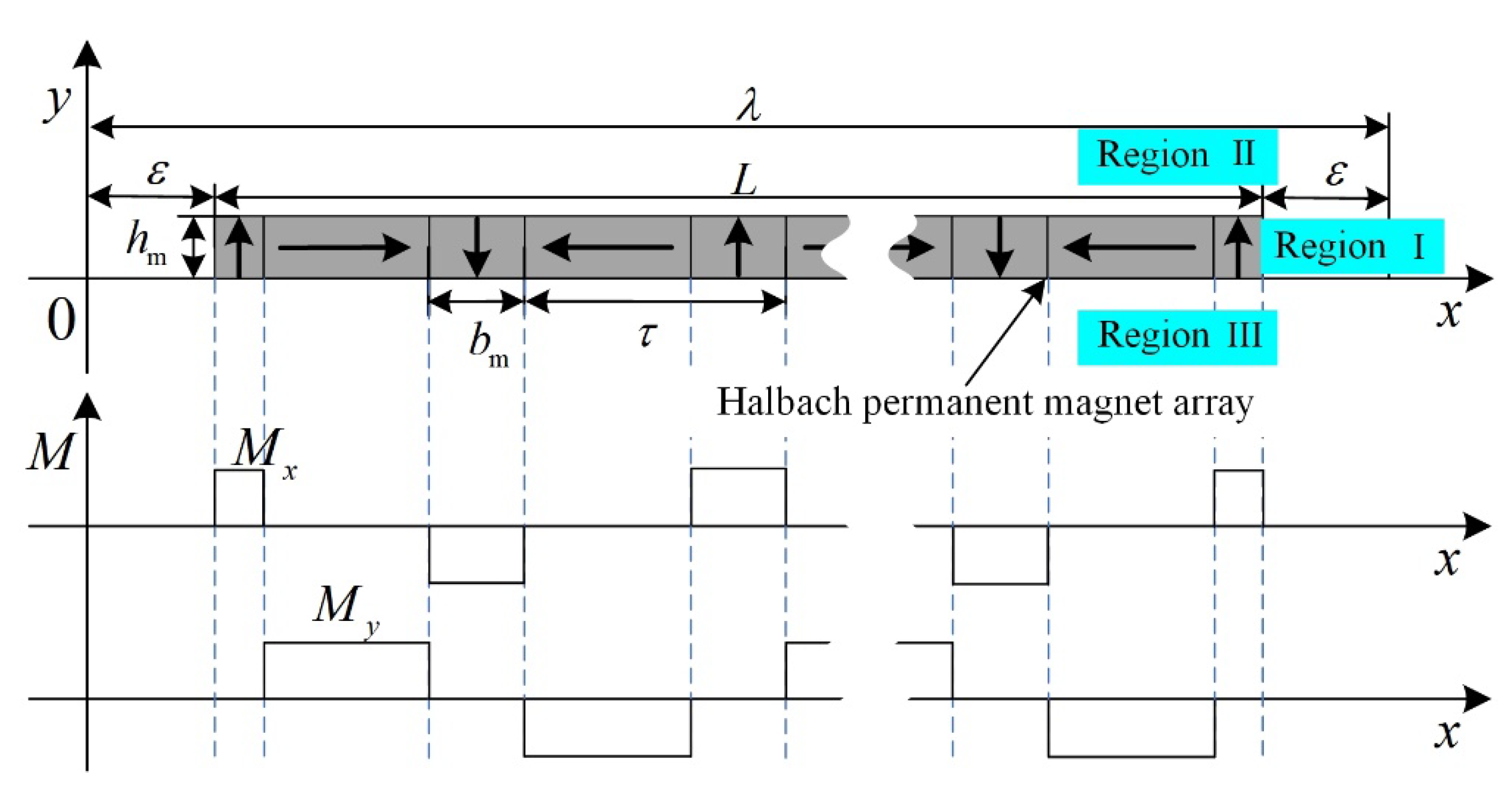
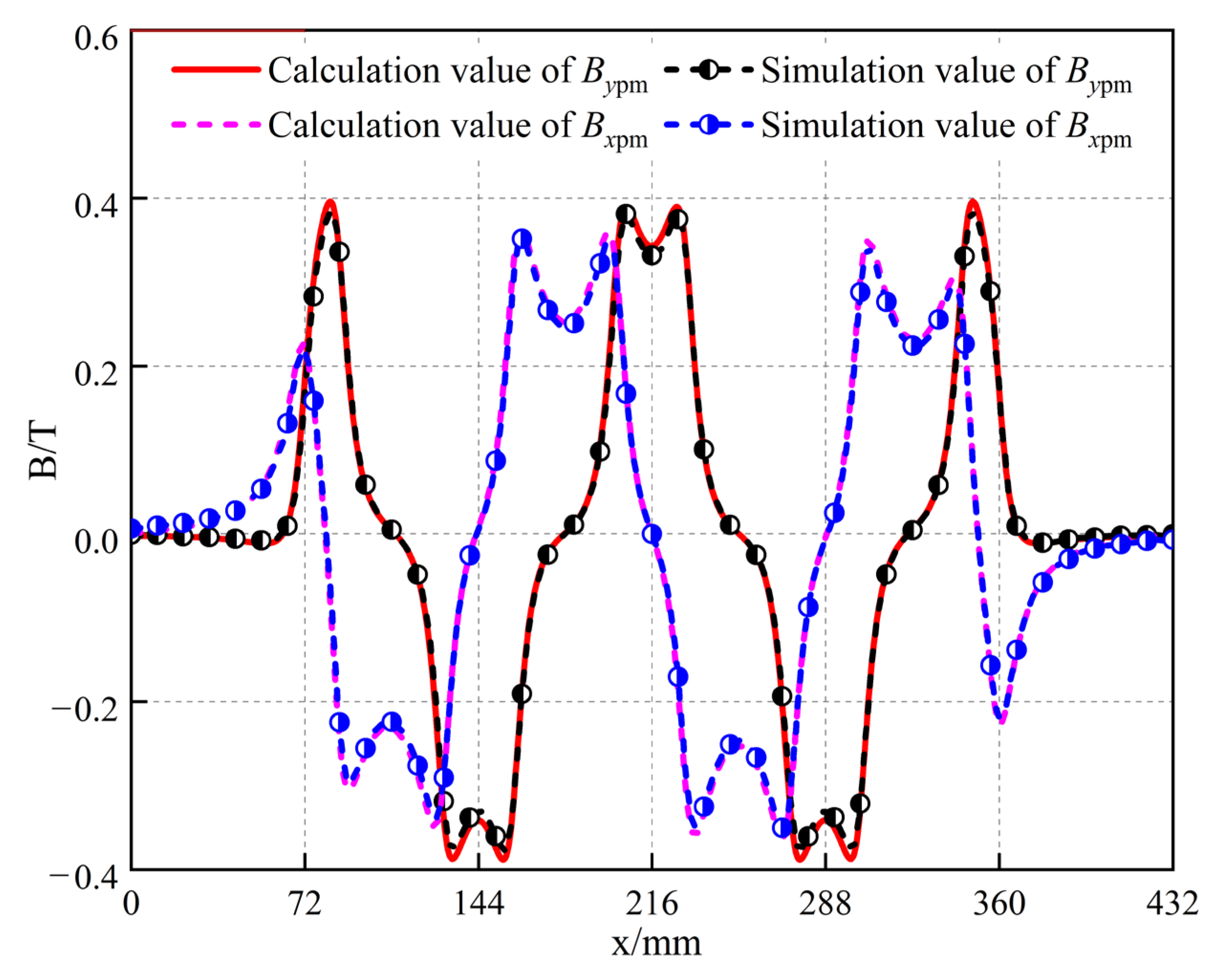
3.2. Halbach Permanent Magnet Array Magnetic Field Analysis and Element Verification
3.3. Primary Winding Magnetic Field Analysis and Finite Element Verification
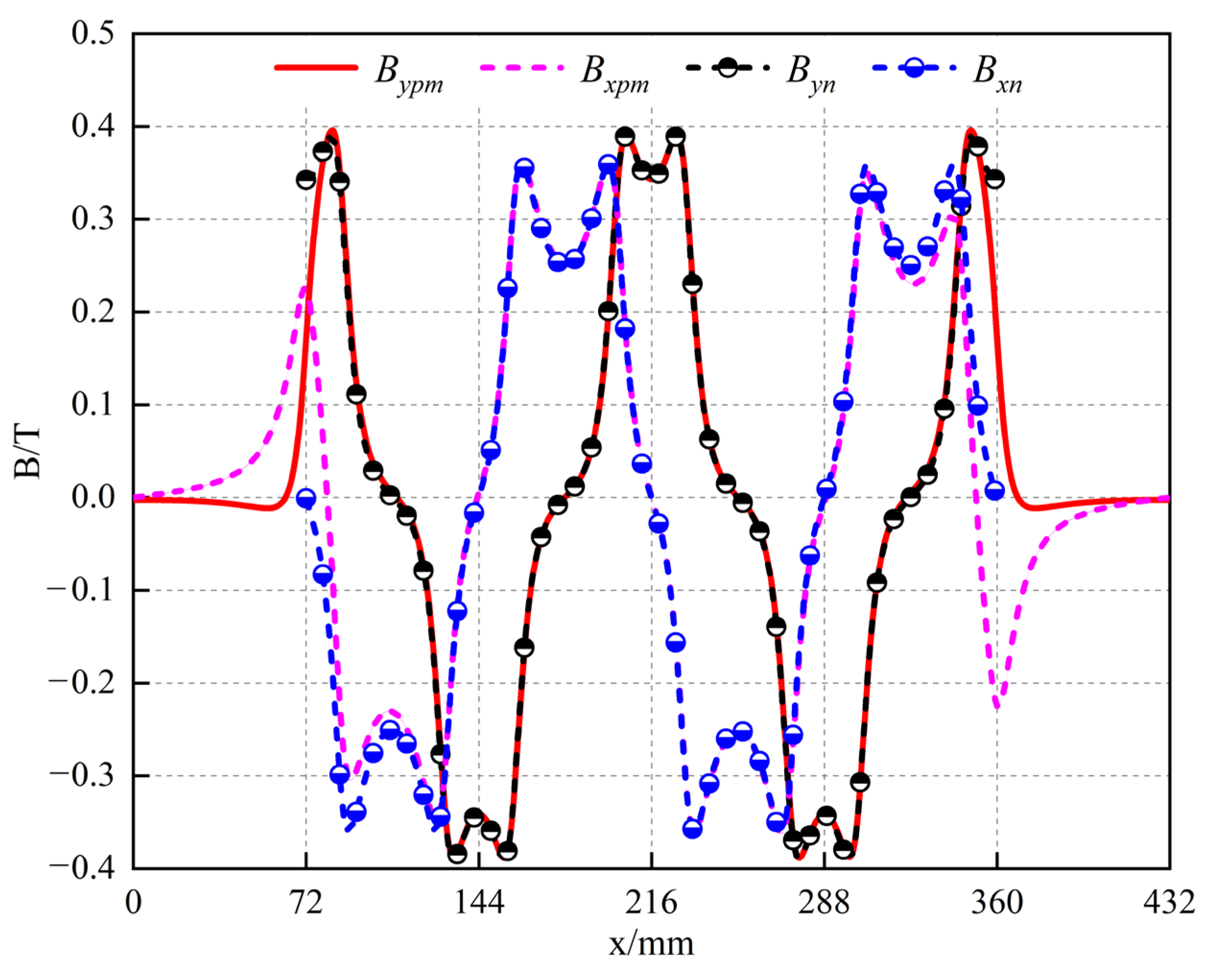
3.4. Air-Gap Synthesis Magnetic Field Analysis and Finite Element Verification
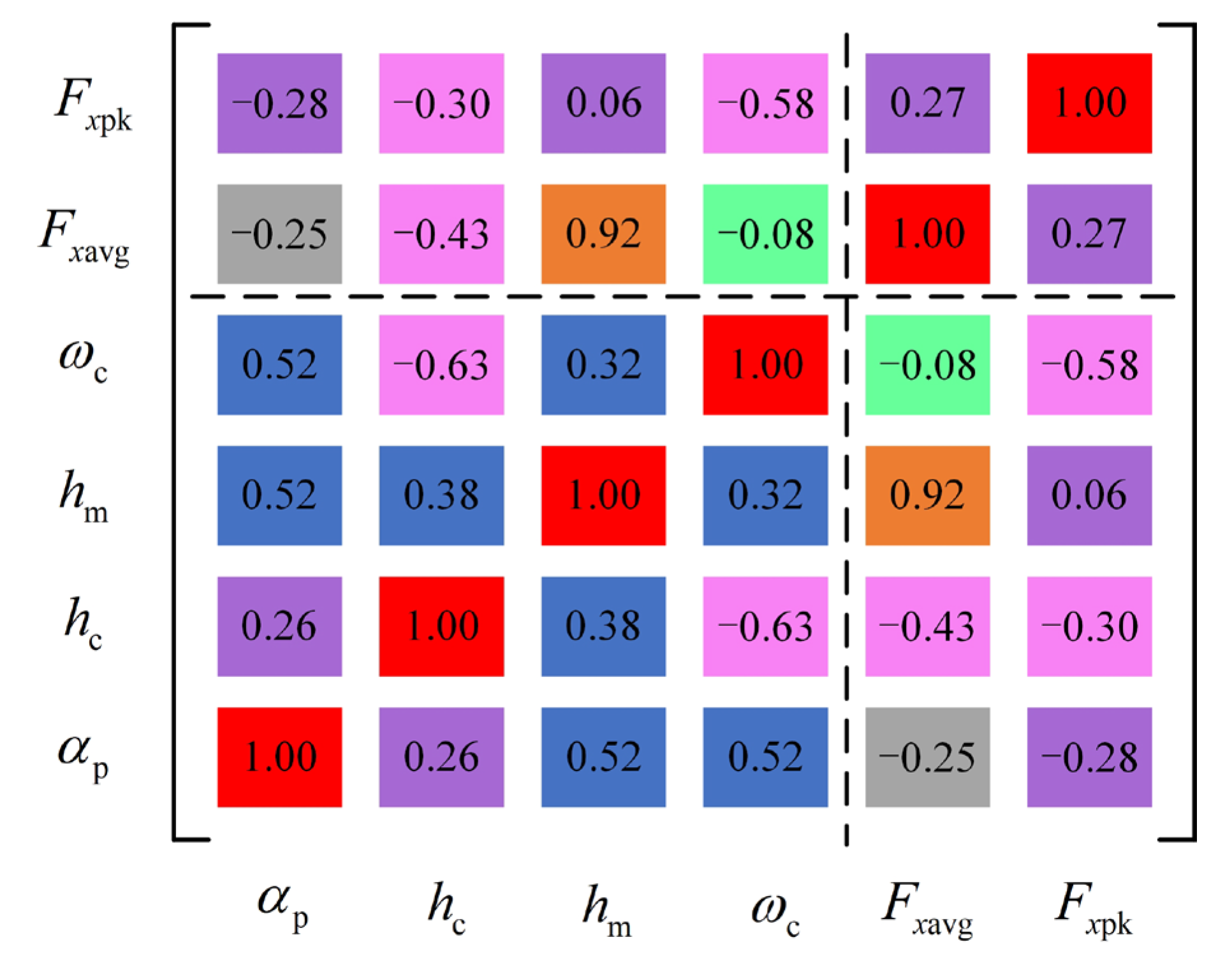
4. Electromagnetic Force Modeling and Optimization
4.1. Electromagnetic Force Calculation
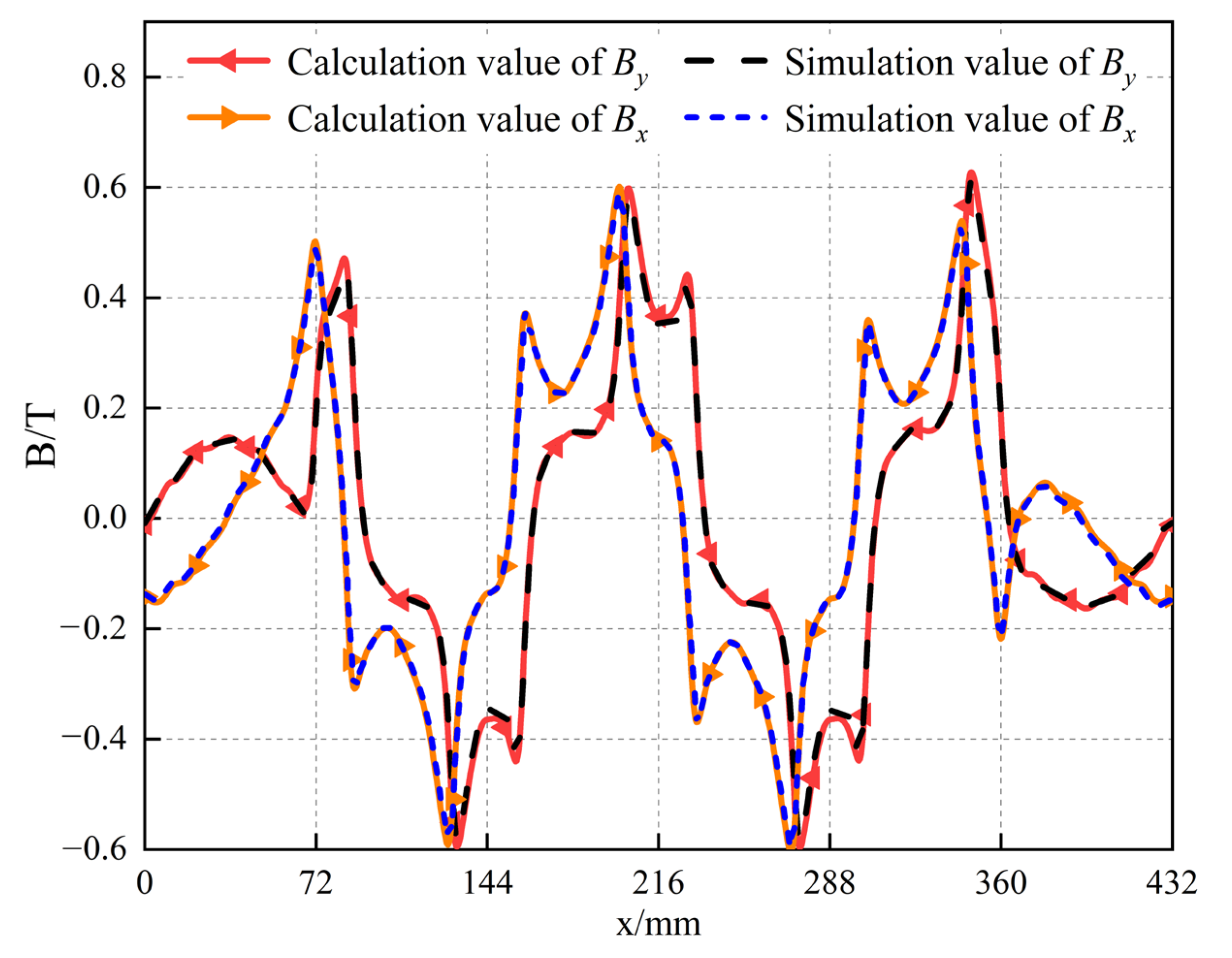
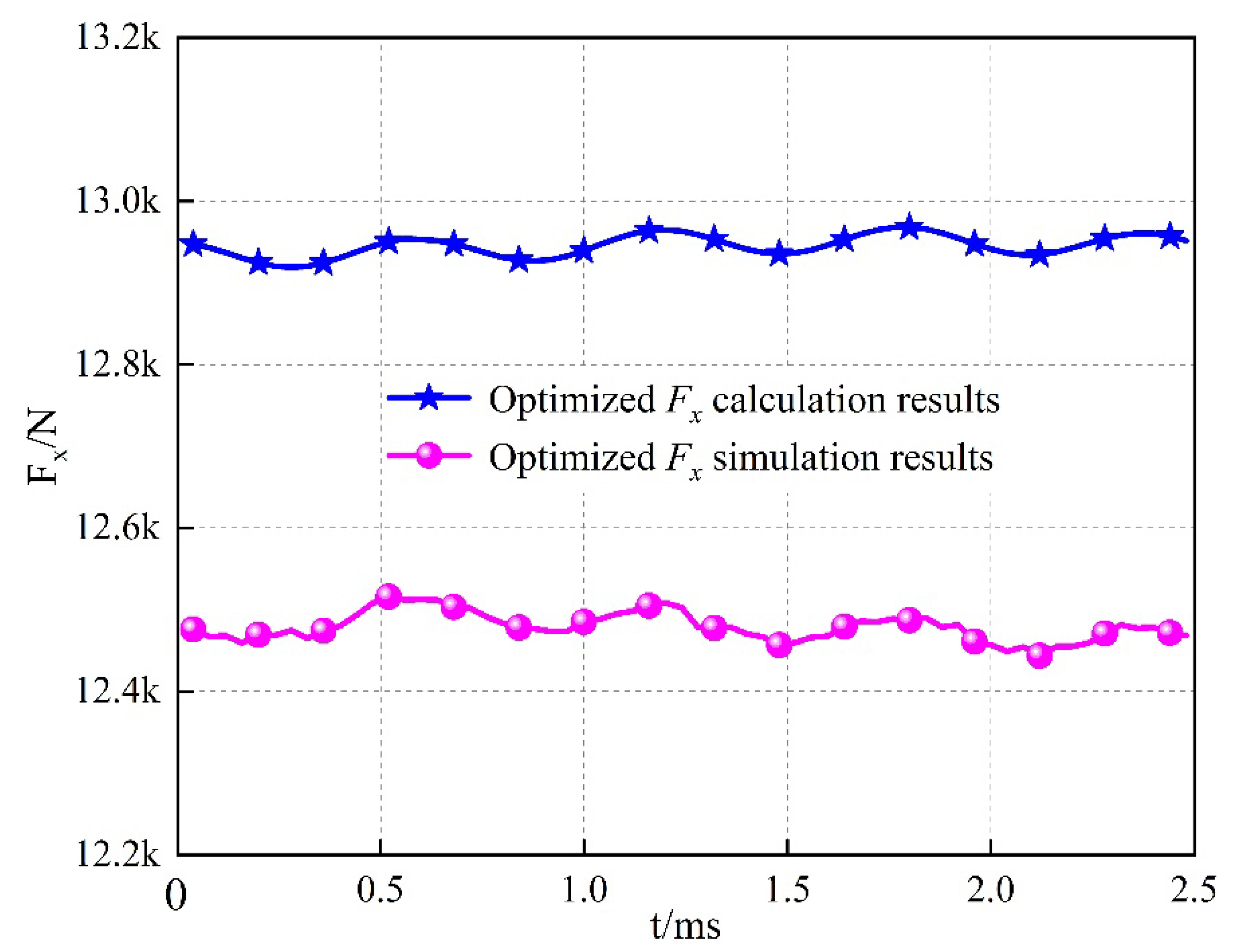
4.2. Finite Element Verification of Electromagnetic Force Calculation Results
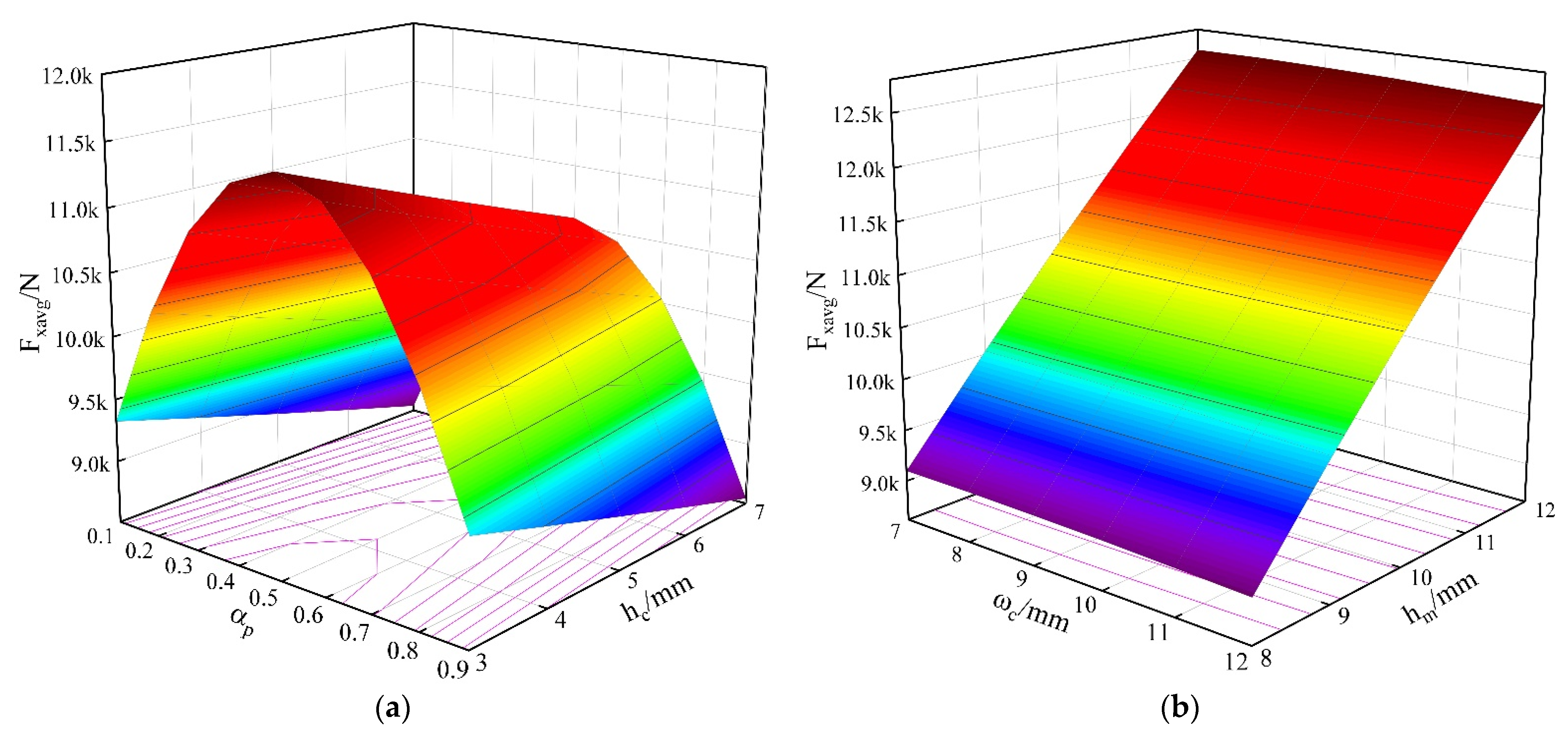
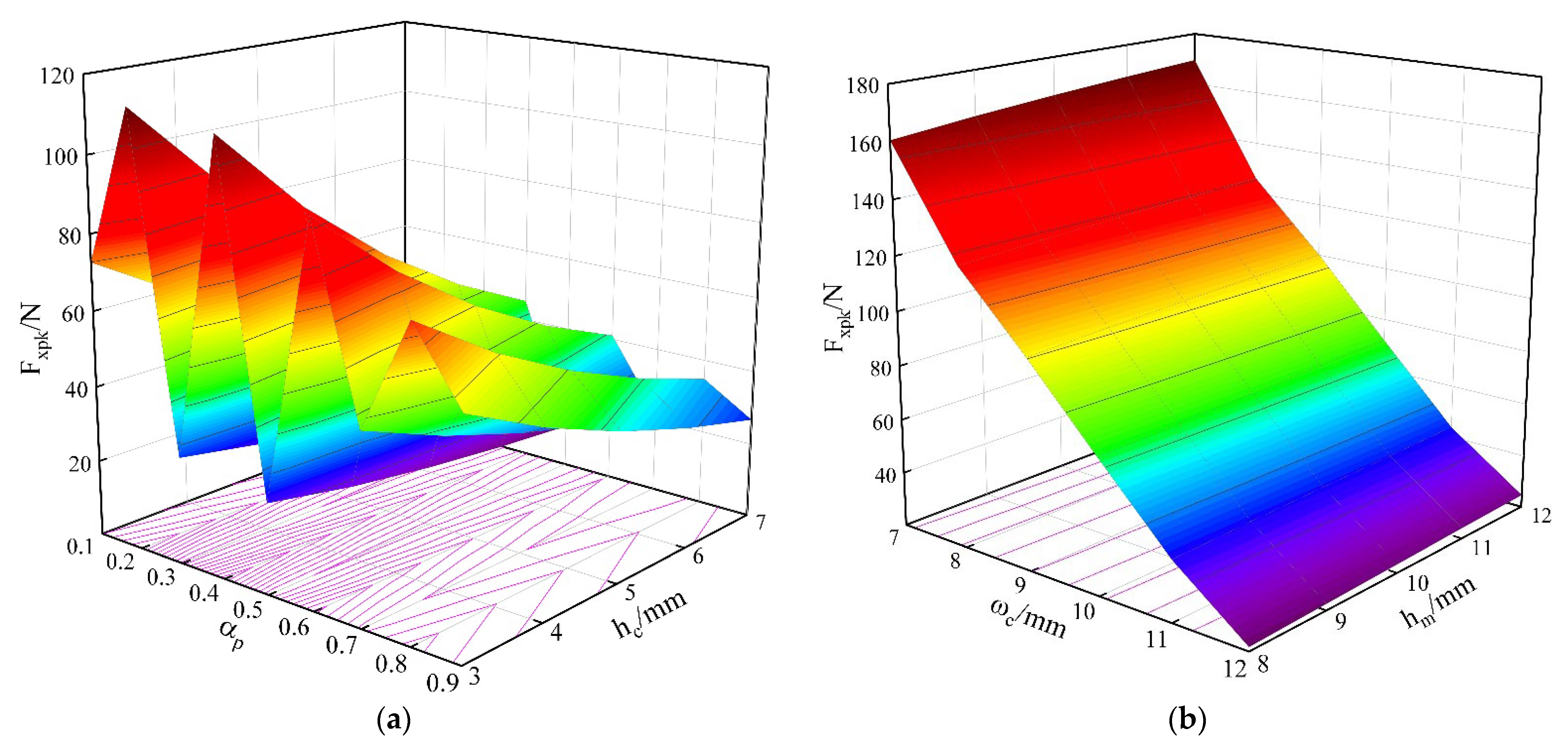
4.3. Electromagnetic Thrust Optimization
5. Conclusions
- (1)
- A single-sided IHPMSLM magnetic field analytical model that can simultaneously solve the primary and secondary air-gap magnetic fields has been established, in which the secondary Halbach permanent magnet array magnetic field is solved by combining the pseudo-periodic idea with the equivalent magnetization strength method, which is less computationally intensive and accurately depicts the air-gap magnetic field in the sinusoidal-like region and the end aberration region of the permanent magnet array. Additionally, the primary six-phase winding magnetic field is solved using the Fourier series expansion method. By superposing the primary and secondary air-gap magnetic fields, the synthetic magnetic field of the IHPMSLM air gap is obtained, which fits the actual distribution of the magnetic field, and the error meets the needs of engineering analysis and matches well with the finite element results, which solves the problem of accurately solving the air-gap magnetic field of the IHPMSLM load.
- (2)
- Based on the solution results of the air-gap magnetic field, the Maxwell tensor method is used to establish the functional relationship between the tangential electromagnetic thrust and the normal electromagnetic force of the unilateral IHPMSLM and the main structural parameters of the motor, and the correctness of the electromagnetic force modeling is verified by the finite element, which provides the theoretical q for the calculation of the motor performance.
- (3)
- Taking the Halbach permanent magnet array and the main structural parameters of the primary winding as the optimization variables, based on the parameter sensitivity analysis and response surface calculation, within the constraints of the values of the optimization variables, the genetic algorithm is used to search for the Pareto optimal solution set of the optimization objective, and the computational results show that the average thrust of the unilateral IHPMSLM following the optimization is increased by 18.75%, the peak-to-peak thrust fluctuation is decreased by 30.27%, and the error is small compared with the finite element results. The decrease of 30.27% and the error with the finite element results are small, which verifies the reasonableness of the optimization method, and the optimization results can be used as a reference for the optimal design of IHPMSLM.
Author Contributions
Funding
Conflicts of Interest
References
- Yu, L.; Chang, S.; He, J.; Sun, H.; Huang, J.; Tian, H. Electromagnetic Design and Analysis of Permanent Magnet Linear Synchronous Motor. Energies 2022, 15, 5441. [Google Scholar] [CrossRef]
- Zhou, W.; Sun, Z.; Cui, F.; Mao, Y. Electromagnetic Design of High-Speed and High-Thrust Cross-Shaped Linear Induction Motor. IEEE Access 2021, 9, 87501–87509. [Google Scholar] [CrossRef]
- Zhang, Z.; Luo, M.; Duan, J.-A.; Kou, B. Design and Modeling of a Novel Permanent Magnet Width Modulation Secondary for Permanent Magnet Linear Synchronous Motor. IEEE Trans. Ind. Electron. 2022, 69, 2749–2758. [Google Scholar] [CrossRef]
- Choi, J.-S.; Yoo, J. Design of a Halbach Magnet Array Based on Optimization Techniques. IEEE Trans. Magn. 2008, 44, 2361–2366. [Google Scholar] [CrossRef]
- Wei, W.; Zhang, J.; Yao, J.; Tang, S.; Zhang, S. Performance Analysis and Optimization of Power Density Enhanced PMSM with Magnetic Stripe on Rotor. Energies 2020, 13, 4457. [Google Scholar] [CrossRef]
- Liu, X.; Zheng, X.; Wang, X. Modeling of Uneven Air Gap Magnetic Field for Disc Planetary Permanent Magnet Machine with Segmented Gap Halbach Array. IEEE Trans. Energy Convers. 2023, 38, 693–702. [Google Scholar] [CrossRef]
- Li, B.; Zhang, J.; Zhao, X.; Liu, B.; Dong, H. Research on Air Gap Magnetic Field Characteristics of Trapezoidal Halbach Permanent Magnet Linear Synchronous Motor Based on Improved Equivalent Surface Current Method. Energies 2023, 16, 793. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, C.; Yu, J.; Du, P.; Li, L. Analytical Model of Magnetic Field of a Permanent Magnet Synchronous Motor with a Trapezoidal Halbach Permanent Magnet Array. IEEE Trans. Magn. 2019, 55, 8105205. [Google Scholar] [CrossRef]
- Ladghem-Chikouche, B.; Boughrara, K.; Dubas, F.; Ibtiouen, R. 2-D Semi-Analytical Magnetic Field Calculation for Flat Permanent-Magnet Linear Machines Using Exact Subdomain Technique. IEEE Trans. Magn. 2021, 57, 8106211. [Google Scholar] [CrossRef]
- Cao, D.; Zhao, W.; Ji, J.; Wang, Y. Parametric Equivalent Magnetic Network Modeling Approach for Multiobjective Optimization of PM Machine. IEEE Trans. Ind. Electron. 2021, 68, 6619–6629. [Google Scholar] [CrossRef]
- Du, Y.; Huang, Y.; Guo, B.; Peng, F.; Dong, J. Semianalytical Model of Multiphase Halbach Array Axial Flux Permanent-Magnet Motor Considering Magnetic Saturation. IEEE Trans. Transp. Electrif. 2023, 9, 2891–2901. [Google Scholar] [CrossRef]
- Li, H.; Li, T. End-Effect Magnetic Field Analysis of the Halbach Array Permanent Magnet Spherical Motor. IEEE Trans. Magn. 2018, 54, 8202209. [Google Scholar] [CrossRef]
- Guo, L.; Zhou, Q.; Galea, M.; Lu, W. Cogging Force Optimization of Double-Sided Tubular Linear Machine with Tooth-Cutting. IEEE Trans. Ind. Electron. 2022, 69, 7161–7169. [Google Scholar] [CrossRef]
- Li, Z.; Xia, J.; Guo, Z.; Lu, B.; Ma, G. Reduction of Pole-Frequency Vibration of Surface-Mounted Permanent Magnet Synchronous Machines with Piecewise Stagger Trapezoidal Poles. IEEE Trans. Transp. Electrif. 2023, 9, 833–844. [Google Scholar] [CrossRef]
- Dreishing, F.; Kreischer, C. Optimization of Force-to-Weight Ratio of Ironless Tubular Linear Motors Using an Analytical Field Calculation Approach. IEEE Trans. Magn. 2022, 58, 7401704. [Google Scholar] [CrossRef]
- Zhao, Y.; Li, Y.; Lu, Q. An Accurate No-Load Analytical Model of Flat Linear Permanent Magnet Synchronous Machine Accounting for End Effects. IEEE Trans. Magn. 2023, 59, 8100111. [Google Scholar] [CrossRef]
- Kim, K.-H.; Cho, H.-K.; Woo, D.-K. 3D Characteristic Analysis of 3-Leg Linear Permanent Magnet Motor with Magnet Skew and Overhang Structure. IEEE Access 2021, 9, 153863–153874. [Google Scholar] [CrossRef]
- Song, Z.; Liu, C.; Feng, K.; Zhao, H.; Yu, J. Field Prediction and Validation of a Slotless Segmented-Halbach Permanent Magnet Synchronous Machine for More Electric Aircraft. IEEE Trans. Transp. Electrif. 2020, 6, 1577–1591. [Google Scholar] [CrossRef]
- Zhao, J.; Mou, Q.; Guo, K.; Liu, X.; Li, J.; Guo, Y. Reduction of the Detent Force in a Flux-Switching Permanent Magnet Linear Motor. IEEE Trans. Energy Convers. 2019, 34, 1695–1705. [Google Scholar] [CrossRef]
- Chi, S.; Yan, J.; Shan, L.; Wang, P. Detent Force Minimizing for Moving-Magnet-Type Linear Synchronous Motor. IEEE Trans. Magn. 2019, 55, 8102005. [Google Scholar] [CrossRef]
- Chung, S.-U.; Lee, J.-Y. Teeth Arrangement and Pole–Slot Combination Design for PMLSM Detent Force Reduction. Energies 2021, 14, 8141. [Google Scholar] [CrossRef]
- Cervone, A.; Slunjski, M.; Levi, E.; Brando, G. Optimal Third-Harmonic Current Injection for Asymmetrical Multiphase Permanent Magnet Synchronous Machines. IEEE Trans. Ind. Electron. 2021, 68, 2772–2783. [Google Scholar] [CrossRef]
- Huang, C.; Kou, B.; Zhao, X.; Niu, X.; Zhang, L. Multi-Objective Optimization Design of a Stator Coreless Multidisc Axial Flux Permanent Magnet Motor. Energies 2022, 15, 4810. [Google Scholar] [CrossRef]
- Grenier, J.-M.; Pérez, R.; Picard, M.; Cros, J. Magnetic FEA Direct Optimization of High-Power Density, Halbach Array Permanent Magnet Electric Motors. Energies 2021, 14, 5939. [Google Scholar] [CrossRef]
- Zhao, W.; Ma, A.; Ji, J.; Chen, X.; Yao, T. Multiobjective Optimization of a Double-Side Linear Vernier PM Motor Using Response Surface Method and Differential Evolution. IEEE Trans. Ind. Electron. 2020, 67, 80–90. [Google Scholar] [CrossRef]





| Symbol | Quantity | Value |
|---|---|---|
| m | phase number | 6 |
| τ | polar pitch | 72 mm |
| d | winding pitch | 2 mm |
| S | windings cross-sectional area | 50 mm2 |
| p1 | primary winding pole pairs | 26 |
| p | permanent magnet array pole pairs | 6 |
| ωc | primary winding width | 10 mm |
| hc | primary winding thickness | 5 mm |
| h1 | primary winding height | 259.6 mm |
| ẟ | mechanical air gap | 5 mm |
| hm | permanent magnet array thickness | 10 mm |
| h2 | permanent magnet array height | 275 mm |
| bm | width of radially magnetized permanent magnets | 28.8 mm |
| bz | width of tangentially magnetized permanent magnets | 43.2 mm |
| Variable | Maximum Value | Minimum Value |
|---|---|---|
| αp | 0.9 | 0.1 |
| hm | 12 mm | 8 mm |
| hc | 7 mm | 3 mm |
| ωc | 12 mm | 7 mm |
| Variable | Value |
|---|---|
| αp | 0.563 |
| hm | 11.8 mm |
| hc | 3.2 mm |
| ωc | 11.6 mm |
| Fx | Fxavg | Fxpk |
|---|---|---|
| calculated value before optimization | 10.901 kN | 70.472 N |
| simulation value before optimization | 10.623 kN | 87.356 N |
| calculated value after optimization | 12.945 kN | 49.140 N |
| simulation value after optimization | 12.478 kN | 62.229 N |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Z.; Jia, G.; Huang, C.; Zhou, W.; Mao, Y.; Lei, Z. Accurate Modeling and Optimization of Electromagnetic Forces in an Ironless Halbach-Type Permanent Magnet Synchronous Linear Motor. Energies 2023, 16, 5785. https://doi.org/10.3390/en16155785
Sun Z, Jia G, Huang C, Zhou W, Mao Y, Lei Z. Accurate Modeling and Optimization of Electromagnetic Forces in an Ironless Halbach-Type Permanent Magnet Synchronous Linear Motor. Energies. 2023; 16(15):5785. https://doi.org/10.3390/en16155785
Chicago/Turabian StyleSun, Zhaolong, Guangyong Jia, Chuibing Huang, Weichang Zhou, Yinhao Mao, and Zhaoran Lei. 2023. "Accurate Modeling and Optimization of Electromagnetic Forces in an Ironless Halbach-Type Permanent Magnet Synchronous Linear Motor" Energies 16, no. 15: 5785. https://doi.org/10.3390/en16155785
APA StyleSun, Z., Jia, G., Huang, C., Zhou, W., Mao, Y., & Lei, Z. (2023). Accurate Modeling and Optimization of Electromagnetic Forces in an Ironless Halbach-Type Permanent Magnet Synchronous Linear Motor. Energies, 16(15), 5785. https://doi.org/10.3390/en16155785







