PhloVer: A Modular and Integrated Tracking Photovoltaic Shading Device for Sustainable Large Urban Spaces—Preliminary Study and Prototyping
Abstract
1. Introduction
- An innovative flower-shaped design for a modular tracking PVSD system intended for integration in coverages of large urban spaces is proposed.
- The flower shape (opened flower petals) increases the electric production of a fixed PV system and has a shade function for the crowded location, not neglecting the architectural aspects.
- Its applicability to a real case study is verified.
- Detailed simulation of the tracking PVSD system is performed using:
- A comparison of the proposed tracking PVSD system with equivalent fixed systems is provided in terms of electricity generation.
- The first small-scale interactive prototype of the system is presented.
2. Literature Review
2.1. Photovoltaics
2.2. Solar Tracking Photovoltaics
2.3. Building-Integrated Photovoltaic (BIPV)
2.4. Photovoltaic Shading Devices (PVSDs)
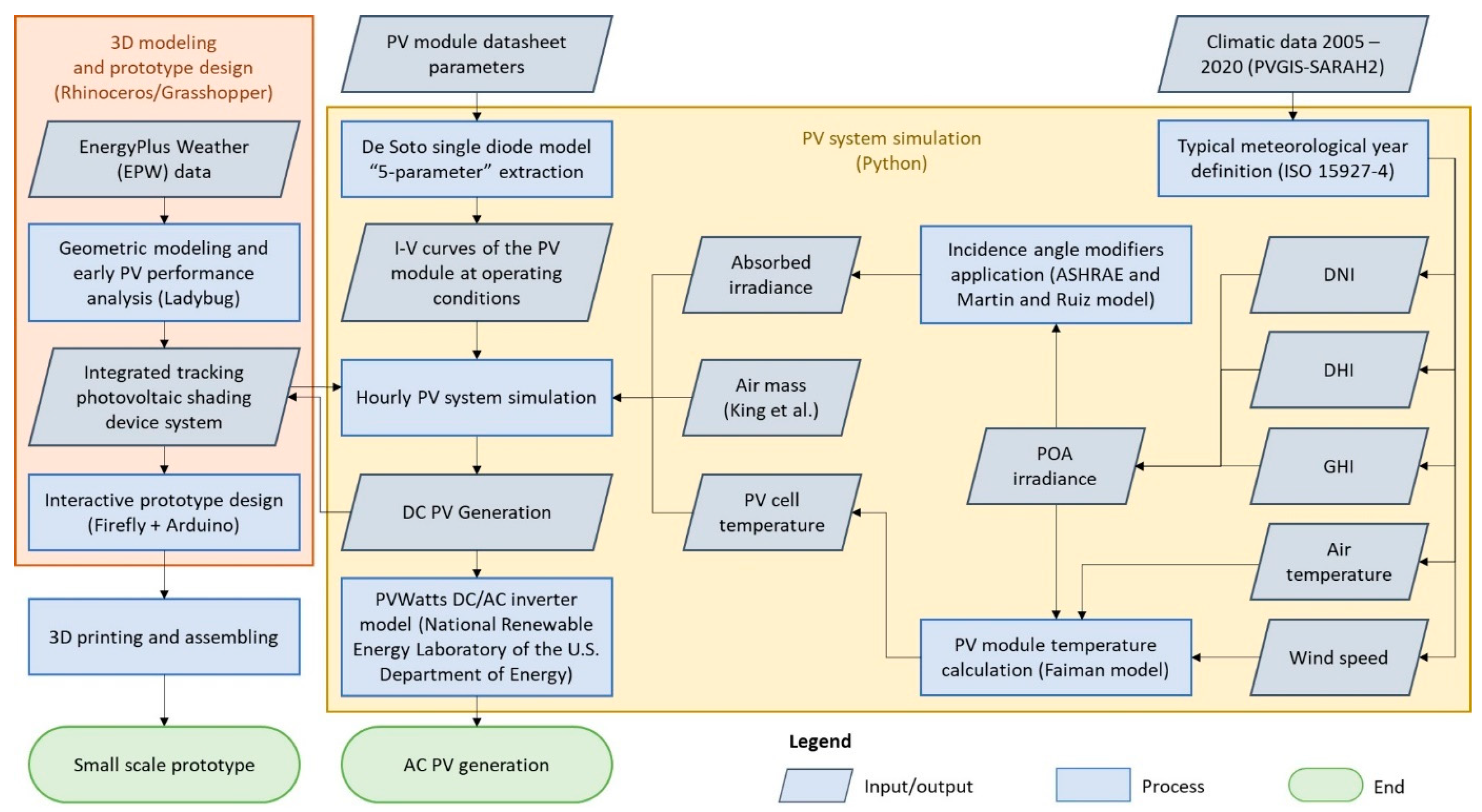
3. Methodology and Case Study
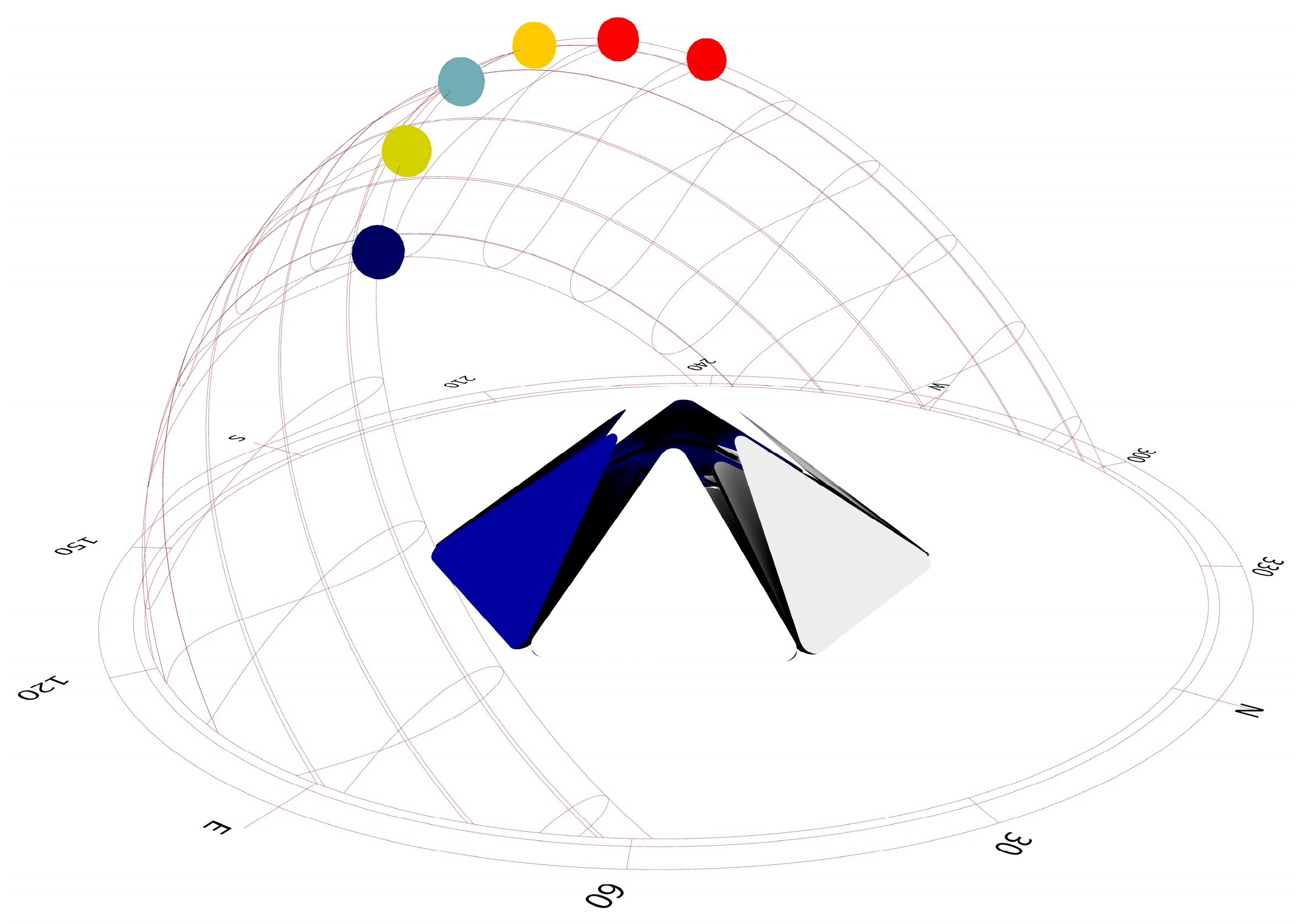
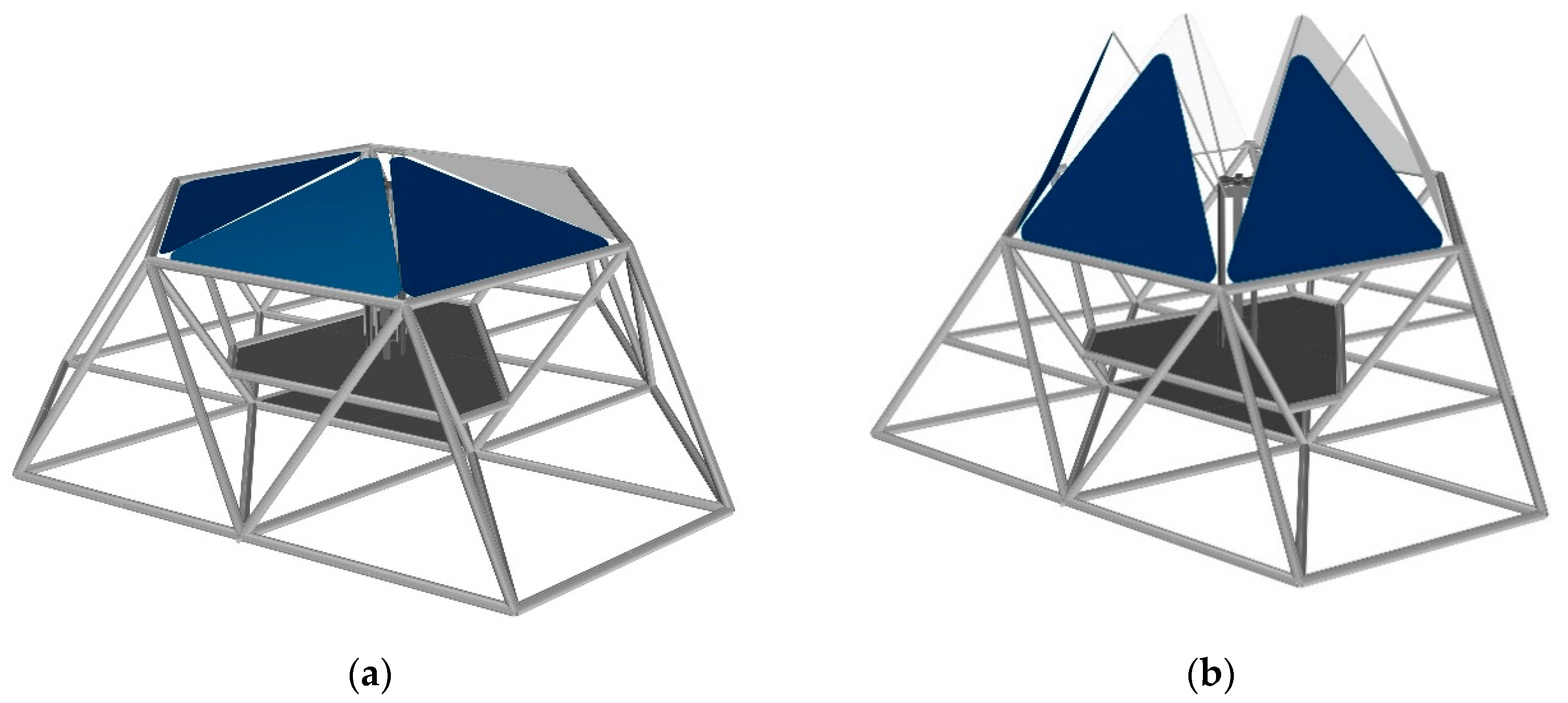
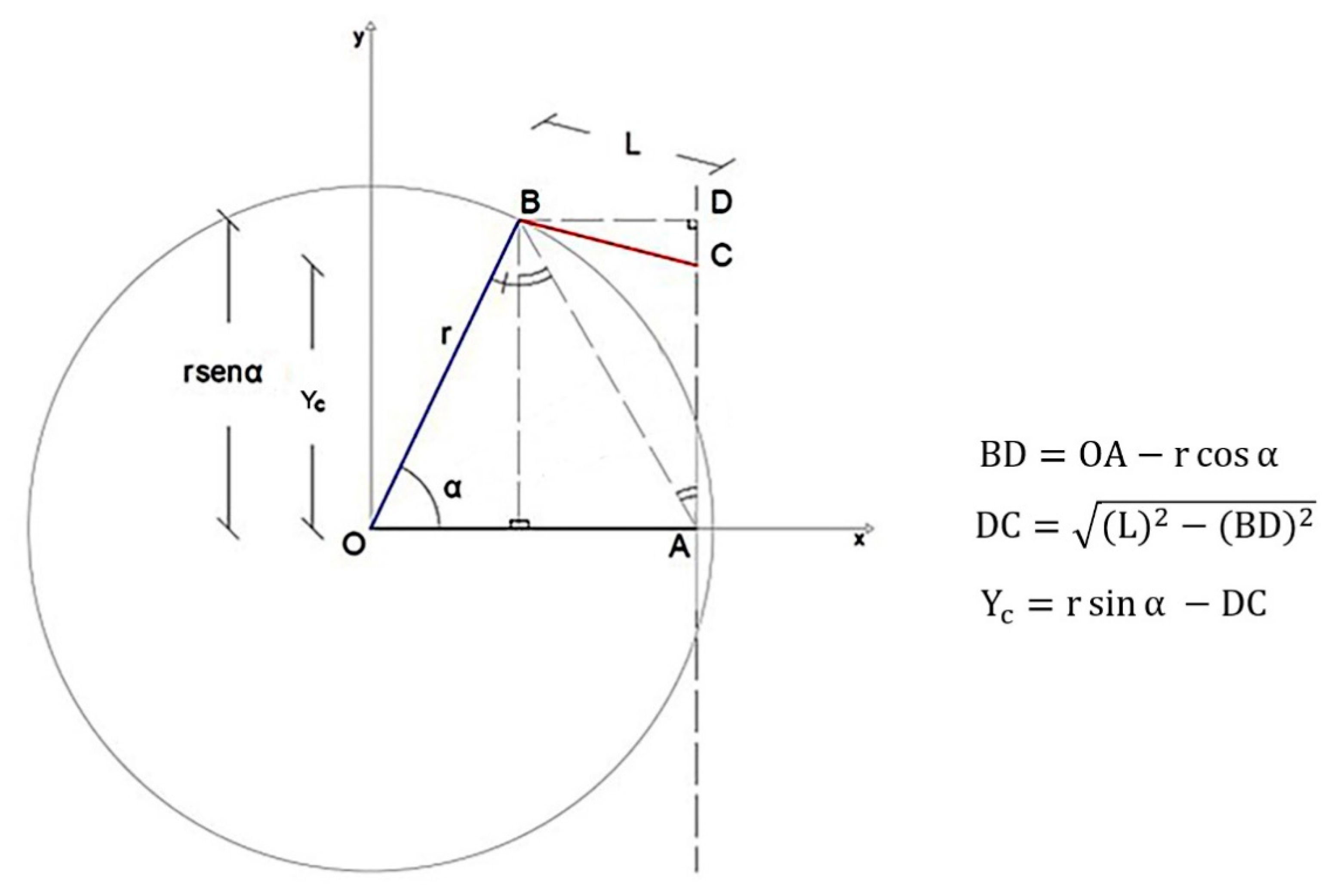
3.1. Design of a Modular Tracking PV System Integrated in Coverages of Large Urban Spaces
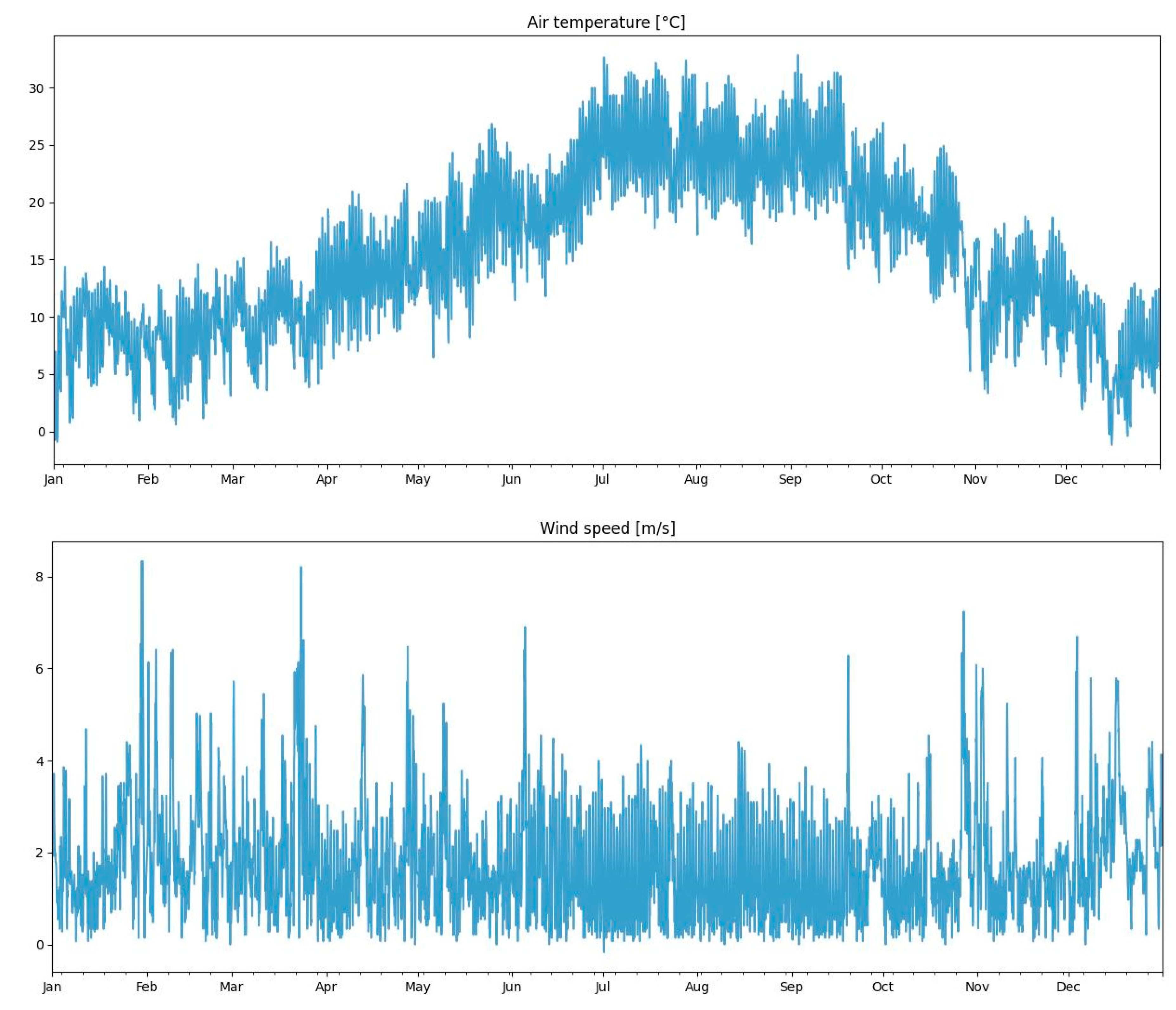
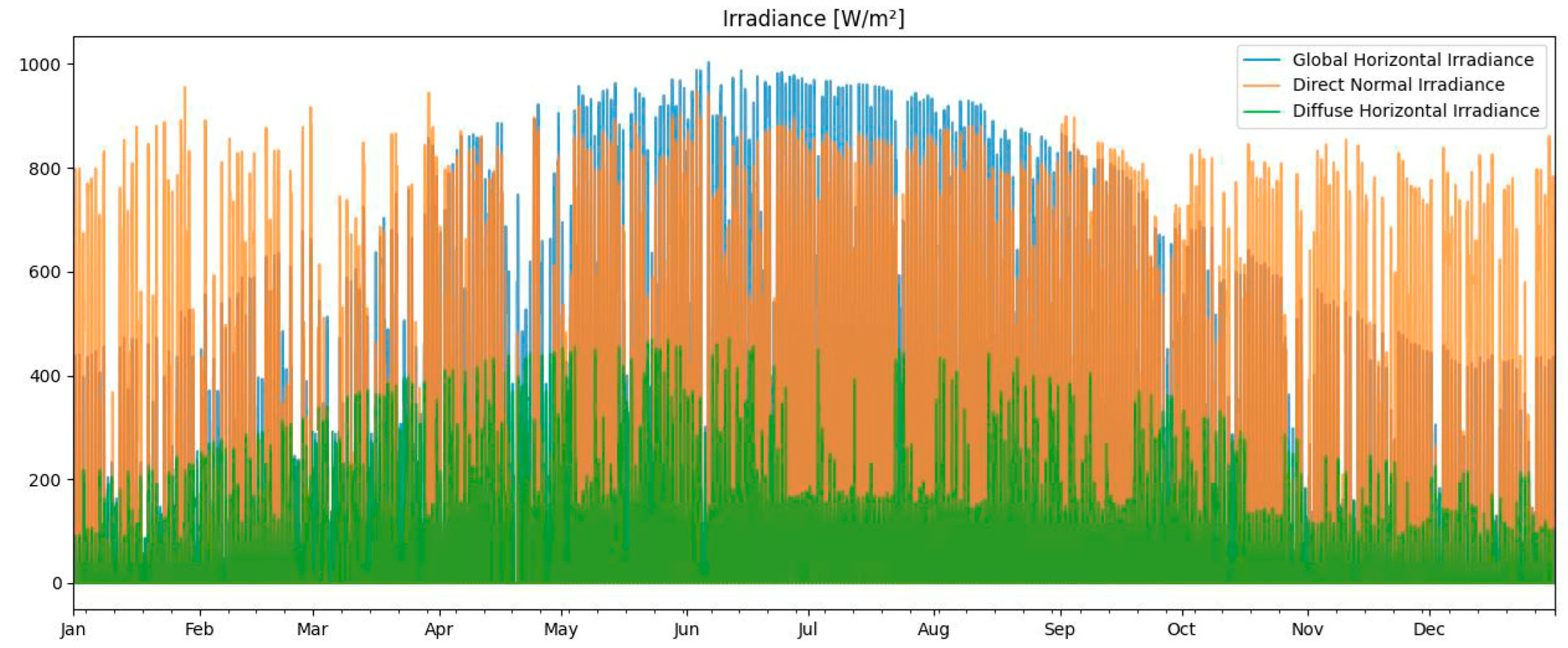
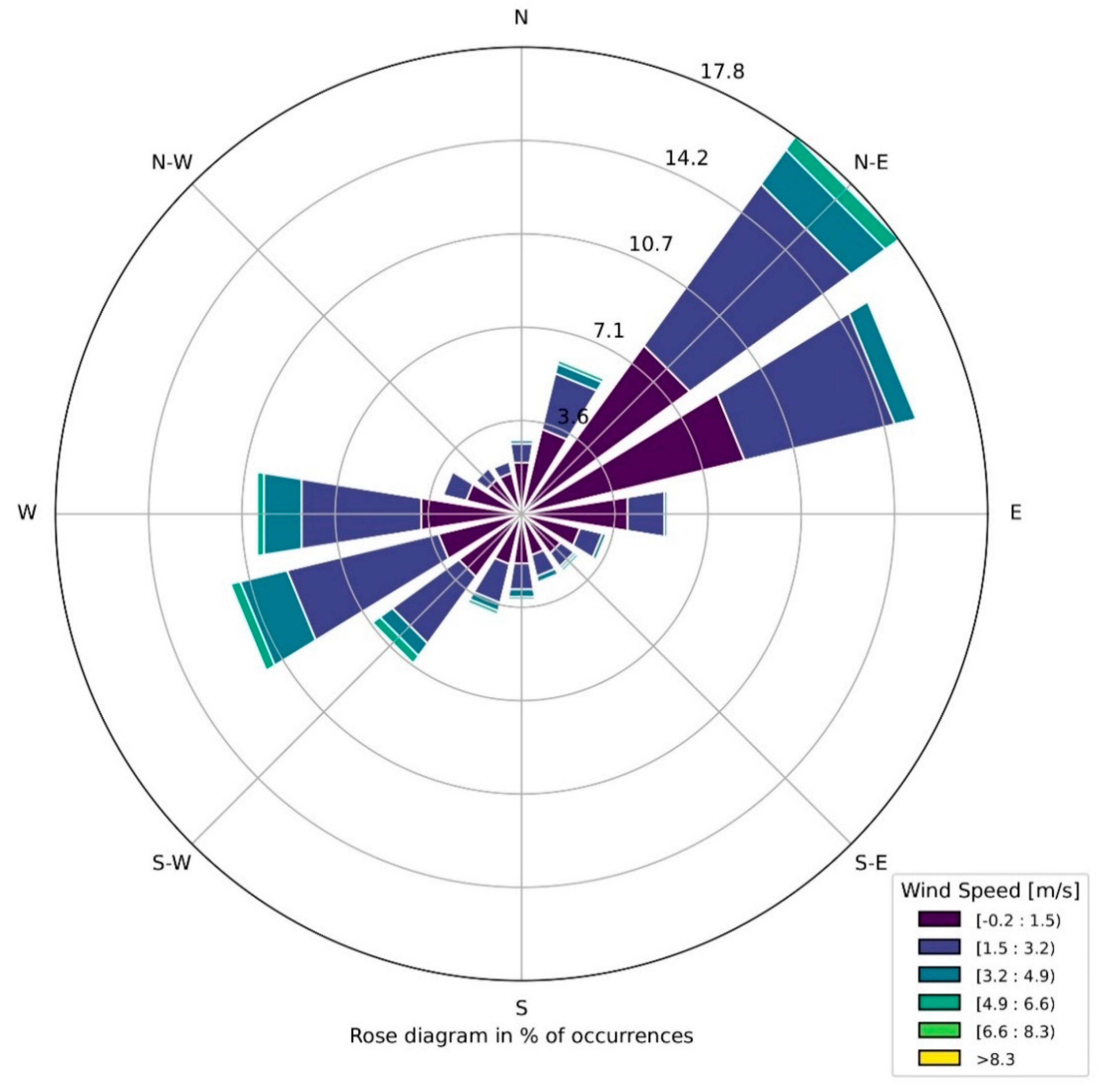
3.2. Climate Data
- Air temperature (°C)
- Wind speed (m/s)
- Direct normal irradiance (DNI) (W/m2)
- Diffuse horizontal irradiance (DHI) (W/m2)
- Global horizontal irradiance (GHI) (W/m2)
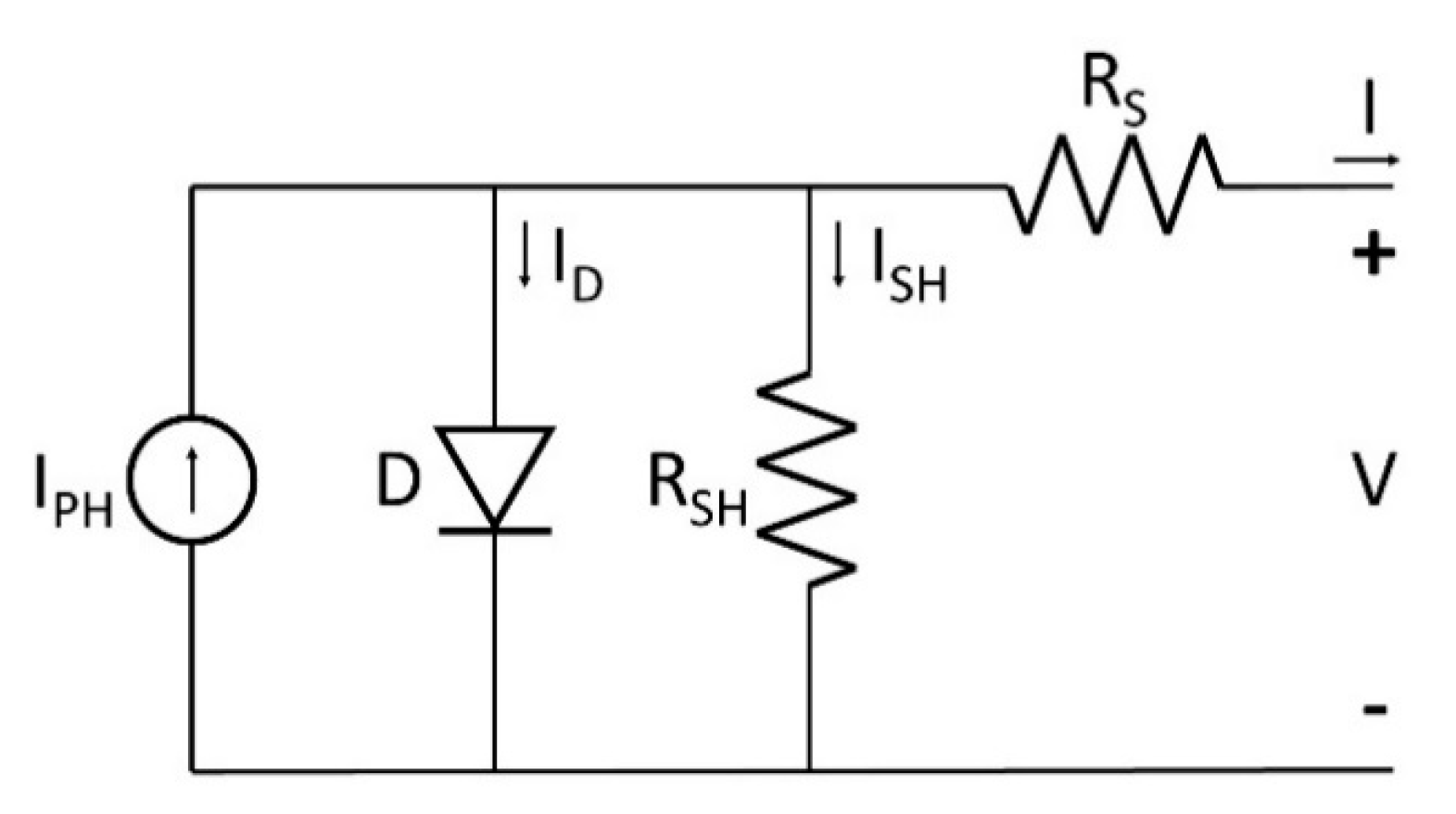
3.3. PV Performance Simulation
- : current of the cell (A)
- : current generated by photovoltaic effect (A)
- : current lost due to recombination (A)
- : current lost due to shunt resistances (A).
- : diode reverse saturation current (A)
- : elementary charge (1.602 × 10−19 C)
- : diode voltage (V)
- : diode ideality factor
- : Boltzmann constant (1.381 × 10−23 J/K)
- : temperature [K]
- : potential of the cell (V)
- : series resistance (Ω).
- : current of the module (A)
- : voltage of the module (V)
- : number of cells in series.
3.4. I–V Parameter Extraction: 5 Parameter Model
- : total absorbed irradiance (W/m2)
- : total absorbed irradiance at STC (W/m2)
- : air mass modifier
- : air mass modifier at STC
- : photocurrent at reference conditions (A)
- : temperature coefficient of short-circuit current (%/°C)
- : temperature of the cell (K)
- : temperature of the cell at reference conditions (K).
- : diode reverse saturation current (A)
- : temperature-dependent bandgap at (eV)
- : temperature-dependent bandgap at reference conditions (eV).
- : shunt resistance at reference conditions (Ω)
- : total irradiance on the horizontal surface (W/m2).
- : irradiance at STC (W/m2)
- : beam component of total irradiance on the horizontal surface (W/m2)
- : diffuse component of total irradiance on the horizontal surface (W/m2)
- : ratio of beam radiation on a tilted surface to that on a horizontal surface (W/m2)
- : incidence angle modifier at beam incidence angle
- : incidence angle modifier for the diffuse component
- : incidence angle modifier for ground reflected component
- : angle of incidence between the module normal vector and the sunbeam vector (°)
- : tilt angle of the panel (°)
- : ground albedo (in this study equal at the albedo of asphalt 0.12).
- : constant parameter (0.05)
- : angle of incidence between the module normal vector and the sunbeam vector (°).
- : angular losses coefficient (typical value for a monocrystalline silicon module is 0.17)
- : fitting parameter
- : fitting parameter (for ).
- : zenith angle
- , , , , : constants available for different PV cell types from Sandia National Laboratories [109].
3.5. Module Temperature Modeling
- : cell temperature (K)
- : ambient air temperature (K)
- : incident irradiance on the plane of array (W/m2)
- : constant heat transfer component (W/(m2K))
- : convective heat transfer component (Ws/(m3K))
- : wind speed (m/s).
3.6. DC/AC Inverter Model
- : nominal inverter efficiency
- : reference inverter efficiency (0.9637)
- and
- : DC power (W)
- : DC power limit of the inverter (W)
- and
3.7. PV Module Parameters
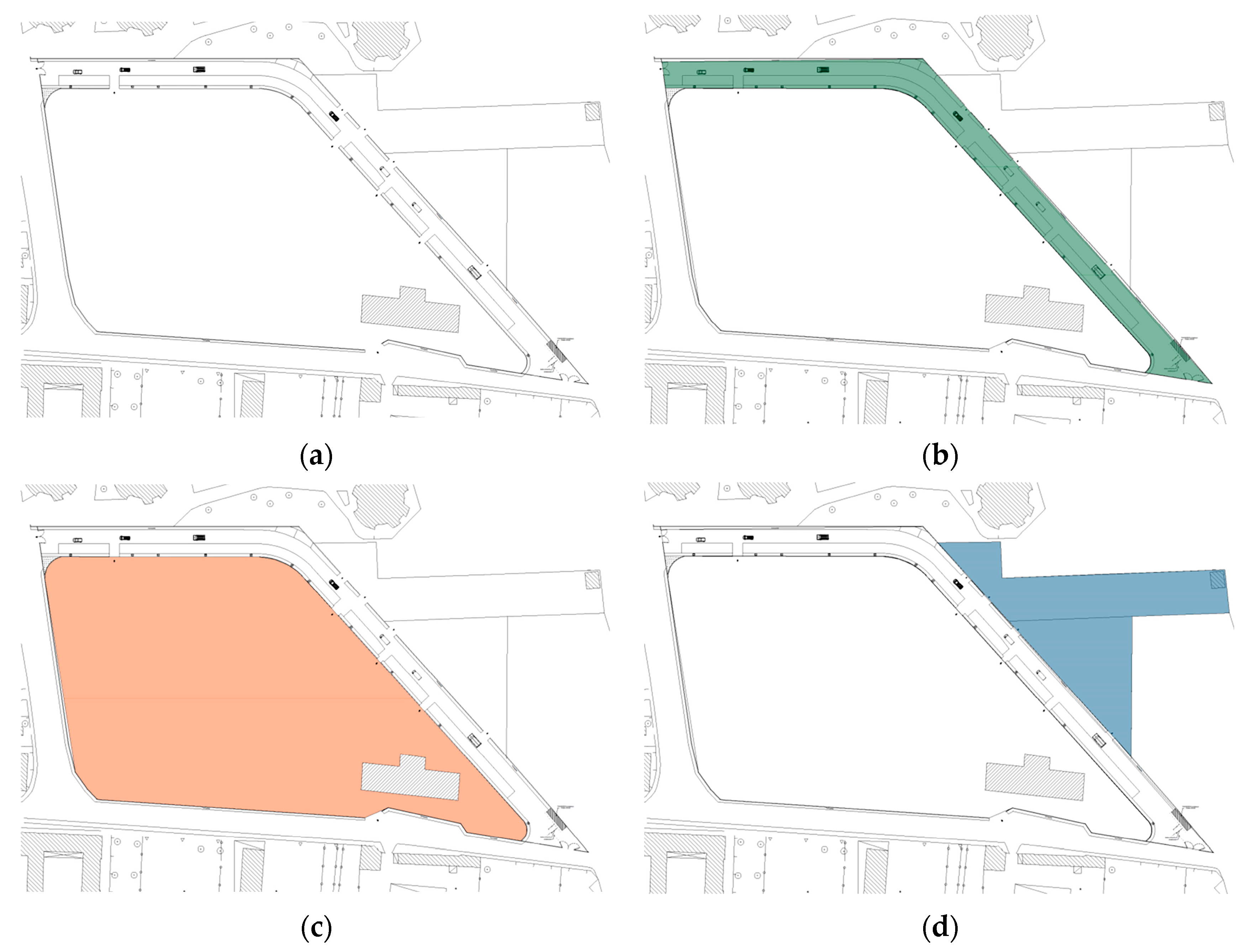
3.8. Case Study
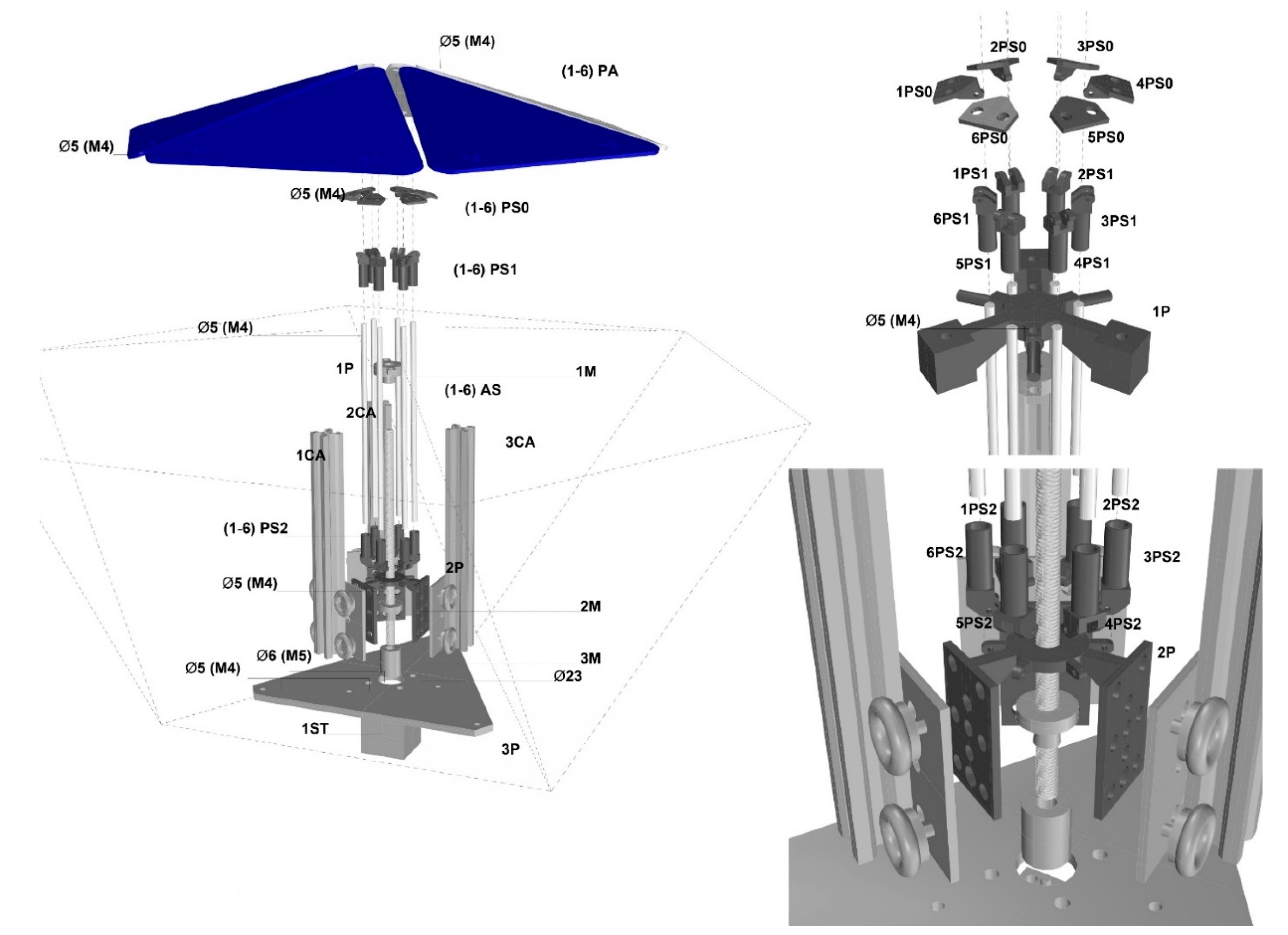
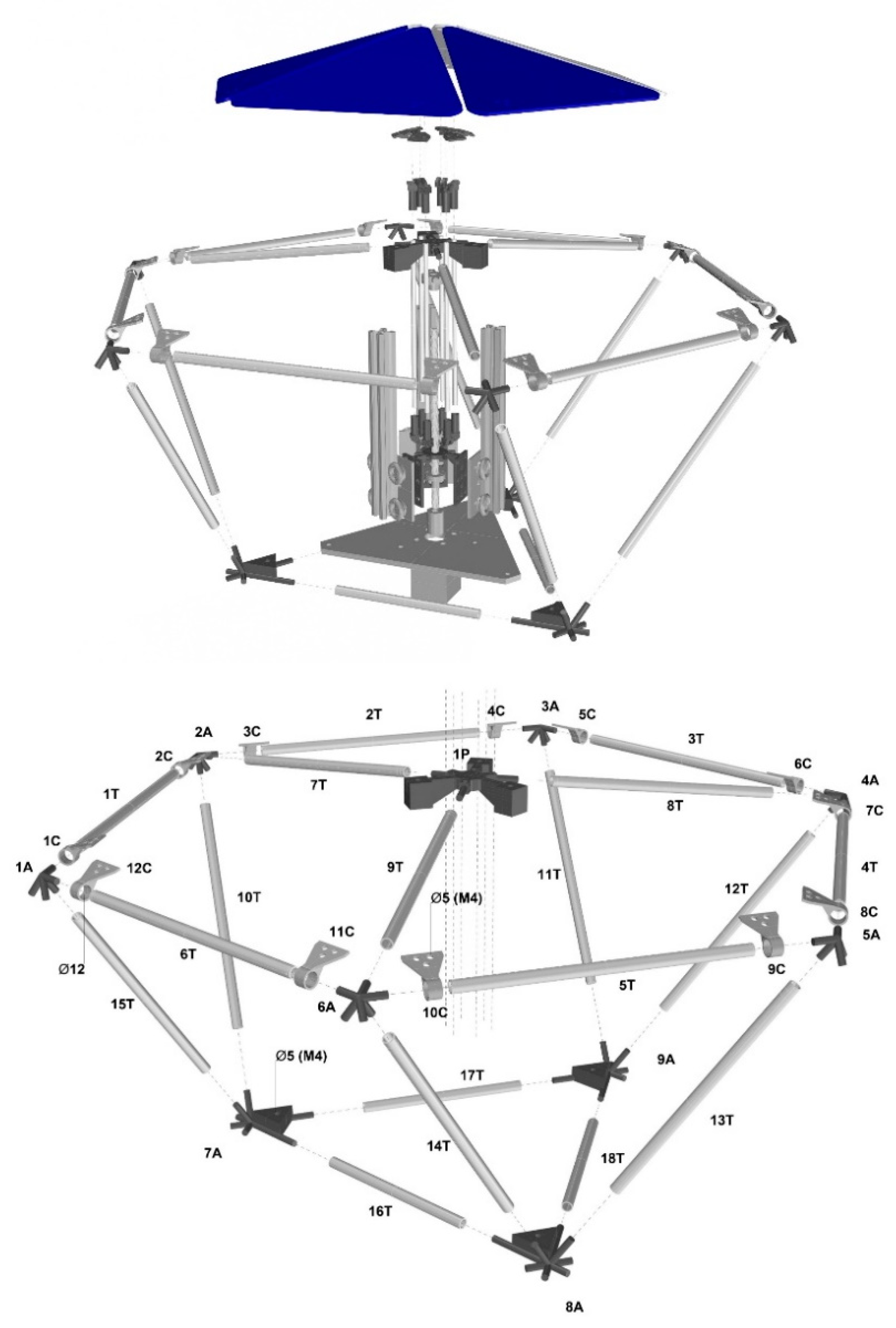
3.9. Prototype
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Acronyms | |
| BAPV | Building Applied Photovoltaic |
| BIPV | Building Integrated Photovoltaic |
| EPBD | Energy Performance of Buildings Directive |
| HVAC | Heating Ventilation and Air Conditioning |
| IPE | Interactive Prototyping Environment |
| KPI | Key Performance Indicator |
| MPPT | Maximum Power Point Tracking |
| nZEB | Nearly Zero Energy Building |
| NZEB | Net Zero Energy Building |
| POA | Plane of Array |
| PVSD | Photovoltaic Shading Device |
| PV | Photovoltaic |
| RES | Renewable Energy Sources |
| STC | Standard Test Conditions |
| TMY | Typical Meteorological Year |
| ZEB | Zero Energy Building |
| Parameters | |
| AC | Alternating current (A) |
| DC | Direct current (A) |
| DHI | Diffuse horizontal irradiance (W/m2) |
| DNI | Direct normal irradiance (W/m2) |
| GHI | Global horizontal irradiance (W/m2) |
References
- European Commission. Fit for 55—Delivering the EU’s 2030 Climate Target on the Way to Climate Neutrality; European Commission: Brussels, Belgium, 2021; p. 15. [Google Scholar]
- European Parliament. Regulation (eu) 2018/842 of the european parliament and of the council of 30 May 2018 on binding annual greenhouse gas emission reductions by Member States from 2021 to 2030 contributing to climate action to meet commitments under the Paris Agreement and amending Regulation (EU) No 525/2013 (Text with EEA relevance). Off. J. Eur. Union 2018, 156, 26–42. [Google Scholar]
- International Energy Agency (IEA). Buildings. A Source of Enormous Untapped Efficiency Potential. [Online]. Available online: https://www.iea.org/topics/buildings (accessed on 25 June 2023).
- Austin, M.C.; Solano, T.; Tejedor-Flores, N.; Quintero, V.; Boya, C.; Mora, D. Bio-inspired Approaches for Sustainable Cities Design in Tropical Climate. In Bionics and Sustainable Design; Palombini, F.L., Muthu, S.S., Eds.; Springer: Berlin/Heidelberg, Germany, 2022; pp. 333–365. [Google Scholar]
- Selvan, S.U.; Saroglou, S.T.; Mosca, F.; Tyc, J.; Joschinski, J.; Calbi, M.; Vogler, V.; Weisser, W.; Grobman, J.Y.; Barath, S. Multi-species Building Envelopes: Developing a multi-criteria design decision-making methodology for cohabitation. In Proceedings of the Human-Centric, Proceedings of the 28th International Conference of the Association for Computer-Aided Architectural Design Research in Asia (CAADRIA), Ahmedebad, India, 18 March 2023; pp. 645–654. [Google Scholar]
- Ciardiello, A.; Dell’Olmo, J.; Rosso, F.; Pastore, L.M.; Ferrero, M.; Salata, F. An Innovative Multi-objective Optimization Digital Workflow for Social Housing Deep Energy Renovation Design Process. In Technological Imagination in the Green and Digital Transition; Arbizzani, E., Cangelli, E., Clemente, C., Cumo, F., Giofrè, F., Giovenale, A.M., Palme, M., Paris, S., Eds.; Springer International Publishing: Berlin/Heidelberg, Germany, 2023; pp. 111–121. [Google Scholar]
- Gálvez, D.M.; Kerdan, I.G.; Carmona-Paredes, G. Assessing the Potential of Implementing a Solar-Based Distributed Energy System for a University Using the Campus Bus Stops. Energies 2022, 15, 3660. [Google Scholar] [CrossRef]
- Kalyan, S.; Sun, Q. Interrogating the Installation Gap and Potential of Solar Photovoltaic Systems Using GIS and Deep Learning. Energies 2022, 15, 3740. [Google Scholar] [CrossRef]
- Dong, J.; Jiang, Y.; Liu, D.; Dou, X.; Liu, Y.; Peng, S. Promoting dynamic pricing implementation considering policy incentives and electricity retailers’ behaviors: An evolutionary game model based on prospect theory. Energy Policy 2022, 167, 113059. [Google Scholar] [CrossRef]
- Barakat, S.; Ibrahim, H.; Elbaset, A.A. Multi-objective optimization of grid-connected PV-wind hybrid system considering reliability, cost, and environmental aspects. Sustain. Cities Soc. 2020, 60, 102178. [Google Scholar] [CrossRef]
- Sinha, S.; Chandel, S.S. Analysis of fixed tilt and sun tracking photovoltaic-micro wind based hybrid power systems. Energy Convers. Manag. 2016, 115, 265–275. [Google Scholar] [CrossRef]
- Calise, F.; Cappiello, F.L.; D’accadia, M.D.; Vicidomini, M. Dynamic modelling and thermoeconomic analysis of micro wind turbines and building integrated photovoltaic panels. Renew. Energy 2020, 160, 633–652. [Google Scholar] [CrossRef]
- Abdul-Ganiyu, S.; Quansah, D.A.; Ramde, E.W.; Seidu, R.; Adaramola, M.S. Techno-economic analysis of solar photovoltaic (PV) and solar photovoltaic thermal (PVT) systems using exergy analysis. Sustain. Energy Technol. Assess. 2021, 47, 101520. [Google Scholar] [CrossRef]
- Renno, C.; Petito, F.; D’agostino, D.; Minichiello, F. Modeling of a CPV/T-ORC Combined System Adopted for an Industrial User. Energies 2020, 13, 3476. [Google Scholar] [CrossRef]
- Bhat, R.; Begovic, M.; Kim, I.; Crittenden, J. Effects of PV on conventional generation. In Proceedings of the Annual Hawaii International Conference on System Sciences, Waikoloa, HI, USA, 6–9 January 2014; pp. 2380–2387. [Google Scholar]
- D’Agostino, D.; Minelli, F.; Minichiello, F. New genetic algorithm-based workflow for multi-objective optimization of Net Zero Energy Buildings integrating robustness assessment. Energy Build. 2023, 284, 112841. [Google Scholar] [CrossRef]
- Zarzavilla, M.; Quintero, A.; Abellán, M.A.; Serrano, F.L.; Austin, M.C.; Tejedor-Flores, N. Comparison of Environmental Impact Assessment Methods in the Assembly and Operation of Photovoltaic Power Plants: A Systematic Review in the Castilla—La Mancha Region. Energies 2022, 15, 1926. [Google Scholar] [CrossRef]
- D’Agostino, D.; Mazzella, S.; Minelli, F.; Minichiello, F. Obtaining the NZEB target by using photovoltaic systems on the roof for multi-storey buildings. Energy Build. 2022, 267, 112147. [Google Scholar] [CrossRef]
- D’Agostino, D.; Minelli, F.; D’Urso, M.; Minichiello, F. Fixed and tracking PV systems for Net Zero Energy Buildings: Comparison between yearly and monthly energy balance. Renew. Energy 2022, 195, 809–824. [Google Scholar] [CrossRef]
- Stadler, M.; Groissböck, M.; Cardoso, G.; Marnay, C. Optimizing Distributed Energy Resources and building retrofits with the strategic DER-CAModel. Appl. Energy 2014, 132, 557–567. [Google Scholar] [CrossRef]
- Almutairi, H.H.; Alajmi, A.F.; Ahmed, N.A. A techno-economic analysis of PV solar modules attached to vertical facades of a residential building in a hot arid climate. J. Eng. Res. 2022, 10, 108–123. [Google Scholar] [CrossRef]
- Kumar, N.M.; Sudhakar, K.; Samykano, M. Performance comparison of BAPV and BIPV systems with c-Si, CIS and CdTe photovoltaic technologies under tropical weather conditions. Case Stud. Therm. Eng. 2019, 13, 100374. [Google Scholar] [CrossRef]
- D’Agostino, P.; Minelli, F. Robustness Assessment of a Low Poly Modeling Strategy for Performance Simulation of Double-Skin Green Facades. In Proceedings of the ICGG 2020—Proceedings of the 19th International Conference on Geometry and Graphics—Advances in Intelligent Systems and Computing, São Paulo, Brazil, 9–13 August 2020; pp. 615–625. [Google Scholar]
- Nicoletti, F.; Carpino, C.; Cucumo, M.A.; Arcuri, N. The Control of Venetian Blinds: A Solution for Reduction of Energy Consumption Preserving Visual Comfort. Energies 2020, 13, 1731. [Google Scholar] [CrossRef]
- Bellia, L.; Diglio, F.; Fragliasso, F. Lighting Quality Self-assessment in Italian Home Offices. J. Daylighting 2022, 9, 177–196. [Google Scholar] [CrossRef]
- Badura, T.; Duchkov, H.; Horv, E. Urban Forestry & Urban Greening The value of the shading function of urban trees: A replacement cost approach. Urban For. Urban Green. 2021, 62, 127166. [Google Scholar]
- Nasrollahi, N.; Namazi, Y.; Taleghani, M. The effect of urban shading and canyon geometry on outdoor thermal comfort in hot climates: A case study of Ahvaz, Iran. Sustain. Cities Soc. 2020, 65, 102638. [Google Scholar] [CrossRef]
- Alawneh, R.; Ghazali, F.; Ali, H.; Sadullah, A.F. A Novel framework for integrating United Nations Sustainable Development Goals into sustainable non-residential building assessment and management in Jordan. Sustain. Cities Soc. 2019, 49, 101612. [Google Scholar] [CrossRef]
- De Soto, W.; Klein, S.; Beckman, W. Improvement and validation of a model for photovoltaic array performance. Sol. Energy 2006, 80, 78–88. [Google Scholar] [CrossRef]
- Faiman, D. Assessing the outdoor operating temperature of photovoltaic modules. Prog. Photovolt. Res. Appl. 2008, 16, 307–315. [Google Scholar] [CrossRef]
- ISO 15927-4:2005; Hygrothermal Performance of Buildings—Calculation and Presentation of Climatic Data—Part 4: Hourly Data for Assessing the Annual Energy Use for Heating and Cooling. ISO: Geneva, Switzerland, 2005.
- Huld, T.; Müller, R.; Gambardella, A. A new solar radiation database for estimating PV performance in Europe and Africa. Sol. Energy 2012, 86, 1803–1815. [Google Scholar] [CrossRef]
- Hernández-Callejo, L.; Gallardo-Saavedra, S.; Alonso-Gómez, V. A review of photovoltaic systems: Design, operation and maintenance. Solar Energy 2019, 188, 426–440. [Google Scholar] [CrossRef]
- Sinke, W.C. Development of photovoltaic technologies for global impact. Renew. Energy 2019, 138, 911–914. [Google Scholar] [CrossRef]
- Yaouba; Bajaj, M.; Welba, C.; Bernard, K.; Kitmo; Kamel, S.; El-Naggar, M.F. An Experimental and Case Study on the Evaluation of the Partial Shading Impact on PV Module Performance Operating Under the Sudano-Sahelian Climate of Cameroon. Front. Energy Res. 2022, 10, 1–13. [Google Scholar] [CrossRef]
- Aste, N.; Del Pero, C.; Leonforte, F. PV technologies performance comparison in temperate climates. Sol. Energy 2014, 109, 1–10. [Google Scholar] [CrossRef]
- Mussard, M. Solar energy under cold climatic conditions: A review. Renew. Sustain. Energy Rev. 2017, 74, 733–745. [Google Scholar] [CrossRef]
- Liu, F.; Bergh, J.C.V.D. Differences in CO2 emissions of solar PV production among technologies and regions: Application to China, EU and USA. Energy Policy 2020, 138, 111234. [Google Scholar] [CrossRef]
- Guzmán, A.B.; Vicencio, R.B.; Ardila-Rey, J.A.; Ahumada, E.N.; Araya, A.G.; Moreno, G.A. A Cost-Effective Methodology for Sizing Solar PV Systems for Existing Irrigation Facilities in Chile. Energies 2018, 11, 1853. [Google Scholar] [CrossRef]
- Skandalos, N.; Karamanis, D. An optimization approach to photovoltaic building integration towards low energy buildings in different climate zones. Appl. Energy 2021, 295, 117017. [Google Scholar] [CrossRef]
- Ciardiello, A.; Dell’Olmo, J.; Ferrero, M.; Pastore, L.M.; Rosso, F.; Salata, F. Energy Retrofit Optimization by Means of Genetic Algorithms as an Answer to Fuel Poverty Mitigation in Social Housing Buildings. Atmosphere 2023, 14, 1. [Google Scholar] [CrossRef]
- Luthander, R.; Widén, J.; Nilsson, D.; Palm, J. Photovoltaic self-consumption in buildings: A review. Appl. Energy 2015, 142, 80–94. [Google Scholar] [CrossRef]
- Erba, S.; Pagliano, L.; Shandiz, S.C.; Pietrobon, M. Energy consumption, thermal comfort and load match: Study of a monitored nearly Zero Energy Building in Mediterranean climate Energy consumption, thermal comfort and load match: Study of a monitored nearly Zero Energy Building in Mediterranean climate. IOP Conf. Ser. Mater. Sci. Eng. 2019, 609, 062026. [Google Scholar] [CrossRef]
- Erba, S.; Pagliano, L. Combining Sufficiency, Efficiency and Flexibility to Achieve Positive Energy Districts Targets. Energies 2021, 14, 4697. [Google Scholar] [CrossRef]
- Weniger, J.; Tjaden, T.; Quaschning, V. Sizing of Residential PV Battery Systems. Energy Procedia 2014, 46, 78–87. [Google Scholar] [CrossRef]
- Abdolmaleki, L.; Berardi, U. Comparative analysis among three solar energy-based systems with hydrogen and electrical battery storage in single houses. Energy Proc. 2021, 19, 321. [Google Scholar]
- Talent, O.; Du, H. Optimal sizing and energy scheduling of photovoltaic-battery systems under different tariff structures. Renew. Energy 2018, 129, 513–526. [Google Scholar] [CrossRef]
- Khatib, T.; Ibrahim, I.A.; Mohamed, A. A review on sizing methodologies of photovoltaic array and storage battery in a standalone photovoltaic system. Energy Convers. Manag. 2016, 120, 430–448. [Google Scholar] [CrossRef]
- Mason, K.; Reno, M.J.; Blakely, L.; Vejdan, S.; Grijalva, S. A deep neural network approach for behind-the-meter residential PV size, tilt and azimuth estimation. Solar Energy 2019, 196, 260–269. [Google Scholar] [CrossRef]
- Linssen, J.; Stenzel, P.; Fleer, J. Techno-economic analysis of photovoltaic battery systems and the influence of different consumer load profiles. Appl. Energy 2017, 185, 2019–2025. [Google Scholar] [CrossRef]
- Singh, R.; Kumar, S.; Gehlot, A.; Pachauri, R. An imperative role of sun trackers in photovoltaic technology: A review. Renew. Sustain. Energy Rev. 2018, 82, 3263–3278. [Google Scholar] [CrossRef]
- Racharla, S.; Rajan, K. Solar tracking system—A review. Int. J. Sustain. Eng. 2017, 10, 72–81. [Google Scholar]
- Awasthi, A.; Shukla, A.K.; Manohar, S.R.M.; Dondariya, C.; Shukla, K.N.; Porwal, D.; Richhariya, G. Review on sun tracking technology in solar PV system. Energy Rep. 2020, 6, 392–405. [Google Scholar] [CrossRef]
- Antonanzas, J.; Urraca, R.; Martinez-De-Pison, F.J.; Antonanzas, F. Optimal solar tracking strategy to increase irradiance in the plane of array under cloudy conditions: A study across Europe. Sol. Energy 2018, 163, 122–130. [Google Scholar] [CrossRef]
- Tina, G.M.; Gagliano, S.; Graditi, G.; Merola, A. Experimental validation of a probabilistic model for estimating the double axis PV tracking energy production. Appl. Energy 2012, 97, 990–998. [Google Scholar] [CrossRef]
- Sumathi, V.; Jayapragash, R.; Bakshi, A.; Akella, P.K. Solar tracking methods to maximize PV system output—A review of the methods adopted in recent decade. Renew. Sustain. Energy Rev. 2017, 74, 130–138. [Google Scholar] [CrossRef]
- Hafez, A.Z.; Yousef, A.M.; Harag, N.M. Solar tracking systems: Technologies and trackers drive types—A review. Renew. Sustain. Energy Rev. 2018, 91, 754–782. [Google Scholar] [CrossRef]
- Vieira, R.; Guerra, F.; Vale, M.; Araújo, M. Comparative performance analysis between static solar panels and single-axis tracking system on a hot climate region near to the equator. Renew. Sustain. Energy Rev. 2016, 64, 672–681. [Google Scholar] [CrossRef]
- Ruelas, J.; Muñoz, F.; Lucero, B.; Palomares, J. PV Tracking Design Methodology Based on an Orientation Efficiency Chart. Appl. Sci. 2019, 9, 894. [Google Scholar] [CrossRef]
- Lim, B.-H.; Lim, C.-S.; Li, H.; Hu, X.-L.; Chong, K.-K.; Zong, J.-L.; Kang, K.; Tan, W.-C. Industrial design and implementation of a large-scale dual-axis sun tracker with a vertical-axis-rotating-platform and multiple-row-elevation structures. Sol. Energy 2020, 199, 596–616. [Google Scholar] [CrossRef]
- Safan, Y.M.; Shaaban, S.; Abu El-Sebah, M.I. Performance evaluation of a multi-degree of freedom hybrid controlled dual axis solar tracking system. Sol. Energy 2018, 170, 576–585. [Google Scholar] [CrossRef]
- Hohne, P.; Kusakana, K.; Numbi, B. Model validation and economic dispatch of a dual axis pv tracking system connected to energy storage with grid connection: A case of a healthcare institution in South Africa. J. Energy Storage 2020, 32, 101986. [Google Scholar] [CrossRef]
- Muñoz-Cerón, E.; Lomas, J.C.; Aguilera, J.; de la Casa, J. Influence of Operation and Maintenance expenditures in the feasibility of photovoltaic projects: The case of a tracking pv plant in Spain. Energy Policy 2018, 121, 506–518. [Google Scholar] [CrossRef]
- Gonzalo, A.P.; Marugán, A.P.; Márquez, F.P.G. Survey of maintenance management for photovoltaic power systems. Renew. Sustain. Energy Rev. 2020, 134, 110347. [Google Scholar] [CrossRef]
- Jaysawal, R.K.; Chakraborty, S.; Elangovan, D.; Padmanaban, S. Concept of net zero energy buildings (NZEB) - A literature review. Clean. Eng. Technol. 2022, 11, 100582. [Google Scholar] [CrossRef]
- Curpek, J.; Cekon, M.; Hraska, J. PCM Integrated in BiPV Ventilated Facąde Concepts: Experimental Test Cell Platform and Initial Full-Scale Measurements. IOP Conf. Ser. Earth Environ. Sci. 2019, 290, 2019. [Google Scholar] [CrossRef]
- Čurpek, J.; Čekon, M. Building performance simulation of a photovoltaic façade enhanced with latent heat storage: Model validation and power generation prediction. J. Energy Storage 2022, 56, 106143. [Google Scholar] [CrossRef]
- Čurpek, J.; Čekon, M.; Šikula, O.; Slávik, R. Thermodynamic responses of adaptive mechanisms in BiPV façade systems coupled with latent thermal energy storage. Energy Build. 2023, 279, 112665. [Google Scholar] [CrossRef]
- Čurpek, J.; Čekon, M. Climate response of a BiPV façade system enhanced with latent PCM-based thermal energy storage. Renew. Energy 2020, 152, 368–384. [Google Scholar] [CrossRef]
- PØstergaard, P.A.; Duic, N.; Noorollahi, Y.; Mikulcic, H.; Kalogirou, S. Sustainable development using renewable energy technology. Renew. Energy 2020, 146, 2430–2437. [Google Scholar] [CrossRef]
- Shono, K.; Yamaguchi, Y.; Perwez, U.; Ma, T.; Dai, Y.; Shimoda, Y. Large-scale building-integrated photovoltaics installation on building façades: Hourly resolution analysis using commercial building stock in Tokyo, Japan. Sol. Energy 2023, 253, 137–153. [Google Scholar] [CrossRef]
- Zhang, X.; Lau, S.K.; Lau, S.S.Y.; Zhao, Y. Photovoltaic integrated shading devices (PVSDs): A review. Solar Energy 2018, 170, 947–968. [Google Scholar] [CrossRef]
- Settino, J.; Carpino, C.; Perrella, S.; Arcuri, N. Multi-Objective Analysis of a Fixed Solar Shading System in Different Climatic Areas. Energies 2020, 13, 3249. [Google Scholar] [CrossRef]
- Al-Masrani, S.M.; Al-Obaidi, K.M. Dynamic shading systems: A review of design parameters, platforms and evaluation strategies. Autom. Constr. 2019, 102, 195–216. [Google Scholar] [CrossRef]
- Kirimtat, A.; Tasgetiren, M.F.; Brida, P.; Krejcar, O. Control of PV integrated shading devices in buildings: A review. Build. Environ. 2022, 214, 108961. [Google Scholar] [CrossRef]
- Valladares-Rendón, L.G.; Schmid, G.; Lo, S.-L. Review on energy savings by solar control techniques and optimal building orientation for the strategic placement of façade shading systems. Energy Build. 2017, 140, 458–479. [Google Scholar] [CrossRef]
- Budhiyanto, A.; Suryabrata, J.A.; Saragih, S. Study of shading device building-integrated photovoltaic performance on energy saving. J. Urban Environ. Eng. 2017, 11, 202–208. [Google Scholar]
- Ibraheem, Y.; Piroozfar, P.; Farr, E.R.P.; Ravenscroft, N. Energy Production Analysis of Photovoltaic Shading Devices (PVSD) in Integrated Façade Systems (IFS). Front. Built Environ. 2020, 6, 1–12. [Google Scholar] [CrossRef]
- Luo, Y.; Zhang, L.; Liu, Z.; Xie, L.; Wang, X.; Wu, J. Experimental study and performance evaluation of a PV-blind embedded double skin façade in winter season. Energy 2018, 165, 326–342. [Google Scholar] [CrossRef]
- Baghoolizadeh, M.; Nadooshan, A.A.; Raisi, A.; Malekshah, E.H. The effect of photovoltaic shading with ideal tilt angle on the energy cost optimization of a building model in European cities. Energy Sustain. Dev. 2022, 71, 505–516. [Google Scholar] [CrossRef]
- Liu, J.; Bi, G.; Gao, G.; Zhao, L. Optimal design method for photovoltaic shading devices (PVSDs) by combining geometric optimization and adaptive control model. J. Build. Eng. 2023, 69, 106101. [Google Scholar] [CrossRef]
- Akbari Paydar, M. Optimum design of building integrated PV module as a movable shading device. Sustain. Cities Soc. 2020, 62, 102368. [Google Scholar] [CrossRef]
- Custódio, I.; Quevedo, T.; Melo, A.; Rüther, R. A holistic approach for assessing architectural integration quality of solar photovoltaic rooftops and shading devices. Sol. Energy 2022, 237, 432–446. [Google Scholar] [CrossRef]
- Mandalaki, M.; Papantoniou, S.; Tsoutsos, T. Assessment of energy production from photovoltaic modules integrated in typical shading devices. Sustain. Cities Soc. 2014, 10, 222–231. [Google Scholar] [CrossRef]
- Tedeschi, A. AAD_Algorithms-Aided Design. Parametric strategies using Grasshopper; Le Penseur: Potenza, Italy, 2018. [Google Scholar]
- Roudsari, M.S.; Pak, M. Ladybug: A parametric environmental plugin for grasshopper to help designers create an environmentally-conscious design. In Proceedings of the BS 2013: 13th Conference of the International Building Performance Simulation Association, Chambery, France, 25–28 August 2013; pp. 3128–3135. [Google Scholar]
- ASHRAE. International Weather files for Energy Calculations (IWEC weather files). User’s manual and CD-ROM; American Society of Heating, Refrigerating and Air-Conditioning Engineers: Atlanta, GA, USA, 2017. [Google Scholar]
- Jentsch, M.F.; James, P.A.B.; Bourikas, L.; Bahaj, A.B.S. Transforming existing weather data for worldwide locations to enable energy and building performance simulation under future climates. Renew. Energy 2013, 55, 514–524. [Google Scholar] [CrossRef]
- Firefly. Available online: http://www.fireflyexperiments.com (accessed on 25 June 2023).
- Arduino. Available online: http://arduino.cc/en/ (accessed on 25 June 2023).
- Duffie, J.A.; Beckman, W.A. Solar Engineering of Thermal Processes, 4th ed.; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2013. [Google Scholar]
- King, D.; Kratochvil, J.; Boyson, W.; Bower, W. Field Experience with a New Performance Characterization Procedure for Photovoltaic Arrays. In Proceedings of the 2nd World Conference and Exhibition on Photovoltaic Solar Energy Conversion, Vienna, Austria, 6–10 July 1998. [Google Scholar]
- Standard 93-77; Methods of Testing to Determine the Thermal Performance of Solar Collectors. ASHRAE: New York, NY, USA, 1977.
- Martin, N.; Ruiz, J.M. Calculation of the PV modules angular losses under field conditions by means of an analytical model. Sol. Energy Mater. Sol. Cells 2001, 70, 25–38. [Google Scholar] [CrossRef]
- Driesse, A.; Jain, P.; Harrison, S. Beyond the curves: Modeling the electrical efficiency of photovoltaic inverters. In Proceedings of the Conference Record of the IEEE Photovoltaic Specialists Conference, San Diego, CA, USA, 11–16 May 2008. [Google Scholar]
- Berardi, U.; Graham, J. Investigation of the impacts of microclimate on PV energy efficiency and outdoor thermal comfort. Sustain. Cities Soc. 2020, 62, 102402. [Google Scholar] [CrossRef]
- Freitas, J.d.S.; Cronemberger, J.; Soares, R.M.; Amorim, C.N.D. Modeling and assessing BIPV envelopes using parametric Rhinoceros plugins Grasshopper and Ladybug. Renew. Energy 2020, 160, 1468–1479. [Google Scholar] [CrossRef]
- Ibrahim, H.; Wagdy, A.; Beccarelli, P.; Carpenter, R.; Chilton, J. Applicability of Flexible Photovoltaic Modules onto Membrane Structures Using Grasshopper Integrative Model. Procedia Eng. 2016, 155, 379–387. [Google Scholar] [CrossRef]
- D’Agostino, P.; Minelli, F. Automated design process for cost-effective sustainable architecture. A performance based approach. Sustain. Mediterr. Constr. 2020, 11, 111–116. [Google Scholar]
- Hamid, Y.S.; Rahim, N.N.A. Optimization on Geometry Design of Double-Layer Space Trusses. In Proceedings of the 5th International Conference on Sustainable Civil Engineering Structures and Construction Materials; Springer Nature: Singapore, 2022; pp. 895–910. [Google Scholar]
- Formisano, A.; Mazzolani, F.M. Numerical Investigation of a New Aluminium Alloy Reticular Space Structure. In Proceedings of the Ninth International Conference on Computational Structures Technology, Athens, Greece, 2–5 September 2008. [Google Scholar]
- Bakhshi, R.; Sadeh, J.; Mosaddegh, H.R. Optimal economic designing of grid-connected photovoltaic systems with multiple inverters using linear and nonlinear module models based on Genetic Algorithm. Renew. Energy 2014, 72, 386–394. [Google Scholar] [CrossRef]
- Urraca, R.; Huld, T.; Lindfors, A.V.; Riihelä, A.; Martinez-de-Pison, F.J.; Sanz-Garcia, A. Quantifying the amplified bias of PV system simulations due to uncertainties in solar radiation estimates. Sol. Energy 2018, 176, 663–677. [Google Scholar] [CrossRef]
- Huld, T.; Súri, M.; Dunlop, E.D.; Albuisson, M.; Wald, L. Integration of HELIOCLIM-1 Database Into PV-GIS to Estimate Solar Electricity Potential in Africa. In Proceedings of the 20th European Photovoltaic Solar Energy Conference and Exhibition, Barcelona, Spain, 6–10 June 2005; p. 2989. [Google Scholar]
- Psiloglou, B.E.; Kambezidis, H.D.; Kaskaoutis, D.G.; Karagiannis, D.; Polo, J.M. Comparison between MRM simulations, CAMS and PVGIS databases with measured solar radiation components at the Methoni station, Greece. Renew. Energy 2020, 146, 1372–1391. [Google Scholar] [CrossRef]
- Huld, T.; Paietta, E.; Zangheri, P.; Pascua, I.P. Assembling Typical Meteorological Year Data Sets for Building Energy Performance Using Reanalysis and Satellite-Based Data. Atmosphere 2018, 9, 53. [Google Scholar] [CrossRef]
- Sumathi, S.; Kumar, L.A.; Surekha, P. Models Used to Assess the Performance of Solar PV Systems. In Solar PV and Wind Energy Conversion Systems, Green Energy and Technology; Springer: Berlin/Heidelberg, Germany, 2015; pp. 651–790. [Google Scholar]
- Ramalingam, K.; Indulkar, C. Solar Energy and Photovoltaic Technology; Elsevier Inc.: Amsterdam, The Netherlands, 2017. [Google Scholar]
- Sandia National Laboratories. Available online: https://www.sandia.gov/ (accessed on 25 June 2023).
- Hottel, H.; Whillier, A. Evaluation of flat plate collector performance. In Transactions of the Conference on the Use of Solar Energy; University of Arizona Press: Tucson, AZ, USA, 1955; Volume 2, p. 74. [Google Scholar]
- Li, W.; Zhang, G.; Pan, T.; Zhang, Z.; Geng, Y.; Wang, J. A Lipschitz Optimization-Based MPPT Algorithm for Photovoltaic System under Partial Shading Condition. IEEE Access 2019, 7, 126323–126333. [Google Scholar] [CrossRef]
- Kitmo; Djidimbélé, R.; Kidmo, D.K.; Tchaya, G.B.; Djongyang, N. Optimization of the power flow of photovoltaic generators in electrical networks by MPPT algorithm and parallel active filters. Energy Rep. 2021, 7, 491–505. [Google Scholar] [CrossRef]
- Dey, A.K.; Sohn, T.; Streng, S.; Kodama, J. iCAP: Interactive Prototyping of Context-Aware Applications. In Proceedings of the Pervasive Computing, Pervasive 2006, Lecture Notes in Computer Science, Sydney, Australia, 19–22 May 2006; pp. 254–271. [Google Scholar]
- Ultimaker Cura. Available online: https://ultimaker.com/ (accessed on 25 June 2023).
- Besagni, G.; Vilà, L.P.; Borgarello, M. Italian household load profiles: A monitoring campaign. Buildings 2020, 10, 217. [Google Scholar] [CrossRef]
- Guarino, F.; Cassarà, P.; Longo, S.; Cellura, M.; Ferro, E. Load match optimisation of a residential building case study: A cross-entropy based electricity storage sizing algorithm. Appl. Energy 2015, 154, 380–391. [Google Scholar] [CrossRef]
- Cao, S.; Hasan, A.; Sirén, K. On-site energy matching indices for buildings with energy conversion, storage and hybrid grid connections. Energy Build. 2013, 64, 423–438. [Google Scholar] [CrossRef]
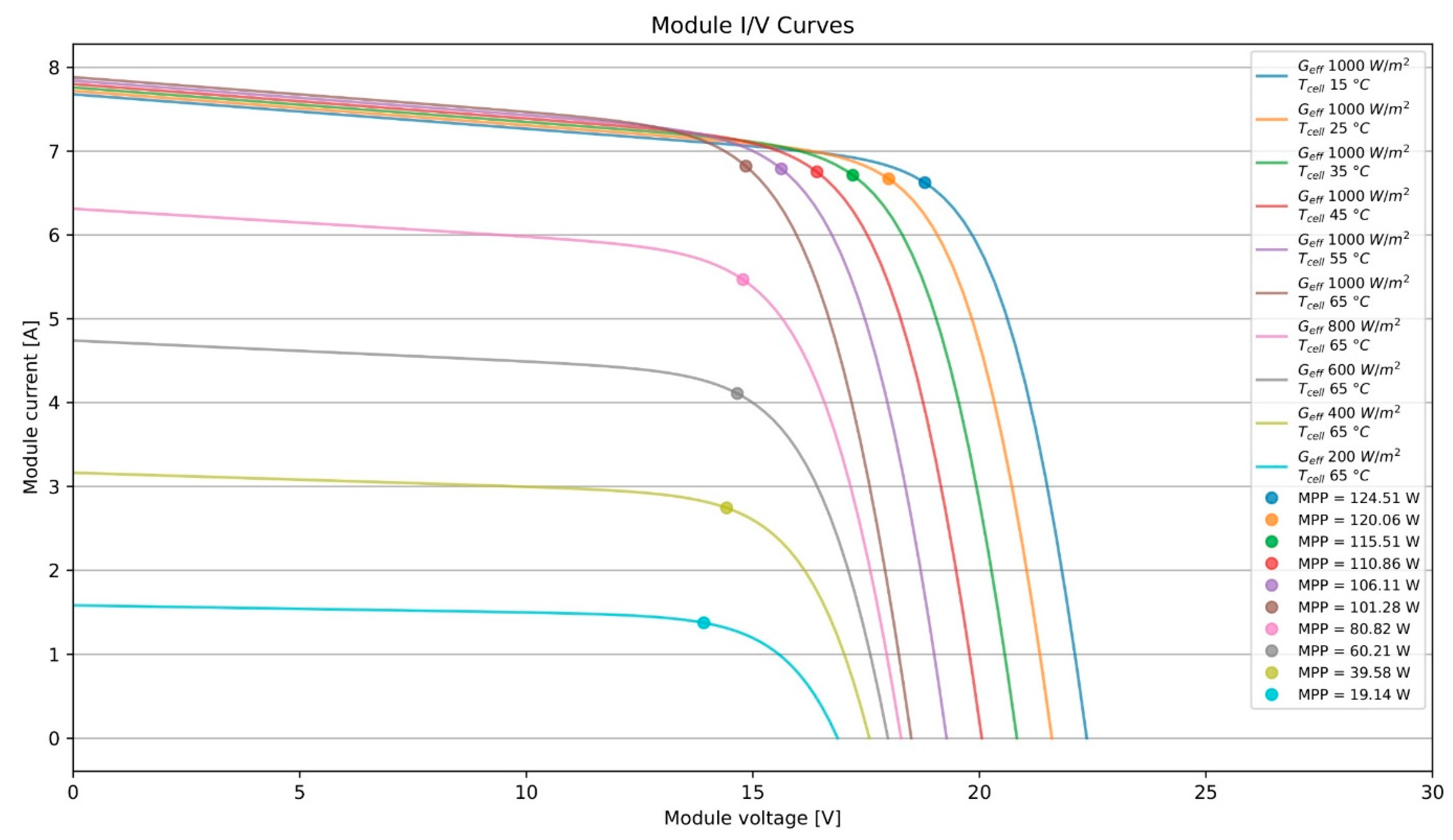







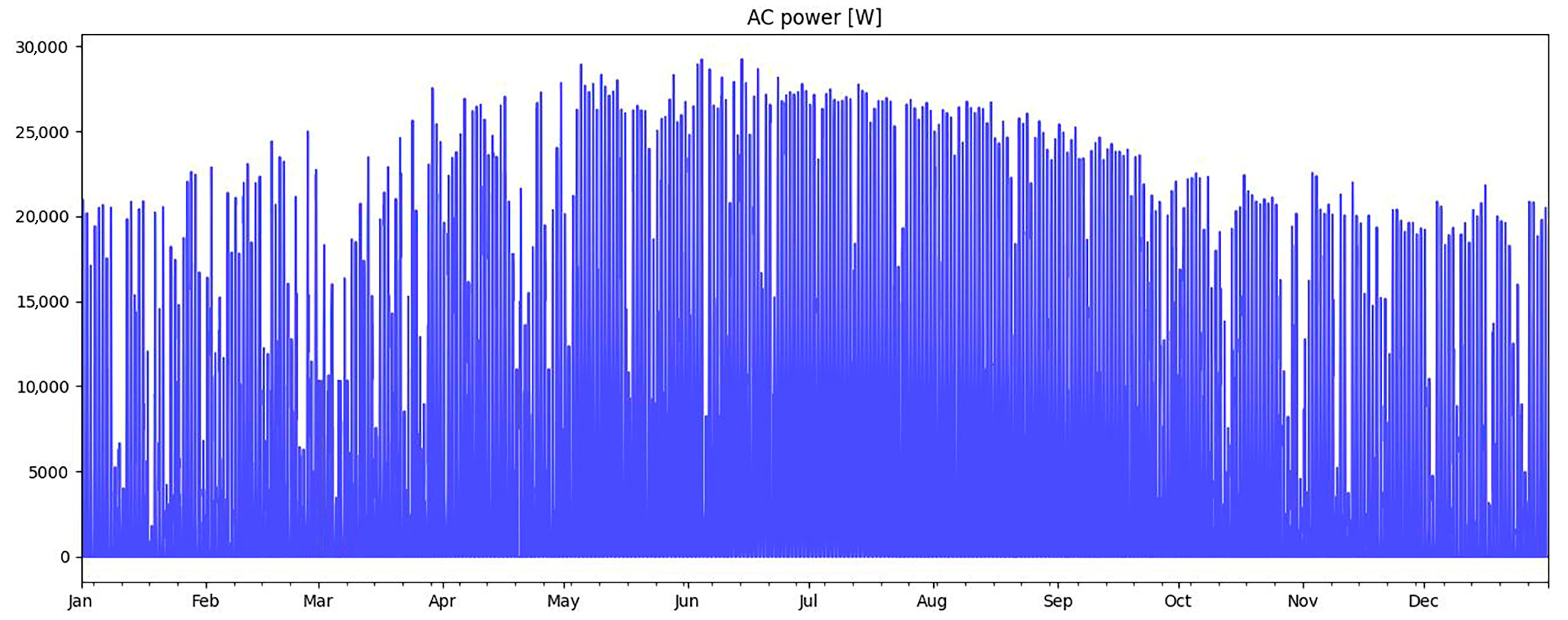
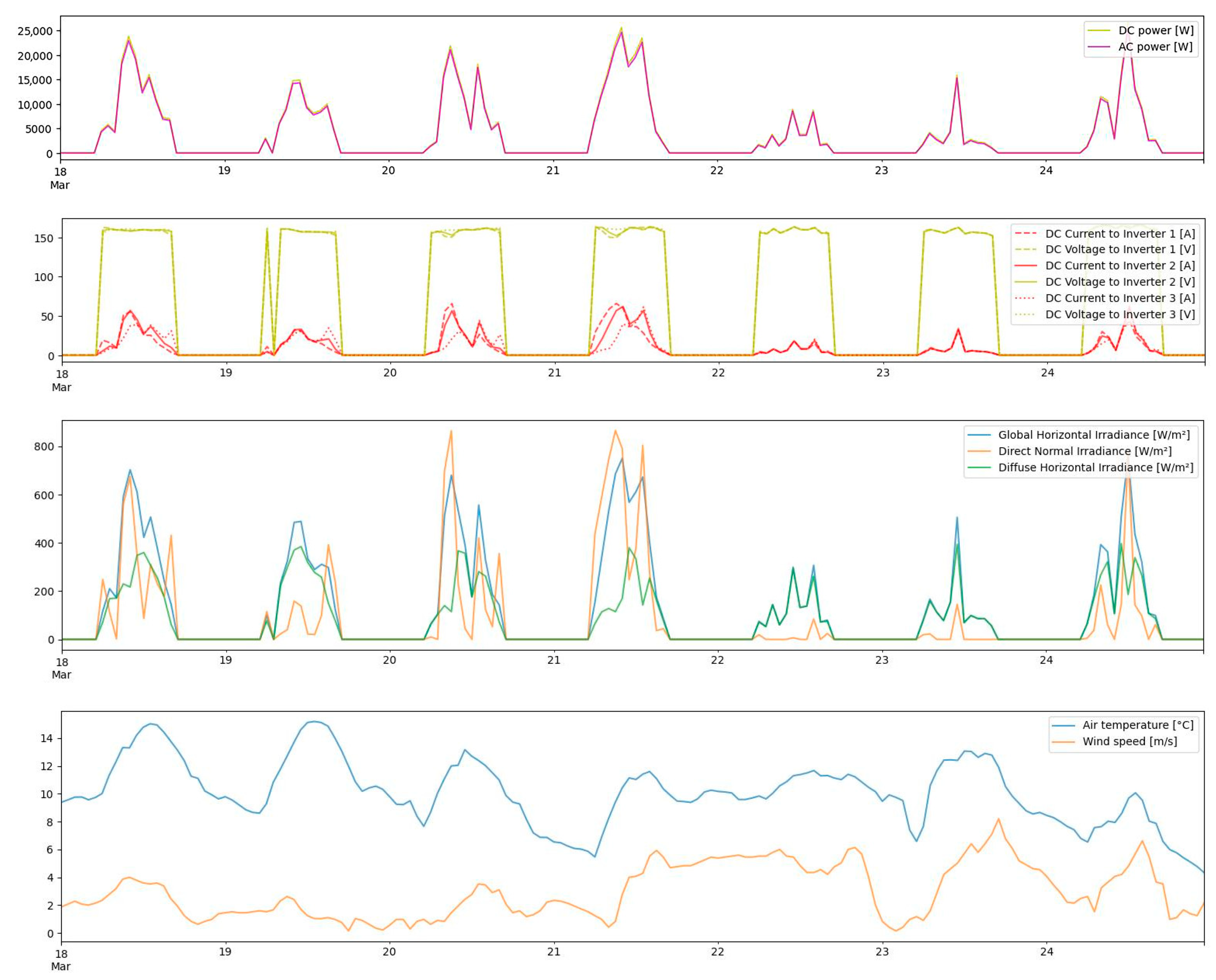
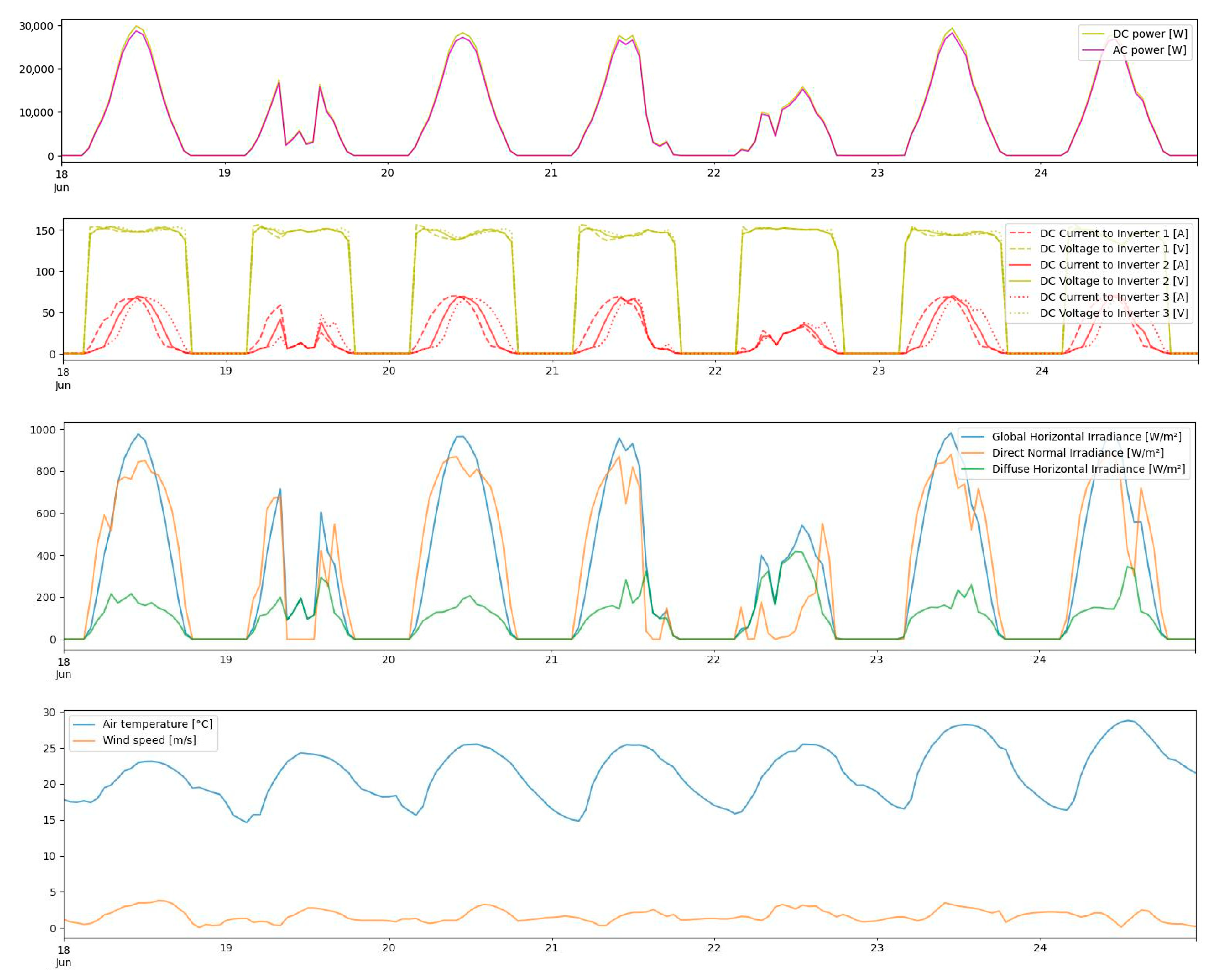

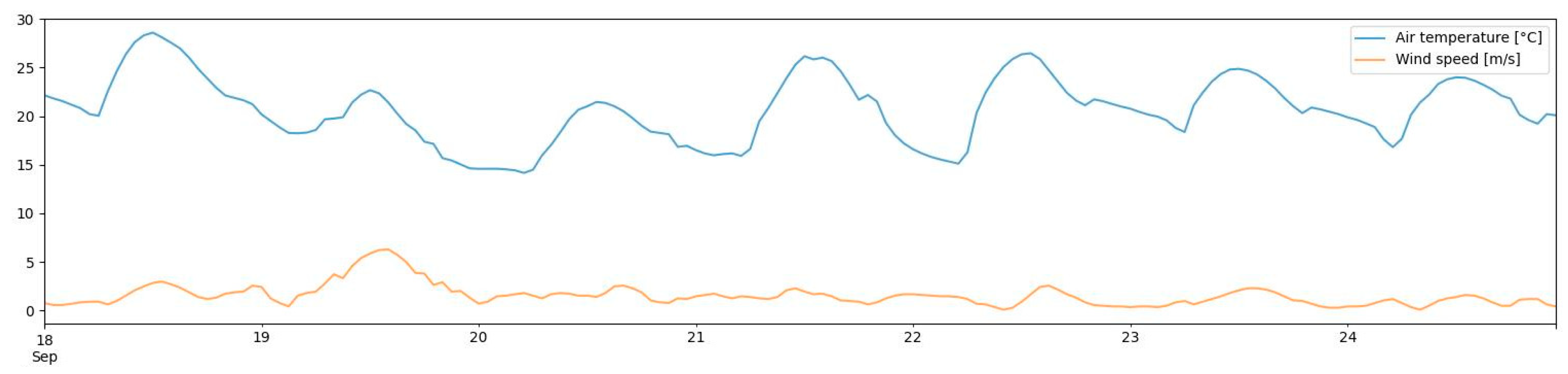
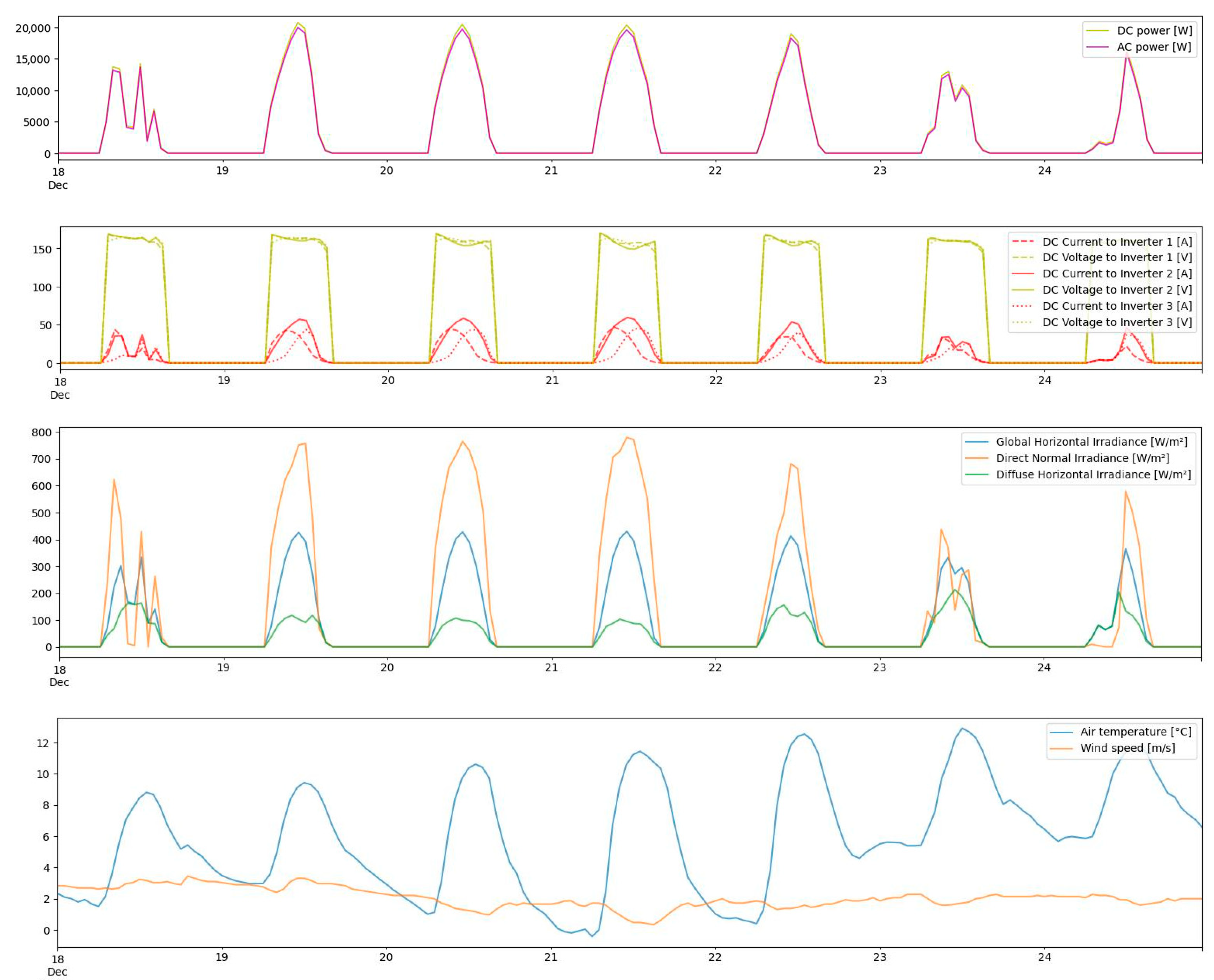
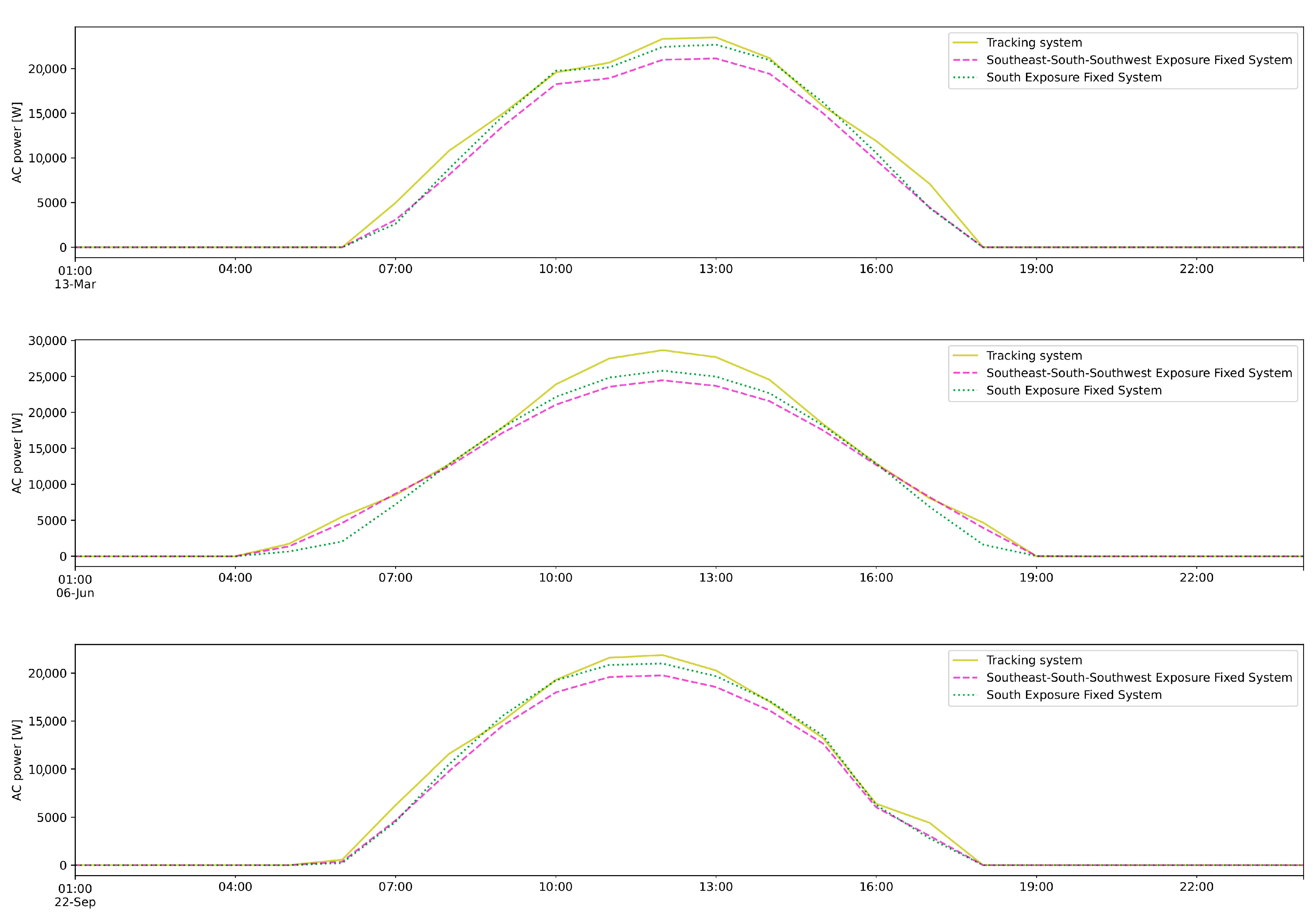
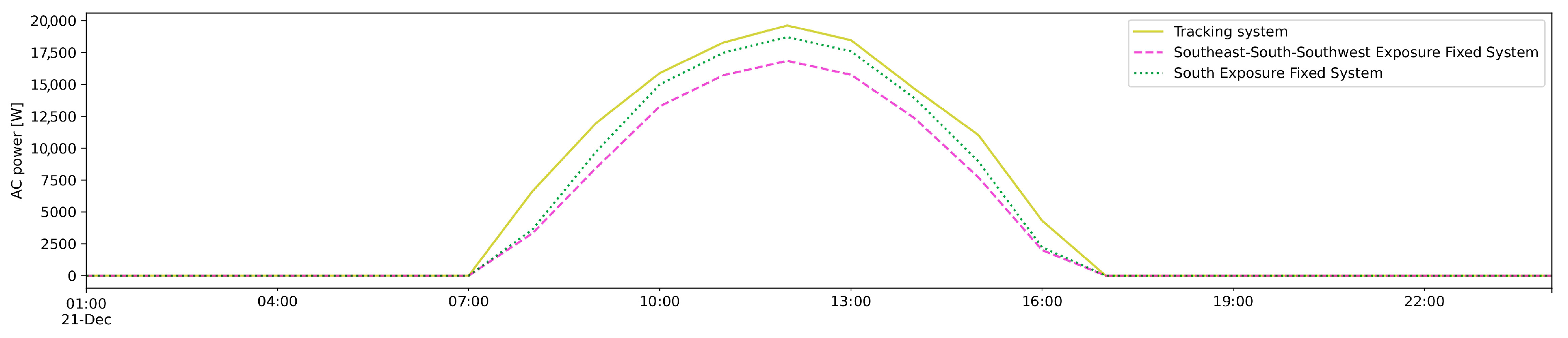
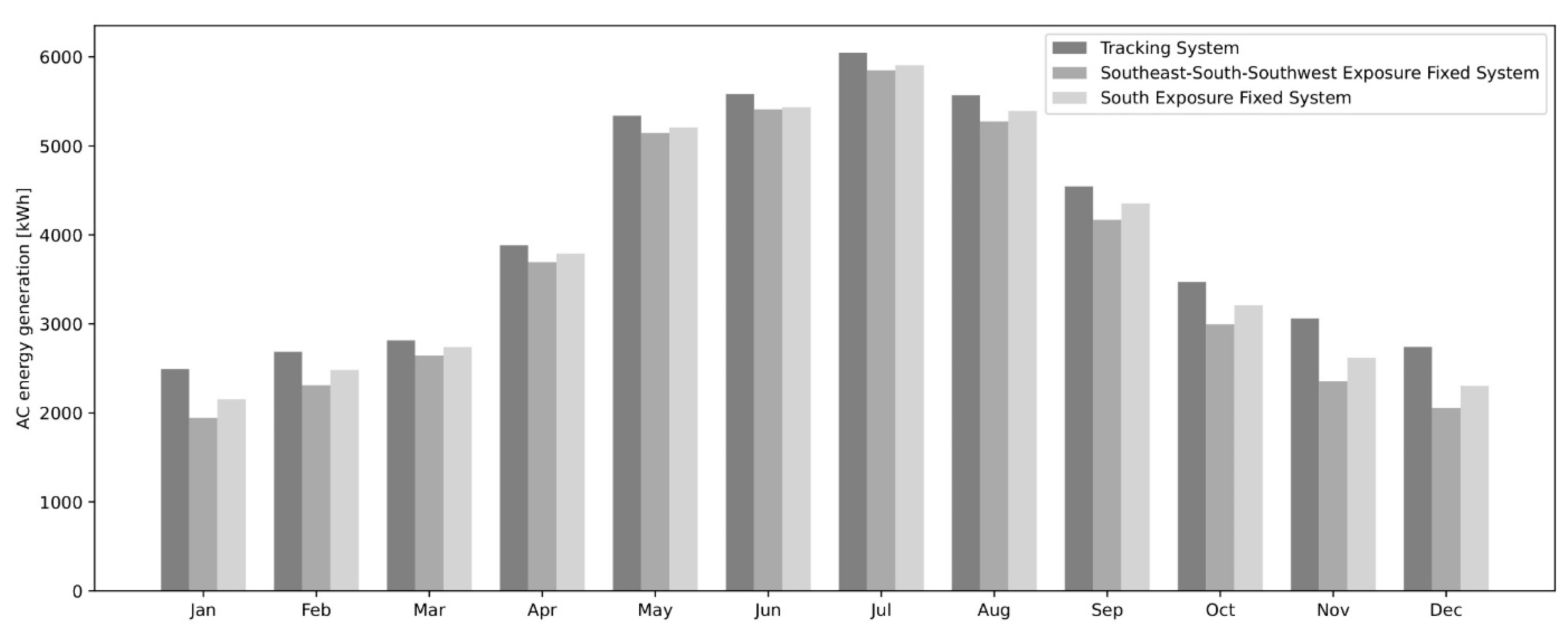


| PV Module Manufacturer Parameters | |
|---|---|
| Cell Type | Monocrystalline Silicon |
| Maximum power (PMAX) (W) | 120 |
| Voltage at maximum power point (VMPP) (V) | 18 |
| Current at maximum power point (IMPP) (A) | 6.67 |
| Open circuit voltage (VOC) (V) | 21.6 |
| Short circuit current (ISC) (A) | 7.72 |
| Temperature coefficient of ISC (%/°C) | 0.035 |
| Temperature coefficient of VOC (%/°C) | 0.37 |
| Cells in series | 4 × 9 |
| STC cell temperature (°C) | 25 |
| STC irradiance (W/m2) | 1000 |
| STC air mass | 1.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Minelli, F.; D’Agostino, D.; Migliozzi, M.; Minichiello, F.; D’Agostino, P. PhloVer: A Modular and Integrated Tracking Photovoltaic Shading Device for Sustainable Large Urban Spaces—Preliminary Study and Prototyping. Energies 2023, 16, 5786. https://doi.org/10.3390/en16155786
Minelli F, D’Agostino D, Migliozzi M, Minichiello F, D’Agostino P. PhloVer: A Modular and Integrated Tracking Photovoltaic Shading Device for Sustainable Large Urban Spaces—Preliminary Study and Prototyping. Energies. 2023; 16(15):5786. https://doi.org/10.3390/en16155786
Chicago/Turabian StyleMinelli, Federico, Diana D’Agostino, Maria Migliozzi, Francesco Minichiello, and Pierpaolo D’Agostino. 2023. "PhloVer: A Modular and Integrated Tracking Photovoltaic Shading Device for Sustainable Large Urban Spaces—Preliminary Study and Prototyping" Energies 16, no. 15: 5786. https://doi.org/10.3390/en16155786
APA StyleMinelli, F., D’Agostino, D., Migliozzi, M., Minichiello, F., & D’Agostino, P. (2023). PhloVer: A Modular and Integrated Tracking Photovoltaic Shading Device for Sustainable Large Urban Spaces—Preliminary Study and Prototyping. Energies, 16(15), 5786. https://doi.org/10.3390/en16155786









