Performance Analysis of Solar Tracking Systems by Five-Position Angles with a Single Axis and Dual Axis
Abstract
:1. Introduction
2. Theory of Solar Radiation
- Latitude (L) is the angle north or south of the equator when measured to the north; positive and negative when measured to the south, ranging from −90 to 90 degrees;
- The hour angle (h) represents the position of the Sun from the local meridian to the east or west. It is negative before the solar-noon period and positive after the solar-noon period, with a value of 15 degrees per hour;
- The declination angle () is the angle between the Sun’s rays in the solar-noon period and the equatorial plane. It is assigned a positive value when measuring north and a negative value when measuring south. The declination angle changes daily between −23.45 and 23.45 degrees. It can be calculated from Equation (1) [17].
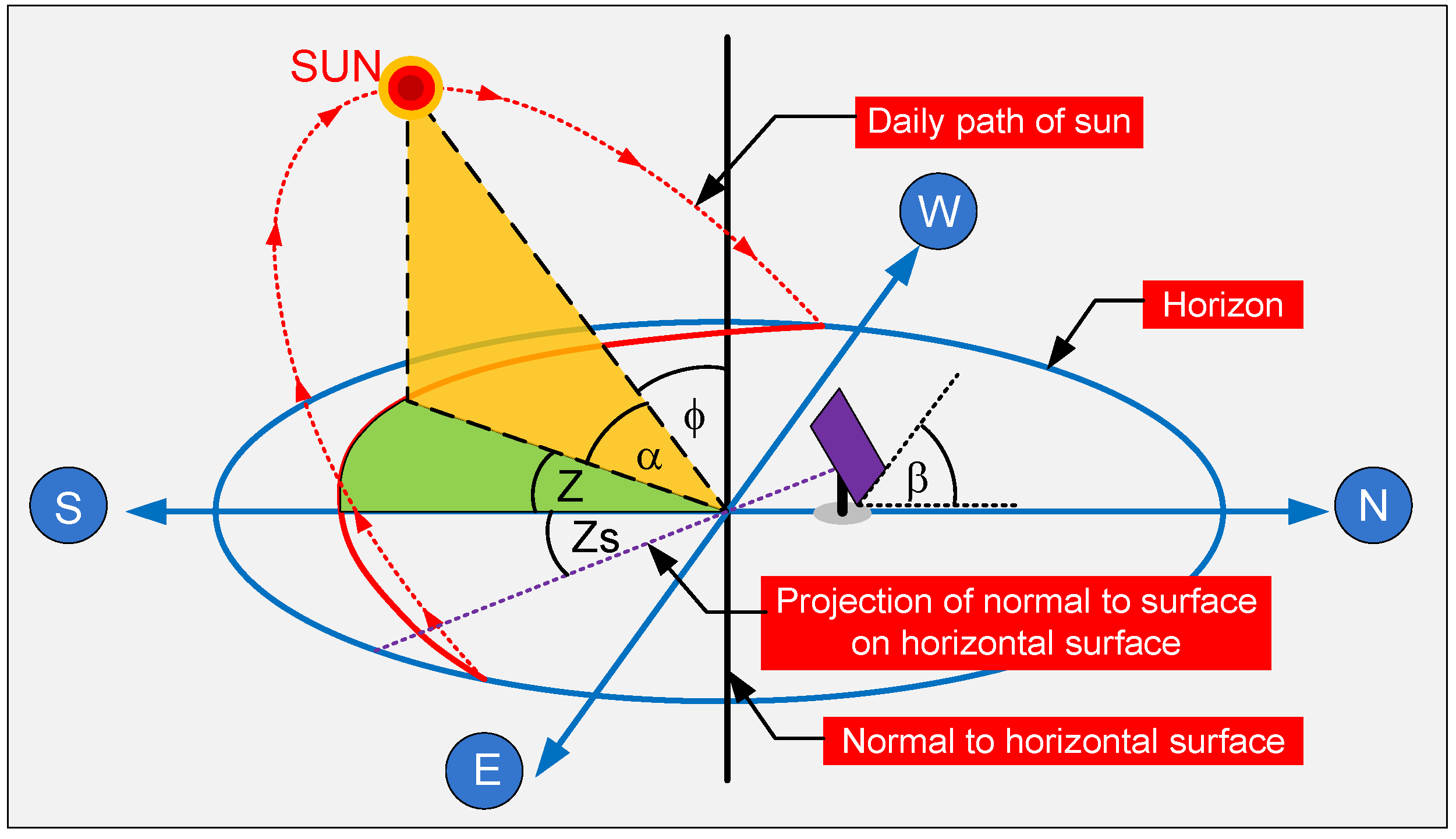
- The solar altitude angle (a) is the angle between the Earth’s plane and the direct solar rays. The solar zenith angle (F) is the angle between natural and vertical solar radiation, as shown in Equation (2) [17].
- The surface azimuth angle (Zs) is the angle between the south and the facing direction of the solar panel. It ranges from −180 to 180 degrees, and is zero, positive, or negative when the direction of the solar panel faces south, west, and east, respectively. Furthermore, b refers to the surface tilt angle from the horizontal plane.
- The solar azimuth angle (Z) is the angle between the Sun’s vertical plane and the local meridian plane. The solar azimuth angle ranges from −180 to 180 degrees. The reference of the solar azimuth angle at the south (true south) is zero, while the south-to-west and south-to-east are positive and negative, respectively. It can be given as Equation (3) [17].
3. Design and Experimental Setup
- I.
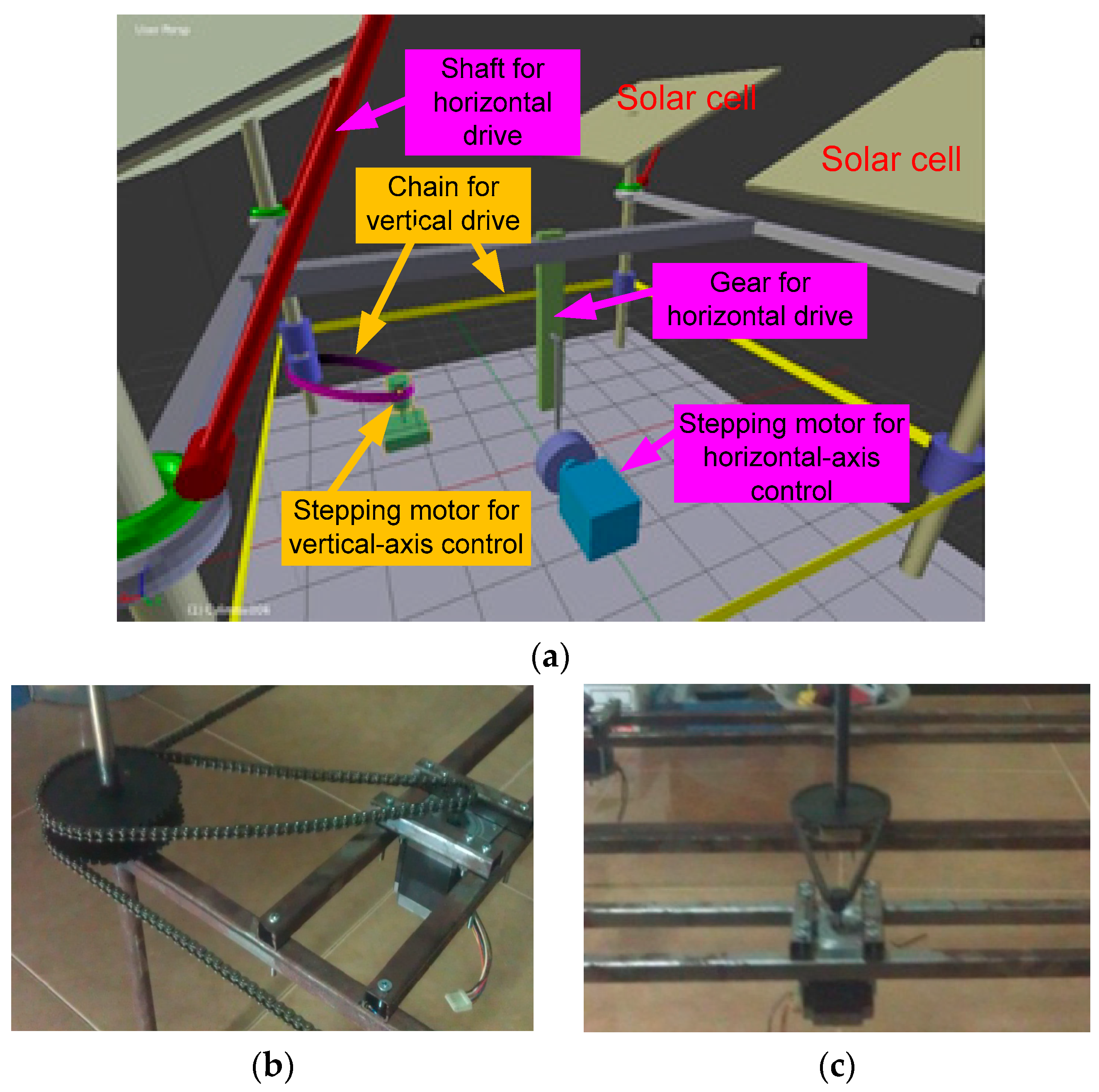
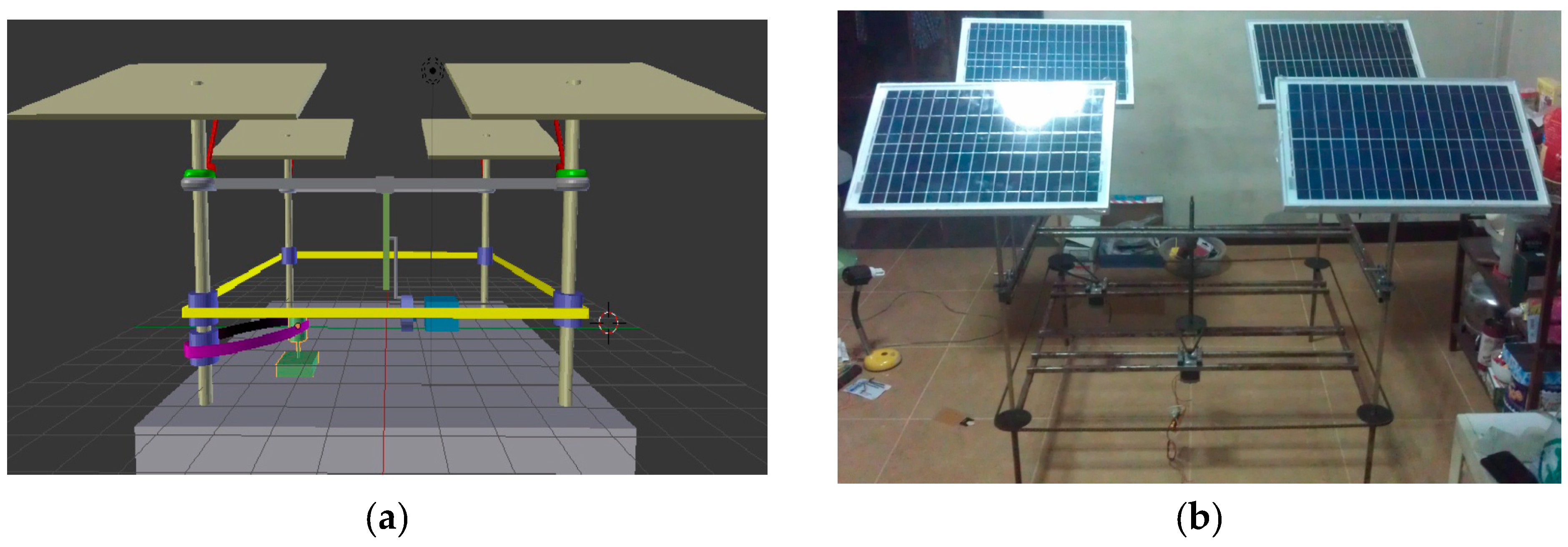
- The structural design comprises four 10 W solar panels and two stepping motors, model syn 103h7124-1011, installed vertically and horizontally to drive the four solar panels moving together, as shown in Figure 3. All four solar panels are moved simultaneously using a chain and gear drive system for both vertical and horizontal axis movement, described as follows [11,22,23]:
- Vertical axis movement uses the stepping motor (green motor in Figure 3a) to drive and transmit power through purple chains and the blue gear. The four rods with solar panels are installed on top, and the blue gears are wrapped around them with yellow chains. When the stepping motor is running, the purple chain mounted on the stepping motor drives the four blue gears mounted on each rod, with the four rods moving simultaneously, as shown in Figure 4.
- Horizontal axis movement uses the stepping motor (blue motor in Figure 3a) to drive the crankshaft system which in turn drives the gray beams for the up-and-down movement of the solar panel. The red shaft is installed with solar panels and a ball-rolling rod. When the gray beams are raised, the red shafts move at a different angle, resulting in the solar panels tilting along the horizontal axis, as shown in Figure 4.
- II.
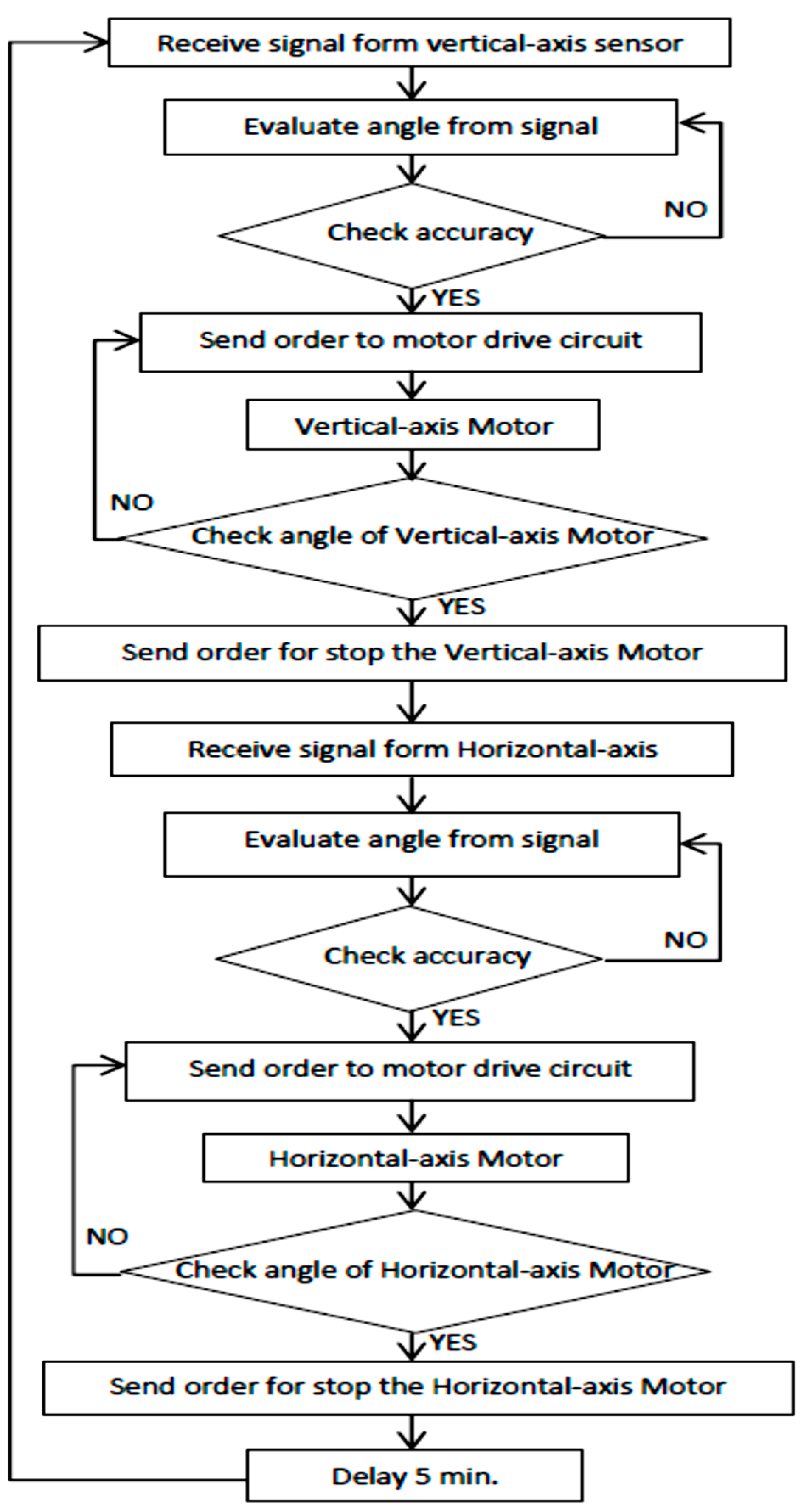
- The control system for both stepping motors to drive the solar panel was designed using an Arduino microcontroller (ET-EASY MEGA 1280). The key component is the vertical and horizontal light receiver circuit, which uses an LDR device for receiving light to control the motion of the motor, processed by a microcontroller [24,25]. The design details of the light-receiving circuit are as follows:
- The vertical light-receiving circuit causes the solar panels to move. The LDR is installed on all four sides of the light-receiving-circuit box in positions V1, V2, V3, and V4. When the LDR is exposed to sunlight, its resistance is lower, as shown in Figure 5.

- b.
- The horizontal light-receiving circuit is used for the horizontal movement of the solar panel. The design shows the LDR installed in all four positions (H1, H2, H3, and H4) on top of the light-receiving circuit box. Between H1, H2, H3, and H4, there is a shading shield in the middle, separating the LDR into two sets, although all LDR light detection operates independently. Figure 6 shows the operation of the microcontroller when the LDR sends the signal for the horizontal movement of five positions (30, 60, 90, 120, and 150 degrees). At sunrise, the H1 and H2 of the LDR can detect the angle between 0 and 45 degrees horizontally with the Earth and send the signal to the microcontroller to adjust the horizontal axis to 30 degrees. When the Sun rises at an angle horizontal to the Earth between 45 and 75 degrees, H1, H2, and H4 can be detected, sending the signal to the microcontroller to adjust the horizontal axis to 45 degrees. The solar panel is perpendicular to the Earth when all horizontal LDRs (H1, H2, H3, and H4) are detected. Likewise, 120 and 150 degrees of the horizontal axis show LDR detection from the operation table presented in Figure 6. However, when all horizontal LDRs (H1, H2, H3, and H4) cannot detect sunlight, the horizontal axis does not move [25].
4. Results and Discussion
4.1. Part A. Analysis of the Energy in Each System
4.2. Part B. Analysis of the Relationship between Irradiation and Tracking Angles
4.3. Part C. Analysis of the Sun-Tracking System
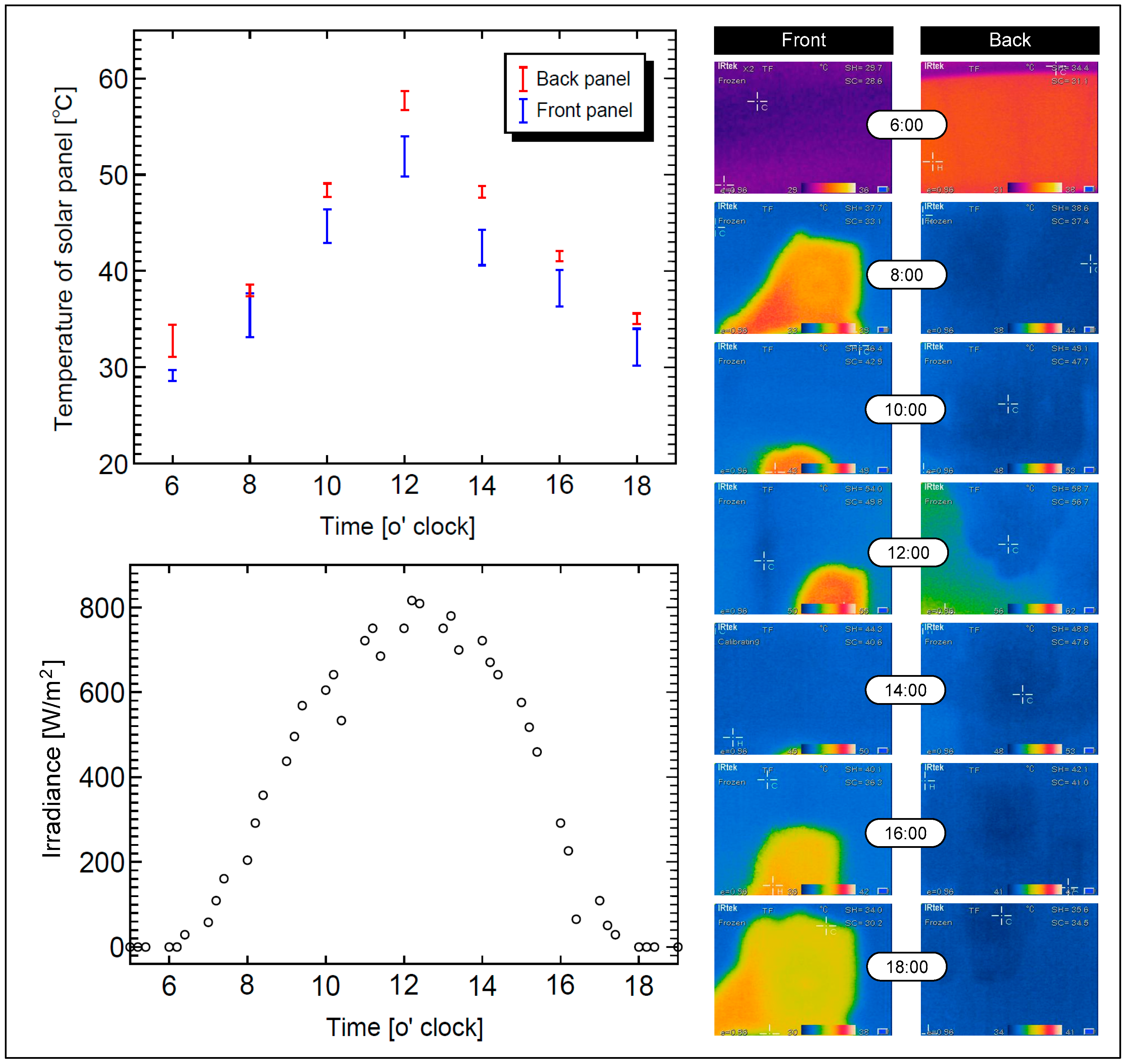
4.4. Part D. Analysis of the Solar Panel Temperature
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Al-Amin, M.; Chowdhury, N.B.; Rabby, F.; Banik, S.C.; Islam, Z. Study of Construction and Analysis of a vehicle using Solar energy with Solar Tracking System. Int. J. Nov. Res. Electr. Mech. Eng. 2014, 1, 44–50. [Google Scholar]
- Sharma, C.; Sharma, A.K.; Mullick, S.C.; Kandpal, T.C. Assessment of solar thermal power generation potential in India. Renew. Sustain. Energy Rev. 2015, 42, 902–912. [Google Scholar] [CrossRef]
- Charafeddine, K.; Tsyruk, S. Automatic Sun-Tracking System. In Proceedings of the 2020 International Russian Automation Conference (RusAutoCon), Sochi, Russia, 29 September 2020. [Google Scholar]
- Kumar, V.S.S.; Suryanarayana, S. Automatic Dual Axis Sun Tracking System using LDR Sensor. Int. J. Curr. Eng. Technol. 2014, 4, 3214–3217. [Google Scholar] [CrossRef] [Green Version]
- Thungsuk, N.; Mungkung, N.; Tanaram, T.; Chaithanakulwat, A.; Arunrungsusmi, S.; Poonthong, W.; Songruk, A.; Tunlasakun, K.; Chunkul, C.; Tanitteerapan, T.; et al. The Characterization Analysis of the Oil-Immersed Transformers Obtained by Area Elimination Method Design. Appl. Sci. 2022, 12, 3970. [Google Scholar] [CrossRef]
- Theraja, B.L.; Theraja, A.K. A Text Book of Electrical Technology; AC & DC Machines in S.I: New Delhi, India; Volume 2.
- Wang, Q.; Zhang, J.; Hu, R.; Shao, Y. Automatic Two Axes Sun-Tracking System Applied to Photovoltaic System for LED Street Light. Appl. Mech. Mater. 2010, 43, 17–20. [Google Scholar] [CrossRef]
- Ponciano, V.D.F.G.; Ponciano, I.D.M.; Alves, D.G.; Saretta, E.; Coelho, R.D. Conversion of solar photovoltaic energy into hydraulic energy applied to irrigation systems using a manual sun tracking. Irrig. Drain. 2020, 25, 508–520. [Google Scholar] [CrossRef]
- Rizi, A.P.; Ashrafzadeh, A.; Ramezani, A. A financial comparative study of solar and regular irrigation pumps: Case studies in eastern and southern Iran. Renew. Energy 2019, 138, 1096–1103. [Google Scholar] [CrossRef]
- Nadia, A.R.; Isa NA, M.; Desa MK, M. Efficient single and dual axis solar tracking system controllers based on adaptive neural fuzzy inference system. J. King Saud Univ. -Eng. Sci. 2020, 32, 459–469. [Google Scholar]
- Al-Rousan, N.; Isa, N.A.M.; Desa, M.K.M. Advances in solar photovoltaic tracking systems: A review. Renew. Sustain. Energy Rev. 2018, 82, 2548–2569. [Google Scholar] [CrossRef]
- Akbar, H.S.; Siddiq, A.I.; Aziz, M.W. Microcontroller based dual axis sun tracking system for maximum solar energy generation. Am. J. Energy Res. 2017, 5, 23–27. [Google Scholar]
- Maharaja, K.; Xavier, R.J.; Amla, L.J.; Balaji, P.P. Intensity based dual axis solar tracking system. Int. J. Appl. Eng. Res. 2015, 10, 19457–19465. [Google Scholar]
- Huang, C.-H.; Pan, H.-Y.; Lin, K.-C. Development of Intelligent Fuzzy Controller for a Two-Axis Solar Tracking System. Appl. Sci. 2016, 6, 130. [Google Scholar] [CrossRef] [Green Version]
- Hijawi, H.; Arafeh, L. Design of dual axis solar tracker system based on fuzzy inference systems. Int. J. Soft Comput. Artif. Intell. Appl. 2016, 2016 5, 23–35. [Google Scholar] [CrossRef]
- Homadi, A.; Hall, T.; Whitman, L. Using solar energy to generate power through a solar wall. J. King Saud Univ. -Eng. Sci. 2020, 32, 470–477. [Google Scholar] [CrossRef]
- Kalogirou, S.A. Solar Energy Engineering Processes and Systems, 2nd ed.; Academic Press (Elsevier): Cambridge, MA, USA, 2014; ISBN 978-0-12-397270-5. [Google Scholar]
- Mahdavi, M.; Li, L.; Zhu, J.; Mekhilef, S. An adaptive Neruo-Fuzzy controller for maximum power point tracking of photovoltaic systems. In Proceeding of the IEEE Region 10 Conference TENCON, Macao, China, 1–4 November 2015. [Google Scholar]
- Hariri, N.G.; AlMutawa, M.A.; Osman, I.S.; AlMadani, I.K.; Almahdi, A.M.; Ali, S. Experimental Investigation of Azimuth- and Sensor-Based Control Strategies for a PV Solar Tracking Application. Appl. Sci. 2022, 12, 4758. [Google Scholar] [CrossRef]
- Angulo-Calderón, M.; Salgado-Tránsito, I.; Trejo-Zúñiga, I.; Paredes-Orta, C.; Kesthkar, S.; Díaz-Ponce, A. Development and Accuracy Assessment of a High-Precision Dual-Axis Pre-Commercial Solar Tracker for Concentrating Photovoltaic Modules. Appl. Sci. 2022, 12, 2625. [Google Scholar] [CrossRef]
- Ruelas, J.; Muñoz, F.; Lucero, B.; Palomares, J. PV Tracking Design Methodology Based on an Orientation Efficiency Chart. Appl. Sci. 2019, 9, 894. [Google Scholar] [CrossRef] [Green Version]
- Sharma, M.; Gupta, S. Adaptive neuro fuzzy inference system technique for photovoltaic array systems. Sol. Energy Mater. Sol. Cells 2015, 46, 1229–1245. [Google Scholar]
- Reddy, K.H.; Ramasamy, S.; Ramanathan, P. Hybrid adaptive neuro fuzzy based speed controller for brushless DC motor. Gazi Univ. J. Sci. 2017, 30, 93–110. [Google Scholar]
- Kiyak, E.; Gol, G. A comparion of fuzzy logic and PID controller for a single-axis solar tracking system. Renew Wind. Water Sol. 2016, 3, 7. [Google Scholar] [CrossRef] [Green Version]
- Aleem, A.; El-Sharief, M.A.; Hassan, M.A.; El-Sebaie, M.G. Implementation of Fuzzy and Adaptive Neuro-Fuzzy Inference Systems in Optimization of Production Inventory Problem. Appl. Math. Inf. Sci. 2017, 11, 289–298. [Google Scholar] [CrossRef]
- Kuttybay, N.; Mekhilef, S.; Saymbetov, A.; Nurgaliyev, M.; Meiirkhanov, A.; Dosymbetova, G.; Kopzhan, Z. An Automated Intelligent Solar Tracking Control System with Adaptive Algorithm for Different Weather Conditions. In Proceedings of the 2019 IEEE International Conference on Automatic Control and Intelligent Systems (I2CACIS), Shah Alam, Malaysia, 29 June 2019; pp. 315–319. [Google Scholar]
- Sidek, M.; Azis, N.; Hasan, W.; Ab Kadir, M.; Shafie, S.; Radzi, M. Automated positioning dual-axis solar tracking system with precision elevation and azimuth angle control. Energy 2017, 124, 160–170. [Google Scholar] [CrossRef]
- Seme, S.; Srpčič, G.; Kavšek, D.; Božičnik, S.; Letnik, T.; Praunseis, Z.; Štumberger, B.; Hadžiselimović, M. Dual-axis photovoltaic tracking system-design and experimental investigation. Energy 2017, 139, 1267–1274. [Google Scholar] [CrossRef]
- Maiga, A. Theoretical Comparative Energy Efficiency Analysis of Dual Axis Solar Tracking Systems. Energy Power Eng. 2021, 13, 448–482. [Google Scholar] [CrossRef]
- Allw, A.S.; Shallal, I. Evaluation of Photovoltaic Solar Power of a Dual-Axis Solar Tracking System. J. Southwest Jiaotong Univ. 2020, 55. [Google Scholar] [CrossRef]
- Ferdaus, R.A.; Mohammed, M.A.; Rahman, S.; Salehin, S.; Mannan, M.A. Energy Efficient Hybrid Dual Axis Solar Tracking System. J. Renew. Energy 2014, 2014, 629717. [Google Scholar] [CrossRef]
- Awasthi, A.; Shukla, A.K.; S.R., M.M.; Dondariya, C.; Shukla, K.N.; Porwal, D.; Richhariya, G. Review on sun tracking technology in solar PV system. Energy Rep. 2020, 6, 392–405. [Google Scholar] [CrossRef]
- Batayneh, W.; Bataineh, A.; Soliman, I.; Hafees, S.A. Investigation of a single-axis discrete solar tracking system for reduced actuations and maximum energy collection. Autom. Constr. 2019, 98, 102–109. [Google Scholar] [CrossRef]
- Seme, S.; Štumberger, B.; Hadžiselimović, M.; Sredenšek, K. Solar Photovoltaic Tracking Systems for Electricity Generation: A Review. Energies 2020, 13, 4224. [Google Scholar] [CrossRef]
- Farrar-Foley, N.; Rongione, N.A.; Wu, H.; Lavine, A.S.; Hu, Y. Total solar spectrum energy converter with integrated pho-tovoltaics, thermos-electrics, and thermal energy storage: System modeling and design. Int. J. Energy Res. 2021, 46, 5731–5744. [Google Scholar] [CrossRef]
- Gbadamosi, S.L. Design and implementation of IoT-based dual-axis solar PV tracking system. Przegląd Elektrotechniczny 2021, 2021, 57. [Google Scholar] [CrossRef]
- Hamad, B.A.; Ibraheem, A.M.; Abdullah, A.G. Design and Practical Implementation of Dual-Axis Solar Tracking System with Smart Monitoring System. Przegląd Elektrotechniczny 2020, 96. [Google Scholar] [CrossRef]
- SKivrak, S.; Gunduzalp, M.; Dincer, F. Theoretical and experimental performance investigation of a two-axis solar tracker under the climatic condition of Denizil, Turkey. Przegląd Elektrotechniczny 2012, 88, 332–336. [Google Scholar]
- Kuttybay, N.; Saymbetov, A.; Mekhilef, S.; Nurgaliyev, M.; Tukymbekov, D.; Dosymbetova, G.; Meiirkhanov, A.; Svanbayev, Y. Optimized Single-Axis Schedule Solar Tracker in Different Weather Conditions. Energies 2020, 13, 5226. [Google Scholar] [CrossRef]
- Božiková, M.; Bilčík, M.; Madola, V.; Szabóová, T.; Kubík, Ľ.; Lendelová, J.; Cviklovič, V. The Effect of Azimuth and Title Anglea. Changes on the Energy Balance of Photovoltaic System Installed in the Southern Slovakia Region. Appl. Sci. 2021, 11, 8998. [Google Scholar] [CrossRef]
- Orłowski, P. Analysis of two-criteria optimization problem with application to automatic orders control system for inventory with long-delay supply with feedback—Feedforward controller and Smith predictor. Przegląd Elektrotechniczny 2016, 92, 218–221. [Google Scholar]
- Utomo, B.R.; Sulistyanto, A.; Riyadi, T.W.B.; Wijayanta, A.T. Enhanced Performance of Combined Photovoltaic–Thermoelectric Generator and Heat Sink Panels with a Dual-Axis Tracking System. Energies 2023, 16, 2658. [Google Scholar] [CrossRef]





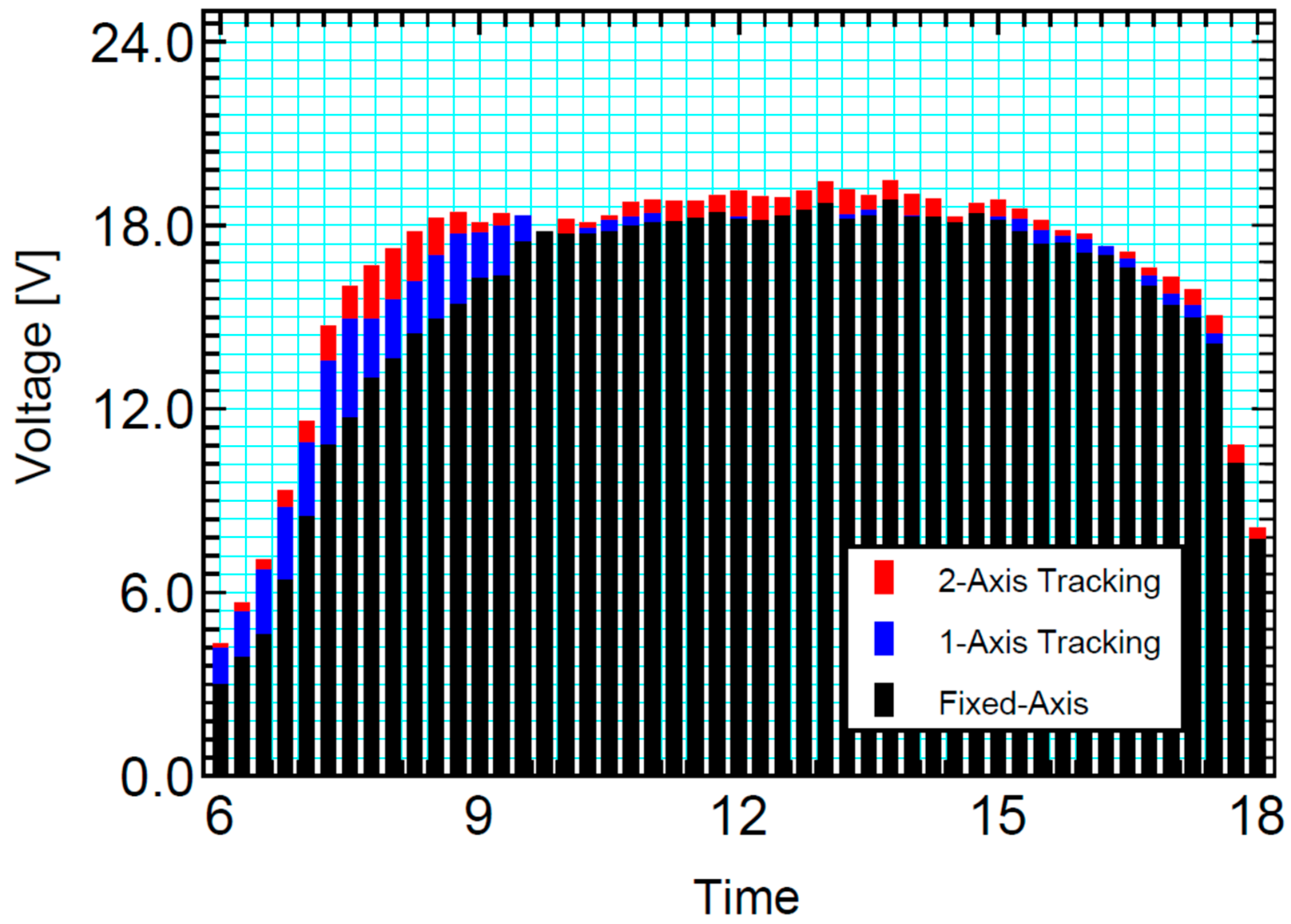
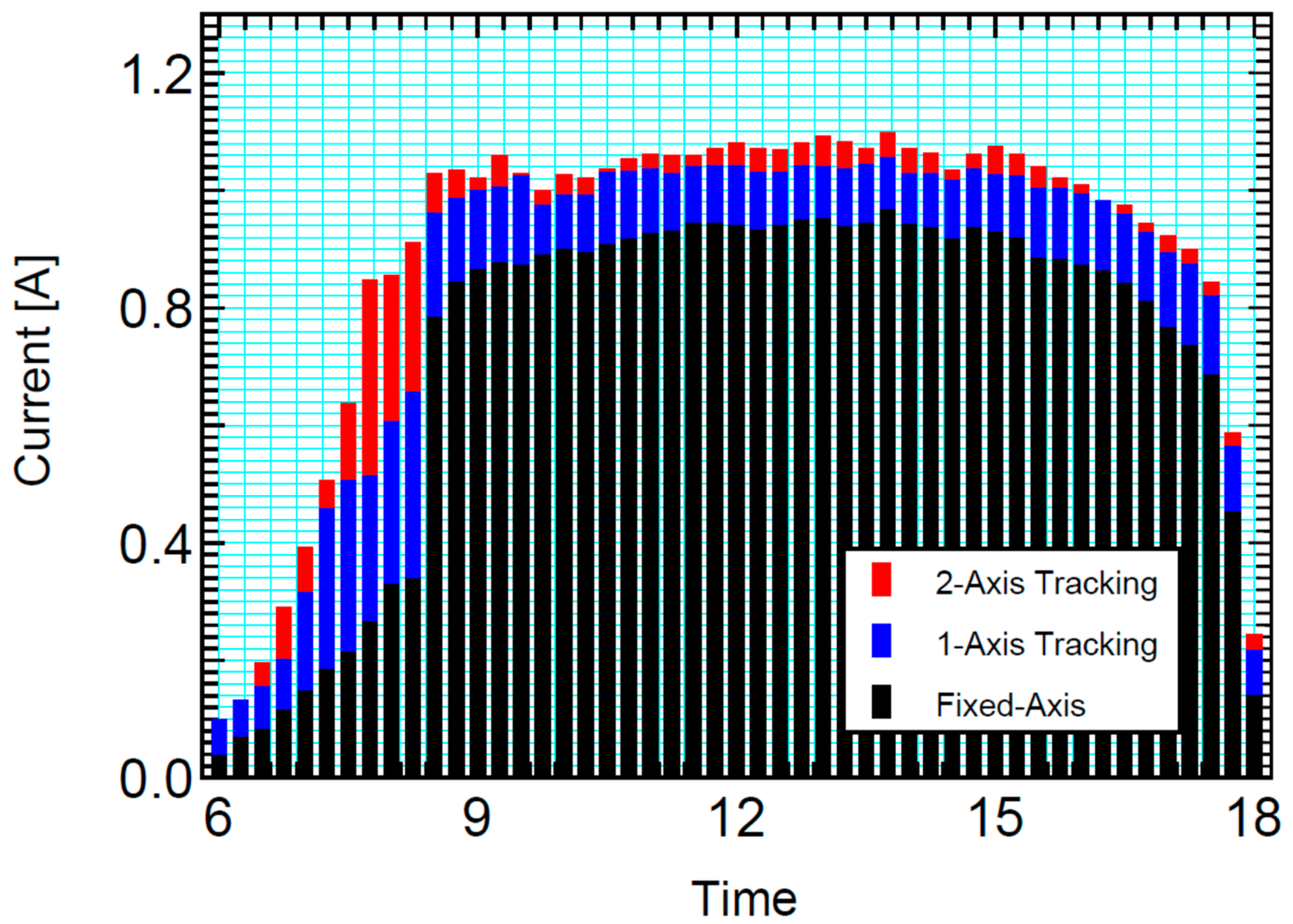


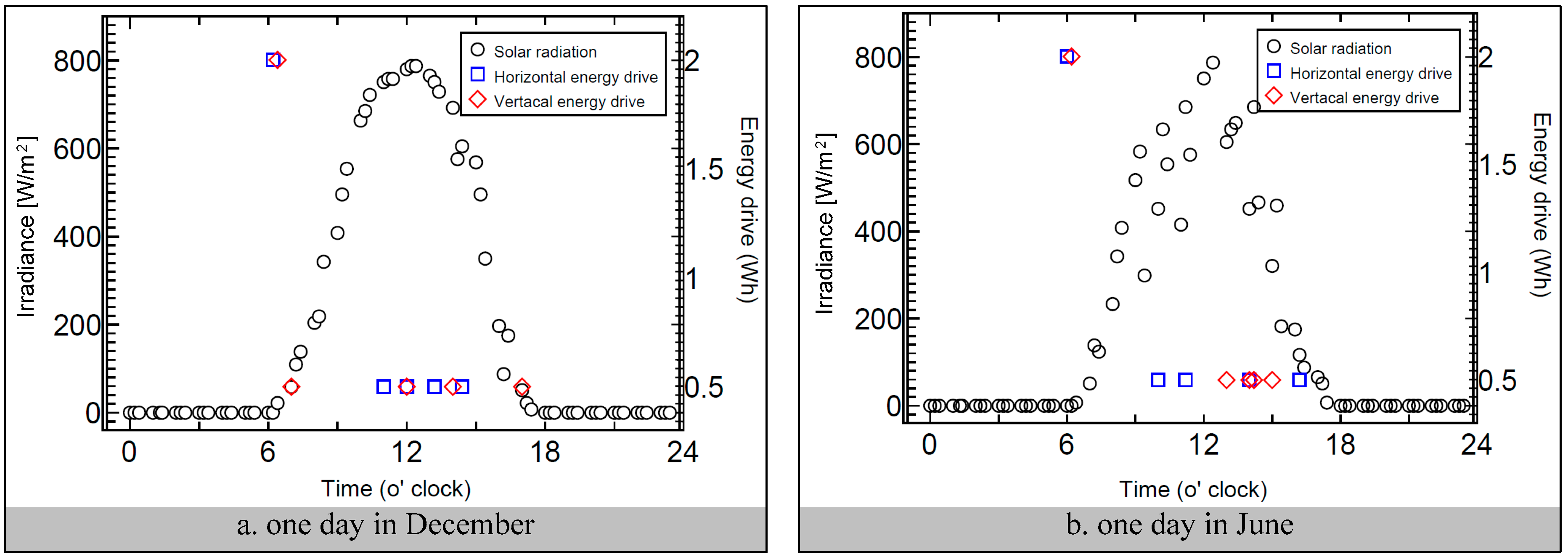
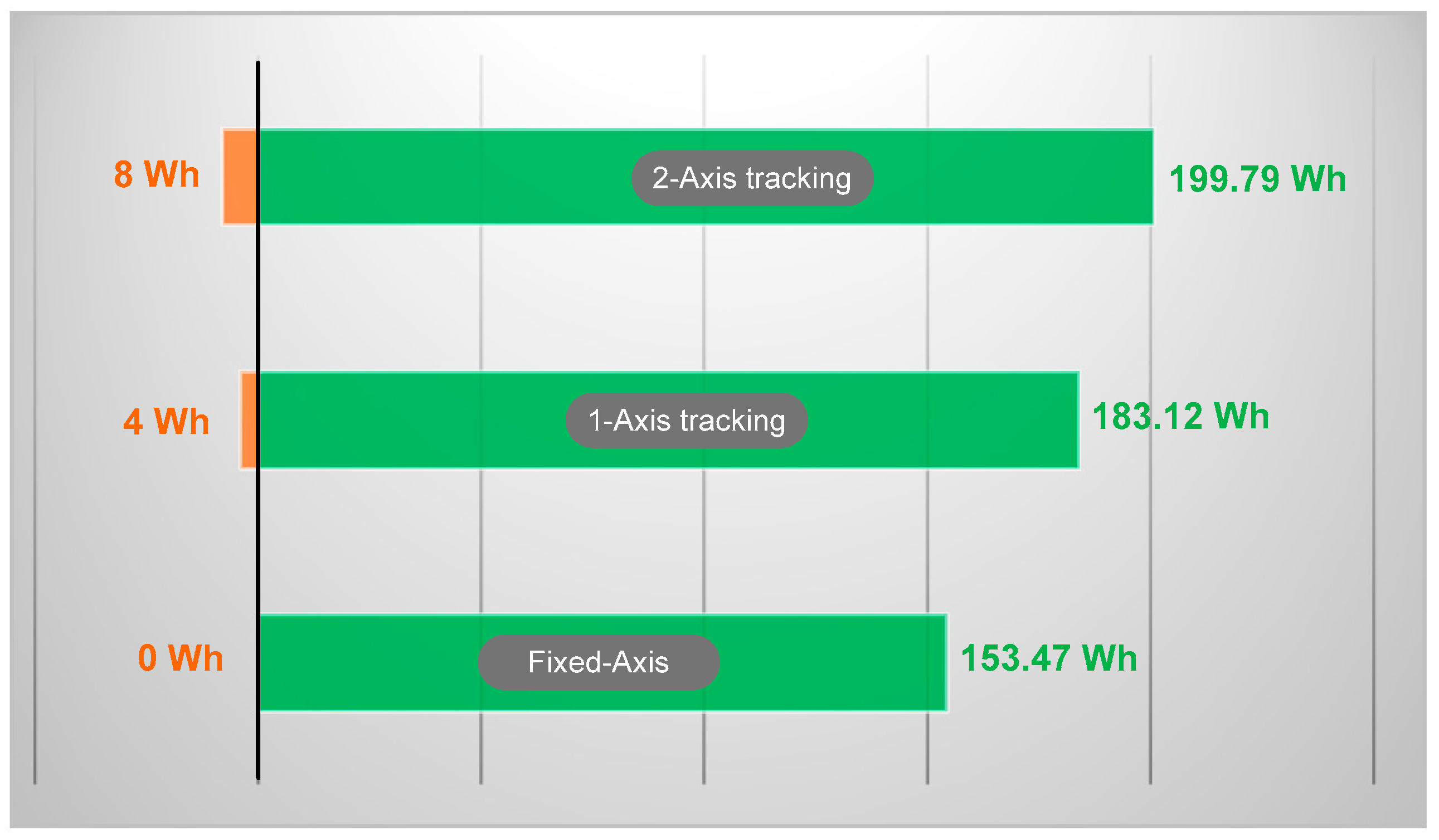
| Axis Tracker | Tracker Sensor | Type | Control | Ref. |
|---|---|---|---|---|
| Single-axis | LDR | All time tracker | PID control | [19] |
| Dual-axis | micro-electromechanical solar sensor | All time tracker | Arduino board in a closed-loop control | [20] |
| Dual-axis | - | 3-point tracker | FPGA boards | [21] |
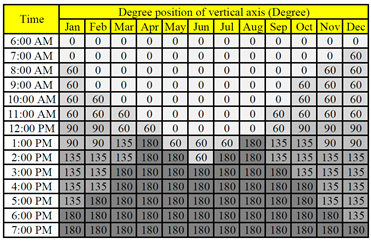 | 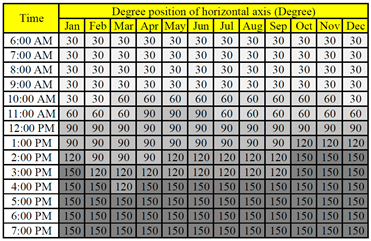 |
| (a) Degree position of the vertical axis | (b) Degree position of the horizontal axis |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Thungsuk, N.; Tanaram, T.; Chaithanakulwat, A.; Savangboon, T.; Songruk, A.; Mungkung, N.; Maneepen, T.; Arunrungrusmi, S.; Poonthong, W.; Kasayapanand, N.; et al. Performance Analysis of Solar Tracking Systems by Five-Position Angles with a Single Axis and Dual Axis. Energies 2023, 16, 5869. https://doi.org/10.3390/en16165869
Thungsuk N, Tanaram T, Chaithanakulwat A, Savangboon T, Songruk A, Mungkung N, Maneepen T, Arunrungrusmi S, Poonthong W, Kasayapanand N, et al. Performance Analysis of Solar Tracking Systems by Five-Position Angles with a Single Axis and Dual Axis. Energies. 2023; 16(16):5869. https://doi.org/10.3390/en16165869
Chicago/Turabian StyleThungsuk, Nuttee, Thaweesak Tanaram, Arckarakit Chaithanakulwat, Teerawut Savangboon, Apidat Songruk, Narong Mungkung, Theerapong Maneepen, Somchai Arunrungrusmi, Wittawat Poonthong, Nat Kasayapanand, and et al. 2023. "Performance Analysis of Solar Tracking Systems by Five-Position Angles with a Single Axis and Dual Axis" Energies 16, no. 16: 5869. https://doi.org/10.3390/en16165869
APA StyleThungsuk, N., Tanaram, T., Chaithanakulwat, A., Savangboon, T., Songruk, A., Mungkung, N., Maneepen, T., Arunrungrusmi, S., Poonthong, W., Kasayapanand, N., Nilwhut, S., Kinoshita, H., & Yuji, T. (2023). Performance Analysis of Solar Tracking Systems by Five-Position Angles with a Single Axis and Dual Axis. Energies, 16(16), 5869. https://doi.org/10.3390/en16165869






