Identification of Lossy Y-Type Two-Port Circuit Models under Measurement Uncertainties: Closed-Form Solution and Statistical–Perturbative Characterization
Abstract
:1. Introduction
2. Nomenclature Summary
3. Problem Formulation for the Real-Valued Case
4. Closed-Form Solution to the Optimization Problem for the Real-Valued Case
5. Special Case of the Parameter Known in the Real-Valued Case
- The second port of the two-port network may be closed by a short-circuit, which corresponds to assuming ; notice that this is an assumption that does not necessarily correspond to a real-world case since, at high frequency, a short-circuit is not necessarily so.
- The equivalent conductance h, in this particular measurement setting, may be measured with negligible measurement error; even this assumption will, most likely, appear just as a case study.
6. Statistical Analysis for the Real-Valued Case
6.1. Statistical Analysis of the Modeling Error
6.2. Statistical Analysis of the Perturbations of the System (12)
- The sequence of random variables is uncorrelated, namely, , where denotes the Kronecker’s delta;
- The sequence is uncorrelated, namely, ;
- The two sequences and are statistically independent, hence , since they were supposed to be zero-mean.
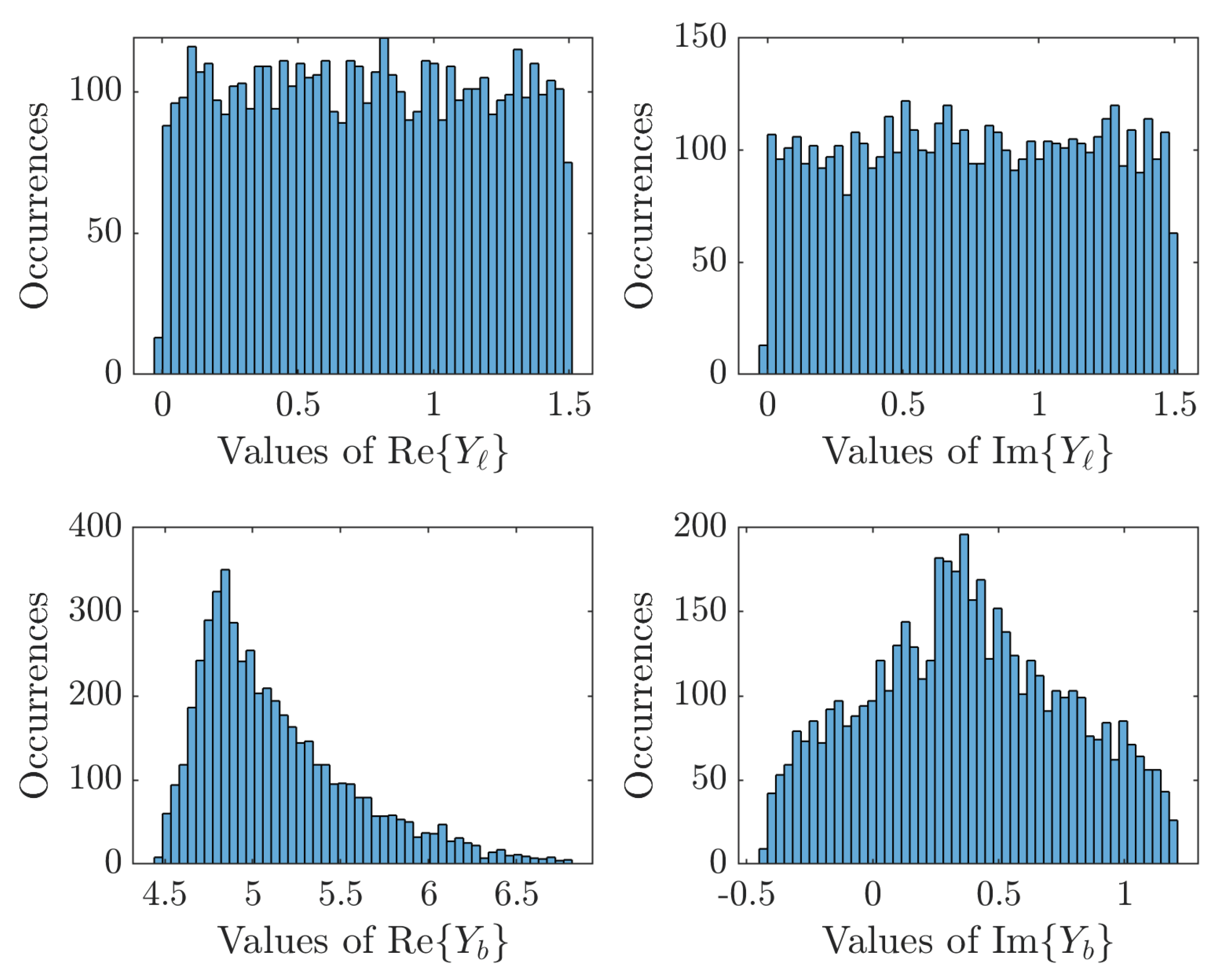
7. Covering of the Complex-Valued Case
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fiori, S.; Wang, J. External identification of a reciprocal lossy multiport circuit under measurement uncertainties by Riemannian gradient descent. Energies 2023, 16, 2585. [Google Scholar] [CrossRef]
- Smith, K.C.A.; Alley, R.E. Electrical Circuits: An Introduction; Electronics Texts for Engineers and Scientists; Cambridge University Press: Cambridge, MA, USA, 1992. [Google Scholar] [CrossRef]
- Alazard, D.; Perez-Gonzalez, J.A.; Loquen, T.; Cumer, C. Two-input two-output port model for mechanical systems. In Proceedings of the Scitech 2015—53rd AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 5–9 January 2015. [Google Scholar]
- Farina, M.; Morini, A.; Rozzi, T. A calibration approach for the segmentation and analysis of microwave circuits. IEEE Trans. Microw. Theory Technol. 2007, 55, 2124–2134. [Google Scholar] [CrossRef]
- Aberle, J. Two-port representation of an antenna with application to non-foster matching networks. IEEE Trans. Antennas Propag. 2008, 56, 1218–1222. [Google Scholar] [CrossRef]
- Duhé, J.F.; Victor, S.; Melchior, P.; Abdelmounen, Y.; Roubertie, F. Two-port network modeling for bio-heat transfers in lungs. IFAC-PapersOnLine 2021, 54, 169–174. [Google Scholar] [CrossRef]
- Lee, H.; Lee, C.; Jang, G.; Kwon, S.H. Harmonic analysis of the Korean high-speed railway using the eight-port representation model. IEEE Trans. Power Deliv. 2006, 21, 979–986. [Google Scholar] [CrossRef]
- Zaman, M.; Mustafa, M.; Hussain, A. Black-box modeling of low dropout voltage regulator based on two-port network parameter identification. In Proceedings of the 2015 IEEE 11th International Colloquium on Signal Processing & Its Applications (CSPA), Kuala Lumpur, Malaysia, 6–8 June 2015; pp. 78–83. [Google Scholar]
- Chou, S.F.; Wang, X.; Blaabjerg, F. Extensions to two-port network modeling method and analysis of multiple-VSC-based systems. In Proceedings of the 2019 20th Workshop on Control and Modeling for Power Electronics (COMPEL), Toronto, ON, Canada, 17–20 June 2019; pp. 1–8. [Google Scholar]
- Mikulecky, D. A network thermodynamic two-port element to represent the coupled flow of salt and current. Improved alternative for the equivalent circuit. Biophys. J. 1979, 25, 323–340. [Google Scholar] [CrossRef] [PubMed]
- Mimani, A.; Munjal, M. Acoustical analysis of a general network of multi-port elements—An impedance matrix approach. Int. J. Acoust. Vib. 2012, 17, 23–46. [Google Scholar]
- Veijola, T. A two-port model for wave propagation along a long circular microchannel. Microfluid. Nanofluid. 2007, 3, 359–368. [Google Scholar] [CrossRef]
- Ballicchia, M.; Farina, M.; Morini, A.; Turchetti, C.; Orcioni, S. A methodology for RF modeling of packages with external pin measurements. Int. J. Microw.-Comput.-Aided Eng. 2014, 24, 623–634. [Google Scholar] [CrossRef]
- Frasch, H.; Kresh, J.; Noordergraaf, A. Two-port analysis of microcirculation: An extension of windkessel. Am. J. Physiol. 1996, 270, 376–385. [Google Scholar] [CrossRef] [PubMed]
- Svoboda, J.A.; Dorf, R.C. Introduction to Electric Circuits, 9th ed.; Wiley: Hoboken, NJ, USA, 2013. [Google Scholar]
- Izadian, A. Two-Port Networks. In Fundamentals of Modern Electric Circuit Analysis and Filter Synthesis: A Transfer Function Approach; Springer International Publishing: Cham, Switzerland, 2023; pp. 609–669. [Google Scholar] [CrossRef]
- Hernández-Escobar, A.; Abdo-Sánchez, E.; Mateos-Ruiz, P.; Esteban, J.; María Martín-Guerrero, T.; Camacho-Peñalosa, C. An Equivalent-Circuit Topology for Lossy Non-Symmetric Reciprocal Two-Ports. IEEE J. Microwaves 2021, 1, 810–820. [Google Scholar] [CrossRef]
- Zappelli, L. Equivalent Circuits of Lossy Two-Port Waveguide Devices. IEEE Trans. Microw. Theory Tech. 2019, 67, 4095–4106. [Google Scholar] [CrossRef]
- Fiori, S. Extended Hebbian learning for blind separation of complex-valued sources. IEEE Trans. Circuits Syst. II Analog. Digit. Signal Process. 2003, 50, 195–202. [Google Scholar] [CrossRef]
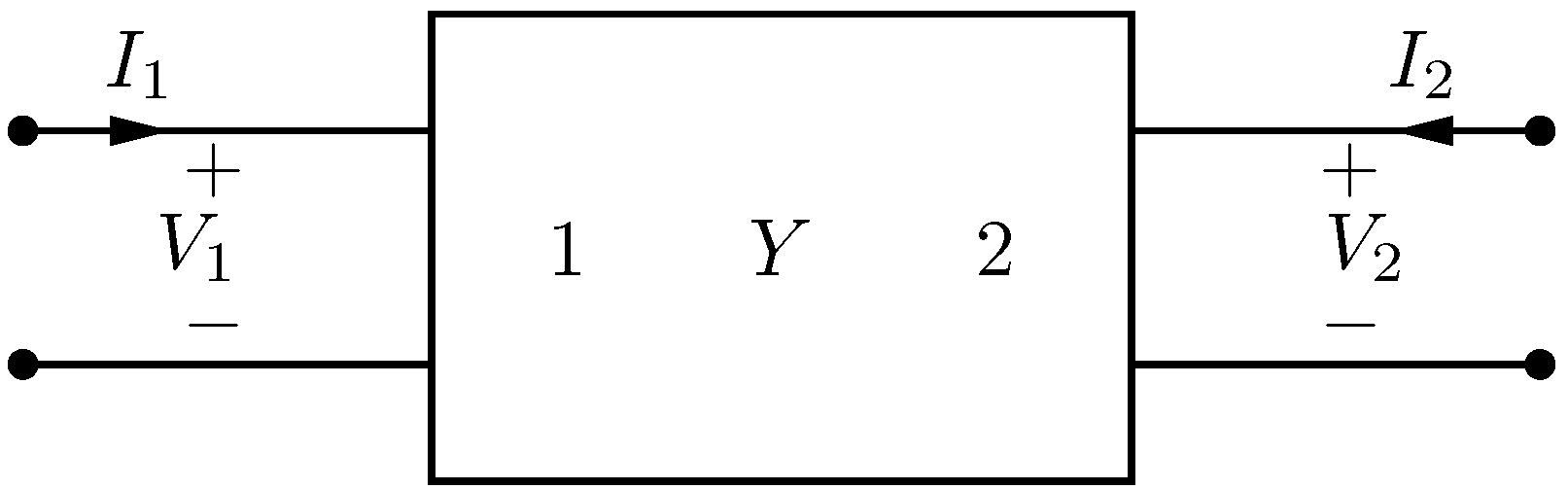
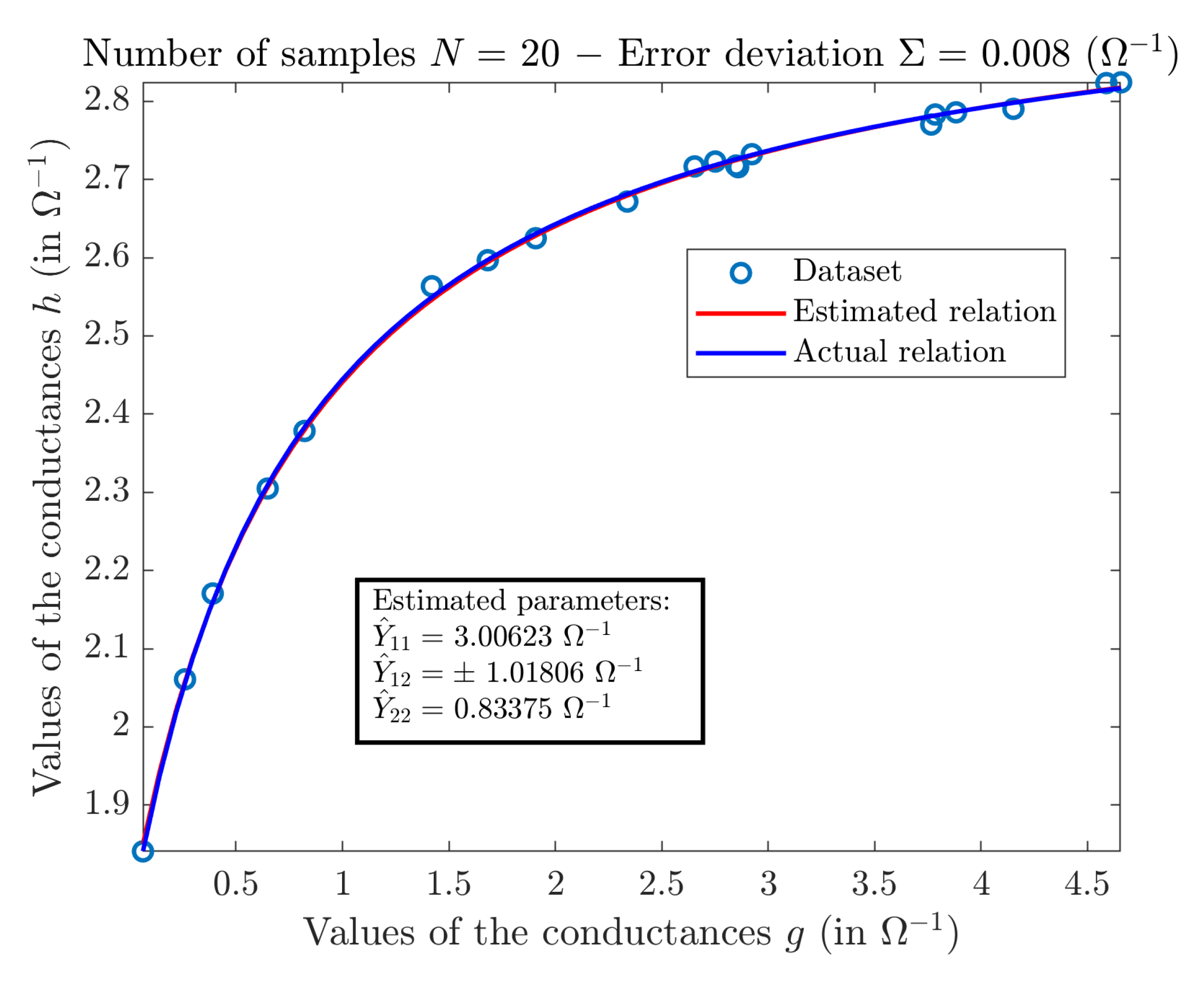
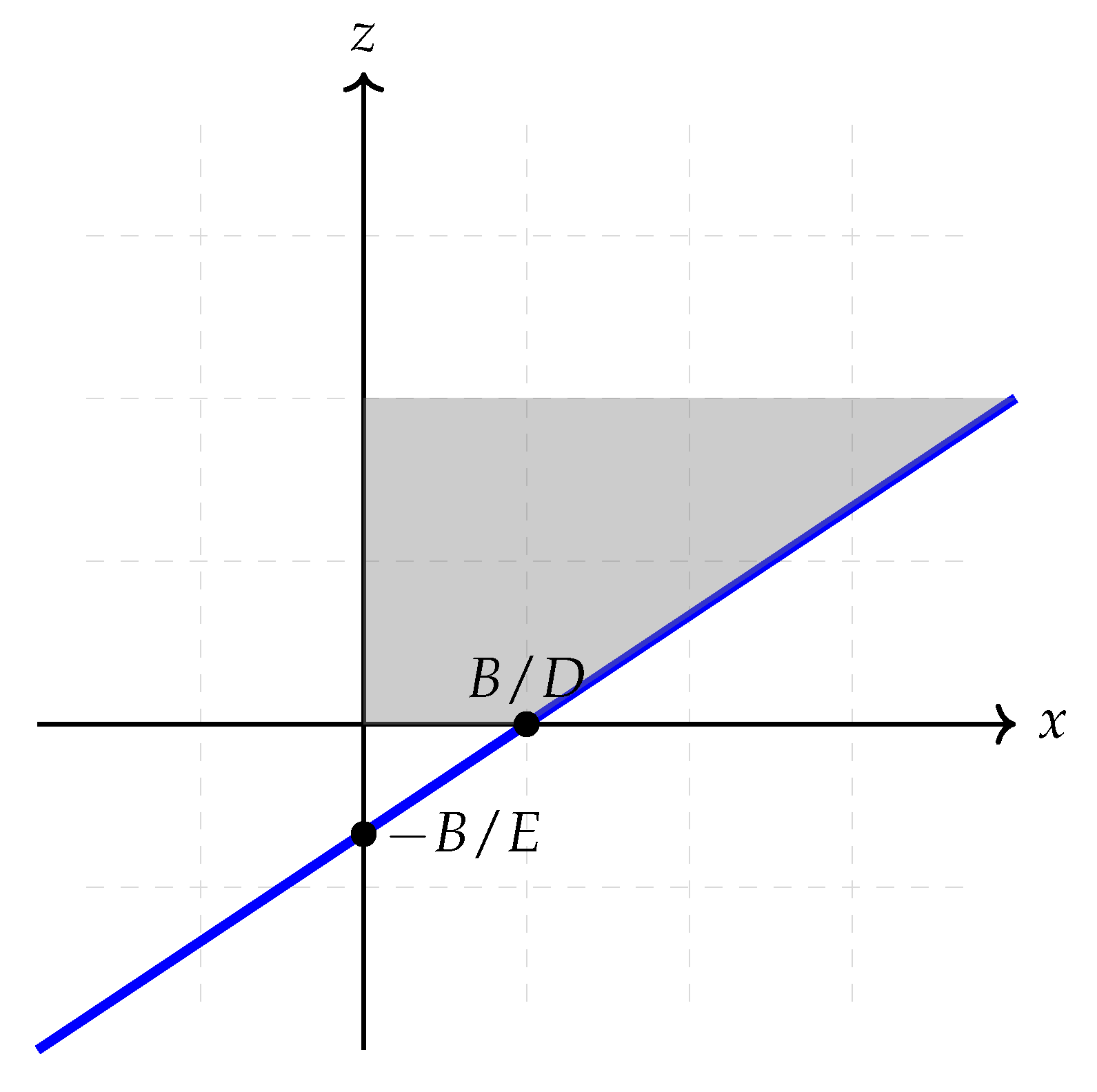

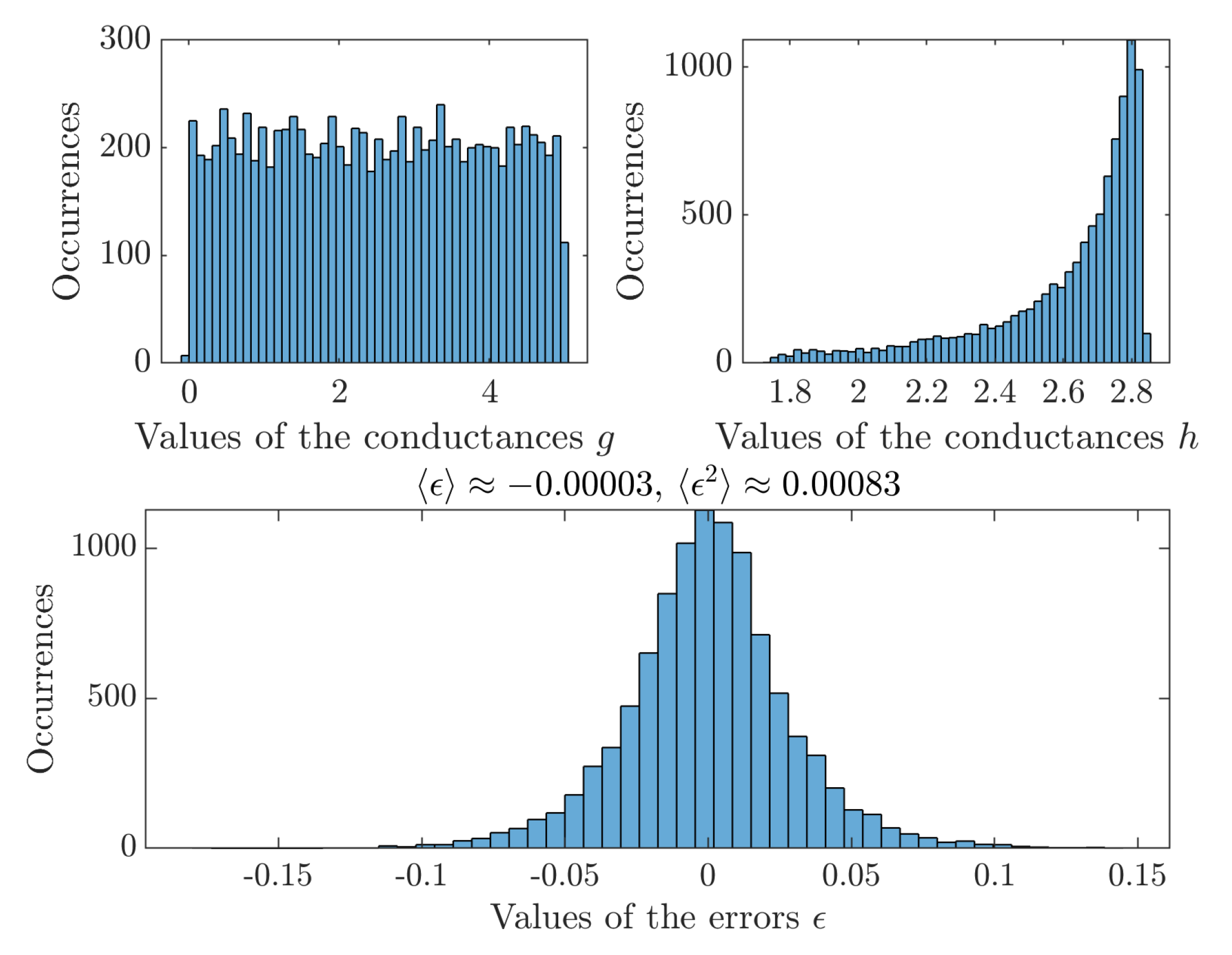
| Method | Advantages | Drawbacks |
|---|---|---|
| Classical [2] | Requires a minimal number of measurements; requires minimal computational efforts. | Assumes errorless measurements and presents a lack of resiliency to measurement errors. |
| Iterative [1] | Deals with measurement errors by an iterative least-squared error approach. | Requires a larger number of measurements (from dozens to hundreds, depending on the size of the multiport network) which may be effected through an inexpensive instrumentation; requires a powerful computation platform. |
| Nonclassical, closed form (proposed) | Deals with measurement errors through a least-squares-error approach; does not requires a powerful computation platform. | Requires a larger number of measurements which may be effected through an inexpensive instrumentation. |
| Symbols | Description |
|---|---|
| Independent parameters of the two-port network to be identified. | |
| Dataset pair to conduct identification. | |
| N | Number of dataset pairs. |
| Specific and global modeling error. | |
| Correlations between data entries to be used in the resolvent system and in the statistical analysis. | |
| Coefficient matrix and vector of the resolvent system. | |
| t | Estimated closed-form solution. |
| Variance of the measurement error. | |
| Mean and variance of estimation mismatch. | |
| Higher-order correlations between data entries to be used in the statistical analysis. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fiori, S.; Cisse, C. Identification of Lossy Y-Type Two-Port Circuit Models under Measurement Uncertainties: Closed-Form Solution and Statistical–Perturbative Characterization. Energies 2023, 16, 6037. https://doi.org/10.3390/en16166037
Fiori S, Cisse C. Identification of Lossy Y-Type Two-Port Circuit Models under Measurement Uncertainties: Closed-Form Solution and Statistical–Perturbative Characterization. Energies. 2023; 16(16):6037. https://doi.org/10.3390/en16166037
Chicago/Turabian StyleFiori, Simone, and Cheikh Cisse. 2023. "Identification of Lossy Y-Type Two-Port Circuit Models under Measurement Uncertainties: Closed-Form Solution and Statistical–Perturbative Characterization" Energies 16, no. 16: 6037. https://doi.org/10.3390/en16166037
APA StyleFiori, S., & Cisse, C. (2023). Identification of Lossy Y-Type Two-Port Circuit Models under Measurement Uncertainties: Closed-Form Solution and Statistical–Perturbative Characterization. Energies, 16(16), 6037. https://doi.org/10.3390/en16166037








