Optimizing Artificial Neural Networks for the Accurate Prediction of Global Solar Radiation: A Performance Comparison with Conventional Methods

Abstract

Obtaining precise solar radiation data is the first stage in determining the availability of solar energy. It is also regarded as one of the major inputs for a variety of solar applications. Due to the scarcity of solar radiation measurement data for many locations throughout the world, many solar radiation models are utilized to predict global solar radiation. Indeed, the most widely used AI technique is artificial neural networks (ANNs). Hitherto, while ANNs have been utilized in various studies to estimate global solar radiation (GSR), limited attention has been given to the architecture of ANN. Thus, this study aimed to: first, optimize the design of one of the faster and most used machine-learning (ML) algorithms, the ANN, to forecast GSR more accurately while saving computation power; second, optimize the number of neurons in the hidden layer to obtain the most significant ANN model for accurate GSR estimation, since it is still lacking; in addition to investigating the impact of varying the number of neurons in the hidden layer on the proficiency of the ANN-based model to predict GSR with high accuracy; and, finally, conduct a comparative study between the ANN and empirical techniques for estimating GSR. The results showed that the best ANN model and the empirical model provided an excellent estimation for the GSR, with a Coefficient of Determination $R^2$ greater than 0.98%. Additionally, ANN architectures with a smaller number of neurons in the single hidden layer (1–3 neurons) provided the best performance, with $R^2$ > 0.98%. Furthermore, the performance of the developed ANN models remained approximately stable and excellent when the number of hidden layer’s neurons was less than ten neurons ($R^2$ > 0.97%), as their performance was very close to each other. However, the ANN models experienced performance instability when the number of hidden layer’s neurons exceeded nine neurons. Furthermore, the performance comparison between the best ANN-based model and the empirical one revealed that both models performed well ($R^2$ > 0.98%). Moreover, while the relative error for the best ANN model slightly exceeded the range, ±10% in November and December, it remained within the range for the empirical model even in the winter months. Additionally, the obtained results of the best ANN model in this work were compared with the recent related work. While it had a good RMSE value of 0.8361 MJ/m² day⁻¹ within the ranges of previous work, its correlation coefficient (r) was the best one. Therefore, the developed models in this study can be utilized for accurate GSR forecasting. The accurate and efficient estimation of global solar radiation using both models can be valuable in designing and performance evaluation for different solar applications.

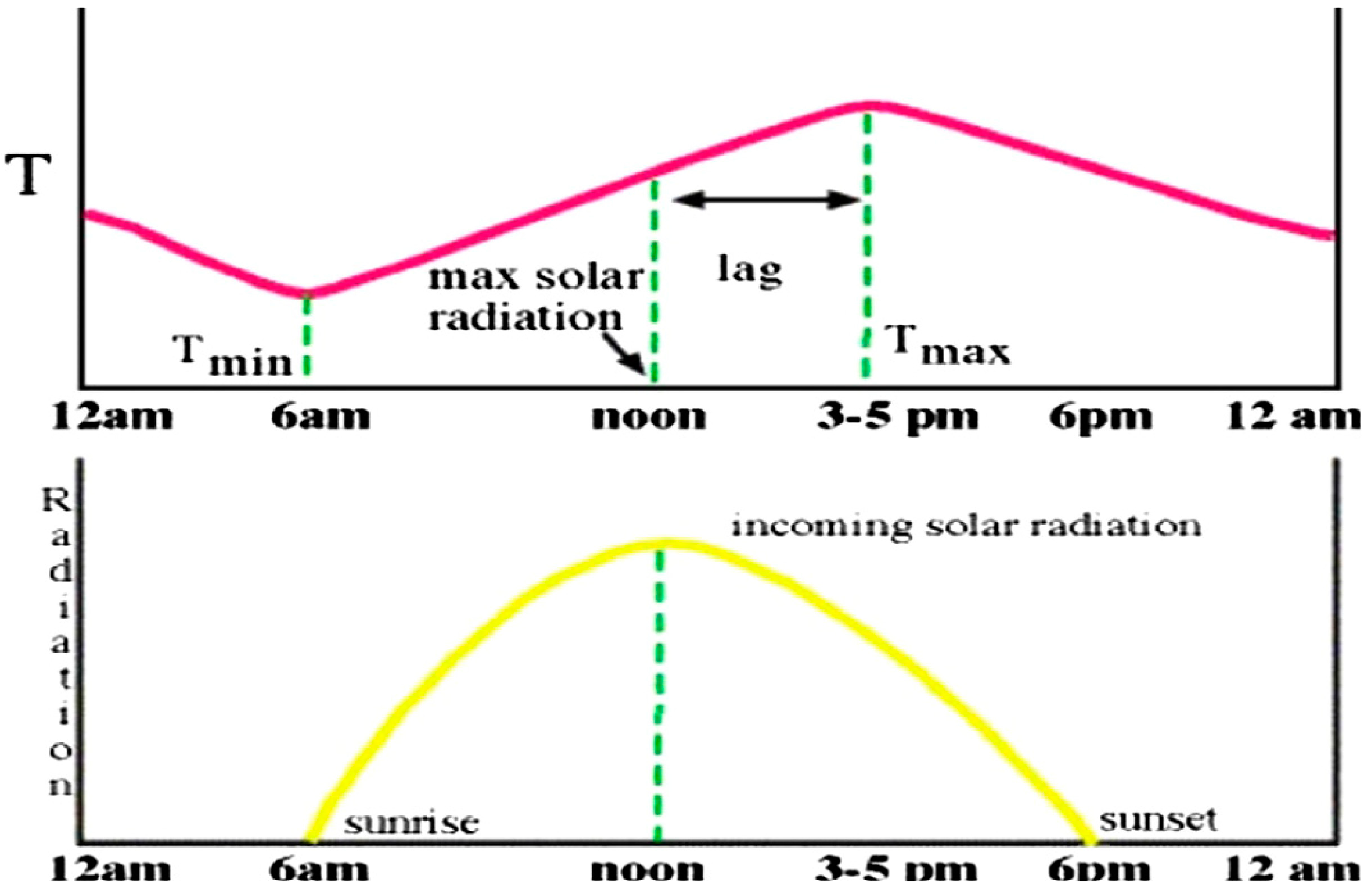
1. Introduction

In recent times, solar energy is considered one of the promising sources of renewable energy in fulfilling an important part of the world’s energy demand [1,2]. Therefore, accurate knowledge of solar radiation is regarded as the basic step in solar energy availability assessment [3]. Additionally, it serves as the first input for different solar energy applications [4,5]. Solar radiation data are unavailable at many sites around the world due to the high cost of the devices, equipment calibration, and maintenance requirements [6,7]. For this reason, several solar radiation models are proposed for estimating global solar radiation (GSR). These models are suggested to forecast solar radiation using various methodologies including empirical methods, geostationary satellite pictures, various artificial intelligence (AI) techniques such as artificial neural networks (ANNs), time series methods, physically radiative transfer models, and stochastic weather methods [8,9,10,11,12,13].

Generally, the empirical approach is the most commonly used one, which mainly relies on the correlation between global solar radiation and different meteorological parameters such as sunshine data, temperature, relative humidity, etc. Ångström [14] originally presented the primary sunshine-based solar radiation model. Ångström’s model was updated by Prescott [15] and has become the most widely employed model globally for predicting solar radiation [16,17]. Youssef et al. [18] assessed the efficacy of 31 non-sunshine-based solar models to forecast global solar radiation on a horizontal plane. The models that provide the most accurate prediction were identified, as well as the best ones among all developed models. Hassan et al. [19] introduced new temperature-based solar models for evaluating global solar radiation. The obtained results showed that the newly presented models have excellent predictions for global solar radiation at various locations. Moreover, the newly suggested formula of the best temperature-based solar model also performs better than the two most accurate sunshine-based solar models from the literature. Mostafa et al. [20] studied the proficiency of fifty-two solar radiation models that utilize sunshine data to compute the global solar radiation on horizontal surfaces, using Jouf City, KSA, as a case study. The results revealed that some models are not suitable for usage in Jouf City, while others exhibited different behavior. Similarly, Mahmoud S. Audi [21] proposed a statistical analysis of nine solar and other climatic parameters in Amman, Jordan. M.A. Alsaad [22] presented a correlation to estimate the average global solar radiation incident on a horizontal plane in Amman, Jordan. Barbaro et al.’s model [23] was updated by Robaa [24] to predict global solar radiation in Egypt. The findings showed that the modified model outperformed other ones in predicting global solar radiation across Egypt. A new model was developed by Ajayi et al. [25] to estimate the daily potential global solar radiation in Nigeria. The results revealed a high level of agreement between model predictions and observed data. El-Metwally presented a simple solar radiation model for computing global solar radiation [26]. According to the results, the developed model provides a good estimation of global solar radiation on a horizontal plane. Quej et al. [27] investigated the efficacy and applicability of thirteen solar models based on various meteorological parameters such as temperature for estimating global solar radiation in the Yucaton Peninsula, Mexico.

However, one limitation of using the empirical method is that it may underperform when applied to model nonlinear systems. With the acknowledgment of its potential, the usage of machine-learning (ML) technology in environmental and renewable energy applications has expanded. The most widely used ML technique is artificial neural networks (ANNs). ANNs provide an alternative to overcome this difficulty. ANNs, which are increasingly employed to tackle complex practical challenges, are known as universal function approximators. Their growing usage in data analysis highlights their potential as a viable alternative to more conventional approaches in various scientific domains. ANNs have the capability of accurately approximating any continuous nonlinear function. ANN-based models have been effectively employed to model various solar radiation parameters, particularly in the meteorological and solar energy resources domains [28,29,30]. Jiang [31] conducted a study on the computation of monthly average daily global solar radiation using ANN and compared it with other empirical models in China. Similarly, Şenkal and Kuleli [32] evaluated solar radiation in Turkey using both artificial neural networks and satellite data. Their ANN model utilized Scale Conjugate Gradient (SCG) and Resilient Propagation (RP) learning algorithms along with the logistic sigmoid transfer function. The results demonstrated a good agreement between the estimated values from both the ANN and satellite, as indicated by the correlation values for the twelve locations considered in the study. Similarly, Rahimikhoob [33] conducted a study on predicting global solar radiation based on temperature data using ANN in a semi-arid environment in Iran. The study also included a comparison with an empirical model, namely the Hargreaves and Samani model [34]. The results demonstrated that the developed ANN model outperformed the empirical model in accurately modeling daily global solar radiation.

In an effort to anticipate daily global solar radiation (GSR) in three locations in southwest Algeria—Bechar, Tindouf, and Naâma—Benatiallah et al. [35] proposed an artificial neural network (ANN) model. The results demonstrated that, over a five-year period, the Cascade-forward Neural Network (CFNN) and Feed-forward Neural Network (FFNN) models provided significantly improved predictions of daily GSR in the selected sites. Kaushika et al. [36] presented a direct method-based ANN model that considered the relationship features of diffuse, direct, and global solar radiations. Their findings revealed that the ANN model exhibited exceptional consistency with the data, yielding an overall mean biased error (MBE) of −0.194% and root mean square error (RMSE) of 5.19% for GSR estimation. To identify the most influential input variables for solar radiation prediction in ANN-based models, Yadav et al. [37] conducted research using WEKA software (Waikato Environment for Knowledge Analysis) on 26 Indian locations with varying climates. The findings indicated that temperature (ambient, minimum, and maximum), sunlight duration, and altitude were deemed the most crucial input components for solar radiation prediction, while longitude and latitude exhibited the least bearing on solar radiation. Yadav and Chandel [38] suggested evaluating existing ANN-based methods for estimating solar radiation and emphasized the need for further research. Their study revealed that ANN algorithms outperformed conventional techniques in accurately predicting solar radiation. In a review paper by Choudhary et al. [39], the development of ANN-based models for solar radiation forecasting was examined. The study concluded that ANN-based models exhibited significantly higher precision compared to other approaches.

Lately, with the availability of vast amounts of gathered data from across the world and developments in computer capabilities, researchers working in this field are increasingly drawn to deep-learning (DL) approaches for constructing prediction models. The DL methods are part of a larger family of ML-based techniques that depend on ANNs with representation-based learning, which became more significant in a variety of fields. For example, the majority of research on the prediction of solar irradiation relies on offline models, such as ML and deep neural networks (DNNs) [40]. In general, DNNs include several algorithms such as long short-term memory (LSTM), gated recurrent unit (GRU), one-dimension convolutional neural networks (CNN1D), and various hybrid configurations such as CNN1D-LSTM are thought to be one of the powerful tools in time series forecasting [41]. In general, models based on ML and DL were created to address complex issues by extracting useful facts from large amounts of data. Furthermore, the performance for both approaches, DL and ML, in GSR prediction (hourly) were compared, as presented in [42]. The results show that while DL techniques provided better GSR prediction than ML techniques, the performance difference was not considerable. Additionally, whereas DL methods showed better GSR prediction performance, it is worth noting that the period for training/testing the ML methods (excluding support vector regression) makes them more preferred, particularly when the computational power is considered. In other words, it can be said that ML-based models use less data and take less time to calculate than DL-based models. The study also revealed that ANN is one of the suitable algorithms for accurate GSR prediction.

ANNs, in general, are the most extensively used ML approach. In the realm of solar radiation estimation or forecasting, the majority of studies have predominantly focused on the utilization of artificial neural network (ANN) techniques and empirical models [43]. This inclination can be attributed to the widespread adoption and extensive utilization of ANN as the leading artificial intelligence (AI) technique in solar radiation prediction. Notably, ANN is often used as a benchmark against which the performance of other AI models is evaluated [43,44,45]. Regarding ANN architecture, single-hidden-layer feed-forward ANNs have been widely acknowledged as versatile approximators capable of representing continuous functions effectively [43,46]. Feed-forward neural network models have garnered significant attention due to their simplicity of implementation and ability to provide accurate representations of measurable functions, particularly in weather prediction [47,48]. Consequently, this study will specifically focus on the ANN architecture with a single-hidden layer, recognizing its importance among various alternatives. For instance, Khosravi et al. [45] developed an ANN model (5, 150, 1) to estimate hourly global solar radiation (GSR). This model comprised an input layer with five parameters, a hidden layer with 150 neurons, and an output layer representing GSR. Their results demonstrated that the developed Multilayer Feed-Forward Neural Network (MLFFNN) yielded optimal performance in GSR estimation. Similarly, Yildirim et al. [49] investigated an ANN model (9, 15, 1) for estimating daily GSR in the Turkish Eastern Mediterranean Region. In another study [50], two ANN-based models, namely the Multi-Layer Perceptron (MLP), were established to estimate hourly Direct Normal Irradiation (DNI) and daily GSR, utilizing ANN architectures of (4, 5, 1) and (7, 10, 1), respectively. The obtained results exhibited a strong correlation between the estimated and recorded values. Moreover, a study [51] proposed an ANN model (7, 10, 1) for forecasting daily GSR on a horizontal surface in major sites across Zimbabwe. The findings revealed that the developed model provided accurate estimations, supported by robust statistical indicators. In Morocco, Ihya et al. [52] introduced two ANN models, MLP with (2, 10, 1) and (3, 10, 1), to estimate hourly and daily diffuse solar fractions in Fez, respectively. Similarly, Elminir et al. [53] developed two ANN models (3, 40, 1) and (5, 40, 1) to estimate diffuse fractions at daily and hourly scales in Egypt. Furthermore, Bosch et al. [54] proposed an ANN model (3, 10, 1) for forecasting daily solar radiation across mountainous areas in Spain. The results indicated that ANN, employing data from a single radiometric station, proved to be an effective and straightforward approach for estimating solar radiation levels in challenging mountainous terrains. Additionally, Ozan Senkal and Tuncay Kuleli [32] introduced an ANN model (6, 6, 1) to predict solar radiation in Turkey. In general, optimizing the architecture of an artificial neural network (ANN) is crucial for achieving efficient performance. It is well known that both under-fitting (low complexity and a small number of neurons) and over-fitting (excessive number of neurons) can result in poor efficiency. Therefore, careful consideration must be given to selecting the appropriate number of neurons in the hidden layer. Currently, there is no mathematically justified method for determining the ideal number of hidden neurons. Utilizing a large number of neurons can increase the network’s training time and compromise its generalization and prediction capabilities. Conversely, using a small number of neurons may fail to capture the relationships between preceding and subsequent values, leading to inadequate modeling. Consequently, the trial-and-error method is commonly employed to determine the optimal number of hidden neurons within the hidden layer [31,55].

Moreover, the literature highlights the lack of attention given to determining the appropriate number of neurons within the hidden layer of an artificial neural network (ANN), which is considered a limitation [56,57]. Thus, it is essential to identify the optimal design of an ANN to effectively address the prediction of global solar radiation (GSR). While ANNs have been widely employed in various studies to estimate GSR, little emphasis has been placed on the design of the ANN model itself, specifically in determining the suitable number of neurons within the hidden layer to achieve an optimal ANN architecture. Given their highly nonlinear nature and ability to capture complex relationships within data without relying on predefined assumptions, Artificial neural networks have proven to be effective tools for simulating solar radiation. Therefore, this article aimed to optimize the design of ANN, one of the widely adopted and faster machine-learning (ML) algorithms, to enhance the accuracy of GSR forecasting while also optimizing computational resources. Consequently, this study focused on optimizing the number of neurons in the hidden layer to obtain the most effective ANN architecture for precise GSR prediction. Additionally, a solar radiation model was developed for a specific study site located at Lat. 30°51′ N and Long. 29°34′ E, which lacks an AI-based model, despite the presence of several proposed solar energy projects in the area, such as the ‘Solar-Greenhouse Desalination System Self-productive of Energy and Irrigating Water Demand’ project and the ‘Multipurpose Applications by Thermodynamic Solar (MATS)’ project. Additional figures and information can be found in the Appendix A. Evaluating solar radiation predictions is an essential initial step in assessing the feasibility and performance of such solar energy application projects.

Thus, the following points summarize the novel aspects and contributions of the presented work:

• The development of an accurate global solar radiation (GSR) model for the study location, which currently lacks an AI-based model, despite the presence of several planned solar energy projects in the area;
• The optimization of the architecture for one of the fastest and most widely used machine-learning algorithms, artificial neural network (ANN), to enhance the precision of solar radiation prediction while conserving computational resources;
• The adoption of hidden layer neurons to establish the most significant ANN model for accurate GSR estimation, addressing the existing research gap in this area;
• The investigation of the impact of varying the number of neurons in the hidden layer on the proficiency of the ANN-based model in achieving high-accuracy GSR prediction;
• The assessment of the performance of the recently introduced Hassan et al. model [19], one of the best temperature-based models for GSR estimation, over a prolonged period of years, and a comparative analysis of its performance against ANN, which has not been previously compared;
• Conducting a comprehensive comparative study between the ANN method and the empirical method for global solar radiation, providing valuable insights for designers, engineers, and stakeholders involved in feasible solar energy applications at the study site.

This detailed study presents significant information that is relevant to designers, engineers, and stakeholders interested in solar energy applications at the study site.

The performance of the established models, including the artificial neural network (ANN) models and the empirical model, was evaluated by comparing their predictions with the observed data of global solar radiation at the study location, New Borg El-Arab, Egypt (Latitude 30°51′ N and Longitude 29°34′ E). The assessment included the computation of commonly used statistical indicators such as Mean Percentage Error (MPE), Mean Bias Error (MBE), Mean Absolute Percentage Error (MAPE), Mean Absolute Bias Error (MABE), Root Mean Square Error (RMSE), Relative Error (e), Coefficient of Determination ($R^2$), and Correlation Coefficient (r) [9,16,58,59,60,61]. These indicators were employed to evaluate the performance of the models and determine the most suitable model for the given task.

The remainder of the manuscript is organized as follows: Section 2.1 provides a description of the utilized dataset, including Global Solar Radiation data and other relevant parameters, as well as the methodology employed for calculating extraterrestrial solar radiation. In Section 2.2 and Section 2.3, an in-depth explanation of AI for solar radiation prediction and ANNs and their functioning are presented, respectively. Section 2.4 and Section 2.5 detail the development of the ANN-based models and the empirical-based model, respectively. Section 3 focuses on discussing the key indicators commonly used to evaluate the performance of the models. The findings and discussion of the results, including a comparative analysis of the performance of both techniques, are presented in Section 4. Finally, Section 5 concludes the manuscript and outlines potential avenues for future research.

2. Materials and Methods

2.1. Dataset

The dataset utilized for establishing and validating the presented models, namely the ANN-based models and the empirical-based model, consisted of temperature and global solar radiation measurements spanning 35 years, from 1 January 1984 to 31 December 2017, and a separate period from 1 January 2020 to 31 December 2020, respectively. These models were designed to predict the monthly average daily global solar radiation on a horizontal surface. The data used in this study were sourced from the power data access provided by the NASA Surface Meteorology and Solar Energy website, which has been widely employed in numerous studies to establish, validate, and evaluate the proficiency of different solar radiation models [18,19,38,45,62,63,64,65,66,67,68,69,70,71,72,73,74]. The NASA weather dataset serves as a comprehensive and continuous record of climatic data derived from satellite measurements, facilitating research on climate and climatic phenomena. Noteworthy characteristics of the NASA dataset include its global coverage and temporal consistency. It has demonstrated a satisfactory level of accuracy when compared to conventional ground-based observations, rendering it a reliable data source. Consequently, the NASA dataset can be effectively utilized in scenarios where ground observations are scarce or unavailable. In this study, the required meteorological parameters were obtained from the NASA data, despite the general perception that terrestrial measurements are more reliable than satellite-based measurements. This decision was based on two main factors. Firstly, the NASA database encompasses all the essential meteorological information for the areas under consideration. Secondly, concerns arise regarding the accuracy of on-site measurements, often due to operational errors, data gaps, or calibration discrepancies, which can lead to inaccuracies in the collected data [62,75].

For clarity, temperature data were utilized in the present work because it was easier to collect in the majority of weather stations than other climatic parameters, which is a considerable benefit. Regarding its dependency with solar radiation, obviously, the close relationship between solar radiation and ambient temperature may be clarified via the behavior of the Earth’s surface with regard to the received solar radiation from the Sun [76]. The Earth’s surface absorbs the solar energy that is released into the atmosphere as shortwave electromagnetic radiation, warming it as a result. The heated surface of the ground releases some of the absorbed energy as longwave radiation, which heats the neighboring ambient air. The surrounding air is heated indirectly by contacting the heated Earth’s surface rather than directly by the Sun’s radiation. The solar radiation and temperature cycles in this process have a phase delay, as seen in Figure 1 [77]. Generally, air temperature variation can be influenced by radiation balancing and air mass advection. The kind of surface cover, the percentage of clouds, the time of day, and the season all have an impact on the local air temperature and radiation balancing. The yearly temperature cycle, which showed a significant relationship between solar energy and ambient temperature, may indicate the regular fluctuation in solar radiation that comes in over a period of a year [76]. As a result, the main emphasis of this work was on establishing distinct relationships between temperature and solar radiation, which is regarded as a significant assertion in this work.

2.2. Artificial Intelligence for Solar Radiastion Prediction

Predicting GSR depending on AI-based techniques such as ML and DL could be accomplished in three forms [40,78,79]. The first relies solely on previous GSR data (ground observation):

$$(y_{t+1},\dots ,y_{t+k})=f(y_{t-n},y_{t-n+1},\dots ,y_t)$$

(1)

where $y_t$ is the real GSR, $y_{t-n}$ refers to the earlier value of GSR, $y_{t+k}$ represents the predicted value of GSR at step k, and $f$ denotes a functional dependency among former and future samples. $tϵ\{1,\dots ,n\}$, n represents the sequence size.

The second is based on numerical weather prediction models, NWP, and projected meteorological characteristics such as Temperature (T), Relative Humidity (RH), Wind Speed (WS), Pressure (P), and cloud (C).

$$(y_{t+1},\dots ,y_{t+k})=f(x_{0t},x_{1t},x_{2t},x_{3t},x_{4t},\dots )$$

(2)

where variables $x_{0t},x_{1t},x_{2t},x_{3t},\mathrm{a}\mathrm{n}\mathrm{d} x_{4t}$ match to T, RH, WS; P, and C, respectively.

The third employs historical GSR information together with meteorological variables:

$$(y_{t+1},\dots ,y_{t+k})=f(y_{t+n},y_{t+n-1},\dots ,x_{0t},x_{1t},x_{2t},x_{3t},x_{4t},\dots )$$

(3)

These methods can be utilized for both one-step ($k=1$) and multistep ($k>1$) predictions.

Generally, DL models differ from other ML models. DL models with different hierarchical structures provide automated learning of the procedures necessary for extracting semantic characteristics from raw data and uncovering relevant patterns. DL, as opposed to ML techniques, learns data and patterns through the use of a complex neural network design. For instance, the recurrent neural network (RNN) based on deep learning is an ANN-type network that employs sequential or time-series input. This paradigm determines the current input and output using information from the prior input. A feedback process for the recurrent layer preserves knowledge of a point in time in a memory cell’s past time-series data. Every layer of an RNN has a common parameter. On the contrary, a network with feed forwarding has distinct weights for every node, but an RNN uses the same weight parameter across the network. During training, its weight is modified via backpropagation and gradient descent [80]. In other words, RNN models, which come in a variety of shapes, offer a new perspective to basic neural networks, such as Multi-Layer Perceptron (MLP). In contrast to ANN feed-forward networks, which use what is learned throughout training to anticipate outputs, RNNs often accept a sequence of inputs, and the model’s choice is impacted by what it has learned in the past [42]. DL models, in general, differ from ML in that they have several hidden layers with distinct weights and biases and numerous activation functions to handle complicated datasets, where the supplied data may have linkages and combinations, and it may not even be in the appropriate structure. For more clarification, the general flow chart of DL techniques is illustrated in Figure 2 [81]. Furthermore, it can be noted that it is rare to use DL-based models to predict long-term solar radiation such as monthly average daily GSR, and, on the contrary, it is mainly employed for short-term forecast horizons (such as minutes and hours) [40,44,80,82]. The DL approach tries to sequence independent machines whereby the output of a particular layer is the input of the following layer because it has the ability to generate and manage the dependency sequence amongst data utilized as input parameters or features [83].

On the other side, the MLP neural networks, as stated before, are a type of nonlinear model that can discover patterns, model data and perform time series analysis. An MLP is based on the structural connection of the data, which is a nonlinear mapping between two or more variables. After the MLP architecture is configured, the data provided to MLP are transferred from the input to the output layer via a hidden layer. The output might be regarded as internalized after the learning period. A good learning algorithm reduces mistakes throughout the training phase. It is important to note that the MLP model’s learning methods rely on back propagation, which is the steepest gradient descent method. The back propagation method’s primary purpose is to decrease network errors. In this regard, the current study utilized ANN (MLP) for predicting monthly average daily global solar radiation. Figure 3 exhibits the flow chart of the proposed ANN models in this work. Thus, this study predicted the GSR using meteorological parameters, specifically the ambient temperature. Though the approach requires no prior knowledge, it is dependent on accurate meteorological data [80]. The forecast only includes a single value of GSR rather than mapping relations between past time-series data (not a time-series forecasting model). The used dataset was divided into two groups, the first one to train the model and the remaining one to validate it, as demonstrated in Figure 3. The temperature data were utilized in this study due to their easy recording at most weather stations compared to other meteorological variables, which is a significant advantage. Additionally, ANN provided well performance in GSR forecasting. Additionally, as mentioned before, while the performance difference between the two approaches, DL and ML, was not significant, it is worth mentioning that the time required for training or testing ML methods makes them preferable, especially when processing power is taken into account [42]. Thus, the optimization of the architecture for one of the fastest and most widely used machine-learning algorithms, ANNs, to enhance the precision of monthly solar radiation prediction while conserving computational resources was one of the main goals of this study.

2.3. Artificial Neural Network

The artificial neural network (ANN) is an artificial intelligence approach that utilizes a black-box-modeling method, making it a powerful non-linear computational algorithm. Its purpose is to process training datasets and learn, store, and recall information, enabling multidimensional transformations between input and output spaces without requiring an explicit understanding of the underlying dynamic relationships. Compared to other mathematical models such as regression, ANN offers greater efficiency and computational speed, making it well-suited for simulating complex engineering problems, including pattern recognition, classification, voice and image processing, and control systems [62,84,85]. The artificial neurons in an ANN-based model serve as interconnected processing components. Figure 4 illustrates the fundamental elements of an artificial neuron, encompassing inputs, biases, weights, a summing junction, a transfer function (also known as an activation function), and an output. Each input was assigned a specific weight associated with the artificial neuron. The sum function was applied to the weighted inputs and biases at the core of the model. The resulting sum passed through the transfer function as the artificial neuron generated its output.

Figure 4 presents a basic ANN model, consisting of interconnected artificial neurons distributed across three layers: input, hidden, and output. During the training phase, the network’s weights were adjusted and modified using various training algorithms until the desired output was reproduced from a set of input data. The training process can be either supervised or unsupervised, depending on the inclusion of desired goals in the training process. The artificial neural network training algorithm enabled the feed-forward and back-propagation of information to minimize the discrepancy between the output and the desired target. Achieving satisfactory training results necessitates a significant allocation of computer resources. Once trained, the ANN model established a non-linear relationship between inputs and outputs, enabling predictions for new input datasets that were not part of the training data. For a more comprehensive understanding of the underlying theories and applications, further exploration can be found in [86].

2.4. ANN-Based Models

This study utilized a feed-forward backpropagation (BP) neural network architecture. Typically, this type of neural network consists of multiple interconnected layers of neurons. The network comprises an input layer, which is the first layer, and an output layer, which is the last layer. Additionally, there may be one or more hidden layers between them. The output of the network, denoted as $y_i$, can be expressed as follows:

$$y_i={\sum }_{j=1}^n{w}_{i,j}\ast x_{i,j}+b_i$$

(4)

where $x_{i,j}$ represents the signal received from the $j\mathrm{t}\mathrm{h}$ neuron at the input level, $w_{i,j}$ denotes the weight associated with the connection from neuron $j$ to neuron $i$ at the hidden level, and $b_i$ corresponds to the bias of neuron $i$. Each $y_i$ is calculated and then adjusted using an activation function, typically chosen from a set of monotonic functions, such as sigmoid functions, which are widely utilized. The ANN-based models developed in this study employed Multilayer Perceptron (MLP) networks with a single hidden layer, as depicted in Figure 5. The weights of the network were fine-tuned using the Levenberg–Marquardt (LM) algorithm. A “PURELIN” linear activation function was applied to the output layer. The network training was performed using the “TRAINLM” method, while the “TANSIG” transfer function, as defined in [31,87], was utilized:

$$f\left(x\right)=\frac{2}{1+\exp (-2x)}-1$$

(5)

The output of a neuron’s activation function in one layer typically served as input for the layer above it, while the final result of the model was generated by the activation function of the last layer. Backpropagation is the process of iteratively computing the error of the output layer to determine the errors for the hidden layers. The weights of the neurons were optimized using the Generalized Delta Rule (GDR), a learning method for backpropagation networks. The design of the ANN network significantly impacts its training process. An excessively large network may not be efficient during training, potentially leading to overfitting and a decline in generalization ability. Conversely, a network that is too small may fail to converge. To address these considerations and leverage the unique characteristics of the present work, a feed-forward backpropagation approach with one hidden layer was employed in this study. During the backpropagation process, the neurons exhibited saturated nonlinear characteristics. This implies that if there was a substantial difference between the input and threshold values, the neuron’s output will tend to be either the highest or the lowest value. To mitigate this issue, the proper management of the network’s input values was essential. Therefore, all input values were normalized from zero to one using Equation (6) before being restored to their initial values upon completion of the simulation [31,33].

The hidden layers commonly employed typical sigmoid functions, such as “TANSIG” and “LOGSIG”, as transfer functions. While using sigmoid transfer functions in the output layer may limit the range of output data, employing linear activation functions, such as the “PURELIN” transfer function, can address more complex problems. The presented ANN model was trained using the MATLAB neural network toolbox. The input layer consisted of two parameters: extra-terrestrial solar radiation and temperature. The output layer produced a single output: global solar radiation. The developed ANN models, specifically MLP, were trained to predict global solar radiation based on ambient air temperature and extra-terrestrial radiation. Given that the initialization of ANN biases and weights was performed randomly, the best results from ten runs were selected to ensure robustness and consistency.

$$X_{norm}=\frac{X-X_{min}}{X_{max}-X_{min}}$$

(6)

When discussing the number of neurons in the hidden layer, it is widely recognized that an ANN performs optimally when its design is finely tuned. Both under-fitting (low complexity and few neurons) and over-fitting (excessive neuron counts) result in suboptimal efficiency. Thus, selecting the appropriate number of neurons in the hidden layer is crucial. Currently, there is no mathematically justified method for determining the ideal number of hidden neurons. Using a large number of neurons increases the network’s training time and diminishes its generalization and prediction capabilities. Conversely, employing a small number of neurons fails to capture the intricate relationships between previous and subsequent values. Consequently, a trial-and-error approach is commonly employed to identify the optimal number of hidden neurons within the hidden layer [31,55,56].

Therefore, one of the main objectives of this study was to address the issue of determining the suitable number of neurons in the hidden layer of the ANN, which is considered a novel contribution. The aim was to establish the best ANN architecture for accurate GSR forecasting. Specifically, it is crucial to strike the right balance in order to avoid under-fitting or over-fitting the model. In this study, an investigation was conducted on the impact of different numbers of hidden layer neurons, ranging from one to fifty. The effectiveness of each architecture was evaluated based on ten independent runs.

The chosen design in this work stems from the fact that single-hidden-layer feed-forward ANNs have been established as universal approximators capable of accurately representing any continuous function [43,44,46]. Furthermore, MLP, being one of the faster learning algorithms commonly employed [88], has been favored for its efficiency. Additionally, feed-forward neural network models have garnered attention due to their ease of use and their ability to provide high-precision representations of measurable functions, especially in the realm of weather forecasting [47,48]. It has been demonstrated that a single hidden layer feed-forward neural network is sufficient to address various regression problems [44]. Moreover, in comparison to other machine-learning (ML) techniques such as the adaptive neuro-fuzzy inference system (ANFIS) and support vector machines (SVM) algorithms, MLP models exhibit exceptional performance in estimating global irradiation [39,89].

2.5. Empirical-Based Model

In general, GSR models rely on both linear and nonlinear approaches, establishing a relationship between global solar radiation incidents on a surface and various meteorological parameters such as cloud cover, relative humidity, sunshine duration, and temperature [90]. In this study, a newly proposed temperature-based solar model, referred to as the Hassan et al. model [19], was employed to assess GSR in the absence of dedicated instruments for radiation estimation. The advantage of utilizing this model lies in the ease and continuous availability of ambient temperature data recorded at most weather stations, which served as a primary benefit for this study (Hassan et al. model, Equation (7)). The mathematical formulation for the developed model in this work is defined as follows [19]:

$$\raisebox{1ex}{$G$}\!\left/ \!\raisebox{-1ex}{$G_0$}\right.=a T^b G_0+c$$

(7)

where T,$G$, and $G_0$ are the monthly average ambient temperature (°C), monthly average daily global solar radiation, and monthly average daily extra-terrestrial solar radiation on a horizontal surface (MJ/m² day⁻¹), respectively. a, b, and c are the empirical coefficients of the developed model.

Extra-terrestrial solar radiation, $G_0$, can be depicted as the radiation that originates outside the atmosphere of the Earth, and it is described as [91]:

$$G_o=\frac{24\times 3600 G_{sc}}{\pi } k\left[\left(\frac{\pi \omega }{180}\right)\mathit{sin}\left(L\right)\mathit{sin}\left(\delta \right)+\mathit{cos}\left(L\right)\mathit{cos}\left(\delta \right)sin\left(\omega \right)\right]$$

(8)

where $G_{sc}$ points to the solar constant ($G_{sc}=$1367 W/m²) [92,93]. k refers to the eccentricity correlation factor of the earth’s orbit, $L$ is the latitude angle (degree), $\omega$ is the hour angle at sunset (degree), and δ is the declination angle (degree). k, δ, and $\omega$ are described as [19,71]:

$$k=\left[1+0.033\mathit{cos}\left(\frac{360 N}{365}\right)\right]$$

(9)

$$\delta =23.45 sin\left[\frac{360}{365}(284+N)\right]$$

(10)

$$\omega ={\mathit{cos}}^{-1}[-\mathit{tan}\left(L\right)tan(\delta \left)\right]$$

(11)

where $N$ is the day number of the year starting from 1 January.

3. Performance Assessment

The performance of the developed models was evaluated using the most popular statistical errors; namely, Root Mean Square Error, RMSE, Mean Percentage Error, MPE, Mean Percentage Absolute Error, MAPE, Mean Absolute Bias Error, MABE, Mean Bias Error, MBE, and Coefficient of Determination, $R^2$, Correlation Coefficient, $r$, t-Test statistic, t-Test, and Relative Error, $e$, [9,16,58,59,94]. The RMSE values offered insights into the short-term performance of the model and are always expressed as positive values. A smaller RMSE indicates a better model performance, with zero representing the ideal case. Mean Bias Error values provide information about the long-term performance of the model, where negative values indicate underestimation and positive values indicate overestimation. A value close to zero is desirable, indicating a minimal bias in the model’s predictions.

The accepted range for RMSE, MPE, MBE, MAPE, and MABE is typically within ±10%. Similarly, the relative error, e, is preferred to be between ±10%. The t-test is used to compare models simultaneously and determine the statistical significance of their predictions, with lower values indicating better model performance [90,95]. The values of ($R^2$R2) show information about the goodness of fit. $R^2$R2 values lie between zero and one (0 ≤ $R^2$ ≤ 1) where the largest value is the desired value [25,60,96]. These statistical indicators are defined as the following:

$$RMSE={\left[\frac{1}{n} \sum _{i=1}^n{(G_{i.c}-G_{i.m})}^2\right]}^{1/2}$$

(12)

$$MABE=\frac{1}{n} {\sum }_{i=1}^n\left|(G_{i.c}-G_{i.m})\right|$$

(13)

$$MAPE=\frac{1}{n} {\sum }_{i=1}^n\left|\left(\frac{G_{i.c}-G_{i.m}}{G_{i.m}}\right)\times 100\right|$$

(14)

$$MBE=\frac{1}{n} {\sum }_{i=1}^n(G_{i.c}-G_{i.m})$$

(15)

$$MPE=\frac{1}{n} {\sum }_{i=1}^n\left(\frac{G_{i.c}-G_{i.m}}{G_{i.m}}\right)\times 100$$

(16)

$$r=\frac{\sum _{i=1}^n(G_{i.m }-\overline{G_m})(G_{i.c }-\overline{G_c})}{{\left[\sum _{i=1}^n{(G_{i.m }-\overline{G_m})}^2\sum _{i=1}^n{(G_{i.c }-\overline{G_c})}^2\right]}^{1/2}}$$

(17)

$$t={\left[\frac{(n-1){\left(MBE\right)}^2}{{\left(RMSE\right)}^2-{\left(MBE\right)}^2}\right]}^{1/2}$$

(18)

$$R^2=1-\frac{\sum _{i=1}^n{(G_{i.m}-{ G}_{i.c})}^2}{\sum _{i=1}^n{(G_{i.m }-\overline{G_m})}^2}$$

(19)

$$e=\left(\frac{G_{i,c}-G_{i,m}}{G_{i,m}}\right)\times 100$$

(20)

where G_i,c and G_i,m are the ith calculated value and the ith measured values, respectively. $\overline{G_m}$ is the average value of the measured values and n is the number of observations.

4. Results and Discussion

This section presents the findings obtained from optimizing the developed ANN models. The number of neurons in the hidden layer was varied from one to fifty to determine the optimal ANN architectures. The measured data of daily ambient temperature and global solar radiation were divided into two sets and averaged to obtain the monthly average daily values. The first set, spanning from 1 January 1984 to 31 December 2017, was used to construct both models. For the empirical model, regression analysis was employed to derive the empirical coefficients corresponding to the actual data of the study location, as outlined in

Table 1. Empirical coefficients for the developed empirical model, Equation (7), at the study location.

a	b	c
0.00163	0.48167	0.41701

[16,25,97]. In contrast, the developed ANN models were trained using the MATLAB neural network toolbox, with all training data normalized between the range of 0 and 1 prior to the training phase.

As mentioned earlier, this study had several objectives: to optimize the design of the ANN, one of the most widely used and efficient machine-learning techniques, for accurate GSR forecasting and computational efficiency. Therefore, determining the appropriate number of neurons in the single hidden layer of the ANN is crucial in developing a robust architecture for precise GSR prediction. Consequently, different numbers of neurons, ranging from one to fifty, were investigated in the hidden layer. Each ANN model was trained, and the best results from ten runs of each model were selected. The optimal performance of each trained ANN model was identified and is summarized in

Table 2. The number of runs at which the best performance for each trained ANN model was obtained, where neurons number in the hidden layer is varied from 1 to 50 neurons.

Hidden Layer’s Neurons Numbers	Iteration Number	Hidden Layer’s Neurons Numbers	Iteration Number
Model_NurnNo._1	6	Model_NurnNo._26	10
Model_NurnNo._2	9	Model_NurnNo._27	6
Model_NurnNo._3	10	Model_NurnNo._28	7
Model_NurnNo._4	10	Model_NurnNo._29	2
Model_NurnNo._5	9	Model_NurnNo._30	2
Model_NurnNo._6	8	Model_NurnNo._31	9
Model_NurnNo._7	10	Model_NurnNo._32	8
Model_NurnNo._8	4	Model_NurnNo._33	2
Model_NurnNo._9	3	Model_NurnNo._34	9
Model_NurnNo._10	4	Model_NurnNo._35	3
Model_NurnNo._11	10	Model_NurnNo._36	3
Model_NurnNo._12	8	Model_NurnNo._37	9
Model_NurnNo._13	5	Model_NurnNo._38	9
Model_NurnNo._14	10	Model_NurnNo._39	10
Model_NurnNo._15	4	Model_NurnNo._40	4
Model_NurnNo._16	9	Model_NurnNo._41	10
Model_NurnNo._17	7	Model_NurnNo._42	3
Model_NurnNo._18	10	Model_NurnNo._43	6
Model_NurnNo._19	9	Model_NurnNo._44	8
Model_NurnNo._20	8	Model_NurnNo._45	9
Model_NurnNo._21	9	Model_NurnNo._46	7
Model_NurnNo._22	5	Model_NurnNo._47	9
Model_NurnNo._23	8	Model_NurnNo._48	7
Model_NurnNo._24	2	Model_NurnNo._49	8
Model_NurnNo._25	10	Model_NurnNo._50	9

.

On the other hand, the second set, covering the period from 1 January 2020 to 31 December 2020, was utilized to evaluate and validate the developed models (empirical and ANN models) using various statistical indicators. The predicted values of the global solar radiation from both models were compared against the measured data at the selected site. The evaluation indicators (MPE, MAPE, RMSE, MBE, MABE, r, and $R^2$) were obtained using Equations (12)–(19) and the best models were recognized and are indicated in bold. The following subsections provide a detailed discussion focusing on the results obtained from both techniques (ANN method and empirical method), as well as their performance comparison.

4.1. Impact of Neurons Numbers Variation on ANN Prediction Accuracy

Regarding the developed ANN-based solar models, the values of various performance indicators such as MBE, MPE, t-Test, RMSE, MAPE, MABE, r, and $R^2$ were calculated for each model. These values are then summarized in

Table 3. Statistical indicators for each developed ANN model are arranged based on the hidden layer’s neuron numbers (1–50).

Model	t-Test	MPE	MBE	RMSE	MAPE	MABE	r	${\mathit{R}}^2$	Rank
Model_NurnNo._1	1.3245	3.1866	0.3330	0.8979	4.5647	0.7259	0.9990	0.9813	2
Model_NurnNo._2	1.3252	3.2125	0.3374	0.9093	4.9410	0.8207	0.9991	0.9809	3
Model_NurnNo._3	0.7968	2.4354	0.1953	0.8361	4.3401	0.7216	0.9991	0.9838	1
Model_NurnNo._4	0.9583	2.9247	0.2551	0.9188	4.7946	0.7811	0.9996	0.9805	4
Model_NurnNo._5	2.0245	4.2101	0.5409	1.0381	5.4992	0.9045	0.9968	0.9751	11
Model_NurnNo._6	1.6643	4.2867	0.4992	1.1131	6.0064	0.9769	0.9984	0.9713	17
Model_NurnNo._7	1.6842	3.5867	0.4183	0.9239	5.0368	0.8171	0.9983	0.9803	5
Model_NurnNo._8	1.4417	3.5178	0.3822	0.9587	5.0704	0.8099	0.9985	0.9787	8
Model_NurnNo._9	1.5307	3.7593	0.4171	0.9952	5.3552	0.8651	0.9989	0.9771	9
Model_NurnNo._10	0.3335	2.3505	0.1205	1.2042	5.9015	1.0355	0.9909	0.9665	26
Model_NurnNo._11	0.2467	1.9073	0.0706	0.9523	5.1224	0.8720	0.9959	0.9790	7
Model_NurnNo._12	1.9155	5.3634	0.7050	1.4097	6.8925	1.1304	0.9917	0.9540	35
Model_NurnNo._13	1.6868	4.6575	0.5489	1.2108	6.2871	0.9978	0.9965	0.9661	27
Model_NurnNo._14	0.9476	5.1520	0.5195	1.8909	9.0598	1.4960	0.9720	0.9173	46
Model_NurnNo._15	2.4363	7.8021	1.2379	2.0910	9.2153	1.6378	0.9693	0.8988	47
Model_NurnNo._16	2.0677	4.3965	0.5499	1.0395	5.6859	0.9152	0.9992	0.9750	12
Model_NurnNo._17	0.8304	3.2031	0.3943	1.6233	7.7703	1.4084	0.9713	0.9390	43
Model_NurnNo._18	1.7570	5.1653	0.6720	1.4356	6.9261	1.1675	0.9891	0.9523	40
Model_NurnNo._19	1.7729	4.3450	0.5337	1.1322	5.7750	0.9423	0.9966	0.9703	19
Model_NurnNo._20	1.4727	4.2452	0.5768	1.4214	6.6163	1.1566	0.9834	0.9533	38
Model_NurnNo._21	0.6326	3.2534	0.2545	1.3586	6.9932	1.1561	0.9880	0.9573	32
Model_NurnNo._22	0.7264	2.7552	0.2353	1.1000	6.0099	1.0436	0.9931	0.9720	16
Model_NurnNo._23	2.1860	8.3605	1.3308	2.4182	9.7377	1.7202	0.9536	0.8647	49
Model_NurnNo._24	1.9135	4.3814	0.5763	1.1532	5.8280	0.9528	0.9941	0.9692	20
Model_NurnNo._25	1.1241	4.2235	0.4407	1.3730	7.2452	1.1468	0.9887	0.9564	33
Model_NurnNo._26	1.7843	4.0408	0.4927	1.0400	5.3938	0.8737	0.9978	0.9750	13
Model_NurnNo._27	1.8753	4.8950	0.6017	1.2225	6.4165	1.0099	0.9964	0.9654	28
Model_NurnNo._28	1.9807	5.0783	0.7248	1.4135	6.9399	1.2398	0.9872	0.9538	37
Model_NurnNo._29	0.7275	2.8267	0.2238	1.0448	5.5863	0.9177	0.9955	0.9747	14
Model_NurnNo._30	1.7596	4.6702	0.5560	1.1863	6.4659	1.0569	0.9977	0.9674	24
Model_NurnNo._31	2.0945	5.6172	0.7434	1.3922	6.8308	1.0935	0.9942	0.9552	34
Model_NurnNo._32	1.1978	2.9893	0.3169	0.9331	4.8235	0.8396	0.9977	0.9799	6
Model_NurnNo._33	1.0223	3.6796	0.3495	1.1866	6.3278	1.0698	0.9956	0.9674	25
Model_NurnNo._34	1.7355	4.8638	0.5929	1.2789	6.8208	1.1401	0.9960	0.9622	31
Model_NurnNo._35	1.7905	4.7620	0.5918	1.2458	6.4519	1.0636	0.9949	0.9641	30
Model_NurnNo._36	1.6011	4.3551	0.5020	1.1546	6.2681	1.0142	0.9973	0.9692	21
Model_NurnNo._37	1.6723	4.5350	0.5328	1.1834	6.3088	1.0366	0.9981	0.9676	23
Model_NurnNo._38	1.3279	4.0845	0.5324	1.4324	6.8530	1.1948	0.9821	0.9525	39
Model_NurnNo._39	1.4119	4.1074	0.4613	1.1778	6.2911	1.0525	0.9951	0.9679	22
Model_NurnNo._40	0.8524	3.7709	0.4601	1.8484	8.1824	1.4720	0.9631	0.9210	45
Model_NurnNo._41	1.8174	6.1221	0.8503	1.7694	8.0014	1.3841	0.9796	0.9276	44
Model_NurnNo._42	1.9298	5.9399	0.7935	1.5777	7.9860	1.2873	0.9857	0.9424	42
Model_NurnNo._43	0.7720	2.9740	0.2563	1.1306	5.8829	1.0089	0.9928	0.9704	18
Model_NurnNo._44	1.8389	5.0259	0.6841	1.4109	6.9763	1.2353	0.9887	0.9539	36
Model_NurnNo._45	2.4297	6.3276	0.8946	1.5137	7.5982	1.2589	0.9913	0.9470	41
Model_NurnNo._46	0.0141	1.2689	0.0199	4.7055	14.9119	2.7546	0.7968	0.4877	50
Model_NurnNo._47	2.1904	4.9419	0.6766	1.2277	5.9423	0.9673	0.9945	0.9651	29
Model_NurnNo._48	0.2430	0.6792	-0.1565	2.1408	8.0687	1.3757	0.9458	0.8940	48
Model_NurnNo._49	1.6216	3.7857	0.4456	1.0145	5.5278	0.8952	0.9967	0.9762	10
Model_NurnNo._50	1.6941	3.9323	0.4758	1.0460	5.5133	0.9301	0.9966	0.9747	15

, utilizing Equations (12)–(19). Based on the revealed results, the statistical errors for all developed ANN models were in the acceptable range ±10%. except for the ANN model which had 46 neurons in its hidden layer, “Model_NurnNo._46”, its MAPE exceeded the acceptable range, MAPE equals 14.9119%. Additionally, while Model_NurnNo._46 had the worst performance, Model_NurnNo._3 provided the best performance followed by Model_NurnNo._1, Model_NurnNo._2, and Model_NurnNo._4, where their Coefficient of Determination, $R^2$, was higher than 0.98%. As mentioned before, $R^2$ suggests a good fitting between the model’s prediction and observed values of global solar radiation. The best ANN model, Model_NurnNo._3, had good values of all indicators, t-test, MPE, MBE, RMSE, MAPE, MABE, $r$, and $R^2$ as 0.7968, 2.4354%, 0.1953 (MJ/m² day⁻¹), 0.8361 (MJ/m² day⁻¹), 4.3401%, 0.7216 (MJ/m² day⁻¹), 0.9991, and 0.9838%, respectively. Figure 6a shows its predictions compared to the measured data throughout the year. The prediction in the winter months was slightly overestimated, and this may return to different weather conditions such as clouds, rains, and winds [19,72,98].

Additionally, it is worthy of note that, firstly, ANN architectures with fewer neurons number in the hidden layer, from 1 to 4 neurons, gave the best performance compared with other models, where their $R^2$ > 0.98%. Secondly, the performance of the developed ANN models was approximately stable and excellent when neurons number were less than 10 neurons in the hidden layer, and they were very close to each other, with $R^2$ > 0.97%, as seen in Table 3. Furthermore, while ANN’s architectures—in some cases—with large neurons number in the hidden layer performed well, like “Model_NurnNo._32” with $R^2$ equals 0.97986%, there were many other ANN models that varied in their performance with $R^2$ ranges from 0.48% to 0.97%, and performance instability was observed. For more clarification, the performance of the developed ANN models against the variation of neuron numbers in the single hidden layer is clarified in Figure 7. Additionally, they were arranged based on their performance (Rank) as seen in

Table 4. Statistical indicators for each developed ANN model are arranged based on their performance, $R^2$.

Model	t-Test	MPE	MBE	RMSE	MAPE	MABE	r	${\mathit{R}}^2$	Rank
Model_NurnNo._3	0.7968	2.4354	0.1953	0.8361	4.3401	0.7216	0.9991	0.9838	1
Model_NurnNo._1	1.3245	3.1866	0.3330	0.8979	4.5647	0.7259	0.9990	0.9813	2
Model_NurnNo._2	1.3252	3.2125	0.3374	0.9093	4.9410	0.8207	0.9991	0.9809	3
Model_NurnNo._4	0.9583	2.9247	0.2551	0.9188	4.7946	0.7811	0.9996	0.9805	4
Model_NurnNo._7	1.6842	3.5867	0.4183	0.9239	5.0368	0.8171	0.9983	0.9803	5
Model_NurnNo._32	1.1978	2.9893	0.3169	0.9331	4.8235	0.8396	0.9977	0.9799	6
Model_NurnNo._11	0.2467	1.9073	0.0706	0.9523	5.1224	0.8720	0.9959	0.9790	7
Model_NurnNo._8	1.4417	3.5178	0.3822	0.9587	5.0704	0.8099	0.9985	0.9787	8
Model_NurnNo._9	1.5307	3.7593	0.4171	0.9952	5.3552	0.8651	0.9989	0.9771	9
Model_NurnNo._49	1.6216	3.7857	0.4456	1.0145	5.5278	0.8952	0.9967	0.9762	10
Model_NurnNo._5	2.0245	4.2101	0.5409	1.0381	5.4992	0.9045	0.9968	0.9751	11
Model_NurnNo._16	2.0677	4.3965	0.5499	1.0395	5.6859	0.9152	0.9992	0.9750	12
Model_NurnNo._26	1.7843	4.0408	0.4927	1.0400	5.3938	0.8737	0.9978	0.9750	13
Model_NurnNo._29	0.7275	2.8267	0.2238	1.0448	5.5863	0.9177	0.9955	0.9747	14
Model_NurnNo._50	1.6941	3.9323	0.4758	1.0460	5.5133	0.9301	0.9966	0.9747	15
Model_NurnNo._22	0.7264	2.7552	0.2353	1.1000	6.0099	1.0436	0.9931	0.9720	16
Model_NurnNo._6	1.6643	4.2867	0.4992	1.1131	6.0064	0.9769	0.9984	0.9713	17
Model_NurnNo._43	0.7720	2.9740	0.2563	1.1306	5.8829	1.0089	0.9928	0.9704	18
Model_NurnNo._19	1.7729	4.3450	0.5337	1.1322	5.7750	0.9423	0.9966	0.9703	19
Model_NurnNo._24	1.9135	4.3814	0.5763	1.1532	5.8280	0.9528	0.9941	0.9692	20
Model_NurnNo._36	1.6011	4.3551	0.5020	1.1546	6.2681	1.0142	0.9973	0.9692	21
Model_NurnNo._39	1.4119	4.1074	0.4613	1.1778	6.2911	1.0525	0.9951	0.9679	22
Model_NurnNo._37	1.6723	4.5350	0.5328	1.1834	6.3088	1.0366	0.9981	0.9676	23
Model_NurnNo._30	1.7596	4.6702	0.5560	1.1863	6.4659	1.0569	0.9977	0.9674	24
Model_NurnNo._33	1.0223	3.6796	0.3495	1.1866	6.3278	1.0698	0.9956	0.9674	25
Model_NurnNo._10	0.3335	2.3505	0.1205	1.2042	5.9015	1.0355	0.9909	0.9665	26
Model_NurnNo._13	1.6868	4.6575	0.5489	1.2108	6.2871	0.9978	0.9965	0.9661	27
Model_NurnNo._27	1.8753	4.8950	0.6017	1.2225	6.4165	1.0099	0.9964	0.9654	28
Model_NurnNo._47	2.1904	4.9419	0.6766	1.2277	5.9423	0.9673	0.9945	0.9651	29
Model_NurnNo._35	1.7905	4.7620	0.5918	1.2458	6.4519	1.0636	0.9949	0.9641	30
Model_NurnNo._34	1.7355	4.8638	0.5929	1.2789	6.8208	1.1401	0.9960	0.9622	31
Model_NurnNo._21	0.6326	3.2534	0.2545	1.3586	6.9932	1.1561	0.9880	0.9573	32
Model_NurnNo._25	1.1241	4.2235	0.4407	1.3730	7.2452	1.1468	0.9887	0.9564	33
Model_NurnNo._31	2.0945	5.6172	0.7434	1.3922	6.8308	1.0935	0.9942	0.9552	34
Model_NurnNo._12	1.9155	5.3634	0.7050	1.4097	6.8925	1.1304	0.9917	0.9540	35
Model_NurnNo._44	1.8389	5.0259	0.6841	1.4109	6.9763	1.2353	0.9887	0.9539	36
Model_NurnNo._28	1.9807	5.0783	0.7248	1.4135	6.9399	1.2398	0.9872	0.9538	37
Model_NurnNo._20	1.4727	4.2452	0.5768	1.4214	6.6163	1.1566	0.9834	0.9533	38
Model_NurnNo._38	1.3279	4.0845	0.5324	1.4324	6.8530	1.1948	0.9821	0.9525	39
Model_NurnNo._18	1.7570	5.1653	0.6720	1.4356	6.9261	1.1675	0.9891	0.9523	40
Model_NurnNo._45	2.4297	6.3276	0.8946	1.5137	7.5982	1.2589	0.9913	0.9470	41
Model_NurnNo._42	1.9298	5.9399	0.7935	1.5777	7.9860	1.2873	0.9857	0.9424	42
Model_NurnNo._17	0.8304	3.2031	0.3943	1.6233	7.7703	1.4084	0.9713	0.9390	43
Model_NurnNo._41	1.8174	6.1221	0.8503	1.7694	8.0014	1.3841	0.9796	0.9276	44
Model_NurnNo._40	0.8524	3.7709	0.4601	1.8484	8.1824	1.4720	0.9631	0.9210	45
Model_NurnNo._14	0.9476	5.1520	0.5195	1.8909	9.0598	1.4960	0.9720	0.9173	46
Model_NurnNo._15	2.4363	7.8021	1.2379	2.0910	9.2153	1.6378	0.9693	0.8988	47
Model_NurnNo._48	0.2430	0.6792	−0.1565	2.1408	8.0687	1.3757	0.9458	0.8940	48
Model_NurnNo._23	2.1860	8.3605	1.3308	2.4182	9.7377	1.7202	0.9536	0.8647	49
Model_NurnNo._46	0.0141	1.2689	0.0199	4.7055	14.9119	2.7546	0.7968	0.4877	50

, where the first ninth-ranked models had few neurons number in the hidden layer (less than ten neurons) except for in Models 11 and 32.

Moreover, the relative error, e, was calculated for each month of all developed ANN models based on Equation (20) and presented in

Table 5. Relative errors for all developed ANN-based solar radiation models throughout the whole year.

Model	Jan	Feb	Mar	Apr	May	Jun	Jul	Aug	Sep	Oct	Nov	Dec
Model_NurnNo._1	9.9	7.8	4.7	−0.2	−0.8	−2.7	−2.4	−1.9	0.2	−0.2	11.9	11.9
Model_NurnNo._2	12.3	8.6	3.5	−2.0	−1.4	−2.3	−2.6	−2.1	2.1	2.3	11.1	9.1
Model_NurnNo._3	8.1	6.1	3.8	−1.9	−1.9	−2.5	−2.2	−2.3	−0.3	−0.3	11.9	10.8
Model_NurnNo._4	13.7	8.2	1.6	−1.2	−1.6	−2.9	−2.3	−3.0	−0.2	2.1	10.0	10.8
Model_NurnNo._5	15.2	6.3	2.5	−1.7	−1.7	−3.0	−1.4	1.7	6.1	2.6	11.3	12.5
Model_NurnNo._6	15.3	9.6	4.4	−2.8	−2.0	−2.5	−2.3	−0.7	1.0	8.0	11.4	12.1
Model_NurnNo._7	14.2	6.7	2.4	−3.1	−1.9	−2.3	−1.5	1.5	2.1	3.0	10.2	11.7
Model_NurnNo._8	14.9	4.9	4.9	−3.2	−1.2	−1.9	−2.6	−0.4	0.3	4.1	9.9	12.6
Model_NurnNo._9	16.6	6.6	4.1	−1.8	−2.6	−2.2	−2.3	−0.7	2.5	2.6	10.1	12.1
Model_NurnNo._10	13.4	6.8	4.6	0.7	−2.6	−2.0	−2.2	−3.2	−11.2	2.9	10.4	10.6
Model_NurnNo._11	13.4	4.4	4.5	−2.7	−1.4	−2.7	−1.9	−1.6	−5.6	−3.4	8.4	11.5
Model_NurnNo._12	17.9	10.7	3.5	−2.4	−1.9	−2.3	−2.1	−0.5	2.3	17.0	10.6	11.5
Model_NurnNo._13	23.2	10.7	4.5	−3.2	−2.3	−1.9	−2.3	0.1	2.4	3.9	10.1	10.9
Model_NurnNo._14	30.0	19.6	5.2	−3.0	−2.9	−1.3	−2.0	−0.1	−14.1	10.4	7.8	12.3
Model_NurnNo._15	20.6	14.2	7.7	−1.7	−1.7	−2.4	−2.7	2.4	22.3	13.6	9.6	11.7
Model_NurnNo._16	14.2	8.4	4.5	−1.0	−1.9	−2.1	−1.9	−0.7	3.0	6.5	10.7	13.2
Model_NurnNo._17	16.3	7.1	4.5	−1.7	−2.5	−3.0	−2.5	7.1	9.8	−17.7	10.8	10.3
Model_NurnNo._18	14.2	18.8	2.4	−2.3	−1.7	−2.7	−3.2	−0.5	11.1	2.3	11.6	12.1
Model_NurnNo._19	14.4	14.9	3.6	−1.1	−1.2	−1.8	−3.9	−0.5	5.0	2.0	9.7	11.1
Model_NurnNo._20	11.1	16.8	5.9	−1.7	−1.3	−2.7	−2.7	0.1	12.8	−5.9	11.2	7.2
Model_NurnNo._21	20.5	17.1	5.3	−1.3	−4.0	−2.8	−1.5	−1.8	−2.8	−8.3	10.1	8.5
Model_NurnNo._22	13.1	7.1	7.6	−2.3	−2.7	−2.8	−2.0	−3.1	3.5	−6.5	11.7	9.6
Model_NurnNo._23	16.0	13.0	7.1	−1.4	−2.6	−2.5	−1.8	2.8	10.9	36.8	9.8	12.1
Model_NurnNo._24	12.5	16.6	7.4	−1.2	−2.2	−1.6	−1.7	0.6	4.7	−2.0	9.9	9.6
Model_NurnNo._25	20.9	15.0	5.6	1.4	−0.3	−2.7	−1.3	−2.7	−2.8	−8.3	13.7	12.1
Model_NurnNo._26	11.9	13.4	2.0	−2.1	−0.8	−1.9	−3.3	0.2	2.0	6.6	10.1	10.4
Model_NurnNo._27	18.1	15.3	6.5	−2.8	−2.1	−2.0	−0.9	0.9	−1.3	4.2	9.7	13.1
Model_NurnNo._28	15.2	7.2	5.5	−3.3	−3.0	−2.5	−2.3	2.2	13.5	6.6	11.4	10.4
Model_NurnNo._29	15.1	9.9	4.7	−1.8	−1.4	−2.7	−1.5	−1.2	−5.7	−2.3	9.1	11.6
Model_NurnNo._30	18.8	8.9	5.8	−2.5	−2.4	−2.1	−3.0	−0.8	4.3	4.3	11.0	13.8
Model_NurnNo._31	14.4	15.7	4.4	−0.4	−2.2	−2.4	−2.3	0.2	0.4	14.7	11.6	13.2
Model_NurnNo._32	8.6	5.4	2.6	1.0	−3.4	−2.3	−2.4	−2.9	0.8	8.9	9.3	10.2
Model_NurnNo._33	13.1	9.3	4.3	−1.3	−2.3	−3.0	−4.8	2.4	−4.5	2.0	14.8	14.1
Model_NurnNo._34	16.4	13.0	3.0	−1.9	−2.2	−2.5	−2.5	−2.8	4.0	10.9	11.2	11.7
Model_NurnNo._35	22.2	10.7	3.2	−2.2	−1.5	−2.1	−2.8	−1.5	6.8	4.9	10.5	9.0
Model_NurnNo._36	12.8	11.8	5.8	−1.0	−1.5	−2.3	−2.6	0.6	−4.0	5.7	13.0	14.0
Model_NurnNo._37	17.2	10.5	7.1	−1.5	−1.5	−2.3	−4.1	−1.3	1.9	5.0	12.9	10.4
Model_NurnNo._38	12.5	6.4	6.5	−2.8	−2.5	−1.8	−1.6	−1.2	14.4	−6.8	12.7	13.2
Model_NurnNo._39	14.7	7.3	5.7	−5.2	−2.0	−1.7	−2.7	−1.7	5.7	1.4	14.5	13.1
Model_NurnNo._40	14.0	12.2	3.8	−3.0	−3.5	−2.9	−2.3	−0.3	19.1	−14.4	11.2	11.4
Model_NurnNo._41	15.0	13.5	4.6	0.8	−2.2	−1.9	−2.8	−4.3	4.7	24.6	10.5	10.9
Model_NurnNo._42	25.3	14.1	8.3	−0.3	−2.3	−2.3	−1.6	0.3	9.9	−5.8	14.4	11.3
Model_NurnNo._43	15.0	5.3	4.9	−1.7	−1.8	−2.6	−2.7	1.9	−8.6	3.8	8.9	13.3
Model_NurnNo._44	15.0	8.5	10.2	−1.4	−2.9	−2.7	−2.9	−1.8	12.2	4.6	10.3	11.3
Model_NurnNo._45	18.2	12.7	3.0	−0.8	−1.9	−1.6	−3.3	0.4	10.2	12.9	12.1	14.1
Model_NurnNo._46	23.9	15.1	1.8	−1.8	−4.2	−3.6	−0.8	2.1	34.1	−71.5	12.6	7.6
Model_NurnNo._47	13.8	7.0	2.7	−0.5	−0.8	−2.6	−2.2	0.6	2.8	14.8	12.8	10.9
Model_NurnNo._48	12.8	13.1	4.9	−1.7	−1.5	−2.7	−2.1	0.8	−1.7	−34.7	9.3	11.6
Model_NurnNo._49	13.3	9.4	−2.4	−2.7	−1.2	−1.9	−2.3	0.6	3.8	5.4	11.4	12.1
Model_NurnNo._50	12.7	8.9	3.3	−0.9	−2.4	−3.0	−3.2	2.5	4.7	0.4	12.3	11.8

. It is worth noting that the values for the best ANN model, Model_NurnNo._3, fell within the preferred range of ±10% for all months, except for November and December, where they slightly exceeded the range at 11.9% and 10.8%, respectively. Similarly, the values of the second and third-ranked models, Model_NurnNo._1 and Model_NurnNo._2, were within the range, except for some winter months where they marginally surpassed the range. This can be attributed to varying climatic conditions, particularly in winter, such as rain, clouds, and wind [19,96,98].

In general, it is evident that while some models exhibited relative error values within the range for all months, such as Model_NurnNo._32, others slightly exceeded the range during certain winter months. On the other hand, certain models significantly surpassed the range, like Model_NurnNo._14 in January, with a relative error of 30%. Furthermore, although many ANN models demonstrated good statistical errors (MBE, MPE, t-test, RMSE, MAPE, MABE, r, and R²), their relative error noticeably exceeded the range, particularly in winter months. For instance, in January, the relative error for Models 13, 14, 15, 21, 25, and 35 exceeded 20%. Finally, the ANN models with the most favorable relative error values were Model_NurnNo._3, Model_NurnNo._32, and Model_NurnNo._1.

4.2. Performance Comparison with Conventional Methods

Of particular interest, the performance of the best ANN model (Model_NurnNo._3) was compared to that of the conventional models (empirical model). As previously mentioned, Hassan et al. [19] recently proposed new temperature-based solar models for estimating global solar radiation, which have not been compared to any ML models before. The empirical coefficients for the best Hassan et al.’s model (Equation (7)) were computed and are presented in Table 1, and its statistical errors were obtained and compared to those of the best ANN model as illustrated in

Table 6. Statistical indicators for the best ANN model (NurnNo._3) against the empirical one (Hassan et al. model, Equation (7)).

Model	t-Test	MPE	MBE	RMSE	MAPE	MABE	r	${\mathit{R}}^2$	Rank
ANN Model (NurnNo._3)	0.7968	2.4354	0.1953	0.8361	4.3401	0.7216	0.9991	0.9838	2
Empirical Model	2.4991	−3.1889	−0.4620	0.7676	3.6733	0.6021	0.9981	0.9864	1

. The results revealed that Hassan et al.’s model demonstrated excellent performance with favorable indicator values, including t-test, MPE, MBE, RMSE, MAPE, MABE, r, and $R^2$, with values of 2.4991, −3.1889%, −0.4620 (MJ/m² day⁻¹), 0.7676 (MJ/m² day⁻¹), 3.6733%, 0.6021 (MJ/m² day⁻¹), 0.9981, and 0.9864%, respectively. Furthermore, while both models (ANN and empirical) exhibited a similar performance, Hassan et al.’s model outperformed the ANN model with the highest $R^2$ value of 0.9864% [25]. The predictions of each model, as well as the comparison with the measured data, are presented in Figure 6a–c. Similarly, their statistical indicators are depicted in Figure 8.

Additionally, the relative errors for the empirical model were calculated using Equation (20) and were compared to those of the best ANN model, as shown in

Table 7. Relative errors for the best ANN model (NurnNo._3) against the empirical one (Hassan et al. model, Equation (7)).

Model	Jan	Feb	Mar	Apr	May	Jun	Jul	Aug	Sep	Oct	Nov	Dec
ANN Model (NurnNo._3)	8.1	6.1	3.8	−1.9	−1.9	−2.5	−2.2	−2.3	−0.3	−0.3	11.9	10.8
Empirical Model	−8.2	−2.8	−0.2	−1.3	1.2	0.7	1.1	−0.9	−2.8	−9.3	−5.6	−10.0

. It is evident that the relative errors of the developed empirical model, Hassan et al. [19], for all months of the year fell within the acceptable range of ±10%, including the winter months. Conversely, the values of the best ANN model, Model_NurnNo._3, slightly exceeded the range in November and December, at 11.9% and 10.8%, respectively. This can be attributed to different weather factors, especially during the winter season, such as clouds, wind, and rain [19,72,97,98]. Figure 9 illustrates the relative errors for both models throughout the year at the study location, New Borg El-Arab City, Alexandria, Egypt.

4.3. Influence of the Learning Rate on ANN Prediction Accuracy

More importantly, the influence of the learning rate was investigated to know its effect on ANN prediction and accuracy. Thus, the best-developed ANN architecture, ANN Model with three neurons in its hidden layer (Model_NurnNo._3) was used to assess the impact of varying learning rates on its performance. Another five learning rates, 0.5, 0.1, 0.05, 0.005, and 0.001, were examined and compared with the most commonly used one, 0.01, where all performance indicators were obtained and are summarized in

Table 8. Influence of the learning rate on the accuracy and prediction of the best ANN architecture (ANN Model_NurnNo._3).

Model	t-Test	MPE	MBE	RMSE	MAPE	MABE	r	${\mathit{R}}^2$	Rank
Model_lr_0.5	1.92878	4.31639	0.53981	1.07379	5.70034	0.93463	0.99823	0.97332	6
Model_lr_0.1	0.37588	2.25109	0.10964	0.97361	5.31092	0.90909	0.99817	0.97807	5
Model_lr_0.05	1.04318	2.70368	0.26045	0.86806	4.48158	0.73888	0.99800	0.98257	3
Model_lr_0.01	0.79676	2.43540	0.19530	0.83610	4.34006	0.72156	0.99905	0.98383	1
Model_lr_0.005	1.72379	3.46941	0.42833	0.92879	5.00093	0.85541	0.99736	0.98004	4
Model_lr_0.001	1.49243	3.18835	0.35135	0.85620	4.33872	0.67601	0.99895	0.98304	2

. The revealed results show that the obtained accuracy for all tested learning rates was very good with R² higher than 97%. Additionally, while ANN models with learning rates of 0.05, 0.01, 0.005, and 0.001 were very close to each other in their performance, the ANN model with a learning rate of 0.01 (the most commonly used one) provided the best accuracy followed by ANN models with learning rates of 0.001, 0.05, and 0.005, respectively. For more clarification, the accuracy of the used leaning rate, 0.01 (best one), is illustrated in Figure 10. Generally, it can be noted that there was no significant effect of learning rate variation on the accuracy and the prediction of the best-developed ANN architecture, where the variance in models’ performance was too small.

4.4. Comparison with Previous Related Work

Furthermore, the obtained results from the study were compared with the related work reported in the state of the art, both at the level of solar radiation prediction (long-term forecast) and at the level of machine-learning and deep-learning techniques. In terms of using DL-based models for long-term GSR prediction, as mentioned before, using the DL technique to forecast in the long term is rare, where it is almost employed in prediction short-term GSR prediction such as minutely and hourly. However, a recent study in an acclaimed journal (Energies Journal) utilized DL algorithms for long-term GSR prediction in four Australian cities [82]. The study employed different DL algorithms such as Deep Neural Networks (DNN) and Deep Belief Networks (DBN) for estimating long-term GSR (monthly scale). Different architectures of both algorithms were investigated and the best-developed DL-based models were compared with the most common ML-based methods such as ANN (single hidden layer), Decision Tree (DT), and Random Forest (RF). For more clarification, the best two architectures of DL-based models and the two best ML-based models were selected and are presented in

Table 9. The RMSE and $r$ values of the two best models of each technique, DL-based models and ML-based models, in the previous work in predicting long-term GSR (monthly) [82].

#	City	RMSE				r
		DL-Based Models		ML-Based Models		DL-Based Models		ML-Based Models
		DBN	DNN	ANN	DT	DBN	DNN	ANN	DT
1	Blacktown	0.546	0.706	0.739	1.309	0.994	0.990	0.989	0.955
2	Adelaide	0.503	0.636	0.653	1.063	0.997	0.996	0.997	0.985
3	Central Victoria	0.614	0.798	1.276	1.696	0.996	0.994	0.984	0.961
4	Townsville	0.773	0.868	0.991	1.181	0.974	0.967	0.972	0.951

. The results showed that the two DL-based models (DNN and DBN) and ANN (ML-based model) outperformed all other data-driven models in terms of accuracy.

More significantly, it is worth of note that the performance of both DL models, DBN and DNN, were very close to each other. However, the DBN model had the best performance at all sites with RMSE values between 0.503 and 0.773 (MJ/m² day⁻¹) and correlation coefficient, $r$, values between 0.974 and 0.997, respectively. Moreover, the ANN (single hidden layer) model provided the best performance compared with all examined ML-based models at the four selected locations, with RMSE and $r$ values ranging from 0.653 to 1.276 (MJ/m² day⁻¹) and from 0.972 and 0.997, successively. This indicates that the performance of ANN and DL-based models was very close to each other, as demonstrated in Table 9. On the other hand, we compared the results of our optimized ANN model with the best DL-based and ML-based models from a previous study [82]. The table below,

Table 10. The RMSE and $r$ values of the optimized ANN model in this work, ANN Model (NurnNo._3), compared with the ranges of the best DL and ML-based models in the previous work [82] in predicting long-term GSR (monthly).

Indicator	Acceptable Ranges	Previous Studies				Current Study
		DL-Based Models		ML-Based Models		Optimized ANN-Based Model
		Min	Max	Min	Max	Value
RMSE	Between: ±10%, (The smallest value is the desired one)	0.503	0.868	0.653	1.696	0.8361
r	Between: 0 and 1, (The biggest value is the desired one)	0.967	0.997	0.951	0.997	0.999

, shows the RMSE and r values for each model. Our optimized ANN model had a very good RMSE value of 0.8361 MJ/m² day⁻¹, which falls within the ranges of both DL and ML techniques. In contrast to the previous study, our optimized ANN model had a better $r$ value of 0.999. For more clarification, the RMSE and $r$ values of the optimized ANN model in this study were compared with those of the previous work and are represented in Figure 11 and Figure 12. It is notable that the optimized artificial neural network (ANN) model in this study demonstrated strong performance, coming very close to the top-performing models based on deep-learning techniques.

Overall, it can be mentioned that while the efficiency difference between DL and ML techniques is insignificant, especially when predicting monthly average daily GSR, it is noteworthy that the period needed to train or test ML techniques makes them advantageous, particularly when computational power is included. Therefore, these revealed results support and strengthen the main objectives of this work, which aim to improve the accuracy of solar radiation forecasts while preserving computing resources by optimizing the design of ANNs, one of the quickest and most popular machine-learning algorithms. Additionally, the obtained results from the current work are in line with the previous up-to-date and related work [42,82].

Based on the obtained results, it can be concluded that the developed models in this study, namely the best ANN model and the empirical model [19], exhibited higher accuracy in estimating Global Solar Radiation. These models, based on temperature, demonstrate a high level of applicability, and can be effectively integrated with various short-term or long-term weather forecasting methods. Furthermore, the development of ANN-based solar radiation models with a limited number of neurons in the single hidden layer (less than 10 neurons) shows great promise for accurately predicting global solar radiation. Additionally, the Hassan et al. model [19], represented by Equation (7), proved to be a reliable empirical tool for accurately predicting global solar radiation.

5. Conclusions and Future Work

This study aimed to optimize the design of the artificial neural network (ANN), one of the widely used machine-learning algorithms, for accurate global solar radiation (GSR) forecasting while minimizing computational requirements. The focus was on optimizing the neurons in the hidden layer, an aspect that has received limited attention in the literature, to develop the most effective ANN architecture for precise GSR estimation. Additionally, the study proposed accurate solar radiation models specifically tailored for the study site, which currently lacks ML-based models, and where several solar energy projects are planned. Furthermore, the study investigated the impact of varying the number of neurons in the hidden layer on the performance of the ANN-based solar radiation model. It also assessed the performance of the Hassan et al. model [19], a leading temperature-based empirical model, which has not been compared with ML-based models such as ANN before. Finally, the study conducted a comparative analysis between the ANN method and the empirical method for estimating global solar radiation on a horizontal plane. To achieve these objectives, the measured data of global solar radiation over a period of 35 years at the study location, New Borg El-Arb, were utilized for model development and validation.

The results demonstrate that the developed models in this study, specifically the best ANN model (Model_NurnNo._3) and the empirical model (Hassan et al. model), provide an excellent estimation of global solar radiation, with a coefficient of determination ($R^2$) exceeding 0.98%. Moreover, their other statistical indicators fell within acceptable ranges. Notably, ANN architectures with a smaller number of neurons in the single hidden layer, ranging from 1 to 4 neurons, exhibited the best performance compared to other ANN models, with $R^2$ values exceeding 0.98%. The performance of the developed ANN models remained stable and excellent when the number of neurons in the hidden layer was less than ten, with $R^2$ values exceeding 0.97%. However, performance instability was observed when the number of neurons in the hidden layer exceeded nine.

Furthermore, the comparison between the best ANN-based model (Model_NurnNo._3) and one of the best empirical-based models, the Hassan et al. model [20], revealed that both models demonstrated an excellent performance, with $R^2$ values exceeding 0.98%. While the performance of both models was quite similar, the Hassan et al. model outperformed the best ANN model, exhibiting the highest $R^2$ value. The performance indicators of the Hassan et al. model included t-test, MPE, MBE, RMSE, MAPE, MABE, r, and $R^2$, with values of 2.4991, −3.1889%, −0.4620 (MJ/m² day⁻¹), 0.7676 (MJ/m² day⁻¹), 3.6733%, 0.6021 (MJ/m² day⁻¹), 0.9981, and 0.9864%, respectively. Additionally, while the relative error for the best ANN model slightly exceeded the acceptable range of ±10% in November and December, the relative error for the empirical model (the Hassan et al. Model) remained within the range, even during winter months.

Additionally, the obtained results of the optimized ANN model in this work were compared with the recent related work, both at the level of solar radiation prediction (long-term forecast) and at the level of machine-learning (ML) and deep-learning (DL) techniques. While it had a good RMSE value of 0.8361 MJ/m² day⁻¹, which falls within the ranges of both DL and ML techniques, its correlation coefficient ($r$) was the best one, which equaled 0.999. This demonstrates its ability in improving the accuracy of solar radiation forecasts while preserving computing resources, since the efficiency difference between DL and ML techniques was insignificant, especially when predicting monthly average daily GSR. Additionally, the influence of the learning rate on its accuracy was examined, where the best one was 0.01. Consequently, the presented models in this study, the best ANN model and the empirical model, demonstrated high accuracy in forecasting global solar radiation, making them suitable for various research projects at the study site. Moreover, the temperature-based solar radiation models developed in this study can be effectively combined with different long or short-term weather forecasting methods, enhancing their applicability.

In future studies, it is recommended to explore additional ANN architectures and training algorithms to evaluate their impact on prediction accuracy. Additionally, the performance of other models (AI-based and empirical-based models) can be investigated and compared with the proposed ones in this study, using different locations, particularly coastal areas.