Proposing a Hybrid BTMS Using a Novel Structure of a Microchannel Cold Plate and PCM
Abstract
:1. Introduction
- The performance of BTMS was analyzed under active and passive cooling techniques using liquid, PCM, and BMCP.
- To evaluate the effect of PCM on the heat dissipation performance of BTMS, the minimum value of PCM weight and ideal thermal performance are suggested.
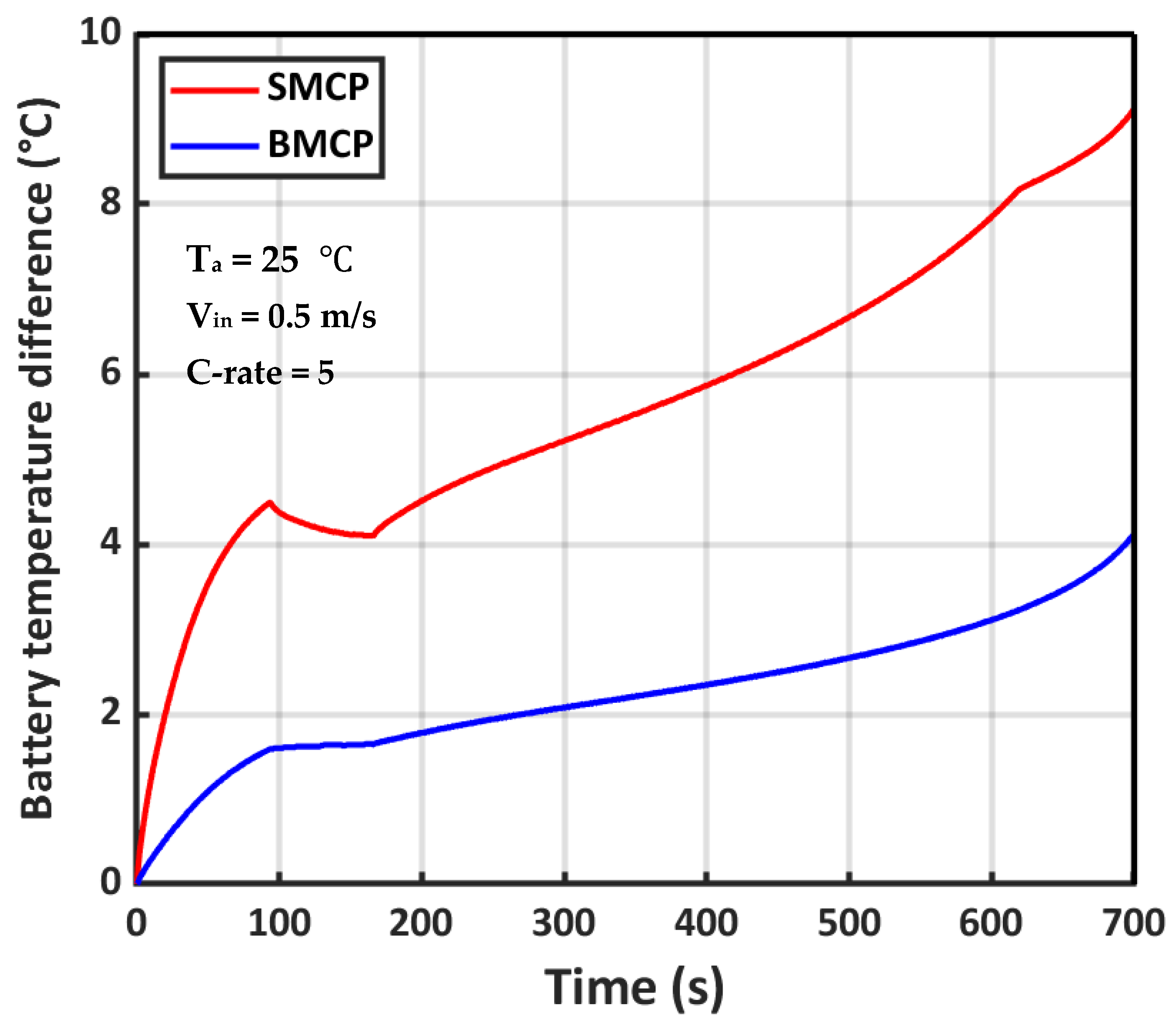
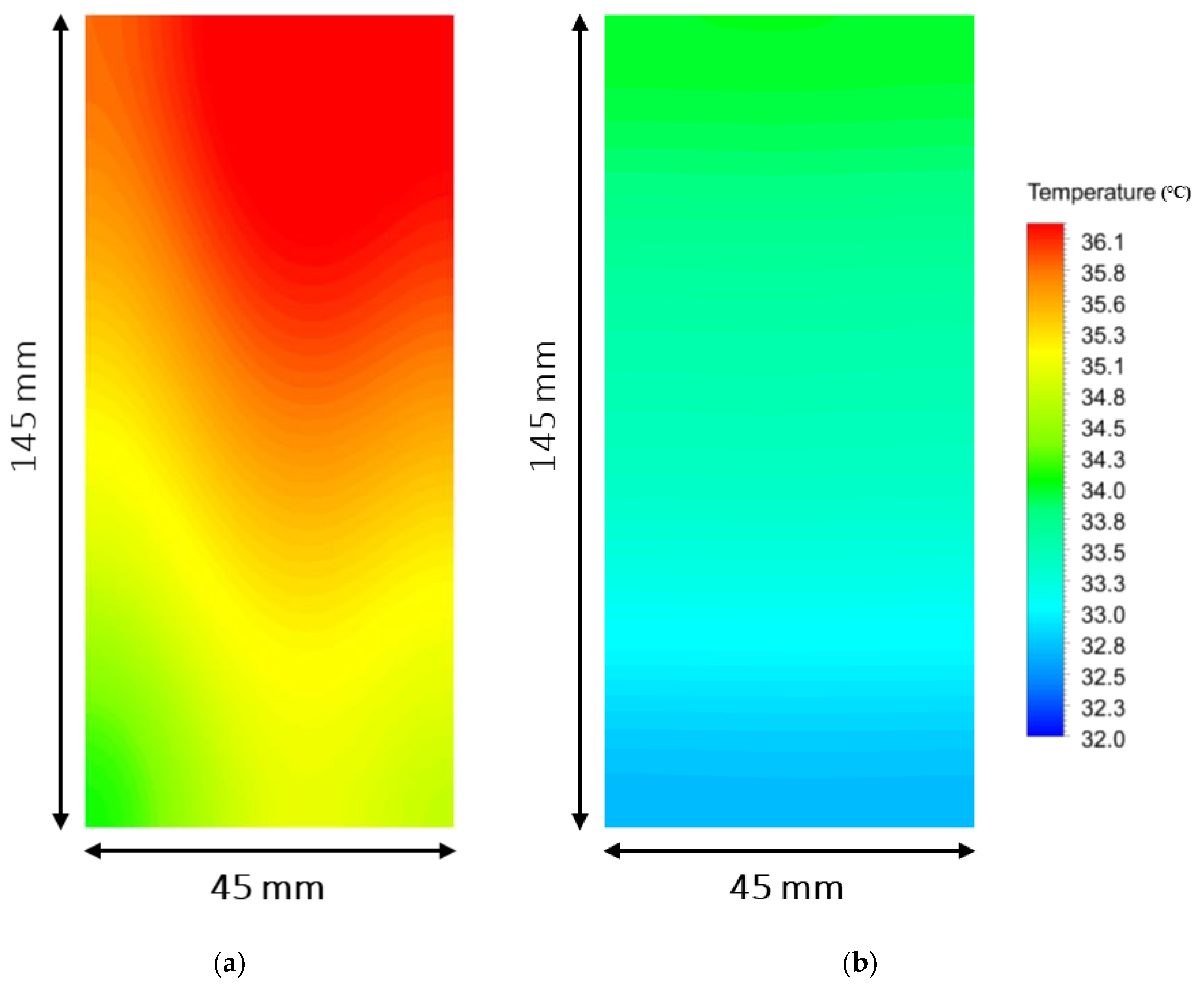
- To prevent thermal runaway, the effect of BMCP with SMCP has been studied as a factor that contributes to maintaining uniform temperature distribution in the cells.
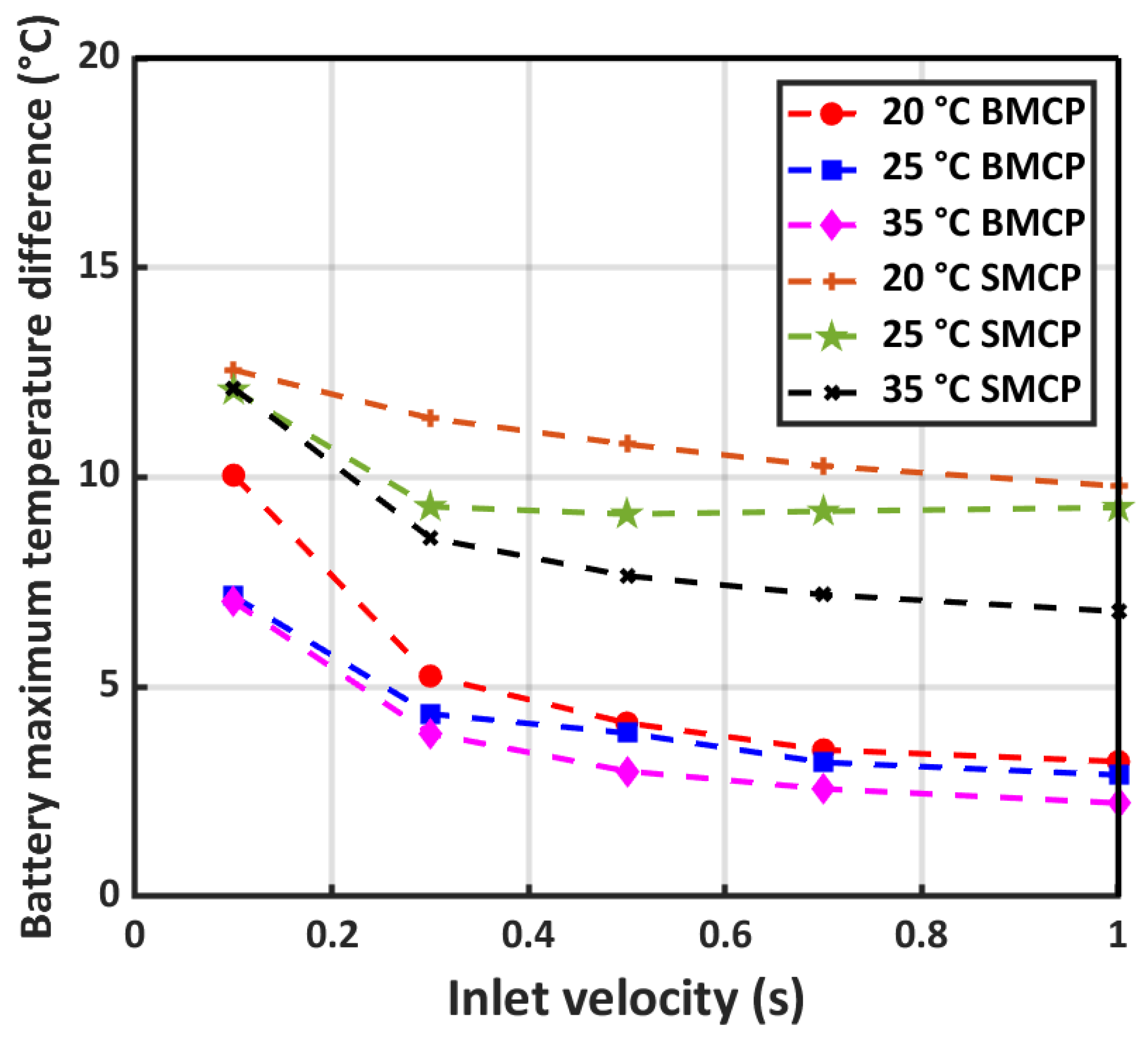
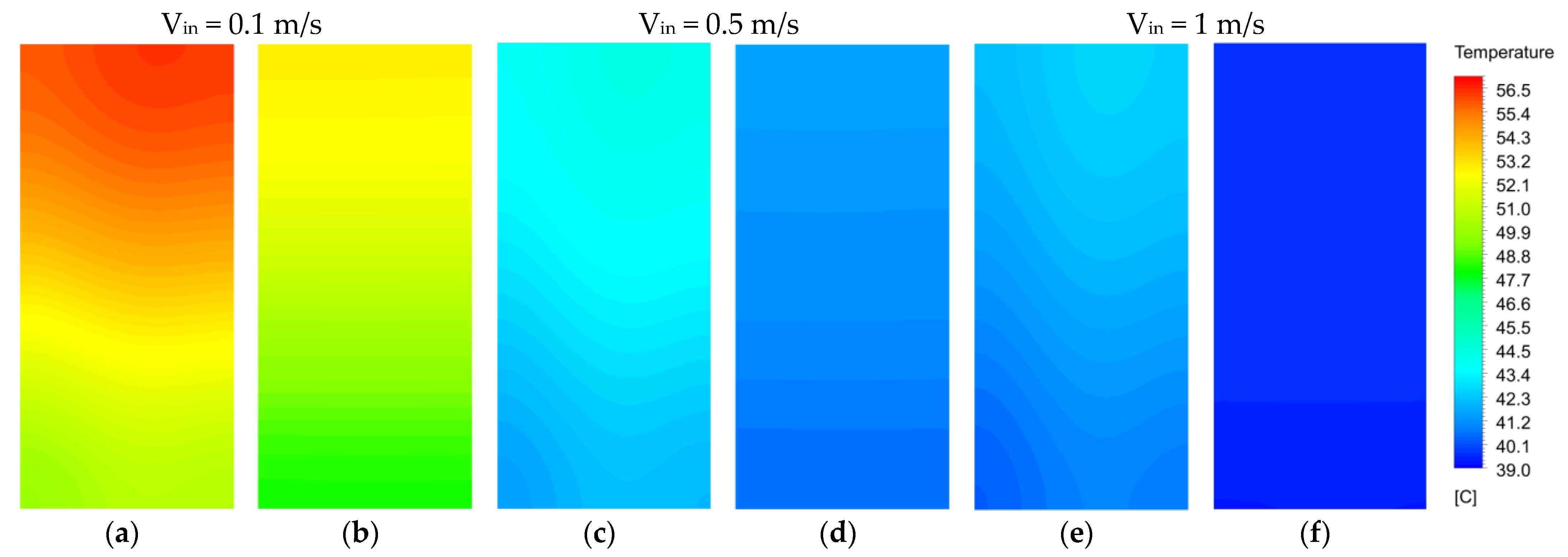
- To achieve the best design, the cooling capability has been analyzed under various environmental conditions to maintain the battery temperature within the optimal range.
2. Materials and Methods
2.1. Model Description
2.2. Governing Equations
2.2.1. Battery Cell
2.2.2. Coolant
2.2.3. Cold plate
2.2.4. PCM
2.3. Initial and Boundary Condition
3. Numerical Method and Mesh Independency
4. Validation of Numerical Model
5. Results and Discussion
5.1. Performance Characteristics of Enhanced BTMS
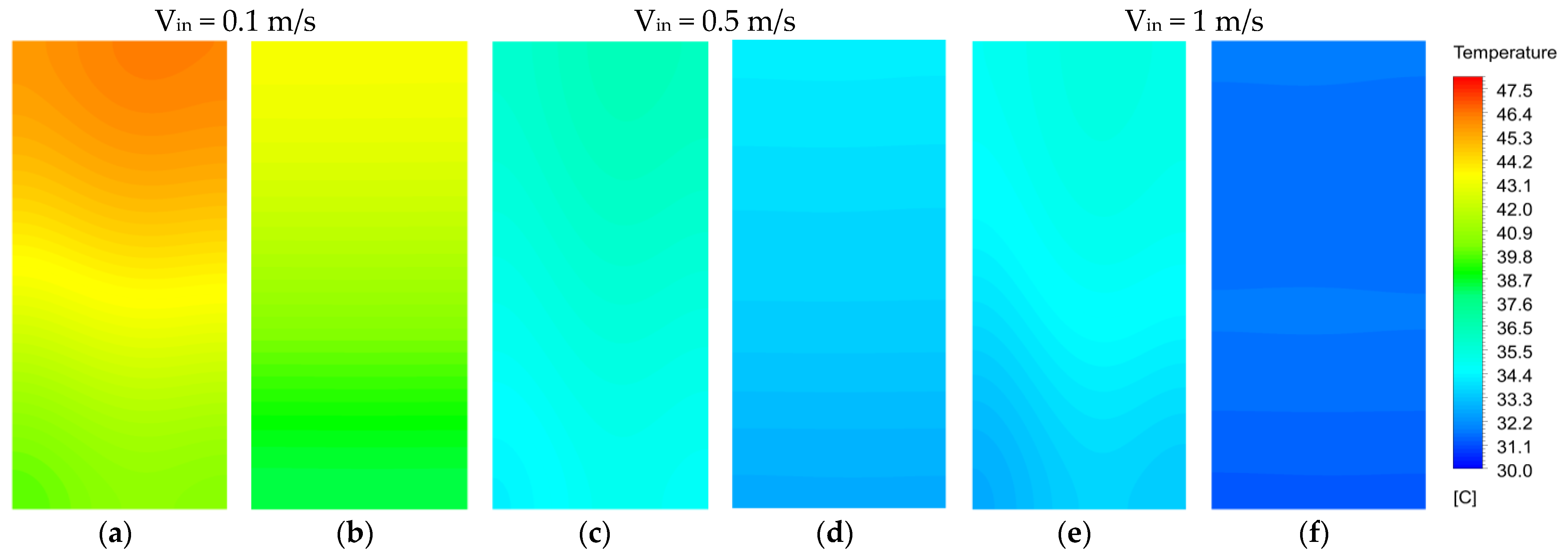
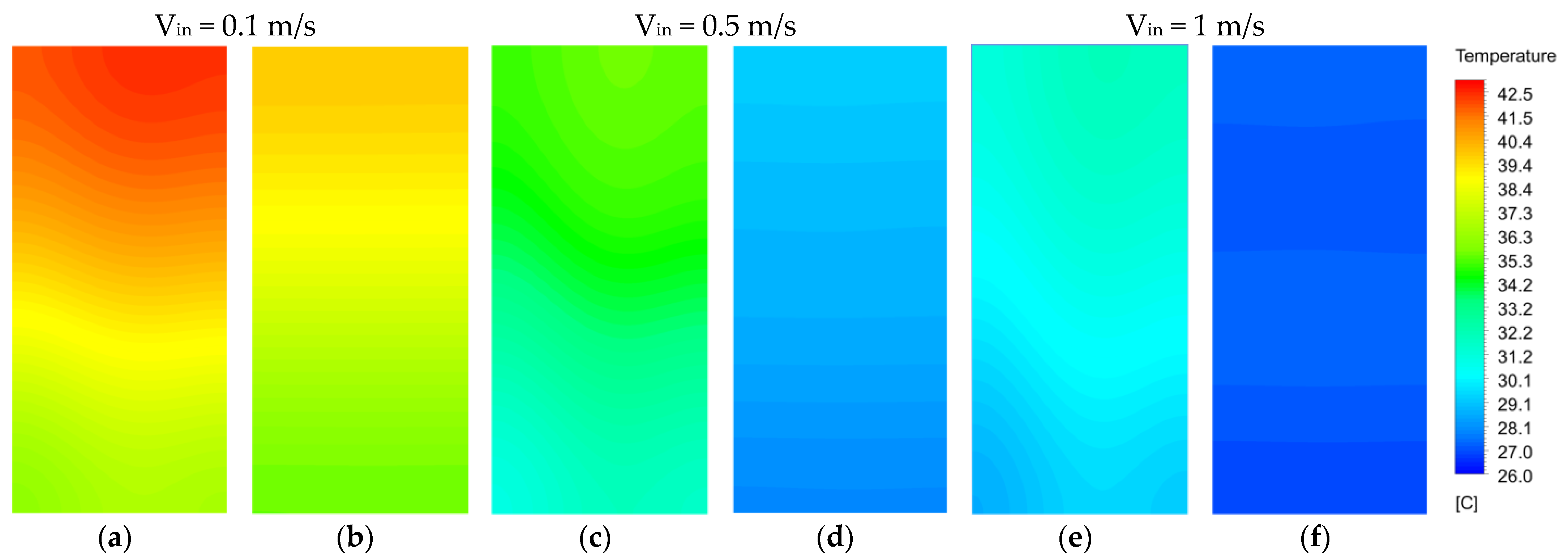
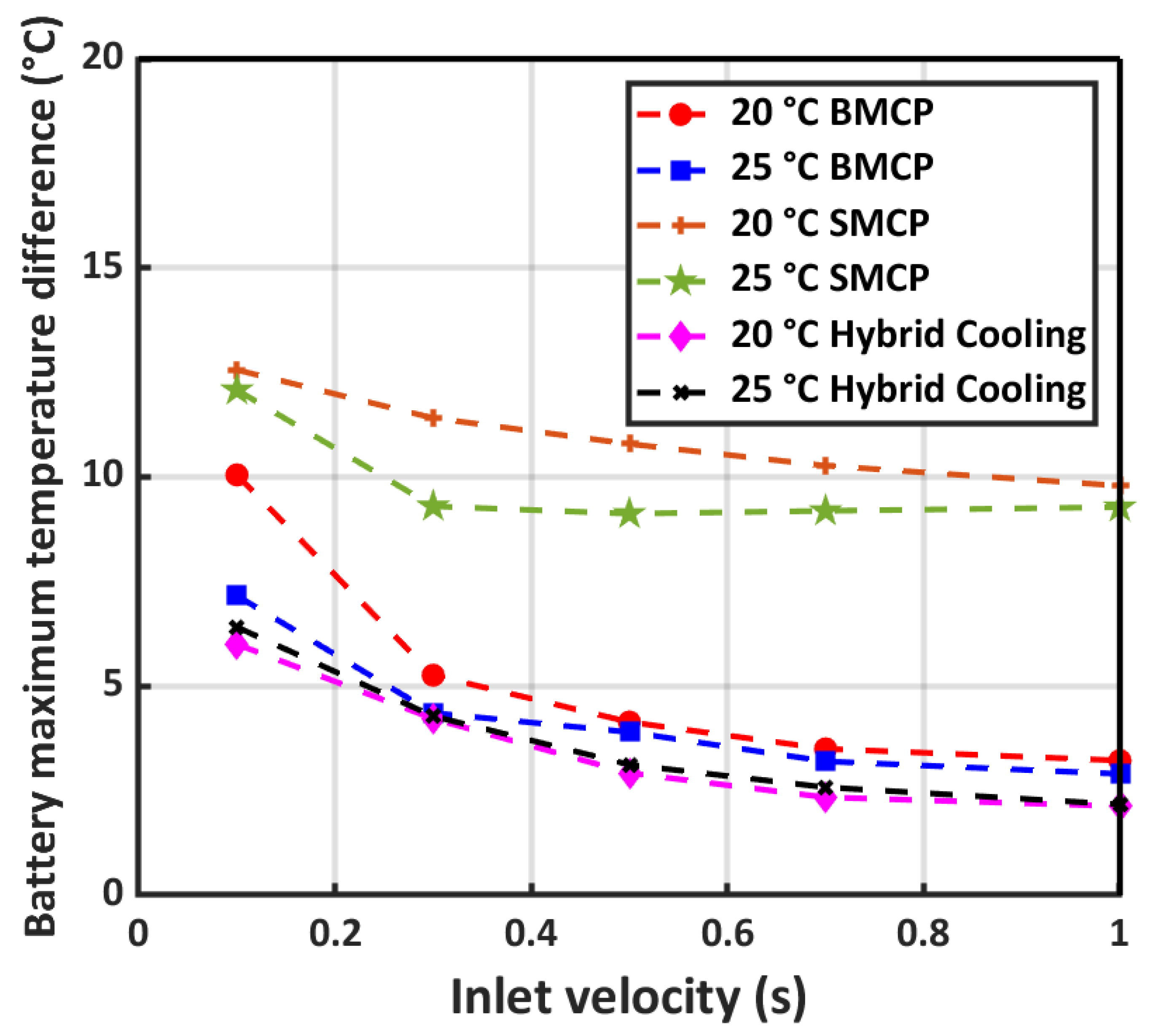
5.2. Effect of Operating Conditions
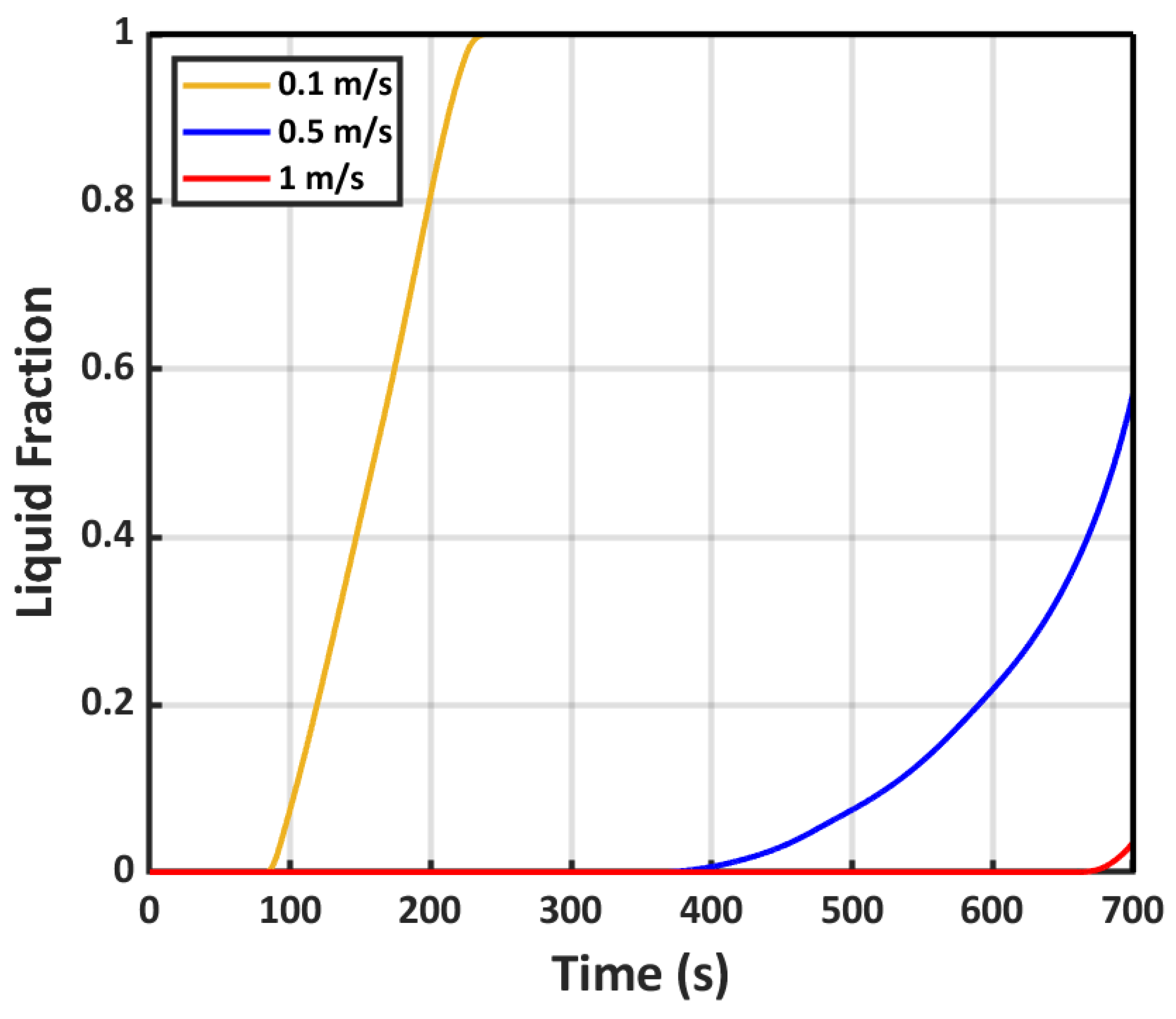
5.3. PCM’s Role in Thermal Performance Enhancement
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhao, Y.; Zou, B.; Zhang, T.; Jiang, Z.; Ding, J.; Ding, Y. A Comprehensive Review of Composite Phase Change Material Based Thermal Management System for Lithium-Ion Batteries. Renew. Sustain. Energy Rev. 2022, 167, 112667. [Google Scholar] [CrossRef]
- Li, W.; Zhou, Y.; Zhang, H.; Tang, X. A Review on Battery Thermal Management for New Energy Vehicles. Energies 2023, 16, 4845. [Google Scholar] [CrossRef]
- Belgibayeva, A.; Rakhmetova, A.; Rakhatkyzy, M.; Kairova, M.; Mukushev, I.; Issatayev, N.; Kalimuldina, G.; Nurpeissova, A.; Sun, Y.K.; Bakenov, Z. Lithium-Ion Batteries for Low-Temperature Applications: Limiting Factors and Solutions. J. Power Sources 2023, 557, 232550. [Google Scholar] [CrossRef]
- Su, X.; Xu, Y.; Wu, Y.; Li, H.; Yang, J.; Liao, Y.; Qu, R.; Zhang, Z. Liquid Electrolytes for Low-Temperature Lithium Batteries: Main Limitations, Current Advances, and Future Perspectives. Energy Storage Mater. 2023, 56, 642–663. [Google Scholar] [CrossRef]
- Liu, C.; Wen, X.; Zhong, J.; Liu, W.; Chen, J.; Zhang, J.; Wang, Z.; Liao, Q. Characterization of Aging Mechanisms and State of Health for Second-Life 21700 Ternary Lithium-Ion Battery. J. Energy Storage 2022, 55, 105511. [Google Scholar] [CrossRef]
- Mehrenjani, J.R.; Gharehghani, A.; Nasrabadi, A.M.; Moghimi, M. Design, Modeling and Optimization of a Renewable-Based System for Power Generation and Hydrogen Production. Int. J. Hydrogen Energy 2022, 47, 14225–14242. [Google Scholar] [CrossRef]
- Kim, J.; Oh, J.; Lee, H. Review on Battery Thermal Management System for Electric Vehicles. Appl. Therm. Eng. 2019, 149, 192–212. [Google Scholar] [CrossRef]
- Wang, Y.; Yu, Y.; Jing, Z.; Wang, C.; Zhou, G.; Zhao, W. Thermal Performance of Lithium-Ion Batteries Applying Forced Air Cooling with an Improved Aluminium Foam Heat Sink Design. Int. J. Heat Mass. Transf. 2021, 167, 120827. [Google Scholar] [CrossRef]
- Andwari, A.M.; Aziz, A.A.; Muhamad Said, M.F.; Latiff, Z.A.; Ghanaati, A. Influence of Hot Burned Gas Utilization on The Exhaust Emission Characteristics of A Controlled Auto-Ignition Two-Stroke Cycle Engine. Int. J. Automot. Mechanical. Eng. 2015, 11, 2396–2404. [Google Scholar] [CrossRef]
- Moradi, J.; Gharehghani, A.; Mirsalim, M. Numerical Comparison of Combustion Characteristics and Cost between Hydrogen, Oxygen and Their Combinations Addition on Natural Gas Fueled HCCI Engine. Energy Convers. Manag. 2020, 222, 113254. [Google Scholar] [CrossRef]
- Gharehghani, A.; Kakoee, A.; Andwari, A.M.; Megaritis, T.; Pesyridis, A. Numerical investigation of an RCCI engine fueled with natural gas/dimethyl-ether in various injection strategies. Energies 2021, 14, 1638. [Google Scholar] [CrossRef]
- Moradi, J.; Gharehghani, A.; Mirsalim, M. Numerical Investigation on the Effect of Oxygen in Combustion Characteristics and to Extend Low Load Operating Range of a Natural-Gas HCCI Engine. Appl. Energy 2020, 276, 115516. [Google Scholar] [CrossRef]
- Mahmoudzadeh Andwari, A.; Aziz, A.A.; Muhamad Said, M.F.; Abdul Latiff, Z. Controlled Auto-Ignition Combustion in a Two-Stroke Cycle Engine Using Hot Burned Gases. Appl. Mech. Mater. 2013, 388, 201–205. [Google Scholar] [CrossRef]
- Ahmadi, S.; Gharehghani, A.; Soltani, M.M.; Fakhari, A.H. Design and Evaluation of Renewable Energies-Based Multi-Generation System for Hydrogen Production, Freshwater and Cooling. Renew. Energy 2022, 198, 916–935. [Google Scholar] [CrossRef]
- Chen, K.; Chen, Y.; Li, Z.; Yuan, F.; Wang, S. Design of the Cell Spacings of Battery Pack in Parallel Air-Cooled Battery Thermal Management System. Int. J. Heat Mass Transf. 2018, 127, 393–401. [Google Scholar] [CrossRef]
- Wang, M.; Hung, T.C.; Xi, H. Numerical Study on Performance Enhancement of the Air-Cooled Battery Thermal Management System by Adding Parallel Plates. Energies 2021, 14, 3096. [Google Scholar] [CrossRef]
- Widyantara, R.D.; Naufal, M.A.; Sambegoro, P.L.; Nurprasetio, I.P.; Triawan, F.; Djamari, D.W.; Bayu, A.; Nandiyanto, D.; Budiman, B.A.; Aziz, M. Low-cost air-cooling system optimization on battery pack of Electric Vehicle. Energies 2021, 14, 7954. [Google Scholar] [CrossRef]
- Le, Q.; Shi, Q.; Liu, Q.; Yao, X.; Ju, X.; Xu, C. Numerical Investigation on Manifold Immersion Cooling Scheme for Lithium Ion Battery Thermal Management Application. Int. J. Heat Mass Transf. 2022, 190, 122750. [Google Scholar] [CrossRef]
- Zhao, D.; Lei, Z.; An, C. Research on Battery Thermal Management System Based on Liquid Cooling Plate with Honeycomb-like Flow Channel. Appl. Therm. Eng. 2022, 218, 119324. [Google Scholar] [CrossRef]
- Wang, H.; Tao, T.; Xu, J.; Mei, X.; Liu, X.; Gou, P. Cooling Capacity of a Novel Modular Liquid-Cooled Battery Thermal Management System for Cylindrical Lithium Ion Batteries. Appl. Therm. Eng. 2020, 178, 115591. [Google Scholar] [CrossRef]
- Li, P.; Zhao, J.; Zhou, S.; Duan, J.; Li, X.; Zhang, H.; Yuan, J. Design and Optimization of a Liquid Cooling Thermal Management System with Flow Distributors and Spiral Channel Cooling Plates for Lithium-Ion Batteries. Energies 2023, 16, 2196. [Google Scholar] [CrossRef]
- Magnini, M.; Thome, J.R. A CFD Study of the Parameters Influencing Heat Transfer in Microchannel Slug Flow Boiling. Int. J. Therm. Sci. 2016, 110, 119–136. [Google Scholar] [CrossRef]
- Li, H.; Hrnjak, P. Flow Visualization of R1234ze(E) in a 0.643 mm Microchannel Tube. Int. J. Heat Mass Transf. 2019, 136, 950–961. [Google Scholar] [CrossRef]
- Wang, X.; Li, B.; Huang, K.; Yan, Y.; Stone, I.; Worrall, S. Experimental Investigation on End Winding Thermal Management with Oil Spray in Electric Vehicles. Case Stud. Therm. Eng. 2022, 35, 102082. [Google Scholar] [CrossRef]
- Jayarajan, S.A.; Azimov, U. CFD Modeling and Thermal Analysis of a Cold Plate Design with a Zig-Zag Serpentine Flow Pattern for Li-Ion Batteries by Dissipation. Energies 2023, 16, 5243. [Google Scholar] [CrossRef]
- Wei, L.; Zou, Y.; Cao, F.; Ma, Z.; Lu, Z.; Jin, L. An Optimization Study on the Operating Parameters of Liquid Cold Plate for Battery Thermal Management of Electric Vehicles. Energies 2022, 15, 9180. [Google Scholar] [CrossRef]
- Dong, J.; Lu, X.; Sun, Y.; Mitin, V.; Xu, H.; Kong, W. Design of Battery Thermal Management System with Considering the Longitudinal and Transverse Temperature Difference. Energies 2022, 15, 7448. [Google Scholar] [CrossRef]
- Lee, P.S.; Garimella, S.V. Saturated Flow Boiling Heat Transfer and Pressure Drop in Silicon Microchannel Arrays. Int. J. Heat Mass Transf. 2008, 51, 789–806. [Google Scholar] [CrossRef]
- Li, H.; Hrnjak, P. Heat Transfer and Pressure Drop of R32 Evaporating in One Pass Microchannel Tube with Parallel Channels. Int. J. Heat Mass Transf. 2018, 127, 526–540. [Google Scholar] [CrossRef]
- Lin, R.; Xie, J.; Liang, R.; Li, X.; Zhang, G.; Li, B. Experiments and Simulation on the Performance of a Liquid-Cooling Thermal Management System Including Composite Silica Gel and Mini-Channel Cold Plates for a Battery Module. Energies 2022, 15, 9103. [Google Scholar] [CrossRef]
- Worwood, D.; Marco, J.; Kellner, Q.; Hosseinzadeh, E.; McGlen, R.; Mullen, D.; Lynn, K.; Greenwood, D. Experimental Analysis of a Novel Cooling Material for Large Format Automotive Lithium-Ion Cells. Energies 2019, 12, 1251. [Google Scholar] [CrossRef]
- Zhao, C.; Zhang, B.; Zheng, Y.; Huang, S.; Yan, T. Hybrid battery thermal management system in Electrical Vehicles: A Review. Energies 2020, 13, 6257. [Google Scholar] [CrossRef]
- Huang, Y.H.; Cheng, W.L.; Zhao, R. Thermal Management of Li-Ion Battery Pack with the Application of Flexible Form-Stable Composite Phase Change Materials. Energy Convers. Manag. 2019, 182, 9–20. [Google Scholar] [CrossRef]
- Choudhari, V.G.; Dhoble, A.S.; Panchal, S.; Fowler, M.; Fraser, R. Numerical Investigation on Thermal Behaviour of 5 × 5 Cell Configured Battery Pack Using Phase Change Material and Fin Structure Layout. J. Energy Storage 2021, 43, 103234. [Google Scholar] [CrossRef]
- Rabiei, M.; Gharehghani, A.; Andwari, A.M. Enhancement of Battery Thermal Management System Using a Novel Structure of Hybrid Liquid Cold Plate. Appl. Therm. Eng. 2023, 232, 121051. [Google Scholar] [CrossRef]
- Ki, S.; Lee, J.; Kim, S.; Seong, J.; Shim, J.; Oh, S.; Cho, S.; Bang, S.; Seo, D.; Kim, J.; et al. An Energy-Efficient Battery Thermal Management System Incorporating a Porous Metal-Based Multiscale Flow Manifold. Energy Convers. Manag. 2022, 269, 116147. [Google Scholar] [CrossRef]
- Weng, J.; He, Y.; Ouyang, D.; Yang, X.; Zhang, G.; Wang, J. Thermal Performance of PCM and Branch-Structured Fins for Cylindrical Power Battery in a High-Temperature Environment. Energy Convers. Manag. 2019, 200, 112106. [Google Scholar] [CrossRef]
- Liu, Y.; Zheng, R.; Li, J. High latent heat phase change materials (PCMs) with low melting temperature for thermal management and storage of electronic devices and power batteries: Critical review. Renew. Sustain. Energy Rev. 2022, 168, 112783. [Google Scholar] [CrossRef]
- Kalkan, O.; Celen, A.; Bakirci, K. Multi-Objective Optimization of a Mini Channeled Cold Plate for Using Thermal Management of a Li-Ion Battery. Energy 2022, 251, 123949. [Google Scholar] [CrossRef]
- Mehrabi-Kermani, M.; Houshfar, E.; Ashjaee, M. A Novel Hybrid Thermal Management for Li-Ion Batteries Using Phase Change Materials Embedded in Copper Foams Combined with Forced-Air Convection. Int. J. Therm. Sci. 2019, 141, 47–61. [Google Scholar] [CrossRef]
- Zhang, W.; Liang, Z.; Ling, G.; Huang, L. Influence of Phase Change Material Dosage on the Heat Dissipation Performance of the Battery Thermal Management System. J. Energy Storage 2021, 41, 102849. [Google Scholar] [CrossRef]
- Lamrani, B.; Lebrouhi, B.E.; Khattari, Y.; Kousksou, T. A Simplified Thermal Model for a Lithium-Ion Battery Pack with Phase Change Material Thermal Management System. J. Energy Storage 2021, 44, 103377. [Google Scholar] [CrossRef]
- Ding, Y.; Wei, M.; Liu, R. Channel Parameters for the Temperature Distribution of a Battery Thermal Management System with Liquid Cooling. Appl. Therm. Eng. 2021, 186, 116494. [Google Scholar] [CrossRef]
- Chen, S.; Bao, N.; Garg, A.; Peng, X.; Gao, L. A Fast Charging–Cooling Coupled Scheduling Method for a Liquid Cooling-Based Thermal Management System for Lithium-Ion Batteries. Engineering 2021, 7, 1165–1176. [Google Scholar] [CrossRef]
- Qi, W.; Huang, W.; Niu, J.; Chen, F.; Chen, B.; Chen, Y. Thermal Management of Power Battery Based on Flexible Swiss Roll Type Liquid Cooling Micro-Channel. Appl. Therm. Eng. 2023, 219, 119491. [Google Scholar] [CrossRef]
- Li, M.; Ma, S.; Jin, H.; Wang, R.; Jiang, Y. Performance Analysis of Liquid Cooling Battery Thermal Management System in Different Cooling Cases. J. Energy Storage 2023, 72, 108651. [Google Scholar] [CrossRef]
- Bernardi, D.; Pawlikowski, E.; Newman, J. General Energy Balance for Battery Systems. Electrochem. Soc. Ext. Abstr. 1984, 132, 164–165. [Google Scholar] [CrossRef]
- Fathabadi, H. A Novel Design Including Cooling Media for Lithium-Ion Batteries Pack Used in Hybrid and Electric Vehicles. J. Power Sources 2014, 245, 495–500. [Google Scholar] [CrossRef]
- Gharehghani, A.; Gholami, J.; Shamsizadeh, P.; Mehranfar, S. Effect Analysis on Performance Improvement of Battery Thermal Management in Cold Weather. J. Energy Storage 2022, 45, 103728. [Google Scholar] [CrossRef]
- Lin, C.; Chen, K.; Sun, F.; Tang, P.; Zhao, H. Research on Thermo-Physical Properties Identification and Thermal Analysis of EV Li-Ion Battery. In Proceedings of the 5th IEEE Vehicle Power and Propulsion Conference VPPC, Dearborn, MI, USA, 7–10 September 2009; pp. 1643–1648. [Google Scholar] [CrossRef]
- Fan, L.; Khodadadi, J.M.; Pesaran, A.A. A Parametric Study on Thermal Management of an Air-Cooled Lithium-Ion Battery Module for Plug-in Hybrid Electric Vehicles. J. Power Sources 2013, 238, 301–312. [Google Scholar] [CrossRef]
- Shmueli, H.; Ziskind, G.; Letan, R. Melting in a Vertical Cylindrical Tube: Numerical Investigation and Comparison with Experiments. Int. J. Heat Mass Transf. 2010, 53, 4082–4091. [Google Scholar] [CrossRef]








| Research | Ref. | Year | Elements of Cooling System | Battery Type | C-Rate | ||
|---|---|---|---|---|---|---|---|
| Kermani et al. | [40] | 2019 | PCM + Copper foam | Pouchy | 5C | 308.9 | 4.6 |
| Zhang et al. | [41] | 2021 | PCM | Prismatic | 5C | 314.5 | 2.5 |
| Lamrani et al. | [42] | 2021 | PCM | Cylindrical | 3C | 305.1 | - |
| Ding et al. | [43] | 2021 | Liquid | Prismatic | 1C | 304.2 | 4.6 |
| Chen et al. | [44] | 2021 | Liquid + Cold plate | Prismatic | 2C | 306.5 | 0.8 |
| Qi et al. | [45] | 2023 | Liquid + Mico channel | Cylindrical | 3C | 300.4 | 3.3 |
| Li et al. | [46] | 2023 | Liquid + Cold plate + SMCP | Prismatic | 5C | 313 | 5 |
| Kalkan et al. | [39] | 2022 | Liquid + Cold plate + BMCP | Prismatic | 5C | 303.6 | 2.3 |
| Current study | - | - | PCM + Liquid + Cold plate + BMCP | Prismatic | 5C | 308.1 | 2 |
| Battery Parameter | Value |
|---|---|
| Size () | 145 × 45 × 9 |
| Density () | 2263 |
| Capacity (mAh) | 7000 |
| Work temperature (°C) | 10–45 |
| Nominal voltage (V) | 3.8 |
| Thermal conductivity (W/m.K) | 43.33/43.331.5 (x/y/z) |
| Positive electrode material | Al |
| Negative electrode material | Cu |
| Specific heat capacity (J/kg.K) | 1532.5 |
| Cold Plate Parameter | Value |
|---|---|
| Size () | |
| Density () | 2719 |
| Thermal conductivity (W/m.K) | 202 |
| Specific heat capacity (J/kg.K) | 871 |
| Specific Heat Capacity (J/kg.K) | Dynamic Viscosity (kg/m s) | Latent Heat (kJ/kg) | Thermal Conductivity (W/m.K) | Size ) | ||
|---|---|---|---|---|---|---|
| Solid | 2500 | - | 870 | 179 | 0.24 | |
| Liquid | 2500 | −1.137439 E − 8 T3 + 1.178188 E − 5 T2 − 0.0041113888T + 0.4857203 | 870 @ 299 K781.5 @ 301 K750 @ 343 K | 179 | 0.15 |
| This Study | Fan et al. [51] | Difference % | |
|---|---|---|---|
| 10.2 | 0.841 | 0.863 | 2.55 |
| 20.4 | 0.832 | 0.823 | 1.08 |
| 30.6 | 0.749 | 0.756 | 1.32 |
| 40.8 | 0.685 | 0.665 | 2.92 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rabiei, M.; Gharehghani, A.; Saeedipour, S.; Andwari, A.M.; Könnö, J. Proposing a Hybrid BTMS Using a Novel Structure of a Microchannel Cold Plate and PCM. Energies 2023, 16, 6238. https://doi.org/10.3390/en16176238
Rabiei M, Gharehghani A, Saeedipour S, Andwari AM, Könnö J. Proposing a Hybrid BTMS Using a Novel Structure of a Microchannel Cold Plate and PCM. Energies. 2023; 16(17):6238. https://doi.org/10.3390/en16176238
Chicago/Turabian StyleRabiei, Moeed, Ayat Gharehghani, Soheil Saeedipour, Amin Mahmoudzadeh Andwari, and Juho Könnö. 2023. "Proposing a Hybrid BTMS Using a Novel Structure of a Microchannel Cold Plate and PCM" Energies 16, no. 17: 6238. https://doi.org/10.3390/en16176238
APA StyleRabiei, M., Gharehghani, A., Saeedipour, S., Andwari, A. M., & Könnö, J. (2023). Proposing a Hybrid BTMS Using a Novel Structure of a Microchannel Cold Plate and PCM. Energies, 16(17), 6238. https://doi.org/10.3390/en16176238







